Cristallographie géométrique/Réseaux de Bravais
La classification des réseaux en réseaux de Bravais est une classification basée sur la topologie des réseaux. Les réseaux de Bravais représentent les types de mailles conventionnelles possibles pour décrire les réseaux. Il n'existe qu'un nombre fini de réseaux de Bravais pour un espace de dimension donnée. Un réseau de Bravais regroupe donc un ensemble infini de réseaux qui ont les mêmes propriétés topologiques et de symétrie, indépendamment des vecteurs de base utilisés pour les décrire.
|
Définition |
|
Deux réseaux appartiennent au même réseau de Bravais si ils appartiennent à la même famille cristalline et si ils possèdent le même mode de réseau. |
Le mode d'un réseau désigne la multiplicité de sa maille conventionnelle. Un mode de réseau primitif signifie que la maille conventionnelle du réseau est primitive.
Espace bidimensionnel[modifier | modifier le wikicode]
Il existe cinq réseaux de Bravais dans l'espace à deux dimensions. Les modes de réseau possibles sont les modes primitif (p) et centré (c). Les réseaux de Bravais bidimensionnels sont notés par deux lettres minuscules italiques. La première désigne la famille cristalline : m, o, t et h. La deuxième désigne le mode de réseau : p et c.
Le mode de réseau centré, c, ne se rencontre que dans le système orthorhombique. Il signifie qu'il existe deux nœuds du réseau dans la maille. Ces deux nœuds sont équivalents par translation d'un vecteur τc tel que :
Cette translation n'est pas valable seulement pour les nœuds du réseau mais aussi pour le volume de la maille, puisque la maille conventionnelle du réseau de Bravais oc a un volume deux fois plus grand que la maille primitive. Tout point A de coordonnées (xA,yA) possède un point équivalent A' dans la maille par translation du vecteur τc, de coordonnées
Si cette translation amène A' dans une maille voisine, il suffit d'effectuer sur A' une translation d'un vecteur bien choisi, combinaison linéaire de a et b, pour trouver le point équivalent de A dans la maille.
La maille primitive d'un réseau orthorhombique de mode centré est une maille monoclinique : l'utilisation de la maille primitive ne permet pas dans ce cas de rendre compte de la symétrie du réseau. C'est pourquoi il vaut mieux utiliser la maille conventionnelle centrée.
Dans la famille monoclinique, le seul mode de réseau possible est le mode primitif. En effet, si dans un réseau une maille monoclinique centrée est trouvée, il est toujours possible de se ramener à une maille monoclinique primitive pour décrire le réseau, sans perdre d'information sur la symétrie du réseau. La maille conventionnelle dans la famille monoclinique est toujours primitive. Ceci est également valable pour la famille tétragonale. Le passage de la maille centrée c à la maille primitive p s'effectue dans ces deux familles par le changement de base suivant :
où ap et bp sont les vecteurs de base de la maille primitive et ac et bc ceux de la maille centrée c.
Dans la famille hexagonale, l'ajout d'un nœud de réseau au centre de la maille primitive ne produit pas un réseau hexagonal centré mais un réseau orthorhombique primitif. Le réseau de Bravais hc n'existe pas car la symétrie hexagonale du réseau est alors détruite.
Espace tridimensionnel[modifier | modifier le wikicode]
Il existe quatorze réseaux de Bravais dans l'espace à trois dimensions. Les modes de réseau possibles sont les modes primitif (P), centré (I), à une face centrée (A, B ou C selon la face qui est centrée), à faces centrées (F) et rhomboédrique (R). La famille cristalline est indiquée par une lettre minuscule italique : a (anortique), m, o, t, h et c. Le mode de réseau est ici indiqué par une lettre majuscule italique, pour différencier les réseaux de Bravais tridimensionnels des réseaux bidimensionnels.
Modes de réseau tridimensionnels[modifier | modifier le wikicode]
Le mode de réseau primitif P signifie que la maille conventionnelle du réseau est primitive.
Le mode de réseau centré I signifie que la maille conventionnelle contient deux nœuds du réseau, à l'origine et au centre de la maille, équivalents par la translation de vecteur τI tel que
Les modes de réseau à face centrée A, B et C signifient que la maille conventionnelle contient deux nœuds, à l'origine et au centre d'une face de la maille, équivalents respectivement par translation de vecteur τA, τB ou τC tels que
Les symboles A, B et C indiquent la face de la maille qui est centrée :
- la face A est définie par les vecteurs b et c ;
- la face B est définie par les vecteurs a et c ;
- la face C est définie par les vecteurs a et b.
Le mode de réseau F contient simultanément les modes de réseau A, B et C : toutes les faces de la maille conventionnelle sont centrées. Un réseau de Bravais F contient quatre nœuds, à l'origine et au centre de chaque face de la maille, équivalents entre eux par translations des vecteurs du réseau τA, τB et τC.
Le mode de réseau R n'existe que dans la famille hexagonale. Il signifie que le système cristallin est trigonal et que la maille contient trois nœuds, équivalents par translations du vecteur τR:
Les translations dues au mode de réseau ne sont pas seulement valables pour les nœuds de la maille mais aussi pour l'ensemble du volume de la maille. En particulier, le motif du cristal est soumis à ces mêmes translations de réseau. Tout point A d'une maille non primitive possède un point équivalent A' dans la maille par translations du mode de réseau. Si ces translations amènent A' dans une maille voisine, il suffit d'effectuer sur A' une translation d'un vecteur bien choisi, combinaison linéaire de a, b et c, pour trouver le point équivalent de A dans la maille. Dans l'exemple de 2τR ci-dessus, il est possible d'ajouter ou de soustraire des vecteurs de base au vecteur de mode de réseau.
Réseaux de Bravais tridimensionnels[modifier | modifier le wikicode]
Les quatorze réseaux de Bravais[modifier | modifier le wikicode]
Le tableau ci-dessous regroupe les quatorze réseaux de Bravais tridimensionnels en fonction des six familles cristallines.
| Triclinique | Monoclinique | ||
|---|---|---|---|
| aP | mP | mC | |
 |
 |

| |
| Orthorhombique | |||
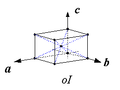
| oP | oI | oS | oF |
 |
 |
 |

|
| Tétragonal | Hexagonal | ||
| tP | tI | hP | hR |
 |
 |
 |

|
| Cubique | |||
| cP | cI | cF | |
 |
 |

| |
Familles triclinique et monoclinique[modifier | modifier le wikicode]
Dans la famille triclinique, seul le mode de réseau primitif est possible. Le réseau de Bravais triclinique est aP.
Dans la famille monoclinique existent deux réseaux de Bravais, mP et mC.
Dans le réseau mC, la face définie par les vecteurs a et b est centrée. La direction b étant par convention perpendiculaire aux directions a et c, le réseau bidimensionnel de tous les plans parallèles au plan (a, b) est oc. Par analogie avec le cas bidimensionnel, la maille conventionnelle d'un réseau mC est centrée afin de mettre en évidence l'orthogonalité des vecteurs a et b : la maille primitive d'un réseau mC est une maille triclinique. D'autre part, le réseau mC est topologiquement équivalent au réseau mA, puisqu'il suffit d'effectuer le changement de base suivant pour passer du réseau mA au réseau mC :
où aA, bA et cA désignent les vecteurs de base de la maille centrée A et aC, bC et cC ceux de la maille centrée C. On appelle par convention C la face centrée de la maille du réseau monoclinique à face centrée.
Il n'existe pas de réseau de Bravais mB : la maille conventionnelle d'un réseau monoclinique à face B centrée est une maille monoclinique primitive, un tel réseau est donc en réalité mP.
Le réseau mI est topologiquement équivalent au réseau mC : un changement des vecteurs de base permet de passer d'un mode de réseau à l'autre. Si aC, bC et cC désignent les vecteurs de base de la maille centrée C et aI, bI et cI ceux de la maille centrée I, les relations entre ces vecteurs sont données par :
ou, en utilisant une autre maille possible également centrée C :
Les deux mailles C ainsi définies et la maille I ont le même volume.

De même, le réseau mF est topologiquement équivalent au réseau mC. Le changement de base permettant de passer d'un mode de réseau à l'autre est
Famille orthorhombique[modifier | modifier le wikicode]
Dans la famille orthorhombique existent quatre réseaux de Bravais, oP, oI, oS et oF. S signifie qu'une des faces de la maille conventionnelle est centrée. Comme aucune des directions de symétrie a, b ou c n'est privilégiée par rapport aux deux autres dans la famille orthorhombique (voir le chapitre sur la symétrie ponctuelle), les réseaux oA, oB et oC sont équivalents et sont regroupés sous le symbole générique oS.
Les quatre réseaux de Bravais oP, oI, oS et oF sont topologiquement différents : il n'est pas possible de passer d'un mode de réseau à un autre par changement de base tout en gardant une maille orthorhombique. Ceci se comprend par analogie dans le cas du réseau de Bravais oS : comme dans le cas du réseau de Bravais bidimensionnel oc, la maille primitive est monoclinique et ne contient pas l'information sur l'orthogonalité des vecteurs de base. Par exemple, la maille primitive d'un réseau de mode A est donnée par :
Le vecteur aP est orthogonal aux vecteurs bP et cP, mais bP et cP ne sont pas orthogonaux entre eux : le produit scalaire bPcP est non nul. La maille primitive est donc monoclinique.
Les changements de base conduisant d'une maille orthorhombique centrée I ou F à la maille primitive correspondante sont :
Ces deux mailles primitives sont tricliniques.
Notons que ces changements de base ne sont pas uniques. Ici sont présentés les changements de base qui conduisent à la plus haute symétrie de la maille primitive lorsque la maille centrée de départ est cubique. Certains programmes, comme Recipe inclus dans X-AREA de Stoe[1], utilisent un changement de matrice différent lors de la réduction automatique de la maille.
Famille tétragonale[modifier | modifier le wikicode]
Dans la famille tétragonale existent deux réseaux de Bravais : tP et tI.
Le réseau tC est topologiquement équivalent au réseau tP. Le changement de base suivant permet de passer de la maille tétragonale primitive à la maille tétragonale centrée C :

D'autre part, le réseau tF est équivalent au réseau tI par le même changement de base qu'entre tC et tP :

Par contre, il n'existe pas de changement de base permettant de passer d'un réseau tI à un réseau tP.
Les modes de réseau A et B n'existent pas dans la famille tétragonale : si une maille tétragonale était centrée A, elle serait aussi centrée B, puisque les directions a et b sont équivalentes par symétrie.
Famille hexagonale[modifier | modifier le wikicode]

Dans la famille hexagonale existent deux réseaux de Bravais : hP et hR. Le mode de réseau P est utilisé pour les réseaux du système cristallin hexagonal. Le mode de réseau R est utilisé pour les réseaux du système cristallin trigonal. La maille hexagonale est compatible avec ces deux systèmes cristallins.
Dans le mode de réseau R, les trois nœuds de la maille hexagonale ont pour coordonnées (0,0,0), (2/3,1/3,1/3) et (1/3,2/3,2/3). Les deux nœuds obtenus par translations du vecteur τR sont alignés le long d'une diagonale principale de la maille, plus précisément le long de la rangée . La maille primitive d'un réseau appartenant au réseau de Bravais hR est un rhomboèdre. Le passage entre la maille hexagonale triple R du réseau de Bravais hR et sa maille primitive P rhomboédrique est donné par :
En particulier, la rangée [111] de la maille rhomboédrique primitive est parallèle à la rangée [001] de la maille hexagonale triple :
Cette rangée est la première direction de symétrie dans le système cristallin trigonal, parallèle à l'axe de rotation ternaire 3 ou .
Famille cubique[modifier | modifier le wikicode]
Dans la famille cubique existent trois réseaux de Bravais : cP, cI et cF.
Les modes de réseau A, B et C n'existent pas dans la famille cubique : les directions a, b et c sont équivalentes par symétrie. Si une face d'une maille cubique est centrée, le mode de réseau est alors forcément F.
Les changements de base conduisant d'une maille cubique centrée I ou F à la maille primitive correspondante sont les mêmes que dans la famille cristalline orthorhombique. La maille primitive du réseau cubique de mode de réseau F est une maille rhomboédrique avec un angle de 60° entre ses vecteurs de base, celle du réseau cubique de mode de réseau I est une maille rhomboédrique avec un angle de 120° entre ses vecteurs de base. Dans les deux cas, la rangée [111] de la maille rhomboédrique primitive est parallèle à la rangée [111] de la maille cubique centrée : il s'agit de la direction de l'axe de rotation ternaire 3 ou .
Notes et références[modifier | modifier le wikicode]
- ↑ anglais « Software - Stoe » (consulté le 4 mars 2013)












![{\displaystyle {\begin{array}{rclcl}\mathbf {\tau } _{R}&=&\displaystyle {{\frac {2}{3}}\mathbf {a} +{\frac {1}{3}}\mathbf {b} +{\frac {1}{3}}\mathbf {c} ,}&&\\[2ex]2\mathbf {\tau } _{R}&=&\displaystyle {{\frac {4}{3}}\mathbf {a} +{\frac {2}{3}}\mathbf {b} +{\frac {2}{3}}\mathbf {c} }&\equiv &\displaystyle {{\frac {1}{3}}\mathbf {a} +{\frac {2}{3}}\mathbf {b} +{\frac {2}{3}}\mathbf {c} .}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/382e1f90d438695cda7b2b463d1f9f0c703b4147)









![{\displaystyle [{\bar {1}}11]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/807e1efd27e06588d647cd69b8cd14b518a646cb)






