Les ressorts
|
LES RESSORTS
navigation rapide dans le livre de technologie
■ préface - SOMMAIRE COMPLET ■ Aspects généraux ■ Éléments de machines |
Le problème des ressorts est l'un des plus complexes qu'ait à traiter le mécanicien.
La recherche de lois de déformation spécifiques, la connaissance des matériaux, de leurs traitements et de leurs modes de dégradation, la mise au point de procédés de fabrications efficaces et stables, sont au programme.
Introduction[modifier | modifier le wikicode]
Les ressorts sont des composants élastiques très répandus dans toutes sortes de machines et d'équipements. En raison de leur souplesse, ils diffèrent radicalement des autres pièces mécaniques dont on cherche, au contraire, à limiter les déformations sous charge.
Attention au terme « déformation » ! Il ne faut pas confondre la déformation d'un élément de volume infiniment petit, tel qu'on le conçoit en résistance des matériaux, et la déformation globale d'un ressort, c'est-à-dire un changement de forme qui se traduit, dans les cas les plus simples, par le déplacement d'une de ses extrémités par rapport à l'autre.
On peut attendre des ressorts :
- qu'ils se déforment d'une certaine façon sous l'effet des charges qu'ils subissent
- ou qu'ils fournissent certains efforts lorsqu'on leur impose une déformation.
Les deux modes de travail à charge imposée ou à déformation imposée ne sont pas équivalents, en particulier pour les ressorts qui, en raison de leur forme ou de leur montage, possèdent plusieurs positions stables de repos.
Un ressort que l'on déforme emmagasine une énergie mécanique qui peut être restituée, idéalement en totalité, lorsque la déformation cesse. Naturellement aucun ressort n'est parfait et une fraction plus ou moins importante de cette énergie mécanique est perdue lors des cycles de fonctionnement et transformée en chaleur.
L'un des premiers ressorts inventé par l'homme n'est autre que l'arc, une pièce de bois courbe et élastique bien plus efficace que le bras humain pour lancer à grande vitesse les flèches utilisées pour la chasse ou pour la guerre. Des peintures rupestres attestent que l'homme a inventé cette arme voici plus de 10 000 ans.
De nos jours, les ressorts assurent toutes sortes de fonctions, par exemple :
- rappel d'une pièce écartée de sa position d'équilibre (portes battantes type « saloon », appareils de mesure),
- maintien d'un serrage (pince à linge),
- suspension des véhicules (ressorts à lames, ressorts hélicoïdaux, systèmes hydropneumatiques),
- émission de sons (boîtes à musique),
- répartition de charges (sommiers et matelas à ressorts),
- accumulation d'énergie (moteurs de jouets, de montres),
- amortissement des chocs (tampons de matériel ferroviaire, systèmes antisismiques pour les bâtiments),
- mesure et/ou consignation de la valeur d'un effort (clé dynamométrique),
- compensation d'une charge ou d'un poids (hayon arrière de voiture, porte abattante de lave-vaisselle),
- établissement ou coupure brutale de contacts électriques,
- guidage de composants mécaniques sur de très faibles distances, en évitant les effets aléatoires des frottements « secs » (capteurs, microrupteurs).
- application d'un effort dans un but thérapeutique (appareils orthodontiques, ...),
- jouets et objets décoratifs (les longs ressorts très souples « Slinky » qui descendent les escaliers),
- etc.
Généralités[modifier | modifier le wikicode]
Les ressorts sont souvent considérés à tort par les bureaux d'études comme de simples accessoires dont on ne se préoccupe qu'une fois les projets achevés. Dans ces conditions, les concepteurs sont souvent contraints de leur donner des caractéristiques inadaptées aux besoins et incompatibles avec une bonne tenue en service. Une fois les mécanismes ou les machines assemblés et mis en marche, on s'aperçoit alors que leur bon fonctionnement dépend uniquement de la durée de vie des ressorts...
Grâce aux soins apportés à leur conception, à leur fabrication et à leur contrôle, les ressorts utilisés pour la suspension des véhicules comptent désormais parmi les composants les plus fiables, bien que les matériaux qui les constituent travaillent à des niveaux très proches de leurs limites.
Du point de vue des modèles utilisés dans la théorie des mécanismes, les ressorts n'introduisent aucun degré de liaison et n'interviennent jamais dans la nomenclature des pièces, en revanche ils fournissent des efforts dont les lois de variation sont a priori connues.
On peut distinguer plusieurs grandes catégories de ressorts en fonction de divers critères, en particulier selon les matériaux utilisés, qui peuvent être des métaux, des élastomères, des matériaux composites ou encore des gaz.
Il faut remarquer aussi que l'introduction d'une certaine élasticité dans un mécanisme peut se faire à l'aide d'un ressort, composant séparé intervenant dans un assemblage, ou en concevant des pièces capables d'assurer, par la totalité ou par une partie seulement de leur matière, la fonction demandée.
Caractéristiques générales des ressorts[modifier | modifier le wikicode]
Lois de comportement[modifier | modifier le wikicode]
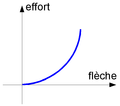
Nous sommes ici dans un domaine où les idées reçues sont légion. Bien que le comportement linéaire soit le plus fréquemment recherché, pour de vrais impératifs techniques ou par facilité, les lois qui relient les déformations globales des ressorts aux efforts qui leur sont appliqués sont beaucoup plus variées que ce que l'on pense généralement ; tout l'art des concepteurs et des fabricants de ressorts consiste à les adapter le mieux possible aux besoins !
 pour en savoir plus : Lois de comportement des ressorts
pour en savoir plus : Lois de comportement des ressorts
Aspects énergétiques[modifier | modifier le wikicode]
Un ressort que l'on déforme absorbe une certaine quantité d'énergie et la conserve sous forme d'énergie potentielle. En général, il en restitue la plus grande partie en reprenant sa forme initiale.
 pour en savoir plus : Aspects énergétiques
pour en savoir plus : Aspects énergétiques
Les impératifs techniques de base[modifier | modifier le wikicode]
Quel qu'en soit le type, un ressort convenablement conçu doit répondre à deux exigences fondamentales :
- résister aux charges maximales qui lui seront appliquées, lesquelles n'engendreront qu'une contrainte au plus égale à la contrainte admissible dans la zone la plus sévèrement sollicitée (condition de résistance).
- se déformer selon les besoins et donc posséder une raideur bien définie (condition de déformation).
Naturellement, d'autres impératifs viennent très vite s'ajouter, à commencer par les limites d'encombrement et de masse. Il faut également tenir compte de la disponibilité de la matière première et des dimensions normalisées des demi-produits, en particulier des diamètres des fils et des barres.
Ce texte vient d'être transféré, toutes les illustrations n'ont pas encore été mises en place dans la suite de ce Wikilivre, merci de votre compréhension.
Ressorts et vitesses de déformation[modifier | modifier le wikicode]
Si la conception d'un ressort de qualité nécessite de solides connaissances dans les domaines de l'analyse des contraintes et de la mécanique rationnelle, la concrétisation d'un projet pose des questions de choix de matériaux (nature, traitements), de mise en forme et surtout de qualité de surface (structure, contraintes résiduelles, rugosités) dès lors que l'on travaille sur un mécanisme en mouvement.
Bien que de nombreux ressorts soient sollicités à des fréquences assez élevées ou très élevées, nous nous limiterons ici à une étude statique ou quasi-statique. Quand les déformations ont lieu à faible vitesse, les variations de charge sont répercutées sans décalage de temps dans toute la masse du ressort. Par contre, dans le cas d'un fonctionnement dynamique à haute fréquence, les charges appliquées à une extrémité d'un ressort ne sont pas transmises instantanément jusqu'à l'autre ; ce retard engendre des phénomènes vibratoires que l'on peut parfois mettre à profit mais qui sont le plus souvent indésirables. Les motoristes, par exemple, n'apprécient guère la « danse » des ressorts de soupapes.
Les lois classiques de la résistance des matériaux sont établies dans le cadre d'hypothèses très restrictives et qui ne sont que très rarement respectées dans le fonctionnement des ressorts industriels. Les formules établies lors de l'étude des poutres s'appliquent relativement bien aux barres de torsion mais, pour la plupart des autres types de ressorts, elles donnent des résultats très imprécis, voire carrément inutilisables. Il faut alors se tourner vers des lois empiriques susceptibles de rendre mieux compte de la réalité. De toute manière, la précision apportée au calcul des ressorts n'a de sens que si l'on dispose des matériaux permettant d'obtenir et surtout de conserver dans la durée les caractéristiques adéquates.
Matériaux et traitements[modifier | modifier le wikicode]
Sans entrer dans le détail pour l'instant, disons qu'un bon matériau pour réaliser des ressorts possède une résistance vive élastique Re2/2.E aussi grande que possible, Re étant la limite d'élasticité et E le module de Young de ce matériau.
Toutefois, une haute limite d'élasticité ne suffit pas, il faut qu'elle s'accompagne d'une bonne résilience et d'une bonne endurance vis-à-vis des efforts alternés. La contrainte limite sous charge est proche de la limite d'élasticité du matériau lorsque l'utilisation est statique ou quasi statique. En revanche, pour les ressorts devant travailler de façon dynamique pendant de longues périodes, il convient d'adopter comme limite pratique du « taux de travail », pour reprendre l'expression couramment employée par les professionnels, des valeurs qui peuvent être deux fois plus faibles.
Matériaux métalliques « habituels »[modifier | modifier le wikicode]
- La « corde à piano » est (en principe) un fil d'acier écroui à 0,8 - 1 % de carbone, dont la surface polie est exempte de défauts ou d'imperfections notables susceptibles d'amorcer des ruptures de fatigue. On atteint normalement une limite d'élasticité Re = 1.210 MPa pour le fil de 0,5 mm et Re = 1.125 MPa pour le fil de 13 mm. Ce matériau peu coûteux est très largement utilisé pour tous les ressorts dont on n'exige pas de performances élevées. Toutefois, il faut se méfier de la « corde à piano » achetée au rayon bricolage du supermarché du coin, car elle risque fort de ne pas approcher ces performances...
- Les aciers au carbone du type XC 70 présentent des caractéristiques plus constantes pouvant atteindre 900 à 1.300 Mpa en traction et 700 à 1.000 Mpa en torsion (cisaillement). Ils sont un peu plus coûteux que la corde à piano mais ils permettent la réalisation de produits de meilleure qualité en raison de leur aptitude aux traitements thermiques.
- Les aciers inoxydables AISI 301 (X10 Cr-Ni 18-8), AISI 302 (Z12 CN 18-8) ou AISI 316 (Z11 CND 17-6) ont des caractéristiques mécaniques très proches de celles des aciers ci-dessus mais ils offrent l'avantage de résister beaucoup mieux à l'oxydation. Leur coût de revient est certes un peu plus important que celui des aciers au carbone mais leur utilisation devient souvent plus économique lorsqu'il faut mettre en œuvre une protection contre la rouille.
 pour en savoir plus : les aciers inoxydables
pour en savoir plus : les aciers inoxydables
- Parmi les aciers alliés, une première famille est celle des aciers mangano-siliceux contenant de 1,5 à 2 % de silicium, 0,6 à 0,7 % de manganèse, 0,4 à 0,6 % de carbone, avec éventuellement un peu de chrome, de tungstène, de molybdène ou de vanadium. Citons les nuances suivantes : 45S7 (ressorts à lames), 55S7, 45SCD6, 60SC7, (barres de torsion), 45SW8. On trouve aussi des aciers au chrome, avec du vanadium, du manganèse ou du silicium-molybdène, par exemple : 45C4, 50CV4. Ces matériaux ne sont disponibles que dans des grosses dimensions : fils de diamètre supérieur à 6 mm, lame d'épaisseur supérieure à 4 mm.
- Le cuivre au béryllium est un matériau trop peu connu mais largement utilisé en construction électrique. L'addition de 1 à 2 % de béryllium dans le cuivre permet de réaliser des ressorts très bons conducteurs de l'électricité et de la chaleur. La limite d'élasticité atteint 1000 MPa, avec une très bonne endurance. Cet alliage requiert un traitement thermique soigné après sa mise en forme, et il est souvent étamé pour en faciliter la soudure. Concernant le dimensionnement des ressorts, la littérature technique ne donne souvent que des indications floues sur les caractéristiques de cet alliage. Lors de travaux de conception de pièces d'armement les caractéristiques suivantes ont été établies expérimentalement et ont servi à dimensionner des ressorts stockés sous contrainte maximale pendant plusieurs dizaines d'années avant d'être utilisés. voici ces données : Alliage CuBe2, approvisionné à l'état recuit. La contrainte maximale pratique en torsion peut être prise à 850 MPa, le module de torsion à considérer est G= 4600 MPa. Enroulé à froid avec un pas très grand correspondant à la flèche par spire sous contrainte maximale, après meulage des extrémités, traitement thermique à 320°C pendant 3 heures. Après refroidissement le ressort est "gymnastiqué" (écrasé à spires jointives puis relâché plusieurs fois) afin de s'assurer de sa stabilité dimensionnelle. S'il est monté en atmosphère corrosive en contact avec de l'acier ou de l'alliage léger, une corrosion galvanique risque de détériorer le mécanisme, pour éviter cela on peut appliquer sur le ressort un nickelage chimique d'épaisseur 15 à 20 micromètres. Il faut éviter les traitements de surfaces à chaud qui altèrent le traitement thermique.
- Il faut noter que cet alliage présente l'avantage d'avoir un module de torsion relativement faible tout en supportant une contrainte de torsion équivalente à celle des meilleurs aciers. Il permet donc une flèche par spire beaucoup plus importante et donc une possibilité de stockage d'énergie améliorée pour un volume donné.
- Les alliages spéciaux sont utilisés pour résoudre des problèmes spécifiques. On sait par exemple que la limite d'élasticité des aciers baisse rapidement lorsque la température s'élève ; les alliages du type INCONEL à base de nickel (45 à 75 %), de chrome (15 %), de cobalt, molybdène, tungstène, titane, fer, et aluminium conservent des propriétés correctes jusqu'à 400-500 °C. Il s'agit là de matériaux très coûteux et utilisés seulement pour des applications particulières, on peut toutefois se les procurer assez facilement.
Matériaux métalliques particuliers[modifier | modifier le wikicode]
- L'ELINVAR (« acier » à 33 % de nickel, 12 % de chrome, 1,2 % de manganèse) a un module d'YOUNG indépendant de la température. Il sert à la fabrication de ressorts de très haute qualité destinés à des appareils de précision (galvanomètres, sismographes, chronomètres, diapasons, etc.). Cet alliage très particulier est réservé à des fabrications spéciales et les fabricants de ressorts ne le fournissent pas. Il faut donc prévoir son approvisionnement avant de penser à une éventuelle utilisation.
- Les alliages à mémoire de forme comme le Nitinol, alliage de nickel, titane et cuivre, constituent une solution intéressante quand la détente du ressort doit être différée dans le temps. Ils présentent plusieurs propriétés très spéciales, entre autres l'effet mémoire simple sens qui permet à l'alliage de retrouver sa forme initiale après une déformation mécanique ou thermique et l'effet mémoire double sens qui le rend capable après « éducation » d'avoir deux positions stables au-dessous et au-dessus d'une certaine « température critique ». Des ressorts peuvent ainsi rester « au repos » à température ambiante et devenir « actifs » si leur température augmente. Ils ont des applications fort intéressantes en orthodontie, dans les systèmes d'assemblage mécanique, les appareillages de sécurité, etc. Les fabricants de systèmes élastiques les utilisent sans doute trop peu actuellement.
- Aux très basses températures (-150 à -200 °C), les aciers sont presque tous extrêmement fragiles mais on peut utiliser d'autres métaux comme... le plomb ! Faut-il préciser qu'un ressort en plomb ne doit jamais être ramené sous charge à la température ambiante ?
Caoutchoucs et élastomères[modifier | modifier le wikicode]
(à développer)
Matériaux divers[modifier | modifier le wikicode]
- Le silicium : ses propriétés élastiques le font parfois employer pour des ressorts destinés à divers micromécanismes et à des montres mécaniques haut de gamme. Ainsi, la société Patek Philippe l'utilise pour fabriquer des ressorts spiraux (Spiromax).
- le carbone est utilisable sous forme de fibres et donc de pièces composites. Malgré un coût élevé par rapport aux matériaux traditionnels, le carbone permet de réaliser des pièces à la fois très résistantes et légères, tout en étant insensibles à la corrosion dans plupart des milieux rencontrés en mécanique.
-
ressort en matériau composite à base de fibres de carbone
Traitements des matériaux métalliques[modifier | modifier le wikicode]
Il n'est pas dans notre intention d'entrer ici dans le détail des procédés de fabrication. Signalons simplement que tous les ressorts sérieux subissent des traitements mécaniques qui, mettant en compression les couches superficielles du métal, minimisent la formation et la propagation des fissures de fatigue. Ces traitements peuvent être le galetage (barres de torsion) ou le grenaillage de précontrainte (en anglais shot peening). La préconformation des ressorts est également une solution pour créer, aux endroits les plus sollicités, les contraintes résiduelles de compression ou de cisaillement adéquates.
Les ressorts sont habituellement livrés huilés ou peints. Les traitements chimiques ou par galvanoplastie ne sont absolument pas conseillés car ils ont généralement pour effet de rendre les ressorts fragiles.
Ressorts dont la matière travaille en torsion[modifier | modifier le wikicode]
Barre de torsion[modifier | modifier le wikicode]
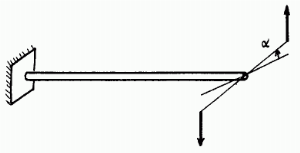
La barre de torsion est un des ressorts les plus simples. Si nous négligeons les extrémités, sa partie active est une barre pleine de diamètre d et de longueur L, ou bien un tube de diamètre intérieur di et de diamètre extérieur de.
L'une des extrémités de la barre est encastrée et considérée comme fixe, l'autre, dite libre, est reliée aux éléments mobiles.
L'application essentielle des barres de torsion est la suspension des véhicules, particulièrement de ceux dont les roues sont indépendantes. On les utilise non seulement sur des véhicules légers, mais aussi sur des engins de masse importante (char d'assaut par exemple) et beaucoup de véhicules tous terrains.
Appelons Mt le moment de torsion appliqué à l'extrémité libre de la barre et α l'angle dont tourne cette extrémité par rapport à l'autre, sous l'effet de ce moment.
Condition de résistance[modifier | modifier le wikicode]
La contrainte maximale de cisaillement dans le ressort vaut :
avec (barre pleine)
ou (tube)
Condition de déformation[modifier | modifier le wikicode]
L'angle de rotation de l'extrémité libre vaut :
avec (barre pleine)
ou (tube)
La raideur vaut
Nous noterons que les inconnues sont faciles à obtenir à partir des formules : en effet, pour un matériau donné, les diamètres de la barre ou du tube sont fixés par la condition de résistance, ensuite la condition de déformation impose la longueur.
Problèmes pratiques[modifier | modifier le wikicode]
Dans les barres de torsion à section circulaire, le problème délicat est celui des attaches, au niveau desquelles il ne faut pas provoquer de concentration de contraintes. Le plus souvent, un cône de demi angle au sommet proche de 30°, raccordé à la barre par un large congé de raccordement (rayon r ~ 1,5.d), permet l'augmentation de diamètre nécessaire au taillage des cannelures ou des dentelures qui seront engagées dans les parties femelles des pièces de liaison. C'est évidemment au niveau des angles rentrants de ces cannelures ou dentelures que les risques de créer des amorces de rupture sont a priori les plus grands mais la réalisation du congé doit être l'objet de toutes les attentions.
Notons la possibilité d'associer une barre et un tube de torsion afin de diminuer l'encombrement en longueur (suspension dite « Dubonnet »).
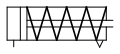
Ressort hélicoïdal de traction ou compression[modifier | modifier le wikicode]
Ce type de ressort, encore appelé « ressort à boudin », peut être considéré comme une barre de torsion que l'on aurait enroulée en hélice. C'est sans doute le plus courant.
-
ressort de compression
-
ressort de traction
La partie active du ressort comporte un fil enroulé selon une hélice régulière, mais il faut tenir compte des extrémités destinées à assurer la liaison avec l'environnement. Le dessin ci-dessous représente un ressort de compression à extrémités rapprochées et meulées.
Retenons immédiatement :
- qu'il existe dans un tel ressort des spires « actives » appelées à se déformer et des « spires inactives » utilisées pour les appuis, avec un passage graduel des unes aux autres par variation de l'angle d'hélice,
- que le nombre TOTAL de spires doit être un multiple impair de 0,5 de façon à mieux répartir les efforts d'appui, surtout lorsque les extrémités ne sont pas meulées.
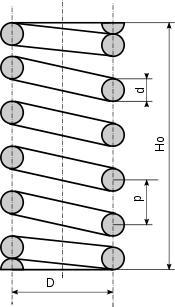
Précisons les notations utilisées :
- D diamètre d'enroulement
- d diamètre du fil
- m = D/d proportions
- De = D + d diamètre extérieur
- Di = D-d diamètre intérieur
- n nombre de spires actives
- n' nombre de spires inactives
- po pas d'enroulement à vide
- px pas d'enroulement sous charge X
- Ho hauteur libre (sans charge)
- Hx hauteur sous charge X
- HP hauteur à spires jointives (à bloc)
- i angle d'inclinaison de l'hélice
- P charge axiale maximale (norme)
- f1 flèche d'une spire sous charge P
- f = Ho-Hp flèche du ressort sous charge P
- T effort tranchant dans le fil (norme)
- N effort normal dans le fil (norme)
- Mf moment de flexion dans le fil (norme)
- Mt moment de torsion dans le fil (norme)
- k = P/f raideur du ressort
- τ contrainte due а la torsion seule
- τm contrainte maximale sous charge P
- K coefficient de correction de contrainte
Nous supposerons dans ce qui suit que les hypothèses suivantes sont vérifiées :
- les sections droites du fil sont et restent circulaires,
- les spires sont faiblement inclinées (i < 7°),
- les appuis du ressort sont perpendiculaires à l'axe et sans frottement,
- les forces extérieures sont appliquées dans l'axe du ressort.
L'application d'un effort axial entraîne l'existence, au niveau d'une section droite quelconque du fil,
- d'un effort normal et d'un effort tangentiel tels que ,
- d'un moment de torsion et d'un moment de flexion tels que leur somme soit tangentielle et que
Compte tenu de la faible inclinaison du fil, nous négligerons le moment de flexion et l'effort normal (le premier produit une rotation d'une extrémité du ressort par rapport à l'autre, rotation qui doit être libre pour conserver leur validité aux calculs). Nous écrirons par ailleurs :
Condition de résistance[modifier | modifier le wikicode]
Il faut examiner ici la répartition des contraintes dans le fil :
Si nous ne tenons compte que du moment de torsion, les contraintes de cisaillement sont réparties comme l'indique la figure 1. Elles sont maximales sur la périphérie du fil, où elles valent :
Cette formule n'est guère utilisable que pour des avant-projets.
Si nous prenons en compte l'effort tranchant, supposé uniformément réparti sur la section du fil, nous arrivons à la répartition indiquée par la figure 2.
Que le ressort travaille en traction ou en compression, les deux contraintes tangentielles s'ajoutent au point I situé à l'intérieur du ressort.
La correction faite est telle que :
Le terme correcteur qu'il faut ajouter est d'autant plus grand que le rapport m = D/d est petit, ce qui caractérise un ressort « raide ». Ceci sera justifié par la suite.
En réalité, il faut encore tenir compte de la courbure de la « poutre » constituant le ressort. La répartition des contraintes n'est pas linéaire et prend l'allure donnée sur la figure 3, avec un maximum très marqué au point intérieur I où s'amorcent presque toujours les ruptures de fatigue, comme celle que l'on peut voir ici :
La contrainte τm se calcule en pratique à partir de la contrainte τ que l'on multiplie par un coefficient correcteur K (ne pas confondre avec la raideur) dépendant du rapport D/d. Ce coefficient K peut être déterminé par lecture sur l'abaque ci-dessous ou encore calculé grâce à des formules plus ou moins empiriques.

Voici par exemple une de ces formules, donnée par ROEVER :
soit
avec en posant m = D/d
Condition de déformation[modifier | modifier le wikicode]
La résistance des matériaux donne la valeur de la flèche par spire active (dans le cadre des hypothèses simplificatrices énoncées plus haut) :
Si nous connaissons la flèche f que doit prendre le ressort sous l'effet de la charge P, nous pouvons très facilement en déduire le nombre de spires actives nécessaires :
soit
La raideur du ressort s'écrit alors :
TIMOSHENKO propose de corriger cette valeur en fonction de la valeur de m :
avec
Une telle correction n'a d'intérêt que si m < 5. Dans le cas contraire le coefficient 9 est très proche de 1 et l'on ne corrige pas (ex : si m = 10, b = 1, 002).
Instabilité latérale[modifier | modifier le wikicode]
Pour les ressorts de compression de grande longueur il est nécessaire de prévoir un guidage pour éviter le phénomène de flambage, lequel est favorisé par le déplacement latéral des appuis, par les vibrations, etc.
La courbe ci-dessous donne la limite à partir de laquelle le flambage devient hautement probable, pour des ressorts dont les appuis sont correctement réalisés.
Variation du diamètre d'enroulement sous charge[modifier | modifier le wikicode]
Lorsqu'un ressort de compression est guidé dans un tube avec un jeu insuffisant, il risque de se trouver bloqué car le fil tend à se dérouler sous l'effet du moment de flexion, ce qui provoque l'augmentation du diamètre extérieur. De étant le diamètre extérieur et p le pas d'enroulement du ressort à vide, on trouve le nouveau diamètre extérieur D'e du ressort chargé à bloc (les spires sont alors jointives) grâce à la formule :
(selon Tools Engineers Book)
Bien que le cas soit nettement plus rare, il pourrait en être de même pour un ressort de traction monté sur une tige de trop fort diamètre, à cause cette fois de la diminution du diamètre intérieur.
Ressorts « légers » et ressorts « forts »[modifier | modifier le wikicode]
Il s'agit ici d'une question de proportions. Les fabricants ont l'habitude de proposer, dans leurs catalogues, différentes séries standardisées répondant à des catégories de besoins spécifiques ; on trouve par exemple un classement en fonction du rapport des diamètres du logement Dl et de l'arbre Da :
- série forte : Dl = 2 Da
- série moyenne : Dl = 1,8 Da
- série légère : Dl = 1,6 Da
- série très légère : Dl = 1,4 Da
Ces rapports tiennent compte des tolérances de fabrication et des variations de diamètre d'enroulement sous charge, le ressort ne devant venir se serrer ni dans le logement, ni sur l'arbre. Le diamètre du fil est donc nettement plus petit que le jeu radial disponible.
Notions sur la fabrication[modifier | modifier le wikicode]
- le rapport m = D/d est presque toujours compris entre 5 et 13 et le plus souvent entre 7 et 10. En dessous de 5, jusqu'à 3,5, on ne peut pratiquement plus enrouler le fil à froid. Au-dessus de 12 ou 13 la détente du fil après enroulement ne permet plus d'assurer avec précision la valeur du diamètre D. On peut exceptionnellement atteindre 17 à 18 pour des fabrications de grande série, après mise au point d'outillages spéciaux.
- le formage du ressort dépend du matériau et du diamètre du fil. L'enroulement se fait généralement à froid au-dessous de 10 mm et systématiquement à chaud au-dessus de 17 mm. Les traitements s'effectuent après le formage.
- la préconformation a pour but d'écrouir les couches superficielles pour en augmenter la limite d'élasticité. Le ressort est enroulé avec un pas plus grand que la valeur calculée puis comprimé à bloc. Il se trouve raccourci après l'opération car dans certaines zones la limite d'élasticité a été dépassée. Cette plastification engendre des contraintes résiduelles qui se déduisent de la contrainte principale régnant au point intérieur I de la section du fil. La maîtrise des divers paramètres (géométrie, contraintes, ...) n'est pas simple.
Dans un fil tordu, tant que l'on reste dans le domaine élastique, les contraintes de cisaillement restent proportionnelles à la distance au centre de la section. Il n'en va pas de même si l'on dépasse la limite d'élasticité : l'écrouissage des zones périphériques s'accompagne d'une limitation des contraintes maximales et d'une surcharge concomitante des zones intérieures. On peut se débrouiller pour que cette situation se produise lorsque le ressort est comprimé à bloc.
Si on relâche l'effort, on ne revient pas à l'état initial, les contraintes dans les zones internes chargent les zones externes en sens contraire.
Une nouvelle charge appliquée au ressort engendrera dans le fil des contraintes qui resteront inférieures à la limite d'élasticité, tant qu'elle restera inférieure à la charge de préconformation, c'est-à-dire tant que le ressort ne sera plus comprimé à bloc. Le domaine d'élasticité du ressort se trouve ainsi étendu, par rapport à ce qu'il serait sans préconformation.
- le grenaillage de précontrainte n'est pas très pratique à mettre en œuvre car le jet de grenaille n'atteint pas facilement la zone intérieure, celle qui peut le plus bénéficier de ce traitement.
Le problème des extrémités[modifier | modifier le wikicode]
Pour les extrémités, on peut se contenter de rapprocher les spires dans le cas de ressorts à bon marché mais le plus souvent on les rapproche et on les meule. Le nombre total de spires est égal au nombre n des spires actives, auquel il convient d'ajouter le nombre n' des spires d'extrémité, lequel vaut usuellement :
| nombre de spires d'extrémité en fonction de m = D/d | ||
| valeurs indicatives de m | 5 | 12 |
| nb de spires meulées | 2 | 1,5 |
| nb de spires non meulées | 3,5 | 3 |
Notons que certains fabricants proposent des ressorts munis de pièces d'appui spécialement étudiées, comme ci-dessous :
Rappelons que pour un bon appui, surtout si les spires terminales ne sont pas meulées, le nombre total de spires doit être un multiple impair de 0,5 :
n + n' = (2 e + 1) 0,5 avec e entier
Les ressorts de traction sont généralement enroulés à spires jointives grâce à une torsion du fil. Il ne faut plus alors les traiter à chaud. La photo ci-dessous montre deux ressorts de traction montés l'un dans l'autre, de façon à obtenir une plus grande raideur dans un encombrement donné.
Les extrémités des ressorts de traction sont munies d'un anneau qui permet de les accrocher aux mécanismes sur lesquels elles doivent agir. Il existe différentes manières de les réaliser :
Les ressorts de compression peuvent être utilisés sans préparation des extrémités à condition d'utiliser des bouchons spécialement adaptés :

Ces bouchons peuvent être munis d'un trou fileté ou d'un trou lisse, ce qui autorise différents types de montage. Ils peuvent également servir à faire travailler le ressort en compression et en traction en le soumettant à des efforts de sens variable.
Calcul d'un ressort en hélice cylindrique[modifier | modifier le wikicode]
Nous disposons d'un certain nombre de données que nous devons exploiter au mieux :
(1) Résistance aux efforts : D/d = m n'étant pas connu a priori, nous ne savons pas quelle valeur adopter pour le coefficient de correction K. Pour nous faire une première idée, nous pouvons choisir un matériau, diminuer de 15 à 20 % sa contrainte admissible de cisaillement et utiliser la formule approchée :
Si nous fixons a priori m, nous fixons également K. Nous pouvons alors remplacer D par m.d dans la formule complète de Roever et en tirer une valeur de d :
Naturellement cette valeur a toutes les chances de ne pas convenir : les diamètres des fils du commerce sont en effet normalisés et il convient de ne pas oublier ce « détail »... Nous choisirons en conséquence le diamètre d dans la série suivante (valeurs en mm) :
0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,50 0,55 0,60 0,65 0,70 0,75 0,80 0,85 0,90 0,95 1 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 2 2,3 2,5 2,8 3 3,2 3,5 3,8 4 4,2 4,5 4,8 5 5,5 6 6,5 7 7,5 8 8,5 9 10 11 12 13 14
(2) Raideur : avec un peu de patience nous aurons peut être fini par tirer de la formule précédente deux valeurs plausibles de d et D. Le nombre de spires sera alors facile à obtenir à partir de la raideur du ressort :
Il faut que nous ayons à nouveau beaucoup de chance pour que ce nombre soit convenable : compte tenu du fait que d et D interviennent à des puissances élevées il est probable que ce calcul nous donnera une valeur aberrante de n, par exemple 250 spires ou 0,47 spire.
(3) Fabrication : elle impose, comme nous l'avons signalé, les proportions du ressort :
(4) Linéarité : elle impose de limiter la valeur de l'angle d'inclinaison d'hélice, on admet généralement la valeur suivante :
(5) Encombrement extérieur : le diamètre De doit rester inférieur à une certaine valeur si le ressort est monté dans un alésage. Attention, dans ce cas, à l'augmentation de De lorsque le ressort est comprimé !
(6) Encombrement intérieur : le diamètre Di doit être supérieur à une certaine valeur si le ressort est enfilé autour d'une tige.
(7) Hauteur maximale : il se peut que la hauteur du ressort monté soit limitée par la place disponible.
(8) Hauteur minimale : on ne peut plus comprimer un ressort dont les spires sont devenues jointives ... ce qui est de toute manière une situation parfaitement anormale en fonctionnement.
La détermination peut être faite au moyen d'abaques et l'on a fabriqué jadis des règles à calcul spéciales. Nous pouvons aussi tracer sur un même graphique les courbes correspondant aux diverses conditions ci-dessus : elles définissent, sauf pour les malheureux qui sont poursuivis par la scoumoune, une zone plus ou moins étendue dans laquelle peuvent être choisies de nombreuses combinaisons de d et D.
On préfère utiliser aujourd'hui des programmes informatiques qui offrent une aide efficace à la conception des ressorts. Reste, dans tous les cas, à mener à bien l'optimisation ...
Abaque pour les ressorts de traction-compression[modifier | modifier le wikicode]
Cet abaque permet de déterminer rapidement les caractéristiques d'un ressort hélicoïdal en « corde à piano », dans le cas où l'on souhaite procéder immédiatement à la réalisation, même si c'est « avec les moyens du bord ». On part de la charge maximale et des proportions D/d, ce qui permet d'obtenir immédiatement le diamètre du fil, le diamètre d'enroulement et la flèche par spire. Compte tenu de la flèche totale, on en déduit le nombre de spires actives.
attention : 520 ko ... mais vous pouvez l'imprimer pour obtenir un document utilisable !
Liens externes[modifier | modifier le wikicode]
Un programme de calcul des ressorts en hélice cylindrique peut être téléchargé à partir du site de la société Ferroflex http://212.71.194.198/fistart.htm
Une feuille de calcul de ressorts de compression existe en ligne proposé par la société Pommeuse Ressorts : http://ressorts.dynomonde.com/compression.php . Les calculs pour les autres sortes de ressorts viendront compléter la collection. Nouvelle adresse d'accès : Calcul de ressort de compression . Je tenterais de maintenir ces deux adresses, mais il est probable qu'à partir de cette dernière adresse, plus de possibilités seront à l'avenir offertes. Depuis peu, le calcul de ressorts de traction est aussi actif, mais encore en version de béta test.
Ressorts apparentés[modifier | modifier le wikicode]
Au lieu d'un fil rond, on peut utiliser d'autres formes, elliptique, rectangulaire, ... Parfois, les ressorts à fil rectangulaire sont obtenus par taillage dans un tube.
Les ressorts coniques sont enroulés à pas constant (sur le ressort à l'état libre, on s'élève d'une même quantité à chaque tour) ou à pente constante (les spires sont de plus en plus serrées au fur et à mesure que l'on se rapproche de l'extrémité de petit diamètre). - dans le premier cas, on peut obtenir une raideur de plus en plus forte au fur et à mesure de la compression (les spires de plus fort diamètre sont les plus souples et se compriment « à bloc » les premières) ou un encombrement minimal une fois la compression réalisée. - dans le second cas, on minimise la variation de raideur, les spires s'écrasent de façon à peu près simultanée mais une fois complètement aplati, le fil prend l'aspect d'une spirale de plus en plus lâche au fur et à mesure que l'on s'éloigne du centre. Notons que tous les ressorts coniques ne peuvent pas se mettre « à plat ».
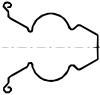
Pour les ressorts en volute, on n'utilise plus du fil mais des bandes de tôle spéciale découpées selon divers profils. Si l'on souhaite une raideur variable, alors il faut adopter une largeur constante de façon que les spires de plus grand diamètre s'affaissent les premières. Si au contraire on souhaite que la raideur reste constante, alors il faut faire en sorte que la section aille en augmentant de l'intérieur vers l'extérieur. Il est également possible de réaliser des ressorts en double volute comme celui qui est (mal) dessiné ci-dessous.
Outre leurs caractéristiques mécaniques un peu spéciales, les ressorts en volute ont la particularité de présenter une structure fermée, limitant les risques de blocage par des corps étrangers. Le ressort en double volute, encore appelés ressort comtois, est très souvent utilisé pour écarter les deux branches des sécateurs. Les jardiniers n'aiment pas beaucoup les sécateurs munis de ressorts hélicoïdaux ordinaires, car les brindilles s'y coincent facilement !
Ressorts dont la matière travaille en flexion[modifier | modifier le wikicode]
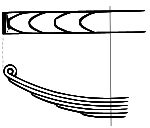
Ressort à lames[modifier | modifier le wikicode]

Nous nous contenterons ici d'un calcul de prédimensionnement (on dit parfois d' « équarrissage ») permettant de se faire une idée pas trop farfelue de l'encombrement qu'aurait un véritable ressort à lames réalisé selon les règles de l'art. Ce type de ressort, qui est une affaire de spécialiste, est surtout utilisé pour la suspensions de véhicules.
Forme de base[modifier | modifier le wikicode]
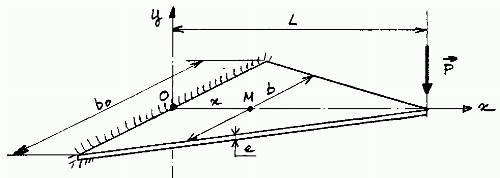
Une lame encastrée à une extrémité et chargée à l'autre peut évidemment servir de ressort mais les contraintes maximales règnent du côté de l'encastrement tandis que l'extrémité libre, qui a le même module de flexion I/v que l'autre, est peu sollicitée.
Pour mieux utiliser la matière, on cherche évidemment à se rapprocher d'une forme d'égale résistance qui est dans ce cas de figure une forme de largeur constante et de hauteur variant selon une loi parabolique (inutilisable ici), ou bien une lame triangulaire de hauteur constante, qui va nous servir de base de calcul.
Si bo est la largeur de cette lame au niveau de l'encastrement et L sa longueur, la largeur de la lame au point M d'abscisse x s'écrit :
Le moment de flexion en M est
La contrainte maximale de flexion est constante tout au long de la lame :
Condition de résistance[modifier | modifier le wikicode]
Elle découle du calcul précédent :
Condition de déformation[modifier | modifier le wikicode]
Dans l'hypothèse, classique mais ici irréaliste, des petits déplacements, nous pouvons calculer la flèche f de l'extrémité libre sous l'effet de la charge P :
Notons que les deux conditions de résistance et de déformation imposent ensemble l'épaisseur maximale de la lame :
Après que nous avons arrondi l'épaisseur à une valeur normalisée, il en résulte la détermination de bo, qui donne généralement des dimensions prohibitives pour la lame ...
Découpage en lames[modifier | modifier le wikicode]
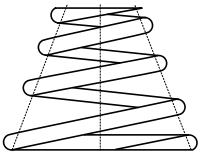
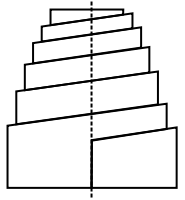
Après avoir découpé la lame triangulaire comme indiqué ci-après, « ressoudé » les morceaux latéraux deux à deux, élargi la lame la plus longue (lame maîtresse), nous pouvons rassembler les lames élémentaires pour former un système étagé que nous supposerons équivalent au précédent.
En pratique, de nombreuses modifications interviennent et rendent très complexe l'étude d'un tel ressort : formes des extrémités des lames, frottements, systèmes d'attache, etc.). Pour réaliser un paquet de lames à peu près « carré » au niveau des attaches, si n est le nombre de lames, il faut écrire :
Si nous choisissons a priori un nombre de lames raisonnable, nous pouvons alors combiner les diverses formules pour trouver la longueur minimale du ressort, lequel sera alors le plus léger que l'on puisse réaliser.
Par exemple, nous pouvons poser bo = n2.e et reporter cette valeur dans les formules :
(résistance)
(flèche)
En éliminant e, nous trouvons :
Ceci ne constitue certes pas LE calcul de détermination d'un ressort à lames, mais nous avons maintenant une idée de l'encombrement que pourrait avoir une solution de ce type.
Quelques problèmes de réalisation[modifier | modifier le wikicode]
Les formes réelles seront assez éloignées de la forme théorique d'égale résistance que nous venons de voir :
- la plus longue lame, ou lame maîtresse, doit avoir une section suffisante pour résister seule à l'effort tranchant, ainsi que pour permettre la liaison avec les éléments extérieurs. Son extrémité n'est donc jamais triangulaire mais toujours façonnée en fonction des besoins.
- pour éviter que le ressort « baille », c'est-à-dire que les lames décollent, on donne à ces dernières une courbure qui croît de la lame maîtresse, la plus longue, aux plus courtes. Il faut alors que les épaisseurs des lames aillent en décroissant, sinon on dépasserait de plus en plus largement la limite d'élasticité.
- l'extrémité des lames n'est jamais taillée en pointe, mais coupée droite, terminée en trapèze ou encore amincie et arrondie selon un profil parabolique.
- les lames ne sont généralement pas de section rectangulaire, elles portent des nervures qui les maintiennent alignées, comme le montre la figure ci-après. Il existe d'ailleurs des profilés normalisés spécialement formés pour la réalisation de ressorts à lames.
- la nécessité de brider les lames au centre impose d'augmenter la longueur du ressort car la partie bridée se trouve raidie.
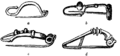
- les attaches peuvent prendre des formes très diverses dites à œil droit (6), renversé (7), épaulé (8), droit à patte (9), épaulé à patte (10), appui à glissoir (11).
Si l'on ajoute la possibilité de réaliser des ressorts à lames étagées de toutes formes, symétriques ou non, à faible ou forte courbure, etc., il devient évident que les formules théoriques établies au début de ce paragraphe doivent être pour le moins revues et corrigées. En fait, chaque ressort nécessite une étude individualisée.
Le frottement entre les lames produit des pertes d'énergie notables (le travail de déformation du ressort est loin d'être intégralement restitué au moment de la détente) mais ces pertes contribuent à l'amortissement des vibrations, par exemple dans le cas des ressorts de suspension. Cependant, outre le fait qu'il fausse un peu plus les formules, le frottement est capable d'engendrer le phénomène de corrosion-frottement (poudre rouge) très destructeur. Pour éviter ou au moins pour freiner cette forme particulière d'usure, une lubrification protectrice est absolument indispensable et il ne faut surtout pas que l'état de surface des lames soit trop bon. Au contraire, il faut utiliser les lames « brutes de laminage ».
Diverses formes[modifier | modifier le wikicode]
Les ressorts à lames peuvent prendre des formes très variées, comme celles relatives à la suspension des véhicules dessinées ci-dessous. Naturellement, cette diversité ne facilite guère les calculs...

Préconformation[modifier | modifier le wikicode]
C'est à propos du ressort à lames que l'on comprend le plus facilement l'intérêt du traitement de préconformation, qui consiste à charger un ressort au-delà du point où il commence à prendre une déformation permanente pour, en quelque sorte, l'endurcir.
- en (a), une lame subit une déformation élastique, le diagramme des contraintes est rectiligne, la limite d'élasticité est atteinte, mais non dépassée, au niveau des couches du métal les plus éloignées de la fibre neutre.
- en (b), on a dépassé la limite d'élasticité dans les zones superficielles qui fluent alors sous charge ; dans ces zones la contrainte peut être considérée comme constante et égale à la limite d'élasticité du métal.
- en (c), on a supprimé la charge, il subsiste une contrainte résiduelle de compression dans la zone qui était tendue et une contrainte résiduelle de tension dans celle qui était comprimée. Le moment non nul créé par ces contraintes résiduelles « externes » est équilibré par d'autres contraintes « internes » qui apparaissent simultanément.
- en (d), on a de nouveau appliqué des efforts de flexion, lesquels donnent naissance à des contraintes réparties selon un diagramme dont la forme est très différente de celui décrit sur la figure (a). La contrainte résiduelle se déduit, en surface, de la contrainte qui serait normalement exercée en l'absence de préconformation, le ressort devient non seulement plus résistant en cas de surcharge, mais aussi moins sensible au phénomène de fatigue.
Ressort spiral à spires nombreuses[modifier | modifier le wikicode]
Le ressort spiral type, à spires non jointives et donc sans frottement, est composé d'un ruban de section rectangulaire encastré à une extrémité B et solidaire à l'autre extrémité 0 d'un axe perpendiculaire au plan d'enroulement.
Nous supposerons que l'axe est mobile sans frottement et, ce qui est moins évident, qu'il ne tend pas à se déplacer radialement lorsqu'on le fait tourner sous l'effet d'un couple C.
Dans ces conditions, tout couple perpendiculaire au plan d'enroulement, appliqué en O, se trouve transmis intégralement en B, ce qui ne serait pas le cas si en ce point l'extrémité n'était pas encastrée mais simplement accrochée, comme ce sera probablement le cas pour cette réalisation industrielle.
Condition de résistance[modifier | modifier le wikicode]
Si la lame élastique a pour largeur b (comptée perpendiculairement au plan d'enroulement) et pour épaisseur e, alors :
Condition de déformation[modifier | modifier le wikicode]
Pour une poutre soumise à la flexion, une variation du moment fléchissant entraîne une variation de la courbure (inverse du rayon de courbure), telle que :
L'intégration sur l'ensemble de la longueur L du ruban fournit l'angle de rotation θ de l'extrémité O :
(θ est évidemment en radians)
En éliminant C entre les deux formules, il vient :
Fabrication[modifier | modifier le wikicode]



Le ressort spiral, essentiellement utilisé dans l'appareillage de précision (montres, appareils électriques...) fait l'objet d'une fabrication très spéciale dont les modes opératoires et les essais sont codifiés par le Centre Technique de l'Industrie Horlogère. L'obtention de spires non jointives et équidistantes nécessite, au départ, une conformation spéciale du ruban. En effet, un ruban élastique rectiligne s'enroule « naturellement » en prenant la forme d'un rouleau compact à spires jointives. À cause des frottements importants entre les couches de cet enroulement, un tel ressort n'aurait donc pas du tout le comportement recherché ; en revanche, une telle disposition convient parfaitement pour les ressorts qui rappellent les mètres à ruban dans leur boîtier.
Lorsque les extrémités du ressort spiral sont liées normalement, c'est-à-dire encastrées et pas simplement accrochées, toute variation du moment de flexion à l'une des extrémités est intégralement transmise à l'autre extrémité : ainsi, dans tous les cas, le moment de flexion le long du ruban est constant.
En un point donné, la courbure de la lame est définie comme l'inverse du rayon de courbure local. Or, comme la section de la lame est constante, toute variation du moment de flexion s'accompagne d'une variation proportionnelle de la courbure :
Nous conviendrons de dire que tout le long du ressort enroulé de façon habituelle, fonctionnant à vide ou en charge, la courbure est positive. La figure ci-contre représente en haut un ressort spiral mis en forme et au-dessous, sa préforme, autrement dit son ébauche. Au niveau de l'extrémité intérieure A et du point M, la courbure de l'ébauche est positive et le reste après enroulement. Le point B correspond à un point d'inflexion de la préforme, où la courbure est nulle. Au point N et à l'extrémité extérieure C, les courbures de la préforme sont négatives. Lors de la mise en forme définitive par enroulement, les courbures positives de la préforme sont accentuées et les courbures négatives deviennent positives.
L'obtention de la forme « en S » est une opération complexe qui demande beaucoup de savoir-faire et d'expérience !
Pour les ressorts spiraux comme ceux des balanciers utilisés en horlogerie, la forme à vide est une spirale d'Archimède dont les courbures toutes positives augmentent ou diminuent au gré des oscillations, fournissant un couple de rappel alternativement négatif ou positif. En réglant la longueur du ruban flexible par un dispositif approprié, on fait varier la raideur du ressort et donc la fréquence des oscillations du balancier, ce qui permet de réduire autant que faire se peut l'avance ou le retard que peut prendre la montre ou la pendule.
Certains ressorts dont le fonctionnement normal se fait toujours en charge peuvent présenter, à vide, la forme « en S » des ébauches. Leur mise en place dans les mécanismes peut se révéler laborieuse, surtout s'ils sont de forte taille et s'ils présentent une raideur importante.
Plus que tout autre, le ressort spiral est une affaire de spécialistes !
Montage[modifier | modifier le wikicode]
Nous avons supposé que l'extrémité du ressort était encastrée et affirmé que dans ces conditions le couple transmis par la lame était identique en tout point de cette dernière. Si par contre l'extrémité du ressort est simplement accrochée en B, le moment est nul en ce point et variable tout au long du ruban, avec un maximum atteignant presque 2C au point A !
Le mode de fixation influe donc énormément sur la contrainte maximale en service et aussi, sur la forme du ressort lorsqu'il est mis en charge.
Ressort hélicoïdal pour la torsion[modifier | modifier le wikicode]
À part la forme spécifique de ses extrémités, ce ressort est identique à un ressort hélicoïdal de traction-compression à très faible angle d'hélice, ou même à un ressort de traction à spires jointives si l'on recherche un certain frottement interne, par exemple pour favoriser l'amortissement de vibrations.
-
Ressort du logement de batterie d'un appareil photo numérique
Nous supposerons que notre ressort a des spires non jointives et très peu inclinées (travaillant en flexion presque pure) et que ses extrémités sont encastrées. Si tel n'était pas le cas la précision des formules serait passablement altérée et la répartition des contraintes modifiée dans un sens nettement défavorable.
Il faut toutefois reconnaître que dans un très grand nombre de mécanismes où les critères de précision sont secondaires, les extrémités sont accrochées ou plus simplement encore appuyées.
Condition de résistance[modifier | modifier le wikicode]
C'est en fait la même que pour le ressort spiral, sauf que l'expression du moment d'inertie est différente. Si le fil n'est soumis qu'à la flexion (extrémités encastrées ...), le moment est alors identique en tout point et donc :
La section du fil peut être quelconque, par exemple carrée ou elliptique. Dans le cas le plus courant d'un fil rond, la formule précédente devient :
Condition de déformation[modifier | modifier le wikicode]
L'angle de rotation θ de l'extrémité mobile par rapport à l'extrémité fixe est là encore, au moment d'inertie près, identique à celle du ressort spiral :
(cas général)
(fil rond)
Fabrication[modifier | modifier le wikicode]
La manière de faire est, grosso modo, la même que pour les ressorts hélicoïdaux de traction-compression. C'est bien sûr la forme des extrémités qui est différente. On se reportera donc au chapitre évoqué ci-dessus, en particulier pour les diamètres de fil.
Il est assez facile de « bricoler » des ressorts de torsion en hélice cylindrique mais il faut généralement faire plusieurs essais si l'on veut approcher une valeur précise de la raideur. Le composant de base, que l'on peut trouver dans les bonnes quincailleries ou grandes surfaces, est la corde à piano. Il en existe de différentes sections et de différentes qualités. Pour fabriquer le ressort, on accroche le fil dans le mandrin d'une perceuse mécanique ou d'un tour et on l'enroule autour d'une tige filetée dont le pas est égal ou légèrement supérieur au diamètre du fil. On fait tourner le mandrin dans le sens antihoraire (comme pour dévisser) tout en maintenant fermement le fil avec un pince de manière à le laisser filer « sous contrôle ». Les résultats sont meilleurs si l'on pince le fil entre deux tasseaux de bois dur maintenus, pendant l'enroulement, en appui sur la tige filetée.
À l'issue de l'opération, le fil se détend, le diamètre d'enroulement augmente et le pas d'enroulement varie aussi, mais dans une moindre mesure. S'il s'agissait de réaliser ainsi un ressort de traction ou de compression, on obtiendrait à peu près n'importe quoi. Pour un ressort de torsion dont le fil travaille en flexion, cela marche assez bien car la raideur dépend essentiellement, pour un diamètre de fil donné, de la longueur totale qui a été enroulée.
Ressorts métalliques divers[modifier | modifier le wikicode]
Rondelles tronconiques[modifier | modifier le wikicode]
Ce type de ressort est fréquemment utilisé lorsque l'on souhaite une faible flexibilité sous forte charge. On le trouve couramment dans le commerce sous la désignation de rondelle BELLEVILLE.

Outre leur faible coût, ces rondelles ont l'avantage de pouvoir être associées de diverses manières, ce qui permet non seulement d'obtenir la raideur souhaitée pour l'ensemble, mais encore de créer des systèmes à raideur variable. Les formules donnant la résistance et la déformation de ces rondelles sont très complexes et sans intérêt pratique puisque généralement ces produits sont achetés dans le commerce. Toutefois, certaines rondelles spéciales, possédant des caractéristiques particulières, peuvent être fabriquées à la demande. La rondelle élémentaire a un diamètre intérieur d, un diamètre extérieur D, une épaisseur e et une hauteur à vide H. La flèche maximale sous charge vaut : h = H - e
Condition de résistance[modifier | modifier le wikicode]

Les rondelles BELLEVILLE sont généralement calculées pour que l'on puisse les aplatir complètement sans les déformer de façon permanente. Il existe donc une charge P dite charge d'aplatissement. Au-delà de cette valeur, la rondelle ne se déforme pratiquement plus et elle peut en fait supporter des charges très élevées sans le moindre risque de rupture, comme le ferait une rondelle plate ordinaire. Il est donc pratiquement impossible de surcharger les rondelles BELLEVILLE, ce que l'on peut considérer comme un avantage considérable !
On notera cependant que ces rondelles présentent, lorsqu'elles sont serrées, une circonférence intérieure travaillant en compression, et l'extérieur étant en traction. La circonférence extérieure est donc très sensible à l'effet d'entaille : tout défaut (fissures, oxydation, ...) pourra servir d'amorce à une rupture qui se propagera de la circonférence extérieure vers l'intérieur. Comme cette surface extérieure est également la plus exposée, on évite donc d'employer ce montage dans des milieux sévères ou pour des applications exigeant une grande fiabilité.
Condition de déformation[modifier | modifier le wikicode]
Les rondelles les plus courantes ont une déformation presque linéaire, de sorte que la raideur peut être exprimée par :
Cependant, il est possible de fabriquer des rondelles ayant des propriétés élastiques très différentes, comme le montrent les courbes charge-flèche en fonction du rapport h/e.
Association de rondelles[modifier | modifier le wikicode]
Les rondelles peuvent être empilées dans le même sens, en « paquets ». Un paquet de n rondelles identiques n'a que la flèche maximale h d'une rondelle unique, mais sa charge d'aplatissement est n P ; si k est la raideur, supposée constante, d'une rondelle unique, la raideur K de l'ensemble est donc :
Si les rondelles sont empilées en opposition, la charge d'aplatissement est la même que pour une rondelle unique, tandis que les flèches s'ajoutent. Un empilement de n rondelles en opposition a donc pour raideur :
Diverses combinaisons sont présentées ci-dessous, permettant d'obtenir des ressorts aux caractéristiques presque linéaires s'ils sont réalisés avec le bon type de rondelles. Remarquons qu'il est facile d'ajuster la raideur d'un empilement contenant un nombre suffisamment important de rondelles.
Si par exemple nous empilons en opposition deux paquets de deux rondelles, la flèche maximale sera 2h et la charge d'aplatissement 2P ... le résultat sera un ressort de même raideur qu'une rondelle unique mais de performances plus étendues. Voici quelques combinaisons usuelles :
Les figures ci-dessous montrent deux limiteurs de couple dans lesquels l'élément élastique est constitué par des rondelles Belleville.
-
limiteur de couple à billes Ringspann
D'autres dispositions sont plus subtiles. Si, par exemple, nous mettons en opposition un paquet de deux rondelles avec une rondelle unique, la flèche maximale sera 2h et la charge d'aplatissement 2P, comme dans le cas précédent. Par contre, la courbe caractéristique sera une ligne brisée et non plus un segment de droite. En effet, il faut considérer deux phases distinctes lors de la compression du système :
- lorsque la charge varie de 0 à P les trois rondelles se déforment linéairement et en même temps, mais pas de la même façon : le paquet de deux rondelles se déforme deux fois moins que la rondelle unique. Lorsque la charge atteint P, la flèche vaut 1,5 h car la rondelle seule se trouve complètement aplatie tandis que le paquet de deux n'est qu'à mi-course. Pendant cette phase la raideur est :
- lorsque la charge varie de P à 2 P la rondelle unique est complètement aplatie et n'intervient plus, la flèche augmente de 0,5 h et la raideur est celle d'un paquet de deux rondelles, soit :
Une telle association donne un ressort d'abord relativement flexible, puis très raide. On peut évidemment inventer de nombreuses autres combinaisons !
Diaphragmes[modifier | modifier le wikicode]
Divers fabricants proposent des pièces standardisées qui fonctionnent comme les rondelles Belleville tout en étant beaucoup moins raides. Il faut consulter leurs catalogues pour plus d'informations.
On voit ci-dessous un ressort-diaphragme en coupelle à lames multiples utilisé en particulier dans certains embrayages, une rondelle Ringspann et un diaphragme conique Borrelly :
Ressorts annulaires[modifier | modifier le wikicode]
On réalise des systèmes élastiques à hauteur variable en empilant des bagues coniques. De tels systèmes, soumis à une charge axiale, diminuent de longueur en raison de la dilatation des bagues extérieures et de la contraction des bagues intérieures. Les anneaux intérieurs « mâles » pénètrent dans les anneaux extérieurs « femelles » :
Lorsque la compression du ressort est très forte, les anneaux intérieurs (ou extérieurs) finissent par entrer en contact entre eux. Lorsque tous les anneaux sont ainsi en contact, cela impose une compression maximale.
Les frottements très importants qui se produisent entre les bagues sont tels que la force axiale fournie lors de la détente de l'empilement est très largement inférieure à celle qui était appliquée lors de la mise en charge. Ils provoquent une perte d'énergie considérable qui correspond à la zone hachurée du diagramme représentant le cycle compression-détente. On peut mettre à profit cette particularité dans certains mécanismes comme les tampons du matériel roulant ferroviaire, où ils contribuent à absorber les chocs.
En remplaçant une ou plusieurs des bagues intérieures complètes par des bagues fendues, on peut donner à ce ressort un tout autre comportement : il devient « mou » au début de sa déformation, puis de plus en plus « dur » :
Rondelles ondulées[modifier | modifier le wikicode]
Il en existe de multiples types. On les utilise par exemple pour rattraper des jeux ou pour remplacer les ressorts à boudin comme ressorts de rappel. Voici quelques exemples industriels (doc. SMALLEY) :
La figure de gauche représente l'utilisation de rondelles élastiques dans un limiteur de débit. Plus la pression de fluide à l'entrée est forte, plus le piston se déplace vers la droite et plus les orifices de sortie du fluide se trouvent rétrécis. Le dessin de droite montre un raccord rapide de tuyauterie avec un système de retenue par billes. Les rondelles assurent le verrouillage des billes qui retiennent la partie mâle (non représentée).
-
Smalley Nested Wave Spring
-
Smalley Wave Spring
Pièces élastiques diverses[modifier | modifier le wikicode]
Il existe d'innombrables pièces élastiques jouant le rôle de ressorts dans beaucoup de mécanismes, avec des caractéristiques spécifiques et donc en-dehors de la production standardisée. Voici par exemple une pièce en fil galbé :
Les joints d'étanchéité Bal-Seal possèdent des ressorts à spires aplaties qui leur donnent l'élasticité radiale nécessaire pour un bon contact intérieur et extérieur sur les pièces à étancher :
De nombreux ressorts sont réalisés à partir de feuillard dit « tôle bleue » découpé et mis en forme à la demande. Pour le matériel électrique, lorsque l'on a besoin de pièces à la fois élastiques et bonnes conductrices, on fait appel dans les mêmes conditions au cuivre au béryllium :
Signalons enfin la possibilité de réaliser des pièces plus complexes par découpage, emboutissage et formage :

Ressorts en élastomères[modifier | modifier le wikicode]
Outre le fait qu'il est beaucoup plus faible que celui des métaux, le module d'élasticité des caoutchoucs varie avec la forme de l'élément élastique, qui varie elle-même beaucoup avec la charge appliquée. Il est donc pratiquement impossible d'obtenir des caractéristiques linéaires, surtout dans le cas des ressorts de compression.
En fait, cette particularité est souvent mise à profit pour amortir les vibrations entre les deux éléments reliés par le ressort. En effet, l'énergie apportée par la vibration sinusoïdale d'un élément va se trouver répartie, à la sortie, entre la fréquence fondamentale et ses harmoniques, qui en sont des multiples. Or, on sait que plus une vibration a une fréquence élevée et plus elle est facile à amortir.
Si les ressorts en caoutchouc ont une très bonne résistance aux sollicitations dynamiques, ils subissent aussi, à des degrés divers, les effets de l'hystérésis mécanique qui fait que la reprise de leur forme initiale n'est pas instantanée après qu'ils ont subi une déformation. Ceci est dû au comportement toujours plus ou moins viscoélastique de ces matériaux. N'oublions pas que le phénomène d'hystérésis est avant tout un phénomène de retard d'un effet sur une cause.
Cet hystérésis provoque la transformation en chaleur, à l'intérieur même du matériau visco-élastique, d'une partie de l'énergie fournie. Le caoutchouc étant mauvais conducteur de la chaleur, il en résulte un échauffement interne susceptible, pour des mécanismes mal étudiés, d'entraîner la dégradation ou la destruction du caoutchouc. Signalons aussi que le module d'élasticité varie avec la température, avec la vitesse d'application de la charge, et qu'il évolue au cours du temps en raison du vieillissement du matériau.
Tous ces facteurs interagissent et dans ces conditions, on comprend facilement que les caractéristiques d'un ressort en caoutchouc ne peuvent pas être définies avec la même précision que celles d'un ressort métallique. Par contre, il est relativement facile d'obtenir des modules d'élasticité et des capacités d'amortissement très variables, en jouant sur la nature et les proportions des constituants du mélange à utiliser.
Ressorts en matériaux composites[modifier | modifier le wikicode]
Ressorts à gaz[modifier | modifier le wikicode]
Objets divers mettant à profit l'élasticité des matériaux[modifier | modifier le wikicode]
C'est un fil métallique enroulé en spirale qui constitue cette fibule antique (période du Halstatt) et permet, par sa déformation, de l'ouvrir ou de la fermer sans faire appel à une construction en plusieurs éléments assemblés :

Images en réserve[modifier | modifier le wikicode]
Fabricants français[modifier | modifier le wikicode]
- SFAM : http://www.sfam.com
- CFT Industrie : http://www.cintrage-fil-tube.com
- RPI LEFEVERE INDUSTRIE : http://www.rpi-cie.com
- RHD : http://www.rhd.fr
- Ressorts Masselin : http://ressorts-maselin.com
- Groupe Simonin : http://www.groupe-simonin.com
- Pommeuse Ressorts : http://pommeuse.ressorts.org - 22 Allée de la ferme - 77515 POMMEUSE - tel 01 64 65 49 95 - pommeuse@ressorts.org
- RVF : http://www.rvf.com
- STYRIA RESSORTS: http://www.styriagroup.com
- VIT Ressorts : http://www.vit-ressort.com/ - Chemin des vignes – BP3 – 05400 Veynes Tél. 04 92 58 17 92 – Fax 04 92 58 17 62 – contactnews@vit-ressort.com
























































































![{\displaystyle L={\sqrt[{5}]{\frac {6\,P\,f^{3}\,E^{3}}{\sigma _{adm}^{4}\,n^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea09a6b82ce656157f4a56e384c2e727d0f8b2e4)