Électricité/Le passage du courant dans un solide : la résistance
Le courant électrique peut se déplacer dans le vide, mais il peut aussi traverser des solides, des liquides, des gaz ou toute autre forme de matière. Mais tous les matériaux ne laissent pas passer le courant de la même manière. Il est intéressant de voir comment les solides et autres matériaux réagissent au courant électrique. Dans ce qui va suivre, nous allons d'abord voir la différence entre isolants et conducteurs, avant de voir dans quel sens se propage le courant dans le matériau. Nous allons aussi voir une propriété électrique particulièrement importante : la résistance.
Les conducteurs et isolants[modifier | modifier le wikicode]
Il semble évident que les charges n'ont aucune difficulté à se déplacer dans le vide. Mais les matériaux solides, liquides ou gazeux ne sont pas dans le même cas. Certains peuvent laisser les charges les traverser facilement, tandis que d'autres vont opposer une résistance au déplacement des charges. Cette différence de comportement est appelée la conductibilité : plus un matériau se laisse traverser par les charges, plus il est conducteur. En théorie, cette conductibilité est un paramètre continu, allant entre deux extrêmes : d'un côté le vide qui n’entraîne aucune résistance et de l'autre les isolants parfaits qui ne laissent passer aucun courant. Mais en pratique, et malgré l'existence de ce continuum, les physiciens classent les matériaux en quelques catégories assez simples : les matériaux conducteurs, isolants, supraconducteurs et semi-conducteurs.
| Type de matériau | Conductibilité | Description | Exemple |
|---|---|---|---|
| Isolants, aussi appelés diélectriques | Conductibilité nulle | Le courant ne passe pas, quelle que soit la situation. | Verre, bois, certains plastiques, autres. |
| Semi-conducteurs | Conductibilité variable selon la situation. | Le courant ne passe pas en temps normal, mais traverse le matériau quand on l'éclaire ou qu'on le chauffe. | Silicium, Germanium, autres. |
| Conducteurs | Conductibilité importante. | Le courant passe quelle que soit la situation, dans une certaine mesure. | Métaux, eau (non-pure), etc. |
| Supraconducteur | Conductibilité maximale, infinie. | Ces matériaux n'opposent aucune résistance au passage du courant. | Hélium liquide, quelques céramiques à basse température, etc. |
Les sous-types de conducteurs[modifier | modifier le wikicode]
De nombreux matériaux sont d’excellents conducteurs et laissent le courant les traverser très facilement, bien plus que pour les autres conducteurs. On peut les classer en deux types : les métaux et les solutions conductrices appelées électrolytes. Les métaux conducteurs les plus connus sont le fer, l'argent, le cuivre, l'or, le mercure ou l'aluminium. Les électrolytes sont moins utilisés, mais certains sont très connus, le cas le plus intuitif étant de loin l'eau.
Les semi-conducteurs sont des intermédiaires entre les isolants et les conducteurs "vrais". Tous les semi-conducteurs ont une résistance qui diminue quand on les chauffe, plus rarement quand on les déforme ou qu'on les soumet à un fort champ électrique. Et cette diminution de résistance est suffisante pour les faire passer d'isolants à conducteurs. Dans le cas des semi-conducteurs intrinsèques, la résistance diminue uniquement en fonction de la température, quand on les chauffe. Mais il existe aussi des semi-conducteurs extrinsèques, dont la résistance varie indépendamment de la température. De nos jours, les semi-conducteurs intrinsèques sont peu utilisés dans la fabrication de composants électriques/électroniques. Il faut dire qu'il faut les porter à haute température pour qu'ils deviennent conducteurs, parfois au-delà de la centaine de degrés. Les semi-conducteurs extrinsèques n'ont pas ce problème, ce qui les rend plus facilement utilisables. L'électronique est friande de semi-conducteurs, qui forment la base de certains composants comme les diodes ou les transistors. Sans eux, pas d'ordinateurs, pas de téléphones portables, pas de consoles de jeux. Le plus utilisé dans les circuits électroniques est de loin le Silicium. Il faut dire qu'il s'agit d'un matériau abondant à la surface de la Terre, qui est d'ailleurs le composant majeur de la croute terrestre, à hauteur de 60%.
Les supraconducteurs ne sont utilisés que dans des circonstances très particulières, qui demandent des investissements conséquents. Le fait est que les supraconducteurs connus ne fonctionnent qu'à de très basses températures, proches du zéro absolu (-273.15°c). Au-delà, ils cessent d'être supraconducteurs et deviennent soit isolants, soit simples conducteurs. Les raisons à cela sont très complexes et font intervenir la physique quantique et la physique du solide. Toujours est-il que l'on ne peut pas les utiliser sans un système de refroidissement onéreux et impraticable. Les physiciens cherchent cependant à comprendre le phénomène de supraconductivité, afin d'obtenir des supraconducteurs à température ambiante. Mais sans succès pour le moment.
Les porteurs de charges[modifier | modifier le wikicode]
Les conducteurs le sont parce qu'ils contiennent des charges qui peuvent se déplacer librement dans le matériau. Ces charges libres, appelées porteurs de charge, peuvent être mises en mouvement sous l'effet d'une force quelconque, et former ainsi des courants électriques. Plus un conducteur est riche en porteurs de charge, plus sa conductibilité sera importante. Les isolants ne possèdent aucun porteur de charge. Leur absence fait que le courant ne peut pas traverser le matériau : si on met une tension aux extrémités d'un diélectrique, le courant ne traverse pas l'isolant. Pour être un isolant, les électrons doivent tous faire partie d'atomes, ils ne doivent pas être libres de leurs mouvements. Même chose pour les ions, qui ne doivent pas pouvoir s'éloigner de leur position d'équilibre dans le cristal/solide.
Dans les métaux, les porteurs de charge sont des électrons, séparés des atomes, qui portent le nom d'électrons libres. Le passage d'un courant dans un métal fait donc intervenir des flux d'électrons libres dans le métal, à savoir un courant de charges négatives.
Dans les semi-conducteurs, ce sont aussi des électrons qui se déplacent. Au repos, les semi-conducteurs ne contiennent presque pas de porteurs de charges, tout du moins pas assez pour être conducteurs. Ils se comportent donc comme des isolants. Quand on les chauffe/déforme/..., les électrons des atomes vont acquérir de l'énergie, suffisamment pour qu'ils se séparent des atomes. Ces électrons vont alors pouvoir circuler librement dans le matériau et servir de porteurs de charges. Ils deviennent donc conducteurs. Ce phénomène a aussi lieu dans les conducteurs et les isolants normaux, à la différence que l'énergie pour arracher les électrons n'est pas la même. Dans les isolants, il faut fournir beaucoup plus d'énergie pour arracher les électrons aux atomes, comparé à ce qui est demandé à un semi-conducteur. Là où il faudrait des températures proches du point de fusion pour rendre un isolant conducteur, les semi-conducteurs le deviennent à des températures beaucoup plus basses. Pour les conducteurs, il existe déjà des électrons libres qui servent de porteurs de charges.
Dans les électrolytes, le courant est composé non d'électrons, mais d'ions (des atomes auxquels on a enlevé ou ajouté des électrons). Il n'est pas rare que les électrolytes contiennent à la fois des charges positives et des charges négatives. Le courant est alors composé d'un courant de charges négatives et d'un second courant de charges positives. À ce propos, l'eau pure n'est pas franchement conductrice, vu qu'elle ne contient que des molécules d'eau et absolument aucun ion. L'eau normale, celle que l'on boit tous les jours, contient des ions dissous qui la rendent conductrice. On y trouve toujours des ions sodium, calcium, potassium, et bien d'autres. Pour l'eau salée, le sel (qui est, rappelons-le, du chlorure de sodium) peut se dissoudre en ions sodium et chlore qui rendent l'eau encore plus conductrice que la normale. Les ions chlore et sodium peuvent se déplacer librement dans l'eau, ce qui permet de transmettre un courant. Pour résumer, l'eau salée conduit mieux l'électricité que l'eau normale, vu qu'elle contient plus d'ions.

La résistance et la conductance[modifier | modifier le wikicode]
On vient tout juste de le voir, un conducteur va laisser plus ou moins bien passer un courant. Cette propriété a reçu un nom de la part des physiciens et techniciens : ils l’appellent la résistance électrique. Plus un matériau s'oppose au passage d'un courant, plus sa résistance électrique est grande. Définir la résistance d'un appareil électrique ou d'un morceau de conducteur est assez simple. Il suffit de placer une tension à ses extrémités et de mesurer le courant qui le traverse. La résistance n’est autre que le rapport entre la tension et le courant.
La conductance est une quantité directement dérivée de la résistance : c'est son inverse ! Son utilité principale est de simplifier certains calculs.
L'ohm et le siemens[modifier | modifier le wikicode]
La résistance est souvent notée avec la lettre R et elle se mesure en ohms (). Un ohm est égal à un volt divisé par un ampère.
Quant à la conductance, elle se note avec la lettre G et est mesurée en siemens. Un siemens est égal à l'inverse d'un ohm, à savoir que cela vaut un ampère divisé par un volt.
La loi d'Ohm[modifier | modifier le wikicode]

La définition de la résistance peut aussi se reformuler sous la forme de l'équation suivante, connue sous le nom de loi d'Ohm. Cette loi est de loin une des plus importantes de ce cours. C'est de loin une des trois lois de base de l’électricité. Vous devez donc la connaitre par cœur pour poursuivre la lecture. Le schéma de droite donne toutes les équations dérivées de cette loi d'Ohm, toutes ses reformulations.
Il faut noter que la résistance et la conductance ne valent que quand on alimente le conducteur avec un courant et une tension constants. Quand on utilise un courant et une tension variables, la relation entre tension et intensité n'est pas linéaire/proportionnelle. Il existe bien une relation entre tension et intensité, mais celle-ci fait intervenir deux autres paramètres appelés capacité et inductance. De plus, l'équation entre intensité et tension fait intervenir des calculs assez compliqués comme des dérivées et des intégrales.
La puissance dissipée par un courant dans un conducteur[modifier | modifier le wikicode]

Tout courant qui parcourt un conducteur va rencontrer de la résistance, qui va lui faire perdre son énergie sous forme d'énergie thermique. Le fait que les conducteurs chauffent quand ils sont parcourus dans un courant porte un nom : c'est l'effet Joule. On peut calculer la puissance ainsi perdue en utilisant la relation vue il y a quelques chapitres :
On peut alors utiliser la loi d'Ohm pour déterminer la tension aux bornes de la résistance. Celle-ci vaut, par définition : . En faisant le remplacement, on a :
Bien d'autres formules peuvent être déduites en combinant la loi d'Ohm et la définition de la résistance. Celles-ci sont résumées dans le cadrant à votre droite.
La résistivité et la conductivité[modifier | modifier le wikicode]
La résistance et la conductance dépendent non seulement du matériau, mais aussi du volume du bloc de conducteur. Pour nous faire comprendre, nous allons prendre deux fils composés du même matériau, mais qui ont un diamètre ou une longueur différente. Ces deux fils n'ont pas forcément la même résistance. Par exemple, prenons deux fils de même diamètre : le fil le plus long aura une résistance supérieure. Intuitivement, cela se comprend : plus le fil est long, plus le courant devra traverser de matériau conducteur et plus la résistance sera grande. Même chose pour des fils de même longueur, mais de diamètre/section différentes. Dans ce cas, la résistance dépend inversement de la section : plus elle est petite, plus la résistance est grande.

Ces deux effets sont plus faciles à comprendre avec une analogie hydraulique. Premièrement, remplaçons le courant par un flux d'eau, ce qui est assez logique pour ce dernier : entre un flux d'électrons et un flux de molécules d'eau, il n'y a qu'un pas. La résistance est alors analogue à un conduit hydraulique qui est parcouru par le flux d'eau. Ce conduit a une résistance hydraulique qui traduit le fait que le conduit oppose une résistance au passage de l'eau. Cette résistance hydraulique provient des frottements de l'eau sur les parois, ce qui est un point de différence avec le flux des électrons dans un conducteur, mais passons ce détail sous silence. Plus le conduit est long, plus les frottements ralentiront le flux d'eau et augmenteront la résistance hydraulique. Pour l'électricité, c'est la même chose : la longueur du fil augmente la résistance électrique. Ensuite, plus la section du conduit est grande, plus le courant aura une intensité importante, comme on l'a vu dans la section sur la densité de courant. Dans les deux cas, le schéma sur votre droite illustre ces deux effets.
Définitions de la résistivité et la conductivité[modifier | modifier le wikicode]
Il est possible de définir une valeur, similaire à la résistance, mais indépendante de la longueur du fil ou de son diamètre. Cette grandeur porte le nom de résistivité électrique et son inverse est appelée la conductivité électrique. Il s'agit d'une résistance par unité de longueur et par unité de surface (ou d'une conductance, pour la conductivité). Il est raisonnable de supposer que la résistance est proportionnelle à la longueur du fil, ainsi qu'inversement proportionnelle à sa section. Dans ce cas, on peut définir la résistivité avec cette équation, où :
- est la résistivité ;
- est la conductivité ;
- est la longueur du fil ;
- est la section du fil.

La loi d'Ohm locale[modifier | modifier le wikicode]
Il faut noter que l'on peut reformuler la loi d'Ohm en utilisant la résistivité, la densité de courant et le champ électrique. Pour cela, partons de la loi d'Ohm :
On injecte alors les relations et .
Ce qui se reformule en :
Le terme de gauche n'est autre que le champ électrique, ce qui donne :
On peut réorganiser les termes pour mettre en avant le courant :
On obtient alors une formulation assez générale de la loi d'Ohm, appelée loi d'Ohm locale. Celle-ci est identique à la loi d'Ohm normale, si ce n'est qu'on a remplacé la tension par le champ électrique, l'intensité par la densité de courant et la résistance par la résistivité/conductivité.
La physique de la conductivité et de la résistance[modifier | modifier le wikicode]
Expliquer l'origine de la résistance revient à expliquer pourquoi la vitesse des charges est proportionnelle au champ électrique dans un matériau, quelle est l'origine de la mobilité des porteurs de charge. Divers modèles ont été inventés pour expliquer ce comportement, mais il ne peut pas exister un modèle général de la conductivité. En effet, les mécanismes de la conduction électrique sont différents selon que l'on parle d'un métal, d'un électrolyte, d'un semi-conducteur, ou d'un autre matériau. Parmi les théories inventées par les physiciens, certaines ne valent que pour les métaux, d'autres fonctionnent pour les matériaux solides, d'autres seulement pour les électrolytes, etc. Le plus simple est de loin le modèle de Drude, qui explique pas trop mal la résistance des métaux malgré son côté extrêmement rudimentaire. Mais il n'est pas le seul et d'autres modèles bien plus complexes existent. Quel dommage qu'ils utilisent tous la physique quantique : nous ne pouvons donc pas en parler dans ce cours...
La mobilité : le lien entre champ électrique et vitesse des charges[modifier | modifier le wikicode]
À ce propos, rappelons que la densité de courant dans un conducteur est égale à :
- , avec v la vitesse des charges et la densité de charge (la charge électrique par unité de volume).
En combinant avec la loi d'Ohm locale , on trouve :
On peut isoler la vitesse des électrons :
On voit que la vitesse des charges est proportionnelle au champ électrique. Le coefficient de proportionnalité est appelé la mobilité des porteurs de charge et est noté . L'équation précédente est reformulée comme suit en utilisant la mobilité :
- , avec .
On utilise alors l'équation , qui dit que le champ électrique est proportionnel à la force électrique qui met en mouvement les charges électriques :
On a donc :
On voit que la vitesse des électrons est proportionnelle à la force à laquelle ils sont soumis. Ce qui est étrange. Les lois de Newton nous disent en effet que la force est proportionnelle à l'accélération, pas la vitesse. Il y a donc anguille sous roche. Mais ce phénomène où une force est proportionnelle à la vitesse n'est cependant pas rare en physique. En réalité, c'est signe qu'il y a des forces de frottements qui sont impliquées.
On a un exemple de ce type avec la chute des corps. Dans le vide, l'accélération d'un corps est proportionnelle à la force appliquée. Mais dans l’atmosphère, les corps subissent des forces de frottement qui font que la vitesse de chute sature, elle cesse d'augmenter au-delà d'un certain stade. Et la vitesse atteinte, la vitesse terminale, est proportionnelle à la force. D'autres situations avec des frottements font elles aussi intervenir une relation entre une vitesse et une force. La résistance est donc le résultat d'une sorte de force de frottement : les électrons sont gênés dans leur passage par les atomes du matériau.
Le modèle classique général[modifier | modifier le wikicode]
Quand on soumet un électron libre à une tension, à un champ électrique, il accélère. Ce champ électrique va lui faire subir une force égale à :
Cette force lui donnera une accélération égale à :
Ce qui lui donne une vitesse de :
On remarque que l'électron voit sa vitesse augmenter sans cesse, ce qui ne donne pas une intensité constante. C'est ce qui se passe dans les super-conducteurs, dans lesquelles la résistance est nulle. Les charges accélèrent tant que le champ électrique est constant. Le seul moyen d'éviter cela est d'ajouter une force de frottement , qui ralentit l'électron, qui est l'origine de la résistance. Le comportement de l'électron est alors défini par l'équation suivante, un simple bilan des forces :
La force de frottement est proportionnelle à la vitesse du fluide, dans le cas hydraulique. Par analogie, la force de freinage est proportionnelle à la vitesse des charges : .
À l'équilibre, on suppose que la vitesse de l'électron est stable, sans quoi le courant serait sans cesse croissant avec le temps. On a alors : , ce qui permet de simplifier fortement l'équation précédente.
Quelques manipulations nous donnent l'équation suivante. Celle-ci nous dit que le champ électrique et la vitesse des charges sont bien proportionnels.
On trouve donc une mobilité et une conductivité constantes, égales à :
- et , avec .
Ce modèle pointe deux sources à la résistance : le nombre de porteurs de charges du matériau et le coefficient de friction. Plus le nombre de porteurs de charges d'un matériau est grand, plus sa conductivité sera importante. La différence entre isolants et conducteurs se situe surtout au niveau du nombre de porteurs de charges : les conducteurs le sont parce qu'ils ont un grand nombre de porteurs de charges, alors que les isolants le sont parce qu'ils n'en ont pas. Pour les semi-conducteurs, la situation est intermédiaire : le nombre de porteurs de charges est très faible en temps normal, mais augmente fortement avec la température, l’éclairement, ou d'autres paramètres physiques. Par exemple, chauffer des semi-conducteurs arrache des électrons aux atomes, les transformant en électrons libres. De ce fait, leur conductivité augmente avec la température, ou autre. Mais il faut aussi signaler que la température ou d'autres paramètres physiques peuvent influencer la mobilité des porteurs de charges, comme nous allons le voir dans la section suivante.
Le modèle de Drude des métaux[modifier | modifier le wikicode]


L'intérieur d'un métal, et d'un solide de manière générale, est assez compliqué à décrire en équations. Pour simplifier la modélisation, le modèle de Drude part du principe que les porteurs de charge des métaux sont des électrons, les atomes et ions étant immobiles. Ces électrons sont dits libres, ce qui veut dire que l'on néglige les interactions des électrons avec les atomes du solide : on part du principe que ces interactions, bien qu'existantes, ne sont pas suffisamment fortes pour être prises en compte. De plus, les électrons sont indépendants dans le sens où l'on néglige aussi les interactions entre électrons, qui sont censés se repousser du fait de leur charge.
Dans le modèle de Drude, la force de freinage de l'électron est causée par les collisions des électrons avec les atomes qui se trouvent sur leur trajectoire. Lors d'une collision, l'électron perd son énergie cinétique, qui est transmise intégralement à l'atome choqué. Un électron va parcourir une certaine distance entre deux collisions, la distance moyenne étant appelée le libre parcours moyen. De même, le temps moyen entre deux collisions est appelé le temps de relaxation. Le mouvement d'un électron dans le métal est illustré dans le schéma de droite.
Entre deux collisions, l'électron est accéléré par le champ électrique, par la tension aux bornes du bout de métal. Au vu des hypothèses, la vitesse moyenne de l’électron est de :
On voit que la vitesse de l’électron est bien proportionnelle au champ électrique. La mobilité déduite du modèle de Drude vaut donc :
La conductivité qui en découle est la suivante :

Le modèle de Drude a cependant de nombreux défauts, qui font qu'il ne s'agit que d'une approximation assez grossière. Déjà, le libre parcours moyen mesuré expérimentalement ne colle pas au modèle. Les valeurs expérimentales donnent, une fois injectées dans le modèle de Drude, des résistances 100 à 1000 fois trop élevées comparé à la réalité. De plus, le libre parcours moyen semble varier en fonction de l'énergie des électrons, chose que le modèle de Drude ne prend pas en compte. De plus, le modèle de Drude ne permet pas d'expliquer un grand nombre de phénomènes. Par exemple, il ne permet pas vraiment d'expliquer la semi-conductivité, pas plus qu'il ne permet d'expliquer la variation de la résistance avec la température. À ce propos, parlons un peu plus en détail de cette dépendance température-résistance.
L'influence de la température[modifier | modifier le wikicode]

Pour la plupart des conducteurs, la résistivité ne dépend pas de la tension ou du courant. Elle ne dépend que du matériau conducteur, mais aussi de la température ou d'autres propriétés physiques. L'influence de la température est intéressante à étudier, car elle commande la résistance des matériaux d'une manière assez importante. Déjà, la variation thermique de la résistance dépend aussi du matériau. Notamment, l'influence de la température dépend selon que l'on parle d'un conducteur, d'un semi-conducteur, d'un supraconducteur ou d'un isolant. L'effet de la température est résumé, dans les grandes lignes, par la loi de Matthiessen, qui dit : la résistance des conducteurs augmente avec la température, alors que celle des isolants diminue. Les semi-conducteurs se comportent dans une certaine mesure comme des isolants. Pour résumer :
- Les supraconducteurs ont une résistance nulle, jusqu'à une certaine température où ils deviennent simplement conducteurs.
- La résistance des métaux/conducteurs augmente linéairement avec la température, sauf pour les basses températures, où elle ne descend pas en-dessous d'une valeur minimale.
- La résistance des semi-conducteurs diminue avec la température, mais ne descend pas en dessous d'une valeur minimale.
- La résistance des isolants diminue avec la température, quelle que soit la température.
 |
 |
Pour les conducteurs, la relation entre résistance et température est grosso modo affine.
Pour les semi-conducteurs intrinsèques, il est possible de démontrer que la résistance et la température suivent la loi suivante :
Le sens du courant[modifier | modifier le wikicode]
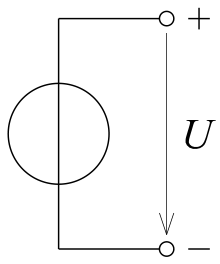
D'ordinaire, les charges se déplacent dans un fil électrique, ce qui fait que le mouvement des charges est guidé, contraint par le fil. Supposons que l'on mette un excès de charges positives à un bout du fil et un excès de charges négatives à l'autre bout. Cette situation peut vous sembler étrange, mais c'est ainsi que fonctionnent les piles, batteries ou autres générateurs de tension/courant. Elles possèdent deux bornes sur lesquelles on connecte des fils électriques : une borne positive (chargée en charges positives) et une borne négative (chargée en charges négatives). Entre ces deux bornes, il existe une tension qui dépend du déséquilibre en charges entre les deux bornes. Imaginons qu'on connecte les deux bornes avec un fil : dans quel sens vont se déplacer les charges dans le fil ?
Cette question a posé pas mal de problèmes aux premiers savants qui se sont penchés sur le sujet. En théorie, les charges positives ou négatives vont du bout où elles sont en excès vers celui où elles sont en déficit. Mais on ne sait pas si ce sont les charges positives qui vont se déplacer ou les charges négatives. Cela laisse trois possibilités :
- seules les charges positives se déplacent, ce qui fait que le courant va de la borne positive vers la borne négative ;
- seules les charges négatives se déplacent, ce qui fait que le courant va de la borne négative vers la borne positive ;
- les charges positives et négatives se déplacent toutes les deux, ce qui fait que le courant réel va dans les deux sens.
Le sens conventionnel du courant[modifier | modifier le wikicode]
Avant de savoir quel était le sens réel du courant, les scientifiques pensaient que les charges qui se déplaçaient dans les métaux étaient des charges positives. C'était avant que l'on découvre l'électron et le fait que les métaux en sont très riches. En conséquence, ils ont pris pour convention que le courant va de la borne positive vers la borne négative. Vu qu'il s'agit d'une convention assez arbitraire, ce sens a reçu le titre de sens conventionnel du courant.
 |
 |
Le sens réel du courant[modifier | modifier le wikicode]
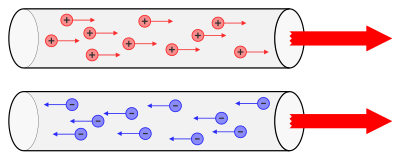
En réalité, le sens réel du courant dépend du matériau et n'est pas le même selon qu'on parle des électrolytes, des semi-conducteurs ou des métaux. Dans les métaux, les charges en mouvement sont négatives : elles vont donc de la borne négative vers la borne positive. Dans les électrolytes, les ions peuvent être chargés aussi bien négativement que positivement. Les ions positifs vont donc se déplacer dans le sens conventionnel, alors que les ions négatifs vont bouger dans l'autre sens. Ces deux sont relativement indépendants et se déplacent en sens inverse.
 |
 |




















































![{\displaystyle R=R_{0}\cdot \left[1+\alpha \cdot \left(T-T_{0}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c2e857d7dc9fd42628d94f86a002af7f2f3ca2b)
