Fonctionnement d'un ordinateur/Les circuits pour l'addition et la soustraction
Tout circuit de calcul peut être conçu par les méthodes vues dans les chapitres précédents. Mais les circuits de calcul actuels manipulent des nombres de 32 ou 64 bits, ce qui demanderait des tables de vérité démesurément grandes : plus de 4 milliards de lignes en 32 bits ! Il faut donc ruser, pour créer des circuits économes en transistors et rapides. Dans ce chapitre, nous allons voir les circuits capables de faire une addition ou une soustraction, ainsi que quelques circuits spécialisés, comme les additionneurs multi-opérande. Précisons cependant que les constructeurs de processeurs, ainsi que des chercheurs en arithmétique des ordinateurs, travaillent d'arrache-pied pour trouver des moyens de rendre ces circuits de calcul plus rapides et plus économes en énergie. Autant vous dire que les circuits que vous allez voir sont vraiment des circuit qui font pâle figure comparé à ce que l'on peut trouver dans un vrai processeur commercial !
Les circuits pour additionner 2 ou 3 bits[modifier | modifier le wikicode]
Pour rappel, l'addition se fait en binaire de la même manière qu'en décimal. On additionne les chiffres/bits colonne par colonne, une éventuelle retenue est propagée à la colonne d'à côté. La soustraction fonctionne sur le même principe, sur le même modèle qu'en décimal.

En clair, additionner deux nombres demande de savoir additionner 2 bits et une retenue sur chaque colonne, et de propager les retenues d'une colonne à l'autre. La propagation des retenues est quelque chose de simple en apparence, mais qui est sujet à des optimisations extraordinairement nombreuses. Aussi, pour simplifier l'exposition, nous allons voir comment gérer une colonne avant de voir comment sont propagées les retenues. Le fait que les additionneurs soient organisés de manière à séparer les deux nous aidera grandement. En effet, tout additionneur est composé d'additionneurs plus simples, capables d'additionner deux ou trois bits suivant la situation. Ceux-ci gèrent ce qui se passe sur une colonne.
Le demi-additionneur[modifier | modifier le wikicode]
Un additionneur deux bits implémente la table d'addition, qui est très simple en binaire. Jugez plutôt :
- 0 + 0 = 0, retenue = 0 ;
- 0 + 1 = 1, retenue = 0 ;
- 1 + 0 = 1, retenue = 0 ;
- 1 + 1 = 0, retenue = 1.
Un circuit capable d'additionner deux bits est donc simple à construire avec les techniques vues dans les premiers chapitres. On voit immédiatement que la colonne des retenues donne une porte ET, alors que celle du bit de somme est calculé par un XOR. Le circuit obtenu est appelé un demi-additionneur. Le voici :
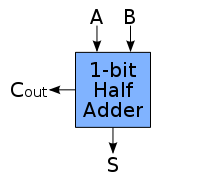 |
 |
L'additionneur complet[modifier | modifier le wikicode]

Si on effectue une addition en colonne, on doit additionner les deux bits sur la colonne, mais aussi additionner une éventuelle retenue. Il faut donc créer un circuit qui additionne trois bits : deux bits de données, plus une retenue. Ce circuit qui additionne trois bits est appelé un additionneur complet. Voici sa table de vérité :
| Retenue entrante | Opérande 1 | Opérande 2 | Retenue sortante | Résultat | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 1 | |
| 0 | 1 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 1 | 0 | |
| 1 | 1 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 |
Il est possible d'en concevoir de plusieurs manières différentes, qui donnent des circuits équivalents, mais avec une organisation en portes logiques différentes. La plus simple consiste à utiliser un tableau de Karnaugh, mais elle donne un résultat sous-optimal. Il existe des circuits équivalents composés seulement de portes NAND ou NOR, plus simples à fabriquer en technologie CMOS.


D'autres méthodes donnent des résultars plus compréhensibles.
L'additionneur complet conçu avec deux demi-additionneurs[modifier | modifier le wikicode]
La solution la plus simple consiste à enchaîner deux demi-additionneurs : un qui additionne les deux bits de données, et un second qui additionne la retenue au résultat. La retenue finale se calcule en combinant les sorties de retenue des deux demi-additionneurs, avec une porte OU. Pour vous en convaincre, établissez la table de vérité de ce circuit, vous verrez que ça marche.

|

|
Avec ce circuit, la somme est calculée avec deux portes XOR l'une à la suite de l'autre. La retenue sortante, quant à elle, est calculée avec un circuit à quatre portes logiques. Les autres versions de l'additionneur complet que nous allons voir sont des dérivés de ce circuit, auquel on a appliqué quelques simplifications. Les simplifications portent surtout sur le circuit de calcul de la retenue. En effet, le calcul de la somme n'est pas simplifié, car on ne peut pas vraiment simplifier deux portes XOR qui se suivent simplement. Par contre, le calcul de la retenue sortante est un cas particulier d'un calcul qui revient souvent en électronique, comme nous allons le voir dans la section suivante.
L'additionneur complet basé sur une porte à majorité[modifier | modifier le wikicode]
Il est possible de calculer la retenue sortante assez simplement, mais à condition de remarquer quelque chose. La retenue sortante vaut 1 seulement si une condition particulière est respectée : au moins 2 des 3 bits d'entrée doivent être à 1. Dit autrement, plus de la moitié des bits d'entrées doivent être à 1. Or,n il existe une porte logique qui fonctionne comme cela : elle met sa sortie à 1 si plus de moitié des entrées vaut 1, et sort un 0 sinon. Cette porte logique complexe s'appelle une porte à majorité. On obtient donc un additionneur en combinant deux portes XOR pour calculer la somme, et une porte à majorité pour la retenue sortante.

L'additionneur complet basé sur un multiplexeur[modifier | modifier le wikicode]
Il est aussi possible de fabriquer un additionneur complet en remplaçant la porte à majorité par un multiplexeur. Le câblage du circuit est cependant totalement différent.
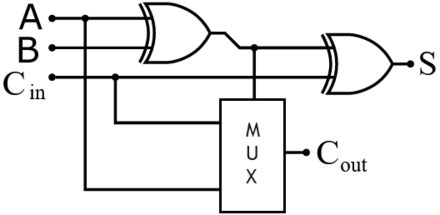
L'additionneur complet basé sur la propagation et la génération de retenue[modifier | modifier le wikicode]
Une autre solution calcule la retenue finale d'une autre manière, en combinant le résultat de deux circuits séparés. Le premier vérifie si l'addition génère une retenue, l'autre si la retenue en entrée est propagée en sortie.
- Une retenue est dite générée si l'addition donne une retenue, quelle que soit la retenue envoyée en entrée (sous-entendu, même si celle-ci vaut 0). Cela arrive quand les bits additionnés valent tous deux 1 : la retenue sera alors de 1, seul le bit du résultat changera. On peut donc calculer si une retenue est générée en faisant un ET entre les deux bits d'entrée.
- Une retenue est propagée si la retenue en sortie est égale à la retenue en entrée. En clair, la retenue n'existe que si on envoie une retenue en entrée. Dans ce cas, la retenue finale vaut 1 quand un seul des deux bits d'entrée vaut 1, et vaut 0 sinon. En clair, on peut déterminer si une retenue est propagée en faisant un XOR entre les deux bits d'entrée.
Vous remarquerez que les signaux P et G sont calculés par le premier demi-additionneur.
Ces deux circuits fournissent deux signaux : un signal G qui indique si une retenue est générée, et un signal P qui indique si une retenue est propagée. En combinant les deux, on peut calculer la retenue finale. Elle vaut 1 soit quand la retenue est générée, soit quand la retenue d'entrée vaut 1 et qu'elle est propagée. Dans les autres cas, elle vaut zéro. La traduction en équation logique dit qu'il suffit de faire un ET entre la retenue d'entrée et le bit P, puis de faire un OU avec le bit G. Le circuit obtenu est strictement identique au circuit précédent.

L'additionneur en Manchester carry chain est une modification de l'additionneur précédent, où les portes logiques en orange dans le schéma précédent sont remplacées par un circuit plus simple, composé de quelques transistors et d'une porte NON. Néanmoins, ce circuit fonctionne en pass transistor logic, avec tous les défauts que cela implique. Le principal est que, vu que la retenue d'entrée est envoyée sur la sortie à travers des interrupteurs/transistors, la tension sur la retenue de sortie est plus faible que la tension de la retenue d'entrée. Ce qui pose des problèmes quand on doit enchainer plusieurs additionneurs de ce type, mais laissons cela pour plus tard. Il existe une version de cet additionneur en logique dynamique, où les transistors sont utilisés comme des condensateurs et sont préchargés avant de faire leurs calculs, mais nous n'en parlerons pas ici.

Il existe des additionneurs qui fournissent les signaux P et G en plus du résultat et de la retenue sortante. Mais il en existe qui ne calculent pas la retenue finale. Par contre, ils calculent les signaux P et G qui disent si l'addition de deux bits génère une retenue, ou si elle propage une retenue provenant d'une colonne précédente. Ils fournissent ces deux signaux sur deux sorties P et G pour indiquer s'il y a propagation et génération de retenue. Un tel additionneur est appelé un additionneur P/G (P/G pour propagation/génération). Ils seront très utiles pour créer des circuits additionneurs comme on le verra plus bas.

|

|
L'additionneur complet basé sur une modification de la retenue sortante[modifier | modifier le wikicode]
Dans les circuits précédents, la retenue sortante et le bit du résultat sont calculés séparément, même si quelques portes logiques sont partagées entre les deux. Une autre méthode, utilisée dans l'unité de calcul de l'Intel 4004 et de l'Intel 8008, fonctionnait autrement. Avec elle, la retenue sortante et calculée en premier, puis on détermine le bit du résultat à partir de la retenue sortante. En effet, le bit du résultat est l'inverse de la retenue sortante, sauf dans deux cas : les trois bits d'entrée sont à 0, où ils sont tous à 1. Dans les deux cas d'exception, le bit du résultat vaut 0, quelque soit la retenue sortante. L'implémentation de cette idée en circuit est assez simple.
Au circuit de calcul de la retenue sortante, il faut ajouter deux circuits, un pour vérifie si tous les bits additionner valent 0, l'autre s'ils valent tous 1. Leur sortie vaut 1 si c'est le cas. Le premier est une simple porte ET, l'autre une porte NOR. Ensuite, on combine le résultat des trois circuits précédents pour obtenir le résultat final. Si un seul des trois circuits a sa sortie à 1, alors la sortie finale doit être à 0. Elle est à 1 sinon. C'est donc une porte NOR qu'il faut utiliser. Le circuit final est donc celui-ci.

- Notons qu'on peut encore optimiser le circuit en fusionnant les deux portes NOR entre elles, mais c'est là un détail.
A ce stade, vous êtes certainement étonné qu'un tel circuit ait pu être utilisé. Il utilise beaucoup plus de portes logiques que le circuit précédent, a une profondeur logique supérieure : il n'a rien d'avantageux. Sauf qu'il était utilisé sur d'anciens processeurs, qui utilisaient des transistors de type TLL, et non des transistors CMOS comme les microprocesseurs actuels. Et avec ces transistors, il est possible d'implémenter des portes logiques complexes, comme les portes ET/OU/NON que nous avons évoqué rapidement dans le chapitre sur les transistors ! Un additionneur complet construit ainsi ne prenait que deux à trois transistors.
Par exemple, l'unité de calcul de l'Intel 8008 utilisait trois transistors : un pour une porte NAND, et deux qui implémentaient chacun une porte ET-OU-NON à plusieurs entrées. Après, l'ALU de ce processeur utilisait un circuit légèrement différent, pour deux raisons. La première est que le circuit prend en entrée l'inverse des bits à additionner, pour des raisons obscures. L'autre est qu'il était capable d'additionner trois bits, mais aussi de faire des opérations logiques dessus, comme des XOR, des ET ou des OU, sans ajouter un seul transistor. le Z-80 utilisait aussi un additionneur de ce type. Et nous reparlerons de ce circuit dans le chapitre suivant.
Les autres implémentations[modifier | modifier le wikicode]
Les implémentations précédentes utilisent des portes logiques, ce qui est simple et facile à comprendre, mais pas forcément le top du top en termes de performances. Mais les additionneurs des processeurs modernes sont nettement plus optimisés que ça. Et pour cela, ils sont optimisés directement au niveau des transistors. Cela permet de les rendre plus rapides, notamment au niveau du calcul de la retenue. Là où l'addition des deux bits d'opérande se doit d'être rapide, le calcul de la retenue doit absolument être le plus rapide possible, c'est crucial pour les circuits qui vont suivre. Outre les optimisations en termes de rapidité, une implémentation à base de transistors peut économiser des transistors. Tout dépend de l'objectif visé, certains circuit optimisant à fond pour la vitesse, d'autres pour le nombre de transistors, d'autres font un compromis entre les deux. Les circuits de ce genre sont très nombreux, trop pour qu'on puisse les citer.
Mais il existe aussi des cas plus rares, où l'implémentation des additionneurs fait au plus simple. C'est le cas sur le premier processeur ARM, l'ARM1, qui implémente ses additionneurs avec des multiplexeurs et des portes NON. Pour rappel, on peut implémenter n'importe quel circuit avec des multiplexeurs, et les additionneurs ne font pas exception. Sur l'ARM1, les concepteurs ont décidé d'implémenter certains circuits avec des multiplexeurs, additionneurs inclus. La raison n'est pas une question de performance ou d'économie de transistors, juste que c'était plus pratique à fabriquer, sachant que le processeur était le premier CPU ARM de l'entreprise. Pour en savoir plus à ce sujet, voici un lien intéressant :
L'implémentation de l'additionneur complet utilisait des multiplexeurs 2 vers 1, mais une version équivalente est la suivante :

L'addition non signée[modifier | modifier le wikicode]
Voyons maintenant un circuit capable d'additionner deux nombres entiers: l'additionneur. Dans la version qu'on va voir, ce circuit manipulera des nombres strictement positifs (et donc les nombres codés en complètement à deux, ou en complément à un).
L'additionneur série[modifier | modifier le wikicode]
Avec un additionneur complet, il est possible d'additionner deux nombres bit par bit. Dit autrement, on peut effectuer l'addition colonne par colonne. Cela demande de coupler l'additionneur avec plusieurs registres à décalages. Les opérandes vont être placées chacune dans un registre à décalage, afin de passer à chaque cycle d'un bit au suivant, d'une colonne à la suivante. Même chose pour le résultat. La retenue de l'addition est stockée dans une bascule de 1 bit, en attente du prochain cycle d'horloge. Un tel additionneur est appelé un additionneur série.

Bien que très simple et économe en transistors, cet additionneur est cependant peu performant. Le temps de calcul est proportionnel à la taille des opérandes. Par exemple, additionner deux nombres de 32 bits prendra deux fois plus de temps que l'addition de deux nombres de 16 bits. L'addition étant une opération fréquente, il vaut mieux utiliser d'autres méthodes d'addition, plus rapides. C'est pour cela que la totalité des autres additionneurs préfère utiliser plus de circuits, quitte à gagner quelque peu en rapidité.
L'additionneur à propagation de retenue[modifier | modifier le wikicode]
L'additionneur à propagation de retenue pose l'addition comme en décimal, en additionnant les bits colonne par colonne avec une éventuelle retenue. Évidemment, on commence par les bits les plus à droite, comme en décimal. Il suffit ainsi de câbler des additionneurs complets les uns à la suite des autres.

Notons la présence de la retenue sortante, qui est utilisée pour détecter les débordements d'entier, ainsi que pour d'autres opérations. Le bit de retenue final est souvent stocké dans un registre spécial du processeur (généralement appelé carry flag).
Notez aussi, sur le schéma précédent, la présence de l’entrée de retenue sur l'additionneur. L'additionneur le plus à droite est bien un additionneur complet, et non un demi-additionneur,c e qui fait qui l'additionneur a une entrée de retenue. Tous les additionneurs ont une entrée de retenue de ce type. Elle est très utile pour l'implémentation de certaines opérations comme l'inversion de signe, la soustraction, l'incrémentation, etc. Certains processeurs sont capables de faire une opération appelée ADC, ADDC ou autre nom signifiant Addition with Carry, qui permet de faire le calcul A + B + Retenue (la retenue en question est la retenue sortante de l'addition précédente, stockée dans le registre carry flag). Son utilité principale est de permettre des additions d'entiers plus grands que ceux supportés par le processeur. Par exemple, cela permet de faire des additions d'entiers 32 bits sur un processeur 16 bits.

Ce circuit utilise plus de portes logiques que l'additionneur série, mais est un peu plus rapide. Il utilise très peu de portes logiques et est assez économe en transistors, ce qui fait qu'il était utilisé sur les tous premiers processeurs 8 et 16 bits. Un défaut de ce circuit est que le calcul des retenues s'effectue en série, l'une après l'autre. En effet, chaque additionneur doit attendre que la retenue de l'addition précédente soit disponible pour donner son résultat. Les retenues doivent se propager à travers le circuit, du premier additionneur jusqu'au dernier. On garde donc un défaut de l'additionneur série, à savoir : le fait que le temps de calcul est proportionnel à la taille des opérandes. Pour éviter cela, les autres additionneurs utilisent diverses solutions : soit calculer les retenues en parallèle, soit éliminer certaines opérations inutiles quand c'est possible.
Une solution est d'utiliser des additionneurs complets de type Manchester carry chain, qui propagent la retenue très rapidement. Néanmoins, l'additionneur de type Manchester carry chain fonctionne en pass transistor logic, avec tous les défauts que cela implique quand on en enchaine plusieurs. L'entrée de retenue est directement connectée sur la sortie de retenue, sans passage par une porte logique. Donc, la tension d'entrée est envoyée directement sur la sortie, sans amplification ou régénération. Si on enchaine plusieurs additionneurs complets de ce type, la tension diminue à chaque passage dans un additionneur complet. En conséquence, on peut difficilement enchainer plus de 4 à 8 additionneurs de type Manchester carry chain à la suite.
Il reste alors à trouver d'autres solutions pour résoudre ce problème de la propagation de retenue. Pour cela, il existe globalement plusieurs solutions, qui donnent quatre types d'additionneurs. Pour résumer ces solutions, en voici une liste rapide :
- Détecter quand le résultat est disponible, plutôt que d'attendre suffisamment pour couvrir le pire des cas.
- Limiter la propagation des retenues sur un petit nombre de bits et concevoir l'additionneur avec cette contrainte.
- Accélérer le calcul de la retenue avec des techniques d'anticipation de retenue.
- Utiliser des représentations binaires qui permettent de se passer de la propagation de retenue.
Les trois premières méthodes donnent, respectivement, les additionneurs à saut de retenue, à sélection de retenue, et à anticipation de retenue. Nous allons les voir dans les sections suivantes. La quatrième méthode sera vue dans le chapitre suivant, qui abordera l'addition multiopérande.
Les accélérations de la propagation de retenue[modifier | modifier le wikicode]
La propagation de la retenue est lente, mais il existe de nombreux moyens de la rendre plus rapide. Dans cette section, nous allons voir quelques additionneurs qui visent à accélérer la propagation de la retenue, mais en gardant la base de l'additionneur de propagation de retenue.

Avant de poursuivre, partons du principe que l'additionneur est conçu en assemblant des additionneurs à plus simples, qui additionnent environ 4 à 5 bits, parfois plus, parfois moins. Ces additionneurs simples seront nommés blocs dans ce qui suit, et l'un d'entre eux est illustré ci-contre. Chaque bloc prend en entrée les deux opérandes à additionner, mais aussi une retenue d'entrée. Il fournit en sortie non seulement le résultat de l'addition, codé sur 4/5 bits, mais aussi une retenue sortante.
En enchaînant plusieurs blocs les uns à la suite des autres, la retenue est propagée d'un bloc au suivant. La retenue sortante d'un bloc est connectée sur l'entrée de retenue du bloc suivant. L'enjeu est, pour un bloc, de calculer les retenues rapidement, plus rapidement qu'un additionneur à propagation de retenue. Le calcul de l'addition dans un bloc n'a pas besoin d'être accéléré, on garde des additionneurs à propagation de retenue.
Les blocs sont tous identiques dans le cas le plus simple, mais il est possible d'utiliser des blocs de taille variable. Par exemple, le premier bloc peut avoir des opérandes de 6 bits, le second des opérandes de 7 bits, etc. Faire ainsi permet de gagner un petit peu en performances, si la taille de chaque bloc est bien choisie. La raison est une question de temps de propagation des retenues. La retenue met plus de temps à se propager à travers 8 blocs qu'à travers 4, ce qui prend plus de temps qu'à travers 2 blocs, etc. En tenir compte fait que la taille des blocs tend à augmenter ou diminuer quand on se rapproche des bits de poids fort.
Le calcul parallèle de la retenue[modifier | modifier le wikicode]

L'optimisation la plus évidente est de calculer la retenue sortante en parallèle de l'addition. Chaque bloc contient, à côté de l'additionneur à propagation de retenue, on trouve un circuit qui calcule la retenue sortante. Il existe de nombreuses manières de calculer la retenue sortante. La plus simple consiste à établir la table de vérité de l'entrée de retenue, puis d'utiliser les techniques du chapitre sur les circuits combinatoire. Cela marche si les blocs sont de petite taille, mais elle devient difficile si le bloc a des opérandes de 2/3 bits ou plus. Mais des techniques alternatives existent.
Un exemple est celui de l'additionneur CMOS 4008, un additionneur de 4 bit. Il est intéressant de voir comment fonctionne ce circuit. Aussi, voici son implémentation. Le circuit est décomposé en trois sections. Une première couche de demi-additionneurs, le circuit de calcul de la retenue sortante, le reste du circuit qui finit l'addition. Le reste du circuit fait que le calcul de l'addition se fait en propageant la retenue, ce qui en fait un additionneur à propagation de retenue. Le circuit de calcul de la retenue sortante prend les résultats des demi-additionneurs, et les utilise pour calculer la retenue sortante. C'est là une constante de tous les circuits qui vont suivre.

Le point important à comprendre est que les demi-additionneurs génèrent les signaux P et G, qui disent si l'additionneur propage ou génère une retenue. Ces signaux sont alors combinés pour déterminer la retenue sortante. La méthode de combinaison des signaux P et G dépend fortement de l'additionneur utilisé. La méthode utilisée sur le 4008 utilise à la fois les signaux P et G, ce qui fait que c'est un hybride entre un additionneur à propagation de retenue, et un additionneur à anticipation de retenue qui sera vu dans la suite du chapitre. Mais il existe des techniques alternatives pour calculer la retenue sortante. La plus simple d'entre elle n'utilise que les signaux de propagation P, sans les signaux de génération. Et nous allons les voir immédiatement.
L'additionneur à saut de retenue[modifier | modifier le wikicode]
L'additionneur à saut de retenue (carry-skip adder) est un additionneur dont le temps de calcul est variable, qui dépend des nombres à additionner. Le calcul prendra quelques cycles d'horloges avec certains opérandes, tandis qu'il sera aussi long qu'avec un additionneur à propagation de retenue avec d'autres. Il n'améliore pas le pire des cas, dans lequel la retenue doit être propagée du début à la fin, du bit de poids faible au bit de poids fort. Dans tous les autres cas, le circuit détecte quand le résultat de l'addition est disponible, quand la retenue a fini de se propager. Il permet d'avoir le résultat en avance, plutôt que d'attendre suffisamment pour couvrir le pire des cas.
L'additionneur à saut de retenue peut, sous certaines conditions, sauter complètement la propagation de la retenue dans le bloc. L'idée est de savoir si, dans le bloc, une retenue est générée par l'addition, ou simplement propagée. Dans le second cas, le bloc ne fait que propager la retenue entrante, sans en générer. La retenue entrante est simplement recopiée sur la retenue sortante. La propagation de retenue dans le bloc est alors skippée (mais elle a quand même lieu). Si une retenue est générée dans le bloc, on envoie cette retenue sur la retenue sortante. Le choix entre les deux est le fait s'un multiplexeur.

Toute la difficulté est de savoir comment commander le multiplexeur. Pour cela, on doit savoir si le circuit propage une retenue ou non. Le bloc propage une retenue si chaque additionneur complet propage la retenue. Les additionneurs complets doivent donc fournir le résultat, mais aussi indiquer s'ils propagent la retenue d'entrée ou non. Le signal de commande du multiplexeur est généré assez simplement : il vaut 1 si tous les additionneurs complets du bloc propagent la retenue précédente. C'est donc un vulgaire ET entre tous ces signaux.

L'additionneur à saut de retenue est construit en assemblant plusieurs blocs de ce type.

L'additionneur à sélection de retenue[modifier | modifier le wikicode]
L'additionneur à sélection de retenue découper les opérandes en blocs, qui sont additionnés indépendamment. L'addition se fait en deux versions : une avec la retenue du bloc précédent valant zéro, et une autre version avec la retenue du bloc précédent valant 1. Il suffira alors de choisir le bon résultat avec un multiplexeur, une fois cette retenue connue. On gagne ainsi du temps en calculant à l'avance les valeurs de certains bits du résultat, sans connaître la valeur de la retenue. Petit détail : sur certains additionneurs à sélection de retenue, les blocs de base n'ont pas la même taille. Cela permet de tenir compte des temps de propagation des retenues entre les blocs.

Dans les exemples du dessus, chaque sous-additionneur étaient des additionneurs à propagation de retenue. Mais ce n'est pas une obligation, et tout autre type d’additionneur peut être utilisé. Par exemple, on peut faire en sorte que les sous-additionneurs soient eux-mêmes des additionneurs à sélection de retenue, et poursuivre ainsi de suite, récursivement. On obtient alors un additionneur à somme conditionnelle, plus rapide que l'additionneur à sélection de retenue, mais qui utilise beaucoup plus de portes logiques.
Les additionneurs à anticipation de retenue[modifier | modifier le wikicode]
Les additionneurs à anticipation de retenue accélèrent le calcul des retenues en les calculant sans les propager. Au lieu de calculer les retenues une par une, ils calculent toutes les retenues en parallèle, à partir de la valeur de tout ou partie des bits précédents. Une fois les retenues pré-calculées, il suffit de les additionner avec les deux bits adéquats, pour obtenir le résultat.

Ces additionneurs sont composés de deux parties :
- un circuit qui pré-calcule la valeur de la retenue d'un étage ;
- et d'un circuit qui additionne les deux bits et la retenue pré-calculée : il s'agit d'une couche d'additionneurs complets simplifiés, qui ne fournissent pas de retenue.

Le circuit qui détermine la valeur de la retenue est lui-même composé de deux grandes parties, qui ont chacune leur utilité. La première partie réutilise des additionneurs qui donnent les signaux de propagation et génération de retenue. L'additionneur commence donc à prendre forme, et est composé de trois parties :
- un circuit qui crée les signaux P et G ;
- un circuit qui déduit la retenue à partir des signaux P et G adéquats ;
- et une couche d'additionneurs qui additionnent chacun deux bits et une retenue.

Il ne nous reste plus qu'à voir comment fabriquer le circuit qui reste. Pour cela, il faut remarquer que la retenue est égale :
- à 1 si l'addition des deux bits génère une retenue ;
- à 1 si l'addition des deux bits propage une retenue ;
- à zéro sinon.
Ainsi, l'addition des bits de rangs i va produire une retenue Ci, qui est égale à Gi+(Pi·Ci−1). Si on utilisait cette formule sans trop réfléchir, on retomberait sur un additionneur à propagation de retenue inutilement compliqué. L'astuce des additionneurs à anticipation de retenue consiste à remplacer le terme Ci−1 par sa valeur calculée avant. Par exemple, je prends un additionneur 4 bits. Je dispose de deux nombres A et B, contenant chacun 4 bits : A3, A2, A1, et A0 pour le nombre A, et B3, B2, B1, et B0 pour le nombre B. Si j'effectue les remplacements, j'obtiens les formules suivantes :
- C1 = G0 + ( P0 · C0 ) ;
- C2 = G1 + ( P1 · G0 ) + ( P1 · P0 · C0 ) ;
- C3 = G2 + ( P2 · G1 ) + ( P2 · P1 · G0 ) + ( P2 · P1 · P0 · C0 ) ;
- C4 = G3 + ( P3 · G2 ) + ( P3 · P2 · G1 ) + ( P3 · P2 · P1 · G0 ) + ( P3 · P2 · P1 · P0 · C0 ).
Ces formules nous permettent de déduire la valeur d'une retenue directement : il reste alors à créer un circuit qui implémente ces formules, et le tour est joué. On peut même simplifier le tout en fusionnant les deux couches d'additionneurs.

Ces additionneurs sont plus rapides que les additionneurs à propagation de retenue. Ceci dit, utiliser un additionneur à anticipation de retenue sur des nombres très grands (16/32bits) utiliserait trop de portes logiques. Pour éviter tout problème, nos additionneurs à anticipation de retenue sont souvent découpés en blocs, avec soit une anticipation de retenue entre les blocs et une propagation de retenue dans les blocs, soit l'inverse.

L'additionneur à calcul parallèle de préfixes[modifier | modifier le wikicode]
Les additionneurs à calcul parallèle de préfixes sont des additionneurs à anticipation de retenue quelque peu améliorés, pour gagner en performances. Ceux-ci sont toujours découpés en trois couches :
- un circuit qui crée les signaux P et G ;
- un circuit qui déduit la retenue à partir des signaux P et G adéquats ;
- et une couche d'additionneurs qui additionnent chacun deux bits et une retenue.
Simplement, ils vont concevoir le circuit de calcul des retenues différemment. Avec eux, le calcul Gi + (Pi · Ci−1) va être modifié pour prendre en entrée non pas la retenue Ci−1, mais les signaux Gi−1 et Pi−1. Dans ce qui va suivre, nous allons noter ce petit calcul o. On peut ainsi écrire que :
- Ci = ((((Gi , Pi) o (Gi−1 , Pi−1) ) o (Gi−2 , Pi−2 )) o (Gi−3 , Pi−3)) …
Si on utilisait cette formule sans trop réfléchir, on retomberait sur un additionneur à propagation de retenue inutilement compliqué. Le truc, c'est que o est associatif, et que cela peut permettre de créer pas mal d'optimisations : il suffit de réorganiser les parenthèses. Cette réorganisation peut se faire de diverses manières qui donnent des additionneurs différents. Les diverses réorganisations donnent l'additionneur de Ladner-Fisher, l'additionneur de Brent-Kung, l'additionneur de Kogge-Stone, ou tout design hybride. L'additionneur de Brent-Kung est le plus lent de tous les additionneurs cités, mais c'est celui qui utilise le moins de portes logiques. L'additionneur de Ladner-Fisher est théoriquement le plus rapide de tous, mais aussi celui qui utilise le plus de portes logiques. Les autres sont des intermédiaires.
 |
 |
L'addition signée et la soustraction[modifier | modifier le wikicode]
Après avoir vu l'addition, il est logique de passer à la soustraction, les deux opérations étant très proches. Si on sait câbler une addition entre entiers positifs, câbler une soustraction n'est pas très compliqué. De plus, la soustraction permet de faire des additions de nombres signés.
Le soustracteur pour opérandes entiers[modifier | modifier le wikicode]
Pour soustraire deux nombres entiers, on peut adapter l'algorithme e soustraction utilisé en décimal, celui que vous avez appris à l'école. Celui-ci ressemble fortement à l'algorithme d'addition : on soustrait les bits de même poids, et on propage éventuellement une retenue sur la colonne suivante. La différence est que la retenue est soustraite, et non ajoutée. La table de soustraction nous dit quel est le résultat de la soustraction de deux bits. La voici :
- 0 - 0 = 0 ;
- 0 - 1 = 1 et une retenue ;
- 1 - 0 = 1 ;
- 1 - 1 = 0.
Cette table de soustraction peut servir de table de vérité pour construire un circuit qui soustrait deux bits. Celui-ci est appelé un demi-soustracteur.

Celui-ci peut être complété afin de prendre en compte une éventuelle retenue, ce qui donne un soustracteur complet. On remarque que le soustracteur complet et composé de deux demi-soustracteurs placés en série. Le calcul de la retenue se fait en combinant les deux retenues des demi-soustracteurs avec une porte OU.

Celui-ci permet de créer des soustracteurs sur le même patron que pour les additionneurs. On peut ainsi créer un soustracteur série, un soustracteur à propagation de retenue, et ainsi de suite.
L'additionneur-soustracteur pour opérandes codées en complément à deux[modifier | modifier le wikicode]
Étudions maintenant le cas de la soustraction en complément à deux, dans l'objectif de créer un circuit soustracteur. Vous savez sûrement que a−b et a+(−b) sont deux expressions équivalentes. Et en complément à deux, − b = not(b) + 1. Dit autrement, a − b = a + not(b) + 1. On pourrait se dire qu'il faut deux additionneurs pour faire le calcul, mais la majorité des additionneurs possède une entrée de retenue pour incrémenter le résultat de l'addition. Un soustracteur en complément à deux est donc simplement composé d'un additionneur et d'un inverseur.

Il est possible de créer un circuit capable d'effectuer soit une addition, soit une soustraction : il suffit de remplacer l'inverseur par un inverseur commandable, qui peut être désactivé. On a vu comment créer un tel inverseur commandable dans le chapitre sur les circuits combinatoires. On peut remarquer que l'entrée de retenue et l'entrée de commande de l'inverseur sont activées en même temps : on peut fusionner les deux signaux en un seul.

Une implémentation alternative est la suivante. Elle remplace l'inverseur commandable par un multiplexeur.

L'additionneur-soustracteur pour opérandes codées en signe-magnitude[modifier | modifier le wikicode]
Passons maintenant aux nombres codés en signe-valeur absolue.
Étudions tout d'abord un circuit d'addition de deux opérandes en signe-magnitude, les deux opérandes étant notée A et B. Suivant les signes des deux opérandes, on a quatre cas possibles : A + B, A − B (B négatif), −A + B (A négatif) et −A − B (A et B négatifs). On remarque que B − A est égal à − (A − B), et − A − B vaut − (A + B). Ainsi, le circuit n'a besoin que de calculer A + B et A − B : il peut les inverser pour obtenir − A − B ou B − A. A + B et A − B peuvent se calculer avec un additionneur-soustracteur. Il suffit de lui ajouter un inverseur commandable pour obtenir le circuit d'addition finale. On peut transformer ce circuit en additionneur-soustracteur en signe-valeur absolue, mais le circuit combinatoire devient plus complexe.

Toute la difficulté tient dans le calcul du bit de signe du résultat, quand interviennent des soustractions. Autant l'addition de deux nombres de même signe ne pose aucun problème, autant l'addition de nombres de signes différents ou les soustractions posent problème. Suivant que ou que , le signe du résultat ne sera pas le même. Intuitivement, on se dit qu'il faut ajouter des comparateurs pour déterminer le signe du résultat. Diverses optimisations permettent cependant de limiter la casse et d'utiliser moins de circuits que prévu. Mais rien d'extraordinaire.
L'additionneur-soustracteur pour opérandes codées en représentation par excès[modifier | modifier le wikicode]
Passons maintenant aux nombres codés en représentation par excès. On pourrait croire que ces nombres s'additionnent comme des nombres non-signés, mais ce serait oublier la présence du biais, qui pose problème. Dans les cas de nombres signés gérés avec un biais, voyons ce que donne l'addition de deux nombres :
Or, le résultat correct serait :
En effectuant l'addition telle quelle, le biais est compté deux fois. On doit donc le soustraire après l'addition pour obtenir le résultat correct.
Même chose pour la soustraction qui donne ceci :
Or, le résultat correct serait :
Il faut rajouter le biais pour obtenir l'exposant correct.
On a donc besoin de deux additionneurs/soustracteurs : un pour additionner/soustraire les représentations binaires des opérandes, et un autre pour ajouter/retirer le biais en trop/manquant.
L'incrémenteur[modifier | modifier le wikicode]
Maintenant, nous allons voir un circuit capable d'incrémenter un nombre, appelé l'incrémenteur. Les circuits incrémenteurs étaient très utilisés sur les premiers processeurs 8 bits, comme le Z-80, le 6502, les premiers processeurs x86 comme le 8008, le 8086, le 8085, et bien d'autres. Il s'agit d'un circuit assez simple, mais qu'il peut être intéressant d'étudier.
Le circuit incrémenteur se construit sur la même base qu'un additionneur, qu'on simplifie. En effet, incrémenter un nombre A revient à calculer A + 1. En clair, l'opération effectuée est la suivante :
+ 0 0 0 0 0 0 0 1 ------------------------------
Le calcul alors très simple : il suffit d'additionner 1 au bit de poids faible, sur la colonne la plus à droite, et propager les retenues pour les autres colonnes. En clair, on n'additionne que deux bits à chaque colonne : un 1 sur celle tout à droite, la retenue de la colonne précédente pour les autres. En clair : un incrémenteur est juste un additionneur normal, dont on a remplacé les additionneurs complets par des demi-additionneurs. Le 1 le plus à droite est injecté sur l'entrée de retenue entrante de l'additionneur. Et cela marche avec tous les types d'additionneurs, que ce soit des additionneurs à propagation de retenue, à anticipation de retenue, etc.
L'incrémenteur à propagation de retenue[modifier | modifier le wikicode]
Un incrémenteur à propagation de retenue est donc constitué de demi-additionneurs enchaînés les uns à la suite des autres. Le circuit incrémenteur basique est équivalent à un additionneur à propagation de retenue, mais où on aurait remplacé tous les additionneurs complets par des demi-additionneurs. L'entrée de retenue entrante est forcément mise à 1, sans quoi l'incrémentation n'a pas lieu.

L'incrémenteur à propagation de retenue était utilisé sur le processeur Intel 8085, avec cependant une optimisation très intéressante. Pour la comprendre, rappelons que les portes logiques sont construites à partir de transistors. Les portes les plus simples à implémenter avec des transistors CMOS et TTL sont les portes NON, NAND et NOR. Le demi-additionneur est donc construit comme ci-dessous

Les ingénieurs ont tenté de se débarrasser de la porte NON, et ont réussit à s'en débarrasser pour une colonne sur deux. L'idée est de prendre les demi-additionneurs deux par deux, par paires. On peut alors regrouper les portes logiques comme ceci :

Les trois portes sont fusionnées, de manière à donner une porte NOR couplée à une porte NON.

- On peut optimiser le tout en fusionnant la porte XOR avec la porte NON pour le calcul de la somme, la porte XOR étant une porte composite. Mais nous n'en parlerons pas plus que ça ici.
Le résultat est que la propagation de la retenue est plus rapide. Au lieu de passer par une porte NAND et une porte NON, il traverse une seule porte : une porte NAND pour les colonnes paires, une porte NOR pour les colonnes impaires. Avec cette optimisation, la retenue se propage presque deux fois plus vite. Mine de rien, cette optimisation économisait des portes logiques et rendait le circuit deux fois plus rapide.
Les incrémenteurs plus complexes sont rares[modifier | modifier le wikicode]
Pour résumer, ce circuit ne paye pas de mine, mais il était largement suffisant sur les premiers microprocesseurs. Ils utilisaient généralement un incrémenteur capable de traiter des nombres de 8 bits, guère plus. Ces processeurs étaient très peu puissants, et fonctionnaient à une fréquence très faible. Ainsi, ils n'avaient pas besoin d'utiliser de circuits plus complexes pour incrémenter un nombre, et se contentaient d'un incrémenteur à propagation de retenues.
Il existe cependant des processeurs qui utilisaient des incrémenteurs complexes, avec anticipation de retenues, voir du carry skip. Par exemple, le processeur Z-80 de Zilog utilisait un incrémenteur pour des nombres de 16 bits, ce qui demandait des performances assez élevées. Et cet incrémenteur utilisait à la fois anticipation de retenues et carry skip. Pour ceux qui veulent en savoir plus sur cet incrémenteur, voici un lien sur le sujet :
L'additionneur BCD[modifier | modifier le wikicode]
Maintenant, voyons un additionneur qui additionne deux entiers au format BCD. Pour cela, nous allons devoir passer par deux étapes. La première est de créer un circuit capable d'additionneur deux chiffres BCD. Ensuite, nous allons voir comment enchaîner ces circuits pour créer un additionneur BCD complet.
L'additionneur BCD qui fait l'opération chiffre par chiffre[modifier | modifier le wikicode]
Nous allons commencer par voir un additionneur qui additionne deux chiffres en BCD. Il fournit un résultat sur 4 bits et une retenue qui est mise à 1 si le résultat dépasse 10 (la limite d'un chiffre BCD). L'additionneur BCD se base sur un additionneur normal, pour des entiers codés en binaire, auquel on ajoute des circuits pour gérer le format BCD. Les deux chiffres sont codés sur 4 bits et sont additionnés en binaire par un additionneur des plus normal, similaire à ceux vus plus haut. Le résultat est alors un entier codé en binaire, sur 5 bits, qu'on cherche à corriger/convertir pour obtenir un chiffre BCD.
Pour corriger le résultat, une idée intuitive serait de prendre le résultat et de faire une division par 10. Le quotient donne la retenue, alors que le reste est le résultat, le chiffre BCD . Mais faire ainsi prendrait beaucoup de circuits, ce qui ne vaut pas le coup. Il existe une autre méthode beaucoup plus simple.
Une autre méthode détecte si le résultat est égal ou supérieur à 10, ce qui correspond à un "débordement" (on dépasse les limites d'un chiffre BCD). Si le résultat est plus petit que 10, il n'y a rien à faire : le résultat est bon et la retenue est de zéro. Par contre, si le résultat vaut 10 ou plus, il faut corriger le résultat et générer une retenue à 1.
Il faut donc ajouter un circuit qui détecte si le résultat est supérieur à 9. La retenue s'obtient facilement : le circuit qui détecte si le résultat est supérieur à 9 donne directement la retenue. Ce circuit peut se fabriquer simplement à partir de sa table de vérité, ou en utilisant les techniques que nous verrons dans un chapitre ultérieur sur les comparateurs. La solution la plus simple est clairement d'utiliser la table de vérité, ce qui est très simple, assez pour être laissé en exercice au lecteur.
Pour comprendre comment corriger le résultat, établissons une table de vérité qui associe le résultat et le résultat corrigé. L'entrée vaut au minimum 10 et au maximum 9 + 9 = 18. On considère la sortie comme un tout, la retenue étant un 5ème bit, le bit de poids fort.
| Entrée | Retenue | Résultat corrigé (sans retenue) | interprétation de la sortie en binaire (retenue inclue) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 0 | (10) | 1 | 0000 | (16) | |
| 0 | 1 | 0 | 1 | 1 | (11) | 1 | 0001 | (17) | |
| 0 | 1 | 1 | 0 | 0 | (12) | 1 | 0010 | (18) | |
| 0 | 1 | 1 | 0 | 1 | (13) | 1 | 0011 | (19) | |
| 0 | 1 | 1 | 1 | 0 | (14) | 1 | 0100 | (20) | |
| 0 | 1 | 1 | 1 | 1 | (15) | 1 | 0101 | (21) | |
| 1 | 0 | 0 | 0 | 0 | (16) | 1 | 0110 | (22) | |
| 1 | 0 | 0 | 0 | 1 | (17) | 1 | 0111 | (23) | |
| 1 | 0 | 0 | 1 | 0 | (18) | 1 | 1000 | (24) | |
En analysant le tableau, on voit que pour corriger le résultat, il suffit d'ajouter 6. La raison est que le résultat déborde d'un nibble à 16 en binaire, mais à 10 en décimal : il suffit d'ajouter la différence entre les deux, à savoir 6, et le débordement binaire fait son travail. Donc, la correction après une addition est très simple : si le résultat dépasse 9, on ajoute 6.
On peut maintenant implémenter l'additionneur BCD au complet, en combinant le comparateur de débordement, le circuit de correction, et l'additionneur. La première solution calcule deux versions du résultat : la version corrigée, la version normale. Le choxi entre les deux est réalisée par un multiplexeur, commandé par le comparateur.

L'autre solution utilise un circuit commandable qui soit additionne 6, soit ne fait rien. Le choix entre les deux est commandé par un bit de commande dédié, calculé par le comparateur.

Une version assez compliquée du circuit final est illustrée ci-dessous. Le circuit commandable est un additionneur, précédé d'un circuit comparateur qui détecte si le résultat est supérieur à 9. Si c'est le cas, ce circuit génère l'opérande 6, et l'envoie en entrée de l'additionneur. Le circuit est simple à concevoir, mais gaspille beaucoup de circuit. Idéalement, il vaudrait mieux utiliser un circuit combinatoire d'addition avec une constante conçu pour.

Pour obtenir un additionneur BCD complet, il suffit d’enchaîner les additionneurs précédents, comme on le ferait avec les additionneurs complets dans un additionneur à propagation de retenue. La seule chose importante est que le circuit précédent est altéré de manière à ce qu'on puisse prendre en compte la retenue. Pour cela, rien de plus simple : il suffit d'utiliser l'entrée de retenue de l'additionneur binaire.
Au final, l'additionneur BCD est beaucoup plus compliqué qu'un additionneur normal. Il rajoute des circuits à un additionneur normal, à savoir un circuit pour détecter si chaque chiffre binaire est >9, un petit additionneur pour ajouter 6 et un multiplexeur. De plus, il est difficile d'appliquer les optimisations disponibles sur les additionneurs non-BCD. Notamment, les circuits d'anticipation de retenue sont totalement à refaire et le résultat est relativement compliqué. c'est ce qui explique pourquoi le BCD a progressivement été abandonné au profit du binaire simple.
L'additionneur BCD par ajustement décimal[modifier | modifier le wikicode]
L'additionneur BCD précédent effectuait son travail chiffre BCD par chiffre BCD. Il additionne et corrige le résultat un chiffre BCD après l'autre, en commençant par le chiffre BCD de poids faible. Mais il existe des additionneurs BCD qui font autrement. L'idée est d’additionner les deux opérandes avec une addition binaire normale, puis de corriger le résultat. Le tout se fait donc en deux étapes : l'addition, puis la correction du résultat. Les deux étapes traitent des opérandes complètes, de 8, 16, voire 32 bits, et non des chiffres BCD seuls.
Une telle technique était utilisée dans le processeur Intel 8085, et de manière générale sur les premiers processeurs x86. Sur ce processeur, les deux étapes d'addition et de correction du résultat étaient séparées dans deux opérations distinctes. Il n'y avait pas d'opération d'addition BCD proprement dit, seulement une addition binaire normale. Par contre, l'addition était secondée par une opération dite d'ajustement décimal qui transformait un nombre binaire en nombre codé en BCD. Effectuer une addition BCD demandait donc de faire deux opérations à la suite : une addition binaire simple, suivie par l'opération d'ajustement décimal. Cela permettait de gérer des nombres entiers en binaire usuel et des entiers BCD sans avoir deux instructions d'addition séparées pour les deux, sans compter que cela simplifiait aussi les circuits d'addition. L'opération d'ajustement décimal lisait l'opérande à manipuler dans un registre (l’accumulateur), et mémorisait le résultat dans ce même registre. Elle prenait une opérande de 8 bits, soit deux chiffres BCD, et fournissait un résultat de la même taille. Elle avait son propre circuit, assez simple, que nous allons voir dans ce qui suit.
L'ajustement décimal s'effectue en ajoutant une constante bien précise à l'opérande à convertir en BCD. L'idée est que la constante est découpée en morceaux de 4 bits, correspondant chacun à un chiffre BCD de l'opérande, chaque morceau contenant soit un 0, soit 6. Cela permet d'ajouter soit 0, soit, à chaque chiffre BCD, et donc de le corriger. La propagation des retenues d'un chiffre à l'autre est effectuée automatiquement par l'addition binaire de la constante. La constante est calculée en deux étapes, sur un principe similaire à celui vu dans l'additionneur précédent. D'abord, on découpe l'opérande en nibbles et on vérifie si chaque nibble est supérieur ou égal à 10. Ensuite, la seconde étape rend les résultats de ces comparaisons et détermine la valeur de chaque nibble de la constante finale. Par exemple, si je prends l'opérande 1001 1110, le nibble de poids faible déborde, alors que celui de poids fort non. La constante sera donc 0000 0110 : 0x06. Inversement, si le nibble de poids fort déborde et pas celui de poids faible, la constante sera alors 0x60. Et la constante est de 0x66 si les deux nibbles débordent, de 0x00 si aucun ne déborde.
Le circuit d’ajustement décimal est donc composé de trois étapes : deux étapes pour calculer la constante, et un circuit d'addition pour additionner cette constante au nombre de départ. La première étape découpe l'opérande en morceaux de 4 bits, en chiffres BCD, et vérifie si chacun d'entre eux vaut 10 ou plus. La seconde étape prend les résultats de la première étape, et les combine pour calculer la constante. Enfin, on trouve l'addition finale, qui était réalisée par un circuit d'addition utilisé à la fois pour l'ajustement décimal et l'addition binaire. La différence entre une addition normale et une opération d'ajustement décimal tient dans le fait que les deux premières étapes sont désactivées dans une addition normale.

Les débordements d'entier lors d'une addition/soustraction[modifier | modifier le wikicode]
Les instructions arithmétiques et quelques autres manipulent des entiers de taille fixe, qui ne peuvent prendre leurs valeurs que dans un intervalle. Pour les nombres positifs, un ordinateur qui code ses entiers sur n bits pourra coder tous les entiers allant de 0 à . Tout nombre en dehors de cet intervalle ne peut pas être représenté. Dans le cas où l'ordinateur gère les nombres négatifs, l'intervalle est différent. Dans le cas général, l'ordinateur peut coder les valeurs comprises de à . Si le résultat d'un calcul sort de cet intervalle, il ne peut pas être représenté par l'ordinateur et il se produit ce qu'on appelle un débordement d'entier.
La valeur haute de débordement désigne la première valeur qui est trop grande pour être représentée par l'ordinateur. Par exemple, pour un ordinateur qui peut coder tous les nombres entre 0 et 7, la valeur haute de débordement est égale à 8. On peut aussi définir la valeur basse de débordement, qui est la première valeur trop petite pour être codée par l'ordinateur. Par exemple, pour un ordinateur qui peut coder tous les nombres entre 8 et 250, la valeur basse de débordement est égale à 7. Pour les nombres entiers, la valeur haute de débordement vaut , alors que la valeur basse vaut (avec et respectivement la plus grande et la plus petite valeur codable par l'ordinateur).
La correction des débordements d'entier : l'arithmétique saturée[modifier | modifier le wikicode]
Quand un débordement d'entier survient, tous les circuits de calcul ne procèdent pas de la même manière. Dans les grandes lignes, il y a deux réactions possibles : soit on corrige automatiquement le résultat du débordement, soit on ne fait rien et on se contente de détecter le débordement.
Si le débordement n'est pas corrigé automatiquement par le circuit, celui-ci ne conserve que les bits de poids faibles du résultat. Les bits en trop sont simplement ignorés. On dit qu'on utilise l'arithmétique modulaire. Le problème avec ce genre d'arithmétique, c'est qu'une opération entre deux grands nombres peut donner un résultat très petit. Par exemple, si je dispose de registres 4 bits et que je souhaite faire l'addition 1111 + 0010 (ce qui donne 15 + 2), le résultat est censé être 10001 (17), ce qui est un résultat plus grand que la taille d'un registre. En conservant les 4 bits de poids faible, j’obtiens 0001 (1). En clair, un résultat très grand est transformé en un résultat très petit. Cela peut poser problèmes si on travaille uniquement avec des nombres positifs, mais c'est aussi utilisé pour coder des nombres en complément à deux. En clair, faire ainsi est parfois une bonne idée, parfois non.
D'autres circuits utilisent ce qu'on appelle l'arithmétique saturée : si un résultat est trop grand au point de générer un débordement, on arrondi le résultat au plus grand entier supporté par le circuit. Les circuits capables de calculer en arithmétique saturée sont un peu tout petit peu plus complexes que leurs collègues qui ne travaillent pas en arithmétique saturée, vu qu'il faut rajouter des circuits pour corriger le résultat en cas de débordement. Il suffit généralement de rajouter un circuit de saturation, qui prend en entrée le résultat en fournit en sortie une version saturée en cas de débordement. Ce circuit de saturation met la valeur maximale en sortie si un débordement survient, mais se contente de recopier le résultat du calcul sur sa sortie s'il n'y a pas de débordement. Typiquement, il est composé d'une ou de deux couches de multiplexeurs, qui sélectionnent quelle valeur mettre sur la sortie : soit le résultat du calcul, soit le plus grand nombre entier géré par le processeur, soit le plus petit (pour les nombres négatifs/soustractions).
L'arithmétique saturée est surtout utilisée pour les additions et soustractions, mais c'est plus rare pour les multiplications/divisions. Une des raisons est que le résultat d'une addition/soustraction prend un bit de plus que le résultat, là où les multiplications doublent le nombre de bits. Cette large différence se traduit par une grande différence pour les résultats qui débordent. Quand une addition déborde, le résultat réel est proche de la valeur maximale codable. mais quand une multiplication déborde, le résultat peut parfois valoir 200 à 60000 fois plus que la valeur maximale codable. Les calculs avec une valeur saturée/corrigée sont donc crédibles pour une suite d'additions, mais pas pour une suite de multiplications. Raison pour laquelle l'arithmétique saturée est utilisée pour les additions/soustractions, là où on préfère corriger les multiplications/divisions par des méthodes logicielles.
La détection des débordements d'entier[modifier | modifier le wikicode]
Et quand un débordement d'entier a eu lieu, il vaut mieux que le circuit prévienne ! Pour cela, les circuits de calculs ont une sortie nommée Overflow, dont la valeur indique si le calcul a donné un débordement d'entier ou non. Reste que détecter un débordement ne se fait pas de la même manière selon que l'on parle d'un additionneur non-signé, d'un additionneur signé, d'un multiplieur non-signé, etc.
Les opérations sur des nombres non-signés[modifier | modifier le wikicode]
Pour le cas des nombres positifs, la détection des débordements dépend assez peu de l'opération. L'idée générale est que le circuit de calcul calcule tous les bits du résultat, quitte à dépasser ce qui est supporté par l'ordinateur. Par exemple, un additionneur 32 bits fournit un résultat sur 33 bits, un multiplieur 32 bits fournit des résultats sur 64 bits, etc. Le circuit de calcul a donc des bits qui sont en trop et doivent être oubliés. Un débordement a lieu quand ces bits oubliés sont pertinents, à savoir quand au moins l'un d'eux est à 1. Par exemple, une addition sur 32 bits déborde quand le 33ème bit est à 1, une multiplication sur 32 bits déborde quand un des 32 bits de poids fort est à 1, etc.
Pour les additionneurs non-signés, la sortie Overflow n'est autre que la retenue finale, celle fournie par le dernier additionneur complet. De plus, le seul type de débordement possible est un débordement par le haut, où le résultat dépasse la valeur maximale. Le circuit de saturation est alors très simple. Il consiste au pire en une seule couche de multiplexeurs. Une solution encore plus simple consiste à utiliser le circuit de mise à la valeur maximale vu dans le chapitre sur les opérations bits à bits.

Les opérations signées[modifier | modifier le wikicode]
Pour les additionneurs non-signés, la gestion des débordements d'entiers dépend fortement de la représentation signée. Dans les grandes lignes, rien ne change avec les représentations en signe-magnitude et par excès, dont les débordements sont gérés de la même manière que pour les nombres positifs. Par contre, il n'en est pas de même pour le complément à deux. Si vous vous rappelez le chapitre 1, j'ai clairement dit que les calculs sur des nombres en complètement à deux utilisent les règles de l'arithmétique modulaire : les calculs sont faits avec un nombre de bits fixé une fois pour toute. Si un résultat dépasse ce nombre de bits fixé, on ne conserve pas les bits en trop. C'est une condition nécessaire pour pouvoir faire nos calculs. À priori, on peut donc penser que dans ces conditions, les débordements d'entiers sont une chose parfaitement normale, qui nous permet d'avoir des résultats corrects. Néanmoins, certains débordements d'entiers peuvent survenir malgré tout et produire des bugs assez ennuyeux.
Si l'on tient en compte les règles du complément à deux, on sait que le bit de poids fort (le plus à gauche) permet de déterminer si le nombre est positif ou négatif : il indique le signe du nombre. Tout se passe comme si les entiers en complément à deux étaient codés sur un bit de moins, et avaient leur longueur amputé du bit de poids fort. Si le résultat d'un calcul a besoin d'un bit de plus que cette longueur, amputée du bit de poids fort, le bit de poids fort sera écrasé; donnant un débordements d'entiers. Il existe une règle simple qui permet de détecter ces débordements d'entiers. L'addition (ou la multiplication) de deux nombres positifs ne peut pas être un nombre négatif : on additionne deux nombres dont le bit de signe est à 0 et que le bit de signe du résultat est à 1, on est certain d'être en face d'un débordements d'entiers. Même chose pour deux nombres négatif : le résultat de l'addition ne peut pas être positif. On peut résumer cela en une phrase : si deux nombres de même signe sont ajoutés, un débordement a lieu quand le bit du signe du résultat a le signe opposé. On peut préciser que cette règle s'applique aussi pour les nombres codés en complément à 1, pour les mêmes raisons que pour le codage en complément à deux. Cette règle est aussi valable pour d'autres opérations, comme les multiplications.
Modifier les circuits d'au-dessus pour qu'ils détectent les débordements en complément à deux est simple comme bonjour : il suffit créer un petit circuit combinatoire qui prenne en entrée les bits de signe des opérandes et du résultat, et qui fasse le calcul de l'indicateur de débordements. Si l'on rédige sa table de vérité, on doit se retrouver avec la table suivante :
| Entrées | Sortie |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 0 |
| 011 | 0 |
| 100 | 0 |
| 101 | 0 |
| 110 | 1 |
| 111 | 0 |
L'équation de ce circuit est la suivante, avec et les signes des deux opérandes, et la retenue de la colonne précédente :
En simplifiant, on obtient alors :
Or, il se trouve que est tout simplement la retenue en sortie du dernier additionneur, que nous noterons . On trouve donc :
Il suffit donc de faire un XOR entre la dernière retenue et la précédente pour obtenir le bit de débordement.




























