Les opérations bit à bit/Les opérations bit à bit

Pour commencer ce livre, nous devons d'abord parler des opérations logiques : que sont-elles, à quoi servent-elles ? Ces opérations logiques travaillent sur des suites de bits d'une longueur fixe, des nombres pour simplifier. Ces opérations modifient directement l'écriture binaire d'un nombre, la suite de bits correspondante. Il en existe de deux types, les instructions bit à bit et les instructions de décalage, que nous allons voir l'une après l'autre. Pour les connaisseurs, nous allons voir quelques opérations iconiques, comme les décalages et les rotations, mais aussi comment concevoir une unité de calcul 2 à 3 bits, les masques et quelques autres opérations.

Les opérations bit à bit proprement dit[modifier | modifier le wikicode]

Les instructions logiques les plus courantes sont au nombre de 4 : le NON, le ET, le OU, et le XOR. Toutes ces instructions vont travailler sur des bits individuels d'un ou de deux nombres, et leur faire subir une opération bien précise. Cette opération prend deux bits (un seul pour le NON) et donne un résultat codé sur un bit. Le fonctionnement de cette opération peut être définie par ce qu'elle fait sur un bit, son comportement étant résumé dans un tableau qu'on appelle la table de vérité. Leur résultat n'est pas vraiment interprétable mathématiquement, ou alors avec un sens vraiment idiosyncratique. La plus simple est clairement l'opération NOT, qui inverse tous les bits d'un nombre. Mais il est aussi possible de prendre deux nombres, de faire un ET/OU/XOR entre les bits de même poids, et de renvoyer le tout en guise de résultat. Formellement, ce sont les seuls types d'opérations bits à bit : l'inversion des bits d'un nombre, un ET entre deux nombres, un OU entre deux nombres, et un XOR entre deux nombres (avec leurs dérivées, tel un NAND ou un NOR).

L’opération d'inversion (NOT)[modifier | modifier le wikicode]

L'inversion bit à bit va inverser tous les bits d'un nombre : les 0 deviennent des 1, et les 1 deviennent des 0. Exemple : le nombre 01110011 va devenir 10001100.

La table de vérité du NOT est celle-ci :

Bit A	Résultat (NOT A)
0	1
1	0

Le NOT d'un bit et/ou d'un nombre sera noté comme ceci : ${\overline {a}}$ .

Notation
dans ce livre	${\overline {x}}$
quelques autres notations	$NOT(x)$	$\neg x$	$\sim x$

On peut remarquer qu'inverser deux fois de suite un bit redonne le bit initial. Autrement dit, ${\overline {\overline {a}}}=a$ .

Le résultat de cette opération dépend de l'encodage du nombre. Plus précisément, l'interprétation du résultat n'est pas la même selon que le nombre inversé soit non-signé, en complément à 1, en complément à 2, etc.

Pour un entier en complément à 1, le NOT sert à obtenir l'opposé d'un nombre : dit autrement, ${\overline {x}}=-x$ .
Pour un entier en complément à deux, le NOT donne l'opposé d'un nombre auquel on aurait retranché 1 : ${\overline {x}}=-x-1$ .
Pour un entier non-signé, le NOT va donner la valeur ${\overline {x}}=2^{n}-1-x$ .

Le dernier résultat est facile à comprendre. On sait que la somme ${\overline {x}}+x$ donne un nombre de n bits dont tous les bits sont à 1. Un tel nombre vaut exactement, par définition, $2^{n}-1$ . On a donc ${\overline {x}}+x=2^{n}-1$ , ce qui donne le résultat précédent avec quelques manipulations algébriques triviales. L'image de droite montre ce que fait l'opérateur NOT sur un entier en complément à deux.

L'opération ET (AND)[modifier | modifier le wikicode]

Vient ensuite le ET bit à bit, aussi appelé AND bit à bit. Celui-ci prend deux nombres en opérandes et donne un nombre comme résultat. Sur ces deux nombres, il va prendre les bits qui sont à la même place et va effectuer dessus une petite opération qui donnera le bit du résultat. Cette opération est un simple AND binaire. Ce AND binaire prend deux bits, A et B, et fonctionne comme ceci :

Bit a	Bit b	Résultat
0	0	0
0	1	0
1	0	0
1	1	1

Cet opérateur AND bit à bit est symbolisé comme ceci : $a.b$ . Le symbole de l'opérateur ET ressemble à celui d'un produit car l'opérateur donne effectivement le résultat de la multiplication bit à bit.

Exemple : $1100.1010=1000$

Notation
dans ce livre	$a.b$
quelques autres notations	a AND b	a & b	$a\land b$

L'instruction AND bit à bit est commutative : $a.b=b.a$

Elle est aussi associative : $(a.b).c=a.(b.c)$

Elle est aussi distributive avec le OR bit à bit : $(a+b).c=(c.b)+(c.a)$

On peut aussi remarquer qu'elle dispose de la propriété d'idempotence : $a.a=a$

Petite remarque : $a.0=0$

De plus, $a.{\overline {a}}=0$

L'opération OU (OR)[modifier | modifier le wikicode]

Vient ensuite le OR bit à bit. Il fonctionne comme le AND bit à bit sauf qu'il effectue un OR binaire entre les bits du nombre. Ce OR binaire prend deux bits, A et B, et fonctionne comme ceci :

Bit a	Bit b	Résultat
0	0	0
0	1	1
1	0	1
1	1	1

Cet opérateur OR bit à bit est symbolisé comme ceci : $a+b$ . Pour éviter toute ambiguïté en présence d'addition, nous utiliserons parfois le symbole $|$ dans la suite du cours.

Exemple : $1100+1010=1110$

Notation
dans ce livre	$a+b$ (a ne pas confondre avec l'addition !)
dans ce livre	$a\|b$
quelques autres notations	a OR b	$a\lor b$

L'opérateur OR est commutatif : $a+b=b+a$

Il est aussi associatif : $(a+b)+c=a+(b+c)$

Il est aussi distributif avec le AND bit à bit : $(a.b)+c=(c+b).(c+a)$

On peut aussi remarquer qu'il dispose de la propriété d'idempotence : $a+a=a$

Petite remarque : $a+0=a$

L'opération OU exclusif (XOR)[modifier | modifier le wikicode]

Vient ensuite le OU exclusif bit à bit, appelé XOR en anglais (eXclusive OR). Il fonctionne comme le AND et le OR bit à bit sauf qu'il effectue un XOR binaire entre les bits du nombre. Ce XOR binaire prend deux bits, A et B, et fonctionne comme ceci :

Bit a	Bit b	Résultat
0	0	0
0	1	1
1	0	1
1	1	0

Le résultat est 0 quand les deux bits sont égaux, et 1 quand les deux bits sont différents.

Cet opérateur XOR bit à bit est symbolisé comme ceci : $a\oplus b$ comme une addition bit à bit sans retenue.

Exemple : $1100\oplus 1010=0110$

Notation
dans ce livre	$a\oplus b$
quelques autres notations	a XOR b	a^b

L'opérateur XOR est commutatif : $a\oplus b=b\oplus a$

Il est aussi associatif : $(a\oplus b)\oplus c=a\oplus (b\oplus c)$

Petite remarque : $a\oplus 0=a$

Autre remarque : $a\oplus a=0$

Les décalages et rotations[modifier | modifier le wikicode]

À côté des opérations précédentes, on trouve les opérations de décalage, qui décalent un nombre binaire de un ou plusieurs rangs vers la gauche ou la droite. A priori, cette opération n'a rien de compliqué, à un détail près : lorsqu'on décale un nombre, certains bits sont inconnus, ce qui laisse des vides qu'il faut combler. Pour résoudre ce petit problème, il existe diverses solutions, qui donnent naissance à plusieurs types de décalages : les décalages logiques, les décalages arithmétiques et les rotations.

Les décalages logiques[modifier | modifier le wikicode]

L'idée la plus immédiate serait de remplir ces vides avec des zéros, ce qui donne un décalage logique. Pour un décalage vers la gauche, l'opération similaire en décimal serait d'ajouter des zéros à la fin d'un nombre, ce qui serait équivalent à multiplier par 10, 100, 1000, bref : par une puissance de 10. Un décalage à droite reviendrait en binaire à décaler la position de la virgule d'un cran vers la gauche et à oublier ce qu'il y a après la virgule, ce qui revient à diviser par une puissance de dix. Cette logique vaut aussi pour le décalage en binaire, si on se rappelle toutefois qu'on doit compter en base 2. Un décalage logique à gauche correspond donc à une multiplication ou division par 2, 4, 8, 16, ..., bref, par une puissance de deux.

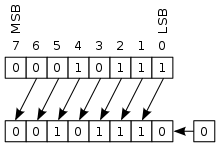L'utilité principale des opérations de décalage est donc qu'elles permettent de faire simplement des multiplications ou divisions par $2^{n}$ , pour les entiers non signés. Précisément, un décalage vers la gauche de $n$ rangs est équivalent à une multiplication par $2^{n}$ , alors que le décalage vers la droite qui revient à diviser un nombre entier par $2^{n}$ . Cette propriété est souvent utilisée par certains compilateurs, qui préfèrent utiliser des instructions de décalages (qui sont des instructions très rapides) à la place d'instructions de multiplication ou de division qui ont une vitesse qui va de moyenne (multiplication) à particulièrement lente (division). Il faut cependant signaler que lorsqu'on effectue un décalage à droite, certains bits de notre nombre vont sortir du résultat et être perdus : le résultat est tronqué ou arrondi vers zéro. Plus précisément, le résultat d'un décalage à droite de n rangs sera égal à la partie entière du résultat de la division par $2^{n}$ .

Le tableau ci-dessous indique les notations utilisées pour les décalages.

Notation
	Décalage à gauche	Décalage à droite
dans ce livre	$x<<n$	$x>>n$
quelques autres notations	$SHL^{n}(x)$	$SHR^{n}(x)$

Les décalages arithmétiques[modifier | modifier le wikicode]

Le décalage logique ne donne cependant pas de bons résultats avec des nombres signés négatifs : on obtient un résultat qui n'a pas grand sens mathématiquement. Il faut dire que le bit de signe est alors remplacé par un zéro, ce qui peut inverser le signe du résultat. Une solution intuitive est de conserver le bit de signe, de ne pas le décaler. Mais en faisant cela, que mettre dans le bit situé juste avant le bit de poids fort après décalage ? On pourrait penser mettre un zéro dedans, mais cela ne donnerait pas le bon résultat avec les nombres négatifs. La solution est en fait de recopier le bit de signe dans ce bit. Tout se passe comme si on faisait le décalage normalement, comme un décalage logique, mais que le bit de poids fort était cependant conservé au lieu d'être remplacé par un zéro. Ce faisant, le bit de signe est conservé et le décalage est malgré tout effectué correctement.

En faisant cela, on obtient un décalage qui effectue correctement des multiplications/divisions par $2^{n}$ sur des nombres signés. De tels décalages sont appelés décalages arithmétiques (arithmetical shift en anglais). La différence avec un décalage logique est la méthode d'arrondi des nombres négatifs. Avec les décalages arithmétiques, les nombres négatifs sont arrondis vers moins l'infini. Pour donner un exemple, 92 sera arrondi en 4, tandis que −92 sera arrondi en −5.

Les rotations de bits[modifier | modifier le wikicode]

Les rotations sont identiques aux décalages, à part que les bits qui sortent du nombre sont ceux qui rentrent pour combler les vides.

Ces opérations sont très utiles en cryptographie, et sont notamment très utilisées dans certains algorithmes de chiffrement. Les rotations sont aussi très utiles dans certains cas particuliers dans lesquels on doit manipuler des données bits par bits. Par exemple, un calcul du nombre de bits à 1 dans un nombre peut s'implémenter de façon naïve avec des instructions de rotation.

Le tableau ci-dessous indique les notations utilisées pour les rotations.

Notation
Rotation à gauche	Rotation à droite
$ROTL^{n}(x)$	$ROTR^{n}(x)$

Quelques règles de calcul utiles[modifier | modifier le wikicode]

Dans la suite du cours, nous ferons souvent usage de quelques équations qui mélangerons les différentes opérations bit à bit. Ne vous étonnez donc pas si vous voyez des équations de ce style :

{\overline {a}}.b.\left[(c+{\overline {d}})\oplus (d+a)\right]

Il existe quelques règles mathématiques qui nous permettront de simplifier de telles équations.

Les règles pour les expressions booléennes[modifier | modifier le wikicode]

Commençons par les règles qui impliquent uniquement des opérations bit à bit/booléens. Nous en avons déjà vu la plus grande partie plus haut, en parlant de la distributivité et de l'associativité des différents opérateurs. En voici la liste complète :

Commutativité	$a+b=b+a$ $a.b=b.a$ $a\oplus b=b\oplus a$
Associativité	$(a+b)+c=a+(b+c)$ $(a.b).c=a.(b.c)$ $(a\oplus b)\oplus c=a\oplus (b\oplus c)$
Distributivité	$(a+b).c=(c.b)+(c.a)$ $(a.b)+c=(c+b).(c+a)$
Idempotence	$a.a=a$ $a+a=a$
Élément nul	$a.0=0$ $a+1=1$
Élément Neutre	$a.1=a$ $a+0=a$ $a\oplus 0=a$
Loi de De Morgan	${\overline {a}}+{\overline {b}}={\overline {a.b}}$ ${\overline {a}}.{\overline {b}}={\overline {a+b}}$
Complémentarité	${\overline {\overline {a}}}=a$ $a+{\overline {a}}=1$ $a.{\overline {a}}=0$ $a\oplus {\overline {a}}=1$ $a\oplus a=0$ $a\oplus 1={\overline {a}}$

Les règles pour les expressions booléennes et arithmétiques[modifier | modifier le wikicode]

Il est parfaitement possible de mixer des opérations booléennes avec des opérations arithmétiques. Par exemple, on peut se demander ce que vaut ${\overline {x-y}}$ , un calcul qui sera notamment beaucoup utilisé dans la suite du cours. Les règles qui régissent les mélanges/interactions entre opérations mathématiques et opérateurs bit à bit dépendent du codage des nombres, notamment pour les nombres signés. Nous allons supposer que les nombres signés sont codés en complètement à deux. Les règles qui en découlent sont résumées dans le tableau suivant :

Addition	$x+y=(x.y)<<1+(x\oplus y)$ $x+y=(x\|y)<<1-(x\oplus y)$ $x+y=(x\|y)+(x.y)$ ${\overline {x+y}}={\overline {x}}-y$
Soustraction	$x-y=x+{\overline {y}}+1$ $x-y=(x.{\overline {y}})-({\overline {x}}.y)$ $x-y=(x\oplus y)-\left[({\overline {x}}.y)<<1\right]$ ${\overline {x-y}}={\overline {x}}+y$
Opposé	$-y={\overline {y}}+1$ $-y={\overline {y-1}}$ ${\overline {y}}=-y-1$ $-{\overline {y}}=y+1$ ${\overline {-y}}=y-1$

Les équations pour l'opposé et la soustraction peuvent se déduire assez facilement de l'équation $-y={\overline {y}}+1$ , définition de l'opposée d'un nombre en complètement à deux. En guise d'exercice, vous pouvez tenter d'en déduire l'équation ${\overline {x-y}}={\overline {x}}+y$ . Si vous utilisez les règles sur les opérateurs booléens, vous devriez y arriver sans trop de peine.

Les règles pour les expressions booléennes et comparaisons[modifier | modifier le wikicode]

Il est parfaitement possible de comparer des expressions booléennes, et certaines égalités ou inégalités sont toujours vraies. On peut rapidement se rendre compte que :