« Cosmologie/Le spectre de puissance des perturbations » : différence entre les versions
| Ligne 64 : | Ligne 64 : | ||
: <math>\frac{\partial^2 \delta}{\partial^2 t} + 2 H \frac{\partial \delta}{\partial t} - 4 \pi G \rho_m \cdot \delta = 0</math> |
: <math>\frac{\partial^2 \delta}{\partial^2 t} + 2 H \frac{\partial \delta}{\partial t} - 4 \pi G \rho_m \cdot \delta = 0</math> |
||
On a vu plus haut que le champ de densité est décrit par la transformée de Fourier suivante : |
|||
: <math>\delta(x,t) = \frac{1}{(2 \pi)^3} \int \overline{\delta}(\vec k) \cdot e^{- i (\vec k \cdot \vec x)} d \vec k</math>, avec <math>\vec k</math> le vecteur d'onde, un vecteur de norme <math>k = \frac{2 \pi}{\lambda}</math>. |
|||
On peut injecter l'équation précédente dans l'équation du début de section. Le résultat, très difficile à obtenir, est pourtant surprenamment simple : |
On peut injecter l'équation précédente dans l'équation du début de section. Le résultat, très difficile à obtenir, est pourtant surprenamment simple : |
||
Version du 17 août 2020 à 14:01
Dans les chapitres précédents, nous sommes parti du principe que la distribution de la densité nous était inconnue. Nous supposions simplement qu'elle existe, mais en savoir plus sur ses propriétés. Et il est vrai que dans le cas général, on ne peut rien dire sur la distribution des perturbations. Par contre, on peut en donner quelques propriétés statistiques plus ou moins pertinentes. Ce champ de densité, peu importe sa forme exacte, a une densité moyenne, une certaine dispersion autour de cette moyenne, et ainsi de suite. Dans ce chapitre, nous allons voir diverses mesures statistiques du champ de densité et voir comment elles se marient avec les équations du chapitre précédent.
La fonction de corrélation
Pour commencer, prenons un exemple assez simple, mais en apparence détaché des perturbations cosmologiques. Si je regarde un point de l'espace et un volume autour de ce point (supposé assez gros à l'échelle cosmologique). Il y a une probabilité que dans le volume , je trouve une galaxie. Si on suppose qu'il y a en moyenne galaxies par unité de volume, alors cette probabilité est de :
De même, en un point , cette probabilité est de :
Maintenant, on souhaite savoir quelle est la probabilité que j'observe une galaxie à la fois au point et au point . Intuitivement, on penserait avoir :
Mais cela ne vaut que si les positions des galaxies sont totalement indépendantes, ce qui n'est pas garanti. Dans les faits, il est possible qu'il y aie une relation dans la distribution des galaxies qui fait que si on observe une galaxie en x, alors sa présence en y est plus probable, en fonction des positions x et y. On doit donc tenir compte de telles corrélations. La formule exacte, qui en tient compte, est la suivante :
- , où est la fonction de corrélation.
Par analogie, on peut utiliser le même formalisme, mais pour prédire non pas la présence d’une galaxie, mais l'intensité d'une fluctuation de densité. On a alors :
- , où est la densité moyenne du champ de densité.
- Il est possible de définir des fonctions de corrélation pour trois points, quatre points, voire beaucoup plus.
L'hypothèse d’homogénéité statistique
Si on considère que l'univers est statistiquement homogène, alors la fonction de corrélation ne dépend que de la distance entre x et y, mais pas de la position exacte de x et y.
Ce qui peut d'écrire comme suit :
- , avec r la distance entre les deux points x et y.
Sous cette hypothèse, le calcul de la densité moyenne est assez simple. Il suffit de prendre la moyenne spatiale de la densité. La corrélation moyenne entre deux points peut se calculer en prenant un grand ombre de points et y et en calculant la corrélation pour chaque paire de points. Il suffit de faire la moyenne des corrélations obtenues, pour obtenir la corrélation moyenne. les mesures semblent montrer que la fonction de corrélation suit une loi de puissance de la forme suivante :
- , avec .
La transformée de Fourier du champ de densité
Une autre manière équivalente de décrire le champ de densité est d'utiliser son spectre de puissance. Pour rappel, le terme est une fonction qui associe une perturbation de densité à tout endroit de l'espace et à chaque instant. On dit aussi que cette fonction décrit un champ de densité. Or, il existe un théorème qui nous dit que tout champ peut être décomposée en champs périodiques semblables à des cosinus ou sinus. Ces champs périodiques sont des formellement des ondes de forme cosinusoïdales ou sinusoïdales. Dans notre cas, la forme de ces ondes est l'équivalent en trois dimension d'un sinus/cosinus. En additionnant un certain nombre (potentiellement infini) de ces ondes de base, pondérées par un coefficient, on peut obtenir n'importe quelle champ résultant. C'est ce qu'on appelle la transformée de Fourier des fonctions continues. Le champ de densité ne fait pas exception et on peut utiliser ce théorème pour décomposer le champ de densité en une somme d'ondes.
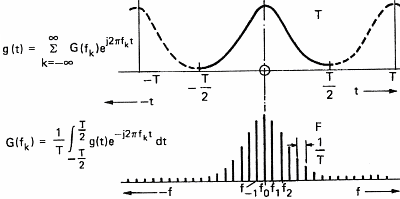
Si on note chaque onde élémentaire , le théorème de Fourier nous donne l'équation suivante :
- , avec le vecteur d'onde, un vecteur de norme .
Le spectre de puissance
Le spectre de puissance donne l'ensemble des amplitudes de chaque onde sinusoïdale. Dit autrement, il donne l'amplitude pour chaque fréquence possible et est donc une fonction du type . Il s'obtient avec la transformée de Fourier.
Le spectre de puissance et la fonction de corrélation sont reliés l'un à l'autre, par la relation suivante :
Dans le cas général, connaitre le spectre de puissance n'est pas suffisant pour décrire complètement le champ de densité, du moins d'un point de vue statistique. Il en est de même avec la fonction de corrélation qui est elle aussi un résumé imparfait de la distribution. Cependant, il existe des distributions statistiques pour lesquelles la connaissance du spectre de puissance et/ou de la fonction de corrélation suffit à décrire totalement les propriétés statistiques du champ décrit. Ce sont les champs aléatoires gaussiens, pour lesquels la densité suit une distribution gaussienne (la fameuse courbe en cloche). Et ce sont ces gaussiennes qui sont utilisées pour modéliser le champ de densité cosmologique, faute de mieux.
L'équation d'évolution des perturbations et le spectre de puissance
Dans le chapitre précédent, nous avions vu que les perturbations se sont formées lors du découplage. Précisément, les perturbations ont évoluées avant le découplage, mais elles se sont gelées lors du découplage. Le spectre de puissance des perturbations est donc un reliquat du découplage et on doit en trouver la trace dans le fond diffus cosmologique (on en dira plus dans quelques chapitres). Les perturbations ayant cessé d'évoluer après le découplage, l'évolution de ces perturbations est donc guidée par l'équation suivante, vue dans le chapitre précédent, qui décrit l'évolution des perturbations après le découplage :
On a vu plus haut que le champ de densité est décrit par la transformée de Fourier suivante :
- , avec le vecteur d'onde, un vecteur de norme .
On peut injecter l'équation précédente dans l'équation du début de section. Le résultat, très difficile à obtenir, est pourtant surprenamment simple :










![{\displaystyle P(x,y)=\left({\overline {n}}\cdot dV\right)^{2}\left[1+\epsilon (x,y)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e2ecb4ca5ae128f1f87bf2acd081c7b85d03131)

![{\displaystyle <\rho (x)\rho (y)>={\overline {\rho }}^{2}\left[1+\epsilon (x,y)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7011cc18e64e77be1fd0d8afe8b5ce486cd3eb70)

![{\displaystyle <\rho (x)\rho (y)>={\overline {\rho }}^{2}\left[1+\epsilon (|x-y|)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e78e420c115ad4823c5451e52d7358973ace1eb)
![{\displaystyle <\rho (x)\rho (y)>={\overline {\rho }}^{2}\left[1+\epsilon (d)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fcfa6c64d2f466b99fc7ba6a221394cbd945a1d)









![{\displaystyle {\frac {\partial ^{2}{\overline {\delta }}(k)}{\partial ^{2}t}}+2H{\frac {\partial {\overline {\delta }}(k)}{\partial t}}-{\frac {1}{a^{2}}}\left[c_{s}^{2}k^{2}+4\pi G\rho _{m}\right]{\overline {\delta }}(k)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2bd8098bac8cd1a829f7a8df83e3654cc4b9431b)