Les fonctions de hachage cryptographiques

On rencontre bien souvent sur les pages de téléchargement des empreintes calculées grâce à des algorithmes comme MD5. Ces « résumés » des fichiers permettent notamment de vérifier la validité et l'intégrité des archives récupérées. Cependant, peu d'utilisateurs connaissent le fonctionnement de ces primitives, les fonctions de hachages, qui sont très répandues. Nous nous intéresserons principalement aux fonctions de hachages dites cryptographiques qui touchent un vaste domaine d'applications. Dès la fin des années 1990, certaines fonctions de hachage populaires ont été analysées puis « cassées ». Cet article examine les enjeux liés à ces algorithmes et leur fonctionnement.
Introduction[modifier | modifier le wikicode]
Dans cet article, nous utiliserons tantôt les termes empreinte ou condensé pour désigner le même concept. On rencontre aussi le terme signature (numérique) qui a un sens plus large car il est normalement lié à un utilisateur. Cette appellation est plutôt utilisée dans le cadre de la cryptographie asymétrique (signature d'un document via une clé privée avec par exemple GnuPG) mais sous certaines conditions, ce mot s'applique aussi aux fonctions de hachage.
Les auteurs de logiciels proposent souvent des empreintes sur les pages dédiées aux téléchargements, on rencontre des fichiers portant l'extension md5 ou sha1 qui contiennent de telles séquences. En comparant l'empreinte de la version téléchargée avec l'empreinte disponible sur le site, l'utilisateur peut s'assurer que sa version n'a pas été corrompue (erreurs de transmission, virus, etc.). Ces condensés sont pour la plupart calculés grâce aux outils md5sum ou sha1sum qui font partie des GNU Core-utils (un ensemble de programmes indispensables pour gérer un système GNU/Linux).
Par exemple, sur le site de la distribution Fedora, on peut lire ceci dans la section téléchargement :
FC3-i386-disc1.iso (md5sum : db8c7254beeb4f6b891d1ed3f689b412)
Après avoir téléchargé l'iso, on peut lancer l'utilitaire md5sum sur le fichier et on devrait retrouver exactement cette séquence. Si la suite varie, ne serait-ce qu'à un seul endroit, alors nous avons affaire à un fichier corrompu ou incomplet. Il est en effet extrêmement peu probable d'obtenir la même empreinte avec deux fichiers différents, nous reviendrons sur ce point essentiel plus tard. Nous allons également voir que les fonctions de hachage ne se limitent pas seulement à cette application.
Définition[modifier | modifier le wikicode]
Les programmes comme md5sum ou sha1sum" utilisent ce que l'on appelle une fonction de hachage. Il y a en fait deux catégories principales de fonctions de hachage, celles qui sont cryptographiques et les autres. Les fonctions de hachage cryptographiques doivent satisfaire des contraintes liées à la sécurité. MD5 et SHA-1 sont cryptographiques mais il en existe bien d'autres. Les premières fonctions de hachage en tant que telles datent de la fin des années 1980 (MD2) mais l'idée est plus ancienne et, toute précaution gardée, a germé dès l'apparition des codes correcteurs d'erreurs dans le cadre de la théorie de l'information. En effet, une somme de contrôle comme CRC-32 (code de redondance cyclique) s'apparente à une fonction de hachage puisqu'elle permet de vérifier la validité des données. La principale différence, c'est que la somme de contrôle est utilisée pour corriger une mauvaise transmission sur un canal bruité, « sans intelligence », alors que les fonctions de hachage doivent résister à des attaques mathématiques ciblées et d'autres tentatives malveillantes dotées d'une « intelligence » (ie. lancées sciemment par l'attaquant).
Une fonction de hachage prend en entrée un message de taille quelconque, applique une série de transformations et réduit ces données. On obtient à la sortie une chaîne de caractères, le condensé qui résume en quelque sorte le fichier. Cette sortie a une taille fixe qui varie selon les algorithmes (128 bits pour MD5 et 160 bits pour SHA-1). Vous aurez remarqué que la séquence calculée par md5sum est codée en hexadécimal, ceci dans le but de limiter la longueur de la chaîne et faciliter les comparaisons entre les empreintes. Il serait en effet assez pénible de devoir comparer deux suites binaires de 128 caractères.
Une fonction de hachage cryptographique doit aussi satisfaire d'autres contraintes. La première stipule qu'il doit être très difficile de retrouver ou générer un texte à partir de l'empreinte (on parle alors de fonction à sens unique). Par très difficile, on entend que même avec une armée de machines dédiées à cette tâche, il sera impossible d'effectuer une telle extraction en un temps raisonnable. Au passage, on ne voit que trop fréquemment sur des forums des assertions erronées comme mot de passe crypté avec MD5. Une fonction de hachage toute seule n'est pas une primitive pour chiffrer. Cependant, des variantes comme SHACAL (basée sur SHA-1) permettent de travailler en mode chiffrement et donc d'obtenir un algorithme de chiffrement par bloc, réversible pour autant que l'on connaisse la clé. Il est aussi possible d'employer la fonction de hachage comme générateur de nombres pseudo-aléatoires ayant pour graine la clé, et d'effectuer un ou-exclusif avec le texte à chiffrer. On obtient alors un chiffrement de flux.
Une autre caractéristique d'une fonction de hachage cryptographique concerne le comportement de l'empreinte selon le fichier en entrée. La moindre modification dans ce fichier doit engendrer un condensé totalement différent. En outre, le hachage doit rendre impossible la création d'un fichier qui donne la même empreinte qu'un autre. Cette dernière contrainte est cruciale pour assurer l'intégrité d'un fichier. Si elle n'était pas respectée, on pourrait facilement générer un fichier corrompu mais valide aux yeux de l'utilisateur. Toutefois, cela ne veut pas dire que des collisions n'existent pas. Comme une empreinte a une taille fixe et que celle-ci est inférieure à la taille des messages que l'on peut mettre à l'entrée de la fonction, alors il existe nécessairement au moins deux messages qui génèrent la même empreinte. Pour être plus exact, avec des entrées dont la taille n'est pas limitée, il existe une infinité de collisions. La solidité de la fonction repose en partie sur l'impossibilité de trouver de tels conflits en un temps raisonnable.
Les fonctions de hachage dans les structures de données[modifier | modifier le wikicode]

Cette résistance aux collisions est aussi recherchée dans les langages de programmation et plus particulièrement dans des structures de données nommées « tables de hachage », « dictionnaires » ou « maps ».
Il s'agit de structures qui peuvent être indexées par des objets ou clés. Un objet se voit attribué un numéro idéalement unique obtenu via une fonction de hachage et cet identifiant permet de retrouver l'objet qui lui est associé dans la table. Par exemple en Java, on peut écrire :
url = table.get("Gentoo")
au lieu d'une indexation classique comme
url = table[10].
La chaîne Gentoo sert de clé pour accéder à l'URL. Bien entendu, il faut éviter que deux objets distincts entrent en collision et accèdent à la même entrée dans la table. Grâce à une fonction de hachage la plus robuste possible sans pénaliser les performances, on évite déjà bien des problèmes mais ce n'est pas toujours suffisant. On peut vite s'apercevoir que la fonction de hachage utilisée par Java n'est pas fiable et nécessite des mécanismes supplémentaires. Par exemple, "Aa".hashcode() = 2112 et "BB".hashcode() = 2112, nous avons donc une collision.
À noter que la méthode hashcode() est disponible pour tous les objets Java. La fonction utilisée est simple à déterminer : "a".hashcode() = 97 et "b".hashcode() = 98. Il s'agit des codes ASCII des caractères considérés. Avec "aa".hashcode() = 3104 et "ab".hashcode() = 3135, nous nous rendons compte que la fonction a cette forme : . Avec trois caractères "abc", le polynôme devient : , et ainsi de suite pour une chaîne plus longue. Si le résultat venait à dépasser la capacité de 32 bits, alors l'excédent serait reporté et servirait de condensé (on effectue un modulo). Au vu de ces caractéristiques, la fonction de Java n'est clairement pas cryptographique mais il ne faut pas oublier que cela n'est pas son but.
En contrepartie, elle est rapidement calculée ce qui est idéal pour accéder à une table. Pour éviter les collisions, on emploie d'autres algorithmes qui prennent le relais dans les cas critiques. Java emploie notamment le système du chaînage. L'implémentation nécessite une liste chaînée ou un arbre mais le principe reste le même. Si une collision se produit lors de l'insertion d'un nouvel objet, alors celui-ci et sa clé sont placés à la suite de l'objet déjà présent dans la structure. Dans notre exemple, "Aa" et "BB" seront insérés dans la structure propre à la "case" 2112. Lors de l'appel à un get("BB"), on pourra accéder à l'emplacement 2112 et en parcourant la liste, on trouvera la clé "BB" et l'objet associé qui sera retourné par la méthode get(). Java utilise encore plusieurs autres concepts pour améliorer les performances. Nous ne les détaillerons pas ici, mais le lecteur intéressé peut consulter le lien donné à la fin.
Nous pouvons encore citer quelques algorithmes qui emploient le hachage . Par exemple, l'algorithme de Rabin-Karp (détection de chaînes dans des textes) ou encore les filtres de Bloom qui sont comparables à des tables probabilistes et qui permettent de déterminer l'appartenance d'un élément à un ensemble particulier.
Vers des fonctions plus robustes[modifier | modifier le wikicode]
Que faut-il pour faire une fonction cryptographique ? Reprenons pour cela l'exemple de Java. L'empreinte générée tient sur seulement 32 bits, le nombre de condensés disponibles se réduit ainsi à environ 4 milliards (232). Cette espace n'est pas utilisé efficacement dans le cas des chaînes de caractères. On assiste de ce fait à un regroupement des condensés dans certains intervalles alors qu'une bonne fonction cryptographique est censée répartir au maximum les résultats dans l'espace disponible.
Pour illustrer cette vulnérabilité, prenons l'exemple d'un attaquant qui intercepte une empreinte calculée avec la fonction de hachage Java. Un espion lui assure que cette empreinte ne concerne qu'un mot de quelques lettres qui ne contient que des majuscules. Le pirate sait que la plus grande empreinte sera obtenue avec une suite de "Z". Avec "ZZZ", l'empreinte Java sera de 89370, on ne peut pas faire plus grand avec trois majuscules. Avec "ZZZZ", le condensé se monte à environ 2,7 millions. Si l'attaquant intercepte une valeur comprise dans cette intervalle, il devine que le mot possède certainement quatre caractères. Avec une résolution de l'équation w + x*31 + y*31*31 + z*31*31*31, on retrouve la solution sans passer par une recherche complète de toutes les possibilités, nous avons réussi à soutirer un peu d'information. On comprend qu'une fonction robuste ne doit pas permettre de telles manipulations et se laisser inverser.
En termes plus techniques, cette recherche d'une entrée possible à partir de l'empreinte est une attaque sur la première préimage. Une attaque sur la seconde préimage consiste quant à elle, à forger des données qui donnent la même empreinte qu'un autre message. Finalement, la troisième attaque se résume à rechercher des collisions quelconques.
La fonction de hachage de Java ne résiste à aucune de ces attaques puisque nous pouvons l'inverser et créer des collisions assez facilement. Les deux premières attaques sont particulièrement redoutables, surtout si elles permettent de forger à peu près n'importe quel message. Comme exemple simple, nous pouvons citer l'insertion de code malveillant dans un exécutable sans que celui-ci ne paraisse corrompu.
Les systèmes de mots de passe[modifier | modifier le wikicode]
Plusieurs systèmes dont GNU/Linux gèrent les mots de passe grâce à un fichier (comme /etc/shadow) qui contient les empreintes des mots de passe. Cela évite de stocker les mots de passe en clair. Quand un utilisateur entre un mot de passe, il suffit de le hacher et de comparer l'empreinte avec le contenu du fichier. Avec une bonne attaque sur la première préimage, on pourrait peut-être retrouver des mots de passe qui seraient acceptés par le système. Pour s'immuniser contre des attaques faciles par dictionnaire, on ajoute un sel qui perturbe le mot de passe ou l'algorithme de hachage et donc l'empreinte. Si deux utilisateurs décident d'employer le même mot de passe alors les empreintes correspondantes ne seront pas identiques dans le fichier. Le sel peut correspondre à la date à laquelle est ajouté un utilisateur ou toute autre composante variable. Il est en général visible et n'est pas soumis à une protection particulière. On peut aussi utiliser une variable qui s'incrémente lors de l'ajout d'un nouvel utilisateur.

Sur la plupart des GNU/Linux, on emploie l'implémentation FreeBSD de MD5. Sur UNIX, on utilise une variante de l'algorithme de chiffrement DES au lieu d'une fonction de hachage. Le hachage repose sur le chiffrement itératif d'une suite de zéros avec le mot de passe servant de clé, l'utilisation d'un algorithme de chiffrement n'est donc pas incompatible avec la notion de hachage. Le sel modifie des variables à l'intérieur de DES ce qui empêche des attaques avec du matériel spécialement conçu pour traiter DES. De plus, les 25 itérations utilisées par UNIX sont supposées ralentir une éventuelle attaque. À noter que DES chiffre des blocs de 64 bits dont 8 bits de parité ce qui réduit la taille effective à 56 bits. À cause de cette contrainte, les mots de passe UNIX ne dépassent pas les 8 caractères. Les mots de passe UNIX tout comme ceux de GNU/Linux peuvent être recherchés avec des utilitaires comme John The Ripper (recherche exhaustive et dictionnaires).
D'autres systèmes comme celui de Windows 9x (LanManager) sont mal pensés et très vulnérables. Un mot de passe LanManager (au maximum 14 caractères) est d'abord coupé en deux parties de 7 caractères chacune. Cette opération est une première erreur. Les minuscules sont ensuite transformées en majuscules ce qui réduit considérablement le nombre de possibilités et représente un vrai trou de sécurité mathématiquement parlant. Une autre vulnérabilité est causée par l'absence de sel. Les deux blocs sont ensuite séparément hachés, ils servent de clés à un DES qui chiffre un message défini dans les spécifications. Au final, nous avons deux blocs complètement indépendants qui forment une empreinte. On détermine très rapidement qu'un mot de passe contient plus de 7 caractères en comparant la deuxième partie de l'empreinte avec celle produite par une chaîne vide.
Pour le reste, une attaque inspirée par les compromis temps-mémoire de Martin Hellman et conçue par Philippe Oechslin permet de déterminer un mot de passe alphanumérique en quelques secondes via des tables (dites tables arc-en-ciel). Depuis Windows NT, le système est basé sur MD4 mais des risques liés à la compatibilité avec les anciennes versions subsistent, il est toutefois possible de désactiver certaines options pour corriger le problème. Dans Windows Server 2003, LanManager est désactivé par défaut.
Stimulation/réponse[modifier | modifier le wikicode]
Le hachage est présent dans un autre concept lié aux authentifications : le challenge (ou stimulation/réponse, voir Preuve à divulgation nulle de connaissance). Un client veut accéder à un serveur mais ne veut pas transmettre des informations en clair sur le réseau. De plus, le système ne dispose pas d'une fonction de chiffrement. On ne veut pas non plus que les données soient identiques lors de chaque connexion. Cela évite une attaque avec un dictionnaire ou alors un envoi ultérieur de la même empreinte par une tierce personne. Le serveur génère pour cela un nombre aléatoire et l'envoie au client. Ce que fait le client avec ce nombre peut varier mais on peut imaginer le scénario simple dans lequel le client concatène le nombre aléatoire avec sa clé secrète. En pratique, ce schéma ne doit pas être suivi et il faut plutôt employer une technique éprouvée comme celle préconisée par le standard HMAC (hashed message authentification code).
Le client hache ensuite cette chaîne et envoie le résultat au serveur. Le serveur effectue la même opération de son côté puisqu'il connaît également la clé secrète du client, il lui suffit de vérifier les deux signatures et d'accepter le client si la comparaison est positive. Un problème apparaît si le serveur venait à être compromis, on pourrait dans ce cas récupérer la clé secrète et avoir accès au serveur de manière transparente en reproduisant la séquence d'accès. Des mesures de protection supplémentaires doivent ainsi être prises pour assurer l'intégrité des différentes parties.
Le paradoxe des anniversaires[modifier | modifier le wikicode]
Outre les problèmes évoqués auparavant, la fonction de hachage de Java présente un grand nombre de collisions. Il est temps d'aborder un résultat qui permet de mieux quantifier la résistance aux collisions : le paradoxe des anniversaires.
- Combien faut-il de lecteurs/lectrices de cet article pour avoir au moins 50% de chance d'obtenir deux personnes avec la même date de naissance ?
Intuitivement, nous serions tenté de répondre qu'il faudrait au moins 183 personnes (la moitié de 365 jours) pour arriver à un résultat positif. Aussi étonnant que cela puisse paraître, nous n'avons pas besoin d'un groupe aussi grand. Il suffit de tirer au sort seulement 23 personnes pour trouver deux dates identiques avec 50% de succès. Pour obtenir un succès de l'ordre de 70%, il faut 30 personnes. Avec 40 personnes, nous nous approchons des 90% de réussite. Ce résultat est bien connu de ceux qui ont déjà eu à travailler avec les probabilités. Il part aussi du principe que les dates de naissance, indépendantes les unes des autres, sont réparties uniformément dans toute l'année. Mathématiquement, si nous avons N possibilités (N=365 dans notre exemple) alors pour obtenir deux résultats identiques (avec 40% de réussite), il suffit d'avoir un échantillon de l'ordre de la racine carrée de N (soit 19 personnes). Pour obtenir un taux de réussite de 70%, il faut multiplier la racine carrée de N par environ 1.56.
Application dans le cadre du hachage[modifier | modifier le wikicode]

Prenons par exemple le SHA-1 et son empreinte de 160 bits : le nombre d'empreintes possibles est immense : 2160 (1048 possibilités). Pour donner un ordre de grandeur, c'est 1000 fois moins que le nombre d'atomes dans notre planète. Il est important de dire que SHA-1 distribue ses empreintes presque uniformément dans l'espace à sa disposition (des tests statistiques ont été effectués pour déterminer ses propriétés en tant que générateur aléatoire), il ne va pas privilégier une zone particulière. Maintenant, si nous voulons trouver une collision quelconque, nous pouvons appliquer le paradoxe des anniversaires. Il en ressort que pour trouver une collision sur SHA-1 avec un taux de réussite de 50%, nous avons besoin d'au moins 280 messages au contenu aléatoire (). Avec 281 messages, nous aurons de forte chance de trouver une collision. Le gain est énorme par rapport aux 2160 du départ mais un facteur comme 280 reste difficilement accessible même pour une grosse organisation (il faudrait compter quelques années).
Mis à part le manque de puissance de calcul, un problème de taille survient. Comment stocker les 280 empreintes pour la comparaison ? À raison de 160 bits par empreinte, cela représente environ 200 millions de milliards de Gb, soit 25 millions de milliard de Go. Il existe toutefois des techniques plus sophistiquées qui évitent le stockage des empreintes. La résistance aux collisions d'une fonction de hachage est donc bornée par le paradoxe des anniversaires mais rien ne dit qu'il n'existe pas un meilleur moyen pour trouver ces collisions en profitant des faiblesses de l'algorithme.
À titre de comparaison, MD5 a un espace plus réduit car son empreinte ne fait que 128 bits, soit une attaque avec 264 messages. À l'instar des concours de factorisation, MD5Crk visait à trouver une collision sur MD5 en faisant appel aux ordinateurs des particuliers. L'algorithme employé était le rho de Pollard, initialement utilisé pour résoudre un autre problème cryptographique : le logarithme discret. Le principe est d'attribuer une empreinte distincte à chaque ordinateur, le programme hache cette empreinte et recommence sur le résultat qu'il vient d'obtenir. Avec suffisamment de temps devant soi, on est assuré de trouver une collision. Précisons avant tout qu'une fonction de hachage est nécessairement cyclique : comme le nombre d'états possibles est limité alors effectuer plus d'itérations que d'états possibles va obligatoirement nous amener à rencontrer un état déjà connu. Ceci explique le nom attribué à cette méthode puisque la forme du chemin parcouru ressemble à la lettre grec rho. Un algorithme de Pollard s'exécutant sur une unique machine doit détecter quand il entre dans un cycle. À ce moment, on sait qu'une collision s'est produite mais pas forcément son emplacement exact. L'algorithme permet de la retrouver ainsi que la paire de messages concernés.
Pour résoudre le problème du stockage dans le cas du calcul distribué, un serveur central conserve des empreintes spécifiques comme par exemple celles dont les 32 premiers bits sont nuls. Si une telle empreinte apparaît deux fois sur le serveur, alors on sait que deux machines ont calculé ce condensé à partir de deux valeurs initiales différentes et qu'une collision s'est produite. Il suffit de parcourir à nouveau la dernière partie du chemin qui a amené à cette collision pour trouver les deux messages. Malheureusement pour ses participants, MD5Crk a du s'interrompre brutalement durant l'été 2004 suite à la découverte d'une collision complète sur MD5. Nous reviendrons sur ces événements à la fin de l'explication sur le MD5.

Dans le listing ci-dessous, vous trouverez un petit script Bash qui permet d'expérimenter les effets du paradoxe des anniversaires sur MD5. Pour limiter les temps de calcul, nous partons du principe qu'une collision se produit si les 8 premiers bits sont identiques, nous avons donc 256 empreintes possibles. Selon le paradoxe, pour trouver une collision avec une chance sur deux, il nous faudrait 16 messages. Pour avoir plus de chance de son côté, le script génère 32 messages au contenu aléatoire grâce à /dev/urandom. Ces 32 messages représentent une assurance de réussite de près de 90%. Il suffit ensuite de calculer les empreintes avec md5sum et de comparer les 8 premiers bits (soit les deux premiers caractères des empreintes exprimées en hexadécimal). Pour faciliter cette comparaison, le script écrit l'empreinte complète suivie de ses 8 premiers bits. N'oubliez pas de changer les droits du script avec chmod +x paradoxe et de le lancer avec :
./paradoxe | sort
de manière à avoir un résultat plus facile à lire. Il se peut qu'aucune collision n'apparaisse lors du premier lancement, il s'agit somme toute d'une chose normale puisque nous travaillons avec des probabilités et que vous avez manqué de chance lors de cette première tentative ! Nous invitons le lecteur à tenter l'opération sur plus de 8 bits (mais peut-être autrement qu'avec un script shell).
#!/bin/bash
for i in $(seq 1 32); do
empreinte=$(head -c 20 /dev/urandom | md5sum)
echo -n $empreinte
echo $(echo $empreinte | head -c 2)
done
Fonctionnement de MD5[modifier | modifier le wikicode]

La fonction MD5 (message digest 5) a été inventée en 1991 par Ronald Rivest, un éminent cryptologue et professeur du MIT qui est aussi à l'origine du RSA (Rivest, Shamir et Adleman), l'un des premiers systèmes de cryptographie asymétrique. Rivest a élaboré d'autres fonctions de hachage comme MD2 et MD4 ainsi que des algorithmes de chiffrement avec la famille des RCx (RC4 est le plus connu puisque il est utilisé dans SSL et WEP).

MD5 utilise une construction de Merkle-Damgård. On découpe le message en blocs de taille fixe de 512 bits. On traite ensuite les blocs séquentiellement grâce à une fonction de compression qui écrase l'espace d'entrée et produit des données qui ne peuvent être inversées (contrairement à la définition habituelle de la compression non-destructive). Les entrées de cette fonction sont un bloc de 512 bits et une variable de 128 bits. Pour le premier bloc du message, on définit un vecteur d'initialisation de 128 bits (imposé par le standard) et on introduit les 512 bits dans la fonction de compression. Celle-ci retourne une empreinte de 128 bits qui est transférée vers les 128 bits de la compression suivante. On traite ainsi les blocs les uns après les autres en chaînant les résultats. La sortie du dernier bloc est l'empreinte finale.

Des mesures doivent être prises si le message n'a pas suffisamment de bits pour remplir complètement le dernier bloc. Cette procédure est le padding (remplissage). Elle consiste à rajouter un bit '1' à la fin du message, suivi d'une séquence de bits '0' dont la taille varie selon le remplissage nécessaire et la longueur du message original codée sur 64 bits à la fin. Le message peut ensuite être haché normalement. Le remplissage satisfait certaines propriétés : si l'on se contentait de rajouter des bits '0' à la fin du message, alors les séquences comme '1010' et 101000' produiraient le même condensé ce qui est inconcevable.
Que se passe-t-il dans cette fonction de compression ? Le bloc de 512 bits provenant du message est divisé en 16 mots de 32 bits. D'autres constantes utilisées dans les transformation sont définies par le standard. Chaque mot du bloc dispose de sa propre boite de transformation. Les différentes boites sont reliées entre elles et ne se comportent pas toutes de la même manière. On dispose pour cela d'un ensemble de quatre fonctions booléennes qui prennent trois mots de 32 bits et fournissent 32 bits en sortie. Une rotation vers la gauche, variable, intervient également dans la transformation. L'inversion est rendue très difficile puisque la sortie d'une boite peut dépendre des sorties d'autres boites au comportement différent. Ce principe de chaînage est employé dans les autres fonctions de hachage comme MD4 ou SHA-1. La différence entre MD4 (1990) et MD5 concerne le type de fonctions utilisées dans les boites (seulement trois, différentes de celles de MD5) et aussi la manière de produire la sortie de chaque boite. Le nombre d'arguments est également inférieur dans MD4. Celui-ci a été le sujet de plusieurs attaques qui au début portaient sur des versions simplifiées de l'algorithme (Den Boer et Bosselaers). Hans Dobbertin a par la suite découvert une méthode pour attaquer un MD4 complet et générer des collisions en moins d'une minute sur un PC standard. Il montre dans Cryptanalysis of MD4 comment réaliser une collision sur des messages au contenu intelligible. L'exemple porte sur la substitution d'un prix dans un contrat en anglais par une autre somme.
Cryptanalyse[modifier | modifier le wikicode]
Qu'en est-il du MD5 ? Lui aussi a subi une cryptanalyse intensive durant une dizaine d'années par les chercheurs cités auparavant. Cette analyse s'est soldée en août 2004 par la découverte d'une collision complète par la Chinoise Xiaoyun Wang et son équipe (Dengguo Feng, Xuejia Lai et Hongbo Yu). Notons au passage que Xuejia Lai est le co-inventeur de l'algorithme de chiffrement symétrique IDEA qui a fait ses preuves dans PGP mais qui reste sous le joug d'une patente. Les confrères de Lai ne se sont pas arrêtés au MD5 puisque Haval, RIPEMD, MD4 ont également fait les frais de leurs recherches avec des collisions complètes avec une complexité moindre pour MD4. D'après leur papier, la méthode permettrait de trouver une collision sur MD4 "à la main". Derrière cette boutade se cache en fait une complexité de l'ordre de 28, soit 256 hachages avec MD4, un nombre tout à fait insignifiant face à la complexité des attaques précédentes. Des implémentations optimisées sont par la suite apparues, et une recherche de collisions dans MD5 est envisageable en l'espace de quelques heures, voire de quelques minutes sur un PC.
Le MD5 n'est donc plus considéré comme cryptographiquement sûr puisque cette attaque permet de faire mieux que le paradoxe des anniversaires avec ses 264 messages. Il en va de même pour RIPEMD (Race Integrity Primitives Evaluation Message Digest) et ses empreintes de 128 bits qui avaient déjà été mis en péril par Dobbertin. Quant à Haval qui date de 1994 mais dont l'utilisation est marginale, c'est la version de 128 bits qui est concernée. Haval se décline également en 160, 192, 224 et 256 bits, des versions qui demeurent intactes à ce jour.
On peut désormais générer une infinité de collisions avec MD5 grâce aux messages M1 et M2 issus de la collision. Il suffit de créer un message X, de le concaténer avec M1 pour obtenir (M1|X) et de la même manière avec M2 (M2|X). En calculant MD5(M1|X), on obtient le même résultat que MD5(M2|X). Ceci est du au fait que le padding est identique et que la sortie de la fonction de compression est identique que ce soit pour M1 ou M2. Ainsi lors du hachage des blocs concernant X, on débute avec le même vecteur d'initialisation.
Présentation de SHA-1[modifier | modifier le wikicode]

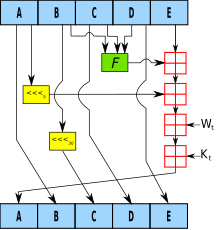
SHA-1 (Secure Hash Algorithm) et son précurseur, w:SHA-0, ressemblent à MD5. Ils utilisent des blocs de 512 bits. Les empreintes sont par contre plus longues : 160 bits. SHA-1 est souvent considéré comme une alternative plus sûre par rapport à MD5, que ce soit dans les protocoles SSL, IPSec ou les codes d'authentification qui allient une clé secrète au hachage afin de produire une signature numérique infalsifiable par une tierce partie (HMAC).
La famille SHA se divise en deux catégories : SHA-1 et SHA-2 (SHA-224, SHA-256, SHA-384 et SHA-512). Ces fonctions ont été conçues par la NSA (Nation Security Agency) et publiées par le NIST, un organisme chargé des standards. Comme le dit Bruce Schneier, auteur du chiffrage Blowfish et de l'ouvrage Applied Cryptography, le SHA-1 est une sorte de « technologie extraterrestre ». On ne sait en effet rien de ses concepteurs, ni des conditions dans lesquelles se sont déroulées son élaboration. En mai 1993, le standard FIPS-180 est publié, il correspond à la première version : SHA-0. Suite à la découverte de faiblesses et sans donner plus de précisions, la NSA publie deux ans plus tard une révision de son standard (FIPS-180-1) : le SHA-1. La seule différence, mais elle est essentielle pour la robustesse, est l'ajout d'une série de rotation vers la gauche.
Étudions maintenant son fonctionnement. SHA-1 est aussi basé sur le principe de Merkle-Damgard. Le message est soumis à un remplissage et il se voit découpé en blocs de 512 bits. Pour chaque bloc de 512 bits, SHA-1 calcule 80 itérations appelées aussi rondes. Elles sont groupées en quatre parties principales avec 20 transformations dans chacune d'entre elle. Ces transformations sont de petites boites noires comme celles présentes dans le MD5. Les 20 boites appartenant à un même groupe utilisent toutes la même fonction, elle prend 3 mots de 32 bits en entrée et fournit un mot de 32 bits en sortie. Par contre, les fonctions diffèrent entre les quatre groupes. SHA-1 n'a ainsi pas une structure semblable selon le numéro du tour. Mais ce n'est pas tout, les boites ont également besoin du bloc de 512 bits à hacher. Pour cela, on le découpe en 16 mots de 32 bits (x[1], x[2], ..., x[16]) et une fonction se charge de générer encore 64 autres mots de 32 bits afin d'en avoir 80, donc un pour chaque ronde. Pour créer ces mots supplémentaires, on applique un ou-exclusif entre quatre mots déjà présents dans la liste : x[i] = x[i-3] XOR x[i-8] XOR x[i-14] XOR x[i-16]. C'est ici qu'intervient la différence entre SHA-0 et SHA-1. Dans SHA-1, ce résultat est soumis à une rotation circulaire vers la gauche de 5 bits. Cela permet de casser une structure trop linéaire qui fut fatale pour SHA-0.

À ce stade, nous avons donc 80 "clés" qui peuvent être envoyées vers les boites noires respectives. Celles-ci prennent plusieurs variables de 32 bits en entrée : A, B, C, D et E. Leurs valeurs initiales pour le premier hachage sont définies par la spécification. À chaque ronde de SHA-1, ces 5 variables sont modifiées et le résultat est transmis à la ronde suivante. On effectue en premier une rotation circulaire vers la gauche de 5 bits sur la variable A, on calcule f(B, C, D) en utilisant la fonction évoquée plus haut. On récupère alors E, ainsi que la "clé" correspondant à cette ronde ainsi qu'une constante définie par le standard qui varie selon les tours. On additionne le tout modulo 32 car nous travaillons avec des registres sur 32 bits et on stocke temporairement cette valeur. Les variables sont ensuite écrasées en prenant bien soin de les permuter lors de l'attribution et d'appliquer quelques rotations intermédiaires sur certaines d'entre elles.
À la fin de la dernière ronde, on additionne les valeurs courantes de A, B, C, D et E avec les valeurs de départ provenant du bloc précédent. En concaténant ces cinq variables de 32 bits, on obtient l'empreinte de 160 bits. Si d'autres blocs doivent être hachés, cette empreinte intermédiaire est passée au bloc suivant en tant que vecteur d'initialisation.
Les raisons pour lesquelles la NSA a invalidé SHA-0 se feront de plus en plus précises grâce à la cryptanalyse effectuée par Antoine Joux et son équipe. Peu avant l'annonce de collision complète sur SHA-0 par Joux, Eli Biham et Rafi Chen présentaient une méthode pour trouver des collisions partielles sur près de 90% des bits présents dans les empreintes. L'attaque de Joux a une complexité de l'ordre de 251 opérations, soit 500 millions de fois moins qu'un paradoxe des anniversaires. Il s'agit d'une version améliorée d'une méthode qu'il avait publié avec Chabaud en 1998 et qui a été implémentée sur un supercalculateur. Elle repose sur la cryptanalyse différentielle. Cette technique a été officiellement publiée par Biham et Shamir au début des années 1990 dans le but d'attaquer l'algorithme de chiffrement symétrique DES. On sait désormais qu'elle était déjà connue des concepteurs de DES à la fin des années 1970 mais gardée secrète pendant une dizaine d'années. Le principe est d'étudier le comportement de l'algorithme lorsque l'on perturbe légèrement les entrées. En inversant certains bits à l'entrée, on provoque un effet avalanche ou diffusion qui comme son nom l'indique, entraîne des modifications de plus en plus significatives dans la structure. L'attaque vise à réduire cette propagation chaotique en compensant l'effet des différences directement dans les messages. Par des corrections successives, on arrive à générer des collisions sur une variante réduite de SHA-0. Pour un SHA-0 complet, la technique a du être optimisée. Elle fait entre autres appel à la méthode dite du bit neutre développée par Biham, on observe en effet que certains bits n'ont aucune influence sur l'effet avalanche pendant un certain nombre d'itérations de l'algorithme. Fait étonnant, Biham et Chen ont prouvé qu'ajouter des rondes n'améliorait pas la sécurité : un SHA-0 de 82 rondes est plus faible que la version avec 80 rondes !
Grâce à la rotation des registres introduites dans SHA-1, ces attaques deviennent caduques. Des attaques sur des versions simplifiées existent (Biham a trouvé une collision complète sur une trentaine de rondes et Vincent Rijmen a écrit un papier sur une collision possible concernant 53 rondes). Cela n'a pas empêché l'équipe chinoise à l'origine de la collision sur MD5 de récidiver avec une collision complète mais théorique nécessitant 269 opérations puis réduite à 265.
On pouvait lire sur la toile cette analogie : si un SHA-1 qui n'est pas cassé représentait un mur avec une épaisseur de 100 mètres alors l'attaque des Chinois réduirait cet ouvrage à seulement 5 centimètres ! Mais ces quelques centimètres nécessitent tout de même une grosse puissance de calcul. Pour l'anecdote, un hachage de 256 bits serait comparable à un mur de 3 années-lumière. Avec 512 bits, en digne successeur du big-bang, il atteindrait 1039 années-lumière. Pour compléter cette comparaison, mentionnons le cassage d'une clé de 64 bits du chiffrement RC5 par le projet "distributed.net". Achevé en 2002, le concours a mobilisé 330 000 participants et une puissance équivalente à 50 000 PC à 2GHz. Cela correspond à un mur de deux millimètres mais cette attaque a duré plus de 1700 jours ! Même si les temps de calcul diffèrent entre SHA-1 et RC5, notre millimètre cryptographique se transforme vite en années.
Conséquences et autres attaques[modifier | modifier le wikicode]
Suite à ces recherches fructueuses, on peut se poser des questions sur la sécurité offerte par les algorithmes de hachage fréquemment utilisés dans les applications. Il est désormais clair que MD5 et SHA-1 ne doivent pas être incorporés dans les nouveaux logiciels. On conseille maintenant d'opter pour des versions plus robustes comme SHA-256 ou même SHA-512. Ces dernières utilisent plus de fonctions (6 au lieu de 4) et pour les versions 384 et 512, la structure travaille sur des mots de 64 bits, ce qui constitue une caractéristique intéressante pour les nouveaux processeurs. Rien ne dit toutefois que des variantes des techniques déployées pour SHA-0 et SHA-1 ne vont pas faire leurs preuves sur les membres de SHA-2. Ceux-ci n'ont pas encore été soumis à beaucoup de cryptanalyse même si des travaux commencent à apparaître (Handschuh et Gilbert). Ce qui est sûr, c'est qu'avec une attaque avec le paradoxe des anniversaires sur SHA-256, on aurait besoin de 2128 messages. Si une attaque similaire à celle des Chinois apparaissait, la complexité serait certainement supérieure à 2100, c'est un nombre qui n'est à la portée de personne à l'heure actuelle.

Une autre attaque présentée par Bruce Schneier et John Kelsey permet d'effectuer une attaque sur la seconde préimage avec une complexité amoindre. Sur SHA-1, une recherche exhaustive (on essaie toutes les possibilités) prendrait en moyenne 2159 hachages. L'optimisation théorique de Schneier et Kelsey permet de réduire cet ordre de grandeur à une moyenne de 2105 calculs d'empreinte mais nécessite de très gros messages (255 octets).
Plus récemment, Arjen Lenstra, Xiaoyun Wang et Benne de Weger ont publié un document expliquant comment ils ont pu générer deux certificats X.509 distincts mais avec la même signature. Cela montre que le système de clés publiques PKI (Public Key Infrastructure) ne peut être raisonnablement considéré comme sûr s'il continue à employer des certificats basés sur MD5. En pratique, cette attaque est plus difficile à mettre en œuvre car la forme des certificats varie et il faut que l'utilisateur suive une procédure particulière pour être vulnérable.
Il devient désormais nécessaire de songer à établir un nouveau standard comme cela a été le cas pour la cryptographie symétrique avec le concours AES (Advanced Encryption Standard) dont le gagnant est l'algorithme Rijndael (de Vincent Rijmen et Joan Daemen) qui a remplacé DES. Un tel projet, NESSIE pour New European Schemes for Signatures, Integrity and Encryption a été lancé avec un résultat en demi-teinte pour les fonctions de hachage puisque parmi les trois candidats (Whirlpool, SHA-1 et la série des SHA-2), seul Whirlpool de Paulo Barreto et Vincent Rijmen était novateur.
Whirlpool reprend des idées présentes dans AES et produit une empreinte de 512 bits ce qui dans le monde du hachage est atypique (citons toutefois SHA-512). On peut parier que Whirlpool refasse parler d'elle de par sa robustesse grâce au schéma de Miyaguchi-Preneel et son design qui diffère des fonctions comme MDx ou SHA. Biham a de son côté également inventé une fonction de hachage : Tiger. Elle se décline en 128 ou 192 bits. Une nouvelle version Tiger-2 vient d'apparaître mais n'apporte que des changements mineurs concernant le remplissage. Mais avant de pouvoir s'imposer, ces fonctions devront faire l'objet d'une cryptanalyse poussée. Une autre alternative pourrait encore venir de la série des RIPEMD (160 bits et plus) mais la présence d'attaques sur la version de 128 bits laisse supposer qu'une meilleure solution doit être trouvée.
En conclusion, nous avons vu que les fonctions de hachage cryptographiques ont été mises à rude épreuve ces derniers temps. Mais pour la plupart des utilisateurs, ces attaques, de par leur nature, leurs limitations et la puissance de calcul nécessaire, sont sans conséquence directes. Il ne faut pas négliger le contexte dans lequel évoluent les primitives cryptographiques et leur relation avec les autres composants du système qui peuvent à leur tour être des cibles potentielles.
La présence de failles laisse toutefois présager que d'autres faiblesses encore inconnues sont dissimulées. Celles-ci pourraient amener à des attaques plus significatives puisque les récentes découvertes ont relancé le débat chez les cryptanalystes. Toutes ces raisons rendent l'utilisation des anciens algorithmes plus délicate voire même déconseillée dans de nouveaux programmes, surtout si ceux-ci nécessitent une grande sécurité.
Liens externes[modifier | modifier le wikicode]
- (anglais) Version PDF complète du livre "Handbook of Applied Cryptography". Un chapitre est consacré aux fonctions de hachage.
- (anglais) Spécification complète du MD5 (RFC 1321)
- (anglais) Spécification complète de la famille SHA
- (anglais) La fonction de hachage Whirlpool par Paulo Barreto et Vincent Rijmen
- (anglais) Description précise de l'attaque sur MD5 par Wang et al.
| À propos de ce document | |
|
Article initialement paru dans le défunt magazine LOGIN. L'auteur, Kévin Drapel, cède le contenu de l'article sous la licence GFDL. | |
- (anglais) Description des attaques sur MD4 et RIPEMD.
- (anglais) Lattaque la plus efficace sur les mots de passe LanManager
- (anglais) Attaque sur les certificats X.509 par Lenstra, Wang et De Weger
- (anglais) Résultats du projet NESSIE.
- (anglais) Programme de hachage en Java
- (anglais) La "rump session" de Crypto'04 avec la présentation des attaques sur MD5, SHA-0, HAVAL et RIPEMD.
- (anglais) Les fonctions de hachage dans les structures de données.



