Cosmologie/Le découplage des photons

Dans les chapitres précédents, nous avons vu quelque chose de très important : la température du rayonnement diminue avec l'expansion. Un point important est que l'univers, à ses débuts, est composé d'un plasma, à savoir un gaz de particules chargées. L'univers ne comprend au départ par d'atomes, mais seulement des électrons, des protons et neutrons, etc. La matière était composée d'un plasma d'électrons libres, de baryons et de photons. A cette époque, le rayonnement interagissait fortement avec les électrons libres, les noyaux d'atomes, les électrons liés aux atomes, bref : avec la matière au sens général. Vu que le rayonnement et la matière interagissaient beaucoup, les deux étaient à la même température. Matière et rayonnement étaient en équilibre thermique, à la même température. Si la matière chauffait trop, elle redistribuait l'excès au rayonnement, et réciproquement. Ce plasma formait un fluide unique, avec une pression, une température, une densité d'énergie, etc.

Les photons interagissaient fortement avec les électrons, par diverses processus (diffusion Compton, et autres), ce qui redistribuait la température. Les photons chauffaient les électrons et réciproquement. Un équilibre thermique s'était ainsi installé entre photons et électrons libres, les deux ayant la même température/énergie cinétique moyenne. Cet équilibre incluait aussi les baryons, bien que les baryons n'interagissaient pas directement avec les photons. Les baryons interagissaient fortement avec les électrons, qui servaient d'intermédiaires avec les photons. Ce plasma avait naturellement des propriétés thermodynamiques simples : une pression, une température, un volume, etc. Sa pression était essentiellement causée par la pression de radiation des photons, avec une participation mineure de la pression des électrons libres et des baryons.

La matière neutre est transparente, ce qui induit un découplage des photons.

Mais la température baissant avec l'expansion, elle a fini par atteindre une température suffisamment basse pour que les atomes se forment. La matière est alors passée de l'état de plasma à un gaz d'atomes. Cela s'est produit 380 000 ans après le big bang, à une température d'environ 3000 degrés. Le résultat est que les interactions entre rayonnement et matière se sont faites plus rares, et surtout que la redistribution d'énergie entre matière et rayonnement s'est faite plus rare, plus lente.On nomme découplage de telles situations où deux populations de particules n'interagissent plus à la suite d'une baisse de température. Et ici, il s'agit du découplage des photons.

Après le découplage, le rayonnement et la matière font leur vie chacun de leur côté et cela s'est ressenti sur leur température et leur évolution. La première conséquence du découplage est que l'équilibre thermique est rompu : les deux populations de particules s'isolent thermiquement et leur températures deviennent indépendantes. La température de la matière est devenue différente de la température des photons. De plus, elles ne se sont pas refroidies de la même manière. La matière garda sa température constante lors de l'expansion, alors que celle du rayonnement chuta avec l'expansion. Le rayonnement s'est refroidi plus vite que la matière, à cause de la diminution de fréquence des photons, abordées il y a quelques chapitres.

Le fond diffus cosmologique

Pour résumer, le plasma s'est divisé en deux gaz indépendants : un gaz de matière et un gaz de photon. Le gaz de matière s'est condensé pour donner des galaxies et autres structures, alors que le gaz de photons a subsisté jusqu’à aujourd'hui sous la forme d'un ensemble de photons de faible température, que l'on peut capter avec certains instruments. Ce gaz est appelé le fond diffus cosmologique, aussi appelé le rayonnement de fond diffus cosmologique, ou encore le CMB (Cosmic Microwave Background).

La même chose a eu lieu pour les neutrinos et anti-neutrinos qui se sont découplés de la matière et des photons un peu avant les photons. Ce fond diffus de neutrinos est malheureusement nettement moins étudié que le fond diffus cosmologique, car les neutrinos n'interagissent pas beaucoup avec la matière, et qu'ils sont donc difficiles à détecter. Nous n'en parlerons donc pas dans ce cours, par manque d'informations à leur sujet. Pour le moment, concentrons-nous sur le découplage des photons.

COBE monopole dipole and primordial perturbations

Le CMB a été théorisé avant d'être découvert. Dans un article de 1948, Alpher et ses collègues théorisèrent l'existence du CMB à partir d'un modèle de big-bang usuel. Mais il fallut attendre 1965 pour que ce signal soit observé pour la première fois, par Penzias et Wilson. Ceux-ci utilisaient une antenne de grandes dimensions, pour tester la fiabilité des communications entre satellites, et étudiaient des interférences radio qui apparaissaient à haute fréquence. Leurs investigations leur ont permis de capter un signal dans la bande de 4Ghz, qui avait des caractéristiques étranges : isotrope, non-polarisé et libre de toute variation saisonnière. L'origine de ce signal est restée inconnue durant quelques années, mais les scientifiques (dont Penzias et Wilson) avaient éliminé toute origine terrestre. Il fallu que Dicke et ses collaborateurs fassent le lien avec l'article d'Alpher. Par la suite, diverses campagnes d'observation ont permis d'obtenir une carte assez détaillée du fond diffus. De nombreux projets d'observations scientifiques ont ainsi observé le fond diffus cosmologique avec une précision de plus en plus grande : COBE, puis WMAP, et enfin la mission PLANCK.

Les observations de Penzias et Wilson montraient un CMB relativement uniforme. Par la suite, les observations du satellite COBE ont montré que le CMB a l'air d'avoir une structure en forme de dipôle, à savoir qu'il a un pôle chaud opposé à un pôle froid. Les observations plus récentes éliminent cet effet Doppler par divers traitements informatiques, et montrent un CMB sans dipôle, mais avec quelques inhomogénéités. On observe notamment une zone plus chaude au niveau de l'équateur, liée à la présence de la voie lactée (notre galaxie), qui réchauffe quelque peu le CMB de par son rayonnement.

La surface de dernière diffusion

Surface de dernière diffusion.

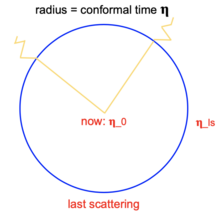
Le fond diffus capté à l'heure actuelle correspond aux photons émis lors du découplage, environ 380 000 ans après le big-bang. Du point de vue de la Terre, les photons du CMB captés par les instruments de mesure sont répartis sur une sphère centrée sur la Terre, appelée la surface de dernière diffusion, dont le diamètre correspond à la distance parcourue par ces photons depuis le découplage.

Pour comprendre pourquoi on parle de surface de dernière diffusion, il faut faire un petit rappel sur les interactions entre photons et matière. Les photons ont en effet tendance se cogner sur les particules qui croisent leur chemin, et à rebondir dessus. Typiquement, ils rebondissent sur des électrons dans un processus appelé la diffusion Compton. Lors de ce choc entre électron et photon,une partie de l'énergie du photon est transférée à l'électron, ou inversement.

Diffusion Compton

Les photons du CMB sont soit des photons qui ont été émis au moment du découplage, soit des photons qui existaient avant, mais ont rebondit une ou plusieurs fois sur des particules de matière. Les diffusions Compton étaient très fréquentes avant le découplage, car les électrons libres étaient très nombreux. Les photons ne pouvaient pas faire un pas sans interagir avec un électron libre, leur temps de libre parcours moyen (temps entre deux collisions avec un électron libre) était très faible. Le mouvement d'un photon dans le plasma primordial était chaotique : les photons ne pouvaient pas aller en ligne droite, mais n'avaient de cesse de se cogner sur les atomes au point où leur trajectoire ressemblait à marche aléatoire, à un mouvement brownien. En conséquence, le plasma primordial avant le CMB était opaque, dans le sens où il ne laissait pas traverser la lumière facilement.

Mais après le découplage, les électrons se sont liés aux atomes, ne laissant presque aucun électron libre pour participer à des diffusions Compton. Les photons du CMB, autrefois diffusés fréquemment, n'ont ensuite plus été diffusé par diffusion Compton, ou presque. Leur libre parcours moyen, la distance parcoure entre deux collisions/diffusions est devenus beaucoup plus grande. Les photons ont alors pu se déplacer en ligne droite entre quelques rares collisions, et donc le plasma primordial est devenu transparent. Le découplage est le moment où ils ont diffusé pour la dernière fois, d'où le fait que l'on parle de surface de dernière diffusion.

Précisons cependant que le découplage ne s'est pas fait instantanément, mais est un processus progressif qui s'est étalé sur un temps non-négligeable. Et cela a un effet sur la surface de dernière diffusion. Il s'agirait bien d'une surface sphérique si le découplage était instantané, mais la réalité est que la surface de dernière diffusion a une certaine épaisseur. Son épaisseur est égale à la distance parcourue par un photon durant la durée du découplage. Cela a des effets mesurables, notamment dans le spectre de puissance du fond diffus, mais nous en reparlerons dans quelques chapitres.

Le CMB est un rayonnement de corps noir

Les observations montrent que, peu importe à quel endroit on le regarde, le CMB est un rayonnement de corps noir quasiment parfait, ce qui est en accord avec la théorie. Le fait que le CMB soit un rayonnement de corps noir signifie que l'on peut lui attribuer une température, une température en chaque point du ciel pour être précis.

Comparaison du CMB avec un rayonnement de corps noir.

Le dipôle du CMB

CMB vu par COBE, sans traitement (en haut), en retirant le dipôle (milieu) et en retirant la luminosité de la voie lactée (en bas).

Le fait que le CMB aie une forme approximativement dipolaire est en soi un gros problème, que l'on arrive pas à bien expliquer théoriquement. On pourrait croire que cela réfute l'idée d'un univers isotrope, mais ce n'est pas forcément le cas.

L'explication usuelle quant à l'existence de ce dipôle est qu'il serait d'origine cinématique, lié au mouvement de la Terre par rapport au CMB. L'explication détaillée part du principe qu'il y aurait un référentiel dans lequel le CMB serait isotrope et sans aucun dipôle. Cependant, la Terre se déplacerait à une certaine vitesse notée v par rapport à ce référentiel. Rappelons que le CMB est avant tout un rayonnement électromagnétique avec une certaine fréquence, fréquence qui dépend de sa température. Or, la fréquence du CMB est alors déformée par une sorte d'effet Doppler, ce qui fait que la température dépend de la direction dans laquelle on se déplace, par rapport au référentiel où le CMB est isotrope. Les zones du CMB qui s'éloignent de nous sont vues comme refroidies, alors que les zones qui s'approchent (opposées, donc) sont vues comme plus chaudes.

Pour rappel, à de faibles vitesse, le CMB subit un décalage vers le rouge de :

$z(v)={\frac {v}{c}}$

La relativité restreinte donne une formule encore plus précise :

$z(v)={\frac {\sqrt {1+{\frac {v}{c}}}}{\sqrt {1-{\frac {v}{c}}}}}-1$

Une explication beaucoup plus détaillée est cependant encore inconnue. On fait face à un cas assez mal compris théoriquement : établir la température d'un objet alors qu'on se déplace par rapport à lui à grande vitesse. Et outre la température, on peut aussi analyser la forme du rayonnement de corps noir observée. Température et corps noirs sont deux concepts de la thermodynamique, une branche de physique parfaitement maitrisée tant qu'on reste dans le cadre de la physique classique de Newton. Mais le cas qui nous intéresse, à savoir à quoi ressemble le fond diffus quand on se déplace à grande vitesse, demande qu'on utilise la relativité restreinte d'Einstein. Et c'est là que le bas blesse : on n'a pas de théorie validée pour la thermodynamique relativiste. La thermodynamique relativiste vise à reformuler les lois de thermodynamique dans le cadre de la relativité restreinte d'Einstein. A l'heure actuelle, les physiciens ont plusieurs théories pour cela, mais elles donnent des résultats complètement contradictoires !

Et pour comprendre pourquoi, faisons quelques rappels de relativité restreinte. La relativité nous dit que quand on se déplace par rapport à un référentiel immobile, les distances et les durées sont modifiées par un facteur appelé le facteur de Lorentz. Ce dernier vaut :

$\gamma ={\frac {c}{\sqrt {c^{2}-v^{2}}}}={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$, avec $v$ est la vitesse de déplacement, et $c$ est la vitesse de la lumière dans le vide.

Concrètement, si je mesure une distance L dans un référentiel immobile, la même distance mesurée en allant à la vitesse v sera de $L \over \gamma$. La distance mesurée est plus petite que dans un référentiel immobile et elle est d'autant plus petite que l'on va vite. C'est l'effet de contraction des longueurs. L'effet est inverse pour les durées, à savoir que la durée d'un évènement/phénoméne n'est pas la même selon la vitesse du référentiel de mesure. La durée mesurée dans un référentiel en mouvement est plus longue que celle mesurée dans un référentiel immobile. Cette fois-ci, une durée D devient $D\times \gamma$. C'est l'effet de dilatation des durées.

Maintenant, prenons le cas où on cherche à calculer la température observée du CMB, ou même de tout autre rayonnement de corps noir observé depuis un objet en mouvement. Le CMB, dans son référentiel où il est isotrope (immobile dirait-on), a une température notée $T_{0}$. L'observateur se déplace à une vitesse $v$ dans une direction bien précise. En théorie, plusieurs situations sont possibles.

• La température observée est égale à $T_{0}\times \gamma$.
• La température observée est égale à $T_{0} \over \gamma$.
• La température observée est égale à $T_{0}$.

A l'heure actuelle, nous ne savons pas quelle est la bonne solution. Les trois possibilités sont impossibles à distinguer expérimentalement, et les trois sont défendues par des arguments théoriques solides. Une revue de ces arguments est disponible dans le document nommé "Black Body Radiation in Moving Frames", par Kamran Derakhshani. Mais l'explication actuelle du dipole du CMB part du principe que l'on a une variante de la seconde solution. En 1968, Bracewell et Conklin ont sorti une étude où ils montraient que, si leur démonstration était correcte, alors un observateur en mouvement dans le CMB mesurait une température anisotrope, à savoir dépendante de la direction. La température mesurée en un point du CMB était la suivante :

$T={\frac {T_{0}}{\gamma \left[1-{v \over c}\times \cos {(\alpha )}\right]}}$, avec $\alpha$ l'angle par rapport à la direction de déplacement.

L'équation nous dit que le CMB doit semble plus chaud à l'avant, et plus froid, par rapport à la direction de déplacement. On retrouve donc le dipole observé dans le CMB, à condition que la vitesse de déplacement ait la bonne valeur. Elle serait d'environ 300 kilomètres par secondes. C'est l'explication actuelle du dipole du CMB.

L'explication précédente du dipôle du CMB est actuellement contestée. A vrai dire, il s'agit d'une hypothèse parmi beaucoup d'autres et elle est juste un consensus assez mou, que les astrophysiciens cherchent à vérifier ou infirmer depuis longtemps. Diverses expériences ont tenté de vérifier l'origine cinétique du dipôle, de plusieurs façons. La première est de vérifier si ce dipôle apparait non seulement dans le CMB, mais aussi dans les observations des quasars et des sources radio lointaines. En théorie, si l'explication cinétique est bonne, alors on devrait retrouver un effet similaire en observant la positions des galaxies très lointaines. Diverses études ont tenté de vérifier cela, mais les résultats ne sont pas encore très fiables. De plus, l'explication cinétique implique qu'il y ait un référentiel dans lequel le CMB serait quasi-uniforme et sans dipôle. Cela pourrait en faire un référentiel privilégié et briserait le principe de relativité avec l'invariance galiléenne/lorentzienne, mais rien n'est moins sûr.

Outre l'existence de ce dipôle, d'autres observations semblent indiquer que le CMB aurait un axe privilégié, nommé l'axe du mal (axis of evil en anglais), qui impacterait le CMB, mais aussi l'expansion de l'univers. Mais le fait que l'axe soit aligné avec le plan de écliptique (le plan sur lequel la Terre tourne autour du Soleil) met le doute quant à son origine. Une origine cinématique locale est en tout cas plus probable qu'une origine cosmologique, sauf coïncidences. Mais là encore, rien n'est moins sûr et il se pourrait que les données soient biaisées, d'autres études n'ayant pas retrouvé cet axe du mal dans leurs données.

L'axe du mal du CMB.

Le découplage et le fond diffus

Au moment du découplage, on sait que le gaz de photons devait avoir la même température que le plasma. Sans expansion, cette température serait égale à la température du plasma au moment du découplage, qui a été conservée par le gaz de photons. Mais l'expansion a décalé ce rayonnement de corps noir vers le rouge, diminuant sa température. La température du fond diffus a donc diminué en conséquence. De nos jours, les mesures donnent une température d'environ 2,735 Kelvin. Mais on est en droit de se demander quelle était sa température au moment de sa formation. On peut aussi se demander combien de temps de refroidissement du CMB a duré.

L'âge de la recombinaison

La température du fond diffus au moment du découplage est estimée à 3000 degrés Kelvin, température de condensation d'un plasma en atomes. À partir de la température mesurée actuellement, et de la valeur théorique de formation d'un plasma, on peut déduire l'âge qui s'est écoulé depuis la formation du CMB. En théorie, on peut déduire la température du CMB en utilisant la formule suivante, établie dans le chapitre "L'évolution de a matière" :

$T(t)=T(t_{0})\cdot {\frac {a(t_{0})}{a(t)}}$

Mais utiliser cette formule présuppose de connaître $a(t_{0})$ et $a(t)$. Cependant, on peut ruser en remplaçant le facteur d'échelle par le redshift. Pour cela, on utilise la formule vue dans le chapitre "L'évolution du rayonnement". Le décalage vers le rouge $z(t)$ est mesuré entre l'époque actuelle et la recombinaison, ce qui fait qu'on le notera $z_{rec}$.

Dans ce qui suit, on suppose que $t_{0}$ est l'instant d'émission de la lumière, alors que l'observation a lieu à l'instant $t$. Avec cette convention, on sait que $1+z(t)={\frac {a(t)}{a(t_{0})}}$. En faisant le remplacement dans l'équation précédente, on trouve :

$T(t)={\frac {T(t_{0})}{1+z}}$

Rappelons que cette formule utilise la convention $t_{0}=t_{emission}$. Ici, le temps d'émission est l'instant où a eu lieu la recombinaison. En clair, la température $T(t_{0})$ est la température de découplage $T_{rec}$.

$T(t)={\frac {T_{rec}}{1+z_{rec}}}$

La température au moment du découplage était d'environ 3000 degrés Kelvin, alors que la température actuelle du fond diffus est d'environ 2,735 degrés Kelvin.

$2,735K={\frac {3000K}{1+z_{rec}}}$

Le redshift calculé ainsi est de :

$z\approx 1100$.

En utilisant un modèle cosmologique, on peut déduire une relation âge-redshift, et donc calculer combien d'années se sont écoulées entre le big-bang et la formation du CMB.

La température de recombinaison

La recombinaison a eu lieu quand l'univers a atteint une certaine température, qu'il est important de connaître. En effet, grâce à elle, on peut calculer quand a eu lieu le découplage, et donc dater le CMB. Autant dire que calculer celle-ci est d'une importance primordiale. En théorie, la température du CMB est la température à laquelle un plasma se condense en atomes quand on le refroidit. Dit autrement, c'est la température d'une transition de phase. Vous avez peut-être déjà entendu que cette température est d'environ 3000 degrés Kelvin, ce qui est la température mesurée sur Terre. Reste qu'il vaut mieux la calculer et en rendre compte théoriquement. Les mesures réalisées sur Terre ne sont peut-être pas représentatives des conditions de l'univers primordial : la pression est plus élevée, la densité différente et j'en passe. Dans cette section, nous allons calculer la température théorique à laquelle le découplage a eu lieu.

L'approximation par l'énergie photonique moyenne

Une première méthode est de comparer l'énergie d'ionisation de l'hydrogène avec l'énergie d'un photon. Dans un gaz de photons de température $T$, l'énergie moyenne d'un photon est de $3k_{B}T$. L'énergie d'ionisation d'un atome d'hydrogène (la plus faible de toutes) est de 13,6 électrons-Volts (l'EV est une unité d'énergie). Si l'énergie moyenne des photons est supérieure à l'énergie d'ionisation de l'hydrogène, alors la matière restera ionisée. Si ce n'est pas le cas, les photons ne sont pas assez énergétiques pour ioniser la matière, qui se condense. On peut alors calculer une approximation de la température de découplage avec le quotient suivant :

$T={\frac {13,6eV}{3k_{B}}}=50000K$

On voit que la température obtenue est diablement haute, comparée aux valeurs réelles : plus de 10 fois la valeur réelle. Cela vient d'un phénomène simple : l'énergie moyenne n'est qu'une moyenne, qui cache le fait que certains photons sont plus énergétiques que la moyenne. Même si l'énergie moyenne d'un photon est de 13,6 eV, de nombreux photons ont une énergie suffisante pour ioniser un atome dans le gaz de photon.

On peut obtenir une approximation plus crédible en étudiant plus en détail la dispersion des énergies des photons. Dans un gaz de photons, tous les photons n'ont pas la même énergie. Et l'énergie n'est pas répartie équitablement entre les photons, mais suit une loi assez compliquée. Mais pour simplifier, on peut estimer que le nombre de photons suit la loi de Boltzmann. Pour résumer, le nombre de photons qui a au moins une énergie $E_{\gamma }$ est proportionnel à l'exponentielle de leur énergie. Mis sous forme de formule, cela donne :

$N_{\gamma }\propto e^{-{\frac {E_{\gamma }}{KT}}}$.

Supposons maintenant qu'il faille un photon par atome à ioniser pour que l'ionisation se fasse. Sachant qu'il y a environ $1,7\times 10^{9}$ photons par baryon.atome, on peut trouver la température de découplage suivante :

$T={\frac {13,6eV}{k_{B}\times \ln {(1,7\times 10^{9})}}}=7400K$

L'approximation par l'équation de Saha

Il est possible d'obtenir une approximation plus précise avec l'équation de Saha. Celle-ci permet de déduire le degré d'ionisation d'un gaz. Le gaz en question correspond à un gaz d'hydrogène, composant principal de l'univers, qui s'est justement formé lors du découplage. Avant le découplage, on peut considérer que l'univers était rempli d'un plasma formé par ionisation du gaz d'hydrogène, à savoir un gaz qui mélangeait protons et électrons. L'équation de Saha nous dit que, si on note :

• $n_{e}$, $n_{p}$ et $n_{H}$ la concentration en électrons, protons et hydrogène ;
• $m_{e}$ la masse de l'électron ;
• $E_{I}$ l'énergie d'ionisation d'un atome d'hydrogène.

${\frac {n_{e}\cdot n_{p}}{n_{H}}}=\left({\frac {m_{e}kT}{2\pi \hbar ^{2}}}\right)^{\frac {3}{2}}\cdot \exp \left({\frac {E_{I}}{kT}}\right)$

Vous remarquerez que l'équation de Saha ressemble beaucoup à la distribution de Boltzmann.

Pour diverses raisons techniques, les physiciens décrivent souvent l'ionisation d'un gaz en utilisant la fraction d'électrons libres. Elle correspond au rapport en nombre d'électrons libres et nombre de protons (libres ou appartenant à un atome d'hydrogène). Elle vaut donc :

$x_{e}={\frac {n_{e}}{n_{p}+n_{H}}}$

Le plasma primordial est neutre électriquement. Or, la neutralité électrique de la matière signifie que $n_{e}=n_{p}$. Avec cette contrainte, l'équation de Saha se réécrit comme suit :

${\frac {x_{e}^{2}}{1-x_{e}}}={\frac {1}{n_{H}+n_{p}}}\cdot \left({\frac {m_{e}kT}{2\pi \hbar ^{2}}}\right)^{\frac {3}{2}}\cdot \exp \left({\frac {E_{I}}{kT}}\right)$

L'équation nous dit que le découplage n'est pas un évènement qui a eu lieu à une température bien précise, mais un processus continu dans lequel l'ionisation a baissé lentement. À 5000 Kelvins, la matière est ionisée à près de 99%. Le taux d'ionisation chute ensuite progressivement avec la température, pour atteindre 50% à 4000 Kelvins, puis 1% à 3000 Kelvins. Les scientifiques estiment, par pure convention, que le découplage a eu lieu quand le degré d'ionisation descend en-dessous de 1%, c'est à dire à une température d'environ 3700 Kelvin.

Les approximations plus précises

Les observations ne sont pas complètement compatibles avec cette approximation, bien que le modèle de Saha colle à-peu-près. Les mesures semblent indiquer non seulement que la température calculée n'est pas tout à fait exacte, mais qu'en plus, le découplage a pris plus de temps, s'est déroulé plus lentement. Pour obtenir des résultats plus précis, divers modèles ont été inventés par les physiciens. Le plus simple de ces modèles est le modèle de Peebles, aussi connu sous le nom de modèle d'atome à trois étages. Il a été complété par de nombreux modèles, qui sont devenus de plus en plus complexes avec le temps, incluant de plus en plus d'acquis théoriques provenant de la physique atomique. Nous ne parlerons pas de ces modèles, qui sont assez compliqués pour ce cours et qui font notamment appel à quelques concepts de physique quantique.