Dynamique
La mécanique d'Aristote
[modifier | modifier le wikicode]Introduction
[modifier | modifier le wikicode]On pense généralement aujourd'hui que la mécanique d'Aristote est dépassée. C'est vrai. Tout comme la mécanique de Newton et la relativité restreinte. Et tout pousse à penser que la relativité générale pourrait être bientôt dépassée. En réalité chacune de ces théories répond à des questions bien précises dans un cadre limité. Les réponses données par ces théories à ces questions sont tout-à-fait pertinentes dans ce cadre. Il est alors important de bien comprendre l'utilité de maintenir la connaissance de ces théories. S'il est naturel aujourd'hui de maintenir dans les universités l'enseignement de la théorie de Newton parce que celle-ci a permis d'envoyer des hommes sur la lune, il est tout aussi important de présenter la théorie d'Aristote parce qu'elle est née de l'évidence et du sens commun et pour cette raison est partagée par tout un chacun. Il est donc très important de marquer bien précisément les limites aux réponses qu'elle peut fournir.
Platon
[modifier | modifier le wikicode]La physique aristotélicienne est intimement liée à la cosmologie de Platon. Celle-ci part d'une idée simple. Platon pense qu'il existe deux mondes tout-à-fait différents : l'un, humain, composé par tout ce qui se trouve au-dessous de la lune et l'autre, divin, composé par tout ce qui est au-dessus.
- "Le monde sublunaire où règnent les apparences [...] est formé de couches étagées; il y a d'abord la Terre, puis l'Eau, l'Air et enfin le Feu se situant tout au-dessus, vers les limites du monde sublunaire. Ce monde dans lequel vivent les hommes est imparfait, corruptible.
- Le monde céleste [...] est le siège des idées. Il est formé de l'Ether, le cinquième élément (ou quintessence. C'est là que se trouvent les astres qui sont des êtres éternels, parfaits, divins et immuables. Parfaits, ils doivent aussi avoir un mouvement parfait autour de la Terre, c'est-à-dire un mouvement circulaire uniforme (MCU), ou éventuellement une combinaison de tels mouvements. Dans l'esprit pythagoricien, le MCU est effectivement le mouvement qui, par ses qualités de symétrie et d'harmonie, est le plus parfait que l'on puisse imaginer."
- Mécanique, E. Lindemann, 1999,DeBoeckUniversité, p.43,44.
C'est dans le cadre de cette cosmologie qu'Aristote va établir sa physique.
Aristote
[modifier | modifier le wikicode]L'idée fondamentale de la dynamique d'Aristote vient de l'observation commune du fait que le mouvement finit toujours par s'arrêter. Ainsi, selon Aristote, il existe pour chacun des cinq éléments qui composent toute chose dans l'univers (la terre, l'eau, l'air, le feu et l'éther) un lieu de repos naturel. Pour la terre, c'est le centre de l'univers (cela implique que le centre de la terre se trouve au centre de l'univers). Pour l'eau, c'est sur la terre. Pour l'air, c'est sur l'eau ou la terre. Pour le feu, c'est au-dessus de l'air (c'est pourquoi le feu monte), mais au-dessous de la lune. Enfin, pour l'éther, c'est au-dessus de la lune.
Cinématique
[modifier | modifier le wikicode]En conséquence, il existe des mouvements dits naturels, ceux qui mènent un objet, selon sa composition, vers son lieu naturel de repos, et des mouvements dits forcés ou violents, ceux qui éloignent l'objet de son lieu naturel de repos. Par exemple, étant essentiellement composée de terre, une pierre qu'on laisse tomber va naturellement rejoindre, au plus près qu'il lui est possible de le faire, le centre de la terre. La chute d'un tel objet est donc un mouvement naturel. Par contre, le mouvement d'un boulet de canon est composé : au début, le boulet, composé de terre, s'élève et ainsi s'éloigne de son lieu naturel de repos, le centre de l'univers. Son mouvement est donc violent. Puis, il s'approche de la lune, lieu divin dans lequel il n'existe qu'un mouvement éternel: le mouvement circulaire uniforme (MCU), c'est-à-dire un mouvement que l'on pourrait dire sans mouvement, un mouvement à vitesse constante. Sa trajectoire prend donc une allure divine, c'est-à-dire tend vers le cercle. C'est la partie haute du mouvement du boulet. Puis, il retombe. Son mouvement redevient donc naturel.
Au total, on distingue donc trois types de mouvement dans la cinématique d'Aristote : les mouvements naturels, les mouvements violents et les mouvements divins. Les deux premiers se font essentiellement en ligne droite. Le dernier est circulaire à vitesse constante.
Dynamique
[modifier | modifier le wikicode]Cette cinématique est complétée par une dynamique en parfaite logique avec la première. Car, si les objets ont un lieu naturel de repos, c'est que leur état naturel est précisément d'être au repos (comme les hommes en quelque sorte, et on peut bien penser que cette comparaison pouvait avoir un sens à cette époque). Ainsi, pour qu'ils restent en mouvement, il faut les y aider en exerçant sur eux une contrainte, une "force" en termes modernes. Pour Aristote, l'état de mouvement est donc directement lié à la force qui lui permet d'exister. Et bien entendu plus cette force est grande, plus l'état de mouvement sera grand, c'est-à-dire plus la vitesse de l'objet sera importante.
On pourrait résumer la dynamique d'Aristote en termes anachroniques en disant que pour lui la force est directement proportionnelle à la vitesse :
Cette théorie est si naturelle qu'elle paraît évidente. Pour l'illustrer, considérons les quatre questions suivantes :
- Un canon pointe verticalement. À l'arrêt, il tire un obus qui lui retombe dessus. Qu'en est-il si le canon se déplace horizontalement, tout en pointant toujours verticalement ? L'obus retombe-t-il derrière le canon, sur le canon ou devant ?
- On laisse tomber un objet du haut de la Tour Eiffel. Étant donné que la terre tourne, celle-ci se déplace. En conséquence, cet objet va-t-il tomber au pied exact de là où il a été lâché, un peu à l'est de ce point ou un peu à l'ouest ?
- Un avion veut remettre des vivres aux rescapés d'un naufrage réunis sur une île déserte. Doit-il lâcher son colis avant l'île, sur l'île ou après elle ?
- Un pirate lâche son couteau du haut de la vigie du grand mat. Le bateau est en pleine poursuite d'un autre vaisseau. Le couteau tombera-t-il du côté de la proue, du côté de la poupe ou au pieds du grand mât du bateau ?
Explications :
Ainsi, la mécanique d'Aristote traduit le fait évident qu'il faut pousser un objet pour qu'il se déplace. Dans la vie de tous les jours, c'est exact parce qu'il y a du frottement. Mais on sait aujourd'hui que cette affirmation est généralement fausse, qu'il n'est pas nécessaire d'exercer une force sur un objet pour qu'il soit en mouvement.
Ainsi on peut dire que la théorie d'Aristote est fausse. Mais on peut aussi la voir comme une bonne théorie pour les cas de la vie courante.
Nous allons voir que la théorie de Newton, si elle résout les erreurs d'Aristote, et donc en ce sens est une théorie plus exacte que celle d'Aristote, a aussi ses propres limitations qui en font aussi une théorie fausse dans certains domaines.
Mécanique de Newton
[modifier | modifier le wikicode]Introduction
[modifier | modifier le wikicode]Newton est avec Einstein le plus grand physicien de tous les temps. C'est lui qui, avec les "Principes mathématiques de la philosophie naturelle" (son principal ouvrage intitulé aussi "Principia mathematica" ; entendez par "philosophie naturelle" la physique) parus en 1687, pose pour la première fois les bases d'une théorie complète du mouvement et de ses causes. Il publie aussi sa fameuse loi de la gravitation, qui détermine une relation d'attraction très générale entre les corps qui ont une masse. Mais l'exceptionnel travail de Newton ne se limite pas à cela. Il porte aussi sur l'optique de son temps, domaine dans lequel il se signale par la découverte des anneaux dits de Newton.
Mécanique
[modifier | modifier le wikicode]Toute la mécanique de Newton repose sur trois axiomes (Le terme d'axiome est intéressant ici puisqu'il souligne que toute la mécanique de Newton peut être logiquement déduite de ces postulats initiaux) ou lois fondamentales. L'invention (au sens de "découverte") de ces lois n'est pas due au hasard, mais dérive directement d'une réflexion en opposition à la physique d'Aristote, comme on va le voir ci-dessous.
Les trois lois de Newton
[modifier | modifier le wikicode]Présentons tout d'abord ces trois lois fondamentales :
Première loi (ou loi de l'inertie)
[modifier | modifier le wikicode]- "Tout corps persévère dans son état de repos ou de mouvement rectiligne uniforme, si et seulement si, la somme des forces qui s'exercent sur lui est nulle."
Le texte exact, traduit par Marie-Françoise Biarnais dans "isaac newton, principia mathematica", Christian Bourgois Éditeur 1985, p.40, dit :
- "Tout corps persévère en son état de repos ou de mouvement rectiligne uniforme, sauf si des forces imprimées le contraignent d'en changer."
Cette loi est en opposition totale avec la notion "d'état de repos" d'Aristote. Pour Aristote, un corps n'est dans son état de repos que s'il ne bouge pas par rapport au centre de l'univers. Ainsi, un état de mouvement ne peut être un état de repos, c'est-à-dire un état qui persévère. Pour lui, le mouvement ne dure pas, à moins qu'on le force à durer. Pour Newton, l'état de repos et l'état de mouvement rectiligne uniforme sont deux choses identiques. Ainsi si, comme pour Aristote, un objet qui ne bouge pas n'est soumis à aucune force, au contraire de lui, pour Newton, un objet qui bouge, plus précisément se déplace en ligne droite et à vitesse constante, n'est pas plus soumis à une quelconque force. En d'autres termes, pour Newton, il n'est pas nécessaire d'exercer une force pour qu'il y ait mouvement.
La traduction mathématique actuelle de la première loi élimine ainsi naturellement la référence à un état de repos pour l'inclure dans la loi en tant que mouvement rectiligne à vitesse constante nulle :
Première loi (version actuelle)
[modifier | modifier le wikicode]La double flèche signifie "si et seulement si". En d'autre termes, on peut lire cette loi dans les deux sens :
- si un objet est en Mouvement Rectiligne Uniforme, alors on peut dire que la somme des forces extérieures qui s'exercent sur lui est nulle ().
- si on sait que la somme des forces qui s'exercent sur un objet est nulle, alors cet objet est en Mouvement Rectiligne Uniforme ().
Seconde loi (loi fondamentale de la dynamique)
[modifier | modifier le wikicode]Le texte exact, traduit par Marie-Françoise Biarnais dans "isaac newton, principia mathématica", Christian Bourgois Éditeur 1985, p.41, dit :
- "Le changement de mouvement est proportionnel à la force motrice imprimée et s'effectue suivant la droite par laquelle cette force est imprimée."
Seconde loi (version actuelle)
[modifier | modifier le wikicode]Cette loi exprime la relation entre cause et effet. La cause du mouvement étant la force totale qui s'exerce sur le système étudié et l'effet étant son accélération, la loi exprime la relation qui existe entre les deux par l'intermédiaire de la masse. Ainsi la cause mène à une expression du mouvement, en l'occurrence l'accélération, qui permet d'obtenir en fin de compte la position de l'objet au cours du temps, comme nous le verrons plus tard.
Par ailleurs nous reviendrons aussi sur la notion de force extérieure.
Troisième loi (loi de l'action et de la réaction)
[modifier | modifier le wikicode]- "La réaction est toujours contraire et égale à l'action : ou encore les actions que deux corps exercent l'un sur l'autre sont toujours égales et dirigées en sens contraire."
C'est le texte exact, traduit par Marie-Françoise Biarnais dans "isaac newton, principia mathematica", Christian Bourgois Éditeur 1985, p. 41.
Troisième loi (version actuelle)
[modifier | modifier le wikicode]Cette loi se traduit mathématiquement par le fait que le vecteur force exercée par un objet A sur un objet B est de mêmes grandeur et direction, mais de sens opposé au vecteur force exercée par l'objet B sur le A.
Cette dernière loi va nous permettre de revenir à la notion de force extérieure utilisée dans la seconde loi. En effet, selon la troisième loi, lorsqu'on pousse un objet pour le mettre en mouvement, celui-ci en réaction nous pousse avec une force de même intensité mais de sens contraire. Il semble donc à première vue, si on utilise par ailleurs la seconde loi, que la somme des forces est nulle. En principe donc, l'accélération devrait être nulle, et l'objet ne devrait pas se mettre en mouvement. Bien entendu, l'expérience montre le contraire. Où est donc le problème ?
En réalité, celui-ci vient du fait que nous n'avons pas considéré uniquement les forces extérieures. Pour bien comprendre cette notion, il est nécessaire de définir (c'est-à-dire choisir) le système dont nous cherchons l'accélération. Cela fait, il ne faut plus considérer dans la seconde loi de Newton, que les forces exercées par un corps autre (c'est-à-dire extérieur) que le système sur le système lui-même. Il ne faut donc alors pas tenir compte des forces exercées par le système sur un objet extérieur à lui.
Pour reprendre précisément l'exemple précédent, on peut dire que si le système dont on cherche l'accélération est l'objet que l'on pousse, il faut considérer dans la seconde loi de Newton uniquement la force que nous exerçons sur lui (force extérieure) et non celle qu'il exerce sur nous (force intérieure). Ainsi donc, même si la troisième loi implique l'existence des deux forces, pour appliquer correctement la seconde loi, il ne faut tenir compte que de la force extérieure.
C'est donc la notion de force qui traduit la cause du mouvement. Cette notion est centrale dans la mécanique de Newton.
Précisons enfin que l'unité de la force est le Newton. Il s'agit de la force nécessaire pour accélérer de 1 m/s² une masse de 1 kg.
Exemples
[modifier | modifier le wikicode]- Une voiture roule en ligne droite à vitesse constante. La force qui lui permet de maintenir sa vitesse vaut 200N. Calculez la force de frottement.
- Réponse :
- comme la voiture roule à vitesse constante et en ligne droite, la première loi de Newton nous indique que la somme des forces qui s'exercent sur elle est nulle. Ainsi, la force poussant la voiture étant vers l'avant et la force de frottement vers l'arrière, on peut dire que la force de frottement vaut aussi 200N.
- Une voiture (de masse m = 2000 kg) accélère de 0 m/s à 100 km/h en 12 secondes. Quelle distance a-t-elle parcouru ? D'où vient la force qui lui permet d'accélérer de telle manière et quelle est sa valeur ?
- Réponse :
- 100 km/h = 27,7 m/s. L'accélération est, par définition : a = (27,7 - 0)/12 = 2,31 m/s². La distance vaut alors : x = 2,31·12²/2 + 0·12 + 0 = 166,6 m.
- La force qui lui permet d'accélérer vient du frottement avec le sol. C'est le sol qui l'exerce. En effet, la force exercée par les pneus sur le sol est clairement vers l'arrière (pensez en effet au sens dans lequel serait projeté un petit caillou collé au pneu au moment du démarrage de la voiture). Ce ne sont donc pas les pneus qui permettent à la voiture de démarrer. D'ailleurs, sur sol gelé, malgré la rotation des pneus, elle ne pourrait pas démarrer. Ainsi, il faut considérer la force exercée par le sol sur les pneus. En effet, selon la troisième loi de Newton, celle-ci, en tant que réaction à l'action vers l'arrière des pneus sur le sol, s'exerce vers l'avant.
- La valeur de la force de frottement se calcule aisément par F = m·a = 2000·2,31 = 4620 N.
- Une voiture (de masse m = 2000 kg) freine sur une distance de 50 m pour éviter une collision avec un mur. Sa vitesse initiale étant de 50 km/h, calculez son accélération et la force qui lui permet de s'arrêter.
- Réponse :
- On ne connaît ni l'accélération, ni le temps d'arrêt. On peut donc soit utiliser les deux équations de la position et de la vitesse (deux équations à deux inconnues) dans lesquelles apparaissent le temps et l'accélération, soit utiliser une relation dérivée de ces deux équations où n'apparaît pas le temps, mais seulement l'accélération. Cette relation est (voir annexe) :
- Avec : , on a :
- Le signe négatif traduit une décélération (le freinage).
- Finalement, la force de freinage vaut : F = m·a = 2000·(-1,93) = 3860 N.
Types de forces
[modifier | modifier le wikicode]La seconde loi de Newton propose donc de faire jouer à la notion de force le rôle de cause du changement du mouvement. Le programme de Newton consiste donc en premier lieu à rechercher les forces qui agissent sur le système étudié. Il est donc fondamental de connaître les principales forces qui peuvent agir. Il y en a beaucoup. On ne pourra les étudier toutes. En fait, il en existe principalement quatre. Ce sont la force de gravitation, la force électromagnétique, la force faible\index{force faible} et la force forte. Elles sont dites fondamentales parce qu'elles sont à l'origine de toutes les autres. En d'autres termes, toutes les autres sont une manifestation de la présence des forces fondamentales.
Dans le cadre de ce cours de mécanique nous en étudierons que quatre, dont une seule fondamentale : la force de gravitation donnant lieu à la loi de la gravitation universelle de Newton.
Loi de la gravitation universelle
[modifier | modifier le wikicode]La force de gravitation exprime l'attraction à distance exercée par une masse sur une autre et réciproquement.
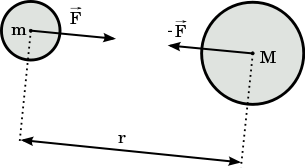 |
L'expression mathématique de cette loi, qui fait référence à la figure 3.1 est la suivante.
Cette loi est présentée ci-dessus sous sa forme vectorielle. Elle traduit donc en même temps la direction (qui lie les centres des deux masses), le sens (attraction des deux corps) et la grandeur du vecteur force . Souvent on utilise une forme plus courante qui ne traduit que la grandeur de la force, mais présente plus clairement la dépendance de cette dernière comme le carré de la distance (r²) :
Remarquons que :
- la loi de la gravitation universelle n'est valable que pour des corps ponctuels ou sphériques,
- qu'elle traduit une action à distance, ce qui posera par la suite de graves problèmes,
- que la constante G est une constante fondamentale appelée "constante de la gravitation universelle", et vaut . Cette constante est très petite. Cela traduit une force relativement faible (même si pour des masses conséquentes comme la terre et le soleil par exemple, elle peut avoir une valeur importante). Nous verrons, avec la force électrique par exemple, un exemple de force beaucoup plus forte.
Le poids
[modifier | modifier le wikicode]On a vu au paragraphe \ref{accg} que l'accélération à la surface de la terre d'un objet en chute libre (c'est-à-dire qui n'est soumis à aucun frottement) vaut . Or, en chute libre, la seule force qui s'exerce est le poids. Ainsi, selon la seconde loi de Newton, on peut écrire :
Évidemment le poids étant une force, il s'exprime en Newton.
On peut aussi comprendre le poids d'une autre manière. On peut considérer que le poids n'est que l'expression de la force de gravitation qui s'exerce entre la terre et le corps considéré placé à la surface de la terre. Ainsi, à l'aide de la loi de la gravitation, on peut écrire :
Attention, il faut bien comprendre que le poids n'est pas une autre force que la force de gravitation, mais qu'il s'agit de la même force! Ainsi, on peut écrire, à la suite de l'équation précédente :
C'est l'expression de l'accélération d'un corps en chute libre à la surface de la terre. On peut donc facilement généraliser cette équation pour un corps autre que la terre :
En particulier aussi, on peut utiliser l'expression de g ci-dessus pour exprimer la variation de l'accélération terrestre en fonction de l'altitude :
où h est l'altitude au-dessus de la surface de la terre. On constate donc que l'accélération diminue avec l'altitude. Par conséquent, le poids aussi. On peut donc se poser la question suivante : "de combien maigrit-on en montant au sommet de l'Everest" :-).
Une des nombreuses applications intéressantes de la loi de la gravitation universelle est la détermination de l'altitude à laquelle il faut placer un satellite en orbite pour qu'il soit géostationnaire. Ce cas est présenté en annexe x.
Le frottement
[modifier | modifier le wikicode]Pour comprendre la force de frottement, il faut réaliser l'expérience suivante :
on tire avec un dynamomètre sur une masse posée sur une table. Pendant un premier temps, la masse ne bouge pas. Cela signifie que la force qu'on exerce est égale à la force de frottement. Même si on tire de plus en plus fort, la masse ne bouge pas. Donc, la force de frottement augmente en même temps et dans la même mesure que celle que l'on exerce. C'est le cas jusqu'à un certain point nommé "imminence de glissement". À ce moment là, la force de frottement, dite "statique" parce que le masse ne bouge pas encore, est maximale. Si on augmente encore ne serait-ce qu'un tout petit peu la force de traction, la masse se met en mouvement et on constate en général que la force de frottement diminue légèrement. Ensuite, même si on augmente la force de traction, la force de frottement ne varie plus. Ce comportement est résumé sur le graphique de la figure 3.2.
 |
Par ailleurs, pour un frottement de type sec, c'est-à-dire entre deux surfaces solides, on montre que la force ne dépend pas de la surface de frottement, mais seulement de la nature des surfaces et de la réaction du sol (la force exercée par le sol sur la masse). Ainsi, on peut écrire :
où est le coefficient de frottement statique qui traduit l'intervention de la nature des surfaces et N est la force de réaction. De la même manière, on a aussi :
où est le coefficient de frottement cinétique.
D'autre part, on a, comme la figure 3.2 le montre, la relation suivante :
Enfin, il faut relever qu'en réalité la situation est plus complexe. Même si le modèle de la force de frottement cinétique présente une force indépendante de la vitesse, on peut observer des variations en fonction de la vitesse (notamment une décroissance). De plus sa linéarité en fonction de la réaction normale du sol n'est pas toujours exacte. Il s'agit donc d'un modèle qui a ses limites.
Pour en savoir plus sur ce sujet il est fortement conseillé de consulter le wikilivre de tribologie.
La force d'un ressort
[modifier | modifier le wikicode]Il est particulièrement intéressant de comprendre comment agit la force d'un ressort. En effet, c'est un premier modèle traduisant les liaisons inter-atomiques à l'intérieur d'un cristal par exemple. Mais beaucoup d'autres cas pourraient être présentés.
Dans le domaine où le ressort à un comportement élastique (c'est-à-dire que son extension est parfaitement réversible), on montre que l'expression donnant le force de rappel par rapport à l'état d'équilibre où le ressort est détendu, est :
 |
Le signe négatif vient du fait que c'est une force de rappel (dirigée dans le sens contraire de l'axe).
Exemples
[modifier | modifier le wikicode]- Déterminez la perte de poids que constate une personne de masse m = 80 kg en passant du bord de la mer au sommet de l'Everest (8000 m).
- Solution :
- L'accélération terrestre au niveau de la mer vaut :
- L'accélération terrestre au niveau du sommet de l'Everest vaut :
- Ainsi, le poids de la personne au niveau de la mer vaut :
- et celui à 8000 m vaut :
- La différence est donc de :
- Au niveau de la mer, cela correspond à une variation de masse qui vaut :
- Calculez la distance de freinage d'une voiture roulant à 50 km/h sur une route mouillée dont les coefficients de frottement avec les pneus valent : . Le conducteur ne sait pas freiner.
- Solution :
- Comme le conducteur ne sait pas freiner, il bloque les roues et elles glissent sur la chaussée. Le coefficient de frottement est donc .
- La force de frottement vaut alors :
- Mais, la seconde loi de Newton implique :
- Par ailleurs, on a aussi :
- Ainsi, on tire :
- Car, 50 km/h = 13,9 m/s et a < 0 pour une décélération.
- On suspend à un ressort de constante k = 200 N/m une masse de 2 kg. Calculez son élongation.
- Solution :
- L'équilibre des forces (le poids vers le bas et la force de rappel du ressort vers le haut) mène à la solution suivante :











































