Fonctionnement d'un ordinateur/Langage machine et assembleur
Ce chapitre va aborder le langage machine, à savoir un standard qui définit les instructions du processeur, le nombre de registres, etc. Dans ce chapitre, on considérera que le processeur est une boîte noire au fonctionnement interne inconnu. Nous verrons le fonctionnement interne d'un processeur dans quelques chapitres. Les concepts que nous allons aborder ne sont rien d'autre que les bases nécessaires pour apprendre l'assembleur. Nous allons surtout parler des instructions du processeur. Pour simplifier, on peut classer les instructions en quatre grands types :
- les échanges de données entre mémoires ;
- les calculs et autres opérations arithmétiques ;
- les instructions de comparaison ;
- les instructions de branchement.
À côté de ceux-ci, on peut trouver d'autres types d'instructions plus exotiques, pour gérer du texte, pour modifier la consommation en électricité de l'ordinateur, pour chiffrer ou de déchiffrer des données de taille fixe, générer des nombres aléatoires, etc. Dans ce chapitre, nous allons voir un aperçu assez large des instructions qui existent. Nous n'allons pas nous limiter aux instructions les plus importantes, mais nous allons aussi parler d'instructions assez exotiques, soit présentes uniquement sur d'anciens ordinateurs, soit très rares, soit franchement tordues. Et certaines de ces instructions exotiques sont assez impressionnantes et risquent de vous surprendre !
Les instructions arithmétiques
[modifier | modifier le wikicode]Tout ordinateur gère des instructions qui font des calculs arithmétiques simples. Une opération mathématique ne se fait pas de la même manière suivant la représentation utilisée pour coder ces nombres : on ne manipule pas de la même façon des nombres signés, des nombres codés en complément à 1, des flottants simple précision, des flottants double précision, etc. Tout dépend du type de la donnée, à savoir est-ce un flottant, un entier codé en BCD, etc.
Dans le cas le plus simple, le processeur dispose d'une instruction par type à manipuler : une instruction de multiplication pour les flottants, une autre pour les entiers codés en complément à deux, etc. Sur d'autres machines assez anciennes, on stockait le type de la donnée dans la mémoire. Chaque nombre manipulé par le processeur incorporait un tag, une petite suite de bits qui permettait de préciser son type. Le processeur ne possédait pas d'instructions en plusieurs exemplaires pour faire la même chose, et utilisait le tag pour déduire comment faire ses calculs. Par exemple, ces processeurs n'avaient qu'une seule instruction d'addition, qui pouvait traiter indifféremment flottants, nombres entiers codés en BCD, en complément à deux, etc. Le traitement effectué par cette instruction dépendait du tag incorporé dans la donnée. Des processeurs de ce type s'appellent des architectures à tags, ou tagged architectures.
Les instructions entières
[modifier | modifier le wikicode]Les instructions arithmétiques sont les plus courantes et comprennent au minimum l'addition, la soustraction, la multiplication, éventuellement la division, parfois les opérations plus complexes comme la racine carrée. La division est une opération très complexe et particulièrement lente, bien plus qu'une addition ou une multiplication. Pour information, sur les processeurs actuels, la division est 20 à 80 fois plus lente qu'une addition/soustraction, et presque 7 à 26 fois plus lente qu'une multiplication. Mais on a de la chance : c'est aussi une opération assez rare.
Les tous premiers ordinateurs pouvaient manipuler des données de taille arbitraire. Alors certes, ces processeurs n'utilisaient pas vraiment les encodages de nombres qu'on a vus au premier chapitre. À la place, ils stockaient leurs nombres dans des chaines de caractères ou des tableaux encodés en BCD. De nos jours, les ordinateurs utilisent des entiers de taille fixe. La taille des données à manipuler peut dépendre de l'instruction. Ainsi, un processeur peut avoir des instructions pour traiter des nombres entiers de 8 bits, et d'autres instructions pour traiter des nombres entiers de 32 bits, par exemple.
La ou les instructions d'addition entière
[modifier | modifier le wikicode]Un processeur implémente au minimum une opération d'addition, même s'il existe de rares exemples de processeurs qui s'en passent. Mieux : certains processeurs implémentent plusieurs instructions d'addition, qui se distinguent par de subtiles différences.
La première différence est la gestion des débordements, qui est parfois gérée en ayant deux instructions d'addition : une pour les additions de nombres signés et une autre pour les nombres non-signés. L’additionneur utilisé pour ces deux instructions est le même, l'addition elle-même ne change pas, mais les débordements d'entiers ne sont pas gérés de la même manière. Comme on le verra plus tard, certains processeurs disposent d'un registre de débordement, de 1 bit, qui indique si une instruction arithmétique a généré un débordement d'entier ou non. Il est mis à 1 en cas de débordement, mais reste à 0 sinon. Ce bit de débordement est mis à jour à chaque addition/multiplication/soustraction. Et les débordements d'entiers sont différents selon que l'addition est signée ou non, d'où l'existence des deux instructions dédiées. D'autres processeurs s'en sortent autrement, en ayant deux bits de débordement : un si le résultat est signé, l'autre pour les résultats non-signés. Mais nous reparlerons de cela plus tard.
Une autre possibilité, présente sur les vieux processeurs, tient dans la gestion de la retenue. A l'époque, les processeurs ne pouvaient gérer que des nombres de 4 à 8 bits, guère plus. Pourtant, la plupart des applications logicielles demandait d'utiliser des entiers de 16 bits. Les opérations comme l'addition ou la soustraction étaient alors réalisées en plusieurs fois. Par exemple, on additionnait les 8 bits de poids faible, puis les 8 bits de poids fort. Dans un cas pareil, il fallait aussi gérer la retenue dans l'addition des 8 bits de poids fort.
Pour cela, la retenue en question était mémorisée dans un registre de 1 bit dédié, semblable au registre de débordement, appelé le bit de retenue. De plus, les processeurs incorporaient une instruction d'addition qui additionnait les deux opérandes avec la retenue en question, instruction souvent appelée ADDC (ADD with Carry). Niveau circuits, cela ne changeait pas grand chose, tous les additionneurs ayant une entrée pour la retenue (qui est utilisée pour implémenter la soustraction, rappelez-vous). L'implémentation de l'instruction ADDC était très simple, n'utilisait presque pas de circuits, et rendait de fiers services aux programmeurs de l'époque. Nous parlons là des vieux processeurs 4 et 8, mais certains processeurs 16, 32, voire 64 bits, sont capables d'effectuer ce genre d'opération, même si ils sont rares.
- Il existe parfois des instructions pour mettre le bit de retenue à 0 ou à 1. C'est le cas sur l'architecture x86. Mais son utilité est marginale, car toutes les instructions arithmétiques modifient le bit de retenue.
La même chose a lieu pour la soustraction, qui demande qu'une "retenue" soit propagée d'une colonne à l'autre (bien que la "retenue" soit utilisée différemment : elle n'est pas additionnée, mais soustraite du résultat de la colonne). Pour cela, les processeurs implémentent l'opération SUBC (Substract with Carry). Et pour mettre en œuvre cette opération, ils ont deux options. La première est d'ajouter un bit pour la "retenue" de la soustraction. Pour une soustraction qui calcule a-b, elle vaut 0 si a>=b et 1 si a<b. Elle est utilisée telle qu'elle par le circuit qui effectue la soustraction, généralement un soustracteur. L'autre option est d'utiliser le but de retenue de l'addition, sans rien modifier. Pour comprendre pourquoi, rappelons que la soustraction est implémentée en complément à deux par le calcul suivant :
Il s'agit d'une addition, qui a donc une retenue lors d'un débordement. On peut alors réutiliser le bit de retenue de l'addition pour la soustraction, en modifiant quelque peu la soustraction à effectuer. Pour comprendre comment faire la modification, précisons tout d'abord que les règles du complément à deux nous disent qu'on a un débordement quand a>=b. Passons maintenant à l'étude d'un exemple théorique : le cas où on veut soustraire deux nombres de 16 bits avec deux opérations SUBC qui travaillent sur 8 bits. Appelons les deux opérandes A et B, et les 8 bits de poids forts de ces opérandes, et et leurs 8 bits de poids faible. Voyons ce qui se passe suivant que la retenue soit de 0 ou 1.
- Si la retenue de l'addition est de 1, on a , ce qui veut dire que la seconde soustraction doit calculer .
- A l'inverse, si la retenue de l'addition est de 0, on a . Cela veut dire que si on posait la soustraction, alors une retenue devrait être propagée à la colonne suivante, ce qui veut dire que la seconde soustraction doit calculer .
Récapitulons dans un tableau.
| Retenue | Opération à effectuer pour la seconde soustraction |
|---|---|
| 0 | |
| 1 |
On voit que ce qu'il faut ajouter à est égal à la retenue. L'opération SUBC fait donc le calcul suivant :
La plupart des processeurs 8 et 16 bits avaient deux instructions de soustraction séparées : une sans gestion de la retenue, une avec. Mais certains processeurs comme le 6502 n'avaient qu'une seule instruction de soustraction : celle qui tient compte de la retenue ! Il n'y avait pas de soustraction normale. Pour éviter tout problème, les programmeurs devaient faire attention. Ils disposaient d'une instruction mettre à 0 ou à 1 le bit de retenue pour éviter tout problème, qu'ils utilisaient avant toute soustraction simple.
Les instructions de multiplication et de division entière
[modifier | modifier le wikicode]Il faut savoir que la division est une opération très lourde pour le processeur : une instruction de division dédiée met au mieux une dizaine de cycles d'horloge pour fournir un résultat, parfois plus de 50 à 70 cycles d’horloge. Heureusement, les divisions les plus courantes sont des divisions par une constante : un programme devant manipuler des nombres décimaux aura tendance à effectuer des divisions par 10, un programme manipulant des durées pourra faire des divisions par 60 (gestion des minutes/secondes) ou 24 (gestion des heures). Or, diverses astuces permettent de les remplacer par des suites d'instructions plus simples, qui donnent le même résultat (l'usage de décalages, la multiplication par un entier réciproque, etc). En-dehors de ce cas, l'usage des divisions est assez rare. Sachant cela, certains processeurs ne possèdent pas d'instruction de division, car les gains de performance seraient modérés et le coût en transistors élevé. D'autres processeurs implémentent toutefois la division dans une instruction machine, avec un circuit dédié, mais c'est signe que le coût en transistors n'est pas un problème pour le concepteur de la puce.
Par contre, l'opération de multiplication entière est très courante, presque tous les processeurs modernes en ont une. Les multiplications sont plus fréquentes dans le code des programmes, sans compter que c'est une opération pas trop lourde à implémenter en circuit. Il en existe parfois plusieurs versions sur un même processeur. Ces différentes versions servent à résoudre un problème quant à la taille du résultat d'une multiplication. En effet, la multiplication de deux opérandes de bits donne un résultat de , ce qui ne tient donc pas dans un registre. Pour résoudre ce problème, il existe plusieurs solutions.
Dans sa version la plus simple, l'instruction de multiplication se contente de garder les bits de poids faible, ce qui peut entraîner l'apparition de débordements d'entiers.
Une autre solution est de calculer soit les bits de poids fort, soit les bits de poids faible, le choix étant laissé au programmeur. Des processeurs disposent de deux instructions de multiplication : une instruction pour calculer les bits de poids fort du résultat et une autre pour les bits de poids faible. Certains processeurs disposent d'une instruction de multiplication configurable, qui permet de choisir quels bits conserver : poids fort ou poids faible.
Une autre version mémorise le résultat dans deux registres : un pour les bits de poids faible et un autre pour les bits de poids fort. Il faut noter que certains processeurs disposent de registres spécialisés pour cela. Par spécialisés, on veut dire qu'ils sont séparés des autres registres. Les autres registres, appelés les registres généraux, mémorisent n'importe quelle opérande entière et sont utilisables pour toutes les opérations. Mais la multiplication mémorise son résultat dans deux registres à part, qu'on nommera HO et LO. Seule l'instruction de multiplication peut écrire un résultat dans ces deux registres, avec HO pour les bits de poids fort, et LO pour les bits de poids faibles. Par contre, n'importe quelle instruction peut les lire, pour récupérer une opérande dans ces deux registres.
Les instructions sur les entiers BCD
[modifier | modifier le wikicode]Enfin, il faut citer les instructions BCD, qui agissent sur des opérandes codées en BCD. Devenues très rares avec la disparition du BCD dans l'informatique grand-public, elles étaient quasiment essentielles sur les tous premiers processeurs 8 bits.
Au tout début de l'informatique, il a existé des processeurs qui travaillaient uniquement en BCD, appelés des processeurs décimaux. Ils avaient uniquement des instructions BCD, pas d'instruction sur des opérandes codées en binaire. Ils étaient assez courants entre les années 60 et 70, même s'ils ne représentent pas la majorité des architectures de l'époque. Il y avait une vraie séparation entre processeurs décimaux et processeurs binaires, sans intermédiaires notables. Le grand avantage des processeurs décimaux est leur très bonne performance dans les tâches de bureautique, de comptabilité, et autres. Les processeurs de l'époque recevaient des entiers codés en BCD de la part des entrées-sorties, et devaient les traiter. Les processeurs binaires devaient faire des conversion BCD-binaire pour communiquer avec les entrées-sorties, mais pas les processeurs décimaux. Le gain en performance pouvait être substantiel dans certaines applications.
Par la suite, dans les années 80, l'augmentation des performances a favorisé les processeurs binaires. Faire des conversions binaires-BCD n'était plus un problème, les conversions étaient suffisamment rapides. Par contre, faire les calculs en BCD était plus lent que faire les calculs en binaire, ce qui fait que le compromis technologique de l'époque favorisaient le binaire. Mais pour obtenir le meilleur des deux mondes, les processeurs binaires ont ajouté un support du BCD. C'était l'époque des architectures 8 bits, puis 16 bits. Intuitivement, on se dit que, les processeurs de l'époque des 8 bits avaient leurs instructions de calcul en double : une instruction pour les calculs entier et une autre pour les calculs BCD. Mais d'autres processeurs faisaient autrement.
A l'époque des processeurs 8-16 bits, certains processeurs ne géraient pas d'instructions BCD proprement dit, mais géraient quand même les calculs en BCD grâce à des instructions spéciales. Concrètement, il n'y avait pas d'instruction d'addition ou de soustraction spécifique pour le BCD. Les programmeurs utilisaient une instruction d'addition ou de soustraction normale, celle utilisée sur les nombres binaires normaux. Le résultat de l'opération n'était évidemment pas le bon, mais il était possible de corriger ce résultat pour obtenir le bon résultat codé en BCD. Les processeurs de l'époque disposaient d'une instruction pour, souvent appelée Decimal Adjust After Addition.
Avant d'aller plus loin, nous devons préciser que les processeurs 8 bits de l'époque pouvaient gérer deux formats de BCD. Le premier est le format Packed, où deux chiffres sont mémorisé dans un octet. Le premier nibble (4bits) mémorise un chiffre BCD, le second nibble mémorise le second. Il s'agit d'un format qui remplit au maximum les bits de l'octet avec des données utiles. L'autre format, appelé Unpacked, ne mémorise qu'un seul chiffre BCD dans un octet. Le chiffre est quasi- tout le temps dans le nibble de poids faible. Il se trouve que la manière de corriger le résultat d'une opération n'est pas la même suivant que le nombre est codé en BCD packed et unpacked.
Pour commencer, étudions le cas des nombres BCD unpacked, plus simples à comprendre. Lors d'une addition, il se peut que le résultat ne soit pas représentable en BCD unpacked. Par exemple, si je fais le calcul 5 + 8, le résultat sera 13 : il tient dans un nibble en décimal, mais pas en BCD ! Cette situation survient quand le résultat d'une addition de deux entiers BCD unpacked dépasse 9, la limite de débordement en BCD unpacked. Nous avons vu dans le chapitre sur les circuits d'addition que la correction est alors toute simple : si le résultat dépasse 9, on ajoute 6. De plus, on doit prévenir que le résultat a débordé et ne tient pas sur un nibble en BCD. Pour cela, on ajoute un bit spécialisé, appelé le half carry flag, indicateur de demi-retenue en français, qui joue le même rôle que le bit de débordement, mais pour le BCD unpacked. Sur les processeurs x86, tout cela est réalisé par une instruction appelée ASCII adjust after addition.
- Pour la soustraction, il faut faire la même chose, sauf qu'il faut soustraire 6, pas l'ajouter. Et il y a aussi une instruction pour cela : ASCII adjust after substraction.
Pour les nombres BCD packed, la procédure est globalement la même, sauf qu'il faut traiter les deux nibbles : on ajoute 6 si le nibble de poids faible dépasse 9, puis on fait la même chose avec le nibble de poids fort. Le bit half carry flag n'est pas mis à jour et est tout simplement ignoré. Notons qu'on modifie d'abord le nibble de poids faible, avant de traiter celui de poids fort. En effet, si on corrige celui de poids faible, la retenue obtenue en ajoutant 6 se propage au nibble suivant, ce qui fait que ce dernier peut voir sa valeur augmenter. Une fois cela fait, le bit de retenue est mis à 1. La procédure est différente, vu qu'il faut traiter deux nibles au lieu d'un, et que le bit half-carry est ignoré au profit du bit de retenue normal'. D'où l'existence d'une instruction séparée pour l'addition des nombres BCD packed, appelée Décimal adjust after addition sur les processeurs x86.
Les processeurs modernes ne supportent plus le BCD, car il est très peu utilisé. Les processeurs ARM et MIPS ont toujours fait sans instructions BCD. Les processeurs x86 des PC désactivent les instructions BCD en mode 64 bits, mais conservent des opérations BCD en mode 32 bits, pour des raisons de compatibilité. Le support du codage BCD est surtout quelque chose qu'on trouve sur les anciens processeurs.
Les instructions flottantes
[modifier | modifier le wikicode]Avant les années 60, les processeurs n'était pas encore capables de faire de calculs avec des nombres flottants. Les calculs flottants étaient émulés soit par une bibliothèque logicielle, soit par le système d'exploitation. Pour améliorer les performances, les concepteurs de processeurs ont conçus des coprocesseurs arithmétiques, des processeurs secondaires spécialisés dans les calculs flottants, qui complémentaient le processeur principal, et avaient leur propre emplacement sur la carte mère. Par la suite, les concepteurs de processeurs ont incorporé des instructions de calculs sur des nombres flottants, rendant le coprocesseur inutile.
Les processeurs modernes disposent d'instructions de calculs sur des nombres flottants, qui sont standardisées. Le standard IEEE 754 standardise aussi quelques instructions sur les flottants : les quatre opérations arithmétiques de base, les comparaisons et la racine carrée. Certains processeurs vont plus loin et implémentent aussi d'autres instructions sur les flottants qui ne sont pas supportées par la norme IEEE 754. Par exemple, certaines fonctions mathématiques telles que sinus, cosinus, tangente, arctangente et d'autres. Le seul problème, c'est que ces instructions peuvent mener à des erreurs de calcul incompatibles avec la norme IEEE 754. Heureusement, les compilateurs peuvent mitiger ces désagréments.
Il faut néanmoins préciser que le support de la norme IEEE 754 n'est pas une obligation : certains processeurs ne la supportent que partiellement. Par exemple, certains processeurs ne supportent que les flottants simple précision, mais pas les double précision (ou inversement). Exemple : les premiers processeurs Intel ne géraient que les flottants double précision étendue. D'autres processeurs ne gèrent pas les underflow, overflow, les NaN, les infinis, ou même les flottants dénormaux. Précisons que même lorsque la gestion des dénormaux est implémentée en hardware (comme c'est le cas sur certains processeurs AMD), celle-ci reste malgré tout très lente.
Si les exceptions ne sont pas supportées, le processeur peut être configuré de façon à soit ignorer les exceptions en fournissant un résultat, soit déclencher une exception matérielle (à ne pas confondre avec les exceptions de la norme). Le choix du mode d'arrondi ou la gestion des exceptions flottantes se fait en configurant un registre dédié, intégré dans le processeur.
Plus rarement, il arrive que certains processeurs gèrent des formats de flottants spéciaux qui ne font pas partie de la norme IEEE 754. Par exemple, certains processeurs utilisent des formats de flottants différents de la norme IEEE 754, avec par exemple des flottants codés sur 8 ou 16 bits, qui sont très utiles pour les applications qui * se contentent très bien d'un résultat approché.
Les instructions logiques
[modifier | modifier le wikicode]À côté des instructions de calcul, on trouve des instructions logiques qui travaillent sur des bits ou des groupes de bits. Les opérations bit à bit ont déjà été vues dans les premiers chapitres, ceux sur l'électronique. Pour rappel, les plus courantes sont :
- La négation, ou encore le NON bit à bit, inverse tous les bits d'un nombre : les 1 deviennent des 0 et les 0 deviennent des 1.
- Le ET bit à bit, qui agit sur deux nombres : il va prendre les bits qui sont à la même place et va effectuer un ET (l’opération effectuée par la porte logique ET). Exemple : 1100·1010=1000.
- Les instructions similaires avec le OU ou le XOR.
Mais d'autres instructions sont intéressantes à étudier.
Les instructions de décalage et de rotation
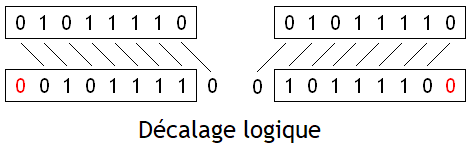
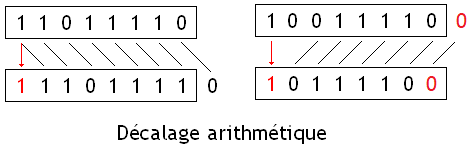
[modifier | modifier le wikicode]Les instructions de décalage décalent tous les bits d'un nombre vers la gauche ou la droite. Pour rappel, il existe plusieurs types de décalages : les rotations, les décalages logiques, et les décalages arithmétiques. Nous avions déjà vu ces trois opérations dans le chapitre sur les circuits de décalage et de rotation, ce qui fait que nous allons simplement faire un rappel dans le tableau suivant. Pour résumer, voici la différence entre les trois opérations :
Pour rappel, les décalages de n rangs sont équivalents à une multiplication/division par 2^n. Un décalage à gauche est une multiplication par 2^n, alors qu'un décalage à droite est une division par 2^n. Les décalages logiques effectuent la multiplication/division pour un nombre non-signé (positif), alors que les décalages arithmétiques sont utilisés pour les nombres signés. Précisons cependant que pour ce qui est des décalages à droite, les décalages logiques et arithmétiques n'arrondissent pas le résultat de la même manière. Les décalages logiques à droite arrondissent vers zéro, alors que les décalages arithmétiques arrondissent vers la valeur inférieure (vers moins l'infini). De plus, les décalages à gauche entraînent des débordements d'entiers qui ne se gèrent pas de la même manière entre décalage logique et décalage arithmétique.
La plupart des processeurs stockent le bit sortant dans un registre, généralement le registre qui stocke le bit de retenue des additions qui est réutilisé pour cette optique. Ils possèdent aussi une variante des instructions de décalage où le bit de retenue est utilisé pour remplir le bit libéré au lieu de mettre un zéro. Cela permet d'enchaîner les décalages sur un nombre de bits plus grand que celui supporté par les instructions en procédant par morceaux. Par exemple, pour un processeur supportant les décalages sur 8 et 16 bits, il peut enchaîner deux décalages de 16 bits pour décaler un nombre de 32 bits ; ou bien un décalage de 8 bits et un autre de 16 bits pour décaler un nombre de 24 bits.

Ils existe une variante des instructions de rotation où le bit de retenue est utilisé. Un bon exemple est celui des instructions LRCY (Left Rotate Through Carry) et RRCY (Right Rotate Through Carry). La première est un décalage/rotation à gauche, l'autre est un décalage/rotation à droite. Les deux décalent un registre de 16 bits, mais on pourrait imaginer la même chose avec des registres de taille différente. Lors du décalage, le bit sortant est mémorisé dans le registre de retenue, alors que le bit de retenue précédent est lui envoyé dans le vide laissé par le décalage. Tout se passe comme s'il s'agissait d'une rotation, sauf que le nombre décalé/rotaté est composé du registre concaténé au bit de retenue, le bit de retenue étant le bit de poids fort pour un décalage à gauche, de poids faible pour un décalage à droite.
Le cas particuliers des processeurs ARM
[modifier | modifier le wikicode]Sur les processeurs ARM, il n'y a pas d'instruction de décalage à proprement parler, ni de rotations. Par contre, les décalages sont fusionnés avec la plupart des opérations arithmétiques ! Toute opération arithmétique prend deux registres d'opérandes et un registre de destination, ainsi qu'un décalage facultatif. Le décalage est appliqué sur la seconde opérande automatiquement, sans avoir à faire une instruction séparée.
A l'intérieur de l'instruction, deux bits précisent quel type de décalage effectuer (logique à droite, arithmétique à droite, à gauche, rotation à droite). Le nombre de rangs dont il faut décaler est soit encodé directement dans l'instruction sur 5-6 bits, soit précisé dans un registre.
Toutes les instructions ne permettent pas de faire un décalage automatique. Seules les opérations simples peuvent le faire, à savoir les additions, soustractions, copies d'un registre à un autre, les opérations logiques, et quelques autres. Et cela se marie très bien avec le fait qu'on applique le décalage sur la seconde opérande fait qu'il se marie très bien avec les calculs d'adresse. En effet, quand un programmeur manipule une structure de données, notamment un tableau, il arrive souvent qu'il fasse des calculs d'adresse cachés. La majeure partie de ces calculs d'adresse sont de la forme : adresse de base + (indice * taille de la donnée). Vu que les données ont très souvent une taille qui est une puissance de deux, le second terme se calcule en décalant l'indice, le calcul total demande une simple addition avec une opérande décalée, ce qui prend une seule instruction sur les processeur ARM.
Les instructions de manipulation de bits
[modifier | modifier le wikicode]D'autres opérations effectuent des calculs non pas bit à bit (on traite en parallèle les bits sur la même colonne), mais qui manipulent les bits à l'intérieur d'un nombre. les plus simples d'entre elles comptent sur les bits.
Une instruction très commune de ce type est l'instruction population count, qui compte le nombre de bits d'un nombre qui sont à 1. Par exemple, pour le nombre 0100 1100 (sur 8 bits), la population count est de 3. Il s'agit d'une instruction utile dans les codes correcteurs d'erreur, très utilisés pour tout et n'importe quoi (trames réseau, sommes de contrôle des secteurs des disques dur, et bien d'autres). De plus, elle permet de calculer facilement le bit de parité d'un nombre, ce qui est utile pour les codes de détection d'erreur. En soi, l'instruction est facultative et l'implémenter est un choix qui n'est pas trivial. Mais cette instruction est très simple à implémenter en circuits, sans compter que son implémentation utilise assez peu de transistors. Le circuit de calcul est ridiculement simple, utilise peu de transistors.
Les processeurs gèrent aussi assez souvent des instructions pour compter les zéros ou les uns après le bit de poids fort/faible. Pour rappel, voici les quatre possibilités :
- Count Trailing Zeros donne le nombre de zéros situés à droite du 1 de poids faible.
- Count Leading Zeros donne le nombre de zéros situés à gauche du 1 de poids fort.
- Count Trailing Ones donnent le nombre de 1 situés à gauche du 0 de poids fort.
- Count Leading Ones donne le nombre de 1 situés à droite du 0 de poids faible.

Comme vous le voyez sur le schéma du dessus, ces quatre opérations de comptage sont liées à quatre autres opérations. Ces dernières donnent la position du 0 ou du 1 de poids faible/fort :
- Find First Set, donne la position du 1 de poids faible.
- Find highest set donne la position du 1 de poids fort.
- Find First Zero donne la position du 0 de poids faible.
- Find Highest Zero donne la position du 0 de poids fort.
Il est rare que des processeurs s’implémentent toutes ces opérations. En effet, le résultat de certaines opérations se calcule à partir des autres. Pour donner un exemple, les processeurs x86 modernes incorporent une extension, appelée Bit manipulation instructions sets (BMI sets), qui ajoute quelques instructions de ce type. Pour le moment, seules les instructions Count Trailing Zeros et Count Leading Zeros sont supportées.
Et il existe bien d'autres instructions de ce type. On peut citer, par exemple, l'instruction BLSI, qui ne garde que le 1 de poids faible et met à zéro tous les autres bits. L'instruction BLSR quant à elle, met à 0 ce 1 de poids faible. Et il y en a bien d'autres, qui impliquent le 1 de poids fort, le 0 de poids faible, le 1 de poids faible, etc.
Les instructions d'extension de registres
[modifier | modifier le wikicode]Certains processeurs sont capables de gérer des données de taille diverses. Ils peuvent par exemple gérer des données codées sur 16 bits ou sur 32 bits comme c'est le cas sur certains processeurs anciens. Comme autre exemple, les processeurs x86 modernes peuvent gérer des données de 8, 16 et 32 bits. Pour cela, ils disposent généralement de registres de taille différentes, certains font 8 bits, d'autres 16, d'autres 32, etc. Dans ce cas, il est courant que l'on ait à faire des conversions vers un nombre de taille plus grande. Par exemple, convertir un nombre de 8 bits en un nombre de 16 bits, ou un nombre de 8 bits en 32 bits. Les processeurs de ce type incorporent des instructions pour ce faire, qui s'appellent les instructions d'extension de nombres.
La seule difficulté de ces instructions tient à la manière dont on remplit les bits de poids forts. Par exemple, si l'on passe de 8 bits à 16 bits, les 8 bits de poids forts sont inconnus. Pareil si on passe de 16 bits à 32 bits : quelle doit être la valeur des 16 bits de poids fort ? Intuitivement, on se dit qu'il suffit de les remplir par des zéros. Faire ainsi marche très bien, mais à condition que le nombre soit un nombre positif ou nul. Mais dans le cas d'un nombre négatif, cela ne marche pas (le résultat n'est pas bon). Pour les nombres codés en complément à deux, il faut remplir les bits manquants par le bit de signe, le bit de poids fort. On a donc deux choix : soit on remplit les bits manquants par des 0, ou par le bit de poids fort. Globalement, les deux choix possibles correspondent à deux instructions : une pour les nombres non-signés et une autre pour les nombres codés en complément à deux. On parle respectivement d'instruction de zero extension et instruction d'extension de signe.
Formellement, les instructions d'extension de nombre sont des copies entre registres : le contenu d'un registre est copié dans un autre plus grand. L'extension de signe est couplée avec cette copie, les deux étant effectués en une instruction. Du moins, c'est le cas sur la plupart des processeurs. On pourrait imaginer séparer les deux en deux instructions séparées, une instruction MOV (qui copie un registre dans un autre, comme on le verra plus bas) et une instruction d'extension de signe/zéro. Dans ce cas, l'instruction d'extension de signe/zéro prend un registre de grande taille et étend la donnée dans ce registre. Par exemple, pour une extension de signe de 16 à 32 bits, l'instruction prendrait un registre de 32 bits, ne considérerait que les 16 bits de poids faible et effectuerait l'extension de signe/zéro à partir de ces derniers. En soi, l'extension avec des zéros est un simple masque, réalisable avec des opérations bit à bit et cette instruction n'a pas besoin d'être implémentée. Par contre, les instructions d'extension de signe sont elles très utiles.
De plus, une instruction d'extension de signe séparée a l'avantage d'être utilisable même sur des architecture avec des registres de taille identique. Mais quel intérêt, me direz-vous ? Il faut savoir que certaines langages de programmation permettent de travailler sur des entiers dont on peut préciser la taille. Un même programme peut ainsi manipuler des entiers de 16 bits et de 32 bits, ou des entiers de 8, d'autres de 16, d'autres de 32, et d'autres de 64. L'intérêt n'est as évident, mais un bon exemple est celui de la rétrocompatibilité entre programmes. Par exemple, un programme 64 bits qui utilise une librairie 32 bits, ou un programme codé en 64 bits qui émule une console 16 bits. Ou encore, la communication entre un programme codé en 16 bits avec un capteur qui mesure des données de 8 bits. Bref, les possibilités sont nombreuses. Imaginons que tout se passe dans des registres de 32 bits. Le processeur peut incorporer des instructions de calcul sur 16 bits, en plus des instructions 32 bits. Dans ce cas, l'extension de signe sert à faire des conversions entre entiers de taille différentes.
Les instructions de permutation d'octets
[modifier | modifier le wikicode]Les instructions de byte swap, aussi appelée instructions de permutation d'octets, échangent de place les octets d'un nombre. Leur implémentation varie grandement selon la taille des entiers. Le cas le plus simple est celui des instructions qui travaillent sur des entiers de 16 bits, soit deux octets. Il n'y a alors qu'une seule solution pour échanger les octets : l'octet de poids fort devient l'octet de poids faible et réciproquement. Les deux octets échangent leur place.
Pour les nombres de 32 bits, soit 4 octets, il y a plusieurs possibilités. La première inverse l'ordre des octets dans le nombre : on échange l'octet de poids faible et de poids fort, mais on échange aussi les deux octets restant entre eux. Une autre solution découpe l'entier en deux morceaux de 16 bits : l'un avec les deux octets de poids fort, l'autre avec les deux octets de poids faible. Les octets sont inversés dans ces blocs de 16 bitzs, mais on n'effectue pas d'autres échanges. On peut aussi échanger les deux morceaux de 16 bits, mais sans changer l'ordre des octets dans les blocs.

L'utilité de ces instructions n'est pas évidente au premier abord, mais elle sert beaucoup dans les opérations de conversion de données. Tout cela devrait devenir plus clair dans le chapitre sur le boutisme.
Les instructions d'accès mémoire
[modifier | modifier le wikicode]Les instructions d’accès mémoire permettent de copier ou d'échanger des données entre le processeur et la RAM. On peut ainsi copier le contenu d'un registre en mémoire, charger une donnée de la RAM dans un registre, initialiser un registre à une valeur bien précise, etc. Il en existe plusieurs, les plus connues étant les suivantes : LOAD, STORE et MOV. D'autres processeurs utilisent une instruction d'accès mémoire généraliste, plus complexe.
Les instructions d'accès à la RAM : LOAD et STORE
[modifier | modifier le wikicode]Les instructions LOAD et STORE sont deux instructions qui permettent d'échanger des données entre la mémoire RAM et les registres. Elles copient le contenu d'un registre dans la mémoire, ou au contraire une portion de mémoire RAM dans un registre.
- L'instruction LOAD est une instruction de lecture : elle copie le contenu d'un ou plusieurs mots mémoire consécutifs dans un registre. Le contenu du registre est remplacé par le contenu des mots mémoire de la mémoire RAM.
- L'instruction STORE fait l'inverse : elle copie le contenu d'un registre dans un ou plusieurs mots mémoire consécutifs en mémoire RAM.

|

|
D'autres instructions d'accès mémoire plus complexes existent. Pour en donner un exemple, citons les instructions de transferts par bloc sur les premiers processeurs ARM. Ces instructions permettent de copier plusieurs registres en mémoire RAM, en une seule instruction. Sur l'ARM1, il y a 16 registres en tout. Les instructions de transfert de bloc peuvent sélectionner n'importe quel sous-ensemble de ces 16 registres, pour les copier en mémoire : on peut sélectionner tous les registres, une partie des registres (5 registres sur 16, ou 7, ou 8, ...), voire aucun registre.
Les instructions de transfert entre registres : MOV et XCHG
[modifier | modifier le wikicode]L'instruction MOV copie le contenu d'un registre dans un autre sans passer par la mémoire. C'est donc un échange de données entre registres, qui n'implique en rien la mémoire RAM, mais MOV est quand même considérée comme une instruction d'accès mémoire. Les données sont copiées d'un registre source vers un registre de destination. Le contenu du registre source est conservé, alors que le contenu du registre de destination est écrasé (il est remplacé par la valeur copiée). Cette instruction est utile pour gérer les registres, notamment sur les architectures avec peu de registres et/ou sur les architectures avec des registres spécialisés.

Mais quelques rares architectures ne disposent pas d'instruction MOV, qui n'est formellement pas nécessaire, même si bien utile. En effet, on peut émuler une instruction MOV avec des instructions logiques utilisées convenablement. L'idée est de faire une opération dont le résultat est l'opérande envoyée, et d'enregistrer le résultat dans le registre de destination. Par exemple, on peut faire un OU entre le registre opérande et 0 : le résultat sera l'opérande. Idem avec un ET et la valeur adéquate. Ou encore, on peut imaginer faire un ET/OU entre un registre et lui-même : le résultat est égal au contenu du registre opérande.
Quelques processeurs assez rares ont des instructions pour échanger le contenu de deux registres. Par exemple, on peut citer l'instruction XCHG sur les processeurs x86 des PC anciens et actuels. Elle permet d'échanger le contenu de deux registres, quel qu'ils soient, il n'y a pas de restrictions sur le registre source et sur le registre de destination. Mais d'autres processeurs ont des restrictions sur les registres source et destination. Par exemple, le processeur Z80 a des instructions d'échanges assez restrictives, comme on le verra dans quelques chapitres.
Sur les processeurs ARM, l'instruction MOV fait partie des instructions qui permettent d'effectuer un décalage sur la seconde opérande. Il s'agit en réalité de décalages/rotations décalées, qui sont fusionnées avec une instruction MOV. L'instruction MOV des processeurs ARM fait soit un MOV normal, soit un décalage.
Les instructions d'accès mémoire complexes
[modifier | modifier le wikicode]Sur certains processeurs, il n'y a pas d'instruction LOAD ou STORE. A la place, on trouve une instruction d'accès mémoire généraliste. Elle est notamment capable de faire une lecture, une écriture, ou une copie entre registres, et parfois une copie d'une adresse mémoire vers une autre. Les trois premières opérations sont presque toujours supportées, mais la copie d'une adresse mémoire vers une autre est beaucoup plus rare.
Sur les processeurs x86, l'instruction généraliste s'appelle l'instruction MOV, mais elle gère la lecture en RAM, l'écriture en RAM, la copie d'un registre vers un autre, l'écriture d'une constante dans un registre ou une adresse. Par contre, elle ne gère pas la copie d'une adresse mémoire vers une autre. Le choix entre les opérations possibles dépend de l'ordre des opérandes et de leurs nature. L'instruction mémoire généraliste utilise deux opérandes, et leur ordre compte. Typiquement, la première opérande désigne la source et l'autre la destination. Par exemple, si les deux opérandes sont des registres, alors le premier registre est copié dans le second. Si la première opérande est un registre, et l'autre une adresse, alors c'est une écriture. Inversez l'adresse et le registre et c'est une lecture.
Pour les transferts entre deux adresses, il existe d'autres instructions mémoires spécialisées. Elles sont connues sous le nom d'instructions de chaines de caractère, bien qu'elles travaillent en réalité plus sur des tableaux ou des zones de mémoire. Fait intéressant, ces instructions mémoires peuvent être répétée automatiquement plusieurs fois, en leur ajoutant un préfixe. Pour cela, le nombre de répétitions doit être stocké dans le registre ECX, qui est décrémenté à chaque exécution de l'instruction. Une fois que ce registre atteint 0, l'instruction n'est plus répété et on passe à l'instruction suivante. En clair, l'instruction décrémente automatiquement ce registre à chaque éxecution et s'arrête quand il atteint zéro.
Pour les échanges entre deux adresses mémoire, les processeurs x86 fournissent une instruction dédiée, appelée MOVS. Pour cela, on doit préciser l'adresse de la source et l'adresse de destination dans deux registres spécifiques. Elle peut être répétée plusieurs fois avec l'ajout du préfixe REP. L'instruction avec préfixe, REPMOVS, permet donc de copier un bloc de mémoire dans un autre, de copier n adresses consécutives ! Les deux registres pour l'adresse source et destination sont modifiés à chaque exécution de l'instruction, afin de pointer vers le mot mémoire suivant. Par modifiés, je veux dire qu'ils peuvent être tous les deux soit incrémentés, soit décrémentés. Cela permet de parcourir la mémoire dans l'ordre montant (adresses croissantes) ou descendant (adresses décroissantes). La direction de parcours de la mémoire est spécifiée dans un bit incorporé dans le processeur, qui vaut 0 (décrémentation) ou 1 (incrémentation). Il peut être altéré par des instructions dédiées, de manière à être mis à 1 ou 0.
D'autres instructions d'accès mémoire peuvent être préfixées avec REP. Par exemple, l'instruction STOS, qui copie le contenu du registre EAX dans une adresse. On peut exécuter cette instruction une fois, ou la répéter plusieurs fois avec le préfixe REP. Là encore, on doit préciser l'adresse à laquelle écrire dans un registre spécifié, puis le nombre de répétitions dans le registre ECX. Là encore, le nombre de répétitions est décrémenté à chaque exécution, alors que l'adresse est incrémentée/décrémentée. L'instruction REPSTOS est très utile pour mettre à zéro une zone de mémoire, ou pour initialiser un tableau avec des données préétablies.
D'autres instructions mémoires effectuent des opérations à l'utilité moins évidente. Sur certains processeurs, on trouve notamment des instructions pour vider la mémoire cache de son contenu, pour la réinitialiser. L'utilité ne vous est pas évidente, mais cela peut servir dans certains scénarios, notamment sur les architectures avec plusieurs processeurs pour synchroniser ces derniers. Cela sert aussi pour le système d'exploitation, qui doit remettre à zéro certains caches (comme la TLB qu'on verra dans le chapitre sur la mémoire virtuelle) quand on exécute plusieurs programmes en même temps.
Les instructions de contrôle (branchements et tests)
[modifier | modifier le wikicode]Un processeur serait sacrément inflexible s'il ne faisait qu'exécuter des instructions dans l'ordre. Certains processeurs ne savent pas faire autre chose, comme le Harvard Mark I, et il est difficile, voire impossible, de coder certains programmes sur de tels ordinateurs. Mais rassurez-vous : il existe de quoi permettre au processeur de faire des choses plus évoluées. Pour rendre notre ordinateur "plus intelligent", on peut par exemple souhaiter que celui-ci n'exécute une suite d'instructions que si une certaine condition est remplie. Ou faire mieux : on peut demander à notre ordinateur de répéter une suite d'instructions tant qu'une condition bien définie est respectée. Diverses structures de contrôle de ce type ont donc étés inventées.
Voici les plus utilisées et les plus courantes : ce sont celles qui reviennent de façon récurrente dans un grand nombre de langages de programmation actuels. Concevoir un programme (dans certains langages de programmation), c'est simplement créer une suite d'instructions, et utiliser ces fameuses structures de contrôle pour l'organiser. D'ailleurs, ceux qui savent déjà programmer auront reconnu ces fameuses structures de contrôle. On peut bien sur en inventer d’autres, en spécialisant certaines structures de contrôle à des cas un peu plus particuliers ou en combinant plusieurs de ces structures de contrôles de base, mais cela dépasse le cadre de ce cours : on ne va pas vous apprendre à programmer.
| Nom de la structure de contrôle | Description |
|---|---|
| SI...ALORS | Exécute une suite d'instructions si une condition est respectée |
| SI...ALORS...SINON | Exécute une suite d'instructions si une condition est respectée ou exécute une autre suite d'instructions si elle ne l'est pas. |
| Boucle WHILE...DO | Répète une suite d'instructions tant qu'une condition est respectée. |
| Boucle DO...WHILE aussi appelée REPEAT UNTIL | Répète une suite d'instructions tant qu'une condition est respectée. La différence, c'est que la boucle DO...WHILE exécute au moins une fois cette suite d'instructions. |
| Boucle FOR | Répète un nombre fixé de fois une suite d'instructions. |
Les conditions à respecter pour qu'une structure de contrôle fasse son office sont généralement très simples. Elles se calculent le plus souvent en comparant deux opérandes (des adresses, ou des nombres entiers ou à virgule flottante). Elles correspondent le plus souvent aux comparaisons suivantes :
- A == B (est-ce que A est égal à B ?) ;
- A != B (est-ce que A est différent de B ?) ;
- A > B (est-ce que A est supérieur à B ?) ;
- A < B (est-ce que A est inférieur à B ?) ;
- A >= B (est-ce que A est supérieur ou égal à B ?) ;
- A <= B (est-ce que A est inférieur ou égal à B ?).
Pour implémenter ces structures de contrôle, on a besoin d'une instruction qui saute en avant ou en arrière dans le programme, suivant le résultat d'une condition. Par exemple, un SI...ALORS zappera une suite d'instruction si une condition n'est pas respectée, ce qui demande de sauter après cette suite d’instruction cas échéant. Répéter une suite d'instruction demande juste de revenir en arrière et de redémarrer l’exécution du programme au début de la suite d'instruction. Nous verrons comment sont implémentées les structures de contrôle plus bas, mais toujours est-il que cela implique de faire des sauts dans le programme. Faire un saut en avant ou en arrière dans le programme est assez simple : il suffit de modifier la valeur stockée dans le program counter, ce qui permet de sauter directement à une instruction et de poursuivre l'exécution à partir de celle-ci. Et un tel saut est réalisé par des instructions spécialisées. Dans ce qui va suivre, nous allons appeler instructions de branchement les instructions qui sautent à un autre endroit du programme. Ce n'est pas la terminologie la plus adaptée, mais elle conviendra pour les explications.
L'implémentation des structures de contrôle demande donc de calculer une condition, puis de faire un saut. Mais il faut savoir que l'implémentation demande parfois de faire un saut, sans avoir à tester de condition. Dans ce cas, l'instruction qui fait un saut sans faire de test de condition est elle aussi une instruction de branchement. Cela nous amène à faire la différence entre un branchement conditionnel et non-conditionnel. La différence entre les deux est simple. Une instruction de branchement conditionnel effectue deux opérations : un test qui vérifie si la condition adéquate est respectée, et un saut dans le programme aussi appelé branchement. Une instruction de branchement inconditionnelle ne teste pas de condition et ne fait qu'un saut dans le programme.
Les structures de contrôle
[modifier | modifier le wikicode]Le IF permet d’exécuter une suite d'instructions si et seulement si une certaine condition est remplie.

Le IF...ELSE sert à effectuer une suite d'instructions différente selon que la condition est respectée ou non : c'est un SI…ALORS contenant un second cas. Une boucle consiste à répéter une suite d'instructions machine tant qu'une condition est valide (ou fausse).

Les boucles sont une variante du IF dont le branchement renvoie le processeur sur une instruction précédente. Commençons par la boucle DO…WHILE : la suite d'instructions est exécutée au moins une fois, et est répétée tant qu'une certaine condition est vérifiée. Pour cela, la suite d'instructions à exécuter est placée avant les instructions de test et de branchement, le branchement permettant de répéter la suite d'instructions si la condition est remplie. Si jamais la condition testée est fausse, on passe tout simplement à la suite du programme.

Une boucle WHILE…DO est identique à une boucle DO…WHILE à un détail près : la suite d'instructions de la boucle n'a pas forcément besoin d'être exécutée au moins une fois. On peut donc adapter une boucle DO…WHILE pour en faire une boucle WHILE…DO : il suffit de tester si la boucle doit être exécutée au moins une fois avec un IF, et exécuter une boucle DO…WHILE équivalente si c'est le cas.

Les branchements conditionnels et leur implémentation
[modifier | modifier le wikicode]Il existe de nombreuses manières de mettre en œuvre les branchements conditionnels et tous les processeurs ne font pas de la même manière. Sur la plupart des processeurs, les branchements conditionnels sont séparés en deux instructions : une instruction de test qui vérifie si la condition voulue est respectée, et une instruction de saut conditionnelle. D'autres processeurs effectuent le test et le saut en une seule instruction machine.

- Plus surprenant, sur quelques rares processeurs, le program counter est un registre qui peut être modifié comme tous les autres. Cela permet de remplacer les branchements par une simple écriture dans le program counter, avec une instruction MOV. Un bon exemple est le processeur ARM1, un des tout premiers processeur ARM. Cette dernière solution n'est presque jamais utilisée, mais elle reste surprenante !
Dans les faits, la solution la plus simple est clairement d'implémenter le tout avec une seule instruction. Mais beaucoup de processeurs anciens utilisent la première méthode, celle qui sépare le branchement conditionnel en deux instructions. Le branchement prend le résultat de l'instruction de test et décide s'il faut passer à l'instruction suivante ou sauter à une autre adresse. Il faut donc mémoriser le résultat de l'instruction de test dans un registre spécialisé, afin qu'il soit disponible pour l'instruction de branchement. L'usage d'un registre intermédiaire pour mémoriser le résultat de l'instruction de test demande d'ajouter un registre au processeur. De plus, le résultat de l'instruction de test varie grandement suivant le processeur, suivant la manière dont on répartit les responsabilités entre test et branchements.
Il existe, dans les grandes lignes, deux techniques pour séparer test et branchement conditionnel. La première impose une séparation stricte entre calcul de la condition et saut : l'instruction de test calcule la condition, le branchement fait ou non le saut dans le programme suivant le résultat de la condition. On a alors une instruction de test proprement dit, qui vérifie si une condition est valide et fournit un résultat sur 1 bit. Nous appellerons ces dernières des comparaisons, car de telles instruction effectuent réellement une comparaison. La seconde méthode procède autrement, avec un calcul de la condition qui est réalisé en partie par l'instruction de test, en partie par le branchement. Cela peut paraitre surprenant, mais il y a de bonnes raisons à cette séparation peu intuitive. La raison est que l'instruction de test est une soustraction déguisée, qui fournit un résultat de plusieurs bits, qui est ensuite utilisé pour calculer la condition voulue par le branchement. l'instruction de test ne fait pas une comparaison proprement dit, mais leur résultat permet de déterminer le résultat d'une comparaison avec quelques manipulations simples.
Les instructions de test proprement dit
[modifier | modifier le wikicode]Les premières sont réellement des instructions de test, qui effectuent une comparaison et disent si deux nombres sont égaux, différents, lequel est supérieur, inférieur, etc. En clair, elles implémentent directement les comparaisons vues précédemment. Au total, on s'attend à ce que les 6 comparaisons précédentes soient implémentées avec 6 instructions de test différentes : une pour l'égalité, une pour la différence, une autre pour la supériorité stricte, etc. Mais certaines de ces comparaisons sont en deux versions : une qui compare des entiers non-signés, et une autre pour les entiers signés. La raison est que comparer deux nombres entiers ne se fait pas de la même manière selon que les opérandes soient signées ou non. Nous avions vu cela dans le chapitre sur les comparateurs, mais un petit rappel ne fait pas de mal. Pour comparer deux entiers signés, il faut tenir compte de leurs signes, et le circuit utilisé n'est pas le même. Cela a des conséquences au niveau des instructions du processeur, ce qui impose d'avoir des opérations séparées pour les entiers signés et non-signés.
Dans les faits, les processeurs actuels utilisent le complément à deux pour les entiers signés, ce qui fait que les comparaisons d'égalité ou de différence A == B et A != B ne sont présentes qu'en un seul exemplaire. En complément à deux, l'égalité se détermine avec la même règle que pour les entiers non-signés : deux nombres sont égaux s'ils ont la même représentation binaire, ils sont différents sinon. Ce ne serait pas le cas avec les entiers en signe-magnitude ou en complément à un, du fait de la présence de deux zéros : un zéro positif et un zéro négatif. Les circuits de comparaison d'égalité et de différence seraient alors légèrement différents pour les entiers signés ou non. Au total, en complément à deux, on trouve donc 10 comparaisons usuelles, vu que les comparaisons de supériorité/infériorité sont en double.
Le résultat d'une comparaison est un bit, qui dit si la condition testée est vraie ou fausse. Dans la majorité des cas, ce bit vaut 1 si la comparaison est vérifiée, et 0 sinon. Une fois que l'instruction a fait son travail, il reste à stocker son résultat quelque part. Pour cela, le processeur utilise un ou plusieurs registres à prédicats, des registres de 1 bit qui peuvent stocker n'importe quel résultat de comparaison. Une comparaison peut enregistrer son résultat dans n'importe quel registre à prédicats : elle a juste à préciser lequel avec son nom de registre.
Les registres à prédicats sont utiles pour accumuler les résultats de plusieurs comparaisons et les combiner par la suite. Par exemple, cela permet d'émuler une instruction qui teste si A >= B à partir de deux instructions qui calculent respectivement A > B et A == B. Pour cela, certains processeurs incorporent des instructions pour faire des opérations logiques sur les registres à prédicats. Ces opérations permettent de faire un ET, OU, XOR entre deux registres à prédicats et de stocker le résultat dans un registre à prédicat quelconque.
D'autres instructions permettent de lire le résultat d'un registre à prédicat, de calculer une condition, de combiner son résultat avec la valeur lue et d'altérer le registre à prédicat sélectionné. Par exemple, sur l'architecture IA-64, il existe une instruction cmp.eq.or, qui calcule une condition, lit un registre à prédicat fait un OU logique entre le registre lu et le résultat de la condition, et enregistre le tout dans un autre registre à prédicat. De telles instructions facilitent grandement le codage de certaines fonctions, qui demandent que plusieurs conditions soient vérifiées pour exécuter un morceau de code.
Les instructions de test qui sont des soustractions déguisées
[modifier | modifier le wikicode]Le second type d'instruction de test ne calcule pas ces conditions directement, mais elle fournit un résultat de quelques bits qui permet de les calculer avec quelques manipulations simples. Sur ces processeurs, il n'y a qu'une seule instruction de comparaison, qui est une soustraction déguisée. Le résultat de la soustraction n'est pas sauvegardé dans un registre et est simplement perdu. C'est le cas sur certains processeurs ARM ou sur les processeurs x86. Par exemple, un processeur x86 possède une instruction CMP qui n'est qu'une soustraction déguisée dans un opcode différent.
Le résultat de cette soustraction déguisée est un résultat portant sur 4 bits, qui donne des informations sur le résultat de la soustraction. Le premier bit, appelé bit null, indique si le résultat est nul ou non. Le second bit indique le signe du résultat, s'il est positif ou négatif. Enfin, deux autres bits précisent si la soustraction a donné lieu à un débordement d'entier. Il y a deux bits, car on vérifie deux types de débordement : un débordement non-signé (une retenue sortante de l'additionneur), et le débordement signé (débordement en complément à deux). Pour mémoriser le résultat d'une soustraction déguisée, le processeur incorpore un registre d'état. Le registre d'état stocke des bits qui ont chacun une signification prédéterminée lors de la conception du processeur et il sert à beaucoup de choses. Dans le cas qui nous intéresse, le registre d'état mémorise les résultats de l'instruction de test : les deux bit de débordement, le bit qui précise que le résultat d'une instruction vaut zéro, le bit de retenue pour le bit de signe.
La condition en elle-même est réalisée par le branchement. L'instruction de branchement fait donc deux choses : calculer la condition à partir du registre d'état, et effectuer le saut si la condition est valide. Le calcul des conditions se fait à partir des 4 bits de résultat. Le bit null permet de savoir si les deux opérandes sont égales ou non : si le résultat d'une soustraction est nul, cela implique que les deux opérandes sont égales. Le bit de signe permet de déterminer si le première opérande est supérieur ou inférieure à la seconde : le résultat de la soustraction est positif si A >= B, négatif sinon. Les bits de débordements permettent de faire la différence entre infériorité stricte ou non. Tout cela sera expliqué plus en détail dans le paragraphe suivant.

La conséquence est qu'il y a autant d'instructions de branchements que de conditions possibles. Aussi, on a une instruction de test, mais environ une dizaine d'instructions de branchements. C'est l'inverse de ce qu'on a avec des instructions de test proprement dites, où on a autant d'instructions de test que de conditions, mais un seul branchement. Un bon exemple est celui des processeurs x86. Le registre d'état des CPU x86 contient 5 bits appelés OF, SF, ZF, CF et PF : ZF indique que le résultat de la soustraction vaut 0, SF indique son signe, CF est le bit de retenue et de débordement non-signé, OF le bit de débordement signé, et PF le bit qui donne la parité du résultat. Il existe plusieurs branchements, certains testant un seul bit du registre d'état, et d'autres une combinaison de plusieurs bits.
| Instruction de branchement | Bit du registre d'état testé | Condition testée si on compare deux nombres A et B avec une instruction de test |
|---|---|---|
| JS (Jump if Sign) | SF = 1 | Le résultat est négatif |
| JNS (Jump if not Sign) | SF = 0 | Le résultat est positif |
| JO (Jump if Overflow) | OF = 1 | Le calcul arithmétique précédent a généré un débordement signé |
| JNO (Jump if Not Overflow) | OF = 0 | Le calcul arithmétique précédent n'a pas généré de débordement signé |
| JNE (Jump if Not equal) | ZF = 1 | Les deux nombres A et B sont égaux |
| JE (Jump if Equal) | ZF = 0 | Les deux nombres A et B sont différents |
| JB (Jump if below) | CF = 1 | A < B, avec A et B non-signés |
| JAE (Jump if Above or Equal) | CF = 0 | A >= B, avec A et B non-signés |
| (JBE) Jump if below or equal | CF OU ZF = 1 | A >= B si A et B sont non-signés |
| JA (Jump if above) | CF ET ZF = 0 | A > B si A et B sont non-signés |
| JL (Jump if less) | SF != OF | si A < B, si A et B sont signés |
| JGE (Jump if Greater or Equal) | SF = OF | si A >= B, si A et B sont signés |
| JLE (Jump if less or equal) | (SF != OF) OU ZF = 1 | si A <= B, si A et B sont signés |
| JGE (Jump if Greater) | (SF = OF) ET (NOT ZF) = 1 | si A > B, si A et B sont signés |
Les instructions à prédicat
[modifier | modifier le wikicode]Les instructions à prédicat sont des instructions qui ne font quelque chose que si une condition est respectée, et se comportent comme un NOP (une instruction qui ne fait rien) sinon. Elles lisent le résultat d'une comparaison, dans le registre d'état ou un registre à prédicat, et s’exécutent ou non suivant sa valeur. En théorie, les instructions à prédicats sont des instructions en plus des instructions normales, pas à prédicat. L'instruction à prédicat la plus représentative, présente sur de nombreux processeurs, est l'instruction CMOV, qui copie un registre dans un autre si une condition est remplie. Elle permet de faire certaines opérations assez simples, comme calculer la valeur absolue d'un nombre, le maximum de deux nombres, etc.
Mais sur certains processeurs, assez rares, toutes les instructions sont des instructions à prédicat : on parle de prédication totale. Cela peut paraitre étranger, vu que certaines instructions ne sont pas dans une structure de contrôle et doivent toujours s’exécuter, peu importe les conditions testées avant. Mais rassurez-vous, sur les processeurs à prédication totale, il y a toujours un moyen pour spécifier que certaines instructions doivent toujours s’exécuter, de manière inconditionnelle. Par exemple, sur les processeurs d'architecture HP IA-64, un des registre à prédicat, le tout premier, contient la valeur 1 et ne peut pas être modifié. Si on veut une instruction inconditionnelle, il suffit qu'elle précise que le registre à prédicat à lire est ce registre.
Sur les processeurs disposant d'instructions à prédicats, les instructions de test s'adaptent sur plusieurs points. L'un d'entre eux est que les instructions de test utilisent souvent des registres à prédicats. L'utilité principale des instructions à prédicats est d'éliminer les branchements, qui posent des problèmes sur les architectures modernes pour des raisons que nous verrons dans les derniers chapitres de ce cours. Toujours est-il que l'usage d'un registre d'état se marierait un petit peu mal avec cet objectif. Avec des registres à prédicats, on peut ajouter des instructions pour faire un ET, un OU ou un XOR entre registres à prédicats, comme dit plus haut. Cela permet de tester des combinaisons de conditions, voire des conditions complexes, sans faire appel au moindre branchement. Et ces conditions complexes ne sont pas rares, ce qui rend l'usage de registres à prédicats très utiles avec les instructions à prédicats. Les processeurs avec un registre d'état n'ont généralement que de la prédication partielle, le plus souvent limitée à une seule instruction CMOV. Alors que qui dit prédication totale dit systématiquement registres à prédicats.
Une autre adaptation est que les instructions de test tendent à fournir deux résultats : le résultat de la condition, et le résultat de la condition inverse. Les deux résultats sont l'inverse l'un de l'autre : si le premier vaut 1, l'autre vaut 0 (et réciproquement). Les deux résultats sont naturellement fournis dans deux registres à prédicats distincts. L'utilité de cette adaptation est que les instructions à prédicats servent à implémenter des structures de contrôle SI...ALORS simples, qui ont deux morceaux de code : un qui s’exécute si une condition est remplie, l'autre si elle ne l'est pas. pour le dire autrement, le premier morceau de code s’exécute quand la condition est remplie, l'autre quand la condition inverse est remplie. On comprend donc mieux l'utilité pour les isntructions de test de fournir deux résultats, l'un étant l'inverse de l'autre.
L'instruction SKIP
[modifier | modifier le wikicode]L'instruction SKIP permet de zapper l'instruction suivante si une condition testée est fausse. Il en existe deux versions. La première est fusionnée avec l'instruction de test. La condition est calculée par l'instruction SKIP, qui décide s'il faut sauter l'instruction suivante. Dans un autre cas, l'instruction SKIP est précédée d'une instruction de test, récupère son résultat dans un registre de prédicat ou dans le registre d'état, et effectue le saut. On peut la voir comme une forme particulière de branchement conditionnel, qui brancherait deux instructions plus loin.
Son utilité n'est pas évidente, mais on peut classer ses utilisations en trois catégories. La première permet d'émuler une instruction de branchement conditionnel en combinant une instruction SKIP avec un branchement inconditionnel. Le branchement inconditionnel est skippé si la condition est remplie/fausse, mais éxecuté dans le cas contraire : c'est le comportement d'un branchement conditionnel. Une autre utilisation permet d'émuler une instruction à prédicat en faisant précéder une instruction normale par une instruction SKIP. Enfin, elles servent à implémenter des structures de controle IF à condition que le code du IF se résume à une vulgaire instruction. C'est assez rare, mais certains calculs comme la valeur absolue ou le calcul du minimum peuvent se calculer ainsi.

Vous pourriez imaginer des versions améliorées de l'instruction, qui permettent de zapper plusieurs instructions, mais de telles instructions ne sont autres que des instructions de branchement conditionnelles spécifiques, comme nous le verrons dans le chapitre sur les modes d'adressage.
Les méta-instructions REPEAT et EXECUTE
[modifier | modifier le wikicode]Enfin, il faut aussi citer les méta-instructions, des instructions qui agissent sur l’exécution d'autres instructions. Il en existe deux : REPEAT et EXECUTE. Elles servent techniquement à manipuler le flot de contrôle d'un programme, et ont quelques ressemblances avec les branchements ou les boucles. Elles sont extrêmement rares et on ne les trouve que sur des anciens processeurs (généralement micro-codés), ou sur certaines processeurs spécialisés dans le traitement de signal appelés des DSP, qui feront l'objet d'un chapitre à eux seuls.
L’instruction REPEAT et le Zero-overhead looping
[modifier | modifier le wikicode]La première est la méta-instruction REPEAT, qui permet de simplifier l'implémentation des boucles. Dans sa version la plus simple, elle fait en sorte que l'instruction qui la suit soit répétée plusieurs fois. Le nombre de répétition est soit un nombre fixe, toujours le même, soit l'instruction se répète tant qu'une condition n'est pas remplie. Les deux situations ne se rencontrent pas sur les mêmes processeurs. Par exemple, l'UNIVAC 1103 possède une instruction REPEAT très simple, qui répète l'instruction cible un nombre fixe de fois, mais ne gère pas les conditions.
Le GE-600/Honeywell 6000 series incorpore trois instructions REPEAT de ce type. La première répète l'instruction suivante soit un nombre fixe de fois, soit quand une condition est remplie. La seconde répète les deux instructions suivantes, l'une après l'autre. Enfin, la dernière répète l'instruction suivante jusqu'à : soit qu'une condition soit remplie, soit qu'une adresse bien précise soit atteinte. Elle servait sans doute à implémenter le parcours d'une liste chainée pour trouver un item bien précis.
Une version améliorée de l'instruction REPEAT permet de répéter un bloc de plusieurs instructions, ce qui permet d'implémenter une boucle en une seule instruction. On parle d'ailleurs de Zero-overhead looping. Elles sont fréquentes sur certains processeurs de traitement de signal, qui doivent exécuter fréquemment des boucles. Typiquement, elles permettent d'implémenter des boucles FOR dont le nombre d’exécution est fixe, ou du moins stocké dans un registres. La répétition de la boucle est contrôlée par un registre de boucle, qui mémorise le nombre de répétitions, et qui est décrémenté à chaque itération.
- Les instructions REP mentionnées plus haut, ne sont PAS des exemples d'instruction REPEAT. Le préfixe REP des processeurs x86 est une instruction qui se répète elle-même. Mais l'instruction REPEAT force la répétition de l'instruction suivante ! Elle agit sur une autre instruction, d'où son caractère de méta-instruction.
L'instruction EXECUTE
[modifier | modifier le wikicode]La méta-instruction EXECUTE fournit l'adresse d'une instruction cible, qui est exécutée en lieu et place de l'instruction EXECUTE. Quand le processeur exécute l'instruction EXECUTE, il prend l'adresse cible, charge l'instruction dans l'adresse cible, et l’exécute à la place de l'instruction EXECUTE. Il est possible de comprendre l'instruction EXECUTE comme un branchement spécial. Tout se passe comme si l'instruction EXECUTE effectuait un branchement vers l'instruction cible, mais que le processeur ne poursuivait pas l’exécution à la suite de l’instruction cible, et revenait à la suite de l'instruction cible.
Il y a souvent des contraintes sur l'instruction cible, qui est pointée par l'adresse cible. Généralement, il n'est pas possible que l'instruction cible soit elle-même une autre instruction EXECUTE. De même, beaucoup de processeurs interdisent que l’instruction cible soit un branchement. Mais d'autres processeurs n'ont pas ces contraintes et autorisent à utiliser des branchements pour l'instruction cible.
L'utilité d'une telle instruction est tout sauf évidente. Elle servait pourtant à beaucoup de choses sur les processeurs où elle était implémentée. Précisons qu'elle était surtout présente sur des vieux ordinateurs, dans les années 50-60, et quelques processeurs des années 70. Elle a disparu dès les années 80 et n'est présentée que par souci d'exhaustivité et intérêt historique pour les curieux. Cette précision permet de comprendre que cette instruction servait pour résoudre des problèmes qui sont actuellement résolus autrement.
L'adresse cible peut être soit intégrée dans l'instruction, soit dans un registre. Dans le second cas, l'adresse peut être incrémentée ou modifiée afin que l'instruction EXECUTE change de cible à chaque exécution. Tout se passe comme si le registre contenant l'adresse cible servait à émuler un program counter. En mettant une instruction EXECUTE dans une boucle et en complétant le tout avec du code annexe, on peut exécuter du code extérieur sans modifier le véritable program counter. L'utilité est de faciliter l'implémentation des logiciels debuggers, des émulateurs, ou d'autres programmes dans le même genre.
Les autres utilisations sont assez nombreuses, mais aussi difficiles à expliquer pour qui n'a pas de connaissances poussées en programmation. La première utilité est l'implémentation de certaines fonctionnalités des langages de programmation évolués, à savoir le late binding, les fonctions virtuelles, et quelques autres. Elle facilite aussi l'implémentation des compilateurs à la volée, en permettant d’exécuter du code produit à volée sans faire tiquer les mécanismes de protection mémoire implémentés dans le processeur. Elle permet d'émuler du code automodifiant pour les logiciels qui gagnaient autrefois à l'utiliser. Et il y en a d'autres.
Les instructions exotiques
[modifier | modifier le wikicode]Pour résumer, les instructions les plus courantes sont les suivantes :
| Instruction | Utilité |
|---|---|
| Instructions arithmétiques | Ces instructions font simplement des calculs sur des nombres. On peut citer par exemple :
|
| Instructions logiques | Elles travaillent sur des bits ou des groupes de bits. On peut citer :
|
| Instructions de test et de contrôle (branchements) | Elles permettent de contrôler la façon dont notre programme s’exécute sur notre ordinateur. Elles permettent notamment de choisir la prochaine instruction à exécuter, histoire de répéter des suites d'instructions, de ne pas exécuter des blocs d'instructions dans certains cas, et bien d'autres choses. |
| Instructions d’accès mémoire | Elles permettent d'échanger des données entre le processeur et la mémoire, ou encore permettent de gérer la mémoire et son adressage. Les deux les plus courantes sont les suivantes :
|
En plus de ces instructions, beaucoup de processeurs ajoutent d'autres instructions. La plupart sont utilisées par le système d'exploitation pour configurer certaines fonctionnalités importante : la protection mémoire, la mémoire virtuelle, les modes de compatibilité du processeur, la gestion de l'alimentation, l'arrêt ou la mise en veille, etc.
On peut aussi trouver des instructions spécialisées dans les calculs cryptographiques : certaines instructions permettent de chiffrer ou de déchiffrer des données de taille fixe. De même, certains processeurs ont une instruction permettant de générer des nombres aléatoires. Et on peut trouver bien d'autres exemples...
Mais d'autres sont franchement exotiques. Par exemple, certains processeurs sont capables d'effectuer des instructions sur du texte directement. Pour stocker du texte, la technique la plus simple utilise une suite de lettres, stockées les unes à la suite des autres dans la mémoire, dans l'ordre dans lesquelles elles sont placées dans le texte. Quelques ordinateurs disposent d'instructions pour traiter ces suites de lettres. D'ailleurs, n'importe quel PC x86 actuel dispose de telles instructions, bien qu'elles ne soient pas utilisées car paradoxalement trop lente comparé aux solutions logicielles ! Cela peut paraître surprenant, mais il y a une explication assez simple qui sera compréhensible dans quelques chapitres (les instructions en question sont microcodées).