Fonctionnement d'un ordinateur/Les circuits combinatoires
Dans ce chapitre, nous allons aborder les circuits combinatoires. Ces circuits font comme tous les autres circuits : ils prennent des données sur leurs entrées, et fournissent un résultat en sortie. Le truc, c'est que ce qui est fourni en sortie ne dépend que du résultat sur les entrées, et de rien d'autre (ce n'est pas le cas pour tous les circuits). Pour donner quelques exemples, on peut citer les circuits qui effectuent des additions, des multiplications, ou d'autres opérations arithmétiques du genre.
Quelle que soit la complexité du circuit combinatoire à créer, celui-ci peut être construit en reliant des portes logiques entre elles. La conception d'un circuit combinatoire demande cependant de respecter quelques contraintes. La première est qu'il n'y ait pas de boucles dans le circuit : impossible de relier la sortie d'une porte logique sur son entrée, ou de faire la même chose avec un morceau de circuit. Si une boucle est présente dans un circuit, celui-ci n'est pas un circuit combinatoire, mais appartient à la classe des circuits séquentiels, que nous verrons dans le prochain chapitre.
Dans ce qui va suivre, nous allons voir comment concevoir ce genre de circuits. Il existe des méthodes et procédures assez simples qui permettent à n'importe qui de créer n'importe quel circuit combinatoire. Nous allons voir comment créer des circuits combinatoires à plusieurs entrées, mais à une seule sortie. Pour simplifier, on peut considérer que les bits envoyés en entrée sont un nombre, et que le circuit calcule un bit à partir du nombre envoyé en entrée.

C'est à partir de circuits de ce genre que l'on peut créer des circuits à plusieurs sorties : il suffit d'assembler plusieurs circuits à une sortie. La méthode pour ce faire est très simple : chaque sortie est calculée indépendamment des autres, uniquement à partir des entrées. Ainsi, pour chaque sortie du circuit, on crée un circuit à plusieurs entrées et une sortie : ce circuit déduit quoi mettre sur cette sortie à partir des entrées. En assemblant ces circuits à plusieurs entrées et une sortie, on peut ainsi calculer toutes les sorties.

Décrire un circuit : tables de vérité et équations logiques
[modifier | modifier le wikicode]Dans ce qui va suivre, nous aurons besoin de décrire un circuit électronique, le plus souvent un circuit que l'on souhaite concevoir ou utiliser. Et pour cela, il existe plusieurs grandes méthodes : la table de vérité, les équations logiques et un schéma du circuit. Les schémas de circuits électroniques ne sont rien de plus que les schémas avec des portes logiques, que nous avons déjà utilisé dans les chapitres précédents. Reste à voir la table de vérité et les équations logiques. La différence entre les deux est que la table de vérité décrit ce que fait un circuit, alors qu'une équation logique décrit la manière dont il est câblé. D'un côté la table de vérité considère le circuit comme une boite noire dont elle décrit le fonctionnement, de l'autre les équations décrivent ce qu'il y a à l'intérieur.
La table de vérité
[modifier | modifier le wikicode]La table de vérité décrit ce que fait le circuit, mais ne se préoccupe pas de dire comment. Elle ne dit pas quelles sont les portes logiques utilisées pour fabriquer le circuit, ni comment celles-ci sont reliées. Il s'agit d'une description du comportement du circuit, pas du circuit lui-même. En effet, elle se borne à donner la valeur de la sortie pour chaque entrée. Pour l'obtenir, il suffit de lister la valeur de chaque sortie pour toute valeur possible en entrée : on obtient alors la table de vérité du circuit. Pour créer cette table de vérité, il faut commencer par lister toutes les valeurs possibles des entrées dans un tableau, et écrire à côté les valeurs des sorties qui correspondent à ces entrées. Cela peut être assez long : pour un circuit ayant entrées, ce tableau aura lignes. Mais c'est la méthode la plus simple, la plus facile à appliquer.
Un premier exemple
[modifier | modifier le wikicode]Le premier exemple sera très simple. Le circuit que l'on va créer sera un inverseur commandable, qui fonctionnera soit comme une porte NON, soit se contentera de recopier le bit fournit en entrée. Pour faire le choix du mode de fonctionnement (inverseur ou non), un bit de commande dira s'il faut que le circuit inverse ou non l'autre bit d'entrée :
- quand le bit de commande vaut zéro, l'autre bit est recopié sur la sortie ;
- quand il vaut 1, le bit de sortie est égal à l'inverse du bit d'entrée (pas le bit de commande, l'autre).
La table de vérité obtenue est celle d'une porte XOR :
| Entrées | Sortie |
|---|---|
| 00 | 0 |
| 01 | 1 |
| 10 | 1 |
| 11 | 0 |
Un second exemple
[modifier | modifier le wikicode]Pour donner un autre exemple, on va prendre un circuit calculant le bit de parité d'un nombre. Ce bit de parité est un bit qu'on ajoute aux données à stocker afin de détecter des erreurs de transmission ou d’éventuelles corruptions de données. Le but d'un bit de parité est que le nombre de bits à 1 dans le nombre à stocker, bit de parité inclus, soit toujours un nombre pair. Ce bit de parité vaut : zéro si le nombre de bits à 1 dans le nombre à stocker (bit de parité exclu) est pair et 1 si ce nombre est impair. Détecter une erreur demande de compter le nombre de 1 dans le nombre stocké, bit de parité inclus : si ce nombre est impair, on sait qu'un nombre impair de bits a été modifié. Dans notre cas, on va créer un circuit qui calcule le bit de parité d'un nombre de 3 bits.
| Entrées | Sortie |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 1 |
| 011 | 0 |
| 100 | 1 |
| 101 | 0 |
| 110 | 0 |
| 111 | 1 |
Un troisième exemple
[modifier | modifier le wikicode]Pour le dernier exemple, nous allons prendre en entrée un nombre de 3 bits. Le but du circuit à concevoir sera de déterminer le bit majoritaire dans ce nombre : celui-ci contient-il plus de 1 ou de 0 ? Par exemple :
- le nombre 010 contient deux 0 et un seul 1 : le bit majoritaire est 0 ;
- le nombre 011 contient deux 1 et un seul 0 : le bit majoritaire est 1 ;
- le nombre 000 contient trois 0 et aucun 1 : le bit majoritaire est 0 ;
- le nombre 110 contient deux 1 et un seul 0 : le bit majoritaire est 1 ;
- etc.
| Entrées | Sortie |
|---|---|
| 000 | 0 |
| 001 | 0 |
| 010 | 0 |
| 011 | 1 |
| 100 | 0 |
| 101 | 1 |
| 110 | 1 |
| 111 | 1 |
Les équations logiques
[modifier | modifier le wikicode]Il peut être utile d'écrire un circuit non sous forme d'une table de vérité, ou d'un schéma, mais sous forme d'équations logiques. Mais attention : il ne s'agit pas des équations auxquelles vous êtes habitués. Ces équations logiques ne font que travailler avec des 1 et des 0, et n'effectuent pas d'opérations arithmétiques mais seulement des ET, des OU, et des NON. Dans le détail, les variables sont des bits (les entrées du circuit considéré), alors que les opérations sont des ET, OU et NON. Voici résumé dans ce tableau les différentes opérations, ainsi que leur notation. a et b sont des bits.
| Opérateur | Notation 1 | Notation 2 |
|---|---|---|
| NON a | ||
| a ET b | a.b | |
| a OU b | a+b | |
| a XOR b |
Avec ce petit tableau, vous savez comment écrire des équations logiques… Enfin presque, il ne faut pas oublier le plus important : les parenthèses, pour éviter quelques ambiguïtés. C'est un peu comme avec des équations normales : donne un résultat différent de . Avec nos équations logiques, on peut trouver des situations similaires : par exemple, est différent de .
Les formes normales conjonctives et disjonctives
[modifier | modifier le wikicode]Dans la jungle des équations logiques, deux types se démarquent des autres. Ces deux catégories portent les noms barbares de formes normales conjonctives et de formes normales disjonctives. Derrière ces termes se cache cependant deux concepts assez simples. Il s'agit d'équations qui impliquent uniquement des portes ET, OU et NON. Pour simplifier, ces équations décrivent des circuits composés de trois couches de portes logiques : une couche de portes NON, une couche de portes ET et une couche de portes OU. La couche de portes NON est placée immédiatement à la suite des entrées, dont elle inverse certains bits. Les couches de portes ET et OU sont placées après la couche de portes NON, et deux cas sont alors possibles : soit on met la couche de portes ET avant la couche de OU, soit on fait l'inverse. Le premier cas, avec les portes ET avant les portes OU, donne une forme normale disjonctive. La forme normale conjonctive est l'exact inverse, à savoir celui où la couche de portes OU est placée avant la couche de portes ET.
Les équations obtenues ont une forme similaire aux exemples qui vont suivre. Ces exemples sont donnés pour un circuit à trois entrées nommées a, b et c, et une sortie s. On voit que certaines entrées sont inversées avec une porte NON, et que le résultat de l'inversion est ensuite combiné avec des portes ET et OU.
- Exemple de forme normale conjonctive : .
- Exemple de forme normale disjonctive : .
Il faut savoir que tout circuit combinatoire peut se décrire avec une forme normale conjonctive et avec une forme normale disjonctive. Mais l'équation obtenue n'est pas forcément la manière idéale de concevoir un circuit. Celui-ci peut par exemple être simplifié en utilisant des portes XOR, ou en remaniant le circuit. Mais obtenir une forme normale est très souvent utile, quitte à simplifier celle-ci par la suite. D'ailleurs, les méthodes que nous allons voir plus bas ne font que cela : elles traduisent une table de vérité en forme normale conjonctive ou disjonctive, avant de la simplifier et de traduire le tout en circuit.
Conversions entre équation, circuit et table de vérité
[modifier | modifier le wikicode]
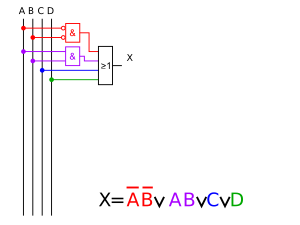
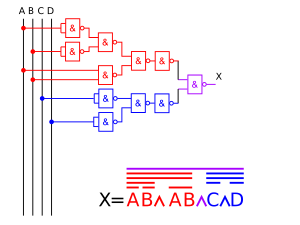
Une équation logique se traduit en circuit assez facilement : il suffit de substituer chaque terme de l'équation avec la porte logique qui correspond. Les parenthèses et priorités opératoires indiquent l'ordre dans lequel relier les différentes portes logiques. Elles donnent une idée de comment doit être faite cette substitution. Les schémas ci-dessous montrent un exemple d'équation logique et le circuit qui correspond, tout en montrant les différentes substitutions intermédiaires. À ce propos, concevoir un circuit demande simplement d'établir son équation logique : il suffit de traduire l'équation obtenue en circuit, et le tour est joué !
La signification symboles sur les exemples est donnée dans la section « Les équations logiques » ci-dessus.
|

|
|
 |
Il est aussi intéressant de parler des liens entre tables de vérité et équation logique. Il faut savoir qu'il est possible de trouver l'équation d'un circuit à partir de sa table de vérité, et réciproquement. C'est d'ailleurs ce que font les méthodes de conception de circuit que nous allons voir plus bas : elles traduisent la table de vérité d'un circuit en équation logique. On commence par établir la table de vérité, ce qui est assez simple, avant d'établir une équation logique et de la traduire en circuit. On pourrait croire qu'à chaque table de vérité correspond une seule équation logique, mais ce n'est pas le cas. En réalité, il existe plusieurs équations logiques différentes pour chaque table de vérité. La raison à cela est que des équations différentes peuvent donner des circuits qui se comportent de la même manière. Après tout, on peut concevoir un circuit de différente manières et des circuits câblés différemment peuvent parfaitement faire la même chose. Des équations logiques qui décrivent la même table de vérité sont dites équivalentes. Par équivalente, on veut dire qu'elles décrivent des circuits différents, mais qui ont la même table de vérité - ils font la même chose. À ce propos, il faut savoir qu'il est possible de convertir une équation logique en une autre équation équivalente., chose que nous apprendrons à faire dans la suite de ce chapitre.
Concevoir un circuit combinatoire avec la méthode des minterms
[modifier | modifier le wikicode]Comme dit plus haut, créer un circuit demande d'établir sa table de vérité, avant de la traduire en équation logique, puis en circuit. Nous allons maintenant voir la première étape, celle de la conversion entre table de vérité et équation. Il existe deux grandes méthodes de ce type, pour concevoir un circuit intégré, qui portent les noms de méthode des minterms et de méthode des maxterms. La différence entre les deux est que la première donne une forme normale disjonctive, alors que la seconde donne une forme normale conjonctive. Dans cette section, nous allons voir la méthode des minterms, avant de voir la méthode des maxterms. Pour chaque méthode, nous allons commencer par montrer comment appliquer ces méthodes sans rentrer dans le formalisme, avant de montrer le formalisme en question. Précisons cependant que ces deux méthodes font la même chose : elles traduisent une table de vérité en équation logique. La première étape de ces deux méthodes est donc d'établir la table de vérité. Voyons un peu de quoi il retourne.
La méthode des minterms, expliquée sans formalisme
[modifier | modifier le wikicode]La méthode des minterms est de loin la plus simple à comprendre. Ses principes sont en effet assez intuitifs et elle est assez facile à appliquer, pour qui connaît ses principes sous-jacents. Pour l'expliquer, nous allons commencer par voir un circuit, qui compare son entrée avec une constante, dépendante du circuit. Par la suite, nous allons voir comment combiner ce circuit avec des portes logiques pour obtenir le circuit désiré.
Les minterms (comparateurs avec une constante)
[modifier | modifier le wikicode]Nous allons maintenant étudier un comparateur qui vérifie si le nombre d'entrée est égal à une certaine constante (2, 3, 5, 8, ou tout autre nombre) qui dépend du circuit et renvoie un 1 seulement si c’est le cas. Ainsi, on peut créer un circuit qui mettra sa sortie à 1 uniquement si on envoie le nombre 5 sur ses entrées. Ou encore, créer un circuit qui met sa sortie à 1 uniquement quand l'entrée vaut 126. Et ainsi de suite : tout nombre peut servir de constante à vérifier. Le circuit possède plusieurs entrées, sur lesquelles on place les bits du nombre à comparer. Sa sortie est un simple bit, qui vaut 1 si le nombre en entrée est égal à la constante et 0 sinon. Nous allons voir qu'il y en a deux types, qui ressemblent aux deux types de comparateurs avec zéro. Le premier type est basé sur une porte NOR, à laquelle on ajoute des portes NON. Le second est basé sur une porte ET précédée de portes NON.
Le premier circuit de ce type est composé d'une couche de portes NON et d'une porte ET à plusieurs entrées. Créer un tel circuit se fait en trois étapes. En premier lieu, il faut convertir la constante à vérifier en binaire : dans ce qui suit, nous nommerons cette constante k. En second lieu, il faut créer la couche de portes NON. Pour cela, rien de plus simple : on place des portes NON pour les entrées de la constante k qui sont à 0, et on ne met rien pour les bits à 1. Par la suite, on place une porte ET à plusieurs entrées à la suite de la couche de portes NON.

Pour comprendre pourquoi on procède ainsi, il faut simplement regarder ce que l'on trouve en sortie de la couche de portes NON :
- si on envoie la constante, tous les bits à 0 seront inversés alors que les autres resteront à 1 : on se retrouve avec un nombre dont tous les bits sont à 1 ;
- si on envoie un autre nombre, soit certains 0 du nombre en entrée ne seront pas inversés, ou alors des bits à 1 le seront : il y aura au moins un bit à 0 en sortie de la couche de portes NON.
Ainsi, on sait que le nombre envoyé en entrée est égal à la constante k si et seulement si tous les bits sont à 1 en sortie de la couche de portes NON. Dit autrement, la sortie du circuit doit être à 1 si et seulement si tous les bits en sortie des portes NON sont à 1 : il ne reste plus qu'à trouver un circuit qui prenne ces bits en entrée et ne mette sa sortie à 1 que si tous les bits d'entrée sont à 1. Il existe une porte logique qui fonctionne ainsi : il s'agit de la porte ET à plusieurs entrées.

Le second type de comparateur avec une constante est fabriqué avec une porte NOR précédée de portes NON. Il se fabrique comme le comparateur précédent, sauf que cette fois-ci, il faut mettre une porte NON pour chaque bit à 1 de l'opérande, et non chaque bit à zéro. En clair, la couche de portes NON est l'exact inverse de celle du circuit précédent. Le tout est suivi par une porte NOR.

Pour comprendre pourquoi on procède ainsi, il faut simplement regarder ce que l'on trouve en sortie de la couche de portes NON :
- si on envoie la constante, tous les bits à 0 seront inversés alors que les autres resteront à 1 : on se retrouve avec un zéro en sortie ;
- si on envoie un autre nombre, soit certains 1 du nombre en entrée ne seront pas inversés, ou alors des bits à 0 le seront : il y aura au moins un bit à 1 en sortie de la couche de portes NON.
La porte NOR, quant à elle est un comparateur avec zéro, comme on l'a vu plus haut. Pour résumer, la première couche de portes NON transforme l'opérande et que la porte NOR vérifie si l'opérande transformée vaut zéro. La transformation de l'opérande est telle que son résultat est nul seulement si l’opérande est égale à la constante testée.

Combiner les comparateurs avec une constante
[modifier | modifier le wikicode]On peut créer n'importe quel circuit à une seule sortie avec ces comparateurs, en les couplant avec une porte OU à plusieurs entrées. Pour comprendre pourquoi, rappelons que les entrées du circuit peuvent prendre plusieurs valeurs : pour une entrée de bits, on peut placer valeurs différentes sur l'entrée. Mais seules certaines valeurs doivent mettre la sortie à 1, les autres la laissant à 0. Les valeurs d'entrée qui mettent la sortie 1 sont aussi appelées des minterms. Ainsi, pour savoir s’il faut mettre un 1 en sortie, il suffit de vérifier que l'entrée est égale à un minterm. Pour savoir si l'entrée est égale à un minterm, on doit utiliser un comparateur avec une constante pour chaque minterm. Par exemple, pour un circuit dont la sortie est à 1 si son entrée vaut 0000, 0010, 0111 ou 1111, il suffit d'utiliser :
- un comparateur qui vérifie si l'entrée vaut 0000 ;
- un comparateur qui vérifie si l'entrée vaut 0010 ;
- un comparateur qui vérifie si l'entrée vaut 0111 ;
- et un comparateur qui vérifie si l'entrée vaut 1111.
Reste à combiner les sorties de ces comparateurs pour obtenir une seule sortie, ce qui est fait en utilisant un circuit relativement simple. On peut remarquer que la sortie du circuit est à 1 si un seul comparateur a sa sortie à 1. Or, on connaît un circuit qui fonctionne comme cela : la porte OU à plusieurs entrées. En clair, on peut créer tout circuit avec seulement des comparateurs et une porte OU à plusieurs entrées.

Méthode des minterms, version formalisée
[modifier | modifier le wikicode]On peut formaliser la méthode précédente, ce qui donne la méthode des minterms. Celle-ci permet d'obtenir un circuit à partir d'une description basique du circuit. Mais le circuit n'est pas vraiment optimisé et peut être fortement simplifié. Nous verrons plus tard comment simplifier des circuits obtenus avec la méthode que nous allons exposer.
Lister les entrées de la table de vérité qui valident l'entrée
[modifier | modifier le wikicode]La première étape demande d'établir la table de vérité du circuit, afin de déterminer ce que fait le circuit voulu. Maintenant que l'on a la table de vérité, il faut lister les valeurs en entrée pour lesquelles la sortie vaut 1. On rappelle que ces valeurs sont appelées des minterms. Il faudra utiliser un comparateur avec une constante pour chaque minterm afin d'obtenir le circuit final. Pour l'exemple, nous allons reprendre le circuit de calcul d'inverseur commandable, vu plus haut.
| Entrées | Sortie |
|---|---|
| 00 | 0 |
| 01 | 1 |
| 10 | 1 |
| 11 | 0 |
Listons les lignes de la table où la sortie vaut 1.
| Entrées | Sortie |
|---|---|
| 01 | 1 |
| 10 | 1 |
Pour ce circuit, la sortie vaut 1 si et seulement si l'entrée du circuit vaut 01 ou 10. Dans ce cas, on doit créer deux comparateurs qui vérifient si leur entrée vaut respectivement 01 et 10. Une fois ces deux comparateurs crée, il faut ajouter la porte OU.
Établir l'équation du circuit
[modifier | modifier le wikicode]Les deux étapes précédentes sont les seules réellement nécessaires : quelqu'un qui sait créer un comparateur avec une constante (ce qu'on a vu plus haut), devrait pouvoir s'en sortir. Reste à savoir comment transformer une table de vérité en équations logiques, et enfin en circuit. Pour cela, il n'y a pas trente-six solutions : on va écrire une équation logique qui permettra de calculer la valeur (0 ou 1) d'une sortie en fonction de toutes les entrées du circuit. Et on fera cela pour toutes les sorties du circuit que l'on veut concevoir. Pour ce faire, on peut utiliser ce qu'on appelle la méthode des minterms, qui est strictement équivalente à la méthode vue au-dessus. Elle permet de créer un circuit en quelques étapes simples :
- lister les lignes de la table de vérité pour lesquelles la sortie vaut 1 (comme avant) ;
- écrire l'équation logique pour chacune de ces lignes (qui est celle d'un comparateur) ;
- faire un OU entre toutes ces équations logiques, en n'oubliant pas de les entourer par des parenthèses.
Pour écrire l'équation logique d'une ligne, il faut simplement :
- lister toutes les entrées de la ligne ;
- faire un NON sur chaque entrée à 0 ;
- et faire un ET avec le tout.
Vous remarquerez que la succession d'étapes précédente permet de créer un comparateur qui vérifie que l'entrée est égale à la valeur sur la ligne sélectionnée.
Pour illustrer le tout, on va reprendre notre exemple avec le bit de parité. La première étape consiste donc à lister les lignes de la table de vérité dont la sortie est à 1.
| Entrées | Sortie |
|---|---|
| 001 | 1 |
| 010 | 1 |
| 100 | 1 |
| 111 | 1 |
On a alors :
- la première ligne où l'entrée vaut 001 : son équation logique vaut ;
- la seconde ligne où l'entrée vaut 010 : son équation logique vaut ;
- la troisième ligne où l'entrée vaut 100 : son équation logique vaut ;
- la quatrième ligne où l'entrée vaut 111 : son équation logique vaut .
On a alors obtenu nos équations logiques. Reste à faire un OU entre toutes ces équations, et le tour est joué !
Nous allons maintenant montrer un deuxième exemple, avec le circuit de calcul du bit majoritaire vu juste au-dessus. Première étape, lister les lignes de la table de vérité dont la sortie vaut 1 :
| Entrées | Sortie |
|---|---|
| 011 | 1 |
| 101 | 1 |
| 110 | 1 |
| 111 | 1 |
Seconde étape, écrire les équations de chaque ligne. Essayez par vous-même, avant de voir la solution ci-dessous.
- Pour la première ligne, l'équation obtenue est : .
- Pour la seconde ligne, l'équation obtenue est : .
- Pour la troisième ligne, l'équation obtenue est : .
- Pour la quatrième ligne, l'équation obtenue est : .
Il suffit ensuite de faire un OU entre les équations obtenues au-dessus.
Traduire l'équation en circuit
[modifier | modifier le wikicode]Enfin, il est temps de traduire l'équation obtenue en circuit, en remplaçant chaque terme de l'équation par le circuit équivalent. Notons que les parenthèses donnent une idée de comment doit être faite cette substitution.
Concevoir un circuit avec la méthode des maxterms
[modifier | modifier le wikicode]La méthode des minterms, vue précédemment, n'est pas la seule qui permet de traduire une table de vérité en équation logique. Elle est secondée par une méthode assez similaire : la méthode des maxterms. Les deux donnent des équations logiques, et donc des circuits, différents. Les deux commencent par une couche de portes NON, suivie par deux couches de portes ET et OU, mais l'ordre des portes ET et OU est inversé. Dit autrement, la méthode des minterms donne une forme normale disjonctive, alors que celle des maxterms donnera une forme normale conjonctive.
La méthode des maxterms : formalisme
[modifier | modifier le wikicode]La méthode des maxterms fonctionne sur un principe assez tordu, mais qui fonctionne cependant. Avec celle-ci, on effectue trois étapes, chacune correspondant à l'exact inverse de l'étape équivalente avec les minterms. Les 0 sont remplacés par des 1 et les portes ET par des portes OU.
- Premièrement on doit lister les lignes de la table de vérité qui mettent la sortie à 0, ce qui est l'exact inverse de l'étape équivalente avec les minterms.
- Ensuite, on traduit chaque ligne en équation logique. La traduction de chaque ligne en équation logique est aussi inversée par rapport à la méthode des minterms : on doit inverser les bits à 1 avec une porte NON et faire un OU entre chaque bit.
- Et enfin, on doit faire un ET entre tous les résultats précédents.
Un exemple d'application
[modifier | modifier le wikicode]Par exemple, prenons la table de vérité suivante :
| Entrée a | Entrée b | Entrée c | Sortie S | |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 0 |
La première étape est de lister les entrées associées à une sortie à 0. Ce qui donne :
| Entrée a | Entrée b | Entrée c | Sortie S | |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 0 |
Vient ensuite la traduction de chaque ligne en équation logique. Cette fois-ci, les bits à 1 dans l'entrée sont ceux qui doivent être inversés, les autres restants tels quels. De plus, on doit faire un OU entre ces bits. On a donc :
- pour la première ligne ;
- pour la seconde ligne ;
- pour la troisième ligne.
Et enfin, il faut faire un ET entre ces maxterms. Ce qui donne l'équation suivante :
Quelle méthode choisir ?
[modifier | modifier le wikicode]On peut se demander quelle méthode choisir entre minterms et maxterms. L'exemple précédent nous donne un indice. Si on applique la méthode des minterms sur l'exemple précédent, vous allez prendre du temps et obtenir une équation logique bien plus compliquée, avec beaucoup de minterms. Alors que c'est plus rapide avec les maxterms, l'équation obtenue étant beaucoup plus simple. Cela vient du fait que dans l'exemple précédent, il y a beaucoup de lignes associées à une sortie à 1. On a donc plus de minterms que de maxterms, ce qui rend la méthode des minterms plus longue. Par contre, on pourrait trouver des exemples où c'est l'inverse. Si un circuit a plus de lignes où la sortie est à 0, alors la méthode des minterms sera plus rapide. Bref, tout dépend du nombre de minterms/maxterms dans la table de vérité. En comptant le nombre de cas où la sortie est à 1 ou à 0, on peut savoir quelle méthode est la plus rapide : minterm si on a plus de cas avec une sortie à 0, maxterm sinon.
Le principe caché derrière la méthode des maxterms
[modifier | modifier le wikicode]La méthode des maxterms fonctionne sur un principe un peu différent de la méthode des minterms. Rappelons que chaque valeur d'entrée qui met une sortie à 0 est appelée un maxterm, alors que celles qui la mettent à 1 sont des minterms. Un circuit conçu selon avec des minterms vérifie si l'entrée met la sortie à 1, alors qu'un circuit maxterm vérifie si l'entrée ne met pas la sortie à 0. Dit autrement, ils vérifient soit que l'entrée est un minterm, soit que l'entrée n'est pas un maxterm.
L’aperçu complet de la méthode
[modifier | modifier le wikicode]Pour cela, un circuit conçu avec la méthode des maxterms procède en deux étapes : il compare l'entrée avec chaque maxterm possible, et combine les résultats avec une porte à plusieurs entrées.
- Pour commencer, le circuit vérifie si l'entrée est un maxterm avec plusieurs comparateurs avec une constante modifiée : un pour chaque maxterm. Chaque comparateur dit si l'entrée est différente du maxterm associé : il renvoie un 1 si l'entrée ne correspond pas au maxterm et 0 sinon.
- La seconde étape combine les résultats de tous les maxterms pour déduire la sortie. Si tous les comparateurs renvoient un 1, cela signifie que l'entrée est différente de tous les maxterms : ce n'en est pas un. La sortie doit alors être mise à 1. Si l'entrée correspond à un maxterm, alors le comparateur associé au maxterm donnera un 0 en sortie : il y aura au moins un comparateur qui donnera un 0. Dans ce cas, la sortie doit être mise à 0. On remarque rapidement que ce comportement est celui d'une porte ET à plusieurs entrées.

Le circuit de comparaison
[modifier | modifier le wikicode]Le circuit de comparaison fonctionne sur le principe suivant : il compare l'entrée avec le maxterm bit par bit, chaque bit étant comparé indépendamment des autres, en parallèle. Les résultats des comparaisons sont ensuite combinées pour donner le bit de résultat.
Le circuit de comparaison donne un 1 quand les bits sont différents et un 0 s'ils sont égaux. La comparaison bit à bit est effectuée par une simple porte logique, qui n'est autre que la porte NON en entrée du circuit (ou son absence). Pour comprendre pourquoi, regardons la table de vérité du circuit de comparaison, illustré ci-dessous. On voit que si le bit du maxterm est 0, alors la sortie est égale au bit d'entrée. Mais si le bit du maxterm est à 1, alors la sortie est l'inverse du bit d'entrée.
| Bit du maxterm | Bit d'entrée | Bit de sortie | |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
Maintenant, passons à la combinaison des résultats. Si au moins un bit d'entrée est différent du bit du maxterm, alors l'entrée ne correspond pas au maxterm. On devine donc qu'on doit combiner les résultats avec une porte OU.
Simplifier un circuit
[modifier | modifier le wikicode]Comme on l'a vu, la méthode précédente donne une équation logique qui décrit un circuit. Mais quelle équation : on se retrouve avec un gros paquet de ET et de OU ! heureusement, il est possible de simplifier cette équation. Pour donner un exemple, sachez que cette équation : ; peut se simplifier en : avec les règles de simplifications que nous allons voir. Dans cet exemple, on passe donc de 17 portes logiques à seulement 3 ! Bien sûr, on peut simplifier cette équation juste pour se simplifier la vie lors de la traduction de cette équation en circuit, mais cela sert aussi à autre chose : cela permet d'obtenir un circuit plus rapide et/ou utilisant moins de portes logiques. Autant vous dire qu'apprendre à simplifier ces équations est quelque chose de crucial, particulièrement si vous voulez concevoir des circuits un tant soit peu rapides.
L'algèbre de Boole
[modifier | modifier le wikicode]Pour simplifier une équation logique, on peut utiliser certaines propriétés mathématiques simples pour factoriser ou développer comme on le ferait avec une équation mathématique normale. Ces propriétés forment ce qu'on appelle l’algèbre de Boole. En utilisant ces règles algébriques, on peut factoriser ou développer certaines expressions, comme on le ferait avec une équation normale, ce qui permet de simplifier une équation logique assez intuitivement. Le tout est de bien faire ces simplifications en appliquant correctement ces règles, ce qui peut demander un peu de réflexion.
Les théorèmes de base de l’algèbre de Boole peuvent se classer en plusieurs types séparés, qui sont les suivantes :
- l'associativité, la commutativité et la distributivité ;
- la double négation et les lois de de Morgan ;
- les autres règles, appelées règles bit à bit.
L'associativité, la distributivité et la commutativité des opérateurs logiques
[modifier | modifier le wikicode]L'associativité, la commutativité et la distributivité ressemblent beaucoup aux règles arithmétiques usuelles, ce qui fait qu'on ne les détaillera pas ici.
| Commutativité |
|
|---|---|
| Associativité |
|
| Distributivité |
|
Les autres règles sont par contre plus importantes.
Les règles de type bit à bit
[modifier | modifier le wikicode]Les règles bit à bit ne sont utiles que dans le cas où certaines entrées d'un circuit sont fixées, ou lors de la simplification de certaines équations logiques. Elles regroupent plusieurs cas distincts :
- soit on fait un ET/OU/XOR entre un bit et lui-même ;
- soit on fait un ET/OU/XOR entre un bit et son inverse ;
- soit on fait un ET/OU/XOR entre un bit et 1 ;
- soit on fait un ET/OU/XOR entre un bit et 0.
Le premier cas regroupe les trois formules suivantes :
Le second cas regroupe les trois formules suivantes :
- ,
- .
Le troisième cas regroupe les trois formules suivantes :
- ,
- .
Le dernier cas regroupe les trois formules suivantes :
- ,
- .
Voici la liste de ces règles, classées par leur nom mathématique :
| Idempotence |
|
|---|---|
| Élément nul |
|
| Élément Neutre |
|
| Complémentarité |
|
Ces relations permettent de simplifier des équations logiques, mais peuvent avoir des utilisations totalement différentes.
Nous avons déjà utilisé implicitement les formules du premier cas, à savoir et dans le chapitre sur les portes logiques. En effet, nous avions vu qu'il est possible de fabriquer une porte NON à partir d'une porte NAND ou d'une porte NOR. L'idée était d'envoyer le bit à inverser sur les deux entrées d'une NOR/NAND, le ET/OU recopiant le bit sur sa sortie et le NON l'inversant. Pour retrouver ce résultat, il suffit d'ajouter une porte NON dans les formules et , ce qui donne :
Au passage, la formule nous dit pourquoi cela ne marcherait pas du tout avec une porte XOR.
Pour la formule , elle sert dans certaines situations particulières, où l'on veut initialiser un nombre à zéro, peu importe que ce nombre soit une variable, la sortie d'un circuit combinatoire ou un registre. La formule nous dit que le résultat d'un XOR entre un bit et lui-même est toujours zéro. Et cela s'applique aussi à des nombres : si on XOR un nombre avec lui-même, chacun de ses bits est XORé avec lui-même et est donc mis à zéro. Conséquence : un nombre XOR lui-même donnera toujours zéro. Cette propriété est utilisée pour mettre à zéro un registre, pour le calcul des bits de parité ou pour échanger une valeur entre deux registres. Les formules du second cas, à savoir , et , permettent de faire quelque chose de similaire. La première formule dit que faire un ET entre un nombre et son inverse donnera toujours zéro, comme un XOR entre un nombre et lui-même. Pour les deux autres formules, elles disent que le résultat sera toujours un bit à 1. Cela sert cette fois-ci si on veut initialiser une variable, un registre ou une sortie de circuit à une valeur où tous les bits sont à 1.
Les formules du troisième et quatrième cas seront utilisées dans le chapitre sur les circuits de calcul logique et bit à bit, dans la section sur les masques. C'est dans cette section que nous verrons en quoi ces formules sont utiles en dehors du cas d'une simplification de circuit. Pour le moment, nous ne pouvons pas en dire plus.
Les lois de de Morgan et la double négation
[modifier | modifier le wikicode]Parmi les règles de l’algèbre de Boole, les lois de de Morgan et la double négation sont de loin les plus importantes à retenir. Elles sont les seules à impliquer les négations. Voici ces deux règles :
| Double négation | |
|---|---|
| Loi de De Morgan |
|
La première loi de de Morgan nous dit simplement qu'une porte NAND peut se fabriquer avec une porte OU précédée de deux portes NON, comme nous l'avions vu au chapitre précédent.

La seconde loi, quant à elle, dit qu'une porte NOR peut se fabriquer avec une porte ET précédée de deux portes NON, comme nous l'avions vu au chapitre précédent.

Les règles de Morgan pour deux entrées sont résumées dans le tableau ci-dessous.

| |

|
Les lois de de Morgan peut se généraliser pour plus de deux entrées.
- 1ère loi de de Morgan :
- 2nd loi de de Morgan :
En les combinant avec la loi de la double négation, les lois de de Morgan permettent de transformer une équation écrite sous forme normale conjonctive en une équation équivalente sous forme normale disjonctive, et réciproquement. Elles permettent de passer d'une équation obtenue avec les minterms à l'équation obtenue avec les maxterms.
La formule équivalente de la porte XOR et de la porte NXOR
[modifier | modifier le wikicode]Avec les règles précédentes, il est possible de démontrer que les portes XOR et NXOR peuvent se construire avec uniquement des portes ET/OU/NON. Nous l'avions vu dans le chapitre précédent, et montré quelques exemples de circuits équivalents.
En utilisant la méthode des minterms, on arrive à l'expression suivante pour la porte XOR et la porte NXOR :
- XOR :
- NXOR :
La formule obtenue avec les minterms pour la porte XOR donne ce circuit :

La formule obtenue avec les minterms pour la porte NXOR donne ce circuit :

Il est possible d'obtenir une formule équivalente pour la porte XOR, en utilisant l’algèbre de Boole sur les formules précédentes. Pour cela, partons de l'équation de la porte NXOR obtenue avec la méthode des minterms :
Appliquons une porte NON pour obtenir la porte XOR :
Appliquons la loi de de Morgan entre les parenthèses :
Appliquons la loi de de Morgan dans les parenthèses :
Simplifions les doubles négations :

Il est possible de faire la même chose, mais pour la porte NXOR. Pour cela, partons de l'équation de la porte XOR obtenue avec la méthode des minterms :
Une porte NXOR est, par définition, l'inverse d'une porte XOR. En appliquant un NON sur l'équation précédente, on trouve donc :
On applique la loi de de Morgan pour le OU entre les parenthèses :
On applique la loi de de Morgan, mais cette fois-ci à l'intérieur des parenthèses :
On simplifie les doubles inversions :
La formule est similaire à celle d'un XOR, la seule différence étant qu'il faut inverser de place les ET et les OU : le ET est dans les parenthèses pour le XOR et entre pour le NXOR, et inversement pour le OU.
Dans les deux exemples précédents, on voit que l'on a pu passer d'une forme normale conjonctive à une forme normale disjonctive et réciproquement, en utilisant la loi de de Morgan. C'est un principe assez général qui se retrouve souvent dans les démonstrations d'équations logiques.
Exemples complets
[modifier | modifier le wikicode]Comme premier exemple, nous allons travailler sur cette équation : . On peut la simplifier en trois étapes :
- Appliquer la règle de distributivité du ET sur le OU pour factoriser le facteur e1.e0, ce qui donne ;
- Appliquer la règle de complémentarité sur le terme entre parenthèses , ce qui donne 1.e1.e0 ;
- Et enfin, utiliser la règle de l’élément neutre du ET, qui nous dit que a.1=a, ce qui donne : e1.e0.
En guise de second exemple, nous allons simplifier . Cela se fait en suivant les étapes suivantes :
- Factoriser e0, ce qui donne : ;
- Utiliser la règle du XOR qui dit que , ce qui donne .
Les tableaux de Karnaugh
[modifier | modifier le wikicode]Il existe d'autres méthodes pour simplifier nos circuits. Les plus connues étant les tableaux de Karnaugh et l'algorithme de Quine Mc Cluskey. On ne parlera pas de la dernière méthode, trop complexe pour ce cours. Ces deux méthodes possèdent quelques défauts qui nous empêchent de créer de très gros circuits avec. Pour le dire franchement, elles sont trop longues à utiliser quand le nombre d'entrée du circuit dépasse 5 ou 6. Nous allons cependant aborder la méthode du tableau de Karnaugh, qui peut être assez utile pour des circuits simples. La simplification des équations avec un tableau de Karnaugh demande plusieurs étapes, que nous allons maintenant décrire.
Première étape : créer le tableau de Karnaugh
[modifier | modifier le wikicode]
D'abord, il faut créer une table de vérité pour chaque bit de sortie du circuit à simplifier, qu'on utilise pour construire ce tableau. La première étape consiste à obtenir un tableau plus ou moins carré à partir d'une table de vérité, organisé en lignes et colonnes. Si on a n variables, on crée deux paquets avec le même nombre de variables (à une variable près pour un nombre impair de variables). Par exemple, supposons que j'aie quatre variables : a, b, c et d. Je peux créer deux paquets en regroupant les quatre variables comme ceci : ab et cd. Ou encore comme ceci : ac et bd. Il arrive que le nombre de variables soit impair : dans ce cas, il y a aura un paquet qui aura une variable de plus.
Seconde étape : remplir ce tableau
[modifier | modifier le wikicode]Ensuite, pour le premier paquet, on place les valeurs que peut prendre ce paquet sur la première ligne. Pour faire simple, considérez ce paquet de variables comme un nombre, et écrivez toutes les valeurs que peut prendre ce paquet en binaire. Rien de bien compliqué, mais ces variables doivent être encodées en code Gray : on ne doit changer qu'un seul bit en passant d'une ligne à sa voisine. Pour le second paquet, faites pareil, mais avec les colonnes. Là encore, les valeurs doivent être codées en code Gray.
Pour chaque ligne et chaque colonne, on prend les deux paquets : ces deux paquets sont avant tout des rassemblements de variables, dans lesquels chacune a une valeur bien précise. Ces deux paquets précisent ainsi les valeurs de toutes les entrées, et correspondent donc à une ligne dans la table de vérité. Sur cette ligne, on prend le bit de la sortie, et on le place à l'intersection de la ligne et de la colonne. On fait cela pour chaque case du tableau, et on le remplit totalement.
Troisième étape : faire des regroupements
[modifier | modifier le wikicode]Troisième étape de l'algorithme : faire des regroupements. Par regroupement, on veut dire que les 1 dans le tableau doivent être regroupés en paquets de 1, 2, 4, 8, 16, 32, etc. Le nombre de 1 dans un paquet doit TOUJOURS être une puissance de deux. De plus, ces regroupements doivent obligatoirement former des rectangles dans le tableau de Karnaugh. De manière générale, il vaut mieux faire des paquets les plus gros possible, afin de simplifier l'équation au maximum.
 |
 |

Il faut noter que les regroupements peuvent se recouvrir. Non seulement c'est possible, mais c'est même conseillé : cela permet d'obtenir des regroupements plus gros. De plus, ces regroupements peuvent passer au travers des bords du tableau : il suffit de les faire revenir de l'autre côté. Et c'est possible aussi bien pour les bords horizontaux (gauche et droite) que pour les bords verticaux (haut et bas). Le même principe peut s'appliquer aux coins.
Quatrième étape : convertir chaque regroupement en équation logique
[modifier | modifier le wikicode]Trouver l'équation qui correspond à un regroupement est un processus en plusieurs étapes, que nous illustrerons dans ce qui va suivre. Ce processus demande de :
- trouver la variable qui ne varie pas dans les lignes et colonnes attribuées au regroupement ;
- inverser la variable si celle-ci vaut toujours zéro dans le regroupement ;
- faire un ET entre les variables qui ne varient pas.
- faire un OU entre les équations de chaque regroupement, et on obtient l'équation finale de la sortie.








































































![{\displaystyle e0.[({\overline {e2}}.e1)+(e2.{\overline {e1}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95a5d00477a179e003e1d4d6dd3fa79137262380)
