Fonctionnement d'un ordinateur/Les circuits de conversion analogique-numérique

Dans ce chapitre, nous allons voir un dernier type de circuits, qui font les conversion entre de l'analogique et du numérique. Il en existe deux types . Le circuit qui convertit un signal analogique en signal numérique cela est un CAN (convertisseur analogique-numérique). Le circuit qui fait la conversion inverse est un CNA (convertisseur numérique-analogique). On verra que ces circuits sont utilisés dans les cartes son et dans les anciennes cartes graphiques. Par exemple, il y a un CAN intégré à la carte son, qui sert à convertir le signal provenant d'un microphone en un signal numérique utilisable par la carte son. Il existe aussi un CNA, qui cette fois convertit le signal provenant de la carte son en signal analogique à destination des haut-parleurs. Mais nous reverrons cela dans quelques chapitres.

CAN & CNA

Le convertisseur numérique-analogique

Les CNA sont plus simples à étudier que les CAN, ce qui fait que nous allons les voir en premier. Les CNA convertissent un nombre en binaire codé sur $N$ bits en tension analogique. la tension de sortie est comprise dans un intervalle, qui va du 0 volts à une tension maximale $U_{max}$. Un 0 binaire sera convertie en une tension de 0 volts, tandis que la valeur binaire $2^{N}-1$ est codée avec la tension maximale. Tout nombre entre les deux est compris entre la tension maximale et minimale. Le lien entre nombre binaire et tension de sortie varie pas mal selon le CNA, mais la plupart sont des convertisseurs dits linéaires.

CNA de 8 bits.

Exemple avec un CNA de 2 bits : chaque nombre binaire de 2 bits correspond à un intervalle de tension précis, tous identiques.

On peut expliquer leur fonctionnement de deux manières différentes. Une première manière de voir un CAN linéaire est de regarder l'association entre tension de sortie et nombre binaire. L'intervalle de la tension de sortie est découpé en sous-intervalles de même taille, chacun d'entre eux se voyant attribuer un nombre binaire. Des sous-intervalles consécutifs codent des intervalles consécutifs, le premier codant un 0 et le dernier la valeur maximale $2^{N}-1$.

La taille de chaque sous-intervalle est appelé le quantum de tension et vaut $U_{max} \over 2^{N}$. Il s'agit de la différence de tension minimale que l'on obtient en changeant l'entrée. En clair, la différence de tension en sortie entre deux nombres binaires consécutifs, est toujours la même, égale au quantum de tension. Par exemple, supposons qu'un 5 et un 6 en binaire donneront des tensions différentes de 1 volt. Alors ce sera la même différence de tension entre un 10 binaire et un 11, entre un 1000 et 1001, etc. La seconde manière de les voir est de considérer que la tension de sortie est proportionnelle au nombre à convertir, le coefficient de proportionnalité n'étant autre que le quantum de tension.

CNA linéaire.

Les CNA uniformes (non-pondérés)

Le CNA peut être construit de diverses manières, qui utilisent toutes des composants analogiques nommés résistances et amplificateurs analogiques, que vous avez certainement vu en cours de collège ou de lycée.

Le premier type utilise autant de générateurs de tension qu'il y a de valeurs possibles en sortie. En clair, ce CNA possède $2^{N}$ générateurs de tension (en comptant la masse et la tension d'alimentation). L'idée est de connecter le générateur qui fournit la tension de sortie et de déconnecter les autres. Chaque connexion/déconnexion se fait par l'intermédiaire d'un interrupteur commandable, à savoir un transistor. Pour faire le lien entre chaque transistor et la valeur binaire, on utilise un décodeur. Il suffit de relier chaque sortie du décodeur (qui correspond à une entrée unique) au transistor (la tension) qui correspond.

CNA uniforme (non-pondéré).

Les CNA pondérés en binaire

Il est maintenant temps de passer aux CNA pondérés. L'idée qui se cache derrière les circuits que nous allons voir est très simple. Partons d'un nombre binaire de $N$ bits $a_{N},a_{n-1},a_{N-2},...,a_{2},a_{1},a_{0}$. Si le bit $a_{0}$ correspond à un quantum de tension $U$, alors la tension correspondant au bit $a_{1}$ est de $2U$, celle de $a_{2}$ est de $4U$, etc. Une fois chaque bit convertit en tension, il suffit d'additionner les tension obtenues pour obtenir la tension finale. Toute la difficulté est de convertir chaque bit en tension, puis d'additionner le tout. C’est surtout l'addition des tensions qui pose problème, ce qui fait que la plupart des circuits convertit les bits en courants, plus faciles à additionner, avant de convertir le résultat final en tension. Dans ce qui va suivre, nous allons voir deux circuits : les CNA pondérés à résistances équilibrées et non-équilibrées.

Le CNA à résistances non-équilibrées

Le circuit suivant utilise des résistances pour convertir un bit en un courant proportionnel à sa valeur. Rappelons que chaque bit est codé par une tension égale à la tension d'alimentation (pour un 1) ou un 0 volt (pour un 0). Cette tension est convertie en courant par un interrupteur, une tension et une résistance. Le courant est obtenu en faisant passer une tension à travers une résistance, l'interrupteur ouvrant ou fermant le circuit selon le bit à coder. Quand le bit est de zéro, l'interrupteur s'ouvre, et le courant ne passe pas : il vaut 0. Quand le bit est à 1, l'interrupteur se ferme et le courant est alors mis à sa valeur de conversion. La valeur de la résistance permet de multiplier chaque bit par son poids (par 1, 2, 4, , 16, ...) : c'est pour cela qu'il y a des résistances de valeur R, 2R, 4R, 8R, etc. Les courants en sortie de chaque résistance sont ensuite additionnés par le reste du circuit, avant d'être transformé en une tension proportionnelle.

Convertisseur numérique-analogique

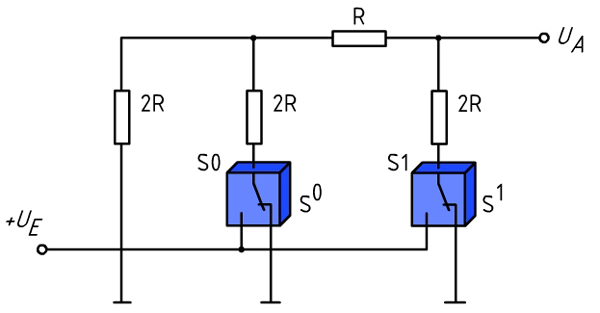
Le CNA à résistances équilibrées

Le circuit précédent a pour défaut d'utiliser des résistances de valeurs fort différentes : R, 2R, 4R, etc. Mais la valeur d'une résistance est rarement très fiable, surtout quand on commence à utiliser des résistances assez fortes. Chaque résistance a une petit marge d'erreur, qui fait que sa résistance véritable n'est pas tout à fait égale à sa valeur idéale. Avec des résistances fort variées, les marges d'erreurs s'accumulent et influencent le fonctionnement du circuit. Si on veut un circuit réellement fiable, il vaut mieux utiliser des résistances qui ont des marges d'erreur similaires. Et qui dit marges d'erreur similaire dit résistances de valeur similaires. Pas question d'utiliser une résistance de valeur R avec une autre de valeur 16R ou 32R. Pour éviter cela, on doit modifier le circuit précédent de manière à utiliser des résistances de même valeur ou presque. Cela donne le circuit suivant.

Convertisseur numérique analogique R-2R

Le convertisseur analogique-numérique

Les convertisseurs analogique-numérique convertissent une tension en un nombre binaire codé sur $N$ bits. Comme pour les CNA, la tension d'entrée peut prendre toutes les valeurs dans un intervalle de tension allant de 0 à une tension maximale. L'intervalle de tension est découpé en sous-intervalles de même taille, chacun se voyant attribuer un nombre binaire. Si la tension d'entrée tombe dans un de ces intervalle, le nombre binaire en sortie est celui qui correspond à cet intervalle. Des intervalles consécutifs correspondent à des nombres binaires consécutifs, le premier intervalle codant un 0 et le dernier le nombre $2^{N}-1$. En clair, le nombre binaire est plus ou moins proportionnel à la tension d'entrée. La taille de chaque intervalle est appelé le quantum de tension, comme pour les CNA.

La conversion d'un signal analogique se fait en plusieurs étapes. La toute première consiste à mesurer régulièrement le signal analogique, pour déterminer sa valeur. Il est en effet impossible de faire la conversion au fil de l'eau, en temps réel. À la place, on doit échantillonner à intervalle réguliers la tension, pour ensuite la convertir. La seconde étape consiste à convertir celle-ci en un signal numérique, un signal discret. Enfin, ce dernier est convertit en binaire. Ces trois étapes portent le nom d’échantillonnage, la quantification et le codage.

signal échantillonné.

Signal discrétisé.

L'échantillonnage

L’échantillonnage mesure régulièrement le signal analogique, afin de fournir un flux de valeurs à convertir en numérique. Il a lieu régulièrement, ce qui signifie que le temps entre deux mesures est le même. Ce temps entre deux mesures est appelée la période d'échantillonnage, notée $T_{e}$. Le nombre de fois que la tension est mesurée par seconde s'appelle la fréquence d'échantillonnage. Elle n'est autre que l'inverse de la période d’échantillonnage : $f_{e}={\frac {1}{T_{e}}}$. Plus celle-ci est élevée, plus la conversion sera de bonne qualité et fidèle au signal original. Les deux schémas ci-dessous montrent ce qui se passe quand on augmente la fréquence d’échantillonnage : le signal à gauche est échantillonné à faible fréquence, alors que le second l'est à une fréquence plus haute.

Signal échantillonné à basse fréquence.

Signal échantillonné à haute fréquence.

L’échantillonnage est réalisé par un circuit appelé l’échantillonneur-bloqueur. L'échantillonneur-bloqueur le plus simple ressemble au circuit du schéma ci-dessous. Les triangles de ce schéma sont ce qu'on appelle des amplificateurs opérationnels, mais on n'a pas vraiment à s'en préoccuper. Dans ce montage, ils servent juste à isoler le condensateur du reste du circuit, en ne laissant passer les tensions que dans un sens. L'entrée C est reliée à un signal d'horloge qui ouvre ou ferme l'interrupteur à fréquence régulière. La tension va remplir le condensateur quand l'interrupteur se ferme. Une fois le condensateur remplit, l'interrupteur est déconnecté isolant le condensateur de la tension d'entrée. Celui-ci mémorisera alors la tension d'entrée jusqu'au prochain échantillonnage.

Echantillonneur-bloqueur.

La quantification et le codage

Le signal échantillonné est ensuite convertit en un signal numérique, codé sur plusieurs bits. Le nombre de bits du résultat est ce qu'on appelle la résolution du CAN. Plus celle-ci est important,e plus le signal codé sera fidèle au signal d'origine. La précision du CAN sera plus importante avec une résolution importante. Malgré tout, un signal analogique ne peut pas être traduit en numérique sans pertes, l'infinité de valeurs d'un intervalle de tension ne pouvant être codé sur un nombre fini de bits. La tension envoyée va ainsi être arrondie à une tension qui peut être traduite en un entier sans problème. Cette perte de précision va donner lieu à de petites imprécisions qui forment ce qu'on appelle le bruit de quantification. Plus le nombre de bits utilisé pour encoder la valeur numérique est élevée, plus ce bruit est faible.

Résolution d'un CAN.

Le CAN Flash

Un CAN peut être construit de diverses manières, à partir de composants nommés résistances et amplificateurs analogiques. Par exemple, voici à quoi ressemble un CAN Flash, le type de CAN le plus performant. C'est aussi le plus simple à comprendre, bizarrement. Pour comprendre comment celui-ci fonctionne, précisons que le CAN code la tension analogique sur $N$ bits, soit des valeurs comprises entre 0 et $2^{N}-1$. Chaque nombre binaire est associée à la tension d'entrée qui correspond. L'idée est de comparer la tension avec toutes les $2^{N}$ valeurs de tension correspondantes. On utilise pour cela un comparateur pour chaque tension, qui fournit un résultat codé sur un bit : ce dernier vaut 1 si la tension d'entrée est supérieure à la valeur, 0 sinon. Les résultats de chaque comparateur sont combinés entre eux pour déterminer la tension la plus grande qui est proche du résultat. La combinaison des résultats est réalisée avec un encodeur à priorité. Les résultats des comparateurs sont envoyés sur l'entrée adéquate de l'encodeur, qui convertit aussi cette tension en nombre binaire.

Comparateur flash

Ce circuit, bien que très simple, a cependant de nombreux défauts. Le principal est qu'il prend beaucoup de place : les comparateurs de tension sont des dispositifs encombrants, sans compter l'encodeur. Mais le défaut principal est le nombre de comparateurs à utiliser. Sachant qu'il en faut un par valeur, on doit utiliser $2^{N}$ comparateurs pour un CAN de $N$ bits. En clair, le nombre de comparateurs à utiliser croît exponentiellement avec le nombre de bits. En conséquence, les CAN Flash ne sont utilisables que pour de petits convertisseurs, limités à quelques bits. Mais il existe des CAN construits autrement qui n'ont pas ce genre de problèmes.

Le CAN simple rampe

Le CAN simple rampe est un CAN construit avec un compteur, un générateur de tension, un comparateur de tension et un signal d'horloge. L'idée derrière ce circuit est assez simple : au lieu de faire toutes les comparaisons en parallèle, comme avec un CAN Flash, celles-ci sont faites une par une, une tension après l'autre. Ce faisant, on n'a besoin que d'un seul comparateur de tension. Les tensions sont générées successivement par un générateur de rampe, à savoir un circuit qui crée une tension qui croit linéairement. La tension en sortie du générateur de rampe commence à 0, puis monte régulièrement jusqu’à une valeur maximale. Celle-ci est alors comparée à la tension d'entrée. Tant que la tension générée est plus faible, la sortie du comparateur est à 0. Quand la tension en sortie du générateur de rampe dépasse à la tension d'entrée, le comparateur renvoie un 1.

Tout ce système permet de faire les comparaisons de tension, mais il n'est alors plus possible d'utiliser un encodeur pour faire la traduction (tension -> nombre binaire). L'encodeur est remplacé par un autre circuit, qui n'est autre que le compteur. Le compteur est initialisé à 0, mais est incrémenté régulièrement, ce qui fait qu'il balaye toutes les valeurs que peut prendre la sortie numérique. L'idée est que le compteur et la tension du générateur de rampe se suivent : quand l'un augmente, l'autre augmente dans la même proportion. Ainsi, la valeur dans le compteur correspondra systématiquement à la tension de sortie du générateur. Pour cela, on synchronise les deux circuits avec un signal d'horloge. À chaque cycle, le compteur est incrémenté, tandis que le générateur augmente d'un quantum de tension. Ce faisant, quand le comparateur renverra un 0, on saura que la tension d'entrée est égale à celle du générateur. Au même cycle d'horloge, le compteur contient la valeur binaire qui lui correspond. Il suffit alors d’arrêter le compteur et de recopier son contenu sur la sortie.

Comparateur simple rampe.

Ce CAN a l'avantage de prendre bien moins de place que son prédécesseur, sans compter qu'il utilise très peu de circuits. Pas besoin de beaucoup de comparateurs de tension, ni d'un encodeur très compliqué : quelques circuits très simples et peu encombrants suffisent. Ce qui est un avantage certain pour les CAN avec beaucoup de bits. Mais ce CAN a cependant des défauts assez importants. Le défaut principal de ce CAN est qu'il est très lent. Déjà, la conversion est plus rapide pour les tensions faibles, mais très lente pour les grosses tensions, vu qu'il faut balayer les tensions unes par unes. On gagne en place ce qu'on perd en vitesse.

Le CAN delta

Le CAN delta peut être vu comme une amélioration du circuit précédent. Il est lui aussi organisé autour d'un compteur, initialisé à 0, qui est incrémenté jusqu'à tomber sur la valeur de sortie. Encore une fois, ce compteur contient un nombre binaire et celui-ci est associé à une tension équivalente. Sauf que cette fois-ci, la tension équivalente n'est pas générée par un générateur synchronisé avec le compteur, mais directement à partir du compteur lui-même. Le compteur relié à un CNA, qui génère la tension équivalente. La tension équivalente est alors comparée avec la tension d'entrée, et le comparateur commande l'incrémentation du compteur, comme dans le circuit précédent.

Convertisseur CAN de type Delta.

Le CAN par approximations successives

Le CAN par approximations successives effectue une comparaison par étapes, en suivant une procédure dite de dichotomie. Chaque étape correspond à un cycle d'horloge du CAN, qui met donc plusieurs cycles d'horloges pour faire une conversion. Le CAN essaye d'encadrer la tension dans un intervalle, est divisé en deux à chaque étape. L'intervalle à la première étape est de [0 , Tension maximale en entrée ], puis il se réduit progressivement, jusqu'à atteindre un encadrement suffisant, compatible avec la résolution du CAN. À chaque étape, le CAN découpe l'intervalle en deux parties égales, séparées au niveau d'une tension médiane. Il compare l'entrée à la tension médiane et en déduit un bit du résultat, qui est ajouté dans un registre à décalage.

Pour comprendre le concept, prenons l’exemple d'un CAN qui prend en entrée une tension comprise entre 0 et 5 Volts.

• Lors de la première étape, le CAN vérifie si la tension d'entrée est supérieure/inférieure à 2,5 V.
• Lors de la seconde étape, il vérifie si la tension d'entrée est supérieure/inférieure 3,75 V ou de 1,25 Volts, selon le résultat de l'étape précédente : 1,25 V si l'entrée est inférieure à 2,5 V, 3,75 V si elle est supérieure.
• Et on procède sur le même schéma, jusqu’à la dernière étape.

Pour faire son travail, ce CAN comprend un comparateur, un registre et un CNA. Le comparateur est utilisé pour comparer la tension d'entrée avec la tension médiane. Le registre à décalage sert à accumuler les bits calculés à chaque étape, dans le bon ordre. En réfléchissant un petit peu, on devine que les bits sont calculés en partant du bit de poids fort vers le bit de poids faible : le bit de poids fort est calculé dans la première étape, le bit de poids faible lors de la dernière, .... Le CNA sert à générer la tension médiane de chaque étape, à partir de la valeur du registre. L'ensemble est organisé comme illustré dans le schéma ci-dessous.

CAN à approximations successives.