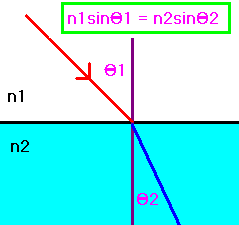
Si la lumière vient d'en haut:
n
2
⋅
sin
i
2
=
n
1
⋅
sin
i
1
{\displaystyle n_{2}\cdot \sin i_{2}=n_{1}\cdot \sin i_{1}}
i
2
=
arcsin
(
n
1
n
2
⋅
sin
(
i
1
)
)
{\displaystyle i_{2}=\arcsin \left({\frac {n_{1}}{n_{2}}}\cdot \sin(i_{1})\right)}
En sens inverse, si la lumière vient d'en bas:
tant que i2 ne dépasse pas l'angle
i
2
m
a
x
=
λ
=
arcsin
(
n
1
n
2
⋅
)
{\displaystyle i_{2max}=\lambda =\arcsin \left({\frac {n_{1}}{n_{2}}}\cdot \right)}
i
1
=
arcsin
(
n
2
n
1
⋅
sin
(
i
2
)
)
{\displaystyle i_{1}=\arcsin \left({\frac {n_{2}}{n_{1}}}\cdot \sin(i_{2})\right)}
2 >i2max
On montre que la relation sur les angles peut aux petits angles, c'est-à-dire dans des conditions de stigmatisme approché, s'écrire:
n
1
.
C
A
1
S
A
1
=
n
2
.
C
A
2
S
A
2
{\displaystyle {\frac {n_{1}.CA_{1}}{SA_{1}}}={\frac {n_{2}.CA_{2}}{SA_{2}}}}
n
1
.
(
a
1
−
c
)
(
a
1
−
s
)
=
n
2
.
(
a
2
−
c
)
(
a
2
−
s
)
{\displaystyle {\frac {n_{1}.(a_{1}-c)}{(a_{1}-s)}}={\frac {n_{2}.(a_{2}-c)}{(a_{2}-s)}}}
ce que l'on peut écrire après un peu d'algèbre :
n
1
(
a
1
−
s
)
−
n
2
(
a
2
−
s
)
=
n
1
−
n
2
(
c
−
s
)
{\displaystyle {\frac {n_{1}}{(a_{1}-s)}}-{\frac {n_{2}}{(a_{2}-s)}}={\frac {n_{1}-n_{2}}{(c-s)}}}
et en prenant comme origine le point S : ce qui revient à prendre s=0
n
1
a
1
−
n
2
a
2
=
n
1
−
n
2
c
{\displaystyle {\frac {n_{1}}{a_{1}}}-{\frac {n_{2}}{a_{2}}}={\frac {n_{1}-n_{2}}{c}}}
et en utilisant comme notation xo = a1, xi=a2, fo=n1 c/(n1-n2)et fi= - n2 c /(n1-n2):
x
i
=
f
i
∗
x
o
(
x
o
−
f
o
)
{\displaystyle x_{i}={\frac {f_{i}*x_{o}}{(x_{o}-f_{o})}}}
y
i
=
−
f
o
∗
y
o
(
x
o
−
f
o
)
{\displaystyle y_{i}={\frac {-f_{o}*y_{o}}{(x_{o}-f_{o})}}}
n
1
a
1
−
n
2
a
2
=
n
1
−
n
2
c
1
{\displaystyle {\frac {n_{1}}{a_{1}}}-{\frac {n_{2}}{a_{2}}}={\frac {n_{1}-n_{2}}{c_{1}}}}
et au deuxième dioptre
n
2
a
2
−
n
3
a
3
=
n
2
−
n
3
c
2
{\displaystyle {\frac {n_{2}}{a_{2}}}-{\frac {n_{3}}{a_{3}}}={\frac {n_{2}-n_{3}}{c_{2}}}}
En additionnant ces deux formules :
n
1
a
1
−
n
3
a
3
=
n
1
−
n
2
c
1
+
n
2
−
n
3
c
2
{\displaystyle {\frac {n_{1}}{a_{1}}}-{\frac {n_{3}}{a_{3}}}={\frac {n_{1}-n_{2}}{c_{1}}}+{\frac {n_{2}-n_{3}}{c_{2}}}}
on obtient la formule des lentilles.
Si les milieux 1 et 3 sont de l'air, d'indice 1 (approxmativement), la formule se simplifie :
1
a
1
−
1
a
3
=
1
−
n
c
1
+
n
−
1
c
2
=
1
f
{\displaystyle {\frac {1}{a_{1}}}-{\frac {1}{a_{3}}}={\frac {1-n}{c_{1}}}+{\frac {n-1}{c_{2}}}={\frac {1}{f}}}
où
a 1 et a 3 sont les abscisses de l'objet et de l'image après passage des deux dioptres qui constituent la lentille mince,f est l'abscisse du foyer objet etf ′ = - f est l'abscisse du foyer image.On trouve aussi comme notation dans les pays anglo-saxons :
fo l'abscisse du foyer objet,fi = - fo est l'abscisse du foyer image,Si xo et xi sont les abscisses de l'objet et de l'image, alors
1
x
o
−
1
x
i
=
1
−
n
c
1
+
n
−
1
c
2
=
1
f
o
=
−
1
f
i
{\displaystyle {\frac {1}{x_{o}}}-{\frac {1}{x_{i}}}={\frac {1-n}{c_{1}}}+{\frac {n-1}{c_{2}}}={\frac {1}{f_{o}}}={\frac {-1}{f_{i}}}}
c'est la formule dite de Descartes, qui avec deux lignes d'algèbre s'écrit :
(
x
i
−
f
i
)
=
f
i
×
f
o
(
x
o
−
f
o
)
{\displaystyle (x_{i}-f_{i})={\frac {f_{i}\times f_{o}}{(x_{o}-f_{o})}}}
formule dite de Newton
On a
x
i
=
f
i
×
f
o
(
x
o
−
f
o
)
+
f
i
{\displaystyle x_{i}={\frac {f_{i}\times f_{o}}{(x_{o}-f_{o})}}+f_{i}}
et donc
x
i
=
f
i
×
x
o
(
x
o
−
f
o
)
{\displaystyle x_{i}={\frac {f_{i}\times x_{o}}{(x_{o}-f_{o})}}}
y
i
=
−
f
o
×
y
o
(
x
o
−
f
o
)
{\displaystyle y_{i}={\frac {-f_{o}\times y_{o}}{(x_{o}-f_{o})}}}
