ISN Numérisation

Numérisation des données

Savoirs :	L'ordinateur manipule uniquement des valeurs numériques. Une étape de numérisation des objets du monde physique est donc indispensable.
Capacités :	Coder un nombre, un caractère au travers d'un code standard, un texte sous forme d'une liste de valeurs numériques. Numériser une image ou un son sous forme d'un tableau de valeurs numériques. Modifier format, taille, contraste ou luminance d'images numériques. Filtrer et détecter des informations spécifiques. Créer une image à l'aide d'un logiciel de modélisation.
Observation :	Il est ici utile de faire référence à des notions technologiques introduites à propos des architectures matérielles. Les images et les sons sont choisis comme contexte applicatif et sont manipulés via des logiciels de traitement ou de synthèse. Le traitement numérique de la lumière et du son est en lien avec les principes physiques sous-jacents, qu'il est utile d'évoquer au moment voulu.

Signal analogique, signal numérique

Un signal analogique se présente souvent sous forme d'une tension électrique qui varie avec le temps. On dit que le signal est analogique quand n'importe quelle valeur de la tension électrique a de la signification. Un signal numérique est aussi une tension qui varie avec le temps, mais seules quelques valeurs de tension ont une signification précise.

Numérisation d'un signal

Un convertisseur analogique numérique (CAN) reçoit en entrée un signal analogique (par exemple,le signal électrique venu d'un microphone,qui représente les variations de la pression acoustique), et un signal d'horloge. À chaque top de l'horloge, le convertisseur CAN doit présenter sur son bus de sortie une valeur binaire qui représente au mieux le signal analogique d'entrée.

Pour obtenir une numérisation de haute qualité, il faut :

• un signal d'horloge assez rapide : le nombre de tops d'horloge à chaque seconde s'appelle la fréquence d'échantillonnage ; elle doit être plus rapide que les variations typiques du signal analogique à numériser.
• une résolution suffisante pour les données en sortie : si le bus de sortie possède $n$ bits, alors il peut représenter $2^{n}$ valeurs numériques différentes.

Un exemple de numérisation

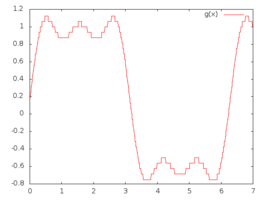
Graphique d'un signal analogique	Numérisation du signal	Graphique d'un signal numérique

Dans les exemples présentés ci-dessus, la numérisation du signal analogique a été réalisée en distinguant 32 valeurs différentes (et 32 seulement : codage possible sur 5 bits) dans l'intervalle compris entre -1 V et +1 V. Un millier d'échantillons de du signal analogique ont été évalués pour effectuer la numérisation.

Exercice : analogique/numérique

• À quoi ressemblerait le signal numérique si celui-ci était codé sur 2 bits, c'est à dire que 4 valeurs différentes seulement du signal peuvent exister ?
• Supposons que le signal numérique ait une forte résolution (par exemple 10 bits, ce qui permet 1024 valeurs significatives distinctes), mais que les échantillons soient peu nombreux. À quoi ressemblerait le signal numérisé s'il n' avait que deux échantillons numérisés pendant la durée représentée sur le graphique ?... et s'il n'y avait qu'un seul échantillon ?

Images numériques

Les appareils photo et les caméras les plus utilisés maintenant fonctionnent avec des capteurs CCD, qui sont des matrices formées de petits rectangles sensibles à la lumière. L'électronique associé au capteur CCD échantillonne sur commande les valeur des charges électriques apparues sur chaque petit rectangle, qui dépend de la lumière reçue. La valeur de chacune de ces charges électriques est numérisée, et un tableau de valeurs numériques est enregistré dans une mémoire.

Les appareils de bonne qualité utilisent de grandes quantités de mémoire, quand les images et les vidéos sont conservées sans chercher à comprimer les données (formats de type "RAW"). De nombreux appareils grand public compriment systématiquement les données afin de pouvoir en emmagasiner plus dans la même mémoire.

Comparaison entre formats de fichiers pour des images

Format de fichier	BMP	XPM	PNG (couleurs indexées)	JPG
principales caractéristiques	non comprimé, 32 bits par pixel	non comprimé, indexé, fichier texte lisible	comprimé, sans perte	comprimé, avec des pertes
Taille en kilo-octets	16,5	4,5	0,6	2,5

L'image choisie pour le tableau ci-dessus mesure $64\times 64$ pixels, elle comporte 4096 pixels indépendants. On peut remarquer que les tailles de certains fichiers non-comprimés sont prévisibles :

• format BMP : Présence d'un en-tête, plus 4 octets par pixels : $4\times 64\times 64=16384$, pour un total de 16,6 kO.
• format XPM : présence d'un en-tête, plus un octet par pixel : $1\times 64\times 64=4096$, pour un total de 4,5 kO.

Les systèmes de compression ont des efficacités variables selon le type d'image à encoder. Comme l'image choisie a un nombre limité de couleurs (huit) la compression PNG réussit très bien : le fichier pèse moins d'un kilo-octet. Le fichier JPG pèse plus du double. Observez bien les pixels de ce dernier fichier : on distingue des altérations.

Les composantes R, V, B d'une image en couleur

Les écran et les vidéoprojecteurs connectés aux ordinateurs utilisent la synthèse additive pour créer les palettes de couleurs qui nous sont présentées.

En synthèse additive, les couleurs primaires sont rouge, vert, bleu (RVB en français, RGB en anglais).

Ci dessous, voici une table de synthèse additive pour les couleurs primaires. Les notations rgb(x,y,z) sont des triplets de valeurs permettant de donner la composition d'une lumière. Les valeurs de x, y et z sont dans un intervalle de 0 (le minimum) à 255 (le maximum). Le couleurs primaires correspondent aux notation suivantes :

• R rgb(255,0,0)
• V rgb(0,255,0)
• B rgb(0,0,255)

$+$	R	V	B
R		J rgb(255,255,0)	M rgb(255,0,255)
V	J rgb(255,255,0)		C rgb(0,255,255)
B	M rgb(255,0,255)	C rgb(0,255,255)

Le couleurs J, M, C sont respectivement le jaune, le magenta et le cyan. Le noir (N rgb(0,0,0)) est l'absence de lumière (ni R, ni V, ni B), le blanc (Bl rgb(255,255,255)) s'obtient en additionnant R, V et B.

Transformer une image par calcul

On peut représenter les images dans un ordinateur par un tableau rectangulaire de nombres représentant chacun un pixel de l'image. Il est quelque fois commode de considérer trois tableaux de même dimension, pour les trois composantes RVB de l'image.

Des calculs appliqués aux cases du tableau rectangulaire qui représente une image permettent de créer des images nouvelles aux propriétés intéressantes.

On peut par exemple remplacer le chiffre dans chaque case par une moyenne (avec coefficients) des chiffres de cases voisines. En choisissant bien les coefficients, on peut obtenir des opérations nommées « filtres », pour simuler un flou, un flou cinétique, pour accentuer les détails, ou pour extraire les bords d'objets contrastés.

Un exemple d'algorithme

debut
  {les données de l'images sont dans la table t}
  largeur, hauteur := taille(t)
  t1 := nouvelle table(hauteur,largeur)
  pour y dans intervalle(0,hauteur)
    pour x dans intervalle(0,largeur)
      t1[y,x] := traitement (t, y, x)
    fin pour
  fin pour
  resultat := t1
fin

Les données de l'image de départ se présentent sous forme d'une table t, organisée en hauteur lignes et largeur colonnes.

Une nouvelle table t1 de même dimension est créée pour contenir la nouvelle image.

Deux boucles indicées par les variables x et y permettent de parcourir chaque pixel de la table t1, qui résulte d'un calcul basé sur les valeurs contenues dans la table t et les coordonnées (x,y). Le calcul est réalisé par la fonction nommée traitement.

Les implémentations ci-dessous utilisent une petite table nommée « filtre » contenant un jeu de coefficients. Une moyenne est faite des valeurs de pixels de la table t, en utilisant les coefficients du filtre. Cette méthode permet entre autres de flouter l'image de départ.

Exemple en Python

#!/usr/bin/python
# -*- coding: utf-8 -*-

import Image

##########################################################
#   un filtre pour obtenir un peu de flou "gaussien"     #
##########################################################
fFlou=[
    [0.5,0.7,0.5],
    [0.7,1.0,0.5],
    [0.5,0.7,0.5],
    ]

#############################################################
#   un filtre pour mettre en valeur les zones contrastées   #
#############################################################
fContraste=[
    [-0.05,-0.2,-0.05],
    [-0.2,1.01,-0.2],
    [-0.05,-0.2,-0.05],
    ]

##########################################################
#   implémentation de l'algorithme suggéré plus haut     #
##########################################################
def appliqueFiltre(t,f):
    """
    Applique un filtre sur un tableau d'image.
    Les valeurs du filtre sont des coefficients utilisées pour faire des
    moyennes pondérées entre pixels voisins
    @param t tableau encodant une image en gris
    @param f un filtre (tableau plus petit)
    @return un tableau de la même taille que t, après passage du filtre
    """
    h=len(t)     #hauteur de t
    w=len(t[0])  #largeur de t

    result=[]
    for y in range(h):
        line=[]
        for x in range(w):
            line.append(traitement(t, y, x, f))
        result.append(line)
    return result

##########################################################
#   implémentation de la fonction "traitement"           #
##########################################################
def traitement(t, y, x, f):
    """
    calcule la valeur d'un pixel nouveau en utilisant une image originale
    et un jeu de coordonnées. Une table de coefficients est utilisée.
    @param t la table del'image originale
    @param y désigne une ligne dans l'image
    @param x désigne une colonne dans l'image
    @param f une table de coefficients(un filtre)
    @return une valeur utilisable pour créer un nouveau pixel
    """
    h=len(f)     #hauteur de f
    w=len(f[0])  #largeur de f
    ifx=range(-w/2,(w+1)/2) # intervalle de même largeur que f centré sur 0
    ify=range(-h/2,(h+1)/2) # intervalle de même hauteur que f centré sur 0
    dfx=w/2 # décalage horizontal de f
    dfy=h/2 # décalage vertical de f

    h=len(t)     #hauteur de t
    w=len(t[0])  #largeur de t
    s=0
    n=0
    for iy in ify:
        for ix in ifx:
            jx=ix+x # coordonnées à prendre encompte dans
            jy=iy+y # le tableau de départ t
            kx=ix+dfx # coordonnées dans le filtre
            ky=iy+dfy # nécessairement positives ou nulles
            if jx in range(w) and jy in range(h):
                # si les coordonnées sont dans le tableau t
                coef=f[ky][kx]
                n+=coef
                s+=t[jy][jx]*coef
    return s/n

##########################################################
#   quelques fonctions utilitaires ci-dessous, pour      #
#   fabriquer des tables explicites à partir d'images    #
#   en utilisant le module python Image.                 #
##########################################################
def troisCanaux(filename):
    """
    Ouvre un fichier image et extrait troix canaux de couleur de l'image
    du fichier
    @param filename le nom du fichier à ouvrir
    @result un triplet d'images en niveau de gris pour rouge, vert et bleu
    """
    im=Image.open(filename)
    im=im.convert("RGB")
    return im.split()

def canalVersTable(canal):
    """
    récupère lesdonnées d'un canal de type L (valeurs de gris)
    dans un tableau
    @param canal un canal de gris
    @return un tableau avec les valeurs organisées dedans
    """
    w,h=canal.size
    result=[]
    for y in range(h):
        line=[]
        for x in range(w):
            line.append(canal.getpixel((x,y)))
        result.append(line)
    return result

def tableVersCanal(t):
    """
    convertit une table rectangulaire de nombres
    vers un canal de valeurs de gris d'image
    """
    h=len(t)
    w=len(t[0])
    result=Image.new("L",(w,h))
    for y in range(h):
        for x in range(w):
            result.putpixel((x,y),t[y][x])
    return result



########################################################
#  programme à effectuer quand ce fichier est invoqué  #
#  directement. On peut invoquer ce fichier suivi du   #
#  nom d'un fichier d'image, ou donner le nom d'un     #
#  fichier d'image interactivement pendant que ce      #
#  programme fonctionne.                               #
########################################################
import sys, os.path
if __name__ == "__main__":
    if len(sys.argv)>1:
        nomFichier=sys.argv[1]
    else:
        nomFichier=raw_input("Tapez le nom d'un fichier d'image")
    r, v, b = troisCanaux(nomFichier)
    t=canalVersTable(r)
    t1=appliqueFiltre(t,fFlou)
    r1=tableVersCanal(t1)
    r.show()
    raw_input("Voici le canal R de %s. Appuyez sur Entrée" %nomFichier)
    r1.show()
    raw_input("Voici l'image obtenue après application du filtre de flou. Appuyez sur Entrée")
    t2=appliqueFiltre(t,fContraste)
    r2=tableVersCanal(t2)
    r2.show()
    raw_input("Voici l'image obtenue après le filtre d'accentuation. Appuyez sur Entrée")
    t3=appliqueFiltre(t1,fContraste)
    r3=tableVersCanal(t3)
    r3.show()
    raw_input("Enfin, on applique le filtre de flou après l'autre. Appuyez sur Entrée")

    # enregistre les nouvelles images.
    path, ext = os.path.splitext(nomFichier)
    nf="%s%d%s" %(path, 0, ext)
    r.save(nf)
    print "fichier sauvé :", nf
    nf="%s%d%s" %(path, 1, ext)
    r1.save(nf)
    print "fichier sauvé :", nf
    nf="%s%d%s" %(path, 2, ext)
    r2.save(nf)
    print "fichier sauvé :", nf
    nf="%s%d%s" %(path, 3, ext)
    r3.save(nf)
    print "fichier sauvé :", nf

Exécution du programme

Voici une trace de l'exécution de ce programme dans une console :

$ ./filtreImages.py logo.png 
Voici le canal R de logo.png. Appuyez sur Entrée
Voici l'image obtenue après application du filtre de flou. Appuyez sur Entrée
Voici l'image obtenue après le filtre d'accentuation. Appuyez sur Entrée
Enfin, on applique le filtre de flou après l'autre. Appuyez sur Entrée
fichier sauvé : logo0.png
fichier sauvé : logo1.png
fichier sauvé : logo2.png
fichier sauvé : logo3.png

L'image d'origine est celle- ci :

Voici les images affichées :

• le canal R de l'image :
• le canal R de l'image après application du filtre de flou :
• le canal R de l'image après application du filtre d'accentuation :
• le canal R de l'image après application des deux filtres :