Électronique/Les filtres électriques
Les filtres électriques sont des quadripôles, qui prennent en entrée une tension en fournissent en sortie une version atténuée de la tension d'entrée. Ceux-ci sont des composants qui atténuent les signaux dans une certaine gamme de fréquence. Ils vont par exemple laisser passer les signaux à basse fréquence, mais filtrer les hautes fréquences, ou inversement. Plus précisément, les filtres vont modifier l'ensemble des sinusoïdes qui leur parviennent. Si on leur envoie un signal (une tension ou courant quelconque) sur leur entrée, ils vont traiter ce signal et fournir une version traitée sur leur sortie. Pour donner quelques exemples, les circuits RC, RL, et RLC sont des filtres parmi tant d'autres. On a vu dans le chapitre sur l'impédance que ceux-ci fournissent une tension de sortie (aux bornes du condensateur ou de la bobine), quand on leur fournit une tension d'entrée. Leur étude dans le chapitre sur l'impédance a servi en quelque sorte d'introduction à l'étude des filtres électriques, là où ce chapitre porte sur l'étude des filtres de manière plus générale.
Il existe un grand nombre de filtres électroniques, qui ont chacun leurs avantages et inconvénients. Les critères utilisés pour classer les filtres sont assez nombreux : on peut les classer en fonction de leur bande passante, de leur ordre, de leur caractère actif/passif ou de certaines propriétés mathématiques. Dans ce qui va suivre, nous allons voir quelques classifications assez courantes des filtres. Nous allons d'abord voir la différence entre les filtres passe-haut, passe-bas, passe-bande et coupe-bande, qui ont chacun un comportement en fréquence bien précise. Puis, nous enchaînerons avec une classification plus élaborée qui distingue les filtres de Bessel, Butterworth, Tchebychev et Legendre.
La réponse en fréquence d'un filtre électronique
[modifier | modifier le wikicode]Lorsqu'on envoie un signal sinusoïdal en entrée d'un filtre, on retrouve en sortie un signal sinusoïdal d'une amplitude plus faible qu'à l'entrée. En quelque sorte, les filtres sont l'inverse d'un amplificateur : au lieu d'amplifier un signal, ils l'atténuent. Cette atténuation dépend de la fréquence du signal d'entrée : elle est minimale, voire nulle pour certaines fréquences, plus importante pour d'autres. Pour certaines fréquences, le signal de sortie est si faible qu'il est négligeable : la fréquence qui correspond est alors filtrée, atténuée, éliminée du signal original.
La relation atténuation-fréquence
[modifier | modifier le wikicode]Si on étudie la variation du gain en fonction des fréquences, on peut tomber sur plusieurs possibilités. Les quatre principales sont les suivantes :
- Le gain augmente avec la fréquence. Le filtre atténue les basses fréquences, mais laisse passer les hautes fréquences. Le filtre est dit un filtre passe-haut.
- Le gain diminue avec la fréquence. Le filtre laisse passer les basses fréquences, mais atténue les hautes fréquences. Le filtre est dit un filtre passe-bas.
- Le gain augmente jusqu'à une fréquence maximale avant de diminuer. Dit autrement, le gain est minimal pour les hautes et basses fréquences, maximal pour un intervalle bien précis. Le filtre laisse passer les fréquences contenues dans un intervalle, mais atténue les fréquences situées en dehors de celui-ci. C'est le comportement d'un filtre passe-bande.
- Le gain est maximal pour les hautes et basses fréquences, mais minimal dans un intervalle précis. Le gain diminue jusqu'à une fréquence maximale avant de remonter. Le filtre laisse passer les fréquences situées en dehors d'un intervalle, mais atténue les fréquences situées dans l'intervalle. C'est le comportement d'un filtre coupe-bande.
Certains filtres ont un comportement plus complexe et fonctionnent comme la superposition de filtres plus simples. Par exemple, certains filtres se comportent comme un filtre passe-bas aux basses fréquences, mais laissent passer une bande de fréquence dans certaines hautes fréquences. Et les exemples de ce type sont nombreux.

On considère arbitrairement qu'un filtre ne laisse pas passer les fréquences dont l’atténuation est de moitié, les autres n'étant pas filtrées. Si on fait les calculs, cela correspond à un gain diminué de 3 dB. La fréquence qui correspond à une atténuation réduite de moitié, c'est à dire où la puissance dissipée par le filtre est la moitié de celle fournie en entrée, est appelée la fréquence de coupure. En clair, le signal voit son amplitude en tension ou en courant divisée par , soit égale à 70,7% du signal originel. Une illustration est donnée ci-dessous pour un filtre passe-bas et un filtre passe-haut.
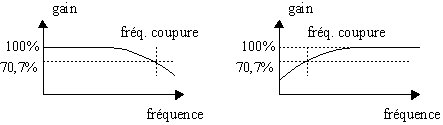
Pour la plupart des filtres, il existe entre une et deux fréquences de coupures, qui délimitent une bande de fréquences qui ne sont que peu filtrées. La largeur de cet intervalle est appelée la bande passante du filtre.

La relation déphasage-fréquence
[modifier | modifier le wikicode]Si le gain varie avec la fréquence, il en est de même pour la phase. Les signaux envoyés à un filtre en ressortent avec un déphasage par rapport à l'entrée. Qui plus est, ce décalage est généralement dépendant de la fréquence, la relation exacte variant selon le filtre considéré. L'origine de ce déphasage est que les signaux mettent un certain temps pour parcourir le filtre, pour faire le chemin de l'entrée vers la sortie, ce temps de parcours se traduisant par déphasage entre entrée et sortie. Généralement, plus un filtre contient de composants enchaînés les uns à la suite des autres, plus ce déphasage est important.
Tous les types de filtres introduisent un décalage constant pour toutes les fréquences. Attention : par décalage constant, on veut dire que le temps de parcours du filtre est identique pour toutes les fréquences. Si on regarde le déphasage, cela se traduit par un déphasage proportionnel à la fréquence. Par exemple, si le déphasage est de 20° à une fréquence de 5 KHz, alors il est de 40° pour 10 KHz, de 80° pour 20 KHz, de 800° pour 2000 KHz, etc. Ce temps de décalage est appelé le retard de groupe, nom qui traduit le fait que toutes les fréquences sont touchées de la même manière. Un signal envoyé sur un filtre ne sera pas modifié par le retard de groupe, vu que toutes les harmoniques du signal seront retardées de la même manière. Il n'implique donc aucune distorsion du signal d'entrée.
Si certains types n'introduisent que ce décalage de groupe, sans autres formes de retard supplémentaires, ce n'est pas le cas pour la majorité des filtres. Divers retards dépendant de la fréquence viennent s'ajouter au retard de groupe et ajoutent un déphasage dépendant de la fréquence. Une conséquence de cette approche se voit quand on envoie des signaux non-sinusoïdaux en entrée de tels filtres. Les diverses harmoniques du signal traversent le filtre à des vitesses différentes et ressortent chacune avec un délai différent de leur voisine. Les harmoniques ont chacune leur propre déphasage, ce qui donne un signal d'entrée déformé. Le résultat est une distorsion du signal, qui est d'autant plus importante que les retards dépendant de la fréquence sont importants.
La transmittance d'un filtre : propriétés mathématiques
[modifier | modifier le wikicode]De manière générale, la transmittance d'un filtre s'exprime avec une fraction, composée d'un numérateur et d'un dénominateur (respectivement, la tension d'entrée et de sortie), qui dépendent tous deux de la fréquence de la tension d'entrée.
Le numérateur et le dénominateur sont tous deux des polynômes, dont la fréquence d'entrée est la seule variable. De manière générale, on peut écrire la transmittance de tout filtre de cette manière :
L'ordre d'un filtre
[modifier | modifier le wikicode]L'exposant le plus élevé dans le dénominateur est appelé l'ordre du filtre. Par exemple, on dira que le filtre est d'ordre 2 si la fréquence est élevée au carré dans le dénominateur, d'ordre 4 si elle est élevée à la puissance 4, etc. Il a un rôle tout particulier à jouer, car elle décrit la sensibilité du filtre à la fréquence. Plus la puissance est élevée, plus le filtre aura un filtrage efficace. Par exemple, pour un filtre passe-bas, l'atténuation sera d'autant plus rapide que l'ordre du filtre est important. Par contre, plus l'ordre d'un filtre est élevé, plus il contient de composants électroniques : il est donc plus complexe, plus difficile à produire, plus coûteux, etc.
Pour un filtre du premier ordre, la transmittance est une équation qui dépend de la fréquence de coupure . Si vous étudiez les formules qui vont suivre, vous verrez qu'elles ressemblent aux formules obtenues pour les filtres RC et RL. Le fait est que les filtres RC et RL sont des filtres du premier ordre.
| Filtre passe-bas | |
|---|---|
| Filtre passe-haut |
La transmittance des filtres du second ordre est une équation quadratique qui contient deux constantes et , dépendantes du circuit, appelées respectivement facteur d'amortissement et facteur de qualité. Le facteur de qualité est défini comme le rapport entre la fréquence propre , celle où le gain est maximal, et la largeur de la bande passante. Le facteur d'amortissement est défini à partir du facteur de qualité, comme étant la moitié de son inverse. On a donc :
| Filtre passe-bas | |
|---|---|
| Filtre passe-haut | |
| Filtre passe-bande | |
| Filtre coupe-bande |
- Si vous étudiez les formules qui vont suivre, vous verrez qu'elles ressemblent aux formules obtenues pour le filtre RLC. Le fait est que le filtre RLC est du second ordre, à savoir que la fréquence est mise au carré dans l'équation de la transmittance.
Les zéros et pôles d'un filtre
[modifier | modifier le wikicode]On peut reformuler les formules pour la transmittance en se souvenant que tout polynôme peut être factorisé en utilisant ses racines. Ainsi, tout polynôme de la forme peut se reformuler comme suit : , avec les racines du polynôme. En reformulant ainsi les polynômes de la transmittance, on a :
Les racines du numérateur sont appelées les zéros et les racines du dénominateur sont appelées les pôles. Ce sont des nombres complexes, avec chacun une partie réelle et une partie imaginaire. Il est possible de placer ces pôles et zéros sur un plan complexe, ce qui donne le graphe des pôles d'un filtre. Il est très utilisé pour déterminer si certaines fréquences rendent le filtre instable. En effet, les pôles sont des valeurs pour lesquelles le dénominateur de la transmittance est nul, et où la transmittance est donc infinie. Si un pôle se situe sur la moitié gauche du graphe des pôles, cela n'a pas trop d'importance, vu qu'il s'agit de valeurs que l'on ne peut pas observer en réalité (une partie réelle négative signifie un gain négatif, chose qui n'a pas vraiment de sens). Mais la présence d'un pôle sur la partie droite est plus problématique. Si le pôle se situe sur l'axe des abscisses, la transmittance augmente exponentiellement jusqu'à ce que la fréquence atteigne ce pôle (où elle est alors infinie). Si elle est en dehors, cela signifie que le déphasage et/ou le gain peuvent devenir infinis et donc que le filtre est extrêmement instable.
Certains filtres n'ont pas de zéros du tout, du moins tant que la fréquence reste finie. De tels filtres sont appelés des filtres tous pôles. Pour de tels filtres, la transmittance peut tendre vers zéro, mais seulement quand la fréquence tend elle aussi vers zéro. En clair : on peut avoir . Cette condition à la limite impose qu'au-delà d'une certaine fréquence, la transmittance baisse. En conséquence, de tels filtres sont forcément des filtres de type passe-bas ou passe-bande, mais ne peuvent pas être des filtres passe-haut ou coupe-bande. Vu l'absence de zéros, la fonction de transfert de ces filtres est la suivante :
La décomposition d'un filtre en filtres plus simples
[modifier | modifier le wikicode]Reprenons maintenant à partir de l'expression suivante de la transmittance :
Il est possible de regrouper les termes par groupes de deux, ce qui donne :
En développant chaque produit, on peut réécrire la formule comme suit :
En clair, la transmittance de tout filtre peut s'exprimer comme le produit de termes de la forme , avec P1 et P2 deux polynômes du premier ou du second degré. La traduction en termes électroniques est que tout filtre peut se décomposer en filtres plus simples, du premier ou du second ordre. C'est d'ailleurs souvent ainsi que sont fabriqués les filtres d'un ordre > 2 : ils sont formés par assemblage de filtres du 1er/2nd ordre.
Les types de filtres en fonction de la formule mathématique de leur transmittance
[modifier | modifier le wikicode]
Suivant les propriétés mathématiques de ces polynômes, on peut distinguer plusieurs types de filtres. Dans cette section, nous allons voir une classification basée sur des propriétés mathématiques précises, qui distingue les filtres de Bessel, Butterworth, Tchebychev et Legendre. Nous utiliserons beaucoup le diagramme gain-fréquence dans ce qui suit, le fameux diagramme de Bode. On verra qu'à l’exception des filtres de Butterworth celui-ci présente des vagues en forme de morceaux de sinusoïdes sur le diagramme gain-fréquence.
| Type de filtre | Caractéristiques |
|---|---|
| Filtre de Bessel | Délai constant en bande passante |
| Filtre de Butterworth | Gain le plus constant possible dans la bande passante |
| Filtre de Tchebychev | Meilleure atténuation en dehors de la bande passante, mais transmittance fluctuante dans la bande passante |
| Filtre de Legendre | Graphe de transmittance sans fluctuations/ondulations et avec une forte pente au voisinage de la fréquence de coupure |
Les filtres de Butterworth
[modifier | modifier le wikicode]Les filtres de Butterworth ont un gain presque totalement constant sur toute la bande passante. En dehors de la bande passante, le gain diminue régulièrement avec la fréquence, mais à un rythme assez faible comparé aux autres filtres. Par exemple, un filtre peut avoir un gain qui diminue de 5 décibels à chaque fois que la fréquence est multipliée par 10, guère plus. Cela en fait des filtres qui éliminent mal les fréquences non-désirées.
Si on regarde le diagramme de Bode (relation gain-fréquence), celui-ci est plat dans la bande passante et a une forme de droite en dehors. Il y a une légère courbure autour de la fréquence de coupure, plus ou moins prononcée selon l'ordre du filtre. Quant au déphasage, il est minimal dans la bande passante, mais augmente progressivement en dehors, avant de se stabiliser pour les fréquences très éloignées de la bande passante.

Ci-dessous sont illustrés les diagrammes de Bode pour un filtre de Butterworth de type passe-bas et passe-haut.
 |
 |
La formule de la transmittance d'un tel filtre est la suivante :
- , avec n l'ordre du filtre.
Le gain qui correspond est donc le module de la transmittance, qui vaut :
- , avec n l'ordre du filtre.
À la fréquence de coupure, la transmittance et le gain sont donc de :
- et , avec n l'ordre du filtre.
Les filtres de Chebyshev
[modifier | modifier le wikicode]
Les filtres de Chebyshev ont un comportement inverse des filtres de Butterworth. Ils ont une chute rapide de transmittance dans la bande non-passante, ce qui en fait des filtres qui coupent bien les fréquences non-désirées, contrairement aux filtres de Butterworth. Par contre, la transmittance varie dans la bande passante, là où un filtre de Butterworth garde un gain constant. Si on observe ce qui se passe dans la bande passante, on voit que le gain oscille quand la fréquence augmente. Sur le graphe gain-fréquence ci-contre, on voit une sorte de sinusoïde déformée dans la bande passante, dont les vagues se font de plus en plus proches en approchant de la fréquence de coupure. Les vagues ont toutes la même hauteur, hauteur qui est minimisée dans le cadre des filtres de Chebyshev. Le nombre de cycles, de vagues sinusoïdales, est égal à l'ordre du filtre. Par exemple, le schéma ci-contre possède deux cycles ce qui fait qu'il s'agit d'un filtre d'ordre 2.
Précisons que le déphasage est maximal près de la fréquence de coupure pour de tels filtres.

La formule de la transmittance d'un tel filtre est la suivante :
- , pour .
- , pour .
- , pour .




























![{\displaystyle T(\omega )={\frac {T_{0}}{1+\zeta ^{2}\cdot \cos ^{2}\left[N\cdot \cos ^{-1}\left({\frac {\omega }{\omega _{0}}}\right)\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/455a92c8612e38d883f25c4bb91bec8f1ca00bed)

![{\displaystyle T(\omega )={\frac {T_{0}}{1+\zeta ^{2}\cdot \cosh ^{2}\left[N\cdot \cosh ^{-1}\left({\frac {\omega }{\omega _{0}}}\right)\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c510d5dfc802034dcd947d211a5744b4be08dc9e)


