Électronique/Les oscillateurs (générateurs de fréquence)
Les oscillateurs électroniques sont des circuits qui fournissent une tension périodique. Ils sont aussi appelés des générateurs de fréquence. Leur utilité principale est de créer un signal d'horloge, de forme sinusoïdale, carrée, triangulaire, etc. Mais ils peuvent avoir d'autres utilités, comme créer la porteuse pour un signal modulé en fréquence ou en phase. On distingue plusieurs types oscillateurs, suivant la forme du signal périodique créé.
- Les oscillateurs linéaires fabriquent un signal sinusoïdal. Leur nom est quelque peu trompeur, une sinusoïde n'étant pas un signal linéaire. Heureusement, on peut aussi les appeler oscillateurs harmoniques, nom qui trahit le fait qu'ils créent des sinusoïdes (des harmoniques).
- Les autres oscillateurs fabriquent des signaux carrés, triangulaires, ou autre. Pour les opposer aux oscillateurs linéaires, on les appelle improprement oscillateurs non-linéaires, ou encore générateurs de fonction, voire oscillateurs à relaxation.

Les oscillateurs harmoniques fournissent une tension sinusoïdale. Il en existe un très grand nombre et tous ne sont pas fabriqués sur le même modèle. Néanmoins, si on analyse le fonctionnement de tous les oscillateurs harmoniques, on peut remarquer qu'on peut les classer en deux grands types. Tous les oscillateurs appartiennent à une de ces deux catégories, qui décrivent le principe de fabrication de l'oscillateur. On distingue donc les oscillateurs à rétroaction et les oscillateurs à résistance négative.
Dans ce qui va suivre, nous allons d'abord voir les oscillateurs harmoniques à résistance négative, avant de passer aux oscillateurs à rétroaction, puis les oscillateurs à relaxation.
Les oscillateurs à résistance négative
[modifier | modifier le wikicode]
Les oscillateurs à résistance négative sont fabriqués en mettant en série un circuit résonant avec une résistance négative.
Une résistance négative n'est pas un composant électronique unique à proprement parler, mais un circuit qui simule une résistance un peu particulière, appelée résistance négative. Dans le cas qui nous intéresse, la résistance en question peut être aussi bien une résistance négative statique que dynamique. Dans le premier cas, on veut dire que la tension et le courant à ses bornes ne sont pas dans le bon. Pour une résistance normale, la tension et le courant sont des sens opposés : la tension va d'une borne à l'autre, le courant va dans le sens inverse. Mais pour une résistance négative, les deux sont dans le même sens. Pour une résistance dynamique négative, le courant qui passe dans la résistance diminue quand on augmente la tension, jusqu'à un certain point.
 |
 |
Le circuit résonant est un circuit qui se comporte approximativement comme un oscillateur en lui-même. Le cas le plus connu est le circuit LC, où un condensateur et une inductance sont placés en série/parallèle. Un autre exemple est un cristal de Quartz soumis à un échelon de tension. De tels circuits ont un comportement périodique, qui peut être utilisé pour fabriquer une tension sinusoïdale. Cependant, de tels circuits sont rarement parfaits : ils ont une résistance interne qui amortit leurs oscillations. Pour éliminer l’amortissement, il suffit de compenser leur résistance interne par quelque chose, ce quelque chose étant une résistance négative égale. En plaçant la résistance négative en série, on arrive à annuler la somme des deux résistances (interne et négative), ne laissant que le circuit résonant parfait, qui fonctionne comme un oscillateur.
Les oscillateurs (R)LC sans résistance négative
[modifier | modifier le wikicode]
Un circuit LC, composé d'une bobine et d'un condensateur en série/parallèle, est en soi un oscillateur isolé. La tension aux bornes d'un tel circuit est en effet égale à :
La tension mesurée aux bornes du condensateur est une tension alternative sinusoïdale et il en est de même aux bornes de la bobine, à cause de la loi des mailles. La tension et le courant sont illustrés dans la figure de droite. La tension sinusoïdale a une fréquence égale à :

Mais cela ne vaut que pour des oscillateurs idéaux, basés sur des bobines et des condensateurs idéaux. Mais dans la réalité, les bobines ont une résistance non-nulle. Il n'existe donc pas de circuit LC pur, dans la réalité. Tous les circuits LC réels se comportent comme des circuits RLC idéaux. Et quand on le soumet à une impulsion (un échelon de tension brutal, par exemple), un circuit RLC ne fournit pas de tensions sinusoïdale en sortie. À la place, la tension de sortie ressemble à une sinusoïde qui s'atténue avec le temps, une sinusoïde amortie. Une telle sinusoïde est illustrée ci-dessous. La vitesse d'amortissement de la sinusoïde dépend de la résistance, plus précisément du facteur d'amortissement du circuit qui est proportionnel à la résistance.

Pour supprimer l'amortissement, il faut éliminer la résistance. En compensant la résistance du circuit avec une résistance négative, on obtient bien un oscillateur. La résistance négative a juste à être placée en série du circuit (R)LC, avec une valeur de résistance exactement calibrée.

En guise de résistance négative, on peut utiliser divers montages ou composants électroniques. On peut utiliser les montages à AOP, des transistors câblés d'une manière bien précise, etc. Et chaque possibilité donne naissance à un oscillateur bien particulier.
L'oscillateur avec une résistance négative émulée par un AOP
[modifier | modifier le wikicode]Il est possible d'émuler une résistance négative par un montage à AOP. Les montages en question sont illustrés ci-dessous.
 |
 |
En utilisant un tel circuit dans un oscillateur à résistance négative, on obtient ce circuit :

L'oscillateur à diode Gunn
[modifier | modifier le wikicode]L'exemple qui suit, utilise une diode Gunn, un composant qui a une résistance dynamique négative. Nous n'en dirons pas plus sur ce composant pour le moment, tout ce qu'il y a à savoir est qu'elle a une résistance dynamique négative. La diode est placée en série du circuit (R)LC. Elle est choisie de manière à avoir une résistance exactement opposée à la résistance du circuit RLC. Le circuit en question est illustré ci-contre.
Notons que le circuit ne fonctionne que si une tension est placée de manière à charger le circuit (R)LC. Il faut donc ajouter un générateur de tension couplé à un interrupteur. L’interrupteur est fermé pour charger le circuit, et s'ouvre une fois l'oscillateur chargé. Le circuit complet est illustré ci-dessous.

Les oscillateurs à rétroaction
[modifier | modifier le wikicode]
Les oscillateurs du premier type sont les oscillateurs à rétroaction. Leur nom trahit le fait que ce sont des circuits à rétroaction, comme ceux que nous avons vu dans le chapitre sur la rétroaction. Et pour être précis, ce sont des circuits à rétroaction positive. Rappelons que ces circuits sont composé de deux circuits mis en boucle l'un avec l'autre. Le premier est ici un AOP, qui multiplie par son entrée. L'autre circuit fait la même chose, sauf que le coefficient est différent et est noté . Pour résumer, est le coefficient d'amplification de l'AOP, alors que est le coefficient d'amplification du circuit de rétroaction. Dans le cas présent, un oscillateur à rétroaction est basé sur un AOP mis en boucle avec un filtre passe-bande.
On pourrait croire que l'on peut réutiliser les acquis vus dans le chapitre sur la rétroaction, mais il n'en est rien. Dans le chapitre mentionné, nous avions parlé des oscillateurs stables, dans le sens où le circuit voit sa sortie se stabiliser à une valeur fixe. La transmittance d'un tel circuit est égal à :
Or, un oscillateur ne fonctionne pas en régime stable, mais en régime instable. En clair, sa transmittance doit être infinie, à savoir que sa sortie doit être finie pour une entrée nulle.
Pour cela, il faut que le produit . En conséquence, le filtre passe-bande est tel qu'il annule l'amplification de l'AOP : son est l'inverse de l' de l'AOP, ce qui fait que leur produit vaut 1. Un signifie que le gain d'un tour de la boucle (un passage par l'AOP, puis dans le circuit de rétroaction) est de 1 : le signal n'est ni amplifié, ni atténué lors d'un passage das la boucle.
Précisons que ce critère n'est réalisé que pour une fréquence bien définie, la fréquence du signal à produire. Pour les autres fréquences, le produit est inférieur à 1. En conséquence, la fréquence sélectionnée va rester, alors que toutes les autres fréquences vont progressivement être atténuées. Le circuit va donc reproduite la fréquence voulue, mais les autres fréquences seront supprimées.
Reste qu'un circuit à rétroaction est censé avoir une entrée. En théorie, on pourrait ajouter une entrée au circuit, qui envoie un signal quelconque. Mais les oscillateurs à rétroaction sont différents. Il n'y a pas nécessité d'avoir une entrée. En réalité, le fil en entrée de l'AOP subit toujours de petites variations de tension, liées à des perturbations électromagnétiques ou à des variations de tension aléatoires. Ces variations sont une forme de bruit, qui a diverses origines : bruit d'origine thermique lié au déplacement thermique des charges du métal, autres. Ce bruit est, comme tout signal, la superposition d'une infinité de fréquences, la fréquence voulue en faisant partie. La fréquence voulue sera alors amplifiée par l'AOP, passé au filtre passe-bande, et cela plusieurs fois de suite. Les autres fréquences finiront par être atténuées, ne laissant que la fréquence voulue.

Les oscillateurs RC et LC à rétroaction
[modifier | modifier le wikicode]Le filtre passe-bande utilisé peut être un circuit RC, un circuit LC, un filtre actif, voire un filtre fabriqué avec un cristal de Quartz. Les oscillateurs RC utilisent un réseau de résistances et de condensateurs comme filtre passe-bande. Les oscillateurs LC utilisent, quant à eux, un réseau d'inductances et de condensateurs. Ils sont plus rares et les plus connus sont les oscillateurs Coolpits et Hartley. Ils ont un circuit LC pour filtre passe-bande et l'amplificateur du montage est implémenté avec un transistor unique.
 |
 |
L'oscillateur de Wien
[modifier | modifier le wikicode]
L'oscillateur de Wien est fabriqué en couplant un montage non-inverseur à un réseau RC. Le réseau RC est composé d'un circuit RC série placé en série avec un circuit RC parallèle. Le circuit est illustré ci-contre. Le réseau RC agit comme un filtre passe-bande assez particulier. Le circuit RC série agit comme un filtre passe-haut, alors que le circuit RC parallèle agit comme un filtre passe-bas (il est alimenté par un courant, compte tenu de la configuration du circuit, ce qui lui permet d'agir comme un filtre passe-bas). L'ensemble du réseau RC agit donc comme un filtre passe-bande.
Le gain de boucle de ce circuit est égal au produit de deux termes : le gain du montage non-inverseur et le gain du réseau RC.
Le gain du montage non-inverseur est égal à :
Pour le réseau RC, la transmittance dépend de l'impédance du circuit série , et de celle du circuit parallèle . En analysant le circuit, on trouve que sa transmittance est égale à :
Le gain de boucle vaut donc :
En remplaçant les valeurs d'impédances par leur valeur respective, on trouve :
Pour permette une oscillation, il faut que le déphasage entre entrée et sortie de la boucle soit nul. Cela signifie que la transmittance doit être un nombre réel. Pour cela, il faut que , ce qui n'est possible que pour . À cette fréquence, on a :
Pour que , il faut que .
L'oscillateur à déphasage
[modifier | modifier le wikicode]
L'oscillateur à déphasage couple un AOP à gain négatif à un réseau RC qui sert de filtre passe-bande.
Par AOP à gain négatif, on veut simplement dire que l'AOP amplifie la tension d'entrée et change son signe. Dans le cas le plus simple, l'AOP à gain négatif est implémenté par un simple montage inverseur. Le gain d'un tel montage est négatif, égal à :
Le fait que l'AOP ait un gain négatif signifie qu'il déphase le signal d'entrée de 180°. Le réseau RC doit donc avoir lui aussi in déphasage de 180°, pour que le déphasage de la boucle soit nul. Sans quoi, il ne peut pas y avoir d'oscillations. Le réseau RC est en trois sections, trois circuits RC placés en série l'un de l'autre. Le nombre de cellules RC mises en série n'est pas anodin : le circuit ne fonctionnerait pas avec moins de trois cellules. En effet, un réseau RC à une ou deux cellules en série ne peut pas avoir de déphasage égal à 180°. il faut absolument au moins trois cellules pour cela.
La fréquence d'un tel circuit est de :
L'oscillateur à Quartz
[modifier | modifier le wikicode]Les oscillateurs RC et LC sont utilisés pour fournir des signaux de faible fréquence, de moins de 100 Mhz. Difficile de les utiliser au-delà, en raison de la taille des condensateurs et des résistances. Pour des fréquences plus élevées, on doit utiliser des oscillateurs à Quartz.
Les cristaux de Quartz comme filtres passe-bande
[modifier | modifier le wikicode]Avec ceux-ci, le filtre passe-bande, le circuit de rétroaction, est composé d'un cristal de Quartz qui se comporte comme un filtre passe-bande mécanique. Cela vient d'une des propriétés des cristaux de Quartz : la piézoélectricité. Un matériau piézoélectrique, comme le Quartz, se déforme en réaction à un champ électrique. Et réciproquement, leur déformation déplace leurs charges internes et un champ électrique apparait sur les faces du cristal. Si on applique une tension périodique sur le cristal, il va se déformer et ces déformations vont elles-mêmes générer une tension périodique en réponse. Le cristal se comporte donc comme un composant, qui prend en entrée une tension et fournit en sortie une autre tension.

Le cristal de Quartz se comporte comme un circuit RLC avec une capacité en parallèle, comme illustré ci-contre. Sachant qu'un filtre RLC est un filtre passe-bande, le cristal se comporte comme un filtre passe-bande. La transmittance inverse d'un cristal de Quartz est donc égale à :
En éliminant l'influence de la résistance, on trouve une transmittance de :
On peut reformuler l'équation précédente comme suit :
L'analyse des équations précédentes nous dit que le cristal a deux fréquences de résonance, deux fréquences d'oscillation possibles.
- Une résonance série égale à :
- Une résonance parallèle égale à :
Si on étudie l'impédance du cristal en fonction de la fréquence, on obtient un spectre semblable à celui-ci :
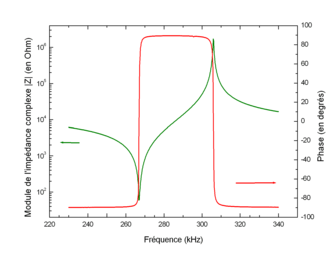
L'oscillateur de Pierce
[modifier | modifier le wikicode]L’oscillateur à Quartz le plus souvent abordé dans les cours d'électronique est l'oscillateur de Pierce. Dans celui-ci, l'amplificateur est implémenté avec une porte logique NON. Le filtre passe-bande est réalisé avec un cristal de Quartz en parallèle avec une résistance, auquel on a couplé deux condensateurs. Le circuit est illustré ci-dessous.

Les oscillateurs non-linéaires
[modifier | modifier le wikicode]Les oscillateurs non-linéaires fournissent une tension de sortie qui n'est pas sinusoïdale, mais carrée, triangulaire ou autre. Globalement, les oscillateurs non-linéaires sont fabriqués à partir de blocs de base, appelés multivibrateurs. Ces derniers se subdivisent en plusieurs types, qui sont appelés les circuits astables, bistables et monostable. Un exemple de circuit bistable n'est ni plus ni moins que le montage comparateur à seuil, que nous avions vu dans le chapitre sur les montages à amplificateurs opérationnels. N'hésitez pas à relire la section associée si vous avez oublié comment fonctionne ce circuit. Nous aurons à l'utiliser dans les circuits qui vont suivre.
Les types principaux d'oscillateurs non-linéaires
[modifier | modifier le wikicode]Les oscillateurs à relaxation sont composés de deux circuits : un circuit de charge et un circuit d'accumulation. Le circuit d'accumulation peut accumuler des charges électriques et se charger/décharger jusqu'à une certaine limite. Le circuit de charge s'occupe à intervalle régulier de remplir, puis de vider le circuit d'accumulation, à une fréquence bien définie. Le circuit d'accumulation est composé d'un condensateur ou d'une inductance, parfois des deux. Le circuit de charge est composé soit d'un AOP, soit d'un transistor, soit d'un comparateur, soit d'un relai, soit d'une résistance négative, etc. La fréquence du circuit dépend de la constante de temps du circuit d'accumulation (du produit RC ou RL).
D'autres oscillateurs non-linéaires sont fabriqués en couplant un oscillateur sinusoïdal avec un circuit qui transforme celle-ci en signal carré/triangulaire/autre. Pour obtenir un signal carré, il faut coupler l'oscillateur avec un circuit dit bistable. Un circuit bistable est un circuit dont la sortie ne peut prendre que deux valeurs : une tension maximale positive, ou une tension minimale nulle/négative. Le passage d'une tension à l'autre se produit en fonction de ce qu'on place sur l'entrée. Un exemple de circuit bistable est le comparateur à un seuil, vu il y a quelques chapitres. Pour rappel, le comparateur à un seuil est un circuit qui fournit une tension positive si la tension d'entrée dépasse un certain seuil, et une tension nulle/négative en dessous de ce seuil. Le comparateur à deux seuils, lui aussi vu il y a quelques chapitres, est aussi un circuit bistable. En couplant un oscillateur sinusoïdal avec un comparateur à un ou deux seuils, on obtient donc un signal carré.
Le cas le plus simple est celui où on couple un oscillateur linéaire avec un comparateur à un seuil. Si le signal d'entrée est une sinusoïde parfaite, alors le signal de sortie sera un signal carré presque parfait. Dans le détail, plus le slew rate de l'AOP est bon, plus le signal sera proche d'un signal carré. Si le signal n'est pas parfait, mais a de petites sautes brutales, l'usage d'un comparateur à un seul seuil peut poser quelques problèmes : les sautes du signal d'entrée peuvent se voir sur la sortie. Si une petite variation fait passer la tension sous le seuil ou au-dessus, alors le signal de sortie va s'inverser. Pour mitiger ce problème, on peut remplacer le comparateur à un seuil par un comparateur à deux seuils. Les sautes brutales de la tension d'entrée ne se voient plus systématiquement sur la sortie. Pour cela, il faut qu'elles passent sous le second seuil, qui est plus bas que le seuil unique du comparateur à un seuil.
Le multivibrateur astable
[modifier | modifier le wikicode]
L'oscillateur que nous allons voir dans cette section est construit à partir d'un circuit bistable, comme un comparateur à deux seuils. En couplant le circuit bistable avec un circuit RC série, on obtient l'oscillateur. Le circuit bistable peut s'implémenter de beaucoup de manières différentes, que ce soit avec des AOP, des transistors, voire d'autres composants moins bien connus.
Les multivibrateurs astables à AOP
[modifier | modifier le wikicode]Pour le cas qui nous intéresse, le circuit bistable en question est un vulgaire comparateur à deux seuils, fabriqué avec des AOP. Le circuit est donc composé d'un AOP avec deux boucles de rétroaction : une boucle de rétroaction positive pour le montage comparateur à deux seuils, et une boucle de rétroaction négative avec le circuit RC. Dans le circuit RC, le condensateur sert de circuit d'accumulation, la résistance n'étant utile que comme intermédiaire à travers lequel on charge/décharge le condensateur. Le circuit est illustré ci-contre, ainsi que ci-dessous.
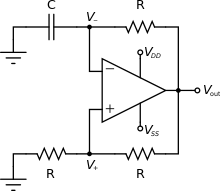 |
 |
Pour comprendre comment fonctionne un tel circuit, imaginons que la sortie du comparateur soit égale à la tension maximale. Dans ce cas, on a une tension positive en entrée du circuit RC, ce qui fait que le condensateur se charge jusqu'à atteindre cette tension. Cependant, la sortie du circuit RC est reliée à l'entrée négative de l'AOP (via la boucle de rétroaction négative). En conséquence, l'augmentation de la tension aux bornes du condensateur se répercute sur l'entrée du comparateur. Quand la tension d'entrée atteint le bon seuil, le comparateur bascule et sa tension de sortie passe dans le négatif, à sa tension minimale. Le comportement du circuit s'inverse alors. Le condensateur est soumis à une tension plus faible que celle à ses bornes, ce qui fait qu'il se vide. La tension à ses bornes diminue, ce qui se répercute à l'inverse sur l'entrée du comparateur. La tension d'entrée du comparateur augmente alors progressivement, au fur et à mesure que le condensateur se vide. Quand la tension d'entrée atteint le second seuil, le circuit rebascule. Et la boucle est bouclée, le circuit recommence de zéro.
La fréquence du circuit est égale à :
- , avec .
Un tel circuit fournit une tension carrée d'un côté du circuit, mais une tension triangulaire déformée sur l'autre côté. En sortie du comparateur, on observe un signal carré, signe que la sortie du comparateur bascule entre sa tension maximale et sa tension minimale d'un seul coup. En sortie du réseau RC, on trouve la tension triangulaire, illustré ci-dessous. Vous reconnaîtrez peut-être que chaque morceau de la courbe ressemble à une courbe de charge ou de décharge d'un condensateur, ce qui est compatible avec ce qu'on a dit précédemment.

En modifiant quelque peu le circuit précédent, on peut obtenir une tension triangulaire en lieu et place de la tension de charge/décharge exponentielle. Pour cela, il faut remplacer le circuit RC série par un montage intégrateur. Ce faisant, le condensateur accumule des charges, mais la tension de sortie du montage est le produit : tension de sortie du comparateur temps. Cette quantité augmente linéairement, ce qui lui donne un aspect de droite sur le graphique. En clair, les courbes de charge/décharge sont remplacées par des segments, ce qui en fait une tension triangulaire.
Les multivibrateurs astables à transistors
[modifier | modifier le wikicode]Il est possible d'implémenter le circuit astable en utilisant des transistors, des composants électroniques qui agissent comme des amplificateurs non-linéaires. Une implémentation d'un circuit astable est illustrée ci-dessous. Mais comprendre le fonctionnement de ce circuit demanderait de connaître en détail le fonctionnement d'un transistor, ce qui sera vu dans les chapitres suivants. Nous n'en parlerons pas ici, donc.

Les multivibrateurs astables à lampe à néon
[modifier | modifier le wikicode]
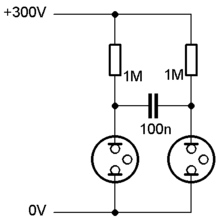
Comme autre exemple, il était autrefois possible de fabriquer des oscillateurs avec des lampes à néon ! En couplant celles-ci avec un circuit RC série, on obtenait un oscillateur assez rustique, mais qui marchait. Le fonctionnement de ce montage est lié au fonctionnement de la lampe à néon, et plus précisément à ce qu'on appelle l'effet Pearson–Anson. Celui-ci dit que si l'on connecte une lampe à néon en parallèle avec un condensateur, et qu'on alimente le tout avec un courant continu, alors la tension de sortie du montage oscille spontanément. Le circuit lampe à néon + condensateur se comporte donc comme un oscillateur. Pour obtenir le courant continu, on peut utiliser un générateur de courant continu, ou alors une tension continue en série avec une résistance.

La tension de sortie d'un tel oscillateur à lampe à néon était une tension presque triangulaire, semblable à la tension de sortie non-lissée de l'oscillateur astable à AOP. Il faut dire que le fonctionnement du montage est presque identique. La lampe à néon fonctionne comme une résistance variable à deux seuils. Pour faire simple, prenons le cas où la tension à ses bornes augmente progressivement. Dans ce cas, elle a une résistance élevée au-dessous d'une tension seuil, mais une résistance plus faible au-delà de la tension seuil. Quand la tension à ses bornes descend, c'est la même chose, sauf que le seuil est différent. Les seuils pour faire commuter la résistance sont respectivement élevé pour la faire baisser, faible pour la faire augmenter. Quand on connecte le montage, le condensateur est vide et la tension à ses bornes est basse. Vu que cette tension alimente la lampe à néon, la lampe à néon ne conduit pas et le condensateur se charge à travers la résistance. Mais quand la tension du condensateur dépasse la tension seuil haute, la lampe se met à conduire et le condensateur se décharge à travers la lampe à néon. La tension chute alors et descend tant qu'elle reste supérieure à la tension seuil basse. Une fois cette tension seuil basse atteinte, la lampe cesse de conduire le courant. Et rebelote : un nouveau cycle commence.

Il était même possible d’enchaîner plusieurs lampes à néon pour améliorer la tension en sortie de l'oscillateur.
 |
 |
















![{\displaystyle \alpha \beta ={\frac {1+R_{4}/R_{3}}{3+j\left[RC\cdot \left(\omega +{\frac {1}{\omega }}\right)\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65f91d5f0a68a4d82fc011011f80be7629d03c9c)








![{\displaystyle {\frac {1}{T(\omega )}}=j\omega C_{0}+{\frac {(j\omega )^{2}+(1/L\cdot C_{1})}{(j\omega )^{2}+\left[(C_{0}+C_{1})/(L\cdot C_{0}\cdot C_{1})\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1a2b2628d45877a9ff5c204e0d9f2ff01a63cc1)


![{\displaystyle T=2\cdot RC\cdot \ln \left[{\frac {1+\beta }{1-\beta }}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0d155461011a1b72d882a7874163d8e95d0c285)

