Électronique/Version imprimable
Une version à jour et éditable de ce livre est disponible sur Wikilivres,
une bibliothèque de livres pédagogiques, à l'URL :
https://fr.wikibooks.org/wiki/%C3%89lectronique
Les amplificateurs électriques
Dans ce chapitre, nous allons étudier les amplificateurs opérationnels, à savoir les composants qui amplifient une tension ou un courant. Il en existe de nombreux types, mais tous sont des quadripôles (pour rappel, des composants avec quatre broches) : deux broches servent d'entrée et reçoivent une tension ou un courant, alors que les deux autres fournissent une tension ou un courant en sortie. On distingue les amplificateurs selon qu'ils amplifient la tension d'entrée, le courant, ou la puissance.
- Pour une amplification en tension, la tension de sortie est un multiple de celle d'entrée.
- Pour une amplification en courant, le courant fournit en sortie est un multiple de celui envoyé sur l'entrée.
- Certains amplificateurs font à la fois de l'amplification de tension et de courant : on parle d'amplification de puissance.
La relation entre tension d'entrée et de sortie
[modifier | modifier le wikicode]
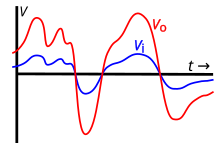
À noter que si l'entrée et la sortie sont proportionnelles, courants et tension de sortie ne peuvent cependant pas dépasser une valeur maximale (souvent proche de la tension ou du courant d'alimentation). Le schéma ci-contre illustre la relation entre entrée et sortie, dans le cas d'un amplificateur en tension. On voit qu’en-deça d'une certaine tension d'entrée, tension d'entrée et de sortie sont proportionnelles. On dit alors que l'amplificateur est en régime linéaire, ce qui trahit la relation entre entrée et sortie. Mais au-delà d'une certaine tension d'entrée, la tension de sortie sature et reste à sa valeur maximale, quelle que soit la tension d'entrée. On dit que l'amplificateur est en régime de saturation, ce qui trahit le fait que la tension de sortie "sature".
Le régime linéaire : gain et transmittance
[modifier | modifier le wikicode]Commencons par étudier le régime linéaire, le régime non-linéaire étant pour plus tard. Si l'on envoie une tension sinusoïdale sur l'entrée d'un amplificateur, la sortie fournit une tension sinusoïdale de même fréquence, mais dont la phase et l'amplitude peuvent être différentes (même chose pour un courant, mais nous utiliserons des tensions dans ce qui suit, pour simplifier les explications). On peut calculer le rapport entre la tension d'entrée et la tension de sortie . Celui-ci s'appelle la fonction de transfert, bien que le terme transmittance soit aussi très utilisé, et se note . La transmittance d'un amplificateur n'est évidemment pas la même selon la fréquence, ce qui traduit le fait que certaines fréquences sont atténuées et d'autres amplifiées. Voici sa formule de calcul.
Si on utilise des phaseurs pour les tensions d'entrée et de sortie, leur rapport est un nombre complexe, qui dépend de la fréquence du signal d'entrée/sortie. La transmittance ainsi calculée est appelée la transmittance complexe et se note .
Vu qu'il s'agit d'un nombre complexe, la transmittance possède un module et un argument, dont les interprétations sont les suivantes :
- L'argument est le déphasage entre signal de sortie et d'entrée.
- Le module est le rapport entre amplitudes d'entrée et de sortie. Il porte le nom d'amplification. Elle n'est évidemment pas la même selon la fréquence, ce qui traduit le fait que certaines fréquences sont plus amplifiées que d'autres.
Il est fréquent d'utiliser des diagrammes qui relient l'amplification/atténuation à la fréquence. Analyser ces diagrammes est cependant assez compliqué si l'on utilise une échelle linéaire. Par exemple, la courbe tracée par un simple condensateur ou une bobine donnent une courbe exponentielle. Pour éviter un tel écueil, il est d'usage d'utiliser une courbe logarithmique, histoire que l'amplification causée par les récepteurs non-linéaires (condensateur et bobine) donnent des droites. Pour cela, on calcule une fonction dérivée du logarithme de l'amplification : le gain. Celui-ci vaut :
Les non-linéarités : distorsion et bruit
[modifier | modifier le wikicode]
Un amplificateur n'est pas un composant parfait et sa linéarité n'est qu'une approximation. Dans le monde réel de la réalité véritable, les amplificateurs ont de petites imperfections qui rendent la relation sortie-entrée non-linéaire. Dans la plupart des cas, cette non-linéarité est négligeable et ne se ressent pas. Mais pour certaines applications ou certains signaux, la non-linéarité devient sensible et commence à poser des problèmes. Les sources de non-linéarité sont variables, mais leur résultat est le même : le signal d'entrée et le signal de sortie n'ont pas la même forme. Cela veut dire que si l'on envoie une sinusoïde en entrée, la sortie n'est plus une sinusoïde. Le signal subit ce qu'on appelle une distorsion. À la distorsion, il faut ajouter du bruit, à savoir des variations aléatoires du signal de sortie, causé par divers mécanismes physiques.
Le premier type de distorsion est lié au fait que des sinusoïdes de fréquences différentes ne sont pas amplifiées de la même manière (certaines le sont plus que d'autres). Or, le théorème de Fourier nous dit que tout signal est composé d'une somme de sinusoïdes et de cosinusoïdes. Si les différentes sinusoïdes d'un signal ne sont pas amplifiées de la même manière, le signal de sortie ne ressemblera pas au signal d'entrée. Ce phénomène est appelé la distorsion d'amplitude. La distorsion de phase est similaire, sauf que la phase des sinusoïdes est décalée par l'amplificateur, chaque sinusoïde l'étant d'une manière différente. Les différentes sinusoïdes se déphasent progressivement, ce qui fait que le signal d'entrée ne ressemble plus au signal de sortie. Ces deux formes de distorsion ont une même cause : la transmittance varie selon les fréquences (que ce soit son module ou son argument). Une conséquence est que ces distorsions ne touchent pas les sinusoïdes pures : un signal sinusoïdal en entrée donne une sinusoïde en sortie. Seuls les signaux complexes, avec des harmoniques, sont déformés et distordus.
En temps normal, pour des entrées assez faibles, la saturation ne pose pas de problèmes. Mais si l'entrée devient trop importante, la sortie sature. Par exemple, prenons le cas d'un signal sinusoïdal, qu'on envoie en entrée d'un amplificateur. Si le signal d'entrée est assez faible, la tension d'entrée restera dans le régime linéaire et la tension de sortie est elle aussi une sinusoïde. Mais si le signal d'entrée est assez importante, elle peut passer dans le régime de saturation : la sortie ne donne alors pas une sinusoïde, mais un signal déformé du fait de la saturation. Ce phénomène porte un nom : on l'appelle la distorsion harmonique.
Les catégories d'amplificateurs selon leur étage de sortie
[modifier | modifier le wikicode]
Il existe de nombreuses classifications pour les amplificateurs électroniques, qui catégorisent ceux-ci selon des critères assez variés. L'une d'entre elle se base sur ce qu'il advient du signal en sortie de l'amplificateur, quand on envoie un signal sinusoïdal sur l'entrée différentielle. Le signal de sortie peut alors être : soit sinusoïdal, soit ne conserver que les tensions positives (ou négatives), soit ne garder que les tensions au-delà d'une tension seuil positive ou négative. Cela donne quatre classes principales, appelées classes A, B, AB et C. Il existe des classes plus marginales, appelées D, E, F, G, et encore d'autres, mais nous les aborderons pas ici. Les quatre classes A, B, AB et C sont illustrées ci-contre et ci-dessous.
- Les amplificateurs de classe A donnent un signal non-déformé en sortie : une sinusoïde en entrée reste une sinusoïde.
- Les amplificateurs de classe B ne gardent que les tensions positives (ou négatives, selon l'amplificateur) et mettent à zéro la tension quand l'entrée devient négative (réciproquement positive).
- Les amplificateurs de classe AB et C mettent la tension de sortie à zéro quand elle dépasse un seuil de tension. La différence est que :
- les amplificateurs de classe AB ont une tension de seuil négative ;
- les amplificateurs de classe C ont une tension de seuil positive.
 |
 |
 |
 |
On peut reformuler les classes précédentes en se basant sur la durée durant laquelle l'amplificateur amplifie réellement le signal. Partons du principe qu'on envoie une sinusoïde de période P sur l'entrée. Les amplificateurs n'amplifient le signal que sur une portion précise de la période (sauf les amplificateurs de classe A, qui amplifient tout le temps). Quand ils mettent la sortie à 0, ils ne l'amplifient pas. On peut alors dire que tel amplificateur amplifie le signal durant 50% de la période, tel autre durant 100%, celui-ci à peine 20% de la période P, etc.
- Un amplificateur de classe A amplifie le signal sur 100% de la période du signal d'entrée.
- Un amplificateur de classe B amplifie le signal sur 50% de la période du signal d'entrée (quand la tension est positive sur certaines amplificateurs, ou négative sur d'autres).
- Un amplificateur de classe AB amplifie le signal pour une durée comprise entre 50 et 100% de la période du signal d'entrée.
- Un amplificateur de classe C amplifie le signal pour une durée comprise entre 0 et 50% de la période du signal d'entrée.
| Classe | % de période | Description |
|---|---|---|
| Classe C | 0-50% | Amplifie durant une fraction de la demi-période positive/négative (selon l'amplificateur). |
| Classe B | 50% | Amplifie durant la demi-période positive/négative (selon l'amplificateur). |
| Classe AB | 50-100% | Amplifie durant la demi-période positive/négative (selon l'amplificateur) et une fraction de l'autre demi-période. |
| Classe A | 100% | Amplifie durant toute la période. |
Les amplificateurs opérationnels
Dans le chapitre précédent, nous avons vu les amplificateurs, au sens général du terme. Dans ce chapitre, nous allons voir une classe particulière d'amplificateurs : les amplificateurs opérationnels (AOP). Ils sont très utilisés de nos jours, et l'étaient encore plus du temps des calculateurs analogiques, avant l’invention de l'informatique. De nos jours, ils sont à la base de presque tous les circuits analogiques, que ce soit les régulateurs de tension, les oscillateurs électriques, les générateurs de fréquence, les servomoteurs (des circuits qui commandent un moteur) et bien d'autres. Ils sont formés de transistors, de résistances, ou d'autres composants du genre, mais on ne se préoccupera pas de ce qu'il y a à l'intérieur pour le moment.
Un AOP a plusieurs broches : des broches d'alimentation symétriques par rapport à la masse sur lesquelles placer VCC et son inverse (-VCC), une sortie (ce qui est normal) et deux entrées (ce qui est moins intuitif). Il existe deux symboles pour représenter les AOPs : un dit américain et un autre dit européen. Les deux notations sont données dans le schéma ci-dessous.

L'AOP réel
[modifier | modifier le wikicode]La présence de deux entrées s'explique par le fait qu'un AOP est ce que l'on appelle un amplificateur différentiel : il amplifie la différence entre deux tensions. Il prend les deux tensions d'entrée, soustrait la seconde à la première, et amplifie le résultat. Le coefficient d'amplification est appelé le gain différentiel de l'AOP, ou encore le gain en boucle ouverte. Si les deux tensions sont égales, l'AOP fournit une tension nulle, propriété appelée rejet du mode commun. Les tensions sur les deux broches d'entrée sont notées et , alors que la tension de sortie est notée . Pour un AOP, on a :
- , avec le gain différentiel de l'amplificateur.
 |
 |
La relation entre entrées et sortie
[modifier | modifier le wikicode]Un AOP présente quelques propriétés qui sont des défauts pour l'électronicien. Pour comprendre ces défauts, nous allons voir en premier lieu les défauts qui apparaissent en courant continu. Nous allons repartir de l'équation vue plus haut, qui décrit le fonctionnement idéal d'un AOP et l’améliorer pour rendre compte de ces défauts :
- , avec le gain différentiel de l'amplificateur.

Un premier défaut est que, pour , la tension de sortie est non-nulle. La tension de sortie obtenue sous ses conditions, à savoir quand les deux entrées sont mises à la masse, est appelée la tension d'offset. Elle peut être positive ou négative : tout dépend de l'AOP utilisé. En temps normal, elle vaut entre 1 mV et 5 mV, guère plus. Elle a pour origine la structure interne de l'AOP, qui est composé de transistors et de composants passifs, qui sont loin d'être parfaits. Notons que la tension d'offset peut varier selon la température, ce qui fait qu'elle est souvent difficile à corriger via un circuit quelconque.
- , avec la tension d'offset.
Ensuite, il faut ajouter l'influence de la tension en mode commun (la moyenne arithmétique des deux tensions d'entrée). Celle-ci est aussi amplifiée et se retrouve dans la tension de sortie. Le coefficient d'amplification lié à la tension en mode commun est appelée le gain en mode commun.
- , avec le gain en mode commun.
Si on note la tension différentielle et la tension en mode commun , on a une version plus simple de l'équation qui est :
| Mesure du gain en mode commun |
|---|
| Si on place la même tension sur les deux entrées et , on a :
En prenant une tension de 1 Volt, la tension de sortie est égale au gain en mode commun. |
| Mesure du gain différentiel |
| Si on place une tension sur une borne et son opposée sur l'autre, on a alors :
En utilisant une tension de 0,5 Volts, la sortie est égale au gain en mode différentiel. |
On peut reformuler l'équation en utilisant une grandeur appelée le taux de rejet en mode commun, qui est égal à :
On a alors :
Les impédances et courants d'entrée/sortie
[modifier | modifier le wikicode]
Les entrées d'un AOP réel sont traversées par un courant, même quand on n'y place aucune tension dessus. Si on place les deux entrées à la masse, on observera un courant d'entrée sur l'entrée et un autre sur l'entrée , qui seront notés et . Les électroniciens utilisent la moyenne de ces deux courants, , auxquels ils donnent le nom de courant de polarisation. Ils utilisent aussi la différence entre ces deux courants, , qui porte le nom de courant d'offset.

Enfin, précisons que l'AOP réel dispose d'une impédance de sortie non-nulle, ainsi que de plusieurs impédances d'entrée (une par entrée et une pour la liaison entre les deux). Le schéma ci-dessous montre quelles sont ces impédances et comment elles sont reliées aux différentes entrées. On voit qu'il existe une impédance pour chaque entrée, qui relie celle-ci à la masse. On trouve aussi une impédance d'entrée située entre les deux entrées, qui porte le nom d'impédance d'entrée différentielle. Chaque impédance d'entrée est constituée d'une résistance en parallèle avec un condensateur, ce qui a des implications sur le fonctionnement de l'AOP à haute fréquence. Mais laissons cela pour plus tard.

La bande passante d'un AOP
[modifier | modifier le wikicode]En courant alternatif, d'autres défauts font leur apparition. Le premier d'entre eux est que le gain différentiel varie avec la fréquence. Plus précisément, le gain différentiel diminue quand la fréquence augmente, les exceptions étant très rares. On peut mettre cela en équation assez simplement, avec la formule suivante (que nous étudierons plus en détail dans le chapitre sur les filtres électroniques) qui exprime la gain en nombre complexe :
- , avec le gain en courant continu (f = 0), f la fréquence du signal d'entrée, et une fréquence particulière appelée fréquence de coupure.

Qui plus est, le gain et la fréquence de coupure sont reliés entre eux : plus le gain est grand, plus la fréquence de coupure sera basse. Pour le dire autrement, la bande passante d'un AOP varie selon le gain configuré.
 |
 |
La vitesse de balayage
[modifier | modifier le wikicode]
Un autre défaut se manifeste pour des signaux de fréquence élevée : l'amplificateur n'arrive pas à suivre le signal d'entrée, qui va trop vite pour lui. La raison est que la tension de sortie ne peut pas augmenter soudainement et met un certain temps avant d'atteindre la valeur voulue. Si on place un front de tension (la tension passe immédiatement de 0 à 5 Volts, par exemple), la tension de sortie va monter progressivement et former une sorte de rampe, comme illustré ci-contre. Pour résumer, les variations de la tension de sortie ne sont pas instantanées. La vitesse à laquelle la tension de sortie évolue est appelée la vitesse de balayage (slew rate en anglais). Elle est définie par :
Si la tension d'entrée évolue plus vite que la vitesse de balayage (en clair, si ), le signal de sortie est alors déformé. Pour un signal sinusoïdal, cela arrive au-delà d'une certaine fréquence. Pour la calculer, prenons ce signal :
On a alors la dérivée suivante :
La vitesse maximale du signal est donc de . Si la vitesse de balayage est inférieure à cette valeur maximale, le signal sera déformé. Alors qu'il ne subira pas de distorsion liée à la vitesse de balayage dans le cas contraire. On sait donc que la fréquence maximale est celle pour laquelle :
- , avec la vitesse de balayage.
Ce qui donne :
L'AOP idéal (parfait)
[modifier | modifier le wikicode]L'AOP réel est un circuit très complexe, dont les propriétés ne sont pas forcément importantes quand on étudie des circuits électroniques. Pour se simplifier la vie, les électroniciens utilisent un modèle simplifié d'AOP appelé AOP parfait, ou encore AOP idéal. Un tel AOP respecte plusieurs conditions irréalistes, mais qui permettent de simplifier l'étude de nombreux circuits électroniques. Celui-ci diffère de l'AOP réel sur de nombreux points. Bon nombre des propriétés de l'AOP réel sont négligées dans l'AOP idéal, ce qui simplifie les calculs et l'analyse. Dans cette section, nous allons voir en quoi l'AOP parfait diffère de l'AOP réel.

Pour rappel, les propriétés principales de l'AOP réel sont résumées dans le schéma de droite. Elles regroupent :
- Des impédances d'entrée assez fortes.
- Une impédance de sortie faible, mais non-nulle.
- Des courants de sortie et d'entrée liés aux impédances précitées.
- Une tension d'offset (non-représentée sur le schéma ci-contre).
- Un gain en mode commun faible, mais non-nul.
- Un gain différentiel assez important, qui diminue avec la fréquence.
- Une vitesse de balayage finie (non-représentée sur le schéma ci-contre).
Les simplifications de l'AOP parfait
[modifier | modifier le wikicode]Une première simplification est de négliger les impédances d'entrée et de sortie. Sur un AOP réel, les impédances d'entrée sont très grandes, alors que l'impédance de sortie est très faible. Pour donner quelques chiffres, l'impédance d'entrée d'un AOP réel est comprise entre et Ohms, ce qui est énorme. Dans ces conditions, on peut considérer que l'impédance est infinie. En clair, les entrées se comportent comme des morceaux de fils non-reliés au reste du circuit interne de l'AOP : il n'y a pas de courants d'entrée. On peut aussi négliger l'impédance de sortie, qui est très faible. Pour un AOP réel, elle est comprise entre 10 et 500 Ohms, rarement plus. Autant ne pas en tenir compte dans les calculs et la supposer nulle. À noter que cette simplification vaut tant que l'on relie l'AOP à des résistances de l'ordre du millier d'Ohm ou plus.

Une autre simplification est de négliger le gain en mode commun et la tension d'offset. La tension de sortie d'un tel AOP est toujours égale à , sans que le courant de sortie ait une quelconque importance. Un AOP est donc une source de tension parfaite, sans impédances parasites. Il est aussi d'usage de supposer que le gain d'un AOP parfait est très grand, suffisamment grand pour être infini. Cela veut dire que la tension de sortie sature entre la tension d'alimentation et son opposé. La caractéristique / d'un AOP parfait est illustrée ci-dessous.

Enfin, le gain différentiel est supposé identique pour toutes les fréquences, ce qui fait qu'il a une bande passante infinie.
Résumé
[modifier | modifier le wikicode]Les propriétés d'un AOP réel et d'un AOP idéal sont comparées ci-dessous. Toutes ces simplifications permettent de simplifier l'étude des circuits qui vont suivre.
| Propriété | AOP idéal | AOP réel |
|---|---|---|
| Impédance d'entrée | Infinie | Finie |
| Impédance de sortie | Nulle | Non-nulle |
| Vitesse de balayage (slew rate) | Infinie | Finie, non-négligeable |
| Bande passante | Infinie | Finie |
| Gain différentiel | Infini (ou du moins très grand) | Fini, non-négligeable |
| Gain en mode commun | Nul | Non-nul |
| Tension d'offset | Nulle | Non-nulle |
La rétroaction linéaire et l'amplification
Les AOP sont rarement utilisés seuls, mais sont souvent utilisés dans des circuits qui combinent un AOP avec des résistances, des bobines, des condensateurs, ou d'autres composants passifs. Dans beaucoup de cas, la sortie de l'AOP est envoyée dans un circuit passif, qui lui-même est relié à l'entrée. Ce genre de circuit est un cas particulier de ce qu'on appelle des circuits à rétroaction. Ce sont des circuits dans lesquels la sortie du circuit est traitée, puis renvoyée sur l'entrée. Renvoyer la sortie sur l'entrée est ce qu'on appelle une rétroaction, d'où le nom donné à ces circuits. En soit, la rétroaction peut s'utiliser pour des raisons très différentes.
Les circuits à rétroaction ont une forme illustrée ci-dessous. La tension d'entrée est notée X(s) et la tension de sortie est notée Y(s). On voit qu'il y a deux circuits distincts. Le premier circuit transforme l'entrée X(s) en sa sortie Y(s) et il a une transmittance notée G(s). Nous l’appellerons le circuit direct, car il connecte directement l'entrée à la sortie. Le second circuit, de transmittance H(s), traite la sortie et renvoie son résultat sur l'entrée. Nous l’appellerons le circuit de rétroaction. Il existe deux types de rétroaction, suivant comment on traite le résultat du circuit de rétroaction. Avec la rétroaction positive, l'entrée est additionnée au signal de rétroaction. Avec la rétroaction négative, le signal de rétroaction est soustrait du signal d'entrée.

Dans ce qui suit, nous allons supposer que le circuit direct et le circuit de rétroaction sont des circuits linéaires, c'est à dire que la sortie et l'entrée sont proportionnels. Le circuit direct multiplie son entrée par un coefficient , alors que le circuit de rétroaction multiplie sa sortie par . Le coefficient est appelé le gain en boucle ouverte et correspond ni plus moins qu'au gain de l'amplificateur. Il est à différencier du gain du circuit complet, qui est défini par le rapport entre entrée et sortie du circuit, soit Y(s)/X(s). Ce dernier est appelé le gain en boucle fermée. Les noms gain en boucle fermée et gain en boucle ouverte parlent d'eux-mêmes : le premier est mesuré sans la rétroaction, donc avec la boucle ouverte, alors que le second est mesuré avec le circuit de rétroaction, donc quand la boucle est fermée.

Dans ce chapitre, nous allons voir comment fonctionnent les circuits à rétroaction de manière générale. Nous verrons dans le chapitre suivant quels montages on peut obtenir avec une rétroaction simple. Nous utiliserons aussi les acquis de ce chapitre dans les chapitres sur les filtres et les oscillateurs. Dans ce qui va suivre, nous allons voir la rétroaction négative avant de voir la rétroaction positive.
La rétroaction négative
[modifier | modifier le wikicode]Avec la rétroaction négative, le résultat de la rétroaction est soustrait au signal d'entrée. Dans le cas des AOP, elle peut servir à corriger les défauts de l'AOP utilisé. Cela peut permettre de rendre le gain moins sensible aux défauts de l'AOP, à augmenter la bande passante, à réduire l'effet du bruit et des perturbations, à réduire les distorsions non-linéaires, où à modifier les résistances d'entrée et de sortie. Mais, si elle est utilisée intelligemment, elle permet de créer des circuits complexes en utilisant un AOP central. On peut ainsi créer des filtres, des oscillateurs ou des circuits additionneur/soustracteurs/multiplieurs/intégrateur/dérivateurs/autres.
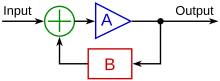
Un circuit à rétroaction négative a la forme donnée ci-dessous. Il prend un signal d'entrée (Signal) et fournit un signal de sortie (Output), le signal de rétroaction est noté .
Le signal O(s) est multiplié par par le circuit de rétroaction, ce qui donne :
Le signal d'entrée S se voit soustrait le signal de rétroaction R, de qui donne un résultat temporaire I qui vaut :
Ce dernier est amplifié par l'AOP, qui a un gain , ce qui donne une sortie égale à :

La transmittance d'un circuit à rétroaction
[modifier | modifier le wikicode]Maintenant, reprenons l'équation précédente et développons.
Divisons par S :
Par définition, n'est autre que la transmittance du circuit complet. En notant celle-ci , on a :
Regroupons les termes avec la transmittance :
Factorisons la transmittance :
Et isolons la transmittance :
Le terme est appelé le gain de boucle. Pour que la rétroaction soit négative, il faut que celui-ci soit positif. Le terme , au dénominateur de la transmittance est appelé la quantité de rétroaction.
 |
Le circuit illustré a une transmittance égale à . |
Au passage, dans la plupart des applications, on a . Dans de telles conditions, la transmittance devient :
Cela signifie que le comportement du circuit est totalement déterminé par le circuit de rétroaction, pas par l'amplificateur. Cela ne signifie pas que le circuit direct est inutile, mais que la sortie sera peu sensible au gain de l'AOP central.
Usage de la rétroaction négative
[modifier | modifier le wikicode]Maintenant, nous allons voir quels sont les avantages de la rétroaction négative, ce à quoi elle peut servir.
Une augmentation de la bande passante
[modifier | modifier le wikicode]La rétroaction négative augmente la bande passante de l'AOP. Notons que cette augmentation de la bande passante est proportionnelle à la réduction du gain en boucle fermée. Plus le gain en boucle fermée est réduit, par rapport au gain en boucle ouverte, plus la bande passante sera élargie. On peut prouver, à partir de résultats mathématiques non-triviaux, que le produit bande passante gain est une constante. En conséquence, une réduction de x% du gain en boucle fermée se traduira par une augmentation de x% de la bande passante.

Traditionnellement, on étudie le cas où le gain de l'AOP diminue avec la fréquence. Le gain de l'amplificateur dépend de la fréquence en suivant l'équation suivante :
On peut alors combiner cette équation avec la formule de la transmittance . On obtient alors :
En simplifiant, on a :
La situation étudiée est illustrée dans le schéma ci-dessous.

Réduction de la sensibilité à l'AOP du gain
[modifier | modifier le wikicode]La première utilisation est la réduction du gain du circuit, de sa sensibilité au gain de l'AOP. Une variation massive du gain de l'AOP se traduit par une réduction beaucoup plus faible du gain du circuit total. Pour comprendre en quoi, partons de la transmittance du circuit à rétroaction :
Dérivons l'équation précédente, pour voir comment le gain varie.
Divisons par la transmittance :
Le terme correspond à une modification en pourcentage du gain en boucle fermée, alors que le terme est une variation en pourcentage du gain en boucle ouverte. On voit que le terme est le coefficient de proportionnalité entre les deux gains en boucle fermée et ouverte. Ce terme est généralement plus petit que 1, beaucoup plus petit. Le gain en boucle fermée du circuit est donc stabilisé, il dépend peu du gain en boucle ouverte de l'AOP.
La réduction des interférences
[modifier | modifier le wikicode]Une autre utilité de la rétroaction est qu'elle permet de réduire l'intensité des perturbations extérieures. Pour comprendre pourquoi, imaginons qu'une perturbation D survienne et perturbe la sortie. Intuitivement, le circuit de rétroaction amplifiera la perturbation D et le signal de rétroaction sera de . Le signal intermédiaire I est donc amputé de , ce qui fait que la sortie est approximativement réduite de . Si on , alors la perturbation est supprimée immédiatement après son apparition. Il suffit que la distorsion se propage dans le circuit de rétroaction, puis dans l'AOP central, et la sortie revient à la normale.

Au niveau mathématique, on peut comparer ce qui se passe avec une perturbation D, avec et sans rétroaction.
Si la rétroaction n'avait pas d'effet sur la perturbation, alors la perturbation s'ajouterait à la sortie directement. Ce qui fait que l'on aurait :
Or, les calculs nous disent qu'avec la perturbation, le circuit à rétroaction négative a une sortie égale à :
|
Démonstration |
|
Pour cela, on suppose que la perturbation s'ajoute à la sortie de l'AOP, pour donner la sortie. En clair, on a :
On combine alors avec On développe : On regroupe les termes avec O : On factorise O : On divise par : |
On voit que l'effet de la perturbation est multiplié par , qui est généralement inférieur à 1. En clair : l'effet de la perturbation est réduit du fait de la rétroaction. Si jamais une interférence électromagnétique peu intense survient, un circuit à rétroaction se comportera normalement. Sa sortie restera relativement stable et ne sera pas trop perturbée par la perturbation.
La rétroaction positive
[modifier | modifier le wikicode]Un circuit à rétroaction positive est identique au circuit à rétroaction négative, sauf que le signal de rétroaction est ajouté au signal d'entrée. Dans ces conditions, on a :
Développons l'équation précédente :
Divisons par S pour obtenir la transmittance :
Regroupons les termes avec la transmittance :
Factorisons la transmittance :
Et isolons la transmittance :
Effets de la rétroaction positive
[modifier | modifier le wikicode]La rétroaction positive a divers effets que nous allons aborder ici.
Réduction de la sensibilité à l'AOP du gain
[modifier | modifier le wikicode]Comme pour la rétroaction négative, la rétroaction positive tend à réduire la sensibilité du gain en boucle fermée au gain en boucle ouverte. Pour le prouver, reprenons le gain en boucle fermée :
Dérivons l'équation précédente et divisons par la transmittance :
Comme pour la rétroaction négative, le terme est un coefficient de proportionnalité qui relie les gains en boucle fermée et ouverte. Ce terme est généralement plus petit que 1, ce qui fait le des variations du gain en boucle ouverte n'ont que peu d'effet sur le gain en boucle fermée.
Réduction de la bande passante
[modifier | modifier le wikicode]Contrairement à la rétroaction négative, la rétroaction positive réduit la bande passante. Il faut dire que l'augmentation du gain doit forcément se traduire par une réduction de la bande passante, du fait de la constante du produit gain bande passante.
Amplification des perturbations
[modifier | modifier le wikicode]Un autre défaut est que la rétroaction positive augmente l'effet des perturbations. Pour le montrer, procédons comme auparavant et ajoutons une perturbation sur la sortie du circuit. Comparons maintenant le résultat avec et sans la rétroaction.
Sans la rétroaction, le circuit a une sortie égale à :
Or, les calculs nous disent qu'avec la perturbation, le circuit à rétroaction positive a une sortie égale à :
|
Démonstration |
|
Pour cela, on suppose que la perturbation s'ajoute à la sortie de l'AOP, pour donner la sortie. En clair, on a :
On combine alors avec On développe : On regroupe les termes avec O : On factorise O : On divise par : |
On voit que les perturbations sont amplifiées, du fait du terme .
La stabilité d'un circuit à rétroaction négative
[modifier | modifier le wikicode]Il existe des valeurs de pour lesquelles la transmittance peut s'annuler ou au contraire devenir infinie. La transmittance est toujours écrite sous la forme d'une fraction avec un numérateur et un dénominateur. Elle s'annule si le numérateur est égal à 0, alors qu'elle devient infinie/indéfinie si le dénominateur s'annule. Les valeurs pour lesquelles sont appelées les zéros de la transmittance, alors que celles où sont appelées des pôles. Si la présence de zéros n'est pas en soi un problème, la présence de pôle en est un. Dans un cas pareil, le circuit est dit instable. On pourrait croire que les pôles n'ont pas de signification physique. Mais il n’en est rien ! Il est parfaitement possible de créer des circuits avec des pôles. En effet, certains oscillateurs (des générateurs de fréquences) sont fabriqués en utilisant cette possibilité. Concrètement, sur un pôle, la sortie du circuit est finie et non-nulle alors que l'entrée est nulle. Dans la plupart des cas, le circuit se met à osciller, à savoir que sa sortie est une tension sinusoïdale ou tout du moins une tension périodique. Ce n'est pas systématique, mais c'est une possibilité, tout dépend du circuit.
Si on compare les circuits à rétroaction positive et négative, on voit que les pôles surviennent pour des valeurs différentes de . Rappelons que pour le dénominateur est égal à et , respectivement. Pour un circuit à rétroaction négative, un pôle correspond au cas où . Cela demande que la condition suivante soit respectée : . Pour un circuit à rétroaction positive, il faut que la quantité de rétroaction s'annule, ce qui arrive si . Cela demande que la condition suivante soit respectée : .
Un problème similaire survient si la transmittance devient négative. Le cas est un petit peu plus complexe, mais le circuit est là aussi instable. Dans ce cas, la transmittance reste finie, mais la tension de sortie a quelques propriétés bizarres. Les méthodes classiques d'analyse des circuits linéaires ne fonctionnent pas et il faut utiliser d'autres méthodes d'analyse spécifiques. Les circuits qui fonctionnent avec cette condition sont les circuits oscillateurs, comme les multivibrateurs, les circuits bistables, etc. Cela arrive si devient négatif, pour un circuit à rétroaction négative. Pour un circuit à rétroaction positive, il faut que . Avec cette condition, la quantité de rétroaction est négative et la transmittance aussi.
En théorie, il suffirait de choisir et pour éviter un tel cas d'instabilité. C'est simple à faire si les deux coefficients ne dépendant pas de la fréquence et sont des constantes. Mais dans la réalité, les AOP et circuits linéaires ne se comportent pas ainsi. Dans la réalité, les circuits ont une transmittance qui dépend de la fréquence. Et il est possible que, pour certaines fréquences, on ait . Il faut absolument éviter ce cas de figure lors de la conception du filtre. Pour cela, il existe quelques techniques, dont l'usage du critère de Nyquist, qui permettent de détecter la présence d'une instabilité ou son absence. L'analyse de la stabilité d'un circuit à rétroaction positive se fait avec les mêmes outils que pour un circuit à rétroaction négative, avec quelques petites différences mineures (la valeur de n'est pas la même pour obtenir un pôle).
Le diagramme de Nyquist
[modifier | modifier le wikicode]Le diagramme de Nyquist est relativement simple. Il s'agit d'une courbe dessinée dans le plan complexe. Rappelons que la transmittance est un nombre complexe, son module correspondant au rapport entre tension d'entrée et de sortie, alors que l'argument donne le déphasage entre les deux tensions. Mais contrairement à ce que l'on peut penser, on ne trace par la transmittance du circuit sur ce diagramme, ce qui ne nous permettrait pas de détecter les situations où elle devient infinie. À la place, chaque point de la courbe est associée au produit mesuré à une fréquence, différente en chaque point.
Pour un circuit à rétroaction, le circuit devient instable pour une valeur finie de , ce qui peut se voir sur le plan complexe. Rappelons que la valeur est égale à -1 pour un circuit à rétroaction négative. La courbe dessinée sur le diagramme de Nyquist donne donc toutes les valeurs possibles de ce produit, et l'on peut vérifier si la courbe passe par -1. Si le circuit peut être instable, alors il passe forcément par le point de coordonnées (-1,0).
 |
 |
 |
La réponse impulsionnelle d'un circuit à rétroaction
[modifier | modifier le wikicode]Précisons maintenant comment se comporte un circuit suivant ce que l'on voit sur le diagramme de Nyquist. Nous allons voir comment il se comporte quand on place un échelon de tension sur son entrée. Par échelon de tension, on veut dire que l'on place une tension finie sur son entrée, durant un temps très faible, trop faible pour être considéré comme un signal d'entrée clair. Si le circuit est stable, la sortie du circuit va dépasser zéro durant un certain temps, avant de diminuer et de repasser à 0. La réduction de la tension de sortie peut être progressive, ou se faire par oscillations progressives, mais celles-ci sont amorties. Si le circuit instable, la sortie du circuit peut soit osciller de manière périodique, soit s’emballer et diverger totalement. Ci-dessous, on voit ce qui se passe suivant la valeur du facteur de rétroaction. Si il reste supérieur à -1, le circuit reste stable suite à un échelon de tension. Si il passe par -1, la sortie du circuit se met à osciller périodiquement. Et enfin, si jamais il devient inférieur à -1, la sortie du circuit diverge totalement.

Les quatre topologies des circuits à rétroaction à amplificateurs opérationnels
[modifier | modifier le wikicode]Dans ce qui précède, nous avons parlé de la rétroaction dans le cas général. Tout ce que l'on a dit marche pour beaucoup de choses, en électronique, mais aussi en mécanique, en électromécanique, en hydraulique, voire en dehors de l’ingénierie. Nous avons abordé la rétroaction dans le cadre général de la théorie du contrôle des systèmes dynamiques. Il est maintenant temps d'aborder des connaissances plus ancrées dans l'électronique.
Montage en série et en shunt de l'AOP central et du circuit de rétroaction
[modifier | modifier le wikicode]

Dans un circuit à rétroaction électronique, on trouve un AOP central bouclé à un circuit de rétroaction. Les deux, l'AOP central et le circuit de rétroaction, sont des quadripôles, à savoir des circuits qui ont quatre bornes. Deux de ces bornes sont des bornes d'entrée, sur lesquelles on peut placer une tension ou un courant, alors que les deux autres fournissent la sortie. En théorie, un quadripôle (idéal ou réel) a pour circuit équivalent les deux circuits ci-contre.
Suivant que l'on mette une tension ou un courant sur l'entrée, on dit que le circuit est en série ou en shunt. Dans le cas en série, on place une tension sur l'entrée. Dans le cas qui nous intéresse, on place la tension d'entrée sur une borne, alors que l'autre reçoit la tension fournie par le circuit de rétroaction. En faisant cela, on est certain que c'est la différence entre ces deux tensions qui est envoyée en entrée de l'AOP. Dans le cas en shunt, on place des courants sur l'entrée. Le courant sur la première borne est le courant du signal d'entrée, celui sur la seconde borne est fourni par le circuit de rétroaction.

Il est possible de faire la même chose, mais pour le circuit de rétroaction. Ce faisant, on peut se retrouver avec quatre possibilités :
- Un shunt sur l'entrée de l'AOP central et du circuit de rétroaction.
- Une série sur l'entrée de l'AOP central et du circuit de rétroaction.
- Un shunt sur l'entrée de l'AOP central et une série sur l'entrée du circuit de rétroaction.
- Une série sur l'entrée de l'AOP central et un shunt sur l'entrée du circuit de rétroaction.
Les explications précédentes peuvent sembler très techniques, en raison du jargon utilisé. Pour le dire autrement, le circuit à rétroaction peut prendre en entrée soit un courant, soit une tension. Et c'est la même chose pour ce qui est fourni en sortie du circuit : c'est soit une tension, soit un courant. Ces quatre possibilités correspondent aux cas suivants :
- L'amplificateur en tension, aussi appelé cas série-shunt, où le circuit prend en entrée une tension et fournit en sortie une tension.
- L'amplificateur en courant, aussi appelé cas shunt-série, où le circuit prend en entrée un courant et fournit en sortie un courant.
- L'amplificateur en transimpédance, aussi appelé cas série-série, où le circuit prend en entrée un courant et fournit en sortie une tension.
- L'amplificateur en transconductance, aussi appelé cas shunt-shunt, où le circuit prend en entrée une tension et fournit en sortie un courant.
Pour résumer, il y a quatre façons de relier entre eux deux quadripôles, qui sont illustrées ci-dessous. Elles correspondent respectivement à l'amplificateur en tension (droite, haut), à l’amplificateur en courant (gauche, bas), à l'amplificateur en transconductance (droite, bas) et l'amplificateur en transimpédance (gauche, haut).

Le montage série-shunt
[modifier | modifier le wikicode]Commençons par étudier l'amplificateur en tension, le montage série-shunt. Nous allons voir que l'amplificateur en tension est censé avoir une résistance d'entrée forte, alors que sa résistance de sortie doit être la plus faible possible. Et l'usage de la rétroaction permet justement de réduire la résistance de sortie, tout en augmentant la résistance d'entrée.
Pour commencer, nous allons préciser qu'il faut faire la distinction entre la tension et la tension : la première est celle envoyée en entrée du circuit, alors que la seconde est celle en entrée de l'AOP. Pareil pour les courants d'entrée : il y en a deux, que nous noterons et , qui correspondent aux courants d'entrée du circuit et de l'AOP. Même chose pour les résistances d'entrée du circuit et de l'AOP qui sont respectivement notées et .
Dans ce qui suit, nous supposons que l'AOP est un quadripôle réel, alors que le circuit de rétroaction est un quadripôle idéal.
La résistance d'entrée du montage
[modifier | modifier le wikicode]Dans ce qui suit, nous supposons que l'AOP central est un quadripôle réel, avec une résistance d'entrée et une résistance de sortie . Par définition, cette résistance est définie par le rapport entre la tension en entrée de l'AOP et le courant d'entrée, par la relation :
Maintenant, calculons la résistance d'entrée du circuit complet, pas celle de l'AOP, mais celle du circuit complet. Elle est égale, par définition, au rapport entre la tension d'entrée et le courant d'entrée. Si l'on suppose que le circuit de rétroaction est un quadripôle idéal, alors le courant d'entrée est égal au courant d'entrée de l'AOP (il n'y a pas d'autre résistance sur l'entrée du circuit). Dans ce cas, la résistance d'entrée du circuit vaut :
On combine les deux équations précédentes :
Maintenant, on applique la formule :
On voit que ce montage augmente la résistance d'entrée.
La résistance de sortie du montage
[modifier | modifier le wikicode]Maintenant, étudions la résistance de sortie du montage, et formulons-la à partir de la résistance d'entrée de l'AOP. Nous supposons que l'AOP est un quadripôle réel, alors que le circuit de rétroaction est un quadripôle idéal. L'AOP est composé d'une résistance en série avec un générateur de tension. Le générateur de tension en question fournit une tension égale à :
Si on met la sortie en court-circuit, la tension de sortie est nulle. La tension de rétroaction s'annule elle aussi, en conséquence. La tension d'entrée de l'AOP est donc la tension d'entrée du circuit, ce qui donne :
De plus, le courant de sortie du circuit est égal au courant de sortie de l'AOP. On a donc :
La résistance d'entrée du circuit est égale, par définition, à :
En combinant avec les équations précédentes, on trouve :
On voit que le montage réduit la résistance d'entrée.
Les montages à amplificateurs opérationnels

Les AOP sont rarement utilisés seuls, mais sont souvent utilisés dans des circuits qui combinent un AOP avec des résistances, des bobines, des condensateurs, ou d'autres composants passifs. Dans presque tous les cas, la sortie de l'AOP est reliée à une entrée, ce qui porte le nom de rétroaction. On a alors deux cas : soit l'entrée , soit la . Dans le premier cas, la rétroaction est dite positive, alors qu'elle est dite négative pour le second cas. Les deux situations sont très différentes et l'AOP fonctionne dans deux modes différent selon que la rétroaction est positive ou négative.
- Avec une rétroaction négative, une augmentation de la tension de sortie réduit la différence des entrées, ce qui tend à réduire la tension de sortie. La tension tend à se stabiliser à une valeur précise, d'équilibre. L'AOP est alors dit en mode linéaire, ce qui trahit le fait que la tension de sortie ne sature pas (du moins, pas systématiquement).
- Avec une rétroaction positive, une augmentation de la tension de sortie augmente la différence entre entrée, ce qui augmente encore la tension de sortie et rebelote. La tension augmente ou baisse alors jusqu’à ce qu'elle arrive à la tension de sortie maximale/minimale.
Les montages en mode linéaire (rétroaction négative)
[modifier | modifier le wikicode]Dans ce chapitre, nous allons voir les montages les plus utilisés, en supposant l'AOP idéal. Pour rappel, un AOP parfait respecte les hypothèses suivantes :
- Il n'a pas de courants d'entrée : .
- Son gain différentiel est infini : .
- On néglige les tensions d'offset et le gain en mode commun, ce qui donne : .
En combinant les deux expressions, et en supposant le mode linéaire (contre-réaction négative), on a :
Les deux tensions d'entrée sont donc égales, sous condition qu'il y ait une contre-réaction sur l'entrée . Intuitivement, on peut interpréter ce résultat comme suit.
Pour commencer, étudions le cas où l'AOP a un gain égal à 1. Supposons que les deux tensions d'entrée soient égales : la sortie est alors égale à 0. Maintenant, imaginons que la tension augmente : cela entraine l'apparition d'une tension différentielle et la tension de sortie prend la même valeur (si le gain est de 1). Cette tension différentielle est envoyée sur l'entrée par l'intermédiaire de la contre-réaction : augmente et les augmentations de et se compensent exactement (dans le cas où le gain est de 1).
Si l'AOP a un gain différent de 1, le principe reste valable, même si le déroulement des faits est plus compliqué. On retrouve la même logique qui veut que si augmente, alors fait de même. Par contre, les deux tensions ne se compensent pas exactement du premier coup : à la place, on voit apparaitre une nouvelle tension différentielle, qui modifie elle aussi la tension et ainsi de suite. Le circuit évolue donc continuellement, mais finir par atteindre un état d'équilibre au bout d'un temps assez court. Et à l'équilibre, les augmentations de et se compensent parfaitement et les tensions d'entrée sont égales.
Le montage suiveur
[modifier | modifier le wikicode]
Le montage le plus simple à étudier est le montage suiveur, illustré ci-contre. Il se limite à une contre-réaction négative, à savoir une liaison de la sortie sur l'entrée .
En appliquant la loi des mailles, on trouve :
- , avec la différence de tension entre et .
Vu que cette dernière vaut zéro, on a :
En clair, ce montage reproduit la tension d'entrée sur sa sortie.
|
Démonstration |
|
On peut aussi analyser ce circuit en utilisant les équations vues au chapitre précédent. Rappelons que l'on a vu que la transmittance d'un circuit à rétroaction négative est donnée par la formule suivante, avec le gain de l'AOP et le gain du circuit de rétroaction. Dans le montage suiveur, le circuit de rétroaction est un simple, ce qui fait que sa transmittance est de 1 (le signal d'entrée est égal au signal de sortie). On a donc : |
Le montage non-inverseur
[modifier | modifier le wikicode]
Le montage non-inverseur est illustré dans le schéma ci-contre.

Rappelons que le courant d'entrée d'un AOP parfait est nul. Avec cette hypothèse, on peut calculer la tension par un simple pont diviseur de tension :
On a aussi, de par les hypothèses de l'AOP parfait :
Ce qui donne :
Multiplions par :
Divisons par
Simplifions la fraction :
- Le montage suiveur peut être vu comme un cas particulier du montage non-inverseur, pour lequel on aurait : et . Les calculs redonnent bien ce qu'on a établi pour le montage suiveur, à savoir :
- :
Le montage convertisseur courant-tension
[modifier | modifier le wikicode]
La particularité de ce montage est que l'entrée ne reçoit pas une tension, mais un courant d'entrée . Vu que l'AOP n'absorbe pas de courant (ses courants sur les entrées sont nuls), tout le courant passe dans la résistance.
L'entrée est reliée à la masse, ce qui fait que . Si l'AOP est parfait, on a donc :
La loi des mailles donne alors :
- , avec la tension aux bornes de la résistance R.
Dit autrement, on a :
Ce montage convertit donc le courant d'entrée en une tension, par l'intermédiaire de la résistance R.
Le montage inverseur
[modifier | modifier le wikicode]
Le montage illustré ci-contre est appelée le montage inverseur. Ce nom vient de ce que fait ce montage. Sa tension de sortie est l'inverse (en réalité l'opposée) de la tension d'entrée, pondérée par un coefficient lié aux résistances.

La démonstration la plus simple utilise les approximations du début du chapitre. Vu que les courants d'entrée de l'AOP sont nuls, le circuit est alors composé de deux résistances en séries, alimentées aux deux bouts par une tension : d'un côté, de l'autre. C'est la situation parfaite pour utiliser le théorème de superposition (aussi appelé théorème de Millmann). Si on ne garde que et qu'on met à 0, le circuit devient un simple pont diviseur. Idem si l'on met à 0 en conservant . La tension d'entrée est la somme de ces deux ponts diviseurs, ce qui donne :
Mais vu que l'entrée est connectée à la masse, on a :
Ce qui donne :
On multiplie par : des deux côtés :
On divise par des deux côtés :
- }}
Il existe aussi un autre moyen de faire la démonstration, sans faire d'approximations simplificatrices.
|
Démonstration |
|
La tension de sortie de l'AOP est donnée, par définition, par la formule suivante : Le schéma montre que l'entrée est reliée à la masse et vaut donc 0, ce qui simplifie la formule précédente en : La tension provient de la somme de deux ponts diviseur entre la tension d'entrée et de sortie, ce qui donne : On combine alors avec la formule qui donne la tension : On développe : On réorganise les termes : On factorise le terme de gauche : On met au même dénominateur dans le terme de gauche : On simplifie : On isole alors : On simplifie : Si on suppose que est très grand par rapport aux valeurs des résistances, on a alors : |

On peut aussi reformuler ce développement comme suit. On peut voir ce montage inverseur comme une amélioration du montage précédent, auquel on aurait rajouté une résistance sur l'entrée. Cette résistance convertit la tension d'entrée en un courant, qui est convertit par le reste du montage en une tension. Cela fonctionne parce que la tension sur l'entrée est nulle, ce qui fait que schéma équivalent du montage est celui illustré ci-contre. Vu que le courant d'entrée de l'AOP est nul, tout le courant passe dans les deux résistances. On a donc :
Quelques manipulations algébriques redonnent bien l'équation précédente.
On peut reformuler cette équation de manière à obtenir le gain de l'amplificateur :
On voit que le gain obtenu n'est pas égal au gain différentiel (ou au gain en mode commun). D'un côté le gain différentiel est supposé infini, de l'autre le gain réel dépend de la valeur des résistances. Cela nous amène à faire la distinction entre deux gains : le gain différentiel vu précédemment, et le gain obtenu avec les calculs de cette section. Le gain différentiel est une propriété de l'AOP quand celui-ci n'a pas de rétroaction, ce qui lui vaut son appellation de gain en boucle ouverte. Par contre, le gain mesuré dans un montage avec une rétroaction est différent. Ce gain est appelé gain en boucle fermée, pour signifier qu'il implique une boucle de rétroaction (négative).
Le montage sommateur-inverseur
[modifier | modifier le wikicode]
Le montage sommateur-inverseur est une amélioration du montage précédent, la différence étant que l'on a plusieurs tensions/résistances reliées à l'entrée . Le montage additionne les tensions placées sur cette entrée et fournit en sortie l'inverse de cette somme. Pour le démontrer, repartons du second développement du montage inverseur. On sait que la tension est nulle.
Pour le courant qui circule dans la résistance , on a :
On peut aussi calculer la somme des courants qui circulent dans chaque résistance d'entrée, ce qui donne :
Vu que le courant d'entrée de l'AOP est nul, les deux courants sont égaux :
En multipliant par , on a :
Ce circuit additionne donc les tensions pondérées par chaque résistance.
Le montage amplificateur différentiel
[modifier | modifier le wikicode]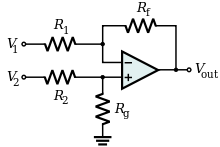
Le montage en amplificateur différentiel est le même que le montage inverseur, si ce n'est qu'on a ajouté un pont diviseur sur la tension d'entrée.
La tension se calcule exactement comme avec le montage inverseur (théorème de Millmann/superposition), ce qui donne :
La tension se calcule avec un pont diviseur de tension :
Les deux tensions sont égales, par les hypothèses de l'AOP parfait :
On soustrait : des deux côtés :
On divise des deux côtés par : :
On développe :
On simplifie et on réarrange les termes :
Deux cas particuliers sont intéressants à étudier :
- Quand et , on a :
- Quand et , on obtient le montage soustracteur :
Le montage amplificateur d'instrumentation
[modifier | modifier le wikicode]Le montage amplificateur d'instrumentation est une amélioration de l'amplificateur différentiel. Il suffit d'ajouter deux suiveurs sur les deux entrées du circuit pour obtenir un amplificateur d'instrumentation. Ce faisant, on est certain que les courants d'entrée de l'AOP (qui sont non-nuls pour un AOP réel) ne perturbent pas le fonctionnement du circuit.
Sur certains montages, on ajoute quelques résistances : une dans chaque boucle du suiveur, et une autre pour relier les deux boucles, afin d'améliorer le fonctionnement du circuit.
Le montage intégrateur
[modifier | modifier le wikicode]
Le montage intégrateur ressemble au montage inverseur, si ce n'est qu'on a remplacé une résistance par un condensateur. Le montage est illustré ci-contre.
Si on suppose l'AOP parfait, il n'y a pas de courants d'entrée.
Aux bornes de la résistance, on a :
Au bornes du condensateur, on a :
Le courant circule dans le circuit série formé par la résistance et le condensateur, ce qui fait qu'il est identique en tout point du circuit. Les deux courants des équations précédentes sont égaux, ce qui donne :
Divisons par C :
Intégrons pour trouver :
Simplifions :
Ce circuit calcule donc l'intégrale de la tension d'entrée au cours du temps (pondérée par le produit RC). D'où son nom de montage intégrateur.
Le montage dérivateur
[modifier | modifier le wikicode]
Si on inverse de place la résistance et le condensateur, le comportement du montage est changé du tout au tout. De montage intégrateur, il passe à un montage dérivateur, qui calcule la dérivée de la tension d'entrée. Pour le démontrer, il faut refaire les développements de la section précédente. La seule différence est que la tension d'entrée et de sortie seront inversées. Évidemment, on suppose l'AOP parfait, ce qui fait qu'il n'y a pas de courants d'entrée.
Aux bornes de la résistance, on a :
Au bornes du condensateur, on a :
Les deux courants précédents sont égaux, ce qui donne :
Multiplions par R :
Ce circuit calcule donc la dérivée de la tension d'entrée au cours du temps (pondérée par le produit RC).
Le montage exponentiel
[modifier | modifier le wikicode]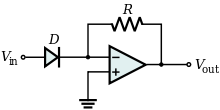
Le montage exponentiel est une amélioration du montage convertisseur courant-tension : on a rajouté une diode sur l'entrée du montage. Et cette fois-ci, on envoie une tension sur l'entrée du montage, et non un courant.
La diode ne change pas grand chose au fonctionnement du montage, vu que la chute de tension à ses bornes est négligeable. On a toujours :
Par contre, on peut le courant qui parcourt le circuit est le courant fournit par la diode (en fonction de la tension d'entrée). Celui-ci vaut, d'après l'équation de Schokley vue il y a quelques chapitres :
En combinant les deux expressions précédentes, on a :
En clair, ce montage calcule l'exponentielle de la tension d'entrée, à un coefficient de proportionnalité près.
- En réalité, l'équation de Schokley d'une diode n'est pas , mais : . Cela modifie quelque peu les calculs, ce qui donne l'équation suivante :
Le montage logarithmique
[modifier | modifier le wikicode]
Le montage logarithmique est une variante du montage précédent, dans lequel la diode et la résistance échangent leurs places.
Ici, la diode est alimentée par la tension , ce qui fait que le courant qui traverse le circuit est de :
On a toujours , ce qui donne :
En combinant les deux expressions précédentes, on a :
On peut reformuler l'expression comme suit :
Prenons le logarithme des deux côtés :
Multiplions par la tension de seuil de la diode :
En clair, ce montage calcule le logarithme de la tension d'entrée, à un coefficient de proportionnalité près.
- En réalité, l'équation de Schokley d'une diode n'est pas , mais : . Cela modifie quelque peu les calculs, ce qui donne l'équation suivante :
Nous en aurons besoin dans la section suivante.
Le montage multiplieur
[modifier | modifier le wikicode]Le montage multiplieur fournit en sortie le produit des deux tensions d'entrée. Il est composé avec l'aide des circuits exponentiels, logarithmiques, inverseurs et sommateurs vus plus haut. L'idée qui se cache derrière ce circuit est redoutablement simple, pour qui connait les propriétés des logarithmes. On sait que le logarithme d'un produit est égal à la somme des logarithmes. Cette propriété a durant longtemps été exploitée pour faire des multiplications à la main, pour des opérandes étaient assez grandes. Il suffit de réutiliser ce principe ici : on prend les logarithmes de chaque entrée, on les additionne, puis on prend l'exponentielle du résultat pour obtenir le résultat final. En clair, on a un montage logarithmique sur chaque entrée, un circuit sommateur, et enfin un montage exponentiel. Le circuit final est illustré ci-dessous.

On peut créer le circuit sommateur de plusieurs manières. La méthode la plus évidente est d'utiliser un montage inverseur-sommateur, suivi par un montage inverseur (pour compenser l'inversion réalisée par le montage inverseur-sommateur). Mais il existe une autre solution, bien plus élégante. Avec elle, les sorties des montages logarithmiques sont placées en série avec une résistance, pour transformer la tension (le logarithme), en un courant proportionnel. Puis, les deux fils sont reliés/fusionnés : la loi des nœuds fait que les deux courants sont additionnés. Enfin, on fait passer le courant obtenu (la somme des courants logarithmiques) dans un montage de conversion courant-tension. Le circuit total, montages exponentiels et logarithmiques inclus, est celui-ci :

En réalité, ce montage ne marche pas parfaitement, pour une raison simple : le montage logarithmique ne calcule pas exactement le logarithme, mais fait le calcul suivant :
La somme des deux logarithmes donne donc :
En appliquant la règle on a :
En appliquant le montage exponentiel, on trouve :
Ce qui se simplifie en :
Il faut donc ajouter les deux tensions d'entrée au résultat pour obtenir le bon résultat. Il suffit d'ajouter un montage sommateur, ce qui donne le circuit suivant :

Les montages en mode comparateur (rétroaction positive ou absence de rétroaction)
[modifier | modifier le wikicode]Les montages précédents utilisent tous une contre-réaction négative, à savoir qu'ils relient la sortie à l'entrée . Cette contre-réaction négative fait fonctionner l'AOP dans le régime linéaire et la sortie tend à être stable autour d'une valeur d'équilibre. Mais il est aussi possible de relier la sortie à l'entrée positive . Dans ce cas, le circuit fonctionne tout autrement. Le circuit fonctionne alors en mode de saturation, à savoir que sa sortie est égale à la valeur maximale ou minimale que peut fournir l'AOP. Les circuits qui utilisent cette propriété sont généralement des comparateurs de tension, qui comparent les deux tensions d'entrée entre elles, ou qui comparent une tension d'entrée à un seuil prédéfini. Dans cette section, nous allons voir les montages qui utilisent une contre-réaction positive, et notamment les comparateurs.
Le comparateur à un seuil (absence de rétroaction)
[modifier | modifier le wikicode]Pour commencer cette section, je me dois de faire une digression sur l'AOP en mode de saturation. Un AOP parfait est, par définition, un comparateur. En effet, son comportement en régime de saturation est défini par les deux équations suivantes :
- Si :
- Si :
Un simple AOP, sans contre-réaction, permet de réaliser un circuit qui compare la tension d'entrée à un seuil. Si la tension est sous le seuil, . Mais si la tension d'entrée dépasse ce seuil : . Pour cela, il suffit de placer la tension de seuil sur l'entrée et de mettre la tension d'entrée sur l'entrée . Ce circuit est appelé un comparateur à un seuil.
Le schéma ci-dessous illustre un comparateur à un seuil qui compare la tension d'entrée au seuil .

Le circuit comparateur à deux seuils (trigger de Schmitt)
[modifier | modifier le wikicode]Le circuit précédent n'utilise pas de rétroaction. Les circuits que nous allons voir dans cette section utilisent une rétroaction positive, qui garantit qu'ils fonctionnent en saturation. Pour comprendre pourquoi l'AOP fonctionne en saturation, étudions ce qui se passe quand la tension différentielle est positive. En clair la tension d'entrée du circuit est telle que la sortie de l'AOP est positive. La tension de sortie positive est alors renvoyée en entrée, où elle s'ajoute à la tension d'entrée préexistante. La tension d'entrée finale augmente donc, ce qui fait encore augmenter la tension de sortie de l'AOP. Et la boucle recommence, la tension de sortie augmentant jusqu’à ce que l'AOP atteigne sa tension maximale. Pour le cas où la tension d'entrée fait que la tension d'entrée est négative, c'est le même raisonnement, si ce n'est que la tension de sortie sera négative. On voit donc que la rétroaction fait que le processus 'emballe : de petites différences d'entrées s'amplifient de plus en plus, jusqu’à ce que l'AOP atteigne sa tension maximale ou minimale.
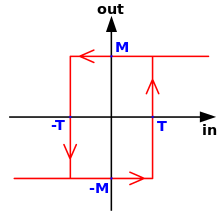
Le comparateur à deux seuils est un comparateur un peu spécial. Il dispose non pas d'un seuil, mais de deux seuils de basculement. Lorsque le premier seuil est franchit, le circuit voit sa sortie passer de -VCC à +VCC. Le second seuil est pour l'opération inverse : quand la tension d'entrée descend en-dessous de ce second seuil, la sortie passe de +VCC à -VCC. Le premier seuil (passage de -VCC à +VCC) est appelé le seuil positif, alors que l'autre est appelé le seuil négatif. La raison est, pour la majorité des montages, ces deux seuils ont la même valeur absolue, mais des signes différents.
Le fonctionnement de ce circuit est résumé dans le schéma ci-contre. Ce schéma est appelé une courbe d'Hystérésis. L'interprétation de cette courbe est la suivante. Supposons que la tension d'entrée soit comprise au-delà du seuil T : la sortie est donc égale à +VCC. Imaginons maintenant qu'elle descende en-dessous du seuil T, mais reste supérieure à -T. Dans ce cas, la sortie restera à +VCC. Ce n'est que quand elle descendra sous le seuil - T que la sortie basculera à -VCC. Ensuite, imaginons que l'entrée, initialement sous le seuil -T, dépasse ce seuil et augmente progressivement. Rien ne se passe tant que l'entrée n'a pas dépassé le seuil de basculement T et la sortie reste à -VCC. Ce n'est qu'une fois le seuil T dépassé que la sortie bascule à +VCC. Les flèches indiquent comment interpréter ces basculements et les hausses/baisses de tension de sortie selon l'entrée.
Pour résumer :
- Si l'entrée est en-dessous du seuil négatif -T, la sortie est à -VCC.
- Si l'entrée est au-dessus du seuil positif +T, la sortie est à +VCC.
- Entre les deux, la sortie garde sa valeur précédente, qui est de +VCC ou de -VCC selon l'histoire du circuit.
Le comparateur à deux seuils inverseur
[modifier | modifier le wikicode]
Il existe deux circuits comparateurs à deux seuils, qui ressemblent aux circuits inverseur et non-inverseur obtenus avec contre-réaction négative. La seule différence est que la contre-réaction est ici placée sur la borne et non . Le circuit inverseur est montré ci-contre.
On voit immédiatement que la tension est obtenue par un pont diviseur de tension, ce qui donne :
Vu que l'AOP est en mode de saturation, peut prendre deux valeurs possibles : +VCC et -VCC. En injectant ces deux valeurs dans l'équation précédente, on trouve l'expression des deux seuils :
- : seuil positif.
- : seuil négatif.
Le comparateur à deux seuils non-inverseur
[modifier | modifier le wikicode]
Passons maintenant au circuit non-inverseur.
Cette fois-ci, on doit utiliser le théorème de superposition (ou de Milmann, c'est selon) pour analyser ce circuit (comme on l'avait fait avec le montage non-inverseur). On a alors :
Vu que l'AOP est en mode de saturation, peut prendre deux valeurs possibles : +VCC et -VCC. En injectant ces deux valeurs dans l'équation précédente, on trouve a :
Reste alors à trouver la tension qui annule la tension différentielle (et donc la tension ), pour trouver les tensions de seuil. Quelques manipulations algébriques triviales donnent alors :
- : seuil positif.
- : seuil positif.
Les filtres électriques
Les filtres électriques sont des quadripôles, qui prennent en entrée une tension en fournissent en sortie une version atténuée de la tension d'entrée. Ceux-ci sont des composants qui atténuent les signaux dans une certaine gamme de fréquence. Ils vont par exemple laisser passer les signaux à basse fréquence, mais filtrer les hautes fréquences, ou inversement. Plus précisément, les filtres vont modifier l'ensemble des sinusoïdes qui leur parviennent. Si on leur envoie un signal (une tension ou courant quelconque) sur leur entrée, ils vont traiter ce signal et fournir une version traitée sur leur sortie. Pour donner quelques exemples, les circuits RC, RL, et RLC sont des filtres parmi tant d'autres. On a vu dans le chapitre sur l'impédance que ceux-ci fournissent une tension de sortie (aux bornes du condensateur ou de la bobine), quand on leur fournit une tension d'entrée. Leur étude dans le chapitre sur l'impédance a servi en quelque sorte d'introduction à l'étude des filtres électriques, là où ce chapitre porte sur l'étude des filtres de manière plus générale.
Il existe un grand nombre de filtres électroniques, qui ont chacun leurs avantages et inconvénients. Les critères utilisés pour classer les filtres sont assez nombreux : on peut les classer en fonction de leur bande passante, de leur ordre, de leur caractère actif/passif ou de certaines propriétés mathématiques. Dans ce qui va suivre, nous allons voir quelques classifications assez courantes des filtres. Nous allons d'abord voir la différence entre les filtres passe-haut, passe-bas, passe-bande et coupe-bande, qui ont chacun un comportement en fréquence bien précise. Puis, nous enchaînerons avec une classification plus élaborée qui distingue les filtres de Bessel, Butterworth, Tchebychev et Legendre.
La réponse en fréquence d'un filtre électronique
[modifier | modifier le wikicode]Lorsqu'on envoie un signal sinusoïdal en entrée d'un filtre, on retrouve en sortie un signal sinusoïdal d'une amplitude plus faible qu'à l'entrée. En quelque sorte, les filtres sont l'inverse d'un amplificateur : au lieu d'amplifier un signal, ils l'atténuent. Cette atténuation dépend de la fréquence du signal d'entrée : elle est minimale, voire nulle pour certaines fréquences, plus importante pour d'autres. Pour certaines fréquences, le signal de sortie est si faible qu'il est négligeable : la fréquence qui correspond est alors filtrée, atténuée, éliminée du signal original.
La relation atténuation-fréquence
[modifier | modifier le wikicode]Si on étudie la variation du gain en fonction des fréquences, on peut tomber sur plusieurs possibilités. Les quatre principales sont les suivantes :
- Le gain augmente avec la fréquence. Le filtre atténue les basses fréquences, mais laisse passer les hautes fréquences. Le filtre est dit un filtre passe-haut.
- Le gain diminue avec la fréquence. Le filtre laisse passer les basses fréquences, mais atténue les hautes fréquences. Le filtre est dit un filtre passe-bas.
- Le gain augmente jusqu'à une fréquence maximale avant de diminuer. Dit autrement, le gain est minimal pour les hautes et basses fréquences, maximal pour un intervalle bien précis. Le filtre laisse passer les fréquences contenues dans un intervalle, mais atténue les fréquences situées en dehors de celui-ci. C'est le comportement d'un filtre passe-bande.
- Le gain est maximal pour les hautes et basses fréquences, mais minimal dans un intervalle précis. Le gain diminue jusqu'à une fréquence maximale avant de remonter. Le filtre laisse passer les fréquences situées en dehors d'un intervalle, mais atténue les fréquences situées dans l'intervalle. C'est le comportement d'un filtre coupe-bande.
Certains filtres ont un comportement plus complexe et fonctionnent comme la superposition de filtres plus simples. Par exemple, certains filtres se comportent comme un filtre passe-bas aux basses fréquences, mais laissent passer une bande de fréquence dans certaines hautes fréquences. Et les exemples de ce type sont nombreux.

On considère arbitrairement qu'un filtre ne laisse pas passer les fréquences dont l’atténuation est de moitié, les autres n'étant pas filtrées. Si on fait les calculs, cela correspond à un gain diminué de 3 dB. La fréquence qui correspond à une atténuation réduite de moitié, c'est à dire où la puissance dissipée par le filtre est la moitié de celle fournie en entrée, est appelée la fréquence de coupure. En clair, le signal voit son amplitude en tension ou en courant divisée par , soit égale à 70,7% du signal originel. Une illustration est donnée ci-dessous pour un filtre passe-bas et un filtre passe-haut.
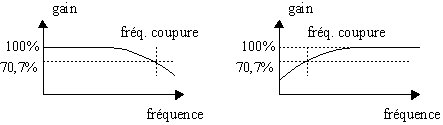
Pour la plupart des filtres, il existe entre une et deux fréquences de coupures, qui délimitent une bande de fréquences qui ne sont que peu filtrées. La largeur de cet intervalle est appelée la bande passante du filtre.

La relation déphasage-fréquence
[modifier | modifier le wikicode]Si le gain varie avec la fréquence, il en est de même pour la phase. Les signaux envoyés à un filtre en ressortent avec un déphasage par rapport à l'entrée. Qui plus est, ce décalage est généralement dépendant de la fréquence, la relation exacte variant selon le filtre considéré. L'origine de ce déphasage est que les signaux mettent un certain temps pour parcourir le filtre, pour faire le chemin de l'entrée vers la sortie, ce temps de parcours se traduisant par déphasage entre entrée et sortie. Généralement, plus un filtre contient de composants enchaînés les uns à la suite des autres, plus ce déphasage est important.
Tous les types de filtres introduisent un décalage constant pour toutes les fréquences. Attention : par décalage constant, on veut dire que le temps de parcours du filtre est identique pour toutes les fréquences. Si on regarde le déphasage, cela se traduit par un déphasage proportionnel à la fréquence. Par exemple, si le déphasage est de 20° à une fréquence de 5 KHz, alors il est de 40° pour 10 KHz, de 80° pour 20 KHz, de 800° pour 2000 KHz, etc. Ce temps de décalage est appelé le retard de groupe, nom qui traduit le fait que toutes les fréquences sont touchées de la même manière. Un signal envoyé sur un filtre ne sera pas modifié par le retard de groupe, vu que toutes les harmoniques du signal seront retardées de la même manière. Il n'implique donc aucune distorsion du signal d'entrée.
Si certains types n'introduisent que ce décalage de groupe, sans autres formes de retard supplémentaires, ce n'est pas le cas pour la majorité des filtres. Divers retards dépendant de la fréquence viennent s'ajouter au retard de groupe et ajoutent un déphasage dépendant de la fréquence. Une conséquence de cette approche se voit quand on envoie des signaux non-sinusoïdaux en entrée de tels filtres. Les diverses harmoniques du signal traversent le filtre à des vitesses différentes et ressortent chacune avec un délai différent de leur voisine. Les harmoniques ont chacune leur propre déphasage, ce qui donne un signal d'entrée déformé. Le résultat est une distorsion du signal, qui est d'autant plus importante que les retards dépendant de la fréquence sont importants.
La transmittance d'un filtre : propriétés mathématiques
[modifier | modifier le wikicode]De manière générale, la transmittance d'un filtre s'exprime avec une fraction, composée d'un numérateur et d'un dénominateur (respectivement, la tension d'entrée et de sortie), qui dépendent tous deux de la fréquence de la tension d'entrée.
Le numérateur et le dénominateur sont tous deux des polynômes, dont la fréquence d'entrée est la seule variable. De manière générale, on peut écrire la transmittance de tout filtre de cette manière :
L'ordre d'un filtre
[modifier | modifier le wikicode]L'exposant le plus élevé dans le dénominateur est appelé l'ordre du filtre. Par exemple, on dira que le filtre est d'ordre 2 si la fréquence est élevée au carré dans le dénominateur, d'ordre 4 si elle est élevée à la puissance 4, etc. Il a un rôle tout particulier à jouer, car elle décrit la sensibilité du filtre à la fréquence. Plus la puissance est élevée, plus le filtre aura un filtrage efficace. Par exemple, pour un filtre passe-bas, l'atténuation sera d'autant plus rapide que l'ordre du filtre est important. Par contre, plus l'ordre d'un filtre est élevé, plus il contient de composants électroniques : il est donc plus complexe, plus difficile à produire, plus coûteux, etc.
Pour un filtre du premier ordre, la transmittance est une équation qui dépend de la fréquence de coupure . Si vous étudiez les formules qui vont suivre, vous verrez qu'elles ressemblent aux formules obtenues pour les filtres RC et RL. Le fait est que les filtres RC et RL sont des filtres du premier ordre.
| Filtre passe-bas | |
|---|---|
| Filtre passe-haut |
La transmittance des filtres du second ordre est une équation quadratique qui contient deux constantes et , dépendantes du circuit, appelées respectivement facteur d'amortissement et facteur de qualité. Le facteur de qualité est défini comme le rapport entre la fréquence propre , celle où le gain est maximal, et la largeur de la bande passante. Le facteur d'amortissement est défini à partir du facteur de qualité, comme étant la moitié de son inverse. On a donc :
| Filtre passe-bas | |
|---|---|
| Filtre passe-haut | |
| Filtre passe-bande | |
| Filtre coupe-bande |
- Si vous étudiez les formules qui vont suivre, vous verrez qu'elles ressemblent aux formules obtenues pour le filtre RLC. Le fait est que le filtre RLC est du second ordre, à savoir que la fréquence est mise au carré dans l'équation de la transmittance.
Les zéros et pôles d'un filtre
[modifier | modifier le wikicode]On peut reformuler les formules pour la transmittance en se souvenant que tout polynôme peut être factorisé en utilisant ses racines. Ainsi, tout polynôme de la forme peut se reformuler comme suit : , avec les racines du polynôme. En reformulant ainsi les polynômes de la transmittance, on a :
Les racines du numérateur sont appelées les zéros et les racines du dénominateur sont appelées les pôles. Ce sont des nombres complexes, avec chacun une partie réelle et une partie imaginaire. Il est possible de placer ces pôles et zéros sur un plan complexe, ce qui donne le graphe des pôles d'un filtre. Il est très utilisé pour déterminer si certaines fréquences rendent le filtre instable. En effet, les pôles sont des valeurs pour lesquelles le dénominateur de la transmittance est nul, et où la transmittance est donc infinie. Si un pôle se situe sur la moitié gauche du graphe des pôles, cela n'a pas trop d'importance, vu qu'il s'agit de valeurs que l'on ne peut pas observer en réalité (une partie réelle négative signifie un gain négatif, chose qui n'a pas vraiment de sens). Mais la présence d'un pôle sur la partie droite est plus problématique. Si le pôle se situe sur l'axe des abscisses, la transmittance augmente exponentiellement jusqu'à ce que la fréquence atteigne ce pôle (où elle est alors infinie). Si elle est en dehors, cela signifie que le déphasage et/ou le gain peuvent devenir infinis et donc que le filtre est extrêmement instable.
Certains filtres n'ont pas de zéros du tout, du moins tant que la fréquence reste finie. De tels filtres sont appelés des filtres tous pôles. Pour de tels filtres, la transmittance peut tendre vers zéro, mais seulement quand la fréquence tend elle aussi vers zéro. En clair : on peut avoir . Cette condition à la limite impose qu'au-delà d'une certaine fréquence, la transmittance baisse. En conséquence, de tels filtres sont forcément des filtres de type passe-bas ou passe-bande, mais ne peuvent pas être des filtres passe-haut ou coupe-bande. Vu l'absence de zéros, la fonction de transfert de ces filtres est la suivante :
La décomposition d'un filtre en filtres plus simples
[modifier | modifier le wikicode]Reprenons maintenant à partir de l'expression suivante de la transmittance :
Il est possible de regrouper les termes par groupes de deux, ce qui donne :
En développant chaque produit, on peut réécrire la formule comme suit :
En clair, la transmittance de tout filtre peut s'exprimer comme le produit de termes de la forme , avec P1 et P2 deux polynômes du premier ou du second degré. La traduction en termes électroniques est que tout filtre peut se décomposer en filtres plus simples, du premier ou du second ordre. C'est d'ailleurs souvent ainsi que sont fabriqués les filtres d'un ordre > 2 : ils sont formés par assemblage de filtres du 1er/2nd ordre.
Les types de filtres en fonction de la formule mathématique de leur transmittance
[modifier | modifier le wikicode]
Suivant les propriétés mathématiques de ces polynômes, on peut distinguer plusieurs types de filtres. Dans cette section, nous allons voir une classification basée sur des propriétés mathématiques précises, qui distingue les filtres de Bessel, Butterworth, Tchebychev et Legendre. Nous utiliserons beaucoup le diagramme gain-fréquence dans ce qui suit, le fameux diagramme de Bode. On verra qu'à l’exception des filtres de Butterworth celui-ci présente des vagues en forme de morceaux de sinusoïdes sur le diagramme gain-fréquence.
| Type de filtre | Caractéristiques |
|---|---|
| Filtre de Bessel | Délai constant en bande passante |
| Filtre de Butterworth | Gain le plus constant possible dans la bande passante |
| Filtre de Tchebychev | Meilleure atténuation en dehors de la bande passante, mais transmittance fluctuante dans la bande passante |
| Filtre de Legendre | Graphe de transmittance sans fluctuations/ondulations et avec une forte pente au voisinage de la fréquence de coupure |
Les filtres de Butterworth
[modifier | modifier le wikicode]Les filtres de Butterworth ont un gain presque totalement constant sur toute la bande passante. En dehors de la bande passante, le gain diminue régulièrement avec la fréquence, mais à un rythme assez faible comparé aux autres filtres. Par exemple, un filtre peut avoir un gain qui diminue de 5 décibels à chaque fois que la fréquence est multipliée par 10, guère plus. Cela en fait des filtres qui éliminent mal les fréquences non-désirées.
Si on regarde le diagramme de Bode (relation gain-fréquence), celui-ci est plat dans la bande passante et a une forme de droite en dehors. Il y a une légère courbure autour de la fréquence de coupure, plus ou moins prononcée selon l'ordre du filtre. Quant au déphasage, il est minimal dans la bande passante, mais augmente progressivement en dehors, avant de se stabiliser pour les fréquences très éloignées de la bande passante.

Ci-dessous sont illustrés les diagrammes de Bode pour un filtre de Butterworth de type passe-bas et passe-haut.
 |
 |
La formule de la transmittance d'un tel filtre est la suivante :
- , avec n l'ordre du filtre.
Le gain qui correspond est donc le module de la transmittance, qui vaut :
- , avec n l'ordre du filtre.
À la fréquence de coupure, la transmittance et le gain sont donc de :
- et , avec n l'ordre du filtre.
Les filtres de Chebyshev
[modifier | modifier le wikicode]
Les filtres de Chebyshev ont un comportement inverse des filtres de Butterworth. Ils ont une chute rapide de transmittance dans la bande non-passante, ce qui en fait des filtres qui coupent bien les fréquences non-désirées, contrairement aux filtres de Butterworth. Par contre, la transmittance varie dans la bande passante, là où un filtre de Butterworth garde un gain constant. Si on observe ce qui se passe dans la bande passante, on voit que le gain oscille quand la fréquence augmente. Sur le graphe gain-fréquence ci-contre, on voit une sorte de sinusoïde déformée dans la bande passante, dont les vagues se font de plus en plus proches en approchant de la fréquence de coupure. Les vagues ont toutes la même hauteur, hauteur qui est minimisée dans le cadre des filtres de Chebyshev. Le nombre de cycles, de vagues sinusoïdales, est égal à l'ordre du filtre. Par exemple, le schéma ci-contre possède deux cycles ce qui fait qu'il s'agit d'un filtre d'ordre 2.
Précisons que le déphasage est maximal près de la fréquence de coupure pour de tels filtres.

La formule de la transmittance d'un tel filtre est la suivante :
- , pour .
- , pour .
- , pour .
Les filtres du premier et second ordre
Dans ce chapitre, nous allons voir les filtres du premier et du second ordre, plus précisément la manière dont ils sont fabriqués à partir de composants plus simples. Vous pouvez vous demander en quoi ces filtres méritent qu'on leur attribue un chapitre entier. La raison est que ces filtres de base sont souvent utilisés pour fabriquer des filtres plus compliqués. Il est parfaitement possible de créer des filtres extrêmement puissants en combinant les filtres simples que nous allons voir dans cette section.
Pour rappel, il existe deux grands types de filtres : les filtres passifs d'un côté, les filtres actifs de l'autre. Les filtres passifs sont composés intégralement de composants passifs, d'où leur nom. Ils ne contiennent donc que des résistances, des condensateurs et des bobines. Ils regroupent des filtres classiques, comme les filtres RC, RL et RLC que nous allons voir dans ce qui suit. À l'inverse, les filtres actifs contiennent des composants actifs, comme des amplificateurs opérationnels. Dans ce chapitre, nous allons d'abord voir les filtres passifs, avant de voir les filtres actifs.
Les filtres passifs du premier et second ordre
[modifier | modifier le wikicode]Dans cette section, nous allons voir les filtres passifs les plus courants : les circuits RC, RL, et RLC.
- Une étude détaillée des circuits RC, RL et RLC est disponible dans le chapitre Les circuits RL, RC et RLC du wikilivre sur l’électricité. Je conseille vivement de lire ce lien avant de terminer la lecture de ce chapitre.
Le circuit RC série
[modifier | modifier le wikicode]
Le filtre RC série est composé d'une résistance et d'un condensateur placés en série. La tension d'entrée est envoyée sur la résistance, alors que la tension de sortie est récupérée aux bornes du condensateur. Le montage est équivalent à un pont diviseur et on peut calculer la tension de sortie à partir de la tension d'entrée et des impédances et du condensateur et de la résistance :
On obtient donc la transmittance complexe suivante :
- pour le circuit RC.
Maintenant, étudions le circuit RC quand la fréquence de la tension d'entrée varie. Il se trouve que les choses varient selon que l'on étudie la tension aux bornes de la résistance ou du condensateur. Pour les hautes fréquences, on a :
A basse fréquence, on a :
On voit que la tension aux bornes du condensateur est maximale à basse fréquence et nulle à haute fréquence. Ce montage agit donc comme un filtre passe-bas, à savoir qu'il laisse passer les basses fréquences, mais filtre, atténue les hautes fréquences. La tension aux bornes de la résistance fait exactement l'inverse : elle est maximale à haute fréquence et nulle à basse fréquence. Il s'agit donc d'un filtre passe-haut, à savoir qui filtre les basses fréquences mais n'atténue pas les hautes.
 |
 |
Le circuit RL série
[modifier | modifier le wikicode]
Le filtre RL série est composé d'une résistance et d'une bobine placées en série. La tension d'entrée est envoyée sur la résistance, alors que la tension de sortie est récupérée aux bornes de la bobine.
On peut obtenir la relation suivante à partir des lois élémentaires de l'électricité :
On obtient donc la transmittance complexe suivante :
- pour le circuit RL.
Passons au cas du circuit RL. Il se trouve que les choses varient selon que l'on étudie la tension aux bornes de la résistance ou du condensateur. Pour les hautes fréquences, on a :
A basse fréquence, on a :
On voit que la tension aux bornes de la résistance est maximale à basse fréquence et nulle à haute fréquence. Ce montage agit donc comme un filtre passe-bas, à savoir qu'il laisse passer les basses fréquences, mais filtre, atténue les hautes fréquences. La tension aux bornes de la bobine fait exactement l'inverse : elle est maximale à haute fréquence et nulle à basse fréquence. Il s'agit donc d'un filtre passe-haut, à savoir qui filtre les basses fréquences mais n'atténue pas les hautes. Ce circuit est donc l'exact opposé du circuit RC.
Le circuit RLC série
[modifier | modifier le wikicode]
Le filtre RLC série est composé d'une résistance, d'un condensateur et d'une bobine placées en série. La tension d'entrée est envoyée sur la résistance, alors que la tension de sortie est récupérée aux bornes de la bobine.
On peut obtenir la relation suivante à partir des lois élémentaires de l'électricité :
On peut calculer la tension aux bornes de la résistance en fonction de la tension d'entrée :
On a donc la transmittance suivante :
Le comportement de cette transmittance est intermédiaire entre celui d'un filtre passe-bas et passe-haut. Rien d'étonnant à cela, vu que ce circuit est un mélange entre un circuit RC et RL, qui sont respectivement passe-haut et passe-bas. Rien d'étonnant à ce qu'elle hérite des propriétés des circuits dont elle est composée. Son impédance est très élevée pour les hautes et basses fréquences, avec un minimum pour une bande de fréquences qui dépend du circuit. Elle filtre aussi bien les basses que hautes fréquences, ce qui fait qu'elle ne laisse passer que les fréquences intermédiaires. On dit qu'il s'agit d'un filtre passe-bande, sous-entendu qui ne laisse passer que les fréquences comprises dans un certain intervalle, une bande de fréquences.
Les filtres actifs
[modifier | modifier le wikicode]Les filtres passifs précédents sont les plus simples à étudier et à comprendre. Mais il existe aussi des filtres actifs basés sur des amplificateurs opérationnels, des transistors ou des diodes, parfois d'autres composants. De nos jours, la méthode la plus utilisée dans l'industrie est celle des filtres actifs à capacité commutée, mais bien d'autres existent. Dans les grandes lignes, les filtres actifs fonctionnent à peu près comme leur équivalent passif, avec quelques différences mineures. Dans le détail, certains composants, comme les inductances ou les résistances, sont remplacés par un circuit équivalent qui comprend un AOP ou des transistors. La raison à cela est que, pour des circuits à basse fréquence, les inductances demandées par un filtre passif sont encombrantes et peu pratiques. De plus, il est difficile d'intégrer des inductances dans des circuits intégrés modernes, du fait des techniques de fabrication actuellement en vigueur. Même chose pour les résistances, qui ne sont pas simples à intégrer dans les circuits actuels. Heureusement, on peut fabriquer des filtres efficaces en se passant d'inductances et de résistances, en utilisant intelligemment des composants actifs. Les méthodes pour ce faire sont assez nombreuses, comme vous allez le voir dans ce qui suit.

Les filtres actifs les plus simples sont construits sur le même modèle qu'un circuit passif, sauf que l'inductance est remplacée par un petit circuit. Ils sont construits autour d'un AOP, entouré de résistances et de condensateurs. Cela leur vaut le nom de filtres actifs à réseau RC. Dans de tels filtres, l'inductance est remplacée par un petit circuit composé d'un AOP, d'une résistance et d'un condensateur. De tels circuits, qui simulent une inductance, sont appelés des simulateurs d'inductance. Il en existe un grand nombre, celui illustré ci-contre n'étant qu'un exemple parmi tant d'autres. Nous n'allons pas tous les étudier, mais sachez que celui qui est le plus utilisé actuellement est celui crée par Antoniou en 1969. Il a pour particularité d'être le seul qui soit très tolérant aux défauts de l'AOP utilisé, ce qui en fait le meilleur circuit possible actuellement connu. Par contre, il simule une inductance placée en parallèle du reste du circuit (remarquez dans le schéma ci-dessous qu'il n'y a qu'une seule connexion avec le reste du circuit).


Dans les filtres à capacités commutées, les résistances sont remplacées par des condensateurs couplés à des interrupteurs (des transistors, le plus souvent). Le principe de cette technique est que les deux interrupteurs sont commandés par un signal d'horloge. Le premier interrupteur s'ouvre sur un front montant et se ferme sur un front descendant, alors que le second fait l'inverse. Ainsi, le condensateur se charge suite au front montant, puis se décharge suite au front descendant. Sur une période, il laisse passer un courant bien précis, qui dépend de la tension d'entrée (qui sert de tension de charge), ce qui fait qu'il se comporte comme une résistance. Lors d'une période, il accumule, puis relâche une quantité de charges électriques. Le courant associé est donc de . Cela donne une résistance égale à : . Les circuits à capacité commutée remplacent donc les résistances par le circuit illustré ci-contre. Cela ne se fait cependant pas sans heurts, le circuit devant souvent être modifié de manière à accommoder ce changement. Le simple remplacement ne suffit généralement pas et d'autres modifications assez tordues sont parfois nécessaires.
Dans ce qui suit, nous allons voir les filtres de type RC, sans voir en détail les filtres à capacité commutées. Pour faire simple, dites-vous que ces derniers sont fabriqués en remplaçant les résistances par des capacités commutées. Ce n'est pas totalement faux, mais c'est une simplification acceptable pour ce cours. Dans ce ui va suivre, nous allons donc voir les filtres les plus simples, les plus connus, en commençant par les filtres du premier ordre.
Les filtres actifs RC du premier ordre
[modifier | modifier le wikicode]Il existe plusieurs filtres actifs RC de premier ordre. En voici quelques exemples, illustrés dans le tableau ci-dessous. Notez que ceux-ci n'utilisent pas le circuit de simulation d'inductance d'Antiniou.
| Réponse en fréquence | Schéma du circuit | Formule de la transmittance |
|---|---|---|
| Filtre passe-bas |  |
, avec |
| Filtre passe-haut |  |
, avec |
Les filtres du second ordre sont beaucoup plus nombreux, tant les méthodes pour les fabriquer sont différentes.
Les filtres actifs RC de type Sallen-Key
[modifier | modifier le wikicode]Une des nombreuses méthodes pour fabriquer de tels filtres se base sur la topologie Sallen-Key, aussi appelée voltage control voltage source (VCVS). Elle est illustrée ci-dessous, dans le cas général et pour les filtres passe-bas et passe-haut. Elle a pour avantage d'être assez peu sensible aux défauts de l'AOP. La raison est que l'AOP est utilisé en tant qu'amplificateur seul, et non dans un montage intégrateur (comme des les autres filtres). Cela permet un fonctionnement à haute fréquence du montage, chose que les autres filtres ont du mal à faire sans AOP de grande qualité. Un autre avantage de cette topologie est qu'elle utilise des résistances et des condensateurs relativement similaires. Entre la plus petite résistance du montage et la plus grande, il n'y a guère qu'un ordre de grandeur en terme de conductance. Pareil pour les capacités, la plus petite étant plus faible d'à peine un ordre de grandeur de la plus grande. Par contre, de tels filtres sont assez difficile à régler, pour obtenir la bande passante exactement souhaitée.
| Réponse en fréquence | Schéma du circuit | Formule de la transmittance |
|---|---|---|
| Topologie générale | 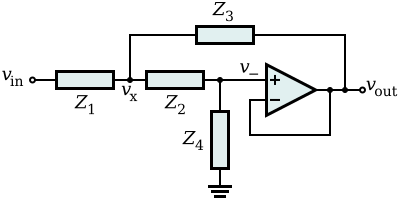
|
|
| Filtre passe-bas | 
|
|
| Filtre passe-haut | 
|
Les filtres actifs RC à rétroaction multiple
[modifier | modifier le wikicode]Une autre méthode est celle des filtres à rétroaction multiple, illustré ci-dessous. Il a les défauts et qualités inverses de celles des filtres Sallen-Key : bande passante assez mauvaise, fonctionnement à haute fréquence compliqué, résistances et condensateurs déséquilibrées, mais réglage facile.

Les filtres actifs RC de type Biquad
[modifier | modifier le wikicode]Les filtres Biquad et les filtres à état variable sont deux types de filtres assez proches l'un de l'autre. Ils ont des avantages et inconvénients similaires aux filtres à rétroaction multiple. Une de leur particularité est que suivant où l'on prend la tension de sortie, la tension sera filtrée en passe-bas, passe-haut, ou passe-bande. Le même circuit peut donc servir à la fois de passe-bas, de passe-haut et passe-bande.
Détaillons un peu ces filtres. Ils sont composés d'un ou deux intégrateur en série, couplés à d'autres montages/composants. Dans le cas des filtres Biquad, ils sont formés de plusieurs montages à AOP mis en série : un sommateur, deux intégrateurs et éventuellement des montages multiplieurs. Dans certaines variantes optimisées, on arrive à n'utiliser qu'un seul intégrateur, mais le fonctionnement du circuit devient plus complexe. Pour comprendre comment fonctionne un filtre Biquad, il faut partir de l'équation de la transmittance d'un filtre du second ordre. Pour un filtre passe-haut, celle-ci peut s'écrire comme suit :
On peut réécrire cette équation comme ceci :
Il se trouve que le terme s'obtient avec un simple sommateur. De même, le terme s'obtient en faisant passer la tension dans un intégrateur dont la constante de temps est égale à . Un second passage dans un intégrateur identique donne le terme manquant . D'où la présence d'un montage sommateur et de deux montages intégrateurs à AOP. Reste ensuite à ajouter des multiplieurs pour tenir compte de divers facteurs multiplicatifs comme le facteur K et le facteur de qualité Q.
Maintenant, reprenons l'équation du filtre passe-haut vu en début de section. En la multipliant par , on obtient l’équation d'un filtre passe-bande du second ordre ! Or, multiplier la tension de sortie initiale par est exactement ce que fait le premier intégrateur. En clair, la sortie du premier intégrateur se comporte comme un filtre passe-bande, dont le facteur de qualité est le même que le filtre passe-haut initial. Et si on re-multiplie encore par , on obtient l'équation d'un filtre passe-bas, cette fois-ci. En clair, la sortie du second intégrateur est un filtre passe-bas dont le facteur de qualité est le même que les deux autres filtres précédents. On a donc trois filtres en un !

Précisons qu'il existe plusieurs manières de traduire cette équation en circuit, de nombreuses simplifications et optimisations étant possibles. La version la plus proche de l'équation, sans optimisations particulières, donnerait un circuit semblable à celui-ci :

Une autre possibilité est la suivante :

Et enfin, voici une dernière possibilité :

Il est possible de ruser pour éliminer des AOP au point de n'en conserver qu'un seul, ce qui donne un filtre Biquad à amplificateur unique. L'idée est de remplacer les AOP, sauf un, par un réseau RC, c'est à dire composé de résistances et de condensateurs. Ce réseau RC est placé dans une boucle, qui relie la sortie de l'AOP à son entrée. La conception du réseau RC est relativement complexe, aussi je n'en parlerais pas ici. Au niveau de leurs caractéristiques, ces circuits ont de moins bonnes performances, comme un gain ou une bande passante limitée. Mais ils sont parfaitement adapté aux circuits basse-consommation, pour lesquels un grand nombre d'AOP a tendance à faire augmenter la consommation plus que raison.
Il existe de nombreux autres types de filtres du second-ordre. Les voir en détail ne serait pas utile, ce qui fait que nous allons nous arrêter là pour cette section.
Les oscillateurs (générateurs de fréquence)
Les oscillateurs électroniques sont des circuits qui fournissent une tension périodique. Ils sont aussi appelés des générateurs de fréquence. Leur utilité principale est de créer un signal d'horloge, de forme sinusoïdale, carrée, triangulaire, etc. Mais ils peuvent avoir d'autres utilités, comme créer la porteuse pour un signal modulé en fréquence ou en phase. On distingue plusieurs types oscillateurs, suivant la forme du signal périodique créé.
- Les oscillateurs linéaires fabriquent un signal sinusoïdal. Leur nom est quelque peu trompeur, une sinusoïde n'étant pas un signal linéaire. Heureusement, on peut aussi les appeler oscillateurs harmoniques, nom qui trahit le fait qu'ils créent des sinusoïdes (des harmoniques).
- Les autres oscillateurs fabriquent des signaux carrés, triangulaires, ou autre. Pour les opposer aux oscillateurs linéaires, on les appelle improprement oscillateurs non-linéaires, ou encore générateurs de fonction, voire oscillateurs à relaxation.

Les oscillateurs harmoniques fournissent une tension sinusoïdale. Il en existe un très grand nombre et tous ne sont pas fabriqués sur le même modèle. Néanmoins, si on analyse le fonctionnement de tous les oscillateurs harmoniques, on peut remarquer qu'on peut les classer en deux grands types. Tous les oscillateurs appartiennent à une de ces deux catégories, qui décrivent le principe de fabrication de l'oscillateur. On distingue donc les oscillateurs à rétroaction et les oscillateurs à résistance négative.
Dans ce qui va suivre, nous allons d'abord voir les oscillateurs harmoniques à résistance négative, avant de passer aux oscillateurs à rétroaction, puis les oscillateurs à relaxation.
Les oscillateurs à résistance négative
[modifier | modifier le wikicode]
Les oscillateurs à résistance négative sont fabriqués en mettant en série un circuit résonant avec une résistance négative.
Une résistance négative n'est pas un composant électronique unique à proprement parler, mais un circuit qui simule une résistance un peu particulière, appelée résistance négative. Dans le cas qui nous intéresse, la résistance en question peut être aussi bien une résistance négative statique que dynamique. Dans le premier cas, on veut dire que la tension et le courant à ses bornes ne sont pas dans le bon. Pour une résistance normale, la tension et le courant sont des sens opposés : la tension va d'une borne à l'autre, le courant va dans le sens inverse. Mais pour une résistance négative, les deux sont dans le même sens. Pour une résistance dynamique négative, le courant qui passe dans la résistance diminue quand on augmente la tension, jusqu'à un certain point.
 |
 |
Le circuit résonant est un circuit qui se comporte approximativement comme un oscillateur en lui-même. Le cas le plus connu est le circuit LC, où un condensateur et une inductance sont placés en série/parallèle. Un autre exemple est un cristal de Quartz soumis à un échelon de tension. De tels circuits ont un comportement périodique, qui peut être utilisé pour fabriquer une tension sinusoïdale. Cependant, de tels circuits sont rarement parfaits : ils ont une résistance interne qui amortit leurs oscillations. Pour éliminer l’amortissement, il suffit de compenser leur résistance interne par quelque chose, ce quelque chose étant une résistance négative égale. En plaçant la résistance négative en série, on arrive à annuler la somme des deux résistances (interne et négative), ne laissant que le circuit résonant parfait, qui fonctionne comme un oscillateur.
Les oscillateurs (R)LC sans résistance négative
[modifier | modifier le wikicode]
Un circuit LC, composé d'une bobine et d'un condensateur en série/parallèle, est en soi un oscillateur isolé. La tension aux bornes d'un tel circuit est en effet égale à :
La tension mesurée aux bornes du condensateur est une tension alternative sinusoïdale et il en est de même aux bornes de la bobine, à cause de la loi des mailles. La tension et le courant sont illustrés dans la figure de droite. La tension sinusoïdale a une fréquence égale à :

Mais cela ne vaut que pour des oscillateurs idéaux, basés sur des bobines et des condensateurs idéaux. Mais dans la réalité, les bobines ont une résistance non-nulle. Il n'existe donc pas de circuit LC pur, dans la réalité. Tous les circuits LC réels se comportent comme des circuits RLC idéaux. Et quand on le soumet à une impulsion (un échelon de tension brutal, par exemple), un circuit RLC ne fournit pas de tensions sinusoïdale en sortie. À la place, la tension de sortie ressemble à une sinusoïde qui s'atténue avec le temps, une sinusoïde amortie. Une telle sinusoïde est illustrée ci-dessous. La vitesse d'amortissement de la sinusoïde dépend de la résistance, plus précisément du facteur d'amortissement du circuit qui est proportionnel à la résistance.

Pour supprimer l'amortissement, il faut éliminer la résistance. En compensant la résistance du circuit avec une résistance négative, on obtient bien un oscillateur. La résistance négative a juste à être placée en série du circuit (R)LC, avec une valeur de résistance exactement calibrée.

En guise de résistance négative, on peut utiliser divers montages ou composants électroniques. On peut utiliser les montages à AOP, des transistors câblés d'une manière bien précise, etc. Et chaque possibilité donne naissance à un oscillateur bien particulier.
L'oscillateur avec une résistance négative émulée par un AOP
[modifier | modifier le wikicode]Il est possible d'émuler une résistance négative par un montage à AOP. Les montages en question sont illustrés ci-dessous.
 |
 |
En utilisant un tel circuit dans un oscillateur à résistance négative, on obtient ce circuit :

L'oscillateur à diode Gunn
[modifier | modifier le wikicode]L'exemple qui suit, utilise une diode Gunn, un composant qui a une résistance dynamique négative. Nous n'en dirons pas plus sur ce composant pour le moment, tout ce qu'il y a à savoir est qu'elle a une résistance dynamique négative. La diode est placée en série du circuit (R)LC. Elle est choisie de manière à avoir une résistance exactement opposée à la résistance du circuit RLC. Le circuit en question est illustré ci-contre.
Notons que le circuit ne fonctionne que si une tension est placée de manière à charger le circuit (R)LC. Il faut donc ajouter un générateur de tension couplé à un interrupteur. L’interrupteur est fermé pour charger le circuit, et s'ouvre une fois l'oscillateur chargé. Le circuit complet est illustré ci-dessous.

Les oscillateurs à rétroaction
[modifier | modifier le wikicode]
Les oscillateurs du premier type sont les oscillateurs à rétroaction. Leur nom trahit le fait que ce sont des circuits à rétroaction, comme ceux que nous avons vu dans le chapitre sur la rétroaction. Et pour être précis, ce sont des circuits à rétroaction positive. Rappelons que ces circuits sont composé de deux circuits mis en boucle l'un avec l'autre. Le premier est ici un AOP, qui multiplie par son entrée. L'autre circuit fait la même chose, sauf que le coefficient est différent et est noté . Pour résumer, est le coefficient d'amplification de l'AOP, alors que est le coefficient d'amplification du circuit de rétroaction. Dans le cas présent, un oscillateur à rétroaction est basé sur un AOP mis en boucle avec un filtre passe-bande.
On pourrait croire que l'on peut réutiliser les acquis vus dans le chapitre sur la rétroaction, mais il n'en est rien. Dans le chapitre mentionné, nous avions parlé des oscillateurs stables, dans le sens où le circuit voit sa sortie se stabiliser à une valeur fixe. La transmittance d'un tel circuit est égal à :
Or, un oscillateur ne fonctionne pas en régime stable, mais en régime instable. En clair, sa transmittance doit être infinie, à savoir que sa sortie doit être finie pour une entrée nulle.
Pour cela, il faut que le produit . En conséquence, le filtre passe-bande est tel qu'il annule l'amplification de l'AOP : son est l'inverse de l' de l'AOP, ce qui fait que leur produit vaut 1. Un signifie que le gain d'un tour de la boucle (un passage par l'AOP, puis dans le circuit de rétroaction) est de 1 : le signal n'est ni amplifié, ni atténué lors d'un passage das la boucle.
Précisons que ce critère n'est réalisé que pour une fréquence bien définie, la fréquence du signal à produire. Pour les autres fréquences, le produit est inférieur à 1. En conséquence, la fréquence sélectionnée va rester, alors que toutes les autres fréquences vont progressivement être atténuées. Le circuit va donc reproduite la fréquence voulue, mais les autres fréquences seront supprimées.
Reste qu'un circuit à rétroaction est censé avoir une entrée. En théorie, on pourrait ajouter une entrée au circuit, qui envoie un signal quelconque. Mais les oscillateurs à rétroaction sont différents. Il n'y a pas nécessité d'avoir une entrée. En réalité, le fil en entrée de l'AOP subit toujours de petites variations de tension, liées à des perturbations électromagnétiques ou à des variations de tension aléatoires. Ces variations sont une forme de bruit, qui a diverses origines : bruit d'origine thermique lié au déplacement thermique des charges du métal, autres. Ce bruit est, comme tout signal, la superposition d'une infinité de fréquences, la fréquence voulue en faisant partie. La fréquence voulue sera alors amplifiée par l'AOP, passé au filtre passe-bande, et cela plusieurs fois de suite. Les autres fréquences finiront par être atténuées, ne laissant que la fréquence voulue.

Les oscillateurs RC et LC à rétroaction
[modifier | modifier le wikicode]Le filtre passe-bande utilisé peut être un circuit RC, un circuit LC, un filtre actif, voire un filtre fabriqué avec un cristal de Quartz. Les oscillateurs RC utilisent un réseau de résistances et de condensateurs comme filtre passe-bande. Les oscillateurs LC utilisent, quant à eux, un réseau d'inductances et de condensateurs. Ils sont plus rares et les plus connus sont les oscillateurs Coolpits et Hartley. Ils ont un circuit LC pour filtre passe-bande et l'amplificateur du montage est implémenté avec un transistor unique.
 |
 |
L'oscillateur de Wien
[modifier | modifier le wikicode]
L'oscillateur de Wien est fabriqué en couplant un montage non-inverseur à un réseau RC. Le réseau RC est composé d'un circuit RC série placé en série avec un circuit RC parallèle. Le circuit est illustré ci-contre. Le réseau RC agit comme un filtre passe-bande assez particulier. Le circuit RC série agit comme un filtre passe-haut, alors que le circuit RC parallèle agit comme un filtre passe-bas (il est alimenté par un courant, compte tenu de la configuration du circuit, ce qui lui permet d'agir comme un filtre passe-bas). L'ensemble du réseau RC agit donc comme un filtre passe-bande.
Le gain de boucle de ce circuit est égal au produit de deux termes : le gain du montage non-inverseur et le gain du réseau RC.
Le gain du montage non-inverseur est égal à :
Pour le réseau RC, la transmittance dépend de l'impédance du circuit série , et de celle du circuit parallèle . En analysant le circuit, on trouve que sa transmittance est égale à :
Le gain de boucle vaut donc :
En remplaçant les valeurs d'impédances par leur valeur respective, on trouve :
Pour permette une oscillation, il faut que le déphasage entre entrée et sortie de la boucle soit nul. Cela signifie que la transmittance doit être un nombre réel. Pour cela, il faut que , ce qui n'est possible que pour . À cette fréquence, on a :
Pour que , il faut que .
L'oscillateur à déphasage
[modifier | modifier le wikicode]
L'oscillateur à déphasage couple un AOP à gain négatif à un réseau RC qui sert de filtre passe-bande.
Par AOP à gain négatif, on veut simplement dire que l'AOP amplifie la tension d'entrée et change son signe. Dans le cas le plus simple, l'AOP à gain négatif est implémenté par un simple montage inverseur. Le gain d'un tel montage est négatif, égal à :
Le fait que l'AOP ait un gain négatif signifie qu'il déphase le signal d'entrée de 180°. Le réseau RC doit donc avoir lui aussi in déphasage de 180°, pour que le déphasage de la boucle soit nul. Sans quoi, il ne peut pas y avoir d'oscillations. Le réseau RC est en trois sections, trois circuits RC placés en série l'un de l'autre. Le nombre de cellules RC mises en série n'est pas anodin : le circuit ne fonctionnerait pas avec moins de trois cellules. En effet, un réseau RC à une ou deux cellules en série ne peut pas avoir de déphasage égal à 180°. il faut absolument au moins trois cellules pour cela.
La fréquence d'un tel circuit est de :
L'oscillateur à Quartz
[modifier | modifier le wikicode]Les oscillateurs RC et LC sont utilisés pour fournir des signaux de faible fréquence, de moins de 100 Mhz. Difficile de les utiliser au-delà, en raison de la taille des condensateurs et des résistances. Pour des fréquences plus élevées, on doit utiliser des oscillateurs à Quartz.
Les cristaux de Quartz comme filtres passe-bande
[modifier | modifier le wikicode]Avec ceux-ci, le filtre passe-bande, le circuit de rétroaction, est composé d'un cristal de Quartz qui se comporte comme un filtre passe-bande mécanique. Cela vient d'une des propriétés des cristaux de Quartz : la piézoélectricité. Un matériau piézoélectrique, comme le Quartz, se déforme en réaction à un champ électrique. Et réciproquement, leur déformation déplace leurs charges internes et un champ électrique apparait sur les faces du cristal. Si on applique une tension périodique sur le cristal, il va se déformer et ces déformations vont elles-mêmes générer une tension périodique en réponse. Le cristal se comporte donc comme un composant, qui prend en entrée une tension et fournit en sortie une autre tension.

Le cristal de Quartz se comporte comme un circuit RLC avec une capacité en parallèle, comme illustré ci-contre. Sachant qu'un filtre RLC est un filtre passe-bande, le cristal se comporte comme un filtre passe-bande. La transmittance inverse d'un cristal de Quartz est donc égale à :
En éliminant l'influence de la résistance, on trouve une transmittance de :
On peut reformuler l'équation précédente comme suit :
L'analyse des équations précédentes nous dit que le cristal a deux fréquences de résonance, deux fréquences d'oscillation possibles.
- Une résonance série égale à :
- Une résonance parallèle égale à :
Si on étudie l'impédance du cristal en fonction de la fréquence, on obtient un spectre semblable à celui-ci :
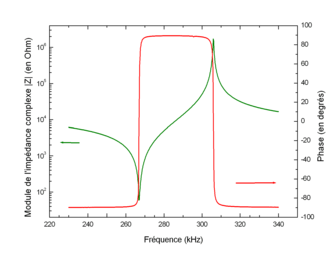
L'oscillateur de Pierce
[modifier | modifier le wikicode]L’oscillateur à Quartz le plus souvent abordé dans les cours d'électronique est l'oscillateur de Pierce. Dans celui-ci, l'amplificateur est implémenté avec une porte logique NON. Le filtre passe-bande est réalisé avec un cristal de Quartz en parallèle avec une résistance, auquel on a couplé deux condensateurs. Le circuit est illustré ci-dessous.

Les oscillateurs non-linéaires
[modifier | modifier le wikicode]Les oscillateurs non-linéaires fournissent une tension de sortie qui n'est pas sinusoïdale, mais carrée, triangulaire ou autre. Globalement, les oscillateurs non-linéaires sont fabriqués à partir de blocs de base, appelés multivibrateurs. Ces derniers se subdivisent en plusieurs types, qui sont appelés les circuits astables, bistables et monostable. Un exemple de circuit bistable n'est ni plus ni moins que le montage comparateur à seuil, que nous avions vu dans le chapitre sur les montages à amplificateurs opérationnels. N'hésitez pas à relire la section associée si vous avez oublié comment fonctionne ce circuit. Nous aurons à l'utiliser dans les circuits qui vont suivre.
Les types principaux d'oscillateurs non-linéaires
[modifier | modifier le wikicode]Les oscillateurs à relaxation sont composés de deux circuits : un circuit de charge et un circuit d'accumulation. Le circuit d'accumulation peut accumuler des charges électriques et se charger/décharger jusqu'à une certaine limite. Le circuit de charge s'occupe à intervalle régulier de remplir, puis de vider le circuit d'accumulation, à une fréquence bien définie. Le circuit d'accumulation est composé d'un condensateur ou d'une inductance, parfois des deux. Le circuit de charge est composé soit d'un AOP, soit d'un transistor, soit d'un comparateur, soit d'un relai, soit d'une résistance négative, etc. La fréquence du circuit dépend de la constante de temps du circuit d'accumulation (du produit RC ou RL).
D'autres oscillateurs non-linéaires sont fabriqués en couplant un oscillateur sinusoïdal avec un circuit qui transforme celle-ci en signal carré/triangulaire/autre. Pour obtenir un signal carré, il faut coupler l'oscillateur avec un circuit dit bistable. Un circuit bistable est un circuit dont la sortie ne peut prendre que deux valeurs : une tension maximale positive, ou une tension minimale nulle/négative. Le passage d'une tension à l'autre se produit en fonction de ce qu'on place sur l'entrée. Un exemple de circuit bistable est le comparateur à un seuil, vu il y a quelques chapitres. Pour rappel, le comparateur à un seuil est un circuit qui fournit une tension positive si la tension d'entrée dépasse un certain seuil, et une tension nulle/négative en dessous de ce seuil. Le comparateur à deux seuils, lui aussi vu il y a quelques chapitres, est aussi un circuit bistable. En couplant un oscillateur sinusoïdal avec un comparateur à un ou deux seuils, on obtient donc un signal carré.
Le cas le plus simple est celui où on couple un oscillateur linéaire avec un comparateur à un seuil. Si le signal d'entrée est une sinusoïde parfaite, alors le signal de sortie sera un signal carré presque parfait. Dans le détail, plus le slew rate de l'AOP est bon, plus le signal sera proche d'un signal carré. Si le signal n'est pas parfait, mais a de petites sautes brutales, l'usage d'un comparateur à un seul seuil peut poser quelques problèmes : les sautes du signal d'entrée peuvent se voir sur la sortie. Si une petite variation fait passer la tension sous le seuil ou au-dessus, alors le signal de sortie va s'inverser. Pour mitiger ce problème, on peut remplacer le comparateur à un seuil par un comparateur à deux seuils. Les sautes brutales de la tension d'entrée ne se voient plus systématiquement sur la sortie. Pour cela, il faut qu'elles passent sous le second seuil, qui est plus bas que le seuil unique du comparateur à un seuil.
Le multivibrateur astable
[modifier | modifier le wikicode]
L'oscillateur que nous allons voir dans cette section est construit à partir d'un circuit bistable, comme un comparateur à deux seuils. En couplant le circuit bistable avec un circuit RC série, on obtient l'oscillateur. Le circuit bistable peut s'implémenter de beaucoup de manières différentes, que ce soit avec des AOP, des transistors, voire d'autres composants moins bien connus.
Les multivibrateurs astables à AOP
[modifier | modifier le wikicode]Pour le cas qui nous intéresse, le circuit bistable en question est un vulgaire comparateur à deux seuils, fabriqué avec des AOP. Le circuit est donc composé d'un AOP avec deux boucles de rétroaction : une boucle de rétroaction positive pour le montage comparateur à deux seuils, et une boucle de rétroaction négative avec le circuit RC. Dans le circuit RC, le condensateur sert de circuit d'accumulation, la résistance n'étant utile que comme intermédiaire à travers lequel on charge/décharge le condensateur. Le circuit est illustré ci-contre, ainsi que ci-dessous.
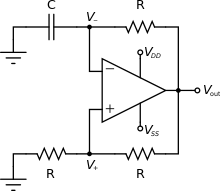 |
 |
Pour comprendre comment fonctionne un tel circuit, imaginons que la sortie du comparateur soit égale à la tension maximale. Dans ce cas, on a une tension positive en entrée du circuit RC, ce qui fait que le condensateur se charge jusqu'à atteindre cette tension. Cependant, la sortie du circuit RC est reliée à l'entrée négative de l'AOP (via la boucle de rétroaction négative). En conséquence, l'augmentation de la tension aux bornes du condensateur se répercute sur l'entrée du comparateur. Quand la tension d'entrée atteint le bon seuil, le comparateur bascule et sa tension de sortie passe dans le négatif, à sa tension minimale. Le comportement du circuit s'inverse alors. Le condensateur est soumis à une tension plus faible que celle à ses bornes, ce qui fait qu'il se vide. La tension à ses bornes diminue, ce qui se répercute à l'inverse sur l'entrée du comparateur. La tension d'entrée du comparateur augmente alors progressivement, au fur et à mesure que le condensateur se vide. Quand la tension d'entrée atteint le second seuil, le circuit rebascule. Et la boucle est bouclée, le circuit recommence de zéro.
La fréquence du circuit est égale à :
- , avec .
Un tel circuit fournit une tension carrée d'un côté du circuit, mais une tension triangulaire déformée sur l'autre côté. En sortie du comparateur, on observe un signal carré, signe que la sortie du comparateur bascule entre sa tension maximale et sa tension minimale d'un seul coup. En sortie du réseau RC, on trouve la tension triangulaire, illustré ci-dessous. Vous reconnaîtrez peut-être que chaque morceau de la courbe ressemble à une courbe de charge ou de décharge d'un condensateur, ce qui est compatible avec ce qu'on a dit précédemment.

En modifiant quelque peu le circuit précédent, on peut obtenir une tension triangulaire en lieu et place de la tension de charge/décharge exponentielle. Pour cela, il faut remplacer le circuit RC série par un montage intégrateur. Ce faisant, le condensateur accumule des charges, mais la tension de sortie du montage est le produit : tension de sortie du comparateur temps. Cette quantité augmente linéairement, ce qui lui donne un aspect de droite sur le graphique. En clair, les courbes de charge/décharge sont remplacées par des segments, ce qui en fait une tension triangulaire.
Les multivibrateurs astables à transistors
[modifier | modifier le wikicode]Il est possible d'implémenter le circuit astable en utilisant des transistors, des composants électroniques qui agissent comme des amplificateurs non-linéaires. Une implémentation d'un circuit astable est illustrée ci-dessous. Mais comprendre le fonctionnement de ce circuit demanderait de connaître en détail le fonctionnement d'un transistor, ce qui sera vu dans les chapitres suivants. Nous n'en parlerons pas ici, donc.

Les multivibrateurs astables à lampe à néon
[modifier | modifier le wikicode]
Comme autre exemple, il était autrefois possible de fabriquer des oscillateurs avec des lampes à néon ! En couplant celles-ci avec un circuit RC série, on obtenait un oscillateur assez rustique, mais qui marchait. Le fonctionnement de ce montage est lié au fonctionnement de la lampe à néon, et plus précisément à ce qu'on appelle l'effet Pearson–Anson. Celui-ci dit que si l'on connecte une lampe à néon en parallèle avec un condensateur, et qu'on alimente le tout avec un courant continu, alors la tension de sortie du montage oscille spontanément. Le circuit lampe à néon + condensateur se comporte donc comme un oscillateur. Pour obtenir le courant continu, on peut utiliser un générateur de courant continu, ou alors une tension continue en série avec une résistance.

La tension de sortie d'un tel oscillateur à lampe à néon était une tension presque triangulaire, semblable à la tension de sortie non-lissée de l'oscillateur astable à AOP. Il faut dire que le fonctionnement du montage est presque identique. La lampe à néon fonctionne comme une résistance variable à deux seuils. Pour faire simple, prenons le cas où la tension à ses bornes augmente progressivement. Dans ce cas, elle a une résistance élevée au-dessous d'une tension seuil, mais une résistance plus faible au-delà de la tension seuil. Quand la tension à ses bornes descend, c'est la même chose, sauf que le seuil est différent. Les seuils pour faire commuter la résistance sont respectivement élevé pour la faire baisser, faible pour la faire augmenter. Quand on connecte le montage, le condensateur est vide et la tension à ses bornes est basse. Vu que cette tension alimente la lampe à néon, la lampe à néon ne conduit pas et le condensateur se charge à travers la résistance. Mais quand la tension du condensateur dépasse la tension seuil haute, la lampe se met à conduire et le condensateur se décharge à travers la lampe à néon. La tension chute alors et descend tant qu'elle reste supérieure à la tension seuil basse. Une fois cette tension seuil basse atteinte, la lampe cesse de conduire le courant. Et rebelote : un nouveau cycle commence.

Il était même possible d’enchaîner plusieurs lampes à néon pour améliorer la tension en sortie de l'oscillateur.
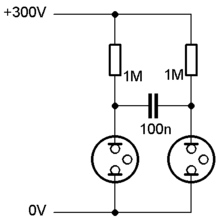 |
 |
Les semi-conducteurs
Les semi-conducteurs sont des solides dont la résistance varie selon la température ou d'autres paramètres physiques. Ce comportement s'explique par le fait que les électrons des atomes deviennent des électrons libres si on leur donne une énergie suffisante. Les électrons arrachés aux atomes deviennent des porteurs de charge, qui peuvent alors conduire le courant. Le courant dans les semi-conducteurs est dominé par les électrons libres créés par "ionisation" du solide, ce qui fait que l'étude de cette "ionisation" est importante.
La théorie des bandes des solides
[modifier | modifier le wikicode]
La théorie des bandes est une théorie physique qui décrit le fonctionnement des semi-conducteurs, mais aussi des conducteurs et des isolants. Nous allons la présenter sous une forme vulgarisée et particulièrement simplifiée. Pour résumer simplement, cette théorie dit que les électrons dans un solide peuvent être dans deux états : soit ils sont fortement liés aux atomes, soit ce sont des électrons libres. Si les électrons libres peuvent servir de porteurs de charges, ce n'est pas le cas des électrons liés. Là où les électrons libres peuvent parcourir la totalité du solide, les électrons liés confinés dans les atomes, d'où ils ne peuvent pas sortir. Les électrons liés appartiennent aux atomes (ils orbitent autour du noyau atomique) et participent aux liaisons chimiques entre atomes.
La différence entre les deux tient dans leur énergie : l'attraction atomique enlève un peu d'énergie aux électrons, pour des raisons que nous éludons ici. Les électrons de faible énergie sont liés aux atomes et ne peuvent pas servir de porteurs de charges. À l'inverse, les électrons à forte énergie sont des électrons libres, qui ont quitté l’attraction atomique du fait de leur forte énergie. Dans un solide, l'énergie d'un électron se trouve systématiquement dans deux intervalles possibles : un intervalle de faible énergie et un autre où elle est plus forte. Les électrons liés ont une énergie dans l'intervalle de faible énergie, appelé la bande de valence. À l'inverse, l'intervalle d'énergie des électrons libres est appelé la bande de conduction. Entre les deux, on peut trouver un intervalle d'énergie dans lequel aucun électron ne peut se trouver : la bande interdite.

On peut déjà comprendre pourquoi certains matériaux sont naturellement conducteurs ou non. Au zéro absolu, les porteurs de charge vont se répartir dans les bandes de conduction et de valence, selon leur énergie. L'énergie maximale que peut avoir un électron au zéro absolu est appelée l'énergie de Fermi. Selon que cette énergie de Fermi se situe dans la bande de conduction ou non, on se trouve face à deux situations différentes.
- Premier cas : l'énergie de Fermi se situe dans la bande de conduction. Des électrons se trouvent alors dans la bande de conduction, même au zéro absolu. Ce qui veut dire que le matériau contient naturellement des porteurs de charges pouvant conduire le courant et est donc conducteur.
- Deuxième cas : l'énergie de Fermi se situe dans la bande de valence ou interdite. Dans ce cas, tous les électrons seront dans la bande de valence. Tous les électrons du matériau sont donc liés et aucun porteur de charge n'est disponible. Le matériau est alors isolant ou semi-conducteur (on verra pourquoi les semi-conducteurs sont dans ce cas juste après).
Semi-conducteurs et isolants
[modifier | modifier le wikicode]
Pour comprendre la différence entre semi-conducteurs et isolants, il faut étudier comment des électrons peuvent transiter entre les bandes de valence et de conduction. Il est possible de dé-confiner un électron en lui fournissant assez d'énergie, ce qui lui permet de vaincre l'attraction atomique et de quitter l'atome. Un bon moyen pour cela est d'augmenter la température du solide, ce qui augmente l'énergie cinétique des électrons. Dit autrement, dé-confiner un électron demande juste de lui fournir assez d'énergie pour passer de la bande de valence vers la bande de conduction. L'énergie qu'il faut fournir pour cela, à savoir la différence d'énergie entre bande de valence et de conduction, est appelée le gap d'énergie. On peut le voir grossièrement comme une énergie d'ionisation pour un électron dans un solide.
La différence entre semi-conducteurs et isolants tient dans le gap d'énergie.
- Pour les isolants, le gap d'énergie est important : il faut fournir une grande quantité d’énergie pour dé-confiner un électron. À des températures normales, la totalité des électrons sont des électrons liés aux atomes et le solide ne contient aucun porteur de charges. À de plus hautes températures, il est cependant possible de créer quelques électrons libres, mais rien de bien folichon.
- Pour les semi-conducteurs, il faut une faible énergie pour dé-confiner un électron. Une petite augmentation de température suffit pour faire passer des électrons de la bande de valence vers la bande de conduction. Dit autrement, une augmentation de température assez faible permet de créer suffisamment d'électrons libres pour conduire le courant.
- Pour les métaux, il n'y a pas besoin de fournir de l'énergie pour dé-confiner les électrons. Le métal contient naturellement des électrons libres, même à de faibles températures. Il conduit donc naturellement le courant. Les métaux sont naturellement ionisés, et on peut les voir comme un cristal ionisé qui baigne dans un fluide d'électrons libres. La bande de valence et de conduction se chevauchent.

Les trous quantiques
[modifier | modifier le wikicode]
Quand un électron lié devient un électron libre, l'atome initial s'ionise et obtient une charge positive opposée à celle de l'électron. D'après les règles compliquées de la physique quantique, on peut considérer qu'un déficit de charge se comporte comme une particule de charge positive, appelée trou. Il ne s'agit pas d'une vraie particule, mais on peut parfaitement faire comme si c'était le cas. Donc, toute formation d'un électron libre donne naissance à un trou dans l'atome qu'il quitte. Le processus inverse, à savoir la disparition d'un trou par capture d'un électron libre, est aussi possible. Il est possible qu'un électron libre se lie à un atome "ionisé", faisant disparaitre le trou. Ce processus est appelé la recombinaison.
Chose importante, les trous peuvent parfaitement se déplacer dans le solide, en sautant d'atome en atome, de proche en proche. Ils se comportent comme des porteurs de charge qui circulent dans le solide et permettent de conduire le courant. Pour comprendre pourquoi, il faut rappeler qu'un trou est un déficit d'électron dans un atome. Ce déficit d'électron peut être compensé par recombinaison avec un électron libre, mais aussi par un électron lié provenant d'un atome voisin. Dans ce cas, l'atome fournisseur de l’électron, initialement neutre, hérite du déficit de charge. Ainsi, le déficit d'électron se déplace dans le métal en sautant d'atomes en atomes, de proche en proche. Les électrons de valence étant attirés eux aussi par la borne positive, ils vont sauter d'atomes en atomes avec une préférence pour la direction positive. Ainsi, le courant dans les semi-conducteurs provient de deux sources : un courant d'électrons libres, et le déplacement des électrons atomiques d'atomes en atomes. Le courant de proche en proche des électrons se reformule alors comme un courant de trous, qui sont donc des porteurs de charge.
Les semi-conducteurs intrinsèques et extrinsèques
[modifier | modifier le wikicode]Les semi-conducteurs se différencient selon leur densité de trous et d'électron, qui peut varier selon divers paramètres. La température est déterminante pour certains semi-conducteurs, alors qu'elle l'est moins pour d'autres. Cela permet de classer les semi-conducteurs en deux types :
- les semi-conducteurs intrinsèques ;
- les semi-conducteurs extrinsèques.
Les semi-conducteurs intrinsèques
[modifier | modifier le wikicode]Les semi-conducteurs intrinsèques sont des semi-conducteurs pour lesquels la résistance dépend de la température. Ils sont totalement isolants au zéro absolu, mais leur résistance diminue quand on les chauffe. Dans ces semi-conducteurs, la formation des électrons-libres est liée exclusivement à la température. La formation des paires électrons-trous a lieu quand un électron reçoit suffisamment d'énergie thermique pour s'arracher de son atome. Il va de soi que plus la température est forte, plus cela a de chances d'arriver : le nombre d'électrons libres augmente donc avec la température, ce qui se répercute sur la conductivité. On peut remarquer que, la formation de chaque électron libre laisse un trou dans le solide. Dit autrement, si on note n la concentration en électrons libres et p la concentration en trous, on a :
On peut aussi reformuler l'équation précédente de la manière suivante, qui a l'avantage d'être aussi valable pour les semi-conducteurs extrinsèques.

Les physiciens ont démontré une formule qui permet de calculer directement la valeur de n (et donc de p). Dans celle-ci, on utilise les notations suivantes : A une constante qui dépend du matériau étudié, T pour la température, K pour la constante de Boltzmann, la largeur de la bande interdite (la bande de Fermi). Ce dernier paramètre est l'énergie minimum qu'il faut pour générer une paire électron-trou. C’est aussi l'énergie nécessaire pour briser une liaison covalente entre deux atomes, ce qui permet de transformer un électron lié en électron libre.
Les semi-conducteurs extrinsèques
[modifier | modifier le wikicode]Mais à côté des semi-conducteurs intrinsèques, on trouve les semi-conducteurs extrinsèques, dont la conduction ne dépend pas que de la température. Leur caractéristique principale est qu'ils ont des porteurs de charges disponibles, même au zéro absolu. On distingue les semi-conducteurs qui contiennent des trous au zéro absolu de ceux qui ont des électrons libres. Les premiers sont appelés semi-conducteurs P et les seconds des semi-conducteurs N. Les schémas ci-dessous illustrent cette distinction. Les trous sont en blanc, alors que les électrons libres sont en noir.
Il faut noter que des paires électrons-trous peuvent se former sous l'effet de la température, dans un semi-conducteur extrinsèque. Le semi-conducteur extrinsèque fonctionne donc comme un semi-conducteur intrinsèque, la différence étant dans le nombre de porteur de charge total. Là où le semi-conducteur intrinsèque n'a aucun porteur de charges au zéro absolu, le semi-conducteur extrinsèque part avec un peu d'avance. Cela fait que les semi-conducteurs extrinsèques ont naturellement une meilleure conductivité, vu qu'ils possèdent plus de porteurs de charges. Le nombre total de porteurs de charges dépend de la température, mais on peut cependant faire une remarque importante. Pour les deux types de semi-conducteurs, il se forme autant d'électrons libres que de trous sous l'effet de la température. Mais les semi-conducteurs extrinsèques possèdent un déséquilibre de charges au zéro absolu : ils vont avoir plus d'électrons que de trous au zéro absolu, ou l'inverse. Et cet excès n'est pas compensé par la formation de paires électrons-trous : ce déséquilibre est permanent. En clair, à la différence des semi-conducteurs intrinsèques, la quantité de trous n'est pas égale à la quantité d'électrons libres pour les semi-conducteurs extrinsèques. La relation entre nombre de porteurs de charges, valable pour les deux types de semi-conducteurs, est la suivante :
Le dopage de semi-conducteurs
[modifier | modifier le wikicode]Les semi-conducteurs extrinsèques sont fabriqués en ajoutant des impuretés à un semi-conducteur intrinsèque. Les impuretés ajoutent des trous ou des électrons libres au matériau de base, i, ce qui en fait un semi-conducteur extrinsèque. Ce processus d'ajout d'impuretés s'appelle le dopage, d'où le nom de semi-conducteur dopés qui est parfois donné aux semi-conducteurs extrinsèques. Lors du dopage, les impuretés vont se lier chimiquement aux atomes du semi-conducteur. Cependant, il restera un électron ou un trou en trop suite à ce processus, qui serviront de porteurs de charges.
- Pour les semi-conducteurs de type N, les impuretés sont plus riches en électrons que les atomes du solide. Il y a alors un électron en trop après dopage, qui devient un électron libre.
- Pour les semi-conducteurs de type P, les impuretés sont plus pauvres en électrons que les atomes du solide. Il manque un électron suite au dopage, ce qui donne un trou.
D'ordinaire, le dopage part d'un morceau de silicium et y ajoute des impuretés en Bore ou en Phosphore. Le silicium peut se lier chimiquement avec quatre atomes via ce qu'on appelle une liaison covalente. Avec celle-ci, l'atome de Silicium partage un électron avec un atome voisin : l'électron appartient alors aux deux atomes.Vu que le silicium peut participer à quatre liaisons covalentes, il peut fournir quatre électrons en tout. Les impuretés vont aussi former des liaisons covalentes avec le silicium, sauf qu'elles peuvent partager 3 ou 5 électrons dans des liaisons covalentes.
- Par exemple, le Phosphore partage 5 électrons, et peut former 5 liaisons covalentes. Un atome de Phosphore prendra la place d'un atome de Silicium dans le solide et ne tissera que quatre liaisons covalentes (il ne peut pas en faire plus pour des raisons assez compliquées). Quatre électrons seront donc utilisés dans ces liaisons, ce qui laisse un électron en trop, qui quitte l'atome et devient un électron libre. Le dopage obtenu est dit de type N, à savoir qu'il ajoute des électrons libres dans le Silicium.
- Le bore est dans la situation inverse, à savoir qu'il peut partager 3 électrons, ce qui donne trois liaisons covalentes. Il tisse bien quatre liaisons covalentes, le Silicium lui fournissant les électrons manquant, mais il manque quand même un électron. Ce manque n'est autre qu'un trou. Le dopage obtenu est dit de type P, à savoir qu'il ajoute des trous dans le Silicium.
Effet du dopage sur les bandes de conduction et de valence
[modifier | modifier le wikicode]Le dopage a un effet sur les bandes de valence et de conduction, en augmentant ou diminuant leurs extrémités. Le dopage de type N abaisse la bande de conduction, alors celui de type P remonte la bande de valence. Dans les deux cas, la bande interdite se réduit, ce qui facilite le dé-confinement des électrons.
La conductivité d'un semi-conducteur
[modifier | modifier le wikicode]Les parties précédentes ont surtout abordé la quantité de trous et d'électrons présente dans un semi-conducteur. Si nous avons passé beaucoup de temps à étudier ce sujet, c'est parce que celle-ci explique pourquoi la conductivité des semi-conducteurs varie. Dans cette section, nous allons voir qu'il existe un lien très fort entre la résistance d'un matériau et le nombre de porteurs de charges. Plus il y a de porteurs de charges (électrons libres ou trous), plus le matériau pourra conduire facilement le courant. Et donc, tout ce qui peut faire varier le nombre de porteur de charge a une influence directe sur la résistance du matériau. Prenons par exemple un semi-conducteur intrinsèque : une augmentation de la température va augmenter la quantité d'électrons et de trous, ce qui va diminuer la résistance du semi-conducteur. Voyons ce mécanisme plus en détails.
Les semi-conducteurs peuvent conduire le courant grâce à deux mécanismes distincts. Le premier est à l'origine de la résistance du matériau et se décrit assez bien avec la loi d'Ohm. Il donne naissance à un courant appelé courant de dérive. Le second permet d'homogénéiser la densité de charge dans le matériau, celles-ci tendant à se répartir uniformément dans l'espace. Cela induit un déplacement de charge appelé courant de diffusion. Le courant dans un semi-conducteur est la somme d'un courant de dérive et du courant de diffusion .
Le courant de dérive
[modifier | modifier le wikicode]Le premier, appelé le courant de dérive, est aussi présent chez les conducteurs normaux (comprendre les métaux et électrolytes). Il apparait quand on soumet le semi-conducteur à une tension/un champ électrique et sa valeur dépend de cette première ainsi que de la résistance du matériau. C'est lui qui intervient dans la loi d'Ohm pour les conducteurs. La conductivité d'un matériau, définie pour le courant de dérive, dépend de la densité de porteurs de charges et de leur mobilité .
Cette équation nous dit que plus le nombre de porteurs de charges d'un matériau est grand, plus sa conductivité sera importante. On retrouve donc ce qu'on a dit plus haut : les conducteurs le sont parce qu'ils ont un grand nombre de porteurs de charges, alors que les isolants le sont parce qu'ils n'en ont pas. Pour les semi-conducteurs, la situation est intermédiaire : le nombre de porteurs de charges est très faible en temps normal, mais augmente fortement avec la température, l’éclairement, ou d'autres paramètres physiques. Pour les semi-conducteurs, cette formule s'applique partiellement (il faut rajouter un second courant dit de diffusion qui provient de la concentration des porteurs de charges). Quoiqu’il en soit, on a un courant de trous et un autre courant d'électrons. Ces deux types de charges ont certes la même charge, mais leur densité n'est pas la même, pas plus que leurs mobilités et . En faisant la somme des deux courants, on a :
Le courant de diffusion
[modifier | modifier le wikicode]Outre le courant de dérive vu dans le section précédente, les semi-conducteurs sont parcourus par un second type de courant. Celui-ci, le courant de diffusion, vient d'une différence de concentration des porteurs de charges. Ceux-ci ne sont pas forcément répartis de manière homogène dans le matériau, du fait des hasards de la formation des paires électrons-trous. Il arrive donc que les électrons soient plus nombreux à un endroit du matériau que dans d'autres. Dit autrement, la concentration en électrons libres et/ou en trous n'est pas uniforme et varie dans le matériau. Mais ces différences de concentration se traduisent par une répartition inhomogène des charges : le matériau sera chargé négativement là où il y a un excès d'électrons, positivement là où il en manque, en suivant le gradient de concentration. Ce mouvement de charges donne naissance à un courant dit de diffusion, régit par les lois physiques de la diffusion et décrit par l'équation de la diffusion :
- j est la densité de courant en un point du matériau ;
- e est la charge électrique d'un électron/trou ;
- D est un coefficient appelé coefficient de diffusion ;
- est le gradient de concentration des charges.
Voici l'équation pour le courant d'électrons libres :
Et voici l'équation pour les trous :
Il existe une relation entre le coefficient de diffusion et la mobilité des porteurs de charge. Celle-ci est appelée la relation d'Einstein :
Le terme : est appelé la tension thermique.
Les jonctions PN
Les résistances, condensateurs et bobines, vus dans les chapitres précédents, sont fabriqués avec des matériaux conducteurs et isolants. Mais certains récepteurs sont fabriqués avec des matériaux semi-conducteurs. Parmi ceux-ci, on peut citer les diodes et les transistors. Dans ce chapitre, nous allons parler des semi-conducteurs, ainsi que des composants fabriqués à partir de ceux-ci. Nous allons notamment parler des diodes et des transistors. Pour cela, nous allons devoir parler des briques de base des diodes et transistors. : les jonctions PN. Celles-ci sont composées d'un morceau de semi-conducteur dopé P accolé à un semi-conducteur dopé N.

La jonction PN au repos
[modifier | modifier le wikicode]Pour commencer, nous allons étudier une jonction PN au repos, c’est-à-dire non-soumise à une tension extérieure. On pourrait croire que décrire cette jonction est très simple : ce n'est que deux morceaux de semi-conducteurs placés côte-à-côte, rien de bien sorcier. Mais dans les faits, ce n'est pas le cas. La raison à cela est qu'il va s'établir un courant de diffusion à travers les régions P et N, ainsi qu'un courant de dérive. Le courant de diffusion transfigure la jonction PN et transforme celle-ci d'une manière fort intéressante. Les propriétés surprenantes des jonctions PN proviennent de cette transfiguration, de cette métamorphose de la jonction PN. Sans elle, nous n'aurions pas de transistors, ni de diodes, et encore moins de composants électroniques de haut niveau. Aussi, vaut mieux passer du temps à étudier ce qui se passe dans une jonction PN au repos.
L'influence du courant de diffusion
[modifier | modifier le wikicode]Quand on place du morceau P à côté d'un morceau N, des échanges de porteurs de charges vont avoir lieu. Des courants de diffusion vont alors naître, avec un courant d’électrons libre d'un côté, et un courant de trous de l'autre. Les électrons de la région N vont diffuser dans la région P et y se recombiner avec les trous présents. Même chose pour les trous de la région P, qui vont diffuser dans la région N et s'y recombiner avec les électrons autochtones. Le bord de la région P va ainsi voir ses trous disparaître progressivement, alors que celui de la région N s'appauvrit en électrons. Si les régions P et N étaient intégralement neutre électriquement, ce qui n'est plus le cas après diffusion des porteurs de charges. La région N perd des électrons et devient donc positive, alors que la disparition des trous donne une charge négative à la région P. Il va rester une zone sans trous ou électrons, intercalée entre les régions P et N "normales", non-chargées. Cette zone de déplétion est composée d'une zone chargée positivement collée à une zone de charge négative.
 |
 |
La tension de déplétion
[modifier | modifier le wikicode]
Les charges présentes dans la zone de déplétion vont entraîner l'apparition d'une tension entre les régions N et P. Les électrons et trous auront du mal à passer cette barrière de tension, qui les repousse. Les électrons ont alors du mal à se diffuser vers la région P, de même que les trous sont empêchés de passer dans la région N. À l'équilibre, les courants d'électrons et de trous vont se compenser parfaitement, donnant un équilibre stable. Il existe alors une légère tension aux bornes de la zone de déplétion. Nous appellerons celle-ci tension de déplétion. Petite précision : cette tension est purement interne à la jonction PN et ne se retrouve pas à ses bornes. Dit autrement, la tension aux bornes d'une jonction PN au repos est nulle, même si la tension de déplétion ne l'est pas. La raison à cela tient au fait que cette tension est perdue dans les contacts métalliques qui relient la jonction à ses bornes. La physique des semi-conducteurs nous fournit une équation qui donne la tension de déplétion en fonction de la tension thermique et des concentrations de charges des régions N et P notées et :
On peut comprendre plus facilement l'origine de la zone de déplétion en regardant les niveaux des bandes de conduction et de valence entre les régions P et N. Rappelons que le dopage fait monter ou descendre la bande interdite (l'intervalle d'énergie où aucun électron ne peut se trouver). Dans le cas du dopage de type N, la bande de conduction (le plafond de la bande interdite) descend. Pour le dopage de type P, c'est la bande de Fermi (le plancher de la bande interdite) qui remonte. Si on place une région P à côté d'une région N, les bandes interdites des deux régions ne seront pas alignées : on observera une discontinuité. L'établissement de la zone de déplétion rend la transition entre les deux bandes interdites plus continue, plus graduelle. À l'équilibre, la transition a la forme d'une marche, dont la hauteur n'est autre que l'énergie qu'il faut fournir pour faire passer un électron de la région N vers la région P.

La longueur de la zone de déplétion
[modifier | modifier le wikicode]La zone de déplétion a une taille limitée dans le semi-conducteur, une certaine longueur. Quelques arguments purement physiques permettent de calculer cette longueur , avec l'équation suivante :
Il faut noter que la zone de déplétion est composée d'une zone chargée positivement et d'une autre chargée négativement, qui ont les longueurs respectives et . Et ces deux sous-zones ne sont pas forcément d'égales longueurs : tout dépend des dopages des régions P et N. Si les concentrations et sont égales, alors les deux régions sont d'égales longueurs. Mais si , alors une région sera plus grande que l'autre. Pour être précis, la région de déplétion pénètre plus profondément dans le matériau le moins dopé. Pour comprendre pourquoi, rappelons que la zone de déplétion reste neutre électriquement, la région positive compensant la région négative. Donc, moins la région est concentrée en charge, plus elle devra être grande pour atteindre la charge assurant la neutralité. On peut vérifier cela mathématiquement en partant de l'équation qui donne l'égalité des charges :
- , avec A la section de la jonction PN.
Quelques manipulations algébriques triviales donnent :
En combinant les équations précédentes avec l'équation , on obtient les équations suivantes :
Ces équations formulent mathématiquement le résultat précédent : la région de déplétion pénétrera plus profondément dans le matériau le moins dopé.
La quantité de charges contenues dans la zone de déplétion au repos
[modifier | modifier le wikicode]On peut calculer la quantité de charge dans la zone de déplétion en utilisant les équations précédentes :
- , avec A la section de la jonction PN.
- et
On trouve alors :
L'influence du courant de dérive
[modifier | modifier le wikicode]Outre le courant de diffusion, il existe aussi un courant de dérive dans la jonction PN. À tout instant, des paires électron-trous vont se former dans le semi-conducteur, que ce soit dans la portion N ou la portion P. Certaines vont se former près de la région de déplétion, et vont être bloquées ou emportées par la tension de déplétion. Par exemple, prenons une paire électron-trou qui se forme dans la région N : si les électrons vont être bloqués par la tension de déplétion, les trous vont au contraire être attirés par celle-ci et vont passer dans la région P. Il se passe le phénomène inverse dans la région P : les électrons qui s'y forment sont emportés de l'autre côté par la tension de déplétion, alors que les trous y sont confinés. On se retrouve avec deux courants : un pour les déplacements de trous de la région N vers la région P, et celui des électrons qui vont dans l'autre sens. Ces deux courants s'additionnent et forment un courant de dérive à l'intérieur de la jonction PN.
À l'équilibre, pour une jonction PN au repos, le courant de dérive et le courant de diffusion s'annulent l'un l'autre. Si on pose le courant de diffusion et le courant de dérive, on a :
La jonction PN soumise à une tension
[modifier | modifier le wikicode]Maintenant, étudions ce qui se passe quand on met une tension aux bornes de la jonction PN. Suivant que la tension est positive ou négative, deux cas sont possibles :
- Si on place le + sur la jonction P et la borne - sur la jonction N, on dit la jonction est alimentée en sens direct[1].
- Si on met le + sur la portion N et le - sur la portion P, on dit que la jonction est alimentée en sens inverse.
Pour comprendre ce qui se passe dans le sens inverse et le sens direct, rappelons ce qui se passe dans une jonction PN au repos. On y trouve deux courants : un courant de dérive et un courant de diffusion. Le courant de diffusion dépend fortement de la barrière de potentiel : plus la tension de déplétion est forte, plus les charges auront du mal à traverser la zone de déplétion par diffusion. Pour le courant de dérive, ce n'est pas le cas : son intensité ne varie pas et ne dépend pas de la tension de déplétion. Dans les sens direct et inverse, la barrière de potentiel sera modifiée par l'application d'une tension externe . La tension va s'ajouter ou se soustraire à la tension de déplétion : cela renforce ou réduit la barrière de potentiel et modifie donc le courant de diffusion. Celui-ci ne sera alors plus égal au courant de dérive, ce qui rend la jonction PN conductrice (elle laisse passer un courant).
- Dans le sens inverse, la tension externe va s'ajouter à la tension de déplétion . La barrière de potentiel de la zone de déplétion va donc être plus grande. Le courant de diffusion sera alors fortement réduit et peut même s'annuler si la tension est suffisante. Dans ce cas, seul le courant de dérive subsiste. En clair : une jonction PN en sens laisse passer un courant de dérive tr_s faible, de l'ordre de quelques milliampères.
- Dans le sens direct, la tension externe va se soustraire à la tension de déplétion . La barrière de potentiel vaut donc , ce qui est plus faible qu'au repos. La barrière de potentiel va alors laisser passer plus facilement les charges et le courant de diffusion va augmenter. La jonction laisse passer un courant de diffusion, dont la valeur dépend seulement de la tension externe.
La longueur de déplétion en sens direct et inverse
[modifier | modifier le wikicode]L'équation de la section précédente, qui donne la longueur de la zone de déplétion, marche aussi en sens direct et inverse après quelques modifications. Il suffit de remplacer la tension de déplétion par sa valeur modifiée, celle à laquelle on a ajouté ou soustrait . On a donc :
- en sens inverse.
- en sens direct.
Cela se comprend assez facilement quand on analyse les recombinaisons qui ont lieu dans la zone de déplétion et à ses bords. Dans le cas où on place le générateur dans le sens direct, les électrons et trous sont attirés à travers la zone de déplétion et vont s'en approcher. Des phénomènes de recombinaison ont alors lieu, ce qui réduit la taille de la zone de déplétion. Dans le sens inverse, ces courants vont appauvrir les bords de la zone de déplétion en porteurs de charges, ce qui va l'agrandir. Pour résumer, la taille de la zone de déplétion varie suivant la tension qu'on met aux bornes de la diode.
 |
 |
De ce fait, la transition dans la zone de déplétion va évoluer et devenir plus abrupte ou plus douce. La largeur de la zone de déplétion évolue en conséquence, mais aussi la hauteur de la marche de transition : la tension de déplétion varie. Du fait de la variation de tension de déplétion, le passage des charges entre les deux régions est facilité ou rendu plus difficile, selon la situation.
 |
 |
La quantité de charges contenues dans la zone de déplétion au repos
[modifier | modifier le wikicode]La quantité de charge dans la zone de déplétion change quand on met la jonction sous tension. Comme précédemment, est remplacée par /
On peut simplifier cette relation comme suit :
- , avec
On voit que la relation entre charge et tension dans la jonction PN n'est pas linéaire. On ne peut donc pas définir de capacitance pour une jonction PN, du moins dans le cas général. S'il y a bien un stockage de charges dans la jonction PN, la non-linéarité de la relation précédente ne colle pas avec la définition de la capacité (). Néanmoins, on peut cependant définir une pseudo-capacité définie par :
On peut reformuler la capacité dans le cas général comme suit :
- , avec la pseudo-capacité de la jonction PN au repos (avec ).
Références
[modifier | modifier le wikicode]
Les diodes et jonctions PN

Les jonctions PN sont utilisées pour fabriquer des composants appelés diodes. À l'exception de quelques diodes très spécialisées, une diode n'est rien d'autre qu'une jonction PN, identique à celle vue dans la section précédente. Ses deux bornes sont appelées respectivement anode et cathode. L'anode correspond au semi-conducteur dopé P, alors que la cathode correspond au semi-conducteur dopé N.

L'usage le plus courant d'une diode est de ne laisser passer le courant que dans un sens, de l'anode vers la cathode, mais pas dans l'autre sens. La diode est dite bloquée quand elle ne laisse pas passer le courant, passante quand le courant passe. Pour vous donner un exemple, les deux circuits illustrés ci-dessous montrent ce qui se passe quand on branche une diode dans le sens passant, puis bloqué. Dans le premier cas, du courant va circuler dans le circuit. Dans le second, le circuit sera équivalent à un circuit ouvert.
 |
 |
Tout cela nous dit que la diode est un dipôle non-symétrique, ce qui signifie qu'il faut faire attention quand on branche une diode dans un circuit électrique : la mettre dans le mauvais sens fait dysfonctionner le circuit. Pour éviter toute confusion, l'anode et la cathode sont souvent indiquées sur les diodes, grâce à un petit cercle noir qui entoure la cathode.
L'équation de Schokley d'une diode/jonction PN
[modifier | modifier le wikicode]La caractéristique d'une jonction PN peut se mettre en équations, l'équation obtenue étant appelée l'équation de Shockley. Elle est déduite de la théorie des semi-conducteurs, appliquée aux jonctions PN. Mais celle-ci est assez complexe, aussi il est rare de l'utiliser dans des exercices typiques. La voici :
- est la tension aux bornes de la diode ;
- est la tension thermique, égale à ;
- est un paramètre dépendant de la diode, appelé courant de saturation.
On peut aussi réécrire cette équation pour obtenir la tension aux bornes de la diode.
L'équation de Schokley n'est autre que celle de la caractéristique I-U d'une diode, d'une jonction PN idéale, représentée dans les graphiques ci-dessous. On distingue deux régimes de fonctionnement sur cette courbe : le régime direct pour des courants positifs, le régime inverse pour les courants négatifs.
- Pour des courants négatifs, les diodes ne laissent pas vraiment passer le courant et se comportent presque comme des circuits ouverts, parce qu'elles laissent malgré tout passer un léger courant appelé le courant de saturation. Mais ce courant ne fait que quelques nanoampères et peut être négligé dans la plupart des cas.
- Pour les courants positifs, la diode laisse passer le courant comme tout conducteur, avec cependant une résistance qui diminue exponentiellement avec le courant. Il est d'usage de dire que la tension d'une diode devient significative au-delà d'une certaine tension de seuil, dont la détermination dépend du fabricant. Cette tension de seuil est cependant approximative et ne correspond à rien de concret, une exponentielle n'ayant pas de point d'inflexion.
 |
 |

Il faut noter que la caractéristique I-U dépend du matériau utilisé pour fabriquer la diode. À ce jour, les diodes sont surtout fabriquées en Silicium et en Germanium, deux semi-conducteurs assez simples à travailler. Les diodes en silicium ont une caractéristique I-U assez différente des diodes fabriquées en germanium. Le graphique ci-dessous montre ces deux caractéristiques, pour que vous puissiez comparer. Dans les grandes lignes, les diodes en Silicium fonctionnent dans une gamme de températures plus grandes que celles en Germanium, ce qui est un grand avantage pour la plupart des applications industrielles. Si une diode à Germanium rend l'âme vers 100°C, les diodes à Silicium peuvent tolérer des températures maximales doubles, de près de 200°C. Et c'est la même chose pour la tension maximale : les diodes au Silicium supportent des tensions pouvant aller jusqu'à 1000 Volts, soit bien plus que les 400 Volts des diodes au Germanium. Cependant, cela ne signifie pas que les diodes au Silicium n'ont que des avantages par rapport à la concurrence. Leur défaut principal est que leur caractéristique I-U est décalée vers la droite par rapport au diodes à Germanium. En clair, elles commencent à conduire le courant à partir d'une tension de seuil assez importante : 0.7 Volts, contre 0.3 Volts pour les diodes au Germanium.
Le régime inverse
[modifier | modifier le wikicode]Dans le régime inverse, les diodes laissent passer un léger courant en état bloqué. Mais ce courant est extrêmement faible de l'ordre du milliardième d'ampère, ce qui fait qu'on peut presque tout le temps le négliger. On peut faire l'approximation suivante : en régime inverse, la diode est totalement bloquée et ne laisse passer aucun courant. Dans ce régime inverse, la pente de la courbe est très faible et le courant très faible, ce qui fait qu'on peut considérer que le courant est en fait nul. Cette approximation est particulièrement bonne et donne de très bons résultats quand il s'agit d'analyser des circuits. Pour nous en rendre compte, partons de l'équation de Schokley, écrite ainsi :
Avec une tension négative , on a :
On peut raisonnablement supposer que le terme est très petit et on peut le négliger. On a alors :
Le courant de saturation étant extrêmement petit, on peut totalement le négliger.
Le régime direct
[modifier | modifier le wikicode]Étudions maintenant le régime direct. Pour cela, partons de l'équation de Schokley, écrite ainsi :
L'approximation exponentielle
[modifier | modifier le wikicode]Pour le régime direct, une approximation possible est de regarder ce qui se passe quand le courant est important. Dans ce cas, le courant est largement supérieur au courant de saturation : . On peut donc négliger le terme dans l'équation de Schokley, ce qui donne un courant exponentiel. Le graphe obtenu avec cette approximation exponentielle est représenté ci-contre à droite.
Qu'on peut reformuler comme suit :
L'approximation affine/linéaire
[modifier | modifier le wikicode]
Pour le régime direct, on peut approximer l'exponentielle par une fonction affine. En somme, l’exponentielle correspond bien à une fonction linéaire, qui commencerait non par à l'origine, mais à une tension légèrement positive. Cette tension positive sert de seuil à partir duquel la diode commence à conduire, ce qui lui vaut le nom de tension de seuil. La diode est bloquée pour une tension sous le seuil, alors que la relation entre courant et tension devient linéaire au-delà. Cela se traduit alors par l'équation suivante, illustrée par le graphique à droite. Dit autrement, la diode a une résistance dynamique non-nulle au-delà du seuil. Un tel modèle de diode est appelée une diode résistive avec seuil. Le graphe de cette approximation est représenté ci-contre à droite.
La résistance de la diode n'est autre que la résistance dynamique de la diode. Celle-ci est, par définition, la dérivée suivante :
Pour la calculer, nous allons partir de l'équation de début de section :
Dérivons par :
Dans l'équation précédente, le terme : n'est autre que le courant qui traverse la diode. En faisant le remplacement, on trouve la conductance dynamique :
Ce qui donne la résistance dynamique suivante:
L'approximation de la diode idéale
[modifier | modifier le wikicode]
On peut encore simplifier ce modèle en remplaçant la portion linéaire par une droite verticale au-delà de la tension de seuil : cela donne le modèle de la diode avec seuil.
On peut simplifier le modèle précédent en éliminant la tension de seuil, ce qui donne une diode parfaite. La diode parfaite n'est qu'un cas particulier de diode avec seuil, pour laquelle le seuil en question est une tension nulle. Le schéma ci-dessous montre la caractéristique I-U d'une diode idéale. Pour un courant négatif, sa conductance est nulle (résistance infinie), ce qui signifie qu'elle ne laisse pas passer de courant, comme un interrupteur ouvert. Mais sa résistance est nulle pour un courant positif : elle se comporte comme un fil parfait (sans résistance). En clair, elle laisse passer un courant positif, mais bloque totalement un courant négatif, du moins dans une certaine mesure. Ce modèle colle assez bien au fonctionnement des diodes réelles, tout en étant assez simple à manipuler.
Pour résumer, le schéma ci-dessous illustre les deux modèles simplifiés de diodes (diode linéaire avec seuil et diode idéale).

Le régime de claquage et les diodes Zener
[modifier | modifier le wikicode]En-deça d'une tension appelée la tension de claquage, la diode cède et finit par laisser passer le courant. Elle fonctionne alors dans le régime de claquage.
Les diodes Zener
[modifier | modifier le wikicode]
Les diodes normales ne survivent généralement pas à ce régime, qui les endommage assez rapidement. Mais certaines diodes, appelées diodes Zener, sont conçues pour fonctionner sans problèmes au-delà de la tension de claquage.

La relation I-U en régime de claquage
[modifier | modifier le wikicode]En régime de claquage, la courbe I-U est quasiment une droite. Ce qui signifie que l'on peut définir une résistance dynamique , égale à l'inverse de la pente de la courbe :
Comme pour le régime directe, on peut approximer la relation I-U en régime de claquage par une relation affine :
- , avec la résistance dynamique et la tension de claquage.
Ce qui fait que le circuit équivalent d'une diode Zener (ou de toute diode placée en régime de claquage) est composé d'une résistance (terme ) et d'une source de tension (la tension de claquage ).

Pour une diode Zener idéale, la courbe I-U est verticale.
Les transistors bipolaires

Après avoir vu la diode, il est temps de passer à un composant bien plus connu : le transistor. Les transistors sont surtout utilisés pour fabriquer des circuits électroniques, comme des ordinateurs, des téléphones et bien d'autres objets numériques du quotidien. Pour donner un exemple, sachez que les derniers modèles de processeurs peuvent utiliser près d'un milliard de transistors. Ils sont utilisés dans de nombreux circuits, qu'il s'agisse de filtres, de stabilisateurs de tension, et bien d'autres fonctions. Il s'agit de composants à trois broches, sur lesquelles peut s'appliquer une tension électrique.
Ils sont utilisés de deux manières différentes : soit comme interrupteurs, soit comme amplificateurs.
- Le plus souvent, ils servent d'interrupteurs commandables, à savoir des interrupteurs commandés par leur troisième broche. Ils se comportent comme un interrupteur fermé ou ouvert selon ce qu'on met sur la troisième broche.
- Ils servent aussi d'amplificateurs. Ils amplifient une tension ou un courant qui les traverse. Le coefficient d'amplification est déterminé par la tension et le courant placé sur la troisième broche. Plus précisément, les transistors bipolaires sont des amplificateurs de courant. Ils reçoivent un courant sur la broche d'entrée, et en fournissent une version multipliée sur leur sortie. Le coefficient multiplicateur dépend du courant ou de la tension sur la broche de contrôle.
 |
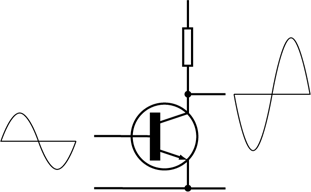 |
Il existe différents types de transistors, les deux classes principales étant les transistors bipolaires et à effet de champ. Les transistors bipolaires sont souvent abréviés transistors BJT (Bipolar Junction Transistor) alors que les transistors à effet de champ sont abréviés FET (Field-Effect Transistor). Nous réutiliserons ces abréviations dans le reste du cours. Dans cette section, nous allons nous limiter aux transistors BJT, les transistors FET seront vus dans la section suivante.
Les transistors NPN et PNP
[modifier | modifier le wikicode]Il existe deux types de transistors BJT : les transistors NPN et les transistors PNP. Ils se distinguent sur de nombreux points, que nous verrons dans ce qui suit. Leurs symboles sont illustrés ci-dessous. Remarquez que la différence entre les deux tient dans le sens de la flèche : elle sort de la base pour les NPN et elle va vers la base pour les PNP. Comme leurs symboles l'indiquent, les transistors BJT possèdent trois bornes, appelées broches, sur lesquelles on peut appliquer une tension électrique. Les trois broches portent les noms suivants : Collecteur, Base et Émetteur. Le fait qu'il existe trois broches au lieu de deux a plusieurs conséquences. Déjà, il existe une tension entre chaque paire de broche, ainsi qu'un courant qui passe dans chaque broche. Cela fait en tout trois tensions notées , et et trois courants notés , et . Ceux-ci sont reliés par l'équation suivante, que nous démontrerons bientôt :
- et
 |
 |
 |
 |
L'intérieur d'un transistor bipolaire
[modifier | modifier le wikicode]
Vous aurez remarqué que les termes NPN et PNP font penser aux jonctions PN. Ce n'est pas un hasard : tout BJT est constitué de deux jonctions PN mises en série. Vu qu'une jonction PN est une diode, on peut considérer, à quelques détails près, qu'un transistor est composé de deux diodes mises en série dans des sens opposés.
L'ensemble donne un groupe de trois morceaux de semi-conducteurs mis côte-à-côte. Pour les transistors NPN, on trouve une portion dopée P entre deux portions dopées N. Pour les transistors PNP, c'est l'inverse : on a une part dopée N entre deux portions dopées P. Chaque broche est connectée directement sur des portions de semi-conducteur : celle de gauche est connectée à l'émetteur, celle du milieu est connectée à la base et celle de droite au collecteur. Un transistor a donc deux jonctions : une entre l'émetteur et la base, et une autre entre la base et le collecteur.
 |
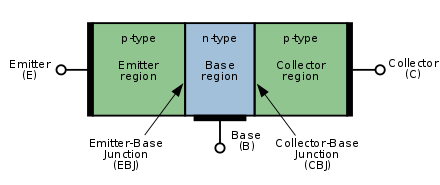 |
 |
 |
Pour comprendre le fonctionnement du transistor, nous allons prendre l'exemple du transistor NPN. Pour cela, mettons l'émetteur à la masse et mettons une tension sur le collecteur, ainsi qu'une autre tension (plus faible) sur la base. Dans cette situation, la "diode" entre base et émetteur est polarisée en direct, dans le sens passant : le courant va donc passer entre la base et l'émetteur. Il faut préciser qu'il s'agit d'un courant de trous, et non pas d'électrons. Par contre, le courant ne passera pas dans l'autre sens, à savoir de la base vers le collecteur, vu que la "diode" est polarisée dans l'autre sens, dans le sens bloqué. Les trous ne peuvent pas passer dans ce sens.
Par contre, un courant d'électrons va passer de l'émetteur vers le collecteur, du fait de la tension VCE. Ce courant va traverser tout le transistor, en passant par la base. On pourrait croire que la diode base-collecteur ne laisserait pas passer le courant, mais ce n'est pas le cas. Les électrons ne vont pas faire comme les trous et vont bien traverser la base (pas immédiatement, mais il y arriveront). Une partie de ce courant d'électron va se recombiner avec les trous dans la section intermédiaire de type P, naturellement riche en trous.

Maintenant, faisons la somme des courants pour la base, le collecteur et l'émetteur.
- Le courant est la somme du courant d'électrons et de trous.
- Le courant de base est égal au courant de trous auquel il faut ajouter la recombinaison des trous avec les électrons.
- Le courant de collecteur est le courant d'électrons qui arrive jusqu'au collecteur, à savoir le courant d'électrons, moins le courant de recombinaison.
On a donc :
Le fonctionnement d'un BJT
[modifier | modifier le wikicode]Le fonctionnement d'un BJT dépend du courant de base utilisé. Si on place une tension entre émetteur et collecteur, le circuit va se comporter différemment selon le courant de base. On peut distinguer trois régimes de fonctionnement (en réalité seulement deux, mais passons) :
- Le courant de base est nul, de même que le courant de collecteur : le transistor est en régime bloqué et se comporte comme un banal interrupteur ouvert.
- Un courant de base non nul ouvre le circuit et le transistor amplifie le courant envoyé sur sa base : le transistor est alors dit en régime linéaire.
- Le courant de collecteur ne peut pas aller au-delà d'une valeur maximale. Si la limite est atteinte, le courant de collecteur reste à sa valeur maximale, quel que soit la valeur de . Le transistor se comporte alors comme un interrupteur fermé, dans une certaine mesure. Le transistor est alors en régime de saturation.
Le réseau des caractéristiques courant-tension
[modifier | modifier le wikicode]Dans cette section, nous allons prendre un transistor NPN et étudier son fonctionnement. Le transistor PNP sera étudié juste après, son traitement étant quasiment similaire. Nous allons prendre un transistor dont l'émetteur est relié à la masse, ce qui donne un montage appelé "montage à émetteur commun". Celui-ci permet d'étudier les relations entre les courants et avec les tensions VCE et VBE, qui servent de caractéristiques courant-tension pour le transistor. L'ensemble de ces relations porte un nom assez barbare : on l'appelle réseau des caractéristiques du transistor. Mais derrière ce terme se cache une simple liste de trois équations, qui servent de caractéristiques courant-tension pour un transistor :
- la relation entre et ;
- la relation entre et ;
- et la relation entre et .
Relations entre courants : Alpha et Bêta d'un transistor
[modifier | modifier le wikicode]
Dans le régime linéaire, le courant qui traverse le collecteur est un multiple du courant d'émetteur et du courant de base. Cela permet de définir deux coefficients de proportionnalité, appelés l'alpha et le béta du transistor.
Détaillons maintenant un peu le calcul de l'alpha et du bêta.
On a donc les équations suivantes :
Relations entre Vbe et courants
[modifier | modifier le wikicode]On a vu plus haut qu'il y a une jonction PN entre la base et l'émetteur. On devine donc que la relation entre Ib et Vbe est celle d'une jonction PN, celle d'une diode. Compte tenu de la relation entre Ic et Ib, on devine qu'il en est de même pour la relation entre Vbe et Ic. On a donc les équations suivantes, qui sont celles d'une diode :
 |
 |
Relations entre Vce et courants
[modifier | modifier le wikicode]La relation théorique entre Ic et Vce est illustrée dans le schéma ci-dessous. On voit bien la différence entre la zone linéaire et la zone de saturation. Dans la zone linéaire, Ic ne dépend que de Ib et pas de Vce : la courbe est donc "plate", signe de l'indépendance de Ic et de Vce. Par contre, dans la zone de saturation, le courant Ic augmente avec la tension VCE. Cette description est cependant assez schématique, du moins pour le fonctionnement de la zone linéaire.

En réalité, la tension Vce a une influence sur le courant Ic, certes assez mineure, mais qu'il faut parfois prendre en compte. Cette influence est cependant indirecte, la tension Vce influençant le courant de base. Cela vient d'un effet physique, appelé l'effet Early : la tension Vce modifie la taille de la zone P ou N attachée à la base, ce qui module le courant de base. On peut rendre compte de ce phénomène avec l'équation suivante, qui donne le bêta du transistor en fonction de la tension Vce.
La tension VE de l'équation précédente est appelée la tension d'Early. Elle s'obtient en prolongeant le courant de saturation sur le graphe Ic/Vce. Un exemple est illustré ci-dessous.

La relation entre courant Ic et tensions Vce et Vbe est assez facile à déduire à partir des équations précédentes. Il suffit de combiner l'équation qui décrit le courant Ib avec la définition précédente du béta, ce qui donne :
Résumé
[modifier | modifier le wikicode]
Le tableau et l'image ci-dessous résument ces trois relations.
| Relation | Description | Équation |
|---|---|---|
| Relation | Définition du béta d'un transistor | |
| Relation | Relation identique à celle d'une diode, équation de Schokley. | |
| Relation | Relation complexe. |
L'état d'un transistor est défini par la tension VCE et le courant IC, l'état de la base se déduisant de ceux-ci. Comme on l'a dit plus haut, le courant IC ne peut pas dépasser une valeur maximale. Il en est de même pour la tension VCE, comme le montrent la relation entre VCE et IC. Ce qui fait que tous les couples VCE-IC ne sont pas permis pour le transistor. De plus, un BJT a aussi une puissance limite, au-delà de laquelle il ne peut pas aller. Si on résume tout cela, on obtient le schéma ci-contre, qui donne les points de fonctionnement possibles pour un BJT.

Les modèles de circuit équivalents d'un BJT
[modifier | modifier le wikicode]Vu ce qui a été expliqué précédemment, on se doute qu'un transistor est un composant assez compliqué et qu'en donner un circuit équivalent n'est pas de tout repos. Mais quelques chercheurs se sont attelés à cette tâche et ont découvert des circuits à base de diodes et de générateurs qui fonctionnent exactement comme des transistors. Ces circuits équivalents d'un transistor bipolaire vont être vus dans ce qui suit.
Le (faux) modèle à base de diodes
[modifier | modifier le wikicode]
Un premier modèle, particulièrement simple, est simplement composé de deux diodes tête-bêche. En effet, rappelons qu'une diode est une simple jonction PN : en en mettant deux l'une à côté de l'autre (sans conducteurs entre les deux), on retrouve bien un transistor NPN ou PNP. Ce modèle fonctionne bien pour décrire un transistor en régime bloqué ou de saturation, quand on l'utilise comme interrupteur commandé. Mais ce modèle, bien que très simple, a de nombreux défauts. Et le principal est clairement qu'il ne modélise pas l'amplification des courants par le transistor. Autant dire que ce modèle est juste complètement faux. On doit donc l'améliorer pour ajouter de quoi amplifier le courants de base, et c'est exactement ce que fait le modèle suivant.
Le modèle d'Ebers–Moll
[modifier | modifier le wikicode]Le modèle d'Ebers-Moll reprend le modèle précédent, avec deux diodes placées tête-bêche, mais ajoute deux générateurs de courant en parallèles de celles-ci. Chaque générateur fournit un courant proportionnel au courant qui traverse la diode située de l'autre (celle avec laquelle il n'est pas en parallèle). Le courant va dans l'autre sens que celui qui traverse la diode située en parallèle. Les sens sont inversés entre les transistors NPN et PNP.
| Modèle Ebers-Moll d'un NPN | Modèle Ebers-Moll d'un PNP |
|---|---|

|

|
Il est intéressant d'étudier le modèle précédent quand on branche une tension aux bornes du transistor, entre l'émetteur et le collecteur. Deux sens sont possibles : soit la tension va de l'émetteur vers le collecteur, soit elle va dans le sens inverse. Dans les deux cas, une des deux diode sera bloquée et le générateur qui correspond ne produira pas de courant. Le circuit se simplifie alors, comme le montre le schéma ci-contre.
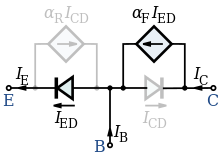

Le modèle donne la valeur des courants de collecteur, d'émetteur et de base, notés IC, IE et IB, avec les équations suivantes. Rappelons que dans ces équations, .
Vu la complexité de ces équations, on préfère souvent utiliser les versions simplifiées que voici.
Le modèle de contrôle de charge de Gummel–Poon
[modifier | modifier le wikicode]
Le modèle d'Ebers-Moll n'est cependant pas la panacée et ne modélise pas à la perfection un transistor BJT. Aussi les chercheurs ont inventé d'autres circuits équivalents, plus détaillés. Mais ces modèles plus complexes sont cependant particulièrement difficiles à comprendre et encore plus à expliquer. Par exemple, prenez le modèle de contrôle de charge de Gummel–Poon, illustré ci-contre. Vous voyez bien que celui-ci est particulièrement touffu, avec un grand nombre de résistances, de diodes, de condensateurs et d'un générateur de courant. Il faut dire qu'avec 41 variables, on comprend que ce modèle n'est pas conçu pour être pédagogique, mais pour être le plus fidèle possible à la réalité. Cependant, quelques modèle intermédiaires existent, mais ceux-ci ne servent que dans des cas particuliers. C'est notamment le cas des modèles pour petits signaux que nous allons voir dans ce qui suit.
Les transistors à effet de champ
Les transistors des circuits électroniques actuels ne sont pas de transistors bipolaires, mais des transistors à effet de champ ou transistors FET. Ils fonctionnent de la même manière que les transistors bipolaires : comme ces derniers, ils peuvent servir d’interrupteurs ou d'amplificateurs. Cependant, les transistors à effet de champ sont un petit peu différents du transistor bipolaire, ce qui fait qu'ils sont vus dans des chapitres à part. La classification des transistors FET est assez complexe, avec de nombreux sous-types assez précis. Dans les grandes lignes, il en existe deux types principaux, appelés transistors JFET et IGFET, eux-mêmes subdivisés en de nombreuses sous-classes. Ce chapitre va surtout se concentrer sur les transistors dits JFET et MOS (Metal Oxyde Silicium), qui sont de loin les plus utilisés.

Les transistors JFET
[modifier | modifier le wikicode]
Les premiers transistors FET que nous allons étudier sont les transistors à effet de champ à jonction, aussi appelés JFET (Junction Field Effect Transistor). Les points communs avec les transistors bipolaires sont nombreux : ils servent eux aussi d'amplificateur et d'interrupteur, ce sont des composants à trois broches, etc. Mais contrairement au transistor bipolaire, leurs broches sont appelées la grille, le drain et la source. Elles correspondent respectivement à la base (grille), le collecteur (drain) et l'émetteur (source). Il faut noter qu'il existe un équivalent des PNP et NPN pour les JFET, qui portent les noms de JFET à canal P et à canal N.
 |
 |
L'intérieur d'un transistor FET
[modifier | modifier le wikicode]
L'intérieur d'un transistor FET est similaire à celui d'un bipolaire, à savoir qu'on y retrouve deux jonctions PN mises bout à bout. On trouve deux portions P et une N pour les JFET à canal N et deux portions N et une P pour ceux à canal P. L'exemple d'un JFET à canal N est illustré ci-contre. On voit que les portions P sont mises face l'une à l'autre, avec la portion N qui est coincée entre les deux. On dit qu'il existe un canal N entre les deux portions P, canal dans lequel les charges peuvent circuler librement.
Le courant entre la source et le drain circule donc dans le canal N, entre les deux portions P. Plus la distance entre les portions P est grande, plus le courant peut passer facilement. Dit autrement, l'intensité du courant drain-source dépend de la largeur du canal N. Or, il se trouve que cette largeur varie selon la tension qu'on place sur la grille. Quand on place une tension sur la grille, les charges du semi-conducteur vont être repoussées de la grille. Les portions P vont donc s'étendre, la largeur du canal N va se réduire, diminuant le courant drain-source. Si la tension est suffisante, le canal N peut carrément se fermer, disparaître complètement : aucun courant ne peut passer. On comprend donc que le courant drain-source est modulé par la tension sur la grille. Cela nous donne une première différence avec le transistor bipolaire : l'équivalent du "courant de collecteur" est commandé par la tension et non le courant de base.

Le réseau de caractéristiques d'un transistor JFET
[modifier | modifier le wikicode]Les caractéristiques d'un JFET sont moins nombreuses que celles du transistor bipolaire. Les seules relations importantes sont celles entre le courant drain-source, la tension sur la grille et la tension entre drain et source. Celles-ci sont notées IDS pour le courant drain-source, VG pour la tension de grille, et VDS pour la tension drain-source. Voici l'équation générale qui décrit le comportement d'un JFET :
On peut décomposer cette équation en deux relations : une pour relier IDS et VGS, et une autre pour relier IDS et VDS. Ces deux relations sont illustrées dans le schéma ci-dessous.

La relation VGS-IDS
[modifier | modifier le wikicode]
La relation entre VGS et IDS se déduit directement du fonctionnement du transistor. Plus la tension augmente, plus le canal N rétrécit et le courant faiblit en conséquence. On a donc une relation décroissante entre VGS et ID. On voit aussi que le courant s'annule au-delà d'une certaine tension, quand le canal N disparaît. Cette tension particulière, notée dans le schéma ci-dessous, est appelée la tension de pincement.
Dans la région linéaire, on peut considérer un JFET comme une résistance contrôlée en tension (la valeur de la résistance dépend de la tension . La valeur de la résistance est approximativement décrite par l'équation suivante :
L'équation précédente peut se réécrire avec le courant .
On peut enfin reformuler le tout pour mettre en avant la tension VGS :
La relation VDS-IDS
[modifier | modifier le wikicode]
La relation entre IDS et VDS ressemble à celle observée sur les transistors bipolaires, entre la tension VCE et le courant IC. Encore une fois, on observe une différence entre une région dite linéaire et une région dite saturée. Dans la région linéaire, le courant IDS est proportionnel à la tension VDS (au moins approximativement). Le JFET est alors en régime linéaire et peut servir d'amplificateur sans problème. Mais le courant IDS débité par le JFET n'est pas illimité et il existe une limite physique au-delà de laquelle le transistor ne peut pas aller. Quand le courant maximal du transistor est atteint, le courant IDS ne varie plus selon la tension VDS : on dit que le JFET est en régime de saturation. Cela arrive quand la tension dépasse une valeur appelée tension de saturation, qui sera notée VP dans ce qui suit.
Les transistors MOS
[modifier | modifier le wikicode]
Après avoir vu les JFET, nous allons passer à une seconde classe de transistors FET : les transistors de type Metal Oxyde Semiconductor Field Effect Transistor, abréviés transistors MOS (ou encore MOSFET). Comme les JFET, celui-ci possède trois broches nommées grille, drain et source.
On peut les classer en deux types, ceux à enrichissement ou à appauvrissement, la différence tenant dans le fait que les premiers ne conduisent pas quand on les polarise (on met une tension entre drain et source), alors les seconds font l'inverse.
De plus, chaque type est subdivisé en deux sous-types, qui diffèrent entre autre par le bit qu'il faut mettre sur la grille pour les ouvrir/fermer :
- les transistors NMOS qui s'ouvrent lorsqu'on envoie un zéro sur la grille et se ferment si la grille est à un ;
- et les PMOS se ferment lorsque la grille est à zéro, et s'ouvrent si la grille est à un.
| NMOS/PMOS | MOS à enrichissement | MOS à appauvrissement |
|---|---|---|
| PMOS | 
|
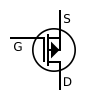
|
| NMOS | 
|

|
L'intérieur d'un transistor MOS
[modifier | modifier le wikicode]À l'intérieur du transistor MOS, on trouve une plaque en métal reliée à la grille appelée l'armature, un bout de semi-conducteur entre la source et le drain, et un morceau d'isolant entre les deux.

La portion de semi-conducteur est encore une fois composée de deux portions dopées P coincées entre une portion dopée N, comme indiqué dans le schéma ci-dessous.

Le fonctionnement du transistor MOS
[modifier | modifier le wikicode]Suivant la tension que l'on place sur la grille, celle-ci va se remplir avec des charges négatives ou positives. Cela va entrainer une modification de la répartition des charges dans le semi-conducteur, ce qui modulera la résistance du conducteur.

Prenons par exemple le cas d'un transistor NMOS et étudions ce qui se passe selon la tension placée sur la grille. Si on met un zéro, la grille sera vide de charges et le semi-conducteur se comportera comme un isolant : le courant ne passera pas. En clair, le transistor sera équivalent à un interrupteur ouvert. Si on met un 1 sur la grille, celle-ci va se remplir de charges. Le semi-conducteur va réagir et se mettre à conduire le courant. En clair, le transistor se comporte comme un interrupteur fermé.

|

|
Prenons par exemple le cas d'un transistor NMOS et étudions ce qui se passe selon la tension placée sur la grille.
- Si on laisse la grille tranquille, l'armature est vide d'électrons et n'a aucun effet sur le circuit. Le semi-conducteur est alors équivalent à deux diodes placées dans des sens opposées, une pour chaque jonction PN, ce qui fait bloque le passage du courant ne passe pas. La liaison source-drain a une résistance très élevée, de plusieurs milliers de milliards d'Ohms ().
- Si on place une tension entre la source et le drain, des charges s'accumulent dans l'armature jusqu'à ce que la grille soit remplie. Ces charges vont repousser leurs congénères dans le semi-conducteur, ce qui va créer un canal de conduction que le courant va emprunter : le courant passe entre la source et le drain. Dans un transistor NMOS, des charges positives vont s'accumuler dans l'armature métallique de la grille. Celles-ci vont attirer les électrons du semi-conducteur et repousser les trous. Les électrons libres des zones N vont aussi être attirés et vont s'accumuler sous la grille. Ces électrons libres sous la grille peuvent conduire le courant, la zone dans laquelle ils se situent formant le canal de conduction. Pour le transistor PMOS, c'est l'inverse : des électrons s'accumulent dans l'armature et les trous des régions P migrent sous la grille. Ces trous permettent de conduire le courant, formant un canal de conduction.
| Transistor MOS avec grille hors-tension. | Transistor MOS avec grille sous tension. |
|---|---|

|

|
Les caractéristiques d'un transistor MOS
[modifier | modifier le wikicode]On comprend avec les explications précédentes que les MOS sont des transistors commandés en tension : suivant la tension placée sur la grille, le courant passe plus ou moins bien entre source et drain. Reste à voir quelles sont les équations qui relient les courants et les tensions aux bornes du transistor.
Déjà, on peut directement déduire que le courant de grille est nul. L'isolant placé sous la grille, qui sépare l'armature métallique du semi-conducteur, empêche tout courant de passer à travers la grille. Le seul courant qui traverse le MOSFET est celui qui passe entre drain et source. On a donc :
- ,
Le courant IDS dépend de la tension VGS, comme pour les JFET, avec quelques différences dans les équations qui relient IDS, VGS et VDS. Pour un MOSFET, la relation entre ID et VDS est une simple relation de proportionnalité, le transistor se comportant comme une simple résistance. Pour simplifier, le MOSFET est une résistance commandée en tension et plus précisément par la tension de grille VGS. Cependant, cela n'est vrai que pour une tension drain-source assez faible. Il existe, comme pour le JFET, une tension au-delà de laquelle le courant ID ne peut plus augmenter : le courant ID finit donc par saturer au-delà d'une tension VDS trop forte. Le transistor fonctionne donc en deux régimes : un régime linéaire où ID et VDS sont proportionnels, et un régime de saturation où ID sature et est découplé de VDS.

Le schéma ci-dessous montre ce qui se passe à l'intérieur du transistor MOSFET selon les différents régimes de fonctionnement.

Maintenant, démontrons tout cela.
Le régime linéaire
[modifier | modifier le wikicode]Commençons par démontrer que le courant ID et la tension VDS sont proportionnels dans le régime linéaire. Pour cela, nous allons supposer que le canal de conduction est donc une zone dans le semi-conducteur où l'on trouve des charges libres, pouvant conduire le courant. Et on peut facilement déduire la relation entre tensions VDS et VGS, avec le courant ID. Pour calculer la valeur du courant ID, il suffit de multiplier la vitesse des charges dans le canal de conduction par la charge linéique (la charge par unité de longueur du canal). Commençons par calculer la charge linéique, avant de calculer la vitesse des charges dans le canal de conduction.
Dans la section suivante, on va supposer que le canal a une forme de parallélépipède et a donc une épaisseur, une largeur et une longueur. On changera cette hypothèse dans la suite du cours, vu qu'elle est fausse, mais elle sera utile pour le moment. La quantité de charges contenu dans ce canal se calcule assez facilement, quand on sait que la grille est un condensateur dont le canal de conduction est la seconde armature. On peut appliquer la formule , reste à trouver la tension adéquate. On peut préciser que la grille ne commence à se charger que si la tension VGS dépasse une valeur seuil, appelée tension de seuil. En notant la tension de seuil , on a :
On peut reformuler cette formule en utilisant non pas la capacité, mais la capacité par unité de surface de l'armature. En prenant les notations suivantes, on a :
- la longueur du canal ;
- la largeur du canal ;
- la capacité surfacique.
La charge linéique est donc :
La tension entre source et drain donne naissance à un champ électrique dans le semi-conducteur, égal à :
La vitesse des charges dans le semi-conducteur est donc égale à ce champ électrique, multiplié par la mobilité des charges :
On a donc :
On voit que la relation entre et est linéaire, ce qui permet de définir une conductance. En reformulant l'équation précédente, on trouve :
- , avec
Cette conductance source-drain est appelée la conductance de sortie du FET. On voit qu'elle dépend de trois paramètres :
- le produit , qui est appelé le paramètre de transconductance de processus ;
- le rapport entre largeur et longueur du canal de conduction ;
- la différence de tension .
Le régime de pré-saturation
[modifier | modifier le wikicode]Maintenant, étudions la forme exacte de la région linéaire du courant ID, juste avant le passage au régime de saturation. La saturation du transistor (et le régime de pré-saturation) est lié à la relation entre l'épaisseur du canal et la tension VDS. Car, contrairement à ce que laissait supposer la simplification du canal parallélépipède, le canal de conduction a une forme légèrement effilée. Le canal est plus épais du côté de la source que du côté du drain. Et cela influence la relation ID/VDS dans le régime linéaire, à des tensions proches du régime de saturation. Plus la tension VDS augmente, plus le canal sera penché, avec une forme de plus en plus effilée. Au-delà d'une certaine tension, le canal ne peut plus s'approfondir et son épaisseur reste constante : le transistor est alors en régime de saturation.

|

|

|

Un bon moyen de modéliser cela est de modifier l'équation précédente :
- , avec
Il suffit de remplacer la tension par celle-ci :
Ce qui donne :
- , avec
En reformulant, on trouve l'équation du second degré suivante :
- , avec
Celui-ci donne la belle parabole ci-contre quand on en trace le graphe.
Le régime de saturation
[modifier | modifier le wikicode]Dans le régime de saturation, la relation ID-VDS devient celle-ci :
- , avec
Néanmoins, il faut préciser qu'un équivalent de l'effet Early des BJT se manifeste, ce qui se traduit par une légère dépendance entre VDS et ID. Ce qui donne l'équation suivante :
- , avec
Le fonctionnement en petits signaux des transistors
Dans le chapitre précédent, nous avons vu quelles sont les relations entre tensions et courants d'entrée/sortie d'un transistor. Dans cette section, nous allons étudier ce qui se passe quand on place un signal alternatif sur l'entrée d'un transistor. Pour être plus précis, nous allons étudier le fonctionnement d'un transistor soumis à des petits signaux. Par "petits signaux", on veut dire les signaux de faible amplitude, qui sont des déviations par rapport à une tension continue. Dans le reste du cours, nous allons décomposer les signaux en deux sous-signaux : un signal continu qui sert à polariser le transistor, et un signal effectif, qui est amplifié par le transistor. Le premier sera écrit en majuscules, alors que l'autre l'est en minuscules. Par exemple, la tension se décompose comme suit :
- , avec .
Précisons que la plupart des équations d'un transistor ne sont pas conservées quand on rentre dans le cadre du "petit signal". À la place, elles sont remplacées par des équations en petits signaux, qui décrivent comment un transistor réagit quand on lui envoie des signaux alternatifs de petite amplitude sur son entrée. On peut les dériver des équations habituelles, en décomposant chaque variable entre composante alternative et continue, avant de faire diverses manipulations algébriques. En règle générale, les équations en petits signaux s'obtiennent en prenant la dérivée des équations normales. Une conséquence est que les équations linéaires sont conservées telles qu’elles en petits signaux. Précisons que, par exemple, c'est le cas de l'équation , qui devient :
L'analyse d'un circuit en petit signal demande de faire quelques manipulations, surtout s'il utilise des transistors (bipolaire ou à effet de champ). Toutes ces manipulations doivent être faites sur le schéma électrique du circuit. Rappelons que les circuits qui fonctionnent en petits signaux doivent être polarisés, histoire de régler les entrées et sorties à des valeurs adéquates.
- Premièrement, il faut remplacer le transistor par un modèle équivalent en petits signaux des transistors utilisés. Et il faut calculer les différents paramètres de ce modèle équivalent à partir des données du circuit.
- Deuxièmement, il faut remplacer les sources de tension et de courant continu, qui disparaissent du circuit. Les sources de tension sont remplacées par un court-circuit, et les sources de courant par un circuit ouvert. De plus, la tension d'alimentation est remplacée par la masse. Intuitivement, c'est lié au fait que l'on filtre les tensions/courants continus pour ne garder que les signaux alternatifs. Pas besoin de tenir compte des tensions/courants continus, ce qui fait que leurs sources disparaissent.
Dans ce qui suit, nous allons établir les différents modèles équivalents d'un transistor en petits signaux. Nous allons commencer par voir les BJT, avant de passer aux FET (aux MOSFET pour être plus précis). Nous allons d'abord voir les MOSFET avant de passer aux BJT. La raison à cela est que tout est plus simple avec les MOSFETs, alors que l'étude est plus compliquée pour les BJTs.
Les FETs en petits signaux
[modifier | modifier le wikicode]
Le modèle équivalent d'un transistor en petit signaux, sur lequel on ne représente que les petits signaux, est illustré ci-contre. On voit qu'il se résume en une source de courant (définie par le produit de la transconductance et de ), qui est mise en parallèle d'une conductance de sortie, liée à l'effet Early. En général, on ne doit pas tenir compte de la résistance de sortie, car elle a une valeur assez faible sur les MOSFET. Et c'est la même chose pour la résistance d'entrée, qui est tellement importante qu'on peut considérer qu'elle est équivalente à un circuit ouvert. Le MOSFET se résume alors à une source de courant définie par sa transconductance.
La transconductance d'un FET
[modifier | modifier le wikicode]Dans ce qui va suivre, nous allons déterminer la transconductance dynamique d'un FET. Partons de l'équation suivante, démontrée dans le chapitre sur les FET :
On décompose la tension Vgs en sa composante continue et le signal alternatif . En injectant dans l'équation précédente, on trouve :
En développant, on trouve :
Le premier terme est la composante continue et on peut l'éliminer pour ne garder que la composante alternative. Ce qui donne :
Le second terme est une distortion qui ruine la linéarité de la relation entre et . Mais on peut la négliger si la tension est assez faible. On a alors :
On peut reformuler cette équation comme suit :
- , avec : .
La conductance d'Early
[modifier | modifier le wikicode]Au modèle précédent, on peut rajouter une résistance pour modéliser l'effet Early et sa valeur est d'ailleurs la suivante, avec Va la tension d'Early :
Les BJTs en petits signaux
[modifier | modifier le wikicode]Il existe plusieurs modèles équivalents d'un BJT, le plus connu étant appelé le modèle hydride-pi. Celui-ci est illustré ci-contre. Il s'agit d'un modèle très simple, mais qui suffit pour une étude approchée. On voit qu'il se résume en une source de courant en série avec une conductance base-émetteur. Le générateur de courant fournit le courant de collecteur , qui est égal au produit de la transconductance et de . La résistance d'entrée est placée entre la base et l'émetteur et est parcourue par le courant , alors que la tension à ses bornes est la tension . En clair, on peut résumer ce modèle avec les trois équations suivantes :
On peut lui rajouter une résistance pour modéliser l'effet Early.
 |
 |
Un autre modèle équivalent est le modèle en T, qui ressemble beaucoup au modèle hybride-pi, mais avec un placement différent des résistances. Encore une fois, on peut placer une résistance d'Early pour simuler la tension d'Early. L'application de la loi des mailles et de la loi des nœuds donne les trois équations suivantes :
 |
 |
Le calcul de la transconductance d'un BJT
[modifier | modifier le wikicode]Pour commencer, calculons la transconductance du BJT en petits signaux, qui est définie par l'équation suivante :
Partons de l'équation qui donne le courant de collecteur à partir de la tension d'entrée.
On peut injecter dans la dernière équation, ce qui donne :
On développe l'exponentielle.
Par définition, on a : : , ce qui simplifie l'équation précédente en :
Si , on peut approximer l'équation précédente en :
On développe le terme de droite et on regroupe les termes continus :
Cette forme sépare le terme de droite en une composante continue et le signal alternatif. On a donc :
Cette équation se réécrit sous la forme en posant :
On voit que le gain du transistor dépend du courant de collecteur et donc de la polarisation du transistor.
Le calcul de la résistance base-émetteur et du bêta
[modifier | modifier le wikicode]Dans cette section, nous allons calculer la résistance base-émetteur en petits signaux, qui n'est autre que la résistance du modèle hybride-pi.
C'est une résistance dynamique, définie par l'équation suivante :
Pour la calculer, nous avons besoin de calculer . Pour cela, on utilise l'équation : . On a alors :
On a vu plus haut que : , ce qui simplifie l'équation précédente en :
On peut reformuler cette équation en :
Le calcul de la résistance base-émetteur
[modifier | modifier le wikicode]Dans cette section, nous allons calculer la résistance base-émetteur du modèle en T, définie par l'équation suivante :
Pour la calculer, nous avons besoin de calculer . Pour cela, on utilise l'équation : . On a alors :
On a vu plus haut que , ce qui simplifie l'équation précédente en :
On peut aller plus loin en se souvenant que :
Ce qui se simplifie en :
Le calcul du courant d'émetteur dans le modèle hybride-pi
[modifier | modifier le wikicode]Dans cette section, nous allons calculer le courant d'émetteur en partant des données du modèle hybride-pi, et montrer que l'on retombe bien sur la relation du modèle en T. Pour cela, partons de l'équation qui définit le courant d'émetteur, à savoir :
En injectant , issue du modèle hybride-pi, dans l'équation précédente, on trouve :
On sait que, par définition,
Le calcul du courant de base dans le modèle en T
[modifier | modifier le wikicode]Dans cette section, nous allons calculer le courant de base en partant des données du modèle en T, et montrer que l'on retombe bien sur la relation du modèle hybride-pi. Pour cela, partons de l'équation qui définit le courant de base dans le modèle en T, à savoir :
En injectant : et dans l'équation précédente, on trouve :
Factorisons :
On sait que, par définition,
Simplifions :
Vu que , on a :
On retrouve bien l'équation du modèle hybride-pi.
Polarisation des transistors BJT et FET
Dans ce chapitre, nous allons étudier de montages à base de transistors, de résistances et de sources de tension/courant, qui sont utilisés pour fabriquer des amplificateurs à base de transistors, mais aussi pour d'autres fonctions. Toujours est-il que nous avons besoin de parler en détail de ces montages et de la polarisation d'un transistor en général, avant de passer aux chapitres suivants.
La polarisation d'un transistor est l'état dans lequel il est tant qu'on ne lui envoie pas le moindre signal, état définit par les courants continus qui le traversent et les tensions continues à ses bornes. Polariser un transistor revient à régler les tensions et courants continus qui le traversent. C'est un processus important pour fabriquer des amplificateurs avec un transistor, en utilisant son fonctionnement en petits signaux. L'idée est que si on envoie un signal quelconque en entrée du transistor, celui-ci sera modifié d'une manière non-linéaire, ce qui ne permet pas de fabriquer des amplificateurs utilisables. Cependant, le fonctionnement en petit signal d'un transistor est linéaire, ce qui fait qu'il peut amplifier des petits signaux de manière linéaire. Les signaux amplifiés sont des déviations par rapport à une tension de base, la tension de polarisation, qui garantit que le transistor est en régime linéaire. Imposer la tension de polarisation se fait en polarisant le transistor, avec les montages que l'on va voir dans ce chapitre.
La polarisation d'un FET
[modifier | modifier le wikicode]Polariser un FET demande à fixer le courant Id et la tension VDS du FET, de manière à ce que celui-ci fonctionne dans la région de saturation. Il existe plusieurs méthodes pour cela, chacune avec ses avantages et inconvénients.
La polarisation par réglage de VGS
[modifier | modifier le wikicode]
La méthode de polarisation la plus simple demande de placer la tension VGS adéquate, pour obtenir le courant ID souhaité. La tension VGS peut être obtenue telle qu'elle, en utilisant une source de tension qu'on connecte sur la grille. On parle alors de polarisation directe, ou encore de polarisation par biais fixe. C'est la méthode la plus simple et la plus intuitive, mais elle a l’inconvénient de consommer plus de place et de circuits, pour la source de tension.
Alternativement, la tension VGS peut être obtenue à partir de la tension d'alimentation en utilisant un simple pont diviseur, ce qui élimine le besoin d'utiliser une tension supplémentaire pour VGS. Cette méthode porte le nom de polarisation par pont diviseur. C'est souvent cette solution qui est utilisée pour fabriquer la tension voulue et l'envoyer sur la grille du transistor. Elle est simple et a aussi l'avantage de faciliter le câblage du circuit, vu que la tension d'alimentation est généralement reliée au drain du transistor, par l'intermédiaire d'une résistance, et est donc toute proche de la grille.
Mais utiliser naïvement l'équation n'est pas une solution viable. Le fait est que les transistors FET d'une même série sont certes fabriqués de la même manière, mais qu'ils n'ont pas exactement les mêmes caractéristiques. Leur capacité, leur longueur de canal, et bien d'autres paramètres varient quelque peu d'un transistor à l'autre. En clair, deux transistors sortant d'une même usine et d'un même modèle auront un coefficient K différent. Fixer une tension VGS précise donnera alors des courants de saturation Id forts différents et la polarisation obtenue ne sera pas la même d'un transistor à l'autre. Il faut donc trouver d'autres méthodes pour compenser ce genre de défauts.
La polarisation d'un BJT
[modifier | modifier le wikicode]Dans cette section, nous allons étudier les montages pour polariser un BJT avec des résistances et des sources de tension. Nous allons étudier les montages de ce type qui sont les plus communs, les plus répandus. Pour détailler, nous allons voir les montages suivants :
- le montage à biais fixe (fixed bias circuit) ;
- le montage à biais fixe avec résistance d’émetteur (emitted-stabilized fixed bias circuit) ;
- le montage à biais par pont diviseur ;
- le montage à biais à rétroaction de voltage ;
- le montage à biais collecteur-base.
La polarisation à biais fixe
[modifier | modifier le wikicode]Pour commencer, nous allons étudier le circuit illustré ci-contre. Comme on le voit, la base et le collecteur sont reliés à la même source de tension, à travers des résistances différentes, judicieusement nommées et . L'émetteur est connecté à la masse. Ce circuit est souvent représenté avec des condensateurs sur son entrée et sa sortie, qui servent à filtrer les tensions continues. Ils servent quand le transistor est utilisé comme amplificateur, ce qui est leur utilisation principale. Lorsqu'on envoie un signal à amplifier au transistor, sa composante continue doit être supprimée, seule la composante alternative devant être amplifiée. Pour être plus précis, la composante continue est remplacée par la tension de polarisation, générée par le montage que l'on va voir. Pour cela, les deux condensateurs sont utilisés pour éliminer la composante continue tout en laissant passer le signal alternatif. Le circuit avec et sans condensateurs est illustré ci-dessous.
 |
 |
On peut résumer le fonctionnement de ce montage sur un graphique avec la tension VCE en abscisse et le courant IC en ordonnée, graphique qui est illustré ci-dessous. Sur ce graphique, on peut tracer les deux équations ci-dessous.
La première est tout simplement tirée de l'application de la loi des mailles dans le circuit. Elle donne un segment de droite décroissant, de pente égale ) -1/Rc.
La seconde décrit la relation entre IC et VCE pour un transistor BJT et nous l'avons déjà rencontrée dans le chapitre sur les BJTs. Elle donne une courbe en forme de marche, avec une montée rapide suivie d'un plateau.
Ces deux équations doivent être respectées simultanément, ce qui fait que le point d'intersection des deux courbes donne les valeurs exactes de IC et VCE.

Le circuit précédent a quelques qualités, mais aussi quelques défauts qui ne se voient pas au premier abord. Au niveau des qualités, il utilise peu de composants (quelques résistances) et est très simple à fabriquer. On peut configurer la tension de polarisation facilement en réglant les valeurs des résistances. Mais les défauts sont nombreux. En premier lieu, le courant de collecteur est assez instable et varie assez fortement avec la température, ce qui se répercute sur la tension de polarisation. Ensuite, le moindre changement dans la tension VBE entraine des variations dans le courant de collecteur, ce qui pose problème quand on veut utiliser VBE comme tension d'entrée dans un amplificateur. Enfin, le béta varie pas mal selon le transistor : changez-le par un autre de même modèle, mais d'une série différente, et le bêta sera totalement différent. Bref, ce montage n'est presque jamais utilisé tel quel, sans optimisations destinée à régler ces problèmes.
La polarisation à biais fixe, avec résistance d'émetteur
[modifier | modifier le wikicode]Pour résoudre les problèmes du montage précédent, il est possible d'ajouter une résistance entre l'émetteur et la masse. Le circuit obtenu est illustré ci-dessous. Le fonctionnement du montage n'est pas beaucoup changé et les équations ressemblent beaucoup à celles du montage précédent.
 |
 |
L'application de la loi des mailles dans le premier chemin donne cette équation.
Sachant qu'on a , on a :
La loi des mailles dans l'autre boucle donne ceci :
En injectant et en faisant quelques modifications, on trouve :
Et donc, on peut trouver le IC qui correspond en multipliant par le bêta.
Si on choisit les résistances tel que , on obtient l'équation suivante :
Le courant de collecteur devient donc assez insensible au bêta. Le résultat est que le circuit est plus stable : la tension de polarisation change un peu moins suite à une variation de température, un changement de VBE ou toute autre modification.
Si on trace les deux équations obtenues sur un graphe IC-VCE, on trouve à peu-près la même chose que pour le circuit précédent. L'équation donne une droite décroissante, alors que l'autre donne une courbe croissante en forme de marche "logarithmique". La différence est que la droite est plus pentue, et que la marche est un peu plus pentue.
La polarisation à pont diviseur
[modifier | modifier le wikicode]Le montage à pont diviseur est une amélioration du montage précédent, auquel on a rajouté une résistance entre la base et la masse. Son nom vient du fait que la tension sur la base est établie par un pont diviseur. Son avantage est que la tension de polarisation est encore plus indépendante du bêta et que le circuit est bien plus stable que les précédents.
 |
 |
Les montages amplificateurs à transistors
On a vu dans les chapitres précédents que les transistors sont des amplificateurs un peu particuliers. Rien d'étonnant donc à ce qu'il existe des circuits amplificateurs qui soient fabriqués avec des transistors bipolaires ou FET. Précisons cependant qu'un amplificateur est un quadripôle, alors que le transistor n'a que trois broches. Pour l'utiliser comme un "quadripôle" en mettant une de ses broches à la masse. Pour un transistor bipolaire, cela donne trois possibilités différentes, selon qu'on place la masse sur le collecteur, l'émetteur ou la base : montage à collecteur commun, à émetteur commun ou à base commune. Pour un transistor MOS, les montages équivalents sont appelés à source commune, à drain commun et à grille commune.

Les chapitres précédents nous ont appris que la relation entre tension et courant aux bornes d'un transistor n'est pas linéaire, ce qui fait qu'on ne peut pas assimiler un MOSFET à une résistance commandée en tension. De plus, il n'est pas possible de corriger les non-linéarités du transistor pour en faire un amplificateur linéaire, du moins pas facilement et pas de manière effectivement exploitable. Par contre, les choses changent quand on étudie le fonctionnement en petits signaux du transistor. Pour ce faire, on polarise le transistor à une tension non-nulle, généralement la moitié de VCC. Les signaux amplifiés sont des déviations par rapport à cette tension de polarisation, qui sont amplifiés par l'intermédiaire des montages que nous allons voir dans ce qui suit.
Rappelons comment procéder à l'analyse d'un circuit en petits signaux, sans quoi nous ne pourrons pas analyser les montages qui vont suivre.
- Remplacer le transistor par son modèle équivalent en petits signaux.
- Remplacer les sources de tension par un court-circuit et les sources de courant par un circuit ouvert. La tension d'alimentation est remplacée par la masse.
Les montages à transistors bipolaires
[modifier | modifier le wikicode]Il existe trois montages qui utilisent un BJT seul comme amplificateur. On les obtient en plaçant une des trois bornes du BJT à la masse, d'où l'existence de trois montages : un où la base est à la masse, un autre où c'est l'émetteur, et un dernier avec le collecteur. Ces trois montages sont appelés respectivement montage à base commune, à émetteur commun et à collecteur commun. Dans cette section, nous allons étudier ces trois montages. Précisons que ces trois montages doivent être polarisés pour fonctionner, vu qu'ils amplifient des petits signaux.
Pour vous en donner un aperçu, voici les trois montages illustrés ci-dessous pour un BJT de type NPN. Sur ces schémas, la tension ou le courant d'entrée est représenté par le générateur à gauche. La sortie est reliée à une charge, ici représentée par une résistance. Pour le reste, on voit que le montage contient des résistances et des condensateurs. Pour détailler, voici leurs fonctions :
- La plupart des résistances du montage et la source de tension forment un circuit de polarisation, dont le rôle est de mettre l'entrée et la sortie à une tension non-nulle. Le transistor est alors en régime de saturation et peut fonctionner comme amplificateur de petits signaux.
- Les condensateurs C1, C2 et C3 servent à filtrer les composantes continues, pour éviter toute interférences sur ou de la part du circuit de polarisation. C'est pourquoi on place des condensateurs, qui sont équivalents à des interrupteurs ouverts en continu, mais qui laissent passer les signaux alternatifs (au-delà d'une certaine fréquence, mais c'est un détail si la capacité des condensateurs est bien choisie). Ce faisant, on garantit que la polarisation du transistor n'est pas influencée par la conductance des circuits connectés sur l'entrée ou la sortie du montage. Sans eux, la polarisation du BJT influencerait le circuit d'entrée ou de sortie.
 |
 |
 |
Pour étudier ces montages, nous allons éliminer les tensions continues des schémas électriques et remplacer le BJT par son modèle en petit signal (soit le modèle hybride-pi, soit le modèle en T).
Le montage à émetteur commun
[modifier | modifier le wikicode]
On a vu dans les chapitres précédents que les transistors peuvent être vus comme des amplificateurs simples. Le courant qui les traverse dépend de la tension sur leur base/grille, ce qui fait qu'ils amplifient une tension d'entrée pour donner un courant de sortie analogue à la tension d'entrée. De tels convertisseurs tension-courant sont aussi appelés des amplificateurs en transconductance. Leur comportement est défini par la relation suivante :
- , avec le coefficient de transconductance.
Pour fabriquer un amplificateur de tension avec un amplificateur en transconductance, il suffit de transformer le courant de sortie en une tension proportionnelle, ce qui est fait en le faisant passer dans une simple résistance. On a alors :
En théorie, on devrait avoir :
On utilise alors la définition du gain de l'amplificateur en petit signal à savoir : :

Mais dans la réalité, les choses sont différentes. La résistance en question est placée en série avec le transistor. Si on omet le circuit de polarisation et les condensateurs du montage, le circuit obtenus sont illustrés ci-contre. De plus, la tension de sortie n'est pas prise aux bornes de la résistance R, mais au niveau du collecteur/drain, pour conserver une masse identique dans tout le circuit. La tension de sortie est donc inversée par rapport à la tension d'entrée : quand on augmente VBE, cela fait baisser VCE (et inversement). Dit autrement, le coefficient d'amplification est négatif.
|
Démonstration |
|
On peut le montrer avec le raisonnement suivant. D'après la loi des mailles, la tension de sortie est donc égale à : On injecte alors dans l'équation précédente. On décompose VBE en composante continue et alternative : On développe l'exponentielle. Par définition, on a : : , ce qui simplifie l'équation précédente en : Si , on peut approximer l'équation précédente en : On développe le terme de droite et on regroupe les termes continus : Cette forme sépare le terme de droite en une composante continue et le signal alternatif. On a donc :
Si on se rappelle que la tension VBE est la tension d'entrée, on voit bien que le gain en alternatif est de : |

Si on prend en compte le circuit de polarisation, le montage change quelque peu. Par exemple, prenons le montage illustré ci-contre. Pour analyser un tel montage, on doit remplacer le BJT par son circuit équivalent, et appliquer la méthode d'analyse en petits signaux. Le résultat est illustré dans le schéma ci-dessous.

On peut alors calculer la tension aux bornes de chaque résistance et étudier le circuit. On retrouve bien les résultats précédents, avec le même gain et la même tension de sortie, à peu de choses près. En faisant cela, on trouve les caractéristiques du tableau ci-dessous.
| Caractéristique | Expression/Approximation |
|---|---|
| Impédance d'entrée | : si on prend un modèle comme modèle équivalent en petits signaux, la résistance d'entrée est celle du modèle équivalent. |
| Impédance de sortie | |
| Gain en courant | 1, pas d'amplification |
| Gain en tension |
Le montage à émetteur commun avec résistance de dégénération d'émetteur
[modifier | modifier le wikicode]
Il est possible d'améliorer le montage précédent en ajoutant une résistance entre l'émetteur et la masse. Nous appelons celle-ci la résistance de dégénération d'émetteur, ce qui donne son nom à ce montage, et nous la noterons . Le circuit obtenu est illustré ci-contre, sans le circuit de polarisation.
Pour comprendre comment la résistance modifie le montage, il faut remplacer le transistor par son modèle équivalent en T. En faisant cela, on voit que la résistance d'émetteur du transistor est mise en série avec la résistance . On pourrait croire que cela augmente la résistance d'entrée de , mais il n'en est rien. Une analyse attentive du montage nous dit que la résistance d'entrée augmente de . Pour le prouver, faisons les calculs. La résistance d'entrée est par définition égale à :
On combine alors l'équation précédente avec l'équation :
On combine ensuite l'équation précédente avec l'équation :
L'équation précédente nous dit que la résistance d'entrée est égale à fois la résistance totale de l'émetteur. Par résistance totale, on veut dire la somme de la résistance d'émetteur du transistor et celle de la résistance .
Le rapport entre résistance d'entrée avec et sans résistance d'émetteur est donc égal à :
Le concepteur du montage peut donc contrôler la résistance d'entrée en choisissant bien la résistance de dégénération d'émetteur.
Le calcul du gain du montage montre que celui-ci est quelques peu réduit. Pour le montrer, partons de l'équation :
On injecte l'équation
On combine ensuite l'équation précédente avec l'équation :
On divise par pour obtenir le gain :
On factorise alors , ce qui donne :
On voit que le gain est réduit par rapport au gain de du montage à émetteur commun simple.
La résistance de sortie est inchangée.
Le montage à base commune
[modifier | modifier le wikicode]
Le montage à base commune est celui où la base d'un transistor bipolaire est reliée à la masse. Le signal d'entrée est envoyé sur l'émetteur et la sortie est sur le collecteur. Le schéma équivalent en petits signaux est illustré ci-dessous. La résistance RL est la résistance de la charge, branchée sur la sortie. La tension et le courant d'entrée sont représentées par la source de tension Vs et la résistance Rs. La résistance RC est la résistance de charge du montage, alors que le reste est le schéma équivalent du BJT, plus précisément le modèle hybride-pi.

Avec ce système, les courants d'entrée et de sortie sont égaux. En effet, le courant de base est nul, vu que la base est reliée à la masse. Combinez ce fait avec l'équation , et vous trouverez bien que : . Il n'y a donc pas d'amplification de courant, contrairement au montage précédent. L'amplification en tension est identique à celle obtenue avec le montage en émetteur commun, à quelques détails près. Mais surtout l'impédance d'entrée est extrêmement faible comparé aux montages précédents.
| Caractéristique | Expression/Approximation |
|---|---|
| Gain en courant | 1, pas d'amplification |
| Gain en tension | |
| Impédance d'entrée | |
| Impédance de sortie |
Le montage à collecteur commun
[modifier | modifier le wikicode]Le montage à collecteur commun utilise un transistor bipolaire dont le collecteur est connecté au VCC, la base servant d'entrée et l'émetteur de sortie. Le circuit exact est illustré ci-dessous, à la fois pour un transistor NPN et un PNP.
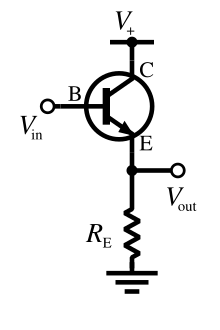 |
 |
Une analyse poussée du montage a un gain en tension très proche de l'unité, ce qui signifie que les signaux envoyés sur l'entrée sont quasiment reproduits à l'identique sur la sortie. Il ne s'agit donc pas d'un amplificateur de tension à proprement parler. Par contre, le gain en courant est le bêta du transistor, ce qui fait que ce montage sert d'amplificateur de courant !
| Caractéristique | Expression/Approximation |
|---|---|
| Gain en courant | |
| Gain en tension | Presque 1, pas d'amplification |
| Impédance d'entrée |
On peut démontrer le gain en tension assez simplement, pour ce montage.
|
Démonstration |
|
Pour le premier montage, la démonstration néglige les résistances d'entrée du transistor, ainsi que les résistances de charge sur l'entrée et la sortie. On utilise la loi des mailles sur la maille avec , et le transistor. On a alors : Or, sachant que , on a : Sachant que VBE est une tension assez faible, on peut la négliger, ce qui donne : |
Pour l'amplification en courant, on peut démontrer assez facilement que le gain est assez proche du du transistor.
|
Démonstration |
|
Pour cela, on applique la loi des nœuds dans le circuit, ce qui nous permet de déduire que le courant de sortie est égal au courant qui circule dans la résistance . Or, ce courant n'est autre que le courant d'émetteur du transistor, qui est égal à : On peut alors calculer le gain en courant en divisant le courant de sortie par le courant d'entrée , ce qui donne : |
Le schéma équivalent de ce montage est le suivant. La source de tension et la résistance Rs représentent la tension d'entrée et le courant associé. La résistance Rl est la résistance reliée à l'émetteur du BJT. Le reste est le schéma équivalent du BJT, provenant du modèle hybride-pi.

Les montages à transistors à effet de champ
[modifier | modifier le wikicode]Les trois montages des transistors bipolaires ont leur équivalent en transistors à effet de champ et réciproquement. Avec les FET, les trois montages sont appelés montage à source commune, à drain commun et à grille commune. Les amplificateurs à transistors à effet de champ ont des propriétés assez intéressantes. Par exemple, ils ont souvent des impédances d'entrée ou de sortie très fortes ou très faibles, ce qui provient de leur faible impédance d'entrée (qu'on peut considérer comme infinie).
Le montage à source commune (transistor à effet de champ)
[modifier | modifier le wikicode]
Le montage à source commune est illustré ci-contre.
On remarque rapidement que l'on envoie la tension d'entrée sur la grille, qui sert d'entrée au montage. En conséquence, la résistance d'entrée du montage est très importante, vu que la grille d'un FET a une résistance très forte (infinie en théorie, très importante en pratique). Il est raisonnable de supposer que le courant d'entrée est négligeable, approximativement nul. Par contre, le courant de sortie n'est pas nul, et encore moins négligeable : il dépend du courant qui circule dans le circuit, et de la résistance du circuit branché sur la sortie. En conséquence, l'amplification en courant du montage est très importante, mais ne peut pas être exploitée en pratique. Le montage a une forte amplification en courant, mais on ne peut pas l'utiliser comme amplificateur de courant. L'avantage de ce montage réside surtout dans le courant d'entrée nul, la forte résistance d'entrée, qui facilite son utilisation.
Pour ce qui est de son fonctionnement, ce montage suit la même logique que le montage à émetteur commun des transistors bipolaires. Le transistor convertit la tension d'entrée en courant, courant qui est envoyé dans une résistance pour être reconvertit en tension à la sortie. La tension de sortie pourrait être prise aux bornes de la résistance R, mais on préfère la prendre au niveau du collecteur/drain, pour conserver une masse identique dans tout le circuit. D'après la loi des mailles, la tension de sortie est donc égale à :
On peut décomposer le courant en ses composantes continue et alternative, et faire de même pour la tension de sortie :
On développe :
On voit rapidement, en analysant les termes, que : . En soustrayant de deux côtés, on a :
On injecte alors l'équation :
On a alors l'amplification en tension du montage, en se rappelant que : :
On peut résumer tout cela dans ce tableau.
| Caractéristique | Expression/Approximation | |
|---|---|---|
| Gain en courant | (courant d'entrée nul, courant de sortie non-nul) | |
| Gain en tension | ||
| Impédance d'entrée | , pas de courant d'entrée | |
| Impédance de sortie | ||
Le circuit équivalent en petits signaux de ce circuit est illustré ci-dessous. Le générateur de tension et la résistance à sa suite représentent la tension d'entrée. La résistance Rl est la résistance de la charge, le circuit placé sur la sortie. Le modèle utilisé pour le MOSFET est un modèle hybride-pi.

Le montage à grille commune
[modifier | modifier le wikicode]
Le montage à grille commune relie l'entrée à la source et la sortie sur le drain, la grille étant mise à la masse. Il est illustré ci-contre, dans sa version la plus simple, sans circuits de polarisation et condensateurs de découplage. Si on établit le circuit équivalent en petits signaux, on trouve le circuit illustré ci-dessous. Le générateur de courant et la résistance du bas représentent la tension d'entrée.

L'analyse détaillée de ce circuit permet d'obtenir les résultats présentés dans le tableau ci-dessous.
| Caractéristique | Expression/Approximation | |
|---|---|---|
| Gain en courant | 1, pas d'amplification | |
| Gain en tension | ||
| Impédance d'entrée | ||
| Impédance de sortie | ||
La version illustrée ci-dessous contient les condensateurs de découplage et les circuits de polarisation.

Les portes logiques
Diodes et transistors sont des composants dits analogiques, ce qui signifie qu'ils manipulent des variables continues, comme des courants ou des tensions. Mais l'électronique ne se limite pas à l'électronique dite analogique, centrée sur l'étude des signaux continus. À côté d'elle, l'électronique numérique étudie les signaux purement digitaux, souvent codés en binaire. Les circuits qui manipulent des données binaires sont fabriqués à partir de composants : les portes logiques.
Les différentes portes logiques
[modifier | modifier le wikicode]Les portes logiques sont des petits circuits qui prennent un ou plusieurs bit en entrée et fournissent un bit de résultat. Elles-mêmes sont fabriquées à partir de transistors ou de diodes, selon la technologie utilisée. Dans ce chapitre, nous allons voir ce que sont ces portes logiques et comment elles fonctionnent. Nous verrons dans un prochain chapitre comment elles sont fabriquées à partir de transistors.
- Sur les schémas qui vont suivre, les entrées des portes logiques seront à gauche et les sorties à droite !
La porte NON
[modifier | modifier le wikicode]
La première porte fondamentale est la porte NON, qui agit sur un seul bit : la sortie d'une porte NON est exactement le contraire de l'entrée.
Pour simplifier la compréhension, je vais rassembler les états de sortie en fonction des entrées pour chaque porte logique dans un tableau que l'on appelle table de vérité.
| Entrée | Sortie |
|---|---|
| 0 | 1 |
| 1 | 0 |
La porte ET
[modifier | modifier le wikicode]
La porte ET possède plusieurs entrées, mais une seule sortie. Cette porte logique met sa sortie à 1 quand toutes ses entrées valent 1. Dans le cas le plus simple, une porte ET possède deux entrées.
| Entrée 1 | Entrée 2 | Sortie |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Il existe des portes ET qui ont plus de deux entrées, et peuvent en avoir 3, 4, 5, 6, 7, etc. Là encore, leur sortie ne vaut 1 que si toutes les entrées valent 1 : dans le cas contraire, la sortie de la porte ET vaut 0. Dit autrement, si une seule entrée vaut 0, la sortie de la porte ET vaut 0.
Porte NAND
[modifier | modifier le wikicode]
La porte NAND donne l'exact inverse de la sortie d'une porte ET. En clair, sa sortie ne vaut 1 que si au moins une entrée est nulle. Dans le cas contraire, si toutes les entrées sont à 1, la sortie vaut 0. Dans le cas le plus simple, une porte NAND a deux entrées. Là encore, il existe des portes NAND ont plus de deux entrées : elles peuvent en avoir 3, 4, 5, 6, 7, etc. Là encore, leur sortie ne vaut 1 que si au moins une entrée est nulle : dans le cas contraire, la sortie de la porte NAND vaut 0. Dit autrement, si toutes les entrées sont à 1, la sortie vaut 0.
| Entrée 1 | Entrée 2 | Sortie |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Au fait, si vous regardez le schéma de la porte NAND, vous verrez que son symbole est presque identique à celui d'une porte ET : seul le petit rond sur la sortie de la porte a été rajouté. Il s'agit d'une sorte de raccourci pour schématiser une porte NON.
La porte OU
[modifier | modifier le wikicode]
La porte OU est une porte dont la sortie vaut 1 si et seulement si au moins une entrée vaut 1. Dit autrement, sa sortie est à 0 si toutes les entrées sont à 0. Dans le cas le plus simple, la porte OU possède deux entrées, ainsi qu'une seule sortie. Cette porte logique met sa sortie à 1 quand au moins une de ses entrées vaut 1. Là encore, il existe des portes OU ont plus de deux entrées. Là encore, leur sortie est à 0 si et seulement si toutes les entrées sont à 0 : si une seule entrée est à 1, alors la sortie vaut 1.
| Entrée 1 | Entrée 2 | Sortie |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Porte NOR
[modifier | modifier le wikicode]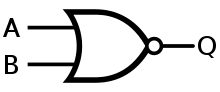
La porte NOR donne l'exact inverse de la sortie d'une porte OU. Là encore, il en existe une version avec deux entrées, et des versions avec plus de deux entrées. Les tableaux et symboles qui suivent sont ceux d'une porte NOR à deux entrées.
| Entrée 1 | Entrée 2 | Sortie |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Porte XOR
[modifier | modifier le wikicode]
Avec une porte OU, deux ET et deux portes NON, on peut créer une porte nommée XOR. Cette porte est souvent appelée porte OU exclusif. Sa sortie est à 1 quand les deux bits placés sur ses entrées sont différents, et vaut 0 sinon.
| Entrée 1 | Entrée 2 | Sortie |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Porte NXOR
[modifier | modifier le wikicode]
La porte XOR possède une petite sœur : la NXOR. Sa sortie est à 1 quand les deux entrées sont identiques, et vaut 0 sinon (elle est équivalente à une porte XOR suivie d'une porte NON).
| Entrée 1 | Entrée 2 | Sortie |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Les propriétés des portes logiques
[modifier | modifier le wikicode]Les portes logiques ont toutes diverses propriétés que l'électronicien doit connaitre. Par exemple, elles mettent du temps à réagir quand on change leur entrée, de même qu'il existe une relation entre la tension de sortie et celle d'entrée, etc. Dans ce qui va suivre, nous allons voir ces propriétés dans le cas le plus simple : celui d'une porte NON, une simple porte inverseuse. Tout ce qui sera dit dans cette section peut se généraliser, avec un petit effort, aux autres portes logiques plus complexes. Si les portes NON sont plus simples à étudier, c'est parce qu'elles n'ont qu'une seule entrée, alors que les autres portes logiques en ont plusieurs. Nous allons d'abord voir la relation entre tension d'entrée et tension de sortie, puis voir le délai de transmission entre entrée et sortie, avant de poursuivre par quelques propriétés annexes comme le fan-out.
La caractéristique tension d'entrée-tension de sortie
[modifier | modifier le wikicode]Le rapport entre tension à l'entrée et tension de sortie d'une porte NON, aussi appelée caractéristique en tension, est assez complexe, aussi il vaut mieux commencer par étudier une version simplifiée de celui-ci. Pour simplifier, le rapport entre et est illustré par le schéma ci-dessous. Pour caricaturer, on peut décomposer cette caractéristique en trois parties : deux zones dites de saturation et une zone d'amplification. Dans la zone de saturation, la tension est approximativement égale à la tension maximale ou minimale, ce qui fait qu'elle code pour un 0 ou un 1. Les seuils pour coder un 0 ou un 1 ne sont pas les mêmes entre l’entrée d'une porte NON et sa sortie. Ils sont beaucoup plus resserrés sur l'entrée, la marge de sécurité entre 1 et 0 étant plus faible. Un signal qui ne correspondrait pas à un 0 ou un 1 en sortie peut l'être en entrée. Entre ces deux zones extrêmes, la tension de sortie dépend linéairement de la tension d'entrée (si on omet l'inversion). Dans cette zone, la porte logique amplifie le signal d'entrée en plus de l'inverser.
Il existe deux tensions d'entrée qui servent de limites aux zones de saturation/amplification. La première, notée (V Input Low), est la tension d'entrée maximale qui code un 0 en entrée : toute tension inférieure code un 0. La seconde, notée (V Input High), est la tension minimale pour coder un 1 : au-delà, toute tension code un 1. À ces deux tensions d'entrée correspondent respectivement la tension de sortie minimale et maximale, notées et (V output Low et V Output High). Entre les deux, on se trouve dans la zone de saturation. Une porte NON est d'autant meilleure qu'elle a une zone d'amplification la plus petite possible. Le cas parfait est celui où la zone d'amplification est d'épaisseur nulle, celui où la tension passe directement de 0 à 1 en passant une tension seuil. Ce cas parfait d'une porte NON idéale est irréaliste et n'est jamais réalisé en pratique.

En réalité, la caractéristique en tension est plus lisse, moins droite que dans le schéma précédent. Il n'y a pas de frontière nette entre les zones de saturation et d'amplification, mais une transition progressive d'un régime à l'autre. La courbe réelle est illustrée ci-dessous et on voit qu'elle ressemble approximativement à une sigmoïde. La frontière entre zones de saturation et d'amplification est définie arbitrairement à partir de la pente de la courbe. On passe de l'un à l'autre quand la pente vaut -1.

Le temps de propagation
[modifier | modifier le wikicode]Un circuit électronique n'est pas un système parfait, et reste soumis aux lois de la physique. Notamment, il n'a pas une évolution instantanée et met toujours un petit peu de temps avant de changer d'état. Quand le bit sur l'entrée d'une porte logique change, elle met du temps avant de changer sa sortie. Ce temps de réaction pour propager un changement sur les entrées vers la sortie s'appelle le temps de propagation.
Pour les portes logiques, le temps de propagation est causé par le fonctionnement des transistors CMOS/MOS ou TTL qui composent la porte logique. Les liaisons entre broches se comportent comme des condensateurs et ont donc une capacité parasite. Lorsque l'on change l'entrée, ces capacités parasites vont se vider ou se remplir, ce qui prend un peu de temps. Il faut noter que plus le courant d'entrée est fort, plus ces capacités vont se remplir/vider rapidement, ce qui aura son importance pour la suite. On peut cependant en déduire que plus les courants en entrée/sortie d'une porte logique sont importants, plus les temps de propagation sont courts et plus celle-ci est rapide.
Pour une porte logique, il existe deux temps de propagation : un temps pour passer la sortie de 0 à 1, et un temps pour la passer de 1 à 0. Les électroniciens utilisent souvent la moyenne entre ces deux temps de propagation, et la nomment le retard de propagation, noté .

Les temps et permettent de déduire quelle est la vitesse maximale d'un circuit, à savoir le nombre de fois maximal qu'il peut changer d'état par secondes. Pour simplifier, on part du principe que la porte logique change d'état sans cesse et passe de 0 à 1 et inversement. En clair, elle évolue de manière cyclique, sa sortie s'inversant régulièrement. Le temps d'un cycle (passage de 0 à 1 et de 1 à 0) est appelé la période de commutation et vaut :
La vitesse maximale, aussi appelée fréquence de commutation, est l'inverse de cette durée. Elle correspond au nombre de cycles que la porte peut subir par secondes :
La sortance
[modifier | modifier le wikicode]Dans les circuits complexes, il n'est pas rare que la sortie d'une porte logique soit reliée à plusieurs entrées (d'autre portes logiques). Quand cela arrive, le nombre d'entrée connectée à la sortie se voit attribuer un nom : c'est la sortance de la sortie. La sortie doit alimenter en énergie les entrées des autres portes. Il faut bien maintenir un 1 sur ces entrées, ce qui demande de maintenir une tension sur les entrées et donc de les alimenter en électricité/courant. Évidemment, la sortie a une capacité limitée pour ce faire et rend les armes si on la branche à trop d'entrées. En clair, le nombre d'entrées auxquelles brancher une sortie est limitée et ce nombre maximal porte un nom : c'est la sortance maximale.
Il existe plusieurs manières de quantifier la sortance, qui ne sont pas équivalentes. L'une d'entre elle est de comparer le courant en sortie de la porte logique comparé au courant d'entrée. Si une porte logique a un courant d'entrée de , ce courant est répartis sur plusieurs portes logiques, chacune ayant un courant d'entrée . Le nombre de portes maximal supporté est alors de :
Cette définition fonctionne bien pour les portes logiques basées sur des transistors bipolaires, mais n'a pas trop de sens pour les portes conçues avec des transistors FET et assimilés. Ces portes ont en effet un courant d'entrée presque nul (nul pour une porte idéale, mais très faible en pratique). La définition précédente de la sortance, appliquée à ces portes logiques, donne une sortance théorique de 100 à 500. Mais ce chiffre surestime la réalité et néglige divers phénomènes physiques liés aux transistors FET. Elle n'est donc pas applicable dans ce genre de cas.
Les familles MOS : PMOS, NMOS et CMOS
Les portes logiques vues dans le chapitre précédent sont fabriquées en utilisant des transistors. Il existe de nombreuses manières pour concevoir des circuits à base de transistors, auxquelles on a donné le nom de familles logiques.. les plus connues portent les noms de DTL, RTL, TLL, CMOS et bien d'autre. En voici la liste et une description sommaire :
- Les logiques MOS (Metal Oxyde Silicium) utilisent des transistors à effet de champ, parfois couplés à des résistances. On distingue :
- La logique NMOS, qui utilise des transistors NMOS associés à des résistances.
- La logique PMOS, qui utilise des transistors PMOS associés à des résistances.
- La logique CMOS, qui utilise des transistors PMOS et NMOS, sans résistances associées.
- Les autres logiques utilisent des transistors bipolaires et/ou des diodes
- La logique à diodes n'utilise que des diodes pour fabriquer des portes logiques ;
- La logique RTL (Resistance-Transistor Logic) utilise des résistances couplées à des transistors bipolaires ;
- La logique DTL (Diode-Transistor Logic) utilise des diodes couplées à des transistors bipolaires ;
- La logique TTL (Transistor-Transistor Logic) utilise uniquement des transistors bipolaires.
- Les logiques Emitter-coupled logic (ECL), Integrated injection logic, Gunning transceiver logic sont des techniques évoluées à base de transistors bipolaires.
Ce chapitre aborde les familles logiques qui utilisent des transistors à effet de champ. Il s'agit des technologies MOS, PMOS, NMOS et CMOS.
La technologie NMOS
[modifier | modifier le wikicode]Nous allons commencer avec la technologie NMOS, mais les circuits PMOS sont relativement similaires. Les deux technologies étaient utilisées avant l'invention de la technologie CMOS, quand on ne savait pas comment faire pour avoir à la fois des transistors PMOS et NMOS sur la même puce électronique, mais sont aujourd'hui révolues.
Le fonctionnement des logiques NMOS et PMOS
[modifier | modifier le wikicode]Avec la technologie NMOS, les portes logiques sont fabriqués avec des transistors NMOS intercalés avec une résistance.

Leur fonctionnement est assez facile à expliquer. Quand la sortie doit être à 1, tous les transistors sont ouverts. Il n'y a pas de chemin qui relie la sortie à la masse. Par contre, la sortie est connectée à la tension d'alimentation, ce qui fait qu'elle est mise à 1. On place une résistance entre la tension d'alimentation et la sortie pour éviter que le courant qui la traverse soit trop fort dans cette situation. Quand la sortie doit être à 0, il y a au moins un transistor NMOS qui se ferme. Mais si un transistor NMOS se ferme et connecte l'alimentation à la masse, les choses changent. Les lois compliquées de l'électricité nous disent alors que la sortie est connectée à la masse, soit au zéro volts. Elle est donc mise à 0.

Les circuits PMOS sont construits d'une manière assez similaire aux circuits CMOS, si ce n'est que les transistors NMOS sont remplacés par une résistance qui relie ici la masse à la sortie. Rien d'étonnant à cela, les deux types de transistors, PMOS et NMOS, ayant un fonctionnement inverse.
Les portes logiques de base en NMOS
[modifier | modifier le wikicode]Que ce soit en logique PMOS ou NMOS, les portes de base sont les portes NON, NAND et NOR. Les portes ET et OU sont fabriqués en combinant des portes de base, par exemple plaçant une porte NON à la suite d'une porte NAND/NOR pour obtenir un ET ou un OU. Voici les circuits obtenus en NMOS et PMOS:
| NMOS | |||||
|---|---|---|---|---|---|
| Portes de base | 
|

|
| ||
| Portes composites | 
|

| |||
Voyons maintenant comment fonctionne les portes de base en NMOS.
La porte NON
[modifier | modifier le wikicode]Le circuit d'une porte NON en technologie NMOS est illustré ci-dessous. Le principe de ce circuit est assez simple : l'étude de seulement deux cas permet de le comprendre en détail. Si on envoie un 0 sur la grille du transistor, celui-ci s'ouvre et la sortie est reliée à la tension d'alimentation. À l'inverse, quand on met un 1 sur la grille, le transistor se ferme et la sortie est reliée à la masse, mise à 0. Le résultat est bien un circuit inverseur.

|
La porte NOR
[modifier | modifier le wikicode]La porte NOR est similaire à la porte NON, si ce n'est qu'il y a maintenant deux transistors en parallèles. Si une des grilles est mise à 1, un des transistors se fermera et la sortie est mise à 0. Par contre, quand les deux entrées sont à 0, les transistors s'ouvrent tous deux et la sortie est mise à 1. Le comportement obtenu est bien celui d'une NOR.

|

|
La porte NAND
[modifier | modifier le wikicode]La porte NAND fonctionne sur un principe similaire au précédent, si ce n'est qu'il faut que les deux grilles soient à zéro pour obtenir une sortie à 1. Pour mettre la sortie à 0 quand seulement les deux transistors sont ouverts, il suffit de les mettre en série, comme dans le schéma ci-dessous. Le circuit obtenu est bien une porte NAND.
 |
 |
Il existe des variantes de la porte précédente, où la résistance est remplacée par un générateur de courant, fabriqué avec des transistors NMOS.

|
|
La technologie PMOS
[modifier | modifier le wikicode]Les circuits en technologie PMOS ressemblent beaucoup aux circuits en technologie NMOS, si ce n'est qu'ils sont inversés. Rien d'étonnant à cela, les deux types de transistors, PMOS et NMOS, ayant un fonctionnement inverse.
La technologie PMOS avec des résistances entre la tension d'alimentation et la sortie
[modifier | modifier le wikicode]Avec les circuits PMOS, les transistors sont placés entre la tension d'alimentation et la sortie. De plus, les transistors NMOS sont remplacés par une résistance qui relie ici la masse à la sortie.

|

|

|
La technologie PMOS avec des résistances entre la masse et la sortie
[modifier | modifier le wikicode]Il est aussi possible de câbler les portes logiques autrement, en remplaçant les transistors NMOS d'un circuit NMOS par des PMOS. Mais dans ce cas, la tensions liée à la résistance doit être négative, égale à l'opposé de la tension d’alimentation.

|

|

|
La technologie CMOS
[modifier | modifier le wikicode]Dans cette section, nous allons montrer comment fabriquer des portes logiques en utilisant la technologie CMOS. Avec celle-ci, chaque porte logique est fabriquée à la fois avec des transistors NMOS et des transistors PMOS. On peut la voir comme un mélange entre la technologie PMOS et NMOS. Tout circuit CMOS est divisé en deux parties : une intégralement composée de transistors PMOS et une autre de transistors NMOS. Chacune relie la sortie du circuit soit à la masse, soit à la tension d'alimentation.

La première partie relie la tension d'alimentation à la sortie, mais uniquement quand la sortie doit être à 1. Si la sortie doit être à 1, des transistors PMOS vont se fermer et connecter tension et sortie. Dans le cas contraire, des transistors s'ouvrent et cela déconnecte la liaison entre sortie et tension d'alimentation. L'autre partie du circuit fonctionne de la même manière que la partie de PMOS, sauf qu'elle relie la sortie à la masse et qu'elle se ferme quand la sortie doit être mise à 0

La porte NON
[modifier | modifier le wikicode]Cette porte est fabriquée avec seulement deux transistors, comme indiqué ci-dessous.

Si on met un 1 en entrée de ce circuit, le transistor du haut va fonctionner comme un interrupteur ouvert, et celui du bas comme un interrupteur fermé : la sortie est reliée au zéro volt, et vaut donc 0. Inversement, si on met un 0 en entrée de ce petit montage électronique, le transistor du bas va fonctionner comme un interrupteur ouvert, et celui du haut comme un interrupteur fermé : la sortie est reliée à la tension d'alimentation, et vaut donc 1.

La porte NAND
[modifier | modifier le wikicode]Voici en exclusivité comment créer une porte NAND à deux entrées avec des transistors CMOS !


La porte NOR
[modifier | modifier le wikicode]Implémenter une porte NOR à deux entrées avec des transistors CMOS ressemble à ce qu'on a fait pour la porte NAND.


Les portes XOR et NXOR
[modifier | modifier le wikicode]Il est possible de créer une porte XOR en combinant d'autres portes logiques. Mais d'autres implémentations optimisent le tout directement au niveau des transistors. Le circuit ci-dessous en est un exemple. Le fonctionnement du circuit est simple et il s'explique facilement si on découpe le circuit en quatre : les deux transistors en haut à gauche, les deux en haut à droite, les deux en bas à gauche et les deux en bas à droite. Si les deux entrées sont à 1, alors les deux transistors en bas à gauche vont se fermer et connecter la sortie au 0 volts, les trois autres groupes ayant au moins un transistor ouvert. Si les deux entrées sont à 0, alors les deux transistors en bas à droite vont se fermer et connecter la sortie au 0 volts, les autres quadrants ayant au moins un transistor ouvert. Et pareil quand les deux bits sont différents : un des deux quadrants aura ses deux transistors fermés, alors que les autres auront au moins un transistor ouvert, ce qui connecte la sortie à la tension d'alimentation.

En ajoutant les deux portes NON nécessaires pour calculer l'inverse des deux entrées, on trouve :

La logique pass transistor logic
[modifier | modifier le wikicode]La pass transistor logic est une forme particulière de technologie CMOS, une version non-conventionnelle. Avec le CMOS normal, la porte de base est la porte NON. En modifiant celle-ci, on arrive à fabriquer des portes NAND, NOR, puis les autres portes logiques. Les transistors sont conçus de manière à connecter la sortie, soit la tension d'alimentation, soit la masse. Avec la pass transistor logic, le montage de base est un circuit interrupteur, qui fonctionne autrement. Cette version du CMOS a été utilisée dans des processeurs commerciaux, comme dans l'ARM1. Dans la suite du cours, nous verrons quelques circuits qui utilisent cette technologie, mais ils seront rares. Nous l'utiliserons quand nous parlerons des additionneurs, ou les multiplexeurs, guère plus. Mais il est sympathique de savoir que cette technologie existe.
La porte à transmission
[modifier | modifier le wikicode]Le circuit de base est un interrupteur construit avec deux transistors. Pourquoi ne pas utiliser un seul transistor par interrupteur ? C'est parce que la logique CMOS fait que tout transistor PMOS doit être associé à un transistor NMOS et réciproquement. Donc, deux transistors. Le montage interrupteur de base est appelé une porte à transmission. C'est un petit circuit avec trois entrées : une entrée de commande, une entrée et une sortie. Le circuit peut soit connecter l'entrée et la sortie, soit déconnecter la sortie de l'entrée. Le choix entre les deux dépend de l’entrée de commande. Le montage de base est le suivant :

- Les deux entrée A et /A sont l'inverse l'une de l'autre, ce qui fait qu'il faut en théorie rajouter une porte NON CMOS normale, pour obtenir le circuit complet. Mais dans les faits, on arrive souvent à s'en passer. Ce qui fait que la porte à transmission est définie comme étant le circuit à deux transistors précédents.
Le schéma ci-dessous nous permet de comprendre quels sont les défauts de la pass transistor logic. Il n'y a ni tension d'alimentation, ni masse (O Volts). Par contre, la sortie d'une porte à transmission est alimentée par la tension d'entrée, ce qui fait qu'il n'y a pas d'amplification de la tension d'entrée. Et vu que les transistors ne sont pas parfaits, on a toujours une petite perte de tension en sortie d'une porte à transmission. Le résultat est que si on enchaine les portes à transmission, la tension de sortie a tendance à diminuer, et ce d'autant plus vite qu'on a enchainé de portes à transmission. le résultat est qu'il faut souvent rajouter des portes amplificatrices pour restaurer les tensions adéquates, à divers endroits du circuit. Ces portes amplificatrices sont composées d'une ou de deux portes NON en CMOS normal. La pass transistor logic mélange donc porte NON CMOS normales avec des portes à transmission. De plus, afin de faire des économies de circuit, on n'utilise souvent qu'une seule porte NON CMOS comme amplificateur, ce qui fait que de nombreux signaux sont inversés dans le circuit.
Par contre, ce défaut entraine aussi des avantages. Notamment, la consommation d'énergie est fortement diminuée. Seules les portes amplificatrices, les portes NON CMOS, sont alimentées en tension/courant. Le reste des circuits n'est pas alimenté, car il n'y a pas de connexion à la tension d'alimentation et la masse.
Les portes à transmission sont très utilisés dans certains circuits très communs, que nous aborderons dans quelques chapitres, comme les multiplexeurs ou les démultiplexeurs.
La porte XOR en pass transistor logic
[modifier | modifier le wikicode]Il est facile d'implémenter une porte XOR avec des portes à transmission. Cela demande deux portes à transmission, plus quelques portes NON, pas plus.

La version précédente est une porte XOR où les signaux d'entrée sont doublés : on a le bit d'entrée original, et son inverse. C'est quelque chose de fréquent dans les circuits en pass transistor logic, où les signaux/bits sont doublés. Mais il est possible de créer des version normales, sans duplication des bits d'entrée. La solution la plus simple de rajouter deux portes NON, pour inverser les deux entrées. Le circuit passe donc de 4 à 8 transistors, ce qui reste peu. Mais on peut ruser, ce qui donne le circuit ci-dessous. Comme vous pouvez les voir, il mélange porte à transmission et portes NON CMOS normales.

Une autre version n'utilise que l'inverse de la première entrée.

Dans les deux cas, l'économie en transistors est drastique comparé au CMOS normal. Plus haut, nous avons illustré plusieurs versions possible d'une porte XOR en CMOS normal : toutes allaient de 8 à 12 transistors. Ici, on va de 6 transistors maximum, à seulement 4 ou 5 pour les versions plus simples. Le gain est clairement significatif, suffisamment pour que les circuits avec beaucoup de portes XOR gagnent à être implémentés avec la pass transistor logic.
Les avantages et inconvénients respectifs du NMOS, PMOS et CMOS
[modifier | modifier le wikicode]De nos jours, la quasi-totalité des circuits électroniques est basé sur une technologie CMOS, les technologies NMOS et PMOS étant quasiment abandonnées. Les raisons à cela sont multiples, chaque technologie ayant des avantages et des inconvénients divers. L'avantage principal du CMOS sur les autres technologies tient surtout à sa faible consommation en énergie. Pour comprendre pourquoi le CMOS consomme moins, reprenons les schémas précédent pour une porte NON (les raisonnements que nous allons suivre valent pour toutes les portes logiques, mais sont plus simples avec une porte NON).
Avec les technologies NMOS et PMOS, la sortie est reliée à la tension VDD par une résistance. Quand la sortie est à 1, le courant passe dans la résistance, ce qui fait qu'une puissance égale à est dissipée par la résistance. Il s'agit d'une perte sèche d'énergie, une consommation d'énergie inutile. Vu que cette perte continue tant que la sortie est maintenue à 1, on lui donne le nom de consommation statique. Par contre, les circuits CMOS n'ont pas de résistances, mais uniquement des transistors, ce qui fait qu'il n'y a pas de dissipation statique de puissance.
Cela ne signifie pas qu'il n'y a pas de consommation d'énergie dans les transistors. Par exemple, ils dissipent un peu d'énergie quand on les fait passer de l'état bloqué à passant (ou inversement). Mais cette consommation d'énergie n'a pas lieu en permanence, tant que la sortie est maintenue. Il faut au contraire que la sortie change de valeur pour que de l'énergie soit dissipée, raison pour laquelle cette consommation d'énergie est appelée la consommation dynamique. Elle est présente dans les circuits CMOS, mais aussi dans les NMOS et les PMOS, qui sont à égalité de ce point de vue. Pour résumer, si tous les circuits ont une dissipation d'énergie d'origine dynamique, les CMOS n'ont pas de consommation statique, ce qui leur donne un avantage en terme de consommation d'électricité.
Les familles bipolaires : à diodes, DTL, ETL, TTL et ECL
Après avoir vu les technologies utilisant des transistors MOS, nous allons voir les technologies à transistors bipolaires. Celles-ci regroupent les technologies suivantes :
- La logique à diodes n'utilise que des diodes pour fabriquer des portes logiques ;
- La logique RTL (Resistance-Transistor Logic) utilise des résistances couplées à des transistors bipolaires ;
- La logique DTL (Diode-Transistor Logic) utilise des diodes couplées à des transistors bipolaires ;
- La logique TTL (Transistor-Transistor Logic) utilise uniquement des transistors bipolaires ;
- Les logiques Emitter-coupled logic (ECL), Integrated injection logic, Gunning transceiver logic sont des techniques évoluées à base de transistors bipolaires.
La logique à diode
[modifier | modifier le wikicode]La logique à diode est la première à avoir été inventée. Comme son nom l'indique, elle n'utilise que des diodes et pas de transistors, pour fabriquer des portes logiques. Son défaut principal est qu'elle ne permet pas de créer toutes les portes logiques possibles, mais seulement les portes ET et OU. Il n'est pas possible de fabriquer une porte NON avec cette famille logique, ce qui la raison pour laquelle les autres portes ne sont pas synthétisables.
La porte OU
[modifier | modifier le wikicode]Le circuit de la porte OU est illustré ci-dessous.

Son fonctionnement est de loin le plus simple, bien plus que celui de la porte ET. Si une entrée est à 1, la diode associée sera passante et la tension sera reproduite sur la sortie. Mais si les deux diodes reçoivent un 0, alors la sortie est simplement mise à 0.

La porte ET
[modifier | modifier le wikicode]Le circuit de la porte ET est illustré ci-dessous.
Le fonctionnement de cette porte s'explique assez facilement en regardant ce qui se passe quand on met un 0 ou un 1 sur une entrée. Chaque entrée est reliée à la tension d'alimentation à travers une résistance. Si on envoie un 0 sur l'entrée, la diode conduira. La sortie est alors reliée à la masse, ce qui la met à 0. Mais si on met un 1, la diode sera bloquée et se comporte comme un interrupteur ouvert. La sortie n'est donc pas reliée à la masse, mais est connectée à la tension d'alimentation : elle est donc à 1. On voit que si une seule entrée est à 0, la sortie sera connectée à la masse et donc à 0. Mais si toutes les entrées sont à 1, les deux diodes se bloquent et la sortie est à 1.

La logique RTL (Resistor-Transistor Logic)
[modifier | modifier le wikicode]La logique RTL (Resistor-Transistor Logic) utilise des résistances et un ou plusieurs transistors bipolaires pour construire une porte logique. La plus simple est de loin la porte NON, les autres portes simples (ET, OU, NAND et NOR) n'étant qu'une extension de la porte NON.
La porte NON en RTL
[modifier | modifier le wikicode]
Le circuit d'une porte NON en RTL est illustré ci-contre. On voit que le montage utilise un transistor en émetteur commun. Le transistor est couplé à deux résistances : une sur sa base et une autre sur son collecteur, que l'on nommera "résistance de base" et "résistance de collecteur". Le collecteur est relié à la tension d'alimentation par le biais d'une des deux résistances. On remarque aussi que la sortie est reliée au collecteur du transistor bipolaire. Le fonctionnement du circuit est assez simple, et on peut résumer le transistor à un simple interrupteur ouvert ou fermé. Quand aux résistances, elles transforment une tension (la tension d'alimentation ou la tension de base) en courant.
- Si on place un 1 sur l'entrée, une tension élevée est placée aux bornes de la résistance de base. Du fait de la loi d'Ohm, le courant de base est non-nul et le transistor est en état passant. la tension est alors reliée à la masse. La tension au niveau de l'émetteur est alors égale à la tension , entre l'émetteur et le collecteur (la masse). Cette tension est très faible, ce qui fait que la tension de sortie l'est aussi : c'est un 0.
- Si on place un 0 sur l'entrée, la tension aux bornes de la résistance de base est nulle. Il n'y a donc aucun courant qui traverse la base, ce qui met le transistor en état bloqué. La sortie est alors reliée directement à la tension d'alimentation, ce qui la met à 1.
 |
 |
Les autres portes en technologie RTL
[modifier | modifier le wikicode]Les portes NAND et NOR ont, en technologie RTL, un câblage similaire à celui des technologies MOS. Leur conception est similaire à celle de la porte NON, si ce n'est qu'on ajoute des résistances et éventuellement des transistors. Le transistor et la résistance en plus sont placés en série du premier pour les portes NAND, en parallèle pour les portes NOR.
La porte NOR
[modifier | modifier le wikicode]Le schéma ci-dessous montre ce qu'il en est pour les portes NOR. On voit qu'il y a un transistor par entrée, avec une résistance d'entrée entre l'entrée et le transistor associé.

Le fonctionnement d'une porte à deux entrées est illustré ci-dessous. Chaque schéma indique les tensions dans le montage, pour une combinaison particulière des entrées.
 |
 |
Précisons que dans le cas d'une porte NOR à deux entrées, on peut simplifier le montage en n'utilisant non pas un transistor par entrée, mais un seul transistor pour tout le montage. Pour cela, il suffit d'utiliser le montage ci-dessous. L'idée est que les résistances d'entrée sont couplées avec une troisième résistance. Le réseau de résistance avant la base additionne les tensions d'entrée, tandis que le transistor compare la tension d'entrée à un seuil d'environ 0.7 volts. Les valeurs des résistances sont choisies avec soin de manière à ce qu'un 1 sur une seule entrée suffise à ce la tension de base dépasse le seuil du transistor.

La porte NAND
[modifier | modifier le wikicode]La porte NAND en technologie RTL est similaire à la porte NOR, sauf que les transistors sont placés en série et non en parallèle.

Les autres portes logiques
[modifier | modifier le wikicode]Les portes ET et OU sont conçues à l'identique, sauf que le circuit est inversé, ce qui inverse le comportement du circuit. La sortie est reliée au collecteur ou à l'émetteur des transistors et ces transistors sont placés entre la tension d'alimentation et la sortie.
| Porte ET | Porte OU |
|---|---|
 |
 |
La logique DTL (Diode-Transistor Logic)
[modifier | modifier le wikicode]La logique DTL (Diode-Transistor Logic) est un mélange de la logique à diode avec la technologie RTL. Avec cette technologie, les portes ET et OU sont fabriquées en utilisant la logique à diode, tandis que les portes NON sont fabriquées à partir de la technologie RTL. Et il est alors possible de fabriquer des portes NOR et NAND en plaçant une porte NON de type RTL à la suite d'une porte ET/OU de type logique à diode.

Cette logique marche assez bien, mais il y a un problème : la tension en sortie de la porte à diode n'est pas adaptée au seuil du transistor. Pour cela, on doit rajouter un étage d'adaptation entre la porte à diode et le transistor inverseur, qui adapte la tension. Dans le cas le plus simple, cet étage est un vulgaire pont diviseur de tension.

Cependant, il est possible de concevoir l'étage d'adaptation en utilisant un montage à base de diodes en série, ou de diodes associées à des résistances. L'idée est que chaque diode réduit un petit peu la tension à adapter, d'environ le seuil de transmission de la diode.

Si l'idée générale suffit largement, il existe des montages optimisés pour simplifier la conception du circuit, éliminer des bruits parasites, rendre le circuit plus tolérant au bruit, etc. Ces circuits sont des améliorations des circuits précédents, où on rajoute des résistances, des condensateurs, des diodes, etc. Par exemple, il est intéressant de rajouter un condensateur, comme montré dans le schéma ci-dessous. Celui-ci permet de vider plus rapidement la base du transistor quand on veut le fermer, et de la remplir plus rapidement quand on veut l'ouvrir.

La logique TTL (Transistor-Transistor Logic)
[modifier | modifier le wikicode]La logique TTL (Transistor-Transistor Logic) est une amélioration de la logique DTL. Les diodes utilisées pour les portes NOR et NAND sont remplacées par un seul transistor dont l'émetteur (la broche) est multiple - en clair, le transistor a plusieurs émetteurs.
| Porte NON | Porte NAND |
|---|---|

|

|
Les circuits intégrés

On peut utiliser des portes logiques et/ou des transistors pour créer des circuits plus compliqués, souvent appelés circuits intégrés. Ces circuits ont, comme les portes logiques, des broches métalliques sur lesquelles on envoie des tensions, chaque broche pouvant servir soit d'entrée, soit de sortie (rarement les deux). Certaines de ces broches vont recevoir la tension d'alimentation (broche VCC), d'autres vont être reliées à la masse (broche GND), d'autres vont recevoir des bits de données. À l'intérieur de ces circuits intégré, on trouve un grand nombre de transistors et de portes logiques qui sont reliés entre eux et/ou connectés aux broches d'entrée/sortie.
Les broches
[modifier | modifier le wikicode]La plupart des circuits complexes, comme les processeurs et mémoires des ordinateurs, comprennent un grand nombre de broches : plusieurs centaines ! Si on prend l'exemple du processeur MC68000, un vieux processeur inventé en 1979 présent dans les calculatrices TI-89 et TI-92, celui-ci contient 68000 transistors (d'où son nom : MC68000). Il s'agit d'un vieux processeur complètement obsolète et particulièrement simple. Et pourtant, celui-ci contient pas mal de broches : 37 au total ! Pour comparer, sachez que les processeurs actuels utilisent entre 700 et 1300 broches d'entrée et de sortie. À ce jeu là, notre pauvre petit MC68000 passe pour un gringalet !
Pour être plus précis, le nombre de broches (entrées et sorties) d'un processeur dépend du socket de la carte mère. Par exemple, un socket LGA775 est conçu pour les processeurs comportant 775 broches d'entrée et de sortie, tandis qu'un socket AM2 est conçu pour des processeurs de 640 broches. Certains sockets peuvent carrément utiliser 2000 broches (c'est le cas du socket G34 utilisé pour certains processeurs AMD Opteron). Pour la mémoire, le nombre de broches dépend du format utilisé pour la barrette de mémoire (il existe trois formats différents), ainsi que du type de mémoire. Certaines mémoires obsolètes (les mémoires FPM-RAM et EDO-RAM) se contentaient de 30 broches, tandis que la mémoire DDR2 utilise entre 204 et 244 broches.
Les sorties et leurs types
[modifier | modifier le wikicode]Les sorties des circuits intégrés peuvent se classer en plusieurs types, selon leur fonctionnement. On distingue principalement les sorties totem-pole, les sorties à drain ouvert et les sorties trois-état.
Les sorties totem-pole sont les plus communes pour les circuits CMOS. Ce sont des sorties qui sont connectées à deux transistors : un qui relie la sortie à la masse, et un autre qui la relie à la tension d'alimentation. En technologie CMOS, elles sont équivalentes à des sorties connectées à une porte logique.

Les sorties à drain ouvert sont reliées à un seul transistor, comme indiqué dans le schéma ci-contre. Le transistor relie la sortie à la masse, mais rien ne relie la sortie à la tension d'alimentation. La sortie peut être mise à 0 par le circuit intégré, mais elle ne peut pas être mise à 1 sans intervention extérieure. Pour utiliser une sortie à drain ouvert, il faut relier la sortie à la tension d'alimentation à travers une résistance, appelée résistance de rappel. Dans ce cas, la sortie est mise à 0 ou 1 selon que le transistor est ouvert ou fermé. Si le transistor est ouvert, la sortie n'est pas reliée au circuit. À la place, elle est connectée à la tension d'alimentation, ce qui fait que la sortie est à 1. Si le transistor est fermé, la tension d'alimentation est reliée à la masse et il en est de même pour la sortie. En clair, elle est à 0.
Les sorties à totem-pole ont pour caractéristique de toujours être connectées soit à la masse, soit à la tension d'alimentation. Les sorties à drain ouvert ne sont pas dans ce cas là, du moins sans résistance de rappel. Si on regard bien, elles peuvent être connectées soit à la masse, soit à rien. Cet état où elles ne sont pas connectées à quoi que ce soit n'est pas utilisé tel quel. Par contre, le troisième type de sortie en fait bon usage. Il s'agit des sorties trois-état. leur caractéristique principale est qu'elles peuvent prendre trois états, comme leur nom l'indique. Soit elles sont connectées à la masse, soit elles sont reliées à la tension d'alimentation, soit elles ne sont connectée ni à l'une ni à l'autre. Si les deux premiers cas correspondent à un 0 et à un 1, l'état déconnecté ne correspond à aucun des deux. Il s'agit d'un état utilisé quand on souhaite déconnecter ou connecter à la demande certains composants dans un circuit. Vous comprendrez en quoi ces sorties sont utiles quand nous parlerons des mémoires et des bus de communication.

 GFDL GFDL
|
Vous avez la permission de copier, distribuer et/ou modifier ce document selon les termes de la licence de documentation libre GNU, version 1.2 ou plus récente publiée par la Free Software Foundation ; sans sections inaltérables, sans texte de première page de couverture et sans texte de dernière page de couverture. |



























































![{\displaystyle O(\omega )=\alpha \cdot I=\alpha \cdot \left[S(\omega )-\beta \cdot O(\omega )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86a5e5ad2c5da37cb87b08d45b6aea9285441acd)
















![{\displaystyle T(\omega )={\frac {\alpha _{0}/(1+j(f/f_{o}))}{1-\beta \cdot \alpha _{0}[1+j(f/f_{o})]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b19c9610e6690214305714b6e26cf99b5d002e0)



















![{\displaystyle O(\omega )=\alpha \cdot \left[S(\omega )+\beta \cdot O(\omega )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7f41b899ebac743240f25076e2f117f614590b1)












































































































































![{\displaystyle U_{sum}=-U_{t}\times \left[\log {\left({\frac {U_{1}}{R\times I_{s}}}+1\right)}+\log {\left({\frac {U_{1}}{R\times I_{s}}}+1\right)}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c07d6cc5039316f2f7b631c5ad1eb54d498b77b)

![{\displaystyle U_{sum}=-U_{t}\times \log {\left[\left({\frac {U_{1}}{R\times I_{s}}}+1\right)\times \left({\frac {U_{1}}{R\times I_{s}}}+1\right)\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c7c0bd8e54ce7ed97ba7c2ef6b547fe383092e5)










































![{\displaystyle T(\omega )={\frac {T_{0}}{1+\zeta ^{2}\cdot \cos ^{2}\left[N\cdot \cos ^{-1}\left({\frac {\omega }{\omega _{0}}}\right)\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/455a92c8612e38d883f25c4bb91bec8f1ca00bed)

![{\displaystyle T(\omega )={\frac {T_{0}}{1+\zeta ^{2}\cdot \cosh ^{2}\left[N\cdot \cosh ^{-1}\left({\frac {\omega }{\omega _{0}}}\right)\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c510d5dfc802034dcd947d211a5744b4be08dc9e)














































![{\displaystyle \alpha \beta ={\frac {1+R_{4}/R_{3}}{3+j\left[RC\cdot \left(\omega +{\frac {1}{\omega }}\right)\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65f91d5f0a68a4d82fc011011f80be7629d03c9c)








![{\displaystyle {\frac {1}{T(\omega )}}=j\omega C_{0}+{\frac {(j\omega )^{2}+(1/L\cdot C_{1})}{(j\omega )^{2}+\left[(C_{0}+C_{1})/(L\cdot C_{0}\cdot C_{1})\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1a2b2628d45877a9ff5c204e0d9f2ff01a63cc1)


![{\displaystyle T=2\cdot RC\cdot \ln \left[{\frac {1+\beta }{1-\beta }}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0d155461011a1b72d882a7874163d8e95d0c285)









































































































![{\displaystyle I_{C}\approx \beta \left[I_{0}\cdot \exp {\left({\frac {V_{be}}{V_{th}}}\right)}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10b03806ec381695f4694536d6fe69f42e802e87)
![{\displaystyle \beta =\beta _{0}\cdot \left[1+{\frac {V_{ce}}{V_{E}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3348d8e2abb4a0ff427ccbad4f91bc4f2d1d299)
![{\displaystyle I_{C}=\left(I_{s}\cdot \exp {\frac {V_{be}}{V_{th}}}\right)\cdot \beta _{0}\left[1+{\frac {V_{ce}}{V_{E}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb7c59f86bfade2bd358df458f811f9959a1d49b)





![{\displaystyle I_{C}=\beta \left[1+{\frac {V_{ce}}{V_{EA}}}\right]\cdot I_{s}\exp {\left({\frac {V_{be}}{V_{th}}}\right)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f8bafdd28ee83b144621c7d645680dd6ff2830a)

![{\displaystyle I_{C}=I_{S}\cdot \left[\left(e^{\frac {V_{BE}}{V_{T}}}-e^{\frac {V_{BC}}{V_{T}}}\right)-{\frac {1}{\beta }}\left(e^{\frac {V_{BC}}{V_{T}}}-1\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85a80fe44c9b6e6591dc21d4b43983ca477ebeab)
![{\displaystyle I_{E}=I_{S}\cdot \left[{\frac {1}{\beta }}\left(e^{\frac {V_{BE}}{V_{T}}}-1\right)+{\frac {1}{\beta }}\left(e^{\frac {V_{BC}}{V_{T}}}-1\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af3ad854e1b6c083075b8a41b997ae470c493007)
![{\displaystyle I_{B}=I_{S}\cdot \left[\left(e^{\frac {V_{BE}}{V_{T}}}-e^{\frac {V_{BC}}{V_{T}}}\right)-{\frac {1}{\beta }}\left(e^{\frac {V_{BE}}{V_{T}}}-1\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36d4ae1a8abd25d727a1e0e9e28f1f43154f5f3d)























![{\displaystyle I_{D}=v\cdot {\frac {Q}{L}}=\mu {\frac {V_{DS}}{L}}\cdot [C_{s}\cdot l\cdot (V_{GS}-V_{T})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59bbb05a814d579702f6b1be5eb6f753393f87e3)









![{\displaystyle I_{D}=k\cdot V_{DS}\cdot \left[(V_{GS}-V_{T})-{\frac {1}{2}}V_{DS}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7167aad45c88f4b97e4ea1edc9c9b828eed0f110)

![{\displaystyle I_{D}=k\cdot \left[V_{DS}\cdot (V_{GS}-V_{T})\right]-{\frac {1}{2}}V_{DS}^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9baa221b18ce226329d5a29b2b6be6c66b8b555d)







































































![{\displaystyle I_{C}=\beta \cdot I_{B}=\beta \cdot \left[1+{\frac {V_{ce}}{V_{EA}}}\right]\cdot I_{s}\exp {\left({\frac {V_{be}}{V_{th}}}\right)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5acdadedf81f03eabaa386267c0f792960013b93)



























































![{\displaystyle V_{OUT}+v_{out}=VCC-R\cdot [ID+i_{d}(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcf13d3b0d4ae09c8e36506270e198f7554c512f)


























