Cosmologie/Le paradoxe d'Olbers
Nous allons commencer ce cours avec une question simple, qui est paradoxalement une excellente introduction à la cosmologie :
- Pourquoi la nuit est-elle noire ?
Cette question peut sembler étrange, tant nous sommes habitués à voir les étoiles sur un fond noir. Bien que la lumière artificielle nous cache les étoiles et éclaire le ciel nocturne, nous savons que cette lumière cache le noir de la nuit, ses étoiles et la Lune. Mais pour un scientifique, même les choses évidentes sont dignes d'intérêt et demandent à être expliquées.
Les astronomes de l'antiquité n'étaient eux-mêmes pas surpris par l'obscurité de la nuit. Pour simplifier, ils pensaient les étoiles attachées à une sphère céleste, une sorte de sphère/coupole géante qui recouvre le ciel. S'ils supposaient que la Terre tourne sur elle-même, ils supposaient la sphère céleste fixe, expliquant le mouvement des étoiles au cours de la nuit et des saisons. Pour être plus précis, leur pensée utilisait plusieurs sphères : une pour le Soleil, une pour la Lune, une pour les étoiles proches, une pour les étoiles fixes des constellations (la plus lointaine) et bien d'autres. L'explication au noir de la nuit était que les étoiles étaient en nombre limitées et à des endroits bien précis, elles ne recouvraient pas entièrement le ciel. Beaucoup de savants avaient compris que ce modèle de sphères concentriques était un artifice de calcul utile, mais fondamentalement faux. Néanmoins, l'explication fondamentale au noir de la nuit restait valide : il n'y avait pas assez d'étoiles pour illuminer le ciel.
 |
 |
Avec les progrès de l'astronomie, et notamment l'arrivée des modèles géocentriques et héliocentriques, ce modèle de sphères emboîtées fût remis en cause. Pour les astronomes du moyen-âge et de la renaissance, les étoiles et astres n'étaient pas fixés sur des sphères proches, mais peuvent emplir tout l'espace. Leur vision de l'univers évolua vers un modèle d'univers infini, immobile, éternel, homogène. Par immobile, on veut dire que les effets de la gravité des astres s'annulent mutuellement sur de grandes distances. Chaque galaxie s'éloigne ou se rapproche de la nôtre, mais dans l'ensemble, ces différents mouvements se compensent et la moyenne des vitesses des galaxies est nulle. Par infini, on veut dire que l'univers a un volume infini : il n'a pas de début ni de fin, pas de frontières ou de bords, etc. Par éternel, on veut dire qu'il a un âge infini, qu'il n'a pas de début et de fin. Et par homogène, on veut dire que la répartition des étoiles est supposée globalement uniforme à grande échelle.
Mais les astronomes du moyen-âge et de la renaissance comprirent rapidement que le noir de la nuit était incompatible avec ce qu'ils savaient de l'univers.
Le paradoxe d'Olbers
[modifier | modifier le wikicode]Le modèle d'un univers infini, immobile, éternel, homogène est assez logique, limite intuitive, mais elle entre en conflit avec le noir de la nuit. Plusieurs savant ont en effet montré qu'un tel univers devrait avoir une nuit extrêmement lumineuse, et certainement pas une nuit noire. Cela peut paraitre étonnant, mais plusieurs astronomes l'ont déduit mathématiquement ou sur la base d'arguments logiques. C'est un paradoxe, appelé paradoxe d'Olbers, nommé ainsi en l'honneur d'Olbers , un des astronomes à avoir évoqué ce paradoxe. D'autres astronomes avaient autrefois évoqué ce paradoxe, comme Thomas Digges en 1576, Johannes Kepler en 1605 ou Edmond Halley au XVIIIe siècle, mais pas aussi explicitement qu'Olbers.
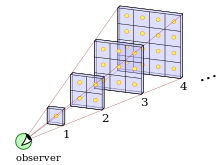
Logiquement, on s'attend à ce que la nuit soit noire car les étoiles lointaines nous envoient directement moins de lumière que les étoiles proches. Après tout, la lumière émise par un objet est répartie dans toutes les directions, ce qui fait que plus un objet est lointain, moins on reçoit sa lumière. La luminosité perçue depuis la Terre diminue avec la distance, et plus précisément avec le carré de la distance. Mais il se trouve que le diamètre apparent fait de même. Le résultat est que pour une portion du ciel d'une surface bien précise, on peut mettre soit peu d'étoiles proches, soit beaucoup d'étoiles lointaines. Il se trouve que sous certaines conditions, respectées dans l'univers infini, éternel et homogène, les deux phénomènes se compensent et que la luminosité d'une portion du ciel est globalement constante.
La lumière des étoiles se déplaçant dans le vide intersidéral en ligne droite, les étoiles sont visibles depuis la Terre tant qu'il n'y a pas d'obstacle entre elles et la Terre. Or, si l'univers est infini, éternel et homogène, alors on est certain qu'en tout point du ciel, on tombera sur au moins une étoile. Si l’univers est infini, il contient une infinité d'étoiles. Et s'il existe depuis un temps infini, la lumière de toutes ces étoiles a eu le temps d'atteindre la Terre. En conséquence, le ciel devrait être éclairé par une infinité d'étoiles. La répartition homogène des étoiles assure que ces étoiles soient réparties équitablement sur la sphère céleste, ce qui fait que peu importe où on regarde de la voûte céleste, on devrait y voir une étoile à cet endroit.
Avec ces conditions, la baisse de quantité de lumière reçue avec la distance est compensée par le plus grand nombre d'étoiles observables. Le schéma ci-contre illustre ce fait. Pour résumer, le ciel devrait être empli de lumière, cachant totalement le Soleil. C'était pour eux un paradoxe, appelé paradoxe d'Olbers, du nom de l'astronome qui le formalisa (d'autres astronomes, comme Kepler, avaient cependant mentionné ce paradoxe dans certains écrits, mais pas aussi explicitement qu'Olbers).
Pour mieux comprendre le problème, nous allons reprendre un développement mathématique assez connu qui formalise l'argument d'Olbers.
Modélisation de la répartition des étoiles
[modifier | modifier le wikicode]En premier lieu, on découpe l'univers en sphères concentriques. Chaque couche, chaque sphère, a une épaisseur égale à la distance moyenne entre deux étoiles. De plus, chaque couche est à une distance de la Terre.

Calcul du nombre d'étoile dans chaque couche
[modifier | modifier le wikicode]En second lieu, on calcule le nombre d'étoiles présentes dans chaque "sphère", dans chaque coque.
Pour cela, on utilise l'hypothèse suivante :
- H1 : Les étoiles sont uniformément réparties.
Cette hypothèse dit que la densité d'étoile, à savoir le nombre d'étoiles par unité de volume, est constante. Dans ce qui suit, nous allons la noter .
Chaque "sphère", chaque coque, contient un nombre d'étoile égal à son volume multiplié par :
Le volume d'une coque est approximativement égal à sa surface S multipliée par son épaisseur (la distance moyenne entre deux étoiles, notée D), ce qui donne :
En combinant les deux équations précédentes, on a :
Calcul du flux de lumière émis par les étoiles d'une couche
[modifier | modifier le wikicode]En troisième lieu, on calcule le flux de lumière émis par une couche.
Pour cela, on part de l'hypothèse suivante :
- H2 : Toutes les étoiles ont la même luminosité L.
On va utiliser cette hypothèse pour calculer le flux de lumière de chaque étoile. La physique du rayonnement nous dit que ce flux est égal à :
Le flux émis par toutes les étoiles d'une couche est la somme des flux de chaque étoile de la couche :
On utilise alors l'équation , démontrée plus haut :
On simplifie :
Cette équation nous dit que toutes les couches émettent la même quantité de lumière, ce qui n'est pas intuitif...
Calcul de la luminosité du ciel
[modifier | modifier le wikicode]En quatrième lieu, on combine la luminosité de toutes les couches pour trouver la luminosité totale du ciel.
Pour cela, on utilise les hypothèses suivantes :
- H3 : Toutes les étoiles sont visibles depuis la Terre, il n'y a pas d'obstacle entre une étoile et la Terre.
Cela signifie qu'il faut prendre en compte toutes les couches dans le calculs.
- H4 : L'univers est infini.
Le fait que l'univers est infini nous dit qu'il existe une infinité de couches concentriques.
- H4 : L'univers est éternel.
Le fait que l'univers est éternel nous dit que la lumière de toutes les étoiles a eu le temps d'atteindre la Terre.
Il faut donc additionner la luminosité de toutes les couches existantes pour trouver le flux de lumière visible dans le ciel, en faisant une intégrale. Nous n'allons pas faire le calcul, car il se trouve qu'on obtient un résultat infini. Intuitivement, la troisième étape suffit à comprendre pourquoi : chaque couche a une luminosité finie et identique à celle des autres couches, et il y a une infinité de couches. Le ciel devrait être infiniment lumineux !
Les "solutions" du paradoxe d'Olbers
[modifier | modifier le wikicode]Divers savants se sont écharpés sur le paradoxe d'Olbers et de nombreuses réponses y ont été apportées. La démonstration d'Olbers n'ayant pas de problèmes mathématiques particuliers, il fallut se rendre à l'évidence : certaines hypothèses utilisées dans la démonstration sont fausses. Reste à trouver lesquelles.
On peut remettre en cause l'hypothèse de la luminosité fixe des étoiles, mais cela ne mène à rien. Même en supposant que certaines étoiles émettent peu ou pas de lumière, on se retrouve quand même avec une somme infinie.
Remettre en cause la répartition des étoiles a été envisagé, notamment dans des théories qui supposaient que la répartition des étoiles/galaxies était une distribution fractale. Ces théories sont cependant restées au stade de théories irréalistes, dont l'utilité est de montrer que telle piste de recherche est envisageable. La raison à cela est que les résultats empiriques ne suivent pas : dans ces théories, on devrait avoir des endroits du ciel qui seraient extrêmement lumineux, bien plus que le Soleil. Les observations astronomiques montrent de plus que si l'univers est assez hétérogène à petite distance, il est fortement homogène à grande distance.
Une première possibilité "crédible" était que les étoiles lointaines ne sont pas visibles depuis la Terre. Leur lumière est bien émise mais n'arrive pas à destination, reste à en trouver la raison. Une première explication fût que la lumière était absorbée par des nuages de gaz, de poussière, ou tout autre obstacle entre les étoiles et la Terre. Mais cette explication était incorrecte. L'obstacle en question absorbe le rayonnement de l'étoile, ce qui le chauffe. Or, tout corps chauffé émet un rayonnement dit de corps noir, dont l'intensité augmente avec la température. À force de chauffer, l'obstacle atteint une température d'équilibre, où le rayonnement absorbé par l'obstacle est intégralement réémis vers la Terre. L'obstacle est alors aussi lumineux que l'étoile qui le chauffe. Retour à la case départ.
La seule solution est que l'univers n'est pas infini et/ou qu'il a un âge fini. Les deux solutions font que l'on ne doit additionner que les couches les plus proches de la Terre, situées en-dessous d'un rayon maximal .
- Si l'univers a un volume fini, il a de de facto un rayon maximal .
- S'il a un âge fini , la lumière des étoiles très éloignées n'a pas eu le temps d'arriver sur Terre. Au-delà de la distance ( est la vitesse de la lumière), la lumière n'a pas encore pu arriver jusqu’à la Terre.














