Cosmologie/Le décalage vers le rouge (redshift)
Peu après la découverte des galaxies, à la moitié des années 20, les astronomes ont entrepris d'étudier les étoiles et les galaxies à partir de la lumière qu'elles émettent. Les observations actuelles utilisent soit des étoiles variables (des céphéides), soit des étoiles qui explosent : les supernovas. Plus précisément, les astronomes utilisent une classe bien précise de supernovas, qui ont pour particularité de générer systématiquement la même luminosité : les supernovas de type Ia. La luminosité perçue depuis la Terre de ces supernovas est proportionnelle à la distance.
Les astronomes analysent la lumière émise par les étoiles et galaxies, afin d'en déduire énormément de chose. Ils ne se contentent pas d'analyser la luminosité ou la couleur des objets, ils étudient le spectre de la lumière émise. Par spectre, on veut dire l'ensemble des fréquences présente dans la lumière émise. Les galaxies et étoiles émettent de la lumière qui est une superposition d'onde électromagnétiques aux fréquences très diverses. L'ensemble forme ce qu'on appelle le spectre de la lumière et il ressemble à ceci :

Les trous dans le spectre, les bandes noires, s'expliquent par l'absorption de la lumière par les atomes. Les atomes absorbent la lumière dans des bandes de fréquence très précises, bandes qui sont des endroits très précis suivant l’élément chimique en question. La position des bandes permet de déterminer la composition chimique des étoiles/galaxies. L'étude des spectres de la lumière s'appelle la spectroscopie et astronomes l'utilisent beaucoup dans leurs observations astronomiques.

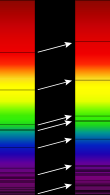
Le redshift des galaxies
[modifier | modifier le wikicode]Si vous étudiez le spectre d'une galaxie, bous allez tomber sur la situation ci-contre. Les bandes semblent décalées par rapport à la fréquence habituelle. Les distances entre les bandes sont conservées, toutes les bandes semblent s'être décalées en bloc. Tout se passe comme si la lumière semble être décalée vers les basses fréquences (le rouge), comparée à sa couleur d'émission. Ce phénomène s'appelle le décalage vers le rouge ou encore le redshift.
Il est possible de quantifier le redshift par un paramètre mathématique noté . Pour quantifier ce phénomène, les physiciens utilisent le rapport entre le décalage des longueurs d'onde, et la longueur d'onde normale, attendue, celle mesurée sur Terre. Cette quantité, notée , est appelée le décalage vers le rouge, ou encore le redshift.
- , avec la longueur d'onde actuelle, mesurée lors d'une observation, et la longueur d'onde lors de l'émission du rayonnement.
Les observations sur les galaxies ont montré la présence de ce décalage vers le rouge, sans pour autant pouvoir l'expliquer. Un point intriguant est que le redshift varie fortement avec la distance. Plus une galaxie est éloignée, plus son spectre sera décalé vers le rouge.
La loi de Hubble
[modifier | modifier le wikicode]Hubble a été le premier astronome à mettre en équation ce comportement, dans son article daté de 1929. Il étudia un grand nombre d'observations provenant de ses collègues, ainsi que les observations qu'il avait effectuées lui-même. De ces observations, il induit une loi statistique, du nom de loi de Hubble. Dans sa formulation la plus fiable, elle dit que pour les galaxies proches, le redshift est proportionnel à la distance.
Suite à la découverte de Hubble, de nombreuses campagnes d'observations ont suivi et se sont poursuivies durant des décennies. Un exemple de résultats obtenus est le suivant. On voit que la relation de Hubble

La loi de Hubble ne fonctionne pas à longue distance
[modifier | modifier le wikicode]Insistons sur le fait que la loi de Hubble ne fonctionne que pour des objets cosmologiques "proches". Par proche, on veut dire que leur décalage vers le rouge est proche de 1, guère plus. Pour de tels objets astronomiques, la concordance est franchement bonne. Mais pour les objets astronomiques plus lointains, la loi de Hubble ne fonctionne tout simplement pas et la relation entre distance et redshift devient tout autre. Elle cesse d'être linéaire, et devient alors beaucoup plus complexe.
Idéalement, il faudrait trouver une équation du redshift qui marche tout le temps. De telles formules empiriques existent, de même que d'autres formules basées sur la théorie de la relativité générale. Les scientifiques ont des logiciels dédiés pour faire les calculs et on peut trouver des calculateurs en ligne pour. Par exemple, vous pouvez utiliser ce site pour faire quelques calculs de distance en fonction du redshift :
L'interprétation de la relation redshift-distance
[modifier | modifier le wikicode]Maintenant que nous connaissons la relation entre distance et redshift, encore faut-il l'expliquer. Et c'est là que le bât blesse ! Pour expliquer le décalage vers le rouge, il existe plusieurs solutions. Mais, comme nous allons le voir, les explications classiques sont rapidement mises en défaut.
L'explication par l'effet Doppler
[modifier | modifier le wikicode]Pour expliquer le décalage vers le rouge des galaxies, Hubble pensa à l'effet Doppler-Fizeau, que les étudiants en physique connaissent bien. Quand un objet s'éloigne de nous à une certaine vitesse, la fréquence de la lumière qu'il émet baisse et la lumière parait rougie par rapport à la normale. Et réciproquement, un objet qui s'approche émettra une lumière plus bleuie, dont la fréquence a légèrement augmenté. Le redshift est alors causé par la vitesse de l'objet qui s'approche ou s'éloigne.
La loi de Hubble proprement dite
[modifier | modifier le wikicode]Il existe une formule qui associe la vitesse de l'objet et le décalage vers le rouge, qui est différente selon que l'on travaille en physique newtonienne, en relativité restreinte ou en relativité générale. La physique classique donne la formule suivante, entre la vitesse de l'objet en mouvement et le décalage vers le rouge qui en découle.
On peut réécrire la formule précédente de manière à obtenir la vitesse de l'objet à partir de son redshift :
En utilisant cette formule et en combinant celle-ci à ses observations sur le redshift, Hubble formula une loi statistique, du nom de loi de Hubble, dit que la vitesse d'éloignement d'une galaxie est proportionnelle à sa distance. Le facteur de proportionnalité nommée paramètre de Hubble, il est noté H.
- , où v est la vitesse extrapolée du redshift, d la distance de la galaxie et H le facteur de Hubble.
La formule précédente est en réalité une extrapolation basée sur l'hypothèse que le redshift est bien causé par une vitesse. En réalité, ce qu'Hubble avait observé, c'est que le redshift était égal à :
La loi de Hubble est approximative, car les galaxies ne s'éloignent pas toutes à la même vitesse. Certaines vont plus vite, d'autres moins vite. Il faut faire la différence entre la vitesse donnée par la loi de Hubble, qui est une moyenne, et la différence avec la vitesse moyenne.

L'interprétation en termes de vitesse était tout simplement fausse et il n'a pas fallu longtemps pour s'en rendre compte. Appliquées de manière naïve à des galaxies lointaines, les redshift observés correspondent à des vitesses supérieures à celle de la lumière dans le vide. De telles vitesses supraluminiques sont un signe que la cause du décalage vers le rouge demande une explication relativiste. Une manière de sauver le tout serait d'utiliser des formules d'effet Doppler tirées de la relativité restreinte, plus adaptées aux forts redshifts, mais nous verrons plus bas que de telles explications ne marchent pas.
L'expansion de l'univers
[modifier | modifier le wikicode]
L'interprétation initiale, à base d'effet Doppler, indique que les galaxies s'éloignent toutes de nous, comme si nous étions au centre de l'univers, et que les galaxies tentaient de le fuir. La conclusion est claire : l'univers s'étend, gonfle. Les astronomes ont appelé ce phénomène l'expansion de l'univers. Pourtant, on aurait dû s'attendre à l'inverse : la gravité est censée rapprocher les galaxies les unes des autres.
A cause de l'expansion de l'univers, il est évident que l'univers devait être plus "petit" par le passé (plus précisément, la portion de l'univers qui correspond aujourd'hui à l'univers observable). En renversant l'écoulement du temps, l'univers se contracte progressivement, et on peut facilement imaginer qu'après un certain temps, tout le contenu de l'univers soit rassemblé en un seul point : la singularité initiale. L'univers serait alors né d'une dilatation de cette singularité initiale, dilatation qui porte le nom de big-bang.
Mais cette vue de l'esprit pose de nombreux problèmes mathématiques. En effet, cette singularité implique que de nombreux calculs dépendant des distances donnent des divisions par zéro. Par exemple, le calcul de la pression, de la température, de la densité, ou d'autres paramètres physiques ne sont pas calculables. Tout ce que peuvent faire les scientifiques, c'est étudier ce qu'il s'est passé quelques secondes ou minutes après le temps qui correspond à cette singularité hypothétique. Les calculs actuels ne donnent plus de résultats crédibles au-delà d'une certaine durée, la durée de Planck. Celle-ci vaut environ secondes.
L'expansion de l'univers est une manière d'expliquer les observations de Hubble, qui est compatible avec l'interprétation du redshift comme un effet Doppler. Cependant, le fait que les redshift donnent des vitesses supra-luminiques semblent indiquer qu'il faut expliquer tout cela avec une théorie relativiste. Voyons ce que la relativité peut dire là dessus.
L'explication par le décalage vers le rouge gravitationnel
[modifier | modifier le wikicode]Une autre explication est le décalage vers le rouge gravitationnel, aussi appelé décalage d'Einstein. Il s'agit d'une conséquence de la relativité générale, observé expérimentalement. Sans rentrer dans les détails, il dit que la fréquence de la lumière change quand elle traverse un champ gravitationnel. Précisément, si on prend une masse M qui génère un champ de gravité, la lumière bleuit en se rapprochant de la masse, elle rougit en s'en éloignant.

Vous avez peut-être pensé que c'était le candidat idéal pour expliquer le redshift des galaxies, mais c'est en réalité le pire. La gravité de la terre ou de notre galaxie est une mauvaise explication : elle a tendance à faire bleuir la lumière qui s'approche de nous, sans compter que les calculs montrent que cela n'explique pas la relation redshift-distance.
En réalité, la lumière émise par les galaxies se rapproche de nous, elle rougit, ce qui signifie qu'elle s'éloigne de la source de gravité responsable du décalage vers le rouge. Et le redshift est observé pour toutes les galaxies, dans tous les sens, peu importe où on regarde sur la voute céleste. Cela signifie que la distribution des masses serait franchement bizarre, avec la terre au beau milieu d'un creux gravitationnel. Chose étrange, sachant qu'on est dans une galaxie et que la distribution des galaxies est assez homogène dans l'univers... Le décalage d'Einstein n'est pas la solution.
L'hypothèse de la lumière fatiguée
[modifier | modifier le wikicode]Les deux idées précédentes font que l'univers n'est pas statique :, il est en expansion avec l'explication par l'effet Doppler, en contraction gravitationnelle avec le décalage d'Einstein. Mais l'intuition nous ferait plutôt penser à un univers statique, sans expansion ni contraction. Aussi, diverses théories ont tenté d'expliquer les redshifts galactiques sans recourir à un univers en expansion/contraction.
La théorie de la lumière fatiguée est une ancienne hypothèse visant à expliquer le redshift et sa variation en fonction de la distance avec un univers statique. L'idée est que sur de longues distances, la lumière interagit avec la matière, ce qui lui fait perdre de l'énergie, ce qui réduit sa fréquence et la décale vers le rouge. Plus la distance est grande, plus la lumière a interagit avec la matière et plus le décalage vers le rouge serait grand. L'idée a été formalisée dans de nombreuses théories différentes, qui se distinguaient par des détails. Mais l'idée de base est la même pour toutes ces théories.
Mais elle a de nombreux défaut, comme le fait que les images de galaxies lointaines devraient être plus floues qu'observé, du fait de la dispersion de la lumière lors des interactions lumière-matière. Cela ne veut pas dire que la lumière n'a pas interagit avec la matière lors de son trajet, mais cela ne suffit pas à expliquer la loi de Hubble.
De plus, d'autres observations vont contre ce mécanisme. Par exemple, la luminosité angulaire des galaxies devrait être constante dans un univers sans expansion avec lumière fatiguée, alors que les observations montrent qu'elle diminue avec la distance. La formalisation de cet argument a donné naissance au test empirique nommé le test de luminosité surfacique de Tolamn (Tolman surface brightness test). Et les résultats de ce test ont montré que les théories de la lumière fatiguée ne tiennent pas la route. D'autres observations plus complexes à expliquer vont à l'encontre des théories de la lumière fatiguée, comme des observations sur les courbes de luminosité des Supernovae, mais surtout : les observations du fond diffus cosmologique qu'on verra dans quelques chapitres.

L'explication du redshift cosmologique par la relativité générale
[modifier | modifier le wikicode]Aussi bizarre que cela puisse paraitre, les savants de l'époque n'étaient pas étonnés de voir apparaitre loi de Hubble, ni des galaxies aux vitesses supra-luminiques. La théorie de la relativité générale, qui existait déjà à l'époque, avait déjà permis de prédire que de telles situations pouvaient arriver. Et la relativité générale fournit un cadre explicatif parfait pour rendre compte des observations sur le redshift. De plus, la théorie de la relativité générale, appliquée à l'univers, explique parfaitement le paradoxe d'Olbers vu au chapitre précédent.
L'interprétation du redshift comme un effet Doppler son aujourd'hui abandonnée, au profit d'une explication totalement différente, basée sur la relativité générale. Dans cette interprétation, la relation est toujours valable, c'est l'équation pour le redshift qui est fausse. Et nous allons détailler cette explication dans le chapitre suivant.










