Cosmologie/Les processus de baryogenèse et nucléosynthèse
Au tout début de sa formation, l'univers était clairement chaud et dense. Les températures quelques microsecondes après le big-bang dépassaient le million voire le milliard de degrés. L'univers était en première approximation un gaz parfait de particules très différentes : neutrons, protons, neutrinos, électrons, photons, quarks, et autres. Les températures étaient tellement fortes que toutes les populations de particules réagissaient entre elles. N'importe quelle particule pouvait échanger de l'énergie avec n'importe quelle autre, homogénéisant les températures. Le mélange était tel que l'on pouvait définir une température moyenne valable pour tous les types de particules : les neutrons avaient une température moyenne similaire à celle des protons, elle-même identiques à celle des quarks, etc. On dit que l'équilibre thermique est respecté.
Pendant cette phase, l'univers était dominé par le rayonnement, avec énormément plus de photons que de particules. Les calculs disent qu'il y avait plusieurs milliards de photons pour une seule particule matérielle. De plus, la température était très élevée et les autres particules étaient ultra-relativistes. Or, rappelez-vous le résultat du chapitre précédent : la température du rayonnement diminue comme l'inverse du facteur d'échelle (), et c'est approximativement la même chose pour les particules ultra-relativistes. Le gaz de particules élémentaires s'est donc progressivement refroidit à cause de l'expansion.
Du fait du refroidissement, le plasma primordial s'est progressivement condensé, donnant naissance à des particules composites. D'une soupe de particules se sont ainsi formés les nucléons, puis les noyaux et enfin les atomes. Puis, l'univers s'est refroidi en raison de l'expansion. En se diluant avec l'expansion, sa densité a diminué, les particules se sont espacées entre elles. Elles se sont éloignées au point que leurs interactions sont devenues plus rares. Leur proximité rendait leurs interactions faciles, chaque particule ayant rapidement accès à une voisine pour échanger de la quantité de mouvement. Mais avec la dilution, les particules se sont progressivement isolées les unes des autres, rendant les échanges de plus en plus difficiles. De nombreuses interactions ont disparues, perturbant les processus de mélange thermique.
La distribution de Maxwell-Boltzmann
[modifier | modifier le wikicode]Avant toute chose, précisons que lorsque la température n'est pas trop forte, un gaz de particules peut être décrit par ce qu'on appelle la distribution de Maxwell-Boltzmann. Elle permet de savoir quelle est la quantité de particules par unité de volume N, pour une particule de masse , en fonction de la température. L'équation qui lie ces trois paramètres, température, densité de particule, et masse, est la suivante :
Une équation plus précise est la suivante :
Elle ne peut s'appliquer qu'à la condition que . En clair, l'énergie de masse de la particule doit être largement supérieure à l'énergie thermique ambiante. De ce fait, la particule peut se former sans être complétement détruite par le chaos thermique ambiant.
Notons que cette relation permet de calculer des rapports, comme le nombre de protons pour un neutron, combien il y a de neutrinos pour un proton, etc. Sauf pour les particules sans masse, comme les photons, évidemment. Elle permet de calculer des choses comme le rapport protons/neutrons, etc. Pour comparer la densité d'une particule avec celle d'une particule , on calcule le rapport . On a alors :
En simplifiant, on a :
La baryogenèse et le découplage des neutrinos
[modifier | modifier le wikicode]Au tout début, on pouvait voir l'univers comme un mélange de plusieurs gaz composés de particules élémentaires. Du temps des fortes températures, quelques micro-secondes avant le big-bang, l'univers était peuplé par un plasma quark-gluons, à savoir un gaz de quarks et de particules liées, accompagné de photons et de neutrinos très énergétiques. Les protons et neutrons ne pouvaient pas se former à partir de quarks. La température trop intense faisait que les particules composites étaient brisées par le chaos ambiant quelques microsecondes après leur formation. C'était essentiellement les photons et neutrinos qui réagissaient avec la matière et brisaient les structures ainsi formées.
Il a fallu attendre que la température du rayonnement baisse pour que les quarks puissent s'assembler en protons et neutrons sans interagir avec un photon qui passe sur le chemin. Ce processus de formation des protons et neutrons s'appelle la baryogenèse, ce qui signifie formation des baryons (les protons et neutrons sont des exemples de baryons, d'où le nom). La théorie du big-bang nous permet de déterminer comment s'est produit ce processus. Une réussite de la théorie tient dans le fait qu'elle prédit le rapport entre le nombre de protons et de neutrons dans l’univers.
Juste après la baryogenèse
[modifier | modifier le wikicode]Pour décrire ce qui se passe après la baryogenèse, nous devons d'abord parler du fait que les protons se transforment parfois en neutrons et réciproquement.
Les transformations les plus connues sont des réactions nucléaires appelées désintégrations bêta, qui sont souvent présentées dans les manuels de physique qui parlent de la radioactivité. La transformation d'un proton en neutron est connue sous le nom de désintégration bêta +, la transformation d'un neutron en proton est une désintégration beta -. Ce sont des réactions spontanées, qui impliquent l'émission ou la de particules assez diverses, à savoir : des électrons, des positrons (l'anti-particule associée à l'électron), ainsi que des particules très légères appelées des neutrinos.
- Avec radioactivité bêta plus, un proton se transforme en un neutron, un positron et un neutrino.
- Avec la radioactivité bêta moins, un neutron se transforme en un proton, un électron et un anti-neutrino.
 |
 |
Mais il existe aussi des désintégration bêta inverses, où un proton/neutron absorbe un neutrino, ce qui le transmute. Par exemple, il est possible de transformer un proton en neutron en lui faisant absorber un anti-neutrino : le résultat est un neutron accompagné de l'émission d'un électron.
Il existe une relation inverse, qui transforme un neutron en proton :
Enfin, il existe aussi une relation où un proton capture un électron, donnant un neutron :
L'existence des réactions bêta peut vous paraitre surprenante, car les neutrinos ont la réputation de très peu interagir avec la matière. Et c'est sans doute pour cela que les manuels de physique sur la radioactivité n'en parlent pas, vu que ces réactions sont très fortement improbables sur Terre. Mais tout cela n'est valide que pour les neutrinos peu énergétiques. Les neutrinos très énergétiques interagissent assez facilement avec la matière, leur section efficace est beaucoup plus importante. Les conséquences à cela sont variées, mais n'impactent que la physique des supernovas et surtout : la baryogenèse !
A forte température, les neutrinos sont très énergétiques et ils interagissent facilement avec les protons/neutrons. Les réactions bêta inverses ont donc lieu assez facilement si les neutrinos sont assez énergétiques, si la température est très élevée. A fortes températures, les désintégrations bêta inverses étaient très fréquentes, aussi fréquentes que les désintégrations bêta usuelles. Le résultat est que le rapport entre protons et neutrons était approximativement égal. De plus, le nombre d'électron est aussi égal au nombre de positrons.
Par la suite, en à peine quelques secondes, la température du plasma a diminué avec l'expansion, ce qui a réduit la température des neutrinos assez rapidement. Les réactions bêta inverses se sont alors faites plus rares, alors que les désintégrations bêta se sont poursuivies normalement, au même rythme. Le résultat est que le nombre de protons et de neutrons a évolué. Le résultat de ces réactions est un déséquilibre entre protons et neutrons, qui s'est aggravé avec la baisse de température.
Dans le plasma primordial, la distribution de Maxwell-Boltzmann s'applique. Ainsi, on peut calculer le rapport entre protons et neutrons, en utilisant l'équation vue au début de ce chapitre, qui est la suivante :
Si on fait les calculs à des températures différentes, on voit que le rapport augmente progressivement, en partant d'un rapport proche de 1 à forte température, vers un rapport de plus en plus grand quand la température baisse.
Le découplage des neutrinos
[modifier | modifier le wikicode]Mais cela ne se poursuit pas indéfiniment. Quand le produit descend en-dessous d'environ 1 Mev, les neutrinos ne sont plus assez énergétiques pour interagir avec la matière. Ils cessent d'interagir avec les protons et les neutrons, les réactions bêta inverses deviennent de plus en plus rares et s’arrêtent. La conséquence est que l'équilibre thermique du plasma est brisé : la température des neutrinos se découple de la température du reste du plasma, car il n'y a pas d'échange d'énergie entre neutrinos et le reste du plasma. La température des neutrinos évolue dans son coin, sans lien avec l'évolution thermique de la matière. Le phénomène porte le nom de découplage des neutrinos.
Au moment du découplage des neutrinos, les réactions bêta inverse cessent, la quantité de protons et de neutrons n'évolue plus. Le rapport proton/neutron gèle, il cesse d'évoluer avec le temps. Le rapport proton/neutron final peut se calculer en prenant l'équation précédente, et en y injectant la température du découplage des neutrinos. Les calculs donnent 6 protons pour 1 neutron : . Dit autrement, ème de la matière baryonique est sous la forme de neutrons, alors que ème sont des protons. Cela correspond à environ 12% de neutrons pour 88% de protons.
Un autre point est que malgré le découplage, la température des neutrinos va évoluer au même rythme que celle des photons, du moins au début. La raison est que les neutrinos et les photons ont une température qui évolue de la même manière. L'expansion agit sur les photons et les neutrinos de la même manière, les deux ont une température qui diminue au même rythme. Et vu que neutrinos et photons partent de la même température, leurs températures seront égales, du moins durant un certain temps. Mais à une température égale au double de la masse de l'électron, un phénomène physique va changer la donne.
L'arrêt du phénomène de production de paires
[modifier | modifier le wikicode]Au-dessus d'une certaine température, les réactions entre électrons, positrons et photons sont assez simples. Les principales sont les suivantes :
- La réaction dite de production de paires, qui transforme un photons en une paire contenant un électron et un positron.
- La réaction inverse, dite d'annihilation électron-positron, où un électron et un positron s'annihilent tous deux, pour donner deux photons.

La réaction de production de paires n'est cependant possible que si le photon est assez énergétique. La conservation de l'énergie dit que le photon doit avoir autant d'énergie que la paire produite. De fait, l'énergie minimale du photon est la somme de l'énergie de masse de l'électron et de celle du positron.
La masse d'un électron et d'un positron étant égales, on a alors :
- , avec la masse de l'électron.
L'énergie de masse d'un électron est proche de 500 kilo-électron-volt (0.511 MeV, pour être précis), ce qui donne :
- , avec la masse de l'électron.
Et cela n'est possible que si la température est suffisamment élevée. Il faut au minimum une température proche de . Sous cette température, le phénomène de production de paire n'est plus possible, les photons n'ont plus assez d'énergie. Le résultat est que seul le phénomène d’annihilation électron-positron a lieu.
Le résultat est que les électrons disparaissent, mais que l'univers se remplit de photons assez énergétiques, ce qui réchauffe le plasma primordial, en augmentant sa température. On peut voir la réaction d'annihilation de paires comme un phénomène endothermique (qui absorbe de la chaleur), alors que la réaction de production de paire est exothermique (elle dégage de la chaleur). L'arrêt des productions de paire fait que le plasma absorbe moins la chaleur, sa température augmente donc. Le résultat est que la température des photons augmente, ce qui fait qu'elle se découple effectivement de celle des neutrinos. Les neutrinos ne sont pas concernés par l'arrêt de la production de paire, les photons le sont.
Il est possible de calculer la température après et avant l'arrêt de la production de paire. L'équation est la suivante :
La température avant est celle que les neutrinos vont conserver, alors que celle d'après sera celle des photons. Le résultat est donc que la température des photons et des neutrinos sera donc la suivante :
L'équation restera la même par la suite, l'expansion n'y changera rien. L'expansion va faire baisser la température des photons et des neutrinos, mais au même rythme, ce qui fait que l'équation restera valable.
La nucléosynthèse primordiale
[modifier | modifier le wikicode]Une fois les protons et neutrons formés, l'univers était rempli de protons, de neutrons, d'électrons et de neutrinos, qui formaient un gaz à haute température. Durant un temps assez court, protons et neutrons ne pouvaient pas s'assembler pour former des noyaux, la température brisant les noyaux qui avaient l'occasion de se former. Mais, la température diminuant, cela ne dura guère. Après un certain temps, protons et neutrons ont pu s'assembler pour former des noyaux, quand la température a atteint un certain seuil.
La formation des premiers noyaux porte le nom de nucléosynthèse primordiale. Un nom barbare assez simple à comprendre : nucléosynthèse veut dire "synthèse de noyaux atomiques", et primordiale pour dire qu'elle a eu lieu peu après le big-bang. Ce terme sert à la distinguer de la nucléosynthèse qui a lieu actuellement au cours des étoiles, la nucléosynthèse stellaire. Les différences entre les deux sont assez nombreuses. Déjà, la nucléosynthèse primordiale s'est faite sur un temps très court, d'à peine quelques secondes grand maximum, alors que la nucléosynthèse des étoiles est un processus continu qui dure durant plusieurs milliards d'années. Ensuite, la nucléosynthèse primordiale a majoritairement créé des éléments chimiques légers, mais guère plus. Elle a permis de fabriquer de l'hydrogène, de l'hélium, du béryllium et du lithium, mais pas plus. Les autres éléments chimiques ont été fabriqués ultérieurement par la nucléosynthèse stellaire, qui a donné naissance à du carbone, de l'oxygène, de l'azote, et d'autres noyaux lourds.

Suite à la nucléosynthèse primordiale, la quasi-totalité de la matière est composée d’hydrogène et d'hélium : environ 3/4 d'hydrogène et 1/4 d'hélium, le reste étant présent en quantités négligeables. C'est pour cela que la quasi-totalité de la matière des étoiles et planètes est sous la forme d'hélium et d'hydrogène, des particules formées par l'assemblage de neutrons et de protons. Pour rappel, Un noyau d'hydrogène est formé d'un simple proton, le nombre de neutrons variant de zéro à deux neutrons. La plupart de l'hydrogène ne contient pas de neutron, cette forme d'hydrogène étant appelé du protium. L'isotope avec un neutron est appelé le deutérium, alors que celui avec deux neutrons est appelé le tritium. Le protium est de loin la forme d’hydrogène dominante, les autres formes n'étant présentes que dans les étoiles, rarement dans le milieu interstellaire. Quant à l'hélium, il possède deux protons, avec un nombre variable de neutrons. Ses deux isotopes les plus fréquents possèdent deux neutrons pour l'hélium-4, un seul pour l'hélium-3.
Les réactions de la nucléosynthèse primordiale
[modifier | modifier le wikicode]
La nucléosynthèse commence avec la fabrication de deutérium, un des isotopes de l'hydrogène. C'est à partir du deutérium que peuvent s'enclencher les réactions qui donnent naissance au tritium, à l'hélium, au lithium et au béryllium.
- Dans ce qui suit, on notera D un noyau de deutérium, T un noyau de tritium, p un proton et n un neutron.
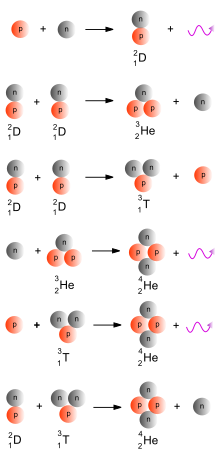
Le deutérium se forme en fusionnant un proton avec un neutron. La formation du deutérium ne s'est produite qu'une fois la température suffisamment basse. Au-dessus de cette température, les noyaux de deutérium ne survivent pas bien longtemps, à cause de la photodissociation. Les photons énergétiques brisent ces noyaux en quelques microsecondes, ne laissant que des protons et des neutrons. Mais une fois que la température descend sous la température critique du deutérium, les photons ne sont plus assez énergétiques pour briser les noyaux de deutérium, qui survivent.
Une fois le deutérium formé, des réactions donnent naissance soit à de l'hélium-3, soit à du tritium. L'hélium-3 peut se former de deux manières : soit par addition d'un proton, soit par fusion de deux noyaux de deutérium.
Le tritium peut lui aussi se former de deux manières différentes. Dans le premier cas, il est formé par la fusion de deux noyaux de deutérium. Dans le second cas, il est formé à partir d'un noyau d'hélium-3, dans lequel on remplace un proton par un neutron (par désintégration bêta, ou par capture/émission de nucléons).
Une fois le tritium ou l'hélium-3 formé, l'hélium-4 peut enfin apparaître. Il se forme soit à partir d'hélium-3, soit à partir de tritium. Et les méthodes pour ce faire assez diverses. Dans les deux cas, il se forme en ajoutant un noyau de deutérium, suivi par l'émission d'un nucléon. Le nucléon émit est un proton pour la fusion avec l'hélium-3, un neutron pour la fusion avec le tritium. Une autre manière consiste à ajouter un proton à du tritium, ou du neutron à de l'hélium-3.
Enfin, les autres éléments légers peuvent se former à partir de l'hélium-4. En fusionnant de l'hélium-4 avec soit du tritium, soit de l'hélium-3, on obtient respectivement du lithium et du béryllium. Le lithium peut aussi se former à partir du béryllium, par remplacement d'un neutron en proton. De plus, le lithium peut fusionner avec un proton pour donner deux noyaux d'hélium-4.
L'ensemble de ces réactions est résumé dans le schéma ci-dessous.
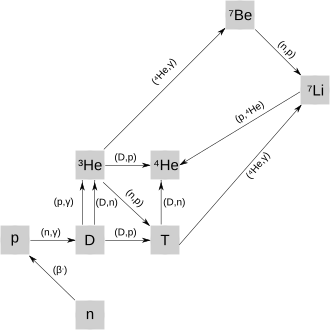
Le calcul de l'abondance de l'Hélium
[modifier | modifier le wikicode]Des calculs théoriques poussés, basés sur la physique nucléaire, nous disent que la concentration en éléments chimiques a évolué rapidement au cours de la nucléosynthèse primordiale, avant de stabiliser. Le résultat est que les deux éléments majoritaires sont l'hydrogène (le protium) et l'hélium-4. Le deutérium et l'hélium-3 sont plus rares et ont une concentration assez similaire. Le tritium et les neutrons libres sont eux encore plus rares. Enfin, le lithium et le béryllium ferment la marche et sont les éléments les plus rares. Pour simplifier, on peut dire que l'univers est rempli presque exclusivement d'hydrogène et d'hélium-4. Les autres éléments sont tellement rares qu'ils sont presque négligeables.

Sans recourir à ces calculs compliqués, on peut calculer l'abondance des éléments principaux. L'idéal est de se concentrer sur l'hydrogène (le protium) et l'hélium-4 uniquement. Négliger les autres éléments n'est pas un problème tant ils sont rares. En faisant cela, on doit considérer que tous les neutrons ont été capturés dans les noyaux d'hélium-4, vu qu'il n'y en a pas dans les noyaux de protium.
Rappelons que le rapport protons/neutrons est de 1/7. Cela veut dire que sur 16 baryons, 2 sont des neutrons et 14 sont des protons (ce qui est équivalent à dire que sur 8 baryons, 1 est un neutron et 7 sont des protons). Avec ces 16 baryons, on peut créer un atome d'hélium-4 avec 2 neutrons et 2 protons, ce qui laisse 12 protons. On a donc 12 noyaux d’hydrogènes pour un noyau d'hélium-4. Vous avez peut-être vu d'autres chiffres dans la vulgarisation, notamment un rapport de 75% d'hydrogène contre 25% d'hélium. Mais ces pourcentages sont exprimés en termes de masse, non de nombre d'atomes. Pour retrouver ce rapport 75%/25%, il faut prendre en compte la masse relative des noyaux d'hélium-4 et d'hydrogène. Un noyau d'hélium-4 étant approximativement 4 fois plus massif qu'un noyau d'hydrogène, il faut diviser le nombre de noyaux d'hydrogène par 4 pour utiliser la même unité de masse. En faisant cela, on trouve alors que 75% de la masse de l'univers est composée d'hydrogène et les 25% restants d'hélium-4.

Il est possible de retrouver ces résultats par le calcul, ce que nous allons faire de ce pas. Dans les calculs qui vont suivre, nous noterons le nombre d'atomes d'hélium alors que le nombre d'atomes de protium sera noté . Les nombres de neutrons et de protons seront notés et . L'hypothèse comme quoi tous les neutrons sont capturés dans les noyaux d'hélium-4 signifie que :
- , car il y a deux neutrons dans un noyau d'hélium-4.
La première étape est de calculer la quantité totale de baryons enfermés dans les noyaux d'hélium-4. Un atome d'hélium-4 contient 4 baryons, deux neutrons et deux protons. En multipliant par le nombre de noyaux, on obtient cette quantité totale, égale à :
Pour la seconde étape, on a besoin du nombre total de baryons dans l'univers. Par définition, il est égal à la somme (la somme du nombre de protons et de neutrons). En combinant les deux équations précédentes, on obtient le rapport entre le nombre de baryons dans les atomes d'hélium et le nombre total de noyaux, que nous noterons .
On utilise alors l'équation :
On peut réécrire cette équation en utilisant uniquement le rapport protons/neutrons calculé dans la section précédente. Il suffit pour cela de diviser l'équation précédente par le nombre de protons. On a alors :
On a vu dans la section précédente que le le rapport protons/neutrons suite au big-bang est de . En utilisant cette valeur, on trouve que , ce qui veut dire que 75% de la masse de l'univers est composé d'hydrogène et 25% d'hélium-4. Cette valeur est très proche de la valeur observée. À l'heure actuelle, 74% de la masse de l'univers est composée d'hydrogène et 25% d'hélium-4, le reste se partageant le 1 % restant. Précisons qu'il s'agit d'un pourcentage en masse, non en nombre d'atomes.









![{\displaystyle {N_{1} \over N_{2}}={\frac {m_{1}^{3/2}\times \exp \left[{\frac {m_{1}c^{2}}{k_{B}T}}\right]}{m_{2}^{3/2}\times \exp \left[{\frac {m_{2}c^{2}}{k_{B}T}}\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ccb2350b7d440bed448092b220e1ceb9dd88bdb)
![{\displaystyle {N_{1} \over N_{2}}={\frac {m_{1}}{m_{2}}}^{3/2}\times \exp \left[{\frac {(m_{1}-m_{2})c^{2}}{k_{B}T}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4c8a8b47108d5b87f640805e209c53d160eaf6a)



![{\displaystyle {\frac {N_{p}}{N_{n}}}={\frac {m_{p}}{m_{n}}}^{3/2}\times \exp \left[{\frac {(m_{p}-m_{n})c^{2}}{k_{B}T}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0e0aab15367c5131465a3a687bc9d20b23b568b)




































