Goélette Cardabela/Calcul des espars/Version collection

Goelette Cardabela

Calcul des espars

Dans la construction navale

Le Contenu est configuré pour être imprimé en livret A5 à l'échelle d'impression de 120% et marges de 15 mm.
Les Version imprimable et Version collection sont configurée pour être imprimées en livret A5 à l'échelle d'impression de 120% et marges de 15 mm.
La Couverture complète du livret « Calcul_des_espars » doit être imprimée séparément à l'échelle 120% et marges de 15 mm.

Page de titre.
Page de titre avec logo WIKILIVRES
Elle se positionne juste après la garde blanche ou la page de faux-titre qui suit la couverture d'un livre ou un livret.

Construction navale

Le calcul des espars

Éditeur : Goélette Cardabela

Sommaire

    1 Introduction - Définition de l'« espar »
    2 Unités de mesure
    3 Les mâts
        3.1 Généralités sur les mâts
        3.2 Calcul de résistance des mâts à la compression
            3.2.1 Exemple de calcul pour des mât ronds pleins en mélèze
                3.2.1.1 Calcul pour un mât en mélèze de 10 cm de diamètre
                3.2.1.2 Corollaire pour un mât en mélèze de 20 cm de diamètre
            3.2.2 Exemple pour un mât creux en aluminium
                3.2.2.1 Calcul pour un mât de 5,4 kg par mètre
            3.2.3 Conclusion
        3.3 Calcul de la résistance des mâts au flambage
            3.3.1 Formule générale à la rupture
                3.3.1.1 Charge critique au flambage
                    3.3.1.1.1 Charge critique pour les espars guidés aux extrémités
                    (Exemples pour le bois et l'aluminium)
                3.3.1.2 Charge pratique de résistance au flambage
            3.3.2 Exemple de calcul pour un mât plein en mélèze
            3.3.3 Exemple de calcul pour un mât rond creux en aluminium
            3.3.4 Exemple de calcul pour un mât elliptique creux en aluminium
            3.3.5 Conclusion
        3.4 Notes et références
    4 Les épontilles
        4.1 Calcul des épontilles de sections rectangulaires
    5 Les beauprés
        5.1 Calcul de beauprés de sections rectangulaires
        5.2 Comment effectuer ce calcul de compression du beaupré ?
        5.3 Exemple pratique
            5.3.1 Quelle doit être la section du beaupré en bois ?
            5.3.2 Résistance au travail de compression
            5.3.3 Charge limite au flambage
            5.3.4 Conclusion
        5.4 Notes et références
    6 Liens


Goélette Cardabela Calcul des espars Dans la construction navale

Couverture du livre compilé

Le Contenu est configuré pour être imprimé en livret A5 à l'échelle d'impression de 120% et marges de 15 mm.
Les Version imprimable et Version collection sont configurée pour être imprimées en livret A5 à l'échelle d'impression de 120% et marges de 15 mm.
La Couverture complète du livret « Calcul_des_espars » doit être imprimée séparément à l'échelle 120% et marges de 15 mm.

Cet article est inclus dans la Collection des livrets techniques de la goélette Cardabela

Introduction - Définition de l'« espar »

ikipedia : « Sur un bateau, un espar (mot étymologiquement apparenté à l'allemand Spiere et à l'anglais spar, qui ont la même signification) est un élément de gréement long et rigide, originellement en bois, et ayant un rôle technique à jouer dans la propulsion (à voile) et les manœuvres.
Entrent dans la catégorie des espars les mâts, bômes, vergues, bouts-dehors, queues de malet, livardes, wishbones. On peut aussi y associer les éléments mobiles tels que avirons, barres, tangons, etc. »

1 daN ≅ 1 kg_f Calcul du gréement de la goélette Cardabela.

Unités de mesure

Remarques concernant l'expression des unités de mesures dans ce chapitre

Nous utilisons le système d'unités CGS^[1] plus proche de notre perception qu'avec les unités du Système international SI.

Nous utilisons cependant l'expression kg_f du Kilogramme-force^[2] qui est une ancienne expression de la force, indépendante du Système de mesures CGS et du Système international d'unités^[3]. Le kg_f est à la fois une unité de force et de poids : le kg_p ou encore le kg que tout le monde connaît en faisant ses courses.
On devrait utiliser le dyne comme unité de force, mais qui ? a une notion réaliste de cette mesure ?

Les formules mathématiques sont en LaTeX^[4], le rendu des expressions à l'écran est différent du rendu imprimé. Nous avons essayé de minimiser cet effet.

↑ https://fr.wikipedia.org/wiki/Système_CGS
↑ https://fr.wikipedia.org/wiki/Kilogramme-force
↑ https://fr.wikipedia.org/wiki/Système_international_d'unités
↑ Livre détaillé : https://fr.wikibooks.org/wiki/LaTeX

Les mâts

Généralités sur les mâts

Les mâts en aluminium sont souvent plus légers que les câbles en acier inoxydable qui les maintiennent.

Les mâts en bois plein sont très lourds.

Les mâts en bois peuvent être creux en bois contrecollé ou lamellé-collé de formes variables. Ces mâts restent lourds lorsque l'on veut une résistance importante à la compression et au flambage.

La section, ou le poids linéaire, des mâts détermine leur résistance à la compression^[1]. C'est la contrainte maximale admissible par un matériau soumis à une charge d’écrasement^[2].

Le profil d'un mât, rond ou elliptique, détermine sa résistance au flambage^[3] longitudinal et latéral. Le flambage est également appelé le flambement. Lorsqu'une structure est compressée dans le sens de la longueur, elle a tendance à fléchir perpendiculairement à l'axe de la force appliquée, en raison d'un phénomène d'instabilité élastique.
- Le petit diamètre, plus sensible au flambage, supporte les barres de flèches latérales.
- Lorsqu'il est nécessaire de maintenir le mât au flambage dans sa section longitudinale, on adopte parfois un étai de trinquette avec des bastaques largables ou non.

La longueur du mât : Le mât est approximativement égal ou plus grand que la longueur de coque du voilier. Selon le type de bateau; croisière hauturière, plaisance pour l'été, voilier pour la course, cette longueur va être adaptée. Le mât sera plus long pour chercher le vent en hauteur, donc pour la course, il sera plus court pour faciliter la manipulation des voiles par un équipage très réduit. En ce début de ce XXI^e siècle les mâts à enrouleurs sont devenus plus populaires et facilitent les manœuvres, on va très probablement voir apparaître des mâts plus longs.

Lien intéressant : Méthodes de fabrication des mâts en aluminium et carbone sur le site nauticaltrek.com^[4].

Calcul de résistance des mâts à la compression

Pour un même matériau, la résistance à la compression ne dépend que du poids linéaire du mât. En effet le poids linéaire est le produit d'une section par une longueur et une densité. Le poids linéaire ne dépend que de la section.

Exemple de calcul pour des mâts ronds pleins en mélèze

Caractéristiques du mélèze :

 Poids sec : 600 kg le mètre cube ou 0,6 kg le dm³
 Résistance à la compression : 53 MPa (Méga-Pascal), ou 530 kg_f/cm²

Calcul pour un mât en mélèze de 10 cm de diamètre

La résistance de travail à la compression pour le bois devrait être égale au cinquième de la résistance à la rupture; on adopte ici 100 kg_f par cm² pour tenir compte des défauts, de la fatigue des matériaux^[1], et du coefficient de sécurité^[2].

 Surface de compression : (3,14 x 10 x 10) / 4 = 78,5 cm²
 Résistance au travail : 78,5 x 100 = 7 850 kg_f
 Poids : (78,5 / 1 000) x 0,6 = 4,71 kg par mètre

Remarque : Section * densité / longueur => 78,5 * 0,6 = 47,1 grammes-poids par cm ou 4,71 kg / mètre

Pourquoi prendre pour exemple un diamètre de 10 cm ?
Il suffit d'élever au carré le rapport des diamètres pour évaluer un autre mât ! Exemple : Pour un mât de 20 cm de diamètre, il suffit d'élever au carré le rapport 20/10, soit quatre fois la valeur des résultats précédents.

Corollaire pour un mât en mélèze de 20 cm de diamètre

 Résistance au travail : 7 850 x 4 = 31 400 kg_f
 Poids : 4,71 x 4 = 18,84 kg par mètre

On imagine le poids des premiers mâts du voilier Joshua de Bernard Moitessier : avec des poteaux télégraphiques comme mâts et des câbles EDF en gréement dormant^[3]
Avec un tel mât planté au travers du pont, à vue de nez il ne sera pas nécessaire de l'étayer avec des barres de flèche et des câbles lourds en acier galvanisé.

Exemple pour un mât creux en aluminium

Caractéristiques de l'aluminium :

 Résistance de rupture à la compression de l'aluminium : 60 kg/mm² ou 6 000 kg/cm²
 ⇒ Résistance au travail avec un coefficient de sécurité de 3 : 2 000 kg/cm²
 Poids de l'aluminium pour 1 décimètre-cube (densité) : 2,7 kg/dm³

Calcul pour un mât de 5,4 kg par mètre

 Poids du mât pour 1 dm : 0,54 kg
 Surface à la compression d'une section transversale du mât : 0,54/2,7 = 0,2 dm² ou 20 cm²
 Résistance au travail à la compression : 20 x 2 000 = 40 000 kg_f

Pour un mât cylindrique de 20 cm de diamètre moyen ou un mât ovale de 22 x 18 cm :

 Circonférence du tube : 3,14 x 20 = 62,8 cm
 Épaisseur du tube : 20 / 62,8 = 0,32 cm

Conclusion

Les longs mâts en bois pleins sont très lourds, ils sont à proscrire car ils rendent le voilier instable.

Les mâts en bois creux seront défavorisés par rapport aux mâts en aluminium car la résistance au travail à la compression, qui est déterminant dans les calculs des mats, est de 100 kg_f par cm² contre 2 000 kg_f par cm² pour l'aluminium.
Le poids linéaire du bois est environ trois fois plus léger que l'aluminium. Pour un mât en bois creux : Afin d'obtenir la même résistance à la compression que pour un mât en aluminium il faudrait concevoir un mâts d'un poids linéaire d'environ 2 000/300 = 6,6 fois plus important. Pour l'équivalent d'un mât en aluminium de 5,4 kg par mètre il faudrait un mât en bois de 5,4 * 6,66 = 35 kg par mètre.

L'aluminium a bien l'avantage sur le bois !

Calcul de la résistance des mâts au flambage

Ce sont les formes qui offrent une résistance au flambage. Un mât en bois plein est résistant mais il est très lourd. Pour alléger le poids du mât tout en garantissant sa résistance à la compression on utilise des matériaux légers, en général l'aluminium d'un prix acceptable, avec une section elliptique avec un côté large, là où l'on ne peut pas facilement disposer de raidisseur et un côté moins large où l'on peut fixer des raidisseurs (Barres de flèche et haubans)

Plus le matériau est dur plus il résistera au flambage.

Formule générale à la rupture

Selon l'article Flambage^[4] sur Wikipédia : $F={\frac {\pi ^{2}EI}{l_{k}^{2}}}$

où, dans le système international d'unités, $E$ est le module d'Young^[5] du matériau ; 70 GPa (Giga Pascal) pour l'aluminium, entre 10 et 13 GPa pour le bois.

$I$ est le moment quadratique^[6] de la poutre, en m⁴
$l_{k}$ est la longueur de flambement de la poutre, en mètre.

Cette charge critique est évidemment limitée par la résistance en section de la poutre (en dessous d'un certain élancement, la rupture par compression est atteinte avant l'apparition du flambage). Dans le cas réel, la rupture par flambage est atteinte encore plus précocement en raison notamment des imperfections de production et de mise en œuvre (voir ci-dessous).

Charge critique au flambage

Selon le Müller^[7], bible des ingénieurs d'autrefois :

  $Pr=k{\frac {\pi ^{2}EI}{l^{2}}}$  
 avec : l en cm, E en kg/cm², I en cm⁴ et Pr en Kg_f

Avec cette formule transposée dans le système CGS, comme on les trouvait avant les dernières directives sur les unités de mesure^[8].

 k = 1 pour les extrémités guidées. (Cas des mâts posés sur le pont)
 k = 0,25 pour une extrémité encastrée et l'autre extrémité mobile.
 k = 2 pour une extrémité encastrée et l'autre extrémité guidée. (Cas de Joshua première version)
 k = 4 pour les deux extrémités encastrées.

Charge critique pour les espars guidés aux extrémités (Exemples pour le bois et l'aluminium)

Rappels :

 k = 1, 
 Pour le bois E = 11 GPa ou 110 000 Kg/cm²

Charge critique au flambage pour les espars en bois (formule bâtarde) :

 Pr = 110 I / L² avec I en cm⁴, L en mètre, E = 11·10⁴ kg/cm².

Charge critique au flambage pour les espars en aluminium (formule bâtarde) :

 Pr = 700 I / L² avec I en cm⁴, L en mètre, E = 70·10⁴ Kg/cm².

Charge pratique de résistance au flambage

Éléments de calcul des moments quadratiques de la section S pour un espar rond creux :

$I_{x}={\frac {\pi \cdot (D^{4}-d^{4})}{64}}$ moment quadratique par rapport à l'axe des x.
$I_{y}={\frac {\pi \cdot (D^{4}-d^{4})}{64}}$ moment quadratique par rapport à l'axe des y.
$I_{S}={\frac {\pi \cdot (D^{4}-d^{4})}{32}}$ avec D et d en cm

Pour évaluer la résistance au flambage d'un mât elliptique on prend $I=2\cdot I_{x}$ ou $I=2\cdot I_{y}$ Dans cette même page :
#Exemple_de_calcul_pour_un_mât_elliptique_creux_en_aluminium

Charge pratique au flambage :

 Pp = Pr / n
 n est un coefficient de sécurité.
 n = 5 pour les métaux homogènes.
 n = 8 pour la fonte.
 n = 7 pour le bois.

Résumé, pour les espars en aluminium :

Charge pratique pour les espars en aluminium, mâts, barres de flèches, tangons. (Formule bâtarde)

 Pp = 140 I / L²
Coefficient de sécurité = 5; Pp en kg_f, I en cm⁴, L en mètre.

Exemple de calcul pour un mât plein en mélèze

Diamètre : 20 cm, longueur : 15 mètres; encastré dans la coque sur 2 mètres.

Rappels :

 k = 2 pour une extrémité encastrée et l'autre extrémité guidée. (Cas de Joshua première version)
  $I=\pi /32\cdot (D^{4}-d^{4})$  avec D et d en cm
 I = (3,14 / 32) * 20 * 20 * 20 * 20 => 15 708 cm⁴
  $Pr=110\ I/L^{2}$

Charge critique :

 pr = 110 * 15 708 / (13 * 13) = 10 224 Kg_f

Charge pratique pour un mât rond plein en mélèze de diamètre 20 cm et d'une longueur de 13 mètres
hors encastrement, au dessus du pont, sans barre de flèche

 Pp = 10 224 / 7 = 1 460 Kg_f

☞	Avec un étayage à mi-hauteur on aurait une charge pratique quatre fois plus importante, de l'ordre de 5 842 Kg_f. Ceci est à comparer à la résistance au travail calculé dans la section précédente : 31 400 Kg_f : #Corollaire_pour_un_mât_en_mélèze_de_20_cm_de_diamètre

Exemple de calcul pour un mât rond creux en aluminium

On reprend l' exemple pour un mât de 13 mètres en aluminium, posé sur le pont; 5,4 kg par mètre; diamètre 20 cm; épaisseur 3,2 mm. Rappels :

 k = 1 pour les extrémités guidées.
 I = π/32 (D⁴ - d⁴)avec D, diamètre extérieur; et d = D - 2e
 I = 3,14 / 32 * (20⁴ - 19,36⁴) = 1 916 cm⁴
 Pr = 700 I / L² avec I₀ en cm⁴; L = 13 m; E = 7 000 kg/m².
 Pr = 700 * 1 916 / 169 = 7 936 kg_f

Charge pratique pour un mât en aluminium de diamètre 20 cm; d'une épaisseur de 3,2 mm; de longueur 13 mètres; guidé aux extrémités.

 Pp = 7 936 / 5 = 1 587 Kg_f

Avec un étayage à mi-hauteur on aurait une charge pratique quatre fois plus importante, de l'ordre de 6 349 Kg_f
Avec deux barres de flèches : 14 286 Kg_f

☞	Ceci est à comparer à la Résistance au travail à la compression calculé dans la section précédente ; 40 00O Kg_f: #Calcul_pour_un_mât_de_5,4_kg_par_mètre

Exemple de calcul pour un mât elliptique creux en aluminium

L'inertie quadratique moyenne par rapport à un point extérieur aura la même valeur pour le mât elliptique creux et le mât rond creux. Du fait de son écrasement les valeurs de l'inertie quadratique selon les axes x et y sera différent.

Rappel de la définition sur wikipedia :

w:Moment_quadratique#Définition_générale :

 Moment quadratique de la section  $S$  par rapport à l’axe  $O{\vec {x}}$  :
  $I_{x}=\int _{S}y^{2}\,\mathrm {d} s=\iint _{S}y^{2}\,\mathrm {d} x\mathrm {d} y$ 
 Moment quadratique de la section  $S$  par rapport à l’axe  $O{\vec {y}}$  :
  $I_{y}=\int _{S}x^{2}\,\mathrm {d} s=\iint _{S}x^{2}\,\mathrm {d} x\mathrm {d} y$ 
 Moment quadratique (polaire) de  $S$  par rapport au point  $O$  :
  $I_{O}=\int _{S}r^{2}\,\mathrm {d} s=\iint _{S}r^{2}\,\mathrm {d} x\mathrm {d} y$

Remarques :
On a $I_{G}=I_{x}+I_{y}$ puisque $r^{2}=x^{2}+y^{2}$ (Théorème de Pythagore).

Il découle de ces définitions que plus les éléments de la section sont situés loin de l'axe, plus le moment quadratique sera important.

Définitions :
Avec les mêmes caractéristiques que le mât rond creux mais ovalisé à 22 cm x 18 cm

 Grand diamètre gd = 22; 
 Petit diamètre pd = 18;
 Diamètre moyen  $D={\frac {gd+pd}{2}}$  est égal au diamètre moyen du mât rond creux
  $I_{G}=Igd+Ipd$

Inertie quadratique :

 Inertie quadratique selon l'axe de grand diamètre :
  $Igd=I_{G}\cdot {\frac {gd}{2\cdot D}}$ 
 Inertie quadratique selon l'axe de petit diamètre :
  $Ipd=I_{G}\cdot {\frac {pd}{2\cdot D}}$

La partie la plus sensible au flambage est le petit diamètre :

Pour l'évaluation du flambage à la compression on prend I = 2·Ipd

Charge limite pour le flambage :
Inertie quadratique avec D = (gd + pd) / 2, gd = 22 cm, pd = 18 cm, e = 0,32 cm, d = D - 2·e en cm

   $I_{G}=\pi /32\cdot (D^{4}-d^{4})$ 
  I_G = 3,14 / 32 * (20⁴ - 19,36⁴) = 1 916
  I = 2·Ipd = 2·I_G * pd / 2·D
  I = 2 * 1 916 * 18 / (2 * 20) = 1 916 * 18 / 20 = 1 724 cm⁴

Charge limite avec trois étages guidés à 4 m, 8 m et 13 m

  Pr = 700·I / L²
  Pour la plus grande longueur guidée de 4 mètres : L² = 16
  Pr = 700 * 1 724 / 16 = 83 825 Kg_f

Charge pratique pour un mât elliptique en aluminium de 22x18 cm, d'une épaisseur de 3,2 mm, de longueur 13 mètres, guidé par deux barres de flèches à 4 et 8 mètres.

 Pp = 83 825 / 5 = 16 765 Kg_f

Conclusion

Dans la conclusion du chapitre précédent sur la résistance des mâts à la compression :
... Pour l'équivalent d'un mât en aluminium de 5,4 kg par mètre il faudrait un mât en bois de 5,4 * 6,66 = 35 kg par mètre.
L'aluminium a bien l'avantage sur le bois !

Pour le flambage : Si le mât creux en bois n'est pas conditionné par une évaluation de sa résistance à la compression comme ci-dessus, on détermine sa section en fonction de la charge estimée, sa section peut être rectangulaire ou ronde. On agit sur les dimensions de la section puis on évalue les risques de flambage selon les longueurs libres guidées ou non par des barres de flèches et les étais. On corrige les dimensions de la section sans changer sa surface de compression jusqu'à obtenir satisfaction. Il faudra sûrement trouver des compromis !

Le mât en bois n'est pas à proscrire. Sur un Voilier ancien, un Vieux Gréement, un mât en aluminium n'est pas de mise.

Notes et références

↑ https://fr.wikipedia.org/wiki/Fatigue_(matériau)
↑ https://fr.wikipedia.org/wiki/Coefficient_de_sécurité
↑ https://fr.wikipedia.org/wiki/Bernard_Moitessier#Joshua Mâts en bois plein de Joshua voilier de B Moitessier dans sa première version.
↑ https://fr.wikipedia.org/wiki/Flambage
↑ https://fr.wikipedia.org/wiki/Module_de_Young
↑ https://fr.wikipedia.org/wiki/Moment_quadratique
↑ Formulaire technique de mécanique générale de Jacques MÜLLER (ISBN 2853140016)
↑ https://fr.wikipedia.org/wiki/Unité_de_mesure#Unités_hors_du_Système_international_d'unités

Les épontilles

Calcul des épontilles de sections rectangulaires

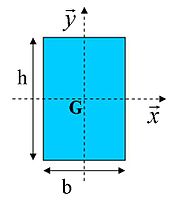
Les épontilles sont des poutres ou des tubes disposés verticalement pour supporter les mâts des bateaux, elles évitent un écrasement du pont.

Compression pour les épontilles en bois de sections rectangulaires

Section S = b * h b et h en cm S en cm² Charge pratique à la compression :

  $Pp=100*S$ 
 pour un coefficient de sécurité de 5

Flambage

$I_{x}={\frac {b\cdot h^{3}}{12}}$
$I_{y}={\frac {h\cdot b^{3}}{12}}$
$I_{G}={\frac {b\cdot h}{12}}\cdot (b^{2}+h^{2})$ Pour le calcul des épontilles on utilise généralement $I=2\cdot I_{y}$ en cm⁴

Charge limite

k = 4 pour deux extrémités pseudo encastrées (maintien par le plancher ou par les aménagements)
$Pr=k\cdot 110\ I/L^{2}$ avec I₀ en cm⁴; L en mètre, et E = 110000 kg/cm² (11GPa)

Charge pratique pour le bois Pp = Pr / 7
Rappel : Pr / 5 pour l'aluminium

Exemple pour une épontille en kotibé de 4 x 20 cm et 2 m de hauteur

Pr = 4 x 110 x 2 x 20 x 4³ / 12 x 2² = 23 466 kg
Pp = 23 466/7 = 3 352 kg

Les beauprés

Calcul de beauprés de sections rectangulaires

1 : Bout-dehors ou bâton de foc volant
2 : Beaupré
3 : Étai de trinquette
4 : Étai de foc ou de génois
8 : Amure de foc volant
13 : Sous-barbe

Le mât de beaupré ou beaupré se trouve à la proue d'un navire, fortement incliné vers l'avant.

Il est destiné à avancer le centre de voilure, il supporte les étais avant du mât le plus à l'avant (généralement le mât de misaine), Il est souvent prolongé par un bout-dehors.

La compression du beaupré dépend de l'effort supporté par l'étai de foc. L'effort est repris par la sous-barbe.

Comment effectuer ce calcul de compression du beaupré ?

On peut l'évaluer en connaissant la résistance du câble de sous-barbe, de l'angle α qu'il fait avec le beaupré, et de l'ange β que fait l'étai de foc avec ce même beaupré.
Par exemple avec une sous-barbe en câble d'acier inoxydable de 12 mm et un angle α de 30°, de charge maximale d'utilisation 1 654 kg_f et une rupture à 8 270 kg_f

Pour effectuer ce calcul on peut utiliser des vecteurs sur une feuille de papier millimétré ou calculer le couple qui s’exerce sur l'extrémité du beaupré de longueur L :
La force du couple qui tire le beaupré vers le haut est égal au produit de la projection de la force de traction du hauban ${\vec {F}}h$ perpendiculairement au beaupré par la longueur du beaupré : $Fh\cdot \sin \beta \cdot L$
La force du couple qui tire le beaupré vers le bas est égal au produit de la projection de la force de traction de la sous barbe $Fs$ perpendiculairement au beaupré par la longueur du beaupré : $Fs\cdot \sin \alpha \cdot L$ où $Fs$ est la résistance du câble de sous-barbe.

On connaît cette force  $Fs$  maximale d'utilisation du câble : 1 654 kg_f

La force du couple qui tire vers le haut doit être égale à la force du couple qui tire vers le bas.
La force qui s'exerce sur le beaupré est la somme des projections vectorielles des deux forces ${\vec {Fh}}\ et\ {\vec {Fs}}$ sur le beaupré :

 $Fh\cdot \sin \beta \cdot L=Fs\cdot \sin \alpha \cdot L$ 
 $Fh=Fs{\frac {\sin \alpha }{\sin \beta }}$  (pour  $\sin \beta$  ≠ 0)

Compression sur le beaupré :

 $Fh\cdot \cos {\beta }+Fs\cdot \cos {\alpha }$ 
 $Fs{\frac {\sin \alpha }{\sin \beta }}\cdot {\cos \beta }+Fs\cdot \cos {\alpha }$  ⇔  $Fs\cdot (\coth {\beta }\cdot \sin \alpha +\cos {\alpha })$

$\coth {\beta }$ n'est autre que le rapport de la distance qui sépare le pied du mât au point d'amure par la hauteur du mât, qui sont les points d'attaches du hauban.

Exemple pratique

Calculer l'effort de compression et la résistance au flambage du beaupré avec un mât de 13,5 m, une distance du point d'amure au pied du mât de 6 m, un angle $\alpha$ de 30°, une sous-babe inox de diamètre 12 : $\sin {\alpha }=0,5\ et\cos {\alpha }=0,866$

Compression pratique = 1 654 * (6/13,5 * 0,5 + 0,866) = 1 799 kg_f

Quelle doit être la section du beaupré en bois ?

La charge à adopter est de 100 kg par cm² pour un bois de bonne qualité tel que le Kotibé^[1] droit de fil avec un coefficient de sécurité de 5.

Résistance au travail de compression

Résistance au travail de compression : Pp = 100 *S = 1 800 kg
Section minimale : 1 800 / 100 = 18 cm²

Le beaupré est une pièce importante sur un petit voilier, il y a des risques de chocs et de poussées latérales. On préfère utiliser un bois plus adapté à ces risques. En multipliant la section par 10 on doit pouvoir supporter une collision 18 000 kg.
La section adoptée pour la goélette Cardabela a été de 10 x 12 cm pour 12 000 kg_f (60 tonnes à la rupture).

Charge limite au flambage

Comme pour l'épontille au chapitre précédent, on prend I = 2 I_y
I = 2 * 12 * 10³ / 12 = 2 000 cm⁴

k = 1 pour les espars en bois guidés aux extrémités.

Pr = k * 110 I / L² (L= 2,52 m)
Pp = Pr /7

Pr = 110 * 2 000 / 2,52² = 34 643 kg_f
Pp = Pr/7 = 34 643 / 7 = 4 949 kg_f

Conclusion

Un beaupré de section 10 x 12 cm est très largement suffisant pour assurer sa fonction, et est capable de supporter certains inconvénients comme les collisions et les chocs latéraux.^[2]

Notes et références

Liens

Calcul des espars – Dans la construction navale

: Sur un bateau, un espar est un élément de gréement long et rigide, originellement en bois, et ayant un rôle technique à jouer dans la propulsion (à voile) et les manœuvres.

Entrent dans la catégorie des espars les mâts, bômes, vergues, bouts-dehors, queues de malet, livardes, wishbones. On peut aussi y associer les éléments mobiles tels que avirons, barre, tangons, etc.

La section, ou le poids linéaire, des espars détermine leur résistance à la compression.

Le profil d'un espar, rond ou elliptique, détermine sa résistance au flambage longitudinal et latéral.

Cet article donne des exemples de calculs des mâts, épontilles et beauprés.

Image de couverture : https://fr.wikibooks.org/wiki/Le_Belem_par_petit_vent.jpg
Attribution : Jickye

[1] https://fr.wikipedia.org/wiki/Système_CGS

[2] https://fr.wikipedia.org/wiki/Kilogramme-force

[3] https://fr.wikipedia.org/wiki/Système_international_d'unités

[4] Livre détaillé : https://fr.wikibooks.org/wiki/LaTeX

[5] ttps://fr.wikipedia.org/wiki/Essai_de_compression

[6] ttp://www.instron.fr/fr-fr/our-company/library/glossary/c/compressive-strength

[7] ttps://fr.wikipedia.org/wiki/Flambage

[8] ttps://nauticaltrek.com/trucs-et-astuces/construction/mat-aluminium-carbone/comment-page-1/#comment-12174]

[9] ttps://fr.wikipedia.org/wiki/Fatigue_(matériau)

[10] ttps://fr.wikipedia.org/wiki/Coefficient_de_sécurité

[11] ttps://fr.wikipedia.org/wiki/Bernard_Moitessier#Joshua Mâts en bois plein de Joshua voilier de B Moitessier dans sa première version.

[12] ttps://fr.wikipedia.org/wiki/Flambage

[13] ttps://fr.wikipedia.org/wiki/Module_de_Young

[14] ttps://fr.wikipedia.org/wiki/Moment_quadratique

[15] Formulaire technique de mécanique générale de Jacques MÜLLER (ISBN 2853140016)

[16] ttps://fr.wikipedia.org/wiki/Unité_de_mesure#Unités_hors_du_Système_international_d'unités

[17] ttps://fr.wiktionary.org/wiki/kotibé

[18] ttp://appgm.asso.free.fr/wiki/index.php/Abordages/Péripéties_d'un_abordage

[1]

[2]

[3]

[4]

[1]

[2]

[3]

[4]

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[1]

[2]