Les suites et séries/Les suites numériques
Les suites sont des outils mathématiques assez généraux, que l'on peut définir comme des suites d'objets mathématiques, placés dans un certain ordre.. Les exemples les plus simples sont de loin les suites de nombres. Les suites les plus simples sont de banales suites de nombres, comme on peut en trouver dans des tests de QI ou dans diverses énigmes mathématiques. Par exemple, ceci est une suite : 1, 2, 4, 8, 16, 32, 64, ... L'exemple précédent est une suite numérique, à savoir une suite de nombres (numérique = nombre). On a bien des objets mathématiques, ici des nombres, placés dans un certain ordre. Il ne faut pas plus pour obtenir une suite !
Mais les suites numériques ne sont pas les seules : il existe de nombreux autres types de suites, comme des suites de fonctions, de polynômes, ou autres. Après tout, rien n’empêche de ranger des fonctions mathématiques dans un certain ordre, ou d'ordonner des polynômes, bref : tant que l'on met des truc mathématiques dans un certain ordre, on obtient une suite. Le terme objet mathématique est volontairement vague, l'objet mathématique en question pouvant être n'importe quoi. Les objets mathématiques d'une suite, qu'ils soient des nombres ou non, sont nommés les termes de la suite. Une suite est donc un ensemble de termes rangés dans un certain ordre.
Pour définir une suite, il faut naturellement préciser ses termes, mais pas seulement : il faut aussi préciser dans quel ordre sont rangés les objets mathématiques. Pour rendre compte de cet ordre, les termes de la suite sont numérotés dans leur ordre dans la suite. Chaque terme est associé à un nombre qui définit sa place dans la suite, ce nombre étant appelé le rang du terme dans la suite, ou encore son indice. Dans la quasi-totalité des cas, la numérotation des termes commence à partir de 1. Cette convention est intuitive : le premier terme a pour rang 1, le second est de rang 2, et ainsi de suite. Cependant, rien n’empêche de commencer à compter non à partir de 1, mais à partir d'un autre rang. Il est par exemple possible de commencer à compter les rangs à partir de 0 : cette convention est notamment très utilisée par les informaticiens, quand ils doivent manipuler des suites. Dans tous les cas, le énième terme de la suite est appelé le terme de rang . Une petite remarque au niveau des notations :
- le terme de rang est noté ;
- la suite en elle-même est notée .
| Rang | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ... |
|---|---|---|---|---|---|---|---|---|
| Terme | 1 | 2 | 4 | 8 | 16 | 32 | 64 | ... |
| Rang | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... |
|---|---|---|---|---|---|---|---|---|---|
| Terme | ... |
Les suites récurrentes et paramétrées
[modifier | modifier le wikicode]Supposons que vous souhaitiez créer une suite quelconque. Pour cela, vous avez deux méthodes qui fonctionnent bien, la première donnant des suites paramètres, l'autre des suites récurrentes. Il faut noter que les deux types de suites ne sont pas mutuellement exclusifs : certaines suites sont à la fois récurrentes et paramétrées. La plupart des suites que nous allons étudier dans la suite du cours sont dans ce cas.
Les suites paramétrées
[modifier | modifier le wikicode]Les suites paramétrées sont simplement des suites définies par une fonction mathématique . En clair, construire la suite demande simplement de dire que tel rang est associé à tel terme de manière univoque. Comme exemple de suite paramètres, on peut citer la suite définie par . Celle-ci est illustrée dans le tableau ci-dessous.
| Rang | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ... |
|---|---|---|---|---|---|---|---|---|
| Terme | 1 | 4 | 9 | 16 | 25 | 36 | 49 | ... |
Comme autres exemples de suites paramétrées, nous allons prendre les suites de Riemann, des suites où chaque terme est une puissance de l'inverse d'un entier... Pour le dire plus clairement, ce sont des suites de la forme :
- , avec r un coefficient appelé la raison de la suite.

La suite de Riemann la plus simple est la suite harmonique, la suite de l'inverse des entiers naturels.
On peut modifier la suite harmonique en inversant les signes d'un terme à l'autre : on obtient alors la suite harmonique alternée.
Une autre suite de Riemann, que nous étudierons dans les chapitres suivants, est la suite de l'inverse des carrés. Elle est définie par :
Les suites récurrentes
[modifier | modifier le wikicode]Une autre méthode consiste à définir comment passer d'un terme au suivant. Dans ce cas, la suite est définie par une fonction de la forme . On voit que le cas précédent marche dans le cas où chaque terme dépend de la valeur du terme précédent. Mais on peut généraliser au cas où chaque terme dépend de plusieurs termes précédents, avec des fonctions de la forme . Ces suites sont appelées des suites récurrentes.
Ces suites sont définies par la fonction qui permet de calculer un terme en fonction des précédents, mais pas seulement ! En effet, une même fonction peut donner plusieurs suites, selon le premier terme utilisé. Par exemple, la fonction peut donner les deux suites (1, 2, 4, 8, 16, 32, 64, ...) et (3, 6, 12, 24, 48, 96, ...). En plus de préciser la fonction, on doit préciser le ou les premiers termes.
Comme exemple de suite récurrente, nous donnant dans le tableau ci-dessous un exemple de suite récurrente assez simple : celle définie par la fonction et le premier terme 1.
| Rang | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ... |
|---|---|---|---|---|---|---|---|---|
| Terme | 1 | 0.5 | 0.25 | 0.125 | 0.0625 | 0.03125 | 0.015625 | ... |
L'étude des suites récurrentes se limite souvent à trouver une expression non-récurrente (paramétrée), plus simple à manipuler. Quand cela n'est pas possible, il est intéressant d'étudier le comportement de la suite quand n devient grand, pour savoir si les termes grandissent, diminuent, si la suite se stabilise, etc.
L'exemple de la suite de Fibonnaci
[modifier | modifier le wikicode]Un exemple très connu de suite récurrente est la suite de Fibonnaci, une suite souvent abordée dans les livres de mathématiques récréatives. Elle est apparue pour la première fois dans un problème de mathématiques récréatives impliquait un problème de lapins qui se reproduisent dans un enclos. Ce problème était l’œuvre de par Leonardo Fibonacci, qui donna son nom à cette suite. Voici l'énoncé de ce problème :
| « | |
| Quelqu’un a déposé un couple de lapins dans un certain lieu, clos de toutes parts, pour savoir combien de couples seraient issus de cette paire en une année, car il est dans leur nature de générer un autre couple en un seul mois, et qu’ils enfantent dans le second mois après leur naissance. | |
| » | |
| — Leonardo Fibonacci |
Si on fait un graphique, on devrait trouver ceci :

Mais une autre manière de résoudre le problème est de concevoir une suite dont le énième terme donne le nombre de lapins dans l'enclos à l’énième mois. Pour le mois numéro n, on peut calculer le nombre de couples présents dans l'enclos assez simplement : il est la somme du nombre de couples au mois précédent, qui sont encore vivants, et du nombre de nouveaux couples ajoutés par la reproduction. Et ce dernier est égal au nombre de lapins d'il y a deux mois auparavant, car les lapins mettent deux mois à se reproduire. Les deux dernières phrases se résument mathématiquement avec la relation de récurrence suivante :
L'énoncé nous dit que le premier terme de la suite est 1, car il n'y a qu'un seul couple pour le premier mois. Le second terme est identique, car il faut deux mois aux lapins pour se reproduire. Les deux premiers termes de la suite de Fibonacci sont respectivement 1 et 1, ce qui donne la suite suivante. On peut faire commencer la suite avec 0 et 1, mais il s'agit d'une définition alternative presque totalement équivalente.

La suite de Fibonnaci ne paye pas de mine au premier abord, mais elle a des propriétés assez intéressantes, avec notamment des liens avec le nombre d'or. Mais n'en disons pas plus pour le moment.
Les propriétés d'une suite
[modifier | modifier le wikicode]Les suites ont divers propriétés assez simples, basées sur des définitions somme toute triviales, que nous allons décrire dans cette section. Ces propriétés sont souvent assez importantes mathématiquement et leur présence est source de beaucoup de propriétés ou de théorèmes intéressants. Pour donner un exemple simple, on peut parler de la distinction entre suite finie et infinie. Les suites finies ont un nombre de termes fini et se terminent sur un dernier terme, alors que ce n'est pas le cas des suites infinies, qui ont autant de termes qu'il y a d'entiers naturels. Cette propriété est assez simple à comprendre, mais elle est à l'origine de grandes différences : là où les suites finies possèdent très peu de propriétés mathématiques intéressantes, les suites infinies sont un sujet d'étude très riche. C'en est au point que ce cours ne parlera que des suites infinies, tant elles possèdent de propriétés supplémentaires par rapport aux suites finies ! Et d'autres propriétés simples donnent le même résultat, d'où l'importance de détailler ces propriétés. Les propriétés que nous allons voir permettent de distinguer les suites bornées, croissantes, décroissantes, constantes, monotones, stationnaires, etc.
Les suites majorées, minorées et bornées
[modifier | modifier le wikicode]Une suite majorée est une suite dont tous les termes sont plus petits qu'une constante définie. Dit autrement, pour tout , . La constante, plus grande que tous les termes de la suite, est appelée un majorant. On peut cependant préciser que toute suite qui a un majorant en a une infinité ! Par exemple, prenons une suite quelconque qui est majorée par 100 : elle est aussi majorée par 101, 102, 103, etc. Tous les nombres supérieurs à un majorant sont eux-mêmes des majorants. Parmi tous ces majorants, il en existe un qui est plus petit que les autres, ce qui lui vaut le nom de borne supérieure de la suite.
Une suite minorée est une suite dont tous les termes sont plus grands qu'une constante définie. Dit autrement, pour tout , . La constante, plus petite que tous les termes de la suite, est appelée un minorant. Encore une fois, toute suite qui a un minorant en a une infinité : tout nombre plus petit qu'un minorant est lui-même un minorant. Parmi tous ces minorants, il en existe un qui est plus petit que les autres, ce qui lui vaut le nom de borne inférieure de la suite.
Une suite bornée est une suite qui est à la fois minorée et majorée, ce qui fait que tous les termes de la suite sont pris dans un intervalle.

Les suites monotones et constantes
[modifier | modifier le wikicode]Les suites numériques ont souvent des propriétés que d’autres suites n’ont pas forcément, la raison étant que les nombres peuvent être ordonnés : on peut dire si un nombre est supérieur, inférieur ou égal à un autre. Cela permet donc de comparer les termes consécutifs d'une suite. Dans quelques cas, les termes consécutifs d'une suite sont les mêmes, que ce soit dès le début de la suite, ou alors au-delà d'un certain rang.
- Si chaque terme est égal au précédent, la suite est dite constante.
- Il existe des suites qui sont constantes au-delà d'un certain rang, mais pas avant celui-ci : on les appelle des suites stationnaires.
D'autres suites ont des termes différents : chaque terme est plus grand ou plus petit que le précédent.
- Dans le cas où chaque terme de la suite est plus grand que le précédent (pour tout rang , on a : ), la suite est dite strictement croissante.
- Dans le cas contraire, on a pour tout rang et la suite est dite strictement décroissante.
- Si , la suite est dite décroissante.
- Si , la suite est dite croissante.
Certaines suites récurrentes sont soit croissantes, soit décroissantes, selon leur premier terme ou la fonction utilisée. Tel est le cas de la suite définie par la relation : la fonction est décroissante avec et croissante avec . Pour éviter de dire qu’une catégorie de suite est soit croissante, soit décroissante, on préfère dire qu’elle est monotone. À noter que certaines suites deviennent monotones au-delà d'un certain rang, mais ne le sont pas forcément avant. Ces suites sont aux suites monotones ce que les suites stationnaires sont aux suites constantes. Mais il faut avouer que ces suites sont assez rares et que nous n'aurons pas à en manipuler beaucoup dans ce cours.
Démontrer qu'une suite est constante, croissante ou décroissante est généralement assez facile.
- Si une suite est croissante, pour tout rang , .
- Si une suite décroissante, pour tout rang , .
- Si une suite est constante, pour tout rang , , on est face à une suite constante.
Une bonne manière pour déterminer la croissance/constance/décroissance d'une suite est de calculer la différence . Son signe varie selon le rang si elle n'est pas monotone, alors qu'il est le même si la suite est monotone. Elle est toujours nulle pour une suite constante, toujours positive si la suite est strictement décroissante, toujours négative pour une suite strictement décroissante. Pour vous donner un exemple type de démonstration de ce genre, nous allons prendre le cas de la suite harmonique, la suite de l'inverse des entiers naturels. La voici :
Pour montrer qu'elle est décroissante, nous allons calculer , qui vaut alors :
On voit bien que la différence est positive : la suite harmonique est donc décroissante.
Les suite périodiques et ultimement périodiques
[modifier | modifier le wikicode]Une suite périodique forme un cycle, les mêmes valeurs revenant périodiquement au-delà d'un certain rang. De manière générale, une suite périodique est une suite telle que les termes forment une séquence de la forme : . Le nombre de termes répétés est appelé la période de la suite. Au fait, si une suite est (ultimement ou non) périodique de période , alors elle est aussi périodique de période , , , , ... Les suites périodiques sont définies de telle sorte que, quel que soit le rang : . En voici quelques exemples :
- Les suites constantes sont des suites périodiques de période 1.
- Un autre exemple de suite périodique est la suite définie par : , qui a une période de 2.
Les suites ultimement périodiques sont similaires aux suites périodiques, à un détail près : le début de la suite n'est pas périodique, la suite n'étant périodique qu'au-delà d'un certain rang. Par exemple, les suites stationnaires (constantes au-delà d'un certain rang) sont des suites ultimement périodiques de période 1.
Les suites périodiques et quasi-périodiques sont toutes bornées. Cela parait évident à démontrer : chaque période, chaque cycle, ne renferme qu'un nombre limité de valeurs différentes ( valeurs pour être exact), ce qui est incompatible avec une suite non-bornée. Les suites périodiques sont donc bornées entre la plus grande de ces valeurs et la plus petite. Quant aux suites quasi-périodiques, elles possèdent fatalement un nombre fini de termes avant de devenir périodique, ce qui fait que le même raisonnement s'applique.
Il existe des suites pour lesquelles on n'a pas encore réussit à prouver si elles sont ou non (quasi-)périodiques. Le meilleur exemple est la suite de Syracuse, définie par la relation de récurrence suivante :
Dans la totalité des cas connus, la suite de Syracuse se stabilise au bout d’un certain temps : la fin de la suite sera une succession de 1, 4, 2, 1, 4, 2, etc. Les tentatives de trouver des contre-exemples se sont retrouvées infructueuses, même en utilisant des ordinateurs très puissants pour tester N jusqu’à des valeurs extraordinairement grandes. Faute de contre-exemples connus à l'heure actuelle, les mathématiciens ont conjecturé que la suite est quasi-périodique pour toutes les valeurs possibles du N initial. Mais à ce jour, les mathématiciens n'en ont pas la preuve et ils n'arrivent pas non plus à démontrer le contraire. La situation est telle que le grand mathématicien feu Paul Erdős a déclaré à propos de cette suite que "Les mathématiques ne sont pas encore prêtes pour de tels problèmes".
Un exemple : les suites arithmético-géométriques
[modifier | modifier le wikicode]Tout cours sur les suites aborde rapidement les fameuses suites arithmétiques, géométriques et arithmético-géométriques. Il faut dire que ces suites sont assez utilisées dans de nombreux domaines et il est important de les connaître par cœur. Elles sont de plus assez simples à comprendre, ce qui fait que nous allons les étudier maintenant.
Les suites arithmétiques
[modifier | modifier le wikicode]Les suites arithmétiques sont des suites où les termes augmentent d'un pas régulier : on compte de 2 en 2, de 3 en 3, de 1.6 en 1.6, de 39 en 39, etc.
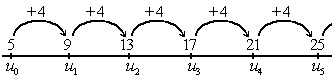
Dit autrement, la différence entre un terme et le suivant est une constante et chaque terme s’obtient en additionnant une constante au terme précédent. En clair, on a :
L'équation précédente peut aussi se réécrire comme suit :
La constante , le pas de la suite, est appelée la raison de la suite La raison d'une suite arithmétique peut être aussi bien positive que négative, et même nulle ! Et le signe de la raison influence la croissance ou décroissance de la suite.
- Si la raison est nulle, chaque terme est égal au précédent : la suite est constante.
- Si la raison est positive, les termes de la suite ne cessent d'augmenter avec le rang : la suite est croissante.
- Si la raison est négative, les termes diminuent progressivement quand le rang augmente : la suite est décroissante.
Les suites arithmétiques sont donc soit croissantes, soit décroissantes : ce sont donc des suites monotones.
Les suites géométriques
[modifier | modifier le wikicode]Les suites géométriques sont assez similaires aux suites arithmétiques, la seule différence étant que l'addition est remplacée par une multiplication : chaque terme est un multiple du précédent

Une suite de ce type est définie par la fonction de récurrence suivante :
L'équation précédente peut se réécrire comme suit :
La constante est encore une fois appelée la raison de la suite et elle peut être aussi bien positive que négative.
Contrairement aux suites arithmétiques, les suites géométriques ne sont pas forcément monotones. Et cette fois-ci, la croissance ou décroissance de la suite ne dépend pas que du signe de la raison, mais aussi de sa valeur. Dans les grandes lignes, tout dépend si la raison est négative ou positive, et si sa valeur absolue est comprise entre 0 et 1.
- Si la raison est positive, la suite est obligatoirement monotone.
- Si la raison est supérieure à 1, chaque terme sera plus grand que le précédent et la suite est croissante.
- Si la raison est de 1, chaque terme est égal au précédent : la suite est constante.
- Si la raison est plus petite que 1 mais malgré tout positive, chaque terme sera plus petit que le précédent, mais reste positif : la suite est décroissante.
- Si la raison est négative, chaque terme positif est suivi d'un négatif et réciproquement : la suite est alors dite alternée.

|

Les suites arithmético-géométriques
[modifier | modifier le wikicode]Les suites arithmético-géométriques sont des généralisations des suites géométriques et arithmétiques : elles sont en quelque sorte les deux à la fois. Chaque terme se calcule en multipliant le précédent, avant d'ajouter une autre constante. La constante par laquelle on multiplie le terme précédent est appelé la raison de la suite, alors que l'autre constante additionnée est appelée la constante additive.
- On peut signaler qu'une suite arithmétique est une suite arithmético-géométrique de raison multiplicative 1, alors qu'une suite géométrique est une suite arithmético-géométrique où la constante additive nulle.
Obtenir l'expression paramétrée de la suite est possible, bien que compliqué. Pour cela, nous allons déterminer la différence entre la suite arithmético-géométrique voulue et une suite géométrique de même raison et de premier terme identique. Nous allons voir ce que cela donne sur un exemple, avant de généraliser.
| Rang | Suite géométrique | Suite arithmético-géométrique | Différence entre les deux suites |
|---|---|---|---|
| 1 | 0 | ||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| ... | ... | ... | ... |
| n | |||
| ... | ... | ... | ... |
On verra dans le chapitre sur les sommes partielles, que . En faisant le remplacement, on a :
On obtient avec pas mal de manipulations algébriques :
Il est possible de démontrer cette relation autrement, bien que la démonstration soit moins intuitive. En voici une démonstration juste en-dessous.
|
Démonstration |
|
Pour faire cette démonstration, nous allons tenter de nous ramener d'une suite arithmético-géométrique à une simple suite géométrique, que l'on sait traiter. Pour cela, nous allons étudier la suite définie par :
On a alors : Vu que : La suite est donc une suite géométrique. On a donc : En remplaçant par sa valeur , on trouve : |

















































































