Planétologie/Les influences gravitationnelles

Loi de la gravitation universelle de Newton.

La pesanteur joue aussi un rôle assez important dans l'évolution des planètes et des satellites. Elle est à l'origine du phénomène de différentiation, de la convection, de la persistance des atmosphères, attire les astéroïdes et est à l'origine de certaines formes d'érosion. Mais en plus de ces influences indirectes, la gravité influence fortement la topographie planétaire. Ce chapitre se propose de voir comment la gravité façonne directement la topographie et la forme des planètes, ainsi que leurs intérieurs. Nous allons y parler des forces de marées et de divers phénomènes similaires.

Le géoïde et la forme des planètes

Si les planètes étaient purement fluides, elles auraient une forme approximativement sphérique, avec une topographie assez mineure. Les planètes telluriques de grande taille sont toutes sphériques, ce qui s'explique par le fait qu'elles ont été entièrement fondues dans leur passé. Elles ont donc eu le temps de prendre une forme sphérique avant de se solidifier. Les petits astéroïdes, formés par agglomération de petits corps solides, n'ont eu aucune chance de devenir sphérique, du moins si leur gravité n'est pas suffisante. La forme des planètes, de forte masse, est donc le fait de la gravité. Mais il ne faut pas oublier le fait que les planètes tournent sur elles-mêmes. Cette rotation donne naissance à une force de Coriolis, qui donne une forme ellipsoïdale aux planètes. Les planètes sont naturellement aplaties, avec un renflement proche de l'équateur.

L'aplatissement des planètes

Pour comprendre pourquoi les planètes en rotation sont de forme ellipsoïdale, il faut détailler un peu comment la gravité et la force centrifuge interagissent. La force de gravité ne dépend que de la distance au centre de la planète. Par contre, la force centrifuge dépend de la distance à l'axe de rotation. Ces deux forces ne sont donc pas orientées dans le même sens. La gravité agit toujours à la verticale, tandis que la force centrifuge fait un angle avec celle-ci, angle qui dépend de la latitude. Peu importe la latitude, la gravité a une intensité qui ne dépend que du rayon de la planète. Mais pour la force centrifuge, ce n'est pas le cas : elle dépend de la latitude. En effet, plus la latitude augmente, plus la distance avec l'axe de rotation diminue, ce qui diminue la force centrifuge. Précisément, l'accélération de la gravité vaut :

g={\frac {GM}{R^{2}}}

Par contre, l'accélération causée par la force centrifuge vaut, avec $D$ la distance à l'axe de rotation et $w$ la vitesse de rotation angulaire :

a_{c}=w^{2}D

Par définition, si la planète est sphérique, on a $D=R\cos {a}$ , avec $a$ la latitude. Ce qui donne :

a_{c}=w^{2}R\cos {a}

À l'équateur, la force centrifuge est maximale et parallèle à la gravité, mais orientée dans le sens opposé. La force centrifuge compense un petit peu la gravité, ce qui fait que l'équateur doit être légèrement surélevé. Aux pôles, la force centrifuge est tout simplement nulle. Ainsi, la gravité agit sans être compensée. Aux latitudes intermédiaires, la force centrifuge est inférieure à celle observée à l'équateur, mais non-nulle : la surface est donc un peu surélevée par rapport aux pôles, mais pas autant qu'à l'équateur. Si on modélise le tout mathématiquement, on voit que la surface où force centrifuge et gravité se compensent forme une ellipsoïde.

L'effet de la topographie sur le champ de gravité

Effet d'une montagne sur le champ de gravité local proche.

La forme exacte des planètes n'est pas une ellipsoïde exacte : elle possède des montagnes, des dépressions, des creux, des failles, etc. La forme exacte de la planète influence naturellement son champ de gravité. Par exemple, les montagnes sont des accumulations de matière, source de gravité supplémentaire. À proximité d'une montagne, la pesanteur est donc influencée par le poids de la montagne. Si on place un fil à plomb, censé indiquer la verticale, celui-ci sera attiré un petit peu par la montagne et déviera vers la montagne. Il formera donc un angle avec la verticale. Évidemment, cet effet est d'autant plus important que le fil à plomb est disposé près de la montagne.

On peut rendre compte du champ de gravité d'une planète en dressant ce qu'on appelle un géoïde. Celui-ci est ce qu'on appelle une surface équipotentielle, à savoir une surface sur laquelle le potentiel gravitationnel est le même (si vous ne savez pas ce que c'est, un livre de physique basique devrait vous éclairer). Sa forme est loin d'être sphérique ou ellipsoïde, du fait de la topographie. Mais sa forme n'est pas identique à celle de la topographie, vu qu'il dépend aussi de la répartition des masses sous le sol. Sur Terre, celui-ci est assez bien approximé par les océans. Leur nature liquide leur permet de se déformer pour minimiser leur énergie potentielle, et donc épouser une surface équipotentielle. Les continents ne sont pas dans ce cas, ce qui signifie que la détermination du géoïde sur les continents est assez difficile.

L'influence de la gravité sur la topographie

Il est évident qu'aucun corps tellurique n'est complètement plat : entre les cratères d'impact et les effets de la tectonique, la topographie a de quoi s'exprimer. Beaucoup de corps telluriques ont des chaînes de montagne ou des volcans, voire quelques dépressions. Ces reliefs se forment essentiellement en augmentant ou en diminuant l'épaisseur de la croûte : les chaînes de montagne et les volcans sont autant de phénomènes qui épaississent la croûte, là où les déprécions sont des zones où la croûte s'amincit. Sédimentation et érosion peuvent aussi épaissir la croûte ou l'amincir, en ajoutant ou enlevant des sédiments. Toute accumulation de matière appuie sur la lithosphère, quel que soit son origine. Évidemment, cette pression entraîne une réorganisation du manteau sous-jacent, ainsi que des tensions crustales. Ces tensions peuvent limiter la hauteur de la croûte, quand elles ne la fracturent pas. Un exemple est ainsi celui de la Valles Marineris sur Mars, qui s'est formée suite à la formation d'une zone volcanique proche : le dôme de Tharsis. L'accumulation de grandes quantités de lave dans le dôme de Tharsis a pesé sur la croûte, qui a fini par se fendre, donnant une fracture de grande taille : la Valles Marineris était née. L'augmentation du poids de la croûte a aussi des effets sur le champ de gravité à proximité. Chose étrange, on peut remarquer que le champ de gravité à longue distance est cependant compensé par des processus mantelliques, comme nous le verrons dans la seconde partie.

La hauteur maximale du relief

Le poids de la croûte peut limiter la taille des volcans et autres montagnes : si elles dépassent une certaine taille, la croûte finit par céder et par raboter les montagnes. Ce relief, cette montagne, est soumise à deux forces : une force de gravité qui la pousse à s'effondrer sur elle-même, et une force de résistance qui empêche ses roches de se déformer. Ces deux forces s’équilibrent jusqu’à une certaine hauteur où la force de gravité surmonte la force de résistance : la montagne s'effondre alors sur elle-même, jusqu’à atteindre la taille maximale permise par la gravité. Pour faire simple, les roches de la montagne se fracturent et se plissent quand elles sont soumises à une pression trop forte. Il existe un seuil autour duquel toute roche commence à plier et casser, seuil qui ne doit pas être dépassé. Les roches situées à la base de la montagne sont naturellement soumises à une pression, causée par le poids de la montagne située au-dessus. Tant que la pression reste sous le seuil de fluage, la montagne garde sa taille. Mais si le seuil est dépassé, les roches se compriment, plient et cassent, ce qui fait rapetisser la montagne. Les roches sont notamment déplacées sur les côtés par la pression : la montagne s'étale, ce qui lui fait perdre de l'altitude.

Calcul

Dans cette section, nous allons calculer la hauteur maximale que peut avoir un relief (une montagne, par exemple) sur un corps tellurique. Pour calculer à quelle hauteur de montagne ce phénomène a lieu, il faut calculer la pression à la base de la montagne. Quelques développements relativement triviaux nous disent que cette pression est égale à l'équation suivante, en posant :

$g$ l'accélération de la pesanteur ;
$p$ la densité des roches de la montagne ;
$h$ la hauteur de la montagne.

P=p\times g\times h


Démonstration
La force de gravité à laquelle est soumise la montagne est égale au produit de sa masse $M$ par l'accélération de la pesanteur $g$ : $F_{g}=g\times M$ Cette force est répartie sur la base de la montagne, sur une surface $S$ . La pression à la base de la montagne est simplement égale à $F \over S$ . $P={\frac {F_{g}}{S}}={\frac {g\times M}{S}}$ La masse de la montagne est naturellement égale au produit de sa densité par son volume, ce qui donne : $P={\frac {g\times \left(\rho \times V\right)}{S}}$ En simplifiant, on trouve l'équation suivante : $P=g\times \rho \times h$

On peut alors déterminer la taille maximale de la montagne $h_{0}$ , si on connaît le seuil de résistance maximal des roches. Si on note $P_{0}$ le seuil de fluage des roches, on a :

h_{0}={\frac {P_{0}}{g\times \rho }}

Résultats

En utilisant une densité moyenne égale à celle de la croûte continentale et un seuil de $3\times 10^{8}$ (proche de celui mesuré en laboratoire), on trouve que la hauteur maximale d'un montagne sur Terre est de 10 kilomètres maximum. Sur Mars, les montages ne peuvent dépasser 27 kilomètres. Ces résultats sont remarquablement précis, en parfait accord avec les mesures. Pour donner un exemple, la plus haute montagne terrestre est un volcan hawaïen qui fait approximativement 10 kilomètres de haut ! Quant au plus haut relief martien, il s'agit du volcan Olympus Mons qui fait 22 kilomètres de haut.

L'isostasie et la topographie

On a vu que le poids des chaînes de montagne et volcans peut fracturer la croûte, au point de limiter leur taille. Mais la croûte va aussi peser sur le manteau sous-jacent et entraîner des déplacements de masse. Par exemple, les continents semblent monter ou descendre à la suite d'une variation de poids. Lors de la disparition d'un glacier, d'une montagne ou d'une couche sédimentaire, tout se passe comme si le continent remontait, libéré du poids imposé par le relief. Dans certaines situations, on observe l'effet inverse : le continent s'enfonce à la suite d'un ajout de poids, comme la formation d'un glacier, un empilement de couches sédimentaires ou la formation d'un relief. La lithosphère subit ainsi, sur de longues périodes, des mouvements verticaux particulièrement lents. Ces déplacements de masse tendent à compenser le surpoids ou le manque de masse de la lithosphère, ce qui réduit quelque peu la topographie. La topographie crustale est donc compensée dans le manteau, par divers processus. Il en est de même pour le géoïde : on pourrait croire que les accumulations de matière se traduisent par une gravité supérieure à leur verticale, les dépressions donnant quant à elle une réduction de gravité comparé aux alentours. Mais tel n'est pas le cas : en réalité, le champ de gravité est relativement uniforme, la topographie le modifiant assez peu. Seules quelques accumulations de matière mantelliques causent des variations du géoïde de grande ampleur. Pour expliquer ce genre de phénomène, les géologues ont inventé des modèles qui font tous appel à l'isostasie. Celle-ci explique pourquoi les chaînes de montagnes ont une racine, une zone de croûte nettement plus épaisse que la normale. Elle permet aussi d'expliquer les modifications d'altitude liées à l'érosion, notamment pour les chaînes de montagnes (chose qui permet d'expliquer la formation de certains granites).

L'équilibre isostatique

Pour rappel, le manteau de la Terre a un comportement assez particulier : il a beau être solide, celui-ci est très déformable et se comporte comme un fluide sur de longues périodes de temps (millions d'années). Par "se comporte comme un fluide", on ne veut pas dire que celui-ci est liquide ou gazeux, mais que les roches du manteau sont suffisamment molles pour s'"écouler" lentement, un peu comme le ferait un vieux fromage qui commence à ramollir. Dans ces conditions, les lois de la mécanique des fluides s'appliquent au manteau. On se retrouve donc avec une lithosphère solide partiellement immergée dans un manteau fluide. S'il n'y avait pas de force qui vienne compenser exactement l'effet du poids de la croûte, celle-ci coulerait dans le manteau plus fluide. Quelle est cette force qui vient contrecarrer le poids de la croûte en dehors des zones de subduction ? Eh bien, c'est la même force que celle qui fait flotter les icebergs ou les navires sur l'océan. Eh oui, vous avez bien lu : les plaques lithosphériques flottent sur le manteau grâce à la poussée d'Archimède.

Pour rappel, le principe d’Archimède stipule que tout corps solide plongé dans un fluide subira une force, dirigée de bas en haut : la poussée d’Archimède. Elle a initialement été décrite dans les liquides, mais sa formulation actuelle fonctionne avec n'importe quel fluide, et les roches du manteau ne font pas exception. Mais cette poussée d'Archimède ne suffit pas toujours à faire flotter un objet : il faut aussi que le solide soit moins dense que le fluide. Dans le cas contraire, le solide coule. Cela arrive dans certaines zones de subduction, où la plaque tectonique subductée, plus dense que le manteau, coule spontanément. Mais dans tous les autres cas, le manteau est nettement plus dense que la croûte, et il en est de même pour la lithosphère, plus dense que l'asthénosphère. Dans ces conditions, la poussée d'Archimède contrecarre totalement le poids de la croûte : la croûte flotte sur le manteau, un peu comme la glace flotte sur l'eau. D'après les lois de l'hydrostatique, plus le volume immergé est grand, plus la poussée d’Archimède sera grande elle aussi. Et cela vaut aussi pour la croûte immergée dans le manteau. En comparaison, le poids d'un morceau de croûte (un continent) provient de tout son volume.

À l'équilibre, il n'y a pas de mouvement vertical de la lithosphère causé par la différence de densité : la force de flottabilité s'équilibre avec le poids de la croûte. Donc, quand le continent ne s'enfonce pas ou qu'il ne remonte pas, force de flottabilité et poids du continent sont égales. On parle d'équilibre isostatique. Cet équilibre permet de définir une surface de compensation, une surface horizontale où la pression est la même partout. Celle-ci se situe approximativement dans le manteau, et plus précisément dans l’asthénosphère.

Maintenant, regardons ce qui se passe dans le cas d'un changement du poids de la lithosphère. Il existe de nombreux processus capables de changer ce poids en ajoutant de la masse : un apport de masse via la sédimentation, la formation d'une chaîne de montagne, la naissance d'un volcan, etc. L'érosion peut aussi retirer de la matière, diminuant ainsi le poids du continent. Bref, les mécanismes sont nombreux (et on donnera de nombreux exemples plus tard). Intuitivement, plus on ajoute du poids, plus la croûte s'enfonce profondément dans le manteau. De même, diminuer le poids aura tendance à faire remonter la croûte. Pour résumer, un changement de masse est suivi par un mouvement vertical qui ramène la lithosphère à l'équilibre isostatique. Le processus a lieu comme suit. Si on ajoute de la masse sur le continent, son poids augmente. Par contre, le volume immergé dans le manteau et la poussée d’Archimède qui va avec ne changeront pas. En conséquence, le poids du continent deviendra supérieur à la poussée hydrostatique. La somme du poids et de la poussée donnera une force dirigée vers le bas : le continent s'enfonce. Lors de son enfoncement, le volume immergé dans le manteau augmentera, ce qui augmentera progressivement la poussée d’Archimède. Le processus continue jusqu'à ce que l'équilibre isostatique soit atteint. On peut tenir le même raisonnement dans le cas où on enlève de la masse sur le continent. Dans ce cas, le continent remonte jusqu'à ce que l'équilibre isostatique soit atteint.

Le processus se déroule comme décrit précédemment sous condition que les ajouts ou retraits de matières soient très rapides. Le manteau n'a pas le temps de se déformer pendant que la masse du continent change, les mouvements du manteau étant très lents. Dans ces conditions, les mouvements verticaux qui ramènent la lithosphère à l'équilibre isostatique mettent du temps à se mettre en place. C'est souvent le cas dans la réalité, vu que les roches se déforment très lentement et que les processus tectoniques ou d'érosion sont nettement plus rapides.

Il est raisonnable de supposer que toute variation d'épaisseur de la croûte se répercute intégralement sur le manteau en dessous : le poids ne génère pas de contraintes horizontales, il ne "déborde" pas. Cette dernière hypothèse est appelée l'hypothèse d'équilibre isostatique local. En réalité, cette hypothèse est irréaliste compte tenu du comportement des roches. La rigidité des plaques et celle du manteau font que la pression d'une chaîne de montagne va se répartir non seulement à la verticale, mais aussi sur les côtés, à l'horizontal. Ainsi, les racines d'une chaîne de montagne s'étalent, et les bassins sont légèrement surélevés sur les bords. L’équilibre isostatique local est brisé, et on parle plutôt d’équilibre isostatique régional. Il existe divers modèles qui formalisent l'effet de cette déformation de la lithosphère. Dans ces modèles, la surface de compensation n'est pas forcément située à la base de la lithosphère ou de la croûte : elle peut se situer un peu plus bas, dans l'asthénosphère. Ces deux hypothèses sont valides dans des circonstances différentes : tout dépend de l'épaisseur de la lithosphère et de la taille de la déformation crustale. Si la lithosphère est très épaisse, il n'y a pas de compensation isostatique. L'isostasie est alors inexistante et la topographie est maximale. Si la déformation devient assez grande, comparé à l'épaisseur de la lithosphère, l'isostasie se fait sentir. Il s'agit alors d'une isostasie régionale, qui traduit la flexure de la lithosphère. Enfin, si la déformation est très grande et que la lithosphère est très fine en comparaison, l'isostasie locale domine.

Il nous reste à formaliser la notion d'isostasie mathématiquement, ce qu'ont fait certains géophysiciens. Il existe de nombreux modèles de l'isostasie, et je vais vous présenter les deux modèles les plus connus. Petite précision : ces modèles ne fonctionnent qu'une fois l'équilibre isostatique atteint : il ne doit pas y avoir de mouvement verticaux.

Le modèle de Airy

Le modèle de Airy s'applique pour une lithosphère et un manteau de densités constantes et rend compte de son équilibre isostatique quand elle s’épaissit ou s’amincit. Elle rend compte, par exemple, des épaississements de la lithosphère comme les chaînes de montagnes et aux volcans éteints. En effet, les chaînes de montagnes ne sont que la partie émergée d'un épaississement de la lithosphère : les montagnes ont des racines, des zones où la lithosphère est épaissie en profondeur et fait saillie dans l’asthénosphère. Pour une montagne, le modèle d'Airy permet de calculer la profondeur de sa racine crustale. On peut aussi l'appliquer dans le cas des amincissements de la lithosphère, comme un bassin sédimentaire, ou un cratère d'impact. Sous ces structures, le manteau tend à remonter pour remplacer le déficit de lithosphère lié à l'amincissement. Le modèle de Airy permet alors de calculer la hauteur de remontée du manteau.Nous étudierons les deux cas, montagne et bassin, dans ce qui suit.

Ce modèle suppose que toute la lithosphère est une zone de densité uniforme, même dans les chaînes de montagne ou les bassins sédimentaires. De plus, ce modèle suppose aussi que le manteau a une densité uniforme. Il postule aussi que la lithosphère est composée de plusieurs blocs de hauteurs différentes, mais de même densité. On suppose que les effets aux bords des blocs sont négligeables et que toute variation d'épaisseur se répercute intégralement sur l'asthénosphère située en-dessous : le poids ne génère pas de contraintes horizontales, il ne "déborde" pas. Ces deux conditions garantissent que l'hypothèse d'équilibre isostatique local est respectée. Rappelons que ce modèle ne fonctionne que dans le cas où l'équilibre isostatique est atteint (il ne doit pas y avoir de mouvement verticaux) : il ne fonctionne pas si l'équilibre isostatique n'est pas atteint. Par exemple, ce modèle ne fonctionne pas pour des chaînes de montagnes qui continuent de grandir : l'Himalaya ne respecte pas cette règle, par exemple. La chaîne de montagne doit aussi avoir une érosion assez faible, sans quoi elle rapetisse : l'équilibre isostatique est alors brisé par perte de masse.

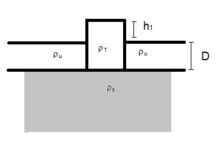
Le modèle de Airy modélise la montagne ou le volcan d'une manière assez sommaire : un simple pavé, comme illustré ci-dessous. La hauteur de la montagne est notée $h_{l}$ , la profondeur de la racine crustale $r_{l}$ et l'épaisseur normale de la lithosphère $e$ . Pour simplifier, on suppose que la surface de compensation est située dans le manteau. La conséquence directe de cette supposition est que la surface de compensation est située à la base de la racine de la chaîne de montagne. En effet, si on ajoute une hauteur $h$ de manteau avant d'arriver à la surface de compensation, on ajoute juste un terme $h\times d_{m}$ à la pression sous la croûte normale, ainsi que sous la chaîne de montagne : on reste sur une nouvelle surface de compensation. Reste à calculer la pression à la base de la chaîne de montagne, et la pression à la même profondeur dans le manteau (ces deux pressions sont situées sur la surface de compensation).

On a vu dans le paragraphe précédent que la pression à la base d'un pavé de roche est égale à : $d\times g\times h$ .

Au niveau de la montagne, on a $h=h_{1}+e+r_{1}$ , ce qui donne une pression de :

d_{c}\times g\times (h1+e+r1)

À la même profondeur, sous la lithosphère normale (sans montagne ni bassin), la pression est la somme de la pression causée par la lithosphère d'épaisseur $e$ et celle causée par le poids du manteau d'épaisseur $r1$ . Elle vaut :

g\times (e\times d_{c}+r_{1}\times d_{m})

Or, selon le principe même de l'isostasie, les deux pressions égales :

d_{c}\times g\times (h_{1}+e+r_{1})=g\times (e\times d_{c}+r_{1}\times d_{m})

On peut alors calculer la profondeur de la racine d'une chaîne de montagne en fonction de sa hauteur, et des densités :

r_{1}=h_{1}\times {\frac {d_{c}}{d_{m}-d_{l}}}

Vu que les densités de la lithosphère et de l'asthénosphère sont connues, le second terme peut être calculé assez facilement. On trouve donc qu'à l'équilibre isostatique, la racine d'une montagne a une taille environ 6 fois plus importante que l'altitude de la montagne.

r_{1}\approx 6\times h_{1}

Le modèle d'Airy s'applique aussi aux amincissements de la croûte, comme on peut en trouver dans les bassins sédimentaires ou les cratères d'impact. En-dessous de ces amincissements lithosphériques, le manteau remonte dans le vide laissé par la diminution d'épaisseur. Le modèle en question est illustré ci-contre. L'amincissement de la lithosphère en surface est noté $h_{1}$ , tandis que l'amincissement en profondeur est noté $r_{1}$ . Les calculs qui vont suivre supposent que la surface de compensation est située à la profondeur normale de la lithosphère, comme illustré ci-dessous.

La pression à la base de la lithosphère normale, sans bassin ni montagne vaut :

e\times d_{l}

À la même profondeur, mais sous le bassin, la pression est la somme de la pression de la lithosphère amincie et de l'asthénosphère qui a pris la place, ce qui donne :

(e-r_{1}-h_{1})\times d_{l}+r_{1}\times d_{a}

Les deux pressions sont égales, et quelques manipulations algébriques donnent :

r_{1}=h_{1}\times {\frac {d_{l}}{d_{a}-d_{l}}}

Si on ajoute le fait que la dépression est remplie par un océan ou des sédiments, l'analyse reste la même : il suffit de rajouter un terme lors du calcul de la pression sous le bassin. Cela demande juste de connaître la densité du matériel qui remplit la dépression, que l'on notera $d_{e}$ . On obtient alors :

r_{1}=h_{1}\times {\frac {d_{l}-d_{e}}{d_{a}-d_{l}}}

Mais attention : si ce modèle fonctionne pour les bassins, il ne fonctionne pas pour un rift ou une dorsale : la densité des matériaux n'est pas constante, une bonne partie des variations d'épaisseur étant causée par des différences de température.

Le modèle de Pratt

Comparaison entre le modèle de Airy et de Pratt.

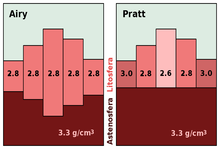
Le modèle de Pratt a été inventé pour rendre compte d'une autre situation : celle d'une lithosphère de densité variable posée sur un manteau de densité uniforme. Ce modèle modélise bien les situations où les variations d'épaisseur proviennent de variations de température du manteau, qui chauffe la lithosphère par en dessous. Dans ces conditions, la lithosphère se dilate, ce qui a tendance à la bomber de quelques centaines de mètres de hauteur. Dans tous les cas, la plaque est très chaude au-dessus de la source de chaleur, mais elle refroidit en s'en éloignant. Cela arrive sous certaines dorsales océaniques, riches en volcans, où les plaques s'écartent à une vitesse largement supérieure aux autres dorsales, et qui ont un rift central très limité (voire pas de rift du tout) : ces dorsales sont appelées des dorsales rapides. On trouve un équivalent continental de ces dorsales : les rifts actifs. Certains points chauds vont aussi chauffer les plaques qu'ils transpercent par en dessous, et le modèle de Pratt est alors tout indiqué. On peut aussi étudier le cas de la subsidence thermique, dans laquelle la lithosphère s'amincit quand on la refroidit. Le traitement mathématique est alors similaire, mais fait appel à quelques hypothèses supplémentaires.

Sous un point chaud ou une dorsale, le bombement n'est pas totalement causé par l'augmentation de température de la croûte. La source de chaleur mantellique remonte vers la surface à cause de la poussée d’Archimède et appuie sous la lithosphère, ce qui crée un bombement supplémentaire. Mais le modèle de Pratt donne malgré tout de bons résultats.

Dans ce modèle, la lithosphère est composée de blocs, comme dans le modèle de Airy. Encore une fois, les effets aux bords des blocs sont négligés, et l'équilibre isostatique local supposé valide. La différence avec le modèle d'Airy, c'est que chaque bloc a une densité différente. Ces blocs s’enfoncent tous à la même profondeur dans le manteau/l'asthénosphère : c'est leur altitude qui varie suivant la densité. Typiquement, les blocs les plus chauds se dilatent vers le haut, et ils ont donc une hauteur supérieure. Le but du modèle de Pratt est de calculer la densité de la lithosphère, en connaissant sa hauteur.

Sous une lithosphère normale, sans dilatation ou contraction thermique, la densité de la croûte est normale, égale à $d_{c}$ . La pression à la base est donc proportionnelle à :

e\times d_{c}

Sous la lithosphère chauffée, elle vaut :

(h_{1}+e)\times d_{1}

, avec

d_{1}

la densité recherchée

On se rappelle alors que la surface de compensation se situe à la base de la lithosphère ou de la croûte, vu que le manteau a une densité homogène. En conséquence, les deux pressions calculées plus haut sont égales :

e\times d_{c}=(h_{1}+e)\times d_{1}

Quelques manipulations algébriques donnent alors :

d_{1}={\frac {e}{e+h_{1}}}\times d_{c}

Les ruptures de l'équilibre isostatique

Des mouvements tectoniques ou un changement dans l'épaisseur de la lithosphère peuvent rompre l'équilibre isostatique. La poussée isostatique se charge alors de ramener la lithosphère à l'équilibre, et des mouvements verticaux se mettent en place. Mais la lithosphère a une certaine viscosité, et met un certain temps avant de se remettre en place : les mouvements du manteau mettent un certain temps avant de faire remonter la lithosphère à l'équilibre isostatique. Par exemple, la variation du niveau des mers entraîne une rupture de l'équilibre isostatique. En effet, l'océan pèse sur le plateau continental et la croûte océanique, ce qui peut entraîner des mouvements isostatiques assez prononcés. Une simple augmentation de la quantité d'eau océanique, ou une variation de la superficie des océans est suffisante. D'autres situations sont possibles, et en faire la liste serait beaucoup trop long. Nous allons donc voir les cas les plus intéressants en planétologie, ainsi que quelques exemples purement terrestres assez intéressants.

Sur Terre, le cas le plus connu est celui du rebond post-glaciaire. Comme vous le savez peut-être, la Terre a subi des épisodes de glaciation plus ou moins prononcés, durant lesquels de grands glaciers se sont mis en place, notamment près des pôles. Ces glaciers recouvraient les continents sur plusieurs kilomètres, et formaient ce qu'on appelle un inlandsis. Lors de la fonte de ces glaciers, au sortir de la glaciation, le continent s'est vu allégé du poids que lui imposaient les glaciers. Cette perte de masse a donc donné naissance à un rebond : la lithosphère est remontée de quelques centaines de mètres. Cette remontée ne s'est cependant pas faite brusquement, mais s'est étalée sur plusieurs millions d'années. Le relâchement de la pression des glaciers a été à l'origine de nombreux tremblements de terre, et d'une fracturation de la lithosphère. L'exemple actuel le mieux connu est celui du nord du Canada, et du golfe de Botnie en Suède et Finlande. La remontée de la lithosphère se poursuit toujours dans le golfe de Botnie, à un rythme de 9 millimètres par an.

La sédimentation/érosion a aussi un rôle à jouer sur l'isostasie. Quand beaucoup de sédiments s'accumulent à un endroit, la masse de ces sédiments pèse sur la lithosphère continentale ou océanique. On en trouve de nombreux exemples dans les bassins sédimentaires, des creux dans la lithosphère qui se remplissent de sédiments : le remplissage de ces cuvettes aggrave la descente et le creusement de la lithosphère. Quant à l'érosion, elle permet de diminuer la charge posée sur la lithosphère : elle enlève de la masse. C'est ce qu'on observe dans les chaînes de montagnes mortes, qui ne grandissent plus : l'érosion entraîne la remontée des roches profondes par isostasie. Pour remonter, ces roches doivent se plier, ce qui donne naissance à de nombreux plis. Dans certains cas extrêmes, cela peut faire fondre ces roches. Il faut dire que les roches profondes, enfouies sous les chaînes de montagnes sont soumises à des températures élevées. En remontant, elles gardent leur température, mais la pression baisse. La pression peut baisser suffisamment pour que la roche fonde, donnant naissance à un magma. De nombreux granites se forment de cette façon dans les chaînes de montagnes érodées.

Le cas le plus courant dans le système solaire est celui de la naissance d'une montagne ou d'un volcan, qui va rapidement épaissir la lithosphère. Cet épaississement peut être si rapide que la lithosphère n'est pas en équilibre isostatique : des mouvements verticaux sont alors à prévoir pour équilibrer le tout. C'est le cas lorsqu'un volcan naît sur le fond de l'océan, notamment pour les volcans de point chaud. Dans ce cas, de grandes quantités de lave vont s'accumuler sur le plancher océanique, durant à peine quelques milliers d'années. Le volcan peut même émerger et donner naissance à une île, qui est alors colonisée par diverses espèces vivantes : le volcan peut notamment s'entourer d'une barrière de corail. Mais très vite, le volcan commence à s'enfoncer par isostasie. Le volcan finit par être immergé, mais la barrière de corail peut subsister à l'air libre : un atoll s'est formé.

La formation d'un cratère d'impact entraîne aussi une rupture de l'équilibre isostatique sous le cratère. L'impact va en effet retirer une épaisseur plus ou moins importante de croûte, qui devra être compensée par le manteau. Cela n'a pas d'incidence pour les petits impacts, mais les gros cratères sont souvent le siège d'une compensation isostatique. Le manteau remonte sous le cratère, surélevant celui-ci. Dans certains cas, cette poussée mantellique entraîne la fracturation de la croûte autour du cratère, formant des failles concentriques d'effondrement (des grabens circulaires). Dans d'autres cas, cela entraîne la formation de plis concentriques autour du cratère. La bosse centrale des cratères complexes peut, dans certains cas, provenir de ce phénomène. En étudiant la taille de ces grabens ou plis, on peut connaître assez approximativement la viscosité du manteau et l'épaisseur de la croûte du corps tellurique.

Les forces de marées

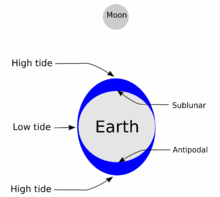
Tous les corps du système solaire sont soumis à des forces de marées, et les satellites et anneaux ne font pas exception. Vu que les forces de marées sont très importantes dans le fonctionnement des systèmes planète-satellite, nous allons les aborder dans ce chapitre. Sur Terre, la marée se traduit par une modification du niveau de la mer au cours de la journée. Ces marées proviennent de deux bourrelets où les océans sont surélevés de quelques mètres : un juste en face de la Lune, un autre opposé à celle-ci. La cause des variations du niveau de la mer est la force de gravité de la Lune et du Soleil, qui attirent les océans vers eux. Cette attraction ne touche pas que les océans, mais aussi l'ensemble de la planète et du satellite : cela déforme la croûte terrestre, l'intérieur du manteau, etc. Il est souvent dit que ces déformations de la croûte et du manteau peuvent parfois causer quelques séismes. Certains séismes lunaires pourraient d'ailleurs provenir des phénomènes de marées. On verra des quelques chapitres que les forces de marées peuvent être à l'origine de frictions dans le manteau, ce qui augmente sa chaleur. Le satellite de Jupiter nommé Io a d'ailleurs un manteau partiellement fondu grâce à ce mécanisme de chauffage par les marées, seule cause du volcanisme intense de ce satellite.

Influence de la Lune et du Soleil sur l'onde de marée.

Il faut cependant signaler que les forces de marées sont des forces assez générales, qui ne se limitent pas à l'action d'un satellite sur une planète (et réciproquement). Par exemple, la gravité du Soleil est à l'origine d'effets de marée sur Terre ou sur les autres planètes. Il existe même des forces de marée galactiques, causées par l'attraction d'une galaxie sur ses étoiles. Si on prend le cas de la Terre, tout corps suffisamment massif du système solaire a un effet sur la marée. C'est ainsi que le Soleil influence fortement la marée : son attraction gravitationnelle accentue du réduit la force de la marée lunaire. En théorie, la gravité des autres planètes du système solaire, comme Venus ou Jupiter, créent des forces de marrées sur Terre, qui s'ajoutent aux contributions de la Lune et du Soleil. Mais cette influence est trop faible pour être mesurable : seuls la Lune et le Soleil ont un effet sensible sur la marée terrestre. Lorsque le Soleil et la Lune sont plus ou moins alignés, leurs attractions gravitationnelles se superposent, accentuant la montée des eaux : c'est la période de vives-eaux, à opposer à la période de mortes-eaux où la Lune et le Soleil sont en opposition. On observe deux marées par jour en France, ni pourquoi d'autres endroits du globe en ont beaucoup plus ou beaucoup moins. Certaines zones sont même vierges de toute marée : en certains points, nommés points amphidromiques, les marées sont inexistantes. Certes, la forme des rivages ou certaines particularités peuvent faire que la marée n'arrive pas aux cotes, mais cela ne suffit pas à tout expliquer.

L'origine des marées

Expliquer les marées à partir de l'attraction gravitationnelle est séduisante. C'est d'ailleurs ainsi que sont expliquées les marées dans les ouvrages ou articles de vulgarisation. Mais cela n’explique pas d'où vient le bourrelet situé à l'opposé de la Lune ? Certains mettent en avant la force centrifuge, mais la raison est en fait plus complexe. La force centrifuge n'est pas une explication, car elle touche tout le satellite et la planète : elle doit agir à l'identique aussi bien sur le bourrelet avant que sur le côté opposé. Les marées sont en réalité causées par le fait que deux points d'un astre ne sont pas forcément soumis à la même force de gravité.

L'effet de marée traduit le fait que si l'on s'éloigne d'un astre massif, la force de gravité diminue avec la distance. Prenons une planète massive, qui attire les objets alentours et sert de "source gravitationnelle", et qualifions-la d'"attracteur". Deux points situés à des distances différentes seront soumis à des forces de gravité différentes. De même, si un objet s'éloigne de la planète, il sentira la pesanteur diminuer légèrement en s'éloignant. L'effet de marée quantifie cette diminution, mais pour un déplacement extrêmement petit, infinitésimal. Mathématiquement, c'est la dérivée de la force de gravité en fonction de la distance (ou encore la dérivée de l'accélération de la pesanteur, ce qui est équivalent), à savoir le vecteur :

{\vec {m}}={\frac {d{\vec {F(r)}}}{dr}}={\frac {d{\vec {a(r)}}}{dr}}

, avec

r

la distance avec le centre de l'attracteur,

{\vec {F}}

la force de gravité et

{\vec {a}}

l'accélération de la pesanteur.

Les points d'un satellite qui sont plus proches de la planète seront plus attirés que les points situés plus loin (vu que la gravité varie avec la distance). Cette différence de force gravitationnelle entre deux points éloignés, appartenant à un même corps, est appelée la force de marée.

Pour calculer celle-ci nous allons prendre deux points appartenant à un même corps tellurique. Les notations utilisées dans ce chapitre sont illustrées sur le schéma ci-dessous :

La force de marée se calcule en faisant la différence entre la force de gravité subie par le premier point et celle subie par le second. On a donc :

\Delta F_{gravite}={\frac {GMm}{(d-r)^{2}}}-{\frac {GMm}{(d+r)^{2}}}

\Delta F_{gravite}=GMm\left({\frac {1}{(d-r)^{2}}}-{\frac {1}{(d+r)^{2}}}\right)

En mettant au même dénominateur les termes ${\frac {1}{(d-r)^{2}}}-{\frac {1}{(d+r)^{2}}}$ , on trouve que : $2dr \over d^{4}+d^{2}r^{2}+2d^{3}r$ .

\Delta F_{gravite}=GMm{\frac {4dr}{d^{4}+r^{4}-2d^{2}r^{2}}}

En supposant que le rayon r est très petit, on peut simplifier les calculs. Avec cette hypothèse, on peut négliger le terme $r$ au dénominateur de l'expression ${\frac {4dr}{d^{4}+r^{4}-2d^{2}r^{2}}}$ . Celle-ci se simplifie en : ${\frac {4r}{d^{3}}}$ . La force de marée vaut donc :

F_{maree}=GMm{\frac {4r}{d^{3}}}

Le champ de marée

Les calculs précédents sont simplifiés, dans le sens où ils prennent deux points alignés avec le corps attirant (ici, la planète). Mais les calculs sont plus complexes quand les deux points sont situés ailleurs sur le satellite. Par exemple, deux points situés à égale distance subiront la même force de gravité, mais dans des directions différentes. Le bilan des forces fait que ces points seront en quelque sorte attirés l'un vers l'autre, en plus de l'être par le corps massif. Ce qui explique que les forces de marées donnent une forme ovoïde aux satellites et planètes.

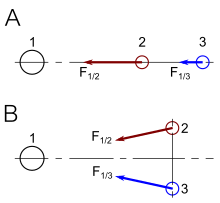
Enfin, il faut aussi tenir compte de la force centrifuge, qui dépend elle aussi de la distance. On peut cependant faire les calculs numériquement, et montrer l’influence de la gravitation sur chaque point du corps attiré. On oit alors que la gravité exacte est celle-ci :

◄ Retour vers « Les magnétosphères planétaires »

Sommaire du livre

Continuer vers « Les orbites des planètes et satellites » ►