Planétologie/Les orbites des planètes et satellites
Les planètes tournent autour du Soleil en suivant une trajectoire bien précise, appelée l'orbite de la planète. Cette orbite est une courbe fermée périodique, ce qui signifie que la planète revient à sa position initiale après un certain temps. En clair, elle parcourt cette trajectoire à l'identique de manière cyclique, chaque passage ayant la même durée que les autres. Décrire les orbites et les calculer est du domaine de la mécanique céleste, une branche de la physique dédiée au mouvement des planètes, satellites, petits corps et autres objets astronomiques. C'est elle qui se cache derrière le calendrier, derrière les saisons, les heures de lever et de coucher du Soleil, et bien d'autres choses du quotidien. Bien que le domaine soit très vaste et que les développements mathématiques soient légion, nous n'allons pas le voir en détail dans ce chapitre et allons simplement voir les bases du domaine, celles nécessaires dans un cours de planétologie.
Les trois lois de Kepler
[modifier | modifier le wikicode]
Sans rentrer dans les détails de l'histoire, la mécanique céleste a beaucoup progressé lors de la renaissance. Durant l'antiquité, les savants pensaient que la Terre était au centre du monde et que le Soleil et autres corps tournaient tout autour. Ce modèle géocentrique était assez intuitif et correspond bien aux observations naïves du quotidien. Après tout, le Soleil semble tourner autour de la Terre : il se lève à l'est et se coucher à l'ouest. Même chose pour les étoiles, qui se déplacent dans le ciel dans la même direction. Certes, ce n'est pas parfait et certaines planètes avaient des mouvements légèrement différents d'un mouvement circulaire, mais la théorie géocentrique tenait assez bien la route pour l'époque. Ses prédictions mathématiques permettaient de prédire le mouvement de astres avec une précision assez appréciable dans la plupart des cas. Cependant, les astronomes finirent par se rallier au modèle dit héliocentrique, où le Soleil est au centre du système solaire et où les planètes tournent autour de lui.
À la suite de cette révolution scientifique, les astronomes purent décrire plus précisément les orbites des planètes. Au 16ème siècle, Kepler établit ses fameuses lois du mouvement des planètes, sur la base de nombreuses observations astronomiques. Comme tout grand astronome de son temps, Kepler avait effectué des années d'observations et accumulé des quantités de données astronomiques assez importantes sur le mouvement des planètes. À partir de ces données, il établit trois lois qui servent encore aujourd'hui à décrire les orbites : la loi des orbites, la loi des aires et la loi des périodes.
La première loi de Kepler
[modifier | modifier le wikicode]Rappelons rapidement ce qu'est une ellipse, afin de bien comprendre de quoi il retourne. Intuitivement, une ellipse est une sorte de cercle aplati. Dans les faits, les cercles sont des cas particuliers d'ellipses, ces dernières étant une sorte de cercle à deux centres. Une ellipse demande, pour être tracée, de préciser deux points A et B, qui sont appelés les foyers. Chaque point de l'ellipse est situé à une distance du point A et à une distance du point B. Pour tout point de l'ellipse, la somme est la même.

La première loi dit que les orbites planétaires sont des ellipses, dont le Soleil occupe un des foyers.

Lorsqu'une planète se déplace sur son orbite, il y a un point où elle est la plus proche du Soleil et un autre où elle en est la plus éloignée. Ces deux points sont appelés respectivement la périapside et la apoapside. L'apoapside est la distance maximale entre l'objet en orbite et le foyer où se trouve le Soleil, alors que la périapside est la distance minimale. Dans le cas où l'on parle de l'orbite d'un corps qui tourne autour du Soleil (une planète, par exemple), on parle aussi de périhélie et d'aphélie.

La seconde loi de Kepler
[modifier | modifier le wikicode]La seconde loi porte sur la vitesse de la planète sur son orbite. Si l'on prend une durée T (peu importe sa valeur), la planète va parcourir une petite portion de l'ellipse, un arc d'ellipse (si on peut faire l'analogie avec un arc de cercle). Il est possible de rejoindre les extrémités de cet arc d'ellipse avec le foyer occupé par le Soleil. Ce faisant, on décrit une surface qui ressemble approximativement à un triangle, dont la base serait en réalité un arc d'ellipse. La seconde loi dit que pour une durée fixée, l'aire de cette surface reste la même, quelle que soit la position de l'arc d'ellipse.

La troisième loi de Kepler
[modifier | modifier le wikicode]La troisième loi de Kepler donne une relation entre la période orbitale, à savoir le temps que met la planète à faire un tour complet de son orbite, et le demi-grand axe de l'orbite. La troisième loi de Kepler dit que le carré de celle-ci est proportionnel au cube du demi-grand axe de l'orbite. Mathématiquement, elle vaut :
- , avec la période orbitale et le demi-grand axe de l’orbite.

Les paramètres orbitaux
[modifier | modifier le wikicode]Décrire l'orbite d'une planète dans le système solaire demande de fournir plusieurs paramètres, au moins six. Les paramètres en question sont appelés les paramètres orbitaux. Ils portent respectivement les noms de demi-grand axe, d'excentricité, d'inclinaison, de longitude du nœud ascendant, d'argument du périastre et de position de l'objet sur son orbite. Les deux premiers décrivent la forme de l'orbite, la forme de l'ellipse, les deux suivants indiquent la position du plan de l'orbite, l'avant-dernier donne la position de l'ellipse sur le plan de l'orbite et le dernier donne la position de la planète ou du satellite sur l'orbite. Le schéma ci-dessous illustre les paramètres orbitaux, mais ne suffira pas à lui seul pour les comprendre. Aussi, dans cette section, nous allons voir en détail à quoi correspondent ces paramètres orbitaux.

La description de l'ellipse orbitale
[modifier | modifier le wikicode]Les premiers paramètres décrivent la forme de l'ellipse qui constitue l'orbite. On peut décrire cette ellipse de plusieurs manières, mais la plus simple fait appel à deux paramètres appelés le petit axe et le grand axe. Il s'agit de deux distances qui passent par le centre de l'ellipse, le petit axe étant la plus grande distance et le grand axe la plus grande. Le grand axe est aligné avec les deux foyers, alors que le petit axe passe au milieu de ceux-ci (c'est la médiatrice du segment formé par les deux foyers). On peut aussi utiliser non pas le petit axe et le grand axe, mais leur moitié. En mathématique, ces deux grandeurs sont appelées le demi-petit axe et le demi-grand axe.

Mais les astronomes n'utilisent pas le demi-grande axe et le demi-petit axe. À la place, ils utilisent deux paramètres appelés le demi-grand axe et l’excentricité. Le demi-grand axe n'est autre que la moitié du grand axe vu précédemment. Par contre, le petit axe est remplacé par un paramètre appelé l'excentricité, qui décrit l’aplatissement de l'ellipse, l'écart entre l'ellipse et un cercle parfait. L'excentricité est comprise entre 0 et 1 : elle vaut 0 pour un cercle, 1 pour une ellipse totalement aplatie (un segment).

L'excentricité peut se calculer à partir de la distance entre les deux foyers, notée , et la longueur du grand-axe.
- , avec le demi-grand axe.
L'excentricité peut se calculer à partir du demi-petit axe et du demi-grand axe, avec la formule suivante :
Enfin, on peut aussi utiliser la formule suivante :
- , avec c la distance entre le centre de l'ellipse et un foyer, qui vaut .
Une autre définition équivalente est donnée par la formule suivante :
On peut relier l'excentricité avec périapside et apoapside. Dans ce qui suit, on note la périapside et l'apoapside, alors que l'excentricité est notée . On a, par définition de l'excentricité :
La description du plan orbital
[modifier | modifier le wikicode]L'ellipse qui forme l'orbite est orientée d'une certaine manière dans l'espace. Elle est comprise dans un plan que nous allons appeler plan orbital. Le plan orbital est repéré par rapport à un plan de référence, choisi de manière adéquate. Le plan de référence varie fortement suivant la situation, mais le corps situé au foyer de l'ellipse est forcément situé sur ce plan. Par exemple, si on veut décrire l'orbite de la Terre autour du Soleil, le plan de référence doit contenir le Soleil en un de ses points. Même chose si on étudie l'orbite de la Lune autour de la Terre : la Terre doit être dans le plan de référence. Pour les planètes du système solaire, le plan utilisé est l'écliptique, le plan qui contient l'orbite de la Terre.

Il est rare que le plan de référence se confonde avec le plan orbital : un tel cas n'aurait aucun intérêt. Dans les faits, les astronomes n'étudient que des situations où le plan de référence est différent du plan orbital, et où les deux plans ne sont pas parallèles. Les deux plans vont donc se couper, ils s'interpénètrent sur une droite. L'orbite coupe le plan de référence en deux points : le nœud ascendant et le nœud descendant. Leur nom est lié au mouvement du corps sur l'orbite : la planète monte par rapport au plan de référence quand elle passe le nœud ascendant, alors qu'elle descend quand elle passe au nœud descendant. Les deux nœuds sont reliés par une ligne, qui est la ligne des nœuds, sur laquelle le plan de l’orbite et le plan de référence se coupent l'un l'autre, s'interpénètrent.
Le plan orbital est incliné par rapport au plan de référence, sans compter qu'il est légèrement tourné. En tout, cela fait deux paramètres : l'angle d'inclinaison et l'angle de rotation entre les deux plans. Pour l'inclinaison, on suppose que le plan de référence définit l'horizontale. Le plan orbital est penché par rapport à cette horizontale, avec un certain angle, qui n'est autre que l'inclinaison. L'angle d'inclinaison est assez facile à mesurer, l'angle en question étant une mesure absolue. Par contre, l'angle de rotation entre les deux plans est lui relatif. C'est à dire qu'il faut préciser une direction bien précise pour dire que les deux plans sont tournés par rapport à cette direction. En plus du plan de référence, il faut donc préciser une direction de référence sur le plan de référence. La direction pointe vers un point de la sphère céleste qui s'appelle le point vernal.
Pour résumer, on doit définir deux paramètres pour décrire le plan orbital et la manière dont il est orienté par rapport au plan de référence.
- Le premier est l'inclinaison, l'angle entre les deux plans.
- Le second est la longitude du nœud ascendant/descendant, à savoir l'angle entre la ligne des nœuds et la direction de référence.
Enfin, on peut ajouter l'argument du périapside, l'angle formé entre le périapside et la ligne des nœuds. Formellement, ce paramètre n'aide pas à décrire l'orientation du plan orbital. Mais il est souvent regroupé avec les deux paramètres précédents. Nous en reparlerons dans la section suivante, par souci de cohérence.

La description de la position du corps sur l'orbite
[modifier | modifier le wikicode]Pour terminer la description de l'orbite d'une planète, il faut indiquer comment l'ellipse est orientée sur le plan orbital, et où se trouve le corps sur l'orbite.
L'orientation de l'ellipse sur le plan orbital est décrit par un angle, l'argument du périapside dont nous avons parlé plus haut. Il s'agit de l'angle formé entre le périapside et la ligne des nœuds.
La position de la planète à un instant t peut se décrire de plusieurs manières différentes, mais la plus utilisée est l'anomalie vraie, à savoir l'angle entre la planète et la périapside.

Le mouvement de la planète sur l'orbite
[modifier | modifier le wikicode]On peut décrire le mouvement de la planète sur l'orbite avec divers paramètres. Le premier est le temps mis pour faire un tour complet de l'orbite, le second est la vitesse de déplacement de la planète sur l'orbite et le troisième est le sens de déplacement.
Le sens de déplacement orbital
[modifier | modifier le wikicode]
Une planète peut parcourir son orbite dans deux sens différents, appelés sens rétrograde et sens prograde. Si l'on regarde le Soleil par-dessus, par le pôle nord, la majorité des planètes vont dans le sens inverse des aiguilles d'une montre. Le mouvement de ces planètes est dit prograde, ou encore dans le sens prograde. Mais une minorité de planètes et de petits corps va dans l'autre sens, dans le sens des aiguilles d'une montre. On dit qu'elles vont en sens rétrograde.
La période de révolution
[modifier | modifier le wikicode]La période de révolution est le temps que met la planète pour faire une révolution (un tour complet), c’est-à-dire pour revernir à sa position initiale sur l'orbite. La troisième loi de Kepler nous dit qu'elle dépend de la longueur du demi-grand axe. La mécanique céleste et les lois de Newton nous permettent d'obtenir une relation plus fine. Si on considère que la planète a une masse très petite devant celle du Soleil, on a :
- , avec la longueur du demi-grand axe, est la constante de gravitation et la masse du Soleil.
La vitesse orbitale
[modifier | modifier le wikicode]La vitesse de la planète est plus grande près du Soleil que quand elle est loin. La vitesse de la planète est maximale au périhélie (la position de l'orbite la plus proche du Soleil) et minimale à l'aphélie (la position la plus éloignée du Soleil sur l'orbite). Quand la planète s'approche du périhélie, elle accélère. Quand elle s'en éloigne et s'approche du périhélie, elle ralentit. D'ailleurs, ce n'est ni plus ni moins que ce que traduit la seconde loi de Kepler.
La vitesse en un point quelconque, situé à une distance d du corps central (ici, le Soleil) se calcule avec la formule suivante :
La vitesse au périapside se calcule avec la formule suivante :
- , avec .
La vitesse à l'apoapside se calcule avec la formule suivante :
- , avec .
L'évolution des orbites au cours du temps
[modifier | modifier le wikicode]
Tout ce qu'on a dit plus haut est valable pour un corps qui orbite autour d'un autre, cette situation portant le doux nom de problème à deux corps. Sous ces conditions, les orbites sont parfaitement elliptiques et ne changent pas de place une fois qu'elles sont installées. Mais dans la réalité, le système solaire comprend bien plus que deux objets et tous s'influencent mutuellement. Si on prend en compte toutes les influences gravitationnelles, les orbites des planètes sont perturbées. Sur un temps très court (quelques millénaires), l'orbite est stable et correspond aux orbites elliptiques idéales des lois de Kepler. L'orbite mesurée ainsi est appelée l'orbite osculatrice. Mais sur un temps plus long, les interactions gravitationnelles modifient la forme et le tracé des orbites, ce qui fait dériver les planètes progressivement. Après un certain temps, assez long, l’orbite réelle est une orbite perturbée qui ne correspond pas à l'orbite osculatrice initiale.
Les interactions gravitaires à l'origine de ce mouvement des orbites sont assez diverses, mais elles impliquent le plus souvent le disque protoplanétaire ou des interactions entre planètes. On peut globalement les classer dans les types suivants :
- Premièrement, les forces de marée influencent la forme des orbites. C'est ce qui explique que la Lune s'éloigne de nous de quelques centimètres chaque année, par exemple.
- Deuxièmement, les planètes s’attirent entre elles, ce qui rend leurs trajectoires assez chaotiques sur le long terme.
- Troisièmement, les planètes vont « frotter » contre le disque interplanétaire, ce qui tend à les ralentir.
D'autres phénomènes peuvent survenir sur les petits corps, en lien avec la luminosité solaire.
Le tidal locking et la rotation synchrone
[modifier | modifier le wikicode]
Les forces de marées, couplées à la rotation d'une planète et/ou de son satellite sont à l'origine d'un phénomène appelé la synchronisation de la rotation (tidal locking en anglais). Pour faire simple, c'est ce qui fait que la Lune nous présente toujours une face cachée et une face visible. Il en est de même pour de nombreux satellites du système solaire, qui font toujours face à leur planète. Et c'est pareil pour certaines planètes, qui font toujours face au Soleil : Mercure, par exemple, présente toujours la même face au Soleil. Dans tous les cas, cela vient du fait que les satellites tournent autour de leur planète à la même vitesse qu'ils tournent sur eux-mêmes : vitesse angulaire de rotation et de révolution sont égales. Pourtant, lors de la formation du système solaire, rien de tout cela n'était en place : la Lune tournait sur elle-même plus vite qu'aujourd'hui. Mais la Lune a fini par synchroniser sa vitesse de rotation avec sa vitesse de révolution (pareil pour les autres satellites ou planètes). La raison vient justement de l'interaction entre marées et rotation des planètes/satellites.
Les mécanismes du tidal locking
[modifier | modifier le wikicode]
Pour comprendre pourquoi, rappelons que les forces de marées déforment la planète et/ou le satellite, leur donnant une forme ovoïde. Dit autrement, un bourrelet de manière rocheuse se forme en face et à l'opposé de la planète et/ou du satellite attracteur. Mais vu que la planète tourne sur elle-même, ce bourrelet va être entraîné par la rotation de la planète, plus vite que le satellite. Ce faisant, la rotation tend à faire tourner ce bourrelet autour de l'axe de la planète à une certaine vitesse. Mais le satellite va aussi attirer ce bourrelet à lui. Vu l'angle formé entre le bourrelet et le satellite, cette attraction va attirer le bourrelet dans un sens légèrement différent de celui de la rotation. Cela va quelque peu freiner le bourrelet, qui entraînera a planète avec elle : elle tournera moins vite. La même chose se produit sur le satellite. Ainsi, les deux finissent par ralentir jusqu'à ce que le bourrelet (et donc la planète), tourne à la même vitesse que le satellite autour de la planète. Dans ces conditions, le déplacement du bourrelet sera exactement compensé par le déplacement du satellite, qui restera à la verticale du bourrelet. La rotation synchrone est alors atteinte.

L'effet se visualise bien si on regarde le champ de marée, c’est-à-dire les forces de marées en chaque point de la planète. On voit qu'il est asymétrique, ce qui signifie que la force de marée impose un couple (une différence de force entre deux points dont la résultante est nulle, mais qui force l'objet soumis à tourner). Ce couple est dans le sens opposé à a rotation de la planète, ce qui fait que la planète ralentit progressivement du fait de ce couple. Du fait de ce phénomène, la rotation de la planète et du satellite sont quelque peu ralentie à chaque marée.

La conservation du moment cinétique et le tidal locking
[modifier | modifier le wikicode]
Notons que la planète et le satellite tournent tous deux de moins en moins vite avec le temps. Cependant, cela a des conséquences sur la forme de leurs orbites, qui augmentent de rayon avec le temps. Le tidal locking ne fait pas que ralentir la rotation des planètes/satellites, mais elle les éloigne aussi les uns des autres. C'est ce phénomène qui explique que la Lune s'éloigne de nous à une vitesse moyenne de 3,8 cm par an. En effet, la Lune et la Terre n'ont pas des orbites totalement verrouillées. La lune a encore un petit mouvement de rotation dit de libration , qui fait qu'elle ne nous présente pas tout à fait la même face d'un jour sur l'autre. Et ce phénomène fait que les forces de marées peuvent causer un phénomène de tidal locking assez faible, mais suffisant pour perturber l'orbite de la Lune. Et le résultat est qu'elle s'éloigne de nous. Dans le passé, la Lune était beaucoup plus proche de la Terre qu'actuellement, mais elle s'est éloignée au cours des temps géologiques, en même temps que sa révolution devenait de plus en plus synchrone avec la rotation de la Terre.
Pour comprendre pourquoi le ralentissement de la rotation force les planètes/satellites à s'éloigner, il faut faire un petit peu de physique assez basique. Un théorème de mécanique classique nous dit que le moment cinétique total se conserve. Pour rappel, le moment cinétique est un vecteur qui encode les informations sur la rotation d'un objet : sa direction est l'axe de rotation et sa norme dépend de la vitesse de rotation. Pour une planète ou un satellite, ce moment angulaire est la somme de deux moments : celui de sa rotation sur lui-même et celui de sa révolution sur son orbite. Le moment angulaire associé à la rotation est appelé le moment cinétique intrinsèque, alors que celui lié à la rotation est appelé le moment cinétique orbital.
Le moment cinétique orbital se calcule à partir de la formule suivante :
- , avec r le rayon de l'orbite, m la masse de l'astre et v sa vitesse.
Le moment cinétique intrinsèque se calcule quant à lui à partir de la formule suivante :
- , avec w la vitesse de rotation angulaire (le nombre de tours par seconde) et I une quantité appelée le moment d'inertie (un équivalent de la masse pour la rotation).

L'effet de tidal locking entraîne une réduction de la vitesse de rotation, c'est-à-dire une diminution du moment cinétique intrinsèque. Vu que le moment cinétique total se conserve, le moment cinétique orbital doit augmenter pour compenser. En conséquence, la planète doit se déplacer plus vite sur son orbite et finit donc par s'éloigner. L'augmentation du moment cinétique orbital peut se traduire de deux manières : soit une augmentation de la vitesse de révolution de la planète, soit une augmentation du rayon de l'orbite. Dans les faits, l'astre va d'abord commencer par accélérer, ce qui va le forcer à s'éloigner de la planète. En s'éloignant, une partie de son énergie cinétique va alors se transformer en énergie potentielle de gravitation et l'astre ralentit. Au final, l'astre s'est éloigné, dans le sens où le rayon de son orbite a augmenté, et la vitesse de révolution s'ajuste alors à la nouvelle orbite.
Les résonances orbitales
[modifier | modifier le wikicode]Le phénomène de résonance orbitale se manifeste quand deux planètes/satellites ont des périodes de révolution qui sont commensurables, c’est-à-dire que leur rapport est un nombre fractionnaire. Pour le dire autrement, prenons deux planètes qui tournent autour du Soleil avec respectivement comme période de révolution et . La résonance a lieu si :
- , avec n et p deux nombres entiers.
La résonance précédente est souvent notée n:p. Cette notation indique que la planète A fait n tours, pendant que la planète B en fait p.
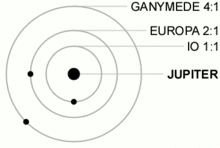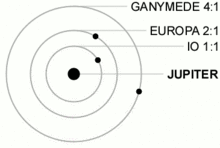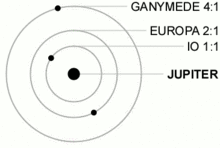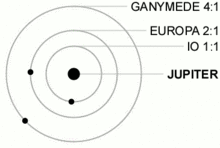
Dans le système solaire, peu de planètes sont en résonance. On peut citer le cas de Pluton (on va dire que c'est une planète...) qui est en résonance 3:2 avec Neptune, ce qui signifie qu'elle fait 3 révolutions pendant que Neptune en fait 2. Mais les résonances sont beaucoup plus nombreuses quand on regarde ce qu'il en est pour les satellites. Le cas le plus connu est celui des lunes de Jupiter, qui sont toutes en résonance les unes avec les autres. Dans le détail, Ganymède, Europe et Io sont dans une résonance 1:2:4. C'est-à-dire que pendant que Ganymède fait une révolution complète sur son orbite, Europe en fait deux et Io en fait quatre.
Les résonances orbitales ont un effet assez franc sur la stabilité des orbites. L'existence d'une résonance entre deux corps peut tout aussi bien stabiliser leurs orbites respectives que les déstabiliser, suivant divers paramètres orbitaux. Dans le système solaire, on a de nombreux exemples. En plusieurs endroits de la ceinture d'astéroïdes, on devrait trouver des corps en résonance avec Jupiter. Mais à l'endroit où devrait se trouver ces résonances, on s’aperçoit qu'il y a un trou dans la ceinture d'astéroïde. Les orbites en question sont vides, ce qui laisse une sorte d'anneau vide dans la ceinture d'astéroïde. De telles vides sont appelées les lacunes de Kirkwood, du nom de leur découvreur. Leur origine tient au fait que les corps présents originellement à cet endroit ont été expulsé par la résonance avec Jupiter. On observe la même chose dans les anneaux de Saturne, où des lacunes semblables ont été creusées par des résonances avec la planète Saturne.

Les résonances orbitales séculaires
[modifier | modifier le wikicode]Outre le phénomène précédent, le terme résonance orbitale recouvre aussi d'autres formes de résonances qui n'ont rien à voir avec la précédente. Pour éviter les confusions, on distingue donc la résonance décrite précédemment, appelée aussi résonance orbitale de mouvement moyen (mean-motion orbital resonance), les phénomènes de résonance séculaire et quelques autres encore.

Les résonances séculaires proviennent du fait que les ellipses orbitales ne sont pas fixes dans le temps : elles peuvent tourner progressivement sur elles-mêmes. Ce phénomène fait que les périapses se déplacent dans le temps, leur mouvement décrivant paradoxalement une sorte d'ellipse (non-confondue avec l'orbite). Ce mouvement est illustré dans le schéma ci-contre. Ce phénomène est appelé la précession des apsides et on dit que le périapse précesse. Formellement, cette précession des apsides modifie l'argument du périapse. D'ailleurs, la précession apsidale est définie par la dérivée temporelle de l'argument du périapse. Notons que le périapse précesse en formant une trajectoire fermée, ellipsoïdale (dans un cas idéal). Et naturellement, le périapse met un certain temps pour faire un tour complet de cette trajectoire : ce temps est appelé la période apsidale.
En raison de ce phénomène, deux orbites peuvent avoir des périapses qui précessent à la même vitesse, ce qui induit des interactions gravitationnelles entre orbites commensurables. Le résultat de cette interaction est une modification de l'inclinaison et de l'excentricité de l'orbite. Si on se limite au cas avec trois corps (un corps central, deux planètes/satellites qui tournent autour), alors les résonances séculaires peuvent modifier l'excentricité et l'inclinaison, mais la quantité reste constante. Dit autrement ce mécanisme permet d'échanger de l'excentricité contre de l'inclinaison et réciproquement.
Les interactions avec le disque protoplanétaire
[modifier | modifier le wikicode]Outre les forces de marées, d'autres interactions peuvent modifier l'orbite des planètes et satellites. Comme dit plus haut, il faut aussi tenir compte du fait que les planètes frottent sur le disque protoplanétaire, peu après leur formation. Ce phénomène peut prendre des formes très différentes selon la masse de la planète.
Pour les planètes peu massives, ce frottement est dû à des ondes de densité que la planète va former lors de son parcours du disque. Lors de chaque passage, la planète attire vers elle les astéroïdes, qui s'éloigneront une fois la planète éloignée. Sion suit les astéroïdes, on voit que ceux-ci s'éloignent puis s'approchent de l'orbite de la planète, dans un mouvement ondulatoire. Si on fait la somme de tous les mouvements astéroïdaux, on voit que la densité du disque augmente quand la planète passe et diminue quand elle s'éloigne. L'onde de densité qui en résulte attire la planète à chaque passage, réduisant sa vitesse. À cause de ce phénomène, la planète ralentit et se rapproche de son étoile. On parle de migration de type 1.
Pour les grosses planètes, comme Jupiter, ce phénomène ne dure qu'un temps. La planète fait le vide autour d'elle en quelque passage, tous les petits corps s'écrasant sur sa surface. Elle fait un véritable trou circulaire dans le disque, réduisant à néant le phénomène de migration de type 1. Mais divers phénomènes annexes prennent la relève et permettent une migration de type 2.
Les orbites des petits corps
[modifier | modifier le wikicode]Maintenant, intéressons-nous aux orbites des petits corps. Par petits corps, on veut parler des astéroïdes et des comètes, mais aussi de la poussière qu'on retrouve dans les anneaux planétaires ou dans l'espace inter-planétaire. Les petits corps orbitent autour du Soleil ou autour d'une planète, voire d'un satellite, en suivant une orbite elliptique. Pour ces petits corps, la lumière du Soleil agit sur les orbites des petits corps. Divers phénomènes physiques et thermiques liés à la lumière solaire et au vent solaire, comme la pression de radiation, l'effet Yarkovsky et l’entraînement de Poynting-Robertson, influencent l'orbite des petits corps. En toute généralité, ces phénomènes touchent tout corps gravitant autour d'une étoile, ici le Soleil. Ils agissent sur la surface des corps, seule à recevoir la lumière et le vent solaire, et non sur leur volume comme le fait la gravité. En conséquence, ces forces se manifestent quand le rapport surface/volume est assez important, ce qui n'est possible que pour les petits corps. Ils sont négligeables pour les planètes, planètes naines et autres corps relativement sphériques. Seuls les astéroïdes et les poussières sont significativement influencés par ces phénomènes.
Nous ne détaillerons pas les effets du vent solaire et du gaz interplanétaire. Tout au plus peut-on dire que le vent solaire souffle sur les petits corps et les éloigne lentement du Soleil. Pour ce qui est des gaz interplanétaires, on va se borner à dire que les petits corps vont frotter sur les gaz du disque interplanétaire, ce qui a tendance à les ralentir. Ce mécanisme est analogue à la friction de l'air qui ralentit les astéroïdes qui rentrent dans l’atmosphère, mais avec une intensité nettement moindre. Ce ralentissement dépend naturellement de la densité du gaz, ce qui explique sa faiblesse comparée à l'entrée dans l'atmosphère.
L'effet de la pression de radiation
[modifier | modifier le wikicode]La pression de radiation est la pression que la lumière exerce sur les corps qu'elle illumine. Toute onde électromagnétique (ou tout photon) transporte une certaine impulsion, une certaine "quantité de mouvement". Dans ce qui suit, nous la désignerons sous le terme d'impulsion lumineuse. Les lois de la physique nous disent que l'impulsion de la lumière est égale à son énergie divisée par la vitesse de la lumière, en vertu de l'équation :
- , avec E l'énergie et p l'impulsion.
La force liée à la pression de radiation n'est autre que la quantité d'impulsion lumineuse qu'un corps absorbe durant une unité de temps. Elle est donc égale à :
On utilise alors la définition de la luminosité L, à savoir .
Mais sur l'impulsion lumineuse incidente, seule une partie est absorbée. Lorsque la lumière interagit avec un objet, elle peut lui céder tout ou partie de son impulsion, qui sera convertie en quantité de mouvement. Si la lumière est absorbée, toute son impulsion sera transformée en quantité de mouvement. Si elle est réfléchie, une partie de son impulsion peut être transmise, mais la lumière changera alors de longueur d'onde : on est dans un cas de diffusion inélastique. Dans ce qui va suivre, nous allons supposer qu'une portion de l'impulsion du rayonnement incident est absorbée. Pour le dire autrement, seule une portion de l'impulsion passe de la lumière au corps solide considéré. Le coefficient vaut 1 pour un corps totalement absorbant et diminue en même temps que l'albédo augmente. Il faut donc ajouter ce coefficient dans l'équation précédente :
La luminosité reçue par le petit corps est, comme on l'a vu dans le chapitre sur la température de surface, égale à :
- , avec R la distance au Soleil et S la surface du petit corps.
En combinant les deux équations précédentes, on trouve que la force induite par la pression de radiation dans le cas du Soleil est donnée par l'équation suivante.
Vu que la pression de radiation et la force de gravité ont toutes deux une dépendance en , on peut reformuler la gravité vue par l’astéroïde comme suit :
- , avec
L'effet Poynting-Robertson
[modifier | modifier le wikicode]L'effet Poynting-Robertson fait que les petits corps éclairés par le Soleil acquièrent une trajectoire en spirale. Il apparaît quand de la poussière se déplace par rapport au Soleil. Il est dû au fait que la lumière absorbée par le petit corps est réémise avec un angle différent de l'angle d'absorption. Pour les besoins de l’explication, supposons que la lumière est absorbée perpendiculairement à la trajectoire de la particule. Du point de vue du petit corps, qui avance à une vitesse non-négligeable, la lumière semblera arriver avec un angle non-perpendiculaire mais sera réémise à la perpendiculaire. Du point de vue d'un observateur extérieur, la lumière du Soleil arrivera à la perpendiculaire, mais sera réémise avec un léger angle qui augmente avec la vitesse. Dans les deux cas, la lumière absorbée n'est pas réémise dans la même direction, ce qui fait que le bilan en quantité de mouvement est déséquilibré. En conséquence, le petit corps absorbe un peu de quantité de mouvement, ce qui le déplace de sa trajectoire originelle.

La force liée à cet effet se calcule avec la formule suivante :
- , où est la puissance irradiée par la particule (égale au rayonnement incident), est la vitesse de la particule, est la vitesse de la lumière.
Une autre formule, équivalente, est la suivante :
- , où est le rayon de l'objet, la constante de gravitation universelle, est la masse du Soleil, est la luminosité solaire et est le rayon orbital de l'objet.
L'effet Yarkovsky
[modifier | modifier le wikicode]
L'effet Yarkovsky, du nom de son découvreur, agit sur des petits corps d'un diamètre de maximum 30 à 40 kilomètres de diamètre. Il s'agit d'un effet extrêmement faible, bine plus que l'effet de la gravitation. En conséquence, il n'agit que sur des durées très longues, de plusieurs millions d'années.
Il apparaît quand un astéroïde est éclairé par le Soleil et provient de la rotation de l'astéroïde et de son inertie thermique. Dans les grandes lignes, l'astéroïde absorbe le rayonnement solaire et le réémet un peu plus tard sous la forme d'un rayonnement de corps noir. Vu que le rayonnement transporte de l'impulsion, de la quantité de mouvement, qui dit émission de lumière dit émission de quantité de mouvement. En réémettant de la lumière, l'astéroïde réémet de la quantité de mouvement et subit donc un léger recul. Cette fuite de quantité de mouvement n'est pas censée engendrer de force si l'émission est isotrope, mais ce n'est pas le cas si l'astéroïde tourne sur lui-même.
Le petit corps est chauffé par le Soleil, durant la journée. La portion éclairée du satellite devient ainsi plus chaude que la portion non-éclairée. Mais le sol de l'astéroïde a une certaine inertie thermique : il met du temps à refroidir quand la nuit tombe. Ce faisant, la portion de l’astéroïde qui est en soirée et s’apprête à passer dans la nuit sera encore assez chaude. Par contre, la portion matinale de l’astéroïde sera totalement refroidie. Il existe donc une différence de température entre les deux côtés soirée-matinée de l'astéroïde. Les deux portions de l’astéroïde émettront de la lumière, mais la partie en soirée émettra plus de lumière. Du fait des différences de température entre matinée et soirée, ce n'est pas le cas : les fuites ne sont pas isotropes. Ce faisant, la différence de fuite de quantité de mouvement entre la soirée et le matin engendrera un couple, et une force de Yarkovsky qui dévieront l’astéroïde de sa trajectoire. Cela pousse l’astéroïde dans le sens opposé de la portion en soirée, soit dans le sens de rotation de l'objet.
Les migrations planétaires et le modèle de Nice
[modifier | modifier le wikicode]Le modèle qui explique au mieux la mise en place des orbites du système solaire à l'heure actuelle est le Grand Tack. Mais celui-ci est assez compliqué, aussi je vais vous parler d'un modèle antérieur, sur lequel se base le Grand Tack : le modèle de Nice.
Pour simplifier, ce modèle commence juste après que la poussière du disque protoplanétaire se soit dissipée, avec des planètes bien formées. Dans cette situation initiale les planètes telluriques avaient des orbites proches de leurs orbites actuelles, mais que les orbites des planètes géantes étaient totalement différentes. En premier lieu, leurs orbites étaient quasiment circulaires, tant leur excentricité était faible. De plus, Jupiter était plus éloigné qu'actuellement alors que les autres planètes géantes étaient beaucoup plus proches du Soleil. À la suite d'interactions gravitaires avec les planétésimaux, la trajectoire des planètes s'est modifiée et leurs orbites ont évolué. Saturne, Neptune et Uranus ont été éjectées vers l'extérieur à la suite d'interactions avec des planétésimaux, alors que Jupiter s'est rapprochée du Soleil. De plus, les orbites des planètes géantes sont devenus plus excentriques et les planètes se sont rapprochées ou éloignées du Soleil.
Dans le détail, les planètes géantes se sont éloignées du Soleil, à l'exception de Jupiter. Au début, cette migration fût lente et progressive et les orbites sont restées quasi-circulaires. Mais, à force de se rapprocher, Jupiter et Saturne sont entrés dans un phénomène gravitationnel dit de "résonance orbitale". Leur orbite s'est alors subitement modifiée, devenant nettement plus courbe et elliptique. Saturne s'est alors déplacée sur son orbite actuelle, de même que Jupiter. L'arrivée de Saturne sur son orbite déstabilise les orbites d'Uranus et de Neptune, qui deviennent plus elliptiques et les éloigne du Soleil. Pour résumer, les planètes géantes ont été éjectées vers l'extérieur du système solaire sur des orbites elliptiques, à l'exception de Jupiter qui a été projeté vers l'intérieur du système solaire.
Ces modifications d'orbite ont eu de nombreuses conséquences sur l'organisation du système solaire. Par exemple, le rapprochement de Jupiter a perturbé la ceinture d’astéroïdes proche. Des astéroïdes de la ceinture ont été déstabilisés par la gravité de Jupiter et ont vu leurs orbites devenir elliptiques, voire paraboliques. Le bilan est que de nombreux astéroïdes ont été éjectés vers le système solaire interne, et se sont écrasés sur les planètes telluriques et leurs satellites. Cela explique que, aux alentours de 600 millions d'années d'existence, le taux de chute d’astéroïdes a fortement augmenté. À cette période, les planètes ont reçu un véritable bombardement d’astéroïdes, qui était nettement plus violent qu'auparavant : ce phénomène a été appelé le grand bombardement tardif. Cela provient du fait que les astéroïdes déplacés par Neptune et Uranus sont retombés vers l'intérieur, sur les planètes telluriques.
Une autre conséquence est que Uranus et Neptune ont fait leur entrée dans le disque externe, faisant le ménage dans celui-ci. De nombreux corps transneptuniens se sont alors écrasés sur Uranus et Neptune, sans compter ceux dont les orbites ont été déstabilisées et qui ont été envoyés au-delà de Neptune. Pour résumer, ces deux planètes ont fait le ménage dans le disque externe, le privant de plus de 90% de sa masse et le repoussant au-delà de Neptune. Ces interactions ont aussi permis aux planètes de se placer sur leurs orbites actuelles, en rendant celles-ci plus circulaires, moins elliptiques.



















































