|
|
plan du chapitre en cours
|
|
Le présent formulaire sert à la vérification de l'état limite en service (ELS). La poutre ayant déjà été vérifiée à l'ELU (voir Formulaire des poutres simples - Efforts de cohésion), on sait qu'elle ne risque pas de rompre. Mais elle se déforme élastiquement sous l'effet du chargement ; il faut donc vérifier que la flèche que prend la poutre reste compatible avec son usage. En particulier, s'il existe un jeu fonctionnel, il faut s'assurer que la flèche est inférieure au jeu.
La flèche est également un élément esthétique, de compatibilité avec les éléments posés dessus (par exemple un plancher), et permet d'avoir des renseignements sur le comportement dynamique (vibrations). En génie civil, on admet typiquement une flèche égale :
- à L/150 (soit 1/150 de la portée L) pour les parties d'ouvrage en console n'ayant pas à supporter couramment une circulation (auvents, débords de toiture), pour les tubes d'une structure supportant un poste électrique HTB (RTE[1]) ;
- à L/200 pour les pièces supportant directement des éléments de couverture (chevrons, liteaux), la charpente d'une structure supportant un poste électrique HTB (RTE)
- à L/250 pour une poutre, dalle ou console soumise à des charges quasi-permanentes (clause 7.4.1.4 de l'Eurocode 2. Béton armé) ;
- à L/300 pour une solive supportant un plancher, les pannes, les pièces supportant directement des matériaux verriers, les consoles supportant une circulation (montage ou entretien), les poteaux avec ponts roulants, les poteaux avec remplissage en maçonnerie prenant appui sur le poteau, les poteaux destinés à recevoir un vitrage sur plus de la moitié de leur hauteur, les éléments fléchis reposant sur deux ou plusieurs appuis, et ne supportant pas d'éléments de remplissage ;
- à L/400 pour les ouvrages fléchis autres que les consoles, et supportant une circulation (montage ou entretien) ou un remplissage ;
- à L/500 pour un linteau de menuiserie ;
- L/600 pour un pont forestier neuf acier-bois (Ministère des ressources naturelles, Québec) ;
- …
De manière un peu plus générale[2] :
- on peut imposer une flèche absolue (en mm) si l'on ne veut pas que la poutre touche un élément proche (par exemple une vitre) ;
- la flèche maximale typique pour une structure métallique (hangar, hall industriel…) vaut L/200 ;
- la flèche ne sera pas visible à l'œil nu si elle est inférieure à L/300 ;
- si la poutre est voisine d'un élément rectiligne parallèle, par exemple proche du sol pour une poutre horizontale, la flèche ne sera pas visible si elle est inférieure à L/500.
La fibre neutre prend une forme appelée « déformée », qui s'exprime par une fonction déplacement y = u(x ) ; par la suite, on la note simplement y(x ). La flèche est l'extremum de cette fonction :
 .
.
La pente est la dérivée de la déformée (coefficient directeur de la tangente) ; comme elle est faible (on suppose des petites déformations), cela correspond approximativement à l'angle θ en radians que fait la tangente avec l'horizontale :
 .
.
La courbure, définie comme l'inverse du rayon de courbure, est la dérivée seconde de la déformée :

et est donnée par
- la valeur du moment fléchissant Mf ;
- la rigidité de la poutre, qui dépend
- de la rigidité propre au matériau, donnée par le module de Young E (MPa),
- la rigidité due à la forme de la section, donnée par le moment quadratique IGz, noté par la suite I.
On obtient l'équation différentielle
 .
.
La résolution de cette équation donne y.
Dans le cas de sollicitations composées, on ne peut pas ajouter les flèches ; il faut ajouter les équations des déformées, puis rechercher les extrema de cette nouvelle fonction.
| Sollicitation
|
Flèche
|
Pente
|
| Équation de la déformée
|

force concentrée en son centre
|


|

|

|
force concentrée
|


|


|


|

force concentrée à l'extérieur des appuis
|



|



|

 , , 
|

charge uniforme
|


|

|

|
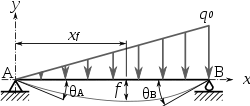
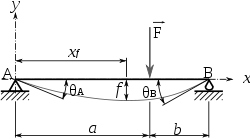
charge linéaire croissante
|


|


|

|

couple concentré en A
|


|


|

|

couple concentré en x = a
|


|


|

|
La poutre est encastrée à gauche (A) et libre à droite. On a toujours θA = 0 et xf = L.
La poutre est encastrée à gauche (A) et appuyée à droite (B). On a toujours θA = 0.
| Sollicitation
|
Flèche
|
Pente
|
| Équation de la déformée
|

charge concentrée au milieu
|


|

|
|
|

charge concentrée en x = a
|
 (Référence nécessaire) (Référence nécessaire)


|

|
|
|
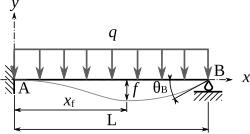
charge uniforme
|


|

|
|
|

charge linéaire décroissante q(x ) = q0(1 - x/L)
|


|

|
|
|
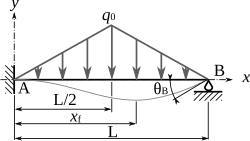
charge triangulaire symétrique
|


|

|
|
|

couple en B
|


|

|
|
|

couple en x = a
|
|
|
|
|
| Sollicitation
|
Flèche
|
Pente
|
| Équation de la déformée
|

charge concentrée au milieu d'une travée
|
[[Image: poutre
charge]]
|
|
|
|
La poutre est encastrée en A et en B, on a toujours θA = θB = 0.
- ↑ norme RTE EDF Transport — Réseau de transport de l'électricité
- ↑ « Déformations des éléments de structure », sur NotionsStructures.be (consulté le 11 janvier 2024).