Technologie/Éléments théoriques et pratiques/Résistance des matériaux/Formulaire des poutres simples - Efforts de cohésion
|
plan du chapitre en cours
|
navigation rapide dans le livre de technologie
■ préface - SOMMAIRE COMPLET ■ Aspects généraux ■ Éléments de machines | ||||||
La poutre est un modèle utilisé dans le domaine de la résistance des matériaux et désignant un objet dont la longueur est grande par rapport aux dimensions transverses (section fine).
Le présent formulaire sert à la validation de l'état limite ultime (ELU), c'est-à-dire à la vérification que la pièce n'est pas endommagée (la limite ultime n'est pas atteinte en service) :
- σmax ≤ Rpe
avec
- σmax : contrainte normale maximale (MPa) ;
- Rpe : résistance pratique à l'extension.
On a en général
avec
- Re : limite élastique (MPa), dont la définition dépend de la forme courbe de traction et du contexte de l'étude : ReH ou ReL pour une courbe avec limite élastique franche, Rp 0,2 % pour une courbe sans limite élastique franche, Rm pour un matériau cassant dans le domaine élastique ;
- s : coefficient de sécurité, dépendant du contexte.
La contrainte normale maximale se calcule par
où
- Mfz max : moment fléchissant maximal (en Nmm) ;
- wz : module de flexion de la poutre (mm3).
On a
où
- IGz : moment quadratique de la section droite (mm4), noté ci-après simplement I ;
- V : valeur absolue de l'ordonnée la plus éloignée de la fibre neutre (mm),
- pour une section à symétrie horizontale de hauteur h, V = h/2,
- pour une section circulaire, V = R (rayon).
L'effet de l'effort tranchant est en général ignoré.
On utilise la convention des efforts à droite de la coupure.

Pour les cas de charge, on ne représente que les efforts de charge. Les efforts à la liaison A sont notés RA pour la force et MA pour le moment.
Problèmes isostatiques
[modifier | modifier le wikicode]Poutres bi-appuyées
[modifier | modifier le wikicode]La force qu'exerce l'appui de gauche sur la poutre est appelée , celle de l'appui de droite est appelée . Par simplicité, on note et .
Poutre console
[modifier | modifier le wikicode]La poutre est encastrée à gauche et libre à droite (porte-à-faux). Les indices, le sens des effort et le sens des déformation sont omis lorsqu'il n'y a pas d'ambiguïté. La force d'encastrement est appelée La force qu'exerce l'appui de gauche sur la poutre est appelée , on note ; le moment d'encastrement est noté MA.
Problèmes hyperstatiques de degré 1
[modifier | modifier le wikicode]Poutre encastrée-appuyée
[modifier | modifier le wikicode]La poutre est encastrée en A et appuyée en B, sans charge en porte-à-faux. La force qu'exerce l'encastrement sur la poutre est appelée , celle de l'appui de droite est appelée . Par simplicité, on note et . Le moment d'encastrement est noté MA.
Poutre continue à deux travées égales
[modifier | modifier le wikicode]La poutre est appuyée sur trois appuis répartis symétriquement. La force l'appui de gauche sur la poutre est appelée , celle de l'appui central est appelée et celle de l'appui de droite est appelée . Par simplicité, on note , et .
Problèmes hyperstatiques de degré 2
[modifier | modifier le wikicode]Poutre bi-encastrée
[modifier | modifier le wikicode]La poutre est encastrée en A et en B, sans charge en porte-à-faux. La force qu'exerce l'encastrement sur la poutre est appelée , celle de l'appui de droite est appelée . Par simplicité, on note et . Les moments d'encastrement sont notés MA et MB.
| Sollicitation | Actions aux liaisons | Effort tranchant | Moment fléchissant |
|---|---|---|---|
 charge concentrée au centre |
|

|

|
 charge excentrée (p. ex. charge roulante) |
|

|

|
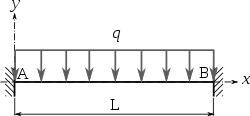 charge uniforme |
|

|

|