Approfondissements de lycée
Avant de commencer : Ce chapitre suppose des connaissances en
- Permutations et combinaisons vues dans le chapitre Dénombrement de base,
- Méthode de fractions partielles et,
- Compétence en manipulation de signes de sommation
Les séries de puissances formelles sont très utiles pour résoudre des problèmes comme :

où
 ; n = 1, 2, 3
; n = 1, 2, 3
Combien de solutions uniques existe-t'il si  ?
?
Avant d'attaquer ce problème, considérons le polynôme infini :

Nous voulons obtenir une forme fermée de ce polynôme infini. La forme fermée est simplement une manière d'exprimer le polynôme pour qu'il implique seulement un nombre fini d'opérations.

Donc, la forme fermée de

est

Nous pouvons les égaliser (en fait, nous ne pouvons pas. Cf. info).

Les deux expressions ne sont pas égales. C'est simplement le cas pour certaines valeurs de x (-1 < x < -1), nous pouvons faire une approximation du côté droit aussi près que possible en ajoutant un grand nombre de termes du côté gauche. Par exemple, supposons x = 1/2, le côté droit = 2; l'approximation du côté gauche en utilisant seulement 5 termes 1 + 1/2 + 1/4 + 1/8 + 1/16 = 1,9375, qui est proche de 2, comme vous pouvez l'imaginer, en additionnant de plus en plus de termes, nous approcherons de 2.
Pour une discussion plus détaillée de ceci, voir Infini et processus infinis.
De toute manière, nous ne ferons attention qu'aux belles propriétés algébriques et non aux valeurs numériques. À partir de maintenant, nous omettrons la condition pour que l'égalité soit vraie lorsque nous écrivons les séries de puissances.
Considérons un cas plus général :

où A et B sont des constantes.
Nous pouvons déduire la forme fermée comme suit :

L'identité suivante que l'on a déduit ci-dessus prend du temps et un effort de mémorisation.

1. Trouver la forme fermée :
- (a)

- (b)

- (c)

- (d)

- (e)

2. Pour une forme fermée donnée, trouver une fonction f(n) pour les coefficients de xn:
- (a)
 (Astuce : noter le signe plus au dénominateur)
(Astuce : noter le signe plus au dénominateur)
- (b)
 (Astuce : obtenir la série de puissances pour
(Astuce : obtenir la série de puissances pour  d'abord, puis multiplier par l'expression appropriée)
d'abord, puis multiplier par l'expression appropriée)
- (c)
 (Astuce : scinder en une somme de deux formes fermées distinctes)
(Astuce : scinder en une somme de deux formes fermées distinctes)
Soit la forme suivante donnée :

Nous pouvons obtenir beaucoup d'autres fonctions génératrices par substitution.
Par exemple : si  , nous avons :
, nous avons :

De manière similaire

est obtenue en substituant z = Bx puis en multipliant l'expression entière par A.
1. Quels sont les coefficients des puissances de x :

2. Quels sont les coefficients des puissances de x (Astuce : extraire un facteur d'1/2) :

3. En regardant une expression appropriée de deux manières différentes, conclure que

Sont-elles réellement égales ?
La suite de Fibonacci
- 1, 1, 2, 3, 5, 8, 13, 21, 34, 55...
où chaque nombre, excepté les 2 premiers (1 et 1), est la somme des deux nombres précédents. Nous disons que les nombres sont reliés si la valeur qu'un nombre prend dépend des valeurs précédentes dans la suite. La suite de Fibonacci est un exemple de relation de récurrence, elle est exprimée par :

où  est le (n+ 1)ème nombre de la suite. Noter que le premier nombre dans la suite est noté
est le (n+ 1)ème nombre de la suite. Noter que le premier nombre dans la suite est noté  . Cette relation de récurrence donnée, la question que nous voulons poser est "pouvons-nous trouver une formule pour le (n+1)ème nombre dans la suite ?". La réponse est oui, mais avant cela, regardons quelques exemples.
. Cette relation de récurrence donnée, la question que nous voulons poser est "pouvons-nous trouver une formule pour le (n+1)ème nombre dans la suite ?". La réponse est oui, mais avant cela, regardons quelques exemples.
Les expressions

définit une relation de récurrence. La suite est : 1, 1, 5, 13, 41, 121, 365... Trouver une formule pour le (n+1)ème nombre dans la suite.
Solution
Soit G(z) la série de puissances de la suite, ce qui signifie que le coefficient de chaque puissance (en ordre croissant) est le nombre correspondant dans la suite. Donc, la série de puissances ressemble à

Maintenant, par une série de manipulations algébriques, nous pouvons trouver la forme fermée de la série de puissances et à partir de là, la formule pour chaque coefficient


par définition 

par la méthode des fractions partielles, nous obtenons :

chaque partie de la somme est une forme fermée reconnaissable. Nous pouvons conclure que :

le lecteur peut facilement vérifier la précision de la formule.

Trouver une formule non-récurrente pour  .
.
Solution
Soit G(z), la série de puissances de la suite décrite ci-dessus.



Par conséquent  , quel que soit n.
, quel que soit n.
Une relation de récurrence linéaire est définie par :

Trouver la formule générale pour  .
.
Solution
Soit G(z) la série de puissances de la relation de récurrence.






Par conséquent

1. Déduire la formule pour le (n+1)ème nombre dans la suite définie par les relations de récurrence :

2. Déduire la formule pour le (n+1)ème nombre dans la suite définie par les relations de récurrence :

3. (Facultatif) Déduire la formule pour le (n+1)ème nombre de Fibonacci.
Considérons l'équation
 ;
;  sont des nombres entiers
sont des nombres entiers
Pour un nombre entier positif fixé n, combien de solutions existe-t'il ? Nous pouvons compter le nombre de solutions :
- 0 + n = n
- 1 + (n - 1) = n
- 2 + (n - 2) = n
- ...
- n + 0 = n
Comme vous pouvez le voir, il existe (n + 1) solutions. Une autre manière de résoudre le problème est de considérer la série de puissance

Soit  , i.e.
, i.e.

Le coefficient de  dans H(z) est le nombre de solutions de
dans H(z) est le nombre de solutions de  .
.
Considérons

Soit

il s'ensuit


Maintenant, nous pouvons voir que le coefficient de zn (pour n ≥ 0) est clairement le nombre de solutions de a + b = n (a, b > 0).
Nous sommes prêts maintenant à déduire un résultat très important : soit  , le nombre de solutions de
, le nombre de solutions de  . Alors, la série de puissance pour la suite
. Alors, la série de puissance pour la suite  est
est


i.e.

Considérons le nombre de solutions de l'équation suivante :

où  ; i = 1, 2, ... m. En appliquant la méthode discutée précédemment, si
; i = 1, 2, ... m. En appliquant la méthode discutée précédemment, si  est le nombre de solutions de l'équation ci-dessus lorsque n = k. La série de puissance pour
est le nombre de solutions de l'équation ci-dessus lorsque n = k. La série de puissance pour  est
est

mais qu'est-ce que  ? Tant que vous n'avez pas appris l'analyse, il est difficile de déduire une formule simplement en regardant l'équation de T(z). Sans supposer de connaissance en analyse, nous considérons le problème de dénombrement suivant.
? Tant que vous n'avez pas appris l'analyse, il est difficile de déduire une formule simplement en regardant l'équation de T(z). Sans supposer de connaissance en analyse, nous considérons le problème de dénombrement suivant.
"Vous avez trois sœurs, et n (n ≥ 3) poupées. Vous décidez de donner à chacune de vos sœurs au moins une poupée. De combien de manières pouvez-vous le faire ?"
Une manière de résoudre le problème est d'aligner toutes les poupées sur la table. Puisqu'il y a n poupées, il y a (n - 1) espaces entre elles (comme vous avez 5 doigts sur chaque mains et 4 espaces entre eux). Maintenant, à partir des (n - 1) espaces disponibles, choisir 2 et mettre un diviseur dans chaque espace que vous avez choisi ! Alors, vous avez divisé les n poupées en trois parts, une pour chaque sœur. Il y a  manière de le faire ! Si vous avez 4 sœurs, alors il y a
manière de le faire ! Si vous avez 4 sœurs, alors il y a  manières de le faire. Si vous avez m sœurs, il y a
manières de le faire. Si vous avez m sœurs, il y a  manières de le faire.
manières de le faire.
Maintenant, considérons ; "Vous avez trois sœurs, et vous avez n poupées. Vous décidez de donner à chacune d'elles une certaine quantité de poupées (sans restriction sur la quantité donnée à chaque sœur). De combien de manières peut-on le faire ?"
Notons que nous venons de résoudre :

où ai ≥ 0; i = 1, 2, 3.
Vous pouvez résoudre le problème en alignant n + 3 poupées sur la table. Prenons deux diviseurs et choisissons 2 espaces à partir des n + 2 espaces disponibles. Maintenant que vous avez divisé n + 3 poupées en 3 parts, dont chaque part a 1 ou plus de poupées. Maintenant, reprenons 1 poupée de chaque part, et vous avez résolu le problème ! Donc, le nombre de solutions est  . Plus généralement, si vous avez m sœurs et n poupées, le nombre de manières pour partager les poupées est
. Plus généralement, si vous avez m sœurs et n poupées, le nombre de manières pour partager les poupées est
 .
.
Un petit conseil, si vous avez des sœurs, donnez-leur une quantité égale de poupées, parce qu'elles sont toutes adorables.
Maintenant, comme discuté ci-dessus, le nombre de solutions de

où  est
est

i.e.

La forme réduite d'une série de puissance T(z) est

et tk est le coefficient de zk est T(z). Trouver une formule explicite pour tk.
Solution

Par conséquent, tk = k
Trouver le nombre de solutions de :
- a + b + c + d = n
pour tous les entiers positifs n (incluant zéro) avec la restriction  .
.
Solution
Par la formule

donc
- le nombre de solutions est

Nous tournons un problème légèrement plus difficile de la même manière. Supposons que nous comptions le nombre de solutions de :

pour un certain entier  , avec a, b, et c aussi plus grand ou égal à zéro. Nous pouvons écrite la forme réduite, nous notons le coefficient de xn de :
, avec a, b, et c aussi plus grand ou égal à zéro. Nous pouvons écrite la forme réduite, nous notons le coefficient de xn de :

est la solution requise. Ceci est dû au fait, de nouveau, que lorsque les puissances sont multipliées, les indices s'ajoutent.
Pour obtenir le nombre de solutions, nous scindons l'expression en formes réduites reconnaissables par la méthode des fractions partielles.
Soit  le nombre de solutions de l'équation suivante :
le nombre de solutions de l'équation suivante :

Trouver la série de puissances pour  , puis trouver une formule explicite pour
, puis trouver une formule explicite pour  en termes de n.
en termes de n.
Solution
Soit T(z) la série de puissances de 


Il n'est pas difficile de voir que


Soit  le nombre de solutions de l'équation suivante :
le nombre de solutions de l'équation suivante :

Trouver la série de puissances pour  , puis trouver une formule explicite pour
, puis trouver une formule explicite pour  en termes de n.
en termes de n.
Solution
Soit T(z) la série de puissances de 




- A = -1/4, B = 3/4, C = 1/4


1. Soit

la série de puissances de  (k = 0, 1, 2 ...). Trouver une formule explicite pour
(k = 0, 1, 2 ...). Trouver une formule explicite pour  en termes de k.
en termes de k.
2. Combien de solutions ont les équations suivantes si m est une constante donnée

où a, b et c ≥ 0
Cette section et la section sur la *technique de dérivation* peuvent être passées si vous êtes déjà familier avec l'analyse/dérivation.
En analyse, la dérivation est une des opérations les plus importantes appliquées aux fonctions de nombres réels. Pour dériver une fonction f(x), nous évaluons simplement la limite

où  signifie que nous faisons tendre h vers 0. Néanmoins, pour l'instant, nous pouvons simplement penser cela comme égalant h à 0, i.e., h = 0 à un temps approprié. Il existe plusieurs notations diverses pour le résultat de la dérivation (appelée la dérivée), par exemple
signifie que nous faisons tendre h vers 0. Néanmoins, pour l'instant, nous pouvons simplement penser cela comme égalant h à 0, i.e., h = 0 à un temps approprié. Il existe plusieurs notations diverses pour le résultat de la dérivation (appelée la dérivée), par exemple

et

veulent dire la même chose. Nous posons, f'(x) est la dérivée de f(x). La dérivation est très utile pour beaucoup d'usages, mais nous n'allons pas exposer les raisons de l'invention de l'analyse, mais plutôt comment nous pouvons appliquer l'analyse à l'étude des séries de puissances.
Il devrait être clair que si
- g(x) = f(x)
alors
- g'(x) = f'(x)
La loi ci-dessus est importante. Si g(x) une forme réduite de f(x), alors la dérivation des deux côtés est valide pour obtenir une nouvelle série de puissances.
Aussi, si
- h(x) = g(x) + f(x)
alors
- h'(x) = g'(x) + f'(x)
Ceci peut être vérifié en examinant les propriétés des limites.
Dérivons f(x) où

Premièrement, nous formons le quotient différentiel

Nous ne pouvons pas fixer h à 0 pour évaluer la limite à ce point. Pouvez-vous voir pourquoi ? Nous devons développer le facteur quadratique d'abord.


Nous pouvons maintenant extraire h pour obtenir maintenant

à partir duquel nous pouvons faire tendre h vers zéro de manière sure pour obtenir la dérivée, 2x. Donc
- f'(x) = 2x
ou de manière équivalente :

Dériver  .
.
Nous démarrons à partir du quotient différentiel :

Par le théorème du binôme, nous avons :

Le premier xn s'annule avec le dernier, pour obtenir

Maintenant, nous mettons la constante 1/h entre parenthèses

et le résultat devient :

Résultat important
Si

alors

Comme vous pouvez le voir, la dérivation implique d'extraire la dérivée d'une fonction à travers une manipulation algébrique, et pour cette raison, cette section est algébriquement très difficile.
Supposons que si
- h(x) = f(x) + g(x)
alors
- h'(x) = f'(x) + g'(x)
Dérivons 
Solution
Soit 

Montrer que si  alors
alors

Solution

Dériver

Solution

1. Dériver

2. Dériver

3. Dériver

4. Dériver

5. Prouver le résultat supposé dans l'exemple 3 ci-dessus, ie., que si  .
.
Conseil : utiliser les limites.
Nous voulons dériver un résultat vital dans cette section, nommément, dériver la dérivée de

où  et n un entier. Nous montrerons un certain nombre de manières pour arriver au résultat.
et n un entier. Nous montrerons un certain nombre de manières pour arriver au résultat.
Commençons par :

Développons le côté droit en utilisant le développement du binôme

dérivons les deux côtés

maintenant nous utilisons 

il existe certaines annulations

prenons un facteur commun de -n, et rappelons que 1! = 0! = 1 nous obtenons

soit j = i - 1, nous obtenons

mais ceci est justement le développement de (1 - z)n-1

De manière similaire à la dérivation 1, nous utilisons à la place de la définition d'une dérivée :

développons en utilisant le théorème du binôme

factorisons

prenons la limite à l'intérieur (rappelons-nous que [Af(x)]' = Af'(x) )

l'intérieur est justement la dérivée de zi

exactement comme pour la dérivation 1, nous obtenons

Exemple
Dérivons 
Solution 1



Solution 2
Par le résultat déduit de ce qui précède, nous avons

En imitant la méthode utilisée ci-dessus ou autrement, dériver :
1. 
2. 
3. 
4. (plus difficile)  (conseil : Utiliser la définition de la dérivée)
(conseil : Utiliser la définition de la dérivée)
Nous apprendrons comment dériver des fonctions de la forme :

i.e. des fonctions dont les inverses sont aussi des fonctions. Nous commençons, par la définition de la dérivation :



par

où g est une fonction de z, nous obtenons

qui confirme le résultat déduit en utilisant un argument de dénombrement.
Dériver
1. 
2. 
3. 
4. Montrer que 
Maintenant que nous sommes familiers avec la dérivation, nous devrions considérer :

Nous savons que

dérivons les deux côtés


par conséquent, nous pouvons conclure que

Noter que nous pouvons obtenir le résultat ci-dessus par la méthode de substitution,

en remplaçant z = x2, cela nous donne le résultat requis.
L'exemple précédent a montré que nous ne sommes pas concernés par les dérivations difficiles. Plutôt, pour obtenir les résultats d'une manière facile, nous devons seulement dériver les formes de base et appliquer la méthode de substitution. Par formes basiques, nous voulons dire les séries de puissances de la forme :

pour  .
.
Considérons le nombre de solutions de

pour  pour
pour  .
.
Nous savons que pour tout m, le nombre de solutions est le coefficient de :

comme discuté précédemment.
Nous démarrons à partir de :

et dérivons les deux côtés (noter que 1 = 1!)

nous dérivons de nouveau

et ainsi de suite pour (n-1) fois

nous divisons les deux côtés par (n-1)!

ceci confirme le résultat déduit en utilisant un argument de dénombrement.
1. Une Nouvelle Compagnie a emprunté 250 000 € pour le capital initial de démarrage, et la banque prend un intérêt mensuel de 3 %. Avant la fin de chaque mois, ils envisagent de rendre x € et l'intérêt est compté le dernier jour de ce mois.
Soit  la dette qui reste après n mois.
la dette qui reste après n mois.
a)Définir  récursivement.
récursivement.
b)Trouver les valeurs minimales de x.
c)Extraire la formule générale pour  .
.
d)Ainsi, déterminer combien de mois sont nécessaires pour tout rembourser s'ils rendent 12 000 € chaque mois.
2. Un arbre binaire est un arbre où à partir de chaque nœud, on peut avoir deux nœuds. Montrer que la figure suivante est un exemple d'arbre binaire.
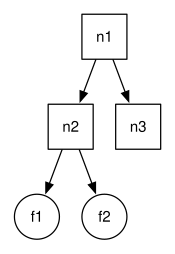
a)Soit  le nombre d'arrangements uniques d'un arbre binaire avec n nœuds au total. Soit C(z), une série de puissances de
le nombre d'arrangements uniques d'un arbre binaire avec n nœuds au total. Soit C(z), une série de puissances de  .
.
(i)Définir C(z) en utilisant la récursion.
(ii)Puis, trouver la forme réduite de C(z).
b)Soit  une série de puissances.
une série de puissances.
(i)En considérant la dérivée n-ième de P(x), trouver une formule pour  .
.
(ii)En utilisant les résultats à partir de a) et b)(i) , ou autrement, déduire une formule pour for  .
.
Conseil : Au lieu de faire une récursion pour rechercher le changement dans  lorsqu'on ajoute des nœuds à la base, essayer de penser à la manière opposée, et à la direction. (Et non, sans supprime de nœuds)
lorsqu'on ajoute des nœuds à la base, essayer de penser à la manière opposée, et à la direction. (Et non, sans supprime de nœuds)





























































































































































































