Cosmologie/L'énergie noire et la constante cosmologique
Les équations de Friedmann nous disent une chose assez importante : l'univers est en expansion. La première équation de Friedmann donne la vitesse de l'expansion, la seconde donne l'accélération de l'expansion de l'univers. Elle nous dit si l'expansion accélère ou ralentit, en fonction de la densité de la pression de l'univers.
Rien de surprenant en soi, nous savons aujourd'hui que l'univers est en expansion. Mais à l'époque où ces équations ont été déduites à partir de la relativité générale, c'était une surprise. L'expansion de l'univers n'était pas encore connue et la loi de Hubble n'avait pas encore été découverte. Le consensus commun de l'époque était que l'univers était statique et un univers en expansion paraissait contre-intuitif. Il fallait réconcilier un univers statique avec ces équations, ce qu'a fait Einstein.
Quand Einstein vit que les équations de Friedmann impliquaient un univers en expansion, il leur ajouta un terme censé corriger ce qui était un "problème" à l'époque. Le terme , ajouté aux équations de Friedmann, a reçu le nom de constante cosmologique. L'existence de cette constante était totalement justifiée par la relativité générale, où elle sert de constante d'intégration lors de certains calculs. Les équations de Friedmann étaient modifiées par la prise en compte de ce terme, ce qui donnait ceci :
L'ajout de la constante cosmologique permet d'obtenir un univers statique sous certaines conditions, qui sont détaillées dans un chapitre annexe de ce wikilivres, mais qui ne sont pas très intéressantes à étudier. Toujours est-il que la découverte de l'expansion de l'univers a mis au placard la constante cosmologique. Cependant, quelques décennies plus tard, les physiciens la réutilisèrent pour expliquer un autre phénomène : l'accélération de l'expansion.
L'accélération de l'expansion : la réintroduction de la constante cosmologique
[modifier | modifier le wikicode]Il a longtemps été cru que l'expansion de l'univers devait décélérer avec le temps, car c'était une conséquences des équations de Friedmann. Mais quelques observations ont remis cette affirmation en cause. Deux expériences ont fait voler en éclat ce consensus, en faisant état d'une accélération de l'expansion : le Supernova Cosmology Project et le High-Z supernovae search team. Ces observations ont été confirmées par des observations faites avec le télescope Hubble, à l'heure où j'écris ces lignes (fin 2016). Autant dire que la découverte de l'accélération de l'univers remettait en question les équations de Friedmann telles qu'elles sont formulées dans les chapitres précédents.
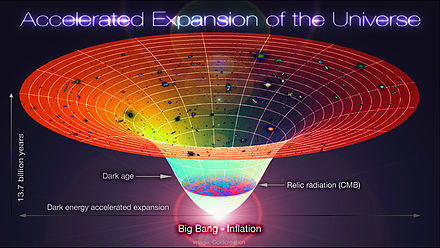
La réintroduction de la constante cosmologique
[modifier | modifier le wikicode]Pour comprendre en quoi l'accélération de l'expansion pose problème, rappelons que l'accélération de l'expansion est donnée par la dérivée seconde du facteur d'échelle. Or, la seconde équation de Friedmann sans constante cosmologique nous donne justement cette dérivée seconde, qui vaut :
La densité et la pression sont forcément positives pour la matière et le rayonnement, le terme entre parenthèses est donc positif, ce qui fait que la dérivée seconde est négative en raison du signe moins. Et un négatif signifie que l'expansion décélère.
Pour résoudre le problème, les physiciens ont ressorti la constante cosmologique du placard. On peut rendre compte de l'accélération de l'expansion assez facilement en réutilisant les équations de Friedmann avec une constante cosmologique. Pour rappel, il s'agit des deux équations suivantes :
L'accélération de l'expansion est donnée par la seconde équation, avec la dérivée seconde du facteur d'échelle. On peut remarquer que cette équation ne contient pas de terme de courbure. En effet, la courbure cause une expansion constante, linéaire, sans accélération ni décélération. Et vu que le terme s'additionne aux autres termes, il n'a pas d'effet sur l'accélération de l'expansion, juste sur la vitesse de l'expansion. Par contre, la constante cosmologique apparaît comme un terme positif, qui permet de faire passer la dérivée seconde au-dessus de zéro. Le terme de densité est positif, ce qui donne une décélération. La dérivée seconde est positive sous la condition suivante :
- Il est en théorie possible de rendre le terme de densité négatif en faisant des hypothèses hardies, comme une matière à pression négative, mais cela serait équivalent à une constante cosmologique.
L'univers dominé par la constante cosmologique
[modifier | modifier le wikicode]Étudions maintenant le cas d'un univers avec une constante cosmologique, mais sans matière, ni rayonnement, ni courbure, ni quoique ce soit d'autre. Un tel univers hypothétique est appelé un univers de De Sitter. Sous ces hypothèses, les équations de Friedmann deviennent celles-ci :
Tous les paramètres de cette équation, , c et les autres, sont tous constants, ce qui fait que le facteur de Hubble l'est aussi. Le fait que le facteur de Hubble est constant est à la base des développements mathématiques qui vont suivre.
La constance du facteur de Hubble a des conséquences assez intéressantes, qui peuvent se déduire de la définition du facteur de Hubble. Pour rappel, la définition du facteur de Hubble en fonction du facteur d'échelle donne :
Multiplions par des deux côtés :
Intégrons sur :
Dans le premier terme, H est une constante, ce qui donne :
Dans le second terme, l'intégrale n'est autre que l'âge de l'univers. Dans ce qui suit, nous noterons l'âge de l'univers . Le calcul de l'intégrale de droite donne :
Prenons l'exponentielle des deux côtés :
En injectant l'équation , on a alors :
Dans ce modèle, le facteur d'échelle suit une relation exponentielle avec le temps. Il s'agit donc d'un cas particulier de modèle à croissance exponentielle, ces derniers ayant déjà été abordés dans le chapitre "Une introduction aux modèles cosmologiques". Tout ce qui a été dit sur ces modèles peut donc s'adapter à ce modèle d'univers dominé par la constante cosmologique. Par exemple, leur facteur de décélération est toujours positif, égal à -1. Un tel univers va donc une croissance exponentiellement croissante, ce qui est beaucoup plus rapide que dans les deux prochains modèles, où la croissance est plus lente. Ce plus, on sait aussi qu'un tel l'univers a un âge infini : vu qu'une exponentielle ne peut être nulle, le facteur d'échelle et le volume de l'univers ne peuvent pas être nuls. Dit autrement : la singularité initiale est totalement évitée !
Les univers vides, avec constante cosmologique et courbure
[modifier | modifier le wikicode]Évidemment, le modèle précédent est irréaliste car l'univers contient aussi de la matière et du rayonnement. Mais le cas général n'a pas de solutions analytiques et il faut recourir à des calculs sur ordinateurs. Les rares solutions analytiques sont connues dans le cas d'un univers vide, à savoir sans matière ni rayonnement, mais avec une courbure positive ou négative. Dans les équations de Friedmann, il suffit de poser que la densité et la pression sont nulles. Sous ces conditions, l'équation du fluide disparaît et les deux autres équations de Friedmann deviennent alors :
- La disparition de l'équation du fluide est assez simple à comprendre. Cette équation décrit comment la matière et le rayonnement sont dilués par l'expansion. Mais sans matière et rayonnement, il n'y a rien à diluer avec l'expansion, et donc cette équation devient inutile. La dilution de la matière et du rayonnement avec l'expansion n'existant pas, on devine que cela a des conséquences sur la dynamique de l'expansion.
Résoudre ces équations dans le cas général, avec une courbure non-nulle et une constante cosmologique, est assez difficile et donne des équations relativement complexes. Mais il est beaucoup plus facile d'obtenir des résultats simples dans le cas où la courbure vaut soit 1, soit 0, soit -1. On obtient alors les résultats suivants :
L'énergie noire
[modifier | modifier le wikicode]Pour expliquer l'accélération de l'expansion, il existe une solution alternative à la constante cosmologique. Elle part du principe que les équations de Friedmann du chapitre précédent sont valides, mais que l'univers est empli d'une forme de matière/énergie aux propriétés particulières. Précisément, l'équation d'état est calibrée de manière à ce que la seconde équation de Friedmann donne une expansion accélérée.
Pour cela, prenons la seconde équation de Friedmann et posons la condition que l'univers soit en expansion. On a alors :
En simplifiant, on trouve :
Cette condition est remplie si et seulement si :
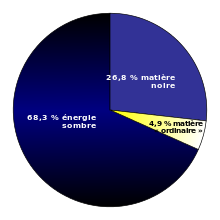
En clair, l'univers peut être en expansion à condition que l'univers contienne quelque chose qui a une densité positive, mais une pression négative. Ce quelque chose, ils l'ont appelé l'énergie noire. Cette énergie noire assez mal connue serait quelque chose de physique, qui contient une certaine densité d'énergie, sous la forme de masse et de pression. Mais les caractéristiques de cette énergie noire font qu'elle ne se comporte pas comme de la matière ordinaire ou du rayonnement. Les observations semblent indiquer que 30% de l'univers est composé de matière, tandis que le reste de la densité d'énergie est intégralement composé d'énergie noire.
Les propriétés de l'énergie noire
[modifier | modifier le wikicode]L'énergie noire a une masse positive, mais a aussi une pression négative. Or, la relativité générale nous dit que la pression est une forme d'énergie, qui a donc un effet gravitationnel. Dans cette théorie, toute énergie a un poids, une sorte de masse fictive, et la pression ne fait pas exception. Mais pour la matière ordinaire, la pression est positive, c'est à dire qu'elle a un effet gravitationnel normal, similaire à une masse positive. Elle a donc tendance à ralentir l'expansion, dans une certaine mesure. Mais l'énergie noire a une pression négative, ce qui est particulièrement original (même si on observe des phénomènes similaires dans certains cristaux ou lors de changements de phases). Du point de vue de la relativité générale, une pression négative implique un effet anti-gravitationnel, une attraction gravitaire dirigée vers l'extérieur. En clair, elle agit comme une force répulsive qui contrecarre la gravité et augmente l'expansion au lieu de la ralentir.
L'énergie noire se caractériserait par une densité constante au cours du temps, même en tenant compte de l'expansion de l'univers. La constance de la densité d'énergie noire a une conséquence assez intéressante : la densité étant constante, le facteur de Hubble est constant lui aussi. On peut remarquer que cela implique que l'énergie de l'univers ne se conserve pas, vu que cette densité constante est couplée à une augmentation du volume de l'univers par l'expansion.
Les scientifiques ont tenté d'expliquer cette énergie noire de plusieurs manières. La tentative la plus connue se base sur une prédiction assez singulière de la théorie quantique des champs., à savoir que le vide est censé être rempli d'une énergie appelé énergie du vide. C'était le candidat idéal pour expliquer l'énergie noire, jusqu'à ce que les calculs montrent que l'expansion mesurée implique une énergie du vide près de fois plus grande qu'observée. Ce résultat est aujourd'hui considéré comme la "pire prédiction théorique de l'histoire de la physique".
Il faut préciser que l'énergie noire et la constante cosmologique sont quasiment équivalentes en terme d'équation de Friedmann. La constante cosmologique est équivalente à une énergie noire d'équation .
Énergie noire et équations de Friedmann
[modifier | modifier le wikicode]La constante de la densité d'énergie noire permet de simplifier la première équation de Friedmann, en utilisant la densité d'énergie noire .
Rappelons que la densité de matière, de rayonnement et de courbure suivent les relations suivantes : , et . En substituant dans l'équation de Friedmann, on trouve :
Par définition, . En faisant le remplacement dans l'équation précédente et en faisant quelques manipulations algébriques, on trouve :
On multiplie par :
À l'heure actuelle, la constante cosmologique n'est qu'un paramètre ad-hoc qui permet de faire coller prédictions théoriques et observations. On ne connaît pas encore son origine, même si les physiciens ont quelques pistes. L'interprétation de ce terme varie suivant les physiciens.
Il est possible de reformuler la première équation de Friedmann avec le paramètre de densité, à savoir le rapport entre la densité réelle et la densité critique obtenue quand on considère un univers de courbure nulle.







































