La politique monétaire/Version imprimable

La politique monétaire

Une version à jour et éditable de ce livre est disponible sur Wikilivres,
une bibliothèque de livres pédagogiques, à l'URL :
https://fr.wikibooks.org/wiki/La_politique_mon%C3%A9taire

Vous avez la permission de copier, distribuer et/ou modifier ce document selon les termes de la Licence de documentation libre GNU, version 1.2 ou plus récente publiée par la Free Software Foundation ; sans sections inaltérables, sans texte de première page de couverture et sans Texte de dernière page de couverture. Une copie de cette licence est incluse dans l'annexe nommée « Licence de documentation libre GNU ».

La monnaie

Toutes les civilisations historiques n'ont pas forcément utilisé de monnaie. Par exemple, les hommes de la préhistoire n'avaient pas de pièces et de billets dans leurs poches. La monnaie est une construction sociale, quelque chose que l'humain a inventé pour résoudre certains problèmes sociaux.

Vous avez peut-être entendu dire qu'avant l’invention de la monnaie, le commerce se fondait sur le troc, à savoir l'échange direct d'un objet ou service contre un autre, mais que ses défauts auraient favorisé son remplacement par la monnaie. En fait, les anthropologues et historiens ne sont pas d'accord avec cette explication, certes intuitive, mais fausse. Aucune société ancienne n'a utilisé massivement le troc comme mécanisme d'échange économique principal. Mais le mythe du troc a cependant une certaine force logique qui fait qu'il est malheureusement assez répandu dans la population générale. Et les manuels d'économie n'aident malheureusement pas, car tout cours sur la monnaie compare la monnaie au troc, pour des raisons pédagogiques. Et nous n'allons pas y échapper.

Les fonctions de la monnaie

Même si le troc n'a jamais été l’échange économique principal, nous allons faire comme si c'était le cas et le comparer à l'échange monétaire (basé sur la monnaie). Cela va nous permettre de comprendre assez simplement pourquoi la monnaie existe et surtout : ce qu'est la monnaie. La monnaie a des avantages que le troc n'a pas et sont ces avantages qui définissent ce qu'est la monnaie. La monnaie remplit trois grandes fonctions par rapport au troc, qui portent les noms barbares d'intermédiation des échanges, de réserve de valeur et d'unité de compte. Voyons cela en détail.

La monnaie comparé au troc

Le problème principal du troc est que l'échange suppose que chaque participant ait quelque chose d'utile à l'autre. Ainsi, si quelqu'un veut échanger des moutons avec un fermier, il faut qu'il ait quelque chose qui intéresse le fermier. Si ce n'est pas le cas, il n'y a pas d'échange. C'est le problème de la double coïncidence des biens. Et ce problème explique pourquoi le troc n'a jamais été utilisé : une situation de double coïncidence est exceptionnelle.

Mais ce problème ne survient pas si on utilise un intermédiaire qui s'échange contre des biens, tout en évitant les problèmes du troc. Les agents économiques peuvent donc échanger un bien/service contre une certaine quantité de cet intermédiaire, qui lui-même peut être échangé plus tard contre un autre bien/service. Tout intermédiaire qui joue ce rôle est qualifié de monnaie, à condition qu'il puisse remplir certaines fonctions bien précises. Cette fonction d'intermédiaire des échanges est une première étape pour être qualifié de monnaie, mais elle n'est cependant pas suffisante.

La première est que l'intermédiaire puisse être conservé sur de longues périodes. Un bien périssable, comme de la nourriture, peut donc difficilement servir de monnaie, quand bien même on pourrait s'en servir comme intermédiaire des échanges. En revanche, un métal comme l'or, qui met énormément de temps avant de se dégrader, est apte à servir de support pour de la monnaie. Cette fonction de réserve de valeur permet notamment de différer ses paiements.

Ensuite, l'intermédiaire doit servir d'unité de compte, dans le sens où il permet d'établir un système de prix qui donne de la valeur aux biens vendus ou achetés.

La monnaie face aux actifs (non-)financiers

Pour résumer, une monnaie est quelque chose qui sert à la fois d'intermédiaire des échanges, de réserve de valeur, et d'unité de compte. Le troc, quant à lui, n'a ni intermédiaire des échanges, ni réserve de valeur, ni unité de compte. Il est donc l'opposé total de la monnaie, ce qui fait qu'on vient de comparer la monnaie au troc en guise d'introduction. Mais entre la monnaie et le troc, il existe de nombreux instruments intermédiaires, comme l'or, les crypto-monnaies, et bien d'autres encore. Certains servent d'intermédiaire des échanges, mais sont de terribles réserves de valeur (les crypto-monnaies aux cours fluctuants sont de bons exemples), d'autres sont de bonnes réserves de valeur mais de piètres intermédiaires des échanges (actions, or, immobilier, autres), et j'en passe.

Le cas le plus simple est celui des placements financiers ou immobiliers qui servent de réserves de valeur, mais ne sont pourtant pas de la monnaie, comme les actions, les dettes d'états, les dettes d’entreprises, et j'en passe. De tels supports, qui servent de réserves de valeur sans pour autant être de la monnaie, sont appelés des actifs. Par exemple, un bien immobilier sert de réserve de valeur, dans le sens où sa valeur de revente a peu de chances de diminuer au cours du temps (même si cela reste possible en cas de crise immobilière). Mais l'immobilier n'est pas un intermédiaire des échanges : on n'échange pas des maisons pour s'acheter du pain.

Comme exemple d'actif, on pourrait citer l'or, qui est utilisé comme placement, comme réserve de valeur, mais qui ne sert plus d’intermédiaire des échanges. Si autrefois l'or était utilisé pour les paiements, ce n'est plus le cas aujourd'hui. Par contre, l'or garde une valeur relativement constante, ce qui fait qu'il est parfois utilisé comme placement (risqué, mais supposé protégé de l'inflation).

Les différentes formes de monnaie

Au cours des âges, la monnaie a évolué de formes relativement simples à des formes de plus en plus complexes et abstraites. Il est donc utile de voir quelles sont les différentes formes de la monnaie, qu'il s’agisse des formes anciennes ou des formes que vous utilisez tous les jours. Et à ce petit jeu, il s'est passé pas mal de choses avant l'invention des pièces et des billets. Sans rentrer dans les détails, il est important de distinguer les monnaies historiques basées sur la valeur d'un bien (du métal, comme l'or, l'argent), des monnaies basées purement sur la confiance.Cette distinction permet de séparer les monnaies marchandise des monnaies fiduciaires. Détaillons cela, en commençant par la forme de monnaie la plus ancienne, puis en suivant par les monnaies fiduciaires.

Les formes historiques

La première forme de monnaie utilisait une marchandise particulière, comme le blé ou le sel, qui servait de monnaie : on parle de monnaie marchandise. Cet intermédiaire était souvent composé de biens consommables ou utiles : céréales, alcool, sucre, etc. Mais pour d'autres civilisations, cet intermédiaire était composé d'objets inutiles et sans valeur, comme des coquillages, des dents d'animaux ou des pierres. Par exemple, certaines tribus utilisaient de l'obsidienne, une roche volcanique noire et vitreuse.

Plus tard, les hommes inventèrent la monnaie métallique, composée de pièces de monnaies forgées dans un métal précieux comme l'or ou l'argent. La valeur des pièces dépendait de la quantité de métal précieux qu'elles contenaient. Les premières pièces en métal ont été réalisées par le roi de Lydie, Gygès, en 687 avant Jésus-Christ. Et ce fut le début d'une longue série, les empires romains et chinois commençant à utiliser de plus en plus de monnaie.

Ce système fonctionna longtemps, plusieurs siècles, avant de cesser. En effet, l'économie dépendait de la valeur de l'or, qui elle-même dépendait des stocks d'or. La quantité de monnaie en circulation dépendait des stocks d'or extraits des mines et gisements. La monnaie était donc une quantité relativement fixe, qui n'augmentait que très lentement avec les extractions des mines et gisements. La découverte d'un gros gisement d'or augmentait fortement la quantité d'or en circulation et faisait donc varier la valeur de la monnaie : la monnaie se dévaluait, elle perdait de sa valeur. Voilà une chose assez curieuse pour une construction sociale : dépendre d'un paramètre physique réel…

La monnaie fiduciaire

Par la suite, cette contrainte fut progressivement relâchée : la valeur d'une monnaie ne dépendait plus de la valeur du métal qui composait la pièce. La monnaie fiduciaire correspond à l'ensemble des billets de banques et des pièces qui ne fondent plus leur valeur sur une quantité de métal mais sur la confiance que lui accordent ses usagers : si ceux-ci refusent d'utiliser votre monnaie, elle ne vaut plus rien. Lors de crises économiques particulièrement graves, certaines monnaies n'ont plus la confiance du public et les vendeurs refusent les paiements dans cette monnaie : soit une monnaie étrangère est utilisée, soit le troc reprend ses droits.

Mais outre les billets et pièces, d'autres formes d'argent existent. Quand vous allez à la banque, vous pouvez faire des transferts entre comptes bancaires, être payé sans recevoir directement l'argent et ainsi de suite. L'argent n'est alors qu'une simple fiction informatique, une somme mémorisée dans un ordinateur ou un livre de compte à l'intérieur de la banque. Cela correspond à l'argent sur vos comptes bancaires, par exemple. De telles formes de monnaies sont appelées des monnaies scripturales. Cette forme de monnaie est la plus importante de nos jours, au point de représenter 90 % de la quantité totale de monnaie en circulation dans la zone Euro, les espèces se limitant aux 10 % restants.

Les agrégats monétaires

Mesurer la quantité totale d'argent en circulation dans l'économie est assez compliqué. Il faut dire que cet argent peut être placé sur divers types de supports, qu'il s'agisse de comptes courants, de livrets bancaires, ou d'autres types de placements. Mesurer la quantité d'argent stockée ou en circulation est assez difficile, surtout quand on prend en compte la monnaie fiduciaire. Pour en faire la mesure, il existe plusieurs instruments statistiques, qui permettent de mesurer certaines formes de monnaies. Ils portent le nom d'agrégats monétaires. Ceux-ci sont définis par leur liquidité, à savoir la facilité à les utiliser dans les transactions. Les supports faiblement liquides sont difficiles à transformer en pièces ou billets, cette transformation pouvant prendre du temps. À l'inverse, les supports fortement liquides sont très simples à transformer en monnaie, la transformation étant très rapide. Voyons un peu dans le détail quels sont ces agrégats.

Les deux agrégats monétaires les plus simples sont appelés la masse monétaire et la base monétaire. Ils correspondent à deux concepts bien différents. La quantité totale de monnaie en circulation dans l'économie porte le nom de masse monétaire. Elle correspond à la monnaie qui peut circuler de main en main, celle qui peut servir pour les transactions. À l'inverse, la base monétaire correspond majoritairement à de la monnaie conservée par les banques, dans leurs coffres ou sur leurs comptes. Là où le public peut utiliser la masse monétaire pour les transactions, la base monétaire correspond à de l'argent dormant à l'intérieur des banques, ainsi qu'aux espèces en circulation.

La masse monétaire

L'argent stocké sur des comptes à la banque est soit de la monnaie scripturale, soit des espèces qu'elle place dans ses coffres. Si vous avez déjà un compte bancaire, vous savez sûrement que certains comptes ne sont pas rémunérés : ce sont les comptes courants. L'avantage de ces comptes est que l'argent peut être retiré à tout moment, contrairement aux comptes d’épargne : l'argent de ces comptes peut être transformé en billets ou en pièces que vous pouvez retirer au distributeur. Dans la comptabilité nationale, la somme des dépôts, des pièces et billets forme de que l'on appelle l'agrégat monétaire M1.

En plus de ces comptes courants, vous pouvez avoir des comptes d’épargne qui sont rémunérés : tous les mois ou tous les ans, la banque verse des intérêts sur ces comptes. Cependant, la majorité d'entre eux demande que l'argent soit immobilisé durant quelques mois ou années et il ne peut pas être retiré à tout moment. La liquidité de ces comptes, à savoir la facilité de retrait, est donc inférieure à celle des comptes courants. Généralement, plus le taux d'intérêt est élevé, plus la liquidité sera faible. L'agrégat M2 prend en compte une partie de ces comptes d'épargne. Plus précisément, il prend en compte les comptes bancaires/livrets dont on peut récupérer le contenu en moins de 3 mois. Des livrets bancaires, tels les livrets A et autres supports à fortes liquidité, peuvent techniquement être considérés comme de la quasi-monnaie et font partie de cet agrégat. L'agrégat M2 prend aussi en compte les dépôts à terme, aussi appelés comptes à termes, tant que ceux-ci ont une maturité inférieure à 2 ans.

Enfin, il faut prendre en compte l'argent placé sur des fonds d'investissements monétaires, ainsi que d'autres formes d'investissement monétaire moins liquides et plus rentables. Typiquement, on pourrait citer les SICAV ou OPCVM monétaires, les certificats de dépôt, et les obligations/créances inférieures ou égale à deux ans. C'est le rôle de l'agrégat M3.

La base monétaire

À côté de ces agrégats, on peut aussi citer la base monétaire, un agrégat assez difficile à appréhender, mais dont nous parlerons beaucoup dans certains chapitres de ce cours. Pour faire simple, c'est la somme des espèces en circulation et de l'argent que les banques conservent. Les banques peuvent décider de conserver leur argent sous deux formes : soit sous la forme d'espèces dans leurs coffres, soit sous la forme de réserves bancaires, aussi appelées dépôts banque centrale.

Ces dernières correspondent, comme leur nom l'indique, à l'argent que les banques commerciales conservent à la banque centrale. En effet, les banques peuvent choisir de déposer de l'argent à la banque centrale, sur des comptes courants dédiés. Elles s'en servent surtout pour y stocker de la monnaie électronique, le stockage de monnaie physique à la banque centrale étant tombé en désuétude. Les banques commerciales peuvent conserver des réserves à la banque centrale pour plusieurs raisons : parce qu'elles sont obligées par la loi d'y placer un certain montant, parce qu'il s'agit d'un placement intéressant en terme de rendement/sécurité, ou parce qu'elles le souhaitent pour d'autres raisons. Les réserves en question regroupent à la fois l'argent physique stocké dans les coffres de la banque centrale, et les dépôts sous forme électronique. Si on consolide le tout, on voit que la base monétaire est la somme des espèces, sous toutes leurs formes, pièces et billets, et des réserves bancaires.

Base monétaire = Espèces + Dépôts électroniques à la banque centrale = Espèces en circulation + Réserves bancaires ( Espèces conservées par les banques commerciales + Dépôts à la banque centrale ).

Base et masse monétaires, octobre 2009.

Les taux d'intérêts

Pour rappel, les taux d'intérêts servent soit à exprimer le rendement d'un placement, soit à donner le coût d'un emprunt. Un emprunteur doit payer des intérêts mensuels ou annuels à la banque préteuse, alors que les placements sont rémunérés avec un intérêt régulier. La monnaie n'offre qu'un faible taux d'intérêt, quand celui-ci n'est pas tout simplement nul. Si la monnaie sur un livret d'épargne a un taux d'intérêt non-nul, ce n'est pas le cas pour des pièces et des billets. Mais dans tous les cas, le taux est très faible comparé aux autres instruments financiers (obligations, actions...). Ces taux d'intérêts ont une place particulièrement importante dans l'étude de la politique monétaire. D'ailleurs, nous verrons dans quelques chapitres que les banques centrales utilisent beaucoup le contrôle des taux d'intérêts pour implémenter leur politique monétaire. C'en est à tel point que les théories macroéconomiques actuelles sont presque exclusivement basées sur l'étude des taux et non sur l'analyse des agrégats monétaires ! Autant dire que nous aurons besoin de bien comprendre ce que sont les taux d'intérêts avant de poursuivre ce cours. D'où la présence de ce chapitre.

Les taux réels

En premier lieu, nous devons parler de l'influence de l'inflation, la hausse généralisée des prix, sur les taux d'intérêts. Rappelons que l'inflation $\pi$ est la variation en pourcentage du prix moyen $P$ : $\pi ={\frac {\Delta P}{P}}$. Le taux réel est un taux d'intérêt corrigé de l'inflation, à savoir le rendement réel d'un intérêt quand on élimine l'effet de l'inflation sur le pouvoir d'achat. Nous allons d'abord commencer par voir quelle est sa valeur exacte, avant d'en fournir une approximation plus simple à utiliser.

La définition mathématique du taux réel

Partons d'un exemple. Supposons que vous investissiez/épargnez une somme d'argent $A$, rémunérée au taux d'intérêt $i$. Ce taux n'est pas corrigé de l'inflation, ce qui fait qu'il est appelé le taux nominal. Vous toucherez, intérêt compris, la somme de : $A\times (1+i)$. Cependant, ce taux nominal est un mauvais indicateur du rendement réel, corrigé de l'inflation. En effet, rien ne sert d'investir à 2% si l'inflation est de 15%. Durant la durée de votre investissement, les prix ont augmenté au même rythme que l'inflation $\pi$, à savoir qu'ils ont été multipliés par $(1+\pi )$. Si on compare l'avant et l'après en termes de biens ou de services que l'on peut acheter, on a :

Avant l'investissement : $A \over P$ ; Après le versement des intérêts : $A\times (1+i) \over P\times (1+\pi )$.

Si on compare le nombre de biens $N$ que l'on peut acheter avant ($N_{t}$) et après ($N_{t+1}$), on trouve que le rendement corrigé de l'inflation $r$ vaut :

$1+r={\frac {1+i}{1+\pi }}$

Soustrayons 1 des deux côtés.

$r={\frac {1+i}{1+\pi }}-1$

Notons que $1={\frac {1+\pi }{1+\pi }}$ et faisons le remplacement :

$r={\frac {1+i}{1+\pi }}-{\frac {1+\pi }{1+\pi }}$

Regroupons les deux termes à droite.

$r={\frac {(1+i)-(1+\pi )}{1+\pi }}$

Puis simplifions :

$r={\frac {i-\pi }{1+\pi }}$

L'équation de Fisher des taux d’intérêt

L'équation précédente n'est cependant pas facile à utiliser. Heureusement, il existe une approximation particulièrement pratique, que nous allons démontrer dans ce qui suit. Pour cela, partons de l'équation précédente :

$1+r={\frac {1+i}{1+\pi }}$

Reformulons-la comme suit et développons :

$1+i=(1+r)\times (1+\pi )=1+r+\pi +r\times \pi$

Soustrayons 1 des deux côtés de l'équation :

$i=r+\pi +r\times \pi$

Si on part du principe que l'inflation et le taux nominal sont tout deux faibles, le terme $r\times \pi$ peut être négligé, ce qui donne :

$i\approx r+\pi$

Dit autrement, le taux nominal est à peu près égal à la somme de l'inflation et du taux d'intérêt réel (corrigé de l'inflation). Cette formule vaut aussi bien pour les taux réels anticipés que les taux obtenus.

L'origine des taux d'intérêts

Les taux d'intérêts ne sortent pas de nulle part et il est important de comprendre leur origine pour la suite. Plusieurs "théories" tentent d'expliquer cela et nous n'allons pas toutes les citer, certaines étant très techniques et dépassant le cadre de ce chapitre. Dans ce chapitre, nous allons voir les trois suivantes : la théorie des fonds prêtables, la théorie classique et la théorie de la préférence pour la liquidité de Keynes.

La théorie des fonds prêtables

Rencontre entre offre et demande de fonds prêtables.

La théorie des fonds prêtables explique les taux d'intérêts par la rencontre de l'épargne avec les besoins des emprunteurs. Les emprunteurs et les préteurs se mettent en relation par l'intermédiaire des établissements de crédit, des banques, des caisses d'épargne, et tout autre intermédiaire financier. Les emprunteurs et préteurs échangent de l'argent, des liquidités, en échange d'une reconnaissance de dette (un contrat de prêt, une obligation d'état ou d'entreprise, peu importe). Dit autrement, il existe une offre de liquidités de la part des préteurs et une demande de la part des emprunteurs. Et la rencontre cette offre et cette demande entraîne l'apparition d'un prix d'équilibre, qui n'est autre que le taux d'intérêt, le "loyer" de l'argent.

L'offre de liquidités provient des préteurs, alors que la demande vient des emprunteurs. Cela parait intuitif, mais cela aurait parfaitement pu être l'inverse. Rappelons que déterminer qui est l'offre et qui est la demande implique d'étudier la variation des quantités en fonction des prix. Ici, il s'agit d'étudier comment emprunt et épargne évoluent en fonction des taux.

• Il existe une relation entre taux et montant des emprunts : des taux élevés rendent l'emprunt coûteux et défavorable, alors que des taux faibles le rendent plus sûr et plus rentable. La relation entre emprunt et taux est donc décroissante, ce qui traduit le fait qu'il s'agisse d'une courbe de demande.
• À l'inverse, la courbe qui relie épargne et taux est croissante, ce qui trahit le fait que c'est une courbe d'offre. En effet, les taux sont le rendement de l'épargne : plus ils sont élevés, plus l'épargne est intéressante. Des taux élevés vont alors inciter les agents économiques à épargner, quitte à réduire un peu leur consommation.

Maintenant, étudions ce qui se passe quand la demande ou l'offre varie, en commençant par la demande. Imaginons que la demande d'emprunt augmente, peu importe la raison. La courbe de demande est alors déplacée vers la droite, ce qui donne une augmentation des taux. De nombreux emprunteurs vont venir sur le marché des capitaux et une partie sera prête à payer des taux élevés pour leur emprunt. Les préteurs vont de préférence prêter aux agents qui acceptent de payer plus cher que les autres, le taux d'intérêt va donc augmenter. La situation est inverse si la demande d'emprunt baisse : la courbe de demande se déplace vers la gauche, de qui donne une baisse des taux. Ce qui se passe est que les préteurs n'ont pas d'autre choix que de prêter leur argent à des taux plus bas, le vivier d'emprunteurs à fort taux se tarissant.

Le cas où l'offre de fonds prêtables diminue ou augmente est assez similaire, avec cependant quelques différences notables. Une augmentation de ceux-ci se traduit par un déplacement vers la droite de la courbe d'offre, alors qu'une réduction donnera un décalage vers la gauche. Cela donne respectivement une baisse ou une hausse des taux. Prenons le cas où l'offre augmente. Le surplus sera alors prêté à de nouveaux emprunteurs. Vu que les emprunteurs à fort taux ont déjà étés servis par les fonds précédents, il ne reste que des emprunteurs à taux plus faibles sur le marché. Les préteurs n'ont pas le choix que de prêter à des taux plus bas et le taux ne peut que baisser. Une pénurie de fonds prêtables a l'effet inverse : l'épargne devenant rare, seuls les emprunteurs qui payent le plus cher seront servis. Ce qui se traduit par des taux élevés.

La théorie classique des taux d'intérêts

Rencontre entre offre et demande de fonds prêtables.

La théorie classique des taux d'intérêts peut être vu comme un cas particulier du précédent. Dans le cadre de la théorie classique, on suppose que la demande d'emprunt est une demande d'investissement, alors que l'offre n'est autre que l'épargne. Notez qu'on fait deux hypothèses : en premier, on confond investissement et emprunt, en second, on confond épargne et offre de fonds prêtables. Avec ces hypothèses, le modèle offre-demande devient un modèle où une demande d'investissement rencontre une offre d'épargne. Le prix qui découle de la rencontre offre-demande est le taux d'intérêt réel, non le taux nominal.

À l'équilibre, l'investissement réalisé est égal à l'épargne effective, du fait de la rencontre offre-demande. On a donc :

$I=S$, avec I l'investissement et S l'épargne (Savings en anglais).

Petite remarque : cette identité a donné son nom à la courbe IS (courbe Investment-Savings), que nous aborderons plus tard dans ce cours.

Il existe divers moyens de démontrer cette égalité, en utilisant des définitions comptables du PIB, mais elles posent quelques problèmes d'interprétation assez forts. Mais nous reparlerons de tout cela dans le chapitre sur le canal des taux d'intérêt.

Notons que ces deux hypothèses, à savoir les égalités emprunt-investissement et épargne-prêt, sont critiquables et ne sont valables que sous certaines conditions.

• Premièrement que tout emprunt soit utilisé pour financer un investissement. Ce n'est pas le cas en pratique : beaucoup de crédits accordés par les banques sont des découverts bancaires, des facilités de trésorerie ou des prêts à la consommation. Néanmoins, une portion non-négligeable de la demande d'emprunts provient de l'investissement des ménages, mais aussi des entreprises et de l'état : les entreprises achètent des machines ou des outils de production, les états empruntent pour des dépenses d'infrastructure, les ménages achètent des maisons (ce qui est une forme d'investissement), etc. Il n'est donc pas si stupide de confondre investissement et emprunt.
• Ensuite, il faut que les emprunts soient financés par une épargne préexistante , ce qui là encore est faux. On verra dans la suite de ce cours que toute l'épargne n'est pas prêtée par les banques, pour plusieurs raisons. Déjà, une partie est thésaurisée, ce qui veut dire qu'elle n'est pas placée dans les banques et est conservée sous forme d'espèce ou d'autres instruments. De plus, les banques doivent conserver une partie de l'épargne sous la forme de réserves bancaires, qui ne sont pas prêtées. Enfin, il faut aussi prendre en compte la création monétaire, la capacité qu'ont les banques à créer de la monnaie (ce qui fera l'objet de plusieurs chapitres futurs). Mais là encore, faisons abstraction de cela et oublions la thésaurisation et les réserves bancaires.

La théorie de la préférence pour la liquidité

Illustration de la théorie de la préférence pour la liquidité de Keynes.

La théorie de la préférence pour la liquidité de Keynes est une théorie assez complexe, que nous survolerons ici. Nous la détaillerons dans les chapitres de fin du cours, pour des raisons pédagogiques. Pour simplifier, cette théorie dit que les agents économiques font un arbitrage entre monnaie et autres actifs. Les agents économiques peuvent répartir leur richesse entre monnaie, obligations, actions, immobiliers et autres biens durables.

Par souci de simplicité, nous n'allons prendre en compte que deux types d'actifs : la monnaie proprement dite et les obligations. La monnaie ne rapporte pas d'intérêt (ou alors très peu), alors que les autres actifs peuvent verser un intérêt parfois important. En contrepartie, la monnaie est parfaitement liquide alors que les autres actifs ne le sont pas. Faire un virement est beaucoup plus facile que vendre un actif sur un marché boursier. Les agents font donc un arbitrage entre le fait de recevoir un intérêt et abandonner la liquidité de leur argent. Le taux d'intérêt est donc le prix à payer pour que les agents abandonnent la liquidité de la monnaie. En terme technique, il s'agit du coût d'opportunité de la possession de monnaie, à savoir le coût que l'on pourrait avoir si cette monnaie était convertie sous la forme d'actifs. Plus ce coût d'opportunité est élevé, plus les actifs sont favorisés par rapport à la monnaie.

Les ménages souhaitent détenir une partie de leur épargne sous la forme de monnaie, le reste étant sous la forme d'actifs rémunérés illiquides. La quantité de monnaie que les agents économiques souhaitent détenir est influencée par les taux d'intérêts. Si les taux sont élevés, les agents préfèrent conserver leur fortune sous la forme d'actifs, qui versent un intérêt. Mais si les taux sont trop bas, le rendement des actifs ne compense pas leur illiquidité et les agents vont préférer la monnaie. En clair, plus les taux sont élevés, plus les agents mettent leur argent dans des obligations et moins ils ont de monnaie. Si on trace la masse monétaire en fonction des taux d'intérêt, on voit que celle-ci forme une courbe, appelée courbe de demande de monnaie et notée $M_{d}$. Pour résumer, la masse monétaire est une fonction décroissante des taux.

Sur le marché des capitaux, la demande de monnaie rencontre une offre de monnaie, qui n'est autre que la quantité totale de monnaie en circulation dans l'économie, la masse monétaire. Cette offre est fournie par la banque centrale, qui crée la monnaie quand elle le doit : c'est cette banque qui imprime les billets, fabrique les pièces, crée l'argent fiduciaire, etc. L'offre de monnaie de la banque centrale va donc rencontrer une demande de monnaie de la part des ménages et entreprises. À l'équilibre, offre et demande de monnaie sont égales : $M_{d}=M_{s}$. Or, qui dit équilibre entre offre et demande dit prix, ici le prix qu'il faut payer pour obtenir de la monnaie. Ce prix n'est autre que le taux d'intérêt, ce qui lui vaut parfois le surnom de loyer de l'argent. Le croisement des deux courbes d'offre et de demande donne le taux d'intérêt en fonction de la quantité de monnaie créée par la banque centrale.

Nous reparlerons plus en détail de cette théorie à la fin du cours, dans le chapitre sur la demande de monnaie.

Les liens entre ces théories

Il faut noter que ces théories ont potentiellement des liens entre elles, mais ils sont encore débattus. Tandis que certains économistes voient ces théories comme des approches complémentaires, voire équivalentes, d'autres les pensent totalement incompatibles et irréconciliables. Une explication serait que le taux d'intérêt décrit serait différent pour chaque théorie. Pour rappel, il existe de nombreux taux d'intérêt dans l'économie : le taux directeur des banques centrales les taux de prêts bancaires, les taux de la dette d'état, et j'en passe. Ajoutons à cela qu'il faut aussi distinguer les taux réels et les taux nominaux, ce qui double encore le nombre de taux d'intérêt à prendre en compte.

L'interprétation qu'on retrouve dans beaucoup de livres d'introduction à la macroéconomie, est que les taux nominaux seraient déterminés par la théorie de la préférence pour la liquidité, alors que les taux réels seraient déterminés par la théorie classique et/ou celle des fonds prêtables.

Une autre interprétation serait que chaque théorie explique un marché différent. La théorie de la préférence pour la liquidité expliquerait les taux d'intérêt sur le marché monétaire, un marché où s'échangent des instruments financiers proches de la monnaie papier. Ce marché fait intervenir des prêts entre banques de courte maturité, des prêts de monnaie, des dépôts monétaires à la banque centrale, et quelques autres instruments financiers du genre. Nous reviendrons sur ce marché dans quelques chapitres, vous n'avez pas besoin d'en savoir plus pour le moment, si ce n'est que les taux sur ce marché sont adossés à des prêts à très court-terme : quelques jours, quelques semaines, quelques mois grand maximum. À l'inverse, le marché des fonds prêtables impliquerait des prêts de plus long-terme, comme les prêts bancaires, les prêts immobiliers, les achats de dette d'état, de dettes d'entreprises, etc. On aurait donc la préférence pour la liquidité pour les taux de court-terme sur les instruments liquides, et la théorie des fonds prêtables pour les taux de long-terme.

L'inflation

L'inflation est définie comme l'augmentation de la moyenne des prix. Cette définition possède quelques subtilités qu'il vaut mieux comprendre, pour éviter tout malentendu. Certains prix peuvent varier plus que d'autres, sans que soit un effet concret de l'inflation. Par exemple, de mauvaises conditions climatiques peuvent entraîner une hausse du prix des céréales. Mais ce n'est pas pour autant de l'inflation proprement dit : il s'agit simplement d'une variation sectorielle toute bête, qui ne présume pas de l'évolution des autres prix. En réalité, l'inflation est une variation de la moyenne des prix, au-dessus de laquelle les fluctuations sectorielles s'ajoutent. Pour résumer, l'inflation $\pi$ est la variation en pourcentage du prix moyen.

Il existe diverses méthodes pour mesurer la moyenne des prix : IPC, déflateur du PIB, mais nous n'en parlerons pas ici. À la place, nous allons nous concentrer sur deux choses : quels sont les effets de l'inflation sur l'économie, et quel est son taux optimal. Ces développements seront cruciaux pour les prochains chapitres. Ils permettront notamment de comprendre pourquoi les banques centrales tentent de contrôler l'inflation, mais aussi pourquoi ce rôle est dévolu à la banque centrale.

Les causes de l'inflation

Équilibre entre offre et demande, sur le marché des biens et services.

L'inflation ne sort pas de nulle part, et plusieurs raisons peuvent l'expliquer. Pour comprendre d'où vient l'inflation, il nous faut repartir du modèle de base qui permet d'expliquer l'origine des prix : l'offre et la demande sur le marché des biens et services. Au niveau macroéconomique, la description offre-demande est formalisée mathématiquement dans un modèle appelé modèle AD/AS, illustré ci-contre. Il est aujourd'hui remplacé par des alternatives plus crédibles, mais il est très adapté pour parler des causes de l'inflation, d'où son introduction dans ce chapitre.

Sur le marché des biens et services, les ménages dépensent une certaine somme d'argent, en échange de biens et de services produits par les entreprises. En clair : la demande des ménages acheteurs rencontre l'offre des entreprises vendeuses. La demande et l'offre sont représentées sur le graphique ci-contre par deux courbes. La courbe de demande totale de l'économie est supposée être une fonction décroissance : plus les prix augmentent, moins les ménages achètent. À l'inverse, la courbe d'offre est censée être croissante, convexe : plus les prix sont élevés, plus les quantités vendues augmentent. Le point d'intersection des deux courbes correspond au prix qui satisfait à la fois les acheteurs et les vendeurs, et les quantités vendues correspondantes. Tout mouvement du point d'intersection entraîne une variation du niveau des prix et/ou du PIB, ce qui se traduit par de l'inflation et/ou de la croissance. L'effet exact dépend alors de la forme respective des courbes de demande et d'offre.

Les trois origines de l'inflation

Il y a plusieurs raisons qui peuvent déplacer le point d'intersection : un mouvement de la courbe de demande, ou un déplacement de la courbe d'offre.

• Un mouvement de la courbe de demande est ce qu'on appelle un choc de demande et entraîne une inflation par la demande. Elle traduit le fait que les ménages souhaitent acheter plus de choses, ce qui pousse les entreprises à augmenter leurs prix. Cette forme d'inflation est généralement causée par une augmentation des salaires et/ou une forte réduction du chômage.
• Un déplacement de la courbe d'offre est un choc d'offre, qui cause une inflation par l'offre. Ces chocs d'offre correspondent à une augmentation des coûts de production, que les entreprises doivent répercuter sur les prix. Mais il ne s'agit pas d'une augmentation localisée, circonscrite à une ou quelques entreprises, mais une augmentation globale des prix qui touche la majeure partie des entreprises et toute l'économie. Or, les évènements qui impactent toute l'économie sont généralement des désastres de grande ampleur : une grève générale prolongée, une crise financière, une guerre, une pandémie, un désastre naturel, ou toute autre cause du genre. Comme autre cause, on peut aussi citer une augmentation des prix du pétrole, des difficultés d'approvisionnement énergétique, etc.

Il existe une troisième raison, qui n'est pas immédiatement visible sur ce graphique : l’inflation est anticipée par les agents économiques et ces anticipations sont performatives. Quand les agents économiques anticipent de l'inflation, ils perdent confiance en leur monnaie et vont réagir pour se prémunir de l'inflation. Mais à l'échelle macroéconomique, la somme de ces réactions individuelles va justement induire de l'inflation, soit de l'inflation par la demande, soit de l'inflation par l'offre, soit les deux. Les anticipations de l'inflation vont donc se matérialiser d'elles-mêmes. Nous parlerons plus en détail des anticipations d'inflation dans le prochain chapitre.

Tout ce qu'il faut retenir est qu'il existe trois grandes causes à l'inflation : une augmentation de la demande (inflation par la demande), une augmentation des coûts de production globaux (inflation par l'offre), une inflation dirigée par les anticipations des agents économiques. L'expliquer mathématiquement demande de mettre les courbes de demande et d'offre en équation, à partir d'un modèle macroéconomique crédible. Mais sans même faire appel à ces théories, on peut dire rapidement ce qui détermine la demande et l'offre macroéconomique.

L'inflation par la demande

La demande dépend du revenu total des agents économiques : plus les gens ont d'argent à dépenser, plus la demande augmentera. Le meilleur moyen de doper la demande est d'utiliser la politique monétaire pour créer de la monnaie, ce que peuvent faire les banques centrales. La monnaie, une fois mise en circulation, atterrira dans les mains des agents, qui vont la dépenser pour acheter des biens et services. Cela va donc gonfler la demande et se répercuter en totalité ou en partie sur le niveau des prix. Une forte injection de monnaie dans l'économie va donc entraîner de l'inflation, sauf cas exceptionnels. Dans les grandes lignes, augmenter la quantité de monnaie dans l'économie a un effet stimulant sur l'activité économique et entraîne une augmentation du PIB et/ou de l'inflation. On dit alors que la politique monétaire est une politique monétaire accommodante. Par contre, restreindre la création monétaire freine l'économie : la croissance et l'inflation se font plus faibles. La politique monétaire est alors une politique monétaire restrictive. Les banques centrales actuelles utilisent indirectement la création monétaire pour atteindre leur cible d'inflation et/ou de PIB. La banque centrale utilise une politique restrictive si l'inflation dépasse une cible prédéfinie, alors que sa politique est accommodante si l'inflation est inférieure.

Un autre moyen pour donner de l'argent est d'utiliser la politique fiscale en baissant les impôts ou en augmentant les dépenses gouvernementales. Dans ce cas, c'est l'état qui va mettre de l'argent dans les mains de ses administrés, dopant la demande. Diminuer les impôts et augmenter les dépenses gouvernementales va stimuler la demande, ce qui lui vaut le nom de politique fiscale accommodante, par analogie avec la politique monétaire. L'inverse, à savoir une hausse des impôts et/ou une baisse des dépenses a l'effet inverse et réduit la demande. C'est ce qui lui vaut son nom de politique fiscale restrictive, parfois appelée politique d'austérité. Politiques fiscale et monétaire sont donc symétriques, l'une pouvant subvenir à l'autre. La différence principale est que la politique monétaire n'augmente pas la dette de l'état, ce qui fait qu'elle est privilégiée à l'heure actuelle. Mais sa transmission aux agents économiques est moins directe, ce qui fait qu'elle peut parfois se retrouver inefficace.

Les conséquences de l'inflation

L'inflation a des conséquences assez variées, qui touchent aussi bien les grandeurs macroéconomiques que microéconomiques. À peu près toutes les variables exprimées en monnaie (euros/dollars/autres) sont touchées par l'inflation. Par exemple, les salaires ont tendance à suivre l'inflation, de même que les taux d'intérêts ou les taux de change. On doit alors faire la différence entre les salaires/taux corrigés de l'inflation de ceux qu ne le sont pas. Les premières sont appelées les variables réelles, alors que les variables non-corrigées sont dites nominales. Pour simplifier, les variables nominales sont généralement proportionnelles au niveau général des prix ou à l'inflation. Les variables réelles sont souvent appelées les variables à prix constants, alors que les variables nominales sont dites à prix courants. L'effet de l'inflation dépend alors de son effet sur les variables réelles, qui est bien moins intuitif que ce qu'on pourrait croire.

Dans ce qui va suivre, nous allons voir quels sont les effets de l'inflation sur l'économie. Nous n'allons cependant pas être totalement exhaustifs et allons seulement voir les effets les plus faciles à comprendre, à ce stade du cours. D'autres effets de l'inflation seront vus plus tard dans le cours, dans des chapitres ultérieurs. Par exemple, nous allons voir l'effet de l'inflation sur les taux de change dans des chapitres ultérieurs.

L'effet sur les salaires : une baisse temporaire du pouvoir d'achat

Si on demande quels sont les défauts de l'inflation à une personne lambda, celle-ci dira que l'inflation cause une perte du pouvoir d'achat en rognant les salaires. C'est intuitif : à salaire égal, une hausse des prix réduit le pouvoir d'achat des salaires d'autant. Mais un économiste ne serait pas d'accord avec ce raisonnement. Dans la réalité, l'inflation fait monter tous les prix de l'économie, y compris les salaires et les taux d'intérêts (qui sont respectivement le prix du travail et de l'épargne). Une inflation égale à 5% fera certes monter les prix des biens et services de 5%, mais les salaires vont croître au même pourcentage. En clair, les salaires tendent à suivre l'inflation, même quand ils ne sont pas indexés à celle-ci. L'inflation et les salaires évoluent de la même façon, covarient exactement. L'inflation n’entraîne donc pas de perte de pouvoir d'achat des salaires, quand on regarde les moyennes macroéconomiques.

Du moins, ce n'est vrai que dans une certaine mesure. Les salaires n'évoluent pas immédiatement en fonction de l'inflation. Il existe toujours un petit délai entre une hausse des prix et la hausse des salaires induite. On peut toujours réduire ce temps de réaction en indexant légalement les salaires sur l'inflation. De tels dispositifs étaient autrefois utilisés dans de nombreux pays, mais ont été supprimés suite aux périodes de stagflation des années 1970 (une période où l'inflation élevée était associée à un fort chômage de masse, chose mal comprise à l'époque). De nos jours, les salaires sont réévalués moins fréquemment, et surtout sans trop de lien avec l'inflation. Mais les salaires tendent approximativement à suivre l'inflation, avec un peu plus de retard il est vrai. La perte de pouvoir d'achat induite par l'inflation est donc minime.

Un autre paramètre, beaucoup plus important, tient aux inégalités de salaires. En effet, les raisonnements précédents sont valables quand on regarde la moyenne nationale des salaires. Mais en fait, les salaires sont inégalement distribués. Et l'inflation n'a pas le même effet sur les employés qui touchent bas salaire et sur ceux qui ont un salaire élevé. En effet, les salaires élevés se rencontrent dans les secteurs économiques qui sont au plein emploi, ou presque. Par contre, les bas salaires sont le signe que l'emploi est dans un secteur loin du plein emploi, avec beaucoup de prétendants pour peu de postes. Les hauts salaires ont la capacité de négocier leur salaire et sont les premiers à toucher une augmentation, alors que les bas/moyens salaires n'ont pas de pouvoir de négociation suffisant. Or, lors d'une période d'inflation forte, les hauts salaires seront plus à même de se protéger de l'inflation par des hausses de salaire, voire d'en profiter, alors que les bas salaires verront leurs salaires stagner. L'inflation entraînera donc une baisse de pouvoir d'achat pour les bas salaires, alors que les hauts salaires verront plutôt leur pouvoir d'achat augmenter avec l'inflation. L'inflation entraîne donc un transfert de pouvoir d'achat des bas salaires vers les hauts salaires.

L'effet sur les taux d'intérêts

Rappelons que l'inflation et les taux réels/nominaux sont reliés par l'équation de Fisher, vue il y a quelques chapitres :

$i\approx r+\pi$, avec i le taux nominal et r le taux réel.

Vu que l'inflation n'est pas fixe, on peut se demander comment les taux nominaux et réels réagissent à ses variations. Par exemple, si l'inflation augmente, que va-t-il se passer au niveau des taux nominaux : vont-ils rester les mêmes ou augmenter ? Pour répondre à cette question, on peut dériver l'équation de Fisher par rapport à l'inflation, ce qui donne :

${\frac {di}{d\pi }}\approx {\frac {dr}{d\pi }}+{\frac {d\pi }{d\pi }}=1+{\frac {dr}{d\pi }}$

Tout dépend alors du terme ${\frac {dr}{d\pi }}$, qui traduit la variation du taux réel en fonction de l'inflation. Globalement, il y a trois cas, que nous allons voir de suite.

Le cas le plus simple est celui où les taux réels ne dépendent pas de l'inflation. Cette hypothèse se traduit mathématiquement par la formule suivante ${\frac {dr}{d\pi }}=0$, grâce à laquelle l'équation précédente devient : ${\frac {di}{d\pi }}\approx 1$. Dit autrement, les taux nominaux varient de la même manière que l'inflation. Une augmentation de 1% de l'inflation se traduit par une hausse identique des taux nominaux, alors que les taux réels restent les mêmes. Mais ce cas simple n'est cependant pas vraiment réaliste. Il est valable sur le très long-terme, c’est-à-dire qu'il s'agit d'un comportement moyen sur de longues périodes de temps. En réalité, tout dépend de la manière dont la banque centrale fixe ses taux nominaux (et indirectement les autres taux nominaux dans l'économie).

Le second cas est celui où les taux réels sont influencés par l'inflation. C'est la situation courante dans les pays développés où la banque centrale influence les taux réels en suivant une sorte de règle assez stricte, appelée règle de Taylor, pour des raisons que nous expliquerons dans quelques chapitres. Pour faire simple, cette règle dit que les taux réels doivent varier dans le même sens que l'inflation : si l'inflation augmente, la banque centrale augmente les taux réels, et inversement pour une baisse. Pour cela, les taux nominaux doivent augmentent plus vite que l'inflation (même chose pour une baisse). Les variations des taux nominaux sont en quelque sorte plus amples que les variations de l'inflation. En clair, le taux nominal et le taux réel tendent tous deux à suivre l'inflation et à covarier avec elle. On a donc : ${\frac {dr}{d\pi }}>0$, ce qui donne ${\frac {di}{d\pi }}>1$.

Le dernier cas est celui où les taux nominaux sont fixes. Une situation assez réaliste est celle où les taux nominaux tombent à 0. La banque centrale ne peut alors pas les baisser plus et on se retrouve avec des taux nominaux fixes. Une autre situation est celle où la banque centrale fixe les taux nominaux, mais ce cas est irréaliste comparé au précédent (pour le moment, aucune banque centrale n'a mis en œuvre une telle politique). Dans les deux cas, on a : ${\frac {di}{d\pi }}=0$, ce qui donne ${\frac {dr}{d\pi }}=-1$. Cela veut dire que les taux réels varient en sens inverse de l'inflation (le signe -) et dans les mêmes proportions (une variation de 1% de l'inflation entraîne une variation de 1% des taux réels).

L'effet sur les crédits : un allègement de certains crédits

On dit qu'une hausse de l'inflation allège le poids des crédits et emprunts, mais cela n'est pas forcément le cas. En réalité, tout dépend de l'effet de l'inflation sur les taux réels. Ce qu'on a vu précédemment sur les taux d'intérêts, s'applique aux taux d'intérêt des crédits. Ici, l'effet dépend de si la dette est à taux fixe ou à taux variable.

• Les dettes indexées sur l'inflation voient leurs taux nominaux covarier avec elle. Toute hausse/baisse de l'inflation entraînant une variation équivalente des taux nominaux, ce qui fait que les taux réels restent les mêmes.
• Les dettes à taux variables, c'est-à-dire dont les taux peuvent varier, voient généralement leurs taux varier selon la règle de Taylor. En clair, le taux réel covarie avec l'inflation, l'inflation faisant augmenter à la fois leur taux nominal et leur taux réel. Une hausse de x% de l'inflation entraîne une hausse supérieure à x% des taux.
• Les dettes à taux fixes sont elles rognées par l'inflation. Leur taux nominal est fixé une fois pour toutes et leur taux réel dépend alors des variations de l'inflation. Par exemple, si vous contractez un emprunt immobilier à 2% (nominal), une hausse de l'inflation réduira le taux réel, ce qui allègera le poids de votre crédit et facilitera son remboursement.

Pour résumer, une hausse de l'inflation aide donc les emprunteurs à taux fixe, défavorise les emprunteurs à taux variable et mais n'a pas d'effet sur les dettes indexées à l'inflation. L'effet macroéconomique des variations de l'inflation dépend donc des proportions d'emprunts à taux fixe/variable/indexés sur l'inflation. Difficile d'en dire plus, sauf à analyser la proportion de chaque type de dette dans la population et leur répartition selon les revenus ou le patrimoine. L'effet redistributif est difficile à déterminer et dépend surtout du système bancaire du pays étudié et de sa régulation.

L'effet sur l'épargne : la vraie-fausse euthanasie du rentier

Une autre conséquence d'une hausse/baisse de l'inflation est son effet sur l'épargne. Intuitivement, une hausse des prix entraîne une baisse du pouvoir d'achat de l'épargne, si celle-ci reste constante. Sauf que ce n'est pas le cas en réalité. Tout dépend, encore une fois de l'effet de l'inflation sur les taux d'intérêts des placements. Il faut, encore une fois, faire la différence entre les placements à taux fixes et les placements à taux variables.

• Certains placements sont indexés sur l'inflation, ce qui fait que leurs taux nominaux évoluent avec celle-ci (dit autrement, leurs taux réels sont fixes). C'est par exemple le cas des obligations indexées sur l'inflation, mais aussi des actions ou de l’immobilier, dont le rendement/prix augmente en même temps que l'inflation, si ce n'est plus. C'est la même chose pour certains placements monétaires, assez rares il est vrai, dont les taux sont au minimum égal à l'inflation (en 2018, c'est le cas du Livret A, du LDDS et du LEP : leur rendement est au minimum égal à l'inflation, d'après la loi). Il va de soi que l'inflation n'a aucun effet sur ce type de placements.
• D'autres placements sont à taux fixes, à savoir que leur taux est garanti et fixé par la loi ou un contrat quelconque. C'est le cas par exemple des comptes à termes, dont les taux sont fixés lors de la signature du contrat et garantis par la loi. Pour ces placements à taux nominal fixe, une augmentation de l'inflation se répercute sur le taux réel. L'inflation est alors mauvaise pour l'épargnant à taux fixe, elle lui fait perdre son pouvoir d'achat. Ce qui est souvent résumé en disant que "l'inflation est l'euthanasie des rentiers" (affirmation que nous nuancerons par la suite). Mais précisons qu'il s'agit là de l'effet d'une hausse de l'inflation. Si l'inflation est stable, elle est prévue par les agents économiques, et les taux d'intérêts s'ajustent.
• D'autres placements ont des taux de rendement variables, qui évoluent dans le temps. Pour ces placements à taux variables, l'inflation tend à se répercuter sur les taux nominaux, sans toucher de beaucoup les taux réels. Les prix des logements à Paris ou le niveau du CAC40 sont là pour en témoigner... Pour ces placements, toute hausse de x% de l'inflation entraîne une hausse identique des taux d'intérêt qui compense la hausse de l'inflation. La réalité est plus complexe, les taux augmentant ou baissant plus fort que l'inflation : une hausse de 2% de l'inflation entraînera une hausse des taux de plus de 2%, et inversement pour une baisse.

Là encore, l'effet redistributif dépend de la proportion de chaque type de placement selon le revenu. Généralement, les ménages pauvres ou de la classe moyenne investissent en actifs sûrs, en placements monétaires qui sont les plus touchés par une hausse de l'inflation. À l'inverse, les ménages riches ont surtout des actions et de l'immobilier, qui sont protégés des hausses de l'inflation.

L'effet précédent est lié à une hausse/baisse de l'inflation, mais sa valeur absolue a aussi des conséquences. Plus l'inflation est forte, plus les agents sont incités à investir en actions et/ou immobilier, ce qui pourrait avoir un impact sur la croissance économique. L'inflation incite à investir non pas dans des titres de dettes sensibles à l'inflation, mais dans du capital productif (actions, immobilier, titres de propriété autres, ...). En clair, cela peut stimuler l'investissement sous la forme de capital, qui lui-même agirait positivement sur la croissance économique. Une telle chaîne "inflation -> investissement en capital -> croissance" porte le nom d'effet Tobin, du nom de son créateur, James Tobin. Pour l'anecdote, Tobin est l'économiste à l'origine de la fameuse taxe Tobin (souvent mal expliquée et mal comprise, mais c'est pour un autre cours), sans compter qu'il a créé un modèle de croissance monétaire qui modélise l'effet Tobin.

L'effet sur la monnaie : la taxe d'inflation

Le cas le plus intéressant à étudier n'est cependant pas celui des rentiers, mais le cas général de tout un chacun, à savoir celui de la monnaie. Vu que son taux nominal est nul, son taux de rendement réel étant de $-\pi$. On peut voir l'inflation comme une taxe sur la détention d'espèces, qui touche surtout les ménages qui détiennent une grande partie de leur patrimoine sous la forme de monnaie. Il peut paraître bizarre d'utiliser le terme taxe, mais nous verrons plus tard dans ce cours que l'inflation est une source de revenus pour l'état. Et nous ne parlons pas seulement du fait qu'une hausse des prix signifie une hausse de l'argent récolté par la TVA ou d'autres taxes portant sur les prix. Nous verrons que la création de monnaie par la banque centrale, qui entraîne de l'inflation, est une source de revenus pour l'état. Mais ce sera l'objet d'un chapitre dédié à la fin du cours. Pour le moment, sachez juste que l'inflation entraîne une hausse des revenus réels de l'état par des mécanismes assez complexes.

Il ne faut pas croire que les ménages et entreprises ne réagissent pas à cette taxe d'inflation. Les ménages tentent de s'en prémunir en réduisant leurs encaisses, en dépensant immédiatement leur argent et en réduisant leur épargne de précaution. Cela entraîne l'apparition de divers coûts, appelés coûts de semelle (Shoe leather cost en anglais). Ce nom, d'inspiration comique, vient du fait que les voyages incessants à la banque lors des épisodes de forte inflation sont censés user plus vite les semelles des ménages. Il faut cependant noter que cette taxe d'inflation ne touche pas les placements rémunérés, ce qui incite les épargnants à placer leur argent, plutôt que de le laisser dormir sur un compte courant ou un livret faiblement rémunéré.

Les ménages "riches" ont peu de monnaie, en proportion de leur patrimoine, vu qu'ils préfèrent investir dans des actifs protégés de l'inflation. Par contre, les ménages modestes sont au contraire investis fortement en monnaie. Certains ménages n'ont même que de la monnaie, à savoir que leur épargne se résume à des comptes courants ou des livrets bancaires. Autant vous dire que les ménages pauvres sont les plus touchés par la taxe d'inflation, alors que les ménages riches y sont assez peu exposés. Cela peut paraître assez contre-intuitif, mais cela se comprend mieux avec quelques exemples. Prenons un ménage pauvre dont la seule épargne est un compte courant et un livret A : la taxe d'inflation va toucher tout son patrimoine. Par contre,ce n'est pas le cas pour un ménage riche qui a gardé 5% de son patrimoine en monnaie et le reste en actions et en immobilier. Seul 5% de son patrimoine seront impacté par la taxe d'inflation, les actions et l'immobilier étant exclus. Ce qui fait beaucoup moins, en termes de pourcentage, que le ménage pauvre. Pour résumer, la taxe d'inflation est donc une taxe fiscalement régressive, dont le taux diminue avec le patrimoine et les revenus.

L'effet sur l'investissement et la consommation

Un autre point est que l'inflation modifie les comportements d'investissement, d'épargne et de consommation. Il est difficile de parler des comportements d'épargne/investissement sans parler des comportements de consommation, les deux étant liés. En effet, l'argent dépensé pour consommer est de l'argent qui ne peut plus être investi/épargné. Il y a donc un arbitrage permanent entre consommation et épargne. Du fait de ses effets, l'inflation modifie les comportements de consommation et d'investissement.

Concrètement, les ménages anticipent des hausses de prix et tendent à s'en prémunir en achetant à l'avance. Pour le dire autrement, ils réduisent leur consommation future pour augmenter leur consommation immédiate, ce qui revient à réduire leur épargne pour consommer plus. Les ménages surconsomment à court-terme, en achetant beaucoup de biens et services qu'ils n'auraient pas acheté sans inflation. Mais outre la surconsommation, les ménages peuvent augmenter leurs dépenses sans que cela se traduise par de la consommation immédiate. Par exemple, les ménages font des stocks de denrées dont le prix est censé grimper avec l'inflation. Typiquement, ils font des stocks de denrées alimentaires, d'essence, de savon, ou de tout autre biens durables. Il arrive aussi que les ménages spéculent en utilisant leurs stocks. Certains ménages achètent immédiatement des biens, pour les revendre plus tard, après que les prix aient montés.

Évidemment, l'augmentation de la consommation immédiate réduit les flux d’épargne, ce qui se traduit par un renchérissement des taux d'intérêt. Les entreprises devant payer plus pour attirer les investisseurs. Une entreprise qui a besoin d'emprunter devra fournir un rendement d'autant plus élevé que l'inflation est grande, les investisseurs n'étant pas bêtes et cherchant à se prémunir contre l'inflation. On a donc une surconsommation immédiate couplée à une réduction de l'épargne financière et des difficultés de financement pour les entreprises. Et les difficultés de financement des entreprises sont aggravés par le fait que les ménages cessent d'investir pour acheter des actifs non-productifs qui les protègent de l’inflation. Typiquement, les agents économiques vont délaisser les marchés financiers et les banques pour acheter de l'or, des métaux précieux, des cryptomonnaies. Les ménages délaissent les investissements productifs, dont les rendements sont grignotés par l'inflation, et leur préfèrent des actifs qui couvrent contre l'inflation (peu importe que cette couverture soit réelle ou supposée).

L'influence sur les impôts : des distorsions macroéconomiques

L'inflation influence la perception des impôts par divers mécanismes assez contre-intuitifs. En premier lieu, elle réduit la valeur des impôts reçus par l’état. Il existe un certain temps entre le versement des revenus par les ménages, la perception des impôts et leur dépense par l'état. Et durant ce temps, l'inflation rogne la valeur des impôts perçus. Ensuite, les impôts portent sur des variables nominales, et non sur les valeurs réelles, ce qui peut poser quelques problèmes assez subtils, mais particulièrement importants.

Pour ce qui est de l'impôt sur le revenu, cela pose problème quand l'impôt est perçu par tranches. Dans ce cas, il faut que les seuils de chaque tranche suivent l'inflation pour compenser l'inflation et la hausse des salaires qui va avec. Si ce n'est pas le cas, des ménages qui étaient en dessous d'une tranche vont passer à la suivante, du fait de la hausse des salaires. Les salariés se retrouvent donc à payer des impôts en plus, alors que leur pouvoir d'achat n'a pas augmenté, ce qui réduit la progressivité de l'impôt. Si l'effet est marginal sur une année, il l'est beaucoup moins après quelques décennies. Songez qu'une hausse des salaires de 3% par an se traduit par un doublement en 24 ans... De manière générale, le phénomène a lieu pour tout seuil nominal qui sert dans le calcul des impôts, ce que soit pour le calcul des seuils ou plafonds des niches fiscales/tranches/autres.

Dans le cas des revenus du capital, cela entraîne une augmentation du taux d'imposition par rapport au taux réellement appliqué (celui définit dans la loi). Et si on tient compte de certaines déductions et réductions d'impôts, cela altère l'attractivité de certains investissements. Les niches fiscales deviennent nettement plus attractives que prévu, et les agents sur-investissent dans celles-ci. Il y a beaucoup d'autres effets de l'inflation sur la perception des impôts ou sur les investissements dépendants des taux d'imposition. Tout cela cause un manque à gagner pour l'état, qui doit être compensé d'une manière ou d'une autre, par une réduction des dépenses ou une augmentation des taxes. Et les effets sont très souvent assez larges, bien plus que pour la taxe d'inflation ou les autres effets. On estime que cela réduit les ressources fiscales de quelques pourcents, la valeur exacte dépendant du pays.

Les coûts de menu

Un autre problème est que si l'inflation est vraiment forte, les prix doivent être mis à jour régulièrement par les entreprises. Cette mise à jour des prix n'est pas gratuite pour les entreprises, celles-ci devant changer les étiquettes, les menus, les catalogues, etc. De tels coûts de menu sont préjudiciables à la rentabilité des entreprises. Et il faut aussi parler de la mise à jour des salaires ou des taux d'intérêts.

Si l'inflation est vraiment forte, les entreprises doivent mettre à jour les salaires fréquemment (tous les mois ou tous les ans). Dans certains cas, les salaires peuvent même être indexés sur l'inflation. Dans les deux cas, cela a un coût pour les entreprises, qui cherchent à les minimiser le plus possible. Elles vont, par exemple, retarder les hausses de salaires ou en diminuer la fréquence. Cela fait que de nombreux salaires sont fixes à court-terme et ne sont pas réévalués en même temps que l'inflation, ce qui entraîne une baisse de pouvoir d'achat temporaire, compensée quand les salaires sont "dé-fixés". Cela a autant d'effets positifs que négatifs, mais cela entraîne une baisse temporaire du pouvoir d'achat des salaires.

La volatilité de l'inflation

Volatilité de l'inflation.

Un autre point est qu'une inflation élevée est souvent une inflation fortement variable dans le temps. Cette volatilité de l'inflation favorise les entreprises financières, au détriment des autres. Plusieurs études estiment qu'une hausse de 10% de l'inflation augmente de plusieurs pourcents la part du PIB gagnée par les sociétés financières. En conséquence, l'inflation aide le transfert des ressources aux banques et organismes financiers. De plus, elle empêche les entrepreneurs et investisseurs d'estimer le rendement réel de leurs investissements.

Pour se prémunir contre une mauvaise anticipation d'inflation, les investisseurs vont anticiper le pire des cas, l'inflation la plus haute possible. Les investisseurs augmenteront les taux d'intérêts pour se prémunir contre le risque d'inflation. Cette hausse des taux entraîne une baisse de la production, par des mécanismes que nous aborderons dans quelques chapitres. Ce phénomène disparaît quand la banque centrale s'engage à respecter une cible d'inflation : les agents économiques s'attendront à une inflation égale à la cible, et ne négocieront pas une prime de risque liée à l'inflation. Les taux réels sont donc légèrement abaissés, favorisant la production.

Le taux d'inflation optimal

Comme on le voit, l'inflation a des effets divers et variés sur l'économie d'un pays. Difficile de savoir quel effet va l'emporter sur les autres, ni si leur intensité est vraiment appréciable. C'est pourtant ce qu'il faudrait savoir pour déterminer le taux d'inflation optimal. Le consensus est cependant en faveur d'un taux d'inflation suffisamment faible pour ne pas avoir d'effet négatif notable d'un côté, mais non-nul pour éviter une déflation de l'autre (la déflation est une baisse des prix, une inflation négative, aux conséquences économiques particulièrement fâcheuses - nous en reparlerons dans la fin de ce livre). Un taux autour de 1 à 3% ne semble pas trop éloigné du taux optimal, les banques centrales actuelles préférant un taux de 2%. Mais d'autres travaux, plus anciens il est vrai, sont en faveur d'un taux de 0%, voire un taux négatif ! Las, aucune réponse certaine n'est aujourd'hui disponible.

Pour ceux qui veulent des sources d'études portant sur l'inflation optimale, je vous conseille de lire le document .pdf suivant : The Reader's Guide to Optimal Monetary Policy, par Anthony M. Diercks.

La taxe d'inflation optimale

La taxe d'inflation permet de faire rentrer de l'argent dans les caisses de l'État, sans augmenter les autres impôts. Il s'agit donc d'une source de revenus pour l'état, qui est bien acceptée par la population car relativement invisible. Une hausse de l'inflation est plus facilement acceptée qu'une hausse des impôts sur le revenu ou de la TVA. La raison est que la taxe d'inflation est assez invisible, ses effets ne se voyant que si les prix ont vraiment augmenté, contrairement aux autres hausses d'impôts. Et surtout, personne ne s'imagine que l'état gagne vraiment beaucoup d'argent avec une inflation modérée.

Cependant, il y a un défaut à ce raisonnement. Tous les impôts causent des inefficiences microéconomiques diverses, de par leurs côtés incitatifs ou désincitatifs. La taxe d'inflation cause des distorsions, à savoir qu'elle modifie l'allocation des ressources (ici, la monnaie) par rapport à un équilibre optimal. On a vu plus haut que les agents économiques tentent par tous les moyens de réduire la taxe d'inflation, en se débarrassant de leur monnaie, que ce soit pour la dépenser ou pour l'investir dans d'autres actifs. Plus l'inflation est forte, plus les agents réduisent la quantité de monnaie qu'ils ont. On peut modéliser cela selon une relation entre taux d'inflation et demande de monnaie, relation décroissante. Sans taxe d'inflation, les agents détiendraient la quantité de monnaie optimale pour leur bien-être. Mais ce n'est pas le cas si la taxe d'inflation est positive : la taxe d'inflation modifie l'allocation de la monnaie dans l'économie, ce qui est source d'inefficiences (trop de dépenses ou d'achats d'actifs risqués, comportements microéconomiques sous-optimaux, influence sur le système bancaire et monétaire, ...). Naïvement, on peut en déduire que l'optimum est obtenu avec une taxe d'inflation nulle, qui ne cause pas de distorsions monétaires. Après tout, l'état dispose d'autres impôts mieux fichus pour financer ses dépenses, comme une TVA, un impôt sur le revenu, etc.

Mais c'est oublier que les autres impôts causent aussi des problèmes, liés au fait que les agents souhaitent limiter leur impôt au maximum. Tout impôt cause des distorsions et pas seulement la taxe d'inflation. Dans le cas où l'inflation cause moins de problèmes que d'autres impôts, plus problématiques, elle est à privilégier (et inversement dans le cas contraire). En somme, il y a un arbitrage coûts-bénéfices entre chaque type d'impôts, qui est extrêmement compliqué à analyser. Par exemple, l'inflation a beau être une taxe peu redistributive (et même fiscalement régressive), les autres impôts peuvent être pires (selon le pays ou le gouvernement). Comme autre exemple, si l'inflation modifie l'allocation de l'épargne des agents, une taxe sur le capital ou les dividendes mal fichue peut faire pire (ou mieux, tout dépend des taux, des assiettes, et de bien d'autres choses). Si on fait une synthèse de cet arbitrage entre inflation et autres impôts, on trouve qu'une taxe d'inflation faible mais positive a des avantages certains sans inconvénients majeurs par rapport aux autres impôts. Elle est bien perçue par la population, rapporte de l'argent à l'état, permet de réduire le poids des autres impôts, sans pour autant causer de distorsions majeures. Cela va dans le sens d'une inflation légèrement positive, mais assez faible, quelques pourcents tout au plus.

Un avantage spécifique à la taxe d'inflation est qu'elle taxe tous les détenteurs de monnaie, y compris les étrangers et/ou ceux qui le déclarent pas leurs revenus. Elle permet ainsi de taxer les activités illégales, comme la vente de drogue, qui ne payent pas d'impôts sur leur activité. De plus, elle taxe aussi des détenteurs étrangers. Par exemple, un ménage européen qui détient des dollars sera taxé par l'inflation américaine, sans même s'en rendre compte. Beaucoup de pays ont des réserves de dollars, que ce soit pour faciliter le commerce international, pour fixer leurs taux de change, ou pour d'autres raisons. Les états-unis, avec leur inflation à 2%, taxent ces réserves étrangères de dollars, ce qui leur donne un revenu fiscal assez important. C'est une source de revenus non-négligeable pour les pays dont la monnaie est beaucoup utilisée à l'étranger, comme les états-unis ou la zone euro.

Le coût d'opportunité de la monnaie

Un autre raisonnement, proposé par Milton Friedmann, veut que l'inflation optimale soit obtenue quand les taux nominaux sont nuls. Pour comprendre le raisonnement, il nous faut anticiper les prochains chapitres et parler de la demande de monnaie. Nous avions vu ce concept dans le chapitre précédent, mais dans le cadre de la théorie de la préférence pour la liquidité. Ici, nous allons parler d'un concept légèrement plus général, qui n'est pas spécifique à cette théorie. Pour rappel, c'est l'idée que la quantité de monnaie en circulation dans l'économie dépende des taux d'intérêt. Plus les taux sont élevés, plus la quantité de monnaie circulante est faible. Une manière simple d'expliquer cela est que plus les taux sont forts, moins les agents économiques veulent détenir de monnaie et plus ils la convertissent en dépenses et/ou placements financiers.

Pour détailler le raisonnement, il faut parler du coût d'opportunité de la monnaie. Celui-ci est la perte (ou le non-gain) qu'un agent a à détenir une quantité M de monnaie. En effet, l'agent pourrait faire autre chose de son argent et notamment l'épargner. Entre détenir de la monnaie qui ne rapporte rien (son taux nominal est de 0) et des instruments financiers qui versent un intérêt élevé, le choix est vite fait. Le coût d'opportunité ici correspond à l'intérêt perdu en ne plaçant pas l'argent, c’est-à-dire les intérêts $iM$. Le coût d'opportunité de la monnaie est donc égal à $i$ et plus il est élevé, plus la détention de monnaie est coûteuse par rapport aux autres options de placement. Avec des taux élevés, les agents vont se débarrasser de leur monnaie et la convertir en placements, réduisant la quantité de monnaie totale en circulation. Inversement, une baisse des taux fait que la monnaie va devenir plus intéressante, car elle garde l'avantage de la liquidité : elle peut être dépensée immédiatement, contrairement à des actions, des obligations ou de l'immobilier. Ainsi, plus le taux nominal est élevé, plus le coût d'opportunité de la monnaie est important, plus la détention de monnaie est coûteuse par rapport aux autres options, plus les agents s'en débarrassent, plus la masse monétaire diminue.

Relation entre taux, inflation et demande de monnaie.

Il existe donc une relation entre taux d'intérêt et monnaie, appelée la demande de monnaie. Celle-ci dit est illustrée schématiquement dans le schéma de droite, mais on peut la mettre grossièrement en équation comme suit :

$M=f(i)=f(r+\pi )$, avec M la masse monétaire, i le taux nominal, r le taux réel et pi pour l'inflation.

On voit que pour un taux réel constant, l'inflation fait augmenter les taux nominaux, ce qui réduit la masse monétaire. La raison à cela est que plus l'inflation fait augmenter les taux nominaux, et donc le coût d'opportunité de la monnaie, ce qui fait que les agents convertissent leur monnaie en placements. Le schéma ci-contre montre que la demande de monnaie est maximale quand le taux nominal est nul.

Friedmann postula que le coût de détention de la monnaie devait être égal au coût de la création de cette même monnaie. Or, ce coût de création monétaire est supposé être nul, d'où un coût d'opportunité nul, ce qui implique un taux d'intérêt nul ! L'idée de Friedmann implique qu'avec un taux nul, les agents ne sont pas incités à biaiser leur détention de monnaie à cause de l'inflation, ce qui fait que les conséquences de l'inflation sont alors minimales, voire nulles. En clair, la politique monétaire optimale demande de garder un taux d'intérêt nominal nul, égal à 0. D'après l'équation de Fisher $i=r+\pi$, cela signifie un taux d'inflation optimal négatif, égal à l'opposé du taux réel : $\pi _{optimal}=-r$. La banque centrale doit donc garder le taux nominal à zéro, ce qui est ce qu'on appelle la règle de Friedmann.

Mais de nos jours, on sait que cette règle n'est probablement pas optimale. Si on prend en compte d'autres effets de l'inflation, on se retrouve avec des frictions qui rendent la règle de Friedmann fausse, ou au moins approximative.

Les taux de change

La politique monétaire a un effet sur la quantité de monnaie et les taux d'intérêts, mais aussi sur les taux de change. Aussi, nous avons dédié un chapitre sur ceux-ci. Les taux de change ont de nombreux points communs avec l'inflation ou les taux d'intérêt. Le premier est d'être des variables dites nominales, qui dépendent du niveau général des prix. On peut en donner des valeurs dites réelles, qui suppriment l'effet de l'inflation ou des prix, et les taux de change ne font pas exception : on distingue le taux de change réelle du taux nominal. De plus, le taux de change et l'inflation sont tous deux influencés par des paramètres réels et par la politique monétaire et fiscale du gouvernement. Reste à voir ce que sont ces taux de change et d'où ils proviennent.

Le taux de change : définitions de base

Pour investir à l'étranger ou pour exporter/importer, tout agent devra échanger sa monnaie nationale contre de la monnaie étrangère : des euros s'échangent contre des yens, des dollars s’échangent contre des euros, etc. Mais pour que cet échange ait lieu, il faut obligatoirement un autre agent faisant l'échange strictement inverse : si j'échange 50 euros contre 100 yens, il faut un autre agent avec qui échanger, agent qui voudra échanger 100 yens contre 50 euros. Pour le dire autrement, l'échange de devises est un troc de monnaie, et non un achat ou une vente habituelle.

Le taux de change nominal et réel

Le taux de change nominal est le prix d'échange de deux monnaies. Il définit combien il faut donner de monnaie nationale pour obtenir une unité de monnaie étrangère. Par exemple, si je dois donner 50 euros pour obtenir 30 yens, le taux de change est de 50/30 = 1,6666... De manière générale, le taux de change d'une monnaie nationale envers une monnaie étrangère est égal au rapport entre la somme de monnaie nationale $S_{n}$ qu'il faut dépenser pour obtenir $S_{e}$ unités de monnaies étrangères.

$e={\frac {S_{n}}{S_{e}}}$

À toute variable nominale, il existe une variable réelle équivalente. Le taux de change ne fait pas exception. Le taux de change réel, noté $q$, est la quantité de biens nationaux que l'on peut échanger contre des biens étrangers. En clair, une quantité $Q_{n}$ de biens nationaux s’échange contre la quantité $q\times Q_{e}$ de biens étrangers. Ce qui donne :

$q={\frac {Q_{n}}{Q_{e}}}$

On peut calculer ce taux de change réel en partant de la définition du taux de change nominal précédente. Il faut juste se souvenir que chaque somme d'argent est équivalente à une certaine quantité de biens multipliée par leur prix, ce qui donne :

$e={\frac {S_{n}}{S_{e}}}={\frac {Q_{n}\times P_{n}}{Q_{e}\times P_{e}}}=q\times {\frac {P_{n}}{P_{e}}}$

Le taux de change réel $q$ vaut donc, par définition :

$q=e\times {\frac {P_{e}}{P_{n}}}$, avec $q$ le taux de change réel, $e$ le taux de change nominal, $P_{n}$ le niveau général des prix nationaux et $P_{e}$ le niveau moyen des prix étrangers.

La dépréciation des taux de change nominaux et réels

Le taux de change peut varier au cours du temps, que ce soit à la hausse ou à la baisse. Une baisse du taux de change porte le nom de dépréciation, alors qu'une hausse s'appelle une appréciation. Quelques calculs algébriques nous permettent de calculer les variations du taux de change, à savoir la dépréciation ou l'appréciation de la monnaie. Ces deux valeurs indiquent si le taux de change a augmenté ou diminué de 5%, de 2%, de 15%, etc. Cette variation en pourcentage est au taux de change ce que l'inflation est au niveau des prix. Ce taux de dépréciation de la monnaie nationale est égal, par définition, à :

$d={\frac {\Delta e}{e}}$, avec e le taux de change.

Une dépréciation se traduit par une hausse des prix des biens importés : les biens et services deviennent alors plus cher dans la monnaie nationale. De plus, elle rend moins chères les exportations dans la monnaie étrangère, ce qui rend les biens exportés plus compétitifs à l'étranger par rapport aux biens domestiques. À contrario, une appréciation a les effets inverses : baisse des prix importés, mais exportations plus chères.

À partir de l'équation précédente, on peut calculer comment varie le taux de change réel en fonction d'une variation du taux de change nominal. En clair, on peut calculer la dépréciation du taux de change réel à partir de celle du taux de change nominal. Pour cela, partons de la définition du taux de change réel :

$q=e\times {\frac {P_{e}}{P_{n}}}$

Prenons la variation/dérivée :

$\Delta q=\Delta \left(e\times {\frac {P_{e}}{P_{n}}}\right)$

On applique la formule $\Delta (A\times B)=\Delta A\cdot B+A\cdot \Delta B$ :

$\Delta q=\Delta e\cdot {\frac {P_{e}}{P_{n}}}+e\cdot \Delta \left({\frac {P_{e}}{P_{n}}}\right)$

Divisons par q, ce qui revient à multiplier par ${\frac {1}{e}}{\frac {P_{n}}{P_{e}}}$ :

${\frac {\Delta q}{q}}={\frac {1}{e}}{\frac {P_{n}}{P_{e}}}\left[\Delta e\cdot {\frac {P_{e}}{P_{n}}}+e\cdot \Delta \left({\frac {P_{e}}{P_{n}}}\right)\right]$

Développons et simplifions :

${\frac {\Delta q}{q}}={\frac {\Delta e}{e}}+{\frac {P_{n}}{P_{e}}}\cdot \Delta \left({\frac {P_{e}}{P_{n}}}\right)$

La variation/dérivée d'un quotient se calcule avec la formule $\Delta \left({\frac {A}{B}}\right)={\frac {\Delta A}{B}}-{\frac {A}{B}}{\frac {\Delta B}{B}}$. Dans le cas présent, cela donne :

${\frac {\Delta q}{q}}={\frac {\Delta e}{e}}+{\frac {P_{n}}{P_{e}}}\cdot \left({\frac {\Delta P_{e}}{P_{n}}}-{\frac {P_{e}}{P_{n}}}{\frac {\Delta P_{n}}{P_{n}}}\right)$

En simplifiant, on trouve :

${\frac {\Delta q}{q}}={\frac {\Delta e}{e}}+{\frac {\Delta P_{e}}{P_{e}}}-{\frac {\Delta P_{n}}{P_{n}}}$

Dans le terme de droite, le premier terme est la dépréciation du taux de change nominal, le second est l'inflation du pays étranger, et le troisième est l'inflation du pays domestique. On a alors :

${\frac {\Delta q}{q}}={\frac {\Delta e}{e}}+\pi _{e}-\pi _{n}$

On peut aussi reformuler cette équation comme suit :

${\frac {\Delta e}{e}}={\frac {\Delta q}{q}}+(\pi _{n}-\pi _{e})$

On voit que dans le cas général, la dépréciation des taux de change nominaux est la somme de la dépréciation du taux de change réel et du différentiel d'inflation entre les deux pays considérés. Reste alors à savoir comment l'inflation interagit avec les taux de change.

Les régimes de change fixe et flottant

L'équation précédente nous donne une égalité, mais elle ne dit pas dans quel sens les variables interagissent. Le fait est que cela dépend de comment le gouvernement gère le taux de change. Il peut le laisser flotter, c'est à dire varier suivant les vicissitudes des marchés, ou le fixer, c'est à dire agir afin de le maintenir constant.

De nos jours, la plupart des pays n'interviennent pas sur le marché des changes, ce qui fait qu'ils laissent les taux de change varier suivant les conditions de marché. On parle alors de politique de change flottant. Mais d'autres pays font intervenir le gouvernement et/ou la banque centrale pour contrôler les taux de change. Cela arrive dans beaucoup de pays émergents, qui dépendent beaucoup des importations. Dans ces pays, maintenir l'inflation sous contrôle demande de contrôler les prix des biens importés, et donc le taux de change. La banque centrale a alors pour objectif de maintenir les taux de change fixes, à une valeur qui maintient le prix des biens importés sous contrôle. On dit alors que la politique de taux de change est une politique de change fixe.

Fixer le taux de change nominal est possible si le gouvernement maintient son taux de change fixe par divers moyens légaux et macroéconomiques. Dans ce cas, l'équation précédente nous dit que la dépréciation du taux de change réel est égal au différentiel d'inflation entre les deux pays. Maintenir un taux de change réel fixe demande donc d'avoir la même inflation que l'autre pays considéré. Une conséquence de cela est que si deux pays s'accordent à maintenir leurs taux de change nominaux fixes, alors il faut de préférence que l'inflation soit identique dans les deux pays pour éviter une divergence exponentielle des taux de change réel. Mais ce cas est quelque peu problématique et assez difficile à mettre en place.

Mais si le gouvernement laisse flotter le taux de change nominal, alors les taux de change nominaux sont influencés par l'inflation. Sur le long-terme, le taux de change réel est relativement stable, ce qui fait que taux de change et différentiel d'inflation covarient : toute variation du différentiel d'inflation entraîne une variation identique des taux de change nominaux. À plus court terme, les variations des taux de change nominaux ne sont cependant pas identiques à l'inflation. Le taux de change réel peut alors varier, dans une certaine mesure, et avoir un effet sur l'économie réelle.

La détermination des taux de change

Qui dit échange dit marché. Ici, il s'agit de marchés où les agents économiques échangent des devises, d'où leur noms de marchés de devises. Sur ce marché, des personnes vendent de la monnaie et d'autres veulent en acheter : des agents vont vouloir échanger de la monnaie nationale contre une monnaie étrangère (offre de monnaie nationale), tandis que d'autres voudront faire la conversion inverse (demande de monnaie nationale). Ces marchés permettent ainsi un troc entre monnaies. Dit autrement, une offre de devises rencontre une demande. À l'équilibre, la demande et l'offre sont égales, ce qui fait que la rencontre entre cette offre et cette demande est à l'origine d'un prix : le taux de change nominal.

L'équilibre du marché des changes

La demande du marché des changes est la quantité de devises que les agents souhaitent échanger contre de la monnaie domestique, l'offre étant l'opération inverse. On peut s'en rendre compte facilement : plus le taux de change est fort, plus la conversion d'une unité de devises rapportera de monnaie nationale. L'opération de conversion de devises en monnaie nationale est donc favorable, contrairement à l'autre opération. On a donc un flux entrant d'un côté et un flux sortant de l'autre. L'offre et la demande de devises/monnaie dépendent des flux de capitaux, mais aussi des importations et exportations, ainsi que des interventions des banques centrales sur le marché. Si on omet l'intervention des banques centrales, alors seules comptes les transferts de capitaux et les importations/exportations. Les

Un premier composant de la demande de monnaie nationale provient des exportations. : un exportateur est payé en monnaie étrangère, qu'il doit convertir en monnaie nationale. Par contre, les importateurs doivent transformer leur monnaie nationale en devises étrangères pour payer leurs vendeurs. Ce qui fait que les importations rentrent dans la composition de l'offre de devise nationale. À cela, il faut ajouter les flux de capitaux entrants et sortants, à savoir l'investissement étranger ou à l'étranger. Premièrement, des capitaux vont rentrer sur le territoire national, pour y être investis. Ceux-ci doivent être convertis d'une monnaie étrangère vers la monnaie nationale : ils font donc partie de la demande de monnaie. Les capitaux sortants, qui quittent le pays pour être investis à l'étranger, font partie de l'offre de monnaie nationale.

Si on fait le bilan l'offre sur le marché des change est donc la somme des exportations et du flux de capitaux entrant, les deux représentant l'argent qui rentre dans le pays. Par contre, la demande est la somme de l'argent qui sort du pays : paiement des importations, et flux sortants de capitaux. À l'équilibre, offre et demande sont égaux sur ce marché, le taux de change évoluant de manière à ce que ce soit le cas. On obtient donc l'équation ci-dessous :

$E+C_{e}=I+C_{s}$, avec E pour les exportations, I pour les importations, $C_{s}$ et $C_{e}$ pour les flux de capitaux sortant et entrant.

Il est possible de reformuler cette relation en faisant intervenir la différence entre exportations et importations, ainsi que la différence entre capitaux sortants et entrants.

$E-I=Cs-C_{e}$

Le premier terme est ce qu'on appelle les exportations nettes, alors que le second est le flux de capitaux net sortant. En notant $N_{e}$ les exportations nettes et $F_{c}$ le flux de capitaux net sortant, on a :

$N_{e}=F_{c}$

Cette équation est la vraie équation qui donne l'équilibre sur le marché des change. En effet, les exportations nettes correspondent à la quantité d'argent nette qui doit être convertie en devises. Les importations compensent en partie les exportations, le solde restant étant le seul à convertir. Même chose pour les flux de capitaux : les capitaux entrants compensent les sortants, seule la différence entre les deux devant effectivement être convertie. Cette équation dit que les conversions causées par les exportations nettes doit avoir une contrepartie inverse, pour respecter le fait que le marché des change n'est qu'un troc de monnaie. Cette compensation est, par nature, le fait des flux de capitaux nets.

La manipulation des taux de change par les états ou la banque centrale

Pour manipuler le taux de change, le gouvernement (par le biais de sa banque centrale) doit manipuler l'offre et/ou la demande sur le marché des changes, soit en achetant de la monnaie étrangère avec de la monnaie nationale, soit en vendant de la monnaie étrangère. Quand la banque centrale crée beaucoup d'argent, la monnaie nationale devient moins rare. Son offre va donc augmenter, ce qui fait que son prix extérieur (le taux de change) diminue. À l'inverse, une politique restrictive réduit la quantité de monnaie, la rendant plus rare, ce qui fait grimper son prix : le taux s'apprécie.

Pour avoir des taux de change fixes, la banque centrale laisse flotter le taux de change dans un intervalle très précis, histoire de borner les évolutions du taux de change.

Mechanism of Fixed Exchange Rate System

Quand le taux de change menace de dépasser la borne maximale, c'est signe qu'il y a un excès de demande de monnaie nationale par rapport à l'offre. Dit autrement, c'est signe que la quantité de monnaie nationale est trop forte. Pour éviter cela, la banque centrale doit acheter sa monnaie nationale, avec de la monnaie étrangère. Pour cela, toute banque centrale possède des réserves de devises étrangères qu'elle peut échanger à volonté sur les marchés des devises. Une autre solution est d'utiliser une politique monétaire restrictive.

Excess Demand for Dollars

Inversement, un taux de change trop bas signifie qu'il y a excès d'offre de monnaie étrangère, ou un manque de demande. Dit autrement, la monnaie nationale est trop rare, que la création monétaire est insuffisante. Pour éviter cela, la banque centrale doit vendre sa monnaie nationale, contre de la monnaie étrangère. Pour cela, la banque centrale a juste à créer de la monnaie nationale avec une politique monétaire accommodante.

Excess Supply of Dollars

Les anticipations d'inflation

On ne peut pas créer de théorie macroéconomique sans utiliser les grandes variables que sont le PIB, le niveau des prix, la masse monétaire, les taux, et ainsi de suite. La macroéconomie a pour but de trouver des relations assez stables entre ces variables, afin de pouvoir décrire le fonctionnement de l'économie. Avant les années 1970, ces relations étaient tirées d'études statistiques ou d'observations à grande échelle. Les économistes découvraient des relations statistiques entre le PIB et l'inflation, entre le PIB et le chômage, et ainsi de suite. Certaines de ces relations sont aujourd'hui connues sous le nom de courbe de Phillips, Courbe IS, et ainsi de suite.

Mais en 1970, Lucas émis une critique quant à l'utilisation de telles relations statistiques : elles ne sont pas stables dans le temps et toute tentative des gouvernements d'utiliser ces relations pour relancer l’économie est vaine. Cette critique de Lucas part du principe que les agents anticipent la politique monétaire et réagissent en fonction. Ainsi, toute tentative de modéliser l'économie sans tenir compte des anticipations des agents et leur réaction donnera des modèles incomplets, dont les relations statistiques ne sont en réalité que des artefacts sans grande importance. Ce raisonnement, associé à des modèles théoriques, a eu son heure de gloire suite à la mort de la courbe de Phillips keynésienne, quand on montra que celle-ci dépendait fortement des anticipations des agents. Si on tient compte de ces anticipations, le fonctionnement de l'économie est plus compliqué à comprendre et à modéliser, mais le faire nous donne des résultats particulièrement intéressants.

Il est très important de voir dans le détail ce qui influence les anticipations d'inflation et quel est leur influence sur l'économie. Le présent chapitre va donc détailler les modèles qui utilisent les anticipations des agents économiques et les modélisent. Du point de vue de la politique monétaire, ce sont essentiellement les anticipations d'inflation qui sont importantes.

L'effet des anticipations d'inflation sur l'économie

Les agents économiques essayent de prédire l'inflation future, consciemment ou non, et tiennent compte de ces anticipations lors de leurs décisions. Les décisions d'épargne, de consommation, les revendications salariales, et bien d'autres décisions demandent en effet de prédire l'inflation. Par exemple, une forte inflation anticipée peut pousser les agents à négocier leurs salaires à la hausse, ou à prendre plus de risques pour leurs investissements.

L'effet sur l'inflation

Toutes ces réactions font que l'inflation est performative, à savoir que le simple fait d'anticiper l'inflation suffit à la concrétiser. L'inflation totale est donc la somme d'une inflation anticipée $\pi ^{e}$, à laquelle il faut ajouter une inflation non-anticipée $\pi ^{r}$ :

$\pi =\pi ^{e}+\pi ^{r}$.

Les banques centrales ayant comme mandat un contrôle de l'inflation, elles suivent régulièrement l'évolution de ces anticipations, pour bien faire leur travail.

L'effet sur les taux d'intérêts

Dans le chapitre sur les taux d'intérêts, nous avons vu l'équation qui relie taux réel, inflation et taux nominal :

$i\approx r+\pi$

Elle donne le taux réel d'un investissement/crédit une fois que le versement des intérêts s'est concrétisé. Il s'agit du taux réellement obtenu, aussi appelé le taux réel effectif. Cependant, les investisseurs/emprunteurs ne peuvent connaitre le taux réel à l'avance, quand bien même les taux nominaux sont connus à l'avance et fixés par un contrat. Même si le taux nominal est fixé à l'avance, ce qui n'est pas garantit, l'inflation ne l'est pas et peut varier durant la durée du crédit/placement. Cependant, un investisseur peut quand même faire une estimation du taux réel, en tentant de prédire l'inflation (au moins approximativement). Les investisseurs estiment l'inflation future et en déduisent non pas le taux réel effectif, mais un taux réel anticipé estimé sur la base des anticipations d'inflation. Sous ces conditions, l'équation de Fisher $i\approx r+\pi$ se reformule comme suit :

$i\approx r_{e}+\pi _{e}$, avec $r_{e}$ le taux réel anticipé.

Cette équation nous dit que les anticipations d'inflation vont influencer le taux réel et le taux nominal. Deux cas sont possibles : soit le taux nominal est fixe (cas fréquent à court-terme), soit le taux réel est fixe (cas observé sur le long-terme). Si le taux réel est fixe, les anticipations d'inflation se répercutent sur les taux nominaux, sans grand effet sur l'économie. Mais si le taux nominal est fixe, alors les anticipations influencent le taux réel. Or, les taux réels sont extrêmement importants pour nombre de décisions économiques, l'investissement étant le cas le plus important. Le taux réel influence la volonté d’emprunter des ménages et entreprises et influence les décisions d'épargne. Autant dire que les anticipations d'inflation vont avoir un effet majeur sur l'économie, si les taux nominaux sont fixes.

La modélisation des anticipations

Modéliser les anticipations d'inflation est assez compliqué et plusieurs modèles ont été inventés par les économistes. Pour simplifier, on distingue les anticipations rationnelles des autres, dites adaptatives/extrapolatives.

Les anticipations adaptatives

Les premières théories ont utilisé des anticipations fixes, où les agents ne prennent en compte que la dernière valeur de l'inflation, celle de l'année dernière. Ces anticipations sont définies comme suit, avec $E[\pi _{t+1}]$ l'inflation anticipée pour la prochaine période (l'an prochain, par exemple) et $\pi _{t}$ l'inflation actuelle.

$E[\pi _{t+1}]=\pi _{t}$

Un cas plus général est celui des anticipations adaptatives, où les agents utilisent l'inflation passée pour prédire l'inflation future. Avec elles, les agents extrapolent l'inflation future à partir de l'inflation passée. Plus précisément, ils anticipent l'inflation en faisant une moyenne pondérée des valeurs passées de l'inflation, valeurs passés dont le poids diminue exponentiellement avec le temps.

$E[\pi _{t+1}]=\pi _{t}+\beta \pi _{t-1}+\beta ^{2}\pi _{t-2}+\beta ^{3}\pi _{t-3}+\beta ^{4}\pi _{t-4}+\beta ^{5}\pi _{t-5}+\beta ^{6}\pi _{t-6}+...$

Ce qui se reformule ainsi, pour une forme plus compacte :

$E[\pi _{t+1}]=\beta \sum _{i=0}^{\infty }(1-\beta )^{i}p_{t-i}$

Les anticipations adaptatives ne sont pas parfaites et les utiliser dans des modèles économiques est relativement compliqué. Leur défaut principal est qu'elles sont incomplètes, qu'elles ne décrivent pas parfaitement le comportement des agents économiques. En effet, les agents ne se limitent pas à l'inflation passée pour prédire l'inflation future : ils utilisent d'autres sources d'information, comme les statistiques de la production, les taux d'intérêts de la banque centrale, etc. Par exemple, certains traders peuvent surveiller les taux et la politique monétaire, identifier les chocs d'offre ou de demande, et ainsi de suite.

Les anticipations rationnelles

Pour résoudre ces problèmes, les anticipations adaptatives ont progressivement été remplacées par les anticipations rationnelles, la théorie des anticipations aujourd'hui la plus répandue (non sans être critiquée). Avec cette théorie, les agents économiques anticipent l'inflation en utilisant toute l'information disponible. Cela ne signifie pas que tous les agents se forgeront la même anticipation : au contraire, chaque agent peut se faire sa propre anticipation, fortement différente des anticipations des autres agents. Par exemple, les agents économiques peuvent se tromper avec des anticipations rationnelles. Néanmoins, et c'est là le cœur des anticipations rationnelles, la moyenne des anticipations de tous les agents ne se trompe pas : elle est égale à la valeur réelle qu'aura l'inflation dans le futur, si aucun évènement imprédictible n'a lieu. L'hypothèse des anticipations rationnelle ne postule donc pas des agents rationnels, mais des marchés rationnels : il s'agit plus d'un postulat d'intelligence collective que de rationalité individuelle.

Pour formuler cela mathématiquement, prenons une variable macroéconomique $x_{t}$, que les agents souhaitent anticiper. Celle-ci évolue comme une variable aléatoire, ce qui fait que chaque valeur $x_{i}$ qu'elle peut prendre possède une probabilité $p_{i}$ d'avoir lieu. L'espérance mathématique de cette variable aléatoire est la somme :

$E(x_{t})=\sum _{i}(p_{i}\cdot x_{i})$

Les agents vont anticiper la valeur de $e(x_{t})$ en utilisant toute information pertinente qu'ils ont a disposition lors de la période précédente, cette dernière étant notée $I_{t-1}$. L'espérance qu'ils vont anticiper est une espérance conditionnelle, à savoir que les probabilités sont les probabilités conditionnelles sachant que l'information disponible est réalisée. Donc l'espérance qu'ils calculent est la suivante :

$E[x_{t}|I_{t-1}]=\sum _{i}p_{i}(x_{t}|I_{t-1})\cdot x_{i}$

Évidemment, les agents peuvent se tromper : les valeurs anticipées sont alors différentes de la valeur réalisée. La différence entre les anticipations et la réalité est ce qu'on appelle l'erreur de prédiction. Elle vaut :

$\epsilon _{t}=x_{t}-E[x_{t}|I_{t-1}]$

L'hypothèse des anticipations rationnelles se base sur deux principes de base, qui assurent que les agents utilisent toute l'information disponible et que celle-ci est traitée de manière adéquate.

• L’espérance de l'erreur de prédiction, compte tenu des informations disponibles, est nulle. Physiquement, cela signifie que les agents ne mettent pas de côté les informations pertinentes, ils ne sont pas myopes à certaines données. Les agents n'ont donc pas de biais cognitifs qui rendent certaines données plus saillantes que les autres, et ont des capacités cognitives non-limitantes. En clair : les agents peuvent se tromper, mais pas de manière systématique, pas à chaque fois de la même manière. Et ils ne sont pas censés se tromper en raison d'une interprétation biaisée des informations.

$E[\epsilon _{t}|I_{t-1}]=0$

• L'erreur de prédiction est indépendante de l'information disponible. Cela signifie que les agents utilisent bien toute l'information disponible. Ils ont accès à toute l'information disponible, sans coût, sans erreur, sans biais (ou du moins, tout se passe comme si c'était le cas). Et enfin, ils savent comment fonctionne l'économie, savent quel est le modèle adéquat. L'erreur de prédiction est donc causée par des phénomènes que les agents ne pouvaient pas prévoir sur la base des informations disponibles.

$\epsilon _{t}=x_{t}-E[x_{t}|I_{t-1}]$

Avec des anticipations rationnelles, si les prix/salaires ne sont pas fixes, l'inflation est prédite à la perfection et la politique monétaire a bien un effet sur les variables nominales, mais n'a aucun effet sur le PIB ou les autres variables réelles (les taux réels ou les salaires réels, par exemple). Celle-ci est parfaitement prédite par les agents économiques, qui s'adaptent et annule tout effet qu'elle aurait pu avoir. En théorie, seule l'inflation non-anticipée a un effet sur le PIB ou les taux réels. Certains auteurs ont réussi à rendre compte de l'existence d'un effet à court-terme de la politique monétaire tout en utilisant des anticipations rationnelles, mais cela demande d'ajouter des frictions dans les théories utilisées. Nous détaillerons ce genre de théories dans un chapitre à la fin du cours.

Les chefs d'orchestre : les banques centrales

Avec la création des banques, le pouvoir de création de la monnaie a changé de main. Chaque banque imprimait sa propre monnaie, ces monnaies n'étant pas forcément convertibles d'une banque à l'autre. Lors de cette période de free banking, la monnaie était intégralement créée par le secteur privé et n'était pas vraiment régulée. Quelques économistes récents, dont Frédéric Hayek, ont vanté les mérites d'un tel système, causant quelques controverses dans les rangs de leur profession. Par la suite, le système monétaire est rapidement devenu ce qu'on appelle l'étalon-or. Chaque banque devait garantir la convertibilité de la monnaie en or, ce qui faisait que la quantité de monnaie imprimée était limitée par les quantités d'or disponibles. Rapidement, la création monétaire a changé de main et est devenu le rôle d'une unique banque, dirigée par le gouvernement : la banque centrale. Leur but premier, dans les anciens temps, était simplement d'imprimer les billets et de fabriquer les pièces. Puis, leur rôle de réserve d'or ou de monnaie est devenu prépondérant.

Depuis l'effondrement de l'étalon-or et du système de Bretton-Woods, le système monétaire mis en place est ce qu'on l'appelle un régime d'inflation-targeting, ou encore système monétaire moderne. La création monétaire est gouvernée par une banque centrale qui utilise la monnaie pour atteindre divers objectifs macroéconomiques. Elle n'est pas limitée par la quantité d'or dans ses caisses, ni par une quelconque contrainte physique. Cela est possible grâce à l'existence de la monnaie électronique, qui facilite la création monétaire. La banque centrale peut imprimer des billets, frapper des pièces, fabriquer des chèques, créer de la monnaie sous forme électronique, remplir des comptes bancaires, etc. Avec le temps, celle-ci a gagné beaucoup de pouvoir, notamment celui de réguler les banques et de gouverner tout ce qui a rapport de près ou de loin avec la gestion de la monnaie dans l'économie. Les chapitres qui vont suivre vont expliquer le fonctionnement détaillé du système monétaire actuel.

De nos jours, les banques centrales sont la clé de voûte de la gestion de la monnaie dans l'économie, la fameuse politique monétaire. De nos jours, ces banques centrales influencent l'économie, via la quantité de monnaie en circulation, l'inflation, le taux de chômage et d'autres paramètres assez importants. Elles jouent aussi un rôle de régulation et de surveillance du secteur bancaire.Les rôles, objectifs, et instruments d'une banque centrale constituent ce qu'on appelle la politique monétaire. Chaque pays (ou zone monétaire, dans le cas de l'euro) définit le fonctionnement de sa banque centrale dans des lois ou traités, qui précisent quels sont les objectifs de la banque centrale, son organisation, les procédures de nomination de ses dirigeants, et ainsi de suite. Ceux-ci déterminent le statut juridique de la banque centrale. Par exemple, c'est le traité de Maastricht qui définit le statut juridique de la banque centrale européenne. C'est ce statut juridique que nous allons aborder ici.

Les objectifs d'une banque centrale

La banque centrale peut avoir plusieurs objectifs distincts, qui varient fortement suivant le pays. Néanmoins, on retrouve souvent plus ou moins les mêmes objectifs chez un grand nombre de banques centrales, la stabilité des prix étant l'objectif principal. Certaines banques centrales ont un objectif de stabilité des taux d'intérêts, d'autres ont un objectif de maintien de la croissance ou de soutien de l'emploi. Un autre objectif est de stabiliser l'économie, en complément d'une éventuelle politique fiscale. Cela implique de lutter contre les récessions ou de freiner une économie en surchauffe. Cet objectif de stabilisation demande de manipuler la demande (et non l'offre), la politique monétaire ayant une grande influence sur celle-ci. Les banques centrales actuelles tentent de maintenir l'économie de leur pays en bonne santé, notamment en régulant ou en soutenant le système bancaire.

Certaines banques centrales ont, dans leurs statuts juridiques, plusieurs objectifs qui sont le plus souvent contradictoires. Dans ce cas, les statuts juridiques des banques centrales précisent souvent quel est l'objectif principal de la banque centrale, mais ils peuvent aussi préciser des objectifs annexes. Les statuts de ce type sont des mandats hiérarchiques, qui précisent quels sont les objectifs prioritaires. C'est notamment le cas de la réserve fédérale américaine, qui a un double objectif de lutte contre l'inflation et de soutien à l'emploi. Les origines de cette situation atypique sont à rechercher dans l'histoire du pays : la crise de 1929 et son chômage de masse ont profondément marqué les Américains.

Banque centrale	Description du mandat	Texte de loi exact qui décrit les objectifs
Banque centrale européenne	La banque centrale européenne a un mandat hiérarchique, décrit par l'article 127 du traité de Lisbonne, qui a la stabilité des prix comme objectif principal. Mais la formulation des autres objectifs est vague, se contentant d'évoquer le fonctionnement économique général de la zone. Peu de choses sont connues sur la manière dont les dirigeants interprètent cette formulation et on ne sait pas s'ils tentent d'influer sur le chômage ou la croissance avec leur politique monétaire.	L'objectif principal du Système européen de banques centrales, ci-après dénommé «SEBC», est de maintenir la stabilité des prix. Sans préjudice de l'objectif de stabilité des prix, le SEBC apporte son soutien aux politiques économiques générales dans l'Union, en vue de contribuer à la réalisation des objectifs de l'Union, tels que définis à l'article 3 du traité sur l'Union européenne. Le SEBC agit conformément au principe d'une économie de marché ouverte où la concurrence est libre, en favorisant une allocation efficace des ressources et en respectant les principes fixés à l'article 119.
Réserve fédérale américaine	La réserve fédérale américaine a un mandat triple, qui vise la stabilité des prix, des taux d'intérêts et un emploi maximal. Ces trois objectifs étant contradictoires, les dirigeants de la FED interprètent ces objectifs comme une hiérarchie : la FED lutte d'abord contre l’inflation et ensuite seulement contre le chômage. Le taux de chômage que cherche à atteindre la FED est le taux de chômage minimal qui n’accélère par l'inflation, ou NAIRU : si le taux de chômage descend en dessous de ce taux, l'inflation augmente.	The Board of Governors of the Federal Reserve System and the Federal Open Market Committee shall maintain long run growth of the monetary and credit aggregates commensurate with the economy’s long run potential to increase production, so as to promote effectively the goals of maximum employment, stable prices, and moderate long-term interest rates.

La banque centrale n'a accès qu'à un seul instrument pour sa politique monétaire : soit elle fixe la quantité de monnaie en circulation, soit elle fixe les taux d'intérêts. Or, la règle de Tinbergen, une célèbre règle de politique économique nommée d'après son inventeur, stipule que le nombre d'objectifs doit être égal au nombre d'instruments. Si la banque centrale ou un gouvernement souhaite atteindre plusieurs objectifs distincts avec un seul instrument, il ne pourra pas y parvenir. Tout au plus pourra-t-il faire un arbitrage en ces deux objectifs, et aboutir à un compromis. Cette règle de Tinbergen est souvent secondée par la règle de Mundell, qui stipule que l'instrument choisi pour atteindre un objectif doit être le plus performant possible. La combinaison de ces deux règles est la source principale de la séparation entre politique monétaire et politique fiscale : la première cible l'inflation, tandis que l'autre cible les variables réelles, comme l'emploi ou la production.

De nos jours, les banques centrales ont toutes le même objectif : limiter l'inflation. Ce régime de ciblage de l’inflation n'est cependant pas apparu par hasard. Les objectifs des banques centrales ont changé plusieurs fois au cours de l'histoire, cette évolution ayant mené à la situation actuelle. Dans les grandes lignes, les banques centrales ont débuté leur carrière en contrôlant la quantité de monnaie.

La stabilité du prix de l'or

Avant les années 50, le système monétaire international était basé sur l'étalon-or, où la banque centrale fixait le prix de l'or. Aux états-unis, le prix était fixé à environ $20 par once d'or avec des variations assez mineures. Ce système tire son origine du fait que les pièces étaient autrefois fabriquées en or, et a survécu avec l'apparition de la monnaie papier. Avec ce système, chaque unité de monnaie correspond à un certain poids en or : une pièce de 10 dollar contenait une demi-once d'or, une pièce de 20 dollar contenait une once d'or, etc. La valeur de la pièce dépendait donc de sa teneur en or mesurée en onces, et du prix de l'once d'or. Les banques centrales garantissaient que la convertibilité de la monnaie papier en or. La monnaie papier était échangeable à volonté contre de l'or, du moins en théorie, ce qui explique que l'étalon-or ait survécu à l'invention de la monnaie papier. La création monétaire était ainsi limitée par les dépôts d'or à la banque centrale : sans échange d'or, pas de création monétaire.

Le prix de l'or a eu quelques évolutions et soubresauts sous l'étalon-or. Déjà, le prix de l'once d'or est passé de 19.39 dollars l'once à 20.67 dollars en 1834. En 1837, l'étalon-or a été temporairement suspendu. Puis, durant la période de Bretton-Woods, entre 1934 et 1971, le prix de l'once est monté à 35 dollars l'once. Après 1971, l'étalon-or a totalement disparu.

Évolution du prix de l'once d'or entre 1793 et 2005. On voit que le prix de l'or est resté stable pendant l'étalon-or, mais a ensuite augmenté fortement après sa fin, dans les années 70.

L'or était une monnaie de paiement internationale et les prix de l'or était sensiblement les mêmes dans tous les pays. En conséquence, ce système impliquait des taux de change "fixes", dépendant des dépôts d'or nationaux.

Ce système a perduré durant très longtemps et a fait un travail remarquable durant plusieurs siècles. Il avait cependant de gros défauts, que nous détaillerons dans les chapitres sur le sujet. Avec la révolution industrielle et les guerres mondiales, les défauts de ce système sont devenus de plus en plus insupportables, menant à son abandon.

La stabilité de la masse monétaire

La sortie de l'étalon-or au début du 20ème siècle ne s'est pas faite sans douleur. Au sortir des guerres mondiales, certains pays sont sortis de l'étalon-or en raison du poids important des dettes nationales. Certains pays, au sortir de la guerre, avaient des dettes nationales égales à plus de 2 à 5 fois leur PIB ! Dans de telles conditions, les états ont décidé de rembourser ces dettes en créant de la monnaie, ce qui leur a demandé de sortir de l'étalon-or. Cette création monétaire a entrainé des périodes d'hyperinflation, à savoir des inflations de plus de 50 % par an, qui ont ruiné de nombreuses économies nationales, ainsi que de nombreux épargnants. Autant dire que le contrôle de la monnaie n'était pas l'idée du siècle dans de telles conditions.

Par la suite, dans les années 1980, les états ont progressivement abandonné l'étalon-or, dans une situation où rembourser la dette avec la création monétaire n'était pas à l'ordre du jour. Aucune hyperinflation n’eut lieu, mais cela a quand même entrainé de l'inflation. Les états imprimaient beaucoup de monnaie, ce qui entraina l'apparition d'une inflation élevée avec un taux de chômage lui aussi élevé. Cette coexistence d'un chômage et d'une inflation élevée a valu le nom de stagflation à cette période. Les banques centrales ont alors tenté de contrôler la masse monétaire, en espérant que cela réduirait l'inflation. Un tel regain d'intérêt pour le contrôle de la masse monétaire provenait de l'influence d'une école de pensée économique, le monétarisme, qui mettait au premier plan le rôle économique de la masse monétaire. La création monétaire était alors gouvernée par un principe simple : faire en sorte que la croissance de la masse monétaire soit strictement égale à la croissance de l'économie. Le but était de limiter l'inflation, qui était très importante à l'époque, la politique monétaire étant un des nombreux instruments mis en œuvre à l'époque. Si les tentatives de la banque centrale américaine ont bien permis de limiter l'inflation, elles ont été de véritables échecs pour ce qui est de contrôler la masse monétaire entre 1979 et 1982, les banques centrales ayant systématiquement raté leurs objectifs de masse monétaire. C'est alors que les banques centrales ont abandonné leur idée de contrôler finement la masse monétaire.

La stabilité des taux de change

Suite à la sortie de l'étalon-or, de nombreux pays ont décidé de stabiliser leurs taux de change. Leurs efforts ont mené à la création d'un système monétaire international, nommé le système de Bretton-Woods, en 1944. Sous un tel système, la banque centrale va créer ou détruire de la monnaie afin de garder un taux de change constant. On verra dans quelques chapitres comment la banque centrale influence les taux de change. Cependant, ce système n'était pas très adapté pour garantir la prospérité nationale. Il pouvait imposer de réduire la quantité de monnaie alors que l'économie nationale avait au contraire besoin d'un stimulus monétaire. Par exemple, si les taux de change baissaient en pleine récession, la banque centrale devait réduire fortement la création monétaire pour garder les taux de change fixes, alors que la lutte contre les récessions demandait de faire l'inverse. La politique monétaire avait encore une fois les mains liées et ne pouvait créer de la monnaie comme elle le devait pour garantir le plein emploi.

De nos jours, ce système de contrôle des taux de change est encore utilisé par certains pays. Pour les petits pays, extrêmement dépendants des importations, la stabilité des prix est obtenue par le biais de la stabilité des taux de change, le niveau général des prix étant extrêmement dépendant des prix importés. La plupart de ces petits pays fixent le taux de change de leur monnaie sur une autre monnaie, généralement le dollar, dont les variations sont relativement faibles. La banque centrale de ces pays est généralement une caisse d'émission, à savoir une banque centrale qui se préoccupe de garder les taux de change avec le dollar (plus rarement l'euro) fixe. Ce mécanisme permet de limiter l'inflation et de lutter assez efficacement contre les récessions, qui sont souvent induites par une hausse des prix importés. Par contre, les pays plus grands n'ont pas vraiment de bénéfices à utiliser une caisse d'émission et préfèrent gérer leur monnaie eux-mêmes. Ils utilisent donc des taux de change flottants, et se concentrent sur l'inflation globale, faiblement dépendante des prix importés.

La stabilité des prix

De nos jours, les banques centrales ont pour objectif principal de garantir la stabilité des prix, à savoir limiter l'inflation à des valeurs raisonnables. La stabilité des prix est aujourd'hui l'objectif principal de la plupart des banques centrales actuelles, plus d'un quart d'entre elles n'ayant que cet objectif en tête. Il faut dire que les banques centrales, de par leur possibilité de créer la monnaie, peuvent influencer la valeur de celle-ci et donc le niveau des prix. Le chapitre sur la théorie quantitative de la monnaie donnera un argument fondamental quant au choix de l'objectif de stabilité des prix assigné aux banques centrales. On verra dans quelques chapitres que cibler l'inflation permet de lutter efficacement contre les récessions et stabilise l'économie autour du plein emploi. Quand une récession a lieu, elle se traduit le plus souvent par une diminution de l'inflation, si ce n'est par une déflation. Pour éviter cela, la banque centrale peut alors stimuler la demande et lutter contre la récession directement à la source. Elle n'a pas les mains liées par le contrôle des taux de change ou par les réserves en or. Ce système permet aussi à la banque centrale de créer suffisamment d'argent pour lutter contre la récession, mais pas suffisamment pour entrainer des dégâts. Les situations d'hyperinflation sont notamment impossibles si la banque centrale s'engage à respecter son objectif de 2% d'inflation.

La majorité des banques centrales tente de garder l'inflation proche d'une certaine valeur, appelée cible d'inflation, souvent proche de 2 %. Le choix de la cible d'inflation est à la discrétion de la banque centrale, mais il est admis que la cible d'inflation doit être légèrement positive. Cela a divers avantages comparé à un taux d'inflation nul, notamment celui d'éviter la déflation, dont on verra qu'elle a une influence néfaste sur l'économie d'ici quelques chapitres. De plus, cela permet à la banque centrale de gérer plus facilement ses taux à court-terme, en évitant que ceux-ci butent sur la limite basse des taux (le taux zéro). Mais surtout, cela réduit les effets néfastes de l'inflation sur l'économie, tout en conservant les quelques rares effets positifs. Je vous renvoie au chapitre sur l'inflation, au début de ce livre, pour ceux qui auraient oublié quels sont les effets de l'inflation sur l'économie.

De nos jours, beaucoup de banques centrales ont une cible d'inflation égale à 2%. Il faut préciser que cette cible a cependant une interprétation assez peu intuitive. La cible n'est pas un plafond, mais une valeur moyenne sur une longue période. Par valeur moyenne, on veut dire que la banque centrale est autant inquiète d'une inflation à 3% qu'une inflation à 1%. La cible n'est pas un plafond qu'il ne faut pas dépasser, et que la banque centrale tente de respecter à tout prix. La banque centrale peut accepter des déviations temporaires de la cible, tant qu'elles sont temporaires et qu'elles sont de faible intensité. Par exemple, il est possible que la banque centrale laisse l'inflation dépasser temporairement la cible de 2% suite à une récession où l'inflation était faible. Depuis la crise de 2008, un débat s'est fait jour chez les économistes, certains souhaitant une cible d'inflation plus haute, de l'ordre de 3 à 4%. L'argument est que la banque centrale aura alors plus de marge pour diminuer les taux en cas de récession ou de forte baisse de l'inflation, vu que les taux seront naturellement plus élevés (les taux étant reliés à l'inflation, comme dit dans le chapitre précédent).

Les instruments de politique monétaire

La politique monétaire est le fait de la banque centrale, qui la met en œuvre. Pour mettre en œuvre sa politique monétaire, la banque centrale dispose d'instruments de politique monétaire : les taux d'intérêt directeurs, la base monétaire, le taux de réserve, etc. Elle décide quelle valeur donner aux taux directeurs, combien de monnaie imprimer, s'il faut acheter des obligations sur le marché monétaire, etc. Pour le dire autrement, la banque centrale configure ses instruments de manière à respecter ses objectifs macroéconomiques. De nos jours, l'instrument utilisé est le taux directeur, les autres instruments étant des instruments non-conventionnels, utilisés dans des situations particulières.

Les canaux de transmission et la fonction de réaction de la banque centrale

Les instruments de politique monétaire influencent directement ou indirectement la masse monétaire et les taux d'intérêts. Une variation des taux ou de la masse monétaire se transmet aux autres variables macroéconomiques, ce qui a des conséquences assez diverses sur l'économie. Les taux ou la monnaie peuvent, par exemple, impacter le PIB, l'inflation, le niveau des prix, le taux de change, etc. Dit autrement, la politique monétaire se transmet aux variables macroéconomiques, par divers mécanismes. La transmission peut se faire par des intermédiaires : par exemple, une variation des taux influence l'investissement, qui lui-même influence le PIB, qui influence le chômage et l'inflation, etc. En clair, la transmission de la politique monétaire s'effectue par des chaines de causes à effets, qui portent les noms de canaux de transmission de la politique monétaire. Ceux-ci peuvent être mis en équation, certains assez facilement mais d'autres plus difficilement. De nos jours, les banques centrales tentent de cibler l'inflation, ce qui fait que les canaux de transmission se résument à des équations de la forme :

$\pi =f(i,M,Y,P,...)$, avec Y le PIB, P le niveau des prix, e le taux de change etc.

La banque centrale ne décide pas sa politique arbitrairement, mais sur la base des variables macroéconomiques. Elle analyse le niveau des prix, le PIB, et d'autres variables macroéconomiques, comme les taux de change, et en déduit ce qu'elle doit faire. En clair, elle réagit aux variables macroéconomiques : toute variation pertinente de ces variables doit être perçue par la banque centrale et donner lieu à une réaction si besoin est. Par exemple, la banque centrale doit réagir quand une récession a lieu, afin de la circonvenir. Si elle voit que le PIB chute brutalement et de manière assez importante, elle doit modifier sa politique et revoir ses taux directeurs. On peut résumer le comportement de la banque centrale par une fonction mathématique, la fonction de réaction de la banque centrale, qui donne le niveau des taux ou de la masse/base monétaire en fonction des autres variables économiques. La fonction de réaction est une fonction de la forme suivante, avec $i$ le taux d'intérêt (directeur) et $M$ la masse monétaire. On utilise la première forme dans les modèles Wickseliens, ceux qui supposent que la banque centrale contrôle les taux, et la seconde dans le modèles monétaristes, qui supposent quant à eux que la banque centrale contrôle la masse monétaire.

$i=f(Y,P,\pi ,e,\cdot \cdot \cdot )$, avec Y le PIB, P le niveau des prix, e le taux de change etc.

$M=f(Y,P,\pi ,e,\cdot \cdot \cdot )$, avec Y le PIB, P le niveau des prix, e le taux de change etc.

Relations entre instruments de politique monétaire et variables macroéconomiques. Canaux de transmission et fonction de réaction de la banque centrale.

Les contraintes sur les instruments de politique monétaire

La banque centrale use de ses instruments pour atteindre ses objectifs. Le statut juridique peut contraindre leur usage des instruments ou au contraire laisser une marge de manœuvre à la banque centrale pour ce qui est des moyens employés. La politique monétaire peut être soit discrétionnaire ou basée sur une règle monétaire.

Dans le cas discrétionnaire, la banque centrale pouvant faire ce qu'elle souhaite pour atteindre ses objectifs. Elle peut fixer les taux comme elle le veut ou faire varier la masse monétaire selon ses désirs. Le défaut de cette approche est que le comportement de la banque centrale est imprévisible, ce qui peut totalement contrarier certaines décisions économiques qui demandent de parier sur l'avenir. Quelques études théoriques ont montré que les politiques monétaires discrétionnaires ont tendance à créer plus d'inflation que leurs opposées basées sur une règle. Un tel biais inflationniste a été montré en premier lieu par les travaux de Barro et Gordon, datés de 1983. L'inflation dépasse alors l'inflation normale, ciblée par la banque centrale. Ce biais provient en grande partie de la volonté de la banque centrale de stimuler la production, afin d'augmenter le PIB.

Opposées à la politique discrétionnaire, les règles monétaires contraignent l'utilisation des taux ou de la masse monétaire par la banque centrale. La banque centrale n'est donc pas libre d'utiliser les moyens qu'elle souhaite pour atteindre ses objectifs. Souvent, ces règles contraignent la manière dont la banque centrale doit fixer ses taux en fonction de l'inflation ou de la production. D'autres règles contraignent l'évolution de la masse monétaire. Par exemple, Friedmann a proposé de faire augmenter la masse monétaire d'un pourcentage fixe par an, d'une valeur de 3%. Ce genre de politique monétaire est facilement prédictible, stabilisant ainsi les marchés. Les marchés peuvent en effet plus facilement anticiper les évolutions futures des taux ou de la masse monétaire.

L'indépendance des banques centrales

Une autre variable précisée par les statuts juridiques est l'indépendance de la banque centrale vis-à-vis du pouvoir politique. Quand la banque centrale n'est pas indépendante, celle-ci doit obéir aux injonctions du pouvoir politique, qui décide de la politique monétaire à tenir. Avec une banque centrale indépendante, l’État ne peut pas décider de la politique monétaire. Si cette indépendance est importante, c'est que le pouvoir politique a intérêt à pratiquer une politique monétaire plutôt qu'une autre, que ce soit sous la pression de l'opinion publique, de lobbys, des banques, ou pour favoriser ses chances de réélection. Par exemple, un pays endetté préférera financer sa dette publique par la banque centrale, au lieu de recourir à des hausses d'impôts ou de réduire les dépenses. Comme autre exemple, un gouvernement peut utiliser sa banque centrale pour dévaluer les taux de change afin de booster les exportations.

Vu que ces politiques se traduisent le plus souvent par de l'inflation, on devine que l'inflation sera plus faible et plus stable avec une banque centrale indépendante. Les études sur le sujet semblent indiquer que les pays avec une banque centrale dépendante du pouvoir politique ont une inflation nettement supérieure aux pays avec une banque centrale indépendantes, sans que cela se traduise par des taux de chômage ou de dette publique significativement différents.

Corrélation entre indépendance des banques centrales et inflation nationale.

La banque centrale européenne

La banque centrale européenne, ou BCE, est bien plus indépendante du pouvoir politique que ne le sont la réserve fédérale ou la banque du Japon. On peut clairement dire qu'il s'agit d'une des banques centrales les plus indépendantes au monde. Son indépendance juridique est garantie par le traité de Lisbonne, dans l'article numéro 123, que voici :

"Il est interdit à la Banque centrale européenne et aux banques centrales des États membres, ci-après dénommées « banques centrales nationales », d'accorder des découverts ou tout autre type de crédit aux institutions, organes ou organismes de l'Union, aux administrations centrales, aux autorités régionales ou locales, aux autres autorités publiques, aux autres organismes ou entreprises publics des États membres ; l'acquisition directe, auprès d'eux, par la Banque centrale européenne ou les banques centrales nationales, des instruments de leur dette est également interdite."

"Le paragraphe 1 ne s'applique pas aux établissements publics de crédit qui, dans le cadre de la mise à disposition de liquidités par les banques centrales, bénéficient, de la part des banques centrales nationales et de la Banque centrale européenne, du même traitement que les établissements de crédit privés."

La Bank Of Japan

La banque du Japon est clairement peu indépendante. Si les textes semblent indiquer que "l'autonomie de la Bank Of Japan doit être respectée", d'autres textes précisent que "La Bank Of Japan doit toujours rester en contact étroit avec le gouvernement et procéder à un échange de vues suffisant avec lui". La politique de dévaluation de la banque centrale, menée sous le gouvernement de Shinzo Abe, a clairement montré que la banque centrale est sous le joug du gouvernement japonais.

La communication de la banque centrale

Les banques centrales, même non-contraintes, doivent quand même rendre des comptes sur ce qu'elles font. Ce qui nous amène à parler de la transparence de la politique monétaire, à savoir comment la banque centrale communique sur ses décisions.

Un changement de culture : de la discrétion vers la transparence

Les banques centrales avaient autrefois une culture de la discrétion. Elles ne commentaient pas leurs décisions de politique monétaire et n'en donnaient pas les raisons. Elles communiquaient peu avec les marchés ou les responsables politiques. Les communications de presse étaient sibyllines, peu détaillées, jargonneuses, volontairement incompréhensibles par les marchés. Et c'était à dessein que les banques centrales procédaient ainsi. D'où la boutade d'Allan Greenspan (ancien directeur de la réserve fédérale américaine) : «Si vous avez compris ce que je viens de dire, c’est que vous ne m’avez peut-être pas bien entendu.». Et pire : les banques centrales d’avant aimaient faire des surprises aux marchés. Elles changeaient leurs taux du jour au lendemain, en mettant les marchés devant le fait accompli. Par exemple, il arrivait que la FED d’avant/pendant Greenspan prenne tout le monde au dépourvu en n’annonçant même pas ses changements de taux). En clair, les banques centrales d'avant n'étaient pas transparentes du tout.

De nos jours, les banques centrales sont devenues bien plus transparentes. Elles préviennent de leurs changements de taux à l'avance, tentent de lisser l'évolution des taux pour ne pas brusquer les marchés, font beaucoup de conférences de presse pour expliquer leur politique, justifient chaque décision devant les marchés et responsables politiques, etc. Leur communication tend à être la plus claire possible, histoire d'être interprétée correctement par les marchés, mais aussi plus fréquente qu'avant. La culture de la discrétion autrefois monnaie courante a aujourd'hui totalement disparue. Aux états-unis, ce changement vers plus de transparence a eu lieu lors de la nomination de Ben Bernanke à la tête de la réserve fédérale, en 2005.

Les avantages/inconvénients de la transparence

Les raisons derrière ce changement de comportement sont multiples, allant d'arguments théoriques (anticipations rationnelles, prime de risque liée à l'incertitude), à des arguments purement politiques.

Le premier argument est que la communication des banques centrales aide les agents à former des anticipations correctes. En dévoilant les informations dont elle dispose, ainsi que la manière dont elle les interprète, la banque centrale informe les agents de la situation macroéconomique. Ces informations modifient les anticipations d'inflations des agents économiques pour les rendre plus rationnelles, plus proches de la réalité. En somme, la transparence des banques centrales rend les anticipations des agents plus rationnelles. Cet effet sur les anticipations a un effet macroéconomique notable, vu que, je le rappelle, l'inflation est performative (les anticipations influencent l'inflation réelle). En communiquant correctement, les banques centrales peuvent donc agir sur l'économie réelle par le biais des anticipations. On peut voir la banque centrale comme une sorte de joueur de flute, dont les paroles guident les marchés vers l'objectif souhaité. Il s'agit d'ailleurs d'un des canaux de transmission de la politique monétaire, appelé canal des anticipations. C'est surprenant, mais c'est le cas : la communication de la banque centrale est un instrument de politique monétaire comme un autre !

Le second argument théorique est qu'une banque centrale transparente est plus crédible, ce qui facilite son travail. Une banque centrale crédible est une banque centrale que les marchés croient : ils savent qu'elle ne ment pas, qu'elle ne cherche pas à tromper les marchés. Les agents savent alors qu'ils peuvent utiliser sans risque les informations divulguées par la banque centrale. La communication de la banque centrale est fiable, et peut agir sur les anticipations sans risque. Par contre, une banque centrale non-crédible n'est pas fiable et les informations qu'elle divulgue sont généralement peu dignes de confiance. Par exemple, une banque centrale peut souhaiter mener une politique expansionniste pour des motifs politiques (faire baisser le chômage avant une élection), mais le cacher par une communication un peu arrangée. Soit elle cherche à tromper les marchés en sous-estimant les effets de sa politique, soit elle est incompétente et ses informations sont juste mauvaises. Dans les deux cas, sa communication n'a pas d'effets sur les anticipations des agents, ou alors un effet contraire à celui recherché. En clair, la crédibilité de la banque centrale favorise un fonctionnement correct du canal des anticipations. D'où la nécessité d'une certaine transparence, mais aussi d'une indépendance vis-à-vis du pouvoir politique. Ces deux mesures rendent la banque centrale lus crédible, notamment en luttant contre son biais inflationniste.

Les banques et leur bilan comptable

Le bilan comptable est un "résumé" des possessions et dettes d'une entreprise (ici, la banque), composé d'un actif et d'un passif. L'actif correspond à ce que la banque possède, tandis que le passif est l'ensemble de ce que doit la banque à ses créanciers et investisseurs.

L'actif correspond à l'ensemble des actifs détenus par la banque centrale, essentiellement les prêts qu'elle a accordés, ainsi que des obligations, actions, possessions immobilières et réserves de change. L'actif est précisément calculé en faisant la somme du prix de chaque actif par sa quantité détenue par la banque. L'actif de la banque est composé d'actifs (ici indicés) $A_{i}$, qui ont chacun un prix $P_{i}$. L'actif total de la banque centrale vaut donc :

$A=\sum _{i}A_{i}\times P_{i}$.

La variation de l'actif peut avoir deux sources : soit l'achat d'actifs, soit l'augmentation du prix des actifs déjà achetés.

$\Delta A=\sum _{i}(A_{i}\times \Delta P_{i})+(\Delta A_{i}\times P_{i})$.

Le passif est la somme des dettes de la banque et de son capital (la dette est l'argent dû à ses créanciers, alors que le capital est l'argent que la banque doit à ses actionnaires/propriétaires). Le passif de la banque est composé des dépôts sur ses comptes, des dettes qu'elle doit à divers investisseurs (émission d'obligations ou dettes auprès d'autres banques) et des fonds propres (le capital). Notez que les dépôts sont considérés comme des dettes : quand vous déposez votre argent à la banque, celle-ci vous doit cet argent et accepte d'honorer sa dette à la moindre demande de retrait, ce qui ressemble plus à une dette qu'à du capital. Précisons que l'actif et le passif doivent être égaux, sans quoi le bilan comptable est automatiquement erroné.

Actif	Passif
Prêts : Prêt à la clientèle (particuliers ou professionnels). Prêts à d'autres banques, sur le marché interbancaire.	Dette : Dépôts de la clientèle, dont comptes courants et livrets. Emprunts interbancaires, réalisés auprès d'autres banques, d'assureurs. Emprunts obligataires, réalisés sur le marché obligataire.
Réserves bancaires (obligatoires ou excédentaires)
Titres et autres actifs (obligations, actions et immobilier)	Capital : Fonds propres

Précisons que certains actifs peuvent se déprécier, c'est à dire perdre leur valeur. Par exemple, prenons le cas où une banque détient un patrimoine immobilier à son actif. Si le prix de ses actifs immobiliers diminue, suite par exemple à un retournement du marché immobilier, alors cela se répercute sur l'actif dans son bilan. La colonne de l'actif doit diminuer du même montant que les pertes encaissées. Vu que l'actif doit être systématiquement égal au passif, le passif doit automatiquement diminuer du même montant. Mais la banque ne peut pas répercuter cette baisse sur les dettes qu'elle doit honorer : une entreprise doit être capable de rembourser ses dettes et donc avoir un actif égal au montant des dettes pour les couvrir. Elle est donc obligée de répercuter cette perte sur son capital. Ainsi, les pertes d'une banque ne sont pas encaissées par ses créanciers ou ses déposants, mais par ses actionnaires/propriétaires. Si le capital tombe à zéro, une banque commerciale fait faillite (par contre, ce n'est pas le cas pour une banque centrale, comme on le verra plus loin).

Le bilan comptable de la banque centrale

Le bilan comptable de la banque centrale fait appel aux prêts qu'elle accorde aux banques commerciales, aux actifs qu'elle possède, ainsi qu'aux réserves et espèces.

Actif	Passif
Prêts aux banques et établissements de crédit	Espèces (billets et pièces)
Titres : obligations et actions (obligations d'état, le plus souvent)	Réserves (comptes courants des banques)
Autres, comme les réserves de devises ou d'or	Autres, tels le capital social et les fonds propres (ne font pas partie de la base monétaire)

L'actif d'une banque centrale

Au niveau de l'actif de la banque centrale, on trouve évidemment les prêts qu'elle accorde aux banques commerciales, mais aussi des obligations, des actions, des réserves de change, et d'autres actifs qu'elle a acquis sur le marché. Pour simplifier, on peut classer les actifs d'une banque centrale en plusieurs types principaux : l'or, les réserves de change, le solde du gouvernement et les instruments financiers.

Actif d'une banque centrale

Stocks d'or et de métaux précieux
Solde du gouvernement
Réserves de change	Devises
	Stocks d'or, autres
Instruments financiers	Prêts aux banques et établissements de crédit
	Titres : obligations et actions (obligations d'état, le plus souvent)

L'or détenu par les banques centrales est généralement un reliquat de l'étalon-or, l'ancien système monétaire basé sur l'or qui s'est effondré durant la période comprise entre les années 40 et 80. Ce qui explique que les banques centrales ont souvent beaucoup d'or, comparé au reste des entreprises, souvent plusieurs tonnes par banque centrale. La gestion comptable de cet actif est quelque peu étrange et il n'existe pas de normes comptables pour sa valorisation. Ce qui fait que le traitement des réserves d'or varie beaucoup suivant les banques centrales, chacune faisant à sa sauce. Une partie de l'or détenue fait en fait partie des réserves de change, alors qu'une autre n'a rien à voir avec les marchés des changes. Suivant la banque centrale, la distinction est faite dans le bilan comptable ou non. La valeur des réserves d'or est comptabilisé soit en tenant compte de son prix de marché (le prix de vente actuel), soit du prix auquel la banque centrale a acquis l'or. Là encore, tout dépend de la banque centrale.

Les réserves de change sont des actifs qui sont libellés dans une monnaie étrangère. Par exemple, certaines banques centrales possèdent beaucoup d'obligations d'états de pays étrangers, en raison de leur politique monétaire. Elles peuvent aussi posséder de la monnaie de pays étrangers, sous forme d'espèces ou de dépôts bancaires. C'est surtout le cas pur les banques centrales qui manipulent leur taux de change, ou qui interviennent sur les marchés des devises. Beaucoup de pays en développements sont dans ce cas et leurs réserves de change sont majoritairement en dollars. Évidemment, la valeur des réserves de change varie avec les taux de change, ce qui fait que la banque centrale peut faire des plus-values ou des moins-values suivant la manière dont évoluent les devises.

Pour certaines banques centrales, leur bilan contient l'argent de l'état, le solde du gouvernement L'état, comme tout autre agent économique de grande envergure, a besoin d'avoir un ou plusieurs comptes courants. Certains pays ont fait le choix de déléguer cela à des banques commerciales, qui se chargent de la gestion des deniers publics. C'est un choix adéquat pour les pays sans banques centrales, mais la majorité des pays avec une banque centrale préfère que ce soit la banque centrale qui serve de banque au gouvernement. Pour ces pays avec une banque centrale, l'état a un compte courant à la banque centrale. Les impôts viennent s'accumuler sur ce compte courant, alors que les dépenses du budget général en sortent. L'argent de l'état est alors placé dans les actifs de la banque centrale, au même titre que les réserves de change. Néanmoins, si la banque centrale gère les virements et opérations courantes, la loi limite les opérations qu'elle peut faire sur ce compte courant d'état. Dans de nombreux pays, elle n'a pas le droit d'utiliser la création monétaire pour y ajouter de la monnaie, que ce soit sous forme de don ou de prêts. Dit autrement, elle n'a pas le droit de financer directement les états.

Passons maintenant aux instruments financiers détenus par la banque centrale. On peut noter que les banques centrales préfèrent investir dans des actifs relativement sûrs, essentiellement des obligations d'état. Peu de banques centrales possèdent des actions ou des instruments similaires, la seule exception étant la banque centrale du Japon, qui détient une grande partie des ETFs sur les indices japonais. À titre d'exemples, les graphiques ci-dessous montrent la composition du bilant des banques centrales japonaise et américaines, qui sont majoritairement dominés par les obligations d'état. On voit que la banque centrale japonaise conserve une grosse majorité de ses actifs sous la forme de dette de l'état japonais. La réserve fédérale américaine n'est pas en reste, même si les proportions sont moindres que pour la banque du Japon. On peut remarquer qu'à la suite de la crise économique de 2008, la réserve fédérale américaine a acheté de nombreux actifs basés sur des crédits, les fameux MBS impliqués dans la crise financière de 2008.

Bilan comptable de la Banque du Japon.

Bilan comptable de la Federal Reserve.

Le passif d'une banque centrale

L'argent détenu par la banque centrale, son passif, est la somme de son capital et de ce qu'on appelle la base monétaire. Il est composé d'une faible portion de capital, des espèces en circulation et de ce qu'on appelle les réserves bancaires.

Passif d’une banque centrale

Base monétaire	Espèces en circulation (currency)
	Réserves bancaires	Espèces conservées par les banques (vault cash)
		Dépôts électroniques à la banque centrale (réserves électroniques)
Passif hors base monétaire	Capital de la banque centrale

Les réserves bancaires correspondent à de l'argent que les banques commerciales possèdent. Elles regroupent à la fois la monnaie électronique et l'argent physique possédé par la banque. Outre les pièces et billets stockées dans les coffres de la banque, les banques commerciales conservent leur monnaie électronique sur un compte courant à la banque centrale. Dans ce qui va suivre, nous allons utiliser le terme "réserves électroniques" pour parler de la monnaie électronique stockée à la banque centrale. Au passage, sachez que la banque centrale peut échanger les réserves électroniques contre des espèces à n'importe quel moment, sur simple demande. Cette opération ne fait que convertir de la monnaie électronique en billets ou pièces, mais ne change pas le montant total des réserves de la banque.

Les réserves, électroniques ou en espèces, ont toutes les caractéristiques de la monnaie. Elles peuvent circuler d'une banque à l'autre (lors d'un virement entre banques), être prêtée, être épargnée à la banque centrale, etc. Quand vous faites un virement vers une autre banque, ce n’est rien de plus qu'un mouvement de réserves : votre banque donner un montant équivalent de réserves à la banque réceptrice, argent qui est ensuite crédité au destinataire. Les banques mettent donc en réserve une partie de l'argent de leurs déposants, pour servir efficacement les retraits.

Les réserves proviennent des dépôts des clients, mais peuvent aussi provenir de la banque centrale. La banque centrale a la possibilité de prêter des réserves aux banques commerciales qui en font la demande. Il va de soi que plus le taux est élevé, plus les banques préféreront éviter d'utiliser l'emprunt à la banque centrale : la quantité de réserve sera alors assez faible. Par contre, des taux bas inciteront les banques à emprunter au guichet de la banque centrale, ce qui augmente la quantité de réserves en circulation. In fine, ces réserves pourront alors soit être prêtées, soit servir à acheter des actifs, soit être conservées telles quelles.

Maintenant, précisons ce que l'on veut dire par : "les réserves proviennent en partie des dépôts des clients". Pour être plus précis, elles correspondent à une fraction des dépôts que les banques conservent à la banque centrale, le reste étant prêté ou utilisé d'une manière ou d'une autre par la banque. La raison à cela est qu'elles sont tenues de le faire par la réglementation bancaire, mais aussi parce que ces réserves leur permettent d'assurer les retraits d'argent de leurs clients. Du fait de la réglementation, les banques doivent conserver une fraction minimale des dépôts sous la forme de réserves obligatoires. Précisément, la réglementation financière les oblige à en conserver un certain pourcentage, ce pourcentage étant appelé le taux de réserve. Mais les banques commerciales sont souvent assez prudentes et peuvent mettre en réserve un peu plus que ce qu'oblige la réglementation. La plupart du temps, les banques n'hésitent pas à garder des réserves au-delà de ce qui est requis par le taux de réserve, ces réserves de précaution étant appelées des réserves excédentaires. Pour donner un exemple, de nombreux pays n'imposent pas un niveau minimal de réserves, leur taux de réserve étant nul... Et pourtant, les banques de ces pays gardent environ 1 à 5% de réserves sur leurs comptes.

Enfin, outre les réserves, la base monétaire contient aussi les pièces et billets en circulation dans l'économie. Attention cependant à ne pas confondre avec les espèces conservées par les banques. Il faut bien faire la distinction entre les espèces stockées par les banques dans leur coffre, et les espèces qui ne sont pas dans une banque. Les pièces et billets dans votre porte-monnaie font bien partie de la base monétaire, mais elles ne font pas partie des réserves bancaires vu qu'elles ne sont détenues par aucune banque. Il n'existe pas de terminologie française pour exprimer cette distinction, mais les anglo-saxons font la différence entre vault cash et currency, le premier terme correspondant à l'argent conservé dans les coffres des banques, alors que le second correspondant à l'argent qui circule dans l'économie hors des banques. Cette petite différence a de grandes implications. En effet, les espèces en circulation font partie à la fois de la base monétaire et de la masse monétaire. Par contre, ce n'est pas le cas pour les réserves en espèces, qui font uniquement partie de la base monétaire, mais ne sont pas comptées dans la masse monétaire. Cela a des implications pour la création monétaire stricto sensus, comme nous le verrons plus bas.

Base monétaire

Espèces en circulation (currency)
Réserves bancaires	Espèces conservées par les banques (vault cash)
	Dépôts électroniques à la banque centrale (réserves électroniques)

Après avoir vu la base monétaire, parlons du reste du passif, à savoir le capital de la banque centrale. Les banques centrales ont, comme toutes les banques, une organisation capitalistique, bien qu'elle soit assez spéciale. En tout cas, elles possèdent des fonds propres et des capitaux, sous la forme d'actions. Sauf que les actions de la banque centrale ne sont pas normalement accessibles en bourse, mais sont détenues intégralement par l'état. Par exemple, la banque centrale française est totalement détenue par l'état français, qui en possède la totalité des actions. Il existe cependant quelques exceptions, où la banque centrale est détenue en partie par l'état et en partie par des investisseurs privés. C'est le cas pour les banques centrales des états-unis, du Japon, de Grèce, de Belgique, De Turquie, d'Italie, de Suisse, de l'Afrique du Sud, et de San Marino. Les banques centrales du Japon, de Grèce, de Belgique et de Suisse sont même cotées en bourse ! Mais la plupart de ces banques centrales ne verse pas de dividende et leurs actions sont sans droits de vote.

La situation est un peu plus complexe dans le cas des unions monétaires, où plusieurs pays partagent la même banque centrale. Dans ce cas-là, les différents pays doivent se répartir les actions de la banque centrale. Tel est le cas de l'union européenne, où la banque centrale européenne a pour actionnaires les banques centrales de chaque pays de la zone euro. Le poids de chaque banque dans l'actionnariat de la BCE est proportionnel à sa population et au poids du PIB dans la zone euro.

Répartition des actionnaires de la BCE

Les spécificités comptables des banques centrales

La banque centrale a le pouvoir de créer de la monnaie à partir de rien. Mais ce pouvoir peut être limité par son mandat ou d'autres contraintes légales, qui font que la banque centrale ne peut pas créer de monnaie n'importe comment, ni la donner à n'importe qui. Mais si on met ces contraintes de coté, alors la banque centrale peut créer de la monnaie à partir de rien, sans avoir à produite ou vendre quelque chose. Elle peut théoriquement fabriquer des billets ou des pièces et les mettre en circulation, avec ou sans contreparties. Et elle peut faire la même chose avec de la monnaie électronique, qu'elle peut créer à partir de rien et mettre en circulation. Cependant, la mise en circulation ne se fait pas forcément sans contrepartie : en temps normal, la banque centrale échange la monnaie qu'elle crée contre quelque chose qui a de la valeur (un actif financier en général). La création de la monnaie se fait donc en contrepartie de quelque chose qui a une valeur équivalente, du moins en temps normal.

Du fait de sa création monétaire, la banque centrale peut voir son actif et son passif évoluer dans le temps. Si l'actif de la banque centrale se déprécie, cela doit se répercuter sur le passif, vu que passif et actifs doivent systématiquement rester égaux. Comme pour toutes les banques, cela est réalisé en réduisant le capital de la banque centrale, sans répercussion possible sur ses dettes. Les propriétaires de la banque centrale encaissent donc les pertes, sans que ses créanciers ne soient aucunement touchés. Il est possible que, suite à des dépréciations importantes, le capital de la banque centrale devienne nul, voire négatif. En théorie, si le capital d'une banque commerciale est à zéro, elle fait faillite. Mais ce n'est pas le cas d'une banque centrale, qui peut fonctionner avec un capital négatif indéfiniment, sans aucun problème ! C'est même la définition d'une banque centrale : c'est la seule banque à continuer de fonctionner alors que son capital est nul ou négatif : l'état ne peut pas faire faillite.

Cependant nombre d'états préfèrent respecter les règles appliquées aux autres banques et doivent alors mettre la main au porte-monnaie pour compenser les pertes de la banque centrale. La banque centrale respecte alors certaines règles de comptabilité, communes à toutes les banques. Par exemple, on considère que l'actif et le passif de la banque centrale doivent être égaux. La création monétaire augmentant mécaniquement le passif, elle doit fatalement augmenter l'actif d'un même montant. Ainsi, la création monétaire doit se faire en contrepartie de quelque chose de réel, qui a de la "valeur" : des actifs, tels des contrats de prêt, des actions, obligations, devises ou autres. Cela garantit que la monnaie n'est pas créée sans contrepartie, sans quelque chose qui représente de la valeur dans l'économie.

La création de monnaie sans achat d'actif reste cependant possible, mais n'est pas une politique envisagée à l'heure actuelle. Il s'agit d'une forme de création monétaire qui porte le nom de monnaie hélicoptère (helicopter money). En théorie, la banque centrale doit être recapitalisée par l'état, pour compenser ses pertes. Du moins, c'est le cas si la banque centrale suit les règles de comptabilité usuelles, communes à toutes les banques. Mais en théorie, il est possible de passer outre cette règle, et de ne pas recapitaliser la banque centrale après une période de monnaie hélicoptère. De l'argent est alors créé sans contrepartie, ce qui est la forme la plus pure de "planche à billets".

Le seigneuriage

Il se peut qu'en poursuivant sa politique monétaire, la banque centrale fasse des profits. Par exemple, elle peut recevoir les intérêts sur les prêts qu'elle accorde aux banques, ou recevoir les intérêts des obligations qu'elle détient dans son portefeuille de titres. Elle peut aussi vendre des actifs acquis auparavant, dont la valeur a augmenté depuis leur achat, ce qui arrive souvent avec les obligations. Techniquement, les actifs achetés par la banque centrale versent des intérêts ou des dividendes, source de profit. Il en est de même pour les prêts qu'elle octroie aux banques commerciales, qui versent des intérêts. Le profit de la banque centrale est aussi appelé le seigneuriage.

Le seigneuriage provient de deux sources : la création monétaire elle-même, ainsi que les revenus des actifs (plus-value et intérêts). On peut deviner qu'une politique accommodante, avec beaucoup d'achats d'obligations, va maximiser le seigneuriage. Après tout, les intérêts des obligations détenues par la banque centrale seront reversées à l'état sous forme de dividendes. Et plus la banque centrale possède d'obligations, plus ses revenus obligataires seront élevés. Ainsi, les gouvernements sont naturellement tentés d'utiliser une politique monétaire accommodante, afin que leur banque centrale fasse beaucoup de profits. C'est un bon moyen pour monétiser leur dette.

Le profit de la banque centrale est redistribué à ses actionnaires, à savoir l'état et éventuellement diverses administrations publiques. Il se peut cependant que la banque centrale ne redistribue pas la totalité de ses bénéfices et les conserve pour plus tard. Ce bénéfice non-distribué sert alors à augmenter son capital social (ses fonds propres).

Le bilan des banques commerciales

Les mécanismes comptables vus au début du chapitre valent aussi pour les banques commerciales/privées, qui ont un bilan comptable comme toutes les banques. Si vous regardez les bilans des banques commerciales les plus connues, vous verrez qu'elles ont beaucoup plus de dettes que de capital. Si on regarde le pourcentage du passif sous forme de dettes, on est proche de 90%, voire 97% pour certaines banques. C'est beaucoup plus que pour les autres entreprises et cela met les banques face à un risque de faillite assez élevé. Nous allons expliquer pourquoi elles font cela.

La marge d'intermédiation bancaire

Illustration de la marge d'intermédiation financière.

Le bilan d'une banque est rempli de dette et d'actifs, auxquels on peut adosser un taux d'intérêt, ou du moins un rendement. Qu'il s'agisse des emprunts interbancaires, des prêts financés par la banque, des dépôts bancaires (pensez aux taux des livrets bancaires), des actifs acquis par la banque, des réserves : tous sont rémunérés par un taux d'intérêt (sauf quelques dépôts bancaires, comme les comptes courants, mais c'est un détail). Le fait est que ces taux n'ont pas la même signification selon qu'ils sont adossés à l'actif ou au passif. Les intérêts de ses actifs sont de l'argent qui lui revient. Les intérêts qu'elle perçoit sur ses prêts, sur ses réserves bancaires, ou sur ses actifs, sont autant d'argent qui appartient à la banque. Mais pour les taux des dépôts et dettes de la banque, il s'agit d'un coût : il s'agit des intérêts que la banque doit verser à ses déposants ou à ses créanciers. La banque va naturellement devoir compenser les intérêts qu'elle paye à ses clients/créanciers par les intérêts qu'elle perçoit sur son actif.

La différence entre intérêts perçus sur ses actifs et ceux dus pour son passif est appelée la marge bancaire nette d'intérêt, ou encore la marge d'intermédiation. Il s'agit de l'argent que la banque a réellement gagné une fois qu'elle a versés ses intérêts liés au passif. Évidemment, les intérêts liés à l'actif doivent être supérieurs aux intérêts liés au passif, sans quoi la banque ne peut rembourser ses créanciers/déposants. Pour simplifier, ce n’est possible que si le taux moyen délivré par ses actifs est supérieur au taux moyen de ses dettes (modulo quelques cas particuliers). Ce qui fait que le fonctionnement d'une banque se résume ainsi : emprunter à taux bas pour prêter à taux élevés et empocher la différence entre les deux. Par exemple, prêter à 5% de l'argent emprunté à 3% donne un rendement brut de 2%. La différence entre le taux d'emprunt et le taux de prêt porte un nom : c'est la marge d'intérêt, ou encore le taux de marge d'intermédiation.

Les banques doivent emprunter à un taux plus faible que celui auquel elles prêtent et si possible à un taux le plus bas possible. Pour cela, elles financent leurs prêts en priorité par leurs dépôts, qui ne sont pas rémunérés ou alors avec un taux extrêmement faible. Vous remarquerez que les comptes courants sont pas ou très peu rémunérés, de même que les livrets (qui font partie des dépôts). Ce n'est qu'une fois la quasi-totalité des dépôts utilisés que la banque recourt à l'emprunt interbancaire, dont les taux d'intérêts sont plus élevés que ceux des dépôts. Enfin, elle peut recourir à l'emprunt obligataire, voire à des élevées de capital en bourse, mais le cout de ces opérations est prohibitif et ne peut servir qu'à financer des prêts très rémunérateurs, fort bien rares. Le bilan d'une banque doit donc être composé principalement de dépôts et d'emprunt interbancaire, avec très peu d'emprunts obligataires et un très faible capital.

L'effet de levier bancaire

On vient de voir que les banques empruntent de l'argent pour le prêter, ou du moins pour acheter des actifs rémunérateurs. La banque doit évidemment avoir plus d'intérêts délivrés par ses actifs que d'intérêts à fournir à ses créanciers/déposants. L'utilisation de la dette pour financer des actifs porte un nom : c'est l'effet de levier. Son utilité principale est d'augmenter le rendement d'un investissement, ici ceux de la banque, ce qui plait aux actionnaires/investisseurs. Mais pour cela, il faut paradoxalement maximiser la dette de l'entreprise, du moins tant que le taux de marge d'intérêt est positif. Dans cette section, nous allons voir en quoi l'effet de levier explique pourquoi les banques ont tant recours à l'endettement.

Effet de levier - schéma explicatif

Cependant, les banques ne se financent pas que par l’emprunt, mais aussi sur leurs fonds propres, leur capital : sur l'actif total, une part est financée sur fonds propres et une autre par de l'emprunt. Maintenant, supposons que l'actif a un rendement bien précis, qui sera appelé rendement de l'actif. La part financée sur fonds propres aura un rendement égal au rendement de l'actif, mais ce ne sera pas le cas de la part financée par la dette. La part financée par la dette aura un rendement égal au rendement du capital, auquel il faut enlever le paiement des intérêts de la dette. Le résultat est que la part de l'actif financée par la dette aura un rendement égal à la marge d'intérêt. Rappelons que cette marge d'intérêt est distribuée aux actionnaires uniquement. Par exemple, si les actifs ont un rendement de 5% de rendement et que 3% sont remboursés aux créanciers, les 2% de taux de marge vont aux actionnaires. Le rendement pour les actionnaires dépend du taux de marge d'intérêt (ici, les 2%), mais aussi de la quantité de dettes et de fonds propres et plus précisément du ratio capital/passif. En effet, les 2% sont sur la part financée par la dette, pas sur l'actif total. Le tout est résumé dans le schéma ci-contre. On devine donc qu'à capital égal, il vaut mieux augmenter le plus possible la dette pour profiter de la marge d'intérêt, du moins en tant qu'actionnaire.

Dans ce qui va suivre, nous allons mettre le tout en équations, en posant :

• $i_{a}$ le taux moyen délivré par ses actifs ;
• $i_{d}$ le taux moyen adossé à ses dettes ;
• $A$ son actif et $P$ son passif ;
• $D$ le montant de dettes à son passif (dépôts inclus s'ils sont rémunérés) ;
• $C$ le montant de son capital.

Premièrement, calculons la différence entre ce que la banque touche sur ses actifs et ce qu'elle doit à ses créanciers. Cette différence est destinée à être reversée à ses actionnaires et donne la quantité d'argent auquel le capital donne droit. Nous allons appeler cette différence le rendement net, et nous allons le noter $R_{n}$.

$R_{n}=i_{a}\times A-i_{d}\times D$

Sachant que $A=P=D+C$, on a :

$R_{n}=i_{a}\times (D+C)-i_{d}\times D$

Quelques simplifications algébriques donnent :

$R_{n}=i_{a}\times C+(i_{a}-i_{d})\times D$, où le terme de gauche donne l'argent gagné par investissement en fonds propres, alors que le terme de droite donne l'argent gagné du fait de la marge d'intérêt.

En divisant par C, on trouve le rendement total d'une unité de capital :

${\frac {R_{n}}{C}}=i_{a}+(i_{a}-i_{d})\times {\frac {D}{C}}$

On voit que le rendement d'une banque dépend du rendement de ses actifs $i_{a}$, du taux différentiel d'intermédiation : $(i_{a}-i_{d})$, mais aussi du rapport dette/capital : ${\frac {D}{C}}$. Cela explique pourquoi les banques ont autant de dettes : c'est pour obtenir un rendement maximal pour leurs actionnaires/propriétaires. C'est totalement à l'opposé de ce qu'on observe chez les autres entreprises, où les dépôts sont inexistants et où le capital et les emprunts obligataires sont bien plus importants.

L'utilisation de l'effet de levier n'est pas sans risques, car il fonctionne d'autant mieux que la banque a peu de capital. Le principal est que le ratio capital/passif diminue fortement. Rappelons que pour ne pas faire faillite, la banque doit être capable de répercuter une dépréciation de ses actifs sur son capital, elle doit avoir un capital suffisant pour encaisser des pertes. Or, l'effet de levier augmente fortement la dette et l'actif, sans augmentation du capital. La banque se retrouve donc avec un capital riquiqui et des actifs susceptibles de se déprécier : le risque de faillite est augmenté par l'effet de levier. En conséquence, une banque doit donc faire attention ne pas avoir un ratio capital/dettes trop faible, sans quoi les moindres pertes sur ses actifs peuvent lui faire faire faillite. La réglementation bancaire impose un levier maximal dans la plupart des pays développés, afin de réduire les risques de faillite.

La transformation de maturités

Un point particulier des banques commerciales est qu'elles gèrent des dettes qui ont des liquidités très différentes : d'un côté le passif est composé d'actifs extrêmement liquides, de l'autre l'actif est composé d'actifs assez illiquides. Les dépôts peuvent être retirés quasiment immédiatement, les emprunts interbancaires ont une maturité assez faible : ce sont des instruments très liquides, qui ont une faible maturité. Par contre, les instruments financiers de l'actif ont des maturités plus longues : entre 15 et 30 ans pour les prêts immobiliers, plusieurs années pour les prêts à la consommation, etc. Seules les réserves et les espèces sont liquides et peuvent être virés ou retirés immédiatement. On résume cela par l'adage : "les banques se financent à court-terme et prêtent à long-terme". D'une manière plus technique, on dit que les banques font de la transformation de maturités.

La raison en est simple : c'est pour maximiser le taux de marge d'intérêt. Le fait est qu'il y a une relation mécanique entre maturité d'un prêt et son taux : plus la maturité est longue, plus le risque est important et plus le taux est élevé. Pour profiter de l'effet de levier, les banques sont donc encouragées à emprunter à taux bas, ce qui implique des maturités courtes, pour prêter à des taux hauts, ce qui implique des maturités élevées. La composition du bilan d'une banque s'explique, du moins dans les grandes lignes, par cette utilisation de l'effet de levier bancaire.

Mais la transformation de maturités n'est pas sans risque et expose les banques à un risque de liquidité : si trop de clients retirent leurs encaisses en même temps, les banques n'auront pas assez de liquidités pour rembourser tout le monde. Elles seront alors obligées de revendre leurs titres de dettes pour acquérir les liquidités nécessaires et feront faillite si elles n'y arrivent pas. Pour éviter cela, les banques utilisent une gestion actif-passif, qui consiste à garder suffisamment de liquidités pour garantir les retraits à venir. Elles doivent estimer la quantité de retraits et de remboursements à venir dans les semaines/mois à venir, et elles doivent ajuster leur niveau de liquidités/réserves en fonction.

La création monétaire : vision comptable

Dans ce chapitre, nous allons voir comment la création monétaire se manifeste dans les bilans comptables des banques. Nous allons faire un rappel rapide sur le bilan d'une banque et comment celui-ci est structuré. Nous allons ensuite voir comment les banques peuvent créer de la monnaie, ou du moins semblent le faire, en prêtant. Nous allons voir comment le bilan d'une banque évolue quand elle accorde un prêt.

La création monétaire d'un point de vue comptable

Pour commencer, nous allons analyser la création monétaire d'un point de vue comptable. Précisons que ce mécanisme fonctionne aussi bien pour une banque commerciale que pour les banques centrales : la création monétaire se voit de la même manière dans leurs bilans comptables. Mais faites attention : la vision comptable que nous allons voir ne décrit que d'une manière très imparfaite la création monétaire actuelle. Beaucoup de choses sont passées sous silence et cette vision est même quelque peu trompeuse. Elle cache beaucoup de chose et ne fait que rendre compte d'une partie des faits.

Ne penser qu'en termes de bilan bancaire permet certes de comprendre en partie le processus de création monétaire, mais il amène facilement à des déductions fausses. Par exemple, certains pensent que les banques ne sont pas limitées par les dépôts bancaires ou par la quantité de réserves lorsqu'elles créent de la monnaie. D'autres pensent même que les banques ne sont pas des intermédiaires bancaires et qu'elles ne sont pas tenues de collecter des dépôts pour financer leurs crédits. Mais dans les faits, ce n'est pas du tout le cas. Soyez vigilants quand vous lisez des documents sur le sujet : beaucoup d'erreurs sont dites en se basant purement sur la vision comptable de la création monétaire !

Nous allons voir que, contrairement à ce que les interprétations naïves de la création monétaire font penser, les banques financent leurs crédits/actifs soit par des dépôts, soit par de la dette (en empruntant quand les dépôts viennent à manquer). Elles ne créent pas l'argent des crédits, bien qu'elles aient la capacité de créer de la monnaie (dans une certaine mesure). Tout cela est assez subtil, mais j'espère que la section qui suit l'expliquera clairement. En tout cas, sachez que les interprétations fautives de la création monétaire sont légion sur le net, et que le sujet est bourré de subtilités assez problématiques qui ne se voient pas dans les bilans comptables.

Le cas avec une seule banque

Pour détailler le fonctionnement de la création monétaire, nous allons commencer par un cas très simple où il n'existe qu'une seule banque dans toute l'économie. Nous verrons ensuite ce qui se passe quand on ajoute plusieurs banques dans l'économie, afin de rendre le tableau plus réaliste.

Pour commencer, étudions le cas où une banque achète un actif à un de ses clients, qui a un compte chez elle. Quand la banque achète quelque chose, elle crédite le compte du vendeur de la somme demandée. Ce faisant, son passif augmente de la somme voulue. En même temps, la banque augmente son actif d'une valeur égale à ce qu'elle a acheté. Actif et passif ayant augmenté dans les mêmes proportions, de la monnaie a été créée.

Actif	Passif
+ Actif acheté.	+ Prix de l'actif (sur le compte courant de l'acheteur).

Il en est de même lorsque la banque donne un prêt à un particulier où à une entreprise. Elle crédite le compte courant de la somme prêtée, mais augmente son actif de la valeur du prêt. Ce comportement bizarre peut se résumer par la fameuse maxime : "les crédits font les dépôts". Remarquons cependant que cette création monétaire implique cependant que la banque augmente son passif en même temps, ou au moins dans un temps assez proche. La banque doit avoir quelque chose à mettre en face de la monnaie créée, sans quoi elle n'équilibre pas son bilan. Ce quelque chose, c'est le contrat du prêt lui-même. Ce contrat est en effet un actif qui a une valeur, égale à la somme prêtée et que le créancier doit rembourser.

Actif	Passif
+ Montant du prêt accordé.	+ Montant du crédit sur le compte courant de l'emprunteur.

La situation est la même si le prêt est versé sur un compte dans une autre banque, si ce n'est qu'il faut prendre en compte la répartition de l'actif et du passif entre les banques.

On voit que, si on analyse la situation uniquement d'un point de vue comptable, les banques peuvent fabriquer de la monnaie, semble-t-il à partir de rien. Quand une banque prête, elle crée automatiquement la monnaie qu'elle prête, au moment où elle le verse sur le compte courant du créditeur. Même chose lorsqu'elle achète un actif quelconque. Elle doit simplement faire attention à avoir suffisamment de réserves pour respecter le taux de réserves obligatoires.

Cette analyse comptable peut laisser penser que les banques peuvent créer de la monnaie à partir de rien. Mais dans la réalité, les banques doivent financer leurs prêts à partir des dépôts des clients, d'emprunts réalisés auprès d'autres banques, voire de levées de capital. Les banques doivent acquérir de l'argent avant de pouvoir le prêter, mais cela ne se voit pas dans le bilan comptable, si l'argent est acquis sous la forme de dépôts (ou de dettes). En effet, la banque prête l'argent des dépôts, mais fait croire que ce n'est pas le cas. Si je dépose 1000 euros à la banque, elle ne va pas réduire le montant de mes dépôts si elle en prête une partie. Elle va me faire croire que l'argent des dépôts n'a pas quitté la banque et me dit que j'ai toujours 1000 euros sur mon compte. Or, dans le bilan comptable, ces 1000 euros restent dans la colonne du passif, au même titre que l'argent qu'elle a prêté, d'où l'illusion que la monnaie des crédits est créée à partir de rien. On voit donc que la création monétaire n'est qu'un artifice comptable. Nous reparlerons de tout cela plus en détail dans le chapitre suivant.

Précisons que la majorité des prêts sert à rembourser des prêts préexistants. Beaucoup d'entreprises font cela régulièrement : elles remboursent certains prêts en empruntant l'argent à rembourser. On dit qu'elles rollent leur dette. Dans une telle situation, le prêt remboursé se traduit par une destruction de monnaie, mais l'emprunt réalisé pour rembourser se traduit lui par une création monétaire équivalente. Les deux se compensent : la quantité de monnaie n'a pas changé.

Le cas avec plusieurs banques

Le cas avec plusieurs banques ressemble au précédent, si ce n'est que la banque peut prêter à des emprunteurs extérieurs, qui ont leur compte dans une autre banque. De plus, il faut ajouter les virements entre les banques, entre les clients de banques différentes.

Lors d'un virement, le montant viré passe des dépôts de la banque d'origine vers la banque destinatrice, ce qui diminue d'autant le passif de la banque d'origine et augmente le passif de la banque destinatrice. Le bilan des deux banques doit cependant rester équilibré, ce qui impose que quelque chose doit diminuer ou augmenter au niveau de l'actif. Ce quelque chose, ce sont les réserves bancaires. La banque d'origine du virement voit ses réserves bancaires diminuer du montant viré, alors que la banque réceptrice voit ses réserves augmenter du même montant. Pour faire simple, les réserves bancaires sont envoyées à l'autre banque, pour "payer le virement".

Banque de l'envoyeur

Actif	Passif
- Réserves excédentaires	- Montant du virement

Banque du récepteur

Actif	Passif
+ Réserves bancaires	+ Montant du virement

Pour ce qui est des prêts à des clients extérieurs, tout se passe comme si la banque prêtait de l'argent sur un de ses comptes, avant de faire un virement vers l'extérieur. La banque préteuse "crée la monnaie" du prêt et l'envoie à la banque réceptrice. Cet envoi est un virement interbancaire, qui implique un échange de réserves. Le passif de la banque réceptrice augmente donc du montant du prêt (le client reçoit le versement du prêt), les réserves à son actif augmentent du même montant. Pour la banque préteuse, les réserves échangées sont remplacées par le contrat du prêt, passé avec le client.

Banque préteuse

Actif	Passif
+ Contrat de prêt - Réserves excédentaires	Pas de changements

Banque du client

Actif	Passif
+ Réserves bancaires	+ Montant du prêt

Les mouvements d'argent entre banques sont donc des mouvements de réserves, plus que des mouvements d'argent créé à partir de rien. L'argent créé lors d'un crédit ne peut donc pas passer d'une banque à l'autre. Cela fait dire à certains que cette monnaie-crédit, créée à partir de rien, est en fait une monnaie spécifique à la banque créditrice. Ainsi, la banque "BNP Paribas" aurait une monnaie différente de la monnaie "Banque Populaire", elle-même différente de la monnaie "Crédit agricole", etc. Les échanges de monnaie entre banques se feraient en utilisant une véritable monnaie, spécifique aux échanges interbancaires, à savoir les réserves bancaires. Cette interprétation a le mérite d'expliquer pourquoi les échanges interbancaires se font en réserves bancaires et pas en monnaie scripturale usuelle, mais utilise de manière un peu particulière la notion de monnaie. Avouons que dire que chaque banque a sa propre monnaie n'est pas du tout intuitif, tant le caractère fongible de la monnaie nous est une évidence.

Les banques commerciales sont des intermédiaires financiers

Les banques commerciales sont des intermédiaires financiers, ce qui signifie qu'ils servent d'intermédiaire entre des personnes qui ont de l'argent à placer et des personnes qui ont besoin d'argent pour investir. Pour simplifier, elles servent d'intermédiaire entre des épargnants et des emprunteurs. Les épargnants placent leur argent à la banque, et celle-ci le prête à divers emprunteurs.

Faire ainsi a plusieurs avantages. Déjà, les épargnants n'ont pas besoin de chercher eux-mêmes des emprunteurs, et encore moins de vérifier leur solvabilité : la banque s'en charge. Ensuite, cela permet aux épargnants de diversifier leurs emprunts. Une banque ne prête pas qu'à une seule personne, mais à un grand nombre d'emprunteurs. Et tous ne font pas défauts sur leurs dettes. La plupart des emprunteurs remboursent effectivement leurs dettes, seule une minorité ne le faisant pas. Ainsi, on s'assure que le risque de perte est plus faible, car répartit sur plusieurs emprunteurs différents avec chacun une faible probabilité de défaut. Au lieu de jouer à la roulette russe en choisissant un emprunteur, l'épargnant répartit le risque et s'assure que le risque de pertes est moins volatil.

L'intermédiation financière en termes de bilan comptable

Au niveau des bilans comptables, le système de dépôts est assez simple à comprendre. Sans intermédiation financière, la situation est la suivante, telle qu'illustrée ci-dessous. On voit que l'argent prêté passe du préteur à l'emprunteur, en échange de quoi ce dernier reçoit une reconnaissance de dette. L'argent prêté reste à l'actif, mais change de main, alors que la reconnaissance de dette est un passif pour l'emprunteur et un actif pour le préteur.

Bilan comptable suite à un prêt sans intermédiation financière.

Avec un intermédiaire financier, la situation est légèrement plus différente. L'intermédiaire en question peut être une banque, un courtier de bourse, une assurance, etc. Suivant les cas, les bilans comptables ne sont pas les mêmes, mais la situation globale est la même.

Tout commence quand l'épargnant place son argent auprès de l'intermédiaire financier. L'argent passe donc à l'actif de l'intermédiaire financier (c'est lui qui possède l'argent), tandis qu'un contrat est passé entre l'épargnant et l'intermédiaire. Le contrat en question peut être une reconnaissance de dette ou un titre de propriété. Par exemple, si vous achetez une action d'une entreprise, le contrat sera un titre de propriété de l'entreprise, l'action proprement dite. Si c'est une obligation, ce sera une reconnaissance de dette. Partons du principe que c'est une reconnaissance de dette, pour simplifier les explications.

L'argent est placé et un contrat signé, c'était la première étape. Ensuite, l'intermédiaire financier va prêter cet argent ou l'utiliser pour investir. L'argent se retrouve dans la poche des investisseurs, tandis que l'intermédiaire signe avec lui un contrat (reconnaissance de dette dans le cas présent). La situation est illustrée ci-dessous, en supposant que les contrats sont tous des reconnaissances de dettes. On peut les remplacer par des titres de propriétés, mais qu'importe.

Bilan comptable suite à un prêt avec intermédiation financière.

Les banques sont des intermédiaires financiers comme les autres. Elles empruntent de l'argent pour le prêter : elles empruntent aux épargnants et prêtent aux emprunteurs. Dans le cas des banques, les reconnaissances de dettes des épargnants sont soit des emprunts normaux, soit des dépôts bancaires. L'argent que vous avez sur vos comptes n'est en réalité pas dans les coffres de la banque : il est voué à être prêté, donc à sortir de la banque. Une fois que l'argent est placé, la banque peut le prêter à divers emprunteurs et recevoir un contrat de prêt en contrepartie. Ce qui est résumé par l'adage : "les dépôts font les crédits". Au passage, cela explique que vos comptes soient rémunérés avec des intérêts. Les intérêts de vos comptes bancaires et livrets correspondent donc à l'intérêt d'un prêt.

Par contre, la banque s'engage à vous rendre cet argent dès que vous en faites la demande, au distributeur ou lors d'un virement. C'est la différence principale entre les banques et les autres intermédiaires financiers : les banques acceptent que l'argent placé puisse être retiré à tout moment. Vous pouvez disposer de l'argent sur vos livrets comme bon vous semble, alors que ce n'est pas le cas pour les autres reconnaissances de dettes. Par exemple, vous ne pouvez pas convertir une obligation d'état (de la dette étatique) en argent liquide en demandant au trésor public. Ce dernier n'a jamais promis contractuellement qu'il acceptait de faire un tel remboursement sur demande. En conséquence, les obligations d'état ne sont pas considérées comme de la monnaie. Mais pour les dépôts, c'est l'inverse : vous pouvez les retirer comme bon vous semble, ce qui en fait une dette, mais aussi de la monnaie.

Bilan comptable suite à un prêt avec intermédiation bancaire.

Au passage, cela explique comment les banques peuvent soi-disant créer de la monnaie. Si on reprend l'exemple illustré ci-dessus, on voit qu'il y a plus d'argent dans la situation finale que dans la situation initiale : seulement l'argent en vert dans la situation initiale, l'argent en vert et les dépôts en orange dans la situation finale. Tout se passe comme si l'argent des dépôts avait été créé à partir de rien lors du prêt. Le remboursement du crédit a l'effet inverse et détruit la monnaie que celui-ci avait créé. En quelque sorte, tout se passe comme si l'argent prêté était créé de toutes pièces lors du prêt et détruit lors du remboursement du crédit !

L'explication de la création monétaire par les banques commerciales est donc évidente. Quand elles prêtent, l'argent passe bien de la banque vers l'emprunteur, mais les dépôts sont toujours là. La banque fait croire qu'elle a toujours autant de monnaie dans ses coffres qu'elle n'a de dépôts, alors qu'une bonne partie de ceux-ci ont été convertis en prêts dans son bilan. L'argent réel (des espèces ou des réserves) passe bien de main en main, mais des reconnaissances de dettes sont créés par-ci, par-là et augmentent la masse monétaire. Tout cela trahit le fait que les dépôts bancaires ne sont en réalité pas de la vraie monnaie, mais sont en fait une dette que la banque s'engage à rembourser sous la forme de monnaie, la demande de remboursement n'étant autre qu'un retrait ou un virement. La vraie monnaie est donc limitée à l'argent qui circule réellement dans l'économie (on verra plus tard qu'il s'agit de l'argent crée par la banque centrale, la base monétaire), non l'argent sur les comptes bancaires (la masse monétaire).

La banque fait comme si l'argent déposé restait sur les comptes des déposants, alors que ce n'est pas tout à fait le cas. Ce mécanisme ne pose pas de problèmes tant que ceux-ci ne le retirent pas. D'expérience, la banque sait que les épargnants ne vont pas tous retirer leur argent au même moment, ce qui fait qu'une petite quantité d'argent est réellement retirée chaque année. Une bonne partie de l'argent va rester sur les comptes d'épargne suffisamment longtemps pour que les prêts effectués avec soient remboursés. Mais il n’empêche que si un épargnant retire son argent, la banque doit trouver de l'argent liquide pour rembourser le déposant. Pour cela, la banque ne va pas prêter la totalité des dépôts, mais va en garder une partie en réserve, pour assurer la liquidité de ses placements. Elle a aussi besoin de garder des réserves pour respecter certaines règlementations, comme le taux de réserves, les ratios de liquidité ou d'endettement par effet de levier.

La création monétaire : le cas sans dépôts à la banque centrale

Maintenant, étudions la création monétaire par les banques plus en détail. Peut-être avez-vous déjà lu des documents sur le sujet, que ce soit dans des livres ou sur le net. Les explications que l'on trouve sur le net ou dans les manuels commencent par le cas où une banque effectue des prêts sous forme de monnaie électronique/fiduciaire à ses déposants. Cet exemple est utilisé pour dire que les banques créent l'argent des crédits sans devoir les financer. Mais ce cas est en réalité extrêmement trompeur et les explications associées ne fonctionnent que dans ce cas bien précis et pas dans les autres. Aussi, nous allons prendre un cas tout aussi simple, mais bien moins trompeur et plus intuitif.

Pour expliquer comment se passe la création monétaire par les banques, mieux vaut d'abord étudier le cas où il n'y a pas de réserves bancaires électroniques. Dans l'exemple qui va suivre, nous supposons que la monnaie existe seulement sous forme de dépôts et d'espèces. Les espèces sont fabriquées par le trésor public ou par une banque centrale qui s'occupe uniquement de la création des espèces. Les banques ne peuvent pas placer d'argent à la banque centrale, ou alors leurs dépôts sont en espèces. Dit autrement, l'argent conservé par les banques ne l'est pas sous forme de réserves, mais l'est en espèces dans les coffres des banques, sous la forme de vault cash. Les prêts sont versés en espèces directement ou sous la forme de virements. Nous allons d'abord étudier le cas où les prêts sont versés à l'emprunteur en espèces. Ce cas est assez proche de ce qu'on observe dans les pays en cours de développement, où le micro-crédit est assez courant. Il ressemble aussi à ce qu'on avait avant les années 1800-1900, avant l'apparition des lettres de change, des chèques, des virements interbancaires et autres technologies bancaires élaborées.

Ce cas est illustré ci-dessous. La base monétaire est intégralement composée d'espèces, 1000$ en tout, et elle ne change pas du tout au cours de l'exemple. Au départ, un épargnant dispose de 1000$ en espèces : la masse monétaire est alors égale à la quantité d'espèces en circulation, soit 1000$. Puis, l'épargnant place ces espèces à la banque : la masse monétaire ne change pas, mais les espèces sont converties en dépôts. Les espèces en question disparaissent de la masse monétaire, qui prend en compte les espèces en circulation, mais pas les réserves en cash. Enfin, la banque prête 1000$ en espèces à un emprunteur : la masse monétaire est la somme du dépôt de l'épargnant et des espèces prêtées. Le total fait une masse monétaire supérieure à celle disponible avant le prêt : il y a eu création monétaire

Par contre, on ne peut pas vraiment dire que l'argent du prêt a été créé, comme le disent les interprétations naïves. On voit bien que l'argent prêté est l'argent de l'emprunteur, les espèces qu'il avait au départ. En réalité, la création monétaire vient du fait que la banque fait croire que l'argent prêté n'a pas quitté la banque, en faisant croire au déposant que le dépôt est toujours là. C'est donc l'argent des dépôts qui est créé lors d'un prêt, bien que ce ne soit pas très intuitif à comprendre. Mais on voit, avec cet exemple, que la banque ne peut pas prêter plus d'argent qu'elle n'en a dans ses coffres, plus d'argent qu'on en a déposé chez elle. Mieux : on voit que les espèces déposées se retrouvent dans les mains de l'emprunteur, signe que le dépôt a financé le crédit.

Création monétaire sans banque centrale - cas historique.

Le cas où le prêt est viré sous la forme de dépôts dans une autre banque n'est pas si différent. La banque du préteur envoie 1000$ à la banque de l'emprunteur, et celle-ci crédite son compte courant du même montant. Du point de vue comptable, la situation est identique à celle qu'on aurait si le prêt était accordé sous forme d'espèces, mais que l'emprunteur plaçait ces espèces sur son compte courant.

Création monétaire sans banque centrale - cas avec le prêt viré dans une autre banque.

Enfin, étudions le cas où l'emprunteur est un client de la banque préteuse et a un compte chez elle. Le prêt est donc versé sur un compte de la banque, il reste dans la banque. Dans ce cas, la situation est identique, si ce n'est qu'il n'y a pas besoin de virement. On remarque que les espèces sont adossées au prêt, pas aux dépôts.

Création monétaire sans banque centrale - avec une seule banque.

La création monétaire : le cas avec des dépôts à la banque centrale

Les explications précédentes sont encore valides dans le monde actuel, sous réserve d'une petite modification : les réserves sont un substitut aux espèces, un équivalent électronique aux espèces. La seule correction à faire est de remplacer le vault cash par les réserves bancaires. Le fonctionnement du système bancaire actuel est le même à ce détail près. Les banques ne s'échangent donc pas forcément des espèces, mais peuvent s'échanger de la monnaie électronique, détenue sur des dépôts à la banque centrale.

Les échanges interbancaires de réserves

La monnaie des dépôts circule par le biais des virements, paiements et retraits. Elle passe d'une banque à l'autre et les échanges interbancaires se font avec des réserves. Si je fais un virement de 1000 euros la banque A vers la banque B, la banque A doit envoyer 1000 euros de réserves bancaires à la banque B. Pour être plus général, les banques peuvent aussi d'échanger des actifs autres que les réserves, mais c'est un détail. Cela simplifie fortement les échanges interbancaires, qui peuvent se faire sous forme électronique, sans que cela change grand-chose au fonctionnement de principe du système.

Pour être plus précis, les banques ne s'échangent pas des réserves à chaque virement, mais elles font le solde des échanges. Plus précisément, deux banques A et B font la somme des entrées et sorties et calculent le montant net qu'elles se doivent l'une l'autre, montant qui est échangé ensuite sous la forme de réserves. Les mouvements d'argent entre deux banques ne se compensent pas forcément, certaines recevant un surplus de réserves tandis que d'autres subissent des fuites. Si une banque a trop de fuites, elle perd des réserves excédentaires et se rapproche du seuil du taux de réserves, ce qui est mauvais signe. À l'inverse, une banque avec trop de surplus a des réserves en trop, qu'elle va essayer de faire fructifier d'une manière ou d'une autre. Le système bancaire étant rarement à l'équilibre, on a des banques en manque de réserves et des banques avec des excès de réserves.

Pour équilibrer le tout, les banques peuvent prêter leur excès de réserves aux banque qui en manquent. Si jamais une banque n'a pas assez de réserves, elle peut emprunter les réserves manquantes auprès d'autres banques. Par autres banques, on veut dire à d'autres banques commerciales qui ont des réserves excédentaires, ou à la banque centrale. Ces emprunts interbancaires de réserves s'effectuent sur le marché interbancaire, un marché informel sur lequel interviennent les banques commerciales, la banque centrale, et quelques autres participants. Sur ce marché, les banques peuvent se prêter ou emprunter des réserves. La plupart des prêts sont gagés, ce qui signifie que la banque emprunteuse fournit en contrepartie un ensemble d'actifs financiers appelé collatéral. Ces prêts ont une durée inférieure à deux ans, les durées les plus communes étant de quelques jours à quelques mois. Les emprunts des clients ont des maturités plus longues (supérieures à l'année), ce qui montre bien que les banques emprunter à taux courts pour prêter à taux longs.

Il est souvent dit que si on fait la somme des mouvements sur le marché interbancaire, le montant total de réserves ne change pas. Les échanges entre banques ne peuvent pas créer des réserves ni en détruire, du moins en première approximation. Mais cela n'est qu'une première approximation, qui met de côté plusieurs points.

Le premier est que la banque centrale peut intervenir sur les marchés pour créer ou détruire des réserves. Les banques centrales ont en effet la capacité de créer des réserves à volonté. Les banques commerciales peuvent emprunter des réserves à la banque centrale, réserves qui sont créées lors du prêt. La seconde est que les réserves peuvent disparaître. Rappelons qu'elles peuvent être converties en cash sans restriction, sur simple demande. Les banques commerciales peuvent demander à la banque centrale de convertir des réserves électroniques en cash et la banque centrale n'a aucun moyen de refuser.

De plus, les réserves comprennent aussi le vault cash, qui peut être retiré à tout moment par les dépositaires. Les retraits des clients transforment ainsi des réserves en espèces circulantes, réduisant la quantité de réserves. D'autres mécanismes peuvent convertir des réserves et les faire disparaître ou apparaître. C'est le cas de certaines interventions sur le marché des change, par exemple. Tout cela pour dire que le montant de réserves n'est pas fixe, mais varie d'un jour à l'autre.

Les réserves sont une limite à la création monétaire

Dans les exemples précédents, la banque ne peut pas prêter des espèces qu'elle n'a pas dans ses coffres. Si on analyse la situation avec non pas des espèces, mais des réserves en général, c'est la même chose. Les banques ont besoin de réserves pour prêter et sont donc limitées par la quantité de réserves dont elles disposent. Et cela est encore aggravé par le fait que les banques doivent disposer de réserves obligatoires, ce qui peut limiter sa capacité à fabriquer de la monnaie. Si une banque veut créer de la monnaie, elle doit avoir un encours de réserves excédentaires suffisant pour le faire. Si elle n'a pas assez de réserves, la création d'un nouveau dépôt/crédit risquerait de la faire passer sous le niveau réglementaire.

Par exemple, supposons que la banque prête à ses clients sur des comptes qu'elle gère. En faisant cela, elle augmente son bilan, à savoir que le passif de la banque augmente en même temps que son actif. Dans une telle situation, elle "transforme" les réserves excédentaires en réserves obligatoires. Au bout d'un moment, les réserves obligatoires deviendront insuffisantes et la banque ne pourra pas prêter plus.

Création monétaire et réserves - point de vue comptable

Et il en est de même si la banque prête à des clients extérieurs. Dans ce cas, elle doit transférer des réserves à l'autre banque et remplace les réserves excédentaires par un contrat de prêt dans son bilan. Précisons que ce cas est de loin le plus fréquent. Aux états-unis, près de 90% des prêts sont des prêts immobiliers qui sont versés directement au propriétaire de la maison vendue, pas à l'acheteur. Et si l'acheteur va voir sa banque pour avoir un prêt, rien n'oblige le propriétaire à avoir un compte dans la banque de l'acheteur. La banque doit donc posséder les réserves quand elle verse le prêt, sans quoi le propriétaire ne reçoit pas le virement/versement.

Utilisation des réserves bancaires par les banques, pour acheter des actifs

Pour résumer, la création monétaire est limitée par la quantité de réserves bancaires. Une banque qui veut prêter de l'argent doit avoir suffisamment de réserves bancaires pour ce faire, que ce soit pour respecter le taux de réserves obligatoires ou pour réaliser le virement de la somme prêtée. Les banques peuvent financer leurs prêts soit en utilisant les dépôts, soit en empruntant l'argent nécessaire sur le marché monétaire, voire par d'autres mesures.

À ce propos, il n'est pas rare que certaines banques aient un encours de prêts supérieurs à l'encours de leurs dépôts. Le rapport entre prêt et dépôts est souvent proche de 100% pour la plupart des banques, mais il arrive qu'il dépasse cette limite et atteigne des valeurs de 110%, 120%, etc. Lorsque cela arrive, c'est signe que la banque a financé ses prêts non seulement par ses dépôts, mais aussi par d'autres méthodes. Un rapport prêt/dépôts élevé est souvent mauvais signe pour une banque et est d'ailleurs assez mal vu par les marchés financiers. Précisons que dans certains pays, il existe une limite légale au rapport prêts/dépôts, qui ne peut pas dépasser une valeur maximale précisée par la loi.

La création monétaire : du crédit à la banque centrale

La banque centrale est une banque un petit peu spéciale, qui peut créer de la monnaie à sa guise, condition sine qua non pour lui permettre de remplir ses objectifs. La banque centrale dispose de plusieurs instruments, qui visent à contrôler la quantité de monnaie en circulation dans l'économie. Mais ce contrôle de la quantité de monnaie n'est pas un contrôle direct, les banques commerciales et d'investissement peuvent en effet créer à tout moment de la monnaie, dans une certaine mesure. Aussi bizarre que cela puisse paraître, la création monétaire n'est pas que le fait de la banque centrale, mais aussi des banques commerciales. Pour comprendre pourquoi, nous allons devoir parler plus en détail des banques et de leur fonctionnement. La banque centrale peut créer de la monnaie à loisir, mais les banques commerciales ont aussi leur rôle à jouer.

Pour rappel, la masse monétaire est composée de deux types de monnaie :

• La base monétaire regroupe l'argent détenu et crée par la banque centrale. Il s'agit de l'ensemble des espèces (pièces et billets) et de ce qu'on appelle les réserves bancaires (nous verrons ce que c'est dans ce qui suit).
  • Les espèces regroupent les pièces et les billets. C'est une forme de monnaie que seule la banque centrale peut créer : elle a le monopole de leur fabrication.
  • La monnaie des banques commerciale qui est placée à la banque centrale, qui porte le nom de réserves bancaires. On en reparle dans ce qui suit.
• Le reste est de la monnaie crée par les banques commerciales. Elle est créée lorsque des agents économiques contractent un emprunt auprès d'une banque. En conséquence, nous appellerons cette forme monnaie par le terme monnaie crédit dans ce qui suit. Il s'agit toujours de monnaie scripturale, la banque centrale ayant le monopole de la création d'espèces.

	Monnaie non-scripturale	Monnaie scripturale
Base monétaire	Espèces	Réserves bancaires
Masse monétaire		Monnaie scriptural, sauf réserves

La création monétaire par la banque centrale

La banque centrale a le monopole de l'émission de monnaie centrale, le monopole de création de la base monétaire. Elle peut en théorie créer de la monnaie sans se soucier de l'égalité entre actifs et passif, bien que cela n'ait jamais été tenté jusqu'à présent. Cependant, la création monétaire de la banque centrale ne doit pas être illimitée. Il vaut mieux que la banque centrale ne puisse pas imprimer plus de monnaie que nécessaire pour l'économie. Pour cela, la banque centrale ne peut qu'échanger des actifs contre de la monnaie ou prêter aux banques commerciales.

Politique de création monétaire	Description
Politique monétaire conventionnelle	Contrôle des taux directeurs, via des prêts ou des opérations d'open market.
Assouplissement quantitatif	Rachat de titres (obligations d'état) sur le marché secondaire, avec de la monnaie créée spécialement pour l'occasion.
Monnaie hélicoptère	Création monétaire pure, sans achat d'actifs. Peut se traduire par un versement direct d'argent au public, ou à l'état, ou encore par un prêt au trésor public.

Les prêts de la banque centrale

En temps normal, la création monétaire prend la forme d'un prêt interbancaire, un prêt de la banque centrale aux banques commerciales. La monnaie du prêt est créée de toutes pièces et est détruite une fois le prêt remboursé. Le prêt aux états était autrefois autorisé mais est aujourd'hui interdit, ce genre de politique étant extrêmement inflationniste. Ce n'est que dans les périodes de l'étalon-or (et des accords de Bretton-Woods) que ces prêts étaient autorisés, l'étalon-or limitant fortement la création monétaire par la banque centrale (et donc le volume des prêts aux états). Au passage, les taux d'emprunt à la banque centrale sont appelés les taux directeurs. Retenez bien ce terme, car il reviendra très souvent dans la suite de ce chapitre, et plus généralement de ce cours.

La politique monétaire conventionnelle se borne à modifier les taux directeurs des prêts interbancaires. Une telle politique modifie donc les taux à court-terme, ce qui a une influence sur les autres taux bancaires, comme les taux des crédits immobiliers, les taux des obligations, et bien d'autres. La banque centrale ne s'engage pas à créer une quantité fixe de monnaie, mais doit fournir la liquidité nécessaire pour atteindre sa cible de taux d'intérêt. Mais Quand la gestion des taux court n'est plus possible (quand ceux-ci sont à zéro, par exemple), la banque centrale peut utiliser d'autres méthodes pour relancer l'économie.

Les échanges d'actifs avec la banque centrale

Outre les prêts, la banque centrale peut ainsi créer de la monnaie pour acheter des actifs, ou en détruire en les vendant, la monnaie ayant servi à payer étant détruite. Lorsqu'elle achète des titres à une banque, elle va payer le montant acheté sous la forme de réserves. Lors d'une vente, la banque centrale va retirer le prix des obligations des réserves de la banque commerciale acheteuse.

La banque centrale n'a pas le droit d'acheter n'importe quel actif, mais doit se limiter à une classe d'actifs autorisés, sauf cas particuliers. Et les actifs achetables dépendent de l'objectif de la banque centrale. Citons quelques exemples :

• Du temps de l'étalon-or, la banque centrale achetait de l'or et rien d'autre. Elle se chargeait de convertir de l'or en monnaie et réciproquement, mais les autres échanges d'actifs étaient interdits. Cela permettait de fixer le prix de l'or, à environ 20 dollars par once.
• Si la banque centrale fixe les taux de change, elle ne peut échanger sa monnaie qu'avec des monnaies étrangères. Par exemple, une banque centrale qui fixe sa monnaie sur le cours du dollar ne pourra qu'échanger sa monnaie avec des dollars, mais rien d'autre.
• Si la banque centrale contrôle les taux d'intérêt, elle doit acheter des titres qui sont rémunérés par des intérêts. Les actifs en question sont des obligations ou des instruments du marché monétaire, mais guère plus. Il s'agit le plus souvent d'actifs sûrs, à faible risque, assez liquides. Les obligations d'états qui ont une maturité de court-terme sont les plus indiquées. Il arrive exceptionnellement que la banque centrale soit autorisée à acheter d'autres titres, mais nous en reparlerons plus tard.

En se limitant aux obligations d'états, la banque centrale garantit que la somme (dette d'état + monnaie) reste constante, malgré les achats ou ventes d'actifs. La politique monétaire ne fait que changer la part de cette somme détenue sous la forme de monnaie. Seul l'état peut augmenter ce stock, en créant des obligations. Une telle politique est alors appelée une politique fiscale. La banque centrale ne peut pas acheter directement des dettes d'états lors de leur émission (elle n’achète pas sur la marché dit primaire). Elle ne peut qu'acheter ou vendre des dettes/titres déjà émis et achetés par les banques commerciales (elle achète des obligations sur le marché dit secondaire, le marché de l'occasion des obligations). Cette contrainte empêche aux états de monétiser leur dette, à savoir la faire financer par la banque centrale. Une telle monétisation est en effet extrêmement inflationniste, et tous les pays qui l'ont pratiqué ont subi une hyperinflation, situation où l'inflation est très forte (plus de 30% par mois).

Illustration du fonctionnement de la politique monétaire conventionnelle par opérations d'open market et de l'assouplissement quantitatif, ainsi que de la différence entre politique monétaire et fiscale.

Pour faire ces achats et ventes de titres, la banque centrale peut utiliser deux mécanismes différents. Cet échange peut prendre deux formes différentes, l'une consistant en un échange temporaire, l'autre en un échange permanent. On distingue ainsi les prêts repos et les opérations d'Open Market, les premiers étant un échange temporaire, l'autre un échange permanent. Dans les deux cas, ces ventes ou achats se payent avec des réserves.

• Avec les repos, la banque centrale achète des titres à une banque commerciale, celle-ci s'engageant à les racheter ultérieurement à un prix supérieur. L'achat ou la vente est alors temporaire, et non permanente. On peut voir les repos comme un prêt pour lequel l'emprunteur doit fournir une "hypothèque", un collatéral. Les collatéraux acceptés par la banque centrale sont relativement limités, dans le sens où ils ne doivent contenir que des titres de haute qualité, le plus souvent des dettes d'état. Ce n'est que quand la liquidité se fait rare que la banque centrale accepte des collatéraux risqués. Mais dans tous les cas, la banque centrale applique une décote au prix de marché du collatéral, l'haircut, en fonction de la qualité du prêt.
• Une autre technique consiste à vendre ou acheter des obligations d'états de maturité inférieure à deux mois, sans avoir à les racheter ou les revendre plus tard. On parle alors d'opération d'open market au sens strict.

La monnaie hélicoptère

Enfin, il est possible pour la banque centrale de créer de la monnaie sans l'échanger ou la prêter. La monnaie est alors crée sans contrepartie et est distribuée soit à l'état, soit à ses citoyens. Il s'agit de création monétaire pure, sans contraintes, la monnaie étant créée sans contrepartie. De plus, cette monnaie est créée de manière définitive. En comparaison, l'assouplissement quantitatif crée de la monnaie de manière temporaire : la banque centrale peut toujours retirer cette monnaie de la circulation en vendant les actifs achetés.

À l'heure actuelle, divers arguments théoriques nous disent que création monétaire temporaire et définitive n'ont pas les mêmes effets sur l'économie. Une création monétaire par monnaie-hélicoptère est considérée comme étant la plus inflationnistes. Mais nous en reparlerons dans un chapitre dédié. Tout ce que l'on peut dire est qu'il y a une grande différence entre monnaie hélicoptère d'un côté, et assouplissement quantitatif et politique monétaire conventionnelle de l'autre. D'ailleurs, les théories économiques qui décrivent la monnaie hélicoptère ne sont pas du tout les mêmes que celles qui décrivent une politique monétaire plus normale. Et cela peut se comprendre : il y a une différence entre échanger des actifs contre de l'argent, et recevoir de l'argent sans contrepartie. SI un jour la banque centrale vous fait un don et vire 2000 euros sur votre compte, vous n'allez pas réagir de la même manière que si elle vous propose un rachat d'assurance-vie sans frais.

La création monétaire par les banques commerciales/privées

On vient de voir que la base monétaire et la masse monétaire sont deux grandeurs différentes. On peut se demander s'il existe une relation entre les deux et, si oui, laquelle. Pour répondre à cette question, diverses théories ont étés formulées dès les années 70-80. On peut grossièrement les classer en deux catégories : les théories à monnaie exogène et les théories à monnaie endogène. Les deux s'accordent sur quelques hypothèses de base, communes à la fois aux théories à monnaie exogène et endogène.

• Le premier est que les banques (les banques commerciales, mais aussi la banque centrale) créent de la monnaie par les crédits, quand les agents économiques empruntent. Toute somme empruntée correspond à une création monétaire de valeur équivalente. Inversement, tout remboursement de crédit détruit de la monnaie. Vu que les crédits à destination des ménages et des entreprises sont le fait des banques commerciales, ce sont elles qui sont les responsables finaux de la création monétaire.
• Le second point est que la monnaie crée par les banques circule dans l'économie et passe de mains en mains. Tout emprunteur achète quelque chose avec l'argent d'un prêt, ce qui fait que l'argent va aller au vendeur, vendeur qui dépensera aussi cet argent, et ainsi de suite. À la fin de ce processus de circulation, une partie de la monnaie va être transformée en liquidités (espèces, argent sur un compte courant), alors que le reste sera transformé en dépôts bancaires.

Pour résumer, la première hypothèse dit que "la masse monétaire est endogène", alors que la seconde dit que "les crédits font les dépôts". Si les deux hypothèses sont communes à toutes les théories de la monnaie, les théories à monnaie exogène considèrent que les banques sont des intermédiaires financiers, alors qu'elles ne le sont pas avec la monnaie endogène. Cela pourrait paraître comme un détail, mais a en réalité des conséquences assez profondes. À cause de cette hypothèse, les différences entre monnaie endogène et exogène sont nombreuses.

La première tient dans l'existence ou non d'une limite à la création monétaire, liée à la politique de la banque centrale. Dans les théories à monnaie exogène, les banques sont limitées par la base monétaire, par l'encours de réserves imprimées par la banque centrale. Dans les théories à monnaie endogène, elles sont limitées, mais pas par la quantité de réserves.

La seconde est la causalité entre base monétaire et masse monétaire. Par exemple, si la base monétaire augmente, est-ce que la masse monétaire suivra la danse ? Ou alors est-ce que la base monétaire répond aux variations de la masse monétaire ? Avec les théories à monnaie exogène, la banque centrale créée la base monétaire et la masse monétaire s'en déduit : la base monétaire est donc exogène (sous-entendu, déterminée par la banque centrale) et la masse monétaire est endogène. Avec une monnaie endogène, la masse monétaire est créée par les banques commerciales et la banque centrale adapte la base monétaire en réaction. Dans le second, base et masse monétaire sont indépendantes. On voit donc que l'attribut endogène/exogène est à attribuer à la base monétaire, pas à la masse monétaire.

L'auteur de ce wikilivre pense que les deux types de théories répondent à une question mal posée. Elles pensent en termes d'agrégats monétaires et laissent complètement de côté les taux d'intérêt, qui sont pourtant primordiaux pour la gestion de politique monétaire. Dans un monde où les banques centrales ont abandonné le contrôle de la masse/base monétaire et fixent les taux d'intérêts, mieux vaut penser en premier lieu en termes de taux d'intérêt qu'en termes d'agrégats monétaires. Ainsi, au lieu de se demander si la base monétaire est la source de la masse monétaire ou inversement, il vaudrait mieux se demander si les deux n'ont pas une source commune liée aux taux d'intérêts. Mais cela n’empêche pas de voir en détail ces théories endogène et exogène, qui ont des choses importantes à nous apprendre. Même si elles sont actuellement obsolètes, ces deux visions sont porteuses d'enseignements qu'il est important de connaître, quitte à les critiquer plus tard.

Les théories à monnaie endogène

Les théories à monnaie endogène sont plus simples que les théories à monnaie exogène, ce qui fait que nous allons les voir en premier lieu. Dans ces théories, les banques privées créent la monnaie lors des emprunts. Une fois la monnaie crée, celle-ci circule dans l'économie est transformée en dépôts et en espèces. Les banques privées conservent une partie des dépôts sous la forme de réserves, acquises auprès de la banque centrale. La banque centrale ne limite pas la base monétaire, ce qui veut dire qu'elle imprime les espèces nécessaires et crée la quantité de réserves demandée par les banques privées. Pour résumer, la masse monétaire est imposée par le volume de prêt des banques commerciales. La base monétaire est le fait du souhait plus ou moins important des agents à conserver des liquidités et/ou des réserves. La base monétaire est donc endogène, dans le sens où la banque centrale ne la contrôle pas directement.

Ce schéma décrit le fonctionnement de la création monétaire tel qu'il est décrit par les théories à monnaie endogène.

Mais heureusement, les banques vont limiter la quantité de prêt qu'elles accordent et ce pour plusieurs raisons.

• Premièrement, rappelons que les banques doivent avoir un capital suffisant par rapport à leur actif, sans quoi elles risquent de faire faillite. Cela peut les amener à limiter leurs encours de prêts si elles n'ont pas assez de capital. Mais ces limites ne sont que des limites microéconomiques, pas des limites macroéconomiques. En dehors de cette limite maximale imposée par le capital, les banques prêtent un montant qui dépend des taux en vigueur, ce qui nous amène à la deuxième raison.
• Deuxièmement, la demande de crédit des emprunteurs est naturellement limitée. Non seulement il n'y a pas une infinité d'emprunteurs, mais en plus leur nombre varie fortement selon les taux proposés : certains n'empruntent pas si les taux sont trop élevés, par exemple. Ce qui fait que la création monétaire d'une banque est donc limitée par la demande d'emprunt, qui dépend elle-même des taux d'intérêt. Ainsi, la masse monétaire dépend donc de la demande de crédit de la part des agents économique et du taux choisit par les banques. Cela a tendance à conditionner la masse monétaire a la santé de l'économie : plus l'économie va bien, plus les ménages auront confiance et emprunteront. La masse monétaire dépend alors de ce qui détermine les taux d'intérêts., ce que nous verrons dans le chapitre suivant.

Les théories à monnaie exogène

Après avoir vu les théories à monnaie endogène, il est temps de passer aux théories à monnaie exogène, que l'on peut voir comme une amélioration des théories précédentes. Par amélioration, on veut dire que les mécanismes présents dans les théories à monnaie endogène sont aussi valables pour les théories exogènes. Par contre, les théories exogènes ajoutent une relation causale entre les dépôts et les prêts.

Description du processus de création monétaire par les théories à monnaie exogène. Les ajouts des théories exogènes sont indiqués en jaune.

Le système bancaire à réserves fractionnaires

Dans les théories à monnaie exogène, les banques sont des intermédiaires financiers entre les épargnants et les emprunteurs. Elles prêtent leurs dépôts pour faire des crédits. On dit que "les dépôts font les crédits". L'argent qui est prêté vient des réserves excédentaires des banques. Une banque sans réserves excédentaires a prêté tout l'argent déposé chez elle, sauf pour la part réglementaire de réserves, et ne peut donc pas prêter plus, sauf à acquérir des réserves auprès d'autres banques.

Notons que ce mécanisme est parfaitement compatible avec les explications de la création monétaire basées sur des bilans comptables. Prenons l'exemple suivant : un déposant place 1000 euros dans sa banque, ce qui donne 100 euros de réserves à la banque. La banque en met en réserve 50 euros pour respecter le taux de réserves réglementaire et prête les 950 euros de réserves excédentaires. Les 950 euros sont alors versés sur un compte de dépôt ou convertis en espèces. Rappelons que la banque fait semblant que les dépôts des clients n'ont pas bougés dans son bilan comptable. La masse monétaire est alors composée des 1000 euros déposés initialement et des 950 euros du crédit : la masse monétaire a donc augmenté suite au crédit.

Le mécanisme décrit précédemment ne s’arrête pas là. L'emprunteur va dépenser ou investir l'argent emprunté, ce qui va le faire circuler dans l'économie. L'argent du crédit est soit converti en espèces, soit viré sur un compte de dépôt. Si l'argent est converti en espèces, le circuit s’arrête ici et aucune création monétaire supplémentaire n'a lieu. Dans l'autre cas, le dépôt est la source d'un nouveau prêt. Les dépôts font les prêts, qui eux-mêmes font des dépôts, qui eux-mêmes font des prêts, etc. Un nouveau tour de création monétaire a lieu à chaque dépôt : le mécanisme s'auto-alimente de lui-même !

On pourrait croire que le mécanisme peut s'emballer, mais il n'en est rien. Il est limité par plusieurs grands facteurs : les besoins en réserves obligatoires, l'existence de réserves excédentaires et la demande d'espèces.

• En premier lieu, à chaque fois que quelqu'un dépose de l'argent à la banque, la banque doit en conserver une partie sous la forme de réserves. Dit autrement, à chaque dépôt, une petite partie des dépôts ne peut plus être prêtée et cesse de circuler dans l'économie. Petit à petit, le stock de fonds prêtables diminue à chaque tour de création monétaire, à chaque dépôt. Les réserves obligatoires s’accroissent à chaque nouveau dépôt créé, vu que le taux de réserve frappe la masse monétaire totale. Plus les contraintes en termes de réserves sont fortes, plus la somme prêtable se réduit à chaque dépôt/prêt.
• En second lieu, les banques ne prêtent pas toutes leurs réserves excédentaires, pour diverses raisons. Soit parce qu'elles ne trouvent pas assez d'emprunteurs, soit parce que les emprunteurs ont de bonnes chances de ne pas rembourser, ou pour d'autres raisons. Et ces réserves excédentaires sont autant de monnaie qui ne circule plus dans l'économie et qui est conservée à la banque centrale.
• Enfin, les retraits d'espèces transforment des dépôts appartenant à la masse monétaire en espèces appartenant à la base monétaire.

Ces trois mécanismes limitent la quantité totale de monnaie qui peut être créé dans l'économie. La relation exacte entre base et masse monétaire est donc liée au taux de réserve obligatoire, au taux de réserves excédentaires accepté par les banques et à la propension à détenir des espèces.

Il faut noter que tout ce qui vient d'être dit marche aussi en remplaçant les crédits par les achats d'actifs. Il est en effet possible qu'une banque achète des actions, des obligations ou de l'immobilier avec l'argent des déposants. Cette possibilité est cependant très encadrée par la réglementation bancaire, quand elle n'est pas tout simplement interdite. Mais mettons cela de côté et supposons que la banque ait le droit d'acheter des actifs. Dans ce cas, l'argent donné au vendeur va se retrouver sur un compte de dépôt, au même titre que l'argent d'un crédit. Les mécanismes décrits plus haut fonctionnent donc de la même manière : l'achat d'actifs par une banque commerciale crée de la monnaie ! À vrai dire, on peut interpréter la création monétaire par le biais du crédit comme un cas particulier d'achat rémunéré par un intérêt.

La source primaire de la création monétaire

La présentation précédente peut laisser penser que seuls les dépôts sont la source de la création monétaire. En réalité, il n'est pas rare que les banques se financent par d'autres sources que les dépôts bancaires. Une banque peut prêter quand elle dispose de réserves excédentaires qu'elle peut prêter à ses clients, mais ces réserves ne viennent pas forcément de dépôts. Pour acquérir des réserves, les banques peuvent faire appel aux dépôts des particuliers, mais aussi à l'emprunt auprès d'une autre banque commerciale ou de la banque centrale, sur le marché monétaire. En clair, la banque commerciale emprunte de l'argent pour le prêter et se rémunère sur la différence entre les deux. Pour résumer, si une banque doit financer ses prêts, elle n'a pas forcément besoin de les associer à un montant équivalent de dépôts.

Si on remonte la source de chaque emprunt, on s’aperçoit qu'il provient soit d'un dépôt, soit d'un emprunt auprès d'autres intermédiaires financiers, soit de la création de réserves par la banque centrale. Et si on remonte aussi loin que possible, on s’aperçoit que toute monnaie provient de la banque centrale. C'est une première forme de création monétaire : la base monétaire nait ainsi. Les banques acquièrent ainsi les réserves obligatoires dont elles ont besoin, mais aussi les réserves excédentaires. Mais les banques commerciales n'aiment pas détenir de réserves excédentaires, peu rémunératrices, et s'en débarrassent en les prêtant à leurs clients ou à d'autres banques, ce qui enclenche le processus de création monétaire secondaire vu plus haut. L'activité de prêts injecte de la monnaie dans l'économie, en transformant une partie de la base monétaire (les réserves excédentaires) en monnaie de la masse monétaire. Pour résumer, les banques centrales créent de la monnaie, qui est mise en circulation par les banques commerciales.

Comme on le voit, cette vision, bien que réaliste, repose sur une hypothèse bien précise : les banques commerciales ne souhaitent pas garder de réserves excédentaires et préfèrent les échanger contre d'autres actifs. C'est réaliste quand les autres placements sont une meilleur compromis rendement/risque. Entre des réserves non-rémunérées et des obligation d'état peu risquées rémunérées à, mettons, 3%, le choix est vite fait. Mais depuis la crise de 2008, il est apparu que dans certaines circonstances, les banques commerciales acceptent de conserver de grandes quantités de réserves excédentaires. C'est le signe que les autres placements ne sont pas assez rentables et/ou trop risqués. Cela est aggravé par le fait que les réserves sont rémunérées par la banque centrale, avec un intérêt annuel, ce qui augmente l'attractivité des réserves. Si les banques commerciales conservent leurs réserves au lieu de les prêter, la mise en circulation des réserves ne se fait pas. La banque centrale a beau créer de grandes quantités de réserves, la masse monétaire reste la même.

L'influence de la banque centrale sur la création monétaire

Les théories exogènes décrivent correctement les économies où la banque centrale contrôle la quantité de réserves. Si la banque centrale contrôle la quantité de monnaie, les banques ne peuvent pas emprunter une quantité infinie de monnaie et ne peuvent pas créer autant de monnaie qu'elles le souhaitent. Mais le cas est rare et ne correspond pas aux économies développées où la banque centrale contrôle son taux directeur.

Dans ces économies modernes, on pourrait croire que la banque centrale peut imprimer autant de réserves que possible et que la création monétaire est donc illimitée. Si les banques commerciales manquent de réserves pour prêter, elles ont juste à emprunter à la banque centrale ou sur le marché monétaire. Mais c'est oublier que la banque centrale prête à un taux non-nul, ce qui empêche les banques d'emprunter autant qu'elles le souhaitent. En effet, les banques n'empruntent pas si les taux du marché monétaire sont plus grands que les taux de leurs crédits. Inutile d'emprunter à 5% sur le marché monétaire si les crédits ne rapportent que 2% à la banque. Les banques vont donc adapter leurs emprunts à la banque centrale en fonction des taux directeurs. Des taux trop élevés réduisent l’emprunt de réserves, alors que des taux bas favorisent la création de nouvelles réserves. La base monétaire est donc indirectement contrôlée par la banque centrale.

Pour résumer, ces théories donnent une limite maximale à la masse monétaire, limite qui dépend de la base monétaire. La masse monétaire est donc limitée par la base monétaire, ce qui permet à la banque centrale de contrôler la masse monétaire, par l'intermédiaire de la base monétaire. Quand la banque centrale crée de la monnaie, elle l'injecte dans l'économie, ce qui augmente la quantité de dépôts et d'emprunts. Cela se traduit par une augmentation générale de la masse monétaire, qui est amplifiée par le fait que les dépôts sont prêtés, ce qui crée de nouveaux dépôts, qui eux-mêmes créent de nouveaux prêts, etc. En clair, la masse et la base monétaire covarient, sauf dans le cas où les banques accumulent les réserves excédentaires. Ce qui est un avantage du modèle sur les théories à monnaie endogène : les théories exogènes expliquent pourquoi la banque centrale peut contrôler la masse monétaire et l'inflation, par son action sur la base monétaire et/ou les taux directeurs.

Comment tester empiriquement l'endogénéité/exogénéité de la monnaie ?

Maintenant que les théories en compétition ont été présentées, il est intéressant de regarder quelles peuvent être les moyens de les départager. Au niveau théorique, les versions élaborées de ces théories fonctionnent assez bien. Elles rendent compte de beaucoup d'observations et sont donc des approximations pas trop mauvaises de la réalité. Certes, les deux théories ont des défauts, mais ceux-ci sont généralement mineurs et peuvent se corriger avec quelques ajouts mineurs. Si on veut vraiment départager les deux théories, il faut se concentrer sur des points importants du modèle, qui ne peuvent pas être patchés facilement. Pour cela, on doit partir directement de l'hypothèse de base qui sépare monnaie exogène et endogène : est-ce que les banques sont des intermédiaires financiers ou non ?

Les modèles à monnaie exogène partent du principe que les banques sont des intermédiaires financiers, qui prêtent une épargne pré-existante. En clair, ils adhérent d'une manière ou d'une autre à la théorie des fonds prêtables, que nous avons vue dans le début de ce cours. Pour rappel, celle-ci explique quelle est l'origine des taux d'intérêt sur les marchés, sur le marché du crédit notamment. Elle dit qu'une offre d'épargne pré-existante rencontre une demande de crédits, donnant naissance à un prix du crédit : le taux d'intérêt. De plus, et c'est une chose importante : l'offre de crédit augmente avec les taux d'intérêt. À l'inverse, la monnaie endogène refuse cette interprétation et considère que la courbe de l'offre de crédit est horizontale. Elle n'explique pas les taux d'intérêts autrement que par le fait qu'ils sont décidés par les banques commerciales/centrales.

Notons que les deux théories sont compatibles avec le fait que le taux d'intérêt dépend du taux directeur et d'une prime de risque. Pour la monnaie exogène, les deux paramètres influencent à la fois la demande de crédit et l'offre d'épargne. Pour la monnaie endogène, les banques décident de la quantité de crédit accordée en fonction du risque de leurs clients et du taux directeur.

Équilibre IS dans les théories à monnaie endogène et exogène.

L'effet d'éviction de l'investissement

L'absence/existence d'une offre d'épargne pré-existante a des conséquences macroéconomiques. La différence se fait jour quand la demande de crédit augmente soudainement, peu importe la raison. D'après la théorie des fonds prêtables, la courbe d'offre de crédit reste la même, du moins tant que la banque centrale ne fait rien. Si la banque centrale n'injecte pas de liquidités, l'augmentation de la demande à offre égale se traduit par une hausse des taux d'intérêt. Mais pour la monnaie endogène, rien de tout cela ne se produit. Si la demande de crédit augmente, les banques fournissent les crédits demandés en créant la monnaie à partir de rien et les taux n'ont aucune raison de varier.

Là où la situation devient intéressante, c'est que cette situation hypothétique peut se voir dans le monde réel. En temps normal, l'état est en déficit fiscal, ce qui veut dire qu'il dépense plus qu'il ne collecte en impôt. Pour combler ce déficit, il emprunte l'argent manquant sur les marchés financiers. Le montant des emprunts est assez constant d'une année sur l'autre et il est assez prédictible. Mais il arrive que l'état emprunte soudainement plus que d'habitude. Par exemple, ce peut être parce que l'état lance un grand plan de relance économique, qui consiste à baisser les impôts et à augmenter les dépenses, afin de soutenir l'économie. Ou encore, ce peut être parce qu'un gouvernement nouvellement élu décide de baisser les impôts et/ou d'augmenter les dépenses. Ce faisant, la différence entre dépenses fiscales et impôts se creuse. Cela se traduit par une brutale augmentation des emprunts d'État, et donc par une hausse de la demande de crédit. Avec la monnaie endogène, il ne se passe rien en termes de taux d'intérêt. Mais avec la monnaie exogène, les taux augmentent, du moins si la banque centrale réagit correctement.

La hausse des taux liées à un déficit fiscal est ce qu'on appelle l'effet d'éviction. Le nom vient du fait que l'investissement privé est en partie évincé par l'emprunt public. En effet, la demande de crédit provient de deux sources : l'investissement privé et l'emprunt public. C’est une vision simplifiée, qui considère que tout emprunt par le privé est de l’investissement, mais passons. Sans augmentation du déficit fiscal, cet argent serait parti dans l'investissement privé, pas dans des emprunts d'État. Il y a donc remplacement de l'investissement privé par l'emprunt d'État, d'où le terme d'effet d'éviction.

Pour illustrer le tout, supposons que l'état emprunte 100 milliards de plus que d'habitude et qu'une partie de ces 100 milliards proviennent d'une épargne pré-existante. On précise bien une partie et pas la totalité. En effet, une partie de ces 100 milliards peut être financée par la création monétaire. Les théories à monnaie endogène disent que les 100 milliards proviennent systématiquement de la création monétaire, car les banques ne prêtent pas d'épargne pré-existante. À l'inverse, la monnaie exogène dit qu'une partie des 100 milliards est financée par la création monétaire, le reste par l'épargne. Par exemple, l'effet d'éviction se manifeste si 90 milliards sont créés et que 10 milliards proviennent de l'épargne. Et ce sont ces 10 milliards manquants qui sont à l'origine de la hausse des taux et de l'effet d'éviction.

Les conditions d'observation de l'effet d'éviction suivant le système monétaire

Dans un système monétaire où la banque centrale contrôle la quantité de monnaie, l'offre d'épargne n'est pas constante, mais augmente ou diminue en fonction de ce que décide la banque centrale. L'effet d'éviction se manifeste quand la création monétaire ne finance pas totalement le déficit de l'état. Si la banque centrale crée moins d'épargne que l'état n'en emprunte, le manque (argent crée - création monétaire) doit venir d'une épargne pré-existante qui est redirigée de l'investissement privé vers l'état. Par contre, l'effet d'éviction disparaît quand la banque centrale augmente la quantité d'épargne du même montant que ce que l'état emprunte.

Dans le système monétaire actuel, avec des banques centrales qui contrôlent leurs taux directeurs, il faut que la banque centrale réagisse en augmentant ses taux afin de limiter la création monétaire. Pour cela, il faut que l'état lance une relance fiscale alors que l'économie est assez proche du plein-emploi (certains états l'ont déjà fait). La banque centrale va alors anticiper les effets inflationnistes de cette politique et augmenter ses taux, afin d'annuler l'effet du plan de relance. La banque centrale limite donc sa création monétaire, de manière à ne pas financer totalement le déficit de l'état.

L'existence ou l'absence de l'effet d'éviction permet de dire quelle théorie est vraie : monnaie endogène ou exogène. Nul besoin de vous dire que la bataille fait rage entre les partisans de chaque modèle. Les études économétriques semblent bel et bien démontrer l'existence d'un effet d’éviction, mais sous conditions. Par conditions, on veut dire que la banque centrale doit réagir comme dit plus haut, soit en gardant la quantité de monnaie constante, soit en augmentant ses taux directeurs. Mais il arrive que la banque centrale ne réagisse pas quand l'état creuse son déficit, voire pire : baisse ses taux. C'est le cas suite à une crise économique : la banque centrale baisse ses taux et/ou crée de la monnaie pour complémenter le plan de relance. On ne s'attend pas à ce que l'effet d'éviction se manifeste, vu que la banque centrale baisse ses taux directeurs et que l'offre d'épargne augmente. Un cas particulier est quand la banque centrale crée directement l'argent demandé par l'état : l'état emprunte alors de l'argent frais à la banque centrale. Nous reviendrons sur ce phénomène dans le chapitre sur le modèle IS/LM, qui est le cadre idéal pour expliquer ce phénomène et donner ses conditions d'apparition.

Le multiplicateur du crédit

Dans les deux théories précédentes, il est raisonnable de supposer une relation proportionnelle entre la base monétaire et la masse monétaire. Le coefficient de proportionnalité entre les deux est appelé le multiplicateur du crédit, ou encore le multiplicateur monétaire, plus rarement diviseur du crédit.

Notations :

• $E$ : espèces (pièces et billets) ;
• $D$ : dépôts bancaires ;
• $B$ : la base monétaire $B$ ;
• $M$ : la masse monétaire $B$ ;
• $r$: le taux de réserve.

Le multiplicateur monétaire est défini par cette formule :

$M=c\times B$, ce qui est équivalent à dire que $c={\frac {M}{B}}$

On peut en donner une approximation on ne prend en compte que les réserves et où les espèces sont négligées. La base monétaire se résume alors aux réserves, alors que la masse monétaire se résume aux dépôts bancaires. On a alors :

$M=D$, $B=R$

En combinant les équations précédentes, on a :

$c={\frac {D}{R}}={\frac {1}{r}}$

On voit que le multiplicateur monétaire n'est autre que l'inverse du taux de réserves, dans ce cas particulier.

L'interprétation du multiplicateur monétaire

L'interprétation du coefficient monétaire est différente dans les modèles à monnaie endogène et dans les modèles à monnaie exogène. Les théories à modèle exogène nous disent que ce coefficient doit s'interpréter comme un multiplicateur. Il dit, pour chaque unité de base monétaire crée, de combien la masse monétaire va augmenter. À l'inverse, les théories à monnaie endogène supposent que ce coefficient est un diviseur : la masse monétaire est créée par les banques commerciales et la banque centrale doit créer alors 1/c unités de base monétaire pour chaque unité de masse monétaire crée.

Le diviseur du crédit

Avec une monnaie endogène, ainsi que dans les théories à monnaie exogène moderne, les banques commerciales créent le montant de crédit qu'elles souhaitent et imposent la masse monétaire. Elles vont alors acquérir le montant de réserves nécessaires pour respecter leurs obligations légales, et acquérir suffisamment d'espèces pour couvrir les retraits. Si on omet les espèces, les banques commerciales vont d'abord créer la masse monétaire $M$, puis acquérir une quantité $M\times r$ de réserves. La banque centrale crée ces réserves sur demande, en les prêtant ou en les échangeant contre des actifs. La causalité va donc de la masse monétaire vers la base monétaire, ce qui fait que ce coefficient est à interpréter comme un diviseur de la masse monétaire.

Changer le taux de réserve n'a donc pas d'influence directe sur la masse monétaire et ne permet pas d'augmenter la masse monétaire : cela permet juste de modifier la quantité de réserves à masse monétaire inchangée. Le taux de réserves n'est donc pas un instrument de la politique monétaire et ne peut pas servir pour contrôler ni la masse monétaire, ni l'inflation, ni quoi que ce soit d'autre. Évidemment, cela ne colle pas parfaitement au monde réel, où certaines banques centrales utilisent ou ont utilisé leur taux de réserve comme instrument, avec une certaine réussite. Par exemple, la réserve fédérale américaine a utilisé le taux de réserve comme instrument à l'époque de l'étalon-or. Plus récemment, les banques centrales chinoises, brésiliennes, russes et quelques autres utilisent encore le taux de réserves comme instrument, avec à chaque fois un effet sur la masse monétaire. Les augmentations du taux de réserves réduisent bien la création de nouveaux prêts par les banques, alors que les réductions les facilitent.

Le multiplicateur du crédit

Dans les anciennes théories à monnaie exogène, l'interprétation du multiplicateur du crédit est l'inverse de celle en monnaie endogène. Cette fois-ci, la banque centrale crée la base monétaire, qui est exogène, et le système bancaire s'occupe de fabriquer la masse monétaire à partir des réserves. Dans ce processus, la création monétaire par les banques commerciales fait que la masse monétaire augmente, par rapport à la base monétaire. Au final, la masse monétaire totale devient égale à la base monétaire multipliée par le multiplicateur du crédit. En quelque sorte, la création monétaire des banques commerciales s'occupe de multiplier la base monétaire par le multiplicateur du crédit. La base monétaire est donc exogène, alors que la masse monétaire est endogène.

Pour comprendre comment font les banques pour "multiplier la base monétaire", prenons le cas où la masse monétaire est nulle initialement. La banque centrale crée une base monétaire égale à une certaine somme, qui sert de dépôts bancaires. Les banques commerciales vont alors garder la quantité nécessaire de réserves (avec éventuellement des réserves excédentaires), mais vont prêter le reste. Or, ces  prêts sont considérés comme de la monnaie crée par les banques commerciales. La masse monétaire, initialement du fait de la banque centrale, augmente par le biais des prêts, d'un montant qui dépend du taux de réserves (qui impose de ne pas prêter une certaine quantité des dépôts). Ce processus est illustré dans le schéma ci-contre. Mais ce n'est que la première étape : la monnaie crée ainsi va aussi être déposée, une partie va être mise en réserves, et le reste prêté. La masse monétaire va donc encore augmenter d'un certain montant, plus faible que le montant de l'étape précédente. Et le processus va se répéter ainsi indéfiniment. Nous avions vu ce mécanisme dans le paragraphe sur la monnaie exogène, mais il est intéressant de détailler ce processus étapes par étape, afin de le mettre en équations.

Le tableau ci-dessous donne un exemple de ce processus itéré de création monétaire, étape par étape. On suppose que le taux de réserves est de 10%, et que la masse monétaire initiale est de 100 euros.

Illustration du processus de création monétaire avec un exemple chiffré (taux de réserves = 10%)

Tour de création monétaire	Réserves	Crédits	Dépôts
1			100
2	100 * 10% = 10	100 * 90% = 90	100 + 90 = 190
3	190 * 10% = 19	190 * 90% = 171	190 + 171 = 361
4	361 * 10% = 36.1	361 * 90% = 324.9	361 + 324.9 = 685.9
...
$\infty$	100	900	1000

Il est intéressant de mettre ce processus en équation, en regardant ce qui se passe étape par étape. Dans ce qui suit, nous allons partir d'une quantité de dépôts fixe et regarder quelle est la quantité de crédits créée à chaque étape, et la quantité de dépôts obtenue. Voici le déroulement complet :

1 : La banque centrale crée une quantité $D_{0}$ de dépôts, qui sont placés dans les banques commerciales.

2 : Les banques commerciales vont mettre en réserve une fraction $r$ des dépôts et vont prêter le reste. La quantité de crédit sera alors de $C_{1}=(1-r)D_{0}$. La masse monétaire totale sera égale à la masse monétaire initiale à laquelle il faut ajouter l'encours des nouveaux crédits. On a alors :

$D_{1}=D_{0}+C_{1}=D_{0}+(1-r)D_{0}$

3 : Encore une fois, les banques vont mettre en réserve une fraction $r$ des dépôts et vont prêter le reste. On a alors : $C_{2}=(1-r)D_{1}$. La masse monétaire totale sera égale à la masse monétaire de l'étape précédente à laquelle il faut ajouter l'encours des nouveaux crédits. On a alors :

$D_{2}=D_{1}+C_{2}=D_{1}+(1-r)D_{1}=D_{0}+(1-r)D_{0}+(1-r)^{2}D_{0}$

4 : Même principe que pour les étapes précédentes, ce qui donne :

$D_{3}=D_{0}+(1-r)D_{0}+(1-r)^{2}D_{0}+(1-r)^{3}D_{0}$

Et ainsi de suite. Au énième tour de création monétaire, on a :

$D_{n}=D_{0}+(1-r)D_{0}+(1-r)^{2}D_{0}+(1-r)^{3}D_{0}+...+(1-r)^{n-1}D_{0}+(1-r)^{n}D_{0}$

Le processus se répète indéfiniment (ou presque), ce qui donne, pour une infinité de tours de création monétaire :

$D=\sum (1-r)^{i}D_{0}=D_{0}\sum (1-r)^{i}$

Quelques calculs algébriques nous donnent la somme totale des dépôts :

$D=D_{0}{\frac {1}{r}}$

On peut alors calculer la quantité totale de réserves qui correspond, en multipliant la formule précédente par le taux de réserves, ce qui donne :

$R=D\times r=D_{0}$

Si on néglige totalement l'existence des espèces, la quantité finale de dépôts n'est autre que la masse monétaire et la quantité totale de réserves n'est autre que la base monétaire. On a alors :

$M=B{\frac {1}{r}}$

On retrouve bien la formule simplifiée obtenue pour le multiplicateur monétaire.

Un défaut de ce modèle est qu'il part du principe que la banque centrale crée la base monétaire, qu'elle décide combien de réserves mettre en circulation dans l'économie. Ce qui n'est pas le cas dans le système monétaire actuel, où la banque centrale contrôle les taux directeurs, mais pas la quantité de monnaie qu'elle crée. Un autre défaut est qu'il suppose que les banques ne gardent pas de réserves excédentaires, du moins dans une version naïve du modèle. Si les banques commerciales gardent des réserves excédentaires, la masse monétaire est alors inférieure à celle prédite par la formule naïve du multiplicateur. On peut cependant résoudre ce problème en remplaçant le taux de réserves obligatoires par le taux de réserve effectif (qui prend en compte toutes les réserves, qu'elles soient obligatoires ou excédentaires).

À noter que l'existence des réserves excédentaires peut s'expliquer de plusieurs manières : soit les banques ne veulent pas prêter leurs réserves excédentaires, soit elles ne le peuvent pas. Par exemple, elles peuvent très bien garder leurs réserves excédentaires parce qu'elles sont rémunérées à un taux positif par la banque centrale, parce que les opportunités d'investissements sont mauvaises (préteurs trop risqués, rares, ..). Elles peuvent aussi vouloir les prêter, mais ne pas trouver suffisamment de demande de crédit. On en revient un peu à ce qui était dit dans le paragraphe sur la monnaie endogène. Tout cela pour dire que la théorie du multiplicateur monétaire est une sorte de théorie de l'offre, mais appliquée à la monnaie. Elle considère que la demande de crédit n'est pas un facteur limitant, et que toute réserve pouvant être prêtée l'est. La prise en compte des réserves excédentaires dans le calcul du multiplicateur monétaire résout cependant ce problème.

Les formules de calcul du multiplicateur monétaire

Dans cette section, nous allons donner une formule pour le calcul du multiplicateur qui est un peu plus précise que la formule $c={\frac {1}{r}}$. Nous utiliserons ensuite cette formule plus élaborée pour discuter de l'influence du taux de réserves ou de la présence d'espèces sur la politique monétaire. Il faut noter qu'il existe un multiplicateur différent pour chaque agrégat monétaire : le multiplicateur de l'agrégat M1 n'est pas celui du M2, ou du M3 ! Dans ce qui va suivre, nous allons nous concentrer sur le multiplicateur de l'agrégat M1, histoire de nous concentrer sur le cas le plus simple. Pour rappel, l'agrégat $M1$ regroupe les espèces et l'argent déposé sur les comptes de dépôts. On va aussi prendre en compte le fait que les réserves se décomposent en réserves obligatoires et excédentaires. Notons $R_{o}$ les réserves obligatoires, et $R_{e}$ les réserves excédentaires. Le taux de réserves est égal à $r={\frac {R_{o}}{D}}$. On pose aussi $e={\frac {R_{e}}{D}}$, et $k={\frac {L}{D}}$ (ce dernier est appelé le coefficient de liquidité). On a :

$B=E+R_{o}+R_{e}=kD+rD+eD=(k+r+e)D$

$D={\frac {1}{k+r+e}}B$

Or, de par la relation $M=(1+k)\times D$, il vient :

$M={\frac {1+k}{k+r+e}}B$

$c={\frac {1+k}{k+r+e}}$

Le taux de réserve

La formule précédente permet de déterminer la valeur maximale possible du multiplicateur du crédit, pour une valeur de $r$ fixée. Ce maximum est atteint quand le coefficient k vaut 0 : tout l'argent est alors déposé à la banque, ce qui maximise la création monétaire par le crédit. On obtient alors :

$c={\frac {1}{r+e}}$

Illustration de l'effet du taux de réserve sur la création monétaire maximale, toutes choses égales par ailleurs.

On peut remarquer que le taux de réserves influence le multiplicateur du crédit et donc la quantité totale de monnaie dans l'économie. À ceci près que ce raisonnement prend en compte le taux de réserves excédentaires. Supposons qu'il n'y ait pas de réserves excédentaires, toutes les banques cherchant à prêter leurs réserves au maximum. Dit autrement, on suppose que la demande de crédit de la part des emprunteurs est suffisamment grande pour ne pas avoir d'influence, seule l'offre de crédit de la part des banques étant limitante. Dans ces conditions, l'offre de crédit sera contrainte par les réserves détenues par les banques. Celles-ci seront limitées par le fait qu'elles ne peuvent pas prêter au-delà de ce qu'impose le taux de réserves. Augmenter la base monétaire, diminuer le taux de réserves, permettra aux banques d'avoir plus d'argent à prêter, augmentant ainsi la masse monétaire totale. Du moins, le raisonnement reste valide tant que les banques ne veulent pas garder de réserves excédentaires...

Abaisser le taux de réserves permet ainsi de créer de la monnaie, dans une certaine mesure, et inversement pour une hausse. Comme exemple, on peut citer le cas de la réserve fédérale américaine lors de la dépression de 1929, qui a baissé son taux de réserves pour faire face à la crise (entre autres). Mais de nos jours, cet instrument est peu utilisé par les économies développées, même si quelques utilisations récentes par la Chine ou l'Inde font exception. La raison est que, pour les économies développées, modifier le taux de réserve a peu d'impact sur la masse monétaire. Diminuer le taux de réserve permet de libérer des réserves, devenues excédentaires après modification du taux, mais cela n'implique pas que les banques vont les utiliser. À l'opposé, augmenter le taux de réserves force les banques à accumuler les réserves, mais cela peut mettre en difficulté le système bancaire, par raréfaction des réserves.

En théorie, un taux de réserves non-nul augmente l'efficacité de la politique monétaire, d'où le fait que le taux de réserve soit non-nul dans beaucoup de pays développés. Cependant, beaucoup de pays développés ont supprimé la contrainte du taux de réserve, celui-ci étant nul au Canada, au Royaume-Uni, et dans quelques autres pays. La Banque centrale européenne a gardé un taux de réserves non-nul.

Le coefficient de liquidité

Le coefficient k, qui décrit comment les agents répartissent leur monnaie sous forme d'espèce ou de dépôts, a aussi une influence importante. Ces fuites sous forme d'espèces imposent une seconde limite à la création monétaire. Si la banque crée énormément de monnaie sous la forme de crédit, une part de celle-ci quittera les comptes de la banque, à cause des virements ou des retraits. Au final, une partie pourra être transformée en billets ou en pièces, que la banque devra fournir. Et la banque doit avoir assez de billets et de pièces pour répondre aux besoins : si elle prête trop, l'argent des crédits ne pourra être retiré faute de billets et de pièces en circulation. Au maximum, la création monétaire ne peut pas dépasser une valeur dépendant uniquement du taux de liquidité, qui se calcule en posant le taux de réserve comme nul :

$c={\frac {1+k}{k}}=1+{\frac {1}{k}}$

On voit alors que plus $k$ est petit, plus le multiplicateur du crédit est fort. Cela se comprend intuitivement : plus les personnes préfèrent la monnaie, moins les dépôts seront importants, réduisant les réserves et donc les prêts. Les banques prêtant moins, la monnaie crédit sera alors moins importante, réduisant d'autant la masse monétaire. Il est donc important de comprendre ce qui fait que les agents économiques préfèrent utiliser des dépôts ou des espèces.

• Un premier paramètre est tout simplement la différence de rendement des dépôts comparé aux espèces. Il arrive que les comptes courants soient rémunérés, chose courante dans d'autres pays que la France. Dans cette situation, conserver son argent en dépôts est plus rentable que de convertir en espèces. Les ménages préféreront conserver des dépôts en lieu et place des espèces, faisait augmenter le coefficient $k$.
• Un autre paramètre est le fait que les espèces sont utilisées pour les dépenses. Les ménages qui dépensent une faible partie de leur revenu ont donc moins besoin d'espèces et peuvent préférer conserver leur argent sur des comptes courants. Ces ménages sont souvent des ménages à fort revenus, ou tout du moins dont les revenus couvrent bien plus que leurs dépenses courantes. Le revenu et la richesse globale de l'économie diminuent donc le coefficient $k$.
• L'activité illégale a besoin d'espèces, les transferts d'argent importants étant surveillés sur les réseaux bancaires. Les criminels, vendeurs de drogue et autres malfrats ont besoin d'espèces pour conserver la confidentialité de leurs transactions délictueuses.
• De plus, ce coefficient évolue fortement dans les situations de crises financières et bancaires, quand le risque de faillite d'un grand nombre de banques augmente. Lors de ces crises, les agents économiques tentent de se prémunir d'une éventuelle faillite en retirant leur argent. Dit autrement, ils voient les dépôts comme étant plus risqués et préfèrent donc garder leur monnaie sous forme d'espèces. Le coefficient k augmente alors, pouvant aggraver la situation financière des banques. Si le nombre de retrait est suffisamment important pour aggraver fortement la situation des banques, on parle de situation de bank-run.

Références, en savoir plus

• The money creation paradox : Banks create money, but also have to borrow it

Les relations entre taux et agrégats monétaires

Les deux chapitres précédents ont porté sur la création monétaire, sans faire le lien avec les taux d'intérêt. Mais dans les faits, la masse monétaire dépend des taux d'intérêt en vigueur et réciproquement. Plus les taux sont élevés, plus le crédit baisse, plus la masse monétaire se réduit. Dans ce chapitre, nous allons poursuivre les développements du chapitre précédent et montrer quelles sont les relations entre taux directeur, taux long-terme, masse monétaire et base monétaire. Nous en avions déjà touché un mot avec les théories de la monnaie endogène et exogène, mais nous n'avions pas tout dit. Il nous faut en effet parler plus en détail des différentes relations entre les taux et la monnaie, ce qui est le but de ce chapitre.

La relation entre base monétaire et taux directeur

Pour commencer, il nous faut étudier le lien entre base monétaire et taux directeur, qui sont très dépendants l'un de l'autre. En temps normal, la relation entre les deux est la même qu'entre la masse monétaire et les taux d'intérêt : plus le taux directeur est haut, plus la base monétaire est réduite. La raison à cela tient dans le fonctionnement du marché monétaire. Rappelons que les banques commerciales empruntent à la banque centrale au taux directeur. Plus celui-ci est bas, plus il est intéressant pour les banques d'emprunter à la banque centrale. Or, les banques empruntent des réserves bancaires, qui font partie de la base monétaire. Le lien est donc : taux directeur -> emprunt à la banque centrale -> base monétaire. On peut résumer cette relation décroissante sur un graphique.

Lien entre base monétaire et taux directeurs

Il existe cependant des situations où la base monétaire devient totalement indépendante des taux directeurs, comme nous allons le voir plus bas.

Les origines de la demande de réserves

Il existe toujours une demande de réserve minimale, liée à l'existence du taux de réserve. Les banques étant tenues d'avoir un certain pourcentage de leurs dépôts en réserves à la banque centrale, cela signifie qu'il y a une quantité minimale de réserves, qui dépend des dépôts (et donc de la masse monétaire). Ce qui fait que tant qu'il existe un taux de réserve obligatoire, la demande de réserves ne peut pas être nulle. Mais attention : rien n’empêche les banques commerciales d'avoir plus de réserves que nécessaire, pour diverses raisons. La demande de réserves n’est donc jamais nulle, même avec des taux règlementaires de réserve à 0, et dépasse parfois la demande minimale de réserves obligatoires.

La présence de réserves excédentaires peut s'expliquer, au moins en partie, par le fait que les banques ont besoin des réserves pour assurer les virements interbancaires. Rappelons que les banques s'échangent des réserves pour payer les virements. Lorsqu'on fait un virement d'une banque A vers une banque B, la banque A envoi le montant du virement à la banque B sous la forme de réserves bancaires. La monnaie que s'échangent les banques est donc composée de réserves bancaires, pas de monnaie-crédit (la monnaie de la masse monétaire). Il existe donc une demande de réserves liée aux échanges interbancaires, qui dépend de la banque (certaines auront besoin de beaucoup de réserves, d'autres non). La demande de réserve d'une banque dépend du nombre de virements entrants et sortants. Plus elle a de virement sortants par rapport à ses virements entrants, plus sa demande de réserve sera importante. On peut appeler cette demande de réserve ainsi : "demande de réserve pour motif de transaction". En théorie, cette demande de réserve est indépendante des taux directeurs, les taux n’influençant pas les virements interbancaires, que ce soit en nature ou en nombre. Elle dépend par contre de la masse monétaire totale et de sa vitesse de circulation. Plus précisément, elle dépend de la demande de dépôts en monnaie scripturale, mais pas exactement de la demande de crédits.

Une autre part de la demande de réserves excédentaires sert à faire des prêts, sur le marché interbancaire ou dans l’économie réelle. Les banques empruntent des réserves pour les prêter, soit à d'autres banques en manque de réserves, soit sous la forme de prêts aux entreprises ou à des particuliers. Mais rappelons que ces réserves n'en restent pas longtemps et qu'elles deviennent de la monnaie scripturale une fois prêtées. Cette forme de demande de réserves est donc transitoire : peu de temps après avoir été créées, ces réserves quittent les comptes de la banque centrale pour circuler dans l'économie réelle. Notons que, en théorie, les montants empruntés pour ce motif dépendent uniquement de la prime de risque, pas du montant des taux directeurs proprement dits. Mais les choses sont plus compliquées en pratique.

Une autre origine de la demande de réserve excédentaires tient dans l'anticipation des taux directeurs futurs. Les banques peuvent décider d'emprunter des réserves maintenant pour les prêter dans plusieurs années ou dans plusieurs mois. On peut se demander pourquoi elles empruntent aussi tôt, au lieu d'emprunter juste avant de prêter, mais ce serait omettre que les taux directeurs évoluent. Entre emprunter maintenant à taux bas et emprunter plus tard à taux hauts, le choix est vite fait. Si les banques anticipent une hausse future des taux, elles vont emprunter maintenant au lieu de dans le futur. À l'inverse, si elles anticipent une baisse des taux, elles vont attendre un petit peu avant d'emprunter à la banque centrale. On peut appeler cette demande de réserve ainsi : "demande de réserves pour motif de spéculation". Cette demande de réserves dépend donc naturellement des taux. Plus précisément, cette demande diminue quand les taux augmentent, ce qui donne une relation décroissante.

Pour résumer, la demande de réserves a plusieurs origines : les virements interbancaires, le financement des prêts bancaires, et l'existence des réserves obligatoires.

Excès et pénurie de réserves

Le schéma précédent montre une situation où la demande de réserve existe et fait face au taux directeur de la banque centrale ce qui détermine la quantité de réserves imprimée par la banque centrale. Une autre situation est possible, où la banque centrale décide de la quantité de réserves qu'elle offre, l'intersection offre-demande décidant du taux directeur. Dans les deux cas, on a une demande de monnaie non-nulle, ce qui veut dire que les banques commerciales manquent de réserves et comblent ce manque par un emprunt à la banque centrale. Mais il existe des situations où les banques commerciales ont suffisamment de réserves et où elles n'ont pas besoin d'emprunter : la demande de réserves n'existe pas. Tout dépend de si il y a un manque ou un excès de réserve.

Dans le cas le plus classique, les réserves manquent. Le système bancaire manque globalement de réserves, que ce soit pour répondre à la demande de réserves obligatoires, ou pour financer les prêts. Par globalement, on veut dire que les réserves excédentaires sont insuffisantes. Les banques qui manquent de réserves vont chercher à les acquérir auprès d'autres banques qui ont des réserves excédentaires. Les réserves excédentaires sont alors prêtées aux banques en pénurie, mais cela ne suffit pas à combler le manque. Au final, il restera quelques banques qui manqueront de réserves et devront se fournir auprès de la banque centrale. Pour le dire autrement, pour que la demande de monnaie existe, il faut que le système bancaire soit en pénurie de réserves. On dit que l'on est dans un système à corridor, terme dont nous verrons le sens complet dans le chapitre sur le marché monétaire.

À l'inverse, on peut imaginer une situation où le système bancaire ait un excès global de réserves. Il peut y avoir des banques qui manquent de réserves, mais elles arrivent toutes à se fournir auprès des banques commerciales avec des excès. Ce faisant, aucune banque n'a besoin d'emprunter auprès de la banque centrale. Cela arrive si la banque centrale a autrefois émis trop de réserves et que l'excès s'est maintenu dans le temps. Dans une telle situation, le taux d'emprunt auprès de la banque centrale n'a plus aucun effet sur l'économie et sur le marché interbancaire.

Mais cela ne signifie pas que la banque centrale ne peut plus influencer les taux sur le marché interbancaire. Pour cela, elle doit utiliser un autre instrument : le taux de rémunération des réserves. Il correspond au taux d'intérêt auquel la banque centrale rémunère les réserves, comme si celles-ci étaient placées sur un livret bancaire avec un intérêt positif. Les banques n'ont alors pas intérêt à prêter leurs réserves à un taux inférieur au taux de rémunération des réserves : à quoi bon prêter les réserves à 2%, si la banque centrale les rémunère à 5% ? Ce qui fait que le taux de rémunération influence la quantité de prêts accordés par les banques, ce qui a un impact indirect sur la quantité de réserves (la courbe de demande de réserves est alors horizontale, voire croissante).

Un tel système est appelé un système à plancher (Floor system) et nous l'étudierons plus en détail dans le chapitre sur le marché monétaire. Toujours est-il que dans un tel système, il n'y a pas à proprement parler de courbe de demande de réserves, qui relie le taux de rémunération à la quantité de réserves, ce qui n'a pas d'importance pour ce qui va suivre.

Relation entre base monétaire et taux directeurs, suivant que le système bancaire est en manque ou en excès de réserves

Toujours est-il que la banque centrale peut contrôler l'état du système bancaire : elle peut le mettre en manque ou en excès de réserves en utilisant divers instruments. Par exemple, la banque centrale peut injecter ou retirer des réserves de la circulation comme bon lui semble, avec des opérations d'open market. En achetant/vendant des obligations d'état, elle augmente/réduit la quantité de réserves. Elle peut aussi organiser une pénurie en augmentant le taux de réserves obligatoires. Les banques vont devoir alors garder plus de réserves dans leurs coffres, ce qui augmente la demande de réserves. Pour que sa politique monétaire ait un impact optimal sur l'économie, la banque centrale doit faire en sorte que le système bancaire se trouve en pénurie de réserves, c’est-à-dire qu'il existe une demande non-nulle de réserves agrégées (toutes banques comprises). La banque centrale a le contrôle des taux d'intérêt, ce qui limite de ce fait la création monétaire avec les mécanismes expliqués dans la suite du chapitre.

La relation entre taux directeur et taux d'intérêts bancaires

Rappelons quelques faits : les banques commerciales font face à une demande de crédits de la part des agents économiques souhaitant emprunter. Elles répondent à cette demande en fournissant une partie des emprunts demandés. Dit autrement, une demande de crédits fait face à une offre bancaire de crédits. L'intersection entre cette offre et cette demande donne le volume total de crédit circulant dans l'économie, c’est-à-dire la masse monétaire, mais aussi le taux d'intérêt. Il y a donc une relation entre taux d'intérêt et masse monétaire. Sauf que le taux d'intérêt en question n'est pas le taux directeur, mais le taux proposé par les banques. Ce taux est le taux auquel les agents économiques empruntent, et il est différent du taux directeur de la banque centrale. S'il y a une relation entre ces deux taux, nous allons d'abord voir ce qui se passe si on néglige cette relation, afin de simplifier les explications.

La relation entre masse monétaire et taux d'intérêts

Rappelons que les banques, comme toute entreprise, cherchent à maximiser leurs profits, profits qui lui viennent des intérêts des prêts. Elle va donc fixer un taux d'emprunt qui lui permet de rentabiliser au maximum ses activités de prêts. Dans la théorie que nous allons voir, c'est ce taux d'emprunt qui détermine la création monétaire. Cette "théorie", fabriquée pour l'exemple, dit que la masse monétaire dépend de la volonté des agents de s'endetter, ainsi que de la volonté des banques de maximiser leur profit. La masse monétaire nait de la rencontre entre une demande de crédit de la part des agents économiques et un taux décidé par les banques. Tout se passe comme si la masse monétaire était choisie par les agents économiques. L'ensemble du modèle, base et masse monétaire inclue, est résumé dans le schéma ci-dessous.

Détermination de la masse monétaire dans un modèle de monnaie endogène

L'offre de crédit de la part des banques n'est pas limitée par les réserves bancaires et on voit mal comment la politique monétaire pourrait intervenir pour la limiter, ni même pour la contrôler finement. La politique monétaire est, dans cette théorie, complètement impotente : elle ne peut pas limiter la création monétaire par les banques privées. Chose qui est passablement incompatible avec la réalité : on observe bien que les banques centrales ont bien réussi à contrôler l'inflation et la masse monétaire depuis plusieurs décennies... Avec l'apparition du régime de ciblage de l'inflation, les banques centrales ont toutes réussi à maintenir l'inflation proche de leur cible de 2%, alors que les théories à monnaie endogène disent clairement que c'est impossible.

D'ailleurs, chose liée au problème précédent, la théorie n'explique pas pourquoi les taux d'intérêts servis par les banques dépendent des taux directeurs, les taux d'emprunt à la banque centrale. En théorie, le taux d'intérêt servi par les banques commerciales ne devrait dépendre que de la maximisation de leur profit. Le taux auquel elles empruntent leurs réserves ne devrait pas jouer du tout sur leur profitabilité. Pourtant, dans le monde réel, les taux directeurs et les taux des banques commerciales covarient très fortement : quand l'un monte, l'autre le fait presque exactement dans les mêmes proportions. Une hausse de 1% du taux directeur se répercute à l'identique sur les taux bancaires. Impossible d'expliquer cela sans recourir d'une manière ou d'une autre à un mécanisme de monnaie exogène, ce que les théories concurrentes font très bien !

Qui plus est, la théorie n'explique pas pourquoi le taux de réserve est utilisé par certaines banques centrales comme instrument de leur politique monétaire. Avec un effet macroéconomique sur l'emprunt qui est très loin d'être négligeable.

D'ailleurs, cette théorie n'explique pas pourquoi les banques détiennent des réserves excédentaires. En théorie, les banques devraient limiter au maximum leurs réserves excédentaires, qui ne leur servent à rien. Elles ne peuvent pas les prêter si le besoin s'en fait sentir, mais leur emprunt leur coute beaucoup à cause des taux d'intérêts de la banque centrale. Elles ont besoin d'emprunter juste ce qu'il faut pour respecter les taux de réserves obligatoires, mais pas plus. Limiter au maximum les réserves excédentaires est donc une chose très importante, qui s'est observé durant un long moment (jusqu'à la crise de 2008), mais qui est aujourd'hui incompatible avec le gigantesque niveau de réserves excédentaires. Tout cela semble indiquer que les banques commerciales ont intérêt à avoir des réserves excédentaires, ce qui est incompatible avec le fait que ces réserves leur coutent.

Au passage, le fait que les réserves sont rémunérées à un taux d'intérêt positif n'y change rien : ce taux est de toute façon inférieur au taux d'emprunt de ces réserves. De plus, en zone euro, les banques acceptent des réserves excédentaires alors que le taux de rémunération de celles-ci était négatif !

Et pour finir, cette théorie n'explique pas pourquoi les banques cherchent à attirer des dépôts, ni pourquoi elles empruntent sur les marchés financiers. Pourquoi s’embêtent-elles à rémunérer les livrets, comptes à terme et autres formes dépôts bancaires, alors qu'elles n'en ont pas besoin ? En théorie, elles n'ont pas besoin de dépôts pour fonctionner et on peut s'étonner que les banques aient conservé une activité de banque de détail. Alors pourquoi attirer des fonds en promettant de les rémunérer avec un intérêt ? De même, pourquoi les banques empruntent-elles autant d'argent, au point d'avoir des ratios capital/passif proches du pourcent ? Pourquoi une telle quantité d'emprunts interbancaires, pourquoi empruntent-elles sur les marchés obligataires ? Autant l'emprunt aux banques centrales peut se comprendre, vu qu'elles font face à des contraintes règlementaires qui imposent un taux de réserve minimal. Mais les autres formes d'emprunt ne collent absolument pas avec les théories à monnaie endogène ! Impossible d'expliquer la structure du bilan d'une banque avec ces théories, alors que les théories à monnaie exogène le font parfaitement bien !

Les taux directeurs influencent les taux d'intérêts bancaires

Le modèle précédent, trop simpliste, est une fiction à laquelle aucun économiste ne croit. Il s'agit d'une création de l'auteur, qui a pour but de simplifier les explications qui vont suivre. Ce modèle pédagogique doit naturellement être amendé, au vu de ses nombreux problèmes. Pour cela, nous allons revenir sur une hypothèse : le taux d'intérêt servi par les banques ne dépend que de leur volonté de faire du profit. Si le gout pour l'argent des banques n'est pas à démontrer, il faut cependant ajouter un paramètre : le taux des banques dépend du taux servi par la banque centrale. Dans le monde réel, les taux directeurs et les taux des banques commerciales varient en même temps : quand l'un monte ou descend, l'autre le fait presque exactement dans les mêmes proportions. Mais taux directeur et taux bancaires ne sont pas identiques. Dans les faits, les taux bancaires sont un peu plus élevés que les taux directeurs, pour diverses raisons.

Le mécanisme qui lie les tau directeurs aux taux d'emprunt est assez simple, et se base sur le fait que les banques sont des intermédiaires financiers. Les banques commerciales acquièrent leurs réserves en les empruntant à la banque centrale, à un certain taux : le taux directeur. Le taux directeur va moduler l'offre de crédit et les taux d'intérêts bancaires, par deux mécanismes. Ces mécanismes impliquent des taux différents : le taux d'emprunt à la banque centrale pour le plancher, le taux de rémunération des réserves pour le second.

Pour étudier le premier mécanisme, il faut se mettre dans une situation de pénurie de réserves. Dit autrement, on suppose que les banques commerciales prêtent l'argent qu'elles empruntent à la banque centrale. Prenons l'exemple d'une entreprise qui souhaite emprunter 100 000 euros à sa banque. Si la banque n'a pas les fonds nécessaires pour ce prêt, elle les emprunte sur le marché monétaire. Et seule la banque centrale peut créer la monnaie demandée si celle-ci vient à manquer dans le système économique. La banque commerciale va donc emprunter de l'argent à la banque centrale et le prêter à des entreprises ou des ménages. Évidemment, la banque centrale ne prête pas ses réserves à taux zéro, mais charge ses prêts au taux directeur. Ce système n'est rentable que si le taux du prêt est plus important que le taux directeur. Emprunter à 1% pour prêter à 2/3% est rentable, mais emprunter à 2% pour le prêter à 1% signifie une perte pour la banque. Le taux directeur sert donc de plancher pour le taux auquel prêtent les banques.

L'autre mécanisme se manifeste quand le système bancaire est en excès de réserves, quand les banques n'ont pas besoin de se financer auprès de la banque centrale. Dans ce cas, les banques vont quand même limiter leur création monétaire en réaction à la politique monétaire. En effet, il faut prendre en compte le taux de rémunération des réserves. Si le taux de rémunération des réserves est à 5%, aucune banque n'irait prêter ces réserves à seulement 2 à 3%. Les banques n'auraient d'intérêt à prêter les réserves qu'à un taux supérieur. Ce faisant, le taux de prêt sert donc là aussi de plancher pour les taux auxquels les banques prêtent. Par contre, le taux directeur est différent dans cette situation.

L'existence d'une prime de risque

Les banques ne se contentent pas de prêter des fonds au taux directeur, pour plusieurs raisons. Déjà, la durée d'un emprunt à la banque centrale n'est pas la même que la durée d'un prêt. Une banque ne peut pas emprunter sur 20 ans à la banque centrale, alors qu'elle offre des crédits immobiliers sur 20 ans. Mais surtout, les crédits qu'elle offre sont risqués et il y a un risque de non-remboursement. Pour l'éviter, les banques sélectionnent activement les crédits qu'elles acceptent en fonction du risque de crédit. Mais cela ne suffit pas et elles doivent faire payer à chaque crédit un taux plus élevé que le taux directeur pour compenser le risque pris. Ainsi, si un prêt n'est pas remboursé, le sur-taux des autres prêts compense totalement la perte du crédit.

Les banques commerciales vont fixer leurs taux juste au-dessus du taux directeur, en fixant une marge qui leur permet de couvrir les risques du prêt, mais aussi de gagner un profit et de rémunérer leurs employés. Or, les banques commerciales sont toutes en concurrence, ce qui les pousse à baisser leurs taux ou tout du moins à les garder proches des taux des autres banques. Une banque ne peut pas augmenter ses taux trop haut, sous peine de perdre ses clients, partis voir la concurrence. Du fait de la concurrence, cette marge est réduite au plus possible et se limite à peu près à une prime de risque, qui varie selon le risque de non-remboursement. L'existence du taux directeur limite donc les taux d'emprunt, ce qui décide donc indirectement de la masse monétaire (par l'intermédiaire de la demande de monnaie). Pour résumer, le taux d'intérêt sur les crédits dépend non seulement des taux de la banque centrale, mais aussi d'une prime de risque qui dépend du ménage et de son projet d'investissement/emprunt. Ce qui se résume avec la formule suivante :

$i_{emprunt}=i_{sr}+p_{r}$, avec i le taux d'un crédit, $i_{sr}$ le taux sans risque et $p_{r}$ une prime de risque.

Pour résumer, il y a une relation entre taux monétaires, taux des crédits et création monétaire : plus les taux monétaires sont élevés, plus les banques doivent augmenter les taux longs pour compenser le cout de l'emprunt et moins de crédits sont demandés par les agents économiques. Vu que la banque centrale a le contrôle quasi-total des taux monétaires, elle a un pouvoir de contrôle indirect de la masse monétaire. La banque centrale contrôle les taux courts, ce qui influence les taux longs et donc la masse monétaire. La banque centrale choisit son taux directeur, et les banques doivent suivre. En choisissant son taux directeur, elle peut augmenter ou diminuer les taux bancaires et donc la création de nouveaux crédits. Il lui suffit de remonter ses taux directeurs pour limiter l'expansion du crédit, et de les baisser pour favoriser l'emprunt. Tout ce qui compte est qu'elle adapte les taux pour obtenir la masse monétaire demandée. Par contre, elle n'a pas le choix de sa base monétaire, qui est toujours imposée par le taux de réserves (et plus précisément par le diviseur/multiplicateur du crédit, que nous verrons plus bas). Le modèle complet est illustré ci-dessous.

Modèle de monnaie endogène de type horizontal

On voit que plusieurs défauts de la théorie précédente sont corrigés. D'abord, la banque centrale a enfin un impact sur la masse monétaire, sa politique monétaire n'est plus impotente et elle gagne un certain pouvoir de gestion de l'inflation. Tout cela grâce à son influence sur les taux directeurs, qui se répercutent par l'intermédiaire des taux bancaires sur la masse monétaire. Cela rend le modèle particulièrement intéressant, bien qu'imparfait. En tout cas, c'est une approximation pas trop mauvaise de ce qui se passe dans le monde réel. Mais le modèle n'est pas exempt de défauts. Par exemple, il n'explique pas pourquoi les banques conservent des réserves excédentaires, pourquoi le taux de réserves est utilisé par certaines banques centrales avec la même efficacité que le taux directeur, pourquoi le bilan des banques est ce qu'il est, etc. Il ne dit pas non plus comment les taux et la prime de risque varient avec la masse/base monétaire. Mais des défauts sont des défauts mineurs, qui peuvent se corriger avec quelques ajouts au modèle.

La relation entre base et masse monétaire

Vu ce qu'on vient de dire, il n'y a pas vraiment de relation stable entre la base monétaire et la masse monétaire. Tout dépend des taux directeurs, de la prime de risque et des demandes de réserves et de crédit. Difficile d'en établir une formule mathématique qui permette de faire des prédictions pertinentes. Par exemple, on ne peut pas prédire comment évolue la masse monétaire quand on augmente la base monétaire. Tout dépend de comment les banques et les agents vont réagir, de leurs demandes de monnaie et de crédit respectives et des variations de taux. Le modèle complet, qui tient compte de la base monétaire et de la masse monétaire, est illustré ci-dessous.

Contrôle de la masse et de la base monétaire par l'intermédiaire des taux directeurs

Pour être plus complet, il faut aussi indiquer l'existence d'une demande de réserves minimales, liée aux réserves obligatoires. Cette quantité de réserves obligatoires est imposée par le taux de réserves, mais la base monétaire la dépasse souvent, du fait de l'existence de réserves excédentaires.

Contrôle de la masse et de la base monétaire par l'intermédiaire des taux directeurs, avec réserves obligatoires

On peut raffiner le modèle en ajoutant quelques contraintes sur la manière dont la prime de risque dépend de la masse monétaire. Par exemple, on peut supposer que les banques évitent de trop prêter, pour diverses raisons. Par exemple, on peut supposer que plus leur encours de crédit est fort, plus cela signifie qu'elles ont prêté à des emprunteurs risqués. En effet, les banques prêtent en priorité aux emprunteurs surs, dont elles pensent qu'ils vont rembourser avec certitude. Le proverbe dit bien qu'on ne prête qu'aux riches ! Autant les premiers prêts sont réservés à des emprunteurs extrêmement surs, autant les prêts suivants sont réalisés à des emprunteurs de moins en moins solvables. Plus l'encours de crédits augmente, plus les clients qui restent sont risqués. On peut aussi ajouter une hausse du taux directeur avec la masse monétaire, qui sert à limiter son extension : plus la masse monétaire augmente, plus la banque centrale augmente ses taux pour en limiter les effets, pour contrôler l'inflation, par exemple. Nous en reparlerons dans les chapitres ultérieurs.

Modèle de monnaie endogène de type horizontal, amélioré

En théorie, base et masse monétaire peuvent évoluer indépendamment, suite à une variation de leurs demandes respectives. Tout déplacement des courbes de demande de réserves/crédit se traduit par une variation du multiplicateur du crédit.

Par exemple, une soudaine hausse des primes de risque va augmenter la demande de réserves à dépôts égaux. Pour simplifier, les banques ne souhaitant plus prêter leur argent et vont restreindre leur offre de crédit. La courbe de demande sera la même, mais l'intersection entre taux et demande sera placée plus haut, sur un point où le crédit est plus faible. La quantité de prêts va diminuer, ce qui réduira la masse monétaire (ou du moins, sa croissance). La banque centrale va alors réagir en baissant son taux directeur pour compenser la baisse des crédits et limiter au mieux les effets de la hausse de la prime de risque. Idéalement, la hausse des primes de risque est exactement compensée par la baisse du taux directeur, ce qui fait que le taux bancaire ne change pas. Sous ces conditions, la demande de crédit ne varie pas et la masse monétaire reste donc la même, ce qui contient l'inflation et le niveau des prix au niveau souhaité par la banque centrale. L'effet sur la base monétaire est pas contre tout autre. En théorie, la demande de réserves ne change pas alors que le taux directeur baisse : on se retrouve avec une hausse de la base monétaire, alors que la masse monétaire reste inchangée. On en déduit que le multiplicateur du crédit diminue donc, par augmentation des réserves excédentaires.

Un exemple est celui de la crise financière similaire de 2007. Cette crise est partie des crédits immobiliers dits subprimes, supposés risqués, mais malgré tout "solvables". Avec la soudaine baisse du prix de l'immobilier, lié à la politique de réserve fédérale, ces crédits se sont soudainement retrouvés nettement plus risqués que prévu. Par un effet de cascade, la hausse des primes s'est propagée à l'ensemble des banques, sur tous les types de crédits existants. La forte hausse des taux qui en a découlé a réduit le crédit, diminuant fortement la quantité de monnaie en circulation dans l'économie. Pour parenthèse, cette contraction de la masse monétaire a eu pour conséquence une récession, à savoir un ralentissement de l’activité économique. La banque centrale a alors réagi en baissant ses taux directeurs pour compenser la récession, ainsi que par d'autres mesures d'urgence.

Le marché monétaire

Pour atteindre ses objectifs, la banque centrale doit créer de la monnaie et échanger celle-ci avec les banques commerciales, que ce soit pour en retirer ou pour en injecter dans l'économie. Ces échanges s'effectuent sur le marché monétaire, un marché où les intervenants peuvent se prêter ou emprunter de la monnaie. Les intervenants en question sont très divers : les banques commerciales, la banque centrale, les trésors publics nationaux, les assureurs, les établissements de crédit, etc. En contrepartie du prêt, la banque emprunteuse va donner au créditeur un ensemble d'actifs financiers appelé collatéral. Ces prêts ont une durée inférieure à deux ans, les durées les plus communes étant de quelques jours à quelques mois.

Les prêts sur le marché monétaire impliquent fatalement un ou plusieurs taux d'intérêt, appelés taux d’intérêt interbancaires. Généralement, les taux d'intérêt sur le marché monétaire guident les taux à plus long-terme, les banques répercutant ces taux d'emprunt sur les crédits qu'elles accordent aux particuliers. Influencer le taux interbancaire permet ainsi de manipuler, dans une certaine mesure, le développement du crédit et donc la croissance de la masse monétaire. Dans la suite du chapitre, on verra que ce taux sont influencés par les taux directeurs.

Dans la zone euro, les taux à court-terme sur le marché monétaire sont mesurés au jour le jour par divers indicateurs. Le premier est l'EONIA, le taux moyen des prêts d'une durée égale ou inférieure à la journée. Celui-ci est calculé sur la base des taux demandés par les différentes banques. Tous les jours, les banques commerciales indiquent à quel taux elles souhaitent prêter ou emprunter sur le marché monétaire. Les quatre valeurs les plus élevées et les plus faibles sont négligées, les autres valeurs servant dans le calcul de la moyenne. L'EURIBOR est un ensemble de taux similaires à l'EONIA, si ce n'est qu'ils portent pour les prêts d'une durée égale respectivement à 1, 2, 3 semaines et 1, 2, 3, .. , 12 mois.

Évolution de l'EONIA entre 1999 et 2009.

D'ordinaire, les banques préfèrent emprunter à une autre banque commerciale au lieu de faire appel à la banque centrale, pour diverses raisons un peu obscures. Mais il arrive que certaines banques ne puissent pas trouver assez de réserves chez les autres banques. Ces dernières peuvent refuser de prêter à une banque trop risquée et endettée, par exemple. Les banques très risquées, qui risquent de faire faillite, peuvent cependant demander des prêts de la dernière chance à la banque centrale. La banque centrale est ainsi un préteur de dernier ressort.

Les prêts de dernier ressort sont monnaie courante quand le marché monétaire dysfonctionne complètement. Lorsque cela arrive, les banques n'aient pas accès à suffisamment de liquidité sur le marché monétaire ou refusent de se prêter entre elles. C'est notamment ce qui est arrivé suite à la crise financière de 2008, où les banques considéraient que les prêts sur le marché monétaire étaient trop risqués. La banque centrale a alors dû jouer son rôle de préteur de dernier ressort et a fourni la totalité de la liquidité du marché monétaire suite la crise. Mais ces prêts de dernier ressort ne permettent pas toujours aux banques de survivre. Tel a été le cas de Lehman Brothers, qui n'avait pas assez de collatéral pour obtenir un prêt de dernier ressort, ce qui entraîna sa faillite. Faillite qui déclencha la crise de 2008, mais cela est une autre histoire !

Les taux directeurs

Dans les chapitres précédents, nous avons beaucoup parlé du taux directeur de la banque centrale. Mais dans la réalité, il existe plusieurs taux directeurs différents, qui jouent chacun un rôle assez précis dans la conduite de la politique monétaire. Dans cette section, nous allons voir à quoi correspondent ces taux directeurs.

Pour commencer, rappelons que la banque centrale est la banque des banques commerciales. Elle leur fournit la même gamme de service que ce que font les banques commerciales auprès du grand public. Les banques commerciales peuvent ouvrent un compte courant à la banque centrale, un "livret d'épargne" ou des comptes à termes, et peuvent même y emprunter. Le compte courant est là où les banques commerciales parquent leurs réserves obligatoires et excédentaires, en attendant de les utiliser (pour des prêts, pour les placer ou faire des virements à une autre banque). Certaines banques centrales fournissent aussi un équivalent aux comptes à terme, qui permet aux banques de rémunérer leurs liquidités excédentaires, plutôt que de les laisser dormir sur leur compte courant. En zone euro, ce livret/compte à terme de la banque centrale s'appelle les facilités de dépôts. Les liquidités sont cependant placées sur une durée très courte, à peine 24 heures, voire quelques semaines tout au plus. Enfin, les banques commerciales peuvent emprunter des liquidités à la banque centrale, moyennant intérêt. La banque centrale manipule le marché monétaire en utilisant deux types de taux : le taux d'emprunt et le taux de placement (sur les facilités de dépôt).

Les taux d'emprunt auprès de la banque centrale

La banque centrale peut prêter des réserves aux banques commerciales, avec un système de repos ou d’opération d'Open Market. Le taux d’intérêt des prêts d'une banque centrale est appelé taux directeur. Aux états-unis, la banque centrale utilise plusieurs taux directeurs. Dans les grandes lignes, la réserve fédérale dispose de plusieurs guichets, auxquels les banques commerciales peuvent emprunter, qui correspondent chacun à des durées de prêts plus ou moins longues. Le guichet pour les prêts d'une journée correspond au taux directeur, d'autres guichets étant accessibles à des taux supérieurs. Le taux le plus élevé demandé est appelé le taux d'escompte. Dans la zone euro, ces prêts sont gérés par un système d'appel d'offre relativement complexe, pour deux maturités différentes.

• Le premier appel d'offre porte sur des prêts d'une durée de deux semaines. Chaque banque peut ainsi emprunter des réserves toutes les semaines, à condition que celle-ci rembourse son prêt précédent. Le taux lié à cet appel d'offre est appelé taux de prêt marginal.
• À côté, la banque centrale gère un second guichet pour des prêts quotidiens, d'une durée de un jour maximum. Le taux lié à ces prêts est appelé le taux de refinancement. Le taux de refinancement est toujours inférieur au taux de prêt marginal, de par leurs maturités différentes.

Le taux de rémunération des réserves

Outre les taux précédents, la banque centrale peut rémunérer ou non les réserves et les facilités de dépôt, avec des intérêts, suivant ses objectifs de politique monétaire. Le taux d'intérêt de la banque centrale sur les réserves est appelé le taux de rémunération des dépôts. Comme dans les banques commerciales, le taux sur les placements à la banque centrale est plus faible que le taux d'emprunt. Sans cette contrainte, les agents emprunteraient à un taux faible pour placer l'emprunt sur les facilités de dépôts fortement rémunérées.

Les réserves sont un coût d'opportunité pour les banques : elles pourraient être prêtées ou servir à acheter des actifs, ce qui permettrait aux banques d'en tirer un revenu. En rémunérant les réserves, la banque centrale réduit ou augmente ce coût d'opportunité, afin de stimuler le crédit ou de le limiter. Prenons le cas où la banque centrale souhaite stimuler le crédit. Dans ce cas, elle va rémunérer très faiblement les réserves, voire pas du tout, ce qui rend leur prêt plus rentable que leur dépôt à la banque centrale. Les banques vont alors chercher à prêter les réserves excédentaires pour en minimiser la quantité. Ce faisant, les réserves créées par la banque centrale ou les dépôts vont finir par circuler dans l'économie sous la forme de monnaie, favorisant l'investissement et la consommation. À l'inverse, la banque peut aussi rémunérer les réserves avec un intérêt assez élevé : les banques ne sont alors pas incitées à prêter leurs réserves, vu qu'il est plus rentable de les conserver à la banque centrale. Il arrive aussi que les banques ne fassent pas circuler leurs réserves excédentaires, même si elles ne sont pas rémunérées. Cela arrive quand l’économie va très mal. Dans ce cas, la banque centrale peut alors imposer des taux négatifs sur les réserves, afin d'inciter les banques à faire des crédits.

Les taux à court-terme

La banque centrale agit sur le marché interbancaire de deux façons : soit elle fixe la quantité de réserves qu'elle est prête à échanger, soit elle se fixe une cible pour le taux interbancaire. Si la quantité de réserves (la base monétaire) est fixée par la banque centrale, les taux à court-terme dépendent uniquement de la demande de réserves des banques. Plus les réserves se font rares, plus le taux interbancaire est fort (et réciproquement). Inversement, en fixant le taux d'intérêt, la banque centrale doit fatalement fournir autant de liquidités que les banques demandent à ce taux. De nos jours, les banques centrales fixent leurs taux d'intérêts, ce qui leur impose d'imprimer une certaine quantité de réserve.

Influence d'une opération d'Open Market (création monétaire et achats d'actifs) sur les taux d'intérêt interbancaires.

En utilisant le graphe ci-dessus, on peut distinguer deux portions de la demande de réserve. Dans la première portion, la demande de réserves dépend du taux d'intérêt, la fonction étant décroissante. Dans la seconde, la quantité de réserve est fixe et peut varier sans la moindre influence des taux : elle ne dépend plus du taux directeur. Notons que la banque centrale peut passer d'un régime à l'autre, que ce soit en changeant ses taux directeurs ou en modifiant la quantité de réserves. Ces deux situations correspondent à deux régimes monétaires différents, dans le sens où la banque centrale implémente sa politique monétaire différemment selon la situation. Dans le premier cas, tous les taux directeurs sont utiles, mais le principal est le taux d'emprunt directeur. Dans la seconde situation, le taux principal est le taux de rémunération des réserves.

Le régime de corridor

Le premier cas est le régime normal de fonctionnement de la politique monétaire, où le système bancaire n'est pas saturé de réserves : certaines banques manquent de réserves et font appel à celles qui en ont trop. Dans ce cas, le taux d'intérêt à court-terme sur le marché interbancaire est encadré par les deux taux directeurs, le taux d'emprunt servant de plafond et le taux de rémunération des dépôts servant de plancher. En somme, la banque centrale contrôle le taux directeur en l'encadrant par les deux taux qu'elle contrôle. Le système est appelé un régime de Corridor, en référence à l'encadrement des taux monétaire par les taux directeurs.

Illustration des différents taux pour la zone euro.

Les raisons qui font que cet encadrement fonctionne sont les suivantes. Premièrement, le taux de rémunération des réserves ne peut pas être supérieur au taux directeur sur le marché interbancaire. Si c'était le cas, les banques gagneraient plus en plaçant leur argent à la banque centrale et n'aurait aucun besoin de les prêter sur le marché interbancaire. La fixation d'un taux de rémunération des réserves permet ainsi de garantir un taux directeur minimum. Deuxièmement, les banques commerciales n'ont aucun intérêt à emprunter à un taux supérieur à celui donné par la banque centrale (le taux de prêt marginal), ce qui fait que les banques préteuses aligneront leurs taux de manière à ce que celui-ci reste compétitif face au taux de prêt marginal.

Première situation, appelée régime de type corridor.

Le régime plancher

Dans le second cas, les banques sont complètement saturées en réserves excédentaires et elles n'ont aucun besoin d'en acquérir en plus. En conséquence, elles n'empruntent plus à la banque centrale et il n'y a plus de prêts interbancaires. Cela se traduit par le fait que l'offre de réserves est dans la seconde portion de la courbe de demande de réserves, là où elle est plate. Le taux d'emprunt perd complètement sa pertinence et n'a plus d'influence sur le marché monétaire. Formellement, le taux du marché monétaire est strictement égal au taux de rémunération des dépôts. On est dans un régime qui porte le nom de Floor System, nom qui trahit le fait que le taux monétaire est à sa valeur plancher, sous-entendu au taux de rémunération des réserves.

Seconde situation, appelée régime de type plancher.

Les taux à long-terme

L'influence de la banque centrale porte essentiellement sur les taux de prêt à courte maturité, qu'il s'agisse d'obligations ou d'autres formes d'actifs. Mais il se trouve que les taux des maturités plus longues sont vraisemblablement dépendants des taux courts, ou tout du moins des taux courts futurs anticipés. Un outil très intéressant pour étudier la relation entre taux longs et taux courts est la courbe des taux, qui donne les taux en fonction de la maturité de l'obligation. On peut alors tomber sur plusieurs cas.

• En général, les taux longs (des obligations de long-terme) sont plus importants que les taux courts. De plus, les taux longs augmentent avec la maturité : le taux d'une obligation à 2 ans est plus faible que celui d'une obligation à 5 ans, lui-même plus faible que celui d'une obligation à 10 ans, etc. Dans ce cas, on trouve une courbe croissante des taux en fonction de la maturité, qui est la courbe des taux croissante, la plus habituelle.
• Plus rarement, les taux courts sont plus élevés que les taux longs (au moins sur une partie de la courbe). La courbe des taux devient une courbe des taux inversés.
• Enfin, il est possible que tous les taux soient identiques, ce qui donne une courbe des taux plate.

Courbe des taux normale.

Courbe des taux inversée.

Les théories des relations entre taux longs et courts

Aujourd'hui, il existe plusieurs théories pour expliquer les relations entre taux longs et courts. La théorie de la préférence pour la liquidité de Keynes, que nous avons vu dans le début de ce livre, est l'une d'entre elle. Mais elle n'est pas la seule et il existe de nombreuses autres théories, à la fois concurrentes et complémentaires de la théorie de Keynes. Nous n'allons pas toutes les voir, mais aborder seulement les principales. Si nous ne reviendrons pas sur la théorie de la préférence pour la liquidité, nous allons parler de la théorie des anticipations de la structure des taux d'intérêts (la plus consensuelle) et quelques autres théories complémentaires.

La théorie des marchés obligataires segmentés

La première théorie, la plus simple de toute, dit que les épargnants ne s'occupent que de la maturité et pas du rendement, ce qui fait qu'il n'y a pas d'arbitrage entre les différentes maturités. Quelqu'un qui achète une obligation à 10 ans n’achèterait pas d'obligation à 5 ans à la place, pour diverses raisons. Par exemple, l'acheteur souhaite épargner pour payer une échéance future : pour sa retraite qui arrivera dans 10 ans, pour payer l'université de son fils dans 10 ans, etc. Les obligations ne sont pas substituables, et il existe un marché indépendant pour chaque maturité. Le taux d'une obligation dépend uniquement de la demande et de l'offre pour la maturité demandée, mais pas des taux des autres obligations à maturité plus courte ou plus longue.

On peut expliquer la forme normale de la courbe des taux en supposant que les épargnants préfèrent des obligations à plus court terme. Ils préfèrent prêter à court-terme et non à long-terme, parce qu'ils pensent que c'est moins risqué. En clair, cette explication combine la théorie de la préférence pour la liquidité avec la théorie précédente. Les autres courbes des taux possibles apparaissent dans diverses situations pathologiques, où le prêt à court-terme devient très risqué, mais que le prêt à plus long-terme ne l'est pas (par exemple, une crise de liquidité). Mais tout cela ne permet pas de rendre compte d'un phénomène : toutes les maturités tendent à varier dans le même sens. Quand les taux courts augmentent, les taux longs augmentent, et la théorie des marchés segmentés est mise en défaut par cette observation.

La théorie des anticipations de la structure des taux d'intérêts

La seconde théorie part du principe que les agents économiques n'ont pas de préférence quant aux maturités et ne se réoccupent que du rendement. Dans ce cas, les agents font un arbitrage entre des obligations à long-terme et une succession d'achats d'obligations de court-terme. Les épargnants sur de longues durées peuvent certes acheter des obligations de longue maturité, mais ils peuvent aussi renouveler des placements de court-terme une fois ceux-ci à l'échéance. À l'équilibre, une succession d'obligations courtes et une obligation longue donneront le même rendement.

On pourrait croire que les taux courts et longs sont identiques, mais il faut prendre en compte la variabilité des taux au fil des ans. Dans ce cas, tout agent va anticiper les taux pour chaque année future. L'arbitrage dépend alors des taux courts futurs, anticipés par les agents économiques. La relation entre taux longs et courts dépend donc des anticipations des variations des taux. Dans ce qui suit, on suppose que l'année de début de maturité est l'année 0 et que les obligations sont renouvelées chaque année. L'agent va naturellement anticiper les taux pour l'année 1, l'année 2, etc. Ils prédiront donc des taux $i_{1}$, $i_{2}$, etc. La rémunération d'un renouvellement d’obligations courtes est donc de :

$(1+i_{l})^{n}=(1+i_{1})\times (1+i_{2})\times (1+i_{3})\times (1+i_{4})\times ...\times (1+i_{n})=\left[1+E({\overline {i_{c}}})\right]^{n}$, avec $E({\overline {i_{c}}})$ la "moyenne" des taux courts.

Si les agents économiques pensent que les taux courts vont augmenter ou rester stables, les taux longs dépendront essentiellement des taux courts actuels. On pourrait croire que les deux sont équivalents, si bien que le taux annuel devrait être identique dans les deux cas. Mais c'est oublier qu'un placement unique à long-terme est plus risqué : l'émetteur peut parfaitement faire défaut, l'inflation peut dépasser les valeurs anticipées, etc. Une succession de placements de court-terme n'a pas ces problèmes, les taux et opportunités étant remises à jour à chaque nouvel investissement. Dans ces conditions, ce risque supplémentaire doit être compensé par une rémunération supérieure, une prime de risque, faute de quoi les agents n’achèteraient pas d'obligations à long-terme. Ainsi, les taux longs sont légèrement supérieurs au taux équivalent à une succession de taux courts de durée équivalente. Une variation des taux courts doit donc se propager aux taux longs.

Par contre, si les agents anticipent une baisse des taux, les taux longs peuvent devenir inférieurs aux taux courts. Cela arrive quand les agents anticipent une baisse des taux directeurs de la banque centrale. Les taux courts ne changent pas tant que la banque centrale ne réagit pas. Par contre, les taux longs baissent avec les taux courts anticipés (voir la section précédente). Pour résumer, les taux longs baissent, les taux courts se maintiennent tant que la récession ne s’est pas concrétisée.

La théorie de l'habitat préféré

Les deux théories précédentes sont incompatibles : pas d'arbitrage d'un côté, arbitrage total de l'autre. La première théorie dit que les épargnants se préoccupent uniquement de la maturité, mais pas du rendement, alors que la seconde théorie dit l'inverse. Mais dans les faits, les épargnants prennent sans doute en compte à la fois les rendements et la maturité. Des arbitrages sont possibles, mais pas des arbitrages basés uniquement sur le rendement. Certains épargnants peuvent faire des arbitrages, en fonction de leur appétit pour le risque, mais les maturités rentrent en compte dans les décisions d'arbitrage.

Pour un niveau de risque et une rémunération égale, une obligation à taux court sera donc un substitut parfait pour une obligation longue. Les taux des obligations longues et courtes sont donc semblables, si ce n'est que les obligations longues subissent un risque d'inflation et de taux : il se peut que les taux ou l'inflation anticipée divergent des prédictions. Ce risque n'existe pas avec un renouvellement d'obligations de court-terme. En résumé, les épargnants éviteront d'acheter une obligation longue si une succession d'obligations courtes donne le même rendement, et ne l’achèteront que si celle-ci donne une prime pour compenser le risque. Pour compenser ce risque, les agents vont demander une rémunération supérieure aux obligations de long-terme. La prime de risque permet de rendre compte de la courbe des taux normale croissante. Plus un investissement a une durée longue, plus il est risqué et plus la prime de risque est grande.

Pour résumer cette théorie, il existe une relation entre les taux courts et les taux longs, les deux ayant tendance à évoluer dans le même sens (ils montent ensemble et descendent ensemble). Les taux longs sont vus comme la somme de deux termes : d'un côté la moyenne des taux courts futurs, de l'autre une prime de risque croissante avec la durée du placement. On peut résumer cela avec une équation de la forme :

$\left[1+i_{long}\right]^{n}=\left[1+E({\overline {i_{court}}})\right]^{n}+p_{r}(n)$, avec $p_{r}(n)$ la prime de risque et $E({\overline {i_{court}}})$ la moyenne anticipée des taux courts.

On peut approximer le tout avec cette formule :

$i_{long}\approx E({\overline {i_{court}}})+p_{r}(n)$, avec $p_{r}(n)$ la prime de risque et $E({\overline {i_{court}}})$ la moyenne anticipée des taux courts.

Précisons que la prime de risque compense plusieurs risques différents, comme l'inflation, le non-remboursement d'une obligation, ou sa faible liquidité. On peut schématiquement décomposer la prime de risque en une prime égale à l'inflation anticipée, une prime qui dépend de la probabilité de non-remboursement, et d'une prime de liquidité.

$i_{long}\approx E({\overline {i_{court}}})+\pi _{e}+p(nr)+p_{l}$, avec $p(nr)$ la probabilité de non-remboursement et $p_{l}$ la compensation pour une éventuelle non-liquidité.

Relation entre taux courts et taux longs.

La manipulation des taux longs par la banque centrale

En temps normal, la banque centrale influence les taux longs par son action directe sur les taux courts. Elle baisse son taux directeur, qui entraînent avec eux les taux longs. Cette politique est ce que l'on appelle la politique monétaire conventionnelle. Néanmoins, il se peut que cela ne suffise pas pour maintenir une inflation suffisante. Lorsque cela arrive, la banque centrale peut tenter de faire baisser les taux longs autrement qu'en faisant baisser les taux courts. On dit qu'elle utilise une politique monétaire non-conventionnelle. Pour cela, la banque centrale dispose de deux outils : l'assouplissement quantitatif et la forward guidance.

La politique monétaire non-conventionnelle

La première solution est appelée la forward guidance. Celle-ci consiste à manipuler les anticipations des taux futurs par une stratégie de communication adaptée. La banque centrale s'engage à garder les taux bas durant une longue période de temps (plusieurs années). Les agents ne s'attendent donc pas à une remontée des taux futurs, et savent que les taux courts resteront longtemps bas. Si on reprend la théorie des anticipations de la structure des taux, on remarque que cela se traduit par des taux longs plus bas. Le but de cette méthode est de faire baisser le terme $E({\overline {i_{court}}})$ dans la formule $i_{long}\approx E({\overline {i_{court}}})+p_{r}$. Ainsi, les anticipations des taux futurs seront basses, modifiant la courbe des taux en faisant mécaniquement baisser les taux longs.

L'autre solution porte le nom d'assouplissement quantitatif. Le but de cette méthode est de faire baisser la prime de risque, le terme $p_{r}$ dans la formule $i_{long}\approx E({\overline {i_{court}}})+p_{r}$. En l'absence de Q.E, la banque centrale se contente de moduler le taux sans risque sans modifier la prime de risque. Par contre, avec le Q.E, la banque centrale écrase cette prime de risque pour faire baisser les taux longs et stimuler l’économie. Les épargnants sont alors incités à investir dans des actifs plus risqués, ce qui stimule l’économie par divers mécanismes. Les spécialistes appellent cela le "canal de la prise de risque" (risk taking channel).

Pour ce faire, la banque centrale va créer de la monnaie et l'échanger contre des actifs de long-terme, généralement des obligations d'état. Ces achats d'obligations vont en faire monter le prix, ce qui en fera diminuer les taux d'intérêt. Rappelons que le prix des obligations est relié en sens inverse à leur taux d'intérêt : le taux diminue quand le prix augmente et vice-versa. Quand la banque centrale achète des obligations, la demande d'obligations va augmenter, faisant monter leur prix et baisser leur taux. Inversement, une vente massive d'obligations va les rendre moins rares, faisant baisser leur prix et monter leur taux. Ainsi, l'assouplissement quantitatif vise à contrôler les taux d'intérêt sur la dette d'état de long-terme.

Sans assouplissement quantitatif, la banque centrale ne fait que des échanges avec de la dette de court-terme, ce qui modifie les taux d'intérêt à court-terme. Avec assouplissement quantitatif, la banque centrale doit acheter des titres de moyen ou long-terme qu'elle n'achetait pas auparavant. Elle peut se mettre à acheter des obligations d'état à maturité importante (long-terme), des obligations d'entreprises, des produits basés sur des crédits aux ménages, voire des actions ou des titres immobiliers. Généralement, la banque centrale achète des obligations d'état dont la durée/maturité est importante, mais guère plus. Dit autrement, la banque centrale modifie la courbe des taux, en faisant baisser les taux longs uniquement, sans toucher aux taux bas (qui sont à zéro). On comprend pourquoi cette politique est utilisée quand les taux directeurs sont déjà à zéro.

Si l'effet sur les taux réels a une influence macroéconomique (du moins le pense-t-on), il a aussi des effets problématiques. La prime de risque ne reflète plus le risque des investissements, ce qui perturbe la perception du risque par les marchés. Cela peut mener à la formation de bulles ou à des comportements d’investissements plus risqués que prévu. Par exemple, cela incite les agents prudents à investir dans des actifs risqués comme les actions ou immobilier, alors qu’ils auraient investis en obligations d’état sans Q.E. Cela entraîne une surévaluation du prix de certains actifs, qui disparaîtra une fois le Q.E retiré. Ou encore, cela incite à prendre du levier en excès, ce qui est rarement une bonne idée… Pire : cela peut pousser les banques à faire n’importe quoi pour chercher du rendement, leurs marges étant fortement compressées par la baisse de la prime de risque. Les risques vont d’une surévaluation de la plupart des actifs risqués à des trucs plus graves, comme des crises bancaires causés par une mauvaise perception du risque (à la 2008). À noter que ces effets n’ont pas lieu avec une variation du taux sans risques, qui est la politique monétaire en temps normal.

En théorie, l'assouplissement quantitatif est censé créer de l'inflation. Cependant, les expériences de des banques centrales américaine et européennes lors de la crise de 2008 montrent que ce n'est pas forcément le cas. Si ces politiques ont aidé à augmenter le prix des actifs achetés par la banque centrale, tout en diminuant leurs taux d'intérêts, les effets macroéconomiques sont beaucoup plus faibles, pour ne pas dire inexistants.

Aux États-Unis, la baisse sur les taux de long-terme a été assez importante, de près d'un pour cent, mais les banques n'ont cependant pas décidé d’augmenter le volume de leurs prêts, pour des raisons assez techniques et encore mal comprises. La même chose a été observée lors de la crise japonaise de 1990, les politiques d'assouplissement quantitatif ayant fortement augmenté le bilan de la banque centrale. Pourtant, force est de constater que l'augmentation de la base monétaire a été très importante dans tous les cas étudiés, allant jusqu’à la tripler ou la quadrupler. Les études sur le QE sont assez contrastées, certaines disant qu'il n'a pas eu d'effet vraiment significatif sur l'économie, tandis que d'autres lui attribuent l'origine de plusieurs pourcents de croissance.

Précisons que les obligations achetées par la banque centrale ne sont pas détruites, mais belles et bien conservées par la banque centrale. L'état doit toujours rembourser sa dette, intérêts compris. Seul le destinataire de la dette change : investisseurs privés sans QE, banque centrale avec. Il y a cependant une petite subtilité quant au cout de la dette. Si l'état doit bel et bien rembourser les intérêts, ceux-ci sont considérés comme un profit par la banque centrale, profit qui est redistribué à ses actionnaires, donc à l'état. En clair, les intérêts sont payés par l'état, mais la banque centrale les renvoie en tout ou partie. Mais cette nuance n'a aucune application pratique, car le QE est utilisé quand les taux d'intérêts sont à zéro, ce qui fait que le gain pour l'état sur sa dette est nul. Le QE ne monétise donc pas la dette d'état. Après, on peut imaginer une situation improbable où la banque centrale décide de faire fi de son mandat e d'alléger la charge des intérêts de la dette. Mais dans ce cas, elle a plutôt intérêt à faire baisser ses taux directeurs à zéro que d'utiliser le QE : l'économie en intérêt sera la même et la mesure sera bien plus efficace.

Les différences entre politique conventionnelle, forward guidance et assouplissement quantitatif

Avec ce qu'on vient de dire, il est intéressant de mettre en avant les différences entre types de politiques monétaires conventionnelle/non-conventionnelle. Pour comprendre la différence entre les deux, il faut regarder ce qui se passe pour la courbe des taux. La politique monétaire conventionnelle déplace la courbe des taux, mais ne modifie pas sa forme. Une baisse des taux directeurs entraîne eux les taux longs, ce qui fait que courbe des taux descend, sur le graphique intérêt-maturité. En théorie, la baisse est identique sur toute la courbe des taux, avec la même intensité partout. En pratique, il se peut que les taux bas baissent plus vite que les taux longs, si la transmission n'est pas optimale, mais ce cas est cependant plus pathologique qu'usuel.

Avec la politique monétaire non-conventionnelle, la courbe des taux s’aplatit. Seuls les taux longs baissent, les taux courts restant identiques. Précisons qu'entre forward guidance et assouplissement quantitatif, le mécanisme d’aplatissement de la courbe des taux est différent. L'assouplissement quantitatif réduit la prime de risque, alors que le forward guidance réduit les taux courts anticipés. Les deux canaux décrits dans les théories précédentes sont utilisés : demande pour une maturité précise pour l'assouplissement quantitatif, taux courts anticipés pour le forward guidance.

Influence des politiques monétaires conventionnelle et non-conventionnelle sur la courbe des taux.

Le modèle new-keynésien

Il existe deux manières de décrire la politique monétaire, qui portent les doux noms de « paradigme monétariste » et de « paradigme Wickselien ». La première, le paradigme monétariste, met l'accent sur la quantité de monnaie en circulation et son impact primordial sur le niveau général des prix. Il est représenté par d'anciennes théories comme la théorie quantitative de la monnaie, les théories IS/LM et AD/AS, et quelques autres théories plus complexes. Mais elle n'est pas la plus apte à décrire l'économie actuelle, où les banques centrales actuelles contrôlent les taux directeurs sur le marché monétaire. Ce qui fait que le paradigme Wicksellien est le plus adapté pour expliquer le fonctionnement actuel de l'économie. En conséquence, nous allons d'abord voir le paradigme Wicksellien sur plusieurs chapitres, avant de voir le paradigme monétariste dans les chapitres de fin de cours.

Le modèle IS-MP-PC

Si on analyse les différents canaux de transmission de la politique monétaire, on remarque que la quasi-totalité passe par un même intermédiaire : le PIB. En clair, la politique monétaire impacte le PIB, par diverses voies plus ou moins directes. Les variations du PIB influencent ensuite l'inflation par un mécanisme assez précis. Seuls quelques canaux ne passent pas par l'intermédiaire du PIB et peuvent influencer directement les prix ou l'inflation. On peut donc simplifier les différents canaux de transmission en deux équations : une qui donne l'influence de la politique monétaire sur le PIB, et une relation entre le PIB et l'inflation.

La première équation est la courbe IS, une relation entre les taux réels à long-terme et le PIB. Cette relation est décroissante, ce qui signifie qu'une baisse des taux fait augmenter le PIB et inversement. On peut mettre cette relation en équation, ce qui donne l'équation suivante :

$Y=Y_{0}-f(r)$, avec $r$ le taux d'intérêt réel, $Y$ le PIB et ${\overline {Y}}$ le PIB quand $r=0$.

La seconde équation, qui relie le PIB et l'inflation, est appelée courbe de Phillips. Celle-ci postule que les anticipations d'inflation sont performatives, à savoir qu'elles se concrétisent. L'inflation est donc égale à la somme de l'inflation anticipée et d'une inflation non-anticipée. La détermination de cette dernière dépend du PIB. Pour simplifier, plus le PIB croît, plus l'inflation augmente. La relation entre PIB et inflation est donc croissante. Sa mise en équation donne l'équation suivante :

$\pi =\pi ^{e}+f(Y)$, avec $\pi$ l'inflation, $\pi _{e}$ l'inflation anticipée et f(Y) une valeur/fonction qui dépend de la valeur du PIB.

À ces deux équations, il faut ajouter une équation qui résume l'action de la banque centrale. On suppose que la banque centrale tente de garder l'inflation proche d'une cible d'inflation prédéfinie. Pour cela, elle joue sur son contrôle des taux réels à courts-terme, pour agir sur le PIB et donc sur l'inflation. Dans les faits, elle augmente les taux réels quand l'inflation dépasse sa cible et les baisse quand l'inflation est trop basse. Ce comportement est résumé dans une règle, la règle de Taylor. Celle-ci est résumé dans l'équation suivante, qui décrit comment la banque centrale fixe son taux directeur (réel) :

$r=r_{0}+f(\pi _{t}-\pi _{t}^{*})$, avec $r$ le taux réel, $r_{0}$ le taux réel pour lequel l'inflation est égale à la cible d'inflation, $\pi _{t}$ l'inflation et $\pi _{t}^{*}$ la cible d'inflation de la banque centrale.

Au final, on obtient le modèle néo-kéynésien, une théorie qui se résume en trois équations : une courbe de Phillips, une courbe IS et une fonction de réaction de la banque centrale. Ces trois courbes sont à l'origine du second nom donné à ce modèle : le modèle IS-MP-PC (IS pour la courbe IS, MP pour Monetary Policy et PC pour Phillips curve).

Politique monétaire et modèle à trois équations.

Les équations du modèle avec les taux nominaux

Les trois équations précédentes ont deux problèmes, qui peuvent se corriger assez facilement. En premier lieu, la courbe IS dépend des taux à long-terme, alors que le taux réel de la banque centrale est un taux de court-terme. Les taux pertinents pour l'économie sont les les taux des crédits, des emprunts immobiliers, des obligations, etc. Et ce sont tous des taux longs, pour diverses raisons dont nous reparlerons plus en détail dans la suite du cours. Mais la banque centrale ne peut pas modifier directement les taux longs. À la place, elle contrôle le taux directeur, qui a une influence indirecte sur les autres taux d'intérêts. Rappelons que la relation entre taux courts et taux longs est, en toute généralité, la relation obtenue dans le chapitre sur le marché monétaire. Celle-ci est, pour rappel, la suivante :

$i_{long}\approx E({\overline {i_{court}}})+p_{r}$, avec $p_{r}$ une prime de risque et $E({\overline {i_{court}}})$ la moyenne anticipée des taux courts.

Mais on peut la simplifier fortement, en remplaçant les anticipations des taux futurs par le taux courant. On obtient alors cette équation approximative :

$i_{long}=i_{court}+p_{r}$

Modele IS-MP-PC avec une relation entre taux courts et taux longs

Voyons maintenant le second problème. La banque centrale contrôle un taux directeur nominal, non pas un taux réel. Par contre, l'équation IS et la règle de Taylor contiennent un taux réel. Pour corriger ce défaut, il faut ajouter au modèle la relation de Fisher vue dans les premiers chapitres, à savoir l'équation $r=i-\pi _{e}$. La banque centrale fixe un taux nominal, auquel il faut retirer les anticipations d'inflation pour obtenir le taux réel en découle. Un point important est que les anticipations d'inflation sont stables sur le court-terme. En effet, les prix sont généralement visqueux, ce qui veut dire qu'ils mettent du temps avant de se mettre à jour, qu'il y a un temps de latence avant que se réalise l'égalité de l'offre et la demande sur le marché des biens et services. En conséquence, les agents économiques ne s'attendent pas à une variation soudaine de l'inflation : les anticipations d'inflation sont stable sur le court-terme. Ce qui fait que toute variation des taux nominaux se répercute sur les taux réels et non sur les anticipations d'inflations. La banque centrale, en modifiant le taux nominal, altère donc temporairement le taux réel.

Modèle IS-MP-PC avec relation de Fisher et relation taux courts-longs

L'état d'équilibre du modèle

Sur le long-terme, l'économie est censée être à l'équilibre, ce qui signifie que les grandeurs macroéconomiques n'évoluent plus. C’est là un principe que l'on retrouve dans tous les domaines de l'économie, qui est pris en tant qu'hypothèse. À l'équilibre, les taux d'intérêts sont stables, de même que le PIB, le niveau des prix ou l'inflation. Ces valeurs prennent alors leur valeur d'équilibre, dite valeur naturelle.

• L'inflation mesurée et l'inflation anticipée sont toutes deux égales à la cible d'inflation de la banque centrale.
• La valeur d'équilibre des taux d'intérêts porte le nom de taux naturel. Ces deux valeurs correspondent aux valeurs de PIB et de taux qui gardent l'inflation constante.
• La valeur d’équilibre du PIB s'appelle le PIB potentiel.
• Le taux de chômage est à un niveau bien précis appelé le taux de chômage naturel. C'est, par définition, le taux de chômage obtenu lorsque l'économie est au PIB potentiel.

On peut alors reformuler les trois équations précédentes en faisant appel au PIB potentiel et au taux réel naturel. On obtient alors les trois équations suivantes, avec :

• le PIB $Y$ et le PIB potentiel ${\overline {Y}}$ ;
• le taux d'intérêt réel $r$ et le taux d'intérêt naturel $r_{n}$ ;
• $\pi _{t}$ l'inflation et $\pi _{t}^{*}$ la cible d'inflation de la banque centrale ;
• a, b et c des coefficients multiplicateurs.

$Y={\overline {Y}}-a(r-r_{n})$ : Courbe IS

$\pi =\pi ^{e}+b(Y-{\overline {Y}})$ : Courbe de Phillips

$r=r_{n}+c(\pi _{t}-\pi _{t}^{*})$ : Relation de Taylor

L'effet d'un déséquilibre sur l'économie

Il arrive que l'économie subisse un choc, c'est à dire qu'un variable quitte sa valeur d'équilibre. Dans ce cas, cette variation va entraîner une variation du PIB, des taux et de l'inflation telle que l'économie finit par retourner à l'équilibre. Par exemple, supposons que le PIB augmente soudainement. Cela entraîne une hausse de l'inflation, puis une hausse des taux d'intérêt qui réduit alors le PIB. L'effet de la hausse de l'inflation et des taux compense la hausse du PIB, qui revient à la normale. Généralement, ces chocs entraînent des variations du PIB, puis de l'inflation. Mais la banque centrale réagit et modifie ses taux de manière à stabiliser l'économie. On verra dans quelques chapitres que la politique monétaire a une influence sur l'économie à court-terme, influence provenant de son contrôle sur les taux réels sur le court-terme.

Il est intéressant d'étudier ce qui se passe quand la banque centrale baisse ses taux. Une baisse des taux réels incite les ménages et entreprises à s'endetter, ce qui facilite l'investissement : acheter des machines, des usines, une voiture ou de l'immobilier se fait souvent à crédit. Or, l'investissement fait lui-même partie du PIB. Le surplus d'investissement causé par la baisse des taux entraîne donc une hausse égale du PIB. Dit autrement, la baisse des taux réels injecte de la monnaie dans l'économie sous la forme de prêts, qui seront dépensés. La consommation et l'investissement vont augmenter et les entreprises vont augmenter leurs ventes, induisant une hausse de la production et du PIB. C'est la première étape : la relation IS.

L'augmentation de la production va rapidement être remarquée par les commerçants et producteurs. Du fait du jeu de l'offre et de la demande, ceux-ci vont augmenter leurs prix jusqu'à ce que l'offre et la demande soient égales. On peut en dire plus sur cette transition vers le long-terme, en la résumant en une relation entre PIB et inflation : plus le PIB est élevé, plus l'inflation le sera aussi. C'est l'effet de la relation de Phillips, qui sera abordée en détail d'ici quelques chapitres.

Mais la hausse de l'inflation ne va pas durer très longtemps. La durée de cette phase dépend énormément de la réaction de la banque centrale, de la manière dont elle prend en compte l'inflation. La banque centrale surveille régulièrement l'évolution de l'inflation et réagit si celle-ci devient trop importante. Elle vérifie aussi le PIB, dont les variations permettent de prédire l'inflation, via la courbe de Phillips. Cette réaction se base sur une modification des taux réels, à l'initiative de la banque centrale, par le biais d'une modification des taux nominaux. La banque centrale augmente les taux réels quand l'inflation dépasse sa cible et les baisse quand l'inflation est trop basse, en suivant la règle vue plus haut. On dit qu'elle suit une règle de Taylor.

Du fait de la rigidité des anticipations d'inflation, toute baisse des taux nominaux par la banque centrale se répercute sur les taux réels. Mais sur le long-terme, les anticipations d'inflation et s'adaptent pour devenir de plus en plus précises, et ce d'autant plus que les anticipations d'inflation sont performatives. Finalement, l'inflation finit toujours par être égale à ses anticipations sur le long-terme. Ces anticipations d'inflation des agents économiques vont contrecarrer l'effet de la politique monétaire. Pour simplifier, l'inflation va se répercuter dans les taux nominaux, réduisant le taux réel à sa valeur naturelle. Le PIB évoluera en même temps que les taux, et finira par atteindre le PIB d'équilibre. L'effet sur le PIB de la politique monétaire est alors annulé, au prix d'une variation des prix. Sur le long-terme, le taux reste égal au taux naturel, les anticipations d’inflation s'adaptant naturellement à la politique de la banque centrale, en neutralisant celle-ci.

L’influence des taux sur l'économie

Plus haut, nous avons résumé l'effet d'une variation de taux d'intérêts par la relation IS, à savoir le fait qu'une baisse des taux augmente le PIB (et inversement). Mais dans les faits, les taux d'intérêts ont une influence un peu plus large. Dans le détail, une variation des taux entraine les effets suivants :

• elle fait varier le recours au crédit (ce qui modifie le PIB) ;
• elle modifie les taux de change ;
• elle influe sur les prix de certains actifs ;
• elle modifie les anticipations d'inflation.

Ces effets sont ce qu'on appelle les canaux de transmission de la politique monétaire. C'est grâce à eux que les taux directeurs ont une influence sur l'inflation par divers moyens indirects.

Canaux de transmission de la politique monétaire.

Le canal de l'investissement

La baisse des taux réels a des effets (à court-terme) sur les taux des crédits distribués par les banques. Baisser ces taux favorise l'emprunt, ce qui va naturellement créer de la monnaie-crédit. L'augmentation de la quantité de monnaie qui en découle va naturellement faire augmenter le PIB à court-terme, puis les prix sur le long-terme. En comparaison, une hausse des taux à l'effet inverse, ce qui diminue les tensions inflationnistes d'une économie qui surchauffe. Ce mécanisme porte le nom de canal des taux d'intérêt. Ce canal sera vu en détail dans le chapitre suivant, dans le section sur la courbe IS kéynésienne.

$\downarrow i~\rightarrow ~\downarrow r\rightarrow ~\uparrow {\text{Emprunt}},\uparrow {\text{Investissement}}~\rightarrow ~\uparrow ~PIB$

Les canaux liés à l'emprunt et l'épargne

Outre le canal des taux d'intérêt, d'autres canaux impliquent l'emprunt et le crédit, associés à l'épargne. Ces deux canaux, liés entre eux, disent comment une variation des taux se répercute sur l'arbitrage entre épargne, emprunt et consommation. La microéconomie nous dit que quand le prix d'un produit varie, il se produit deux effets : un effet revenu (on peut acheter moins de ce produit qu'avant) et un effet de substitution (on substitue le produit par un autre). Ici, la logique est analogue, bien que légèrement différente. Quand les taux varient, on a un effet revenu et un effet de substitution. L'effet revenu se traduit par le fait que les mensualités des crédits et la rémunération de l'épargne sont directement touchés par la variation des taux. L'effet de substitution fait que les agents peuvent substituer de l'épargne en consommation. En cas de baisse des taux, les agents tendent à désépargner pour consommer, et inversement.

Le premier effet implique les crédits à taux variables, des crédits dont le taux varie pendant la durée de vie du contrat. Ces crédits ne sont pas très communs en France, mais ils le sont dans de nombreux autres pays européens ou aux état-unis. Pour simplifier, les taux de ces crédits suivent les taux directeurs. Quand la banque centrale hausse son taux directeur, les taux des crédits variables augmentent et les mensualités des crédits suivent. Les ménages perdent alors un peu de revenu disponible, qui part dans l'augmentation des mensualités. Et inversement pour une baisse des taux, qui fait baisser les mensualités et rend du pouvoir d'achat aux emprunteurs. Pour les épargnants, la baisse/hausse des taux se traduit directement par une hausse/baisse de leurs revenus d'épargne, qui peut se répercuter sur leur consommation. Ces deux phénomènes sont regroupés dans ce qu'on appelle le canal du « cashflow ».

Le second effet fait qu'une baisse des taux défavorise l'épargne et favorise la consommation. En effet, les agents économiques font un arbitrage entre consommation et épargne (épargne qui n'est d'ailleurs que de la consommation différée). Et le taux d'intérêt est la rémunération de l'épargne : mieux vaut consommer qu'épargner si elle est trop faible, mieux vaut épargner si elle est forte. Ce canal est appelé en termes techniques : canal de substitution intertemporel. Ce canal sera vu en détail dans un chapitre dédié.

$\downarrow i~\rightarrow ~\downarrow r~\rightarrow ~(\uparrow {\text{Consommation}},\downarrow {\text{Epargne}})~\rightarrow ~\uparrow PIB$

Le canal des prix d'actifs financiers

Les variations du taux d'intérêt ont des effets sur le prix de divers actifs financiers. Elle joue surtout sur la rémunération des obligations, des actifs qui représentent une reconnaissance de dette remboursée après un certain temps avec un intérêt. Mais elle a aussi des effets assez indirects sur le prix des actions ou de l’immobilier. La hausse du prix des actifs a alors plusieurs effets. Premièrement, les détenteurs d'actifs, devenus plus riches, vont augmenter leur consommation. Cet effet est appelé l'effet de richesse : les gens consomment plus quand leur patrimoine augmente, quand ils sont plus riches.

$\downarrow i\rightarrow ~\uparrow P_{o}\rightarrow ~\uparrow {Consommation}$

Le second effet est que les détenteurs d'actifs sont mieux vus par les banques. L'augmentation de leur patrimoine fait qu'ils sont plus sûrs, que leur risque de faillite ou de non-remboursement diminue auprès des banques. En conséquence, ils peuvent emprunter plus d'argent qu'avant, voire avoir accès à des crédits qui leur étaient interdits avant. Cela stimule d'emprunt, et donc l'investissement et la consommation.

$\downarrow i\rightarrow ~\uparrow P_{o}\rightarrow ~\uparrow {Patrimoine~net}\rightarrow ~\uparrow {Emprunt}\rightarrow ~\uparrow PIB$

Le canal des taux de change

On verra dans le chapitre sur la courbe IS que toute modification des taux réels entraine une variation des taux de change. Ainsi, une baisse des taux dévaluera la monnaie, renchérissant les importations et favorisant les exportations.

$\downarrow i\rightarrow ~\downarrow e\rightarrow ~\uparrow NE\rightarrow ~\uparrow PIB\rightarrow ~\uparrow \pi$

À plus court-terme, la modification des taux de change a aussi une influence sur le prix des matières importées : une hausse des taux de change fait grimper le prix des biens importés, tandis qu'une hausse les fait baisser. Ainsi, dévaluer la monnaie d'un pays est un bon moyen de faire repartir l'inflation, tandis que l'apprécier coupe l'herbe sous le pied à d'éventuelles tensions inflationnistes. Soit $e$ le taux de change, $P_{i}$ les prix des importations et $NE$ les exportations nettes, le canal du taux de change a ainsi deux effets :

$\downarrow i\rightarrow ~\downarrow e\rightarrow ~\uparrow P_{i}\rightarrow ~\uparrow \pi$

Le canal des anticipations

La modification des taux va entraîner une variation à la hausse ou à la baisse des anticipations d'inflation réalisées par les agents économiques. Or, on verra dans quelques chapitres que ces anticipations sont quelque peu performatives, dans le sens où les agents tentent de se prémunir contre l'inflation anticipée. Cela passe par des négociations salariales, des demandes de rendements supérieures de la part des investisseurs en cas d'inflation anticipée, des taux de crédit supérieurs, ou des variations de la quantité d'épargne. Et les agents économiques se basent sur les taux pour anticiper l'inflation future.

$\downarrow i\rightarrow ~\uparrow \pi _{e}\rightarrow ~\uparrow \pi$

Un bon moyen pour la banque centrale d'influencer les anticipations d'inflation est de fixer une cible d'inflation. Ainsi, les agents économiques s'attendront à une inflation proche de celle voulue par la banque centrale. Les anticipations seront, en négligeant toute autre influence, égale à la cible d'inflation. Néanmoins, cela ne fonctionne que si la banque centrale est crédible. Si les agents économiques pensent que la banque centrale ne respectera pas son objectif d'inflation, leurs anticipations pourront s'écarter de la cible d'inflation. Ainsi, la crédibilité de la banque centrale est très importante pour ancrer les anticipations d’inflation au niveau de la cible.

La courbe IS

Dans ce chapitre, nous allons voir comment rendre compte de l'influence des taux d'intérêts sur l'économie. Les chapitres précédents nous ont appris qu'il existe plusieurs canaux de transmission, des mécanismes qui font qu'une variation des taux influence le PIB, l'inflation, le taux de change, etc. La plupart de ces canaux de transmission font que le PIB augmente ou diminue quand les taux varient. Les taux d'intérêts ont une relation assez forte avec le PIB réel. Cette relation est représentée graphiquement par la courbe IS, qui lie PIB et taux d'intérêt réel. Ce chapitre va parler en détail de cette fameuses courbe IS. Nous allons voir qu'il en existe deux versions, qui sont tirées de théories différentes : la courbe IS des keynésiens concurrence la version des new keynesian. Autant la première se dérive à partir d'hypothèses assez simples, la seconde est démontrée à partir de la microéconomie. Il va de soit que la première est bien plus simple à étudier que la seconde.

La courbe IS : généralités

Courbe IS

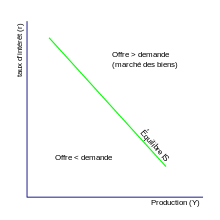
La courbe IS est une fonction décroissante des taux, ce qui traduit le fait que de forts taux diminuent le PIB, là où des taux faibles le stimulent. Il va de soit que la forme exacte de cette courbe est inconnue et que la seule certitude est qu'elle est décroissante. Dans ce qui va suivre, nous allons supposer que cette courbe est linéaire. Cette hypothèse irréaliste nous permettra de simplifier les calculs et le raisonnement, sans trop sacrifier la véracité des conclusions tirées.

Le taux pertinent pour la courbe IS est un taux réel de long-terme

Il faut faire attention au taux d'intérêt pris en compte par la courbe, qui n'est pas le taux directeur de la banque centrale. Le taux pertinent pour la courbe IS est un taux long, pas le taux directeur. La raison à cela est que les agents n'empruntent pas directement à la banque centrale, mais auprès des banques commerciales. Et si les taux des banques commerciales suivent le taux directeur la plupart du temps, les deux taux n'en sont pas moins différents. Pour rappel, les banques prêtent à un taux qui est la somme du taux directeur et d'une prime de risque.

$i=i_{d}+p_{r}$, avec $i$ le taux nominal des prêts commerciaux, $i_{d}$ le taux directeur et $p_{r}$ la prime de risque.

En second lieu, il s'agit du taux réel et non du taux nominal. De plus, le taux réel n'est connu qu'à posteriori, ce qui fait que la courbe IS utilise le taux réel anticipé, un taux ex-ante. La raison à tout cela est que les décisions économiques se basent sur le taux réel. Les agents économiques anticipent l'inflation et estiment le rendement réel, sur lequel ils basent leurs décisions économiques. Pour résumer, le taux de la courbe IS est un taux réel anticipé, qui se calcule à partir des taux nominaux et de l'inflation, grâce à l'équation de Fisher des taux d'intérêts :

$r_{e}=i-\pi _{e}$, avec i le taux nominal et $\pi _{e}$ l'inflation anticipée.

Le taux réel de long-terme dépend des taux directeurs

En combinant les deux équations précédentes, on peut calculer le taux réel de long terme, qui est utilisé dans la courbe IS. Pour cela, partons de l'équation suivante :

$i=i_{d}+p_{r}$

Soustrayons l'inflation anticipée des deux côtés et regroupons les termes comme ceci :

$i-\pi _{e}=(i_{d}-\pi _{e})+p_{r}$

Le terme de gauche est le taux réel de long-terme, alors que le terme entre parenthèses est le taux court/directeur réel. En notant ces taux respectivement $r$ pour le taux réel de long-terme et $r_{d}$ pour le taux directeur réel, on trouve :

$r=r_{d}+p_{r}$

On voit que le taux réel de long-terme est la somme du taux directeur réel et de la prime de risque. Cela nous dit que la politique monétaire a une influence sur le PIB, via l'influence de la politique monétaire, mais aussi que la prime de risque n'est pas à négliger.

Notons que sur le court-terme, les prix sont supposés rigides, ce qui signifie qu'ils restent plus ou moins constants. En conséquence, l'inflation anticipée ne change pas. Ce faisant, les variations du taux nominal se répercutent sur le taux réel. C'est pour cela que sur le court-terme, une modification des taux nominaux implique une variation du PIB, alors que cela ne devrait pas être le cas. Grâce aux prix rigides, une hausse des taux entraîne une baisse du PIB (et inversement). La banque centrale peut donc, en réglant ses taux, fixer le PIB à une valeur compatible avec sa cible d'inflation.

La courbe IS keynésienne

Pour dériver la courbe IS, les keynésiens partent du principe que le PIB dépend fortement de l'investissement, qui est extrêmement sensible au taux d'intérêt. La causalité est donc la suivante : taux d'intérêt -> investissement -> PIB. Les versions plus élaborées tiennent compte d'autres paramètres, comme l'influence des taux sur le taux de change et les exportations nettes, et bien d'autres. Mais nous laissons cela aux chapitres qui vont suivre.

Dans ce qui va suivre, nous allons supposer que cette courbe est linéaire. Cette hypothèse irréaliste nous permettra de simplifier les calculs et le raisonnement, sans trop sacrifier la véracité des conclusions tirées.

L'équation IS sans PIB potentiel

La courbe IS s'exprime aussi sous la forme d'une équation IS, qui peut se décliner en plusieurs versions selon les démonstrations utilisées. La plus simple se contente de faire intervenir le PIB et le taux réel, sans mention du PIB potentiel ou du taux réel naturel. Celle-ci s'écrit comme suit, avec :

$Y=Y_{0}-a\times r$, avec le taux d'intérêt réel $r$, le PIB $Y$, $Y_{0}$ le PIB quand $r=0$ et un coefficient multiplicateur $a$.

En combinant l'équation précédente avec l'équation $r=r_{d}+p_{r}$, on trouve :

$Y=Y_{0}-a\times (r_{d}+p_{r})$

L'équation précédente permet de décrire ce qui se passe lors d'une crise financière similaire à celle de 2008, au moins dans les grandes lignes. Lors d'une crise financière, les banques se retrouvent en mauvaise situation et doivent augmenter la prime de taux pour diverses raisons. Le taux réel des prêts des banques commerciales va donc fortement augmenter. La courbe IS précédente nous dit que cela va réduire le PIB : la production chute suite à la crise financière, à cause de la hausse des taux réels. Une solution possible est de compenser cette hausse par une baisse des taux directeurs, en utilisant la politique monétaire. Cela fonctionne tant que les taux directeurs peuvent baisser, mais la banque centrale doit procéder autrement une fois les taux devenus nuls. Mais nous laissons cela au chapitre sur les trappes à liquidité.

L'équation IS avec PIB potentiel

Une version plus complexe fait intervenir le PIB potentiel et le taux naturel, ainsi que le PIB mesuré et le taux réel courant. Pour comprendre cette équation, il faut juste examiner trois cas : ceux où le taux réel est égal, supérieur et inférieur au taux naturel. Si le taux réel est égal au taux naturel, le PIB est au PIB potentiel. S'il est inférieur, cela signifie que les taux sont relativement bas, ce qui stimule le crédit. La création de monnaie crédit va donc stimuler la demande et la production, augmentant le PIB. Et inversement, un taux réel supérieur au taux naturel signifie que le crédit se renchérit, réduisant la dépense et la production. On pourrait aussi analyser les effets sur l'épargne, favorisée par des taux supérieurs au taux naturel et défavorisée au profit de la consommation par des taux bas. On peut donc résumer le tout dans cette équation :

$Y={\overline {Y}}-a\times (r_{e}-r_{n})$, avec le taux d'intérêt naturel $r_{n}$.

Il est possible de reformuler cette équation en mettant en avant l'écart de production, à savoir la différence entre PIB réel et PIB potentiel. Dans la suite de ce cours, nous noterons cet écart de production $y$, en minuscules. Comme on le verra dans quelques chapitres, cet écart de production est synonyme de tensions inflationnistes (s'il est positif) ou déflationnistes (s'il est négatif). Une manipulation algébrique nous donne l'équation suivante. Celle-ci dit simplement que l'écart de production est proportionnel à l'écart entre taux réel et taux naturel.

$y=Y-{\overline {Y}}=-a\times (r_{e}-r_{n})$

La courbe IS new-keynesian

La courbe IS new-keynesian est une version "améliorée" de la courbe IS, que l'on retrouve dans un modèle macroéconomique appelé le modèle new-keynesian. Nous l'étudierons en détail dans le chapitre nommé "Le canal de substitution intertemporelle", situé à la fin du cours. La raison à cela est qu'elle est dérivée à partir de la microéconomie, sous l'hypothèse d'un agent économique rationnel. Or, pour des raisons pédagogiques, les modèles basés sur cette hypothèse seront vus à la fin du cours, dans une section à part. Pour le moment, nous allons juste faire quelques observations assez simples.

La courbe IS new-keynesian ressemble à la courbe IS précédente, mais elle fait intervenir le PIB anticipé et quelques variables supplémentaires. Elle ne tient pas compte de l'influence des taux sur l'investissement ou les exportations nettes, comme le font les démonstrations keynésiennes. À la place, elle part du principe que la consommation et l'épargne sont influencés par les taux d'intérêt. Plus les taux sont haut, plus l'épargne est rentable par rapport à la consommation et plus les agents vont épargner. Inversement, des taux trop bas rendent la consommation plus intéressante que l'épargne et favorise la dépense. La causalité est donc la suivante : taux d'intérêt -> consommation -> PIB.

La courbe IS new-keynesian est la suivante, dans sa version la plus simple, qui utilise l'écart de production $y_{t}$ :

$y_{t}=E[y_{t+1}]-a\cdot (r_{e}-r_{n})$, avec $E[y_{t}]$ l'écart de production anticipé.

Étudions maintenant les anticipations de l'écart de production futur $E[y_{t+1}]$. On sait que ces anticipations peuvent se tromper, ce qui fait qu'il existera une différence entre le PIB effectivement réalisé et son anticipation. Mathématiquement, cela se traduit ainsi :

$y_{t+1}=E[y_{t+1}]+\epsilon _{t+1}$

Supposons que les anticipations soient rationnelles. Les agents tentent alors de prédire l'écart de production futur à partir de l'équation précédente. Si les anticipations sont rationnelles, sa valeur future est en moyenne égale à sa valeur effectivement prédite. De plus, les agents semblent utiliser bien l'équation $y_{t}=E[y_{t+1}]-a\cdot (r_{e}-r_{n})$ pour prédire l'écart de production futur. Cela ne veut pas dire qu'ils utilisent cette équation dans leur tête, mais ils savent que l'écart de production dépend des taux d'intérêt. Les agents économiques utilisent les taux pour prédire l'écart de production futur. On a alors :

$E[y_{t+1}]=E[y_{t+2}-a\cdot (r_{e}(t+1)-r_{n}(t+1))]$

On peut faire la même chose pour : $E[y_{t+2}]$, ce qui donne :

$E[y_{t+2}]=E[y_{t+3}-a\cdot (r_{e}(t+2)-r_{n}(t+2))]$

Et ainsi de suite. Dans le cas général on trouve :

$E[y_{t+i}]=E[y_{t+i+1}-a\cdot (r_{e}(t+i)-r_{n}(t+i))]$

En combinant l'équation précédente et l'équation $y_{t}=E[y_{t+1}]-a\cdot (r_{e}-r_{n})$, on peut itérer à l'infini et on obtient :

$y_{t}=-\sum _{i=0}^{\infty }a\cdot E[r_{e}(t+i)-r_{n}(t+i)]$

On voit que l'écart de production actuel est déterminé par l'évolution des taux réels futurs. Sachant que ces taux réels dépendent de l'inflation anticipée et des taux nominaux, on a :

$y_{t}=-\sum _{i=0}^{\infty }a\cdot E[i(t+i)-\pi _{e}(t+i)-r_{n}(t+i)]$

On voit que l'écart de production dépend de la politique monétaire future, anticipée, ainsi que de l'évolution de l'inflation et des paramètres structurels de l'économie.

L'influence de la politique monétaire future sur l'écart de production semble être un détail. Mais il s'agit de la raison pour laquelle toutes les banques centrales font de la forward guidance en temps de crise. Rappelons ce qu'est la forward guidance : c'est le fait pour la banque centrale de donner des indications sur sa politique monétaire future. Elle peut par exemple s'engager à garder ses taux bas pour une durée minimale (d'au moins un an, par exemple). Ce faisant, les marchés sont mis au courant que la politique monétaire future sera accommodante et adaptent alors leurs anticipations. Si la banque centrale s'engage à maintenir des taux bas, les agents anticipent un taux nominal bas et l'équation précédente nous dit que cela augmente sur l'écart de production actuel.

Le canal des taux d'intérêts

Il existe plusieurs explications concernant la forme de la courbe IS. Il est possible de la dériver de plusieurs manières, que ce soit via quelques hypothèses ad hoc ou via de véritables fondations microéconomiques. Ces explications sont parfois contradictoires, ou tout du moins portent sur des aspects macro ou microéconomiques forts différents. Nous allons passer celles-ci en revue. La première explication, chère aux keynésiens, part du principe que le PIB est la somme de plusieurs dépenses : la consommation des ménages et entreprises, l'investissement, les dépenses gouvernementales et les exportations et importations (les exportations sont intégrés dans le PIB, alors que les importations en sont soustraites). Ainsi, on a :

$Y+M=C+I+G+E$, avec $Y$ le PIB, $C$ la consommation, $I$ l'investissement, $G$ les dépenses gouvernementales, $E$ les exportations et $M$ les importations.

La courbe IS : l'influence des taux d'intérêt

la consommation est totalement insensible aux variations des taux d'intérêts, du moins dans une certaine mesure, et on peut raisonnablement supposer la même chose pour les dépenses gouvernementales. Par contre, les taux d'intérêt ont une grande influence sur l'investissement. Aussi, il n'est pas étonnant que la macroéconomie keynésienne ait fait grand cas de la relation entre investissements et politique monétaire. Au passage, même si consommation et dépenses ne sont pas influencées par les taux d'intérêts, il est important de les étudier pour comprendre comment la politique fiscale et la politique monétaire interagissent.

La fonction de consommation

La consommation réagit suite à une variation des taux, essentiellement car elle soulage ou durcit la situation des ménages qui ont un crédit à taux variable (très courant dans d'autres pays que la France). Cependant, cette situation a un effet sur l'économie qui peut être négligé dans notre analyse. Une spécification totale de la courbe IS ne se limite pas à l'influence des taux d'intérêts sur la consommation, mais prend aussi en compte l'influence du revenu Y (le PIB) et des encaisses réelles ${\frac {M}{P}}$. Dans le détail, cela amène à trouver une équation qui détermine la consommation sur la base du revenu, des impôts, des encaisses réelles, etc.

La consommation et le revenu disponible

Pour simplifier, la consommation dépend essentiellement du revenu. La consommation dépendante du revenu dépend plus précisément du revenu disponible, le revenu après impôt. Le revenu total avant impôts, au niveau macroéconomique, est par définition égal au produit intérieur brut (nominal ou réel selon qu'on parle du revenu réel ou nominal). Si on note T les impôts/taxes et Y le PIB, le revenu disponible est égal à :

$Y_{disponible}=Y-T$

Les agents économiques sont supposés dépenser une fraction $c$ de leur revenu disponible et épargner le reste, soit la fraction $s=(1-c)$. La fonction de consommation est alors la suivante :

$C=c\cdot Y_{disponible}=c\cdot (Y-T)$

Fonction de consommation.

Pour quelques raisons techniques, il est préférable de rajouter un terme de consommation indépendante du revenu. La consommation devient alors une fonction affine du revenu disponible, à savoir une équation de la forme : $C=a+b(Y_{disponible})$. Dans ce qui va suivre, nous utiliserons la notation suivante :

$C=C_{0}+c\cdot Y_{disponible}=C_{0}+c\cdot (Y-T)$

Il est possible de raffiner l'analyse, en postulant que les impôts sont proportionnels aux revenus (et donc au PIB). Mathématiquement, cela donne : $T=t\times Y$. Les équations précédentes deviennent alors :

$Y_{disponible}=Y-(t\times Y)=Y(1-t)$

$C=C_{0}+c(1-t)\cdot Y$

L'effet d'encaisses réelles

La fonction de consommation précédente, inventée par Keynes, a par la suite été complétée suite aux remarques de Pigou. Divers arguments, liés à des controverses sur l'effet d'une baisse des salaires sur l'emploi, ont poussé Pigou à ajouter les encaisses réelles ${\frac {M}{P}}$ dans la fonction de consommation. Le raisonnement est que la monnaie est une richesse, qui peut être dépensée pour consommer. Plus les agents ont d'argent placé, plus ils auront tendance à consommer. Par exemple, une personne avec plus de 200.000 euros sur son compte courant a de quoi consommer, même si son revenu est nul. La consommation dépend donc non seulement du revenu, mais aussi de l'épargne accumulée (rappelons que l'épargne est de la consommation différée. Pigou a donné un nom à l'influence de l'épargne monétaire sur la consommation : c'est l'effet d'encaisses réelles. La fonction de consommation devient alors :

$C=C_{0}+c(Y-T)+f\left({\frac {M}{P}}\right)$

Dans la suite de ce chapitre, nous négligerons l'effet d'encaisses réelles. Celui-ci sera cependant utilisé dans les chapitres sur les modèles IS/LM et AD/AS, dans la partie du cours portant sur les théories monétaristes. La raison est que cet effet est fondamentalement monétariste, lié aux agrégats monétaires, au point qu'il se marie assez mal avec les théories Wickseliennes (qui se basent sur des taux d'intérêts).

L'investissement et les taux d'intérêts

Courbe concave qui relie l'investissement en fonction du taux réel.

L'investissement est souvent financé par le crédit. Les entreprises empruntent aux banques pour financer leurs investissements ou peuvent recourir à des obligations. Les ménages eux-même peuvent investir dans l'immobilier ou dans une voiture en utilisant le crédit. Le coût du crédit dépend fortement du taux d'intérêt : plus ce dernier est élevé, plus les intérêts seront élevés et moins il sera rentable d'emprunter. Plus les taux sont forts, plus le nombre de crédits sera faible. Il y a donc une relation entre taux d'intérêt et investissement total.

Il faut préciser que les entreprises et ménages basent leurs décisions d'emprunt/investissement sur la base des taux réels, et non sur les taux nominaux. Les investisseurs anticipent l'inflation et en déduisent un taux réel à partir d'un taux nominal. En fonction de ce taux réel anticipé, ils décident d'investir ou non si le taux réel est acceptable. Plus le taux réel est intéressant, plus les investisseurs sont attirés par le rendement. Inversement, un taux réel trop faible fera fuir les investisseurs.

De plus, ce sont les taux longs qui sont utilisés et non les taux courts. Les taux courts, décidés par la banque centrale, sont utilisés sur le marché monétaire pour négocier les crédits d'une durée très courte, trop courte pour financer des investissements qui mettent du temps avant de devenir rentables. Les investisseurs empruntent en fait sur des durées suffisamment longues pour que leurs investissements deviennent rentables. Et les taux associés sont les taux longs, pas les taux courts. Rappelons que les taux longs dépendent des taux courts, qui sont eux-même influencés par la banque centrale.

Pour résumer, l'investissement est une fonction décroissante des taux d'intérêt réels de long-terme. Par souci de simplification, nous allons supposer que l'investissement est une fonction linéairement décroissante du taux long réel. Ce choix est purement arbitraire et ne sert qu'à simplifier les calculs. Mais il va de soit que nous aurions pu prendre n'importe quelle autre forme, comme une forme concave ou convexe, plus réaliste. On obtient alors :

$I(i)=I_{0}-a\cdot (i_{long}-\pi _{e})$

L'équation de la courbe IS

Récapitulons. Nous avons établit les deux équations suivantes, qui donnent la consommation et l'investissement en fonction du revenu et des taux d'intérêt.

$C=C_{0}+c\cdot Y_{disponible}=C_{0}+c\cdot (Y-T)$

$I=I_{0}-a\cdot (i_{long}-\pi _{e})$

Dans ce qui va suivre, nous allons nous concentrer sur le cas d'une économie fermée, à savoir sans échanges commerciaux avec d'autres pays. Dit autrement, les exportations et importations sont nulles, ou tout du moins négligées. L'analyse en économie ouverte (avec prise en compte des exportations et importations) sera vue dans quelques chapitres. Mais que l'économie soit ouverte ou fermée ne change rien (ou presque) aux résultats que nous allons obtenir dans ce chapitre, qui sont valables dans les deux cas. La seule différence est qu'il faut tenir compte de l'impact indirect des taux d'intérêt sur les exportations et importations, ce qui ne fait que complexifier le tout tout en gardant des équations similaires. Toujours est-il qu'avec cette hypothèse, le PIB est définit comme suit :

$Y=C+I+G$

En combinant les équations précédentes, on a :

$Y=C+G+I_{0}-a\cdot (i_{long}-\pi _{e})$

On peut alors regrouper le terme $C+G+I_{0}$ en un seul, que l'on note $Y_{0}$. On retrouve alors l'équation de la courbe IS :

$Y=Y_{0}-a\cdot (i_{long}-\pi _{e})$

Les déplacements de la courbe IS

Déplacement de la courbe IS suite à une politique fiscale ou monétaire restrictive.

On vient de le voir, la courbe IS dépend de nombreux paramètres, certains relevant de la politique monétaire, et d'autres de la politique budgétaire. Pour ce qui est de la politique budgétaire, la consommation dépend essentiellement du taux d'imposition, tandis que les dépenses gouvernementales sont du fait même des états. Par contre, l'investissement et les exportations nettes sont sous le contrôle direct de la banque centrale, ces deux facteurs dépendant essentiellement des taux d'intérêts.

Dans les faits, une politique monétaire accommodante augmente l'investissement et les exportations nettes, ce qui augmente le PIB (la valeur dépendant du multiplicateur keynésien). Une augmentation des dépenses de l'état aura le même effet, à savoir que cette augmentation augmentera le PIB, par le biais du multiplicateur. Par contre, une politique fiscale à base de baisses d’impôts aura un effet plus faible, portant essentiellement sur la consommation (et sur la valeur du multiplicateur fiscal, dans les modèles plus complets). Dans tous les cas, une politique monétaire ou fiscale accommodante (baisse des impôts, hausse des dépenses, taux bas) augmente fortement le PIB, déplaçant la courbe IS vers la droite. Une politique monétaire ou fiscale restrictive aura l'effet inverse (baisse du PIB, ce qui déplacera la courbe IS vers la gauche.

La pente de la courbe IS et les multiplicateurs keynésien

On vient de voir que divers composants du PIB sont dépendants des taux. Mais ceci sont aussi dépendants d'un paramètre nommé le multiplicateur keynésien. Ce multiplicateur n'est pas unique, et il faudrait faire la distinction entre multiplicateur de l'investissement, multiplicateur des dépenses et multiplicateur fiscal.

Précisons que pour les démonstrations qui vont suivre, nous allons devoir faire quelques suppositions. La plus importante tient dans les relations de causalité dans l'équation $Y=C+I+G$. L'hypothèse suppose que I et G sont indépendants, mais aussi que ce sont des variables dites exogènes. Par exogènes, on veut dire que la causalité va dans le sens $I+G\rightarrow Y$, et non dans l'autre sens. Dit autrement, on suppose que les variations de I et de G surviennent "toutes seules", et qu'elles se répercutent sur le PIB et/ou la consommation. Pour cela, il faut que l'investissement ne dépend pas de l'épargne S, qui est égale à $Y-C-T$, avec T les taxes. On fait donc une hypothèse implicite, qui est que l'investissement existe de manière totalement autonome, sans rapport avec l'épargne, la consommation ou quoique ce soit d'autre. Cette vision se marie donc bien avec les théories naïves de la monnaie purement endogène, qui supposent que les banques commerciales créent de la monnaie sans avoir besoin d’une épargne préalable.

Mais on peut aussi interpréter les choses d'une manière différente. On peut considérer que la causalité va du PIB vers ses composantes. Les agents économiques touchent un revenu, payent leurs taxes, et décident combien ils consomment et combien ils épargnent. On a alors l'équation $Y=C+S+T$. Pour simplifier, l'épargne finance l'investissement, alors que les taxes financent les dépenses gouvernementales. Ce qui redonne l'équation $Y=C+I+G$. Dans une telle situation, il n'existe pas de multiplicateur keynésien et il ne peut pas y en avoir. Notons que cette vision se marie mieux avec les théories à monnaie exogène, où les banques ne peuvent investir que de l'épargne préexistante.

Les multiplicateurs keynésiens

Nous allons commencer par le multiplicateur de l'investissement. Celui-ci indique que l'augmentation de l'investissement a un effet sur le PIB qui est supérieur à l'augmentation de l'investissement lui-même. Dans le détail, si l'investissement augmente d'une quantité $\Delta I$, le PIB augmentera d'une quantité égale à :

$\Delta PIB=k_{i}\times \Delta I$, avec $k$ le multiplicateur de l'investissement.

Il existe un multiplicateur équivalent pour une hausse des dépenses gouvernementales, qui dit de combien augmente le PIB suite à une hausse des dépenses G. Il est défini par :

$\Delta PIB=k_{g}\times \Delta G$, avec $k_{g}$ le multiplicateur des dépenses gouvernementales.

Enfin, il existe la même chose, un multiplicateur fiscal pour les impôts et taxes T. Contrairement aux multiplicateurs précédent, il a une valeur négative, ce qui veut dire qu'une hausse des impôts réduit la production. Ce multiplicateur vaut :

$\Delta PIB=k_{t}\times \Delta T$, avec $k_{t}$ le multiplicateur fiscal.

La pente de la courbe IS

Le multiplicateur de l'investissement modifie la pente de la courbe IS. Pour comprendre pourquoi, il faut partir de la formule de l'investissement que nous avons utilisée plus bas. Celle-ci est, pour rappel :

$I(r)=I_{0}-\alpha \cdot r$

En étudiant les variations de I par rapport à r, on trouve (avec $\alpha$ constant) :

${\frac {\Delta I}{\Delta r}}=-\alpha$

On combine cette équation avec la formule du multiplicateur keynésien $\Delta Y=k_{i}\cdot \Delta I$, ce qui permet d'obtenir la variation du PIB provenant d'une variation du taux réel.

${\frac {\Delta Y}{\Delta r}}=-(\alpha \cdot k)$

Si on trace la courbe sur un graphique r-Y, on voit qu'il s'agit d'une fonction affine dont la pente est égale à $k\cdot \alpha$.

Le calcul du multiplicateur keynésien

Reste à calculer le multiplicateur keynésien pour parfaire notre compréhension de la pente de la courbe IS. Pour cela, nous allons calculer le multiplicateur keynésien dans plusieurs cas : avec ou sans impôts, avec des impôts proportionnels, etc.

Le cas sans impôts ni dépenses gouvernementales

Pour commencer, nous allons omettre les impôts et taxes, ainsi que les dépenses gouvernementales. Ce cas est irréaliste, mais permet de simplifier les calculs afin de mettre l'accent sur l'essentiel. L'équation qui définit le PIB devient alors :

$Y=C+I(r)$

Nous allons aussi utiliser la fonction de consommation simplifiée suivante :

$C=c\cdot Y$.

On combine avec l'équation précédente :

$Y=c\cdot Y+I(r)$

On soustrait $c\cdot Y$ :

$Y-c\cdot Y=I(r)$

On factorise :

$Y(1-c)=I(r)$

On divise par $1-c$ :

$Y={\frac {1}{1-c}}I(r)={\frac {1}{s}}I(r)$

L'équation donne le multiplicateur de l'investissement, qui est égal à ${\frac {1}{1-c}}={\frac {1}{s}}$.

Le cas avec des impôts forfaitaires

On peut raffiner l'analyse en utilisant la fonction de consommation suivante :

$C=C_{0}+c(Y-T)$.

On combine l'équation précédente avec l'équation $Y=C+G+I(r)$ qui définit le PIB :

$Y=[C_{0}+c(Y-T)]+G+I(r)$

On développe :

$Y=C_{0}+cY-cT+G+I(r)$

Là encore, on soustrait $c\cdot Y$ et on factorise, et on trouve :

$Y={\frac {1}{s}}[C_{0}-cT+G+I(r)]$

Les calculs sont les mêmes que précédemment, sauf que l'investissement est remplacé par $C_{0}+I+G-cT$. Mais le multiplicateur est le même.

Le cas avec des impôts proportionnels

Il est aussi possible de raffiner l'analyse, en postulant que les impôts sont proportionnels aux revenus (et donc au PIB) : $T=t\times Y$. La fonction de consommation est donc :

$C=C_{0}+c(1-t)Y$

En combinant avec la définition du PIB, on a :

$Y=C_{0}+c(1-t)Y+G+I(r)$

On fait passer les termes avec Y à gauche et on factorise :

$Y[1-c(1-t)]=C_{0}+G+I(r)$

On divise alors par $1-c(1-t)$ :

$Y={\frac {1}{1-c(1-t)}}[C_{0}+G+I(r)]$

Dans ces conditions, le multiplicateur vaut ${\frac {1}{1-c(1-t)}}={\frac {1}{1-c+ct}}={\frac {1}{s+ct}}$.

Pourquoi cette courbe s'appelle-t-elle "courbe IS" ?

Les premières démonstrations de la courbe IS keynésienne/classique partaient de la théorie classique des taux d'intérêt, que nous avions abordée dans les premiers chapitres du cours. Elles se basaient sur l'hypothèse que investissement et épargne sont égaux. Les formulations ultérieures ont réussit à s'affranchir de cette théorie des taux d'intérêt, mais conservent le fait que investissement et épargne sont égaux, bien que ce soit pour des raisons différentes. On a donc :

$I=S$, avec I l'investissement et S l'épargne (Savings en anglais).

Cette identité comptable a d'ailleurs donné son nom à la courbe IS (courbe Investment-Savings).

Les dérivations de I=S à partir des définitions du PIB

Il est possible de retrouver cette égalité à partir de quelques raisonnements sur les identités comptables du style $Y=C+I+G$, ce que nous allons faire dans ce qui suit.

Le cas d'une économie fermée sans état

On peut "démontrer" cette égalité en partant de la définition du PIB. Dans un monde sans état et en économie fermée, les revenus sont soit dépensés, soit épargnés. On a alors :

$Y=C+S$

Du côté de la production, ce qui est produit est soit consommé, soit investit. On a donc :

$Y=C+I$

En combinant les deux équations précédentes, on trouve bien l'identité comptable :

$I=S$

Le cas d'une économie fermée avec état

Interprétation des identités comptables dans la théorie keynésienne.

Maintenant, ajoutons un état qui lève des taxes et dépense. Dans une économie fermée avec état, les revenus sont soit dépensés, soit épargnés, soit utilisés pour payer des taxes.

$Y=C+S+T$, avec Y le revenu (le PIB pour être précis), C la consommation, S l'épargne et T les taxes.

Inversement, si on regarde du côté de la production, le revenu provient soit des dépenses de consommation, soit des dépenses d'investissement, soit des dépenses gouvernementales.

$Y=C+I(r)+G$, avec Y le revenu (le PIB pour être précis), C la consommation, I l'investissement, G les dépenses gouvernementales, E les exportations et M les importations.

On a alors l'égalité suivante :

$C+S+T=C+I(r)+G$

En simplifiant et en isolant S, on trouve l'équation suivante :

$S=I(r)+(G-T)$

Le déficit public de l'état est égal, par définition, à $G-T$, ce qui donne :

$S=I(r)+{\text{déficit publique}}$

Cette équation est assez logique quand on sait qu'un état en déficit public doit trouver de l'argent pour financer ses dépenses, car les impôts ne suffisent pas. La différence entre dépenses et impôts provient soit de l'épargne accumulée par l'état, soit d'un emprunt sur les marchés financier. Vu que les états avec de l'épargne sont rares, on peut considérer que le déficit est ce que doit emprunter l'état pour financer ses dépenses qui dépassent ses impôts. Et cet emprunt remobilise de l'épargne privée non-investie : l'épargne prête par l'état est en fait de l'épargnée privée qui est prêtée à l'état. L'épargne privée se répartit entre investissement et financement du gouvernement. Si l'épargne est donnée, un déficit public réduit l'investissement. On fait face à un effet d'éviction : l'épargne qui aurait été utilisée pour investir est redirigée pour financer l'état. Ce cas est courant, mais il existe des situations où l'effet d'éviction ne se manifeste pas, comme on le verra plus tard.

Le cas d'une économie ouverte avec état

Le cas précédent est celui d'une économie fermée, sans importations ni exportations, qui peu paraitre irréaliste. Mais si on ajoute les exportations et importations, alors le résultat change peu. Les importations s'ajoutent à la demande globale, alors que les exportations s'ajoutent à la production, ce qui donne :

$Y=C+S+T-M$, avec M les importations.

$Y=C+I+G+E$, avec E les exportations.

L'égalité donne donc :

$I+(G-T)=S+(M-E)$

On retrouve le résultat précédent, à ceci près qu'il faut ajouter le terme (M - E). Ce terme n'est autre que le déficit commercial, la différence entre importations et exportations.

Investissement (I) + Déficit public (G - T) = Épargne domestique (S) + Déficit commercial (M - E)

On verra dans le chapitre sur les taux de change que le déficit commercial est égal au flux de capitaux entrant dans le pays. Dit autrement il s'agit d'une épargne étrangère qui est investie dans le pays domestique. On a donc :

Investissement privé (I) + Emprunt public (G - T) = Épargne domestique (S) + Épargne étrangère (M - E)

Le terme de gauche n'est autre que la somme des flux d'emprunts, alors que le terme de droite est l'ensemble des flux d'épargne. l'équation nous dit que l'emprunt est égal à l'épargne, ce qui n'est qu'une reformulation de l'équation $I=S$.

Là encore, on peut étudier ce qui se passe dans divers cas particuliers. En premier lieu, on peut étudier le cas où I et S sont constants tous les deux. Dans ce cas, on voit que toute variation de l'épargne domestique publique est compensée par une variation de l'épargne étrangère. Le déficit commercial est alors égal au déficit public. On a alors un second effet d'éviction dans le sens où l'épargne publique évince l'épargne étrangère. L'un remplace l'autre lors de l'investissement. Dans le cas général, pour une économie au PIB potentiel, on n'a pas exactement cette variation. Cependant, l'effet d'éviction épargne-privée-publique se combine avec l'effet d'éviction épargne étrangère-publique, ce qui fait que déficit commercial, déficit public et épargne privée entrent en compétition. Toute variation de l'une se répercute sur les autres. Ainsi, un déficit public absorbe une partie de l'épargne privée au détriment de l'investissement, mais il va aussi absorber une partie de l'épargne étrangère.

L'interprétation de l'identité I=S

L'égalité entre investissement et épargne peut sembler contre-intuitive. Rappelons que l'épargne est définie comme tout ce qui n'est pas dépensé/taxé. Mais cet argent peut être conservé de bien des manières. Il peut certes être placé dans une banque ou sur les marchés financiers, mais il peut aussi être thésaurisé et mis sous un matelas. Difficile de comprendre comment de l'argent conservé sous forme d'espèces peut donner lieu à de l'investissement... Mais c'est oublier que l'égalité I=S est une identité comptable qui dépend fortement de la nature de ce qui est compté comme investissement et comme épargne. En triturant les définitions, on peut faire en sorte que l'égalité I=S soit toujours vraie, et c'est ce qui est fait dans le monde réel. Nous allons voir pourquoi dans cette section.

Prenons le cas où les agents souhaitent thésauriser, c'est à dire augmenter leur épargne non-placée. On va supposer que les agents gardent leur consommation constante, mais qu'ils remplacent de l'épargne investie par de l'épargne thésaurisée, non-investie. En théorie, l'investissement devrait baisser, mais l'épargne devrait rester la même. L'égalité I=S devrait être violée, même en tenant compte de l'épargnée publique ou étrangère. Cependant, si les agents se mettent soudainement à thésauriser, les entreprises ne le voient pas venir et continuent de produire autant qu'avant. Elles vont alors accumuler des inventaires, des invendus, de la production pas encore consommée, mais destinée à l'être. Or, dans les normes comptables actuelles, les invendus sont comptés dans l'investissement. Et c'est assez logique : un invendu est destiné à être vendu dans le futur, donc à rapporter plus tard, comme tout investissement. Une augmentation de la thésaurisation entraine deux remplacements : le remplacement d'une partie de l'épargne placée par de l'épargne non-placée, et un remplacement d'une partie la consommation par des invendus. L'égalité I=S est donc vérifiée, même si c'est par une sorte de triche assez problématique.

Cependant, les entreprises en continuent pas de produire des invendus durant bien longtemps. Elles remarquent que les invendus s'accumulent et comprennent que la demande a baissée (à cause de la baisse de l'investissement). Elles vont donc réduire leur production, couper leurs dépenses, virer leurs employés, et j'en passe. Le résultat est une baisse de l'investissement, qui entraine une baisse du PIB. Dit autrement, cela cause une récession. Et l'effet est encore plus fort si on prend en compte le multiplicateur keynésien : non seulement l'investissement baisse, mais en plus la consommation suit. Dans tous les cas, la récession réduit les revenus, et donc la capacité d'épargne des agents économiques... Les agents qui souhaitaient épargner plus n'y arrivent plus au bout de quelques temps. Ce raisonnement est ce qu'on appelle le paradoxe de l'épargne, un paradoxe vieux comme le monde qui dit que si tous les agents souhaitent augmenter leur épargne, la capacité d'épargne globale chutera. Résultat valide, mais contre-intuitif, d'où le nom de paradoxe qu'on lui donne.

L’identité I=S et le contrôle des taux d'intérêt

Dans les économies modernes, la banque centrale a le pouvoir de contrôler le taux réel sur le court-terme. On peut se demander comment cela est compatible avec le modèle présenté, dans lequel I=S. En contrôlant les taux, elle contrôle le point d'intersection entre les deux courbes d'investissement désiré et d'épargne souhaitée. Formellement, elle n'a pas le pouvoir d'agir sur la courbe d'investissement, ce qui ne peut être fait que par des politiques budgétaires, financières, d'action pour la recherche et les entreprises technologiques, etc. Par contre le flux et le stock d'épargne peuvent être influencés par la politique monétaire. Rappelons que la banque centrale a le pouvoir d'injecter de la monnaie dans l'économie, par l'intermédiaire du système bancaire. Et une partie de cette monnaie sera épargnée, investie dans les marchés de fonds prêtables et de capitaux, ce qui augmente l'offre de fonds prêtables. En clair, elle déplace la courbe d'offre d'épargne S(r) là où il faut, là où le taux d'intérêt est celui voulu par la banque centrale.

Après, le raisonnement n'est pas parfait et il existe des situations où l'injection de monnaie dans l'économie n'influence pas l'investissement. Peut-être avez-vous déjà entendu, dans les médias, des commentateurs qui accusent les taux bas de réduire l'activité économique. Pour eux, des taux bas incitent les agents économiques à ne pas épargner, ce qui réduit l'investissement, et donc déprime l'activité économique et l'inflation. Néanmoins, ce raisonnement ne vaut pas si l'épargne est remplacée par de la consommation, car le PIB reste alors inchangé. Pour que ce raisonnement soit valide, il faut que les épargnants thésaurisent. S'ils thésaurisent tout l'argent crée par la banque centrale, la courbe d'offre de fonds prêtables ne changera pas. Les taux d'intérêt restent les mêmes et la banque centrale ne peut plus rien faire pour les changer. Quand cela arrive, l'économie tombe dans une trappe à liquidité, une situation où la banque centrale ne peut plus contrôler les taux d'intérêt. En général, cela survient quand les taux sont faibles, proches de zéro. La monnaie devient alors presque identique aux autres investissements. Pourquoi réduire ses liquidités et gagner des clopinettes, alors qu'on peut garder de l'argent liquide au cas où pour un rendement presque identique ? La demande de monnaie augmente alors fortement, alors que l'offre de fonds prêtables s'effondre. La consommation reste la même, mais l'investissement s’effondre effectivement, déclenchant une récession. Mais augmenter les taux ne résout pas forcément le problème : l'effet peut être délétère, suivant la valeur du multiplicateur keynésien, de l'ampleur de la substitution épargne investie-consommation, etc.

Le canal du cashflow

Après avoir vu le canal du taux d'intérêt, il est temps de voir un autre canal de transmission de la politique monétaire. Nous allons parler du canal du cashflow, un canal complémentaire au canal des taux d'intérêt et qui peut s'analyser avec des outils similaires.

Les canaux du cashflow

Le canal du cashflow est en fait la réunion de deux canaux antagonistes. Le premier canal est appelé le canal des intérêts d'emprunt, alors que le second est appelé le canal des intérêts d'épargne.

Le premier canal est causé par le fait que les intérêts des emprunts sont pris sur le revenu disponible. Quand vous remboursez un emprunt, vous remboursez chaque mois un peu du capital emprunté, mais aussi les intérêts. La plupart des crédits sont dits à taux fixe, dans le sens où le taux est déterminé une fois pour toutes lors de la souscription. La mensualité est la même durant toute la durée du prêt et le taux d'intérêt ne varie pas dans le temps. Mais si ces crédits sont majoritaires en France, les autres pays utilisent des crédits à taux variable, où le taux d'intérêt évolue au cours du temps. Le taux est indexé sur d'autres taux techniques, mais on peut considérer qu'il est indirectement indexé sur les taux directeurs. Ce qui fait que quand la banque centrale diminue ses taux directeurs, le taux des emprunts à taux variable baissent et les mensualités d'emprunt font de même. Les emprunteurs voient donc leurs mensualités évoluer avec le temps, en fonction de la politique monétaire. Et une hausse ou baisse des mensualités se répercute sur le revenu disponible et donc sur la consommation et le PIB.

$\downarrow i~\rightarrow ~\downarrow {\text{Mensualités des crédits}}~\rightarrow ~\uparrow {\text{Revenu disponible}}~\rightarrow ~\uparrow C~\rightarrow ~\uparrow Y~\rightarrow ~...$

Les consommateurs ne sont pas les seuls emprunteurs potentiels. De nombreuses entreprises sont endettées, l'endettement étant un bon moyen de financer l'investissement. Une baisse des taux est donc favorable pour elles, dans le sens où elles auront moins d'intérêts à payer. Ce faisant, ces économies d'intérêts peuvent servir à consolider les comptes de l'entreprise ou être reversées en tant que dividendes, mais elles peuvent aussi financer de l'investissement. Les économies d'intérêts sont alors réinvesties pour faire grossir l'entreprise ou l'adapter au marché. Cet investissement supplémentaire, lié non pas à un endettement accru mais à une économie de charges d’intérêt, se répercute sur le PIB.

$\downarrow i~\rightarrow ~\downarrow {\text{Charges de crédit}}~\rightarrow ~\uparrow {\text{Cashflow de l'entreprise}}~\rightarrow ~\uparrow I~\rightarrow ~\uparrow Y~\rightarrow ~...$

Le second canal est le pendant du précédent, mais pour les revenus de l'épargne. En effet, une partie de l'épargne est rémunérée sous la forme d'un intérêt, comme le sont les livrets bancaires, les comptes à terme, les fonds euro d'assurance-vie, et bien d'autres. Et les taux d'intérêt de cette épargne sont indexés sur les taux directeurs, par divers mécanismes qu'on a vu dans les chapitres précédents (courbe de s taux, autres). Ce qui fait que quand la banque centrale réduit ses taux directeurs, tous les autres taux baissent, ce qui impacte la rémunération de l'épargne. Or, la rémunération de l'épargne fait partie du revenu disponible. Sa baisse ou sa hausse se répercute sur le revenu disponible, ce qui impacte la consommation et par la suite le PIB.

$\downarrow i~\rightarrow ~\downarrow i_{\text{épargne}}~\rightarrow ~\downarrow {\text{Revenu disponible}}~\rightarrow ~\downarrow C~\rightarrow ~\downarrow Y~\rightarrow ~...$

La modélisation des deux canaux du cashflow

Dans le chapitre précédent, nous avions vu que le revenu disponible d'un agent est égal à ceci :

$Y_{\text{disponible}}=Y-T$, avec Y ses revenus totaux, et T les taxes et impôts.

Pour un épargnant, les revenus d'épargne sont contenus dans les revenus Y. Mais on peut séparer les revenus d'intérêt et le reste. On a alors :

$Y_{\text{disponible}}=(Y_{N}+i_{s}\cdot S)-T$, avec S son épargne et $i_{s}$ le taux de rémunération de son épargne.

Cela peut se reformuler comme suit :

$Y_{\text{disponible}}=Y_{0}+i_{s}\cdot S$, avec $Y_{0}=Y_{N}-T$.

Pour un emprunteur, il faut retrancher les intérêts à payer sur les crédits et le remboursement du capital.

$Y_{\text{disponible}}=Y-T-R-i_{c}\cdot D$, avec R le remboursement du capital, $i_{c}$ le taux d’emprunt et D le montant de la dette empruntée.

On peut raisonnablement penser que les taux d'intérêt d'épargne et d'emprunt sont reliés par la relation suivante, vue il y a quelques chapitres : $i_{c}=i_{s}+p_{r}$, avec $p_{r}$ une prime de risque qui sert à se couvrir du non-remboursement des crédits. En faisant le remplacement, on trouve :

$Y_{\text{disponible}}=Y-T-R-(i_{s}+p_{r})\cdot D=Y-T-R-p_{r}\cdot D-i_{s}\cdot D$

Dans ce qui suit, la prime de risque est supposée constante et n'est pas influencée par la politique monétaire (ce qui est partiellement faux, mais passons). La formule précédente se reformule alors comme suit :

$Y_{\text{disponible}}=Y_{0}-i_{s}\cdot D$

Les équations précédentes se généralisent au niveau macroéconomique. Elles donnent la variation totale de revenu disponibles de tous les emprunteurs et de tous les épargnants. Si on considère que le revenu disponible est celui de tous les emprunteurs ou de tous les épargnants, on a :

$Y_{\text{emprunteurs}}=Y_{0}+i_{s}\cdot S$, avec D le stock total d'épargne dans l'économie.

$Y_{\text{épargnants}}=Y_{0}-i_{s}\cdot D$, avec D le stock total de dette dans l'économie.

En prenant les variations, et en supposant que S et D sont constants, on trouve :

$\Delta Y_{\text{emprunteurs}}=\Delta i_{s}\cdot S$

$\Delta Y_{\text{épargnants}}=-\Delta i_{s}\cdot D$

L'influence du solde débiteur net

On voit que les deux canaux vont dans des sens opposés : le premier stimule la consommation, alors que le second la réduit. Intuitivement, les deux devraient s'annuler. Un raisonnement simple nous dit en effet que la somme des emprunts devrait être égale à la somme de l'épargne, comme on l'a vu en parlant du canal des taux. Rien d'étonnant à cela, vu que les sommes prêtées viennent de l'épargne préexistante. En théorie, la baisse des taux doit impacter les taux d'emprunt et les taux de l'épargne de la même manière. Si l'un baisse de 1%, l'autre doit faire de même. Ce qui est gagné d'un côté l'est aussi de l'autre. En théorie, une hausse/baisse des taux n'a donc pas d'effets globaux, elle ne change pas le revenu disponible total de tous les agents économiques. Certains vont voir leur revenu disponible augmenter, d'autres vont le voir baisser, mais les hausses compensent les baisses au niveau global. Par exemple, une baisse des taux fait gagner de l'argent aux emprunteurs, mais fait perdre la même somme aux épargnants et le revenu disponible global ne change pas.

Mis en équations, voici ce que cela donne. On a naturellement :

$Y=Y_{\text{emprunteurs}}+Y_{\text{épargnants}}$

Prenons la variation, on a :

$Y=\Delta Y_{\text{emprunteurs}}+\Delta Y_{\text{épargnants}}$

On utilise les équations de la section précédente :

$\Delta Y=\Delta i_{s}\cdot S-\Delta i_{s}\cdot D$

On factorise :

$\Delta Y=\Delta i_{s}(S-D)$

Si on a D = S, alors on a :

$\Delta Y=0$

Mais dans la réalité, l'égalité D=S n'est pas respectée. On a pourtant vu dans le chapitre précédent que l'égalité I=S est tout le temps respectée, mais le diable est dans les détails. La différence D-S est liée à l'existence d'une épargne non-rémunérée par des intérêts, comme l'argent sur les comptes courants. De plus, une partie de la dette est détenue dans des plans d'épargne en prévision de la retraite, du chômage, ou autre. Les intérêts associés ne font pas partie du revenu disponible, ce qui fait que l'épargne associée ne compte pas.

L'influence de la propension à consommer

Outre la différence D-S, il faut aussi prendre en compte la propension à consommer. Les épargnants ont par définition de quoi épargner et ne sont pas spécialement limités par leur revenu disponible pour ce qui est de consommer. Il est naturel de penser qu'un épargnant préfère épargner que consommer, ce qui lui donne une propension à consommer faible. Pour les emprunteurs, c'est l'inverse : ils empruntent car ils n'ont pas assez d'épargne et/ou de revenu pour obtenir ce qu'ils veulent (une maison, une voiture, ou autre). Sans compter qu'il est difficile d'épargner avec un crédit sur les bras. Ils ont donc vraisemblablement une propension à consommer plus grande. En prenant en compte cet effet, une hausse/baisse des taux peut toucher la consommation par le canal du cashflow, même quand épargne et dette sont égales. Avec une baisse des taux, la consommation des emprunteurs augmente et celle des épargnants se réduit, mais l'ensemble ne se compense pas et la consommation augmente. Et cette hausse de la consommation se répercute sur le PIB, par le biais du multiplicateur keynésien. Au final, l'effet n'est pas exactement nul.

Pour mettre cela en équations, nous allons séparer la population en deux catégories : les emprunteurs et les épargnants. Nous allons calculer le revenu disponible total pour chaque catégorie, puis faire de même avec la consommation, et ainsi de suite. La consommation de chaque catégorie est alors la suivante :

$C_{\text{totale}}=C_{\text{emprunteurs}}+C_{\text{épargnants}}\approx c_{1}\cdot Y_{\text{emprunteurs}}+c_{2}\cdot Y_{\text{emprunteurs}}$, avec $c_{1}$ la propension moyenne à consommer des emprunteurs et $c_{2}$ la propension moyenne à consommer des épargnants.

Prenons la variation, en supposant les propensions à consommer constantes :

$\Delta C_{\text{totale}}=\Delta C_{\text{emprunteurs}}+\Delta C_{\text{épargnants}}\approx c_{1}\cdot \Delta Y_{\text{emprunteurs}}+c_{2}\cdot \Delta Y_{\text{emprunteurs}}$

On utilise les équations $\Delta Y_{\text{emprunteurs}}=\Delta i_{s}\cdot S$ et $\Delta Y_{\text{épargnants}}=-\Delta i_{s}\cdot D$ :

$\Delta C\approx c_{1}\cdot \Delta i_{s}\cdot S-c_{2}\cdot \Delta i_{s}\cdot D$

On factorise :

$\Delta C\approx \Delta i_{s}\cdot (c_{1}\cdot S-c_{2}\cdot D)$

On trouve donc une généralisation de l'équation : $\Delta Y\approx \Delta i_{s}\cdot (S-D)$, qui tient compte des propensions à consommer. Mais ce qui est intéressant, c'est d'étudier le cas où D=S. On a alors : :

$\Delta C\approx \Delta i_{s}\cdot (c_{1}\cdot S-c_{2}\cdot S)=\Delta i_{s}\cdot S\cdot (c_{1}-c_{2})$

On voit que la consommation est stimulée par la différence de propension à consommer, même si la dette et l'épargne sont identiques. Et cette différence de consommation se répercute sur le PIB par le biais du multiplicateur keynésien. Pour résumer, le canal du cashflow a un impact par le biais du nombre d'emprunteurs et leur propension à consommer.

Conclusion

Ce chapitre nous a appris que la politique monétaire redistribuait du pouvoir d'achat entre emprunteurs et épargnants. Une baisse des taux sera favorable aux emprunteurs et défavorable aux épargnants, alors qu'une hausse aura l'effet inverse. Si en première approximation, cette redistribution n'a que peu d'impact sur le PIB, il existe quand même un petit effet lié aux propensions à consommer. Vu que les emprunteurs dépensent plus leur revenu que les épargnants, une baisse des taux remet de l'argent en circulation dans l'économie. De l'argent qui aurait été épargné se retrouve dans la consommation, et l'équilibre épargne-consommation est alors chamboulé, ce qui a un impact macroéconomique sur le PIB et l'inflation.

Néanmoins, le canal du cashflow n'est pas le seul à toucher l'équilibre épargne-consommation. À ce titre, on pourrait aussi citer le canal de substitution intertemporel, qui est l'équivalent du canal du cashflow, mais lissé dans le temps. Il décrit comment les agents décident d'épargner ou de consommer en fonction de leurs anticipations de l'avenir. Plus ils pensent avoir des revenus futurs élevés, plus ils auront tendance à consommer maintenant et à peu épargner. Et inversement, les agents peuvent épargner pour se prévenir contre une future baisse de revenus. Et les taux d'intérêt ont leur rôle à jouer dans cet arbitrage, ceux-ci déterminant à quel point l'épargne sera rentable dans le futur. Mais nous verrons cela vers la fin de ce cours. Pour poursuivre ce chapitre, nous allons devoir parler de ce qui se passe pour les épargnants dont l’épargne n'est pas rémunérée sous la forme d’intérêt, mais sous la forme de dividendes, de loyers, ou autres. Et pour cela, nous allons devoir parler du canal des prix d'actifs, ce que se propose de faire le prochain chapitre.

Le canal du prix des actifs

Outre son effet sur l'investissement, les variations du taux d'intérêt ont des effets sur le prix de divers actifs financiers. La politique monétaire influence le prix des obligations (de la dette d'état ou d'entreprise), des actions, voire de l'immobilier. Dans les grandes lignes, une baisse des taux augmente les prix de tous les actifs et inversement pour une hausse. Et cela a des effets indirects susceptibles de faire augmenter l'inflation. Par exemple, une augmentation du prix des actifs va stimuler l'investissement des entreprises cotées, ce qui fera augmenter la demande agrégée. De même, les ménages détenteurs d'actifs, devenus plus riches, vont dépenser plus que prévu et stimuler la demande. Et ainsi de suite. Dans ce qui va suivre, nous allons d'abord voir d'où vient l'effet de la politique monétaire sur les prix d'actifs, avant de voir comment ces variations de prix vont stimuler l'économie.

L'origine de l'influence de la politique monétaire sur le prix des actifs

On peut se demander d'où provient l'augmentation du prix des actifs induite par une modification des taux monétaires. Il existe plusieurs raisons, mais nous n'allons voir que les deux principales. La première est que les agents font un arbitrage entre les différents placements en fonction de leur rendement et de leur risque. Une baisse des taux réduit le rendement des produits de taux (obligations et placements monétaires), ce qui incite les agents à se rabattre sur les autres actifs. L'autre raison est liée au fait que la baisse des taux favorise l'emprunt, qui est utilisé pour acheter des actifs à crédit. Dans les deux cas, certains actifs voient leur demande augmenter, ce qui entraîne une augmentation de leur prix (à offre égale).

L'arbitrage entre actifs

La raison principale est que les investisseurs font face à un choix : placer leur argent soit dans des actifs risqués, soit dans des placements monétaires/obligataires. Les investisseurs font un arbitrage entre la liquidité et la sûreté des placements monétaires/obligataires et le rendement des actifs plus risqués. Ils préféreront l'un ou l'autre selon les variations des rendements.

• Plus les placements monétaires deviennent rentables, plus les agents vont délaisser les actifs risqués au profit des placements monétaires/obligataires. Par exemple, peu d'agents oseraient acheter des actions risquées qui rapportent 5% s'ils ont accès à des placements monétaires qui rapportent 4%. Et les détenteurs d'obligations chercheront à revendre leurs actions pour investir sur les placements sans risque. Ce phénomène de fly-to-quality entraîne une baisse du prix des actifs risqués.
• À l'inverse, une baisse des taux sans risques rend les actifs risqués plus intéressant que les placements monétaires/obligataires, ce qui fait monter leurs prix par hausse de la demande. Par exemple, des taux très bas incitent les agents à acheter des actifs risqués, plus rémunérateurs. Un cas classique est celui des trappes à liquidité, où les taux sans risque restent à 0 durant assez longtemps. Les agents économiques ont alors tendance à aller chercher le rendement là où il est : dans les actifs risqués. Cette hausse de la demande d'actifs fait alors grimper leurs prix. Un bon exemple est celui de l'évolution des bourses mondiales suite à la crise de 2008, quand les banques centrales ont commencé à avoir une politique monétaire agressive. Même chose pour les divers épisodes d'assouplissement quantitatif de cette même époque.

Les prix des obligations varient en sens inverse des taux : une baisse des taux rend les obligations moins rentables, vu que les intérêts versés diminuent avec le taux, et inversement pour une hausse des taux. Cela a une influence sur les taux des actions et de l'immobilier. Si le taux d'intérêt sur les obligations baisse, les épargnants déplacent leur argent vers des actions ou des actifs immobiliers, dont le prix monte. Le cas de l'immobilier est encore différent, vu qu'une baisse des taux se répercute sur les taux des crédits immobiliers. Dans ces conditions, le marché immobilier devient plus dynamique, la demande de logements augmente : les prix font naturellement de même. Reste à expliquer tout cela de manière plus formelle.

Pour la suite, nous noterons le rendement des placements monétaires, le taux sans risque, $i$. Le prix des actifs peut être vu comme la somme des revenus ultérieurs générés par l'investissement, pondérés par le taux des placements monétaires. Imaginons que l'investisseur reçoive un dividende ou un coupon d’obligation régulier, fixe chaque année (ce qui correspond plus au cas d'un coupon, mais on peut généraliser au cas d'un dividende en omettant ses variations annuelles). Ce coupon/dividende sera noté $c$ dans ce qui suit.

L'impact des taux d'intérêt sur le prix des obligations

Pour simplifier, nous allons supposer que le taux sans risque est constant et ne varie jamais. Cette hypothèse est complètement fausse, la banque centrale le faisant varier au besoin, mais elle permet de comprendre comment une modification du taux agit sur le prix des actifs. Nous relâcherons cette hypothèse dans la suite de la section. Nous allons aussi supposer qu'il en est de même pour le dividende/coupon, afin de simplifier l'analyse. On peut alors se demander combien il faudrait placer dans un placement monétaire pour obtenir le même coupon chaque année.

• Pour la première année, l'investisseur aurait dû placer $c \over 1+i$ pour obtenir la même somme en intérêts.
• Pour la deuxième année, il aurait placer $c \over (1+i)^{2}$.
• Pour la troisième année, il aurait placer $c \over (1+i)^{3}$.
• Et ainsi de suite.

Les sommes précédentes sont ce qu'on appelle la valeur actualisée du coupon. Par actualisée, on veut dire qu'elle tient compte du passage du temps et de son effet sur la valeur de la monnaie. En effet, un euro aujourd'hui correspond à (1 + i) euros dans le futur, du moins si on le place sur un placement monétaire. Les valeurs actualisées du coupon permettent de comparer la valeur présent du coupon avec sa valeur future.

On peut raisonnablement supposer que la valeur actuelle d'un investissement en obligation est égale à la somme des valeurs actualisées des coupons. Pour calculer celle-ci, faisons l'addition des valeurs actualisées précédentes, sur une durée supposée infinie. On obtient alors le prix que l'investisseur est près à payer pour l'actif :

$P_{a}={\frac {c}{1+i}}+{\frac {c}{(1+i)^{2}}}+{\frac {c}{(1+i)^{3}}}+{\frac {c}{(1+i)^{4}}}+{\frac {c}{(1+i)^{5}}}+{\frac {c}{(1+i)^{6}}}+...$

Factorisons le coupon c :

$P_{a}=c\times \left[{\frac {1}{1+i}}+{\frac {1}{(1+i)^{2}}}+{\frac {1}{(1+i)^{3}}}+{\frac {1}{(1+i)^{4}}}+{\frac {1}{(1+i)^{5}}}+{\frac {1}{(1+i)^{6}}}+...\right]=c\times \sum _{t}{\frac {1}{(1+i)^{t}}}$

Les règles sur les suites géométriques nous disent que $\sum _{t}{\frac {1}{(1+i)^{t}}}={\frac {1}{i}}$, ce qui donne :

$P_{a}={\frac {c}{i}}$

L'impact des taux d'intérêt sur le prix des actions

Le modèle précédent marche bien pour les obligations, dont le coupon est généralement fixe (il existe quelques obligations à taux variable ou indexées sur l'inflation, mais nous les laissons de coté pour la clarté de l'exposé). Pour ce qui est des actions, on peut le complexifier pour tenir compte de la croissance des dividendes. En effet, les dividendes versés par une entreprises augmentent avec le temps. Non seulement les entreprises sont en croissance, ce qui fait augmenter le dividende avec le temps, mais de plus le dividende est une valeur nominale qui doit suivre l'inflation. Dans ce cas, le modèle est à peine plus compliqué : il suffit de remplacer le dividende $d$ par l'expression $d_{0}\times (1+g)^{t}$, avec t le nombre de période et $g$ le taux de croissance des dividendes. On obtient alors :

$P_{a}={\frac {d_{0}\times (1+g)}{1+i}}+{\frac {d_{0}\times (1+g)^{2}}{(1+i)^{2}}}+{\frac {d_{0}\times (1+g)^{3}}{(1+i)^{3}}}+{\frac {d_{0}\times (1+g)^{4}}{(1+i)^{4}}}+{\frac {d_{0}\times (1+g)^{5}}{(1+i)^{5}}}+{\frac {d_{0}\times (1+g)^{6}}{(1+i)^{6}}}+...$

On factorise $d_{0}$ :

$P_{a}=d_{0}\times \left[{\frac {1+g}{1+i}}+{\frac {(1+g)^{2}}{(1+i)^{2}}}+{\frac {(1+g)^{3}}{(1+i)^{3}}}+{\frac {(1+g)^{4}}{(1+i)^{4}}}+{\frac {(1+g)^{5}}{(1+i)^{5}}}+{\frac {(1+g)^{6}}{(1+i)^{6}}}+...\right]$

Le terme entre crochets peut se réecrire comme ceci :

$P_{a}=d_{0}\sum _{t}{\frac {(1+g)^{t}}{(1+i)^{t}}}$

En utilisant les formules sur les séries géométriques, le tout devient :

$P_{a}=d_{0}{\frac {1+g}{i-g}}$

Allons plus loin : le taux de croissance n'est pas connu à l'avance, mais est donc anticipé par les agents économiques. Et il en est de même pour les taux d'intérêts futurs. En fait, tous les termes de l'équation précédente sont anticipés par les agents économiques. En tenant compte du fait que $d=d_{0}\times (1+g)$ est le dividende de l'année prochaine, on peut reformuler l'équation comme suit.

$P_{a}=E\left[{\frac {d}{i-g}}\right]$

Dans la réalité, les taux et dividendes/coupons futurs ne sont pas constants et varient d'une année sur l'autre. L'équation précédente doit alors se reformuler comme suit.

$P_{a}=d_{0}\times \left[{\frac {1+E(g_{1})}{1+E(i_{1})}}+{\frac {1+E(g_{2})}{1+E(i_{2})}}+{\frac {1+E(g_{3})}{1+E(i_{3})}}+{\frac {1+E(g_{4})}{1+E(i_{4})}}+...\right]$

L'impact d'une variation des taux sur le prix des actifs

Les équations précédentes nous disent que le prix d'un actif dépend du dividende/coupon et du taux monétaire. Si la banque centrale diminue ses taux directeurs, $i$ va baisser et le prix des actifs va augmenter, compte tenu de l'équation précédente. On peut calculer la variation du prix des actifs $\Delta P$ induite par une variation $\Delta i$ des taux, à partir de l'équation précédente. On suppose simplement que le taux sans risque $i$ a été multiplié par $1+x$, pour simplifier les calculs. Les prix avant et après la modification des taux sont alors :

$P_{avant}={\frac {c}{i}}$ et $P_{apres}={\frac {c}{i(1+x)}}={\frac {P_{avant}}{1+x}}$

La variation $\Delta P$ vaut, par définition :

$\Delta P=P_{apres}-P_{avant}={\frac {P_{avant}}{1+x}}-P_{avant}=P_{avant}\left({\frac {1}{1+x}}-1\right)=-{\frac {x}{1+x}}P_{avant}$

On peut alors obtenir la variation en pourcentage du prix des actifs en divisant par le prix initial. Le résultat nous dit que le gain en capital, exprimé en pourcentage du prix initial est de :

${\frac {\Delta P}{P_{avant}}}=-{\frac {x}{1+x}}$

L'emprunt pour l'achat d'actifs

Une autre raison tient dans le fait que les agents empruntent pour acheter des actifs quand les taux sont bas, ce qu'ils rechignent à faire quand les taux sont élevés. Cette logique vaut aussi bien pour l'achat d'immobilier que pour l'achat d'actions ou d’obligations.

Emprunter pour acheter des actifs est rentable tant que les rendements de l'actif sont plus élevés que les intérêts du crédit. La rentabilité liée à la différence entre rendement et taux de crédit est ce qu'on appelle l'effet de levier. Par exemple, de nombreux investisseurs empruntent souvent de l'argent pour acheter de l'immobilier afin de le louer : le rendement des loyers vaut alors plus que la mensualité du crédit. Plus rare, les investisseurs peuvent emprunter sur plusieurs années pour acheter des actions, grâce à des comptes sur marge. Dans les deux cas, l'effet de levier augmente la demande d'actifs, ce qui pousse le prix des actifs à la hausse. Plus les taux d'emprunt sont faibles, plus l'effet de levier sera rentable : les investisseurs vont alors emprunter et acheter des actifs, faisant augmenter leurs prix. À l'inverse, des taux forts vont décourager l'emprunt et la demande d'actif va alors chuter.

L'impact sur le marché immobilier est un cas particulier, même si acheter une maison ou un appartement est un investissement comme un autre. La différence avec les autres actifs est que les biens immobiliers s’achètent presque toujours avec un emprunt, rarement au comptant. Après tout, il y a peu de raisons de contracter un emprunt, si ce n'est pour l'achat immobilier, les travaux et l'achat d'automobiles. Toute variation des taux a donc un effet direct sur l'emprunt immobilier et sur les achats/ventes. Une baisse des taux favorise l'emprunt immobilier, les gens achètent plus facilement maisons et appartements, construisent plus facilement des maisons, etc. La conséquence est une hausse directe des prix immobiliers. L'augmentation des prix immobiliers a diverses conséquences, dont nous allons parler maintenant. Cela cause une augmentation du marché des travaux ou de la construction, ce qui dynamise l'emploi dans ce secteur. Il faut employer des ouvriers pour construire des maisons ou faire des travaux, engager des agents immobiliers, etc. L'emploi redémarre, la production dans le secteur immobilier démarre, et cela entraîne des tensions inflationnistes.

L'influence des prix d'actifs sur la demande agrégée

Une hausse des prix d'actifs va pouvoir stimuler l'investissement ou la consommation par divers canaux distincts. En premier lieu, les agents détenteurs d'actifs se retrouvent avec des plus-values latentes. Ils sont donc plus riches, ce qui peut les pousser à consommer. En second lieu, une hausse des prix des actions peut pousser les entreprises à investir, ce qui stimule la demande agrégée (et donc, l'inflation). Enfin, une hausse des prix d'actif impacte les bilans comptables des agents économiques, ce qui modifie leur comportement.

	Effet sur la consommation	Effet sur l'investissement	Effet sur les bilans actif/passif
Canal de transmission	Effet de richesse	Ratio du Q de Tobin
		Accélérateur flexible
Effet sur la création monétaire	Réduction/augmentation de l'offre de crédit		Accès au crédit facilité/réduit

L'effet sur la consommation

Toute augmentation des prix d'actif, que ce soit des actions ou de l'immobilier, rend leurs détenteurs plus riches. Cette soudaine augmentation de fortune peut pousser les agents à dépenser celle-ci, que ce soit pour consommer ou investir. Cette dépense se traduit par une augmentation mesurée du PIB. Inversement, une hausse des taux fait baisser les prix d'actifs, diminuant la fortune des détenteurs d'actions ou d'immobilier, qui réduisent leurs dépenses. Comme on peut s'en douter, cet effet de richesse induit par la réallocation d'actifs au niveau macro-économique, a peu de chance d'avoir une influence vraiment significative. Aux États-Unis, et dans les pays où la retraite est par capitalisation, l'effet de richesse est assez important. En Europe, du fait de l'existence de systèmes de retraites par répartition, cet effet est cependant plus faible.

De plus, une part de la consommation est financée à crédit. Et les banques ont tendance à faciliter l'accès au crédit à ceux qui ont un bon patrimoine. Il est plus facile d'obtenir un crédit quand on dispose d'un patrimoine boursier/immobilier/... important que quand on n'en a pas. Cela peut paraître étrange, mais certains ménages préfèrent prendre un crédit que financer leurs dépenses en piochant dans leur patrimoine. La raison est que les taux des crédits est largement inférieur au rendement des actifs. Il est plus intéressant d’emprunter à 2% que de vendre des actions/obligations qui en rapportent 5% par an. Quand les prix d'actifs montent, leurs détenteurs sont plus riches et beaucoup plus de ménages deviennent fiables aux yeux des banques. La hausse des prix d'actifs, induite par la politique monétaire, facilite donc l'accès au crédit et in fine la consommation à crédit.

L'impact sur l'investissement

L'effet précédent (meilleur accès au crédit quand le patrimoine augmente) vaut aussi pour les entreprises. Plus le prix de leurs actions monte, plus les banques vont les considérer comme solides et plus elles accepteront de leur prêter. Le résultat est que les entreprises empruntent plus facilement, ce qui leur permet d'investir plus qu'avant. Pour résumer, la hausse des prix d'actifs stimule l'emprunt, et donc l'investissement, ce qui dope la production. L'effet d'une hausse des taux est l'exact inverse.

Un autre effet, spécifique aux actions, est nommé canal du Q de Tobin, implique une relation entre prix des actions et investissement agrégé. L'augmentation du prix des actions est en effet favorable à l'investissement, et donc à l'activité économique. Pour comprendre pourquoi, il faut faire appel à la théorie du Q de Tobin. Ce Q de Tobin est le rapport entre la valeur boursière de l'entreprise (le prix des actions multiplié par leur nombre) et la valeur de l'investissement moyen. Il est supposé que l'investissement permet de remplacer le capital existant, qui se déprécie avec le temps. Le ratio divise donc la valeur boursière de l'entreprise et le coût de remplacement du capital :

$Q={\frac {\mathrm {Valeur~boursi{\grave {e}}re~de~l'entreprise} }{\text{Coût du remplacement du capital}}}$.

Quand ce $Q>1$ l'entreprise a intérêt à investir. En effet, la valeur de l’investissement est alors supérieure à la capitalisation boursière, ce qui est un signal positif pour les investisseurs. La situation est inversé si $Q<1$ .

$\downarrow i\rightarrow \uparrow P_{a}\rightarrow \uparrow I\rightarrow \uparrow PIB\rightarrow \uparrow \pi$

L'impact sur les bilans des ménages, des entreprises et des banques

Un autre effet des prix d'actifs est une modification de l'incertitude économique et une plus grande confiance de la part des banques. Les banques sont soucieuses de bien utiliser leur argent et ne prêtent qu'aux agents sûrs, qui vont les rembourser. Généralement, elles prêtent à des agents assez riches, au patrimoine solide, ou à des entreprises solides et stables. Le proverbe le dit bien : "On ne prête qu’aux riches". Elles sont assez réticentes à prêter aux ménages mal lotis financièrement ou avec un faible patrimoine. La raison à cela est une certaine asymétrie d'information, les banques ayant des difficultés à évaluer la soutenabilité de certains ménages ou entreprises.

Le canal des taux de change

Les taux d'intérêts ont un effet sur les taux de change et cela entraîne une dépréciation ou une appréciation de la monnaie. Pour rappel, l'appréciation de la monnaie nationale est égale, par définition, à ${\frac {\Delta e}{e}}$. Elle indique si le taux de change a augmenté ou diminué de 5%, de 2%, de 15%, etc. Il se trouve qu'il existe diverses relations entre appréciation et taux d'intérêt, ainsi que des relations entre taux de change et PIB/inflation.

Pour commencer ce chapitre, il nous faut expliquer comment la politique monétaire peut avoir le moindre effet sur les taux de change. C’est seulement ensuite que nous verrons quel est l'effet d'une dépréciation/appréciation sur l'économie.

L'effet des taux d'intérêt sur le taux de change

L'effet des taux d'intérêt sur les taux de change varie beaucoup suivant le système monétaire. Il n'est pas le même selon que la banque centrale contrôle la quantité de monnaie ou les taux d'intérêt. De même, il dépend de la manière dont les capitaux circulent d'un pays à l'autre : sans restrictions, avec des restrictions, etc. Nous allons devoir expliquer ce qui se passe quand la banque centrale contrôle les taux, et dériver des relations entre taux d'intérêt et taux de change. Pour commencer, nous allons voir l'influence des taux d'intérêt sur les flux de capitaux.

La relation entre taux d'intérêt, flux de capitaux et taux de change

Les investisseurs investissent en obligations à l'international. Ils achètent des obligations étrangères, en vendent, et font pareil avec les obligations domestiques. Les investisseurs auront tendance à investir dans les pays où les taux sont les plus élevés, mais seulement dans une certaine mesure. N'oublions pas que des taux élevés signifient que l'investissement est risqué, ce qui peut refroidir les investisseurs prudents. Pour simplifier, nous allons omettre ce genre de détails et considérer que les obligations étrangères et nationales sont équivalentes, que ce sont de parfaits substituts (à part pour les taux). En conséquence, les investisseurs investiront là où les taux sont les plus forts. Dit autrement, les flux de capitaux vont donc aller vers les pays avec des taux élevés. On peut aussi dire que plus les taux nationaux sont élevés, moins les investisseurs ont envie d'aller voir ailleurs et plus les flux sortants sont faibles. Si les taux sont assez élevés, le flux peut même être un flux entrant : les investisseurs souhaitent investir dans le pays. Il est possible de modéliser le tout en disant que ce flux net sortant de capitaux est une fonction décroissante du taux réel.

$F_{C}(i)=C_{s}(i)-C_{e}(i)$

Quand un investisseur domestique achète une obligation étrangère, il doit trouver les devises nécessaires pour acheter l'obligation. Il en est de même pour une vente : il récupère des devises qu'il doit convertir en monnaie nationale. Tout cela fait qu'un grand nombre de transactions de change servent à acheter/vendre des obligations à l'international. Les flux de capitaux entrant/sortant d'un pays influencent donc fortement l'équilibre entre offre et demande sur le marché des change. Toute variation des flux de capitaux entraine une modification de l'équilibre sur le marché des change et le taux de change s'adapte pour rétablir l'équilibre. Il y a donc une relation entre flux de capitaux et taux de change. En combinant les deux paragraphes, on en déduit qu'il y a une relation indirecte entre taux d'intérêt et de change, qui passe par l'intermédiaire des flux de capitaux. Les variations des taux d'intérêt, en faisant varier les flux de capitaux, vont apprécier déprécier le taux de change. La relation est décroissante : une augmentation des taux entraîne une appréciation de la monnaie, alors qu'une baisse des taux dévalue la monnaie.

Illustration des relations entre taux d'intérêt réel et taux de change réel.

La théorie de la parité des taux d'intérêts

Parité des taux d'intérêt non-couverte.

On vient de voir qu'une différence entre taux domestique et taux étrangers entraîne une appréciation/dépréciation de la monnaie. Et cette appréciation/dépréciation va retentir sur le rendement des actifs : quand le taux de change varie, la valeur des actifs étrangers fait de même. Si la monnaie se dévalue, les rendements vont diminuer avec la dépréciation de la monnaie, ce qui aura tendance à refroidir les investisseurs (inversement pour une augmentation). Le processus décrit précédemment continue jusqu’à ce qu'il soit autant rentable d’investir chez soi qu'à l'étranger. À l'équilibre, les investissements nationaux et étrangers ont le même rendement. Les taux plus élevés sont compensés par la dépréciation de la monnaie. Quand cela arrive, on a une relation entre les taux de change et les taux d'intérêts.

La relation entre taux d'intérêts nominaux et appréciation des taux de change nominaux

Pour la démontrer, limitons nous à un cas à seulement deux pays. Partons d'un investisseur qui peut investir à domicile à un taux $i_{d}$ ou à l’étranger au taux $i_{e}$. La différence entre les taux entre deux pays est nommée différentiel de taux. Pour investir à l'étranger, il va devoir changer son argent en monnaie étrangère, au taux de change nominal $e$. L'investisseur souhaite retirer son argent quelques temps plus tard, quelques années. L'investisseur anticipe que, lors de ce retrait, le taux de change sera de $e^{*}$. Si les deux investissements sont de rentabilité égale, on a :

$1+i_{d}=(1+i_{e}){\frac {e*}{e}}$

Par définition, on peut écrire : ${\frac {e*}{e}}=1+{\frac {\Delta e}{e}}$. En faisant le remplacement dans l'équation précédente, on a :

$1+i_{d}=(1+i_{e})(1+{\frac {\Delta e}{e}})$

Développons :

$1+i_{d}=1+i_{e}+{\frac {\Delta e}{e}}+i_{e}{\frac {\Delta e}{e}}$

Soustrayons 1 des deux côtés :

$i_{d}=i_{e}+{\frac {\Delta e}{e}}+i_{e}\cdot {\frac {\Delta e}{e}}$

Si les taux sont faibles, on peut négliger le terme $i_{e}\cdot {\frac {\Delta e}{e}}$, ce qui donne :

$i_{d}=i_{e}+{\frac {\Delta e}{e}}$

Que l'on peut aussi écrire :

$i_{d}-i_{e}={\frac {\Delta e}{e}}$, avec le différentiel de taux d'intérêt dans le terme de gauche, et l'appréciation du taux de change dans la seconde.

Cette équation nous dit que la différence entre les taux d'intérêt nominaux de deux pays est égal à l'appréciation du taux de change.

La relation entre taux d'intérêts réels et appréciation des taux de change réels

Il est possible de comparer l'équation précédente avec l'équation qui suit, qui relie la dépréciation nominale et la dépréciation réelle. Pour rappel, cette équation est la suivante :

${\frac {\Delta e}{e}}={\frac {\Delta q}{q}}+(\pi _{n}-\pi _{e})$

En combinant les deux équations précédentes, on trouve :

$i_{d}-i_{e}={\frac {\Delta q}{q}}+(\pi _{n}-\pi _{e})$

Soustrayons le différentiel d'inflation $(\pi _{n}-\pi _{e})$ :

$(i_{d}-i_{e})-(\pi _{n}-\pi _{e})={\frac {\Delta q}{q}}$

Réorganisons les termes :

$(i_{d}-\pi _{n})-(i_{e}-\pi _{e})={\frac {\Delta q}{q}}$

Les deux premiers termes entre parenthèses correspondent respectivement au taux d'intérêt réel national $r_{n}$ et étranger $r_{e}$ :

$r_{d}-r_{e}={\frac {\Delta q}{q}}$

En clair, la différence entre les taux d'intérêt réels de deux pays est égal à l'appréciation de leur taux de change réel.

Le triangle d'incompatibilité de Mundell

Triangle d'incompatibilité de Mundell.

Tout ce qui a été dit auparavant suppose une mobilité parfaite des capitaux, c'est à dire que les capitaux peuvent passer d'un pays à l'autre sans restrictions. Les investisseurs étrangers peuvent investir chez nous comme bon leur semble, et les investisseurs domestiques peuvent faire de même à l'étranger. Cela colle bien au monde réel, où la mondialisation et la libéralisation des services financiers sont des acquis de longue date. Mais si il n'y a pas de mobilité parfaite des capitaux, la relation entre taux de change et taux d'intérêt devient plus compliquée et peut même disparaitre. Une conséquence à cela ce que l'on appelle le triangle d’incompatibilité de Mundell. Il dit simplement qu'il est impossible de combiner à la fois un régime de change fixe, une politique monétaire souveraine et une mobilité parfaite des capitaux. Pour comprendre pourquoi, étudions les deux cas possibles : avec et sans mobilité parfaite des capitaux.

Si les capitaux sont parfaitement mobiles, alors les taux d'intérêt et de change s'influencent mutuellement. Si l'économie est en régime de change flottant, alors la politique monétaire peut faire ce qu'elle veut. Une modification des taux entrainera une variation des changes, mais ce n'est pas un problème avec des changes flottants. Inversement, ce n'est pas le cas en régime de change fixe. Un taux de change fixe implique $i_{d}-i_{e}={\frac {\Delta e}{e}}=0$. Les taux domestiques sont alors égaux aux taux étrangers et la banque centrale n'a pas le contrôle de sa politique monétaire. Elle doit copier les taux étrangers et doit faire varier ses taux domestiques au même rythme que les taux étrangers. La politique monétaire n'est alors pas souveraine, mais totalement dépendante de la politique monétaire du pays sur laquelle les taux de change sont fixés. On voit donc que la mobilité parfaite des capitaux implique soit une politique monétaire souveraine et un taux de change flottant, soit un taux de change fixe et une politique monétaire non-souveraine.

Relaxer la mobilité parfaite des capitaux réduit le lien entre taux de change et taux d'intérêt, ce qui fait que politique monétaire souveraine et taux de change fixe peuvent devenir compatibles, si le gouvernement contrôle suffisamment bien les entrées et sorties de capitaux.

Si on combine les résultats précédents, on voit que seules trois situations sont possibles. La première combine politique monétaire souveraine avec mobilité parfaite des capitaux, mais doit accepter des taux de change flottants. La seconde accepte une politique monétaire souveraine et des change fixes, mais implique un contrôle des capitaux entrants/sortants. Enfin, la troisième possibilité demande des changes fixes avec une mobilité parfaite des capitaux, mais doit accepter une politique monétaire totalement dépendante de l'étranger. Tout cela est une autre manière de reformuler le triangle d'incompatibilité de Mundell.

L'effet des taux de change sur l'économie

Après avoir vu l'effet des taux d'intérêt sur les taux de change, nous allons voir comment ces variations de taux de change influencent l'économie. Dans les grandes lignes, ils ont deux effets : ils influencent le cout des importations et la compétitivité des entreprises domestiques. Dans le premier cas, une variation des taux de change va faire varier le prix des importations. Dans le second cas, elle va améliorer la balance courante, la différence entre exportations et importations.

L'effet sur le niveau général des prix

En premier lieu, le taux de change influence le prix des importations, ce qui a un effet direct sur le niveau général des prix $P$. Une augmentation des prix importés va, toute chose égale par ailleurs, faire monter la moyenne des prix. On peut détailler ce canal de transmission plus en détail, mais les développements en question n'ont rien à voir avec la courbe IS : ils sont à intégrer dans la courbe de Phillips. Aussi, nous les laissons à un chapitre ultérieur. Pour le moment, on peut se contenter de résumer ainsi ce canal de transmission :

$\uparrow e~\rightarrow ~\uparrow P_{imports}~\rightarrow ~\uparrow P~\rightarrow ~\uparrow \pi$

L'effet sur le patrimoine net

Il faut noter que les taux de change influencent les prix des actifs étrangers. Par exemple, un ménage français au patrimoine diversifié est censé détenir beaucoup d'actions étrangères, dont la valeur est exprimée en dollars, ou dans d'autres devises. La valeur en euros de celles-ci variera avec les taux de change. Une dévaluation entraine une hausse du prix des actifs étrangers, une appréciation a l'effet inverse. D'ordinaire, ces variations ne sont pas importantes pour l'agent qui investit à long-terme, car les variations de taux de change finissent par se lisser, les creux compensant les baisses. Il lui est alors bien plus profitable d'investir à l'étranger pour diversifier que de limiter son risque de change, inexistant à long-terme. Mais cela peut moduler l'efficacité du canal des prix d'actif à plus court-terme. Si jamais une devise s'effondre ou s'apprécie, le ménage aura un patrimoine temporairement plus faible ou plus élevé.

La seule exception tient dans un actif particulier : les devises étrangères. Les taux de change ont aussi un effet sur les détenteurs de devises, qui vont voir la valeur de celles-ci augmenter ou diminuer avec les taux de change. Dans ce cas, les devises sont considérées comme des actifs, au même titre que les actions ou l'immobilier. Les taux de change en font alors varier le prix, ce qui fait apparaitre un effet de richesse, ainsi qu'un effet de bilan, comme ceux vus dans le chapitre précédent. Pour l'effet de richesse, les détenteurs de devises, devenus plus riches, vont consommer plus, ce qui stimule la croissance. Pour l'effet de bilan, les détenteurs de devises vont voir leur patrimoine monter (ou descendre), ce qui les rend plus sûr (moins sûr) au niveau des banques. Ils pourront alors plus facilement (plus difficilement) emprunter, ce qui stimule (réduit) la croissance et l'investissement. Dans ce cas, l'effet est alors totalement inverse des autres canaux précédents. Une dévaluation de la monnaie va réduire le patrimoine net des agents détenteurs de devises, réduisant le PIB.

De plus, toutes les valeurs nominales étrangères vont subir une hausse en cas de dévaluation et une baisse en cas d'appréciation. Cet effet se manifeste aussi pour les dettes libellées en devises étrangères. Si une entreprise domestique a emprunté auprès d'une banque étrangère, les variations de taux de change font varier la valeur des dettes : la dette augmente en cas de dévaluation et diminue pour une appréciation. Les entreprises qui ont contracté beaucoup de dettes à l'étranger vont ainsi souffrir en cas de dévaluation. Cela pose de nombreux problèmes dans les pays en voie de développement, pour lesquels les systèmes bancaires sont assez frustres. Les besoins d'emprunt de ces pays ne peuvent être assouvis par leurs banques et leurs entreprises doivent emprunter à l'étranger, les soumettant aux variations de taux de change. Dans ces pays, cet effet va supplanter tous les autres, rendant les dévaluations contractionnistes ! Chose qui l'inverse de l'effet recherché.

Le cas le plus dramatique est illustré par l'exemple des crises bancaires au Mexique, en Indonésie ou dans quelques autres pays. Dans ces pays, les banques étaient endettées auprès de pays étrangers (leurs banques pour être précis). Lorsque ces pays ont dû faire face à une dévaluation, les banques ont vu leur dette fortement augmenter du jour au lendemain. Les dettes étant à très court-terme, à rembourser en quelques jours ou semaines/mois, les banques se sont alors trouvées rapidement face à de forts risques de liquidité. Couplé aux difficultés des emprunteurs domestiques à rembourser, cet effet a rapidement mené à des paniques bancaires. Les banques se sont vues contraintes de couper les crédits et autres services bancaires du genre. La baisse des crédits a alors impacté directement le PIB, le réduisant assez fortement. On a donc des exemples où la dévaluation, par son effet sur les banques et dettes étrangères, a entrainé une baisse du PIB.

L'effet direct sur le PIB (la courbe IS)

Dans ce qui va suivre, nous allons faire intervenir un composant du PIB : les exportations nettes. Les exportations nettes, que nous noterons $NX(e)$, correspondent à la différence entre exportations et importations : $E-I$, libellés dans la monnaie domestique. Rappelons qu'il existe une relation qui nous dit que le flux de capitaux sortants est égal aux exportations nettes. Si on fait le bilan des échanges sur le marché des changes, on peut remarquer que les flux de capitaux et les exportations nettes se compensent : d'un côté le flux sortant est le flux de monnaie domestique à convertir en devises, de l'autre les exportations payées en devises doivent être converties en monnaie domestique. Dit autrement, les exportations nettes correspondent à l'offre de devises, alors que le flux sortant est la demande. À l'équilibre, les deux sont égaux du fait que le marché des changes n'est qu'un troc de monnaie.

$NX(e)=F_{C}(r)$

En remplaçant les exportations nettes par les flux de capitaux, on peut reformuler l'équation IS.

$Y=C+I(r)+G+F_{C}(r)$

On voit que les exportations nettes dépendent du taux de change réel, et que a relation est décroissante. Par décroissante, on veut dire qu'un taux de change faible favorise les exportations nettes, alors qu'un taux fort défavorise celles-ci. L'effet des exportations nettes est le même que celui de l'investissement. Dans les deux cas, une augmentation des taux réels diminue aussi bien l'investissement que les exportations nettes. La courbe IS est donc plus pentue en économie ouverte que dans une économie fermée. Pour résumer, voici comment ce canal fonctionne :

$\downarrow i~\rightarrow ~\uparrow F_{C}(r)~\rightarrow ~\downarrow e~\rightarrow ~\uparrow N_{x}(e),\uparrow PIB~\rightarrow ~\uparrow \pi$

Pour précision, cette explication, bien que classique, oublie un point important : le flux de capitaux net entrant est de l'épargne étrangère qui vient être investie dans le pays domestique. Un raisonnement sur la base d'identités comptables nous avait permis d'obtenir la formule suivante, dans le chapitre sur le canal des taux d'intérêt.

Investissement (I) + Déficit publique (G-T) = Épargne domestique privée (S) + Épargne étrangère (Importations - Exportations)

On voit, avec cette formule, que les importations nettes sont une compensation pour de l'investissement étranger. On peut reformuler l'équation précédente en utilisant le flux de capitaux sortants, ce qui donne :

Investissement (I) + Déficit publique (G-T) = Épargne domestique privée (S) + Épargne domestique publique (T - G) - Flux de capitaux sortants (Exportations - Importations )

En tenant compte cette formule, on voit que les politiques de change n'ont pas d'effet : l'augmentation des exportations nettes augmente le PIB d'un côté, mais réduit d'autant l'investissement de l'autre. L'effet sur l'économie est presque neutre : on a juste remplacé de l'investissement par des exportations. Pour conclure, les politiques de dévaluations/réévaluations n'ont pas d'effet par elles-mêmes.

L'effet sur la balance courante

Les exportations sont exprimées en monnaie nationale, là où les importations sont payées en monnaie étrangères. Le taux de change ne peut pas toucher la valeur des exportations en monnaie nationale (même si leur prix étranger diminue), mais il influence le prix des importations. Une baisse du taux de change va renchérir les importations, ce qui détourne les clients de celles-ci. Les agents vont alors acheter de préférence des produits domestiques et réduire leurs achats d'importations. Les exportations nettes sont donc définies par l'équation suivante, avec e le taux de change :

$N_{x}(e)=E-e\cdot I$

L'effet-volume et l'effet-prix

L'équation précédente nous permet de savoir quel est l'effet d'une variation des taux de change sur les exportations nettes. Pour faire simple, un changement des taux de change a deux effets distincts : un effet-volume et un effet-prix. Prenons l'exemple d'une dévaluation de la monnaie, à savoir une baisse des taux de change. À cause d'elle, le prix des produits domestiques se réduit à l'étranger, alors que le prix des importations augmente. En premier lieu, elle rend les exportations moins chères, ce qui fait que le pays exporte plus. Le volume des exportations augmente, c'est l'effet volume. Maintenant, supposons cependant que le volume exporté reste le même : la baisse des prix fait que les entreprises exportatrices vont moins gagner d'argent. C'est l'effet prix. Reste à savoir quel effet l'emporte : vaut-il mieux vendre plus, mais moins cher, ou moins mais plus cher ? Il n'y a pas de solution claire : tout dépend de la variation des volumes échangés et des prix, l'effet qui l'emporte changeant selon la situation.

Pour l'expliquer plus clairement, prenons quelques chiffres.

• Imaginez que les prix des exports $P_{e}$ diminuent de 2% et que les volumes exportés $V_{e}$ augmentent de 2% aussi. Dans ce cas, le produit $V_{e}\times P_{e}$ reste le même : les deux effets se compensent.
• Imaginez maintenant que les prix diminuent de 3%, mais que les volumes augmentent de seulement 1%. Dans ce cas, le produit $V_{e}\times P_{e}$ diminue (d'environ 2%, la différence entre les taux). L'effet prix l'emporte sur l'effet volume.
• Enfin, dernier cas, imaginez que les prix augmentent de 0%, mais que les volumes augmentent de 30%. L'effet volume l'emporte et l'argent gagné en exportations augmente.

La même chose a lieu pour les importations. Avec l'effet volume, la hausse des prix fait que les acheteurs vont réduire les quantités achetées. En théorie, les consommateurs devraient remplacer les produits importés par des produits domestiques, mais cela ne se produit pas toujours, et la substitution n'est souvent que partielle, voire nulle. Par contre, la hausse des prix signifie, à quantités vendues égales, que les acheteurs vont dépenser plus d'argent. Et les entreprises importatrices vont gagner plus d'argent. Reste encore une fois à savoir quel effet va l'emporter.

Un petit détail, cependant : les effets de volume et de prix n'ont pas lieu en même temps. L'effet prix est immédiat : les importations voient leur prix monter immédiatement après que les taux de change aient bougé. Par contre, l'effet-volume met un certain temps avant de se mettre en place.

La condition de Marshall-Lerner

On peut savoir quel effet l'emporte sur l'autre grâce à la condition de Marshall-Lerner. Celle-ci dit qu'une variation des taux de change n'a d'effet positif que sous des conditions bien précises. La condition exacte implique ce qu'on appelle les élasticité-prix des exportations et importations. Il s'agit de la variation en pourcentage des export/imports quand leur prix varie. Par exemple, supposons qu'une augmentation de 4% des prix induise une réduction de 2% des quantités importées. Alors l'élasticité-prix des importations est le rapport entre les deux pourcentages : - 10% / 4%. Dans ce cas, on peut remarquer que l'effet prix l'emporte : les volumes sont réduits de 2%, mais les prix gagnent 4% : l'argent dépensé dans les importations augmente.

À noter que la variation des prix est strictement égale, en pourcentage, à la variation des taux de change. On peut donc remplacer les prix par les taux de change dans la définition de ces élasticités. Celles-ci sont définies par :

$\epsilon _{E}={\frac {\frac {\partial E}{E}}{\frac {\partial e}{e}}}={\frac {\partial E}{\partial e}}{\frac {e}{E}}$, $\epsilon _{I}={\frac {\frac {\partial I}{I}}{\frac {\partial e}{e}}}={\frac {\partial I}{\partial e}}{\frac {e}{I}}$

Dérivons maintenant la condition de Marshall-Lerner. Pour cela, partons de l'équation précédente :

$N_{E}=E-e\cdot I$

Dérivons cette équation par e :

${\frac {\partial N_{x}(e)}{\partial e}}={\frac {\partial (E-e\cdot I)}{\partial e}}$

On applique la formule qui dit que la dérivée d'une somme est la somme des dérivées :

${\frac {\partial N_{x}(e)}{\partial e}}={\frac {\partial E}{\partial e}}-{\frac {\partial (e\cdot I)}{\partial e}}$

On applique la formule de la dérivée d'un produit :

${\frac {\partial N_{x}(e)}{\partial e}}={\frac {\partial E}{\partial e}}-e\cdot {\frac {\partial I}{\partial e}}-{\frac {\partial e}{\partial e}}\cdot I$

On simplifie :

${\frac {\partial N_{x}(e)}{\partial e}}={\frac {\partial E}{\partial e}}-e\cdot {\frac {\partial I}{\partial e}}-I$

Divisons par les importations :

${\frac {\partial N_{x}(e)}{\partial e}}{\frac {1}{I}}={\frac {1}{I}}{\frac {\partial E}{\partial e}}-{\frac {e}{I}}\cdot {\frac {\partial I}{\partial e}}-1$

À l'équilibre, on a $E=eI$. Injectons cette équation dans le premier terme du côté droit :

${\frac {\partial N_{x}(e)}{\partial e}}{\frac {1}{I}}={\frac {e}{E}}{\frac {\partial E}{\partial e}}-{\frac {e}{I}}\cdot {\frac {\partial I}{\partial e}}-1$

On reconnaît l'élasticité-prix des exportations et importations :

${\frac {\partial N_{x}(e)}{\partial e}}{\frac {1}{I}}=\epsilon _{E}-\epsilon _{I}-1$

C'est la condition de Marshal-Lerner. Celle-ci dit que pour que la dévaluation d'une monnaie ait un impact positif, il faut que le terme de gauche soit positif. Si cela arrive, alors l'effet sur les exportations l'emporte sur les importations. Cela impose alors :

$\epsilon _{E}-\epsilon _{I}>1$

Dit autrement, il faut que l'effet sur les exportations l'emporte sur l'effet sur les importations.

La courbe de Phillips

Ce chapitre va s'attarder sur l'origine de l'inflation, et notamment sur l'inflation par la demande et l'inflation anticipée. La première forme d'inflation est celle déterminée par la demande agrégée. Pour simplifier, on peut dire que cette forme d'inflation dépend essentiellement du PIB. Celui-ci dépend de beaucoup de choses, et notamment de la politique fiscale, du revenu, de la répartition des richesses, du taux de chômage, et de bien d'autres paramètres. Il nous reste à préciser quelle est cette relation entre PIB et inflation, relation aussi appelée improprement courbe de Phillips.

La courbe de Phillips originelle

Courbe de Phillips des années 1960.

La courbe de Phillips originelle est une relation entre le taux de chômage et la croissance des salaires nominaux, découverte par Phillips en 1952. Celle-ci montrait que plus le taux de chômage est bas, plus les salaires croissent. La relation exacte était la suivante, avec $W$ les salaires, $U$ le taux de chômage, a, b et c des coefficients constants.

${\frac {\Delta W}{W}}=-a\cdot U^{b}+c$

Aujourd'hui, les économistes reconnaissent une influence du chômage sur les salaires, sans pour autant accepter la formule vue plus haut. La formule exacte doit être plus compliquée, avec beaucoup plus de paramètres, et il est sans doute vain de chercher une formulation mathématique exacte de la relation entre salaires et chômage. Dans les faits, on peut se contenter d'une relation qualitative du genre :

${\frac {\Delta W}{W}}=f(U)$

Quel est le rapport avec l'inflation, me direz-vous ? Et bien il faut savoir que la croissance des salaires est fortement liée à l'inflation. La première raison à cela est que les entreprises doivent compenser la hausse des salaires, qui est un coût pour elles. Elles répercutent donc la hausse des salaires sur leurs prix. Au niveau macroéconomique, une hausse de la moyenne globale des salaires entraîne donc une hausse de la moyenne des prix. Mais cela ne se traduit pas par une baisse de la production ou du PIB pour une raison simple : le PIB nominal augmente en proportion, vu qu'il est égal à la moyenne macroéconomique des salaires. La croissance des salaires entraîne une hausse des dépenses de même ampleur, qui compense l'impact sur la demande de la hausse des prix. Quoiqu'il en soit, la corrélation découverte par Phillips entre chômage et croissance des salaires s'extrapole en une relation entre taux de chômage et inflation. Un chômage bas entraîne une forte inflation, tandis qu'un chômage haut signifiera inflation basse. Cette relation entre inflation et chômage est appelée la courbe de Phillips.

L'interprétation keynésienne de la courbe de Phillips

Pour comprendre d'où vient cette relation inverse, il nous faut étudier les effets d'une baisse ou d'une hausse sur les négociations salariales. Une baisse du chômage a plusieurs effets. Premièrement, elle donne plus de poids aux employés pour négocier des augmentations de salaires. Cette hausse des salaires permet aux salariés de dépenser plus, ce qui entraîne une hausse des prix et donc de l'inflation. De plus, la baisse du chômage signifie que plus de personnes touchent un revenu, les chômeurs touchant maintenant un salaire. Ces nouveaux salariés dépensent plus, ce qui entraîne une hausse des prix, et donc de l'inflation. En résumé, il existe une relation entre taux de chômage et inflation : plus le chômage baisse, plus l'inflation sera forte.

Pour commencer, faisons le bilan entre l'argent que gagne une entreprise et les salaires qu'elle verse. Une entreprise doit verser un salaire moyen $W$ à $N$ employés. Elle dépense donc la somme suivante en salaire total. De l'autre côté, elle vend $Y$ produits à un prix moyen de $P$ : elle gagne donc $P\cdot Y$ en chiffre d'affaire. Au niveau d'une entreprise seule, le chiffre d'affaire sert à couvrir les salaires, le profit des actionnaires et à payer les inputs (les matières premières et/ou les produits qui sont assemblés pour donner le produit final). Mais au niveau de l'économie au global, les inputs sont produites par d'autres entreprises qui versent des salaires ou des profits. Au final, le chiffre d'affaire $P\cdot Y$ représente une valeur ajoutée totale, qui est versée en salaires ou en profits.

Dans une situation de concurrence pure et parfaite, on peut démontrer que toute la valeur ajoutée est versée sous la forme de salaires. On a alors :

$P\cdot Y=W\cdot N$

Mais quand les entreprises ont un pouvoir de marché, qu'il s'agisse d'une situation de monopole, d'oligopole ou de simple concurrence imparfaite, les entreprises peuvent augmenter les prix/réduire les salaires. Les entreprises peuvent alors dégager un certain profit, exprimé sous la forme d'un pourcentage du salaire. En notant W le salaire, µ le taux de profit et P le prix, on a alors :

$P\cdot Y=(1+\mu )\cdot W\cdot N$

Pour simplifier les calculs, on va diviser des deux côtés par $N$ :

$P\cdot {\frac {Y}{N}}=(1+\mu )\cdot W$

Le terme ${\frac {Y}{N}}$ n'est autre que la productivité des employés, que l'on note y.

$P\cdot y=(1+\mu )\cdot W$

Supposons que le taux de profit µ soit constant et dérivons l'équation précédente.

$\Delta (P\cdot y)=(1+\mu )\Delta W$

Divisons par $P\cdot y=(1+\mu )W$ et simplifions :

${\frac {\Delta P}{P}}+{\frac {\Delta y}{y}}={\frac {\Delta W}{W}}$

Le terme de gauche est par définition la somme de l'inflation et de la croissance de la production (productivité), ce qui nous donne une relation entre inflation et croissance des salaires.

$\pi ={\frac {\Delta W}{W}}-{\frac {\Delta y}{y}}$, ce qui se traduit par : inflation = croissance des salaires - croissance de la productivité

Reprenons l'équation de Phillips ${\frac {\Delta W}{W}}=f(U)$ et injectons-la dans l'équation : $\pi ={\frac {\Delta W}{W}}-{\frac {\Delta y}{y}}$ :

$\pi =f(U)-{\frac {\Delta y}{y}}$

On trouve donc une relation décroissante entre inflation et chômage.

La reformulation avec le PIB

Courbe de Phillips, qui relie le PIB avec l'inflation.

Certains économistes reformulent l'équation précédente en remplaçant le taux de chômage par le PIB. Ce remplacement est rendu possible par une relation entre ces deux variables, qui porte le nom de loi d'Okun. Celle-ci dit que toute augmentation/diminution du PIB au-delà d'un certain seuil entraîne une baisse/hausse du chômage. Si les prix sont stables à l'équilibre, cela signifie que l'inflation est nulle au PIB potentiel, positive si $PIB>PIB_{potentiel}$ et négative si $PIB<PIB_{potentiel}$. En clair : l'inflation a le même signe que l'écart de production. On peut mettre cela en équation en supposant une relation approximativement linéaire, ce qui donne l'équation suivante :

$\pi =\pi _{0}-a\cdot (Y-{\overline {Y}})$, avec $Y-{\overline {Y}}$ est l'écart de production.

À tout cela, on peut aussi ajouter l'influence d'un éventuel choc d'offre, qui induit une inflation $S$.

$\pi =\pi _{0}-a\cdot (Y-{\overline {Y}})+S$

La courbe de Phillips augmentée des anticipations

Courbe de Phillips avec taux de chômage naturel.

La courbe de Phillips précédente indique qu'il existe un arbitrage entre chômage et inflation, que les gouvernements et banques centrales pourraient utiliser pour influencer l'économie. Mais une telle possibilité ne colle pas avec ce que l'on a vu dans les chapitres précédents, à savoir que l'économie finit fatalement par se stabiliser au PIB potentiel. Si la courbe de Phillips est vraie, rien ne peut empêcher la banque centrale de maintenir en permanence le PIB au-delà du PIB potentiel avec une politique monétaire adéquate, ou de stabiliser définitivement le taux de chômage en-dessous du taux de chômage naturel, chose incompatible avec les données empiriques. Cet argument a poussé divers auteurs monétaristes, comme Friedman (1968) et E. Phelps (1967), à théoriser l'absence d'un arbitrage inflation-chômage à long-terme. La seule conclusion possible est que l'arbitrage entre inflation et chômage est une relation de court-terme, qui disparaît avec le temps. À long-terme, la courbe d'offre de l'économie doit être verticale, l'offre ne dépendant plus des prix.

Pour cela, on doit postuler que diverses forces de rappel poussent le PIB à se stabiliser à son taux potentiel, au point d'annuler l'effet de la courbe de Phillips. La force de rappel qui ramène l'économie au PIB potentiel n'est autre que les anticipations d'inflation de la part des agents économiques. En effet, les anticipations d'inflation influencent l'inflation réelle : les anticipations sont performatives. Et il y a plusieurs raisons à cela, la première étant que les agents vont tenter de se prémunir contre l'inflation qu'ils anticipent.

• Premièrement, ils vont dépenser leur argent plus rapidement, pour éviter que le temps leur fasse perdre du pouvoir d'achat. En cas d'inflation anticipée, les agents économiques ont donc tendance à dépenser à l'instant présent pour se prémunir d'une hausse des prix futures, renforçant encore l'inflation (et inversement).
• En second lieu, les salariés et employés tendent à renégocier leurs salaires à la hausse, pour compenser la perte de pouvoir d'achat liée à l'inflation.
• Enfin, les taux nominaux sont fixes sur le court-terme, les banques (centrales et commerciales) mettant un peu de temps avant d'ajuster les taux nominaux. une hausse de l'inflation anticipée va réduire les taux réels anticipés. Or, le taux nominal est égal à la somme du taux réel et de l’inflation anticipée, de part l'équation de Fisher : $i=r+\pi _{e}$. En conséquence, une hausse de l'inflation anticipée à taux nominaux égaux va faire baisser le taux réel. Ce qui va, par le biais de la courbe IS, stimuler l'économie encore plus, et donc aggraver l'inflation.

Ces réactions se traduisent par encore plus d'inflation, mais vont avoir l'effet inverse sur la production et le chômage. Les anticipations vont elles-mêmes induire de l'inflation, elles sont performatives de par leurs effets sur les comportements des agents économiques. Si les gouvernements tentent d'utiliser la courbe de Phillips, ils vont créer de l'inflation supplémentaire et faire baisser le chômage temporairement. Mais les agents économiques ne sont pas stupides et vont anticiper une inflation supérieure à la précédente. Ils vont alors réagir pour se prémunir contre l'inflation et leurs réactions vont certes augmenter l'inflation, mais vont aussi réduire le PIB et augmenter le taux de chômage. Le chômage retourne donc à sa valeur d'équilibre, de même que le PIB, mais l'inflation a augmenté.

La prédiction du courant monétariste s'est réalisée dans les années 1970, la courbe de Phillips s'atténuant progressivement avant de totalement disparaître. En effet, la théorie précédente explique à merveille la disparition de la courbe de Phillips dans les années 1970. Avant les années 1970, l'inflation était proche de zéro et fluctuait aussi bien en-dessous qu'au-dessus de cette moyenne. Mais après les années 1970, l'inflation commença à devenir strictement positive et relativement sensible comparé à avant. Les agents commencèrent à anticiper de plus en plus finement l'inflation, devenue plus prédictible. D'où une disparition de la courbe de Phillips, annulée par les anticipations d'inflation. La réussite de cette prédiction propulsa sur le devant de la scène les théories monétaristes, seules à rendre compte de ce fait, avant que les théories keynésiennes fusionnent avec les théories monétaristes dans le cadre de la synthèse néoclassique. Depuis, tous les économistes font grand cas des anticipations dans leurs modèles économiques.

L'ajout des anticipations d'inflation dans la courbe de Phillips

On peut obtenir l'équation de la courbe de Phillips en additionnant l'inflation anticipée au modèle précédent. Cela donne l'équation suivante, dans laquelle :

$\pi =\pi _{e}+a(Y-{\overline {Y}})+S$

Il faut noter que toute modification d'un des trois termes de l'équation fait se déplacer la courbe de Phillips. Un choc d'offre négatif, qui augmente les coûts de production, va naturellement augmenter l'inflation, à PIB égal. Même chose pour une augmentation des anticipations d'inflation, à PIB égal. Cela se traduit donc par un déplacement vers la gauche de la courbe de Phillips. Une baisse des anticipations d'inflation ou un choc d'offre positif (baisse des coûts de production) a l'effet inverse : la courbe de Phillips se déplace vers la droite.

Déplacement de la courbe de Phillips suite à un choc d'offre, une augmentation des anticipations d'inflation, ou d'une augmentation de l'écart de production.

La courbe de Phillips accélérationniste

On a vu la y a quelques chapitres utilisent divers modèles pour expliquer comment les agents économiques forment des anticipations sur l'inflation future. On a abordé trois modèles cardinaux , qui portent le nom d'anticipations adaptative, par extrapolation et rationnelles. Chacun d'entre eux donne une courbe de Phillips particulière, dont le comportement est différent de celui des autres. Nous allons commencer par étudier ce qui se passe avec des anticipations par extrapolation, où l'inflation prédite est égale à l’inflation précédente. Il est plus réaliste, d'utiliser des anticipations adaptatives, où l'inflation anticipée est alors une moyenne pondérée des valeurs passées de l'inflation. Mais cela ne change pas grand chose : les résultats obtenus sont similaires à ceux obtenus avec des anticipations par extrapolation. La courbe de Phillips obtenu est identique, si ce n'est que le changement de l'inflation, sa mise à jour, est plus lente. L'inflation anticipée agit alors comme une force d'inertie qui tend à lisser l'évolution de l'inflation dans le temps. Quoiqu'il en soit, les anticipations par extrapolation sont définies comme suit :

$E[\pi _{t}]=\pi _{t-1}$

En faisant le remplacement, la courbe de Phillips devient celle-ci :

$\pi _{t}-\pi _{t-1}=a(Y_{t}-{\overline {Y}})$

Le terme de gauche n'est autre que la hausse de l'inflation sur la période étudiée. L'équation nous dit donc ce qui peut faire varier l'inflation de sa valeur passée, ce qui fait que cette version de la courbe de Phillips est appelée la courbe de Phillips accélérationniste. Elle nous dit que tout écart de production entraîne un changement d'inflation. Par contre, un écart de production nul stabilise l'inflation à sa valeur actuelle. Cela a une conséquence assez importante : on ne peut pas effectuer de réduction de l'inflation sans faire passer le PIB en-dessous de sa valeur naturelle. Dit autrement, on ne peut pas faire baisser l'inflation sans passer par une période temporaire où le chômage est supérieur au chômage naturel.

Cette version de la courbe de Phillips permet à la politique monétaire d'avoir un effet réel sur le PIB, ce qui lui permet de le faire monter au-dessus de sa valeur potentielle, quitte à générer de l'inflation. Mais cela ne dure qu'un temps, avant que les anticipations fassent revenir le PIB à la normale. Imaginons que la banque centrale baisse ses taux, afin de réduire le PIB, quitte à générer de l'inflation. La baisse des taux réels par la banque centrale va naturellement stimuler la production et augmenter le PIB. Sur le court-terme, les anticipations d'inflation sont rigides, ce qui fait qu'elles restent assez faibles. L'inflation non-anticipée augmente, mais l'inflation anticipée reste relativement stable. Au total, la courbe de Phillips ne se déplace pas suite à l'action de la banque centrale. Mais avec le temps, les anticipations d'inflation vont augmenter progressivement, les agents anticipant l'inflation de plus en plus finement, faisant remonter l'inflation assez vite. Cela va toucher la courbe de Phillips, qui va se déplacer et devenir de plus en plus pentue. Au final, le déplacement de la courbe de Phillips va totalement annihiler l'action de la banque centrale. La courbe de Phillips va devenir verticale : le PIB potentiel sera atteint, et la banque centrale aura juste réussit à créer de l'inflation. Pour résumer, la politique monétaire a donc des effets sur les variables réelles (salaires réels, PIB, taux réels), mais seulement à court-terme, lors de la transition vers l'équilibre macroéconomique. On voit donc que la politique de ciblage de l'inflation, utilisée par les banques centrales, permet automatiquement d'amener l'économie au PIB potentiel.

La courbe de Phillips avec des anticipations rationnelles

Il est aussi possible d'utiliser une courbe de Phillips dans laquelle les anticipations sont rationnelles. On obtient alors la courbe de Phillips NK (new-keynesian) :

$\pi _{t}=E[\pi _{t}]+a(Y_{t}-{\overline {Y}})$

Par définition, les anticipations d'inflations sont égales à la somme de l'inflation future et d'une erreur d'anticipation : $E[\pi _{t}]=\pi _{t}+\epsilon _{t}$. En injectant cette formule dans l'équation précédente, on a :

$\pi _{t}=\pi _{t}+\epsilon _{t}+a(Y_{t}-{\overline {Y}})$

Ce qui donne :

$\epsilon _{t}=a(Y_{t}-{\overline {Y}})$

L'hypothèse des anticipations rationnelles nous dit que les erreurs d'anticipations sont supposées suivre une courbe de Gauss de moyenne nulle. On peut prendre la moyenne de cette expression sur une durée assez longue. On a donc :

${\overline {\epsilon }}=a{\overline {(Y-{\overline {Y}})}}=0$

En clair, l'économie peut dévier de son état d'équilibre, mais seulement si les agents font des erreurs de prédiction. Ces erreurs étant supposées non-systématiques (leur moyenne dans le temps est nulle), l'économie oscille aléatoirement autour de son état d'équilibre. Si les agents peuvent se tromper sur le court-terme, leurs anticipations donnent des résultats "parfaits" sur le long-terme vu que les erreurs se moyennent. Cela implique une inefficacité totale de la banque centrale à garder un PIB sous le PIB potentiel. Elle aura beau créer autant de monnaie qu'elle veut, les agents anticiperont de l'inflation et réagiront en conséquence. Ce qui va totalement annihiler l'effet de la politique monétaire sur le PIB, ne laissant que son effet sur l'inflation. L'efficacité de la politique monétaire sur le PIB n’apparaît que si la politique menée n'a pas été anticipée, ou alors pas totalement. Ce résultat est appelé la proposition d'inefficacité de la politique monétaire (Monetary Policy Ineffectiveness Proposition).

Outre ce résultat, cette version de la Courbe de Phillips possède quelques défauts. Le premier est qu'elle donne aussi quelques résultats contra-factuels assez importants. Le plus connu est celui identifié par Ball, dans son article de 1994. Il montra qu'avec cette courbe de Phillips, toute désinflation soutenue permet d'augmenter la production au-delà de sa valeur potentielle. Ce résultat est assez contre-intuitif, mais il se comprend assez facilement. Pour cela, il faut que la banque centrale décide de changer ses règles de politique monétaire et souhaite passer à une politique plus stricte. Cependant, elle doit prévenir à l'avance du changement, avant que celui-ci ait lieu. Dans ce cas, le résultat est une baisse de l'inflation suivie par une hausse de la production. Le résultat provient de la logique suivante : les entreprises s'attendent à une réduction de la masse monétaire dans le futur et vont adapter leurs prix en conséquence. Si les prix sont rigides, ils ne le sont pas totalement et une petite baisse des prix s'enclenche suite à l'annonce de la banque centrale, avant même que la politique stricte soit en place. Les consommateurs voyant la baisse des prix, ils en profitent pour augmenter leur consommation, ce qui stimule la production et le PIB. Le fait est que toute politique de désinflation continue pourrait alors maintenir le PIB au-delà de sa valeur potentielle de manière permanente. Chose qui ne respecte pas la fameuse critique de Mc Callum : il n'existe pas de politique monétaire permettant de maintenir le PIB au-delà de sa valeur potentielle.

Il va de soi que ce résultat n'a jamais été observé dans le monde réel. Toute annonce d'une restriction monétaire future se traduit immédiatement par une réduction de la production. Toutes les banques centrales qui ont tenté de réduire l'inflation ont dû le faire avec force fracas sur le PIB, souvent avec des conséquences assez dures. Reste à expliquer ce qui cloche dans le raisonnement qui a mené à la courbe de Phillips NK. Certains pensent que la courbe de Phillips n'est pas en cause, mais que c'est la crédibilité de la banque centrale qui est en jeu : si elle n'est pas crédible, les entreprises ne vont pas croire à la modification future de la politique monétaire, ce qui fait qu'elles ne réduisent pas leurs prix. Mais d'autre pensent que ce raisonnement n'est qu'un pansement sur une jambe de bois, et que la courbe de Phillips NK est juste invalide.

Passons maintenant au second défaut : les relations entre inflation passée et future. Avec la courbe de Phillips de type NK, l'inflation ne dépend alors que des anticipations de l'écart de production. Si on suppose que les agents économiques ont des anticipations rationnelles, on remarque que l'équation de Phillips new-keynesian peut se reformuler ainsi (on rappelle que toute valeur précédée d'un E est une valeur anticipée par les agents économiques) :

$\pi _{t}=\alpha \sum _{k}\beta ^{k}E(y_{t+k})$

Or, une large littérature économétrique montre que l’inflation actuelle est très sensible aux valeurs passées de l'inflation. Chose que cette équation ne permet pas de rendre compte. Ce défaut est suffisamment important pour que certains chercheurs aient tenté d'améliorer l'équation de Phillps new keynesian, afin d'en corriger ce défaut. Un moyen relativement simple pour cela est d'ajouter un terme basé sur des anticipations adaptatives, à savoir sur une moyenne des valeurs passées de l'inflation.

$\pi _{t}=\alpha y+\beta \pi ^{e}+\gamma \sum \limits _{i=0}^{t-1}(\omega \pi _{i})+S$

Une dérivation keynésienne de la courbe de Phillips augmentée des anticipations

La manière la plus simple de dériver la courbe de Phillips augmentée des anticipations se base sur un modèle simplifié du marché du travail : le modèle WS-PS. Cette théorie se base sur le fait que les entreprises et les salariés vont essayer de négocier le salaire à payer/recevoir. Les salaires sont établis par un système de négociation salariales, qui peut ou non faire appel aux syndicats ou corporations de salariés. Quoi qu’il en soit, les employés ou leurs instances représentatives peuvent ou non être en position de force par rapport à l'employeur. Si le chômage est très bas, ce rapport de force est en leur faveur. Les employés peuvent alors négocier un salaire plus élevé, que les entreprises doivent accepter sous peine de voir partir leurs salariés vers une entreprise mieux-disante. Mais si le chômage est important, les employés peuvent être remplacés plus facilement, ce qui incite ceux-ci à ne pas négocier leur salaire, ou du moins intensément.

Au niveau des entreprises, ce modèle part de la relation vue précédemment, qui lie salaires et prix : $P=(1+\mu )\cdot W$. Cette équation est appelée l'équation PS (Price Setting). Elle dit que le salaire réel négocié par l'entreprise est totalement indépendant du taux de chômage. On retrouve donc le résultat dérivé au chapitre précédent :

$\pi ={\frac {\Delta W}{W}}-{\frac {\Delta y}{y}}$

Reste à déterminer ce qui fixe le niveau des salaires. On peut raisonnablement supposer que les négociations portent sur les salaires réels, sur le pouvoir d'achat du salaire. Si on note W le salaire nominal et P le niveau général des prix, le salaire réel est égal à : ${\frac {W}{P}}$. Nous allons étudier quel est le salaire réel que les entreprises vont tenter de négocier, et celui que les ménages souhaitent obtenir. Fait important, les ménages tentent de négocier le salaire réel anticipé. Ils vont anticiper le niveau général des prix, et utiliser ces anticipations lors des négociations salariales. On peut remarquer qu'il y a asymétrie entre l'entreprise, qui décide de fixer ses prix, et les ménages qui doivent anticiper les futurs niveaux des prix. Dans tous les cas, les ménages négocient le salaire réel anticipé ${\frac {W}{P_{e}}}$, qui dépendra du taux de chômage. On obtient alors l'équation WS (Wage Setting).

${\frac {W}{P_{e}}}=F(U)$, souvent formulée comme suit : $W=P_{e}\cdot F(U)$

Dérivons l'équation précédente :

$\Delta W=\Delta P_{e}\cdot F(U)+P_{e}\cdot \Delta F(U)$

Divisons par $W=P_{e}\cdot F(U)$

${\frac {\Delta W}{W}}={\frac {\Delta P_{e}\cdot F(U}{P_{e}\cdot F(U)}}+{\frac {P_{e}\cdot \Delta F(U)}{P_{e}\cdot F(U)}}$

Simplifions :

${\frac {\Delta W}{W}}={\frac {\Delta P_{e}}{P_{e}}}+{\frac {\Delta F(U)}{F(U)}}$

Soustrayons ${\frac {\Delta y}{y}}$ dans les deux termes.

${\frac {\Delta W}{W}}-{\frac {\Delta y}{y}}={\frac {\Delta P_{e}}{P_{e}}}+{\frac {\Delta F(U)}{F(U)}}-{\frac {\Delta y}{y}}$

On identifie alors l'inflation (le terme de gauche) et l'inflation anticipée dans l'équation précédente.

$\pi =\pi _{e}+{\frac {\Delta F(U)}{F(U)}}-{\frac {\Delta y}{y}}$

En supposant que ${\frac {\Delta F(U)}{F(U)}}-{\frac {\Delta y}{y}}=a(U-U_{n})$, on retrouve alors une forme simplifiée de l'équation de la courbe de Phillips augmentée des anticipations.

$\pi =\pi _{e}+a(U-U_{n})$

La courbe de Phillips en économie ouverte

Les développements précédents sont valides pour une économie fermée, c'est à dire sans exportations, ni importations. Mais en économie ouverte, la courbe de Phillips doit être légèrement modifiée. En effet, les prix importés sont pris en compte dans la mesure de l'inflation et influencent directement la courbe de Phillips. En tenir compte fait que l'on peut étudier ce qu'il arrive quand les taux de change varient, par exemple. Dans cette section, nous allons étudier le canal des taux de change, et plus précisément le canal direct des taux de change. Pour rappel, celui-ci tient au fait qu'une variation des taux d'intérêts modifie le taux de change, ce qui se répercute sur les prix importés, et donc sur l'inflation. Il est à opposer au canal des taux indirect, que nous avions vu en détail dans le chapitre sur le canal des taux de change.

$\downarrow i\rightarrow ~\downarrow e\rightarrow ~\uparrow P_{importations}\rightarrow ~\uparrow \pi$

L'influence des prix importés sur le niveau général des prix

En économie ouverte, une partie des produits vendus provient de la production domestique, tandis que le reste est importé. Dans ce qui suit, on note Q la quantité totale de biens et services achetés dans un pays. Cette quantité n'est autre que la somme de la production nationale Y (autrement dit, le PIB), et des importations I.

$Q=Y+I$

Ensuite, on multiplie ces quantités par leurs prix respectifs. Dans ce qui suit, on note P le niveau général des prix, $P_{d}$ la moyenne des prix domestiques et $P_{i}$ la moyenne des prix importés. On a alors :

$P\cdot Q=P_{d}\cdot Y+P_{i}\cdot I$

Le niveau général des prix se calcule à partir de la formule précédente, en divisant par Q :

$P=P_{d}\cdot {\frac {Y}{Q}}+P_{i}\cdot {\frac {I}{Q}}$

Par définition, on a $I=Q-Y$, ce qui donne :

$P=P_{d}\cdot {\frac {Y}{Q}}+P_{i}\cdot {\frac {Q-Y}{Q}}$

On simplifie :

$P=P_{d}\cdot {\frac {Y}{Q}}+P_{i}\cdot \left(1-{\frac {Y}{Q}}\right)$

En posant $\beta ={\frac {Y}{Q}}$, on obtient :

$P=\beta \cdot P_{d}+(1-\beta )\cdot P_{i}$, avec $\beta$ un coefficient qui indique quelle est la part des prix domestiques dans le niveau général des prix.

Cette formule nous dit que le niveau général des prix dépend donc des prix des produits domestiques, mais aussi des prix importés. Elle dit aussi que l'impact sur les prix importés est d'autant plus important que les importations ont une part importante dans la consommation du pays. C'est le cas dans beaucoup de pays émergents ou en développement, qui se fournissent en biens dans les pays développés. Les importations y représentent une bonne partie de l'activité économique du pays et de la consommation de la population. La moindre variation des taux de change se répercute rapidement sur une majorité des biens de consommation, ce qui peut suffire à induire une récession. En conséquence, les banques centrales de ces pays fixent le taux de change de manière à garantir la stabilité des prix. Ce qui explique pourquoi beaucoup de pays africains disposent de caisses d'émission (des banques centrales qui maintiennent les taux de change fixes) et indexent leur monnaie sur une monnaie étrangère (le cas du franc CFA est de loin l'exemple le plus connu). Par contre, les pays développés (les grandes économies ouvertes) n'ont pas vraiment ce genre de problèmes. Les importations sont assez mineures dans leur économie, ou alors celles-ci proviennent d'un grand nombre de pays (et donc de devises) différents.

L'influence des prix importés sur l'inflation

Dans ce qui suit, on suppose que le coefficient $\beta$ est approximativement constant. Cette hypothèse est valide tant que la part des importations dans le PIB ne change pas trop. Si ce n'est pas le cas, les ménages remplacent des produits étrangers par des produits domestiques (ou inversement), ce qui fait que le coefficient change. Mais si ce phénomène de substitution est faible, l'hypothèse est crédible. Précisons que tout changement dans le coefficient $\beta$ a une influence sur la courbe IS, comme on le verra plus loin.

Dérivons l'équation précédente, en posant $\beta$ constant :

$\Delta P=\beta \cdot \Delta P_{d}+(1-\beta )\cdot \Delta P_{i}$

Divisons par P pour obtenir l'inflation dans le terme de gauche :

$\pi =\beta \cdot {\frac {\Delta P_{d}}{P}}+(1-\beta )\cdot {\frac {\Delta P_{i}}{P}}$

Les termes ${\frac {\Delta P_{d}}{P}}$ et ${\frac {\Delta P_{i}}{P}}$ sont respectivement l'inflation des produits domestiques et l'inflation des produits importés. On les note respectivement $\pi _{d}$ et $\pi _{i}$. On a alors :

$\pi =\beta \cdot \pi _{n}+(1-\beta )\pi _{imports}$

Le terme d'inflation domestique n'est autre que la courbe de Phillips donnée dans les sections précédentes. En faisant le remplacement, on trouve l'équation de la courbe de Phillips en économie ouverte :

$\pi =\beta \left[\pi _{e}+a(U-U_{n})\right]+(1-\beta )\pi _{imports}$

En collapsant les produits de constantes et en nommant ceux-ci $\alpha _{1}$, $\alpha _{2}$ et $\alpha _{3}$, on trouve l'équation générale :

$\pi =\alpha _{1}\cdot \pi _{e}+\alpha _{2}\cdot (U-U_{n})+\alpha _{3}\cdot \pi _{imports}$

Pour résumer, nous avons ajouté un terme d'inflation importée à la courbe de Phillips précédente.

Avec cette équation, on peut étudier la dynamique de l'inflation en fonction des prix importés. Si l'inflation importée augmente, alors l'inflation totale augmentera aussi. La banque centrale nationale va alors réagir pour la réduire, en augmentant ses taux d'intérêts. Ce faisant, le PIB national baisse, l'inflation des produits domestiques fait de même, et l'inflation totale est conservée à 2%. On voit que l'impact des prix importés se répercute sur le PIB national. Le truc est que la banque centrale n'a aucun impact sur l'inflation importée, et n'a pas beaucoup d'influence sur le coefficient $\beta$. Tout ce qu'elle peut faire est de réduire/stimuler le PIB, pour agir sur l'inflation des produits domestiques.

L'influence des taux de change sur les prix importés

Le prix des importations dépend directement des taux de change. Si les taux de change se déprécient, les prix des importations augmentent. Alors que si les taux s'apprécient, le prix des importations diminue. En clair : une variation des taux de change se traduit par une inflation approximativement inverse des produits importés. On pourrait croire que l'inflation importée est égale à l'opposé de la variation des taux de change. On aurait alors :

$\pi _{imports}\approx -{\frac {\Delta e}{e}}$, avec e le taux de change nominal.

En injectant cela dans la courbe de Phillips précédente, on trouve :

$\pi =\alpha _{1}\cdot \pi _{e}+\alpha _{2}\cdot (U-U_{n})-\alpha _{3}\cdot {\frac {\Delta e}{e}}$

Sur le principe, la courbe de Phillips précédente est juste. Mais l'effet des taux de change est modéré par un phénomène dit d'exchange rate pass-through, qui veut que la hausse des taux de change ne se répercute partiellement sur les prix importés. Par exemple, si le taux de change varie de 10 %, la variation des prix importés sera de moins de 10%. Les raisons à cela sont multiples, mais elles ne nous intéressent pas ici. Pour modéliser cela mathématiquement, on utilise simplement l'équation suivante, qui relie les variations des prix importés aux variations du taux de change :

$\pi _{imports}=\zeta \cdot {\frac {\Delta e}{e}}$, avec $P_{i}$ les prix importés, e le taux de change et $\zeta$ un coefficient dit de pass-through.

Mais la courbe de Phillips reste sensiblement identique avec ou sans pass-through, seuls les valeurs des coefficients changeant.

L'influence des taux d'intérêt sur la courbe de Phillips

Dans le chapitre sur le canal des taux de change, nous avons vu qu'il existe une relation entre les taux d'intérêt domestiques/étrangers et les taux de change. La relation relie le différentiel de taux d'intérêt domestique/étranger, avec l'appréciation du taux de change. La relation en question est la suivante :

$i_{d}-i_{e}={\frac {\Delta e}{e}}$, avec $i_{d}$ le taux d'intérêt domestique, $i_{e}$ le taux d'intérêt étranger et e le taux de change.

Si on combine cette relation avec la courbe de Phillips précédente, on trouve :

$\pi =\alpha _{1}\cdot \pi _{e}+\alpha _{2}\cdot (U-U_{n})-\alpha _{3}\cdot (i_{d}-i_{e})$

On développe le terme : $-\alpha _{3}\cdot (i_{d}-i_{e})$ :

$\pi =\alpha _{1}\cdot \pi _{e}+\alpha _{2}\cdot (U-U_{n})-\alpha _{3}\cdot i_{d}+\alpha _{3}\cdot i_{e}$

En clair, l'inflation dépend directement du taux d'intérêt, par le canal des taux de change, et indirectement par le biais de l'écart de production (la courbe IS). Le terme : $-\alpha _{3}\cdot i_{d}$ correspond au canal des taux de change direct.

Cette nouvelle courbe de Phillips ne paye pas de mine, mais elle a des implications assez importantes. Elle permet notamment de voir comment les politiques monétaires de différents pays interagissent. Elle permet de savoir ce qui se passe quand un pays étranger change ses taux directeurs. Pour cela, nous allons prendre l'équation précédente et regrouper tous les termes "domestiques", dépendants de variables nationales, dans une inflation domestique $\pi _{d}$ :

$\pi =\pi _{d}+\alpha _{3}\cdot i_{e}$

L'équation précédente nous dit que si un pays étranger augmente ses taux d'intérêt, alors notre pays voit son inflation augmenter (en raison des variations de taux de change associées). Et inversement : une baisse des taux étrangers entraîne naturellement une relance domestique de l'inflation. Un résultat intéressant surgit quand on pousse le résultat plus loin, en prenant en compte la réaction de la banque centrale domestique. Si des banques centrales étrangères baissent leurs taux, l'inflation nationale va baisser et la banque centrale domestique doit assouplir la politique monétaire pour relancer l'inflation nationale. Toutes les banques centrales, nationale et étrangères, baissent leurs taux de concert, l'une en réaction aux autres. Et inversement en cas de hausse des taux : la hausse des taux étrangers stimule l'inflation nationale, ce qui force la banque centrale nationale à monter ses taux. Les politiques monétaires nationales et étrangères sont donc corrélées et tendent à réagir dans le même sens. Évidemment, cette corrélation n'est pas parfaite, vu que les pays ont des systèmes fiscaux différents, des inflations différentes, etc.

Un résultat similaire est que les difficultés d'un pays tendent à se propager aux pays étrangers. Imaginons qu'un pays subisse une crise et que son inflation diminue fortement. La banque centrale étrangère va devoir baisser ses taux pour relancer son économie et son inflation. Au vu de l'équation précédente, l'inflation domestique va aussi chuter : la crise de demande s'est propagée dans notre pays, alors qu'elle provenait de l'étranger. En clair, la corrélation des politiques monétaires n'est qu'un revers de la médaille. L'autre revers est la corrélation des économies, au niveau de l'inflation. Si un pays entre en crise, dans le sens où son économie ralentit (chômage qui augmente et inflation en baisse), alors sa crise se propage aux pays étrangers.

Le contrôle de l'inflation par la banque centrale

Pour contrôler l'inflation, la banque centrale peut agir sur deux leviers : son taux directeur, ou la quantité de monnaie qu'elle émet. Ces deux instruments ne peuvent cependant pas être utilisés en même temps, toute variation des taux entraînant une variation de la quantité de monnaie, et réciproquement. Dans ce chapitre, nous allons étudier deux cas : celui où la banque centrale contrôle les taux d'intérêts et celui où elle contrôle la masse monétaire. Dans le premier cas, nous allons voir comment la banque centrale fixe ses taux d'intérêts, en réaction à l'inflation ou à l'écart de production. Ce n'est que dans la seconde section que nous verrons comment la banque centrale gère la masse monétaire. La raison à cela est que la majorité des banques centrales fixe les taux d'intérêts et non la masse monétaire. Le premier cas est donc plus fréquent dans la réalité, ce qui justifie de le voir en premier.

Le comportement de la banque centrale se modélise relativement bien par une fonction de réaction de la banque centrale, qui détermine comment la banque centrale fixe ses taux d'intérêts ou la masse monétaire en fonction de l'inflation mesurée/anticipée. Cette fonction de réaction est cependant une simplification mathématique qui ne capture pas les subtilités du fonctionnement des banques centrales. Les taux d'intérêts sont décidés par des comités internes aux banques centrales, ce qui rend la modélisation du comportement d'un tel groupe relativement compliquée. Rares sont les banques centrales qui suivent une véritable règle, qui dicterait leur conduite et leur comportement de manière fine. Dans les faits, les banques centrales suivent parfois des politiques discrétionnaires, qui dépendent fortement de la conjoncture économique. Cela arrive notamment dans les situations de crises bancaire ou suite à des récessions. Les fonctions de réaction qui vont suivre sont donc à voir comme des simplifications théoriques, aptes pour la modélisation, mais dont l'intérêt normatif est faible.

Le contrôle de la masse monétaire

Rares sont les banques centrales qui gèrent activement la masse monétaire. Les raisons à cela sont multiples, allant d'une sombre histoire d'instabilité de la demande de monnaie à des contraintes techniques. Une de ces raisons tient dans le fait que la banque centrale contrôle en fait la base monétaire et non la masse monétaire. Cela peut sembler un détail, vu que ces deux grandeurs sont reliées par un multiplicateur monétaire, mais ce dernier n'est pas constant et est soumis à des variations assez soutenues. En conséquence, contrôler la base monétaire ne signifie pas forcément contrôler la masse monétaire.

La règle de Friedmann de croissance de la masse monétaire

Quelques économistes ont tenté de définir ce que serait une politique monétaire optimale, capable de gérer au mieux la masse monétaire. Certains l'ont définie par une règle de fixation de la masse monétaire, équivalente à la règle de Taylor, mais pour la masse monétaire. Le premier à l'avoir fait fût Friedmann, qui donna son nom à la règle de Friedmann de croissance de la masse monétaire. Celle-ci est au demeurant particulièrement simple : elle consiste à faire croître la masse monétaire d'un pourcentage fixe chaque année, proche de 3%.

L'idée cachée derrière cette règle est simplement d'obtenir une politique contracyclique, qui réduit l'ampleur des récessions et des booms. Lors d'une récession, la masse monétaire s'effondre et une forte baisse de l'inflation s'ensuit. La contrer demande de créer de la monnaie bien plus rapidement que la production ne croit, ce qui induit une hausse de l'inflation. À l'inverse, la masse monétaire croit lors des booms, bien plus vite que la production. On peut alors les contrer en utilisant une politique contractionniste, réduisant donc l'inflation. La règle de Friedmman fait exactement ceci, en gardant le taux de croissance de la masse monétaire fixe.

L'abandon du contrôle monétaire

Dans les années 1970-1980, la banque centrale américaine a suivi les conseils des monétaristes et tenté de contrôler la masse monétaire entre 1979 et 1982. Mais cela a été un véritable échec, la banque centrale américaine ayant systématiquement raté leurs objectifs de masse monétaire. Le résultat de cette expérience est que contrôler la quantité de monnaie est clairement une mauvaise idée, contrôler les taux étant de loin plus simple et plus facile. De nos jours, peu de banques centrales contrôlent la quantité de monnaie, notamment dans les pays développés. La plupart des banques centrales ne mesure même plus la quantité de monnaie en circulation et beaucoup n'en tiennent pas compte dans leurs décisions. La macroéconomie actuelle, et notamment les théories du cycle réel ou la théorie néo-keynésienne, sont des théories "sans monnaie", qui ne prennent pas en compte la masse monétaire.

Les raisons à cela sont multiples. Premièrement, mesurer la quantité de monnaie dans l'économie est relativement complexe et donne des résultats assez ambigus : doit-on cibler l'agrégat M1, M2 ou M3 ? De plus, contrôler l'offre de monnaie n'est optimal que sous certaines conditions, comme nous le verrons plus tard dans le chapitre "Le choix de l'instrument de politique monétaire". Or, si ces conditions étaient respectées sous l'étalon-or, elle ne le sont plus depuis les années 70-80. Le contexte institutionnel a changé dans les années 1980, avec l'apparition d'innovations financières comme le distributeur automatique, qui ont rendu la vitesse de circulation de la monnaie plus imprévisible. Dans ces conditions, prédire la masse monétaire optimale est quasiment impossible.

Le contrôle des taux directeurs

La politique monétaire a une action indirecte sur l'inflation, qui passe par l'intermédiaire du PIB. Si la banque centrale a un objectif d'inflation de 2%, elle a juste à régler le taux d'intérêt pour que le PIB corresponde à une inflation de 2% sur la courbe de Phillips. La banque centrale ne fixe jamais son taux d'intérêt de manière permanente : elle l'adapte en fonction des effets de sa politique monétaire. Ainsi, si le PIB augmente trop, ou que l'inflation remonte dangereusement, elle remonte progressivement ses taux d'intérêts de manière à ralentir les effets de sa politique monétaire. Au fur et à mesure que l'inflation ou le PIB s'approchent de leur cible, la banque centrale remonte ou baisse ses taux d'intérêts progressivement. Quand la cible est atteinte, le taux d'intérêt se stabilise au taux d'intérêt naturel.

Le lien entre inflation et taux réels

La courbe IS, combinée avec la courbe de Phillips, nous permet de résumer cet argument. Partons de l'équation de la courbe de Phillips.

$\pi =\pi _{e}+a(Y-{\overline {Y}})$

L'équation de la courbe IS nous dit que $Y-{\overline {Y}}=-b(r-r_{n})$. Injectons celle-ci dans l'équation précédente :

$\pi =\pi _{e}+a\left[-b(r-r_{n})\right]$

Simplifions, en posant $a\cdot b=k$ :

$\pi =\pi _{e}-k(r-r_{n})$

Cette équation n'est autre qu'une relation entre taux réel et inflation. On voit que l'inflation varie en sens inverse du taux réel : elle monte quand le taux réel baisse et inversement.

On voit bien que l'inflation dépend négativement de la différence entre taux réel et taux naturel. Quand le taux réel est supérieur au taux naturel, l'inflation diminue. Inversement, un taux réel inférieur au taux naturel va naturellement stimuler l'inflation. On voit ainsi comment la banque centrale peut cibler l'inflation : il lui suffit de modifier les taux réels, histoire d'obtenir celui qui donne l'inflation voulue. Pour cela, toute variation de l'inflation doit être contrecarrée par une variation des taux nominaux qui est supérieure à la variation de l'inflation. La dernière partie est importante : c'est elle qui garantie que la banque centrale fait bien varier les taux réels. Pour nous en rendre compte, imaginons que la banque centrale modifie les taux nominaux au même rythme que l'inflation : les taux augmentent de 1% quand l'inflation fait de même, baissent de 4% quand l'inflation fait du -4% et ainsi de suite. Dans ce cas, la différence entre taux nominaux et inflation va rester la même : le taux réel ne changera pas. Modifier le taux réel demande donc de varier les taux nominaux plus que l'inflation ne varie : c'est ce qu'on appelle le principe de Taylor.

La règle de Taylor

À l'heure actuelle, les économistes utilisent une approximation pour rendre compte du comportement de la banque centrale : la règle de Taylor. Celle-ci stipule que le taux d'intérêt doit être bas si l'inflation et/ou le PIB sont en-dessous de leur cible, alors qu'il doit augmenter si ceux-ci sont au-dessus de la cible. Ce n'est que la traduction du fait que la politique doit être accommodante si l'inflation ou le PIB sont inférieurs à la cible voulue (restrictive dans le cas contraire). En clair, le taux d’intérêt de la banque centrale i est donné par la formule ci-dessous, avec :

• $\pi _{t}$ l'inflation mesurée au moment de la décision ;
• $\pi _{t}^{*}$ la cible d'inflation de la banque centrale ;
• $Y_{t}$ le PIB et $Y_{n}$ le PIB potentiel ;
• a et b deux coefficients entiers positifs.

$r=r_{n}+a\cdot (\pi _{t}-\pi _{t}^{*})+b\cdot (Y_{t}-Y_{n})$

On peut la simplifier en utilisant l'écart de production $y_{t}$.

$r=r_{n}+a\cdot (\pi _{t}-\pi _{t}^{*})+b\cdot y_{t}$

On voit que la règle de Taylor prend en compte l'écart de production. Il faut dire qu'un écart de production non-nul est synonyme de tensions inflationnistes ou déflationnistes. Celles-ci mettent un peu de temps avant de se manifester, compte tenu de la rigidité des prix, ce qui fait que la banque centrale doit anticiper leur arrivée. Se baser sur l’écart de production permet d'anticiper de futures variations de l'inflation. Compte tenu du temps avant que la politique monétaire fasse son effet, cette anticipation est une nécessité.

Un problème de cette formulation est que la banque centrale fixe non pas un taux réel, mais un taux nominal. Mais on peut passer de l'un à l'autre en utilisant la relation de Fisher $i=r+\pi$. L'inflation à prendre en compte est l'inflation actuelle, non pas l'inflation anticipée. En effet, rappelons que la banque centrale contrôle un taux court, non pas un taux long. Autant parler d'inflation anticipée a du sens pour calculer un taux réel de long-terme, il n'est a pas pour le court-terme. Pour résumer, il suffit d'ajouter l'inflation à l'équation précédente pour passer du taux réel au taux nominal. En faisant le remplacement, on trouve une équation qui donne le taux directeur de la banque central en fonction des autres variables :

$i_{t}=r_{n}+\pi _{t}+a\cdot (\pi _{t}-\pi _{t}^{*})+b\cdot y_{t}$

Pour simplifier, on peut retirer l’écart de production, ce qui permet de comprendre plus facilement comment la banque centrale réagit à une variation de l'inflation. On a alors :

$i_{t}=r_{n}+\pi _{t}+a\cdot (\pi _{t}-\pi _{t}^{*})$

Si on analyse l'équation précédente, on peut comprendre comment la banque centrale adapte son taux directeur avec l'inflation. On voit que si l'inflation augmente d'une unité, la banque centrale augmente son taux nominal de plus d'une unité ! Les variations du taux directeurs sont plus amples que les variations de l'inflation. C'est en raison du terme $a\cdot (\pi _{t}-\pi _{t}^{*})$, sans lequel on n'observerait pas ce comportement. Sans ce terme dans la règle de Taylor, la règle de Taylor deviendrait alors : $i_{t}=r_{n}+\pi _{t}$. En clair, la banque centrale modifierait son taux directeur en suivant la relation de Fisher. La banque centrale compenserait la hausse de l'inflation avec une hausse équivalente des taux nominaux, et inversement pour les baisses. Le taux réel serait alors constant et n'aurait alors aucun effet sur l'économie et l'inflation. La banque centrale ne pourrait pas agir sur le PIB via la courbe IS et la courbe de Phillips. Elle subirait l'inflation sans pouvoir agir dessus. On peut même prouver que l'inflation serait alors égale à sa valeur anticipée ! Et tout dépend de comment les anticipations se forment et de la valeur du taux réel naturel.

La fonction de réaction théorique

Déterminer à quoi pourrait ressembler une fonction de réaction d'une banque centrale n'est pas si compliqué, tant qu'on garde à l'esprit les objectifs qu'elle poursuit. Dans le cas général, celle-ci cherche à atteindre une cible d'inflation, et éventuellement une autre cible de PIB (le fameux PIB potentiel). Évidemment, elle n'y arrive pas toujours, des écarts avec les valeurs cibles étant possibles. Dans ces conditions, la banque centrale va tenter de s'approcher au plus près des valeurs cibles, en limitant ces écarts au maximum. On peut modéliser cela en langage mathématique en posant que la banque centrale souhaite diminuer la variance de l'inflation et du PIB par rapport aux cibles adéquates. Il faut noter que les banques centrales ne donnent pas forcément le même poids à la cible de PIB, souvent au second plan. La banque centrale cherche à tout instant à minimiser cette variance pondérée, qui se calcule avec une fonction appelée fonction de perte.

Le ciblage strict de l'inflation

Pour commencer, nous allons prendre le cas d'une banque centrale qui cible une certaine valeur d'inflation. Sa fonction de perte ne dépend que de la différence entre l'inflation et sa cible, de sa variance pour être précis. Ce qui donne :

$L={\frac {1}{2}}\left(\pi -\pi _{*}\right)^{2}$

Une politique monétaire optimale minimise la fonction de production, ce qui se traduit mathématiquement par la valeur qui annule la dérivée de la fonction précédente. Mathématiquement, nous devons donc avoir :

$L'=\pi -\pi _{*}=0$

On peut alors remplacer l'inflation par sa valeur dérivée de la courbe de Phillips.

$\pi _{e}+\alpha \cdot y-\pi _{*}=0$

Réarrangeons les termes. L'équation obtenue dit que plus l'inflation anticipée est grande comparée à la cible d'inflation, plus la banque centrale devra faire descendre le PIB de sa valeur potentiel.

$\alpha \cdot y=\pi _{e}-\pi _{*}$

Ensuite, remplaçons la valeur de l'écart de production par sa valeur dérivée de la courbe IS.

$\alpha \cdot \beta \cdot \left(r-r_{n}\right)=\pi _{e}-\pi _{*}$

Divisons par $\alpha \cdot \beta$.

$r-r_{n}={\frac {\pi _{e}-\pi _{*}}{\alpha \cdot \beta }}$

On pose $k={\frac {1}{\alpha \cdot \beta }}$.

$r-r_{n}=k\cdot (\pi _{e}-\pi _{*})$

Ajoutons $r_{n}$ à gauche et à droite.

$r=r_{n}+k\cdot (\pi _{e}-\pi _{*})$

On voit donc que la banque centrale réagit aux anticipations d'inflation des agents économiques. Dans le cas où ces anticipations sont rationnelles, l'inflation anticipée sera strictement égale à l'inflation future, ce qui fait que la banque centrale a un comportement idéal. Pour résumer, il s'agit donc d'une fonction de la forme suivante, avec $k$ un coefficient relativement constant qui dépend des paramètres de la courbe IS et de la courbe de Phillips.

$r=r_{n}+k(\pi -\pi _{t}^{*})$

On voit que la banque centrale utilise alors une forme simplifiée de la règle de Taylor, qui ne prend en compte que l'inflation et se moque de l'écart de production.

Le cas général

Maintenant, étudions le cas où la banque centrale ne fait pas que cibler l'inflation, mais souhaite aussi minimiser l'écart de production. Nous allons voir que ce cas donne une fonction de réaction identique à la précédente !

La fonction de perte est égale à :

$L={\frac {1}{2}}\left[(\pi -\pi _{*})^{2}+\omega \cdot y^{2}\right]$

Sa dérivée est donc la suivante.

$L'=\left(\pi -\pi _{*}\right)+\omega \cdot y=0$

On réarrange les termes.

$\omega \cdot y=\pi -\pi _{*}$

Remplaçons l'inflation par sa valeur dérivée de la courbe de Phillips.

$\omega \cdot y=\pi _{e}+\alpha \cdot y-\pi _{*}$

Factorisons l'écart de production.

$\left(\omega +\alpha \right)\cdot y=\pi _{e}-\pi _{*}$

Injectons l'équation de la courbe IS en lieu et place de l'écart de production.

$\left(\omega +\alpha \right)\cdot \beta \cdot \left(r-r_{n}\right)=\pi _{e}-\pi _{*}$

On divise par $\left(\omega +\alpha \right)\cdot \beta$.

$r-r_{n}={\frac {\pi _{e}-\pi _{*}}{\left(\omega +\alpha \right)\cdot \beta }}$

On pose $k={\frac {1}{\left(\omega +\alpha \right)\cdot \beta }}$.

$r-r_{n}=k\cdot \left(\pi _{e}-\pi _{*}\right)$

On ajoute $r_{n}$ des deux côtés.

$r=r_{n}+k\cdot \left(\pi _{e}-\pi _{*}\right)$

On retombe donc sur la fonction de réaction précédente, si ce n'est que le coefficient $k$ change quelque peu. On voit que la banque centrale ne prend en compte que l'inflation et se moque des mesures du chômage ou du PIB, alors que sa fonction de perte en tient compte ! Cibler l'inflation suffit donc parfaitement pour obtenir un résultat optimal au niveau de l'écart de production.

Le plancher des taux zéro

Dans les chapitres précédents, nous avons vu comment la banque centrale contrôlait l'inflation en usant de son taux directeur. Nous avons vu comment une variation des taux directeurs impacte les autres taux à long-terme, et comment leur variation se transmet à l'économie réelle par divers canaux de transmission. Cependant, nous sommes partis du principe que les canaux de transmission fonctionnent et que la banque centrale a effectivement la capacité à agir sur l'économie. Mais la réalité nous a montré par le passé que ce n'est pas toujours le cas. Il arrive que la politique monétaire basée sur un taux directeur perde de son efficacité.

Le cas qui nous intéresse ici est celui où la banque centrale ne peut pas modifier son taux directeur et est forcée par diverses frictions, à garder son taux directeur constant. Le cas le plus classique est celui où le taux nominal atteint zéro, sa borne minimale en-deça de laquelle il ne peut pas descendre. Le résultat est que la banque centrale ne peut plus fixer le taux réel à la valeur souhaitée. Ce cas est alors celui d'une limite des taux nominaux nuls, appelé Zero Lower Bound, que nous abrégerons en ZLB. La limite des taux zéro provient de l'existence des espèces, dont le taux nominal est zéro. Si la banque centrale attribue des taux nominaux négatifs, les placements monétaires (sans risques) seront rémunérés à un taux négatif. Les agents économiques, ne voulant pas perdre leur argent, vont convertir leur argent en espèces dont le taux nominal est nul.

Le phénomène de spirale déflationniste

Dans une économie soumise à la ZLB, l'économie a un comportement quelque peu compliqué, qui ne se décrit pas facilement. Lorsque la banque centrale atteint des taux nominaux nuls, elle n'a plus le moindre effet sur le taux réel. Pour rappel, le taux réel se calcule comme suit :

$r=i-\pi _{e}$

Il vient alors qu'avec des taux nominaux nuls, le taux réel est égal à :

$r=-\pi _{e}$

Le taux réel de la détention de monnaie est alors strictement égal à l'opposé de l'inflation.

Si l'inflation anticipée est positive, une somme d'argent détenue sous forme de monnaie perdra de son pouvoir d'achat avec le temps, à cause de l'augmentation des prix. On peut reformuler cette constatation en disant que le taux réel de la monnaie est négatif. Dans ces conditions, les agents économiques dépensent leur monnaie le plus vite possible, avant que l'inflation ne rogne sa valeur. L'effet sur l'économie sera donc relativement stimulant, se traduisant par une augmentation du PIB.

Par contre, les tensions déflationnistes auront l'effet inverse. Les ménages vont anticiper un taux réel positif, ce qui signifie qu'une somme d'argent donnée permettra d'acheter plus de biens à la fin de l'année qu'au début. Tout se passe comme si l'argent conservé sur les comptes courants était rémunérés à un taux réel égal au taux de déflation, soit l'inverse du taux d'inflation. Placer de l'argent sur un compte courant serait rémunérateur, peut-être plus que de placer ou l'investir. Dans ce cas, les agents économiques ne sont pas incités à dépenser leur argent. Cela incite les agents économiques à conserver leur monnaie et à l'épargner sous forme de monnaie, ce qui fait que la consommation et l'investissement diminuent. Il en découle une réduction de l'activité économique, et donc une baisse du PIB.

Et le phénomène peut s'emballer rapidement : si le PIB diminue, les anticipations d'inflation en font autant, et ainsi de suite. La déflation entraine une augmentation des taux réels, qui fait diminuer le PIB, ce qui entraine une baisse des salaires et de l'emploi, causant une nouvelle baisse de l'inflation. Cette nouvelle baisse de l'inflation se traduira par une nouvelle augmentation des taux réels, et ainsi de suite. En clair, la déflation s'entretient et s'auto-alimente ! D'où le nom de spirale déflationniste donné à cette situation.

Spirale déflationniste.

Une telle situation de déflation peut sembler intéressante intuitivement, la baisse des prix pouvant induire une hausse du pouvoir d'achat. En réalité, ce n'est pas le cas, vu que tous les prix sont touché, y compris les salaires ! La déflation entraine notamment une baisse de la demande (et donc des ventes) et des prix, qui réduiront les revenus des entreprises. Celles-ci vont donc naturellement baisser les salaires pour compenser. Les salaires baissent dans une mesure similaire à la baisse des prix, ce qui fait que les ménages ne voient pas de gain en pouvoir d'achat suit à la déflation. Pire : les ménages peuvent voir une baisse des salaires vu que le PIB, le revenu moyen de l'économie, diminue !

Le PIB lors d'une situation de déflation

Une autre manière de comprendre les situations de ZLB est de regarder ce qui se passe au niveau de la courbe IS seulement. L'important est de regarder comment la courbe IS interagit avec le PIB potentiel. Le PIB potentiel étant une constante, il est représenté par une droite verticale sur le diagramme i-Y. En-dehors d'une situation de ZLB, le PIB potentiel et la courbe IS s'intersectent. Cela signifie que la banque centrale peut, en configurant ses taux, amener l'économie au PIB potentiel. Il y a un équilibre entre la politique monétaire (le taux réel choisit par la banque centrale), et le marché des biens (la courbe IS). Mais dans une situation de ZLB, la situation est celle illustrée ci-dessous. On voit que la courbe IS et le PIB potentiel ne s’intersectent pas. La banque centrale ne peut pas amener l'économie au PIB potentiel, et doit en assumer les conséquences. Le PIB restant sous le PIB potentiel, la courbe de Phillips nous dit que l'inflation diminue. L'économie entre en déflation.

Courbe IS en trappe à liquidité.

L'effet Pigou : une limite aux spirales déflationnistes

Il faut noter que certains mécanismes pourraient limiter ou stopper la spirale déflationniste. Dans les années 50, Pigou a supposé l'existence d'un effet Pigou, pouvant faire cesser une déflation. Ce mécanisme se base sur le fait qu'une baisse des prix augmente la valeur des encaisses monétaires ou des placements financiers. Une somme épargnée S vaudra ainsi plus, en termes réels, après une baisse des prix. Cela augmente donc la richesse des ménages et entreprises, ce qui peut les pousser à consommer. L'augmentation de la dépense qui en découle peut alors limiter, si ce n'est contrecarrer, la spirale déflationniste.

Cet effet suppose cependant que la déflation n'a pas d'effets sur l'épargne. Les taux de rémunération de l'épargne ne peuvent notamment pas devenir négatifs, par exemple. De même, la dette sous forme d’obligation, ne doit pas subir de défauts. Or, dans les économies où les salaires baissent, de nombreux ménages et entreprises peuvent faire défaut sur leurs crédits, entrainant une perte de valeur des obligations ou des prêts. De nombreuses banques peuvent ainsi être menées à la banqueroute et des placements faire faillite, réduisant alors la richesse des ménages. De plus l'effet Pigou ne peut ne pas marcher si la déflation s'installe. Les ménages, oyant les prix baisser régulièrement, vont préférer retarder leurs achats. Pourquoi acheter maintenant alors que les prix seront encore plus bas dans quelques mois ? Ce report des achats se traduit naturellement par une baisse de la consommation, et donc de la demande agrégée. On voit que la spirale déflationniste s'auto-alimente du fait des anticipations, même en tenant compte de l'effet Pigou.

Comment sortir d'une situation de ZLB ?

Sortie d'une situation de ZLB est loin d'être facile. Mais la banque centrale et le gouvernement ont diverses solutions, certes assez inhabituelles, mais efficaces. Dans les grandes lignes, on peut classer ces solutions en plusieurs grands types, selon le mécanisme utilisé. Les premières tentent de faire baisser les taux réels malgré la limite des taux nominaux à zéro. Il existe deux grandes méthodes pour cela : soit imposer des taux nominaux négatifs, soit augmenter l'inflation anticipée. Le second type de solution se base sur une augmentation massive de la base monétaire, sur la création monétaire par la banque centrale. La banque centrale crée alors de grandes quantités d'argent, qu'elle fait circuler dans l'économie. Il s'agit des politiques d'assouplissement quantitatif et de monnaie-hélicoptère. Enfin, le gouvernement peut, en dernier recours, utiliser la politique fiscale pour soutenir la demande agrégée.

Dans les grandes lignes, ces solutions se comprennent assez bien en partant de l'équation de la courbe IS. Celle-ci est, rappelons-le :

$Y=Y_{0}-a\cdot (i_{directeur}+p_{r}-\pi _{e})$, avec $i_{directeur}$ le taux directeur, $p_{r}$ la prime de risque sur les marchés du crédit et $\pi _{e}$ l'inflation anticipée.

Si l'on veut que le PIB remonte, pour atteindre sa valeur potentielle, il faut jouer sur les paramètres de cette équation. Pour cela, le gouvernement peut :

• tenter de diminuer les taux nominaux courts encore plus qu'avant, ce qui revient à les faire passer en territoire négatif ;
• tenter de réduire la prime de risque des investissements, avec une politique d'assouplissement quantitatif ;
• tenter d'influencer l'inflation anticipée, en communiquant sur sa politique future ;
• augmenter le PIB de base $Y_{0}$, avec une politique fiscale adaptée.

Les trois premières politiques ont pour but de réduire le taux réel encore plus qu'avant, en essayent de passer outre la barrière des taux nominaux nuls. Vu qu'il s'agit de politiques de taux, elles sont mises en place par la banque centrale, et font partie de la politique monétaire. Par contre, la dernière est une politique purement fiscale, budgétaire, qui est de la responsabilité du gouvernement et non de la banque centrale. Nous allons détailler ces trois politiques rapidement ci-dessous. Si nous n'avons pas parlé des taux négatifs auparavant dans ce cours, nous avions déjà parlé des politiques d'assouplissement quantitatif ou de forward guidance dans un chapitre antérieur. Nous les avions abordé dans le chapitre sur le marché monétaire, dans la section "La manipulation des taux longs par la banque centrale" en fin de chapitre. Quant à la politique fiscale, nous l'avions effleurée dans le chapitre sur le canal des taux d'intérêt.

Les politiques de taux négatifs

La limite des taux nuls n'est pas absolue. En effet, l'argent sous forme de monnaie a des problèmes que les dépôts n'ont pas : il peut être volé plus facilement, il faut le stocker (dans des coffres ou des locaux sécurisés), ce qui pose quelques problèmes. Les agents économiques peuvent accepter un taux très légèrement négatifs, à condition que ce taux soit avantageux comparé aux couts subjectifs associés à la détention d'argent liquide. Utiliser de tels taux nominaux négatifs permet de réduire quelque peu les taux réels, ce qui a un effet stimulant sur l'économie.

Une implantation de cette politique consiste à imposer les taux négatifs sur le taux de rémunération des réserves. L'idée est de taxer les réserves excédentaires à un taux négatif, histoire que les banques se débarrassent de leurs réserves. Au lieu de les conserver sur un compte à la banque centrale, elles vont les préter et les mettre en circulation, ce qui booste l'offre de crédits et relance l'économie. Mais en-deça d'un taux négatif proche de 0.3 à 0.7%, tout agent économique retirera son argent, limitant l'effet de la politique monétaire. Cette politique est donc limitée dans son intensité. Les taux directeurs les plus bas aujourd'hui observés sont inférieurs au pourcent : -0,75%, pour la banque de Suède (à noter que cette banque n'impose pas de réserves obligatoires).

Les politiques de manipulation des anticipations d'inflation

Une autre solution demande d'utiliser au mieux le canal des anticipations, via diverses politiques. Le but de ces politiques est de maximiser les anticipations d'inflation, pour réduire le taux réel anticipé. Dit autrement, ces politiques visent à faire baisser le plateau de la courbe MP, histoire que la courbe IS se retrouve dans sa portion croissante. La première de ces politiques est connue sous le nom de forward guidance. Celle-ci consiste, comme on l'a vu il y a quelques chapitres, à dire au public que les taux resteront bas (nuls) durant très longtemps, bien après le retour de l'inflation. Ce faisant, les agents économiques anticiperont une inflation plus forte, une fois sorti de la ZLB. Mais l’efficacité de ces politiques est cependant relativement modeste.

Une autre solution, relativement similaire, est d'augmenter la cible d'inflation. Elle n'a encore jamais été tentée et il faut dire qu'elle n'est pas sans défauts. Une telle modification pourrait obérer la crédibilité de la banque centrale, réduisant de fait sa capacité à faire efficacement son travail.

L'assouplissement quantitatif

Les taux directeurs ne sont pas les seuls taux dans l'économie. La banque centrale peut tenter de faire baisser les taux longs ou moyen-terme, afin de profiter au maximum du canal des taux. Une politique d'assouplissement quantitatif est, dans cette optique, un recours possible.

L'utilisation de la politique fiscale

Une dernière solution est de recourir à la politique fiscale, en lançant une politique de relance. Cette politique déplacera la courbe IS, de manière à la replacer sur la portion croissante de la courbe MP. Cependant, une telle politique a tendance à augmenter la dette de l'état, ce qui fait qu'elle n'est pas "gratuite", sans coûts. Il faut donc voir une telle politique comme une solution de dernier recours. Et pour comprendre en quoi la politique fiscale a un impact sur les taux d'intérêt, il nous faut étudier plus en détail l'interaction entre les deux. Ce sera le propos du chapitre suivant.

Utilisation de la politique fiscale pour sortir d'une trappe à liquidité de type ZLB.

Le modèle IS/MP

Le modèle vu précédemment, basé sur trois équations, fonctionne très bien pour décrire l'économie, mais il est difficile à visualiser graphiquement. Pour cela, il est cependant possible de ruser et de simplifier le modèle pour qu'il tienne sur quelques graphiques assez simples. Représenter des modèles simples avec quelques graphes est quelque chose de courant dans les cours d'introduction à l'économie. Les courbes de demande et d'offre en sont un exemple assez connu. Pour représenter le modèle à trois équations, nous devons ruser. Pour cela, on peut étudier deux cas : un cas où on étudie l'économie à court-terme en enlevant la courbe de Phillips, ou en fusionnant deux équations en une seule. La première solution donne le modèle IS/MP, alors que la seconde donne le modèle AD/IA. Nous allons voir les deux dans ce qui suit.

Le modéle IS/MP

Le modèle IS/MP étudie l'économie sur le court-terme, alors que le modèle à trois équations marche sur le moyen et le long-terme. En effet, ce dernier suppose que les prix peuvent évoluer dans le temps, même si pas parfaitement. En clair, le modèle suppose que les prix ont une marge d'évolution, ce qui permet d'existence de la courbe de Phillips. Une flexibilité des prix totale traduit un horizon temporel de long-terme, où l'économie est au PIB potentiel, et où es taux sont déterminés par l'inflation et le taux réel. Il est intéressant de regarder ce que donne le modèle à court-terme, sur un horizon de temps suffisamment court pour que les prix n'aient pas eu le temps d'évoluer. Les prix sont alors considérés comme totalement rigides, ce qui permet de retirer la courbe de Phillips du modèle à trois équations. C'est l'idée du modèle IS-MP.

Présentation du modèle IS/MP

Le modèle IS/MP fait intervenir la courbe IS et la règle de Taylor. La règle de Taylor dit que les taux augmentent avec l'inflation et le PIB, ce qui fait que la relation entre taux directeurs et PIB est croissante. Dans ce qui suit, on va utiliser un graphique qui relie les taux et le PIB. La régle de Taylor est représentée par une courbe croissante, appelée la courbe MP, alors que la courbe IS est décroissante. Le point d'intersection entre les deux courbes donne à la fois le taux réel et le PIB de l'économie, sur le court-terme.

Modèle IS-MP

On peut dériver la courbe MP à partir de l'équation de Taylor vue dans le chapitre précédent, en ne gardant que le taux naturel et l'écart de production (ce qui revient à postuler l'hypothèse de rigidité totale des prix à court-terme). Il existe aussi une autre manière de dériver la courbe MP, plus générale. Nous avons vu dans le chapitre précédent que la banque centrale fixait ses taux à partir de l'équation suivante :

$r=r_{n}+f(\pi -\pi _{*})$

On omet l'influence de la cible d'inflation, pour simplifier les calculs :

$r=r_{n}+f(\pi )$

Remplaçons maintenant l'inflation par sa valeur déduite de l'équation de Phillips. Si on omet les anticipations d'inflation (supposées rigides), l'inflation ne dépend que de l'écart de production

$r=r_{n}+f(y)$

On se retrouve bien avec une relation croissante entre taux directeurs et écart de production, ce qui correspond à la courbe MP.

Les conséquences de la politique monétaire et budgétaire

Le modèle IS/MP est simple à comprendre, mais il permet d'expliquer le fonctionnement de l'économie sur le court-terme. Il permet notamment de voir comment la politique monétaire et la politique budgétaire peuvent influencer l'économie, notamment pour contrer récessions et booms économiques. Dans les grandes lignes, la politique monétaire va influencer la position de la courbe MP : une politique expansionniste la déplace vers la droite, alors qu'une politique restrictive la déplace vers la gauche. La politique budgétaire fait la même chose, mais pour la courbe IS : une politique expansionniste la déplace vers la droite, alors qu'une politique restrictive la déplace vers la gauche. Ce qui est intéressant, c'est de voir ce qui se passe quand on déplace une des deux courbes, ou les deux, ce qui traduit l'effet des politiques économiques sur l'économie.

Dans cette partie, nous allons étudier le modèle en économie fermée. Les conclusions obtenues seront identiques à celles valables pour l'économie ouverte, si l'on omet les exportations nettes : la courbe IS sera tout simplement plus plate en économie ouverte.

Pour commencer, étudions l'effet de la politique budgétaire dans ce modèle. Pour rappel, celle-ci déplace la courbe IS vers la gauche ou la droite. Prenons l'exemple d'une politique budgétaire accommodante (augmentation des dépenses de l'état et/ou baisse des impôts), qui fait se déplacer la courbe IS vers la droite. Cependant, la courbe MP étant croissante, le point d'intersection va remonter, ce qui fait qu'il se déplacera vers la droite d'une longueur inférieure à celle attendue si les taux ne variaient pas. Dit autrement, la politique monétaire va quelque peu contrecarrer la relance budgétaire. La banque centrale va ainsi tenter de limiter, d’adoucir les variations de l'écart de production sur l'inflation. Du fait de la hausse des taux, l'investissement privé va diminuer. Pour résumer, une partie de l'investissement public remplacera l'investissement privé : c'est ce que l'on appelle l'effet d'éviction. Le cas d'une politique restrictive est strictement inverse, aussi il ne sera pas étudié.

Effet d'une politique de relance dans le modèle IS-MP.

La courbe MP monte ou descend en fonction de l'inflation, ce qui explique le passage du court-terme au moyen-long-terme. Lorsque l'inflation augmente, la courbe MP monte. Ce faisant, le point d'intersection des deux courbes va naturellement monter : le taux réel va augmenter. Mais le point d'intersection va aussi se déporter vers la gauche, du fait que la courbe IS est décroissante : le PIB va diminuer. Lorsque l'inflation aura atteint sa valeur cible, le taux d'intérêt sera égal au taux naturel, et le PIB sera égal au PIB potentiel. La situation inverse, à savoir une baisse de l'inflation, se traduit par la dynamique exactement inverse.

Effet d'une augmentation de l'inflation ou d'un resserrement de la politique monétaire dans le modèle IS-MP.

Il faut noter qu'il est possible de coupler les deux politiques, histoire de stabiliser le PIB à une valeur bien précise. Par exemple, imaginons que le gouvernement souhaite réduire les dépenses gouvernementales ou augmenter les impôts, pour diminuer la charge de la dette. Une telle action déplacera la courbe IS vers la gauche, entrainant une baisse du PIB et des taux. Mais la politique monétaire peut réagir à cette politique d'austérité, pour compenser son effet récessif. Pour cela, elle a juste à rendre sa politique monétaire plus accommodante. La baisse des taux induite entrainera une augmentation du PIB, qui compensera la politique budgétaire.

Couplage des politiques budgétaires et monétaires (policy mix) dans le cadre du modèle IS/MP.

Le modèle AD/IA

Le modèle IS/MP est un modèle de court-terme, qui part du principe que les prix sont rigides. Mais il est possible d'étendre la vision de l'économie au moyen-terme, en postulant des prix flexibles. Pour cela, il faut réussir à résumer ces deux courbes en une seule courbe, que l'on pourra combiner à une courbe de Phillips. Cette courbe sera appelée une courbe de demande agrégée.

La courbe de demande agrégée : dérivation

La construire demande de regarder ce qui se passe quand l'inflation augmente ou diminue. Dans une telle situation, la banque centrale doit augmenter les taux réels, ce qui diminue le PIB. On peut résumer ce processus en traçant sur une courbe la relation entre inflation et PIB. Le modèle IS/MP, de court-terme, permet ainsi de dériver une relation entre PIB et inflation appelée courbe de demande agrégée.

Attention : le terme "demande agrégée" est particulièrement trompeur. Peut-être avez-vous fait le lien avec la demande de la microéconomie, celle qu'on utilise dans la loi de l'offre et de la demande, pour décrire le fonctionnement des marchés. Mais en réalité, il n’en est rien. Déjà, la demande de la microéconomie est une relation entre quantités vendues et prix, alors que la demande agrégée est ici une relation entre quantités vendues et inflation. Ensuite, il faut savoir que l'on ne peut pas définir formellement une courbe de demande habituelle pour l'ensemble de l'économie, ce que laisse penser le terme "demande agrégée". Un théorème de la théorie de l'équilibre général, le théorème SMD (théorème de Sonnenschein, Mantel, Debreu) dit que l'on ne peut pas additionner les courbes de demande de chaque individu pour donner la courbe de demande de l'économie toute entière. Derrière ces difficultés techniques se cache le fait que décrire une demande globale revient à additionner des choux et des carottes. Les biens vendus sont hétérogènes, alors qu'une courbe de demande n'est définie que pour un bien unique. Et on voit mal comment additionner les courbes de demande des œufs au plat avec la courbe de demande d'ordinateurs neufs.

La courbe de demande agrégée se déplace suivant la politique monétaire ou budgétaire : toute politique de relance tend à déplacer cette courbe vers la droite, alors que des politiques contractionnistes tendent à la déplacer vers la gauche.

Construction de la courbe de demande agrégée à partir du modèle IS/MP.

La courbe de demande agrégée peut se déplacer, suivant la politique monétaire et budgétaire. Une politique budgétaire et/ou monétaire accommodante déplace cette courbe vers la droite, tandis qu'une politique restrictive la déplace vers la gauche.

Relance et demande agrégée dérivée du modèle IS-MP.

L'équilibre AD/IA

Cette courbe de demande peut être complétée avec la fameuse courbe de Phillips. L'intersection entre les deux courbes donne l'état de l'économie en fonction de l'inflation mesurée.

Modèle AD-AS dérivé du modèle IS-MP.

On peut maintenant étudier quel est l'effet d'une politique monétaire ou budgétaire quelconque sur le PIB et l'inflation à moyen-terme. Une politique de relance déplacera la courbe de demande vers la droite, laissant la courbe de Phillips inchangée. l'inflation augmentera, de même que le PIB. Une politique d'austérité budgétaire ou une politique monétaire restrictive va au contraire faire baisser les prix et le PIB, en déplaçant la courbe de demande vers la gauche.

Politique de relance dans le modèle AD-AS (dérivé d'IS-MP).

L'effet d'un choc d'offre est quelque peu différent. Il se traduit par un déplacement de la courbe de Phillips. Un choc d'offre négatif déplace cette courbe vers la gauche, ce qui se traduit par une augmentation de l'inflation, couplée à une baisse du PIB. Un choc d'offre positif a l'effet inverse : une baisse de l'inflation et une augmentation du PIB. La réaction de la banque centrale à un tel choc d'offre dépend de la durée de celui-ci. D'ordinaire, les chocs d'offre sont temporaires, dans le sens où la courbe de Phillips revient à la normale après un certain temps. Dans ces conditions, la banque centrale n'a pas vraiment intérêt à agir : le temps que sa politique monétaire se fasse sentir, le choc d'offre aura disparu. De plus, contrer le choc d'offre demanderait d'utiliser une politique restrictive, qui déplacerait la courbe de demande vers la gauche. Dans ces conditions, l'inflation reviendrait à la normale, mais au prix d'une baisse encore plus importante du PIB.

Choc d'offre dans le modèle AD-AS (dérivé de IS-MP).

Le cas particulier de la limite des taux zéro

Pour rendre compte des situations de ZLB avec le modéle IS/MP, on doit admettre qu'une partie de la courbe MP est plate, avant de redevenir croissante. Le plateau de la courbe MP est donc égal à l'opposé des anticipations d'inflation. Si le PIB est suffisamment élevé, cela n'a pas vraiment d'impact : la courbe IS entrera en intersection en-dehors de ce plateau. Mais avec un PIB trop bas, la courbe IS coupera le plateau de la courbe MP. Dans une telle situation, le taux réel souhaité par la banque centrale nécessite un taux nominal négatif, ce qui est impossible. Sur cette portion, l'usage de la politique monétaire est tout simplement impossible. Le seul moyen de faire remonter le PIB et les taux est de déplacer la courbe IS via une politique fiscale adaptée.

Modèle IS-MP avec trappe à liquidité.

Sur le moyen-terme, on peut naturellement supposer que les anticipations d'inflation et l'inflation sont égales. Dans ces conditions, le taux réel est l'opposé de l'inflation. Généralement, les ZLB s'accompagnent de tensions déflationnistes, à savoir que l'inflation diminue de plus en plus. Ce faisant, le taux réel augmentera en conséquence. Cette augmentation du taux réel fera naturellement diminuer le PIB (courbe IS), tout comme le ferait une politique monétaire restrictive. Ainsi, la courbe de demande agrégée doit être reformulée dans le cas d'une ZLB : une portion de la courbe de demande devient soudainement croissante (là où la ZLB se fait sentir).

$\downarrow \pi \rightarrow \downarrow \pi _{e}\rightarrow \uparrow r\rightarrow \downarrow PIB$

Demande agrégée et trappe à liquidité (modèle IS-MP).

Les canaux de transmission monétaires

Dans les chapitres précédents, nous avons étudié un cas particulier de modèle dit wickselien, qui explique la politique monétaire par une variation des taux d'intérêt directeurs. Mais la banque centrale peut aussi manipuler la masse monétaire sans passer par l'intermédiaire des taux directeurs. Elle a la capacité de créer de la monnaie à volonté et peut l'utiliser pour racheter des dettes d'état, pour la verser aux citoyens et bien d'autres. Elle dispose des politiques d'assouplissement quantitatif (rachat de dettes d'états), et de monnaie hélicoptère (création monétaire sans contrepartie). Si l'assouplissement quantitatif se marie pas trop mal avec le modèle wickselien, ce n'est pas du tout le cas de la monnaie-hélicoptère. Les conséquences de ces politiques ne peuvent pas s'expliquer parfaitement dans le modèle wickselien et demandent de passer à un modèle plus complet, dit monétaire/monétariste.

Le modèle monétaire, appelé ainsi faute de mieux, ressemble beaucoup au modèle wickselien. À vrai dire, il y a peu de différence, si ce n'est que des canaux de transmission sont rajoutés. Les canaux de transmission du modèle wickselien sont toujours présents, mais on leur ajoute des canaux supplémentaires, qui décrivent l'effet de la création monétaire sur l'économie. Et à ce petit jeu, l'effet du Q.E et de la monnaie-hélicoptère n'est pas la même, les canaux de transmission n'étant pas exactement les mêmes. Le Q.E agit sur l'économie par des effets indirects, alors que la monnaie-hélicoptère a un effet direct sur la consommation et l'investissement. Pour faire simple, on peut identifier quatre canaux de transmission.

• Plusieurs canaux sont communs au Q.E et à la création monétaire directe :
  • Le canal des taux d'intérêts, qui correspondent aux canaux wickseliens, adaptés à un contexte manéétariste.
  • Le canal des anticipations, basé sur les anticipations d'inflation
  • Le canal du crédit, où la création monétaire facilite l'octroi de crédit par les banques
• Et un canal spécifique à la monnaie-hélicoptère : le canal de transmission monétaire direct.

Modèle "monétaire".

Le canal des taux d'intérêt

Les premiers canaux ne sont autres que les canaux wickseliens vus dans les chapitres précédents, mais quelque peu modifiés. Une hausse de la masse/base monétaire entraîne une variation des taux d'intérêt, ce qui a des conséquences assez diverses sur l'économie réelle. Prendre en compte ce canal est assez simple : il suffit de rajouter une relation mathématique entre masse/base monétaire et taux d'intérêt. Cette relation n'est autre que la demande de monnaie, vue il y a quelques chapitres de cela. En théorie, cette relation est décroissante, c'est à dire que toute hausse des taux d'intérêt réduit la masse monétaire. La demande de monnaie est une relation qui résume beaucoup de mécanismes différents, mais nous laissons cela pour une série de chapitres ultérieurs. Tout ce qu'il faut savoir est que masse monétaire et taux d'intérêt sont interdépendants.

L'ajout de cette relation demande d'amender le modèle wickselien sur un point : la règle de Taylor n'est pas utilisable. La politique monétaire décide non pas de la course des taux d'intérêt, mais de la course de la masse monétaire. La fonction de réaction de la banque centrale doit donc d'exprimer comme une relation entre inflation et masse monétaire.

Notons que l'impact d'une hausse de la base monétaire n'a pas le même effet qu'une hausse de la masse monétaire. Et qu'une hausse de la base monétaire n'a pas le même effet selon qu'il s'agisse d'une politique monétaire conventionnelle ou d'un assouplissement quantitatif. Il faut donc distinguer une hausse de la base monétaire normale conventionnelle, l'assouplissement quantitatif, et l'hélicoptère monétaire. Au sens strict les trois politiques modifient la base monétaire et ont un effet sur la masse monétaire. Mais les deux premières ont un effet indirect sur la masse monétaire, qui peut parfois ne pas se manifester, alors que l'hélicoptère monétaire a un impact direct sur la masse monétaire. Il est donc plus simple de dire que politique conventionnelle et Q.E modifient la base monétaire, alors que l'hélicoptère monétaire modifie la masse monétaire.

• Avec une politique d'open market conventionnelle, la base monétaire est augmentée par la banque centrale et les réserves créées servent à acheter des titres de court-terme, sur le marché monétaire. Dans ce cas, les taux d'intérêts touchés sont les taux monétaire, de court-terme. Le résultat est le même qu'une modification du taux directeur et ne diffère pas vraiment d'une politique de contrôle des taux conventionnelle.

$\uparrow B~\rightarrow ~\downarrow i_{court-terme}~\rightarrow ~\downarrow i_{long-terme}~\rightarrow ...~\uparrow \pi$

• Avec l'assouplissement quantitatif, les réserves imprimées par la banque centrale sont échangées contre des dettes d'état de long-terme. Le Q.E a donc pour effet principal de réduire le taux d'intérêt nominal sur la dette de l'état de long-terme. Avec une courbe IS stable, cela entraine une hausse de l'investissement et du PIB, ce qui se répercute sur l'inflation.

$\uparrow B~\rightarrow ~\downarrow i_{long-terme}~\rightarrow ~...~\uparrow \pi$

• Avec l'hélicoptère monétaire, la monnaie créé est injectée dans l'économie réelle directement, en donnant de l'argent aux ménages et/ou à l'état. L'effet exact sur les taux est indirect et dépend de l'effet de la politique sur l'économie réelle. Mais on peut dire que les taux de long-terme sont touchés, tout comme les taux de court-terme. Les taux tendent à baisser sur le court-terme, mais finissent par augmenter sur le long-terme du fait de l'inflation. L'effet de l'hélicoptère monétaire sur les taux est en fait indirect et passe par le canal direct, comme nous le verrons plus tard. Aussi, il n'y a pas de liens entre taux et masse monétaire, dans le cadre strict du canal des taux d'intérêt.

Modèle monétaire et canal des taux d'intérêt.

Le canal des anticipations

Qu'il s'agisse du Q.E ou de monnaie-hélicoptère, la création monétaire agit sur le canal des anticipations. Une création monétaire massive est censée avoir un effet inflationniste, et c'est une constatation assez bien vérifiée au niveau empirique. Les agents vont s'attendre à une hausse du niveau général des prix, et donc anticiper de l'inflation.

$\uparrow ~M\rightarrow ~\uparrow P_{e}~\rightarrow ~\uparrow \pi _{e}~\rightarrow ~...~\rightarrow ~\uparrow \pi$

La hausse des anticipations d'inflation a alors divers effets, qui se matérialisent à la fois sur la courbe IS et la courbe de Phillips.

• En premier lieu, la hausse de l'inflation anticipée se répercute sur le taux réel, ce qui agit via la courbe IS.

$\pi _{e}~\rightarrow ~\downarrow r~\xrightarrow {Courbe~IS} PIB~\xrightarrow {Courbe~de~Phillips} ~\uparrow \pi$

• En second lieu, l'inflation anticipée se répercute dans la courbe de Phillips, ce qui augmente l'inflation directement.

$\uparrow \pi _{e}~\xrightarrow {Courbe~de~Phillips} ~\uparrow \pi$

Les canaux du crédit (asymétries d’information)

Le taux d'intérêt sur les crédits dépend non seulement des taux de la banque centrale, mais aussi d'une prime de risque qui dépend du ménage et de son projet d'investissement/emprunt. Ce qui se résume avec la formule suivante :

$i_{emprunt}=i_{sr}+p_{r}$, avec i le taux d'un crédit, $i_{sr}$ le taux sans risque et $p_{r}$ une prime de risque.

Cependant, il ne faut pas croire que la politique monétaire n'a d'effet que sur les taux sans risques : elle influence aussi les primes de risques des agents économiques. Une politique monétaire expansionniste réduit les primes de risques de certains agents, alors qu'une politique restrictive les augmente. L'offre de crédit est alors impactée : les banques vont prêter plus facilement quand les taux baissent et réduire l'offre de crédit quand les taux montent. Cet effet est ce qu'on appelle le canal du crédit. Là où le canal des taux d'intérêt se concentre sur la demande de crédit de la part des ménages et entreprises, mais oublie de prendre en compte l'offre de crédit de la part des banques.

Précisons qu'il existe en réalité plusieurs canaux du crédit, chacun correspondant à un mécanisme distinct des autres. En voici la liste :

• Le canal restreint du crédit, aussi appelé canal de l'emprunt bancaire.
• Le canal des bilans actif-passif.
• Le canal du rationnement du crédit.

Le canal de l'emprunt bancaire

Le canal de l'emprunt bancaire est lié au fait que les prêts sont financés par divers mécanismes de financement. Par exemple, les banques peuvent emprunter de l'argent à d'autres banques (dont la banque centrale) pour le prêter à leurs clients. Comme autre exemple, les banques prêtent l'argent des dépôts et limitent l'utilisation des autres moyens de financement. Les différents moyens de financement ne sont pas équivalents, on ne peut pas les substituer l'un à l'autre sans contraintes. Parfois, le financement par les dépôts sera plus rentable ou facile, d'autres fois il vaudra mieux emprunter à la banque centrale, et ainsi de suite. En temps normal, les dépôts sont le moyen de financement privilégié est le financement des crédits par les dépôts.

Une politique monétaire expansionniste augmente la quantité totale de dépôts présente dans l'économie, ainsi que la quantité de réserves. Et qui dit augmentation des dépôts signifie augmentation des fonds prêtables : la quantité de crédit fournie par les banques augmente. L'emprunt, et donc l'investissement, augmente, ce qui stimule l'économie et le PIB.

$\uparrow M~\rightarrow ~\uparrow Depots~\rightarrow ~\uparrow Credit~\rightarrow ~\uparrow I~\rightarrow ~\uparrow Y~\rightarrow ~...~\uparrow \pi$

En théorie, les petites entreprises utilisent bien plus l'emprunt bancaire que les grosses entreprises. Les grosses entreprises se financent généralement sur les marchés financiers, souvent par l'émission d'obligations, plus rarement d'actions. Ce que les petites entreprises ne peuvent pas faire, les couts de l'émission d'obligations/actions étant assez élevés. Elles font donc appel aux banques commerciales, et donc au crédit bancaire, plutôt qu'aux banques d'investissement (qui aident les entreprises à émettre des titres sur les marchés financiers).

Le canal des bilans actif-passifs

Les banques sont frileuses quand il s'agit de prêter leur argent. Les raisons à cela sont diverses, mais on peut résumer cela au fait qu'elles sont désavantagées par rapport aux emprunteurs, qu'elles ne savent moins qu'eux. Les emprunteurs savent ce qu'ils vont faire de leur argent, connaissent la probabilité de réussite de leur investissement, et ont une excellente idée de leur situation financière et de leur patrimoine. Les banques sont moins armées de ce point de vue : si elles peuvent avoir une idée de la situation financière des emprunteurs, ou qu'elles peuvent analyser les projets d’emprunt/investissement, elles n'en savent pas autant que les emprunteurs. Elles peuvent alors se faire entraîner dans des projets d'investissements plus risqués que prévu, où l’emprunteur ne rembourse pas ou peu, sans qu'elles le sachent. Elles font donc preuve de mesure dans leurs décisions de prêts et réduisent l'offre de crédit par rapport à une situation où les banques disposent de toutes les informations pertinentes.

Pour analyser la situation financière des emprunteurs, les banques analysent leurs dettes, leurs revenus et leurs patrimoines.

• Plus un emprunteur a un patrimoine important, plus les banques accepteront de leur prêter. Il se trouve que la politique monétaire entraîne une variation du patrimoine des agents, par le biais du canal des prix des actifs, ce qui modifie les dispositions au prêt des banques. Formellement, ce canal de transmission fait partie intégrante du canal des prix d'actifs et nous en avions déjà parlé il y a quelques chapitres.

$\uparrow M~\rightarrow ~\uparrow Patrimoine~\rightarrow ~\uparrow Credit~\rightarrow ~\uparrow I~\rightarrow ~\uparrow Y~\rightarrow ~...~\uparrow \pi$

• Un autre effet est qu'une politique monétaire expansionniste doit se traduire par une hausse des prix et des salaires. Si les dettes restent les mêmes en termes nominaux, l'inflation réduit alors le poids des dettes, comme on l'a vu dans le chapitre sur l'inflation. Dans ce cas, une politique monétaire expansionniste réduit les dettes réelles des agents, qui ont alors plus de marge pour emprunter et investir.

$\uparrow M~\rightarrow ~\downarrow Dettes~\rightarrow ~\uparrow Credit~\rightarrow ~\uparrow I~\rightarrow ~\uparrow Y~\rightarrow ~...~\uparrow \pi$

• Enfin, la politique monétaire doit augmenter les revenus futurs de certains agents. C'est notamment le cas pour certaines entreprises, qui voient leur revenu d'exploitation augmenter suite à une politique monétaire expansionniste. Les banques sont alors plus disposées à préter à de tells entreprises, compte tenu de l'amélioration de leurs revenus et de leur situation financière.

$\uparrow M~\rightarrow ~\downarrow i~\rightarrow ~\uparrow Tresorerie~des~entreprises~\rightarrow ~\uparrow Credit~\rightarrow ~\uparrow I~\rightarrow ~\uparrow Y~\rightarrow ~...~\uparrow \pi$

Le rationnement du crédit

Enfin, un autre mécanisme est que les agents emprunteurs ne présentent pas les mêmes niveaux de risque selon les taux en vigueur. Quand les taux sont élevés, seuls les emprunteurs à haut risque se présentent aux guichets des banques. Les autres préfèrent ne pas emprunter à des taux trop élevés et préfèrent se priver d'emprunt. Seuls les investissements à haut risque sont pris en charge par les banques, qui préfèrent rationner le crédit pour se concentrer sur un sous-ensemble pas trop risqués de crédits. Mais quand les taux sont bas, l'emprunt devient rentable pour les emprunteurs à faible risque, qui font alors appel aux banques. Les banques acceptent plus facilement de prêter à ces emprunteurs, ce qui augmente le volume de prêts accordés. Dit autrement, la quantité de ménages solvable qui emprunte auprès des banques dépend des taux. À de fort taux, les banques font face à une faible quantité de projets risqués et rationnement le crédit pour éviter des emprunts à trop haut risque. À faible taux, elles font face à de nombreux emprunteurs solvables et ont alors plus d'opportunités de prêts peu risqués. Elles prêtent donc plus à faibles taux et moins à de forts taux.

Le canal monétaire direct

La monnaie hélicoptère agit par un canal particulier sur le niveau des prix. Sur le court-terme, elle induit de la consommation, les agents disposant de plus d'argent pour consommer. Cette consommation se traduit par une hausse de l'inflation. Sur le long-terme, la création monétaire entraîne juste une hausse des prix, sans impact sur le PIB, le taux de chômage ou toute autre variable réelle. Elle n'impacte que les variables nominales, comme les prix, l'inflation, les taux d'intérêts nominaux, les taux de change nominaux, etc.

$\uparrow M~\rightarrow ~\uparrow P~\rightarrow ~\uparrow \pi ~\rightarrow ~\uparrow i~\rightarrow ~...$

L'effet se fait ressentir à la fois sur les prix des biens et services, mais aussi sur les prix des actifs. Après tout, quand les agents reçoivent de l'argent sous forme d'hélicoptère monétaire, ils ne dépensent pas tout. Si une portion plus ou moins grande de l’hélicoptère monétaire sert pour consommer, une autre est épargnée. Et si une partie de cette épargne finit en dépôts et sert de carburant au canal du crédit, une autre se retrouve sur les marchés financiers. Le flux d'argent sur les marchés augmente, ce qui augmente la demande d'actif alors que leur offre reste la même. Dans ces conditions, le prix des actifs augmente directement, à taux d'intérêts constants. De là, le canal du prix des actifs fonctionne à plein. Tout se passe comme si le canal des prix d'actif usuel était court-circuité et que la masse monétaire remplaçait le taux d'intérêt.

$\uparrow M~\rightarrow ~\uparrow {\text{Prix des actifs}}~\rightarrow ~...~\uparrow \pi$

Notons que la hausse du prix des actifs réduit leur rendement. Dans le cas des placement rémunérés par un intérêt, cela signifie une diminution de leur taux d'intérêt. Et ce peu importe que les taux soient à court ou long-terme : la logique vaut aussi bien pour les obligations que pour les placements monétaires. En clair, l'hélicoptère monétaire entraine une baisse des taux d'intérêt de court et de long-terme, qui se répercute sur l'économie.

$\uparrow M~\rightarrow ~\uparrow {\text{Prix des actifs}}~\rightarrow ~\downarrow i~\rightarrow ~...~\uparrow \pi$

Enfin, les taux de change sont aussi modifiés par l'hélicoptère monétaire. L'argent de l’hélicoptère monétaire peut servir à acheter des importations ou être placé dans des investissement à l'étranger. Et ces flux d'argent se répercute sur la demande des devises étrangères, et donc sur leur taux de change. Le canal des taux de change est donc court-circuité par l’hélicoptère monétaire ne ne fonctionne pas que par l'intermédiaire des taux d'intérêts.

$\uparrow M~\rightarrow ~\downarrow e~\rightarrow ~...~\uparrow \pi$

La théorie quantitative de la monnaie

Si vous avez déjà lu de vieux manuels d'économie ou de politique monétaire, vous avez remarqué qu'ils portent une grande importance à la quantité de monnaie en circulation dans l'économie. Il faut dire que la masse monétaire, la quantité de monnaie, a longtemps été considérée comme un facteur extrêmement important pour la formation des prix et pour le fonctionnement de l'économie en général. De nos jours, les économistes pensent que la croissance de la masse monétaire a des effets différents selon que l'on mesure ses effets à long-terme ou à court-terme. Sur le long-terme, l'influence de la quantité de monnaie sur l'économie peut se résumer à une action sur les prix et sur les taux d'intérêt. La théorie quantitative de la monnaie, apparue au 19éme siècle et améliorée dans les années 60/70 par les monétaristes, explique quelle est l'influence de la quantité de monnaie sur les prix.

L'équation de Fisher

Prenons un ensemble de transactions, qui peut être complètement quelconque et qu'on peut choisir arbitrairement, dans lesquelles une certaine somme d'argent est échangée. Notons cette somme d'argent N. Par définition, chaque transaction T implique une certaine quantité de biens/services Q, chacun d'entre eux ayant un prix P. L'argent dépensé est alors égal à :

$N=\sum _{i}T_{i}=\sum _{i}P_{i}\times Q_{i}$, où $T_{i}$ correspond à la somme d'argent échangé lors de la transaction T numéro i, $Q_{i}$ est la quantité de biens et services échangé lors de la transaction, et $P_{i}$ le prix de chaque bien/service.

On peut alors définir un prix moyen pour chaque transaction, ce qui donne :

$N=P_{m}\times \sum _{i}Q_{i}$, où $p_{m}$ est le prix moyen des transactions considérées.

Maintenant, comparons la somme d'argent N avec la masse monétaire. D'ordinaire, la somme d'argent dépensée est inférieure à la masse monétaire, signe tous seule une partie de la masse monétaire est impliquée dans les transactions choisies. Mais elle peut être supérieure si on étudie un ensemble de transactions assez grand pour avoir une importance macroéconomique. Par exemple, si on étudie les flux d'argent sur la totalité des marchés financiers action, obligation, de devise, et dérivés, on trouvera un résultat supérieure à la masse monétaire dans certains pays si on compte sur une période de temps assez longue. C'est parce qu'un même euro/dollar/autre passera plusieurs fois sur le marché et sera utilisé dans plusieurs transactions. Pour donner un exemple, un employé peut acheter de la viande avec 20 euros, le boucher peut alors utiliser ces 20 euros pour acheter des livres pour sa fille, le libraire peut ensuite utiliser ces 20 euros pour acheter un nouveau livre à mettre en vente à un éditeur, et ainsi de suite. La monnaie circule et un même euro passe de main en main. Il est possible de mesurer combien de fois un euro passe de main en main, combien de fois il est utilisé dans une transaction. Si on fait la moyenne sur tous les euros, et qu'on fait les comptes sur toute la masse monétaire, on peut définir la vitesse de circulation de la monnaie ou vélocité de la monnaie. La vélocité de la monnaie correspond au nombre de fois en moyenne qu'un euro/dollar/... change de main, sert dans une transaction, durant l'année.

Précisons que la vélocité de la monnaie dépend des transactions considérées. Pour mesurer la vélocité de la monnaie, on doit choisir un ensemble de transactions et faire les comptes dessus. Par exemple, on peut choisir les flux du marchés actions français Euronext entre le 20 janvier 2020 et le 13 novembre 2060, et en calculer le prix moyen, et la vélocité associée. Par définition, si on mesure la vélocité de la monnaie et qu'on la multiplie par la masse monétaire, on obtient la somme d'argent dépensée dans les transactions considérées. On alors :

$N=V\times M$, où $V$ est la vélocité moyenne de la monnaie dans les transactions considérée.

Les deux équations $N=V\times M$ et $N=P_{m}\times \sum _{i}Q_{i}$ sont toujours vraies par définition. En les égalisant, on a :

$M\times V=P_{m}\times \sum _{i}Q_{i}$

Cette équation est une identité comptable appelée l'équation de Fisher.

L'équation de base de la théorie monétariste

Dans ce qui va suivre, nous allons choisir comme transactions comptabilisées dans le PIB Y et seulement celles-ci. On obtient alors l'équation de Fisher. Celle-ci est donnée ci-dessous, avec :

• $M$ la masse monétaire (la quantité de monnaie totale) ;
• $P$ le niveau moyen des prix ;
• $Y$ le volume des ventes de biens et services ;
• $V$ la vitesse de circulation de la monnaie.

$M\times V=Y\times P$

Les économistes choisissent un ensemble de transactions bien précises, regroupée dans ce qu'on appelle souvent le Produit Intérieur Brut (PIB). Avec ce choix, le produit $Y\times P$ est appelé le PIB nominal, alors que le terme $Y$ est ce qu'on appelle le PIB réel. L'ensemble de transactions comprises dans le PIB inclut les dépenses de consommation et d'investissement les plus courantes, ainsi que bien d'autres.

L'épargne est cependant prise en compte dans l'équation, mais d'une manière un peu cachée. Déjà, une partie de l'épargne finance l’investissement. Le reste de l'épargne est de la monnaie qui ne circule pas et n'est donc pas prise en compte dans la vélocité de la monnaie. Si les ménages se mettent à épargner dans une forme d'épargne qui ne circule pas, la vélocité de la monnaie diminue. À ce propos, une interprétation possible de l'équation précédente met en avant la répartition de l'argent en circulation dans l'économie. Les agents économiques peuvent répartir leur argent entre consommation et épargne improductive. Une certaine fraction $k$ du revenu est donc conservé sous forme de monnaie pour des dépenses ou sous forme d'épargne réinjectée dans le circuit économique, et le reste sous forme d'épargne improductive. Seule la fraction $k$ circule dans l'économie, ce qui donne :

$k\times M=P\times Y$

On retrouve bien la théorie quantitative, si la vélocité est l'inverse du coefficient $k$ :

$M{\frac {1}{k}}=PY$

Dans ces conditions, il est implicite que la vélocité de la monnaie peut changer dans le temps, mais les paramètres qui font varier $k$ ne sont pas précisés par la théorie. En réfléchissant un petit peu, on se doute que les taux d'intérêt peuvent influencer le taux d'épargne, et donc la vélocité, mais la théorie quantitative ne le précise pas. Elle va au contraire faire quelques hypothèses simplificatrices qui omettent ce genre d'influence.

Un défaut de la théorie quantitative est qu'elle ne précise pas à quel agrégat monétaire correspond $M$. Vu que l'on utilise le PIB dans l'équation de Fisher, donc une mesure des dépenses courantes, l'agrégat idéal devrait être l'agrégat M1 qui regroupe l'argent facilement mobilisable, à savoir les espèces et dépôts sur compte courants. Cette déduction était valable autrefois, avant que les innovations financières et bancaires rendent facile et rapide le transfert d'argent entre livrets et comptes courants, donc de l'agrégat M2/M3 à l'agrégat M1. Ces modifications font que l'agrégat à utiliser n'est pas très clair de nos jours.

L'effet d'une variation de la masse monétaire

La relation précédente est une identité, c’est-à-dire qu'elle s'applique tout le temps, sans contraintes. De celle-ci, on peut déduire ce qui se passe lors d'une augmentation de la masse monétaire. Imaginons que la masse monétaire croît de 5% : que se passe-t-il ? Pour commencer, il faut définir la croissance de la masse monétaire $g_{m}$, comme étant le rapport ${\frac {\Delta M}{M}}$. De même, la croissance de la vélocité vaut $\Delta V \over V$, tandis que ${\frac {\Delta Y}{Y}}$ et ${\frac {\Delta P}{P}}$ correspondent respectivement à la croissance du PIB et à l'inflation.

Partons de l'équation de base et dérivons-là.

$\Delta (M\times V)=\Delta (P\times Y)$

En appliquant la formule de la dérivée d'un produit, on trouve :

$\Delta M\times V+M\times \Delta V=\Delta P\times Y+P\times \Delta Y$

Divisons maintenant par MV, ce qui est équivalent par diviser par PY. Du fait de cette équivalence, nous allons diviser par MV le terme de gauche, et par PY celui de droite.

${\frac {\Delta M\times V+M\times \Delta V}{M\times V}}={\frac {\Delta P\times Y+P\times \Delta Y}{P\times Y}}$

En simplifiant les fractions, on trouve alors :

${\frac {\Delta M}{M}}+{\frac {\Delta V}{V}}={\frac {\Delta Y}{Y}}+{\frac {\Delta P}{P}}$

Le terme ${\frac {\Delta Y}{Y}}$ n'est autre que la croissance du PIB, notée $g$, et le terme ${\frac {\Delta P}{P}}$ n'est autre que l'inflation. Dit autrement, la croissance de la masse monétaire se traduit par de l'inflation (croissance des prix), une croissance du PIB réel, ou une baisse de la vélocité.

La constance de la vélocité

Toute modification de la quantité de monnaie en circulation peut se traduire par une modification de la vélocité de la monnaie, du PIB réel ou du niveau général des prix, si ce n'est les trois. Sans hypothèses supplémentaires, on ne peut pas prédire ce qui va se passer. Une première simplification, relativement raisonnable, est de considérer que la vélocité de la monnaie est constante sur le long-terme, ou du moins qu'elle n'évolue que très lentement. En appliquant cette simplification dans les équations précédentes, on a :

${\frac {\Delta M}{M}}={\frac {\Delta Y}{Y}}+{\frac {\Delta P}{P}}$

Cette équation nous dit qu'à vélocité constante, la croissance de la masse monétaire est égale à la somme de l'inflation et de la croissance du PIB. Dit autrement, toute variation de la masse monétaire se traduit par une variation du PIB nominal, à savoir soit par une variation des prix, soit par une variation du PIB réel, soit par les deux. Il faut alors poser d'autres hypothèses pour savoir qui du PIB réel ou des prix est impacté.

On verra dans les prochains chapitres que cette hypothèse n'est pas exactement vraie. Les études empiriques montrent que la vélocité a un effet qui suit les cycles économiques : elle baisse lors des récessions/dépressions, et augmente lors des phases d'expansion. Cela lui donne un effet procyclique : la baisse de la vélocité aggrave les récessions et intensifie les expansions. Ce caractère procyclique de la vélocité de la monnaie est clairement établi par les données historiques. Mais on peut considérer que la constance de la vélocité est une approximation assez intéressante à étudier.

La neutralité de la monnaie

Pour la suite, nous allons supposer que la monnaie n'a pas d'influence sur les facteurs dits réels (corrigés du niveau des prix et de l'inflation), comme le PIB ou les taux réels. En clair, on suppose qu'ils dépendent de la politique fiscale, de la productivité, de l'état de la technologie et des progrès techniques, et de bien d'autres choses, mais pas de la quantité de monnaie en circulation. Cette hypothèse est appelée la neutralité de la monnaie.

Pour le dire autrement, l'hypothèse dit que le PIB est égal une valeur indépendante de la politique monétaire, appelée PIB potentiel. L'hypothèse de neutralité de la monnaie nous dit qu'une variation de la masse monétaire n'est pas censée influencer le PIB potentiel, au moins sur le court-terme. Mais le PIB potentiel n'est pas constant, même si l'hypothèse de neutralité de la monnaie est respectée. En effet, le PIB potentiel peut augmenter de lui-même ou suite à diverses politiques fiscales ou réglementaires. Cela permet de reformuler l'équation de la théorie quantitative de la monnaie comme suit :

${\frac {\Delta M}{M}}={\frac {\Delta Y_{potentiel}}{Y_{potentiel}}}+{\frac {\Delta P}{P}}$

Ou encore :

${\frac {\Delta P}{P}}={\frac {\Delta M}{M}}-{\frac {\Delta Y_{potentiel}}{Y_{potentiel}}}$

Cette équation nous dit que la croissance du PIB potentiel a des conséquences différentes selon le rythme de croissance de la masse monétaire. Trois cas sont possibles :

• Si le PIB potentiel et la masse monétaire augmentent au même rythme, les prix restent inchangés.
• Si le PIB potentiel croît plus vite que la masse monétaire, les prix augmentent.
• Si le PIB potentiel croît moins vite que la masse monétaire, les prix baissent.

Si on néglige la croissance du PIB potentiel, on a alors :

${\frac {\Delta M}{M}}={\frac {\Delta P}{P}}$

L'équation nous dit que l'inflation est liée à la croissance de la masse monétaire et uniquement à celle-ci. D'où l'adage énoncé par Friedmann qui veut que "l'inflation est partout et de tout temps un phénomène monétaire".

Les preuves empiriques

Si la théorie quantitative de la monnaie est une théorie bien définie, celle-ci a aussi le luxe d'avoir de nombreuses confirmations empiriques. En pratique, de nombreuses études statistiques ont montré que la monnaie est neutre sur le long-terme. Par exemple, on pourrait citer l'étude de McCandless et Weber datée de 1995, qui a analysé 110 pays sur une période de 30 ans. Cette étude montre des corrélations entre croissance de la masse monétaire et inflation comprises entre 0,92 et 0,96 (ce qui est énorme). Par contre, il n'y a pas de corrélation avec la croissance du PIB réel. Cette étude va dans le sens de nombreuses autres études, qui portaient cependant sur un échantillon plus limité, avec moins de pays, si ce n'est un pays unique par étude. Par exemple, on pourrait citer celle de Lucas, datée de 1980, pour les états-unis. Cette étude étudie le comportement de l'inflation et de la croissance de la masse monétaire des états-unis entre 1955 et 1975. Elle montre que, en enlevant la volatilité à court-terme de l'inflation, la corrélation entre croissance monétaire et inflation est très forte. Cette étude a été répliquée pour une période plus longue par Berentsen, Menzio et Wright en 2008, donnant des résultats similaires. Et il ne s'agit là que d'une étude parmi un océan de confirmations. Cependant, des études récentes semblent montrer que cette relation semble s'estomper pour les pays où l'inflation est très basse, l'étude de Paul DeGrauwe et Magdalena Poland datée de 2001 en étant un bon exemple.

Money supply growth vs inflation rates

Comme autre forme de preuve, on peut aussi citer les cas d'hyperinflation, une situation où l'inflation devient très importante (les prix peuvent augmenter de 5 à 10.000 fois en à peine quelques mois). Tous les épisodes d'hyperinflation ont été accompagnés d'une forte augmentation de la masse monétaire, ainsi qu'à une hausse de la vélocité de la monnaie. On pourrait cependant rétorquer que c'est peut-être l'inflation qui cause l'augmentation de la masse monétaire, et non l'inverse. Mais l'étude des décisions des banques centrales par les historiens permet de décider quelle est la cause de cette corrélation : c'est systématiquement l'augmentation de la masse monétaire qui cause l'inflation, et non l'inverse. À titre d'indice, on peut signaler qu'aucune situation d'hyperinflation n'est à déplorer sous l'étalon-or. Ce n'est qu'une fois celui-ci abandonné ou suspendu que l'hyperinflation a commencé à se manifester au cours de l'histoire. Ce qui est cohérent avec la limitation de la croissance monétaire induite par l'étalon-or.

L'effet Fisher : les taux nominaux à long-terme

L'équation précédente résume bien la théorie quantitative de la monnaie, mais elle ne suffit à elle seule à décrire la macroéconomie d'un pays. Tel n'est pas son rôle, dirons certains. Mais il est possible d'étendre cette théorie avec quelques hypothèses. Dans cette section, nous allons voir comment, avec quelques hypothèses, on peut rendre compte de l'effet de la masse monétaire sur les taux nominaux. Nous allons ajouter une relation entre taux réel, inflation et taux nominal, cette relation étant appelée la relation de Fisher.

L'hypothèse du taux d'intérêt naturel

Effet Fisher.

Sur le long-terme, la politique monétaire est totalement neutre sur le taux d'intérêt réel. Ce taux réel indépendant de la banque centrale est appelé taux d'intérêt naturel. Celui-ci sera noté ${\overline {r}}$ dans la suite du cours.

$i={\overline {r}}+\pi _{e}$

Dans ces conditions, les taux nominaux varient alors exactement comme l'inflation, avec des hausses-baisses de 1 pour 1 : on parle d'effet Fisher. L'inflation dépendant de la croissance de la masse monétaire, la banque centrale devra accommoder son taux nominal : elle n'a pas le contrôle à long-terme du taux nominal, excepté via le contrôle de l'inflation. On voit donc que sur le long-terme, une politique monétaire restrictive fera baisser l'inflation, et donc le taux d'intérêt nominal, tandis qu'une politique accommodante aura l'effet inverse. Dit autrement, un taux d'intérêt bas est le signe que la politique monétaire a été restrictive (accommodante pour un taux haut), compte tenu des délais de transmission de la politique monétaire. C'est exactement l'inverse de ce qu'on observe à court-terme, où des taux bas indiquent une politique accommodante (et réciproquement).

Les preuves empiriques

La réalité de l'effet Fisher est plus ou moins bien établie par la corrélation entre taux d'intérêt à long-terme et inflation, ainsi qu'en taux et croissance de la masse monétaire. Les pays avec une faible inflation tendent à avoir des taux faibles, et inversement. Le lien entre taux à long-terme et croissance de la masse monétaire est illustré par l'étude de Monnet et Weber (2001), qui a étudié 31 pays sur la période 1961-1998. La corrélation entre ces deux variables est alors de 0.87, ce qui est très élevé. Les chiffres sont un peu plus faibles pour les pays développés, la corrélation étant de 0,66.

Un exemple assez intéressant est celui des taux américains. Le graphique ci-dessous montre l'évolution des taux et de l'inflation américaine depuis les années 1950. On voit que les taux tendent à suivre l'inflation de quelques mois ou années. La corrélation entre ces deux variables est proche de 0,75. Dans le détail, on voit que l'inflation américaine a commencé à augmenter dès les années 60, essentiellement à cause des différents chocs pétroliers. L'inflation s'est poursuivie, encouragée par une certaine passivité de la banque centrale américaine. Dans les années 1070, l'inflation était même proche des 11,3%. Cette inflation galopante s’arrêta quand Paul Volcker fut nommé président de la réserve fédérale. Déterminé à remettre l'inflation sur les rails, Volcker rendit la politique monétaire nettement plus restrictive. Cette politique ramena rapidement l'inflation proche des 3%. Il s’avère que les taux suivirent le même mouvement. Ceux-ci augmentèrent rapidement sur le court-terme, à cause de la politique restrictive (ce qui est le comportement attendu, comme nous le verrons dans quelques chapitres). Mais sur le long-terme, ceux-ci diminuèrent rapidement, comme prévu par l'effet Fisher. Le règne Volcker mit fin à la passivité de la réserve fédérale face à l'inflation. C'est à peu près à la même époque que les banques centrales se mirent à cibler l'inflation, et mirent la stabilité des prix au premier plan de leurs objectifs. Les années qui suivirent furent suivies par une baisse des taux mondiaux. Cette période de contrôle de l'inflation et de baisse des taux fût aussi connu sous le nom de grande modération.

Inflation et taux américains.

L'effet sur les taux de change à long-terme

Nous venons de voir comment la masse monétaire influence les taux d'intérêts, par l'intermédiaire de l'inflation. Il est maintenant temps de voir comme la masse monétaire influence les taux de change, une autre variable nominale. Nous allons voir que cette influence passe par le niveau des prix, ainsi que par l'inflation, dans une certaine mesure.

Avant de commencer, rappelons que le taux de change réel, noté $q$, est la quantité de biens nationaux que l'on peut échanger contre des biens étrangers. En clair, une quantité $Q_{n}$ de biens nationaux s’échange contre la quantité $q\times Q_{e}$ de biens étrangers. Ce qui donne :

$q={\frac {Q_{n}}{Q_{e}}}$

Le taux de change nominal, quant à lui, est égal à :

$e=q\cdot {\frac {P_{n}}{P_{e}}}$

La théorie de la parité de pouvoir d'achat

Dans ce qui suit, nous allons poser une hypothèse bien particulière : la loi du prix unique. Elle suppose que la Terre entière soit un gigantesque marché unique, totalement globalisé. En conséquence, on ne peut pas vendre plus cher un produit sur le territoire national qu'à l'étranger, et réciproquement. Si une entreprise tenait de vendre un produit plus cher sur le territoire national, les fournisseurs préféreraient acheter le même produit est le moins cher à l'étranger. Ce faisant, du fait des lois de la concurrence, l’entreprise nationale devra diminuer ses prix pour les amener au même niveau que les prix étranger. Pour résumer, la loi du prix unique dit que des produits identiques ont le même prix, peu importe l'endroit sur Terre.

Une conséquence de cette hypothèse est que le pouvoir d'achat d'une unité monétaire doit être le même à l'étranger. On dit alors que la parité de pouvoir d'achat est respectée. Dit autrement, Une somme d'encaisses réelles doit permettre d'acheter la même quantité $Q$ de biens ou de services que la même somme en monnaie étrangère. Dit autrement, le taux de change réel est égal à 1. On a donc le taux de change nominal qui vaut :

$e={\frac {P_{n}}{P_{e}}}$

L'hypothèse de la parité de pouvoir d'achat implique donc que les taux de change réels sont indépendants de la politique monétaire, qui ne peut qu'influencer les taux nominaux. La monnaie n'a donc pas d'effet réel sur les taux de change réels. En clair, sur le long-terme, la neutralité de la monnaie joue aussi au niveau international.

Petit bémol : la parité de pouvoir d'achat ne tient pas en compte de quelques menus détails. Par exemple, certaines choses ne sont pas importables ou exportables, les services en étant l'exemple parfait. Il ne m'est pas possible d'importer une heure d'enseignement en présentiel depuis le Japon, par exemple. En somme, la théorie de la parité de pouvoir d'achat ne vaut que pour les produits qui peuvent passer d'un pays à un autre. C'est sans doute pour cela que la théorie de la parité de pouvoir d'achat est assez mal vérifiée dans la réalité. Beaucoup d'économistes considèrent qu'elle est une bonne approximation de ce qui se passe à long-terme, mais il est clair que cette théorie ne vaut rien à court-terme. Les taux de change évoluent très souvent à court-terme et semblent suivre une marche aléatoire complètement imprévisible, sans compter que la politique monétaire a un effet sur les taux de change réel.

L'effet Fisher international

Dans le chapitre sur les taux de change, nous avons vu une formule qui permet de relie la dépréciation des taux de change réels avec la dépréciation des taux de change nominaux :

${\frac {\Delta e}{e}}={\frac {\Delta q}{q}}+(\pi _{n}-\pi _{e})$, avec e le taux de change nominal et q le taux de change réel.

L'hypothèse de la parité de pouvoir d'achat implique que le taux de change réel est constant. En injectant cette hypothèse dans l'équation précédente, on trouve :

${\frac {\Delta e}{e}}=\pi _{n}-\pi _{e}$

La relation précédente s'appelle l'effet Fisher international. Elle permet de comprendre l'effet de la politique monétaire sur les taux de change. Une politique monétaire expansionniste va faire grimper l'inflation, ce qui dépréciera la monnaie. Une politique restrictive réduira l'inflation et donc la dépréciation monétaire.

On l'a vu dans le chapitre sur les taux de change, la dépréciation du taux de change réel ${\frac {\Delta q}{q}}$est égal à la différence entre taux réels entre les deux pays $r_{n}-r_{e}$. En clair, l'effet Fisher international dut que les taux réels domestiques et étrangers soient égaux.

Le modèle monétaire des taux de change

Après avoir introduit l'effet Fisher international et la parité de pouvoir d'achat, nous pouvons leur appliquer la théorie quantitative de la monnaie. Nous pouvons notamment déduire la valeur des taux de change à partir des masses monétaires et de la croissance de chaque pays, ainsi qu'en déduire la dépréciation induite par une croissance de la masse monétaire.

Détermination des taux de change

Maintenant, utilisons la théorie quantitative pour déduire les niveaux des prix domestiques et étrangères, à partir de l'équation de Fisher.

$P_{n}={\frac {M_{n}\times V_{n}}{Y_{n}}}$

$P_{e}={\frac {M_{e}\times V_{e}}{Y_{e}}}$

Injectons les deux premières équations dans l'équation $e={\frac {P_{n}}{P_{e}}}$ et faisons quelques manipulations algébriques :

$e={\frac {M_{n}\times V_{n}}{Y_{n}}}\times {\frac {Y_{e}}{M_{e}\times V_{e}}}={\frac {V_{n}}{V_{e}}}{\frac {M_{n}}{M_{e}}}\times {\frac {Y_{e}}{Y_{n}}}$

Nous pouvons simplifier les équations en supposant que les vélocités sont constantes, ce qui donne :

$e=k\times {\frac {M_{n}}{M_{e}}}\times {\frac {Y_{e}}{Y_{n}}}$

On voit que le taux de change est égal au rapport des masses monétaires, pondéré par le rapport des PIB (ainsi que par le rapport des vélocités).

Détermination de la dépréciation

On peut aussi utiliser l'équation de Fisher pour calculer l'appréciation/dépréciation des taux de change. En réutilisant les formules vues dans le chapitre, on trouve alors que :

$\pi _{n}={\frac {\Delta P_{n}}{P_{n}}}={\frac {\Delta M_{n}}{M_{n}}}+{\frac {\Delta V_{n}}{V_{n}}}-{\frac {\Delta Y_{n}}{Y_{n}}}$

$\pi _{e}={\frac {\Delta P_{e}}{P_{e}}}={\frac {\Delta M_{e}}{M_{e}}}+{\frac {\Delta V_{e}}{V_{e}}}-{\frac {\Delta Y_{e}}{Y_{e}}}$

On peut alors injecter ces dérivées dans l'équation Fisher internationale : ${\frac {\Delta e}{e}}=\pi _{n}-\pi _{e}$, ce qui donne :

${\frac {\Delta e}{e}}=\left[{\frac {\Delta M_{n}}{M_{n}}}-{\frac {\Delta M_{e}}{M_{e}}}\right]+\left[{\frac {\Delta V_{n}}{V_{n}}}-{\frac {\Delta V_{e}}{V_{e}}}\right]-\left[{\frac {\Delta Y_{n}}{Y_{n}}}-{\frac {\Delta Y_{e}}{Y_{e}}}\right]$

Cela permet de comprendre comment la politique monétaire d'un pays étranger influence le taux de change, à politique monétaire égale dans le pays domestique. Plus un pays étranger va créer de monnaie, plus celle-ci va se déprécier de son point de vue (et donc s'apprécier du nôtre).

La non-constance de la vélocité de la monnaie

La théorie quantitative de la monnaie se base sur deux hypothèses : la constance de la vélocité de la monnaie et la neutralité de la monnaie. Évidemment, ces deux hypothèses ne sont pas vraiment bien respectées dans le monde réel. Sur le temps long, la neutralité de la monnaie est cependant bien respectée, ce qui en fait une hypothèse valable pour étudier le long-terme. Il en est de même pour la stabilité de la vélocité de la monnaie, encore que celle-ci aie subit des variations assez importantes au cours du siècle dernier. Mais sur le court-terme, la constante de la vélocité de la monnaie ne tient tout simplement pas. Dans ce chapitre, nous allons modifier la théorie quantitative de la monnaie pour tenir compte d'une vélocité non-constante. Mais avant tout, il nous faut montrer pourquoi la vélocité change au cours du temps. Et pour cela, nous allons devoir introduire le concept de demande de monnaie.

La demande de monnaie : définition

La demande de monnaie correspond à la quantité de monnaie que les agents économiques souhaitent détenir compte tenu des conditions macroéconomiques, de leur salaire, de leurs anticipations de l'avenir, et de tout ce qui peut influencer leurs décisions de consommation et d'épargne. Ils vont détenir de la monnaie pour la dépenser en biens de consommation, mais aussi pour investir dans des actifs financiers (actions, obligations, assurances-vies, immobilier, autres), ou tout simplement épargner sur des livrets. Ce faisant, au niveau macroéconomique, on peut définir une demande de monnaie globale qui correspond à la quantité totale d'argent que tous les agents économiques d'un pays souhaitent conserver sur leurs comptes. Par définition, la demande de monnaie peut être fractionnée en plusieurs sous-demandes : une pour la monnaie destinée à être dépensée, une autre pour celle à échanger contre des actifs, une autre qui part en épargne de précaution, une autre qui sert à payer les impôts, etc.

Voici ce que cela donne quand on le dit avec des maths :

$M_{d}=M_{C}+M_{I}+M_{T}+M_{S}$, avec $M_{d}$ la demande de monnaie, $M_{C}$ la monnaie destinée à être consommée, $M_{I}$ la monnaie à investir, $M_{T}$ la monnaie pour payer les taxes et $M_{S}$ pour l'épargne de précaution thésaurisée.

La demande de monnaie réelle

La demande de monnaie précédente est une somme d'argent, exprimée en euros/dollar/autres. Mais la monnaie est censée être dépensée pour acheter des biens qui ont un prix. Une certaine somme de monnaie correspond à un certain pouvoir d'achat, qui dépend de M, mais aussi de P. Il est donc possible de définir une demande de monnaie exprimée non pas en euros/dollar/autre, mais en unités de pouvoir d'achat, en biens/services. Pour cela, il suffit de diviser la demande de monnaie précédente par le niveau des prix. On obtient alors la demande de monnaie réelle, notée comme suit :

$L(...)={\frac {M_{d}}{P}}$

Les parenthèses sont là pour dire que la demande de monnaie réelle dépend de plusieurs paramètres, qui ont été depuis longtemps identifiés par les économistes. Les études économétriques ont montré que la masse monétaire dépend fortement du PIB , des prix et de bien d'autres paramètres. Les trois principaux sont cependant les prix, le PIB et les taux d'intérêt. Les économistes ont depuis longtemps mesuré les dérivées de la demande de monnaie en fonction des prix, du PIB et des taux. Et ils ont obtenu des résultats suivants :

${\frac {\partial M_{d}}{\partial P}}\approx 1$, ${\frac {\partial M_{d}}{\partial Y}}\approx 1-0.5$, ${\frac {\partial M_{d}}{\partial i}}\approx -0.2$

Les chiffres nous disent aussi qu'il faut des variations assez importantes des taux pour causer une variation de la masse monétaire. Pour diviser par deux la masse monétaire, les taux d'intérêts doivent être multipliés par 32. Pour les prix, l'effet est beaucoup plus fort. Diviser par deux la production ou les prix permet de diviser par deux la masse monétaire. Les prix sont quasiment proportionnels à la masse monétaire et il semble en être de même pour le PIB. Pour résumer, la demande de monnaie nominale est donc proportionnelle aux prix, croissante en fonction du PIB et décroissante en fonction des taux. On peut résumer tout cela dans la formule suivante, avec $Y$ le PIB nominal, $P$ le niveau des prix, $i$ le taux d'intérêt, $M_{d}$ la demande de monnaie et L une fonction.

$L(Y,i)={\frac {M_{d}}{P}}$

La fonction L est appelée la demande de monnaie réelle, là où $M_{d}$ est la demande de monnaie nominale. Les deux correspondent à la quantité de monnaie que souhaitent obtenir les agents économiques, la différence étant que la quantité de monnaie est exprimée en unités monétaires (euros, dollar, autre) pour la demande nominale, en pouvoir d'achat pour la demande réelle.

À partir de maintenant, quand on parlera de "demande de monnaie", on parlera de la demande de monnaie réelle, la fonction L(y,i) et non de la demande de monnaie M.

L'équilibre entre demande de monnaie et masse monétaire

Quel que soit le système monétaire, divers mécanismes tendent à faire en sorte que la demande de monnaie nominale soit égale à la masse monétaire. Typiquement, l'égalisation entre demande de monnaie et masse monétaire fait intervenir les taux d'intérêt, ainsi que d'autres mécanismes liés. Mais nous en reparlerons dans les chapitres dédiés, quand nous verrons les modèles IS/LM et quelques autres. Toujours est-il que, peu importe ces mécanismes, la demande de monnaie peut varier, mais que divers mécanismes de rappels font en sorte que la demande de monnaie et la masse monétaire s'égalisent. Soit parce que la banque centrale crée la monnaie demandée par les agents, soit parce que des modifications du PIB ou des taux d'intérêts ramènent la demande de monnaie à l'équilibre.

Par exemple, supposons que la demande de monnaie augmente soudainement, toutes choses égales par ailleurs. Peu importe la raison de cette augmentation, l'important est que la hausse de la demande de monnaie aie lieu alors que les taux d'intérêt et le PIB restent stables. Dans uen telle situation, il se peut que la banque centrale et le système financier réagisse en créant la monnaie demandée. La demande de monnaie augmente, mais la masse monétaire fait de même et les deux s'égalisent. Une autre possibilité est que la masse monétaire reste stable : dans ce cas, on observe une modification des taux d'intérêt et/ou du PIB, qui réduit la demande de monnaie et la ramène à l'équilibre. Toujours est-il que nous pouvons donc postuler l'égalité suivante dans la suite du cours :

$M=M_{d}$

Les variations de la demande de monnaie

Prenons la définition de la demande de monnaie et écrivons-la comme suit :

$M=P\cdot L(Y,i)$

Dérivons maintenant cette équation :

$\Delta M=\Delta [P\cdot L(Y,i)]$

Appliquons la formule qui donne la dérivée d'un produit :

$\Delta M=\Delta P\cdot L(Y,i)+P\cdot \Delta L(Y,i)$

Divisons par $M$ à gauche et par $P\cdot L(Y,i)$ à droite, ce qui revient à diviser par la même quantité des deux côtés :

${\frac {\Delta M}{M}}={\frac {\Delta P}{P}}\cdot {\frac {L(Y,i)}{L(Y,i)}}+{\frac {P}{P}}\cdot {\frac {\Delta L(Y,i)}{L(Y,i)}}$

Simplifions :

${\frac {\Delta M}{M}}={\frac {\Delta P}{P}}+{\frac {\Delta L(Y,i)}{L(Y,i)}}$

Le terme ${\frac {\Delta P}{P}}$ n'est autre que l'inflation, ce qui donne :

${\frac {\Delta M}{M}}=\pi +{\frac {\Delta L(Y,i)}{L(Y,i)}}$

L'équation précédente nous dit que la demande de monnaie nominale peut varier pour plusieurs raisons.

• La première est que les prix influencent la demande de monnaie. Il faut bien de la monnaie pour s'acheter des biens et il en faut d'autant plus qu'ils sont chers. Plus les prix sont élevés, plus il faudra de monnaie pour payer la même chose et plus la demande de monnaie est forte. Il est donc naturel de postuler que la demande de monnaie est proportionnelle aux prix. Les agents économiques ont pour cible une certaine demande de monnaie réelle, et non une demande de monnaie nominale. Si les prix doublent, toutes choses égales par ailleurs, alors la demande de monnaie doit doubler pour conserver le même pouvoir d'achat. En conséquence, prix et demande de monnaie tendent à varier de concert, toute augmentation des prix se répercutant sur la demande de monnaie. Les variations de la demande de monnaie qui en découlent sont appelées des chocs d'inflation, ou encore des chocs de prix.
• Le terme ${\frac {\Delta L(Y,i)}{L(Y,i)}}$ nous dit qu'il existe des variations de demande de monnaie qui ne sont pas liées à une variation des prix. Ces variations de la demande de monnaie sont appelées des chocs de demande de monnaie réelle.

Les chocs d'inflation et de demande de monnaie n'ont pas les mêmes effets macroéconomiques et il faut absolument faire la différence entre les deux, comme nous allons le voir dans la suite.

Too much money chasing too few goods

L'équation précédente nous dit que l'inflation a pour cause une croissance de la masse monétaire supérieure à la croissance de la demande de monnaie réelle. Pour comprendre pourquoi, étudions le scénario suivant, où la banque centrale crée beaucoup de monnaie et la distribue aux agents économiques. Les agents vont conserver une certaine quantité de cette monnaie, mais pas forcément tout. La demande de monnaie réelle va donc augmenter, mais seulement dans une certaine mesure. Si la banque centrale crée trop de monnaie, les agents vont avoir plus de monnaie qu'ils n'en veulent et vont se débarrasser du surplus en l'échangeant contre autre chose : des biens/services, des actifs financiers, etc. L'économie peut absorber une partie de cette demande supplémentaire, jusqu’à un certain point où l'offre reste plus ou moins la même sur tous les marchés (au moins approximativement). Dans de telles conditions, les prix ne peuvent qu'augmenter.

Pour résumer, la banque centrale crée une quantité de monnaie $\Delta M$, mais les agents ne conservent que $\Delta L(Y,i)\cdot P$ de monnaie supplémentaires, la différence partant dans l'augmentation des prix. Ce résultat nous dit que l'inflation nait quand trop de monnaie chasse des biens peu nombreux. La citation anglaise qui résume le phénomène est la suivante : Too much money chasing too few goods. C'est là le moto de la théorie monétariste au sens général, pas seulement celui de la théorie quantitative de la monnaie.

La taxe d'inflation

Une formalisation plus détaillée du raisonnement précédent permet de rendre compte d'un phénomène appelé la taxe d'inflation. Supposons que ce soit l'état qui crée la monnaie $\Delta M$, par le biais de sa banque centrale. La monnaie créée lui appartiendra donc et il sera celui qui en tire profit. Par en tirer profit, on veut dire que son stock de monnaie réelle augmentera, et il pourra l'utiliser pour ce qu'il veut, comme par exemple réduire sa dette publique. Etudions ce qui se passe du point de vu de la demande de monnaie. Pour cela, partons de l'équation suivante, vue dans les démonstrations précédentes :

$\Delta M=P\cdot \Delta L(Y,i)+\Delta P\cdot L(Y,i)$

L'équation peut se traduire ainsi : si la banque centrale crée une quantité $\Delta M$ de monnaie, les agents vont épargner une somme égale à $P\cdot \Delta L(Y,i)$. Mais ils vont dépenser/investir le surplus de monnaie égal à $\Delta P\cdot L(Y,i)$, qui est dépensé et est responsable de l'augmentation des prix.

Ensuite, divisons l'équation précédente par le niveau général des prix P :

${\frac {\Delta M}{P}}=\Delta L(Y,i)+{\frac {\Delta P}{P}}\cdot L(Y,i)=\Delta L(Y,i)+\pi \cdot L(Y,i)$

On voit que lorsque de la monnaie est créé, le stock de monnaie réel évolue lui aussi, pour deux raisons : une liée à l'augmentation de la demande de monnaie, une autre liée à l'inflation.

D'une part, on a bien une augmentation de la demande de monnaie réelle par les agents économiques. Si l'état crée une quantité de monnaie réelle ${\frac {\Delta M}{P}}$, les agents économiques vont décider d'acquérir une quantité $\Delta L(Y,i)$ de monnaie réelle. Pour cela, ils vont échanger quelque chose de valeur contre cette monnaie nouvellement crée, ce qui est un gain net pour l'état. Par exemple, les agents vont pouvoir échanger des obligations d'état ou d'autres actifs financiers en échange de la monnaie nouvellement créé, par le biais d'une opération d'open market. L'état gagne donc de la valeur, en échange de monnaie. Il peut par exemple racheter sa dette publique contre la monnaie nouvelle, via des politiques d'assouplissement quantitatif, voire faire du QE et annuler la dette rachetée (précisons que le cas où l'état annule sa dette après l'avoir racheté plus complexe que ce que les explications précédentes peuvent faire croire).

L'autre source est liée à l'inflation, par le biais du terme $\pi \cdot L(Y,i)$. Il s'agit formellement de ce qu'on appelle la taxe d'inflation. Elle est liée au fait que l'inflation rogne le pouvoir d'achat du stock de monnaie pré-existant. La monnaie perd de sa valeur, ce qui force les gens à s'en procurer plus pour compenser. Et ultimement, les agents se fournissent en monnaie auprès de l'état, auprès de la banque centrale. Ainsi, le pouvoir d'achat perdu par la monnaie est en quelque sorte regagné par le gouvernement. D'où le terme de taxe d'inflation donné à ce phénomène. Dans le terme $\pi \cdot L(Y,i)$, on peut interpréter $\pi$ comme étant le taux de taxation et $L(Y,i)$ l'assiette de taxation.

La relation entre vélocité de la monnaie et demande de monnaie

Les développements précédents étaient assez longs et peut-être n'avez-vous pas vu en quoi ils représentent une reformulation plus générale de la théorie quantitative de la monnaie. Il est maintenant temps de faire explicitement le lien et de voir en détail en quoi la demande de monnaie est un concept plus général que la vélocité de la monnaie. Commençons par dire qu'il existe une relation assez marquée entre demande de monnaie et vélocité de la monnaie. Pour la comprendre, partons de la définition de la demande de monnaie, vue juste auparavant :

$L(Y,i)={\frac {M}{P}}$

L'équation de Fisher, vue dans le chapitre précédent, nous dit que :

$M\cdot V=P\cdot Y$

En combinant les deux équations précédentes, on trouve :

$L(Y,i)={\frac {Y}{V}}$

Une manière équivalente de formuler l'équation précédente est la suivante :

$V={\frac {Y}{L(Y,i)}}$

On voit que la vélocité de la monnaie dépend de la demande de monnaie. Quand la demande de monnaie augmente, la vélocité de la monnaie diminue et inversement. En soit, cela n'a rien d'étonnant. La demande de monnaie varie au jour le jour, au gré des dépenses, des investissements, et de bien d'autres échanges monétaires. Ces échanges monétaires font que la monnaie circule plus ou moins vite dans l'économie, à prix égaux/constants. Une hausse de la demande de monnaie signifie que les agents souhaitent épargner sous forme de monnaie. Et qui dit agents qui épargnent leur monnaie dit agents qui investissent ou consomment moins, et donc monnaie qui ne circule plus. Plus les gens épargnent, moins la monnaie circule vite et plus la demande de monnaie augmente. Plus les gens dépensent, plus la monnaie circule vite et moins les gens en ont (ce qui rentre est dépensé assez rapidement).

Cela éclaire quelque peu les développements des chapitres précédents. La théorie quantitative de la monnaie supposait une vélocité de la monnaie stable, ainsi que la neutralité de la monnaie. Dans sa version la moins élaborée, la neutralité de la monnaie se résume à dire que le PIB reste constant. Or, supposer que le PIB et la vélocité sont constants est équivalent à dire que la demande de monnaie réelle est constante. En clair, la théorie quantitative de la monnaie se base en réalité sur une seule hypothèse : la demande de monnaie réelle est stable, il n'y a pas de chocs de demande de monnaie réelle. Nous avons donc trouvé un moyen de reformuler la théorie quantitative dans un cadre plus général en introduisant la notion de demande de monnaie. Et ce concept est utile quand il s'agit de raisonner en termes macroéconomiques. En effet, si on voit mal pourquoi la vélocité de la monnaie changerait au cours du temps, on comprends plus facilement pourquoi les agents économiques changent d'avis quant à leur demande de monnaie. Si l'hypothèse de constance de la vélocité semble crédible, elle devient tout de suite moins réaliste quand on la reformule en termes de demande de monnaie.

Mais dans le monde réel, la demande de monnaie n'est pas stable et peut varier suivant les anticipations des agents économiques. Par exemple, si les agents s'attendent à un baisse de leurs revenus futurs, voire à une crise économique, ils épargnent dans des actifs non-risqués et liquide, afin de pouvoir réagir rapidement à la situation. La monnaie étant l'actif non-risqué et liquide par exemple, la demande de monnaie va augmenter, ce qui entraînera une réduction de la vélocité de la monnaie. À masse monétaire constante, cela se traduit par une baisse des prix et/ou du PIB, donc par une récession. En soi, cette explication suffit à expliquer la plupart des récessions. Un évènement dangereux survient dans le monde réel ou la sphère financière, les ménages et entreprises prennent peur et épargnent en prévision d'un avenir incertain, la vélocité de la monnaie chute, l'argent ne circule plus et cela entraîne une récession.

Précisons cependant que ce mécanisme ne se manifeste que si la masse monétaire est gardée constante. Dans le cas contraire, la banque centrale peut accommoder la hausse de la demande de monnaie en créant juste ce qu'il faut de monnaie pour satisfaire les agents. Cela demande juste que la banque centrale garde des taux d’intérêt constants.

Les variations de la vélocité et de la demande de monnaie

Partons de l'équation suivante, démontrée plus haut :

$L(Y,i)={\frac {Y}{V}}$

Calculons maintenant la dérivée du total.

$\Delta L(Y,i)=\Delta \left({\frac {Y}{V}}\right)$

On applique la formule qui donne la dérivée d'un quotient : $\left({\frac {u}{v}}\right)^{'}={\frac {u^{'}}{v}}+u\cdot \left({\frac {1}{v}}\right)^{'}$, ce qui donne :

$\Delta L(Y,i)={\frac {\Delta Y}{V}}+Y\cdot \left({\frac {1}{V}}\right)^{'}$

On multiplie par ${\frac {1}{L(Y,i)}}={\frac {V}{Y}}$ :

${\frac {\Delta L(Y,i)}{L(Y,i)}}={\frac {\Delta Y}{Y}}+V\cdot \left({\frac {1}{V}}\right)^{'}$

Le calcul de la dérivée de l'inverse de V donne ceci :

${\frac {\Delta L(Y,i)}{L(Y,i)}}={\frac {\Delta Y}{Y}}+V\cdot {\frac {\Delta V}{V^{2}}}$

On simplifie :

${\frac {\Delta L(Y,i)}{L(Y,i)}}={\frac {\Delta Y}{Y}}-{\frac {\Delta V}{V}}$

Cette équation peut se reformuler comme suit :

${\frac {\Delta L(Y,i)}{L(Y,i)}}=g-v$, avec g la croissance du PIB et v les variations en pourcentage de la vélocité de la monnaie.

L'évolution de la demande de monnaie à court- et long-terme

L'équation précédente permet d'étudier séparément le cas du long-terme et du court-terme. En effet, le court-terme et le long-terme sont dominés par des chocs différents.

Sur le long-terme, les chocs de vélocité ne sont pas si importants et on peut les supposer nuls. La vélocité de la monnaie étant constante, on retrouve les résultats de la théorie quantitative de la monnaie.

Le court-terme est dominé par les chocs de vélocité, alors que la croissance et l'inflation n'y ont pas d'importance. Si on abandonne l'hypothèse de constance de la vélocité, il est cependant possible de conserver l'hypothèse de neutralité de la monnaie, qui veut que les variations de la masse monétaire n'influencent pas le PIB. Ce dernier reste donc constant. Si la masse monétaire est constante, on trouve alors l'équation suivante :

$\pi ={\frac {\Delta V}{V}}$

En clair, la théorie monétariste nous dit que sur le court-terme, les variations des prix sont causées par des variations de la vélocité de la monnaie. Une forte hausse de la demande de monnaie entraîne une chute de la vélocité et donc une forte baisse des prix. Et inversement, une baisse de la demande de monnaie entraîne une hausse des prix et de la vélocité. Le tout explique le comportement des prix sous l'étalon-or, une période où la masse monétaire était gardée assez constante au cours du temps. Sur le court-terme, les prix étaient très variables et pouvaient varier de plusieurs pourcents en quelques semaines ou mois. Ces variations étaient liées aux variations de la vélocité, selon la théorie monétariste, la vélocité n'étant pas des plus stable à court-terme. Mais sur le long-terme, les variations de la vélocité de la monnaie s'annulaient les unes les autres et se lissaient dans le temps, ce qui fait que les prix restaient plus ou moins constants sur le long-terme, la faible croissance de l'époque ne suffisait pas à faire baisser les prix sur le long-terme.

Les rigidités nominales de court-terme

La théorie quantitative de la monnaie se base sur deux hypothèses : la constance de la vélocité de la monnaie et la neutralité de la monnaie. Nous avons vu dans le chapitre précédent que la première hypothèse ne tenait pas la route. Eh bien sachez que la neutralité de la monnaie est une hypothèse qui n'est respectée que si les prix sont flexibles, c'est-à-dire que les entreprises peuvent adapter librement leurs prix en réaction à une variation de la demande ou de l'offre. Mais la flexibilité des prix n'est pas respectée sur le court-terme, du fait des délais de mise à jour des prix, ainsi que pour d'autres raisons. L’ajustement des prix et salaires n'étant pas immédiat, ce qui fait qu'il existe des rigidités nominales, les deux principales étant :

• Une rigidité des prix : les prix mettent un certain temps avant d'égaliser offre et demande, suite à la mise en place d'une politique monétaire quelconque.
• Une rigidité des salaires : les salaires évoluent peu à court-terme, notamment quand il s'agit de les baisser. Peu d'employés accepteraient, à raison, une baisse de salaire, même justifiée par la conjoncture économique.

Dans ce chapitre, nous allons voir quel est l'impact sur l'économie de ces rigidités nominales.

Le lien entre prix et salaires

Dans ce qui va suivre, nous allons montrer qu'il y a un lien entre les salaires nominaux et les prix, la baisse/hausse de l'un entrainant la baisse/hausse de l'autre. Pour comprendre pourquoi, nous devons voir d'où proviennent les salaires. Le modèle que nous allons voir est particulièrement simple : il implique des ménages et des entreprises, qui échangent via un marché des biens/services et un marché du travail. Dans ce modèle, il n'y a pas d'épargne ni de capital (l'un impliquant l'autre). En faisant cela, on garantit que les variations de la vélocité de la monnaie sont nulles, sans compter que l'on ne tient pas compte de l'effet de l'épargne sur l'investissement et donc sur le PIB. Cela simplifie considérablement le modèle.

Le modèle et ses flux

Sur le marché des biens, l'entreprise produit des produits ou services que les ménages achètent. L'entreprise vend ses produits à un prix moyen $P$, les quantités de biens vendues étant notées $Q$. Dans ce cadre, le produit $P\times Q$ est tout simplement égal au PIB nominal et la quantité Q est égale au PIB réel. Le PIB nominal représente donc le chiffre d'affaires total de l'économie, l'ensemble de l'argent qui circule dans l'économie et achète des biens.

$PIB_{nominal}=PIB_{reel}\times P$

Les biens ou services sont produits grâce à deux facteurs de production : le travail des employés, et le capital investit. On omettra le capital dans les raisonnements suivants, ce qui ne change rien à l'idée générale. Étudions maintenant le marché du travail. Sur ce marché, les ménages "vendent" des heures de travail en échange d'un salaire. La somme totale des salaires nominaux est égal au salaire horaire multiplié par le nombre d'heures travaillées. On a alors :

$S_{n}=S_{h}\times L$, avec $S_{n}$ la somme des salaires nominaux, $S_{h}$ le salaire horaire (nominal) et L la quantité de travail.

La quantité de travail fournie correspond à une quantité totale d'heures de travail fournies par les travailleurs. Elle dépend du nombre d'employés (on produit plus avec 1000 employés qu'avec 100), mais aussi du nombre d'heures travaillées par employé (on produit plus en 100 heures de travail qu'en seulement 10).

Pour compléter le modèle, il faut y ajouter ce qui s'appelle une fonction de production, qui est une fonction utilisée dans les théories de la croissance économique. Encore une fois, on omet le stock de capital pour simplifier les explications. Dans ce cas, la production ne dépend que du travail effectué et de la productivité, notée $A$.La fonction de production est alors celle-ci :

$PIB_{reel}=A\times L$

Le modèle au complet est représenté ci-dessous.

Modèle macroéconomique à deux secteurs.

Les variables réelles du modèle

La somme des salaires nominaux n'est autre que le PIB nominal, dans ce modèle. En effet, tout argent dépensé pour acheter quelque chose sera un revenu pour le vendeur. Et ces revenus seront reversés aux salariés, vu que l'on a omis le capital dans le modèle. Ultimement, toute rémunération provient du fait que quelqu'un a payé pour (via les impôts pour les fonctionnaires, directement pour les employés du privé). Donc, les deux équations précédentes sont égales.

$PIB_{reel}\times P=S_{h}\times L$

On divise par le prix, pour isoler le PIB réel.

$PIB_{reel}={\frac {S_{h}}{P}}\times L$

Le terme $S_{h} \over P$ n'est autre que le salaire réel horaire, que nous noterons $S_{r}$.

$PIB_{reel}=S_{r}\times L$

En combinant avec l'équation $PIB_{reel}=A\times L$, on trouve que :

$S_{r}=A$

Cette équation nous dit que le salaire réel est égal à la productivité des employés. Cela explique pourquoi les salaires réels sont généralement rigides : tant que la productivité est stable, les salaires réels doivent rester stables eux aussi. En conséquence, en cas de récession, les salaires réels ne peuvent pas s'adapter pour accommoder la récession.

Les liens entre salaires et prix

Le modèle total est donc composé des équations suivantes :

$PIB_{nominal}=P\times PIB_{reel}=S_{h}\times L$

$PIB_{reel}=S_{r}\times L=A\times L$

${\frac {S_{h}}{P}}=S_{r}=A$

Maintenant, imaginons que les variables nominales soient flexibles, à savoir qu'elles changent sans que les facteurs réels soient modifiés. Dans ce cas, le PIB réel, le salaire réel et la productivité sont inchangés, de même que le niveau d'emploi. Les agents travaillent toujours autant et la productivité ne change pas, les entreprises produisent toujours autant et le PIB réel reste le même. En utilisant l'équation $PIB_{nominal}=P\times PIB_{reel}=S_{h}\times L$, on voit qu'une variation du salaire nominal se répercute sur les prix et le salaire nominal. La seule manière de respecter les équations précédentes est que les salaires suivent les prix : ils doivent baisser ou augmenter dans les mêmes proportions.

Maintenant, ajoutons la rigidité des salaires, ce qui signifie que $S_{h}$ est une constante qui ne varie pas à court-terme. En utilisant l'équation $PIB_{nominal}=S_{h}\times L$, on en déduit que toute variation du PIB nominal se répercute sur l'emploi L : le nombre de chômeurs augmente ou baisse en même temps que le PIB nominal. En injectant la baisse de L dans l'équation $PIB_{reel}=S_{r}\times L$, on voit que la baisse du temps de travail, à productivité égale, se traduit par une baisse du PIB réel et/ou des salaires réels.

• Si le salaire réel ne change pas, alors la productivité est inchangée. En utilisant l'équation $S_{r}=A={\frac {S_{h}}{P}}$, on en déduit que la baisse de $S_{h}$ doit être compensée par une baisse identique de P pour garder A et $S_{r}$ constants. Les prix suivent les salaires : la rigidité des salaires entraîne la rigidité des prix.
• Sinon, le salaire réel doit augmenter pour compenser la baisse de l'emploi. Dans ce cas, vu le lien entre productivité et salaire réel, la productivité doit doubler. Vu que $S_{r}=A={\frac {S_{h}}{P}}$ et que $S_{h}$ est constant, cela signifie que les prix doivent diminuer. On retrouve donc le lien entre baisse du PIB nominal et baisse des prix obtenu avec des prix flexibles. Mais il s'agit d'un cas extrêmement improbable, qui est vraisemblablement irréaliste.

Il faut noter que les raisonnements précédents sont aussi valables quand on remplace la rigidité salariale par la rigidité des prix. Une rigidité des prix a exactement les mêmes conséquences qu'une rigidité salariale, sauf dans le cas improbable de fortes variations de productivité. En cas de réduction du PIB nominal, elle entraîne une réduction du PIB réel et de l'emploi. En cas d'augmentation du PIB nominal, elle entraîne une augmentation du PIB réel et de l'emploi. Qu'il s'agisse de la rigidité des salaires ou de celle des prix, l'une entraîne l'autre, sauf une modification de la productivité aberrante qui sort de nulle part. Et cela n'a rien d'étonnant, quand on sait que les salaires des employés doivent bien venir de quelque part. Le salaire d'un employé est simplement égal à sa productivité multipliée par les prix. Dans ce modèle, si un salarié produit N biens vendus au prix P, il recevra tout l'argent de la vente sous forme de salaires/revenus (il n'y a pas de profit dans ce modèle, vu qu'on a omis le capital). Donc, si les salaires baissent ou montent, les prix doivent suivre le mouvement. Sauf à observer une hausse/baisse de la productivité sortie de nulle part.

On peut interpréter les résultats du modèle précédent à travers la théorie quantitative de la monnaie. On peut noter que le modèle précédent ne prend pas en compte les variations de la vélocité de la monnaie pour une raison simple : nous avons supposé que celle-ci est constante. Le fait est que le modèle précédent ne prend pas en compte l'épargne et donc suppose que la monnaie est exclusivement utilisée pour les transactions (les flèches rouges). Dans ces conditions, la vélocité de la monnaie est non seulement constante, mais de plus égale à 1. Dans ces conditions, toute variation de la masse monétaire entraine une variation égale du PIB nominal. On retrouve alors les résultats du modèle précédent.

• Si les salaires et/ou prix sont flexibles, la politique monétaire n'influence que les prix et pas les variables réelles : on dit que la monnaie est neutre. Les salaires nominaux et les prix évoluent dans les mêmes proportions. L'inflation touche donc aussi bien les prix que les salaires, leurs taux de croissance devant être identiques (ou du moins similaires si on prend en compte d'autres paramètres).
• Si les salaires et/ou prix sont rigides, la politique monétaire influence les variables réelles, essentiellement l'emploi et le PIB réel.

Le lien entre salaires nominaux et emploi

Pour interpréter correctement le modèle précédent, il faut comprendre comment l'évolution des salaires nominaux influence l'emploi. Sans cela, on peut être amené à faire de graves erreurs, notamment quand il faut interpréter des cas de déflation ou les crises économiques. Et c'est un vieux débat de la macroéconomie que celui de l'influence des salaires nominaux sur l'emploi. Encore aujourd'hui, on ne sait pas très bien si une baisse des salaires nominaux augmente ou réduit l'emploi. Le débat a été lancé par Keynes, suite à la publication de son best-seller "Théorie générale de l'emploi, de l'intérêt et de la monnaie". On peut dire qu'il y a un avant et un après Keynes sur cette question. Globalement, Tout dépend de l'interprétation qui est faite de l'équation $PIB_{nominal}=S_{n}\times L=PIB_{reel}\times P$ du modèle précédent.

L'hypothèse classique : l'équilibre de plein-emploi

Pour les économistes classiques, le PIB nominal reste constant dans l'équation $PIB_{nominal}=S_{n}\times L$. Les variations des salaires nominaux sont alors compensées par des variations de l'emploi. Par exemple, une hausse de l'emploi compense la baisse des salaires réels et le PIB nominal reste stable. En clair, une baisse des salaires ne peut qu'inciter les entreprises à embaucher et réduire le chômage.

Pour comprendre cet argument, il faut introduire la modélisation du marché de l'emploi faite par ces économistes. Sur le marché du travail, une offre de travail de la part des ménages rencontre une demande de travail de la part des entreprises. Le prix qui égalise offre et demande est le salaire réel. Avec des prix flexibles, le salaire réel reste le même et la monnaie est neutre, sans effet sur l'emploi. Mais avec des prix fixes, une baisse des salaires nominaux se répercute sur le salaire réel, ce qui stimule l'embauche. On peut résumer cela comme suit :

$\downarrow S_{n}\rightarrow \downarrow S_{r}\rightarrow \uparrow L$

Une conséquence de cette manière de penser est que le chômage ne peut être que frictionnel (lié au fonctionnement imparfait du marché du travail). De plus, les crises économiques sont temporaires et se soignent toutes seules : les salaires (réels et nominaux) tendent à baisser en temps de crise, ce qui entraîne une hausse de l'emploi, ce qui stimule la demande et finit par anéantir progressivement la crise.

Chômage classique et Keynésien.

La théorie de Keynes

Keynes fût le premier à remettre en cause les explications précédentes. Pour lui, dans l'équation $PIB_{nominal}=S_{n}\times L=PIB_{reel}\times P$, la baisse des salaires nominaux se traduit par une baisse de la demande, et donc une baisse identique du PIB nominal : l'emploi reste grosso-modo le même. Une baisse des salaires ne peut palier les crises économiques et il existe un chômage involontaire. Pour lutter contre les récessions, il faut que quelque chose fasse varier les salaires réels, sans toucher les salaires nominaux. En utilisant l'équation $S_{r}={\frac {S_{n}}{P}}$, on devine qu'il suffit de faire varier le niveau des prix grâce à une politique monétaire adaptée. En faisant cela, le salaire réel va baisser du fait de l'inflation, ce qui favorise l'embauche et l'emploi.

$\uparrow P\rightarrow \downarrow {\frac {S_{n}}{P}}\rightarrow \uparrow L$

La conclusion est donc qu'une baisse des salaires ne peut doper l'emploi que si elle est accompagnée d'une baisse du taux d'intérêt et/ou une hausse de la masse monétaire. C'est le seul moyen pour garder le PIB nominal constant. Un tel effet de la politique monétaire sur le chômage ne vaut cependant que si les salaires nominaux sont rigides, mais pas les prix. Ce qui demande des variations de productivité, comme montré dans le modèle précédent.

Le modèle IS/LM

Dans ce chapitre, nous allons expliquer comment fonctionne l'économie avec des rigidités nominales et quel est l'effet de la politique monétaire dans ces conditions. Le modèle IS/LM, d'inspiration keynésienne, explique fort bien le fonctionnement de l'économie quand la masse monétaire est constante et que les prix/salaires sont rigides. Il permet de montrer comment la politique monétaire et le marché des biens interagissent, l'interaction entre ces deux marchés étant le fait des taux d'intérêt.

Les briques de base du modèle : la courbe IS et la courbe LM

Pour obtenir le modèle IS-LM, on doit poser quelques hypothèses simplificatrices, qui seront levées dans le chapitre suivant. Les voici :

• L'offre n'est pas limitée, dans le sens où les entreprises peuvent répondre à toute augmentation de la demande en utilisant des capacités laissées inexploitées (heures supplémentaires, embauches, remise en marche de machines, et ainsi de suite).
• L'hypothèse de rigidité des prix est respectée. En conséquence, toute modification des taux directeurs par la banque centrale entraînera une variation similaire des taux réels dans l'économie, tout du moins à court-terme. La conséquence est que le recours au crédit est favorisé, ce qui booste l'investissement des entreprises, les crédits à la consommation ou les crédits immobiliers. En conséquence de cette augmentation de l'investissement, le PIB augmente.
• La quantité de monnaie est fixée par la banque centrale. Cette hypothèse est fondamentale et sera la base de ce chapitre, ainsi que du suivant.

La courbe IS

La première pièce du modèle IS--LM n'est autre que la courbe IS vue en détail dans les chapitres précédents, à une différence près. Dans le modèle IS/LM, la courbe IS relie le taux d'intérêt nominal au PIB, et non le taux réel.

$Y={\overline {Y}}-a\times i$, avec le PIB Y, le PIB potentiel ${\overline {Y}}$, le taux d'intérêt nominal i.

Cette utilisation de taux nominaux par le modèle lui a valu quelques critiques. Il est possible d'amender le modèle IS/LM pour que la courbe IS utilise un taux réel et non nominal, mais le modèle devient alors difficile à représenter sur un graphique. Cependant, l'usage d'un taux nominal n'est pas vraiment un problème grâce à l'hypothèse de rigidité des prix au modèle. Celle-ci dit que les prix sont considérés comme fixes, au moins à court-terme, ce qui fait que l'inflation anticipée reste la même. En conséquence, toute modification des taux nominaux se répercute à l'identique sur les taux réels. Dans ces conditions, utiliser un taux nominal ou un taux réel ne change pas grand-chose, si ce n'est quelques détails mineurs.

La courbe LM

Illustration du marché monétaire.

Sur le marché monétaire, la banque centrale contrôle la quantité de monnaie en circulation dans l'économie. Cette quantité de monnaie, aussi appelée offre de monnaie, rencontre la courbe de demande de monnaie, la rencontre déterminant le taux d'intérêt. On a vu il y a quelques chapitres que la demande de monnaie est une fonction croissante du PIB et une fonction décroissante des taux. On peut illustrer le tout sur le graphique ci-contre, qui montre la rencontre entre une courbe de demande de monnaie décroissante et une courbe d'offre de monnaie verticale.

Quand le PIB augmente, la demande de monnaie augmente, à taux d'intérêt identique. En conséquence, la courbe de demande de monnaie va se déplacer vers le haut et/ou vers la droite, alors que la courbe d'offre va rester immobile. Le point d'intersection de ces deux courbes va donc remonter, ce qui se traduit par une hausse des taux d'intérêt. Dit autrement, les taux d'intérêt augmentent avec le PIB. On peut résumer le tout avec une courbe qui relie PIB et taux d'intérêt sur le marché monétaire : la courbe LM.

Courbe LM

L'équilibre IS/LM

Équilibre IS-LM

Le modèle complet place les courbes IS et LM sur le même graphique, avec le PIB en abscisse et le taux d'intérêt en ordonnée. Les deux courbes se croisent en un point unique, le point d'équilibre IS/LM, qui donne le taux d'intérêt et le PIB qui prévalent dans l'économie. Il faut noter que la position exacte de ce point d'intersection peut varier. out ce qui fait bouger la courbe IS ou la courbe LM fait bouger ce point, et donc faire varier les taux et le PIB. Dans les grandes lignes, la politique fiscale/budgétaire peut faire bouger la courbe IS, alors que la politique monétaire va faire bouger la courbe LM. Mais d'autres paramètres ont aussi leur importance : une révision des anticipations d'inflation va modifier les deux courbes, une augmentation du taux d’épargne va modifier la courbe IS, etc.

L'effet de la politique budgétaire

Effet d'une politique de relance sur l'équilibre IS/LM.

Maintenant, étudions l'effet de la politique budgétaire, qui modifie la courbe IS, en déplaçant celle-ci vers la gauche ou la droite. Le gouvernement peut faire appel à une politique fiscale accommodante (augmenter les dépenses budgétaires ou baisser les impôts) pour augmenter le PIB, déplaçant la courbe IS vers la droite. Une politique budgétaire restrictive aura l'effet inverse (baisse du PIB), ce qui déplacera la courbe IS vers la gauche.

Prenons l'exemple d'une politique budgétaire accommodante, à savoir une politique de relance qui fait se déplacer la courbe IS vers la droite. Le point d'intersection des deux courbes se déplacera vers la droite : le PIB augmente. Mais la courbe LM étant croissante, le point d'intersection va remonter, ce qui signifie une augmentation des taux d'intérêt. Cette augmentation du taux réduire l'investissement, compensant partiellement l'augmentation du PIB induite par la relance. Dit autrement, la politique monétaire va quelque peu contrecarrer la relance budgétaire. Dans le détail, une partie de l'investissement public remplacera l'investissement privé : c'est ce que l'on appelle l'effet d'éviction.

Dans le cas extrême où la courbe LM est verticale, l'effet d'éviction, est total : toute politique de relance est systématiquement compensée par une baisse identique de l'investissement, et le PIB reste le même. C'est la vision des monétaristes, qui pensent que la courbe LM est verticale, ou tout du moins très proche de la verticale. Dans ces conditions, toute politique de relance est inutile : elle ne fera que faire monter le taux d'intérêt, sans effet sur le PIB. La politique monétaire est alors la seule à pouvoir répondre à une variation soudaine de l'activité.

L'effet de la politique monétaire

Effet d'une augmentation de la masse monétaire et/ou d'une baisse de la demande de monnaie sur l'équilibre IS/LM.

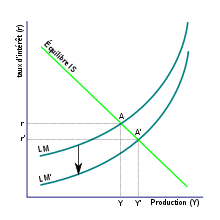
Toute modification de la quantité de monnaie entraîne une variation de la courbe LM. À PIB égal, un accroissement de la quantité de monnaie se traduit par une baisse des taux. Dit autrement, une politique monétaire accommodante entraîne un déplacement vers le bas de la courbe LM, tandis qu'une diminution de l'offre de monnaie la fera monter. La courbe IS restant identique, le point d'intersection des deux courbes va se déplacer vers la droite ou la gauche. Pour une baisse de la courbe LM, cela se traduit par une baisse des taux d'intérêt et une augmentation du PIB. Le mécanisme complet est relativement simple. Une augmentation de la masse monétaire entraîne une baisse des taux d'intérêt, ce qui stimule le crédit et l'investissement : le PIB augmente en proportion. Une diminution de l'offre de monnaie aura l'effet inverse : cela diminuera le PIB, via une contraction de l'investissement.

$\uparrow M~\rightarrow ~\downarrow i~{\xrightarrow {Prix~Fixes}}~\downarrow r~{\xrightarrow {Courbe~IS}}~\uparrow Y$

L'effet d'un choc de demande de monnaie

La demande de monnaie n'est pas fixe, mais peut varier assez fortement dans le temps. Il faut dire qu'elle dépend du comportement des agents économiques, de leur volonté d'épargner, de leur consommation et de bien d'autres choses. On peut comprendre les conséquences d'une variation de la demande de monnaie à partir du schéma offre-demande de monnaie. Une variation de la demande de monnaie, à offre de monnaie égale, se répercute sur les taux : une baisse de la demande de monnaie fait baisser les taux et inversement. Tout cela impacte directement la courbe LM, qui se déplace vers le bas pour une baisse de la demande de monnaie et vers le haut pour une hausse. L'effet se répercute sur le PIB par l’intermédiaire de la courbe IS. Pour comprendre ce qui se passe, prenons l'exemple d'une hausse de la demande de monnaie. À offre de monnaie égale, cela fait augmenter les taux d'intérêt sur le marché monétaire. Cette hausse des taux va, par l'intermédiaire de la courbe IS, réduire le PIB.

$\uparrow M_{d}~\rightarrow ~\uparrow i~\xrightarrow {Prix~fixes} ~\uparrow r~\xrightarrow {Courbe~IS} ~\downarrow Y$

Une conclusion intéressante de ce raisonnement est appelé le paradoxe de l'épargne. Ici, l'épargne considérée est l'épargne monétaire, non-investie sur les marchés financiers ou utilisée pour faire crédit. Dit autrement, il s'agit de l'épargne sous forme de monnaie, que ce soit sous forme d'espèces ou de dépôts bancaires. Si tous les agents économiques augmentent leur épargne monétaire, l'effet sur l'économie est récessif. En effet, l’augmentation de l'épargne monétaire, sous forme de monnaie, se traduit par une forte hausse de la demande de monnaie. L’impact est alors récessif, avec une baisse du PIB. Qui dit hausse de l'épargne monétaire, à masse monétaire constante, dit moins de monnaie pour les transactions, donc moins d'achats et moins de PIB. On peut voir cela comme une baisse de la vélocité de la monnaie induite par un surplus d'effort d'épargne monétaire.

On pourrait croire que l'épargne supplémentaire est utilisée pour l'investissement, ce qui pourrait compenser l'effet précédent. Dans ce cas, la monnaie épargnée est remise en circulation par l'investissement et la vélocité de la monnaie reste la même. C'est effectivement ce qui se passe pour une épargne non-monétaire, investie en crédits ou sur les marchés financiers. Mais le cas en question n’entraîne pas de hausse de la demande de monnaie, vu que l'épargne en question est composée de crédits, de titres ou d'actions, pas de monnaie. Le cas étudié est une hausse de l'épargne monétaire, non-investie, ce qui fait que l'investissement n'augmente pas.

Une autre conséquence est que le contrôle de la masse monétaire n'est pas optimal si la demande de monnaie est instable. Le modèle IS/LM dit que si la banque centrale contrôle la masse monétaire, les fluctuations de $M_{d}$ se répercutent sur le PIB, en sens inverse : une hausse de $M_{d}$ entraîne une baisse de Y et réciproquement. Si la demande de monnaie est instable, à savoir qu'elle fluctue beaucoup, alors le PIB et les variables associées (comme l'emploi et l'inflation) en feront de même. La volatilité de la demande de monnaie se répercute aussi sur l'inflation : elle entraîne une volatilité du PIB, qui se transmet à l'inflation par le biais de la courbe de Phillips. La banque centrale doit alors ajuster sans cesse la quantité de monnaie à sa demande pour garder l'inflation sous contrôle. Rien de tout cela n'a lieu avec un contrôle des taux directeurs, raison pour laquelle cette politique est préférée par les banques centrales.

Les trappes à liquidité

Trappe à liquidité.

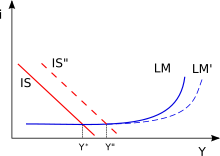
Dans certaines situations, il se peut que la courbe LM soit horizontale sur une portion bien délimitée, là où les taux d'intérêt sont faibles. On parle alors de trappe à liquidité. La raison tient dans le fait que si les taux sont assez faibles, les agents économiques ne font plus la différence entre monnaie et titres de dette sûrs.

En dehors d'une trappe à liquidité keynésienne, les banques préfèrent prêter leurs réserves que de conserver des réserves excédentaires peu ou pas rémunérées. Si la banque centrale injecte de la monnaie sur le marché monétaire, les banques vont prêter la monnaie injectée, ce qui fait que la monnaie est injectée dans l'économie via les prêts des banques. Cet afflux de fonds prêtables fait baisser les taux d'intérêts, par le jeu de l'offre et de la demande entre préteurs et emprunteurs. En conséquence, la création monétaire par la banque centrale modifie les taux d'intérêt. Mais lors d'une trappe à liquidité, les taux sont tellement bas que les banques n'ont pas vraiment intérêt à prêter leurs réserves. À quoi bon prêter leurs réserves à des taux proches de 0.05%, par exemple ? Les banques conservent alors des quantités importantes de réserves excédentaires et toute création monétaire par la banque centrale est épargnée par les banques, elle n'est pas injectée dans l'économie. Dans ces conditions, une variation de la masse monétaire n'a aucun effet sur le taux d'intérêt et cela se traduit par une courbe LM horizontale.

Dans une trappe à liquidité, l'effet d'éviction est strictement nul : une politique de relance n'augmente pas les taux d'intérêt et se traduit par une augmentation du PIB calculée par le multiplicateur keynésien. La politique budgétaire est donc très efficace sur l'économie. Par contre, la politique monétaire ne sert plus à rien, car elle ne permet même pas de modifier les taux d'intérêt. Les canaux de transmission sont presque tous rendus ineffectifs. La courroie de transmission de la politique monétaire casse dès le premier maillon, celui de la relation entre monnaie et taux. La banque centrale a beau créer de la monnaie et l'injecter sur les marchés via des opérations d'open market, les réserves créées sont juste épargnées par les agents économiques en attendant que les taux remontent. La monnaie créée par la banque centrale n'est même pas injectée dans l'économie. Pour résumer, la politique budgétaire est alors efficace, là où la politique monétaire est réduite à une inefficacité totale.

Le modèle CC/LM

Ce chapitre peut être sauté en première lecture, et je conseille au lecteur peu aguerri de passer directement au chapitre suivant. La raison est que ce chapitre est assez complexe et qu'il est nettement moins important que les autres. De plus, sa pertinence empirique est assez faible : les études sur le canal du crédit montrent qu'il est assez peu actif de nos jours.

Le modèle IS/LM est très simple sur de nombreux points et de nombreuses extensions ont tenté de palier cette grande simplicité qui fait la force pédagogique de ce modèle. Parmi ces extensions, celles qui ajoutent un système bancaire au modèle sont assez importantes, du moins pour l'étude de la politique monétaire. Dans ce chapitre, nous allons voir quelques modèles assez simples, dont le modèle CC-LM de Bernanke et Blinder.

Nous avions vu il y a quelques chapitre dans quelques chapitres que la création monétaire influence l'offre de crédit de la part des banques, ce qui porte le nom de canal du crédit. En théorie, une modélisation assez fine du canal du crédit devrait permettre de retrouver une courbe IS après quelques développements mathématiques. Ce n'est ni plus ni moins que ce qu'on fait Bernanke et Blinder, dans leur article daté de 1988. Ils ont élaboré un modèle qui décrit le canal du crédit, à l'exception du canal du rationnement du crédit, et qui a pour résultat une courbe IS décroissante (entre autres résultats). Pour ce faire, le modèle part du bilan des banques, fait quelques hypothèses et arrive à retrouver cette courbe IS spéciale après moult calculs.

Les hypothèses de base du modèle

Le modèle IS-LM faisait une simplification assez importante : il ne faisait pas la distinction entre crédit et obligation. Tout investissement est censé être fait en obligations, ce qui fait que tout argent placé rapporte le même taux et supporte le même risque. Avec cette hypothèse, on peut dériver une courbe IS assez simple. Mais on peut relaxer cette hypothèse, ce qui donne, sous certaines conditions, le modèle de ce chapitre.

Le bilan des banques

Ce modèle fait quelques simplifications qui rendent plus simple l'étude du bilan des banques.

• Le modèle suppose que le passif des banques est composé uniquement des dépôts. Ce qui fait que l'on ne tient pas compte des espèces, des dettes et du capital, tous deux supposés nuls.
• Ensuite, les banques commerciales ont, comme actifs, leurs réserves, des contrats de crédits et des obligations d'état. On néglige les autres actifs, que ce soit les obligations d’entreprise ou les actions, voire l'immobilier.

Avec ces hypothèses, la base monétaire se résume aux réserves bancaires et la masse monétaire aux dépôts. Voici le tout résumé sous forme de tableau :

Actif	Passif
R : Réserves (base monétaire dans le modèle)	D : Dépôts (identique à la masse monétaire dans le modèle)
C : Crédits/emprunts
O : Obligations (dette d'état dans le modèle)

L'actif et le passif sont égaux, par définition, ce qui donne :

$R+C+O=D$

Dans ce qui suit, on note $\sigma$ le taux de réserve (par réserves, on veut dire à la fois les réserves obligatoires et excédentaires). Retranchons les réserves des deux côtés :

$C+O=D(1-\sigma )$

Le multiplicateur du crédit

On peut rajouter qu'il existe une relation entre base monétaire et masse monétaire, par le biais du multiplicateur du crédit. Vu que l'on néglige les espèces, on a :

$D={\frac {1}{\sigma }}R$

En injectant dans l' équation précédente, on a :

$C+O={\frac {1-\sigma }{\sigma }}R$

Cette équation nous dit que les dépôts qu'elle ne met pas en réserve sont prêtés ou investis en obligations. La répartition exacte, à savoir tel pourcentage en obligation, tel autre en crédit et tel autre en réserves excédentaires, est au choix de la banque commerciale. Dans ce qui va suivre, nous allons supposer que la banque alloue un pourcentage $c$ des dépôts libres en crédits.

$C=c\times D(1-\sigma )=c{\frac {1-\sigma }{\sigma }}R$

$O=(1-c)\times D(1-\sigma )=(1-c){\frac {1-\sigma }{\sigma }}R$

L'influence des taux

La valeur de ces coefficients est influencée par les taux, comme nous allons le voir ci-dessous. Si les taux et le risque des crédits et obligations étaient identiques, il n'y aurait pas grand chose à dire. Les banques répartiraient leurs encaisses aléatoirement. Mais dans les faits, crédits et obligations ne sont pas des substituts parfaits : leurs taux sont différents, de même que leur risque. Pour simplifier, on peut établir une relation entre le risque d'un placement et sa rémunération : plus un placement est risqué, plus il doit fournir un taux élevé pour attirer les investisseurs. Ce taux sert par exemple, dans le cas des crédits, à compenser un risque de non-remboursement. Dans ce qui suit, on suppose que les obligations ne sont pas risquées, et que leur taux est un taux sans risque. Cette hypothèse marche bien car les obligations sont un instrument financier assez sûr et sans risque, du moins pour la plupart des obligations d'états ou de grandes entreprises (les plus courantes). Par contre, les crédits sont plus risqués et offrent une sur-rémunération par rapport aux obligations. On peut résumer cela mathématiquement comme suit :

$i_{c}=i_{o}+p_{r}$, avec $i_{c}$ le taux d'intérêt sur les crédits et $i_{o}$ le taux sur les obligations d'état et $p_{r}$ la prime de risque des crédits.

Si on résume les hypothèses du modèle quant aux taux dans un tableau, voici ce qu'on obtient :

Augmentation de :	Masse monétaire	Taux d'intérêt sur les crédits	Taux d'intérêt sur les obligations
Offre d’obligations	$\uparrow$	$\downarrow$	$\downarrow$
Demande d'obligations	$\downarrow$	$\uparrow$	$\uparrow$
Offre de crédit	$\uparrow$	$\uparrow$	$\uparrow$
Demande de crédit	$\downarrow$	$\uparrow$	$\downarrow$

La courbe CC

Maintenant, étudions un peu le coefficient c, qui indique combien de crédits sont accordés. On doit distinguer l'offre de crédits de la part des banques, à savoir la quantité d'argent qu'elles sont disposées à prêter, de la demande de crédits des agents (ménages et entreprises). Et les deux ne sont pas influencés de la même manière par les taux d'intérêt.

Au niveau de l'offre de crédit, les banques peuvent prêter au maximum $D(1-\sigma )$, mais rien ne dit comment elle vont répartir cette somme entre crédit et obligations. Tout dépend de la rentabilité des prêts par rapport aux crédits. Plus les obligations ont un taux élevé, plus les banques vont réduire les crédits pour investir en obligations. Et inversement, plus les taux des crédits sont élevés, plus la banque va les préférer aux obligations. Cela est évidemment modulé par le risque des crédits : plus les crédits sont risqués, plus les banques vont s'en détourner au profit des obligations, considérées comme peu ou pas risquées. Par exemple, les banques peuvent peuvent refuser de prêter à certains clients, par crainte de ne pas être remboursés. Si les taux sont élevés, les obligations deviennent plus intéressantes que les crédits : elles donnent des taux élevés sans risque, alors que les crédits donnent des taux similaires, mais avec un risque bien plus élevé. Par contre, des taux faibles rendent les crédits bien plus rentables que les obligations, ce qui compense le risque pris. Pour résumer, l'offre de crédit des banques est une fonction des taux d'intérêts $i_{c}$ et $i_{o}$, et du risque p.

$C_{s}=c(i_{o},i_{c})\cdot {\frac {1-\sigma }{\sigma }}R$

Ensuite, il se peut que la demande de crédit ne soit pas suffisante : les banques peuvent avoir plus d'argent dans les caisses que de demandes de crédit par les ménages et entreprises. Mathématiquement, cela traduit le fait que l'offre et la demande de crédit s'égalisent. Sachant que la demande de crédit de la part des ménages et entreprises dépend du PIB et des différents taux ($C_{d}(i_{o},i_{c},Y)$), on obtient l'égalité suivante :

$C=C_{d}(i_{o},i_{c},Y)=c(i_{o},i_{c})\cdot {\frac {1-\sigma }{\sigma }}R$

L'investissement I est égal à la quantité de dette circulant dans l'économie, à savoir la somme des obligations et des crédits.

$I=C+O=c(i_{o},i_{c})\cdot {\frac {1-\sigma }{\sigma }}R+(1-c(i_{o},i_{c})){\frac {1-\sigma }{\sigma }}R$

Pour résumer, l'investissement dépend de plusieurs paramètres : les taux sur les crédits et obligations, ainsi que de la quantité de réserves :

$I=f(i_{o},i_{c},R)$

Le PIB est la somme de la consommation, de l'investissement, des exportations nettes et des dépenses gouvernementales. Le PIB dépend donc, par transitivité, des mêmes paramètres que l'investissement, ce qui donne :

$Y=C+I(i_{o},i_{c},R)+G+E=f(i_{o},i_{c},R)$

Cette équation est une version modifiée de la courbe IS vue il y a quelques chapitres. Elle nous dit que le PIB est une fonction non seulement des taux, mais aussi de la quantité de réserves. Toute modification de la base monétaire, des réserves, influence la courbe IS. Ce qui change la donne comparé au modèle IS-LM, où la politique monétaire ne déplace pas la courbe IS, chose que seule la politique fiscale pouvait faire.

L’équilibre CC-LM

Pour clore le modèle, il nous faut ajouter une courbe LM, identique à celle du modèle IS-LM. Les taux d'intérêt pertinents pour cette courbe sont supposés être ceux des obligations et non le taux des crédits. Le tout est résumé par l'équation suivante :

$M=f(i_{b},Y)$

On peut tracer les deux équations, celle qui donne la masse monétaire et celle qui donne le PIB, sur un graphique i-Y. On a alors deux courbes : une courbe LM croissante, et la courbe IS améliorée. On peut alors étudier ce qui se passe quand la politique monétaire change. Une politique monétaire expansionniste augmente la quantité de réserves, ce qui déplace la courbe LM et la courbe IS vers la droite. Une politique restrictive a l'effet inverse.

L'augmentation des réserves fait chuter la différence $(i_{o}-i_{c})$. La raison principale est que plus de réserves signifie plus de dépôts, et donc plus d'argent à prêter : la demande de crédits augmente, ce qui fait chuter le taux des crédits. Le même mécanisme a lieu pour les obligations, mais la demande d'obligations par les ménages se réduit avec le taux d'intérêt. Cela compense l'augmentation de la demande d’obligations de la part des banques. Le taux des obligations chute, mais pas autant que celui des crédits.

$\uparrow R~\rightarrow ~\uparrow D~\rightarrow ~\uparrow C_{d}~\rightarrow ~\downarrow i_{c},\downarrow i_{o}~\rightarrow \downarrow (i_{o}-i_{c})$

On voit donc que la prime de risque des crédits est compréssée par une politique monétaire expansionniste (et inversement pour une politique restrictive). Ce qui décrit bien le fonctionnement du canal du crédit.

Le modèle de Mundell-Flemming

Le modèle IS/LM est un modèle d'économie fermée, ce qui signifie qu'il néglige le taux de change, les exportations et importations, et les échanges entre pays de manière générale. Cependant, on peut le modifier pour en faire un modèle d'économie ouverte, qui tient compte du commerce international et des échanges de capitaux entre pays. Le résultat est une théorie appelée modèle de Mundell-Flemming, qu'il est intéressant d'étudier. Ce modèle nous dit comment la politique monétaire doit se comporter et comment elle agit sur l'économie, que ce soit dans un régime de change fixe ou flexible.

Le modèle : cas général

Le modèle se base sur deux hypothèses.

• Petite économie ouverte : Le modèle décrit une petite économie ouverte, pas les économies assez grandes. Par là, on veut dire une économie ouverte dont les politiques économiques n'ont pas d'impact sur les autres pays. Les autres pays ne sont pas ou très peu influencés par les décisions nationales : le taux d'intérêt et le PIB étrangers ne sont pas influencés par une politique de relance domestique.
• Mobilité parfaite des capitaux : Les capitaux sont libres de circuler d'un pays à un autre, sans aucune forme de frictions. En clair, les agents économiques investissent nationalement et peuvent à tout moment déplacer leur argent d'un pays à un autre. Si un pays a un taux d'intérêt plus élevé que les autres, alors les capitaux affluent dans ce pays, afin de profiter de rendements élevés. Cet afflux de capitaux entraîne une hausse des capitaux prêtables dans le pays et les taux d'intérêts vont baisser en conséquence. Si le taux national est plus faible que pour les autres pays, le mécanisme va en sens inverse. Les capitaux fuient le pays pour être investit dans des pays plus rémunérateurs, ce qui fait baisser le taux national. À l'équilibre, si la mobilité des capitaux est parfaite, le taux d'intérêt national est égal aux taux d'intérêts étrangers.

$i_{national}=i_{etranger}=i^{*}$

La relation entre taux d'intérêt et PIB

Modèle de Mundell-Fleming Model (équilibre IS/LM).

Cette dernière hypothèse se répercute directement sur la courbe IS et la courbe LM. Sur le graphique i-Y, le point d'intersection entre ces deux courbes doit se trouver sur la ligne horizontale définie par $i=i^{*}$. Cette situation est illustrée ci-contre. On voit que les courbes IS et LM s'intersectent au niveau du taux $i^{*}$, quel que soit la situation. Si une courbe bouge, l'autre va automatiquement bouger pour compenser. Les mécanismes exacts dépendent cependant du régime de change : la compensation n'a pas lieu de la même manière suivant que l'on est en régime de change fixe ou flottant.

Pour détailler le modèle, injectons ce taux étranger $i^{*}$ dans leurs équations. Ce taux est fixe, "constant", dans le sens où il n'est pas du ressort de la politique nationale et n'est pas décidé par l'état de l'économie nationale. Il s'agit d'une grandeur exogène, qui est fixée par le modèle. Les seules variables qui peuvent varier sont le PIB/revenu et le taux de change.

$Y=C(Y,...)+G+I(i^{*})+E(e)$

${\frac {M}{P}}=L(Y,i^{*})$

La relation entre taux de change et PIB

Modèle de Mundell-Flemming

Les deux équations précédentes nous montrent comment évoluent les courbes IS et LM. La courbe LM associée est une courbe LM tout ce qu'il y a de plus normale. Par contre, l'équation de la courbe IS change. L'équation précédente nous dit que le PIB ne dépend pas du taux d'intérêt, mais du taux de change. La courbe IS devient une courbe décroissante en fonction du taux de change. Idéalement, on devrait reformuler le modèle en utilisant le taux de change et non le taux d'intérêt, pour voir ce qui se passe quand le taux de change varie. Le modèle se résume alors à deux courbes : une courbe IS décroissante et une courbe LM verticale. Le tout est illustré ci-contre. Le fait que la courbe LM est verticale signifie simplement que la demande de monnaie est indépendante du taux de change, qu'elle est égale à une constante qui dépend du PIB et du taux $i^{*}$. La décroissance de la courbe IS trahit le fait que le PIB augmente quand le taux de change baisse. Du moins, c'est ce que laisse supposer l'équation de la courbe IS, si on suppose que les exportations nettes croissent quand la monnaie se déprécie.

En régime de change flexible

En régime de change flexible, le taux de change peut varier en réaction à la politique fiscale ou monétaire. Sous ce régime, la courbe IS s'adapte aux variations de la courbe LM. L'équilibre est atteint grâce à une modification des taux de change, qui permet au point d'intersection de LM et IS de rester sur la ligne horizontale d'équation $i=i^{*}$. Le fait est que la politique monétaire est contrainte par la contrainte $i_{national}=i_{etranger}=i^{*}$. Elle maintient le taux d'intérêt constant, sous l'effet de la mobilité des capitaux, ce qui fait que la courbe LM se modifie automatiquement.

L'effet de la politique budgétaire

Prenons le cas où la courbe IS se déplace vers la droite, suite à une politique fiscale accommodante. Dans ce cas, l'effet d'éviction va se manifester : de l'investissement public va remplacer l'investissement privé, ce qui cause une hausse du taux d'intérêt. Cette hausse des taux attire les capitaux étrangers et un flux de capitaux supplémentaire va entrer dans le pays. Les flux entrants augmentant, le taux de change va naturellement être impacté et va augmenter. Cette augmentation du taux de change influence les exportations nettes, ce qui se répercute sur le PIB. Au final, la courbe IS revient à sa position initiale. Pour résumer, la politique fiscale ou budgétaire n'a aucune influence en économie ouverte, du moins pour une petite économie ouverte. Elle ne permet pas de relancer l’économie.

$\uparrow Y(\uparrow G\cdot \downarrow T)~{\xrightarrow {effet~d'eviction}}~\uparrow i~\rightarrow ~\uparrow FC(i-i^{*})(flux~entrant~de~capitaux)~\rightarrow ~\uparrow e~\rightarrow ~\downarrow NX(e)~\rightarrow ~\downarrow Y$

Conséquences d'une politique fiscale accommodante en change flexibles. D'abord la courbe IS se déplace vers la droite, mais finit par revenir à sa position initiale, du fait d'une baisse des exportations nettes.

L'effet de la politique monétaire

Prenons maintenant une politique monétaire accommodante, qui augmente la quantité de monnaie domestique. Elle fait baisser le taux d'intérêt domestique, ce qui fait fuir les capitaux étrangers. La fuite des capitaux déprécie le taux de change, ce qui booste les exportations nettes. Les exportations nettes faisant partie intégrante du PIB, ce dernier augmente. Pour être précis, le PIB augmente jusqu’à ce que le taux d'intérêt revienne à sa valeur d'équilibre, le taux d’intérêt étranger. En clair, la politique monétaire est efficace et a un effet net sur le PIB.

$\uparrow M~\rightarrow ~\downarrow i~\rightarrow ~\downarrow FC~\rightarrow ~\downarrow e~\rightarrow ~\uparrow NX(e)~\rightarrow ~\uparrow Y$

Examinons maintenant comment tout cela se traduit graphiquement sur le graphique i-Y. La politique monétaire accommodante a pour effet de déplacer la courbe LM vers la droite. Si la courbe IS reste la même, son point d'intersection avec la courbe LM descend : le taux d'intérêt descend sous le taux étranger. Pour rétablir l'équilibre, la courbe IS doit se déplacer à droite pour que le point d'intersection revienne sur la droite horizontale liée au taux étranger. Ce déplacement est causé, comme dit plus haut, par une variation du taux de change qui ne se voit pas sur le graphique i-Y.

Conséquences d'une politique monétaire accommodante en change flexibles. La courbe LM se déplace vers la droite et la courbe IS suit peu après.

En régime de change fixe

En régime de change fixe, la situation est l'inverse de celle en change flexibles. Cette fois-ci, c'est la courbe LM qui réagit aux variations de la courbe IS et non l'inverse. Encore une fois, cela permet au point d'équilibre IS/LM de rester sur la droite $i=i^{*}$.

Chose importante, le cas d'un régime de change fixe avec taux d'intérêt identique entre pays correspond plus ou moins au cas d'une union monétaire, comme la zone euro. En effet, les taux directeurs sont les mêmes dans toute la zone euro. La politique monétaire est la même partout, vu que la BCE gère toute la zone euro, avec des taux identiques dans tous ses pays. L'hypothèse $i=i^{*}$ est donc valable, si on considère que $i^{*}$ est le taux directeur de la BCE. Pour l'hypothèse de fixité des taux de change, elle est respectée quand tous les pays partagent la même monnaie. Tout se passe comme si les différents pays avaient un taux de change fixe, égal à 1 (la monnaie d'un pays a la même valeur que celle d'un autre). Le modèle présenté ne fait pas la différence entre monnaies différentes de même valeur, et monnaie partagée. Les mathématiques du modèle restent les mêmes dans les deux cas.

L'effet de la politique budgétaire

Prenons une politique budgétaire accommodante. Tout se passe de la même manière que pour les changes flexibles, jusqu'à ce que le taux de change soit modifié. La politique fiscale augmente le PIB, et fait augmenter les taux d'intérêts par effet d'éviction. Les flux entrants de capitaux augmentent alors, ce qui apprécie le taux de change. Et c'est là que les choses changent par rapport aux taux de change flexibles. La banque centrale ne peut pas laisser le taux de change se déprécier et réagit alors. Elle augmente la quantité de monnaie en circulation, ce qui réduit les taux d'intérêt et donc les taux de change. Les taux (intérêt et change) et les exportations nettes reviennent à ce qu'elles étaient avant la politique fiscale, mais le PIB a augmenté, de même que la quantité de monnaie en circulation.

$\uparrow G,\downarrow T~{\xrightarrow {effet~d'eviction}}~\uparrow i~\rightarrow ~\uparrow FC(i-i^{*})(flux~entrant~de~capitaux)~\rightarrow ~\uparrow e,\downarrow NX(e)~{\xrightarrow {Reaction~banque~centrale}}~\uparrow M,\downarrow i,\downarrow e,\uparrow NX(e)\rightarrow \uparrow Y$

Conséquences d'une politique fiscale accommodante en change fixes.

L'effet de la politique monétaire

Passons maintenant à l'étude de la politique monétaire en change fixe. Nous allons étudier le cadre d'un régime de change fixes avec mobilité parfaite des capitaux. Prenons l'exemple d'une politique monétaire accommodante, le cas d'une politique restrictive étant l'exact opposé. Celle-ci fait baisser le taux d'intérêt domestique, ce qui fait fuir les capitaux étrangers et déprécie la monnaie. Pour garder le taux de change fixe, la banque centrale n'a pas le choix que de remonter ses taux à leur valeur initiale. En clair : la politique monétaire n'a plus le contrôle de la quantité de monnaie ou de ses taux, si elle doit contrôler les taux de change. Bien sur, cela ne marche que si les capitaux peuvent fuir, ce qui implique une mobilité des capitaux. Ce résultat ne tient pas si les entrées et sorties de capitaux sont contrôlées par le pays domestique. Un régime de change fixe implique donc : soit une politique monétaire restreinte, soit un contrôle des capitaux.

Conséquences d'une politique monétaire accommodante en change fixes.

Résumé des résultats du modèle

Il est possible de résumer les résultats du modèle dans le tableau à double entrée ci-dessous.

	Taux de change flottant	Taux de change fixe
Politique budgétaire	Inefficace (si mobilité parfaite des capitaux)	Efficace
Politique monétaire	Efficace	Inefficace

Le modèle AD/AS

Le modèle IS/LM a pour défaut d'être un modèle à prix fixes. Pour éliminer cette hypothèse, il faut regarder ce qui se passe quand les prix baissent. L'extension d'IS/LM sans rigidité des prix est un modèle assez connu, nommé modèle AD/AS. Ce modèle est d'une importance capitale pour comprendre certains débats macroéconomiques anciens, comme la controverse entre économistes classiques, monétaristes et keynésiens. Ces deux derniers courants se basaient sur des théories assez simples, toutes dérivées du modèle AD/AS. Les monétaristes et keynésiens acceptaient tous deux les modèles IS/LM ainsi que le modèle AD/AS, mais y ajoutaient quelques hypothèses opposées sur la forme des courbes de demande et d'offre agrégée. En somme, le monétarisme et le keynésianisme sont tous deux des versions particulières du modèle AD/AS, qui est un modèle suffisamment général pour expliquer le fonctionnement de l'économie sous l'étalon-or.

Avec le changement de régime monétaire et l'apparition du contrôle de l'économie par les taux, ces débats sont devenus marginaux, car n'ayant plus de pertinence dans le monde réel. Maintenant que la banque centrale ne contrôle la quantité de monnaie en circulation, les modèles IS/LM et AD/AS sont devenus obsolètes et sont remplacés par les modèles IS/MP et AD/IA. Il n'y a donc plus de controverse entre monétaristes et keynésiens, mais un compromis néo-kéynésien basé sur le modèle à trois équations vu dans les chapitres précédents. Cependant, il est intéressant de comparer les modèles monétaristes et keynésiens, pour comprendre plus finement le fonctionnement de l'économie supposé par ces deux courants. Certains débats ou visions économiques contemporains gardent en effet la trace de ce conflit ancien entre courants économiques opposés et des analogies avec l'économie actuelle peuvent être appliquées.

Description générale du modèle AD/AS

Modèle AD/AS.

Le modèle AD/AS a de fortes ressemblances avec le modèle de base de l'offre et de la demande utilisé en microéconomie. Il fait en effet intervenir deux courbes appelées demande et offre agrégées, qui sont l'équivalent macroéconomique des courbes de demande et d'offre de la microéconomie.

La courbe de demande agrégée indique combien les agents souhaitent acheter en fonction des prix et de leur revenu nominal, la courbe agrégée indiquant quant à elle quelle quantité de biens et services les entreprises vont produire selon les prix. La courbe de demande est naturellement décroissante : plus les prix sont élevés, plus la demande de biens et services diminue.

La situation est moins claire pour la courbe d'offre agrégée, mais il est naturel de supposer que celle-ci est croissante dans la plupart des cas. Des prix plus élevés incitent les producteurs à produire plus pour profiter des prix haut pour faire du profit. Pour faire simple, la demande agrégée n'est autre que la somme des demandes individuelles de chaque marché, de toute l'économie considérée, l'offre agrégée étant la même chose pour les offres de chaque marché. Ces deux courbes donnent chacune de leur côté une relation entre PIB et prix. Ces deux courbes vont s'intersecter en un point qui indique l'état d'équilibre de l'économie, celui dans lequel l'offre agrégée est égale à la demande agrégée. Cet équilibre donne le niveau des prix et la production qui découlent de la rencontre entre l'offre et la demande agrégées.

Précisons que la demande agrégée ressemble à la demande utilisée dans la loi de l'offre et de la demande, mais qu'elle n'a en réalité rien à voir. En effet, le théorème de Sonnenschein, Mantel, Debreu) nous dit qu'on ne peut pas dériver une courbe de demande pour l'ensemble de l'économie, ce que laisse penser le terme "demande agrégée". Derrière ce théorème se cache le fait que décrire une demande globale revient à additionner des choux et des carottes. Les biens vendus sont hétérogènes, alors qu'une courbe de demande n'est définie que pour un bien unique. Et on voit mal comment additionner les courbes de demande des œufs au plat avec la courbe de demande d'ordinateurs neufs. La demande agrégée est de plus démontrée en utilisant des méthodes bien différentes de la microéconomie. Dériver une courbe de demande décroissante en microéconomie demande de postuler des hypothèses assez fortes. Mais la demande agrégée ne demande rien de tout cela et peut exister même si la loi de la demande n'est pas respectée. Pareil pour ce qui est de l'offre. Démontrer que la courbe d'offre microéconomique est croissante demande par exemple des hypothèses sur les rendements factoriels ou une situation de monopole. Mais la courbe d'offre agrégée peut être croissante sans qu'aucune de ces hypothèses ne soit respectée.

L'équilibre entre offre et demande agrégée

Effet d'une variation de la demande avec une courbe d'offre croissante.

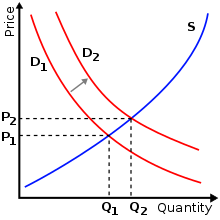
L'équilibre entre offre et demande agrégées peut varier suite à une modification de la demande et/ou de l'offre agrégée. Généralement, les changements de la courbe de demande font suite à un changement de politique monétaire et/ou budgétaire. Des politiques expansionnistes vont déplacer la courbe de demande vers la droite, alors que des politiques interactionnistes vont la déplacer vers la gauche. Par contre, ces politiques n'ont pas d'effet immédiat sur l'offre agrégée. Ce faisant, le point d'équilibre se déplace dans le même sens que la courbe de demande : le PIB et les prix baissent avec une politique restrictive, alors qu'ils augmentent avec une politique expansionniste. Une variation de la courbe d'offre agrégée aura l'effet inverse, selon que l'offre se réduise (déplacement vers la gauche de la courbe) ou augmente (vers la droite). Un déplacement de la courbe d'offre vers la gauche se traduit par une hausse des prix alors que le PIB diminue. À l'inverse, un déplacement vers la droite de l'offre va faire baisser les prix alors que le PIB augmente. On peut ainsi savoir si l'inflation a une origine liée à la demande ou à l'offre : elle va dans le même sens que le PIB si c'est une histoire de demande, en sens inverse pour un problème d'offre.

Différence entre monétarisme et keynésianisme

La différence entre monétarisme et keynésianisme se base sur la forme de la courbe d'offre agrégée et la dérivation de la courbe de demande agrégée. Dans les deux cas, monétaristes et keynésiens s’accordent pour dire que la courbe de demande agrégée est décroissante. Mais les raisons à cela différent grandement selon le courant considéré. Les monétaristes dérivent cette courbe de demande à partir de la théorie quantitative de la monnaie, les keynésiens préférant la démontrer à partir du modèle IS/LM. Cependant, certains monétaristes acceptent le modèle IS/LM comme modèle de l'économie à court-terme, quand les prix sont considérés comme temporairement rigides. Ils font cependant des hypothèses différentes des keynésiens sur la forme de la courbe LM, hypothèses aux conséquences légèrement différentes des prédictions keynésiennes. En réponse à la courbe LM plate des keynésiens, les monétaristes préfèrent une courbe LM verticale. Si la première fait que toute politique monétaire est inefficace alors que la politique fiscale est toute puissante, la seconde hypothèse a les conséquences inverses. Nous verrons cela en détail dans ce qui va suivre, avec une présentation détaillée du modèle monétariste et du modèle keynésien.

Le modèle AD/AS monétariste

Comme dit plus haut, le modèle monétariste se base avant tout sur la théorie quantitative de la monnaie pour décrire le fonctionnement à long-terme de l'économie. À plus court ou moyen terme, ils pensent cependant que l'économie est bien décrite par le modèle IS/LM, dans une certaine mesure. Ils posent cependant quelques contraintes sur la forme des courbes LM et IS, qui traduisent un a priori quant à l'efficacité des politiques monétaires et fiscales. Les keynésiens font pareil, si ce n'est que leurs hypothèses traduisent de a priori inverses. Pour résumer, le modèle monétariste fait quelques hypothèses assez simples :

• la courbe d'offre AS est verticale sur le long-terme ;
• la courbe de demande AD est dérivée de la théorie quantitative de la monnaie pour le long-terme ;
• à court-terme, la courbe LM est verticale.

La courbe d'offre agrégée monétariste

Effet d'une variation de la demande sur les prix avec une courbe d'offre verticale.

Le fait que la courbe AS est verticale traduit le fait que l'économie est, à l'équilibre, au PIB potentiel. Cela traduit le fait que toute variation de la demande agrégée n'a pas d'effet réel : elle n'influence ni le PIB, ni les taux réels. À la place, toute variation de la demande va retenir sur les prix et uniquement sur ceux-ci. Il s'agit tout simplement d'une formalisation de la neutralité de la monnaie. Ce fait est illustré par le graphique sur votre droite. Celui montre ce qui se passe quand la demande agrégée diminue : on voit que le point d'intersection avec l'offre agrégée baisse, ce qui n'a pas d'impact sur le PIB mais en a un sur les prix, qui suivent le mouvement. Une hausse de la demande agrégée aurait l'effet strictement inverse : une hausse des prix, mais un PIB identique. Cela m’amène à faire une petite remarque : tout cela n'est possible que si les prix sont totalement flexibles, toute rigidité des prix étant interdite. Toute variation de la quantité de monnaie doit se répercuter intégralement sur les prix qui doivent évoluer dans le même sens et dans les mêmes proportions que la masse monétaire. Flexibilité des prix, neutralité de la monnaie et courbe d'offre agrégée verticale sont trois formulations différentes de la même hypothèse, du même principe sous-jacent.

La courbe de demande agrégée monétariste

La théorie monétariste dérive la courbe AD à partir de la théorie quantitative de la monnaie. Partons de l'équation $M\times V=Y\times P$. Supposons que le produit $M\times V$ soit une constante K. Dans ces conditions, toute augmentation du PIB devra faire baisser les prix, pour garder leur produit constant. Par exemple, une multiplication par deux du PIB entrainera une division par deux des prix et réciproquement. On peut alors tracer sur un diagramme (P, Y) toutes les combinaisons possibles (P, Y) pour une valeur de M donnée. Le graphe de la fonction obtenue est tout simplement une fonction décroissante du prix en fonction du PIB, soit la courbe AD dérivée plus haut.

Avec cette approche, la courbe AD dépend essentiellement de la quantité de monnaie en circulation. Ainsi, toute hausse ou baisse de l'offre de monnaie entrainera un déplacement de la courbe AD. Une hausse de l'offre de monnaie entrainera une hausse de la constante K, donc du produit $PY$. Ainsi, le PIB sera naturellement supérieur à prix égal, tandis que le prix montera à PIB identique. Cela se traduit graphiquement par un déplacement de la courbe AD vers la droite. Une baisse de l'offre de monnaie aura les conséquences inverses : la courbe AD se déplacera vers la gauche. Cela traduit le fait que, pour les monétaristes, seule la politique monétaire peut jouer un rôle de stabilisation. Lutter contre les récessions et les booms économiques demande d'ajuster la quantité de monnaie en circulation dans l'économie. Une politique fiscale ou budgétaire ne peut pas influencer la masse monétaire et ne peut donc pas influencer la demande agrégée. C'est ce qui es traduit par l'aphorisme de Milton Friedmann : "l'inflation est de tout temps et partout un phénomène monétaire".

Il est possible d'obtenir la courbe AD monétariste à partir du modèle IS/LM, en faisant quelques hypothèses sur la forme de la courbe LM. Ces hypothèses doivent rendre compte du fait que la politique fiscale est totalement inutile et n'a pas d'influence sur le PIB, tandis que la politique monétaire en a un. Pour cela, on peut reprendre ce qu'on a vu dans le chapitre précédent, quand nous avons parlé de l'effet d'éviction. On a vu que lorsque le gouvernement démarre une politique de relance fiscale, cela se traduit par un déplacement de la courbe IS. Pour que cela n'aie pas d'effet sur le PIB, il faut que la courbe LM soit verticale. Dans ce cas bien précis, tout déplacement de la courbe IS ne fera rien sur le PIB, mais aura par contre un effet sur les taux d'intérêts. Cela traduit le fait que la politique de relance subit un effet d'éviction : la hausse de l'investissement public est compensée par une baisse identique de l'investissement privé. Dans le détail, le gouvernement va devoir emprunter de l'argent pour faire sa politique de relance fiscale, en creusant sa dette. Cet emprunt va entrer en concurrence avec l'investissement privé, ce qui fera augmenter les taux d'intérêt. Du fait de l'augmentation des taux, l'investissement va se réduire : c'est un effet d'éviction. Pour résumer, la relance va dévier des fonds destinés à l'investissement privé vers l'achat de dette publique, réduisant d'autant l'investissement privée. Si la courbe LM est verticale, l'effet d'éviction annule totalement l'effet de la relance fiscale. Par contre, la politique monétaire est particulièrement efficace pour modifier la demande, car elle déplace la courbe LM. On retrouve bien l'hypothèse monétariste qui veut que seule la politique monétaire soit efficace.

Le modèle AD/AS Keynésien

Le modèle AD/AS des keynésiens est un peu plus compliqué à comprendre que le modèle monétariste. Cependant, les hypothèses qui le sous-tendent sont assez simples : la courbe d'offre agrégée est plate et la courbe de demande se dérive d'IS/LM avec quelques hypothèses supplémentaires. Pour ceux-ci, la courbe d'offre agrégée est plate, du moins dans une certaine mesure. De plus, la politique monétaire n'a pas d'influence sur la demande agrégée. On va voir que cette hypothèse implique des contraintes sur la forme des courbes IS et LM : la courbe IS doit être plate pour cela. Voyons cela en détail.

La courbe d'offre agrégée keynésienne

Offre agrégée.

Pour les keynésiens, la courbe d'offre agrégée a une forme plus complexe que la courbe AS des monétaristes. Leur version la plus réaliste de la courbe d'offre est illustrée ci-contre. On voit qu'elle est plate pour de faibles niveaux des prix, dans ce qu'on appelle la portion keynésienne. Elle commence ensuite à devenir progressivement croissante, avant de devenir verticale dans sa portion dite classique. L'explication de la forme de la courbe AS est quelque peu compliquée, mais elle fait fatalement intervenir une rigidité des prix ou des salaires d'une manière ou d'une autre.

• Si les prix sont totalement rigides, ceux-ci ne peuvent pas changer quand la demande augmente. En clair, un déplacement vers la gauche ou la droite de la courbe AD ne doit pas changer les prix : cela n'est possible que si la courbe d'offre est plate. Cependant, les keynésiens admettent que la platitude de l'offre ne vaut que si la demande n'est pas trop importante.
• Si la demande est bien plus importante que la capacité maximale de production de l'économie, les entreprises ne pourront pas répondre à la demande en augmentant les quantités vendues. L’économie est alors en situation de plein emploi. Le seul ajustement possible sera alors sur les prix : on retrouve alors la courbe verticale au-delà d'un certain niveau de production/PIB réel.
• Entre les deux, on a une portion de transition qui fait le lien entre offre verticale et horizontale, dans laquelle certaines entreprises ajustent les quantités vendues alors que les autres modifient leurs prix. Dit autrement, le plein emploi est atteint dans certain secteurs, mais pas dans d'autres. Les secteurs en plein emploi ne peuvent qu'augmenter les prix alors que les autres peuvent encore augmenter les quantités. L'effet agrégé est alors un mélange entre hausse des prix et de la production.

La courbe de demande keynésienne

Dérivation de la courbe AD à partir de IS/LM.

La courbe de demande agrégée keynésienne peut se dériver du modèle IS/LM assez simplement. Il est en effet possible de fusionner les courbes IS et LM en une courbe de demande agrégée, qui relie PIB et niveau des prix. Deux mécanismes permettent d'obtenir une relation décroissante : l'effet Pigou d'un côté, et l'effet de la monnaie sur les taux de l'autre.

Commençons par étudier l'effet sur les taux. Quand les prix augmentent, la demande de monnaie $M_{d} \over P$ se réduit alors que l'offre de monnaie reste la même. En conséquence, les taux d'intérêt vont augmenter, ce qui réduira le PIB via la courbe IS. À l'inverse, une baisse des prix entraine une hausse de la demande réelle de monnaie $M_{d} \over P$, ce qui cause une baisse des taux d'intérêt, qui elle-même dope l'investissement, causant finalement une augmentation du PIB par le biais du multiplicateur keynésien. On peut modéliser cette chaîne d'évènements à partir du modèle IS/LM. Avec une hausse des prix, la courbe LM se déplace vers la gauche/le haut. Le point d'intersection se déplace et ont voit que cela augmente les taux et réduit le PIB. Une baisse des prix va déplacer la courbe LM vers la droite/vers lebas, l'équilibre IS/LM est alors lui aussi déplacé vers la droite (la courbe IS reste la même).

$\uparrow P\rightarrow \downarrow {\frac {M_{d}}{P}}\rightarrow \uparrow i\rightarrow \downarrow I\rightarrow \downarrow Y$

En second lieu, il faut prendre en compte l'effet d'encaisses réelles. Pour rappel, celui-ci signifie que les encaisses réelles $M \over P$, détenues par les ménages et entreprises, favorisent la consommation. Plus les agents ont d'argent placé, plus ils auront tendance à consommer. On peut résumer cela avec une relation entre PIB et encaisses réelles qui est de la forme suivante :

$Y=C\left(Y,T,{\frac {M}{P}}\right)+I(r)+G+E(r)$

Si les prix augmentent, les agents voient leurs encaisses réelles diminuer. Bien que les encaisses nominales M restent les mêmes, la hausse des prix leur fait perdre leur pouvoir d'achat. En clair : l'épargne de précaution des agents fond comme neige au soleil et ils réduisent leur consommation pour tenter de la reconstituer. À l'inverse, une baisse des prix augmente la valeur des encaisses réelles, ce qui réduit le besoin d'épargner par précaution. On a donc une relation décroissante entre la dépense (et donc le PIB), et les encaisses réelles.

Un compromis entre théories : la transition entre court et long-terme

On a vu qu'en l'absence de toute forme de rigidité des prix et salaires, la courbe AS est une droite verticale, dont l'abscisse est égale au PIB potentiel. Dans ces conditions, toute variation de la courbe AD se traduira par une variation des prix, sans aucune variation du PIB. Ainsi, politique monétaire et budgétaire n'auraient aucun impact sur le PIB, et ne feraient qu'entrainer de l'inflation. Force est de constater que c'est réellement ce qui se passe à long-terme, comme nous l'avons vu dans le chapitre sur la théorie quantitative de la monnaie. Mais à court-terme, les prix sont rigides et cela entraine une courbe d'offre plate.

Première solution : une courbe d'offre agrégée mi-keynésienne mi-monétariste

Une première solution est de mixer les courbes d'offre agrégée en une seule courbe, capable de rendre compte à la fois des effets keynésiens et monétaristes. La courbe obtenue est subdivisée en trois sections : une section monétariste (aussi dite classique), une section keynésienne, et une section intermédiaire. Dans la portion classique, toute augmentation de la demande entraîne une augmentation immédiate des prix, sans effet sur le PIB. Par contre, toute augmentation dans la portion keynésienne a l'effet inverse : les prix restent stables alors que le PIB augmente. Ce n'est qu'entre les deux que PIB et prix augmentent en même temps, du moins pour un choc positif de demande. Un choc d'offre a un effet similaire sur le PIB, quoique les variations des prix soient inversées. Les prix augmentent pour un choc d'offre négatif, alors que le PIB diminue. Par contre, un choc d'offre positif fait diminuer les prix alors que le PIB augmente.

Graphe AD/AS.

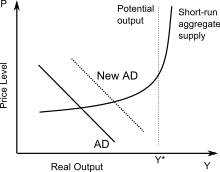
Une différence avec les monétaristes est que les keynésiens supposent que la politique fiscale est très efficace alors que la politique monétaire ne stimule pas la demande. Pour cela, les keynésiens supposent que l'économie est dans une situation de trappe à liquidité, une situation où les taux ne sont pas influencés par la politique monétaire. Dans une telle situation, la courbe LM est totalement horizontale et l'effet d'éviction est totalement nul. Le seul moyen pour augmenter le PIB est de déplacer la courbe IS, ce qui demande une politique fiscale expansionniste.

Seconde solution : deux courbes d'offre agrégée à long et court-terme

Pour réconcilier le court et le long-terme, il est possible d'utiliser deux courbes AS : une courbe AS de long-terme verticale (au PIB potentiel) et une courbe AS de court-terme keynésienne. Le modèle obtenu est alors assez général, au point qu'il met de côté l'efficacité des politiques fiscale et monétaire : les deux sont supposées avoir un effet sur la demande agrégée. L'effet sur la demande est supposé immédiat, ce qui fait que la courbe de demande se déplace une fois pour toute, et ne bouge pas tant que la politique budgétaire ou monétaire ne changent pas. Une politique de relance va ainsi déplacer la demande vers la droite, la courbe s'immobilisant une fois que la politique a fait son effet et restant ainsi tant que la politique est maintenue. À court terme, l'économie suit un fonctionnement keynésien et la courbe d'offre est, au moins partiellement, horizontale. Une politique de relance va donc naturellement augmenter la production sans faire varier les prix. À plus long-terme, l'économie va cependant voir les prix s'adapter et devenir flexibles. La courbe d'offre va alors se modifier et se verticaliser progressivement. Au bout de ce processus, le PIB sera revenu à sa valeur potentielle, mais les prix auront augmentés.

Les raisonnements précédents impliquent que l'effet à court-terme des politiques de relance existe. En effet, il est possible que le PIB dépasse temporairement le PIB potentiel : il suffit que la courbe d'offre horizontale aille au-delà du PIB potentiel et que la relance soit suffisante. Mais cela ne dure pas, les prix finissant par s'adapter et la courbe d'offre finissant par redevenir verticale. Mais à long-terme, l'effet de la relance est nul si l’économie est au PIB potentiel : cela ne sert alors qu'à créer de l'inflation. Par contre, elles ont un sens si l'économie tombe brutalement en-dessous du PIB potentiel, ce qui est le cas lors d'une récession. La banque centrale et le gouvernement peuvent alors relancer l'économie pour la faire revenir à l'équilibre de plein emploi, au PIB potentiel.

La courbe d'offre agrégée croissante

Les méthodes précédentes demandent d'utiliser une courbe croissante pour rendre compte du court-terme, qui devient verticale au long-terme. Pour obtenir sa version à court-terme, il existe deux possibilités : soit postuler que les salaires sont fixes, soit postuler une rigidité des prix. Dans les deux cas, on obtient une courbe croissante, que l'on peut approximativement résumer par une équation de la forme :

$Y={\overline {Y}}+\alpha (P_{1}-P_{2})$

Démonstration

Pour le cas avec les salaires rigides, reprenons le résultat obtenu avec la théorie de Keynes, obtenu dans le chapitre sur les rigidités nominales. On a vu qu'une hausse des prix tend à faire baisser le salaire réel, ce qui favorise l'embauche. $\uparrow P\rightarrow \downarrow {\frac {S_{n}}{P}}\rightarrow \uparrow L$ On peut dérouler le raisonnement plus loin en supposant une relation directe entre emploi et PIB réel : quand le premier augmente, le second suit. Cette hypothèse a quelques défauts. Par exemple, elle suppose que la productivité reste plus ou moins constante, malgré les variations du salaire réel (alors que le modèle du chapitre sur les rigidités nominales supposait l'égalité des deux). De plus, elle suppose que la baisse des salaires réels, qui induit une baisse du pouvoir d'achat, n'impacte pas ou peu le PIB réel. Logiquement, une baisse du pouvoir d'achat des salariés devrait toucher négativement les dépenses et donc le PIB réel. Mais on suppose que la hausse de l'emploi surcompense cet effet. On a alors : $\uparrow P\rightarrow \downarrow {\frac {S_{n}}{P}}\rightarrow \uparrow L\rightarrow \uparrow PIB_{reel}$ On retrouve donc une relation croissante entre niveau des prix et PIB réel, tant que les salaires nominaux restent fixes et si les agents n'anticipent pas les variations des prix. On peut dérouler le modèle comme suit. En premier lieu, les entreprises et ménages négocient un salaire réel $S_{r}={\frac {S_{n}}{P_{1}}}$, mais sur la base des prix au moment de la négociation. Ils n'anticipent pas l'évolution future des prix et supposent que ceux-ci restent constants (ou que les salaires nominaux vont augmenter en même temps que les prix). De ce fait, ils conviennent d'un salaire nominal fixé une fois pour toute. Le salaire réel obtenu est celui qui égalise l'offre et la demande de travail. Ensuite, les prix augmentent et atteignent une valeur $P_{2}$. Cette variation ultérieure des prix, non-prévue, va modifier le salaire réel et doper l'emploi, si les salaires nominaux sont fixes. Pour résumer, on a une relation croissante entre prix et salaires, connue sous le nom de courbe d’offre agrégée. On peut résumer cette relation en supposant que les variations des prix et du PIB réel sont proportionnelles. On a alors : $Y={\overline {Y}}+\alpha (P_{1}-P_{2})$

Démonstration

Pour le cas avec prix rigides, on suppose qu'une fraction $\lambda$ des entreprises met à jour ses prix, alors que le reste ne les met pas à jour. En posant $P_{1}$ le prix d'avant et $P_{2}$ le prix mis à jour, on a : $P=\lambda P_{2}+(1-\lambda )P_{1}=\lambda P_{2}+P_{1}-\lambda P_{1}=P_{1}+\lambda (P_{2}-P_{1})$ On suppose que les prix augmentent avec la production et on décide de le formuler comme suit : $P_{2}=P_{1}+\alpha (Y-{\overline {Y}})$ En combinant les deux équations précédentes, on a : $P=P_{1}+\lambda (P_{1}+\alpha (Y-{\overline {Y}})-P_{1})$ On simplifie : $P=P_{1}+\lambda \alpha (Y-{\overline {Y}})$ On pose alors $\beta =\lambda \alpha$ : $P=P_{1}+\beta (Y-{\overline {Y}})$ La dernière équation est celle d'une courbe d'offre agrégée croissante.

L'étalon-or et le système de Bretton-Woods

On l'a vu dans les chapitres précédents, la quantité de monnaie qui circule dans l'économie est un paramètre primordial pour garantir son bon fonctionnement. Si trop de monnaie se retrouve en circulation, l'inflation surviendra après une période d'embellie économique. Pas assez de monnaie et le spectre de la déflation généralisée des prix menace ! Ce faisant, on peut se demander qui contrôle la quantité de monnaie en circulation, comment est créé la monnaie. Hé bien cette question a eu de nombreuses réponses fort différentes au cours de l'histoire. Entre le système de l'étalon-or, le système de Bretton-woods et le système actuel, il y a eu de nombreuses évolutions. Quoi qu’il en soit, la création de la monnaie et sa mise en circulation est le fait d'institutions regroupées sous le nom de système monétaire. Ces institutions sont assez variées et il n'y a pas qu'un seul et unique modèle existant, bien que tous les pays actuels n'en utilisent qu'un seul. Le premier système monétaire a été basé sur l'or, avant que son échec ne pousse à son abandon. Dans ce chapitre, nous allons voir comment fonctionnait l'économie sous l'étalon-or, avant de passer à ses successeurs.

Avant l'étalon-or

On a vu dans le premier chapitre que les premières monnaies circulaient sous la forme de pièces en métal. Les billets n'existaient pas, pas plus que les chèques ou autres formes d'argent papier ou électronique. La fabrication des pièces est une entreprise exigeante et le choix des métaux à utiliser était crucial. Les métaux utilisés devaient avoir certaines propriétés pour rendre utile l'usage de pièces. En premier lieu, les pièces devaient survivre longtemps et pouvoir être conservées durant plusieurs années. En conséquence, le métal doit résister à la corrosion et être difficile à casser ou à plier . Cependant, il doit être assez malléable pour être travaillée, sans quoi on ne pourrait pas fabriquer de pièces avec. Il ne doit pas non plus avoir d'utilité particulière, ne pas être utilisé dans l'industrie. Sans quoi la fabrication de pièce parasiterait une activité économique utile et divertirait l'usage du métal de celle-ci. Enfin, il doit être assez rare, sans quoi le métal et la pièce n'auront aucune valeur. Divers métaux respectent ce cahier des charges, l'or étant le plus connu, avec l'argent, le cuivre et quelques autres métaux.

Le mono et le bimétallisme

L'or n'était pas le seul métal utilisé dans la fabrication des pièces : certaines étaient en argent ou en cuivre. Mais rares étaient les pays à utiliser plus de deux métaux précieux pour leurs pièces : la plupart utilisaient l'or et l'argent pour leurs pièces, pas plus. Certains pays n'utilisaient qu'un seul métal, le plus souvent l'or, pour leurs pièces. Le système monétaire était alors dit mono-métallique. D'autres pays acceptaient des pièces en deux métaux, par exemple des pièces en or pour les grosses valeurs et des petites pièces en argent. Leur système monétaire était alors dit bimétallique.

À l'époque, la valeur des pièces n'était pas égale à la valeur du métal qui la constitue. Il faut distinguer la valeur faciale (marquée sur la pièce) d'un côté et la valeur des métaux qu'elle contient v. Par exemple, supposons que le prix de l'or soit de 7 sesterces par gramme. Prenons une pièce de 40 sesterces, composée de 5 grammes d'or : sa valeur facile est de 40 sesterces, alors que sa valeur métallique vaut 5 grammes * 7 sesterces par gramme = 35 sesterces. La différence est notable. Quand la valeur métallique d'une pièce devient supérieure à sa valeur faciale, il était plus rentable de fondre la pièce pour revendre le métal. Ce fait bien connu des orfèvres a longtemps été utilisé par ceux-ci pour faire quelques menus profits. Cela fonctionne aussi bien sous monométallisme que sous bimétallisme.

La loi de Gresham

Fait étrange, les premiers systèmes monétaires étaient majoritairement bimétalliques, le monométallisme ayant progressivement remplacé le bimétallisme quand ce dernier a commencé à montrer des signes de faiblesse, résumés par l'adage, émis par Gresham : "La mauvaise monnaie chasse la bonne". Du fait de la loi de Gresham, une des deux monnaie va disparaître, donnant ultimement un système mono-métallique.

La valeur métallique dépend de la valeur de l'or ou de l'argent, ce qui fait que les pièces en or auront donc une valeur différente des pièces en argent, du fait des prix de l'or et de l'argent. Et le fait est que le prix de l'or et de l'argent change régulièrement, ces deux métaux étant vendus et achetés sur un marché des métaux précieux. La valeur des pièces fluctue donc dans le temps, les pièces en or devant plus ou moins chères que les pièces en argent, selon l'état des prix. Il existe donc une sorte de "taux de change métallique" entre pièces et or et en argent, taux de change qui fluctue chaque jour. Par contre, ce taux de change ne se voit pas dans les valeurs faciales des pièces : si une pièce en argent fait 5 sesterces et une pièce en or 40 en valeurs faciales, alors une pièce d'or vaut toujours 8 pièces en argent, et cela ne changera jamais.

Pour résumer, le "taux de change facial" est fixe, alors que le taux de change métallique varie continuellement. Et cette différence entre les taux de change peut être exploitée par les ménages et orfèvres. Pour cela, les agents peuvent échange leurs pièces en or contre des pièces en argent, ou vice-versa. Ce faisant, ils vont acquérir de l'or et/ou de l'argent au cours légal, au taux de change facial. Puis, ils pourront fondre les pièces et vendre l'or ou l'argent au taux de change métallique. Pour résumer, l'échange de pièces permet d'acquérir de l'or/argent à un prix plus bas que le prix de marché : acheter à un prix inférieur pour revendre au prix normal donne naturellement un gain. Si les deux taux de change sont très différents, une telle opération est rapidement rentable. Et ce phénomène ne touche pas que la vente/revente de monnaie, mais joue aussi pour les achats de biens ou services : les agents vont se débarrasser des pièces sous-évaluées et conserver les pièces surévaluées. Ainsi si une monnaie est surévaluée, celle-ci sera rapidement fondue ou thésaurisée, ce qui fait qu'elle disparaîtra au profit de l'autre monnaie. Cela fait qu'une des deux monnaie devient de plus en plus rare, alors que l'autre devient de plus en plus abondante.

L'étalon-or

L'adoption généralisée du monométallisme a été assez lente, mais a fini par se faire avec la victoire de l'or sur l'argent. Ce système perdura assez longtemps, mais fît face rapidement à un défaut : la quantité limitée d'or limitait la création monétaire. Tout l'or du monde ne pouvait pas être utilisé pour fabriquer des pièces, ce qui limitait la quantité de pièces disponibles. Pour résoudre ce problème, les gouvernements ont autorisé l'émission de monnaie-papier, sous la forme de lettres de change, de chèques, de billets et autres. Ceux-ci étaient au départ des instruments pour remplacer les pièces. Tout particulier déposait de l'or à la banque et recevait un billet d'une valeur équivalente, qu'il pouvait utiliser pour les paiements. Ainsi, tout billet était créé en contrepartie d'une quantité d'or équivalente et les banques ne pouvaient émettre plus de billets que leurs réserves d'or ne le permettaient. Du moins, c'est ce que voulait la théorie, mais rien n’empêchait les banques de respecter cette contrainte : certaines banques produisaient plus de billets que prévu, ce qui amenait à des crises bancaires fréquentes. Les ménages qui suspectaient que la banque n'avait pas assez de réserves en or, tentaient de retirer leur argent. Ils convertissaient alors leurs billets en pièces d'or ou en lingots et certains arrivaient quand les caisses de la banque étaient vides : la banque faisait alors faillite.

Pour résoudre ce problème, l'état a alors pris le monopole de la création monétaire, lui seul pouvant créer des billets. Il créa une banque, la banque centrale, seule à pouvoir émettre de la monnaie en échange d'or. Ainsi est né l'étalon-or, un système monétaire où toute monnaie a une contrepartie en or présente dans les caisses de la banque centrale. Sous ce régime, la monnaie était convertible en or (et réciproquement) à un taux fixe, décidé par le gouvernement et gardé stable. Dans de telles conditions, la quantité de monnaie était proportionnelle à la quantité d'or présente dans les caisses des banques centrales et commerciales, le coefficient de proportionnalité étant le taux de change de l'or.

L'inflation sous l'étalon-or

Illustration du CPI historique, pendant et après l'étalon-or.

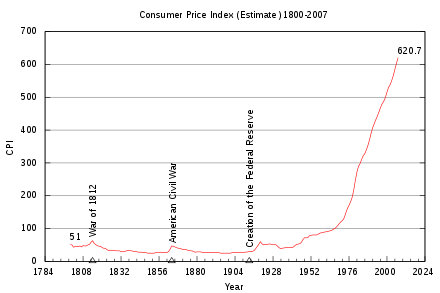
Avec l'étalon-or, la quantité de monnaie est limitée par la quantité d'or minée. La création monétaire dépend alors de l'extraction d'or par les industries minières, mais n'a aucun rapport avec les besoins de l'économie. En conséquence, l'inflation était contrôlée assez facilement : la création monétaire étant frustre, l'inflation qui en découle l'était aussi. Il se trouve que l'inflation, bien que très variable à court-terme, était relativement stable sur le long-terme, si ce n'est nulle. Cependant, l'inflation était beaucoup plus variable sous l'étalon-or, l'économie enchaîna des périodes d'inflation et de déflation assez importantes. Les données historiques montrent que les périodes d'inflation sont aussi fréquentes que les périodes de déflation, inflation et déflation se compensant l'un l'autre : à long-terme l'inflation reste contrôlée.

Il faut cependant noter que la découverte de gisements d'or entraînait une augmentation de la masse monétaire, et donc une forte inflation dans les années ou mois suivants. Ce fût le cas en Espagne, lors de la découverte du nouveau monde et de ses mines d'or, ou aux états-unis suite à la ruée vers l'or californienne de 1848. Ce n'est qu'à la fin de l'étalon-or, dans les années 1950, que la masse monétaire est retombée sous le contrôle des banques centrales. On observe alors une franche remontée des prix et de l'inflation. Des situations d'hyperinflation deviennent possibles, alors qu'elles étaient virtuellement impossibles sous l'étalon-or.

Un système déflationniste

L'étalon-or avait cependant un léger défaut : il s'agit d'un système déflationniste. Il faut en effet préciser que l'économie est en croissance, le PIB réel augmentant quelque peu chaque année. Si la vélocité de la monnaie et la masse monétaire sont constantes (ce qui est le cas ici), alors les prix et le PIB réel doivent baisser chaque année. À court-terme, c'est le PIB réel qui est impacté, avec un effet indirect sur le chômage. À plus long-terme, c'est le niveau des prix qui va s'adapter. Dit autrement, la constance de la masse monétaire entraîne une augmentation du chômage et une réduction de la production, suivie par une déflation généralisée. Or, la déflation est la pire chose qui peut arriver à une économie : elle décourage les ménages de consommer et d'investir, elle réduit les salaires (qui baissent en même temps que les prix), etc. Cette déflation avait un effet sur les taux réels des crédits et des investissements.

Une déflation de x% par an faisait que chaque dollar/franc/... était rémunéré à un taux réel de $r=i-\pi =0-(-x)=x$. Cela limitait drastiquement l'investissement, réduisant d'autant la croissance et la production, et ce pour plusieurs raisons. En premier lieu, les agents économiques n'étaient pas vraiment incités à investir dans des entreprises : celles-ci voient leurs profits baisser en même temps que les prix, alors que l'or gardait la même valeur. Les ménages avaient juste à conserver leur argent sur leur "compte courant" pour le faire fructifier : si son taux nominal était bien nul, son taux réel était en réalité positif compte tenu de la baisse des prix. Nul besoin d'investir et de prendre des risques. Ensuite, les forts taux réels défavorisent les personnes endettées, alors qu'elle favorise fortement les créanciers. En conséquence, peu d'entreprises empruntaient pour financer des investissements ou renouveler l'appareil productif. En conséquence, l'investissement dans l'économie productive était découragé.

Une autre conséquence était que les dépressions et récessions étaient bien plus fortes sous ce système. Tel est le cas de la grande dépression de 1929, la plus sévère de l'histoire des états-unis. D’après les études de Friedmann et Schwartz ont clairement montré que le respect de l'étalon-or a empêché les USA d'utiliser une politique monétaire plus accommodante, qui aurait permis de contenir la dépression. Dans les faits, de nombreux pays sont sortis de l'étalon-or suite à cette dépression, et ce sont ceux qui ont pu sortir de la récession le plus rapidement. Pour résumer, les défauts de l'étalon-or sont :

• une déflation structurelle ;
• une limitation de l'investissement ;
• un effet défavorable sur les personnes endettées (donc pauvres) mais favorable aux créanciers (plus riches) ;
• l'impossibilité de toute politique de stabilisation (lutte contre les récessions) par la politique monétaire.

Des taux de change fixes

Au niveau international, les échanges entre pays étaient payés directement en or, le plus souvent par l'intermédiaire des banques centrales. Cela faisait que les taux de change entre pays étaient fixes, chaque monnaie étant échangeable avec une autre avec un taux fixe. Par exemple, si 5 francs vaut une once d'or et que 10 dollars valent une once d'or, alors 1 franc = 2 dollars. De plus, ce système garantissait des échanges commerciaux équilibrés entre pays, limitant la balance des paiements (la différence entre exportations et importations, pour rappel). Sous l'étalon-or, celle-ci restait nulle, ou tout du moins très faible. La raison est assez simple à expliquer, un mécanisme automatique permettant de contrôler la balance des paiements. Ce mécanisme a été découvert par Hume, d'où le nom de mécanisme de Hume qui lui a été donné. Voyons celui-ci.

Imaginons qu'un pays enregistre un excédent commercial : il a plus d'exportations que d'importations. Le paiement des exportations va se faire en or, ce qui fait que les encaisses d'or de la banque vont augmenter. Ce faisant, la quantité de monnaie va augmenter, ce qui fera augmenter les prix par le biais de l'équation MV = PY. Cette inflation va dégrader la compétitivité : les ménages et entreprises préfèreront acheter des importations que des produits domestiques devenus plus chers. De plus, l'inflation va entraîner une hausse des taux d'intérêts, ce qui augmentera les flux de capitaux entrants, et donc les importations. Les importations étant favorisées, cela va réduire l'excédent commercial initial, les deux mécanismes se compensant totalement quand la balance commerciale est nulle. On peut réutiliser le même raisonnement, mais dans le cas d'un déficit commercial, le résultat étant le même.

Le système de Bretton-Woods

L'étalon-or avait de nombreux défauts, qui ont sonné son glas suite aux deux guerres mondiales. Le financement des dépenses de guerre était une nécessité pour les pays impliqués dans le conflit, mais était contrarié par la fixité de la quantité de monnaie induite par l'étalon-or. L'endettement des états était devenu insoutenable suite aux deux conflits mondiaux, et rembourser la dette de guerre était devenu un défi presque impossible à réaliser, sans compter qu'il fallait reconstruire les pays touchés. Pour résoudre ce problème, de nombreux pays ont abandonné temporairement l'étalon-or pour pouvoir créer de la monnaie à leur guise. Cependant, cela se fit au prix d'une forte inflation, parfois d'une hyperinflation. Mais le mal était fait : l'étalon-or avait déjà été abandonné plusieurs fois par de nombreux pays. Mais l'ambiance était à la paix et à la coopération suit à la fin de la seconde guerre mondiale, et de nombreux pays se coordonnèrent pour créer un nouveau système monétaire international. En 1944, la plupart des pays développés se sont rassemblés dans la conférence de Bretton-woods et sont arrivés à un accord sur le fonctionnement monétaire international. Cet accord entérinait la naissance du FMI et de la banque mondiale, mais aussi celle d'un nouveau système international : le système de Bretton-Woods était né.

Ce système était essentiellement basé sur un système de taux de change fixes entre de nombreux pays. Les pays concernés par l'accord de Bretton-Woods devaient maintenir un taux de change avec le dollar fixe, avec une tolérance de 1%, le dollar étant la seule monnaie à respecter la convertibilité en or. Mais ce système était encore trop proche de l'étalon-or et en héritait des défauts : il limitait la création monétaire, avec un effet nuisible sur la croissance et l'emploi. Il est rapidement apparu que la demande de monnaie ne pouvait pas être garantie par les quantités d'or américaines. Les états-unis ont finalement été obligés d'abandonner la parité entre or et dollar, sous la présidence de Nixon. Le système de Bretton-Woods a été enterré lors des accords de la Jamaïque, qui laissa un système monétaire assez informel basé sur des taux de change flottants (sauf pour quelques pays qui conservent des parités fixes).

Demande de monnaie et taux d'intérêt

Dans le chapitre nommé "La non-constance de la vélocité de la monnaie", nous avons introduit le concept de demande de monnaie, à savoir la quantité de monnaie que les agents souhaitent détenir. Cette dernière dépend de leurs possibilités et de leurs revenus, mais aussi d'autres paramètres. Dans ce chapitre, nous allons voir que les taux d'intérêts influencent la demande de monnaie et nous allons expliquer pourquoi. Le lien entre demande de monnaie et taux d'intérêt est primordial pour comprendre les modèles macroéconomiques complexes, sans compter que cela permet de comprendre pourquoi les banques centrales actuelles ne contrôlent pas la masse monétaire et préférent modifier un taux directeur.

La relation décroissante entre taux d'intérêt et demande de monnaie

Illustration de la courbe de demande de monnaie.

Il existe une relation décroissante entre masse monétaire et taux d'intérêt : plus les taux sont hauts, plus la masse monétaire est basse et réciproquement. Quoi qu’il en soit, on peut représenter cette relation décroissante entre M et i sur un graphique. On voit que celle-ci forme une courbe, appelée courbe de demande de monnaie, notée $M_{d}$. Notons que la position de la courbe de demande de monnaie dépend du niveau des prix et du PIB. En effet, plus les revenus nominaux d'un agent sont élevés, plus les agents vont mettre d'argent de côté et plus ils vont vouloir/pouvoir détenir de monnaie. Et cette intuition se généralise à l'économie toute entière, la somme des revenus nominaux étant égale au produit du PIB par le niveau général des prix. Si prix ou PIB augmentent, la courbe se déplacera vers la droite, et inversement si ils baissent.

À tout instant, l'économie est sur un point de la courbe $M_{d}$, point qui est appelé le point de fonctionnement. Celui-ci est déterminé soit par l'offre de monnaie imprimée par la banque centrale, soit par les taux directeurs qu'elle impose. Cela suppose que la banque centrale peut choisir soit la masse monétaire en circulation dans le premier cas, soit les taux d'intérêts pratiqués par les banques dans le second. Mais en réalité, la banque n'a que deux instruments à sa disposition : la base monétaire et ses taux directeurs. L'influence sur i et sur M est donc indirecte, au mieux.

Pourquoi la courbe de demande de monnaie est-elle décroissante ?

L'influence des taux sur la demande de monnaie se voit sur le diagramme plus haut, mais on est en droit de se demander pourquoi la courbe est décroissante. Il y a diverses raisons à cela.

En premier lieu, taux d'intérêt et création monétaire sont liés par le biais de l'emprunt. Les taux d'intérêt sont le prix que les agents doivent payer pour emprunter de la monnaie. Les taux sont le loyer de l'argent prêté, que le préteur doit verser à l'emprunteur. Et plus la monnaie est rare, plus elle sera chère, d'où la relation entre masse monétaire et taux d'intérêt. Quand les taux sont bas, la monnaie (sous-entendu l’emprunt) n'est pas chère, les agents empruntent plus que d'habitude. Or, chaque emprunt est une création de monnaie, qui augmente la masse monétaire. Inversement, des taux élevés signifie que l'emprunt se paye cher. Peu de personnes acceptent d’emprunter, ce qui réduit la quantité de monnaie en circulation. Nous avons détaillé tout cela dans les chapitres sur la création monétaire, aussi nous ne nous attarderons pas plus là dessus. Mais gardez bien en tête cette interprétation : le taux d'intérêt est le prix de la monnaie, le loyer de l'argent.

En second lieu, les taux influencent la manière dont les agents répartissent leur patrimoine entre monnaie et actifs. Pour simplifier les explications, on suppose que l'argent des agents économiques se répartit entre obligations et monnaie, la répartition dépendant des taux en vigueur. Si les taux varient, les agents vont alors remplacer de la monnaie par des obligations (rémunérées par un intérêt), ou inversement. Par exemple, si les taux montent, les obligations deviennent très rentables par rapport à la monnaie. Les agents vont alors convertir leur monnaie en obligations, ce qui a pour effet de diminuer la quantité de monnaie en circulation. En faisant baisser les taux, la situation inverse prévaut : les agents convertissent leurs obligations en monnaie, augmentant la quantité de monnaie en circulation. En faisant varier le taux d'intérêt, la banque centrale va rendre les obligations plus ou moins intéressantes par rapport à la monnaie et forcer les agents à ajuster la quantité de monnaie en circulation.

Les relations entre demande de monnaie, inflation et taux réel

Si les taux influencent la demande de monnaie, il faut faire la différence entre ce qui tient des taux réels et ce qui tient de l'inflation. Pour cela, partons de l'équation suivante :

${\frac {M_{d}}{P}}=L(Y,i)$

On peut combiner cette équation avec l'équation de Fisher $i=r+\pi$ :

${\frac {M_{d}}{P}}=L(Y,r+\pi )=L(Y,r_{e}+\pi _{e})$

Dans cette équation, on peut étudier deux régimes.

Le premier est le cas, assez irréaliste, où l'inflation n'a pas d'effet sur les taux nominaux, qui restent constants. Par transitivité, on en déduit que l'inflation n'a pas d'effet direct sur la demande de monnaie. Mais l'inflation a un effet indirect sur la demande de monnaie, par le biais du PIB. Les variations induites de la demande de monnaie peuvent alors se répercuter soit sur la masse monétaire, soit sur les prix.

$\uparrow \pi ~\rightarrow ~\downarrow r~\rightarrow ~\uparrow Y~\rightarrow ~\uparrow L(Y,i)~\rightarrow ~\uparrow {\frac {M_{d}}{P}}$

L'autre régime, qui décrit assez bien l'économie sur le long ou le moyen-terme, est celui où le taux réel et le PIB restent fixes. Dans ce cas, ils ne peuvent pas influencer la demande de monnaie, qui se simplifie en :

${\frac {M_{d}}{P}}=L(\pi )$

L'équation nous dit qu'une augmentation de l'inflation (anticipée ou non) réduit la demande de monnaie. Dans le détail, l'inflation se répercute sur les taux nominaux, ce qui réduit la demande de monnaie. L'explication est que l'inflation réduit le pouvoir d'achat de la monnaie avec le temps, ce qui fait que l'inflation rend la détention de monnaie plus couteuse. En conséquence, les agents réagissent à l'inflation (anticipée ou non) en réduisant leurs encaisses réelles.

$\uparrow \pi ~\rightarrow ~\uparrow i~\rightarrow ~\downarrow L(Y,i)~\rightarrow ~\downarrow {\frac {M_{d}}{P}}$

L'influence d'une variation de la masse monétaire sur les taux d'intérêt

Intéressons-nous maintenant à ce qui se passe quand la banque centrale augmente la masse monétaire (le cas où elle la réduit est symétrique). Cette politique expansionniste va naturellement avoir des effets sur les taux d'intérêts. Pour simplifier, plusieurs effets aux conséquences opposées s'affrontent. Le premier, appelé l'effet de liquidité, fait qu'une hausse de la masse monétaire réduit les taux d'intérêt (et inversement en cas de baisse de M). Par contre, les autres effets ont des conséquences strictement inverses : une hausse de la masse monétaire fait monter les taux d'intérêt. L'effet d'une hausse de la masse monétaire sur les taux est donc ambigu. Les économistes estiment que seul le premier effet agit sur le court-terme, alors que les autres effets se manifestent plus tard, sur le long-terme. À court terme, une hausse de la masse monétaire doit donc faire baisser les taux d'intérêt, avant de les faire remonter après un certain temps.

L'effet de liquidité

Le premier effet s'explique en prenant la courbe de demande de monnaie, qui nous dit qu'une hausse de la masse monétaire réduit les taux (et réciproquement). La raison à cela est qu'augmenter la quantité de monnaie en circulation rend la monnaie moins rare, donc moins chère. Inversement, réduire la masse monétaire rend la monnaie plus rare, donc plus chère sur les marchés monétaire, ce qui fait monter son prix (les taux d'intérêt). Cet effet est appelé l'effet de liquidité. Il s'agit d'un effet direct, l'influence de M vers i se faisant sans intermédiaires.

On peut interpréter cet effet à partir de la demande de monnaie ${M \over P}=L(Y,i)$, en supposant que les prix et le PIB sont fixes. Pour le dire autrement, on suppose que la courbe de demande de monnaie est stable, immobile. C’est la condition sine qua non pour que l'effet de liquidité se manifeste. Mais les économistes estiment irréaliste une telle hypothèse. Cependant, si on omet ses variations sur quelques jours ou quelques semaines, alors l'hypothèse n'est pas si problématique et on peut considérer que l'effet de liquidité se manifeste.

Supposons que la banque centrale contrôle la masse monétaire. Si $M$ augmente avec $P$ fixe, alors la demande de monnaie $M/P$ augmente et $L(Y,i)$ doit faire de même. Mais pour faire augmenter ${M \over P}=L(Y,i)$ avec $Y$ fixe, il faut que le taux d'intérêt diminue.

$\uparrow M~{\xrightarrow {Pfixe}}~\uparrow {M \over P}~\rightarrow ~\uparrow L(Y,i)~{\xrightarrow {Yfixe}}~\downarrow i$

Si la banque centrale contrôle le taux d'intérêt, la causalité est inversée et le processus se déroule en sens inverse.

$\downarrow i~\rightarrow ~\uparrow L(Y,i)~\rightarrow ~\uparrow {M \over P}~{\xrightarrow {Pfixe}}~\uparrow M$

Effet de liquidité

Une autre interprétation de l'effet de liquidité est possible. Des économistes ont en effet inventé des modèles théoriques où l'effet de liquidité se manifeste, mais sans que les prix soient fixes, sans avoir une courbe de demande fixe. L'effet de liquidité se manifeste alors si certains agents n'ont pas la possibilité de faire certaines transactions financières. De tels modèles supposent que la monnaie injectée dans l'économie n'est pas répartie également entre tous les agents économiques. Une telle hypothèse est clairement réaliste, bien plus que l'hypothèse des prix fixes (dans le monde réel, les prix sont visqueux et changent avec un certain temps et une inertie non-négligeable). Beaucoup de ménages n'ont pas accès aux marchés financiers et ceux qui y ont accès le font à travers les banques et assurances. Peu d'agents économiques agissent directement sur les marchés monétaires, qui est plus un marché d'intermédiaires financiers. De tels modèles théoriques sont cependant plus compliqués et basés sur des démonstrations microéconomiques complexes, qu'il est difficile d'aborder ici.

Les effets indirects

Dans la section précédente, on a supposé que la courbe de demande de monnaie était stable, dans le sens où elle ne se déplace ni vers la gauche, ni vers la droite. Cela suppose que la masse monétaire est totalement indépendante de la demande de monnaie, ce qui n'est pas le cas dans la réalité. En fait, la masse monétaire a des relations avec le PIB, les prix et les taux d'intérêt, qui influencent la demande de monnaie. Ici, l'effet de la politique monétaire est indirect, dans le sens où il ne passe pas par la courbe de demande de monnaie, mais par d'autres mécanismes. Dans les grandes lignes, une politique monétaire expansionniste déplace la courbe de demande de monnaie vers la droite pour une politique expansionniste et vers la gauche pour une politique restrictive. L'effet sur les taux est alors l'inverse de l'effet de liquidité : une politique expansionniste augmente les taux, alors qu'une politique restrictive les baisse.

Si la banque centrale contrôle la quantité de monnaie, plusieurs effets indirects sont possibles. Un premier mécanisme est le lien entre quantité de monnaie et prix. On verra vers la fin du cours que les deux sont grossièrement proportionnels. En conséquence, une hausse de la masse monétaire entraine une hausse des prix, qui est du même ordre de grandeur. Sous de telles conditions, une hausse de $M$ est compensée par une hausse de $P$, ce qui fait que le rapport $M/P$ reste relativement stable. En théorie, si les prix augmentent du même taux que la masse monétaire, l'effet de liquidité est totalement compensé et la demande de monnaie reste constante. Mais l'effet ne se manifeste qu'à long-terme, ce qui fait qu'il ne compense pas immédiatement l'effet de liquidité. Notons que cet effet peut se compléter si on prend en compte l'effet de l'inflation sur la demande de monnaie. En effet, une hausse de la masse monétaire entraîne une hausse des prix, donc de l'inflation. Si le PIB et le taux réel sont constants, l'inflation se répercute sur les taux nominaux et les fait augmenter. C'est ce qu'on appelle l'effet Fisher. La hausse des taux nominaux réduit ensuite la demande de monnaie. D'autres effets peuvent survenir, mais ils sont généralement mineurs.

Si la banque centrale contrôle les taux nominaux, l'effet principal implique une relation des taux nominaux sur le PIB, lui-même relié aux prix. Les effets en question sont illustrés ci-dessous. Nous détaillerons ces effets dans plusieurs chapitres ultérieurs.

$\uparrow M~\rightarrow ~\uparrow P~\rightarrow ~\uparrow \pi ~\rightarrow ~\uparrow i$

Effets indirects entre M et i.

Dans les faits, le déplacement de la demande de monnaie compense l'effet de liquidité (partiellement ou totalement). Le résultat final est donc un mélange entre les deux, qu'il est bien difficile de décrire. Prenons un exemple simple où l'on double la masse monétaire. Sur le court-terme, les taux d'intérêt chutent, alors que le PIB et les prix restent stables. Seul l'effet de liquidité se manifeste, mais les effets indirects n'ont pas encore eu le temps d'agir. Mais sur le long-terme, les effets indirects se font de plus en plus importants. Les prix et le PIB augmentent, ce qui fait que la demande de monnaie fait de même. Là, tout dépend de l'évolution des prix et du PIB. Si les prix doublent, alors les taux reviennent à ce qu'ils étaient auparavant, avant que la masse monétaire n'augmente.

La demande de monnaie : modèles agrégés

Illustration de la théorie de la préférence pour la liquidité de Keynes.

Souvenez-vous des premiers chapitres, quand nous avons abordé les théories des taux d'intérêts. Nous avons vu que les taux d'intérêt naissent quand une offre de monnaie, offerte par la banque centrale, rencontre une demande de monnaie de la part des agents économiques. La demande de monnaie correspond tout simplement à la quantité de monnaie que les agents économiques souhaitent détenir, que ce soit pour acheter des biens et services ou pour épargner. La masse monétaire dépend du taux d'intérêt : des taux hauts vont inciter les agents à convertir leur monnaie en obligations rémunérés, alors que des taux bas sont une incitation plus faible. Le résultat est que la demande de monnaie diminue avec les taux d'intérêts, la relation entre les deux étant décroissante. Le tout est illustré dans le schéma de droite, la relation entre M et i donnant la courbe de demande de monnaie vue il y a quelques chapitres. Dans ce qui va suivre, nous allons montrer comment est dérivée cette courbe de demande de monnaie, qui joue un rôle particulièrement important quand on étudie la politique monétaire du point de vue des agrégats monétaires.

Les théories globales de la demande de monnaie

Les toutes premières visions de la demande de monnaie la supposaient proportionnelle au PIB. À l'époque, la notion de demande de monnaie était floue et la théorie quantitative ne faisait pas usage de ce concept, du moins pas explicitement. Ce n'est que plus tard qu'on a pu voir le lien entre cette théorie et le concept de demande de monnaie. Le premier économiste à avoir introduit le concept de demande de monnaie fût Keynes, un économiste reconnu dans les années 50 à 80, auteur de la "Théorie générale de l'emploi, de l'intérêt et de la monnaie". Par la suite, d'autres modèles sont apparus, notamment sous l'influence de Milton Friedmann (le chef de file de l'école monétariste), puis Tobin et quelques autres auteurs. Ce n'est qu'après les années 60-70 que des modèles plus sophistiqués sont apparus, peu avant que le domaine de l'étude de la demande de monnaie périclite quelque peu.

La théorie quantitative de la monnaie

Commençons par survoler la toute première théorie de la demande de monnaie, la fameuse théorie quantitative de la monnaie, vue en détail il y a quelques chapitres. Elle suppose l'équation suivante :

${\frac {M_{d}}{P}}=k\cdot Y$, avec k une constante.

Le coefficient k n'est autre que l'inverse de la vélocité de la monnaie. Cette dernière étant supposée constante par la théorie, le coefficient k l'est aussi. La théorie se borne donc à dire que la demande de monnaie est proportionnelle aux revenus et qu'elle n'est pas influencée par les taux d'intérêt, mais seulement par le PIB.

La théorie de la préférence pour la liquidité de Keynes

La théorie suivante a été établie par Keynes. Celui-ci a, parmi ses nombreux écrits, établit la théorie de la préférence pour la liquidité, qui décrit les motifs de détention de monnaie. Cette théorie vise à décrire pourquoi les ménages souhaitent détenir de la monnaie, alors qu'ils ont d'autres actifs rémunérateurs à leur disposition. Pourquoi se priver d'intérêts, perçus grâce à des obligations particulièrement sures, au profit d'une monnaie sans rémunération ? Pour répondre à cette question, cette théorie identifie plusieurs raisons qui font que les agents souhaitent détenir de la monnaie.

Premièrement, les agents souhaitent avoir de la monnaie pour la dépenser, pour consommer. Seule la monnaie peut être échangée contre des biens ou des services. Ce motif, appelé motif de transaction, fait que les agents économiques conservent une certaine quantité de monnaie, qui dépend des dépenses prévues. Cette demande de monnaie dépend essentiellement du revenu, mais pas des taux d'intérêt (ou alors très peu). On peut, en première approximation, considérer que cette demande de monnaie est particulièrement bien décrite par la théorie quantitative de la monnaie.

Ensuite, Keynes a identifié le motif de précaution, le fait que les agents épargnent en cas de coup dur ou de dépenses imprévues. Les sommes épargnées peuvent, en première approximation, être considérées comme constantes (éventuellement proportionnelles aux revenus). On peut cependant signaler que les taux d'intérêt peuvent avoir un effet sur l'épargne de précaution, via un effet de revenu. Des taux forts signifient que les revenus d'intérêts compensent une faible quantité d'épargne de précaution. Si les taux sont bas, les agents économiques vont devoir conserver une grande quantité de monnaie de précaution. Avec des taux haut, les agents peuvent atteindre la quantité de monnaie voulue plus rapidement, du fait de revenus d'épargne plus élevés. La relation entre épargne de précaution et taux est donc décroissante. Cependant, seules les théories plus récentes prennent en compte cet effet.

À cela, il faut ajouter le motif de spéculation, dans lequel les agents décident de conserver une partie de leur monnaie pour l'investir plus tard, en attendant une meilleure occasion. Par exemple, prenons une situation où les taux sont bas et risquent de monter dans le futur : il est plus rentable d'attendre avant d'acheter des obligations, ce qui force l'agent à conserver de la monnaie pour cet achat ultérieur. Dans ce cas, l'argent détenu pour motif de spéculation augmente. Dans le cas contraire, si l'agent anticipe une baisse des taux, les agents vont acheter immédiatement des obligations, réduisant leurs encaisses pour motif de spéculation. L'argent détenu à cause du motif de spéculation dépend fortement des taux d'intérêts anticipés. Des taux haut favorisent l'achat d'obligations, ce qui réduit la demande de monnaie, alors que des taux bas auront la conséquence inverse. La relation entre épargne de spéculation et taux est donc décroissante.

Motif de détention de monnaie	Sensible au revenu	Sensible au taux d'intérêt	Fonction de la monnaie
Motif de transaction	Oui	Non dans la théorie de Keynes. Oui dans les théories plus récentes, comme celle de Baumol-Tobin.	Intermédiaire des échanges
Motif de précaution	Oui dans la théorie de Keynes. Non dans quelques théories plus récentes.	Non dans la théorie de Keynes. Oui dans les théories qui prennent en compte l'effet de revenu. Non dans d'autres classes de modèles.	Réserve de valeur
Motif de spéculation	Non	Oui	Réserve de valeur

Les encaisses réelles sont la somme des trois types de demandes (en termes réels), qui sont respectivement notées $L_{t}$, $L_{p}$ et $L_{s}$ :

${\frac {M_{d}}{P}}=L_{t}+L_{p}+L_{s}$

Keynes supposait que la demande de précaution et de transaction sont proportionnelles au revenu, alors que la demande de spéculation dépendrait uniquement du taux d'intérêt nominal. Cela donne :

${\frac {M_{d}}{P}}=k\cdot Y+L_{s}(i)$

Il est rapidement apparu, suite à des études économétriques, que l'additivité de ces deux demandes n'était pas parfaite. La même quantité de monnaie peut servir à la fois pour plusieurs motifs de détention. Cependant, les intuitions de Keynes restent valables malgré tout, seule la formalisation mathématique de ses idées changeant quelque peu. De manière générale, il faut retenir que les encaisses réelles varient selon deux paramètres : le revenu global (le PIB) et les taux d'intérêt. Plus le revenu est fort, plus les dépenses sont importantes, à cause du motif de transaction. Par contre, des taux d'intérêt favorisent ou défavorisent le motif de spéculation. De manière générale, des taux élevés favoriseront l'épargne, alors que des taux bas favoriseront la conservation de monnaie pour motif de spéculation. Ainsi, cette dernière est donc, une fonction croissante des revenus Y et une fonction décroissante du taux d’intérêt i.

${\frac {M_{d}}{P}}=L(Y,i)$

La demande de monnaie de Friedmann

Après Keynes, une autre formulation de la demande de monnaie fût inventée par Friedmann. Sa théorie est une amélioration de la théorie de Keynes, avec cependant quelques reformulations. Son idée est que la monnaie est un actif parmi d'autres, au même titre que les obligations et les actions. Là où Keynes fusionnait ces actifs en un seul et ne gardait que le taux nominal des obligations, Friedmann intégra plusieurs taux dans la fonction de demande de monnaie. Au taux nominal sur les obligations, il ajoute le taux des actions et de la monnaie.

Déjà, parlons du taux de rémunération de la monnaie. Friedmann part du principe que la demande de monnaie dépend du taux réel de la monnaie. Dans le cas le plus simple, la monnaie est sur un compte courant : le taux nominal de la monnaie est alors de zéro, ce qui donne un taux réel négatif égal à $-\pi$. Du fait de l'inflation, la monnaie perd de son pouvoir d'achat avec le temps. Pour les détenteurs de monnaie, il est plus rentable de la dépenser rapidement, avant que leur argent perdre sa valeur : la consommation augmente et l'argent est dépensé aussi tôt perçu. On peut formuler cette observation en disant que la vélocité de la monnaie augmente, mais on peut aussi dire que la demande de monnaie est alors plus faible vu que les agents économiques ne thésaurisent pas. Dit autrement, la demande de transaction devient sensible à l'inflation, la relation étant négative. Cela est vérifié empiriquement, mais n'est réellement sensible que pour une inflation particulièrement importante, essentiellement dans les cas d'hyperinflation.

${\frac {M_{d}}{P}}=L(Y,\pi _{e},...)$

À cela, il faut ajouter que la monnaie placée sur un compte épargne peut être rémunérée, ce qui nuance l'explication précédente. On a donc :

${\frac {M_{d}}{P}}=L(Y,i_{monnaie}-\pi _{e},...)$

Enfin, il faut ajouter que les obligations et les actions sont en concurrence avec la monnaie en tant qu'actifs. Ils sont rémunérés à un taux ou un rendement qui est supérieur à celui de la monnaie, ce qui les rend plus attractifs pour l'investisseur. Leur sur-rémunération par rapport à la monnaie agit donc négativement sur la demande de monnaie. La fonction de demande de monnaie complète est donc :

${\frac {M_{d}}{P}}=L(Y,i_{monnaie}-\pi _{e},i_{obligations}-i_{monnaie},i_{actions}-i_{monnaie})$

Les modèles du motif de transaction

Diverses théories ont tenté de raffiner l'analyse de Keynes, afin d'en donner des fondations plus solides, plus mathématisées. Certains de ces modèles se sont attaqués à la détention de monnaie pour motif de transaction : ces théories oublient les motifs de spéculation et de précaution. Ces théories, appelées théories d'inventaires, sont relativement nombreuses. Elles expliquent relativement bien la demande de monnaie pour l'agrégat M1, mais fonctionnent mal pour les autres agrégats monétaires. Il faut dire que le M1 est l'agrégat type utilisé pour faire des transactions, contrairement aux autres. La première de ces théories fût le modèle de Baumol-Tobin. Celui-ci a depuis été surmonté par les modèles de type cash in advance, ou money in utility.

Le modèle sans épargne

Nous allons commencer par un modèle extrêmement trivial, qui servira surtout d'introduction pour les modèles suivants. On peut voir ce modèle comme un cas très particulier du modèle de Baumol-Tobin, une simplification très astucieuse. L'extension de ce modèle, appelé modèle sans épargne, donnera directement le modèle de Baumol-Tobin. Ce modèle se base sur les hypothèses suivantes :

• Tout agent économique reçoit à chaque période un revenu, noté $S$ (tous les mois, mettons). Au niveau agrégé, la somme de tous les revenus n'est autre que le PIB nominal $PY$.
• L'agent épargne ce revenu uniquement sous la forme de monnaie.
• Tout agent retire son argent à la banque régulièrement, en $N$ retraits.
• On suppose qu'après ces N retraits (à la fin du mois, mettons), l'agent a retiré l'ensemble de son épargne. Il reçoit alors son prochain revenu, qui renfloue ses caisses du montant du revenu.

Dans ce qui va suivre, nous allons noter $M$ la quantité moyenne de monnaie détenue par l'agent sur une période et $W$ l'épargne initiale.

L'agent retire de son épargne $R={\frac {W}{N}}$ unités monétaires à chaque retrait.

Vu que l'agent retire son argent à intervalle réguliers, la monnaie disponible sur ses dépôts est en moyenne égale à la moitié de son épargne initiale : $M={\frac {W}{2}}$.

Vu que d'après les hypothèses, l'argent épargné provient uniquement du revenu, soit : $W=S=PY$, ce qui donne : $M={\frac {PY}{2}}$.

On voit que la masse monétaire est proportionnelle au revenu nominal, le coefficient de proportionnalité étant par définition la vélocité de la monnaie. Dit autrement, la vélocité de la monnaie est constante. D'après ce modèle très simple, on voit que la vélocité et la monnaie détenue pour motif de transaction ne dépendent pas des taux d'intérêts. Cette constatation reste valide même si la monnaie est rémunérée, du mois si on ne détaille pas plus l'analyse. Cela peut sembler bizarre que la monnaie soit rémunérée, mais c'est le cas en réalité : les livrets bancaires, comme les fameux livrets A/LDDS/LEP, sont considérés comme de la monnaie et font partie de l'agrégat M1/M2. Dans d'autres pays, les comptes courants sont aussi faiblement rémunérés. Dans ces conditions, la rémunération n'impacte que le support d'épargne monétaire : les agents préféreront placer sur leur livret A que sur leur compte courant, mais ils épargneront la même somme avec ou sans rémunération.

Ce modèle, ô combien simple, explique cependant le comportement de beaucoup de ménages dans la zone euro. Certains ménages dépensent tout leur argent en un mois et n'épargnent pas sur le long-terme. En plus des ménages précédents, beaucoup de ménages ne peuvent pas épargner sur les marchés financiers ou dans des placements non-monétaires : peu de ménages ont des assurances-vie, des investissements boursiers ou autres. Enfin, chose plus étrange, ce modèle vaut aussi si les rendements des obligations et placements sont inférieurs aux placements monétaires. Par exemple, si les placements obligataires ont des rendements négatifs, les épargnants vont préférer tout mettre sur leur compte courant ou leurs livrets, ce qui fait que ce modèle sera valide.

Le modèle de Baumol-Tobin

La théorie de Baumol-Tobin ajoute plusieurs hypothèses au modèle précédent :

• Tout agent peut détenir son "épargne" sous la forme de monnaie (non-rémunérée) ou d'"obligations" (en réalité, sous la forme d'instruments rémunérés par un intérêt).
• La conversion d'obligations en monnaie entraine un cout, qui sera noté $C$.

Mathématiquement, la première hypothèse se formule comme suit :

$W=M+B$, avec $W$ la somme épargnée, $M$ la quantité de monnaie épargnée et $B$ l’épargne en obligation.

Vu que l'agent retire son argent à intervalle réguliers, la somme d'argent disponible sur ses dépôts est en moyenne égale à la moitié de son argent : $W={\frac {S}{2}}$.

En moyenne, l'agent retirera donc $R={\frac {S}{N}}$ unités monétaires à chaque retrait.

Il les dépensera à un rythme continu (tous les jours, par exemple), ce qui fait que la somme moyenne de monnaie détenue sous forme d'encaisses monétaires est égale à la moitié de l'argent retiré, ce qui vaut :

$M={\frac {1}{2}}R={\frac {1}{2}}{\frac {S}{N}}={\frac {W}{N}}$

Le coût de la détention de monnaie

L'argent est déposé à la banque sur des dépôts qui lui versent un intérêt $i$ proportionnel à l'argent épargné. Du fait de ces retraits, l'agent se prive des intérêts qu'il aurait perçu s'il avait gardé son argent en dépôt. La perte sèche d'intérêt liée aux retraits est égale à :

$C_{i}=i\times M=i\times {\frac {1}{2}}R={\frac {i}{2}}R$.

Il faut aussi prendre en compte le coût total des retraits, qui vaut $C_{r}=C\times N$. Le coût total $C_{t}$ est donc égal à :

$C_{t}=C_{i}+C_{r}={\frac {i}{2}}R+C\cdot N$

On utilise alors l'équation $N={\frac {S}{R}}$ :

$C_{t}={\frac {i}{2}}R+C{\frac {S}{R}}$

Dans beaucoup de banques, le coût $C$ est composé d'une part fixe et d'une part proportionnelle à la somme retirée : $C=a+bR$, avec $R$ la somme retirée. On a donc :

$C_{t}={\frac {i}{2}}R+\left(a+bR\right){\frac {S}{R}}$

En développant, on a :

$C_{t}={\frac {i}{2}}R+a{\frac {S}{R}}+bS$

Détermination de la demande de monnaie

L'agent économique va chercher à minimiser ce coût, histoire d'économiser le plus possible. Pour déterminer la valeur de la demande de monnaie qui minimise ce coût, nous allons calculer la valeur qui annule la dérivée de l'équation précédente (dérivée par rapport à la demande de monnaie).

${\frac {d(C_{t})}{dR}}=0$

On injecte alors la formule $C_{t}={\frac {i}{2}}R+a{\frac {S}{R}}+b\cdot S$, vue plus haut.

${\frac {d}{dR}}\left({\frac {i}{2}}R+a{\frac {S}{R}}+bS\right)=0$

On applique alors la formule qui dit que la dérivée d'une somme est la somme des dérivées :

${\frac {d}{dR}}\left({\frac {i}{2}}R\right)+{\frac {d}{dR}}\left(a{\frac {S}{R}}\right)+{\frac {d}{dR}}\left(b\cdot S\right)=0$

Le dernier terme, qui représente les couts de transaction proportionnels aux retraits $C=bR$, s'annule. La raison est que le nombre de retraits ne change rien aux couts proportionnels. Retirer une somme en plusieurs fois ou en une seule fois donnera le même coût proportionnel. Dans ce cas, la demande de monnaie dépend du coefficient $b$ et des intérêts : si $b>{\frac {i}{2}}$, il n'est pas rentable d'investir dans des obligations et les épargnants épargnent sur des placements monétaires, en monnaie : on revient dans le cas du modèle sans épargne. Dans l'autre cas, la demande de monnaie est simplement réduite a sa portion congrue. Annulons donc le second terme :

${\frac {d}{dR}}\left({\frac {i}{2}}R\right)+{\frac {d}{dR}}\left(a{\frac {S}{R}}\right)=0$

La dérivée du premier terme vaut $i \over 2$, alors que la dérivée du dernier terme vaut ${\frac {aS}{R^{2}}}$.

${\frac {i}{2}}-{\frac {aS}{R^{2}}}=0$

Ce qui se reformule comme suit :

${\frac {i}{2}}={\frac {aS}{R^{2}}}$

Isolons $R^{2}$ :

${\frac {2aS}{i}}=R^{2}$

Ce qui donne :

$R={\sqrt {\frac {2aS}{i}}}$

On peut alors calculer $M$ à partir de l'équation $M={\frac {1}{2}}R$, ce qui donne :

$M={\frac {1}{2}}{\sqrt {\frac {2aS}{i}}}={\sqrt {\frac {aY}{2i}}}$

Cette équation peut aussi être écrite sous la forme suivante :

$M\propto Y^{\frac {1}{2}}i^{-{\frac {1}{2}}}$

L'élasticité de la demande de monnaie

L'équation précédente nous dit comment la demande de monnaie est influencée par le revenu, le taux d'intérêt, ainsi que par les coûts de retrait. On voit que les taux défavorisent la demande de monnaie quand ils sont hauts. Cette constatation est à l'opposé de la théorie de la préférence pour la liquidité de Keynes, qui postule que le motif de transaction n'est pas influencé par les taux d'intérêt. Enfin, un revenu plus fort augmente naturellement la demande de monnaie, mais cette augmentation n'est pas proportionnelle : elle est proportionnelle à la racine carrée de l'augmentation. On dit en terme technique que l’élasticité de la demande de monnaie est égale à un demi. En comparaison, l'équation nous dit que l'élasticité de la demande de monnaie par rapport aux taux est égale à moins un demi. Enfin, plus les coûts de retrait sont forts, plus la demande de monnaie sera faible.

Les modèles du motif de spéculation

Après avoir vu le motif de transaction, il est maintenant temps de voir les modèles du motif de spéculation. Peu de modèles existent pour modéliser précisément ce motif, les modèles du motif de transaction étant nettement plus nombreux. Néanmoins, la théorie financière a donné de nombreux développement dans ce domaine, avec toutefois une différence de traitement de ce motif. Ces développements abandonnent cependant l'idée de motif de spéculation et ont une vision assez différente de l'idée qu'en avait Keynes. Nous verrons en quoi plus loin dans ce cours.

La théorie de Keynes et formalisation par Tobin

La théorie de Keynes se focalise surtout sur un cas assez particulier d'investissement. Sa théorie se contente d'un marché monétaire et du marché des obligations. La monnaie n'est ainsi en concurrence qu'avec les obligations. Un agent devrait ainsi investir son argent en obligations, histoire de profiter d'un rendement plus élevé. Cependant, il existe une situation où garder son argent permet de faire plus de profits, sans pour autant que les taux des obligations soient négatifs : une future hausse des taux.

On rappelle que le gain que l'investisseur peut obtenir à partir des obligations provient soit des intérêts (le coupon) soit de la plus-value d'une revente des obligations. Or, on a vu il y a quelques chapitres que le prix de revente des obligations dépend des taux d'intérêt. Une baisse des taux entraine une plus-value, ce qui incite à la revente. Et inversement, une hausse des taux entraine une moins-value, ce qui incite l'agent à conserver ses titres. On peut calculer le gain ou la perte en capital induite par une variation $\Delta i$ des taux, à partir de l'équation vue il y a quelques chapitres :

${\frac {\Delta P}{P}}=-{\frac {x}{1+x}}=-{\frac {\Delta i}{i+\Delta i}}$, avec $x=\Delta i \over i$.

Outre ce gain en capital (plus ou moins-value), il faut ajouter les intérêts versés par le coupon. Ce qui donne un gain réel de :

$G=i-{\frac {x}{1+x}}=i-{\frac {\Delta i}{i+\Delta i}}$

Il existe une valeur de $\Delta i$ pour laquelle le gain est nul : le placement est alors identique à la monnaie, le risque en plus. Maintenant, supposons que l’investisseur anticipe une baisse ou une hausse des taux. Il va ainsi faire une anticipation des taux futurs et anticiper un $\Delta i$. Si cette valeur et le taux donnent un gain nul ou négatif, il est plus rentable de garder son argent sous forme de monnaie et ne pas acheter d'obligations. C'est là l'essence du motif de spéculation : ne pas investir à perte, en attendant des jours meilleurs. Évidemment, les raisonnements précédents donnent une forme en tout ou rien, pour un investisseur unique. Mais les agents n'ont pas tous les mêmes anticipations : certains vont anticiper une hausse des taux alors que les autres vont anticiper une baisse, certains vont anticiper une petite baisse et d'autres une baisse importante, etc. Cette hétérogénéité est à l'origine d'une courbe décroissante de la demande de monnaie pour motif de spéculation.

La théorie moderne du portefeuille

De nos jours, la demande spéculative de monnaie est interprétée dans le cadre d'une théorie appelée la théorie moderne du portefeuille. Cette théorie est une théorie générale qui a été inventée par Markowitz en 1952 et qui est aujourd'hui la théorie de référence pour ce qui est de l'investissement. Elle a des défauts et n'est pas parfaite, mais c'est un cadre général qui a fait ses preuves et sert de fondation à l'économie financière actuelle. Précisons qu'il ne s'agit pas d'une théorie qui tente de décrire les marchés financiers ou le comportement réel des investisseurs, mais d'une théorie normative, à savoir une théorie économique qui tente de décrire le comportement optimal/parfait d'un investisseur. Précisément, c'est un modèle qui dit aux investisseurs comment diversifier au mieux leur patrimoine et comment évaluer le prix d'un actif financier. Sa formulation actuelle est le modèle Capital Asset Pricing Model, ou CAPM.

On peut utiliser cette théorie pour expliquer pourquoi les agents économiques détiennent de la monnaie. L'explication tient dans le fait que la monnaie, contrairement aux autres actifs, est un actif sans risques. Le terme sans risques est un peu trompeur, dans le sens où il y a bel et bien des risques liés à la détention de monnaie : l'inflation peut rogner son pouvoir d'achat, et la faillite de votre banque peut vous mettre sur la paille (modulo l'assurance de protection des dépôts, limitée en-deça d'un certain montant). Mais les autres actifs financiers sont eux aussi soumis à ces risques, ainsi qu'à bien d'autres encore. La monnaie est donc l'actif le moins risqué de tous et tout investisseur va en détenir au cas où, par prudence. Précisément, les investisseurs vont répartir leur épargne entre une monnaie sans risque et des actifs risqués, afin d'obtenir un bon compromis entre rendement et risque.

Pour être plus précis, le modèle part du principe qu'un actif est intégralement définit par deux paramètres : son rendement et son risque. Le rendement est tout simplement le taux d'intérêt ou le taux de rendement des dividendes. Plus celui-ci est élevé, plus l'actif est rentable et plus sa détention peut nous rapporter d'argent (du moins, si le rendement reste le même dans le temps). Le risque est définit, dans le cadre du CAPM, par la volatilité du prix de l'actif. L'idée est que le prix d'un actif varie dans le temps autour d'une valeur moyenne. Plus le prix d'une action ou d'une obligation varie dans le temps, plus on considère qu'elle est risquée. On peut rendre compte de l'amplitude de ces variations de prix en calculant l'écart-type et la variance du prix de l'actif. La volatilité n'est ni plus ni moins que la variance du prix de l'actif, ce qui fait qu'elle rend compte de cette variation dans le temps, et donc du risque de l'actif.

La droite d'allocation de capital

Droite d'allocation du capital.

Dans ce qui suit, nous allons supposer que les investisseurs ont accès à seulement deux actifs : la monnaie à et un actif risqué. La monnaie à une volatilité nulle, alors que l'actif risqué a une volatilité $\sigma _{a}$. On suppose que l'agent répartit un pourcentage $m$ de son épargne en monnaie et un pourcentage $1-m$ en actif risqué.

Il se trouve que la volatilité totale du portefeuille (monnaie+actif) est une moyenne pondérée de la volatilité de chaque actif. La monnaie à une volatilité nulle, alors que l'actif risqué a une volatilité $\sigma _{a}$. En clair, on a :

$\sigma =(1-m)\cdot \sigma _{a}$

Il en est de même pour le rendement, à une complication près : la monnaie peut très bien être rémunérée. Elle n'a pas systématiquement un rendement nul, bien que ce soit le cas pour les encaisses les plus courantes. Pensez par exemple à l'argent sur un livret A ou tout autre livret bancaire : c'est bel et bien de la monnaie rémunérée par un intérêt. En toute généralité, on doit donc supposer que la monnaie a un rendement $i_{m}$, assez faible, alors que l'actif a un rendement $i_{a}$ plus élevé. Le rendement total du portefeuille est alors la moyenne pondérée des rendements :

$i=m\cdot i_{m}+(1-m)\cdot i_{a}$

Développons :

$i=m\cdot i_{m}+i_{a}-m\cdot i_{a}$

Factorisons m :

$i=i_{a}+m(i_{m}-i_{a})$

On voit que pour une valeur de m donnée, on obtient la volatilité et le rendement total sont tous deux déterminés : il n'y a, pour cette valeur de m, qu'un unique couple (rendement-volatilité) associé. Si on trace sur un graphique chaque couple (rendement-volatilité) possible, pour toutes les valeurs de m possibles (entre 0 et 1), on voit que le graphe donne une belle droite, appelée la droite d'allocation du capital. Celle-ci est illustrée ci-contre.

La maximisation de l'utilité du couple rendement-volatilité

Les investisseurs font un arbitrage entre la volatilité et le rendement des actifs qu'ils ont à leur disposition. Par exemple, il n'ont aucun intérêt à investir dans un actif très risqué mais dont le rendement est faible : il n'est pas intéressant pour eux de prendre autant de risques, surtout quand d'autres actifs moins risqués ont le même rendement. Les investisseurs n'investirons dans des titres risqués que si le rendement est à la hauteur. Plus la volatilité est élevée, plus l'actif est risqué et plus les investisseurs demanderont un rendement élevé pour détenir ce titre. À l'inverse, ils sont près à accepter des titres à rendements faibles, du moment qu'ils sont sûrs et peu risqués. On peut résumer cela en disant que l'investisseur attribue une utilité à chaque couple rendement-volatilité et souhaite maximiser celle-ci. En notant i le rendement et $\sigma$ la volatilité, on a :

$U=f(i,\sigma )$

L'investisseur souhaite maximiser son utilité U en tombant sur le compromis idéal entre rendement et volatilité. Pour déterminer quel est ce compromis idéal, reprenons le graphe précédent sur lequel on avait tracé la droite d'allocation de capital. Nous allons y ajouter le graphe de la fonction d'utilité, afin de voir ce qui se passe. Ce graphe correspond à tous les couples $i\sigma$ pour lesquels la fonction est maximisée. Tous ces points sont donc équivalents pour l'investisseur (la fonction d'utilité y est maximale), ce qui fait que la courbe obtenue est appelée une courbe d'indifférence. On voit que les deux courbes se coupent en un point, qu'on suppose unique (il faut pour cela que la fonction d'utilité possède certaines caractéristiques, mais passons sur ce genre de détails). Ce point correspond au choix de l'investisseur parmi ceux à sa disposition.

La conclusion est que l'investisseur ne va pas mettre tous ses œufs dans le même panier : il détiendra à la fois de la monnaie et l'actif risqué. La proportion entre monnaie et actif risqué est ajustée de manière à obtenir un couple volatilité-rendement idéal, qui maximise l'utilité de l'investisseur. En conséquence, l'investisseur détient toujours un petit peu de monnaie, afin de réduire la volatilité de son portefeuille. Cela réduit naturellement le rendement de son patrimoine, mais cette réduction est compensée par une réduction du risque encouru. L'agent cherche sans cesse à être à l'équilibre, au point optimal de détention de monnaie. Si l'agent augmentait la quantité de monnaie détenue, il gagnerait du point de vue de la volatilité, mais ce gain ne vaudrait pas la perte de rendement induite. À l'inverse, si l'agent voyait ses encaisses de monnaie réduites, la volatilité de son portefeuille aurait augmenté, sans que cela soit compensé par une hausse psychologiquement suffisante de rendement.

Le choix de l'instrument de politique monétaire

La politique monétaire a un pouvoir de création monétaire, qui lui permet d'imprimer de la monnaie et d'en créer à volonté. Mais la quantité de monnaie imprimée par la banque centrale n'est pas choisie au hasard. On peut intégrer la création monétaire dans les développements précédents en rajoutant une seconde courbe à côté de la demande de monnaie. La demande de monnaie doit être secondée par une courbe d'offre de monnaie, qui indique combien la banque centrale a créée de monnaie en fonction des taux d'intérêt. Si la demande de monnaie indique combien les agents économiques souhaitent conserver de monnaie, alors que l'offre de monnaie est la quantité effective de monnaie que la banque centrale accepte de fabriquer. Les deux courbes se rencontrent en un point, qui indique quels sont les taux et la quantité de réserves/monnaie.

Deux cas extrêmes peuvent être mis en évidence : soit la banque centrale fixe la masse monétaire, soit elle fixe les taux d'intérêt. Le premier cas correspond à une offre de monnaie verticale sur le diagramme i-M, alors que le second est une courbe horizontale. Si la banque centrale choisit la masse monétaire, alors elle doit accepter le taux d'intérêt qui en découle. Et réciproquement, si la banque centrale choisit un taux d'intérêt, la masse monétaire sera déterminée par la courbe de demande de monnaie. Tout ce qu'il faut retenir est que taux d'intérêt et masse monétaire sont deux faces d'une même pièce, deux visages de la demande de monnaie. La banque centrale dispose donc de deux instruments incompatibles. Elle peut contrôler les taux d'intérêts d'un côté, ou contrôler la masse monétaire de l'autre. Les conséquences macroéconomiques sont alors très différentes.

Les conséquences ne sont pas les mêmes selon que M ou i soit fixé par la banque centrale. Pour résumer ce qui va suivre, l'économie est instable si la banque centrale contrôle la masse monétaire. L'inflation et la croissance sont très volatiles. À l'opposé, si la banque centrale garde les taux d'intérêts constants, il y a des risques au niveau de l'inflation. Au passage, le premier cas décrit bien ce qui se passait sous l'étalon-or, quand la quantité de monnaie dépendait des stocks d'or de la banque centrale. Le second cas correspond presque à ce qui se passe dans le système monétaire actuel, où la masse monétaire s'ajuste automatiquement à la demande de monnaie. Mais trêve d'anecdotes, passons à l'étude des deux types de politique monétaire possible : le contrôle des taux directeurs, et le contrôle de la masse monétaire.

Le ciblage de l'inflation avec contrôle de la masse monétaire

Dans les chapitres précédents;, nous avons démontré l'équation suivante :

$\pi ={\frac {\Delta M}{M}}+{\frac {\Delta V}{V}}-{\frac {\Delta Y}{Y}}$, avec M la masse monétaire, V la vélocité de la monnaie et Y le PIB.

Armé de cette équation, nous pouvons étudier ce qui se passe quand la banque centrale contrôle la masse monétaire. La masse monétaire est contrôlée par la banque centrale et la demande réelle de monnaie évolue sans lien avec la politique monétaire. En clair, $M$ et $L(Y,i)$ sont deux variables exogènes, l'inflation dépendant de ces deux variables. En clair, l'équation nous dit que si la banque centrale cible une inflation de 2%, elle doit faire en sorte que :

${\frac {\Delta M}{M}}=g-v+2\%$

Maintenant, étudions ce qui se passe quand la demande de monnaie est stable, puis quand elle ne l'est pas.

La solution optimale si la demande de monnaie est stable

Pour commencer par un cas simple, bien qu'irréaliste. Faisons l'hypothèse que la demande réelle de monnaie $L(Y,i)$ est conservée constante. On a alors ${\frac {\Delta L(Y,i)}{L(Y,i)}}=0$, ce qui donne :

$\pi ={\frac {\Delta M}{M}}$

En soi, ce résultat est tout sauf étonnant. Postuler une demande de monnaie constante revient à postuler une vélocité de la monnaie constante et nous fait donc tomber dans le cadre de la théorie quantitative de la monnaie. Théorie qui a pour résultat que "l'inflation est partout et de tout temps un phénomène monétaire", comme le disait Friedmann. Toute variation de $M$ se répercute totalement sur $P$. La banque centrale peut donc contrôler le niveau des prix et, par conséquence, l'inflation. La banque centrale a juste à augmenter la masse monétaire au rythme de 2% par an pour obtenir une inflation de 2% par an.

Notons que supposer une constance de la demande de monnaie signifie postuler une vélocité constante, mais aussi un PIB constant, d'où le résultat.

Une solution sous-optimale si la demande de monnaie est volatile

L'hypothèse précédente, à savoir que la demande de monnaie reste constante, est irréaliste. Dans les faits, la demande réelle de monnaie subit des chocs de demande de monnaie, des variations de plus ou moins grande ampleur, dont les causes sont variées. Si les variations de $L(Y,i)$ sont de faible amplitude, on peut supposer que $L(Y,i)$ est constante. Sous cette condition, la banque centrale contrôle le niveau des prix assez finement. Mais si les variations de $L(Y,i)$ sont plus amples, alors la banque centrale devra les compenser par une variation de même ampleur de la masse monétaire.

Si la vélocité de la monnaie est constante, on a :

${\frac {\Delta M}{M}}=\pi +g$

Cette équation nous dit que si la banque centrale a juste à faire croître sa masse monétaire au même rythme que le PIB + sa cible d'inflation. Si elle veut une inflation de 2%, elle doit faire croître sa masse monétaire à un taux égal à $g+2\%$. Prédire la croissance sur une année n'est pas tellement compliqué pour la banque centrale, mais n'est jamais un exercice certain. Cependant, elles y arrivent suffisamment bien pour cela ne soit pas un problème.

Mais le monde réel n'est pas aussi idéal que les développements précédents peuvent le laisser penser. Dans le monde réel, la vélocité de la monnaie est variable. Et ces variations viennent mettre leur grain de sel, ce qui perturbe la mise en œuvre de la politique monétaire. En effet, les variations de $L(Y,i)$ sont non seulement de grande ampleur, mais aussi imprévisibles, difficiles à anticiper pour la banque centrale. Ce qui fait que de telles variations sont appelées des chocs de vélocité.

Si la masse monétaire est gardée constante ou qu'elle croît à un rythme constant, la banque centrale n'arrive pas adapter la masse monétaire. Précisons que si la masse monétaire ne peut pas compenser les variations de vélocité, alors autre chose s'en charge. Cet autre chose, ce sont les taux d'intérêts. En clair, le contrôle de la masse monétaire se traduit par des taux d'intérêt extrêmement volatils. Ce qui est intuitif à comprendre, quand on y pense. La courbe de demande de monnaie donne une relation entre masse monétaire et taux d'intérêt. Tout mouvement de cette courbe se répercute soit sur les taux, soit sur la masse monétaire, soit sur les deux. Si la banque centrale contrôle la masse monétaire, alors les taux doivent bouger avec la courbe de demande de monnaie. Et inversement si les taux sont fixés : c'est la masse monétaire qui s'ajuste.

Le résultat précédent permet d'expliquer le comportement des taux d'intérêt lors de la période de l'étalon-or, durant laquelle la masse monétaire était assez bien maintenue constante. La volatilité des taux d'intérêt était assez importante sur le court-terme, avec des variations assez fortes durant la même journée et de fortes fluctuations au cours du mois. La courbe de demande de monnaie n'était pas stable et ses variations se répercutaient au jour le jour sur les taux d'intérêt. Or, les taux d'intérêts (réels) ont en effet un effet à long-terme sur le PIB et l'inflation. Nous détaillerons ces relations dans les chapitres suivants, vu qu'elles ne sont pas nécessaires pour comprendre ce qui va suivre. Tout ce qu'il faut savoir est que la volatilité des taux d'intérêt se répercutent sur le PIB, puis sur le niveau des prix. L'économie est donc assez instable, avec de fortes variations à long ou moyen-terme. Et cela est aggravé par le fait que la demande de monnaie suit les cycles économiques : elle augmente lors des récessions/dépressions, et baisse lors des phases d'expansion. Si la masse monétaire est constante, les variations de la demande de monnaie aggravent les récessions et intensifient les expansions. Ce caractère procyclique est clairement établi par les données historiques.

Le ciblage de l'inflation avec contrôle des taux d'intérêt

Pour résumer, les chocs de vélocité posent de lourds problèmes à la banque centrale. Ils la forcent à revoir sa masse monétaire au jour le jour, pour compenser des chocs de vélocité allant de petits chocs sans grande importance à des fluctuations de grande ampleur. Pire : les chocs de vélocité sont imprédictibles par la banque centrale. Une solution, assez évidente, serait que la banque centrale adapte la masse monétaire en fonction de la demande de monnaie, pour compenser les chocs de vélocité. Et c'est exactement ce qui se passe quand la banque centrale contrôle les taux d'intérêts.

Les taux d'intérêts fixes et la compensation des chocs de vélocité

Si les taux d'intérêts sont fixes, alors les chocs de vélocités sont compensés par une variation égale de la masse monétaire. Dans ce cas, l'offre de monnaie fournie par la banque centrale est horizontale. Elle doit accommoder la quantité de réserves et ses emprunts qui découle de la rencontre entre la courbe horizontale d'offre de monnaie et la demande de monnaie. Elle ne peut pas contrôler la masse monétaire, et doit laisser filer la quantité de monnaie, la laisser s'adapter à la demande.

Dans les grandes lignes, le choix entre contrôle des taux ou de la monnaie dépend de la volatilité de la demande de monnaie. Plus elle est instable, plus le contrôle de la masse monétaire est mauvais et plus le ciblage des taux directeurs est intéressant. Si on contrôle la masse monétaire, les chocs d'inflation sont compensés, mais les chocs de vélocité rendent les taux très volatils, ce qui se répercute sur les marchés financiers, l'investissement, la production et l'emploi assez problématique.

Les chocs d'inflation doivent être compensés par une variation des taux directeurs

Passons maintenant au cas d'un horizon de moyen-terme, où la demande de monnaie varie avec les prix, qui eux-mêmes dépendent de la masse monétaire. Plus la masse monétaire augmente, plus les prix montent (à demande de monnaie égale) et la demande de monnaie suit. En conséquence, toute hausse des prix entraîne une hausse de la demande de monnaie. Si la banque centrale garde ses taux fixes une bonne fois pour toutes, cela peut poser quelques problèmes. En effet, la banque centrale, en ciblant les taux, augmente la masse monétaire au même rythme que la demande de monnaie. Ce faisant, une hausse des prix entraîne une hausse de la demande de monnaie, qui entraîne une hausse de la masse monétaire, qui elle-même entraîne une hausse des prix, et ainsi de suite. L'inflation devrait donc exploser de manière exponentielle. Une politique de taux stables compense les chocs de vélocité, mais les chocs d'inflation s'emballent et l'inflation explose de manière exponentielle. Le contrôle des taux marche donc bien à court-terme, mais pas sur le long-terme. À plus long-terme, les taux doivent varier, afin que la croissance de la masse monétaire ne s'emballe pas.

La morale est que si les chocs de vélocité doivent être compensés par une variation de la masse monétaire, les variations des prix ne le doivent pas. Pour résoudre ce problème, il suffit d'adapter la masse monétaire seulement pour accommoder les variations de la demande de monnaie qui ne sont pas liées aux prix. En clair, les prix ne doivent pas se répercuter sur la masse monétaire, mais les chocs de vélocité le doivent. D'un côté elle autorise la demande de monnaie à fluctuer au même rythme que la vélocité de la monnaie, tout en rendant cette dernière plus stable, de l'autre elle compense l'effet de l'inflation sur la demande de monnaie par une hausse des taux. Le meilleur des deux mondes, en somme : la masse monétaire fluctue avec la vélocité, mais est réduite en réponse à l'inflation.

Pour cela, il suffit de réduire la demande de monnaie quand les prix augmentent, histoire de garder une masse monétaire adaptée. Et pour cela, la banque centrale module ses taux d'intérêt, afin de faire varier la demande de monnaie et/ou d'adapter la masse monétaire. L'idée est que l'inflation doit se répercuter sur les taux d'intérêts (et plus précisément sur les taux réels). Ce comportement est souvent résumé sous la forme d'une règle : la règle de Taylor. Celle-ci dit que la banque centrale doit augmenter ses taux réels quand l'inflation va augmenter et les réduire quand l'inflation menace de baisser. D'un côté, les taux sont constants sur le court-terme (dans une journée, durant un mois, quelques mois, rarement plus), de l'autre ils varient sur le long-terme pour s'adapter aux variations des prix.

L'interaction entre contrôle des taux et politique budgétaire

Dans les chapitres précédents, nous avons étudié la politique monétaire comme si celle-ci était totalement indépendante. Cependant, celle-ci n'est pas totalement indépendante de la politique budgétaire. On a vu dans les chapitres précédents que politiques budgétaire et monétaire peuvent toutes deux agir sur la demande agrégée. Les deux peuvent ainsi être utilisées en tant que politique de stabilisation, pour lutter contre les récessions ou les surchauffes de l'économie. Si la politique monétaire est utilisée en premier lieu, c'est pour sa meilleure réactivité, ainsi que son impact direct sur la quantité de monnaie en circulation (idéal pour contrôler l'inflation). Les deux types de politiques sont indépendants sur le court-terme. Cependant, ce n'est pas le cas sur le long-terme. La politique monétaire peut ainsi avoir un léger impact sur la dynamique de la dette publique de l'état, notamment par son influence sur les taux d’intérêt. Ce chapitre va aborder ce lien, et parler notamment des conséquences de la monétisation de la dette et de la planche à billets.

Rappels : Le budget de l'état

Le gouvernement dépense de l'argent, que ce soit pour des dépenses d'investissement, pour financer la protection sociale, ou pour toute autre chose. En théorie, l'état est censé financer ses dépenses par l'impôt. Cependant, il arrive souvent que l'impôt ne soit pas suffisant pour financer les dépenses du gouvernement, ou au contraire que l'impôt donne naissance à des ressources excédentaires. La différence entre les dépenses gouvernementales et les revenus fiscaux est appelée le déficit budgétaire primaire. Quand celui-ci est nul ou négatif, le gouvernement finance ses dépenses uniquement par l'impôt (et obtient même un surplus en cas de déficit négatif). Mais si le déficit budgétaire est positif, l'état doit trouver des sources alternatives de financement. Il dispose alors de deux possibilités théoriques :

• La première est l'emprunt sur les marchés financiers : l'état peut émettre des obligations (les bons du trésor), achetées par les particuliers ou les banques/assureurs/fonds d'investissement. Cette dette d'état doit être remboursée aux créanciers, avec un intérêt. Les intérêts font partie des dépenses de l'état, raison pour laquelle on les appelle souvent avec le terme de "charge de la dette". Il est d'ailleurs d'usage d'intégrer la charge de la dette dans le déficit : le déficit dont on parler alors est appelé le déficit secondaire.
• Une autre solution est de créer la monnaie nécessaire pour financer les dépenses : l'état peut demander un prêt à la banque centrale ou tout simplement créer la monnaie de nulle part. Le revenu tiré de la création monétaire est appelé le seigneuriage. Pour les économies développées, le seigneuriage est très faible et ne représente que que dixièmes ou centièmes de pourcents du revenu de l'état. De plus, il est interdit dans certains pays, notamment (mais pas que) dans les pays de l'Union Européenne, en raison de son effet inflationniste. Il est donc possible de le négliger, pour simplifier l'analyse, sans que cela ait la moindre conséquence sur les résultats obtenus.

La contrainte budgétaire du gouvernement

Avec ce que l'on vient de dire, on peut faire le bilan des sorties et des entrées d'argent, ce que touche l'état et ce qu'il doit dépenser. Posons les notations suivantes :

• $G$ les dépenses gouvernementales ;
• $T$ les revenus fiscaux ;
• $D$ la dette de l'état ;
• $B$ la base monétaire ;
• $i$ le taux d'intérêt sur la dette de l'état.

Du côté des sorties d'argent, on a les dépenses gouvernementales proprement dites, ainsi que les intérêts de la dette. Du côté des entrées d'argents, on a les taxes, l'emprunt (l’accroissement de la dette) et le financement par création monétaire. Les deux doivent être égaux, ce qui donne :

$G+i\times D=T_{t}+(D_{t}-D_{t-1})+\Delta B$

En réarrangeant les termes, on peut isoler la dette de l'état dans le membre de gauche, ce qui donne :

$D_{t}=(1+i)D_{t-1}+(G_{t}-T_{t})-\Delta B$

Par définition, le déficit primaire vaut $G-T$ et le déficit secondaire $(G-T)+(i_{t-1}\times D_{t-1})$. Dans ce qui suit, nous allons noter le déficit primaire à l'instant t comme suit :$DP_{t}$. L'équation précédente se reformule alors ainsi :

$D_{t}=(1+i)D_{t-1}+DP_{t}-\Delta B$

Cette équation est si souvent utilisée par les économistes qu'ils l'ont affublée du doux nom de contrainte budgétaire gouvernementale. Dans le membre de droite, le premier terme correspond à la dette dite rollée (on emprunte pour rembourser la dette existante), le second est le déficit, et le troisième le seigneuriage utilisé pour rembourser la dette de l'état.

Le seigneuriage peut être négligé dans le système monétaire actuel

Dans ce qui va suivre, nous allons être obligés de négliger le seigneuriage, pour diverses raisons. La raison principale est que le seigneuriage est une source assez faible de revenus à l'heure actuelle. Beaucoup de pays se passent du seigneuriage et préfèrent emprunter de l'argent sur les marchés plutôt qu'à leur banque centrale. Le financement de l'état par la banque centrale a aujourd'hui complètement disparu dans les pays développés, même si l'existence de l'assouplissement quantitatif peut faire croire le contraire. D'ailleurs, il est totalement interdit dans la zone euro, les règles du statut de la BCE étant assez stricts.

De plus, on ne peut pas modéliser l'impact du seigneuriage sur la dette facilement. En effet, la création monétaire impacte les taux d'intérêt et le seigneuriage ne fait pas exception. Si l'état fait financer sa dette par la banque centrale, les taux sur sa dette vont fatalement se mettre à bouger (sauf cas rare de trappe à liquidité). Et modéliser cela n'est pas simple : il faudrait connaître la forme mathématique exacte de la relation M-i, la fameuse courbe de demande de monnaie, chose qui est presque impossible. Et c'est sans compter qu'annoncer soudainement une politique de seigneuriage aurait des conséquences sur la demande de monnaie, chose qu'il est encore plus compliqué de modéliser. Autant dire que ce serait beaucoup de complications pour un résultat franchement peu pertinent.

Mais surtout, il nous faut citer une autre raison, bien plus importante : il existe deux définitions différentes du seigneuriage, l'une faisant intervenir le taux d'intérêt, l'autre faisant intervenir la croissance de la base monétaire $\Delta B$. La première définition est facile à introduire maintenant, sachant que l'on est dans la partie du cours où l'on voit les modèles Wickseliens (sans masse monétaire). Par contre, la seconde définition se marie extrêmement mal avec les modèles Wickseliens et les analyses de ce chapitre. En conséquence, nous laissons le seigneuriage à un chapitre ultérieur. Nous allons rapidement parler de la première définition, mais sans rentrer dans le détail.

L'équation précédente, une fois le seigneuriage supprimé, devient :

$D_{t}=(1+i)D_{t-1}+DP_{t}$

On peut réécrire l'équation précédente en mettant en avant l'augmentation de la dette à l'instant t. Sans seigneuriage, l'augmentation de la dette est égale au déficit secondaire (le déficit primaire + la charge de la dette).

$\Delta D_{t}=DP_{t}+(i_{t-1}\times D_{t-1})$

De cette équation, on peut déduire sous quelles conditions la dette cesse d'augmenter, à savoir les conditions pour que $\Delta D=0$. En injectant dans l'équation précédente et en faisant quelques manipulations algébriques, on en déduit que la dette cesse d'augmenter quand l'état enregistre un surplus primaire (plus de taxes que de dépenses) qui compense la charge de la dette.

$DP_{t}=(i_{t-1}\times D_{t-1})$

L'influence de la politique des taux directeurs sur la charge réelle de la dette

Dans ce qui va suivre, nous allons étudier l'effet de la politique monétaire sur la charge de la dette. Plus précisément, nous allons voir comment le comportement "normal" de la banque centrale influence le montant de la dette, sa soutenabilité, etc. Et par politique monétaire "normale", nous voulons dire : absence de seigneuriage. Le cas du financement par seigneuriage, à savoir le financement des états par création monétaire, est en effet assez spécial, à part, au point qu'on doive l'étudier pour lui-même. En effet, la politique monétaire habituelle modifie les taux d'intérêt, sans influence directe sur le niveau des prix. À l'inverse, le seigneuriage a un impact direct sur le niveau des prix, en plus de son influence sur les taux d'intérêts. Dans cette section, nous allons nous concentrer sur ce qui se passe quand la banque centrale modifie son taux directeur, et uniquement cela.

L'influence de l'inflation sur la charge de la dette

On entend souvent dire que l'inflation permet d'alléger le poids de la dette d'état. Mais en réalité, c'est une erreur de raisonnement. Les agents acceptent de prêter à l'état sous réserve de recevoir un certain rendement réel, et non un rendement nominal. Les investisseurs ne sont pas stupides et savent très bien que l'inflation réduit le poids des dettes et recherchent un taux réel. Pour étudier correctement la situation, nous devons étudier comment la dette est influencée par le niveau des prix et par l'inflation. Nous allons donc devoir reformuler l'équation précédente de manière à : introduire le niveau des prix, introduire l'inflation. Introduire le niveau des prix est assez simple : il suffit de diviser l'équation par le niveau des prix, ce qui donnera une équation utilisant uniquement des termes réels. Il faudra ensuite reformuler les taux d'intérêts de manière à passer des taux nominaux aux taux réels.

Pour commencer, on divise tous les membres de l'équation précédente par le niveau des prix observé à l'instant $t$ :

${\frac {D_{t}}{P_{t}}}=(1+i){\frac {D_{t-1}}{P_{t}}}+{\frac {DP_{t}}{P_{t}}}$

Comme on peut le voir, le terme ${\frac {D_{t-1}}{P_{t}}}$ n'est pas correct : la dette à l'instant $t-1$ est comparée à un prix d'instant $t$ et non aux prix à l'instant $t-1$. Faire la correction demande d'injecter $P_{t}=(1+\pi _{t-1})\cdot P_{t-1}$ dans l'équation :

${\frac {D_{t}}{P_{t}}}={\frac {1+i}{1+\pi }}{\frac {D_{t-1}}{P_{t-1}}}+{\frac {DP_{t}}{P_{t}}}$

Le terme ${\frac {1+i}{1+\pi }}$ est égal au taux réel effectif sur la dette de l'état.

${\frac {D_{t}}{P_{t}}}=(1+r){\frac {D_{t-1}}{P_{t-1}}}+{\frac {DP_{t}}{P_{t}}}$

On voit que la croissance de la dette, en termes réels, dépend des taux réel sur la dette publique. Et l'influence de la banque centrale porte sur les taux nominaux, non les taux réels. Alors certes, les variations des taux nominaux se répercutent sur les taux réels tant que l'inflation reste fixe. Mais quand l'inflation repart, elle emporte les taux nominaux avec elle, et le taux réel remonte.

Si la banque centrale suit une règle de Taylor, elle n'est pas libre de fixer son directeur et ne peut pas aider l'état à monétiser sa dette. La monétisation de la dette d'état est alors dépendante du cycle économique. Quand l'inflation est basse, la banque centrale baisse ses taux, ce qui arrange les affaires de l'état. Ce qui l'aide d'autant plus lors des périodes de récession ou de crise économique : certes les dépenses gouvernementales augmentent pour répondre à la crise, mais la charge de sa dette diminue avec la baisse des taux. Mais quand l'inflation est forte, la hausse des taux ne fait pas l'affaire du gouvernement, du moins pour ce qui est de gérer sa dette publique. Mais ce n'est pas trop un problème, car les périodes de forte inflation sont des périodes de fort dynamisme économique, où le chômage est faible et où les impôts affluent. La dette est donc sous contrôle. Pour résumer, le taux réel varie dans le temps, mais ces variations se compensent. Le taux réel diminue quand l'inflation est basse, mais augmente quand l'inflation est forte. L'inflation étant, en moyenne, égale à sa cible sur une longue période, le taux réel de la dette d'état est en moyenne égal au taux naturel. La banque centrale n'a donc aucune capacité à monétiser la dette publique.

Le cas où la banque centrale ne suit pas une règle de Taylor est plus compliqué et demande d'étudier l'influence des taux nominaux sur la dette publique. Il est étudié dans la section suivante.

L'influence des taux nominaux sur la charge de la dette

Pour étudier l'influence des taux nominaux sur la dette d'état, reprenons l'équation de la dynamique de la dette, et négligeons le terme $-\Delta B$ :

$D_{t}=(1+i)\cdot D_{t-1}+DP_{t}$

Rappelons que la dette publique est une dette à maturité "longue", du moins plus longue que les placements du marché monétaire (encore que). Rappelons que les taux longs et courts sont reliés par l'intermédiaire de la courbe des taux. Pour simplifier, les taux longs sont la somme du taux court (le taux sans risque) et d'une prime de risque : $i_{long}=i_{court}+p_{risque}$. Ici, le taux court est le taux directeur, alors que le taux long est celui de la dette d'état. En injectant cette équation dans la précédente, on trouve :

$D_{t}=(1+i_{directeur}+p_{risque})\cdot D_{t-1}+DP_{t}$

L'équation précédente nous fait croire que l'état a intérêt à ce que les taux directeurs soient les plus bas possibles. Si la prime de risque est constante, plus les taux directeurs sont bas, plus le taux de la dette publique l'est aussi. Et c'est le cas sur le court-terme, dans une certaine mesure. Pas étonnant que certains états souhaitent des taux directeurs les plus bas possibles, idéalement des taux nuls voire négatifs. Mais sur le long-terme, la prime de risque s'adapte et augmente si l'état tente de monétiser sa dette. Rappelez-vous que la prime de risque incorpore tous les risques associés à la dette publique, et en priorité l'inflation et la probabilité de non-remboursement. Et à ce petit jeu, l'équation précédente a gros un défaut : elle néglige l'effet de l'inflation sur les taux nominaux.

Pour résoudre ce problème, on doit reformuler l'équation précédente pour en tenir compte. Sur le long-terme, le taux d'intérêt de la dette publique dépend de l'inflation et du risque de non-remboursement. Pour faire simple, on suppose que le taux est approximativement égal à la somme d'une prime de risque de non-remboursement et de l'inflation anticipée : $i_{D}\approx \pi _{e}+p_{defaut}$. Pour être plus précis, il faudrait aussi ajouter une prime de liquidité, mais laissons cela sous silence. En injectant cette équation dans la précédente, on trouve :

$D_{t}\approx (1+p_{defaut}+\pi _{e})\cdot D_{t-1}+DP_{t}$

En divisant par $P_{t}\approx P_{t-1}\cdot (1+\pi )$, on a :

${\frac {D_{t}}{P_{t}}}\approx (1+p_{defaut}){\frac {D_{t-1}}{P_{t-1}}}+{\frac {DP_{t}}{P_{t}}}$

On peut alors faire l'analogie avec l'équation : ${\frac {D_{t}}{P_{t}}}=(1+r){\frac {D_{t-1}}{P_{t-1}}}+{\frac {DP_{t}}{P_{t}}}$, ce qui donne :

$r\approx 1+p_{defaut}$

Il est raisonnable de considérer que la politique monétaire n'a pas d'effet sur la probabilité de défaut, ce qui fait que le taux réel ne change pas avec la politique monétaire. La raison à cela est que les taux nominaux évoluent en réponse à l'inflation. Si la banque centrale fixe ses taux pour monétiser la dette d'état, cela entraîne une inflation supérieure à la normale. Les agents économiques vont alors réagir à l'inflation et leurs actions vont renchérir les taux sur la dette d'état. Au final, les taux vont remonter jusqu’à ce que l'inflation soit complètement compensée.

L'influence des anticipations d'inflation

Pour étudier en détail le cas d'une monétisation de la dette publique, il faut détailler ce qui passe lors de la transition entre court et long-terme. Ce qui va se passer est que les taux de la dette publique vont se découpler progressivement des taux directeurs, au fur et à mesure que l'inflation augmente. Dans un premier temps, les taux de la dette publique vont baisser en même temps que les taux directeurs. Mais ensuite, les agents économiques vont se rendre compte que la dette est monétisée et ils vont réagir. Leur réaction va entraîner, indirectement, une hausse des taux sur la dette publique, afin de compenser l'inflation causée par la monétisation de la dette. Au final, les taux vont augmenter et complètement compenser l'action de la banque centrale sur les taux réels.

Pour détailler ce qui se passe réellement, imaginons que la banque centrale décide de baisser son taux directeur de quelques pourcents, afin de monétiser la dette publique. Les acheteurs de dette publique vont initialement se faire avoir par une baisse surprise des taux en pensant que la banque centrale sait ce qu'elle fait et en pensant qu'elle continue à cibler l'inflation. Durant quelque temps, ils vont continuer à acheter des obligations d'état en pensant que leur taux réel sera suffisamment intéressant pour mériter d'en acheter. Mais avec le temps, les agents vont se rendre compte que l'inflation a augmentée et réviseront alors leurs anticipations d'inflation. Ils calculeront alors le "vrai" taux réel des obligations d'état et verront qu'il est très faible, bien plus faible que prévu auparavant. En conséquence, ils rechigneront à en acheter et préféreront placer leur argent ailleurs, dans des actions, l'immobilier, ou tout autre actif. La demande d'obligations d'état se réduira donc, ce qui fera augmenter les taux associés. Ce processus continuera jusqu'à ce que le taux réel redevienne ce qu'il était avant : la hausse de l'inflation est alors compensée.

Prenons l'exemple d'un gouvernement qui ciblerait une inflation à 5%, au lieu des 2% habituels, dans le but de réduire sa dette. Ce faisant, les agents économiques se feront avoir par l'inflation surprise. Mais peu après, les agents économiques anticiperont la valeur de la future inflation à sa valeur correcte de 5%. Dans ces conditions, ils demanderont un taux plus élevé sur la dette d'état, histoire de compenser l'inflation : le taux réel convergera vers sa valeur naturelle. Et c'est dans le meilleur des cas, celui où les anticipations des agents sont rationnelles. Dans les faits, les agents peuvent se rendre compte que l'état essaye de les flouer et anticipent le pire. Ils peuvent alors anticiper une monétisation de la dette bien plus forte que prévue et sur-estimer l'inflation. Autant dire que le taux réel réalisé sera alors plus élevé que le taux naturel...

Pour rendre compte de ce phénomène mathématiquement, il faut reformuler l'équation en fonction du taux anticipé sur la dette d'état. Dans ce qui va suivre, nous noterons ce taux ${\overline {r_{t-1}}}$. Pour cela, nous allons devoir trouver une expression du taux réel effectif en fonction du taux réel anticipé. La relation suivante convient bien :

$1+r_{t-1}=(1+{\overline {r_{t-1}}})+(r-{\overline {r_{t-1}}})$

En faisant le remplacement dans l'équation précédente et en développant, on trouve :

${\frac {G}{P_{t}}}-{\frac {T}{P_{t}}}={\frac {D_{t}}{P_{t}}}-\left[(1+{\overline {r_{t-1}}})+(r-{\overline {r_{t-1}}})\right]{\frac {D_{t-1}}{P_{t-1}}}$

${\frac {G}{P_{t}}}-{\frac {T}{P_{t}}}={\frac {D_{t}}{P_{t}}}-(1+{\overline {r_{t-1}}}){\frac {D_{t-1}}{P_{t-1}}}+(r-{\overline {r_{t-1}}}){\frac {D_{t-1}}{P_{t-1}}}$

Or, le facteur $r-{\overline {r_{t-1}}}$ peut se simplifier, par définition des taux réels, en : $(\pi -\pi _{e})$.

${\frac {G}{P_{t}}}-{\frac {T}{P_{t}}}={\frac {D_{t}}{P_{t}}}-(1+{\overline {r_{t-1}}}){\frac {D_{t-1}}{P_{t-1}}}+(\pi -\pi _{e}){\frac {D_{t-1}}{P_{t-1}}}$

On peut remarquer que le terme $(\pi -\pi _{e}){\frac {D_{t-1}}{P_{t-1}}}$ est un revenu qui provient de la part d'inflation non-anticipée par les agents économiques (la différence entre inflation anticipée et inflation non-anticipée).

Pour résumer, l'inflation n'est donc qu'un remède temporaire pour réduire la charge de la dette, celui-ci ne fonctionnant que pour une inflation non-anticipée. Utiliser la politique monétaire pour réduire la charge de la dette est donc vain.

Le seigneuriage

Dans ce chapitre, nous allons étudier le seigneuriage, à savoir l'enrichissement de l'état suite à l'émission de sa monnaie. Le contenu du chapitre est la suite du chapitre précédent, où nous avions étudié l'interaction entre politique fiscale et monétaire. Pour être précis, nous avions seulement regardé l'interaction entre politique de contrôle des taux et dette de l'état, mais avions volontairement omis de parler du seigneuriage. Celui était décrit dans le chapitre précédent comme une création monétaire utilisée pour financer les dépenses de l'état, en remplacement de l'emprunt et/ou des taxes/impôts. Dans ce chapitre, nous allons voir en détail ce seigneuriage.

La définition du seigneuriage

Il existe deux définitions techniques du seigneuriage, qui sont équivalentes sous certaines conditions.

• La première définition du seigneuriage est tout simplement l'accroissement de la base monétaire sur une période fixée (l'année, par exemple) $\Delta B$.
• Une autre définition est le coût d'opportunité de la base monétaire, à savoir le coût qu'il y a à conserver de la monnaie au lieu d'investir celle-ci.

La définition par le coût d'opportunité de la monnaie

Rappelons que la monnaie et la dette publique sont toutes deux un passif pour l'état. Un gouvernement qui souhaite augmenter son passif (et donc acquérir de l'argent), a le choix entre augmenter la base monétaire et émettre de la dette. La différence principale est que là où la dette est adossée à un taux d'intérêt, ce n'est pas le cas de la base monétaire (en première approximation). Et les intérêts sont un coût qui existe avec la dette publique, mais pas avec la monnaie : émettre de la dette a un coût que la création monétaire n'a pas. Le seigneuriage est donc défini comme le coût des intérêts de la dette, l'argent qu'on économise en remplaçant de la dette par de la monnaie, l'intérêt que l'état n'aura pas à verser sur sa monnaie et qu'il aurait dû verser si la base monétaire était de la dette d'état. Pour résumer, cette seconde définition nous dit que le seigneuriage est égal à :

$S=i\times B$.

Petite parenthèse, concernant la relation entre taux d'intérêt et revenus du seigneuriage. La définition $i\times B$ nous laisse croire que plus les taux sont hauts, plus le seigneuriage est important. En réalité, il ne faut pas oublier que la base monétaire dépend fortement des taux d'intérêts et que la relation entre les deux est décroissante : des taux forts vont réduire la base monétaire et des taux faibles d'augmenter. On se retrouve donc avec deux effets de sens contraire : d'un côté des taux forts augmentent le premier terme, de l'autre ils réduisent le second terme. En somme, l'effet des taux nominaux sur le seigneuriage n'est pas clair, pour ce qui est de la théorie. En pratique, les observations historiques nous disent que des taux forts signifient bien souvent un fort seigneuriage perçu par la banque centrale, via les revenus de ses taux directeurs.

L'impact de la rémunération des réserves

L'équation précédente est valide sur le principe, mais il faut rester quelque peu prudent quant à sa validité. Rappelons que la base monétaire est composée d'espèces non-rémunérées, mais aussi de réserves. Et ces réserves peuvent être rémunérées, la banque centrale versant un intérêt tous les ans. Si le taux de rémunération des réserves n'est pas nul, l'économie d'intérêt est moindre et l'équation précédente doit être amendée.

Pour comprendre le principe, comparons deux situations : un financement par l'emprunt et un financement par émission de nouvelles réserves. Pour le premier cas, supposons que l'état emprunte une somme $D$ à un taux $t_{d}$. Le coût pour l'état est donc de $D\times t_{d}$. Dans le second cas, la banque centrale crée une quantité $D$ de réserves qu'elle injecte dans l'économie, le plus généralement avec une politique d'assouplissement quantitatif. L'état n'a alors pas à supporter le coût des intérêts sur une dette qu'elle n'a pas empruntée. On pourrait donc croire que le gain des revenus de seigneuriage est égal au taux d'intérêt économisé, le coût d'opportunité de la monnaie créé. Mais la rémunération des réserves est financée par la banque centrale et le coût n'est pas négligeable pour l'état qui est l'actionnaire de la banque centrale. Pour faire les calculs correctement, il faut donc compter l'économie des intérêts d'un côté, mais soustraire la rémunération des réserves de l'autre.

Le seigneuriage est donc défini comme la différence entre l'économie sur sa dette et la rémunération de la base monétaire.

$S=B\times t_{d}-R\times t_{r}$, avec $B$ la base monétaire, $R$ la quantité de réserves, $t_{r}$ le taux de rémunération des réserves et $t_{d}$ le taux de la dette d'état.

Si on suppose que toute la base monétaire est composée de réserves, on a :

$S=B\times (t_{d}-t_{r})$

L'équation précédente nous permet de déterminer quel est le gain du seigneuriage pour l'état. Et ce gain est souvent plus faible que prévu à cause de la rémunération des réserves et peut même être nul.

• Si le taux sur la dette est égal au taux de rémunération des réserves, ce qui est économisé d'un côté est repris de l'autre. Les intérêts économisés sur la dette d'état sont compensés par la rémunération des réserves par la banque centrale. Un stimulus fiscal financé par l'emprunt et l'émission de réserves sont alors deux politiques identiques.
• Dans le cas contraire, on a un gain positif. Le stimulus fiscal financé par l'emprunt est alors plus cher que la monnaie hélicoptère, car l'économie d'intérêt sur la dette est supérieur à la rémunération des réserves. Les deux politiques ne sont donc pas équivalentes et l'ensemble ressemble plus à une forme de taxation implicite (l'état gagne de l'argent au détriment du secteur privé).

Encore une fois, les revenus de seigneuriage dépendent des taux, mais aussi de la base monétaire, et les deux ne sont pas indépendants. Si des taux élevés sur la dette d'état tendent à réduire la base monétaire, c'est l'inverse pour les taux de rémunération des réserves. Au final, ce qui compte est la différence entre les deux taux. Dette d'état et réserves sont presque identiques en termes de risques, bien que la dette d'état a une probabilité non-nulle de remboursement alors que les réserves sont totalement sans risques. La véritable différence qui fait pencher la balance d'un côté plutôt que de l'autre est réellement le rendement. Plus le taux sur la dette d'état est élevé, par rapport au taux de rémunération des réserves, plus la détention de dette est intéressante. Inversement, plus le taux de rémunération des réserves se rapproche du taux sur la dette d'état, plus les agents privilégient la détention de réserves. Encore une fois, la base monétaire diminue avec le différentiel de taux et on ne peut pas dire à l'avance quel effet va l'emporter.

L’influence de la présence d'espèces

L'équation précédente est une bonne approximation, mais elle met de côté les espèces. Dans la réalité, l'économie exacte dépend du taux de rémunération des réserves, mais aussi de la proportion d'espèces/réserves. Plus le poids des espèces dans la base monétaire est important, plus l'économie est elle aussi importante. Pour nous en rendre compte, faisons les calculs en tenant compte de la présences des espèces. Pour cela, partons de l'équation vue plus haut :

$S=B\times t_{d}-R\times t_{r}$, avec $B$ la base monétaire, $R$ la quantité de réserves, $t_{r}$ le taux de rémunération des réserves et $t_{d}$ le taux de la dette d'état.

La base monétaire est égale à la somme des espèces $E$ et des réserves $R$, ce qui donne :

$S=(R+E)\times t_{d}-R\times t_{r}$

On développe :

$S=E\times t_{d}+R\times t_{d}-R\times t_{r}$

On factorise R :

$S=E\times t_{d}+R\times (t_{d}-t_{r})$

On voit que les espèces donnent un revenu de seigneuriage plus important que les réserves, en raison de leur différence de rémunération. Mais vu la faible utilisation des espèces dans les économies avancées, c'est plus un détail qu'autre chose.

Les deux définitions sont équivalentes, sous certaines conditions

Les deux définitions précédentes sont équivalentes si la base monétaire croit au même rythme qu'un placement rémunéré au taux d'intérêt. Dit autrement, le taux de croissance et le taux d'intérêt sont égaux. Pour comprendre pourquoi, partons de la définition du taux de croissance de la base monétaire.

$S=\Delta B$

Par définition, le taux de croissance de la base monétaire $\Omega$ vaut : $\Omega ={\frac {\Delta B}{B}}$. En injectant dans l'équation précédente, on a :

$S=\Omega \cdot B$

On voit que les deux définitions coïncident si :

$\Omega =i$

Le seigneuriage réel

Dans cette section, nous allons démontrer des équations qui serviront de fil rouge pour ce chapitre. Elles donnent toutes deux la valeur du seigneuriage réel, à savoir la valeur corrigée du niveau des prix du seigneuriage. La première équation par de la définition $S=i\times B$, alors que la seconde équation utilise la définition $S=\Delta B$ du seigneuriage.

Le seigneuriage réel : définition à partir du cout d’opportunité de la monnaie

La première équation part de la définition $S=i\times B$. Elle suppose donc qu'à l'instant t, l'argent économisé par l'état est l'intérêt qu'il économise en émettant de la monnaie au lieu de la dette d'état. Dit autrement, c'est l'intérêt supplémentaire qu'il payerait si la monnaie était convertie en dette.

Pour déterminer la valeur réelle du seigneuriage, on pourrait croire qu'il suffirait de diviser $S=i\times B$ par le niveau général des prix $P$. Mais en réalité, quelques subtilités font que c'est plus compliqué. Rappelons que l'intérêt versé par la dette est versé avec un retard : la dette a une certaine maturité. Dans ce qui va suivre, nous allons partir du principe que l'intérêt est annuel et allons voir ce qui se passe d'une année sur l'autre. À un instant t, l'intérêt économisé est celui qu'aurait versé une dette émise l'année précédente. Si on note $Dv$ cette dette virtuelle, on a :

$S_{t}=i\times Dv_{t-1}$

Sachant que cette dette virtuelle est en fait égale à la base monétaire, on peut remplacer $Dv_{t-1}$ par $B$ :

$S_{t}=i\times B_{t-1}$

On peut alors diviser le tout par le niveau général des prix P pour trouver le seigneuriage réel.

${\frac {S_{t}}{P_{t}}}=i\times {\frac {B_{t-1}}{P_{t}}}$

Le terme ${\frac {B_{t-1}}{P_{t}}}$ est incorrect : il divise deux grandeurs mesurées à des instants différents. Pour corriger cela, on injecte la formule $P_{t}=(1+\pi )\cdot P_{t-1}$ dans l'équation précédente.

${\frac {S_{t}}{P_{t}}}={\frac {i}{1+\pi }}{\frac {B_{t-1}}{P_{t-1}}}$

Le seigneuriage réel : définition à partir de la création monétaire

La seconde équation que nous allons voir est extrêmement importante pour qui veut étudier le seigneuriage réel, en déduire l'impact de l'inflation sur celui-ci, etc. La voici :

$S={\frac {\Omega }{1+\pi }}{\frac {B_{t-1}}{P_{t-1}}}$

Démonstration

Partons de la définition du seigneuriage réel (corrigé du niveau des prix) : $S={\frac {\Delta B}{P_{t}}}={\frac {B_{t}-B_{t-1}}{P_{t}}}$ On peut réécrire cette équation comme ceci : $S={\frac {B_{t}-B_{t-1}}{B_{t-1}}}{\frac {B_{t-1}}{P_{t}}}={\frac {\Delta B}{B_{t-1}}}{\frac {B_{t-1}}{P_{t}}}$ Le premier terme, ${\frac {\Delta B}{B_{t-1}}}$ n'est autre que le taux de croissance de la base monétaire, défini comme suit : $B_{t}=(1+\Omega )B_{t-1}$. Faisons le remplacement : $S=\Omega {\frac {B_{t-1}}{P_{t}}}$ On injecte la formule $P_{t}=(1+\pi )\cdot P_{t-1}$ dans l'équation précédente. $S={\frac {\Omega }{1+\pi }}{\frac {B_{t-1}}{P_{t-1}}}$

Il est possible de reformuler les calculs précédents de manière à distinguer la part du seigneuriage qui vient de l'augmentation de la base monétaire réelle ${\frac {B}{P}}$, et quelle est la part provenant de l'inflation proprement dite. On trouve alors l'équation suivante :

$S=\left[{\frac {B_{t}}{P_{t}}}-{\frac {B_{t-1}}{P_{t-1}}}\right]+\left[{\frac {\pi }{1+\pi }}{\frac {B_{t-1}}{P_{t-1}}}\right]$

Démonstration

Partons de la définition du seigneuriage : $S={\frac {B_{t}-B_{t-1}}{P_{t}}}$ Développons et appliquons la formule $P_{t}=(1+\pi )\cdot P_{t-1}$ : $S={\frac {B_{t}}{P_{t}}}-{\frac {1}{1+\pi }}{\frac {B_{t-1}}{P_{t-1}}}$ Reformulons l'équation précédente comme suit : $S={\frac {B_{t}}{P_{t}}}-{\frac {B_{t-1}}{P_{t-1}}}+{\frac {B_{t-1}}{P_{t-1}}}-{\frac {1}{1+\pi }}{\frac {B_{t-1}}{P_{t-1}}}$ Regroupons les termes ainsi : $S=\left[{\frac {B_{t}}{P_{t}}}-{\frac {B_{t-1}}{P_{t-1}}}\right]+\left[{\frac {B_{t-1}}{P_{t-1}}}-{\frac {1}{1+\pi }}{\frac {B_{t-1}}{P_{t-1}}}\right]$ On factorise le terme de droite : $S=\left[{\frac {B_{t}}{P_{t}}}-{\frac {B_{t-1}}{P_{t-1}}}\right]+\left[{\frac {B_{t-1}}{P_{t-1}}}\left(1-{\frac {1}{1+\pi }}\right)\right]$ On simplifie en utilisant la formule $1-{\frac {1}{1+x}}={\frac {x}{1+x}}$ : $S=\left[{\frac {B_{t}}{P_{t}}}-{\frac {B_{t-1}}{P_{t-1}}}\right]+\left[{\frac {\pi }{1+\pi }}{\frac {B_{t-1}}{P_{t-1}}}\right]$

La taxe d'inflation

Dans l'équation précédente, le premier terme de droite correspond à l'augmentation de la base monétaire réelle, alors que le second est celui de l'équation obtenue précédemment.

$S=\Delta \left({\frac {B}{P}}\right)+{\frac {\pi }{1+\pi }}{\frac {B_{t-1}}{P_{t-1}}}$

Le premier terme, à savoir l'augmentation de la base monétaire réelle, est le fruit d'un échange de ressources entre les agents privés et le gouvernement. Rappelons que la base monétaire est détenue par des agents privés, non par le gouvernement proprement dit. Quand le gouvernement augmente sa base monétaire, elle doit être échangée avec quelque chose pour passer dans les mains des agents privés : le gouvernement peut donc acquérir des ressources réelles en échange de la monnaie qu'il crée. Plus précisément, le gouvernement transfère de la monnaie en échange de titres ou d'autres ressources qui ont une valeur réelle, via des opérations d'open market ou des prêts interbancaires.

Maintenant, étudions le second terme ${\frac {\pi }{1+\pi }}{\frac {B_{t-1}}{P_{t-1}}}$. Il s'agit de revenus de seigneuriage qui ne sont pas le fruit d'un échange de ressources réelles contre de la monnaie. Il s'agit d'un gain net pour le gouvernement et d'une perte sèche sans contrepartie pour les agents privés détenteurs de monnaie.

Les revenus de seigneuriage à base monétaire réelle constante

Pour comprendre à quoi il peut bien correspondre, partons de l'équation suivante, démontrée plus haut :

$S={\frac {\Omega }{1+\pi }}{\frac {B_{t-1}}{P_{t-1}}}$

Supposons que la banque centrale garde la base monétaire réelle constante. Pour cela, la base monétaire doit croître au même niveau que les prix, ce qui donne : $\Omega =\pi$. On pourrait croire que, la base monétaire augmentant au même rythme que les prix, le gouvernement ne devrait pas faire le moindre profit et les revenus de seigneuriage devraient être nuls. Mais les calculs qui vont suivre montrent qu'il n'en est rien. La raison est simple : les revenus de seigneuriage obtenus quand $\Omega =\pi$ sont des revenus causés par l'inflation. En injectant $\Omega =\pi$ dans l'équation précédente, on a :

$S={\frac {\pi }{1+\pi }}{\frac {B_{t-1}}{P_{t-1}}}$

Une autre manière de retrouver ce résultat est de partir de l'équation suivante :

$S=\left[{\frac {B_{t}}{P_{t}}}-{\frac {B_{t-1}}{P_{t-1}}}\right]+\left[{\frac {\pi }{1+\pi }}{\frac {B_{t-1}}{P_{t-1}}}\right]$

Supposer une base monétaire réelle constante revient à dire que : $\left[{\frac {B_{t}}{P_{t}}}-{\frac {B_{t-1}}{P_{t-1}}}\right]=0$. Dans ce cas, on retrouve l'équation vue auparavant :

$S={\frac {\pi }{1+\pi }}{\frac {B_{t-1}}{P_{t-1}}}$

L'origine de la taxe d'inflation

On vient de voir que si l'état garde une base monétaire réelle constante, il gagne quand même des revenus de seigneuriage. Ces revenus sont le résultat de l'inflation, qui rogne le pouvoir d'achat de l'épargne au profit de l'état. Le tout peut s'interpréter comme une sorte de taxe sur les encaisses réelles privées, la taxe d'inflation. Et comme toute taxe, elle est égale au produit d'un taux par une certaine assiette fiscale. Il est possible de calculer le taux et l'assiette de celle-ci. Pour ce qui est de l'assiette, la taxe d'inflation touche la détention de monnaie, précisément sur les encaisses réelles ${\frac {B}{P}}$. Elle est donc payée par les ménages et le secteur privé, en fonction de leur détention d'encaisse réelle. Le taux de la taxe est égal à :

$t_{\pi }={\frac {\pi }{1+\pi }}$

Si l'inflation est elle-même faible, on peut faire l'approximation suivante : ${\frac {\pi }{1+\pi }}\approx \pi$, ce qui donne :

$t_{\pi }\approx \pi$

Vous vous demandez certainement quelle est l'origine de cette taxe d'inflation, mais son nom devrait vous donner une petite idée : l'inflation réduit la valeur de la monnaie, au profit de l'état. L'augmentation des prix causée par le seigneuriage va causer une inflation surprise, qui n'a pas été anticipée par les agents économiques. Or, l'équation de Fisher $i=r+\pi _{e}$ nous dit que les taux d'intérêts ne tiennent compte que de l'inflation anticipée. Les agents économiques décident de leurs investissements en fonction de l'inflation qu'ils anticipent, mais ils ne peuvent rien contre des surprises au niveau des prix. La rémunération de l'épargne est donc capable de compenser l'inflation anticipée, mais elle ne peut rien contre une inflation surprise, que personne n'a vu venir. Le seigneuriage va donc réduire la valeur de la monnaie détenue par les agents économiques. L'épargne monétaire d'un ménage vaudra moins qu'avant du fait de l'inflation surprise.

La dépréciation de la monnaie détenue par les agents se fait au profit de l'état, qui est le détenteur de la monnaie qu'il crée et qui peut acheter ce qu'il veut avec. Et le montant perdu d'un côté est strictement égal au montant perdu de l'autre. Si l'état augmente la base monétaire de x%, cela se fait au prix d'une perte de valeur de la monnaie de x%, et donc d'une inflation surprise de x%. Les ménages vont donc perdre x% en encaisses monétaires réelles. La perte pour les ménages est un gain pour l'état. Ce qui fait que l'inflation causée par le seigneuriage peut être vu comme une taxe d'inflation, chose que nous avons déjà évoqué dans les premiers chapitres où nous avions dit que l'inflation peut être vue comme une taxe sur les encaisses monétaires, mais sans le justifier vraiment. Nous avions juste dit qu'une inflation surprise de x% réduit les encaisses monétaires réelles de x%, ce qui a le même effet qu'une taxe nominale de x% sur ces encaisses nominales. Mais en réalité, l'analogie est bien plus profonde : l'état gagne bien de l'argent par la création monétaire et le montant ainsi gagné est égal au montant de la taxe d'inflation. La taxe d'inflation agit donc comme une vraie taxe, au profit de l'état !

L'assiette de la taxe d'inflation

La taxe d'inflation ne touche que les détenteurs de monnaie, à savoir majoritairement des ménages (souvent les plus pauvres). Les agents économiques relativement "riches", ceux qui ont un patrimoine conséquent sont relativement peu touchés par cette taxe d'inflation. En effet, la majorité de leur patrimoine est composé d'actifs financiers ou immobiliers : obligations, actions ou pierre-papier. La taxe ne touchant que la monnaie proprement dite, seule la faible partie monétaire de leur patrimoine est touchée. En comparaison, les ménages qui dépensent une majorité de leurs revenus sont obligés de conserver une grande partie de leurs revenus sous forme monétaire. Ceux-ci sont plus fortement touchés, en proportion de leurs revenus, par la taxe d'inflation. Pour résumer, la taxe d'inflation est une taxe fiscalement régressive. Cependant, toute la monnaie émise par l'état est touchée, y compris celle détenue sur les résidents étrangers. Là où les impôts traditionnels touchent les ressortissants, le plus souvent les résidents, la taxe d'inflation a une assiette beaucoup plus large.

Chose importante, l'assiette dépend de l'inflation anticipée. Pour nous en rendre compte, prenons de l'équation précédente :

$S=t_{\pi }\cdot {\frac {B}{P}}$

On peut faire l'amalgame entre la base monétaire à la masse monétaire, l'une étant approximativement proportionnelle à l'autre, ce qui donne :

$S\propto t_{\pi }\cdot {\frac {M}{P}}$

Rappelons que ${\frac {M}{P}}$ n'est autre que la demande de monnaie $L$.

$S\propto t_{\pi }\cdot L(Y,i)$

Enfin, on injecte l'équation de Fisher $i=\pi _{e}+r$.

$S\propto t_{\pi }\cdot L(Y,r+\pi _{e})$

On voit que l'assiette dépend de l'inflation anticipée et on peut même déduire que cette relation est décroissante (vu que la relation entre taux et demande de monnaie est décroissante). Les agents réagissent à la taxe d'inflation et réduisent en conséquent leur épargne monétaire. Plus l'inflation est forte, plus les agents réduisent leurs encaisses monétaires, devenue encore moins rentables avec la taxe d'inflation. Rien d'étonnant à cela : plus l'inflation est forte, plus les agents se débarrassent rapidement de leur monnaie, avant qu'elle perde de la valeur. Pour le dire autrement, la vélocité de la monnaie augmente avec l'inflation. Pour le montrer, rappelons que la vélocité de la monnaie est, par définition : $L(Y,r+\pi _{e})={\frac {Y}{V(Y,r+\pi _{e})}}$. En injectant dans l'équation précédente, on trouve :

$S\propto t_{\pi }\cdot {\frac {Y}{V(r+\pi _{e})}}$

Le taux de seigneuriage optimal

Courbe qui lie le taux de seigneuriage réel et l'inflation (sous-entendu, les recettes provenant de la taxe d'inflation). On voit que celle-ci fournit des revenus croissants, sauf au-delà d'un certain point où les revenus décroissent.

Il est souvent dit que trop d'impôt tue l'impôt. Et il se trouve que les modélisations théoriques nous disent que cet argument est vrai dans le cas de la taxe d'inflation. On vient de voir que l'inflation influence non seulement le taux de la taxe d'inflation, mais aussi son assiette. Il doit donc exister un taux de seigneuriage optimal, au delà duquel une hausse de l'inflation diminue les recettes du seigneuriage.

Pour le montrer mathématiquement, partons de la définition simplifiée des revenus de la taxe d'inflation :

$S\propto t_{\pi }\cdot L(Y,r+\pi _{e})$

Il est raisonnable de supposer que le produit intérieur brut et le taux réel sont constants : seules les variables nominales changent. C'est une manière de dire que le seigneuriage ne modifie pas ces valeurs, ou tout du moins n'a pas d'influence dessus. Dans ces conditions, on peut les négliger. On a alors :

$S\approx t_{\pi }\cdot L(\pi _{e})$

On voit donc que l'inflation (anticipée) a deux effets : elle augmente le taux d'un côté, mais réduit l'assiette (la demande de monnaie) de l'autre. Et autant l'augmentation du taux augmente les revenus, la réduction de l'assiette les réduit. Le résultat final dépend de l'influence de ces deux facteurs. Pour simplifier, l'influence du taux prédomine quand l'inflation est faible, mais l'influence de l'assiette prend le dessus pour une inflation trop forte. La courbe qui relie revenus de seigneuriage réel et inflation ressemble donc à une courbe en forme de bosse.. La courbe se divise en deux portions : une où elle est croissante (à gauche du point d'inflexion) et une où elle est décroissante (à droite du point d'inflexion). Et les deux correspondent à des régimes différents. Si l'état ne finance pas sa dette avec le seigneuriage, le seigneuriage est faible et l'état tire des revenus réguliers de seigneuriage. Mais si l'état tente de trop financer sa dette avec le seigneuriage, il passe sur la partie droite de la courbe. Un état rationnel se rendrait compte de cette situation et baisserait alors l'inflation, mais ce n'est pas ce qui se produit en réalité. L'état va en fait augmenter de plus en plus le seigneuriage, sans se rendre compte que cela aggrave la situation. L'inflation prend alors des proportions hallucinantes et il survient l'hyperinflation (une inflation très élevée, permanente, de plus de 100% par an).

Précisons cependant que le taux de seigneuriage maximal n'est pas le taux de seigneuriage optimal. En effet, il faut savoir que l'inflation a tendance à réduire les recettes fiscales des états, à cause de subtilités techniques. Nous avions déjà abordé cela dans le chapitre sur l'inflation au début du cours. Nous avions dit que l'inflation réduit le pouvoir d'achat de toute valeur nominale et que les impôts ne font pas exception. Les impôts sont dus à partir du moment où un évènement taxable survient : une vente en plus-value sur les marchés financiers, la revente d'une maison, la perception d'un revenu exceptionnel. Mais les impôts sont prélevés tous les ans, sauf dans les cas de prélèvement à la source non-régularisables qui ne touchent de toute façon pas tous les évènements taxables. Pour les évènements taxables non-prélevés à la source, il se passe un peu de temps entre le moment entre l'évènement taxable et le paiement effectif. Et l'inflation profite de ce temps pour réduire la valeur de l'impôt. C'est ce qu'on appelle l'effet Tanzi. En soi, l'effet est négligeable si les sommes prélevées sont faibles et que l'inflation est basse. Mais si l'inflation est forte, l'effet Tanzi devient sensible. Au final, le taux de seigneuriage optimal est plus faible que le taux de seigneuriage maximal. L'état gagne avec les revenus de seigneuriage jusqu’à un certain point, mais il perd avec l'effet Tanzi. Et les sont d'autant plus élevés que l'inflation est forte, sous conditions. Le taux optimal est un compromis entre effet Tanzi et revenus de seigneuriage. Le taux optimal est donc forcément inférieur au taux de seigneuriage maximal.

L'utilisation du seigneuriage pour financer la dette publique

Après avoir étudié l'influence des politiques monétaires non-conventionnelles sur la dette d'état, il est temps de voir ce qui se passe quand le gouvernement utilise le seigneuriage pour financer sa dette. L'intuition nous dit que la création monétaire peut permettre de rembourser la dette. Dans le meilleur des cas, l'état peut créer de la monnaie et racheter sa dette avec. Dans le pire des cas, la création monétaire directe augmente le niveau des prix, ce qui réduit la dette réelle. En effet, le stock de dette est une variable nominale parmi tant d'autres, indépendante du niveau des prix. Si le niveau des prix double, le stock de dette restera plus ou moins le même : la dette réelle sera divisée par deux. Tout porte à croire que la création monétaire est l'idéal pour rembourser la dette.

Le seigneuriage a déjà été utilisé par les gouvernements pour réduire le poids de leurs dettes budgétaires. Évidemment, cela signifie que les banques centrales doivent plier face aux gouvernements et s'affranchir de leurs objectifs habituels de contrôle de l'inflation, ce qui n'est pas possible en temps normal. Habituellement, la banque centrale est totalement indifférente au risque de défaut de l'état, elle ne se préoccupe pas du tout de sa politique fiscale et/ou de la gestion de ses comptes. On parle alors de situation de dominance monétaire. Mais certains états ne gèrent pas leurs déficits de manière stricte et n'hésitent pas à faire gonfler leur dette au point qu'elle finit par devenir insoutenable. L'état a alors deux solutions : faire défaut ou faire appel au seigneuriage. Dans le premier cas, la dominance monétaire est respectée : la banque centrale laisse l'état faire défaut sans monétiser la dette. Dans le second cas, la banque centrale se plie à la décision de l'état. On parle alors de dominance fiscale, dans le sens où la politique monétaire est sous contrôle de la politique budgétaire et non des objectifs qui sont assignés à la banque centrale.

Une conséquence : l'hyperinflation

Quand l'état décide de financer sa dette par le seigneuriage, la dette est importante comparée à la masse monétaire totale, ce qui fait que la croissance de la masse monétaire est alors très forte. Si on applique la théorie quantitative, on déduit que l'inflation engendrée est très forte. Dans les faits, toutes les tentatives de financer la dette par la banque centrale se sont soldées par une hyperinflation (une situation où l'inflation devient si importante qu'elle détruit l'économie du pays). Toutes les hyperinflations du 20ᵉ siècle avaient pour origine un déficit budgétaire excessif, finalement financé par la banque centrale. L'indépendance des banques centrales vise justement à empêcher toute monétisation du déficit par seigneuriage. et c'est cette raison qui a conduit l'Union Européenne à interdire tout financement direct des états par la banque centrale, interdiction inscrite dans le traité de Maastricht.

Hyperinflation allemande de 1923.

Un bon exemple est donné par les cas de l'Allemagne des années 1920. Celle-ci devait rembourser une dette de 132 milliards de Marks, causée par les remboursements liés au traité de Versailles ainsi qu'à l'effort de guerre. L’Allemagne n'avait qu'une seule solution pour diminuer une telle dette : l'inflation. En conséquence, la banque centrale Allemande, qui était sous contrôle des autorités politiques, quitta l'étalon-or et se mis à créer une très grande quantité de monnaie : au plus fort de la crise, l'impression des billets mobilisait jour et nuit plus de 30 fabriques de papier, 133 imprimeries, et 1783 presses à billets. Les billets de 5 millions de Marks étaient monnaie courante, les Allemands perdirent confiance en leur monnaie, le troc commença à se développer et de nombreuses banques mirent la clé sous la porte. L’Allemagne changea de monnaie dans les années 1923, mettant fin à cette hyperinflation.

La même situation s'est reproduite avec la Hongrie en 1946 et la Grèce en 1944. La seconde guerre mondiale a forcé certains pays à accumuler une dette de guerre assez importante. Loin de compenser cette dette par les impôts ou les exportations, ces pays ont préféré imprimer de la monnaie pour diminuer la charge de la dette. Dans les années 1980, divers pays d’Amérique latine ont subi des hyperinflations causées par une forte impression de monnaie de la part des banques centrales. Là encore, les pays souhaitaient diminuer la charge de la dette publique grâce à l'inflation.

Billets de banque du Zimbabwe, datant de 2008.

Et ces hyperinflations ne sont pas forcément rares, comme le montre le cas du Zimbabwe lors de l'année 2008. Durant cette période, le président Robert Mugabe a tenté de faire financer sa dette nationale en imprimant de la monnaie dans un contexte géopolitique assez tendu, qui mêle des expropriations de terres, une instabilité politique avec des violences sur l'opposition, une banque centrale dépendante du pouvoir politique, et des sanctions internationales sur le plan commercial contre le régime en place.

La dynamique de la dette avec seigneuriage

Étudions la dynamique de la dette avec le seigneuriage, en repartant de l'équation précédente, établie il y a quelques chapitres :

${\frac {D_{t}}{P_{t}}}=(1+r){\frac {D_{t-1}}{P_{t-1}}}+{\frac {DP_{t}}{P_{t}}}-{\frac {\Delta B}{P_{t}}}$

Injectons l'équation $S={\frac {\Omega }{1+\pi }}{\frac {B_{t-1}}{P_{t-1}}}$, avec $\Omega$ dans la précédente :

${\frac {D_{t}}{P_{t}}}=(1+r){\frac {D_{t-1}}{P_{t-1}}}+{\frac {DP_{t}}{P_{t}}}-{\frac {\Omega }{1+\pi }}{\frac {B_{t-1}}{P_{t-1}}}$

D'après la théorie quantitative de la monnaie, on a : $\Omega =g+\pi -{\overline {v}}$ (le dernier terme est la variation de la vélocité de la monnaie). Lors d'un épisode d'hyperinflation, la croissance est faible par rapport à l'inflation, ce qui fait qu'on peut la négliger dans les calculs. On a alors $\Omega \approx \pi -{\overline {v}}$. En faisant le remplacement dans l'équation précédente, on trouve :

${\frac {D_{t}}{P_{t}}}\approx (1+r){\frac {D_{t-1}}{P_{t-1}}}+{\frac {DP_{t}}{P_{t}}}-{\frac {\pi -{\overline {v}}}{1+\pi }}{\frac {B_{t-1}}{P_{t-1}}}$

Le seigneuriage devient alors :

$S\approx {\frac {\pi -{\overline {v}}}{1+\pi }}{\frac {B_{t-1}}{P_{t-1}}}$

On peut se retrouver avec trois cas, selon l'évolution de la vélocité et de l'inflation :

• Si la vélocité et l'inflation augmentent dans les mêmes proportions, la charge de la dette reste inchangée.
• Si la vélocité augmente plus vite que l'inflation, la charge de la dette est alourdie : l'état y perd.
• Si la vélocité augmente moins vite que l'inflation, la charge de la dette est allégée : l'état y gagne.

Lors d'une hyperinflation, on observe une hausse de la vélocité de la monnaie. La raison est que les ménages se prémunissent contre la taxe d'inflation en se débarrassant au plus vite de leur monnaie, ce qui augmente sa vélocité. Une première conséquence est que les prix augmentent plus vite que la masse monétaire. Une autre conséquence est que l'augmentation de la vélocité compense l'inflation, du point de vue des recettes fiscales. La création monétaire n'est donc pas un si bon plan que cela si elle augmente trop la vélocité. Une trop forte création monétaire peut même avoir l'effet inverse que celui escompté, avec un renchérissement des déficits fiscaux.

Le modèle de Cagan des hyperinflations

Le modèle de Cagan est un modèle dit log-linéarisé, ce qui veut dire que toutes les variables sont remplacées par leur logarithme et qu'une opération d'approximation est réalisée. Dans le détail, l'opération de log-linéarisation se base sur la formule $\log(1+x)\approx x$. La raison à cela est que, pour une grandeur qui croit à un taux de x% par période, le logarithme est une bonne approximation du taux de croissance. L'opération de log-linéarisation transforme donc chaque grandeur en son taux de croissance, ce qui est l'idéal pour étudier les situations d'hyperinflation, où on se préoccupe surtout des taux de croissance de la base monétaire, des prix, et autres grandeurs. Le modèle de Cagan part de l'équation de la théorie quantitative de la monnaie et en prend le logarithme. En réarrangeant les termes, on trouve :

$\log(P_{t})=\log(M_{t})+\log(V_{t})-\log(Y_{t})$

La vélocité de la monnaie dépend des taux d'intérêt, ce qui se modélise avec la relation suivante :

$\log(V_{t})=a\cdot i=a\cdot (r+\pi _{t})$, avec a > 0

En combinant les deux équations précédentes, on trouve :

$\log(P_{t})=\log(M_{t})-\log(Y_{t})-a\cdot (r+\pi _{e})$

Lors des situations d'hyperinflation, le taux réel et le PIB restent constants. On peut alors les négliger, ce qui donne :

$\log(P_{t})=\log(M_{t})+a\cdot \pi _{e}$

Par définition, l'inflation anticipée est égale à : $\pi _{e}=E\left[\log {P_{t+1}}\right]-\log {P_{t}}$. En faisant le remplacement, on trouve :

$\log(P_{t})=\log(M_{t})+a\cdot \left(E\left[\log {P_{t+1}}\right]-\log {P_{t}}\right)$

On développe :

$\log(P_{t})=\log(M_{t})+a\cdot E\left[\log {P_{t+1}}\right]-a\cdot \log {P_{t}}$

On ajoute $a\cdot \log {P_{t}}$ des deux côtés :

$\log(P_{t})\cdot (1+a)=\log(M_{t})+a\cdot E\left[\log {P_{t+1}}\right]$

On divise par (1 + a) des deux côtés :

$\log(P_{t})={\frac {1}{1+a}}\log(M_{t})+{\frac {a}{1+a}}E\left[\log {P_{t+1}}\right]$

Si on suppose des anticipations rationnelles, on a : $E\left[\log {P_{t+1}}\right]=P_{t+1}$. En injectant dans l'équation précédente, on a :

$\log(P_{t})={\frac {1}{1+a}}\log(M_{t})+{\frac {a}{1+a}}P_{t+1}$

On peut alors "dérouler" l'équation, en remplaçant $P_{t+1}$ par : $\log(P_{t+1})={\frac {1}{1-a}}\log(M_{t+1})+{\frac {a}{1-a}}P_{t+2}$, et ainsi de suite avec $P_{t+2}$, $P_{t+3}$, etc. On obtient alors :

$\log(P_{t})={\frac {1}{1+a}}\sum _{i=0}^{\infty }\left({\frac {a}{1+a}}\right)^{i}\log(M_{t+i})$

Cette équation nous dit que le niveau des prix lors d'une hyperinflation est égal à la somme actualisée future de la masse monétaire. On pourrait croire que le niveau des prix est constant, mais ce n'est pas le cas à cause des coefficients. Les coefficients de pondération font que le futur est sous-pesé, les valeurs futures de la masse monétaire sont en quelque sorte "sous-estimées". Le futur a moins de poids que le présent, ce qui fait que les prix restent bas même si les valeurs futures de M sont élevées. Mais au fur et à mesure que le temps passe, M augmente et les valeurs proches dans le temps font de même. Les prix augmentent donc en même temps que la masse monétaire.

L'interaction entre politique budgétaire et création monétaire

Depuis les années 2008, à la suite de la crise financière, les banques centrales se sont mises à effectuer de l'assouplissement quantitatif (QE) à grande échelle. Beaucoup de commentateurs ont alors accusé ces politiques de monétiser la dette de l'état, sous-entendu de financer directement le déficit. Et l'accusation en question est rapide, pour ne pas dire complètement fausse. En soi, cette confusion n'est pas si stupide : le QE a beaucoup de points communs avec le financement de l'état, mais il s'en démarque cependant par de nombreux points. Dans cette section, nous allons dissiper ces malentendus et expliquer quelles sont les différences fondamentales entre helicopter money (HM), QE et financement normal de l'état.

Les différentes politiques de financement d'un stimulus fiscal

Dans ce qui va suivre, nous allons supposer que l'état souhaite effectuer une politique de stimulus fiscal. Cela signifie qu'il souhaite baisser les impôts et taxes, ou alors qu'il souhaite verser de l'argent à ses citoyens. Qu'il s'agisse d'une baisse d'impôt ou d'une hausse des dépenses, il s'agit d'un stimulus fiscal, un stimulus budgétaire. Les dépenses peuvent être réparties comme l'état le souhaite : il peut décider d'augmenter le niveau des minimas sociaux, instaurer un revenu universel, faire un plan de relance de l'investissement, fournir des aides aux entreprises : peu importe. Pareil pour les baisses d'impôt, qui peuvent être générales ou ciblées sur une catégorie de la population. La nature exacte du stimulus, et sa mise en œuvre, spécifient qui touchera l'argent du stimulus fiscal. Et les conséquences ne seront donc pas les mêmes. Suivant comment cet argent est mis en circulation, l'effet macroéconomique favorisera certains secteurs, certaines catégories de la population. Certains deviendront plus riches, ou moins pauvres, d'autres pourront y perdre au change, etc.

Au niveau macroéconomique, le stimulus peut avoir une influence sur le niveau des prix et la production, qui sera différente selon le secteur économique. Au niveau agrégé, le résultat est soit une augmentation des prix, soit une augmentation de la production, soit un mélange des deux. Les économistes estiment que l'effet sur les prix se manifeste surtout à long terme, bien qu'il puisse se manifester dès le court terme sui le stimulus est trop fort. Pour la production, l'effet est maximal à court terme, mais s'atténue avec le temps. En fait, le stimulus mobilise des capacités de production inutilisées par manque de demande. En stimulant la demande, les entreprises répondent en réutilisant les capacités de production qu'elles avaient mises en sommeil ou qui étaient en pause suite à une crise économique. Mais si le stimulus est trop fort, toutes les capacités de production sont utilisées et la demande en surplus se transforme en inflation. Précisons cependant que si les prix augmentent au niveau global, certains prix vont augmenter plus que d'autres. Et l'effet sur chaque prix dépend de l'endroit où la monnaie est injectée dans l'économie et de la manière dont elle se propage, dont elle circule. Cela s’appelle l'effet Cantillon.

Mais ce qui nous importe n'est pas l'effet du stimulus, mais son financement. Il existe plusieurs manières de financer un stimulus, qui se distinguent fortement par leurs effets. Les deux cas les plus simples sont les suivants : soit l'état se finance par le déficit en empruntant sur les marchés, soit la banque centrale finance directement ses dépenses. Plusieurs politiques sont possibles.

• Avec la première, l'état emprunte l'argent du stimulus sur les marchés financiers. Cela mobilise de l'épargne existante, qui est remise en circulation par le stimulus. On parle alors de financement par l'emprunt.
• Dans le second cas, l'état emprunte l'argent sur les marchés, mais la banque centrale rachète la dette associée via assouplissement quantitatif. C'est un cas particulier de financement par l'emprunt où la banque centrale stérilise les effets de l'emprunt.
• Les autres méthodes correspondent au cas où la banque centrale intervient pour faciliter le financement du déficit. Elles sont regroupées sous le terme hélicoptère monétaire, ou encore monnaie-hélicoptère - helicopter money (HM) en anglais.

Précisons que le QE peut être utilisé seul, sans emprunt associé, et ne sert pas forcément à financer les dettes de l'état. Par exemple, une banque centrale peut utiliser le QE pour relancer l'économie, sans que l'état n'utilise de relance fiscale de son côté. Mais le cas est quand même rare.

Modes de financement d'un stimulus fiscal.

Les différentes formes d’hélicoptère monétaire

Il existe plusieurs formes d'hélicoptère monétaire, qui sont considérées comme identiques du fait de leurs caractéristiques fortement semblables et de leurs effets macroéconomiques similaires. Dans les deux premiers cas, la banque centrale crée la monnaie du stimulus et verse celui-ci soit directement à l'état, soit aux ménages. Dans le troisième cas, la banque centrale annule la dette d'état qu'elle détient. S'il faut distinguer versement de la banque centrale à tous les citoyens et versement de la banque centrale à l'état, nous pouvons cependant faire la confusion tant les deux sont similaires du point de vue monétaire. Dans les deux cas, la base monétaire augmente : elle n'est juste pas distribuée aux mêmes agents économiques.

Les trois méthodes permettent de financer le déficit de l'état, bien que ce soit par des moyens différents. Dans le cas où la banque centrale verse de l'argent au ménages, le financement est le plus direct possible. L'argent du stimulus fiscal est versé par la banque centrale, sans passer par le moindre intermédiaire. Dans le cas où la banque centrale donne de l'argent au trésor public, le transfert est indirect : la banque centrale donne de l'argent au trésor qui le redistribue aux ménages. Dans le troisième cas, il y a bien financement du déficit, bien qu'il ne soit pas évident. Le gain est lié au fait que l'état n'a pas à rembourser les échéances des dettes annulées. Les mensualités de remboursement et les intérêts disparaissent, ce qui lui fait de l'argent en moins à payer. Et cet argent en moins à payer est autant de déficit en moins et autant d'argent économisé pour l'état.

L'étude comptable du financement de l'état

Regardons maintenant ce qui se passe au niveau du bilan comptable de la banque centrale, quand l'état se finance. Suivant la situation, le bilan n'évoluera pas de la même manière. Le Q.E, le financement par l'emprunt et la monnaie-hélicoptère ont des conséquences très différentes.

Le financement par l'emprunt n'implique aucune action de la part de la banque centrale, ce qui fait que son bilan reste inchangé.

L'assouplissement quantitatif se traduit par l'augmentation des dettes publiques détenues par la banque centrale, donc une augmentation de son actif. Les dettes sont échangées contre des réserves bancaires par la banque centrale. On a donc une augmentation de l'actif (dettes achetées), mais aussi du passif (hausse des réserves), du même montant.

Bilan comptable de la banque centrale

Actif	Passif
Dette publique $\uparrow$	Réserves bancaires $\uparrow$
-	-

Au niveau comptable, les trois politiques d'hélicoptère monétaire entraînent une baisse des fonds propres de la banque centrale et/ou une création monétaire sans contrepartie.

• Avec le versement d'argent aux ménages, la base monétaire augmente et l'argent crée est versé aux citoyens. Mais pour respecter l'égalité entre actif et passif, quelque chose doit diminuer. Ce quelque chose, c'est les fonds propres de la banque centrale, son capital.

Bilan comptable de la banque centrale

Actif	Passif
-	Base monétaire (Espèces et réserves) $\uparrow$
	Compte du trésor
	Capital de la banque centrale (fonds propres) $\downarrow$

• Avec le versement d'argent à l'état, c'est la même chose, sauf que la base monétaire reste la même. L'argent est versé directement sur le compte du trésor et le capital de la banque centrale diminue du même montant.

Bilan comptable de la banque centrale

Actif	Passif
-	Base monétaire (Espèces et réserves)
	Compte du trésor $\uparrow$
	Capital de la banque centrale (fonds propres) $\downarrow$

• Avec l'annulation de la dette publique, les choses sont plus compliquées. Les dettes sont présentes à l'actif, qui diminue donc du montant des dettes annulées. En conséquence, le passif diminue et c'est encore une fois le capital de la banque centrale qui encaisse le choc.

Bilan comptable de la banque centrale

Actif	Passif
Dette publique $\downarrow$	Base monétaire (Espèces et réserves)
Autres actifs	Compte du trésor
	Capital de la banque centrale (fonds propres) $\downarrow$

L'hypothèse de l'équivalence ricardienne

Les trois politiques sont similaires dans le sens où elles injectent de la monnaie dans l'économie. Mais le sort de cette monnaie ne sera pas le même. Tout dépend de la manière dont les agents économiques vont réagir : vont-ils dépenser ou épargner l'argent du stimulus. S'ils l'épargnent, alors le stimulus n'a aucun effet macroéconomique notable. Les dépenses restent les mêmes, l'inflation reste stable, le chômage aussi, le PIB idem, etc. Par contre, si le stimulus augmente la dépense, alors c'est l'inverse : le chômage baisse, l'inflation repart, etc. Évidemment, la banque centrale peut toujours stériliser ces effets si l'inflation dépasse sa cible. Raison pour laquelle les politique de stimulus fiscal sont utilisées quand les stimulus monétaires ne servent plus, quand les taux d'intérêt sont à zéro et ne peuvent plus baisser, soit en trappe à liquidité.

L'équivalence ricardienne

Mais pourquoi les agents économiques épargneraient l'argent du stimulus ? Et bien tout dépend de s'ils s'attendent à devoir le rembourser plus tard. L'hypothèse de l'équivalence ricardienne nous dit que les ménages vont anticiper les conséquences du stimulus et réagir en conséquence. Prenons un stimulus financé par l'emprunt. Les ménages vont se rendre compte que l'argent du stimulus est attaché à une dette, qui devra être remboursée plus tard. En conséquence, ils s'attendent à une augmentation des impôts et à une réduction des dépenses dans le futur. Ce faisant, ils épargnent l'argent du stimulus, afin de compenser l'austérité future. Et c'est une solution parfaitement rationnelle (trop, même). Si l'état dépense une somme X maintenant, il devra rembourser la somme $X(1+r)^{n}$, avec r le taux d'intérêt réel sur la dette d'état et N le nombre d'années avant remboursement. En plaçant la somme X sur un support rémunéré à r%, les agents pourront rembourser la dette du stimulus.

Ce mécanisme est le même dans le cadre du QE : l'argent injecté dans l'économie peut être retiré par la banque centrale de la circulation. Les ménages vont donc conserver cet argent jusqu’à au moment où la banque centrale décidera de le retirer, afin de ne rien perdre. En théorie, c'est complètement différent pour l'HM. L'HM est supposé être une injection permanente de monnaie dans l'économie, qui ne peut pas être retiré de la circulation. En conséquence, les agents économiques n'ont pas besoin d'épargner l'argent du stimulus et le dépensent comme ils le souhaitent. L'équivalence ricardienne n'a donc aucune raison de tenir, rendant l'HM plus efficace que les autres méthodes pour stimuler l'inflation. La différence fondamentale entre QE et HM est donc son caractère temporaire/permanent : les agents s'attendent à ce que le QE/l'emprunt disparaisse et qu'il soit remboursé d'une manière ou d'une autre, alors que l'HM est permanent et n'est pas censé être remboursé.

Plus précisément, c'est le caractère permanent/temporaire perçu par les agents économiques. Si les agents économiques s'attendent à ce que la création monétaire soit permanente, alors ils vont réagir en conséquence et dépenser l'argent du stimulus. Si à l'inverse ils anticipent que la création monétaire sera temporaire, ils vont décider d'épargner et cela annulera l'efficacité du stimulus. Et si l'HM est réellement permanent, rien n'indique que les agents économiques le verront ainsi, pareil pour le QE. Il se peut que les agents économiques anticipent une réaction de la banque centrale qui ne sera pas celle prévue dans les théories. Par exemple, si la banque centrale n'est pas crédible aux yeux des agents, les marchés réagiront différemment au QE. La banque centrale a beau lancer un QE de grande envergure et jurer que celui-ci sera maintenu durant très longtemps, le QE n'aura que peu d'impact si les agents n'y croient pas et épargnent au cas où.

Une hypothèse respectée pour le Q.E, moins bien pour les autres méthodes de financement

L'équivalence ricardienne semble fonctionner assez bien pour le QE : l'argent des différents QE a été conservé par les banques, au lieu d'être mis en circulation dans l'économie. Les banques ont échangé leurs obligations d'état contre des réserves bancaires, mais n'ont pas prêtées celles-ci.

L'expérience des banques centrales américaines et européennes lors de la crise de 2008 sont assez parlantes : la totalité de l'argent du QE a été épargnée par les banques. La même chose a été observée lors de la crise japonaise de 1990, les politiques d'assouplissement quantitatif ayant fortement augmenté le bilan de la banque centrale. Aux États-Unis, la baisse sur les taux de long terme a été assez importante, de près d'un pour cent, mais les banques n'ont cependant pas décidé d’augmenter le volume de leurs prêts. Les autres pays ont eu une expérience similaire : pas d'augmentation notable du volume de prêts. Et pourtant, force est de constater que l'augmentation de la base monétaire a été très importante dans tous les cas étudiés, allant jusqu’à tripler ou quadrupler la base monétaire.

Évolution de la base monétaire américaine durant les dernières décennies. On voit qu'elle augmente fortement suite aux différents QE de 2008, signe que l'argent du QE a été épargné par les banques sous la forme de réserves bancaires.

Une explication à cela est qu'elles n'avaient pas de demande de crédit à financer et qu'elles n'avaient pas d'autre choix que de les conserver. Une autre explication est que la rémunération des réserves incitait les banques à conserver leurs réserves. Mais on ne peut pas nier que les banques ont anticipé que le QE est une mesure temporaire. Les banques sont remplies de professionnels qui connaissent la finance et la macroéconomie sur le bout des doigts (en théorie), qui connaissent le caractère temporaire du QE. D'où, en théorie, le fait que les banques ont beaucoup épargné l'argent des différents QE.

Bref : le QE permet de financer un stimulus, mais n'est en soi pas spécialement plus inflationniste que l'emprunt direct. L'argent du stimulus fiscal n'est pas complété par une mise en circulation de l'argent du QE.

Précisons cependant que l'hypothèse d'équivalence ricardienne tient assez peu pour le financement par l'emprunt. En effet, beaucoup de ménages ne se rendent pas compte que le stimulus fiscal se traduira par des impôts plus élevés dans le futur. Et s'ils s'y attendent, ils ne vont pas forcément épargner l'argent du stimulus et vont quand même préférer le dépenser. Les ménages de la théorie économique néoclassique sont capables d'anticiper un tel phénomène et de réagir en conséquence, rationnels et optimiseurs qu'ils sont. Les agents économiques du monde réel sont cependant très différents. De plus, divers mécanismes empêchent l'équivalence ricardienne de fonctionner à plein. Quelques études estiment qu'à la louche, environ 50% de l'argent d'un stimulus financé par l'emprunt est dépensé et l'autre moitié est épargnée. Notons cependant que le niveau de dette peut avoir son influence et modérer ou accentuer les effets ricardiens. Si l'état est faiblement endetté, les agents économiques ne se préoccupent pas vraiment d'un emprunt supplémentaire et n'agissent pas de manière ricardienne. Mais pour un état fortement endetté, les agents peuvent réagir autrement : un fort niveau de dette signifie soit un défaut futur probable, soit de très forts impôts pour lesquels il vaut mieux se préparer. D'où l'apparition supposée d'un comportement ricardien à de forts niveaux de dette.

Pour l'H.M, l'équivalence ricardienne n'est de toute façon pas censée se manifester. Mais on peut quand même estimer qu'une partie de l'argent de l'HM sera épargnée malgré tout. Cette politique n'ayant pas été mise en œuvre dans les pays développés, sous en quelques rares occasions et à petite échelle, on ne sait pas ce qu'il en est dans le monde réel. Mais il serait suspect que l'équivalence ricardienne tienne dans un tel cas de figure. Certes, les agents peuvent anticiper une sorte de remboursement de l'HM, sous la forme d'une politique monétaire stricte dans le futur, mais cela ne change rien tant que la banque centrale respecte sa cible d'inflation. L'HM, sous cette condition, est alors permanent dans le sens où il sert à remettre l'inflation sur les rails, comme cela aurait dû être le cas si la trappe à liquidité n'existait pas.

Pour résumer, QE, financement par l'emprunt et HM sont trois politiques qui se placent sur un continuum en termes d'efficacité : le QE est le moins efficace de tous, l'HM est tellement inflationniste qu'il est considéré comme une arme atomique monétaire, alors que le financement par l'emprunt est un intermédiaire.

Politique monétaire non-conventionnelle, coûts de financement et désendettement

Les politiques monétaires non-conventionnelles et la dette de l'état interagissent fortement. L'assouplissement quantitatif demande de racheter de la dette de l'état, certaines formes d'H.M se basent sur une annulation de la dette d'état au détenue par la banque centrale, et j'en passe. Intuitivement, Q.E et H.M permettent à l'état de monétiser leur dette, de se désendetter sans frais, sans avoir à taxer pour trouver de quoi rembourser. Mais comme on va le voir dans ce qui suit, les choses sont plus compliquées. Nous allons voir comment Q.E et H.M aident l'état à financer sa dette, et voir comment les agents privés se désendettent ou non suite à une politique monétaire non-conventionnelle.

Avant de poursuivre, il est intéressant de distinguer les différents coûts liés à un crédit. Quand l'état ou un agent privé emprunte, il doit rembourser deux choses : les intérêts et le principal (la somme empruntée). Cela demande d’acquérir une certaine somme d'argent pour rembourser les intérêts et une autre pour rembourser le principal. La première somme est ce qu'on appelle la charge d'intérêt et l'autre est la charge de principal. La somme de la charge d'intérêt et du remboursement du principal donne la charge totale. Faire la distinction est important, car le Q.E et l'H.M n'impliquent pas les mêmes charges.

L'emprunt sur les marchés : des coûts de financement élevés

Sans politique monétaire conventionnelle, l'état emprunte sur les marchés à un taux défini par les marchés? Et sur les marchés financiers, l'état se trouve en compétition avec les autres sources d'épargne. Si l'état veut emprunter 100 millions d'euros supplémentaires, alors ces 100 millions vont devoir se faire une place entre les autres obligations d'entreprises et les marchés actions. En clair, la demande d'emprunt total (état + privé) va augmenter de 100 millions d'euros. Mais le stock d'épargne préexistant est fixe, du moins sur le court terme. Les marchés vont donc prendre 100 millions d'euros qui auraient dû atterrir en emprunt privé, pour les rediriger vers l’emprunt public.

Pour résumer, l'emprunt public remplacera l'emprunt privé : c'est ce que l'on appelle l'effet d'éviction. Ce faisant, la confrontation demande d'investissement - offre d'épargne va être chamboulée. Si on trace un graphe offre-demande, on voit rapidement que les taux d'intérêt augmentent. L'état doit fournir des taux plus élevés pour attirer les investisseurs. Les autres marchés vont devoir s'adapter et monter eux-mêmes leurs taux au même niveau, ce qui fait que tous les taux augmentent. L'emprunt direct augmente donc les taux d'intérêts, ce qui est un cout direct pour l'état.

Précisons cependant qu'il existe des situations où l'effet d'éviction ne se manifeste pas. Cela arrive notamment lors des situations de trappe à liquidité, y compris quand les taux d'intérêt sont à zéro. Dans ce cas, l'état peut emprunter comme il le souhaite sans que les taux d'intérêts augmentent. Cela n’empêche pas la banque centrale de rajouter une couche de QE par-dessus, histoire de baisser encore plus les couts d'emprunt pour l'état, mais cela n'est pas strictement nécessaire.

L'assouplissement quantitatif : une réduction de la charge d'intérêt

Le financement par QE se base sur un financement sur un financement par l'emprunt, couplé à une politique de QE. Avec QE ou emprunt seul, l'état se finance sur les marchés et mobilise de l'épargne pré-existante et l'effet d'éviction apparaît. Mais le Q.E permet de neutraliser l'effet d'éviction si on le calibre bien. Si l'état veut emprunter 100 millions, la banque centrale place 100 millions sur la table. Les marchés financent l'état à hauteur de 100 millions d'euros, la banque centrale rachète 100 millions d'euros de dettes, puis les marchés réinvestissent les 100 millions dans de l'investissement privé. Si on fait la somme comptable, la demande d'investissement a augmenté autant que l'offre d'épargne. En conséquence, les taux d'intérêt restent les mêmes, ce qui rend la mesure moins coûteuse pour l'état. L'état économise la hausse des taux d'intérêts, qui n'a pas lieu.

De plus, rappelons que la dette de l'état acquise lors d'un Q.E est détenue par la banque centrale. L'état doit toujours la rembourser, mais il rembourse sa banque centrale et non des agents privés. Ce qui fait que le versement des intérêts et du principal se fait à la banque centrale. Au niveau comptable, les intérêts sont comptabilisés comme du profit, profit que la banque centrale reverse à l'état sous la forme de revenus de seigneuriage. Par contre, le principal n'est pas du profit et est comptabilisé comme remboursement d'un crédit. Et rappelons que la monnaie est détruite lors du remboursement d'un crédit, le remboursement de la dette d'état à la banque centrale ne faisant pas exception. En clair, la banque centrale détruit la monnaie du remboursement du principal et reverse tout ou partie des intérêts à l'état. L'économie est donc approximativement égale aux intérêts de la dette d'état, modulo quelques subtilités liées à la rémunération des réserves, comme on le verra plus bas.

Avec ce qu'on vient de dire, on peut quantifier le gain apporté par le Q.E. Il correspond à l'économie d'intérêts apportée par une hausse de la base monétaire. Si l'état emprunte une somme D et que l'état rachète cette dette lors d'un Q.E, le gain est le suivant :

$S=i\times D$, avec D la somme empruntée et i le taux d'intérêt sur la dette.

L'équation précédente devrait vous dire quelque chose si vous avez lu le chapitre précédent, de même que le raisonnement comme quoi le gain est une économie d'intérêt. Vous l'avez compris, ce gain n'est autre que le revenu de seigneuriage du Q.E. Et par revenu de seigneuriage, on veut dire seigneuriage définit comme le coût d'opportunité de la base monétaire. Mais nous avions vu que l'équation précédente n'est qu'une approximation et que la véritable équation prend aussi en compte la rémunération des réserves. Quand l'état fait du Q.E ou de l'hélicoptère monétaire, il n'a pas à emprunter l'argent créé. Il ne paye pas les intérêts sur une dette inexistante, ce qui fait une économie. En contrepartie, il doit rémunérer les réserves créées par sa politique, ce qui lui impose un cout supplémentaire, qui est souvent inférieur à l'économie sur la dette non-contractée. La véritable économie est donc égale à la différence entre économie d'intérêt sur la dette et rémunération des réserves, qui vaut approximativement :

$S=D\times (t_{d}-t_{r})$, avec $t_{r}$ le taux de rémunération des réserves et $t_{d}$ le taux de la dette d'état.

Le taux sur la dette d'état est le taux de long-terme, alors que le taux de rémunération des réserves est un des taux directeur de la banque centrale. On peut alors utiliser la relation : $i_{long}=i_{directeur}+p_{r}$ entre les deux taux. En combinant avec l'équation précédente, on trouve :

$S=D\times p_{r}$, avec $p_{r}$ la prime de risque de l'état.

L'interprétation de cette équation est que le gain du Q.E dépend du risque de non-remboursement de l'état. Après tout, rien d'étonnant à cela, vu que les réserves sont un instrument sans risque, alors que la dette d'état est elle risquée (l'état peut ne pas la rembourser). Le gain pour l'état correspond à l’intérêt que les agents auraient fait payer à l'état pour le risque de non-remboursement de sa dette. De ce point de vue, le Q.E peut être vu assez grossièrement comme un remboursement anticipé de la dette par la banque centrale. Pour les économies développées, qui ont de bonnes chances de rembourser leur dette, l'état est un placement très peu risqué, la prime de risque est donc limité et le gain du Q.E assez faible. Par contre, le Q.E peut être mis en place suite à une récession ou un choc économique majeur, quand les taux sur la dette d'état sont au plafond et que la prime de risque est très élevée. Le Q.E est donc un très bon instrument quand les taux sont à zéro et que la prime de risque est assez élevée.

La monnaie-hélicoptère : une réduction de la charge de la dette totale

L'H.M existe sous plusieurs formes, qui ont des impacts différents sur la dette de l'état. Mais quel que soit la forme d'H.M utilisée, l'effet macroéconomique est plus puissant avec l'H.M que le Q.E. De plus, le désendettement de l'état est plus rapide avec l'H.M qu'avec le Q.E, même si les raisons sont différentes selon que l'on annule la dette de l'état, qu'on la monétise ou qu'on donne de l'argent aux citoyens. Dans les deux premiers cas, le déficit de l'état est réduit et celui-ci peut en profiter pour se désendetter, bien que ce ne soit pas systématique. L'état peut profiter de la baisse du déficit non pas pour réduire sa dette, mais pour dépenser plus, ce qu'il faut faire en cas de récession. Mais avec la monnaie-hélicoptère proprement dite, à savoir donner de l'argent aux citoyens, l'effet sur le déficit n'est qu'indirect. Tout au plus, l'état peut donner de l'argent à ses citoyens sans s'endetter, ce qui lui permet d'augmenter ses dépenses sans coût fiscal direct. Voyons en revue les trois cas.

Le cas le plus évident est celui où la banque centrale annule tout ou partie de la dette de l'état au bien de la banque centrale. Là, l'état se désendette d'une manière assez radicale, l'état n'ayant plus à payer une partie de sa dette. Cela entraîne une réduction de la charge totale, l'état n'ayant pas à rembourser le principal de la dette annulée, pas plus que les intérêts. On a alors une réduction de la charge d'intérêt et de la charge totale. Précisons que ce cas est très différent d'un simple Q.E. Avec le Q.E, l'état rembourse le principal et les intérêts à la banque centrale, cette dernière détruit ensuite la monnaie utilisée pour rembourser le principal et reverse les intérêts à l'état. Là où le Q.E permet à l'état de réduire sa charge d'intérêt et elle seule, l'H.M par annulation de dette d'état permet une réduction de la charge totale. Le désendettement de l'état est plus rapide avec l'H.M par annulation de dette publique que le Q.E et on devine donc que l'effet macroéconomique est plus puissant avec l'H.M que le Q.E.

Précisons cependant que cette annulation n'est pas sans coûts. En effet, l'annulation de la dette impacte négativement le bilan de la banque centrale. Concrètement, son actif et son passif diminuent tous deux, ce qui se répercute sur son capital. Au premier abord, cela n'a rien de bien problématique ni de coûteux, beaucoup de banques centrales ayant un capital négatif (les banques centrales sont d'ailleurs les seules à pouvoir le faire). Par contre, ce capital est généralement reconstitué par la banque centrale, qui va préférer récupérer le capital perdu. Pour cela, il y a deux solutions.

• La première est que l'état recapitalise la banque centrale en injectant des fonds, pour faire revenir le capital de la banque centrale dans le positif. Mais cette situation est improbable et est même assez illogique. Pourquoi gagner de l'argent avec l'annulation, si c'est pour en perdre en recapitalisant la banque centrale ? Certes, l'état peut y gagner, à condition que la dette annulée soit supérieure à ce que l'état doit verser pour recapitaliser la banque centrale. Mais cela fait que le gain net pour l'état est fortement diminué. Concrètement, l'état gagne au maximum une somme équivalente au capital de la banque centrale, pas plus. Ensuite, si un état est en difficulté au point qu'il doive appeler sa banque centrale à annuler sa dette, d'où lui viendrait l'argent nécessaire pour recapitaliser sa banque centrale ? Et surtout, s'il a déjà cet argent, pourquoi ne l'utilise-t-il pas tout simplement pour rembourser sa dette en avance, ou racheter sa dette sur les marchés, ce qui reviendrait de fait à une annulation sans intervention de la banque centrale ?
• Une autre solution est que la banque centrale se recapitalise avec les revenus de seigneuriage. C'est à dire qu'elle ne les verse pas à l'état et qu'elle les accumule pour faire remonter son capital. Ce faisant, on comprend que l'annulation n'est pas une politique sans coûts. Elle consiste à échanger un flux de revenus futurs contre une grosse somme d'argent immédiate. En théorie, on peut appliquer les formules du chapitre sur le canal des prix d'actifs et montrer que les deux solutions sont équivalentes, compte tenu de taux d'intérêts. Ce qu'on gagne d'un côté, on le perd de l'autre. Du moins, en première approximation et en oubliant que l'argent peut être plus utile maintenant que plus tard, par exemple si l'économie est en pleine récession.

Pour le cas où la banque centrale donne de l'argent à l'état pour financer son déficit, l'effet sur la dette de l'état est indirect. Rappelons qu'un déficit budgétaire est généralement financé par l'émission de dette d'état supplémentaire sur les marchés. Le déficit de l'état étant totalement ou partiellement financé, la dette croît moins vite qu'elle n'aurait dû sans H.M. Cela peut aider l'état à faire des économies ou soulager sa pression financière, ce qui peut l'aider à se désendetter ou à garder une dette stable.

Pour l'HM au sens strict, à savoir de l'argent donné aux ménages sans contrepartie, l'état ne se désendette pas, mais l'argent donné peut être utilisé par les agents privés pour se désendetter. Le désendettement est possible, mais est réalisé par les ménages, ce qui a des implications macroéconomiques différentes d'un désendettement de l'état. Notons que l'effet de se désendettement privé induit par l'H.M a des effets ambigus sur la masse monétaire. D'un côté, de la monnaie est créée par la banque centrale, de l'autre le désendettement signifie destruction de monnaie lors des remboursements. Au total, la création monétaire est partiellement compensée par la destruction monétaire par les banques, l'ampleur de la compensation dépendant de l'ampleur du désendettement. Si les deux se compensent totalement et que les taux d'intérêt restent les mêmes, la monnaie créé lors de l'HM est retournée à la banque centrale sous la forme de réserves. Mais dans les faits, l'HM a une influence indirecte sur les taux d'intérêts. Le désendettement entraîne une baisse de l'activité de crédit des banques,mais ces dernières réagissent en baissent leurs taux pour relancer le crédit. Elles sont d'autant plus incitées à le faire que le désendettement induit par l'HM réduit la prime de risque des crédits de nombreux emprunteurs, via les divers canaux du crédit qu'on a vu dans les chapitres antérieurs. Et qui baisse de prime de risque dit baisse des taux bancaires et donc relance de l'activité de crédit. Au final, la masse monétaire augmente bel et bien suite à l'HM , sauf situation exceptionnelle.

Pour résumer, on peut classer les trois mesures suivant leur cout pour l'état : l'emprunt seul est la plus chère, le financement par QE est moins cher que l'emprunt seul, l'HM a un effet encore mal compris mais qui devrait être plus important que celui du Q.E.

Les différences pratiques entre H.M et Q.E

Comme dit plus haut, l'assouplissement quantitatif et la monnaie-hélicoptère n'ont pas les mêmes effets en termes de financement. Mais on peut encore creuser ce point et montrer que les deux politiques n'ont pas les mêmes effets macroéconomiques. Si les deux partagent de nombreux points communs, elles ne se transmettent pas tout à fait de la même manière à l'économie réelle.

Déjà, la mise en œuvre de l’assouplissement quantitatif est bien plus simple. L'assouplissement quantitatif demande juste de procéder à des opérations d'open market, là où la monnaie–hélicoptère au sens strict demande un transfert direct d'argent à l'état ou aux ménages. L'annulation des dettes de l'état au bilan de la banque centrale semble plus simple à mettre en œuvre, bien qu'aucune banque centrale ne l'ai jamais mise en œuvre.

Ensuite, l'assouplissement quantitatif est mieux vu par les marchés que la monnaie-hélicoptère. Elle est considérée comme moins inflationniste et surtout, elle ne remet pas en cause l'indépendance des banques centrales. Rappelons que donner gratuitement de l'argent aux agents économiques est apparenté à une mesure fiscale, et est donc du ressort de l'état, non de la banque centrale. Sans compter que certaines mises en œuvre de la monnaie-hélicoptère se basent sur un transfert direct d'argent de la banque centrale vers l'état, ou une annulation partielle de sa dette... Autant dire que mettre en œuvre cette politique ruinerait la crédibilité de la banque centrale, ce qui pourrait faire plus de mal que de bien, du moins sur le long-terme.

En savoir plus

• Hélicoptère monétaire et relance budgétaire financée par l'emprunt : du pareil au même ?
• Helicopter money: The illusion of a free lunch
• The true costs of helicopter money.

L'équation d'Euler de la consommation

Dans ce chapitre, nous allons étudier le comportement de consommation des agents économiques et allons donc faire quelques rappels sur les théories de la consommation. Nous allons dépasser la simple fonction de consommation keynésienne vue il y a quelques chapitres, à savoir $C=C_{0}+cY$, pour la remplacer par une version plus élaborée, tirée de fondements microéconomiques.

Les axiomes du modèle

Dans ce qui va suivre, nous allons volontairement éluder l'existence de l'investissement et des dépenses gouvernementales pour étudier l'impact des taux d'intérêt sur la consommation. Cela suppose que les agents économiques ne gardent de la monnaie que dans l'optique de la dépenser. Dans ce qui va suivre, nous allons supposer que le temps s'écoule par pas de temps. L'agent économique reçoit un revenu $Y_{t}$ à chaque pas de temps, et dépense en consommation la quantité d'argent $C_{t}$. Il n'est pas si déraisonnable de supposer que l'agent dépense tout son revenu et l'épargne pas. En anglais, cette hypothèse est appelée hypothèse du hand-to-mouth consumer. Mathématiquement, elle dit que la relation entre revenus et consommation est la suivante :

$C_{t}=Y_{t}$.

Mais dans les faits, cette hypothèse est bien trop approximative. Nous ne sommes pas dans un monde où l'épargne n'existe pas et force est de constater que tous les ménages ne sont pas du type hand-to-mouth. Pour comprendre pourquoi, la théorie économique suppose que les agents ne cherchent pas à maximiser leur consommation présente, mais qu'ils prennent en compte l'avenir. Dans cette optique, l’épargne est considérée comme de la consommation différée, tandis que l'emprunt est de la consommation anticipée. Épargner une somme signifie se priver de la consommation qu'elle représente, pour en profiter plus tard dans le temps. L'emprunt est l'exact inverse : la somme empruntée est dépensée tout de suite, mais le remboursement du crédit sera autant de consommation future en moins. En utilisant le formalisme adapté, on peut rendre compte de la manière dont les ménages répartissent leur consommation dans le temps.

L'utilité intertemporelle

Dans ce qui va suivre, nous allons utiliser le formalisme principal de la microéconomie : les fonctions d'utilité. Pour résumer rapidement, les fonctions d'utilité permettent de représenter mathématiquement les préférences, le fait que tel agent préfère tel choix à tel autre. Rien n'est supposée sur l'origine de ces choix, le formalisme se bornant à décrire les préférences des agents économiques. Pour faire simple, chaque choix/possibilité se voit attribuer un nombre, appelé l'utilité espérée, ou encore utilité. Plus l'utilité est importante, plus ce choix sera préférable pour l'agent économique. L'agent économique cherche à maximiser l'utilité de ses choix. Ainsi, si deux choix sont en concurrence, celui dont l'utilité est la plus forte sera choisi par l'agent économique. Les microéconomistes ajoutent quelques contraintes sur cette utilité : les utilités peuvent toujours être comparées entre deux choix, les préférences sont transitives, l'ajout d'options alternatives ne change pas les préférences déjà établies avant l'ajout, etc. Il va de soi que si vous voulez en savoir plus, vous pouvez lire l'article wikipédia sur l'utilité, disponible ici : article wikipédia sur les fonctions d'utilité.

Nous allons supposer que l'agent peut consommer à des périodes bien précises, à des pas de temps distincts. Il peut consommer à l'instant $t$, à l'instant $t+1$, à l'instant $t+2$, à l'instant $t+3$, etc. La consommation totale au cours du temps est appelée la consommation intertemporelle, et elle vaut par définition :

$C=C_{t}+C_{t+1}+C_{t+2}+C_{t+3}+...$

Cependant, nous savons que l'agent ne souhaite pas maximiser sa consommation totale, mais la lisser dans le temps. Pour modéliser cela, nous allons attribuer à la consommation intertemporelle une utilité subjective $U(C)$, qui représente grossièrement la valeur subjective attribuée à la consommation totale. Par définition, l'agent maximise l'utilité de sa consommation intemporelle, qui vaut :

$U(C)=U\left[C_{t}+C_{t+1}+C_{t+2}+C_{t+3}+...\right]$

Il est important de contraindre la fonction d'utilité, sans quoi on ne peut en tirer des résultats intéressants et encore moins faire des calculs. Les contraintes en question sont généralement tirées d'intuitions psychologiques, afin de rendre compte du comportement humain.

La première contrainte est que la fonction est croissante, ce qui traduit le fait que plus la consommation est élevée, plus l'agent en tire d'utilité. Mathématiquement, ceela se traduit par une contrainte sur la dérivée de l'utilité, qui est positive.

$U'(C_{t})>0$ : la fonction d'utilité est croissante.

La seconde contrainte dit que les agents ne considèrent pas chaque unité de consommation comme équivalente : un euro de consommation a bien plus de valeur pour quelqu'un de très pauvre que pour un agent très riche. C'est ainsi : quelqu'un qui ne peut consomme que 500 euros par mois attribuera plus de valeur à une dépense de 100 euros que quelqu'un qui peut se permettre de dépenser 5000 euros pas mois. On peut résumer cela en disant que chaque unité de consommation supplémentaire a moins de valeur que les précédentes. Et mathématiquement, cela veut dire que la fonction $U(C_{t})$ doit être de forme concave, ce qui est équivalent à dire que sa dérivée seconde est négative.

$U''(C_{t})<0$ : la fonction d'utilité est concave.

Ensuite, pour simplifier fortement les calculs, nous devons supposer que la fonction d'utilité est additivement séparable. Ce terme barbare signifie simplement que la fonction d'utilité $U(C)$ se calcule comme suit :

$U(C)=U(C_{t})+U(C_{t+1})+U(C_{t+2})+U(C_{t+3})+...$

Une telle hypothèse peut paraitre simple, mais elle suppose que l'utilité lors d'une période est indépendante de l'utilité des périodes précédentes. Un tel comportement est cependant quelque peu douteux et ne correspond pas trop à l'intuition. Déjà, cela néglige le fait que certains biens de consommation sont durables, à l'opposé des consommables. Là où la consommation d'un bien consommable donne lieu à une "utilité" immédiate mais de courte durée, les biens durables sont utilisés durant un temps assez long, équivalent à plusieurs périodes dans le modèle précédent. Cela, le modèle ne peut pas en rendre compte : seuls les effets immédiats sont modélisés, pas les effets à plus long-terme. Ensuite, un autre phénomène n'est pas pris en compte : l'apparition d'habitudes. Nombreux sont les agents économiques qui réagiraient à une baisse de leur consommation par rapport à leurs habitudes. Notons que les économistes ont un cadre théorique pour rendre compte des habitudes de consommation (le paradigme habit formation, mais cela nous emmènerait trop loin pour ce chapitre.

Introduisons maintenant le second concept, qui est l'élasticité de substitution intertemporelle. Il sert à rendre compte des arbitrage entre présent et futur. Les agents économiques ne donnent pas le même poids à la consommation différée et à la consommation immédiate : certains préféreront dépenser tout de suite plutôt que d'épargner, tandis que d'autres seront dans le cas inverse. Il s'agit en quelque sorte d'un phénomène de préférence pour le présent. Mathématiquement, cela veut dire que l'utilité de la consommation diminue dans le temps. Par exemple, l'utilité d'une consommation immédiate sera plus forte que l'utilité de la consommation future. De même, l'utilité de consommer dans 5 ans est supérieure à l'utilité de consommer dans 10 ans, et ainsi de suite.

Dans les modèles les plus simples, on modélise cela en faisant qu'à chaque pas de temps, l'utilité de la consommation soit multipliée par un coefficient $\beta$, compris entre 0 et 1. On peut poser la définition suivante : $\beta ={\frac {1}{1+p}}$, où p est le coefficient de préférence pour le présent.

$U(C_{t+1})=\beta \cdot U(C_{t})={\frac {1}{1+p}}U(C_{t})$

Cette hypothèse a des propriétés mathématiques sympathiques, comme le fait que les préférences sont consistantes dans le temps. Par exemple, on sait que les préférences ne s'inversent pas au cours du temps : si tel choix A est préféré au B à l'instant t, il le sera toujours à l'instant t+1, t+2, t+3, ... Mais malheureusement, les expériences en psychologie cognitive ne semblent pas corroborer cette hypothèse. Si on omet les controverses liées à la reproductibilité des expériences ou aux modélisations mathématiques du phénomène, les préférences semblent inconsistantes dans le temps. Pour rendre compte de cela, les économistes peuvent utiliser une préférence pour le présent dite hyperbolique, mais les calculs deviennent alors plus compliqués et seuls les modèles évoluées le font.

Le but des agents économiques est de maximiser, non pas la consommation, mais l'utilité totale de la consommation. Ce faisant, ils vont naturellement lisser leur consommation dans le temps, tout en ayant une certaine préférence pour la consommation actuelle. Leur objectif est donc de maximiser :

$U(C)=\sum _{t}\beta ^{t}\cdot U(C_{t})=\sum _{t}{\frac {1}{(1+p)^{t}}}U(C_{t})$

La contrainte de budget

Il faut ensuite ajouter la dernière brique du puzzle pour obtenir le modèle complet : la contrainte de budget. Celle-ci donne les limites à la consommation de l'agent compte tenu de son revenu. Dans ce qui va suivre, nous allons considérer que le présent correspond à la période où $t=0$ et que l'agent vit durant $N$ années. Le cas où $N$ est fini est parfois plus compliqué à traiter mathématiquement, contrairement au cas où $N=\infty$. Ce qui fait que nous allons supposer, pour simplifier les calculs, que les agents vivent indéfiniment. C'est clairement une hypothèse irréaliste, mais qui donne des résultats assez faciles à comprendre. Relaxer cette hypothèse demanderait d'étudier des modèles de type OLG (à générations imbriquées), bien plus compliqués à comprendre et hors de portée de ce cours.

Pour commencer, nous allons nous contenter d'une contrainte simple : au cours du temps qu'il lui reste à vivre, l'agent ne peut dépenser plus que ce qu'il gagne, épargne mise de côté. En clair, sa consommation totale au cours de sa vie est la somme la somme de son épargne initiale et de ses revenus (présents et futurs). Cependant, cette contrainte vaut sur l'ensemble de sa vie. Par exemple, l'agent peut parfaitement consommer moins que ce qu'il gagne : cela lui permet d'épargner une partie de son argent. De même, il peut consommer plus que ce qu'il gagne à un instant t, mais ce sera en puisant dans son épargne ou au prix d'un emprunt à rembourser plus tard. Mais dans tous les cas, l'argent épargné à un instant t sera consommé plus tard, à un instant t+x. Même chose pour un emprunt à l'instant t, qui sera remboursé en tout ou partie à l'instant t+1, t+2, t+3, etc. On pourrait croire que cette contrainte s'écrit comme suit, avec A l'épargne, Y le revenu et C la consommation :

$\sum _{t=0}^{N}C_{t}=A_{0}+\sum _{t=0}^{N}Y_{t}$

Sauf que cette équation a quelques problèmes. Déjà, les valeurs futures de la consommation et du revenu ne sont pas certains, et doivent être anticipées par l'agent économique. Notons quand même que l'agent connaît sa consommation et son revenu présent. L'équation doit se reformuler comme suit :

$C_{0}+\sum _{t=1}^{N}E[C_{t}]=A_{0}+Y_{0}+\sum _{t=1}^{N}E[Y_{t}]$

Ensuite, il faut prendre en compte le coût de l'emprunt et les intérêts sur l'épargne. Pour cela, il faut prendre en compte l'évolution de la valeur de l'argent au cours du temps. Souvenez-vous du chapitre sur le canal des prix d'actif : nous avions déjà utilisé un outil permettant de comparer les valeurs futures et actuelles d'une somme d'argent. Il s'agissait des valeurs actualisées, que nous avions appliquées sur des prix de coupons. Pour rappel, la valeur actualisée d'une somme d'argent est pondérée par le taux d'intérêt. Si on note $V_{a}[E_{t}]$ la valeur actualisée de la valeur $E_{t}$, on a :

$V_{a}[E_{t}]={\frac {E_{t}}{(1+i)^{t}}}$

Dans l'équation précédente, on peut prendre en compte facilement l'écoulement du temps sur la valeur des emprunts et de l'épargne. Il suffit d'utiliser les valeurs actualisées pour la consommation et le revenu. Ce faisant, on prend en compte naturellement l'emprunt et l'épargne dans le processus. Pour simplifier, nous allons supposer que le taux d'intérêt d'actualisation est le même pour les crédits et l'emprunt. De plus, ce taux est égal au taux réel. On doit donc reformuler la contrainte de manière à ce que les sommes pour la consommation et le revenu soient les sommes des valeurs actualisées. On a alors une contrainte de budget qui se formule de la manière suivante. Vous remarquerez que l'épargne initiale n'est pas touchée par l'usage de valeurs actualisées. Si elle est rémunérée par des intérêts, le calcul des valeurs actualisées divise par (1 + r) à chaque période. En conséquence, la rémunération de l'épargne initiale est compensée par l'usage de valeurs actualisées.

$C_{0}+\sum _{i=t+x}^{N}{\frac {E[C_{i}]}{(1+r)^{x}}}=A_{0}+Y_{0}+\sum _{i=t+x}^{N}{\frac {E[Y{i}]}{(1+r)^{x}}}$

On peut reformuler l'équation précédente comme suit, afin de pouvoir l'utiliser dans la suite du chapitre. L'équation obtenue définit la contrainte que doit respecter l'agent économique lorsqu'il maximise l'utilité de consommation.

$\left[C_{0}+\sum _{i=t+x}^{N}{\frac {E[C_{i}]}{(1+r)^{x}}}\right]-\left[A_{0}+Y_{0}+\sum _{i=t+x}^{N}{\frac {E[Y{i}]}{(1+r)^{x}}}\right]=0$

Le cas simplifié à deux périodes

À partir des deux équations de la section précédente, à savoir la fonction d'utilité et la contrainte de budget, on peut déterminer une équation appelée équation d'Euler de la consommation. Celle-ci nous permettra de déduire une nouvelle forme de la courbe IS, qui décrira convenablement le canal de substitution intertemporelle. On pourra alors étudier ce qui se passe quand les taux d'intérêt varient, et en quoi ils impactent la consommation et l'épargne, ainsi que l'arbitrage des agents économiques. Dans ce qui va suivre, nous allons nous concentrer sur deux périodes, ce qui suffit largement pour notre analyse et n'en change pas les résultats.

La contrainte de budget

Afin de simplifier l'analyse, nous allons d'abord étudier le cas à deux périodes. Nous allons nous limiter à un cas simple, où l'agent ne dispose pas de patrimoine en première période. Lors de la première période, l'agent consomme une quantité $C_{t}$ et épargne le reste de son revenu.

$Y_{t}=C_{t}+S_{t}$

Lors de la seconde période, l'agent dépense tout son argent, à savoir son revenu et son épargne.

$C_{t+1}=Y_{t+1}+(1+r)S_{t}$

En réarrangeant les termes, on a :

$S_{t}={\frac {1}{1+r}}\left(Y_{t+1}-C_{t+1}\right)$

En combinant cette équation avec la première, on a :

$C_{t}=Y_{t}+{\frac {1}{1+r}}\left(Y_{t+1}-C_{t+1}\right)$

Développons et faisons passer ${\frac {C_{t+1}}{1+r}}$ de l'autre côté :

$C_{t}+{\frac {C_{t+1}}{1+r}}=Y_{t}+{\frac {Y_{t+1}}{1+r}}$

À l'instant t, l'agent ne connait pas sa consommation future lors de la période suivante, pas plus que son revenu futur. Il doit donc les anticiper, ce qui fait que les valeurs indicées avec t+1 sont en réalité les valeurs anticipées par l'agent. L'équation plus haut devient alors :

$C_{t}+{\frac {E[C_{t+1}]}{1+r}}=A_{t}+Y_{t}+{\frac {E[Y_{t+1}]}{1+r}}$

Contrainte de budget pour deux périodes.

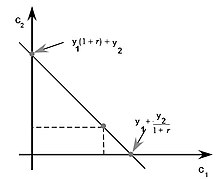
On peut représenter cette équation sur un graphe, dans lequel l'abscisse est $C_{t}$ et l'ordonnée $C_{t+1}$. Le résultat est illustré ci-contre. On voit que la contrainte de budget forme une droite penchée vers la droite. La pente de cette droite n'est autre que $-(1+r)$. Toute augmentation du revenu de l'agent pousse cette droite vers la droite, alors qu'une baisse des revenus la déplace vers la gauche.

Démonstration

Pour démontrer que la droite a une pente de $-(1+r)$, reprenons l'équation précédente et posons que le terme de droite est constant. On a alors : $C_{t}+{\frac {E[C_{t+1}]}{1+r}}=K$ Quelques manipulations algébriques donnent alors une relation entre $E[C_{t+1}]$ et $C_{t}$ : $E[C_{t+1}]=(1+r)\left[K-C_{t}\right]$ En posant $X=(1+r)K$, on a alors : $E[C_{t+1}]=X-(1+r)C_{t}$ Ce qui est une fonction affine, donc une droite de pente $-(1+r)$.

L'intersection de la droite de budget et de la courbe d'utilité

Maintenant, passons à l'équation suivante :

$U=U(C_{t})+\beta U(C_{t+1})$

Cette équation demande de préciser deux paramètres : : $C_{t}$ et : $C_{t+1}$. Il existe de nombreuses paires ($C_{t}$ , $C_{t+1}$) qui donnent la même utilité. L'agent ayant la même utilité pour chaque paire possible, il est totalement indifférent quant au choix de la paire. À ses yeux, elles sont toutes équivalentes et peu importe laquelle est choisie. Maintenant, si toutes les paires se valent en termes d'utilité, certaines ne sont pas compatibles avec la droite de budget. Pour comprendre quelle paire l'agent doit choisir, on doit représenter graphiquement ces paires et les confronter à la droite de budget. Pour cela, on va devoir prendre une utilité quelconque, égale à une valeur X choisie arbitrairement, et en déduire toutes les paires qui donnent cette utilité. L'ensemble des paires forme une courbe concave, appelée courbe d’indifférence.

Si on met les deux équations précédentes sur un graphique, on doit obtenir le schéma suivant où la courbe verte donne l'équation de l'utilité, l'autre courbe étant celle de la contrainte de budget. Si on prend un cas quelconque, il y a alors entre 0 et 2 points d'intersection. Il n'y en a aucun si la courbe d'indifférence est trop éloignée de la droite de budget, au point de ne pas la couper. Cela signifie alors qu'il n'y a pas de combinaison possible qui donne cette utilité. L'agent aura beau épargner ou dépenser de manière optimale, il n'a pas assez de revenus pour obtenir cette utilité. Le cas avec deux points d'intersection est un cas où l'agent peut mieux faire. En augmentant l'utilité, on va déplacer la courbe vers la droite et vers le haut, tout en conservant l’existence d'au moins un point d'intersection. Ce nouveau point d’intersection donne une consommation plus élevée, ce qui est le but recherché par l'agent. Le cas idéal est celui avec un seul point d'intersection : le moindre déplacement donne soit une diminution de l'utilité avec apparition de deux possibilités ($C_{t}$ , $C_{t+1}$), soit une impossibilité par incompatibilité avec la droite de budget. Pour résumer, le cas avec un point d'intersection unique est celui qui optimise au maximum l'utilité, tout en respectant la contrainte de budget. Reste à trouver les coordonnées de ce point.

Équation d'Euler de la consommation : droites de budget et d'utilité.

On vient de voir qu'il n'existe qu'un seul point d'intersection qui maximise l'utilité. En ce point, la courbe d'indifférence et la droite de budget ne font pas que se croiser : elles sont tangentes l'une de l'autre. Dit autrement, la dérivée de l'utilité est égale à la pente de la droite de budget en ce point. Les pentes des deux courbes sont égales par définition à $1+r$ pour la droite de budget et à ${\frac {U'(C_{t})}{\beta \cdot U'(C_{t+1})}}$ pour la courbe d'indifférence. On a donc :

$1+r={\frac {U'(C_{t})}{\beta \cdot U'(C_{t+1})}}$

Quelques manipulations algébriques donnent alors :

$U'(C_{t})=\left({\frac {1+r}{1+p}}\right)U'(C_{t+1})$

Le terme de droite a pour défaut de ne pas être connu à l'instant $t$. Ce faisant, les agents doivent en donner une valeur estimée à partir des informations dont ils disposent. C'est cette valeur anticipée qui est utilisée par les agents, et qui prend alors la place du terme de droite. En reformulant, on trouve l'équation d'Euler de la consommation :

$U'(C_{t})=E\left[\left({\frac {1+r}{1+p}}\right)U'(C_{t+1})\right]$

Cas idéal pour l'intersection des droites de budget et d'utilité.

On peut aussi calculer les coordonnées où ces deux pentes s'égalisent avec le raisonnement suivant.

Démonstration

La fonction d'utilité est maximisée quand sa dérivée s'annule, ce qui donne : $U'=\left[U(C_{t})+\beta U(C_{t+1})\right]'=0$ La dérivée d'une somme est la somme des dérivées, ce qui donne : $U'(C_{t})+\left[\beta U(C_{t+1})\right]'=0$ Appliquons la formule $(aU)'=a\cdot U'$ : $U'(C_{t})+\beta \cdot U'(C_{t+1})=0$ Reformulons : $U'(C_{t})=\beta \cdot U'(C_{t+1})$ On calcule la valeur de $C_{t+1}$ à partir de la contrainte, et on injecte le résultat dans l'équation d'utilité, ce qui donne : $U'(C_{t})=\beta \cdot U'((1+r)[Y_{t}-C_{t}]+Y_{t+1})$ Ce qui donne : $U'(C_{t})=\beta \cdot (1+r)\cdot U'([Y_{t}-C_{t}]+Y_{t+1})$ On peut alors faire le remplacement : $C_{t+1}=[Y_{t}-C_{t}]+Y_{t+1}$ $U'(C_{t})=\beta (1+r)\cdot U'(C_{t+1})$ Quelques remaniements nous donnent : $U'(C_{t})=\left({\frac {1+r}{1+p}}\right)U'(C_{t+1})$ Le terme de droite a pour défaut de ne pas être connu à l'instant $t$. Ce faisant, les agents doivent en donner une valeur estimée à partir des informations dont ils disposent. C'est cette valeur anticipée qui est utilisée par les agents, et qui prend alors la place du terme de droite. En reformulant, on trouve l'équation d'Euler de la consommation : $U'(C_{t})=E\left[\left({\frac {1+r}{1+p}}\right)U'(C_{t+1})\right]$

L'impact d'une variation des taux réels

Maintenant que le point d'équilibre est connu, nous allons étudier ce qui se passe quand le taux réel augmente ou baisse. Rappelons que le taux d'intérêt réel est le prix à payer pour inciter un agent à retarder sa consommation. Des taux forts permettent de rémunérer fortement l'épargne et donc de la rendre plus rentable que la consommation immédiate. Une hausse des taux entraînera une hausse des rendements de l'épargne, rendant celle-ci plus attractive (et inversement pour une baisse des taux). Les agents économiques décideront donc de se priver d'une part de consommation immédiate pour l'épargner (et inversement, une baisse des taux entraînera une dés-épargne et de la consommation), préférant la rémunération de l'épargne à une satisfaction immédiate. Dit dans le langage des économistes, le taux d'intérêt est un coût d'opportunité, la rémunération que les agents doivent recevoir pour épargner leur argent. Plus ce prix est élevé, plus l'incitation à l'épargne est importante aux dépens de la consommation. Cet effet de substitution entre monnaie et actifs, explique la forme de la courbe IS : un faible taux stimule la dépense, et donc le PIB, tandis qu'un fort taux incite à épargner, réduisant d'autant le PIB.

Cependant, cet effet de substitution est secondé par un effet de revenu, non pris en compte dans les calculs qui vont suivre. Celui-ci tient à ce que de forts taux impliquent de gros intérêts. Un ménage qui souhaite épargner une certaine somme cible, pour sa retraite par exemple, devra épargner plus avec un taux faible, comparé à ce qu'elle aurait dû épargner avec un taux plus fort. Les revenus d'épargne futurs augmentant avec les taux, le revenu futur augmente, poussant l'épargnant à consommer maintenant au lieu d'épargner. Cet effet de revenu est important dans quelques pays, dont les États-Unis, où les ménages doivent épargner pour leur retraite (du fait de l'absence de protection sociale développée). Dans les pays européens, ces effets semblent plus faibles. Les économistes ont tendance à négliger l'effet de revenu et ne considèrent que l'effet de substitution dans la construction de la courbe IS.

L'influence de ces deux effets varie fortement suivant que le ménage est emprunteur ou épargnant. Trois cas se présentent : le cas d'un emprunteur, celui d'un épargnant et celui d'un agent qui n'épargne ni n'emprunte. Bref, toujours est-il que l'effet de substitution apparaît pour tous les agents économiques, qu'ils soient emprunteurs ou épargnant. Par contre, l'effet de revenu n’apparaît que pour les épargnants, seuls à avoir des sous de côté. On peut s'en rendre compte en étudiant le graphe précédent assez simplement, en regardant la position sur le graphe du point d'intersection. Les variations du taux réels vont naturellement modifier la pente de la droite de budget, dont je rappelle que la pente est de (1 + r). Une hausse des taux va rendre la droite de budget plus pentue, alors qu'une baisse va la rendre moins pentue, plus plate. De plus, la droite va partir de plus haut suite à une hausse des taux et de plus bas en cas de baisse. Pour résumer, la droite de budget subit une rotation horaire/anti-horaire selon la situation. Dans ce qui va suivre, nous allons étudier le cas d'une hausse des taux, le cas d'une baisse s'en déduisant facilement, les raisonnements étant les mêmes. Les emprunteurs sont ceux dont les revenus actuels sont plus faibles que les revenus futurs, ceux pour lesquels le point d'intersection est situé vers la droite. Par contre, les épargnants sont ceux pour lesquels la consommation future est plus grande que l'actuelle, ce qui fait que le point d'intersection est situé plus à gauche. Les deux cas sont illustrés ci-dessous. On voit qu'une hausse du revenu entraîne une baisse de la consommation pour un emprunteur, alors que l'effet est variable pour les épargnants (tout dépend comment tourne la droite de budget).

Cas d'un emprunteur.

Cas d'un épargnant.

L'équation d'Euler de la consommation : le cas général

L'équation précédente a été dérivée à partir d'un cas particulier. Le cas général est décrit par deux équations un peu plus complexes, qui sont les suivantes :

$U(C)=\sum _{t}\beta ^{t}U(C_{t})=\sum _{t}{\frac {1}{(1+p)^{t}}}U(C_{t})$

$A_{t}+\sum _{t=0}^{N}{\frac {E[Y_{t}]}{(1+r)^{t}}}-\sum _{t=0}^{N}{\frac {E[C_{t}]}{(1+r)^{t}}}=0$

En utilisant les techniques mathématiques adaptées (méthode des multiplicateurs de Lagrange ou théorème de Bellman), on peut montrer que l'équation d'Euler vue précédemment vaut aussi pour le cas général.

$U'(C_{t})=E\left[\left({\frac {1+r}{1+p}}\right)U'(C_{t+1})\right]$

Les microéconomistes considèrent que la préférence pour le présent ne varie pas dans le temps. Il s'agit, dans leurs modèles, d'un paramètre dit structural, dans le sens où il n'est pas modifié par un changement de politique économique. En prenant cela en compte, l'équation d'Euler devient :

$U'(C_{t})={\frac {1}{1+p}}\cdot E\left[(1+r)\cdot U'(C_{t+1})\right]$

Sur le long-terme, on sait que le taux réel converge vers sa valeur naturelle et il est donc raisonnable de postuler que ce taux ne change pas au cours du temps. Sur le plus court-terme, on peut supposer que le taux réel est fixé et ne change pas durant une période. Par exemple, si on prend une période d'un an, le taux réel de la plupart des placements type livrets bancaires ne change pas, la rémunération étant annuelle. L'équation d'Euler devient alors :

$U'(C_{t})={\frac {1+r}{1+p}}\cdot E\left[U'(C_{t+1})\right]$

Le lien entre croissance et équation d'Euler

Il est possible de démontrer l'équation d'Euler en temps continu, ce qui demande quelques manipulations mathématiques assez simples, similaires à celles que nous avons réalisées en temps discret. L'équation d'Euler obtenue peut alors se reformuler comme suit :

$r-p\approx {\frac {U''(C)}{U'(C)}}\cdot {\dot {C}}$, avec ${\dot {C}}$ la dérivée de C.

On peut reformuler l'équation de la manière suivante, qui sera utile dans le prochain chapitre :

$r-p\approx {\frac {U''(C)\cdot C}{U'(C)}}\cdot {\frac {\dot {C}}{C}}$

Dans l'équation précédente, le terme ${\frac {\dot {C}}{C}}$ n'est autre que le taux de croissance de la consommation dans le temps. Si on fait l'amalgame entre la consommation et le PIB, on peut dire qu'il représente aussi le taux de croissance du PIB, le taux de croissance de l'économie réelle. En notant $g$ ce taux de croissance, on a alors :

$r-p\approx g\cdot \left[{\frac {U''(C)\cdot C}{U'(C)}}\right]$

On verra quelle est l'interprétation du terme de droite dans le chapitre suivant.

Conclusion

Pour aller plus loin, il nous faudrait connaître la fonction d'utilité elle-même. Pour cela, nous pouvons faire quelques suppositions raisonnables sur ses propriétés. On a dit plus haut que l'utilité croit avec la consommation : plus la consommation est importante, plus l'utilité dérivée de cette consommation le serait aussi. On a aussi dit que l'utilité doit avoir des rendements décroissants : plus la consommation augmente, plus l'utilité augmente lentement. Dit autrement, l'utilité augmente moins vite que la consommation dont elle dérive. Dans ce qui va suivre, nous allons voir ce qui passe pour quelques fonctions d'utilité particulières, choisies assez arbitrairement, pour voir lesquelles permettent d'expliquer certains faits économiques (comme l'épargne de précaution ou la courbe IS).

Le canal de substitution intertemporelle

Dans le chapitre précédent, nous avons démontré l'équation d'Euler de la consommation. Dans ce chapitre, nous allons l'utiliser pour montrer comment les agents économiques répartissent leur consommation dans le temps. Pour rappel, le chapitre précédent nous a appris que les agents économiques arbitrent épargne et consommation : soit ils consomment maintenant, soit ils reportent leur consommation à plus tard (et épargnent leur argent en attendant). Pour le dire autrement, l'épargne est de la consommation différée. Et les taux influencent la répartition entre consommation et épargne, ce qui impacte l'économie réelle. Cela correspond à un canal de transmission de la politique monétaire, appelé le canal de substitution intemporel. L'ensemble de ce chapitre parlera de la manière dont les ménages lissent leur consommation dans le temps, mais aussi de l'épargne de précaution.

Le lissage de la consommation dans le temps : l'équation d'Euler avec une fonction d'utilité quadratique

L'équation d'Euler nous dit que les ménages souhaitent lisser leur consommation moyenne au cours de leur vie, à savoir qu'ils cherchent à limiter les fortes chutes ou fortes baisses de consommation au cours de leur existence par le biais de l'emprunt ou de l'épargne. Ce lissage de la consommation n'est cependant pas parfait et peu de ménages arrivent à avoir une consommation uniforme au cours de leur vie. Pour décrire ce comportement, les économistes ont été obligés d'introduire certaines notions pour rendre compte de ces raisons. Ces notions ne sont autre que la préférence pour le présent et le taux d'élasticité intertemporel, des termes barbares qui cachent pourtant des concepts simples, intuitifs.

Le modèle de Hall

L'équation d'Euler a été utilisée par Hall, en 1971, dans un article qui lui a valu la renommée. À partir de celle-ci, il a montré qu'avec certaines fonctions d'utilité, la consommation suit une sorte de marche aléatoire. Pour cela, il faut que la fonction d'utilité est quadratique, à savoir un polynôme du second degré de la forme :

$U(C_{t})=aC_{t}^{2}+bC_{t}+c$

Ces fonctions d'utilité, bien que très utilisées dans un but pédagogique, ont cependant des propriétés qui posent quelques problèmes théoriques et empiriques. Par exemple, ces fonctions s'annulent pour une consommation trop grande, ce qui fait qu'elles donnent une consommation maximale, au-delà de laquelle l'utilité de la consommation ne fait que descendre ! Chose qui heurte suffisamment l'intuition pour être considéré comme irréaliste. Un autre gros problème est que sa dérivée troisième est nulle : $U'''(C_{t})=0$, ce qui ne permet pas de rendre compte de phénomènes comme l'épargne de précaution. Mais malgré tout, on peut rendre compte simplement de certains phénomènes avec une telle fonction d'utilité, sans rentrer dans des calculs extrêmement complexes, chose qu'on ne peut pas faire avec des fonctions d'utilité plus réalistes.

Avant de commencer les démonstrations, il faut faire quelques petites hypothèses supplémentaires, pour rendre le tout plus réaliste. Pour commencer, on peut supprimer le terme constant c. Par définition, cette constante est l'utilité dérivée par une consommation nulle. Pour vous en rendre compte, appliquez la formule pour $C_{t}=0$, et vous verrez qu'elle vaut c. Mais il est irréaliste d'avoir une utilité non-nulle pour une consommation nulle. On est donc obligé de postuler que c = 0.

$U(C_{t})=aC_{t}^{2}+bC_{t}$

Pour respecter les contraintes précédentes sur la dérivée première et seconde, le terme de second degré doit être négatif. Le tout donne l'utilité, ainsi que ses dérivées premières et secondes, suivantes :

$U(C_{t})=bC_{t}-aC_{t}^{2}$

$U'(C_{t})=1-2kC_{t}^{2}$

$U''(C_{t})=-2k$

Pour simplifier les calculs, on va étudier le cas où le taux réel et le taux de préférence pour le présent sont égaux : $r=p$, ce qui donne ${\frac {1+r}{1+p}}=1$. Cette hypothèse permet de simplifier l'équation d'Euler, qui devient :

$U'(C_{t})=E\left[U'(C_{t+1})\right]$

En injectant la dérivée première dans l'équation d'Euler, on trouve :

$1-2kC_{t}^{2}=E\left[1-2kC_{t+1}^{2}\right]$

Ce qui se simplifie en :

$C_{t}=E\left[C_{t+1}\right]$

Et vu que l'équation d'Euler tient en permanence, on a :

$C_{t}=E\left[C_{t+1}\right]=E\left[C_{t+2}\right]=E\left[C_{t+3}\right]=E\left[C_{t+4}\right]=...$

On voit que la consommation à un instant t est strictement égale à la consommation future anticipée. Hall postula alors que les agents forgent des anticipations rationnelles, ce qui fait que leur consommation anticipée est imprédictible. Si aucun évènement imprévu n'a lieu, alors la consommation reste stable. Pour que la consommation évolue, il faut que surviennent des évènements imprévus sur la base des informations disponibles. En clair : la consommation suit une sorte de marche aléatoire. Dans ce cas, on a alors :

$C_{t}=C_{t+1}=C_{t+2}=C_{t+3}=...$

En clair : les agents lissent parfaitement leur consommation dans le temps. Ils ne cherchent pas à consommer plus maintenant que plus tard, mais tentent de véritablement répartir leurs dépenses sur l'ensemble de leur vie. Ce qui va nous mener au point suivant. Mais précisons cependant que dans la réalité, les agents ne tentent pas de lisser parfaitement leur consommation dans le temps, pour tout un tas de raisons assez différentes les unes des autres. Le résultat obtenu avec les fonctions quadratiques est un cas particulier, qui est surtout utilisé pour mettre en avant le fait que les agents lissent leur consommation dans le temps. Ce n'est pas une vérité absolue, un cas extrême irréaliste présenté pour rende saillant un phénomène plus discret.

L'hypothèse du revenu permanent de Friedmann

Maintenant, partons de la contrainte de budget vue au-dessus, en négligeant l'épargne :

$C_{0}+\sum _{t}{\frac {E[C_{t}]}{(1+r)^{t}}}=Y_{0}+\sum _{t}{\frac {E[Y{t}]}{(1+r)^{t}}}$

Injectons dedans l'équation obtenue plus haut, à savoir : $C_{t}=E\left[C_{t+1}\right]$. On a alors :

$C_{0}+\sum _{t}{\frac {C_{t}}{(1+r)^{t}}}=Y_{0}+\sum _{t}{\frac {Y{t}}{(1+r)^{t}}}$

Ce qui se simplifie en :

$\sum _{i=t}{\frac {C_{t}}{(1+r)^{x}}}=\sum _{i=t}{\frac {Y_{i}}{(1+r)^{x}}}$

On peut alors en déduire la consommation $C_{t}$ avec quelques manipulations algébriques. Pour commencer, $C_{t}$ étant constant, on peut le sortir de la somme, ce qui donne :

$C_{t}\cdot \sum _{i=t}^{N}{\frac {1}{(1+r)^{x}}}=\sum _{i=t}^{N}{\frac {Y_{i}}{(1+r)^{x}}}$

On peut ensuite utiliser la formule d'une série géométrique pour calculer : $\sum _{i=t}^{N}{\frac {1}{(1+r)^{x}}}$, ce qui donne : $\sum _{i=t}^{N}{\frac {1}{(1+r)^{x}}}={\frac {1+r}{r}}$. En faisant le remplacement, on a alors :

$C_{t}={\frac {r}{1+r}}\cdot \sum _{i=t}^{N}{\frac {Y_{i}}{(1+r)^{x}}}$

On voit donc que la consommation des ménages dépend essentiellement de la moyenne pondérée des revenus futurs. Friedmann appelait cette moyenne le revenu permanent, par opposition aux déviations temporaires à cette moyenne, qui sont un revenu transitoire. Les revenus transitoires n'ont pas d'influence sur la consommation, comme le montre l'équation précédente. Ce qui fait qu'ils sont systématiquement épargnés. E contrario, une augmentation du revenu permanent va forcer l'agent à revoir ses anticipations de revenu futur. Il va alors modifier sa consommation en conséquence.

Cette théorie a quelques conséquences assez particulières. Notamment, elle dit que les politiques de relance fiscale sont inutiles : les agents savent que les revenus provenant d'une politique de relance fiscale ou d'une hausse des dépenses sont temporaires. Ce faisant, l'argent dépensé par l'état ou les baisses d'impôts sont épargnées par les agents et ne servent pas à relancer l'économie (si on met de côté le canal des taux d'intérêt qui induit une hausse de l'investissement). Tout se passe comme si les agents comprenaient que la relance d'aujourd'hui, financée par le déficit public, devra être remboursée un jour par une hausse des impôts. La dépense fiscale actuelle étant l'impôt de demain, les agents anticipent une future baisse des revenus qui compense aujourd'hui la relance fiscale. Ce faisant, les agents épargnent la somme qu'ils reçoivent des impôts pour payer les impôts futurs. Ce résultat est aussi connu sous le nom d'équivalence ricardienne.

L'effet de revenu

Les développements précédents ont volontairement mis de côté l'épargne des agents à l'instant t. Si on la prend en compte, l'équation de la contrainte de budget devient, avec l'équation $C_{t}=E\left[C_{t+1}\right]$ :

$\sum _{i=t}^{N}{\frac {C_{t}}{(1+r)^{x}}}=\sum _{i=t}^{N}\left(A_{t}+{\frac {Y_{i}}{(1+r)^{x}}}\right)$

On peut alors en déduire la consommation $C_{t}$ avec les mêmes manipulations algébriques que dans la section précédente. On trouve alors :

$C_{t}={\frac {r}{1+r}}\cdot A_{t}+{\frac {r}{1+r}}\cdot \sum _{i=t}^{N}{\frac {Y_{i}}{(1+r)^{x}}}$

On voit que la consommation dépend alors non seulement du revenu permanent, mais aussi de la valeur des actifs. Cette constatation est la base de l'effet de revenu que nous avons vu il y a quelques chapitres. Celui-ci dit que quand la valeur des actifs d'un ménage augmente, celui-ci augmente sa consommation. Et réciproquement quand la valeur des actifs diminue.

L'équation d'Euler avec présence d'aversion au risque

Les développements précédents nous disent que l'épargne sert uniquement à lisser la consommation dans le temps. Alors certes, les agents ne connaissent pas exactement leurs revenus futurs et doivent les anticiper. Et naturellement, les agents peuvent se tromper dans l'établissement de leur consommation présente, qui peut se révéler sous-optimale dans le futur. Mais dans les développements précédents, les agents ne cherchent pas à se prémunir contre de telles erreurs de prédiction : ils épargnent uniquement si le taux d'intérêt est supérieur au taux de croissance de la consommation. Et il va de soit que cette prédiction a beau avoir une part de vérité, elle ne suffit pas à décrire l'épargne de la plupart des ménages. Beaucoup de ménages épargnent pour se prémunir contre une dépense imprévue ou contre une baisse imprévue de revenus. Reste à rendre compte de cette épargne de précaution dans le cadre théorique de ce chapitre, ce qui demande de parler de l'aversion au risque.

L'aversion au risque et la prudence

Fonction d'utilité avec aversion au risque.

La théorie de l'utilité espérée nous dit que les réactions des agents face au risque sont de trois types : soit le sujet préfère éviter les choix risqués et fait preuve d'aversion au risque, soit il prend des risques et est alors dit "preneur de risque", soit il est relativement neutre face au risque. L'épargne de précaution survient si les agents économiques sont averses au risque, qu'ils préfèrent être prudents face au risque et s'en prémunir. Mathématiquement, l'aversion au risque fait que la fonction d'utilité respecte certaine contraintes précises sur sa dérivée $U'(c)$, et plus précisément sa courbe. L'aversion au risque donne une courbe $u'(c)$ concave, ce qui se traduit par une dérivée seconde $U''(c)$ positive et par une dérivée troisième telle que $U'''(c)>0$.

Vu que la fonction d'utilité est convexe, on peut utiliser l'inégalité de Jensen, ce qui donne :

$E[U'(c_{t+1})]>U'(E[c_{t+1}])$

On voit que l'utilité espérée de la consommation marginale future est supérieure à sa valeur effectivement réalisée. Dans ces conditions, on a alors :

$C_{t}<E[C_{t+1}]$

On voit que les agents surévaluent l'utilité de la consommation future. L'incertitude sur leurs revenus futurs font que les agents réduisent leur consommation pour épargner. Et surtout, ils épargnent donc plus que s'ils n'avaient pas d'aversion au risque, d'où l'épargne de précaution.

Pour aller plus loin, il nous faut quantifier l'aversion au risque mathématiquement et en déduire les fonctions d'utilité adaptées. Les économistes quantifient l'aversion au risque de deux manières, qui font toutes deux intervenir les fonctions $U'(c)$ et $U''(c)$. Ces deux manières distinguent l'aversion au risque absolue et relative. L'aversion au risque absolue est définie par :

$\mathrm {A} ={\frac {U''(c)}{U'(c)}}$

L'aversion au risque relative est définie par :

$\alpha =A_{a}\cdot C=C\cdot {\frac {U''(c)}{U'(c)}}$, avec C la consommation.

De plus, les économistes définissent une seconde quantité, dérivée de l'aversion au risque : la prudence. Comme pour l'aversion au risque, il existe une prudence absolue et une prudence relative. La première est la prudence absolue, définie par :

$p_{a}={\frac {U'''(c)}{U''(c)}}$

La seconde est la prudence relative, définie par :

$p_{r}=p_{a}\cdot C=C\cdot {\frac {U'''(c)}{U''(c)}}$, avec C la consommation.

Le choix de la fonction d'utilité adéquate

Maintenant que l'on sait cela, il reste à choisir quelle fonction d'utilité permet de modéliser correctement le comportement des agents. La fonction d'utilité quadratique précédente a une dérivée troisième nulle ($U'''(c)=0$), ce qui fait qu'elle ne peut pas rendre compte de l'épargne de précaution. On doit donc en changer pour une autre. Pour cela, on a le choix entre différentes classes de fonctions, mais les deux principales sont les fonctions de type CARA (Constant Absolute Risk Aversion) et CRRA (Constant Relative Risk Aversion). La première classe a une aversion au risque absolue constante, quel que soit le niveau de la consommation, alors que la seconde a une aversion au risque relative constante.

L'utilité de type CARA est assez irréaliste, ce qui fait que, dans la section suivante, nous ne parlerons que des résultats obtenus avec une utilité de type CRRA. Pour comprendre pourquoi, nous devons repartir de l'équation d'Euler du chapitre précédent. Nous avons dit qu'en temps continu, l'équation d'Euler peut se reformuler comme ceci :

$r-p\approx g\cdot \left[{\frac {U''(C)\cdot C}{U'(C)}}\right]$, avec r le taux réel, p le taux de préférence pour le présent et g le taux de croissance de la consommation/du PIB.

Or, on voit que le terme ${\frac {U''(C)\cdot C}{U'(C)}}$ n'est autre que l'aversion au risque relative. En faisant le remplacement, on obtient :

$r-p\approx g\cdot \alpha$

Si on isole le taux de croissance, on obtient :

$g\approx {\frac {r-p}{\alpha }}$

Là où cette équation devient intéressante, c'est qu'on sait que l'économie croit à un taux relativement constant, sans grandes variations. Les périodes de faibles croissance sont monnaie courante, alors que les périodes de forte croissance sont beaucoup plus rares. Pour expliquer cela, il faut que toutes les grandeurs du terme de droite soient aussi constantes. On sait que c'est le cas pour le taux réel et le taux de préférence pour le présent : le taux réel est égal à un taux naturel constant sur une longue période, pendant que p est un paramètre structural lui aussi constant. En conséquence, l'aversion au risque relative doit aussi être constante. Et par définition, seules les fonctions d'utilité de type CRRA respectent cette condition. Elles sont donc plus réalistes que les fonctions de type CARA. Les fonctions d'utilité de type CARA donnent une croissance qui se réduit au cours du temps. Plus précisément, elles donnent une croissance constante du niveau de consommation, à savoir une consommation qui croit de manière linéaire. Ce que l'on observe pas dans la réalité, où la croissance est plutôt "exponentielle".

Fonction d'utilité isoélastique.

La fonction de type CARA la plus utilisée est la suivante :

$U(C)={\frac {e^{-\beta \cdot C}}{\beta }}$

Les fonctions de type CRRA les plus utilisées sont les suivantes :

$U(C)={\frac {C^{1-\alpha }}{1-\alpha }}$, appelée utilité isoélastique.

$U(C)=\log C$, appelée utilité logarithmique.

Il faut noter que la seconde n'est que la limite de la première si $\alpha \rightarrow 1$. Elle correspond au cas particulier où l'effet de substitution et l'effet de revenu se compensent exactement. Dans ces conditions, on peut se contenter d'étudier la fonction isoélastique, le cas logarithmique n'étant qu'un cas particulier que l'on peut déduire de la formulation générale de l'utilité isoélastique.

L'équation d'Euler avec une fonction d'utilité isoélastique

Dans cette section, nous allons dériver la courbe IS new-keynesian à partir de l'équation d'Euler de la consommation et d'une fonction d'utilité isoélastique. Pour rappel, la fonction d'utilité isoélastique est la suivante :

$U(C)={\frac {C^{1-\alpha }}{1-\alpha }}$

Sa dérivée est de :

$U'(C)=C^{-\alpha }$

En injectant dans l'équation d'Euler, on a :

${C_{t}}^{-\alpha }=E\left[{\frac {1+r}{1+p}}\cdot {C_{t+1}}^{-\alpha }\right]$

Si on suppose que les anticipations sont rationnelles, alors l'équation devient :

${C_{t}}^{-\alpha }={\frac {1+r}{1+p}}{C_{t+1}}^{-\alpha }$

La relation entre taux réel, croissance, préférence pour le présent et aversion au risque

L'équation précédente permet de déterminer le taux sans risque, à savoir le taux décidé par la banque centrale. Pour cela, prenons l'équation précédente et reformulons-la comme suit, en divisant par : ${C_{t+1}}^{-\alpha }$ :

${\frac {{C_{t}}^{-\alpha }}{{C_{t+1}}^{-\alpha }}}={\frac {1+r}{1+p}}$

On peut reformuler l'équation en utilisant le taux de croissance de la consommation g, ce qui donne :

$(1+g)^{-\alpha }={\frac {1+r}{1+p}}$

En prenant le logarithme des deux côtés, on trouve l'équation suivante. Rappelons que le logarithme transforme les puissances en produit.

$-\alpha \cdot \log(1+g)=\log \left({\frac {1+r}{1+p}}\right)$

On utilise alors la formule $\log {\frac {a}{b}}=\log a-\log b$ :

$-\alpha \cdot \log(1+g)=\log(1+r)-\log(1+p)$

On peut alors utiliser l'équation $\log(1+x)\approx x$, on a :

$-g\cdot \alpha \approx r-p$

On retrouve donc l'équation vue précédemment, qui donne la relation entre aversion au risque relative, croissance et taux réel :

$g\approx -{\frac {r-p}{\alpha }}$, avec $\alpha$ l'aversion au risque.

Précisons que si l'on avait utilisé une utilité logarithmique, au lieu d'une utilité isoélastique, la relation précédente serait une égalité.

On voit que le taux réel sans risque dépend de plusieurs paramètres.

• L'impatience des agents, à savoir leur préférence pour le présent $(1+p)$, impacte directement le taux réel. Plus les ménages sont impatients (p élevé), plus le taux réel sera élevé. Cela se comprend comme suit : plus les agents sont impatients, plus il faut fixer un taux réel élevé pour les inciter à épargner. Des taux trop faibles ne fournissent pas une incitation suffisante pour que les agents réduisent leur consommation au profit de l'épargne.
• Ensuite, les taux réels sont élevés quand la consommation croit rapidement dans le temps, en raison de l'influence du terme g.
• Enfin, le paramètre $\alpha$ donne la sensibilité du taux réel à la croissance de la consommation. On a vu qu'il signifie à quel point la fonction d'utilité est courbée, convexe. Plus elle l'est, plus les agents souhaitent alors lisser fortement leur consommation dans le temps. Les variations des taux réels sans risque n'ont alors que peu d'impact sur la consommation et il faut une forte variation des taux pour les faire changer leur consommation actuelle.

La courbe IS new-keynesian log-linéarisée

Repartons de l'équation suivante :

${C_{t}}^{-\alpha }={\frac {1+r}{1+p}}\cdot E\left[{C_{t+1}}^{-\alpha }\right]$

Élevons à la puissance : $-{\frac {1}{a}}$ :

$C_{t}=\left({\frac {1+r}{1+p}}\right)^{-{\frac {1}{a}}}E\left[C_{t+1}\right]$

Pour simplifier les calculs qui vont suivre, nous allons prendre le logarithme des deux termes, et faire tous les calculs avec des logarithmes : on dit qu'on log-linéarise l'équation.

$\log {(C_{t})}=\log {\left[\left({\frac {1+r}{1+p}}\right)^{-{\frac {1}{a}}}E\left[C_{t+1}\right]\right]}$

Vu que le logarithme d'un produit est la somme des logarithmes, on a :

$\log {(C_{t})}=E[\log {C_{t+1}}]+\log {\left[\left({\frac {1+r}{1+p}}\right)^{-{\frac {1}{a}}}\right]}$

Pour le terme tout à droite, on utilise la formule $\log(a^{r})=r\cdot \log(a)$ :

$\log {(C_{t})}=E[\log {C_{t+1}}]-{\frac {1}{a}}\log {\left[{\frac {1+r}{1+p}}\right]}$

On utilise la formule suivante : $\log {\left({\frac {a}{b}}\right)}=\log a-\log b$ :

$\log {(C_{t})}=E[\log {C_{t+1}}]-{\frac {1}{a}}\left[\log {(1+r)}-\log {(1+p)}\right]$

On utilise alors l'approximation suivante : $\ln(1+r)\approx r$, ce qui donne :

$\log {C_{t}}=E[\log {C_{t+1}}]-{\frac {r-p}{\alpha }}$

Maintenant, nous allons considérer que la consommation et le PIB sont égaux, ce qui donne :

$\log Y_{t}=E[\log {Y_{t+1}}]-{\frac {r-p}{\alpha }}$

Le logarithme du PIB sera noté $y_{t}$ : $y_{t}=\ln Y_{t}$ et $y_{t+1}=\ln Y_{t+1}$. De manière générale, toutes les valeurs log-linéarisées seront écrites en minuscules dans le reste de ce cours. On a alors :

$y_{t}=E[y_{t+1}]-{\frac {1}{\alpha }}(r-p)$

Il est possible de faire ressortir le PIB potentiel et le taux naturel, ce qui donne l'équation de la courbe IS new-keynesian :

$y_{t}-{\overline {y_{t}}}=E[y_{t+1}-{\overline {y_{t+1}}})]-{\frac {1}{\alpha }}(r-{\overline {r}})$

En posant $\gamma _{t}=y_{t}-{\overline {y_{t}}}$ et $\gamma _{t+1}=y_{t+1}-{\overline {y_{t+1}}}$, on a :

$\gamma _{t}=E[\gamma _{t+1}]-{\frac {1}{\alpha }}(r-{\overline {r}})$

La valeur du coefficient : $-{\frac {1}{\alpha }}$ varie selon l'intensité de l'effet de substitution et de l'effet revenu. Si l'effet de substitution diminue, ce coefficient est négatif, et on retrouve une courbe IS décroissante habituelle. Mais si l'effet revenu domine, alors le coefficient est positif et la courbe IS est alors croissante.

La demande de monnaie : modèle Money in utility

Le modèle Money in utility, qui sera abrévié MIU, est un modèle dit d'équilibre général (il prend en compte un grand nombre de marchés et leurs interactions), qui part du comportement d'un agent qui maximise sa fonction d'utilité. Ce modèle part du principe que la détention de monnaie est source d'utilité, tout comme la consommation. Il s'agit là d'un raccourci assez grotesque : personne ne détient de la monnaie pour elle-même. Les agents détiennent de la monnaie pour divers motifs de transaction ou de précaution, c'est à dire pour ce qu'ils peuvent obtenir en échangeant leur monnaie. Néanmoins, on peut utiliser l'hypothèse que la monnaie elle-même donne de l'utilité à l'agent, pour simplifier les calculs. Cependant, divers modèles plus complets, comme les modèles OLG ou cash-in advance, permettent de dériver l'équation de base du modèle MIU.

Les hypothèses

Le modèle Money In Utility peut être vu comme une extension du modèle des deux chapitres précédents. On y retrouve les mêmes hypothèses globales, à savoir un agent qui maximise son utilité, mais qui est soumis à une contrainte de budget. La différence est que la fonction d'utilité ne tient plus compte que de la consommation, mais aussi de la quantité de monnaie à disposition. De plus, la contrainte de budget est plus compliquée, car elle doit aussi prendre en compte la monnaie, les obligations et le capital.

La fonction d'utilité

La fonction maximisée est la suivante, avec $\beta$ le taux de préférence pour le présent. Ce dernier , pour rappel, vient du fait que l'utilité de quelque chose maintenant est toujours supérieur à l'utilité de la même chose dans le futur.

$U=\sum \beta ^{t}\times U\left(C,{\frac {M_{t}}{P_{t}}}\right)$

On ne peut résoudre le modèle sans avoir une expression plus ou moins exacte de la fonction d'utilité. Dans la littérature, de nombreuses fonctions d'utilité existent : l'utilité CES, isoélastique, quasi-linéaire, exponentielle, etc. Nous n'allons par en choisir une pour le moment, mais allons garder une expression assez générale pour la fonction d'utilité. Ce n'est qu'à la fin du chapitre que nous choisirons une fonction d'utilité pour dériver quelques résultats assez précis. Mais même avec une expression générale, résoudre le modèle demande de faire quelques hypothèses sur la fonction d'utilité, qui doit être connue si on veut faire les calculs avec.

Dans ce qui va suivre, nous allons supposer que l'utilité est la somme de deux utilités séparées : l'utilité de la monnaie d'un côté, l'utilité de la consommation de l'autre. De telles fonctions, dites linéaires séparables, sont courantes en économie et permettent de simplifier les calculs. Dans le cas des modèles MIU, de telles fonctions linéairement séparables induisent le respect de la neutralité de la monnaie. Grâce à elles, la quantité de monnaie n'intervient pas dans la fonction d'utilité et seuls les taux d'intérêt ont une importance pour la politique monétaire. Les modèles Wickseliens peuvent être dérivés avec une fonction d'utilité de ce genre, mais pas les modèles monétaristes. À l'inverse, les fonctions non-linéairement séparables permettent à la politique monétaire d'avoir un effet sur les variables réelles. Mais laissons cela à plus tard. Voici à quoi ressemble la fonction d'utilité séparable :

$U\left(C,{\frac {M_{t}}{P_{t}}}\right)=U\left(C_{t}\right)+U\left({\frac {M_{t}}{P_{t}}}\right)$

La contrainte de budget

Voyons d'abord la contrainte. Nous allons supposer que l'argent (en termes réels) à disposition d'un agent à un instant t est la somme de :

• son revenu réel $Y$ ;
• ses encaisses monétaires réelles ${\frac {M}{P}}$ ;
• des encaisses réelles d'obligations $B \over P$, qui sont les seuls actifs du modèle (du moins, de la version simplifiée que nous allons étudier).

La contrainte de budget est la suivante :

$R_{t}=Y_{t}+{\frac {M_{t-1}}{P_{t}}}+{\frac {(1+i)B_{t-1}}{P_{t}}}$

On utilise alors la formule $P_{t}=(1+\pi )P_{t-1}$ :

$Rt=Y_{t}+{\frac {1}{1+\pi }}{\frac {M_{t-1}}{P_{t-1}}}+(1+r){\frac {B_{t-1}}{P_{t-1}}}$

L'équation précédente nous donne les dépenses. On peut aussi regarder les dépenses et investissements que peut réaliser l'agent. Durant cette période, cet argent peut être consommé, gardé sous la forme d'obligations, de capital ou d'encaisses monétaires. On a alors l'ensemble des dépenses et investissements :

$D_{t}=C_{t}+{\frac {M_{t}}{P_{t}}}+{\frac {B_{t}}{P_{t}}}$

Il va de soit que les deux sont égaux, ce qui donne :

$Y_{t}+{\frac {1}{1+\pi }}{\frac {M_{t-1}}{P_{t-1}}}+(1+r){\frac {B_{t-1}}{P_{t-1}}}=C_{t}+{\frac {M_{t}}{P_{t}}}+{\frac {B_{t}}{P_{t}}}$

On peut reformuler le tout en disant que :

$\left[Y_{t}+{\frac {1}{1+\pi }}{\frac {M_{t-1}}{P_{t-1}}}+(1+r){\frac {B_{t-1}}{P_{t-1}}}\right]-\left[C_{t}+{\frac {M_{t}}{P_{t}}}+{\frac {B_{t}}{P_{t}}}\right]=0$

Voici la contrainte budgétaire telle que nous l'utiliserons plus loin.

La résolution du modèle

Dans ce qui va suivre, nous allons utiliser une méthode appelée méthode des multiplicateurs de Lagrange. Celle-ci permet de maximiser ou minimiser une fonction sous une contrainte. Ici, la fonction à maximiser est évidemment la fonction d'utilité, la contrainte étant que consommation et encaisses monétaires sont limitées par W. Celle-ci commence par définir un lagrangien, une fonction similaire à la fonction à maximiser. Ce lagrangien vaut, pour une fonction $U$ et une contrainte $G=0$ : $L=U(x_{1},x_{2},x_{3},x_{4},...)+\lambda G(x_{1},x_{2},x_{3},x_{4},...)$ Le paramètre $\lambda$ est le multiplicateur de Lagrange. Celui-ci est égal à la dérivée de l'utilité quand on augmente d'une unité la contrainte. Les conditions qui maximisent la fonction U sous la contrainte G sont les suivantes : ${\frac {dL}{dx_{1}}}={\frac {dU}{dx_{1}}}+\lambda {\frac {dG}{dx_{1}}}=F_{1}+\lambda G_{1}=0$ ${\frac {dL}{dx_{2}}}={\frac {dU}{dx_{2}}}+\lambda {\frac {dG}{dx_{2}}}=F_{1}+\lambda G_{2}=0$ ${\frac {dL}{dx_{3}}}={\frac {dU}{dx_{3}}}+\lambda {\frac {dG}{dx_{3}}}=F_{1}+\lambda G_{3}=0$ ${\frac {dL}{dx_{4}}}={\frac {dU}{dx_{4}}}+\lambda {\frac {dG}{dx_{4}}}=F_{1}+\lambda G_{4}=0$ ...

Le lagrangien

Utilisons la méthode des multiplicateurs de Lagrange. Le lagrangien est le suivant.

$L=U+\lambda \left[R_{t}-D_{t}\right]=\sum \beta ^{t}\times U\left(C,{\frac {M_{t}}{P_{t}}}\right)+\lambda \left[R_{t}-D_{t}\right]$

On peut éliminer la somme, ce qui donne :

$L=\beta ^{t}\times U\left(C,{\frac {M_{t}}{P_{t}}}\right)+\lambda \left[R_{t}-D_{t}\right]$

Une fois développé, le lagrangien devrait donc être le suivant :

$L=\beta ^{t}U(C,M,P)+\lambda \left[Y_{t}+{\frac {1}{1+\pi }}{\frac {M_{t-1}}{P_{t-1}}}+(1+r){\frac {B_{t-1}}{P_{t-1}}}\right]-\left[C_{t}+{\frac {M_{t}}{P_{t}}}+{\frac {B_{t}}{P_{t}}}\right]$

Cependant, il faut noter que, d'après la méthode des multiplicateur de Lagrange, les termes avec l'indice t reçoivent un multiplicateur $\lambda _{t}$, alors que ceux d'indice t-1 ont un multiplicateur de $\lambda _{t-1}$. Le lagrangien devient alors :

$L=\beta ^{t}U(C,M,P)+\lambda _{t-1}\left[Y_{t}+{\frac {1}{1+\pi }}{\frac {M_{t-1}}{P_{t-1}}}+(1+r){\frac {B_{t-1}}{P_{t-1}}}\right]-\lambda _{t}\left[C_{t}+{\frac {M_{t}}{P_{t}}}+{\frac {B_{t}}{P_{t}}}\right]$

Le calcul des conditions de premier ordre

Les conditions de premier ordre vont nous demander de calculer beaucoup de dérivés, aussi nous allons les calculer avant de voir les conditions de premier ordre proprement dites, histoire de simplifier la compréhension des calculs.

Commençons par la fonction de dépenses $D_{t}=C_{t}+{\frac {M_{t}}{P_{t}}}+{\frac {B_{t}}{P_{t}}}$. On voit qu'on peut calculer les dérivées en fonction de la consommation, du capital, des encaisses monétaire et obligataires. Les calculs sont triviaux et donnent :

${\frac {dD_{t}}{dC}}=1$, ${\frac {dD_{t}}{dM}}={\frac {1}{P_{t}}}$ et ${\frac {dD_{t}}{dB}}={\frac {1}{P_{t}}}$.

Reste alors à calculer la dérivée des revenus par rapport aux quatre variables. On rappelle que la fonction de revenus est la suivante : $R_{t}=Y_{t}+{\frac {M_{t-1}}{P_{t}}}+{\frac {(1+i)B_{t-1}}{P_{t}}}$. L'absence de la consommation dans cette fonction nous dit que la dérivée correspondante sera nulle. On peut cependant dériver la fonction par rapport aux encaisses monétaires et obligataires. Pour le cas des encaisses, il faut penser à mettre les prix à la bonne période, à savoir utiliser l'équation $P_{t+1}=(1+\pi )P_{t}$. On a alors :

${\frac {dR_{t}}{dC}}=0$, ${\frac {dR_{t}}{dM}}={\frac {1}{1+\pi }}{\frac {1}{P_{t}}}$, ${\frac {dR_{t}}{dB}}=(1+r){\frac {1}{P_{t}}}$

Enfin, la méthode va nous demander de calculer la dérivée de l'utilité en fonction de la consommation, des encaisses monétaires et ainsi de suite. Vu que seule la consommation et les encaisses monétaires influencent la fonction d'utilité, on aura seulement deux dérivées non-nulles :

${\frac {dU}{dC}}>0$, ${\frac {dU}{dM}}>0$, ${\frac {dU}{dB}}=0$

Avec les équations précédentes, on peut calculer la condition de premier ordre pour les obligations.

${\frac {dU}{dB}}+\lambda \left({\frac {dR}{dB}}-{\frac {dD}{dB}}\right)=0$

$\lambda _{t}{\frac {1}{P_{t}}}-\lambda _{t-1}(1+r){\frac {1}{P_{t}}}=0$

$\lambda _{t}-\lambda _{t-1}(1+r)=0$

$\lambda _{t}=\lambda _{t-1}(1+r)$

On peut faire la même chose avec la consommation :

${\frac {dU}{dC}}+\lambda _{t}{\frac {dR_{t}}{dC}}-\lambda _{t}{\frac {dD_{t}}{dC}}=0$

${\frac {dU}{dC}}-\lambda _{t}=0$

${\frac {dU}{dC}}=\lambda _{t}$

On peut alors appliquer la formule $U=\beta ^{t}U(C,M)$, ce qui donne :

$\beta ^{t}{\frac {dU(C,M)}{dC}}=\lambda _{t}$

Les équations générales du modèle

À partir des conditions de premier ordre précédentes, on peut dériver plusieurs équations. On peut notamment déterminer le taux réel, retrouver l'équation d'Euler de la consommation, et déterminer le coût d'opportunité de la monnaie. Les équations qui vont suivre sont valables peut importe la fonction d'utilité choisie. Les équations que nous allons voir sont donc valables pour tous les modèles MIU, qui ne sont qu'une classe de modèles différents, mais qui partagent la même substance.

L'équation d'Euler de la consommation

On peut retrouver l'équation d'Euler de la consommation à partir de l'équation suivante :

$\lambda _{t}=\lambda _{t-1}\times (1+r)$

On y injecte l'équation $\beta ^{t}{\frac {dU(C_{t},M_{t})}{dC}}=\lambda _{t}$ :

$\beta ^{t}{\frac {dU(C_{t},M_{t})}{dC}}=\beta ^{t-1}{\frac {dU(C_{t-1},M_{t-1})}{dC}}\times (1+r)$

En simplifiant par $\beta ^{t}$, on a :

${\frac {dU(C_{t},M_{t})}{dC}}={\frac {dU(C_{t-1},M_{t-1})}{dC}}\times {\frac {1+r}{\beta }}$

De simples manipulations algébriques donnent :

${\frac {dU(C_{t-1},M_{t-1})}{dC}}={\frac {dU(C_{t},M_{t})}{dC}}\times {\frac {\beta }{1+r}}$

La dernière équation n'est autre que l'équation d'Euler de la consommation.

On peut noter que si l'on arrive à dériver l'équation d'Euler, on peut en théorie dériver l'équation de la courbe IS si l'on utilise la fonction d'utilité adéquate. Ce que nous ferons plus bas, dans les sections suivantes.

Le cout d'opportunité de la monnaie

Passons maintenant à la condition de premier ordre pour la monnaie.

${\frac {dU}{dM}}+\lambda \left({\frac {dR}{dM}}-{\frac {dD}{dM}}\right)=0$

${\frac {dU}{dM}}=\lambda \left({\frac {dR}{dM}}-{\frac {dD}{dM}}\right)$

${\frac {dU}{dM}}=\lambda _{t}-{\frac {\lambda _{t-1}}{1+\pi }}$

On applique la condition de premier ordre de la consommation :

${\frac {dU}{dM}}={\frac {dU(C_{t},M_{t})}{dC}}\beta ^{t}-{\frac {1}{1+\pi }}{\frac {dU(C_{t-1},M_{t-1})}{dC}}\beta ^{t-1}$

On utilise alors la formule ${\frac {dU}{dM}}=\beta ^{t}{\frac {dU(C_{t},M_{t})}{dM}}$ :

$\beta ^{t}{\frac {dU(C_{t},M_{t})}{dM}}={\frac {dU(C_{t},M_{t})}{dC}}\beta ^{t}-{\frac {1}{1+\pi }}{\frac {dU(C_{t-1},M_{t-1})}{dC}}\beta ^{t-1}$

On simplifie par $\beta ^{t}$ :

${\frac {dU(C_{t},M_{t})}{dM}}={\frac {dU(C_{t},M_{t})}{dC}}-{\frac {1}{1+\pi }}{\frac {dU(C_{t-1},M_{t-1})}{dC}}{\frac {1}{\beta }}$

On applique l'équation d'Euler de la consommation :

${\frac {dU(C_{t},M_{t})}{dM}}={\frac {dU(C_{t},M_{t})}{dC}}-{\frac {1}{1+\pi }}{\frac {dU(C_{t},M_{t})}{dC}}\times {\frac {\beta }{1+r}}{\frac {1}{\beta }}$

${\frac {dU}{dM}}={\frac {dU(C_{t},M_{t})}{dC}}-{\frac {1}{1+i}}{\frac {dU(C_{t},M_{t})}{dC}}$

${\frac {dU}{dM}}={\frac {dU(C_{t},M_{t})}{dC}}\left(1-{\frac {1}{1+i}}\right)$

${\frac {dU}{dM}}={\frac {dU(C_{t},M_{t})}{dC}}{\frac {i}{1+i}}$

La résolution du modèle MIU

Pour réellement résoudre le modèle Money in utility, il faut introduire une fonction d'utilité dans les équations de la section précédente et faire diverses manipulations algébriques. Nous allons d'abord étudier le cas avec une utilité logarithmique, puis avec une utilité de type CRRA (Constant Relative Risk Aversion). Rappelons que l'utilité logarithmique est un cas particulier de fonction d'utilité CRRA. Dans cette section, nous verrons notamment que l'on peut retrouver un ersatz de modèle IS/LM à partir de ces résultats.

Le cas d'une utilité logarithmique

Dans ce qui va suivre, nous allons supposer que la fonction U est un banal logarithme. Il s'agit en effet d'une fonction d'utilité souvent utilisée pour faire les calculs en microéconomie, du moins dans les manuels d'introduction. Cette fonction a quelques propriétés mathématiques qui la rende intéressante pour une fonction d'utilité. On a alors :

$U\left(C,{\frac {M}{P}}\right)=\ln {C_{t}}+\ln {\frac {M_{t}}{P_{t}}}=\ln {C_{t}}+\ln {M_{t}}-\ln {P_{t}}$

Pour résoudre le modèle, on a besoin des dérivées ${\frac {dU}{dC}}$ et ${\frac {dU}{dM}}$. Dans le cas d'une utilité logarithmique, les dérivées en question sont les suivantes.

${\frac {dU}{dC}}=\beta ^{t}{\frac {1}{C_{t}}}$ et ${\frac {dU}{dM}}=\beta ^{t}{\frac {P_{t}}{M_{t}}}$

Les résultats du modèle

Si on introduit ces dérivées dans l'équation d'Euler, on se retrouve avec un cas particulier de courbe IS de type New Keynesian, telle que dérivée il y a quelques chapitres.

Maintenant, introduisons ces dérivées dans l'équation ${\frac {dU}{dM}}={\frac {dU(C_{t},M_{t})}{dC}}{\frac {i}{1+i}}$.

$\beta ^{t}{\frac {P_{t}}{M_{t}}}=\beta ^{t}{\frac {1}{C_{t}}}{\frac {i}{1+i}}$

On simplifie par $\beta ^{t}$.

${\frac {P_{t}}{M_{t}}}={\frac {1}{C_{t}}}{\frac {i}{1+i}}$

On prend l'inverse de l'équation précédente.

${\frac {M_{t}}{P_{t}}}=C_{t}{\frac {1+i}{i}}$

Si on part du principe que $C=Y$, on a :

${\frac {M_{t}}{P_{t}}}=Y{\frac {1+i}{i}}$

On voit que la demande de monnaie est proportionnelle à la consommation et qu'elle dépend du taux nominal. La vélocité de la monnaie est alors :

$V={\frac {i}{1+i}}$

L'inflation optimale avec une utilité logarithmique

Ce modèle MIU nous permet de calculer l'inflation optimale. Pour cela, partons du principe que la banque centrale cherche à maximiser la fonction d'utilité, sous contrainte que $C=Y$. La valeur qui maximise cette fonction se calcule avec la méthode de Lagrange, ce qui donne :

$L=U+\lambda (Y-C)$

Les conditions de premier ordre obtenues sont donc :

${\frac {dU}{dC}}-\lambda C=0$ et ${\frac {dU}{dM}}={\frac {1}{M}}=0$

Il nous reste alors à déterminer comment faire en sorte d'annuler le terme ${\frac {1}{M}}$. Intuitivement, cela demande une création monétaire forte, pas forcément infinie, mais suffisante. Pour cela, partons de l'équation de demande de monnaie :

$M=PC{\frac {1+i}{i}}$

On a :

${\frac {1}{M}}={\frac {i}{PC(1+i)}}$

On voit que le terme peut s'annuler si $i=0$. Le taux d'intérêt optimal est donc nul. En clair, le taux d'inflation optimal est l'opposé du taux réel : $\pi =-r$. Une telle politique demande donc une certaine forme de déflation, où le taux de déflation est égal au taux réel. Dans ce cas, la monnaie devient un actif rémunéré, du fait de la déflation, au taux égal à $r$. Ce résultat intriguant n'est autre que la règle de Friedmann vue au début du cours.

La résolution avec une utilité de type CRRA

Dans cette section, nous allons voir le cas général, avec une utilité de type CRRA. Rappelons que l'utilité de type CRRA est la suivante :

$U(X)={\frac {X^{1-\alpha }}{1-\alpha }}$

On suppose, comme pour l'utilité logarithmique, que l'utilité est séparable : l'utilité totale est la somme de l'utilité de la consommation et de la monnaie. On a alors :

$U\left(C,{\frac {M}{P}}\right)={\frac {C_{t}^{1-\alpha }}{1-\alpha }}+{\frac {(M_{t}/P_{t})^{1-\alpha }}{1-\alpha }}$

Les dérivées ${\frac {dU}{dC}}$ et ${\frac {dU}{dM}}$ sont les suivantes.

${\frac {dU}{dC}}=C_{t}^{-\alpha }$ et ${\frac {dU}{dM}}=\left({\frac {M_{t}}{P_{t}}}\right)^{-\alpha }$

Il ne nous reste plus qu'à introduire ces dérivées dans l'équation d'Euler et l'équation du coût d'opportunité de la monnaie, pour résoudre le modèle. Pour l'équation d'Euler, les développements sont identiques à ceux du chapitre sur le canal de substitution intertemporel, dans la section sur la résolution de l'équation d'Euler avec une utilité de type CRRA. Inutile donc de les refaire ici. On peut se borner à dire que les développements permettent de retrouver l'équation de la courbe IS, et plus précisément de la courbe IS New Keynesian. Pour l'autre équation, les développements permettent de retrouver une équation de la courbe de demande de monnaie. Pour cela, reprenons l'équation du coût d'opportunité de la monnaie :

${\frac {dU}{dM}}={\frac {dU(C_{t},M_{t})}{dC}}{\frac {i}{1+i}}$

Introduisons la dérivée ${\frac {dU}{dM}}=(M_{t}/P_{t})^{-\alpha }$ :

$\left({\frac {M_{t}}{P_{t}}}\right)^{-\alpha }={\frac {dU(C_{t},M_{t})}{dC}}{\frac {i}{1+i}}$

Introduisons maintenant la dérivée : ${\frac {dU}{dC}}=C_{t}^{-\alpha }$ :

$\left({\frac {M_{t}}{P_{t}}}\right)^{-\alpha }=C_{t}^{-\alpha }{\frac {i}{1+i}}$

Élevons le tout à la puissance $-{\frac {1}{\alpha }}$ :

${\frac {M_{t}}{P_{t}}}=C_{t}\cdot \left({\frac {i}{1+i}}^{-{\frac {1}{\alpha }}}\right)$

L'équation précédent donne la demande de monnaie en fonction de la consommation et du taux d'intérêt. En faisant la confusion entre PIB et consommation, on peut écrire :

${\frac {M}{P}}=Y\cdot \left({\frac {i}{1+i}}^{-{\frac {1}{\alpha }}}\right)$

Et cette équation n'est autre qu'une équation de demande de monnaie en bonne et due forme. Si on couple cette équation avec l'équation de la courbe IS New Keynesian et la relation de Fisher $i+\pi +r$, on retrouve une sorte de modèle IS/LM un peu particulier. Le modèle Money In Utility simple permet donc de micro-fonder le modèle IS/LM, dans une certaine mesure.

Au passage, l'équation précédente permet de déterminer la vélocité de la monnaie, qui vaut alors :

$V=\left({\frac {i}{1+i}}\right)^{-{\frac {1}{\alpha }}}$

L'introduction du capital dans le modèle MIU

Dans les développements précédents, nous sommes partis du principe que les seuls actifs étaient les obligations. Mais on peut aussi ajouter la présence de capital dans le modèle. Plus précisément, on peut l'ajouter dans la contrainte de budget, afin d'affiner le modèle. En prenant en compte l'influence réciproque du revenu et du capital, le modèle MIU se voit ajouter une équation, qui ajoute la croissance économique dans le modèle. Mais les résultats du modèle ne sont pas drastiquement modifiés : l'équation rajoutée ne fait que déterminer le taux réel en fonction du capital, de la croissance et de quelques autres paramètres.

Pour commencer, il nous faut éclaircir les relations entre revenu et capital. La relation entre ces deux variables nous vient du modèle de Solow, un modèle de croissance que nous n'allons pas détailler ici. Tout ce que nous allons dire est que le revenu Y est une fonction croissante du capital. Ceux qui veulent en savoir plus peuvent lire l'encart ci-dessous, mais c'est loin d'être nécessaire pour comprendre la suite.

Les théories de la croissance postulent que le PIB Y dépend non seulement de la force de travail, mais aussi du capital présent dans l'économie. Il peut ainsi se modéliser sous la forme d'une fonction de la forme : $Y=f(L,K)$ Il est raisonnable de supposer des rendements décroissants : une augmentation de K ou L se traduit par une augmentation moindre de la production. Par exemple, si on triple le travail sans tripler le capital, la production n'est pas triplée, mais augmente de moins de trois fois. Cette propriété est relativement crédible : si on double le nombre d'employés sans doubler le nombre de machine, l'entreprise ne pourra pas produire deux fois plus. Par contre, doubler le nombre de machines et d'ouvrier permettra certainement de produire deux fois plus : si on multiplie la force de travail et le capital par deux, la production est doublée. De manière générale, augmenter les deux facteurs dans les mêmes proportions augmentera la production d'autant. On parle alors de rendements d'échelle constants. $Y\times k=f(L\times k,K\times k)$ Pour obtenir le PIB par personne, il suffit de diviser la fonction par L. Vu la présence de rendements d'échelle constants, on a donc : ${\frac {Y}{L}}=f\left({\frac {L}{L}},{\frac {K}{L}}\right)=f\left(1,{\frac {K}{L}}\right)=f\left({\frac {K}{L}}\right)$ Le terme ${\frac {K}{L}}$ est le capital par habitant, aussi appelé intensité capitalistique. Il ne faut cependant pas oublier que les rendements du capital, et donc de l'intensité capitalistique, sont décroissants : on peut doubler le capital, cela ne doublera pas le PIB.

Le lagrangien

Pour commencer, nous allons établir le nouveau lagrangien du modèle. Dans ce qui suit, on postule que le capital a tendance à se déprécier avec le temps, à un taux de $1-\delta$ par période. La contrainte de budget devient alors :

$Y_{t}+{\frac {1}{1+\pi }}{\frac {M_{t-1}}{P_{t-1}}}+(1+r){\frac {B_{t-1}}{P_{t-1}}}+(1-\delta )K_{t-1}=C_{t}+{\frac {M_{t}}{P_{t}}}+{\frac {B_{t}}{P_{t}}}+K_{t}$

On utilise alors la relation $Y_{t}=f(K_{t-1})$ :

$f(K_{t-1})+{\frac {1}{1+\pi }}{\frac {M_{t-1}}{P_{t-1}}}+(1+r){\frac {B_{t-1}}{P_{t-1}}}+(1-\delta )K_{t-1}=C_{t}+{\frac {M_{t}}{P_{t}}}+{\frac {B_{t}}{P_{t}}}+K_{t}$

On peut reformuler le tout comme suit :

$\left[f(K_{t-1})+{\frac {1}{1+\pi }}{\frac {M_{t-1}}{P_{t-1}}}+(1+r){\frac {B_{t-1}}{P_{t-1}}}+(1-\delta )K_{t-1}\right]-\left[C_{t}+{\frac {M_{t}}{P_{t}}}+{\frac {B_{t}}{P_{t}}}+K_{t}\right]=0$

Une fois développé, le lagrangien devrait donc être le suivant :

$L=\beta ^{t}U(C,M,P)+\lambda _{t-1}\left[f(K_{t-1})+{\frac {1}{1+\pi }}{\frac {M_{t-1}}{P_{t-1}}}+(1+r){\frac {B_{t-1}}{P_{t-1}}}+(1-\delta )K_{t-1}\right]-\lambda _{t}\left[C_{t}+{\frac {M_{t}}{P_{t}}}+{\frac {B_{t}}{P_{t}}}+K_{t}\right]$

La détermination du taux réel dans le modèle

Les dérivées vues dans la section précédente ne sont pas modifiées par l'introduction du capital. Par contre, une nouvelle dérivée fait son apparition : la dérivée du lagrangien par rapport au capital. Avec celle-ci, on obtient la condition de premier ordre pour le capital.

${\frac {dU}{dK}}+\lambda \left({\frac {dR}{dK}}-{\frac {dD}{dK}}\right)=0$

Cette équation peut se réécrire comme suit :

$\lambda _{t}-\lambda _{t-1}\left[{\frac {df(K)}{dK}}+(1-\delta )\right]=0$

Ce qui donne, après quelques manipulations basiques :

$\lambda _{t}=\lambda _{t-1}\left[{\frac {df(K)}{dK}}+(1-\delta )\right]$

On utilise alors la relation $\lambda _{t}=\lambda _{t-1}\times (1+r)$ :

$1+r={\frac {df(K)}{dK}}+(1-\delta )$

Ce qui donne :

$r={\frac {df(K)}{dK}}-\delta$

On voit que les facteurs monétaires ne jouent aucun rôle dans la détermination du taux réel, qui est donc un taux naturel. Le modèle nous donne donc une valeur pour le taux naturel, qui dépend des ressources en capital. On peut remarquer que le taux d'intérêt réel est égal au rendement réel du capital, son taux de profit marginal. Il s'agit d'une interprétation assez ancienne, qui date d'avant l'émergence de la macroéconomie Keynésienne, qui est respectée dans ce modèle.

Les microfondations de la courbe de Phillips : les rigidités nominales

Les modèles microfondés des chapitres précédents supposent que la demande et l'offre sur le marché des biens s'équilibre. Dans ces conditions, le PIB est à sa valeur d'équilibre qu'est le PIB potentiel et il n'existe pas de courbe de Phillips. Le seul moyen pour que cette dernière existe est de faire en sorte qu'offre et demande soient en déséquilibre temporaire. Pour cela, il faut que les prix (y compris les salaires et les taux d'intérêts) ne réagissent pas immédiatement à une variation de la demande. Une manière commode de rendre compte de cette inertie des prix et salaires est de supposer qu'ils sont rigides, ce qui veut dire qu'ils mettent du temps avant de s'adapter. Les prix et/ou salaires rigides sont à opposer aux prix dits flexibles, qui peuvent s'adapter selon la loi de l'offre et de la demande. Il existe plusieurs manières différentes de dériver la courbe de Phillips NK (New Keynesian), chacune faisant appel à un modèle particulier. Si la plupart des démonstrations utilisent des prix rigides, il est possible de démontrer la courbe de Phillips avec des prix et salaires flexibles, si on suppose que quelque chose vient mettre son grain de sel (mais nous laissons cela pour la fin du chapitre). On peut schématiquement distinguer plusieurs rigidités principales :

• une rigidité des prix : les prix mettent un certain temps avant d'égaliser offre et demande, suite à la mise en place d'une politique monétaire quelconque ;
• une rigidité des salaires, à savoir que les salaires évoluent peu à court-terme, notamment quand il s'agit de les baisser : peu d'employés accepteraient, à raison, une baisse de salaire, même justifiée par la conjoncture économique.
• une rigidité des anticipations d'inflation, causée par le fait que les agents n'ont pas forcément accès à toute l'information disponible, ce qui rend leurs anticipations d'inflation assez rigides.

Salaires et des prix ont en commun le fait qu'ils sont des variables dites nominales, à savoir dépendantes du niveau général des prix. La rigidité des prix et des salaires sont donc deux formes de ce qu'on appelle des rigidités nominales, à savoir le fait qu'une valeur nominale tend à rester la même et met du temps à s'adapter. La section qui va suivre vise à étudier plus en détail ces rigidités nominales et les théories qui les décrivent. Ces théories sont obligées de postuler l'existence de frictions, d’imperfections de marchés qui empêchent l'offre et la demande de s'égaliser à court-terme. Il existe diverses théories qui visent à rendre compte des rigidités nominales, deux modèles étant le plus souvent utilisés : le modèle de Taylor pour la rigidité des salaires, et le modèle de Calvo pour la rigidité des prix. Mais ces deux modèles sont loin d'être les seuls : il existe des modèles plus réalistes, mais aussi plus compliqués à appréhender.

Le modèle de Rotemberg

Le modèle de Rotemberg est plus simple à comprendre que le modèle de Calvo, sans compter qu'il est vraisemblablement plus réaliste, ce qui fait que nous allons le voir en premier. Ce premier part du principe que mettre à jour les prix entraîne des coûts, appelés coûts de menu, pour l'entreprise. L'entreprise va limiter ces coûts, sans pour autant se priver des gains liés à une hausse des prix. On peut prendre l'exemple d'un restaurant qui doit mettre à jour ses prix. Certes, la mise à jour des prix lui fera gagner de l'argent, en augmentant son chiffre d'affaire. Mais cela demandera aussi de réimprimer à jour la carte des menus, de revoir les procédures de calcul de la TVA et potentiellement d'autres coûts. Autant les coûts peuvent paraître dérisoires dans cet exemple, autant ceux-ci peuvent être coûteux pour d'autres entreprises. Pensez à une multinationale qui doit revoir les prix dans plusieurs pays, mettre à jour son catalogue, ses sites internets, avertir ses distributeurs, etc. De plus, outre ces coûts physiques, il faut prendre en compte la réaction des consommateurs à une éventuelle hausse des prix ! Ceux-ci pourraient ne pas la voir d'un bon œil et aller acheter chez la concurrence. Une telle réaction fait implicitement partie des coûts de menu, le terme coût de menu englobant tout ce qui peut réduire le profit suite à une hausse des prix.

Les calculs par unité produite

Divers modèles micro-économiques permettent d'établir des équations pour les coûts de menu, mais le modèle de Rotemberg ne part pas de celles-ci. À la place, il suppose que ces coûts sont proportionnels à sa production, mais dépendant aussi de la hausse des prix. Dans ce qui va suivre, nous allons travailler avec des coûts ou gains par unité produite/vendue. Le coût de menu est proportionnel au carré de la hausse des prix. Plus précisément, le modèle postule l'équation suivante pour les coûts de menu, avec :

• $C_{m}$ les coûts de menu par unité produite ;
• $\alpha$ un coefficient qui modélise la valeur de la rigidité des prix : plus il est élevé, plus les prix seront rigides;
• $Q$ la production de l’entreprise ;
• $\Delta P$ la valeur de la hausse des prix.

$C_{m}=\alpha (\Delta P)^{2}$

Outre les coûts de menu, l'entreprise va aussi gagner de l'argent en augmentant ses prix. Le gain (par unité produite) n'est autre que la hausse des prix de chaque unité $\Delta P$. Cette hausse va cependant être grignotée par les coûts marginaux, à savoir les coûts nécessaires pour produire une unité supplémentaire. On a donc, en posant $cm$ le coût marginal d'une nouvelle unité produite. Le gain réel d'une entreprise sera donc :

$G=\Delta P-C_{m}-cm=\Delta P-\alpha (\Delta P)^{2}-cm$

Les calculs agrégés

Si on se place du point de vue de l'économie tout entière, on sait que : $\Delta P=\pi _{t}P$. Ce qui donne :

$G_{t}=\pi _{t}P-\alpha (\pi _{t}P)^{2}-cm$

Nous allons multiplier le calcul précédent par le nombre d'unité vendues. On a donc :

$G_{t}=\left[\pi _{t}P-\alpha (\pi _{t}P)^{2}-cm\right]\times Y_{t}$

Comme dans le modèle de Calvo, l’entreprise va sommer l'ensemble des gains réels pour tout les pas de temps, chaque gain étant pondéré du fait de la préférence pour le passé proche. On a donc :

$\sum _{t}\beta ^{t}\left(\pi _{t}P-\alpha (\pi _{t}P)^{2}-cm\right)\times Y_{t}$

L'entreprise cherche à maximiser ce gain. Le maximum peut se calculer assez simplement, vu qu'il va, par définition d'un extremum, annuler sa dérivée. Il nous reste donc à dériver l'équation précédente en fonction du prix, et trouver quelle valeur annule la dérivée. Quelques manipulations algébriques permettent alors de retrouver l'équation de la courbe de Phillips néo-keynésienne.

$\pi =\beta \pi ^{e}+{\frac {1}{\alpha }}y$

Le modèle de Taylor

Le modèle de Taylor est un des tout premiers modèles macroéconomiques des rigidités salariales. Le modèle que nous allons voir est ce qu'on appelle un modèle log-linéarisé, dans lequel on manipule uniquement les logarithmes des valeurs pertinentes. Les économistes adorent ce genre de modèles, qui sont très courants dans le domaine de la macroéconomie. Les raisons pour faire cela sont multiples, mais la principale est que le logarithme d'une valeur est approximativement égal à sa variation en taux.

Le modèle de Taylor fait partie de la classes des modèles de type staggered contracts, où les prix et salaires sont fixés une fois pour toutes. Par exemple, les salaires sont fixés lors de la signature du contrat de travail. Ils peuvent évoluer ensuite, les augmentations n'étant pas un mythe, mais cela prend suffisamment de temps pour qu'on considère qu'un salaire est fixe durant plusieurs mois, plusieurs années. Dit autrement, tous les employés qui commencent à travailler à l'instant $t$ auront leur salaire $W_{t}$ fixé sur plusieurs périodes.

La relation entre prix et salaires

Pour commencer, le modèle que suppose que les prix et les salaires sont reliés par la formule suivante :

$P\cdot y=(1+\mu ){\overline {W}}$

Si on prend le logarithme de cette formule, on trouve :

$\log {(P\cdot y)}=\log {[(1+\mu ){\overline {W}}]}$

On applique alors la formule qui dit que le logarithme d'un produit est la somme des logarithmes : $\log {(A\times B)}=\log A+\log B$.

$\log {P_{t}}+\log {y}=\log {(1+\mu )}+\log {\overline {W}}$

On utilise alors l'approximation $\log {(1+x)}\approx \log x$.

$\log {P_{t}}+\log {y}=\mu +\log {\overline {W}}$

Par la suite, nous noterons le logarithme d'une variable $A$ comme suit : $a$. En clair, les variables en minuscules sont le logarithme de la variable écrite en majuscules. Pour donner un exemple, l'équation précédente devient, avec cette notation, cette formule :

$p_{t}+y_{t}=w_{t}+\mu$

Sur le court-terme, la croissance de la productivité est négligeable et on peut la négliger dans l'équation précédente. La formule précédente devient alors :

$p_{t}=w+\mu$

Si on suppose de plus une situation de concurrence pure et parfaite, le profit disparaît et on se retrouve alors avec :

$p_{t}=w$

C'est une approximation grossière, mais qui donne des résultats assez bons dans le cas où la croissance de la productivité est nulle (ce qui est une bonne approximation sur le cour-terme) et où le profit l'est aussi (la dernière hypothèse est réalisée en concurrence pure et parfaite).

Le salaire moyen sur deux périodes

A un instant t, la moyenne des salaires dépend des contrats signés à l'instant t, mais aussi des contrats anciens, signés dans les périodes antérieures. Dans ce qui suit, on va prendre deux périodes de temps, à savoir l'instant $t$ et l'instant $t-1$. Les salariés signent des contrats à chaque période et négocient un salaire $W_{t}$, qui correspond à un salaire réel $W_{t} \over P_{t}$. Les logarithmes de ces valeurs sont naturellement notés $w_{t}$ et $w_{t}-p_{t}$ (salaire réel). On suppose que le nombre de personnes recrutées à un instant quelconque est constant : il est le même à l'instant $t$ et à l'instant $t-1$. Le logarithme du salaire moyen à l'instant t est donc de :

$w_{m}={\frac {w_{t}+w_{t-1}}{2}}$

Maintenant, on a besoin d'une équation qui fixe l'évolution des salaires dans le temps. Il est raisonnable de supposer que les salaires dépendent certes des prix, mais aussi de l'activité économique. Cela peut se résumer avec une formule de la forme $w_{t}=P_{t}+\gamma \cdot Y_{t}$. Pour simplifier les calculs, nous allons prendre la formule suivante :

$w_{t}={\frac {p_{t}+E[p_{t+1}]}{2}}+\gamma \cdot Y_{t}$

À partir de cette équation, on peut calculer le salaire moyen. Pour cela, commençons par calculer la somme $w_{t}+w_{t-1}$ :

$w_{t}+w_{t-1}=\left[{\frac {p_{t}+E[p_{t+1}]}{2}}+\gamma \cdot Y_{t}\right]+\left[{\frac {p_{t-1}+E[p_{t}]}{2}}+\gamma \cdot Y_{t-1}\right]$

En simplifiant, on trouve :

$w_{t}+w_{t-1}={\frac {p_{t}+E[p_{t+1}]+p_{t-1}+E[p_{t}]}{2}}+\gamma \cdot (Y_{t}+Y_{t-1})$

Maintenant, regardons le terme $E[p_{t}]$. À l'instant t, on sait quel est le niveau des prix et on peut le comparer à la valeur anticipée $E[p_{t}]$. On sait qu'il y aura une différence entre les deux, l'erreur de prédiction, qui est plus ou moins négligeable. Formellement, on a : $E[p_{t}]-p_{t}=\epsilon _{t}$. Nous allons ici faire le choix de négliger l'erreur de prédiction afin de simplifier les calculs. On peut alors remplacer $E[p_{t}]$ par $p_{t}$. L'équation précédente devient alors :

$w_{t}+w_{t-1}={\frac {p_{t}+E[p_{t+1}]+p_{t-1}+p_{t}}{2}}+\gamma \cdot (Y_{t}+Y_{t-1})$

On peut alors simplifier, ce qui donne :

$w_{t}+w_{t-1}=p_{t}+{\frac {E[p_{t+1}]+p_{t-1}}{2}}+\gamma \cdot (Y_{t}+Y_{t-1})$

Divisons par 2 pour obtenir le salaire moyen :

$w_{m}={\frac {p_{t}}{2}}+{\frac {E[p_{t+1}]+p_{t-1}}{4}}+{\frac {1}{2}}\cdot \gamma \cdot (Y_{t}+Y_{t-1})$

Le niveau général des prix et l'inflation

Maintenant, rappelons que le prix moyen $p_{t}$ est égal au salaire moyen, ce qui donne :

$p_{t}={\frac {p_{t}}{2}}+{\frac {E[p_{t+1}]+p_{t-1}}{4}}+{\frac {1}{2}}\cdot \gamma \cdot (Y_{t}+Y_{t-1})$

Soustrayons ${\frac {p_{t}}{2}}$ des deux côtés :

${\frac {1}{2}}p_{t}={\frac {E[p_{t+1}]+p_{t-1}}{4}}+{\frac {1}{2}}\cdot \gamma \cdot (Y_{t}+Y_{t-1})$

En simplifiant par 1/2, on a :

$p_{t}={\frac {E[p_{t+1}]+p_{t-1}}{2}}+\gamma \cdot (Y_{t}+Y_{t-1})$

Le taux d'inflation est égal, par définition, à $\pi _{t}=p_{t}-p_{t-1}$, ce qui donne :

$\pi _{t}=E[\pi _{t+1}]+2\cdot \gamma \cdot (Y_{t}+Y_{t-1})$

On retrouve bien l'équation d'une courbe de Phillips augmentée des anticipations.

Le modèle de Calvo

Le modèle de Calvo est à la base de la théorie New Keynesian, aussi mérite-il d'être abordé ici. Son principe est très simple, ce qui fait que le modèle n'est pas vraiment réalise. Néanmoins, celui-ci donne des prédictions similaires à celles obtenues avec des modèles plus complets et réalistes. De plus, il est assez simple à comprendre (du moins, dans une certaine mesure) et facile à utiliser. Cette simplicité lui a permis d'être la pierre angulaire du traitement des rigidités nominales.

Ce modèle part de deux hypothèses :

• les firmes ne mettent pas à jour leurs prix en permanence, à cause des coûts que cela induirait : les prix sont rigides pour une partie des entreprises et flexibles pour l'autre ;
• les entreprises décident à quel prix elles vendent leurs produits, ce qui n'est possible que si celles-ci sont des monopoles ou oligopoles en compétition les uns avec les autres.

Première hypothèse

La version du modèle que nous allons aborder suppose que l'entreprise peut modifier ses prix à des instants bien précis, séparés par un pas temporel constant. La première version publiée par Calvo utilisait cependant un temps continu, moins facile à manier. Mais cette différence entre temps continu et discret est cependant sans importance sur les résultats. Le point de départ du modèle est de négliger les facteurs qui poussent une entreprise à mettre à jour ses prix. Il est juste supposé qu'à chaque instant t, une entreprise a une probabilité (1 - h) de mettre à jour ses prix et une probabilité h de les garder tels quel. Ainsi, on peut facilement déterminer le niveau général des prix à un instant t+1, à partir des prix à un instant t :

• soit $P_{t}$ le niveau général des prix à l'instant t ;
• $P*$ le prix mis à jour par les entreprises à l'instant t ;
• $\Delta P$ la différence entre $P*-P_{t}$.

$P_{t+1}=(1-h)P*+hP_{t}=(1-h)\left[\Delta P+P_{t}\right]+hP_{t}=(1-h)\Delta P+P_{t}$

Divisons par $P_{t}$ :

$1+\pi =(1-h){\frac {\Delta P}{P_{t}}}+1=(1-h){\frac {P*}{P_{t}}}+h$

On a alors :

${\frac {1+\pi }{1-h}}={\frac {P*}{P_{t}}}+{\frac {h}{1-h}}$

${\frac {1+\pi }{1-h}}-{\frac {h}{1-h}}={\frac {P*}{P_{t}}}$

${\frac {1+\pi -h}{1-h}}P_{t}=P*$

Seconde hypothèse

La firme sait qu'elle va devoir garder ce prix durant un moment, sans vraiment possibilité de l'ajuster précisément à la conjoncture économique. Cela entraînera un manque à gagner, dans le sens où le prix choisit ne sera pas forcément optimal comparé au prix idéal que choisirait l'entreprise si elle pouvait mettre à jour ses prix à la volée. La solution idéale, qui minimise le manque à gagner est de fixer la prix à une valeur précise, qui se calcule assez facilement. Cette valeur est simplement la moyenne du prix idéal, obtenu en mettant les prix continuellement à jour. La moyenne est effectuée sur les prix idéaux anticipés entre la mise en place du prix $P*$ et son abandon (sa mise à jour). Cette moyenne est pondérée, pour une raison simple : le manque à gagner proche dans le temps a plus d'impact qu'un manque à gagner lointain dans le futur. Chaque prix idéal pour un pas de temps se voit donc attribuer un coefficient, coefficient qui diminue avec le temps qui passe. Ce phénomène est assez classique en économie, et est étudié par les économistes qui étudient le choix intertemporel. Ceux-ci ont démontré que pour que les préférences soient stables, la décroissance des coefficients avec le temps doit être exponentielle.

On peut formaliser cela par l’équation suivante :

$P*=(1-h\beta )\sum _{t}(h\beta )^{t}P_{i}(t)$

Si on omet le terme $(1-h\beta )$, l'équation nous dit que le prix choisit est la moyenne des prix idéaux $\sum _{t}P_{i}(t)$, chaque prix étant pondéré par le coefficient $\beta$ en fonction du temps et la probabilité que l'entreprise garde le prix jusqu'à cette période.

Démonstration

On part du principe que l'entreprise souhaite minimiser une fonction de perte $L$, qui prend en compte le manque à gagner. Voici les points qui doivent apparaître dans cette équation : Il faut donc calculer le manque à gagner pour chaque pas de temps et en faire la somme. Si on pose $L_{t}$ le manque à gagner lors du pas de temps t, on a : $L=\sum _{t}L_{t}$ Lors d'un pas temporel, ce manque à gagner est égal à la différence entre le prix choisi et le prix idéal (anticipé par l'entreprise) $P_{i}(t)$ : $P*-P_{i}(t)$. L'entreprise souhaite diminuer la variance du prix choisit par rapport au prix idéal, c'est à dire minimiser l'expression $[P*-P_{i}(t)]^{2}$. L'entreprise a une préférence pour les gains proches comparé aux gains dans un futur lointain. Ainsi, elle donne un poids différent aux manques à gagner proches dans le temps qu'aux lointains. On peut modéliser cela en supposant qu'à chaque pas de temps, le manque à gagner estimé est multiplié par un coefficient $\beta$. A chaque pas de temps, l'entreprise a une probabilité h de ne pas changer son prix, mais aussi une probabilité ( 1 - h ) de les changer. Seul le premier cas doit être pris en compte, alors que le second n’entraîne aucun manque à gagner. En prenant ces faits en compte, on obtient : $L_{t}=\sum _{t}(h\beta )^{t}[P*-P_{i}(t)]^{2}$ Le prix mis à jour est naturellement celui qui minimise le manque à gagner, c'est à dire celui tel que ${\frac {\delta L_{t}}{\delta P*}}=0$. On obtient alors : $\sum _{t}2[P*-P_{i}(t)](h\beta )^{t}=0$ On peut alors factoriser et simplifier par deux, ce qui donne : $\sum _{t}(h\beta )^{t}P*-\sum _{t}(h\beta )^{t}P_{i}(t)=0$ $\sum _{t}(h\beta )^{t}P*=\sum _{t}(h\beta )^{t}P_{i}(t)$ Vu que $P*$ est une constante, on peut la factoriser de la somme, ce qui donne : $P*\sum _{t}(h\beta )^{t}=\sum _{t}(h\beta )^{t}P_{i}(t)$ Pour le terme de gauche, on peut utiliser la formule d'une série géométrique pour simplifier la somme, ce qui donne : $P*\times {\frac {1}{1-h\beta }}=\sum _{t}(h\beta )^{t}P_{i}(t)$ $P*=(1-h\beta )\sum _{t}(h\beta )^{t}P_{i}(t)$

Toute entreprise qui met à jour ses prix a intérêt à choisir le prix $P*$ de manière à maximiser ses profits. On peut formuler cela mathématiquement en disant que le prix sera le somme d'un bénéfice/profit $u$ et du reste, composé de coûts appelés coûts marginaux (salaires, prix des matières premières et autres).

$P=u+cm$

En injectant cette équation dans la précédente, on trouve l'équation de Calvo proprement dite. Il faut cependant signaler que les coûts marginaux sont des coûts anticipés, ce qui fait qu'on leur mettra un indice e.

$P*=(1-h\beta )\sum _{t}(h\beta )^{t}(u+cm_{e})$

La courbe de Phillips néo-keynésienne

On peut alors égaliser avec l'équation ${\frac {1+\pi -h}{1-h}}P_{t}=P*$, ce qui donne :

$(1-h\beta )\sum _{t}(h\beta )^{t}(u+cm_{e})={\frac {1+\pi -h}{1-h}}P_{t}$

$(1-h)(1-h\beta )\sum _{t}(h\beta )^{t}(u+cm_{e})=(1+\pi -h)P_{t}$

$(1-h)(1-h\beta )\sum _{t}(h\beta )^{t}(u+cm_{e})=(1-h)P_{t}+\pi P_{t}$

$(1-h)(1-h\beta )\sum _{t}(h\beta )^{t}(u+cm_{e})-(1-h)P_{t}=\pi P_{t}$

Quelques manipulations algébriques nous donnent l'inflation :

$\pi _{t}=\beta \pi _{e}+{\frac {(1-h)(1-h\beta )}{\beta }}[(u+cm_{e})-P_{t}]$

Le terme $[(u+cm_{e})-P_{t}]$ est appelé le coût marginal réel. Certains ont supposé une relation entre ce coût marginal réel et l'écart de production, sur des arguments qualitatifs. On peut parfaitement supposer que les deux sont proportionnels, ce qui donne :

$\pi _{t}=\beta \pi _{e}+{\frac {(1-h)(1-h\beta )}{\beta }}y_{t}$

On retrouve ainsi l'équation vue au début de ce paragraphe, en posant $\alpha ={\frac {(1-h)(1-h\beta )}{\beta }}$.

$\pi =\beta \pi ^{e}+\alpha y+S$

Les microfondations de la courbe de Phillips : l'information incomplète

Il est possible de dériver la courbe de Phillips en supposant que les prix sont flexibles, mais que les prix mis à jour ne sont pas ceux qui égalisent l'offre et la demande. Pour cela, quelque chose doit empêcher les agents d'estimer correctement la bonne valeur des prix. Ces mauvaises anticipations peuvent avoir des origines diverses, mais on peut les classer en deux types : soit les anticipations des agents ne sont pas rationnelles, soit les agents ont des anticipations rationnelles mais diverses frictions viennent mettre un grain de sable dans les rouages. Par exemple, on peut supposer qu'ils anticipent rationnellement l'inflation, mais sur la base d'informations obsolètes. Ou alors, on peut supposer des anticipations adaptatives, ce qui permet d'obtenir une courbe de Phillips. Dans cette section, nous allons parler de quelques modèles de ce genre, en mettant de côté celui des anticipations adaptatives (qui a déjà été vu il y a quelques chapitres).

L’illusion monétaire (Worker's misperception model)

Milton Friedmann a été le premier à donner, sous une formulation essentiellement verbale, un mécanisme à l'origine des effets réels de la politique monétaire. Celui-ci se base sur l'illusion monétaire, le fait que les salariés ne perçoivent pas correctement une hausse des prix, ou tout du moins mettent du temps avant de s'en rendre compte. Cette illusion monétaire est à l'origine d'une différence entre les salaires réels effectifs et les salaires réels perçus par les entreprises et salariés. Suite à une hausse de l'inflation, les salaires nominaux vont naturellement augmenter, alors que les salaires réels vont rester les mêmes. Les salariés vont voir la hausse des salaires nominaux, mais vont tarder à voir la hausse des prix. Ils vont croire que la hausse des salaires nominaux est synonyme d'une hausse des salaires réels. Cette fausse hausse des salaires réels incite à travailler plus, les heures travaillées augmentent et le taux de chômage baisse. Mais cela ne dure que tant que l'illusion monétaire se fait sentir. Quand les salariés commencent à voir la hausse des prix, ils calculent leur salaire réel et adaptent l'offre de travail en conséquence. Le chômage revient alors à son taux naturel, à savoir le taux de chômage lié au PIB potentiel.

Le modèle des îles de Lucas

Le mécanisme décrit par Friedmann était une formulation essentiellement verbale, et non une théorie mathématique. Il fallut attendre quelque temps avant que Lucas élabore son modèle des îles de Lucas, la première théorie de ce genre, qui a valu un prix Nobel à son auteur. Ce modèle utilise des anticipations rationnelles, sans que cela l’empêche d'obtenir un effet de la politique monétaire sur le PIB et d'autres variables réelles ! C'est pour cela que ce modèle est souvent abordé dans les cursus de macroéconomie. Elle aboutit à la formulation de l'équation suivante, appelée courbe d'offre de Lucas. Celle-ci est une relation entre PIB et prix, exprimée avec des grandeurs logarithmiques (formellement, il s'agit d'une équation dite log-linéarisée). Dans celle-ci, on a :

• $p$ est le logarithme du niveau moyen des prix ;
• $p_{e}$ est le logarithme du niveau futur des prix anticipé par les entreprises ;
• $y$ le logarithme du PIB et ${\overline {y}}$ le logarithme du PIB potentiel ;
• $\alpha$ un coefficient de proportionnalité.

$y_{t}={\overline {y}}+\alpha (p_{t}-p_{e})$

On peut alors reformuler cette équation de la manière suivante :

$p_{t}-p_{e}=a(y_{t}-{\overline {y}})$

Soustrayons maintenant $P_{t-1}$.

$p_{t}-p_{t-1}=p_{e}-p_{t-1}+a(y_{t}-{\overline {y}})$

D'après les règles liées aux logarithmes, $p_{t}-p_{t-1}=\pi _{t}$ et $p_{e}-p_{t-1}=\pi _{e}$. En faisant le remplacement on trouve :

$\pi =\pi _{e}+a(y_{t}-{\overline {y}})$

Le modèle de Mankiw (courbe de Phillips à information rigide)

En 2002, Mankiw, économiste assez reconnu pour ses travaux et pour ses manuels d'économie à destination des étudiants, proposa un modèle de courbe de Phillips particulier. Celui-ci ressemble beaucoup au modèle de Calvo que nous avons vu dans la section précédente, mais avec quelques petites différences qui en corrigent les défauts.

Pour commencer, ce modèle part lui aussi du principe que seule une portion $\lambda$ des entreprises met à jour ses prix à chaque instant, le reste gardant les prix inchangés. À tout instant le niveau général des prix est donc une moyenne des prix fixé par chaque entreprise, à savoir une moyenne pondérée des prix fixés dans le passé par chaque compagnie. On a donc l'équation suivante (que l'on aurait pu utiliser pour démontrer le modèle de Calvo) :

$p_{t}=\lambda \sum _{i=0}^{\infty }\left[(1-\lambda )^{i}\cdot x_{t-i}^{*}\right]$, avec $x_{t}$ le logarithme du niveau général des prix et $p_{t-i}^{*}$ le logarithme des prix de chaque entreprise à l'instant t-i.

Ensuite, le prix idéal fixé par chaque entreprise dépend du prix à l'instant t, mais aussi de l'écart de production (en réalité, du coût marginal de la production, mais c'est presque la même chose du point de vue macroéconomique). On peut résumer cela avec l'équation suivante, qui aurait aussi pu être utilisée pour démontrer le modèle de Calvo :

$p_{t}^{*}=p_{t}+\alpha y_{t}$, avec $p_{t}^{*}$ le log du prix désiré par l'entreprise à l'instant t, $p_{t}$ le log du niveau général des prix et $y_{t}$ le logarithme de l'écart de production.

Jusqu'ici, rien de nouveau par rapport au modèle de Calvo. La différence tient dans l'origine de cette rigidité des prix. Mankiw suppose que les entreprises mettent à jour leurs prix sur la base des informations dont elles disposent à un instant t, sur la base d'anticipations rationnelles. Mais les informations en question mettent du temps avant de se propager et d'arriver aux entreprises. Les entreprises vont donc prendre des décisions sur la base d'informations anciennes, qui leur sont arrivées avec du retard. On peut résumer cela mathématiquement avec la formule suivante, encore une fois écrite avec des variables logarithmiques :

$x_{t}^{i}=E_{t-i}[p_{t}^{*}]$, avec $E_{t-i}[...]$ l’anticipation du prix idéal sur la base des informations datant de la énième période précédente.

En combinant les trois équations précédentes, on trouve l'équation suivante :

$p_{t}=\lambda \sum _{i=0}^{\infty }\left[(1-\lambda )^{i}\cdot E_{t-i}[p_{t}+\alpha y_{t}]\right]$

Avec quelques bidouilles mathématiques assez affreuses, on trouve l'équation de la courbe de Phillips à information rigide :

$\pi _{t}={\frac {\alpha \lambda }{1-\lambda }}y_{t}+\lambda \sum _{i=0}^{\infty }\left[(1-\lambda )^{i}\cdot E_{t-i}[\pi _{t}+\alpha \Delta y_{t}]\right]$, avec $\Delta y_{t}$ la croissance de l'écart de production.

Si on analyse cette équation, on voit que l'inflation dépend de plusieurs choses : de l'écart de production, de l'inflation anticipée, mais aussi des anticipations de l'écart de production. On retrouve donc une équation qui ressemble marginalement à l'équation de Calvo, à une différence près : les anticipations de l'écart de production font leur apparition dans l'équation. De plus, les anticipations utilisées changent par rapport au modèle de Calvo : les anticipations sont établies sur la base d'informations retardées, ce qui fait qu'elles accusent un retard.

L'avantage de cette courbe de Phillips est qu'elle respecte la critique de Mc Callum : elle ne permet pas de maintenir le PIB au-dessus de sa valeur potentielle de manière permanente. Contrairement à la courbe de Phillips New Keynesian, avec laquelle une politique dés-inflationniste permettait d'obtenir ce résultat aberrant. Avec la courbe de Phillips de Mankiw, seule une politique monétaire non-anticipée a un effet sur le PIB, toute politique anticipée n'ayant d'effet que sur l'inflation. En effet, en l'absence de surprise, les anticipations sont correcte, et on a alors : $p_{t}=E_{t-i}[p_{t}]$. L'équation de la courbe de Phillips de Mankiw se simplifie alors de telle manière que l'on a $y_{t}=0$.

GFDL

Vous avez la permission de copier, distribuer et/ou modifier ce document selon les termes de la licence de documentation libre GNU, version 1.2 ou plus récente publiée par la Free Software Foundation ; sans sections inaltérables, sans texte de première page de couverture et sans texte de dernière page de couverture.