Les cartes graphiques/Le rendu d'une scène 3D : shaders et T&L

Le premier jeu à utiliser de la "vraie" 3D fût le jeu Quake, premier du nom. Et depuis sa sortie, la grande majorité des jeux vidéo utilisent de la 3D, même s'il existe encore quelques jeux en 2D. Face à la prolifération des jeux vidéo en 3D, les fabricants de cartes graphiques ont inventé les cartes accélératrices 3D, des cartes vidéo capables d'accélérer le rendu en 3D. Dans ce chapitre, nous allons voir comment elles fonctionnent et comment elles ont évolué dans le temps. Pour comprendre comment celles-ci fonctionnent, il faut faire quelques rapides rappels sur les bases du rendu 3D.

Les bases du rendu 3D

Une scène 3D est composée d'un espace en trois dimensions, dans laquelle le moteur d’un jeu vidéo place des objets et les fait bouger. Cette scène est, en première approche, un simple parallélogramme. Un des coins de ce parallélogramme sert d’origine à un système de coordonnées : il est à la position (0, 0, 0), et les axes partent de ce point en suivant les arêtes. Les objets seront placés à des coordonnées bien précises dans ce parallélogramme.

Les objets 3D et leur géométrie

Dans la quasi-totalité des jeux vidéo actuels, les objets et la scène 3D sont modélisés par un assemblage de triangles collés les uns aux autres, ce qui porte le nom de maillage, (mesh en anglais). Il a été tenté dans le passé d'utiliser des quadrilatères (rendu dit en quad) ou d'autres polygones, mais les contraintes techniques ont fait que ces solutions n'ont pas été retenues.

En général, il est possible de créer un modèle 3D avec autre chose que des triangles ou des quadrilatères, avec des polygones concaves, des courbes de Béziers, et bien d'autres techniques. Mais ces solutions sont peu pratiques et plus complexes.

Les modèles 3D sont définis par leurs sommets, aussi appelés vertices dans le domaine du rendu 3D. Chaque sommet possède trois coordonnées, qui indiquent sa position dans la scène 3D : abscisse, ordonnée, profondeur. Un triangle est donc composé de 9 coordonnées, 3 par sommet.

Un segment qui connecte une paire de sommets s'appelle une arête, comme en géométrie élémentaire. Plusieurs arêtes délimitent une surface fermée, celle-ci est appelée une face, ou encore une primitive.

Les API 3D supportent des primitives assez diverses. Elles gèrent au minimum les points, les lignes et les triangles. Elles gèrent éventuellement les triangle-strip et triangle-fan. Aujourd'hui, OpenGL et DirectX ne gèrent plus le rendu avec des quads est aujourd’hui tombé en désuétude, mais il est parfois supporté par les cartes graphiques actuelles, bien que ce soit souvent par émulation (un quad est rendu avec deux triangles). Pour information, voici les primitives gérées par les premières versions d'OpenGL :

Précisons cependant que le support d'une primitive par une API 3D ne signifie pas que la carte graphique supporte ces primitives. Il se peut que les primitives soient découpées en triangles par la carte graphique lors de l'exécution, alors qu'elles sont supportées par l'API 3D.

La représentation exacte d'un objet est donc une liste plus ou moins structurée de sommets, pouvant contenir une certaine redondance ou des informations en plus. La liste doit préciser les coordonnées de chaque sommet, ainsi que comment les relier pour former des triangles. Pour cela, l'objet est représenté par une structure qui contient la liste des sommets, mais aussi de quoi savoir quels sont les sommets reliés entre eux par un segment. Nous en dirons plus dans le chapitre sur le rendu de la géométrie.

La caméra : le point de vue depuis l'écran

Outre les objets proprement dit, on trouve une caméra, qui représente les yeux du joueur. Cette caméra est définie par :

une position ;
par la direction du regard (un vecteur) ;
le champ de vision (un angle) ;
un plan qui représente l'écran du joueur ;
et un plan limite au-delà duquel on ne voit plus les objets.

Volume délimité par la caméra (*view frustum*).

Ce qui est potentiellement visible du point de vue de la caméra est localisé dans un volume, situé entre le plan de l'écran et le plan limite, appelé le view frustum. Suivant la perspective utilisée, ce volume n'a pas la même forme. Avec la perspective usuelle, le view frustum ressemble à un trapèze en trois dimensions, délimité par plusieurs faces attachées au bords de l'écran et au plan limite. Le tout est parfois appelée, bien que par abus de langage, la pyramide de vision. Avec d'autres perspectives moins utilisées, le view frustum est un pavé, mais nous n'en parlerons pas plus dans le cadre de ce cours car elles ne sont presque pas utilisés dans les jeux vidéos actuels.

Les textures

Tout objet à rendre en 3D est donc composé d'un assemblage de triangles, et ceux-ci sont éclairés et coloriés par divers algorithmes. Pour rajouter de la couleur, les objets sont recouverts par des textures, des images qui servent de papier peint à un objet. Un objet géométrique est donc recouvert par une ou plusieurs textures qui permettent de le colorier ou de lui appliquer du relief.

Notons que les textures sont des images comme les autres, codées pixel par pixel. Pour faire la différence entre les pixels de l'écran et les pixels d'une texture, on appelle ces derniers des texels. Ce terme est assez important, aussi profitez-en pour le mémoriser, nous le réutiliserons dans quelques chapitres.

Un autre point lié au fait que les textures sont des images est leur compression, leur format. N'allez pas croire que les textures sont stockées dans un fichier .jpg, .png ou tout autre format de ce genre. Les textures utilisent des formats spécialisés, comme le DXTC1, le S3TC ou d'autres, plus adaptés à leur rôle de texture. Mais qu'il s'agisse d'images normales (.jpg, .png ou autres) ou de textures, toutes sont compressées. Les textures sont compressées pour prendre moins de mémoire. Songez que la compression de texture est terriblement efficace, souvent capable de diviser par 6 la mémoire occupée par une texture. S'en est au point où les textures restent compressées sur le disque dur, mais aussi dans la mémoire vidéo ! Nous en reparlerons dans le chapitre sur la mémoire d'une carte graphique.

Plaquer une texture sur un objet peut se faire de deux manières, qui portent les noms de placage de texture inverse et direct. Le placage de texture direct a été utilisé au tout début de la 3D, sur des bornes d'arcade et quelques consoles de jeu. La 3DO, la PS1, la Sega Saturn, utilisaient ce genre de rendu. Avec ce genre de rendu, les textures ne sont pas plaquer sur les objets, mais sont en fait écrites directement dans le framebuffer, après avoir été tournées et redimensionnés. Il s'agit d'un rendu très particulier que nous aborderons dans ce cours dans des chapitres dédiés. De nos jours, on utilise uniquement la technique de placage de texture inverse, qui sera décrite plus bas.

La différence entre rastérisation et lancer de rayons

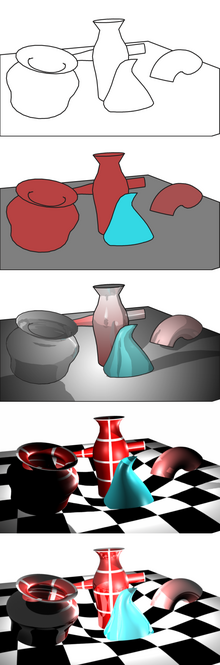
Les techniques de rendu 3D sont nombreuses, mais on peut les classer en deux grands types : le lancer de rayons et la rasterization. Sans décrire les deux techniques, sachez cependant que le lancer de rayon n'est pas beaucoup utilisé pour les jeux vidéo. Il est surtout utilisé dans la production de films d'animation, d'effets spéciaux, ou d'autres rendu spéciaux. Dans les jeux vidéos, il est surtout utilisé pour quelques effets graphiques, la rasterization restant le mode de rendu principal.

La raison principale est que le lancer de rayons demande beaucoup de puissance de calcul. Une autre raison est que créer des cartes accélératrices pour le lancer de rayons n'est pas simple. Il a existé des cartes accélératrices permettant d'accélérer le rendu en lancer de rayons, mais elles sont restées confidentielles. Les cartes graphiques modernes incorporent quelques circuits pour accélérer le lancer de rayons, mais ils restent marginaux des compléments au rendu par rastérization. Un chapitre entier sera dédié aux cartes accélératrices de lancer de rayons et nous verrons pourquoi le lancer de rayons est difficile à implémenter avec des performances convenables, ce qui explique que les jeux vidéo utilisent la rasterization.

La rastérisation est structurée autour de trois étapes principales :

une étape purement logicielle, effectuée par le processeur, où le moteur physique calcule la géométrie de la scène 3D ;
une étape de traitement de la géométrie, qui gère tout ce qui a trait aux sommets et triangles ;
une étape de rastérisation qui effectue beaucoup de traitements différents, mais dont le principal est d'attribuer chaque triangle à un pixel donné de l'écran.

L'étape de traitement de la géométrie et celle de rastérisation sont souvent réalisées dans des circuits ou processeurs séparés, comme on le verra plus tard. Il existe plusieurs rendus différents et l'étape de rastérisation dépend fortement du rendu utilisé. Il existe des rendus sans textures, d'autres avec, d'autres avec éclairage, d'autres sans, etc. Par contre, l'étape de calcul de la géométrie est la même quelque soit le rendu ! Mieux : le calcul de la géométrie se fait de la même manière entre rastérisation et lancer de rayons, il est le même quelque soit la technique de rendu 3D utilisée.

Mais quoiqu'il en soit, le rendu d'une image est décomposé en une succession d'étapes, chacune ayant un rôle bien précis. Le traitement de la géométrie est lui-même composé d'une succession de sous-étapes, la rasterisation est elle-même découpée en plusieurs sous-étapes, et ainsi de suite. Le nombre d'étapes pour une carte graphique moderne dépasse la dizaine. La rastérisation calcule un rendu 3D avec une suite d'étapes consécutives qui doivent s'enchainer dans un ordre bien précis. L'ensemble de ces étapes est appelé le pipeline graphique.

Le calcul de la géométrie

Le traitement de la géométrie se fait lui-même en plusieurs étapes. La principale est l'étape de transformation, qui place les objets dans la scène 3D. Elle combine les différents modèles 3D avec le monde, pour obtenir la géométrie à afficher à l'écran. Elle en profite aussi pour faire d'autres changements de coordonnées, notamment pour centrer l'univers sur la caméra et corriger la perspective.

Le calcul de la géométrie regroupe plusieurs manipulations différentes. La principale demande juste de placer les modèles 3D dans la scène, de placer les objets dans le monde. Puis, il faut centrer la scène 3D sur la caméra. Les deux changements ont pour point commun de demander des changements de repères. Par changement de repères, on veut dire que l'on passe d'un système de coordonnées à un autre. En tout, il existe trois changements de repères distincts qui sont regroupés dans l'étape de transformation : un premier qui place chaque objet 3D dans la scène 3D, un autre qui centre la scène du point de vue de la caméra, et un autre qui corrige la perspective.

Les trois étapes de transformation

La première étape place les objets 3D dans la scène 3D. Un modèle 3D est représentée par un ensemble de sommets, qui sont reliés pour former sa surface. Les données du modèle 3D indiquent, pour chaque sommet, sa position par rapport au centre de l'objet qui a les coordonnées (0, 0, 0). La première étape place l'objet 3D à une position dans la scène 3D, déterminée par le moteur physique, qui a des coordonnées (X, Y, Z). Une fois placé dans la scène 3D, le centre de l'objet passe donc des coordonnées (0, 0, 0) aux coordonnées (X, Y, Z) et tous les sommets de l'objet doivent être mis à jour.

De plus, l'objet a une certaine orientation : il faut aussi le faire tourner. Enfin, l'objet peut aussi subir une mise à l'échelle : on peut le gonfler ou le faire rapetisser, du moment que cela ne modifie pas sa forme, mais simplement sa taille. En clair, le modèle 3D subit une translation, une rotation et une mise à l'échelle, les trois impliquant une modification des coordonnées des sommets..

Une fois le placement des différents objets effectué, la carte graphique effectue un changement de coordonnées pour centrer le monde sur la caméra. Au lieu de considérer un des bords de la scène 3D comme étant le point de coordonnées (0, 0, 0), il va passer dans le référentiel de la caméra. Après cette transformation, le point de coordonnées (0, 0, 0) sera la caméra. La direction de la vue du joueur sera alignée avec l'axe de la profondeur (l'axe Z).

Enfin, il faut aussi corriger la perspective, ce qui est le fait de l'étape de projection, qui modifie la forme du view frustum sans en modifier le contenu. Différents types de perspective existent et celles-ci ont un impact différent les unes des autres sur le view frustum. Dans le cas qui nous intéresse, le view frustum passe d’une forme de trapèze tridimensionnel à une forme de pavé dont l'écran est une des faces.

Les changements de coordonnées se font via des multiplications de matrices

Les trois étapes précédentes demande de faire des changements de coordonnées, chaque sommet voyant ses coordonnées remplacées par de nouvelles. Or, un changement de coordonnée s'effectue assez simplement, avec des matrices, à savoir des tableaux organisés en lignes et en colonnes avec un nombre dans chaque case. Un changement de coordonnées se fait simplement en multipliant le vecteur (X, Y, Z) des coordonnées d'un sommet par une matrice adéquate. Il existe des matrices pour la translation, la mise à l'échelle, d'autres pour la rotation, une autre pour la transformation de la caméra, une autre pour l'étape de projection, etc.

Il se trouve que multiplier des matrices amène certaines simplifications. Au lieu de faire plusieurs multiplications de matrices, il est possible de fusionner les matrices en une seule, ce qui permet de simplifier les calculs. Ce qui fait que le placement des objets, changement de repère pour centrer la caméra, et d'autres traitements forts différents sont regroupés ensemble.

Le traitement de la géométrie implique, sans surprise, des calculs de géométrie dans l'espace. Et cela implique des opérations mathématiques aux noms barbares : produits scalaires, produits vectoriels, et autres calculs impliquant des vecteurs et/ou des matrices. Et les calculs vectoriels/matriciels impliquent beaucoup d'additions, de soustractions, de multiplications, de division, mais aussi des opérations plus complexes : calculs trigonométriques, racines carrées, inverse d'une racine carrée, etc. Au final, un simple processeur peut faire ce genre de calculs, si on lui fournit le programme adéquat, l'implémentation est assez aisée.

Mais on peut aussi implémenter le tout avec un circuit spécialisé, non-programmable. Les deux solutions sont possibles, tant que le circuit dispose d'assez de puissance de calcul. Les cartes graphiques anciennes contenaient un ou plusieurs circuits de multiplication de matrices spécialisés dans l'étape de transformation. Chacun de ces circuits prend un sommet et renvoie le sommet transformé. Ils sont composés d'un gros paquet de multiplieurs et d'additionneurs flottants. Pour plus d'efficacité, les cartes graphiques comportent plusieurs de ces circuits, afin de pouvoir traiter plusieurs sommets en même temps.

L'élimination des surfaces cachées

Un point important du rendu 3D est que ce qui n'est pas visible depuis la caméra ne doit idéalement pas être calculé. A quoi bon calculer des choses qui ne seront pas affichées, après tout ? Ce serait gâcher de la puissance de calcul. Et pour cela, les cartes graphiques et les moteurs graphiques incorporent de nombreuses optimisations pour éliminer les calculs inutiles. Diverses techniques de clipping ou de culling existent pour cela. La différence entre culling et clipping n'est pas fixée et la terminologie n'est pas claire. Dans ce qui va suivre, nous n'utiliserons que le terme culling.

Les différentes formes de culling/clipping

La première forme de culling est le view frustum culling, dont le nom indique qu'il s'agit de l'élimination de tout ce qui est situé en-dehors du view frustum. Elle fait que ce qui est en-dehors du champ de vision de la caméra n'est pas affiché à l'écran n'est pas calculé ou rendu, dans une certaine mesure. De même, certains objets qui sont trop loin ne sont tout simplement pas calculés et remplacé par du brouillard, voire pas remplacé du tout.

Les autres formes de culling visent à éliminer ce qui est dans le view frustum, mais qui n'est pas visible depuis la caméra. Pensez à des objets cachés par un autre objet plus proche, par exemple. Ou encore, pensez aux faces à l'arrière d'un objet opaque qui sont cachées par l'avant. Ces deux cas correspondent à deux types de culling. L'élimination des objets masqués par d'autres est appelé l'occlusion culling. L'élimination des parties arrières d'un objet est appelé le back-face culling. Dans les deux cas, nous parlerons d'élimination des surfaces cachées.

Pour résumer, les portions de la scène 3D qui ne sont pas visibles à l'écran ne doivent pas être calculées. Les cartes graphiques embarquent divers méthodes de culling pour abandonner les calculs quand elles s’aperçoivent que ceux-ci portent sur une partie non-affichée de l'image. Cela fait des économies de puissance de calcul assez appréciables et un gain en performance assez important. Précisons que le culling peut être plus ou moins précoce suivant le type de rendu 3D utilisé, mais nous verrons cela dans la suite du chapitre.

Les techniques de culling/clipping

Il existe plusieurs techniques pour effectuer le culling. Le view frustum culling est assez trivial : il suffit d'éliminer ce qui n'est pas dans le view frustum, quelques calculs de coordonnées assez simples le permette assez facilement. Par contre, l'élimination des surfaces cachées est plus compliqué. Le lancer de rayons n'a pas besoin d'éliminer les surfaces cachées, il ne calcule que les surfaces visibles. Par contre, la rastérisation demande d'éliminer les surfaces cachées. Sans cela, le rendu est incorrect dans le pire des cas, ou alors le rendu calcule des surfaces invisibles pour rien. Il existe de nombreux algorithmes logiciels pour implémenter l'élimination des surfaces cachées.

L'implémentation de ces algorithmes demande de connaitre la distance à la caméra de chaque triangle. La distance à la caméra est appelée la profondeur du triangle. Elle est déterminée à l'étape de rastérisation et est calculée à chaque sommet. Lors de la rastérisation, chaque sommet se voit attribuer trois coordonnées : deux coordonnées x et y qui indiquent sa position à l'écran, et une coordonnée de profondeur notée z.

Pour éliminer les surfaces cachées, la solution la plus simple consiste simplement à rendre les triangles du plus lointain au plus proche. L'idée est que si deux triangles se chevauchent, on doit dessiner celui qui est derrière, puis celui qui est devant. Le dessin du second va recouvrir le premier. Quelque chose qui devrait vous rappeler le rendu 2D, où les sprites sont rendus du plus lointain au plus proche. Un problème est que la solution ne marche pas avec certaines configurations particulières, dans le cas où des polygones un peu complexes se chevauchent plusieurs fois. Mais il se présente rarement dans un rendu 3D normal.

Les anciens jeux en 2.5D comme DOOM ou les DOOM-like, utilisaient une amélioration de l'algorithme précédent. L'"amélioration variait suivant le moteur de jeu utilisé, et donnait soit une technique dite de portal rendering, soit un système de Binary Space Partionning, assez complexes et difficiles à expliquer.

Une autre solution utilise ce qu'on appelle un tampon de profondeur, aussi appelé un z-buffer. Il s'agit d'un tableau, stocké en mémoire vidéo, qui mémorise la coordonnée z de l'objet le plus proche pour chaque pixel. Par défaut, ce tampon de profondeur est initialisé avec la valeur de profondeur maximale. Au fur et à mesure que les triangles sont rastérisés, le tampon de profondeur est mis à jour, conservant ainsi la trace de l'objet le plus proche de la caméra.

Si jamais un triangle a une coordonnée z plus grande que celle du tampon de profondeur, cela veut dire qu'il est situé derrière un objet déjà rendu : il est éliminé et ne poursuit pas sa route au-delà de l'unité de rastérisation. Le tampon de profondeur n'a pas à être mis à jour. Dans le cas contraire, l'objet est plus près de la caméra et sa coordonnée z remplace l'ancienne valeur z dans le tampon de profondeur.

Illustration du processus de mise à jour du Z-buffer.

Toutes les cartes graphiques modernes utilisent un système de z-buffer. C'est la seule solution pour avoir des performances dignes de ce nom.

La rastérisation

L'étape de rastérisation est difficile à expliquer, surtout que son rôle exact dépend de la technique de rendu utilisée. Pour simplifier, elle projette un rendu en 3D sur un écran en 2D. Une autre explication tout aussi vague est qu'elle s'occupe la traduction des triangles en un affichage pixelisé à l'écran. Elle détermine à quoi ressemble la scène visible sur l'écran. C'est par exemple lors de cette étape que sont appliquées certaines techniques de culling, qui éliminent les portions non-visibles de l'image, ainsi qu'une correction de la perspective et diverses opérations d'interpolation dont nous parlerons dans plusieurs chapitres.

L'étape de rastérisation effectue aussi beaucoup de traitements différents, mais l'idée structurante est que rastérisation et placage de textures sont deux opérations très liées entre elles. Il existe deux manières principales pour lier les textures à la géométrie : la méthode directe et la méthode inverse (UV Mapping). Et les deux font que la rastérisation se fait de manière très différente. Précisons cependant que les rendus les plus simples n'utilisent pas de textures du tout. Ils se contentent de colorier les triangles, voire d'un simple rendu en fil de fer basé sur du tracé de lignes. Dans la suite de cette section, nous allons voir les quatre types de rendu principaux : le rendu en fils de fer, le rendu colorié, et deux rendus utilisant des textures.

Le rendu en fil de fer

Le rendu 3D en fils de fer est illustré ci-contre. Il s'agit d'un rendu assez ancien, utilisé au tout début de la 3D, sur des machines qu'on aurait du mal à appeler ordinateurs. Il se contente de tracer des lignes à l'écran, lignes qui connectent deux sommets, qui ne sont autres que les arêtes de la géométrie de la scène rendue. Le tout était suffisant pour réaliser quelques jeux vidéos rudimentaires. Les tout premiers jeux vidéos utilisaient ce rendu, l'un d'entre eux étant Maze War, le tout premier FPS.

Le monde est calculé en 3D, il y a toujours un calcul de la géométrie, la scène est rastérisée normalement, les portions invisbles de l'image sont retirées, mais il n'y a pas d'application de textures après rastérisation. A la place, un algorithme de tracé de ligne trace les lignes à l'écran. Quand un triangle passe l'étape de rastérisation, l'étape de rastérisation fournit la position des trois sommets sur l'écran. En clair, elle fournit les coordonnées de trois pixels, un par sommet. A la suite, un algorithme de tracé de ligne trace trois lignes, une par paire de sommet.

L'implémentation demande juste d'avoir une unité de calcul géométrique, une unité de rastérisation, et un VDC qui supporte le tracé de lignes. Elle est donc assez simple et ne demande pas de circuits de gestion des textures ni de ROP. Le VDC écrit directement dans le framebuffer les lignes à tracer.

Il a existé des proto-cartes graphiques spécialisées dans ce genre de rendu. Un exemple est le Line Drawing System-1 de l'entreprise Eans & Sutherland, qui n'est ni plus ni moins que le toute premier circuit graphique séparé du processeur ayant existé. C'est en un sens la toute première carte graphique, le tout premier GPU. Il prenait la forme d'un périphérique qui se connectait à l'ordinateur d'un côté et était relié à l'écran de l'autre. Il était compatible avec un grand nombre d'ordinateurs et de processeurs existants.

L'intérieur du circuit était assez simple : un circuit de multiplication de matrice pour les calculs géométriques, un rastériser simplifié (le clipping diviser, un circuit de tracé de lignes, et un processeur de contrôle pour commander les autres circuits. Le fait que ces trois circuits soient séparés permettait une implémentation en pipeline, où plusieurs portions de l'image pouvaient être calculées en même temps : pendant que l'une est dans l'unité géométrique, l'autre est dans le rastériseur et une troisième est en cours de tracé.

Architecture du LDS-1. Le processeur de contrôle n'est pas représenté.

Le processeur de contrôle exécute un programme qui se charge de commander l'unité géométrique et les autres circuits. Le programme en question est fourni par le programmeur, le LDS-1 est donc totalement programmable. Il lit directement les données nécessaires pour le rendu dans la mémoire de l’ordinateur et le programme exécuté est lui aussi en mémoire principale. Il n'a pas de mémoire vidéo dédiée, il utilise la RAM de l'ordinateur principal.

Le multiplieur de matrices est plus complexe qu'on pourrait s'y attendre. Il ne s'agit pas que d'un circuit arithmétique tout simple, mais d'un véritable processeur avec des registres et des instructions machine complexes. Il contient plusieurs registres, l'ensemble mémorisant 4 matrices de 16 nombres chacune (4 lignes de 4 colonnes). Un nombre est codé sur 18 bits. Les registres sont reliés à un ensemble de circuits arithmétiques, des additionneurs et des multiplieurs. Le circuit supporte des instructions de copie entre registres, pour copier une ligne d'une matrice à une autre, des instructions LOAD/STORE pour lire ou écrire dans la mémoire RAM, etc. Il supporte aussi des multiplications en 2D et 3D.

Le clipping divider est un circuit assez complexe, contenant un processeur à accumulateur, une mémoire ROM pour le programme du processeur. Le programme exécuté par le processeur est un petit programme de 62 instructions, stocké dans la ROM. L'algorithme du clipping divider est décrite dans le papier de recherche "A clipping divider", écrit par Robert Sproull.

Un détail assez intéressant est que le résultat en sortie de l'unité géométrique et du rastériseur peuvent être envoyés à l'ordinateur en parallèle du rendu. C'était très utile sur les anciens ordinateurs qui étaient connectés à plusieurs terminaux. Le LDS-1 calculait la géométrie et le rendu, et le tout pouvait petre envoyé à d'autres composants, comme des terminaux, une imprimante, etc.

Le rendu à primitives colorées

Exemple de rendu pouvant être obtenu avec des sommets colorés.

Une amélioration du rendu précédent utilise des triangles/quads coloriés. Chaque triangle ou quad est associé à une couleur, et cette couleur est dessinée sur le triangle/quadaprès la rastérisation. Le rendu est une amélioration du rendu en fils de fer. L'idée est que chaque triangle/quad est associé à une couleur, qui est dessinée sur le triangle/quad après la rastérisation. La technique est nommée colored vertices en anglais, nous parlerons de rendu à maillage coloré.

La couleur est propagée lors des calculs géométriques et de la rastérisation, sans subir de modifications. Une fois un rendu en fils de fer effectué, la couleur du triangle est récupérée. Le triangle/quad rendu correspond à un triangle/quad à l'écran. Et l'intérieur de ce triangle/quad est colorié avec la couleur transmise. Pour cela, on utilise encore une fois une fonction du VDC : celle du remplissage de figure géométrique. Nous l’avions vu en parlant des VDC à accélération 2D, mais elle est souvent prise en charge par les blitters. Ils peuvent remplir une figure géométrique avec une couleur unique, on réutilise cette fonction pour colorier le triangle/quad. L'étape de rastérisation fournit les coordonnées des sommets de la figure géométrique, le blitter les utilise pour colorier la figure géométrique.

Niveau matériel, quelques bornes d'arcade ont utilisé ce rendu. Dès 1988, les cartes d'arcades Namco System 21 et les bornes d'arcades Sega Model 1 utilisaient ce genre de rendu. On peut s'en rendre compte en regardant les graphismes des jeux tournant sur ces bornes d'arcade. Des jeux comme Virtua Racing, Virtua Fighter ou Virtua Formula sont assez parlants à ce niveau. Leurs graphismes sont assez anguleux et on voit qu'ils sont basés sur des triangles uniformément colorés.

La Namco System 2 implémentait ce rendu en calculant la géométrie dans des processeurs dédiés, 4 DSP de marque Texas Instruments TMS320C25, cadencés à 24,576 MHz. La carte d'arcade Sega Model 1 utilisait quant à elle un DSP spécialisé dans les calculs géométriques. Les deux cartes n'utilisaient pas de circuit géométrique fixe, mais l'émulaient avec des processeurs programmés avec un firmware/microcode spécialisé pour implémenter le pipeline géométrique et le T&L en logiciel.

Le placage de textures direct

Les deux rendus précédents sont très simples et il n'existe pas de carte graphique qui les implémente. Cependant, une amélioration des rendus précédents a été implémentée sur des cartes graphiques assez anciennes. Le rendu en question est appelé le rendu par placage de texture direct, que nous appellerons rendu direct dans ce qui suit. Le rendu direct a été utilisé sur les anciennes consoles de jeu et sur les anciennes bornes d'arcade, mais il est aujourd'hui abandonné. Il n'a servi que de transition entre rendu 2D et rendu 3D.

L'idée est assez simple et peut utiliser aussi bien des triangles que des quads, mais nous allons partir du principe qu'elle utilise des quads, à savoir que les objets 3D sont composés de quadrilatères. Lorsqu'un quad est rastérisé, sa forme à l'écran est un rectangle déformé par la perspective. On obtient un rectangle si le quad est vu de face, un trapèze si on le voit de biais. Et le sprite doit être déformé de la même manière que le quad.

L'idée est que tout quad est associé à une texture, à un sprite. La figure géométrique qui correspond à un quad à l'écran est remplie non pas par une couleur uniforme, mais par un sprite rectangulaire. Il suffit techniquement de recopier le sprite à l'écran, c'est à dire dans la figure géométrique, au bon endroit dans le framebuffer. Le rendu direct est en effet un intermédiaire entre rendu 2D à base de sprite et rendu 3D moderne. La géométrie est rendue en 3D pour générer des quads, mais ces quads ne servent à guider la copie des sprites/textures dans le framebuffer.

Exemple caricatural de placage de texture sur un *quad*.

La subtilité est que le sprite est déformé de manière à rentrer dans un quadrilatère, qui n'est pas forcément un rectangle à l'écran, mais est déformé par la perspective et son orientation en 3D. Le sprite doit être déformé de deux manières : il doit être agrandi/réduit en fonction de la taille de la figure affichée à l'écran, tourné en fonction de l'orientation du quad, déformé pour gérer la perspective. Pour cela, il faut connaitre les coordonnées de profondeur de chaque bord d'un quad, et de faire quelques calculs. N'importe quel VDC incluant un blitter avec une gestion du zoom/rotation des sprites peut le faire.

Si on veut avoir de beaux graphismes, il vaut mieux appliquer un filtre pour lisser le sprite envoyé dans le trapèze, filtre qui se résume à une opération d'interpolation et n'est pas très différent du filtrage de texture qui lisse les textures à l'écran.

Un autre point est que les quads doivent être rendus du plus lointain au plus proche. Sans cela, on obtient rapidement des erreurs de rendu. L'idée est que si deux quads se chevauchent, on doit dessiner celui qui est derrière, puis celui qui est devant. Le dessin du second va recouvrir le premier. L'écriture du sprite du second quad écrasera les données du premier quad, pour les portions recouvertes, lors de l'écriture du sprite dans le framebuffer. Quelque chose qui devrait vous rappeler le rendu 2D, où les sprites sont rendus du plus lointain au plus proche.

Le rendu inverse utilise très souvent des triangles pour la géométrie, alors que le rendu direct a tendance à utiliser des quads, mais il ne s'agit pas d'une différence stricte. L'usage de triangles/quads peut se faire aussi bien avec un rendu direct comme avec un rendu inverse. Cependant, le rendu en quad se marie très bien au rendu direct, alors que le rendu en triangle colle mieux au rendu inverse.

L'avantage de cette technique est qu'on parcourt les textures dans un ordre bien précis. Par exemple, on peut parcourir la texture ligne par ligne, l'exploiter par blocs de 4*4 pixels, etc. Et accéder à une texture de manière prédictible se marie bien avec l'usage de mémoires caches, ce qui est un avantage en matière de performances. Mais un même pixel du framebuffer est écrit plusieurs fois quand plusieurs quads se superposent, alors que le rendu inverse gère la situation avec une seule écriture (sauf si usage de la transparence). De plus, la gestion de la transparence était compliquée et les jeux devaient ruser en utilisation des solutions logicielles assez complexes.

Niveau implémentation matérielle, une carte graphique en rendu direct demande juste trois circuits. Le premier est un circuit de calcul géométrique, qui rend la scène 3D. Le tri des quads est souvent réalisé par le processeur principal, et non pas par un circuit séparé. Toutes les étapes au-delà de l'étape de rastérisation étaient prises en charge par un VDC amélioré, qui écrivait des sprites/textures directement dans le framebuffer.

Géométrie	Processeurs dédiés programmé pour émuler le pipeline graphique
Tri des quads du plus lointain au plus proche	Processeur principal (implémentation logicielle)
Application des textures	Blitter amélioré, capable de faire tourner et de zoomer sur des sprites.

L'implémentation était très simple et réutilisait des composants déjà existants : des VDC 2D pour l'application des textures, des processeurs dédiés pour la géométrie. Les unités de calcul de la géométrie étaient généralement implémentées avec un ou plusieurs processeurs dédiés. Vu qu'on savait déjà effectuer le rendu géométrique en logiciel, pas besoin de créer un circuit sur mesure. Il suffisait de dédier un processeur spécialisé rien que pour les calculs géométriques et on lui faisait exécuter un code déjà bien connu à la base. En clair, ils utilisaient un code spécifique pour émuler un circuit fixe. C'était clairement la solution la plus adaptée pour l'époque.

Les unités géométriques étaient des processeurs RISC, normalement utilisés dans l'embarqué ou sur des serveurs. Elles utilisaient parfois des DSP. Pour rappel, les DSP des processeurs de traitement de signal assez communs, pas spécialement dédiés aux rendu 3D, mais spécialisé dans le traitement de signal audio, vidéo et autre. Ils avaient un jeu d'instruction assez proche de celui des cartes graphiques actuelles, et supportaient de nombreuses instructions utiles pour le rendu 3D.

L'accélération du rendu 3D sur les bornes d'arcade était déjà bien avancé dès les années 90. Dès 1988, les bornes d'arcade Namco System 21 et Sega Model 1 géraient les calculs géométriques, grâce à plusieurs DSP dédiés au calcul de la géométrie. Quelques années plus tard, les cartes graphiques se sont mises à supporter un éclairage de Gouraud et du placage de texture. Le Namco System 22 et la Sega model 2 supportaient des textures 2D et comme le filtrage de texture (bilinéaire et trilinéaire), le mip-mapping, et quelques autres. Par la suite, elles ont réutilisé le hardware des PC et autres consoles de jeux.

Outre les bornes d'arcade, quelques consoles de 5ème génération utilisaient le rendu direct, avec les mêmes solutions matérielles. La géométrie était calculée sur plusieurs processeurs dédiés. Le reste du pipeline était géré par un VDC 2D qui implémentait le placage de textures. Deux consoles étaient dans ce cas : la 3DO, et la Sega Saturn.

La Sega Saturn incorpore trois processeurs et deux VDC. Les deux VDC sont nommés le VDP1 et le VDP2. Le VDP1 s'occupe des textures/sprites, le VDP2 s'occupe uniquement de l'arrière-plan. La géométrie est calculée par les trois processeurs. Le troisième processeur, la Saturn Control Unit, est un processeur de type DSP, utilisé exclusivement pour les calculs géométriques. Il avait sa propre mémoire RAM dédiée de 32 KB de SRAM. Les transferts entre cette RAM et le reste de l'ordinateur étaient gérés par un contrôleur DMA intégré dans le DSP.

Le placage de textures inverse

Le rendu précédent, le rendu direct, permet d'appliquer des textures directement dans le framebuffer. Mais comme dit plus haut, il existe une seconde technique pour plaquer des textures, appelé le placage de texture inverse, aussi appelé l'UV Mapping. Elle associe une texture complète pour un modèle 3D,contrairement au placage de tecture direct qui associe une texture par quad/triangle. L'idée est que l'on attribue un texel à chaque sommet. Plus précisémment, chaque sommet est associé à des coordonnées de texture, qui précisent quelle texture appliquer, mais aussi où se situe le texel à appliquer dans la texture. Par exemple, la coordonnée de texture peut dire : je veux le pixel qui est à ligne 5, colonne 27 dans cette texture. La correspondance entre texture et géométrie est réalisée lorsque les créateurs de jeu vidéo conçoivent le modèle de l'objet.

Dans les faits, on n'utilise pas de coordonnées entières de ce type, mais deux nombres flottants compris entre 0 et 1. La coordonnée 0,0 correspond au texel en bas à gauche, celui de coordonnée 1,1 est tout en haut à droite. L'avantage est que ces coordonnées sont indépendantes de la résolution de la texture, ce qui aura des avantages pour certaines techniques de rendu, comme le mip-mapping. Les deux coordonnées de texture sont notées u,v avec DirectX, ou encore s,t dans le cas général : u est la coordonnée horizontale, v la verticale.

Avec le placage de texture inverse, la rastérisation se fait grosso-modo en trois étapes : la rastérisation proprement dite, le placage de textures, et les opérations finales qui écrivent un pixel dans le framebuffer. Au niveau du matériel, ainsi que dans la plupart des API 3D, les trois étapes sont réalisées par des circuits séparés.

Lors de la rasterisation, chaque triangle se voit attribuer un ou plusieurs pixels à l'écran. Pour bien comprendre, imaginez une ligne droite qui part de caméra et qui passe par un pixel sur le plan de l'écran. Cette ligne intersecte 0, 1 ou plusieurs objets dans la scène 3D. Les triangles situés ces intersections entre cette ligne et les objets rencontrés seront associés au pixel correspondant. L'étape de rastérisation prend en entrée un triangle et renvoie la coordonnée x,y du pixel associé.

Il s'agit là d'une simplification, car un triangle tend à occuper plusieurs pixels sur l'écran. L'étape de rastérisation fournit la liste de tous les pixels occupés par un triangle, et les traite un par un. Quand un triangle est rastérisé, le rasteriseur détermine la coordonnée x,y du premier pixel, applique une texture dessus, puis passe au suivant, et rebelote jusqu'à ce que tous les pixels occupés par le triangles aient été traités.

L'implémentation matérielle du placage de texture inverse est beaucoup plus complexe que pour les autres techniques. Pour être franc, nous allons passer le reste du cours à parler de l'implémentation matérielle du placage de texture inverse, ce qui prendra plus d'une dizaine de chapitres. L'implémentation simplifiée est que l'on a des unités géométriques, une unité de rastérisation, un circuit de placage de textures et enfin un ROP pour gérer les opérations finales. Du moins sur le principe, car les cartes graphiques modernes ont fortement optimisé l'implémentation et n'ont pas hésité à fusionner certains circuits. Mais nous verrons cela en temps voulu, nous n'allons pas résumer plusieurs décennies d'innovation technologique en quelques paragraphes.

L'éclairage d'une scène 3D

L'éclairage d'une scène 3D calcule les ombres, mais aussi la luminosité de chaque pixel, ainsi que bien d'autres effets graphiques. Les algorithmes d'éclairage ont longtemps été implémentés directement en matériel, les cartes graphiques géraient l'éclairage dans des circuits spécialisés. Aussi, il est important de voir ces algorithmes d'éclairage. Il est possible d'implémenter l'éclairage à deux endroits différents du pipeline : juste avant la rastérisation, et après la rastérisation.

Il est possible d'ajouter une étape d'éclairage dans la phase de traitement de la géométrie. Elle attribue une illumination/couleur à chaque triangle ou à chaque sommet de la scène 3D. L'éclairage obtenu est appelé du vertex lighting, terme qui désigne toute technique où l'éclairage est calculé pour chaque sommet/triangle d’une scène 3D. Il est assez rudimentaire et donne un éclairage très brut, qui ne suffit pas à elle seule à éclairer la scène comme voulu.

L'éclairage par pixel (per-pixel lighting), est calculé pixel par pixel. En clair, l’éclairage est finalisé après l'étape de rastérisation, il ne se fait pas qu'au niveau de la géométrie. Même des algorithmes d'éclairage par pixel très simples demandent une intervention des pixels shaders. Autant dire que cette distinction a été importante dans l'évolution du matériel graphique et l'introduction des shaders. Mais pour comprendre cela, il faut voir comment fonctionnent les algorithmes d'éclairage et voir comment le hardware peut aider à les implémenter.

En général, l'éclairage par pixel a une qualité d'éclairage supérieure aux techniques d'éclairage par sommet, mais il est aussi plus gourmand. L'éclairage par pixel est utilisé dans presque tous les jeux vidéo depuis DOOM 3 (l'un des premiers jeux à utiliser ce genre d'éclairage), en raison de sa meilleure qualité, les ordinateurs actuels étant assez performants. Mais cela n'aurait pas été possible si le matériel n'avait pas évolué de manière à incorporer des algorithmes d'éclairage matériel assez puissants, avant de basculer sur un éclairage programmable.

Les sources de lumière et les couleurs associées

Dans ce qui suit, on part du principe que les modèles 3D ont une surface, sur laquelle on peut placer des points. Vous vous dites que ces points de surface sont tout bêtement les sommets et c'est vrai que c'est une possibilité. Mais sachez que ce n'est pas systématique. On peut aussi faire en sorte que les points de surface soient au centre des triangles du modèle 3D. Pour simplifier, vous pouvez considérer que le terme "point de la surface" correspond à un sommet, ce sera l'idéal et suffira largement pour les explications.

L'éclairage attribue à chaque point de la surface une illumination, à savoir sa luminosité, l'intensité de la lumière réfléchie par la surface. L'illumination d'un point de surface est définie par un niveau de gris. Plus un point de surface a une illumination importante, plus il a une couleur proche du blanc. Et inversement, plus son illumination est faible, plus il est proche du noir. L'attribution d'une illumination à chaque point de surface fait que la scène 3D est éclairée. Mais on peut aussi aller plus loin et colorier la géométrie. Pour cela, il suffit que l'éclairage ne fasse pas que rendre la scène 3D en niveaux de gris, mais que les niveaux de luminosité sont calculés indépendamment pour chaque couleur RGB.

L'éclairage d'une scène 3D provient de sources de lumières, comme des lampes, des torches, etc. Celles-ci sont souvent modélisées comme de simples points, qui ont une couleur bien précise (la couleur de la lumière émise) et émettent une intensité lumineuse codée par un entier. La lumière provenant de ces sources de lumière est appelée la lumière directionnelle.

Mais en plus de ces sources de lumière, il faut ajouter une lumière ambiante, qui sert à simuler l’éclairage ambiant (d’où le terme lumière ambiante). Par exemple, elle correspond à la lumière du cycle jour/nuit pour les environnements extérieurs. On peut simuler un cycle jour-nuit simplement en modifiant la lumière ambiante : nulle en pleine nuit noire, élevée en plein jour. En rendu 3D, la lumière ambiante est définie comme une lumière égale en tout point de la scène 3D, et sert notamment à simuler l’éclairage ambiant (d’où le terme lumière ambiante).

Le calcul exact de l'illumination de chaque point de surface demande de calculer trois illuminations indépendantes, qui ne proviennent pas des mêmes types de sources lumineuses.

L'illumination ambiante correspond à la lumière ambiante réfléchie par la surface.
Les autres formes d'illumination proviennent de la réflexion de a lumière directionnelle. Elles doivent être calculées par la carte graphique, généralement avec des algorithmes compliqués qui demandent de faire des calculs entre vecteurs. Il existe plusieurs sous-types d'illumination d'origine directionnelles, les deux principales étant les deux suivantes :
- L'illumination spéculaire est la couleur de la lumière réfléchie via la réflexion de Snell-Descartes.
- L'illumination diffuse vient du fait que la surface d'un objet diffuse une partie de la lumière qui lui arrive dessus dans toutes les directions. Cette lumière « rebondit » sur la surface de l'objet et une partie s'éparpille dans un peu toutes les directions. La couleur diffuse ne dépend pas vraiment de l'orientation de la caméra par rapport à la surface. Elle dépend uniquement de l'angle entre le rayon de lumière et la verticale de la surface (sa normale).

Elles sont additionnées ensemble pour donner l'illumination finale du point de surface. Chaque composante rouge, bleu, ou verte de la couleur est traitée indépendamment des autres, ce qui donne une scène 3D coloriée.

Le calcul des illuminations ambiantes, spéculaire et diffuse est le fait d'algorithmes plus ou moins compliqués. Et ces algorithmes sont très nombreux, au point où on ne pourrait pas en faire la liste. Les algorithmes varient beaucoup d'un moteur de jeu à l'autre, d'une carte graphique à l'autre. Les plus simples se décrivent en quelques équations, les algorithmes les plus complexes prennent un chapitre à eux seuls dans un livre spécialisé.

Les données nécessaires pour les algorithmes d'illumination

L'algorithme d’illumination a besoin de plusieurs informations, certaines étant des nombres, d'autres des vecteurs, d'autres des angles. Tous les algorithmes d'éclairage directionnel impliquent de faire des calculs trigonométriques dans l'espace, de déterminer des angles, des distances, et bien d'autres choses.

Le premier de ces paramètres est l'intensité de la source de lumière, à quel point elle émet de la lumière. Là encore, cette information est encodée par un simple nombre, un coefficient, spécifié par l'artiste lors de la création du niveau/scène 3D. La couleur de la source de lumière est une version améliorée de l'intensité de la source lumineuse, dans le sens où on a une intensité pour chaque composante RGB.

Le second est un nombre attribué à chaque point de surface : le coefficient de réflexion. Il indique si la surface réfléchit beaucoup la lumière ou pas, et dans quelles proportions. Généralement, chaque point d'une surface a plusieurs coefficients de réflexion, pour chaque couleur : un pour la couleur ambiante, un pour la couleur diffuse, et un pour la couleur spéculaire.

Les calculs de réflexion de la lumière demandent aussi de connaitre l'orientation de la surface. Pour gérer cette orientation, tout point de surface est fourni avec une information qui indique comment est orientée la surface : la normale. Cette normale est un simple vecteur, perpendiculaire à la surface de l'objet, dont l'origine est le point de surface (sommet ou triangle).

Ensuite, il faut aussi préciser l'orientation de la lumière, dans quel sens est orientée. La majorité des sources de lumière émettent de la lumière dans une direction bien précise. Il existe bien quelques sources de lumière qui émettent de manière égale dans toutes les directions, mais nous passons cette situation sous silence. Les sources de lumières habituelles, comme les lampes, émettent dans une direction bien précise, appelée la direction privilégiée. La direction privilégiée est un vecteur, notée v dans le schéma du dessous.

Un autre vecteur important est celui de la ligne entre le point de surface considéré et la caméra (noté w dans le schéma ci-dessous).

Il faut aussi tenir comme du vecteur qui trace la ligne entre la source de lumière et le point de surface (noté L dans le schéma ci-dessous).

Enfin, il faut ajouter le vecteur qui correspond à la lumière réfléchie par la surface au niveau du point de surface. Ce vecteur, noté R et non-indiqué dans le schéma ci-dessous, se calcule à partir du vecteur L et de la normale.

La plupart de ces informations n'a pas à être calculée. C'est le cas de la normale de la surface ou du vecteur L qui sont connus une fois l'étape de transformation réalisée. Même chose pour le coefficient de réflexion ou de l'intensité de la lumière, qui sont connus dès la création du niveau ou de la scène 3D. Par contre, le reste doit être calculé à la volée par la carte graphique à partir de calculs vectoriels.

Le calcul des couleurs par un algorithme d'illumination de Phong

À partir de ces informations, divers algorithmes peuvent éclairer une scène. Dans ce qui va suivre, nous allons voir l'algorithme d'illumination de Phong, la méthode la plus utilisée dans le rendu 3D.S'il n'est peut-être pas l'algorithme le plus utilisé, vous pouvez être certain que c'est au moins une version améliorée ou un autre algorithme proche mais plus poussé qui l'est à sa place.

L'illumination ambiante d'un point de surface s'obtient à partir de la lumière ambiante, mais elle n'est pas strictement égale à celle-ci, c'est légèrement plus compliqué que ça. Deux objets de la même couleur, illuminés par la même lumière ambiante, ne donneront pas la même couleur. Un objet totalement rouge illuminé par une lumière ambiante donnera une couleur ambiante rouge, un objet vert donnera une lumière verte. Et sans même parler des couleurs, certains objets sont plus sombres à certains endroits et plus clairs à d'autres, ce qui fait que leurs différentes parties ne vont pas réagir de la même manière à la lumière ambiante.

La couleur de chaque point de surface de l'objet lui-même est mémorisée dans le modèle 3D, ce qui fait que chaque point de surface se voit attribuer, en plus de ces trois coordonnées, une couleur ambiante qui indique comment celui-ci réagit à la lumière ambiante. La couleur ambiante finale d'un point de surface se calcule en multipliant la couleur ambiante de base par l'intensité de la lumière ambiante. Les deux sont des constantes pré-calculées par les concepteurs du jeu vidéo ou du rendu 3D.

{\text{Illumination ambiante}}=K_{a}\times I_{a}

avec

K_{a}

la couleur ambiante du point de surface et

I_{a}

l'intensité de la lumière ambiante.

L'illumination spéculaire et diffuse sont calculées autrement, à partir des vecteurs indiqués dans le schéma ci-contre. l'illumination diffuse est calculée à partir du coefficient de réflexion diffuse $K_{d}$ qui indique à quel point la surface diffuse de la lumière, l'intensité de la source lumineuse, et l'angle entre N et L. L'angle entre N et L donne la manière dont la surface est penchée par rapport à la surface lumineuse : plus elle est penchée, plus la lumière est diffusée et moins l'illumination diffuse est intense. L'angle en question est noté $omega$ dans l'équation suivante :

{\text{Illumination diffuse}}=K_{d}\times I_{a}\times \cos {(\omega )}=K_{d}\times I_{a}\times ({\vec {N}}\cdot {\vec {L}})

Pour calculer la lumière spéculaire, il faut prendre en compte l'angle que fait la caméra et la lumière réfléchie, c'est à dire l'angle entre v et R, que nous noterons $\Omega$ . Là encore, on doit utiliser le coefficient de réflexion spéculaire $K_{s}$ de la surface et l'intensité de la lumière, ce qui donne :

{\text{Illumination spéculaire}}=K_{s}\times I_{a}\times \cos {(\Omega )}=K_{s}\times I_{a}\times ({\vec {R}}\cdot {\vec {v}})

En additionnant ces trois sources d'illumination, on trouve :

{\text{Illumination ambiante}}=K_{a}\times I_{a}+I_{a}\times \left[K_{d}\times \cos {(\omega )}+K_{s}\times \cos {(\Omega )}\right]

Les algorithmes d'éclairage basiques : par triangle, par sommet et par pixel

Maintenant que l'on sait comment est calculé l'illumination d'un point de surface, passons maintenant aux algorithmes d'éclairage proprement dit. C’est une bonne chose de savoir comment les points de surface (sommets ou triangles) sont éclairés, mais rappelons que ce sont des pixels qui s'affichent à l'écran. L'étape d'éclairage réalisée par la géométrie peut calculer la luminosité/couleur d'un sommet/triangle, mais pas celle d'un pixel. Pour cela, il faut déterminer la luminosité d'un pixel à partir de la luminosité/couleur des sommets du triangle associé. Pour cela, il existe plusieurs algorithmes qui font ce calcul. les trois plus connus sont appelés l'éclairage plat, l'éclairage de Gouraud, et l'éclairage de Phong. Notons que ce dernier n'est pas identique à l'éclairage de Phong vu précédemment.

Dans ce dessin, le triangle a un sommet de couleur bleu foncé, un autre de couleur rouge et un autre de couleur bleu clair. L’interpolation plate et de Gouraud donnent des résultats bien différents.

L'éclairage plat calcule l'éclairage triangle par triangle. Typiquement, l'algorithme d'éclairage part de la normale du triangle, puis effectue les calculs d'éclairage à partir de cette normale. La normale est fournie pour chaque triangle, directement dans le modèle 3D, de même que chaque triangle a un coefficient de réflexion ambiante/spéculaire/diffuse. L'algorithme applique ensuite l’algorithme d'illumination triangle par triangle, ce qui fait que chaque triangle se voit attribuer une couleur, puis l'unité de rastérisation applique cette couleur sur tous les pixels associés à ce triangle.

L'éclairage de Gouraud calcule l'éclairage sommet par sommet. Tous les sommets se voient attribuer une illumination, puis l'algorithme calcule la couleur de chaque pixel à partir des couleurs du sommet du triangle associé. Le calcul en question est une sorte de moyenne, où la couleur de chaque sommet est pondéré par un coefficient qui dépend de la distance avec le pixel. Plus le pixel est loin d'un sommet, plus ce coefficient est petit. Typiquement, le coefficient varie entre 0 et 1 : de 1 si le pixel est sur le sommet, à 0 si le pixel est sur un des sommets adjacents. La moyenne effectuée est généralement une interpolation bilinéaire, mais n'importe quel algorithme d'interpolation peut marcher, qu'il soit simplement linéaire, bilinéaire, cubique, hyperbolique. L'étape d'interpolation est prise en charge soit par l'étape de rastérisation, soit par les pixel shaders.

L'éclairage de Phong est différent des précédents dans le sens où il calcule l'éclairage pixel par pixel. Avec cet algorithme, la géométrie n'est pas éclairée : les couleurs des sommets ne sont pas calculées, seuls les vecteurs adéquats le sont. C'est notamment le cas de la normale, qui est calculée pour chaque sommet. La normale est alors calculée pour chaque pixel, par interpolation des normales des sommets du triangle. Puis, l'algorithme d'illumination de Phong est effectué pour chaque normale interpolée.

Pour simplifier, l'éclairage plat calcule la couleur triangle par triangle, l'éclairage de Gouraud calcule la couleur sommet par sommet, et l'éclairage de Phong calcule la couleur pixel par pixel. La différence entre les trois algorithmes se voit assez facilement. L'éclairage plat donne un éclairage assez carré, avec des frontières assez nettes. l'éclairage de Gouraud donne des ombres plus lisses, dans une certaine mesure, mais pèche à rendre correctement les reflets spéculaires. L'éclairage de Phong est de meilleure qualité, surtout pour les reflets spéculaires.

Flat shading	Gouraud Shading	Phong Shading
Flat shading	Gouraud Shading	Phong Shading
Flat shading	Gouraud Shading	Phong Shading
Flat shading	Gouraud Shading	Phong Shading

L'éclairage de Gouraud et l'éclairage plat sont des cas particulier d'éclairage par sommet (vertex lighting), où l'éclairage est calculé sur la géométrie d'une scène 3D. Les calculs géométriques se ressemblent beaucoup aux calculs d'éclairage plat/Gouraud, car ils impliquent tous deux des calculs vectoriels, comme des produits scalaires et des produits vectoriels, qui agissent sur des sommets/triangles.

L'implémentation des calculs géométriques peut se faire de deux manières : soit avec un processeur dédié, soit avec un circuit fixe, non-programmable. La seconde solution utilise un circuit de Transform & Lightning, qui effectue tous les calculs géométriques, éclairage par sommetinclus (d'où le L de T&L). La première carte graphique à avoir intégré un circuit de T&L était la Geforce 256, qui fût la première à intégrer un circuit dit de Transform & Lightning. A la même époque, les consoles de jeu n'avaient pas de circuit de T&L.

L'éclairage de Gouraud demande, en plus des circuits de T&L, un circuit d'interpolation qui fait normalement partie de l'unité de rastérisation, comme on le verra plus tard dans le chapitre dédié. Pour donner un exemple, la console de jeu Playstation 1 gérait l'éclairage de Gouraud directement en matériel, mais seulement partiellement. Elle n'avait pas de circuit de T&L, mais intégrait un circuit pour interpoler les couleurs de chaque sommet. Sans ce circuit d'interpolation, l'éclairage de Gouraud aurait été impossible, même si le processeur était capable de calculer l'éclairage des sommets.

L'éclairage par pixel demande lui d'agir après l'étape de rastérisation, avant ou après l'unité de textures. Son implémentation demande d'ajouter un circuit d'éclairage par pixel dédié, placé après l'unité de texture. Des fonctionnalités d'éclairage par pixel matériel ont été ajoutées aux cartes graphiques, au cours des années 2000. Mais il s'agissait d'approximations basée sur l'usage de plusieurs textures spécialisées.

Il a existé quelques cartes graphiques capables de faire de l'éclairage de Phong en matériel, sans utiliser de circuit programmable. Un exemple est la carte graphique de la Nintendo DS, la PICA200. Créée par une startup japonaise, elle avait des capacités très intéressantes. Il s'agissait d’une carte graphique avec T&L matérielle, des unités de calcul géométrique programmables et des circuits d'éclairage par pixel. Elle implémentait matériellement un éclairage de Phong, du cel shading, des techniques de normal-mapping, de Shadow Mapping, de light-mapping, du cubemapping, de nombreux effets de post-traitement (bloom, effet de flou cinétique, motion blur, rendu HDR, et autres). Un autre exemple est celui de la Geforce 3, dont l'unité géométrique implémentait un algorithme de Phong pour calculer les normales, et qui envoyait cela au rastériseur, qui s'occupait de calculer l'éclairage pixel par pixel.

Le bump-mapping et autres approximations de l'éclairage par pixel

Les techniques dites de bump-mapping visent à ajouter du relief et des détails sur des surface planes en jouant sur l'éclairage. Les reliefs et autres détails ne sont pas présents dans la géométrie, mais sont ajoutés lors de l'étape d'éclairage. Ils sont mémorisés dans une texture appelée la bump-map, qui est appliquée au-dessus que la texture normale. L'implémentation hardware du bump-mapping demande juste de pouvoir appliquer plusieurs textures sur une surface, et de faire les traitements adéquats sur la bump-map. Les pipelines fixes en sont capables s'ils sont conçu pour.

La technique du normal mapping est assez simple à expliquer, sans compter que plusieurs cartes graphiques l'ont implémentée avec des circuits fixes. Plus haut, nous avions vu que l'éclairage de Phong demande de calculer les lumières pour chaque pixel. Le normal-mapping consiste à précalculer les normales d'une surface dans une texture, appelée la normal-map, qui est utilisée lors de l'application des textures. Avec cette technique, l'éclairage n'est pas géré par pixel, mais par texel, ce qui fait qu'il a une qualité de rendu inférieure à un vrai éclairage de Phong, mais le résultat est assez appréciable.

Différence sans et avec *normal-mapping*.

L'implémentation du normal-mapping demande d'avoir de quoi lire une normal-map et d'utiliser les normales dans cette texture dans des calculs d'éclairage. Les unités de texture normale sont utilisées pour lire la normal-map, des circuits dédiés sont utilisés pour les calculs d'éclairage. Puis, les pixels shaders sont arrivés, ce qui nous amène assez naturellement au chapitre suivant.

Les API 3D

De nos jours, le développement de jeux vidéo, ou tout simplement de tout rendu 3D, utilise des API 3D. Les API 3D les plus connues sont DirectX, OpenGL, et Vulkan. L'enjeu des API est de ne pas avoir à recoder un moteur de jeu différent pour chaque carte graphique ou ordinateur existant. Elles fournissent des fonctions qui effectuent des calculs bien spécifiques de rendu 3D, mais pas que. L'application de rendu 3D utilise des fonctionnalités de ces API 3D, qui elles-mêmes utilisent les autres intermédiaires, les autres maillons de la chaîne. Typiquement, ces API communiquent avec le pilote de la carte graphique et le système d'exploitation.

La description du pipeline graphique

L'API ne fait pas que fournir des morceaux de code que les programmeurs peuvent utiliser. Elles fournissent des contraintes et des règles de programmation assez importantes. Notamment, elles décrivent le pipeline graphique à utiliser. Pour rappel, le pipeline graphique comprend plusieurs étapes : plusieurs étapes de traitement de la géométrie, une phase de rastérisation, puis plusieurs étapes de traitement des pixels. Une API 3D comme DirectX ou OpenGl décrète quelles sont les étapes à faire, ce qu'elles font, et l'ordre dans lesquelles il faut les exécuter.

Il n'existe pas un pipeline graphique unique : chaque API 3D fait à sa sauce. Mais en général, on retrouve les mêmes étapes de base, complétées par des étapes facultatives sont sont apparues après. Par exemple les API récentes supportent certaines étapes comme l'étape de tesselation, qui sont absentes des API anciennes.

Pour donner un exemple, je vais prendre l'exemple d'OpenGL 1.0, une des premières version d'OpenGL, aujourd'hui totalement obsolète. Le pipeline d'OpenGL 1.0 est illustré ci-dessous. On voit qu'il implémente le pipeline graphique de base, avec une phase de traitement de la géométrie (per vertex operations et primitive assembly), la rastérisation, et les traitements sur les pixels (per fragment opertaions). On y voit la présence du framebuffer et de la mémoire dédiée aux textures, les deux étant soit séparées, soit placée dans la même mémoire vidéo. La display list est une liste de commande de rendu que la carte graphique doit traiter d'un seul bloc, chaque display list correspond au rendu d'une image, pour simplifier. Les étapes evaluator et pixel operations sont des étapes facultatives, qui ne sont pas dans le pipeline graphique de base, mais qui sont utiles pour implémenter certains effets graphiques.

Le pipeline d'OpenGL 1.0 vu plus haut est très simple, comparé aux pipelines des API modernes. Pour comparaison, voici des schémas qui décrivent le pipeline de DirextX 10 et 11. Vous voyez que le nombre d'étapes n'est pas le même, que les étapes elles-mêmes sont légèrement différentes, etc. Toutes les API 3D modernes sont organisées plus ou moins de la même manière, ce qui fait que le pipeline des schémas ci-dessous colle assez bien avec les logiciels 3D anciens et modernes, ainsi qu'avec l'organisation des cartes graphiques (anciennes ou modernes).

L'implémentation peut être logicielle ou matérielle

La mise en œuvre d'une API 3D peut se faire en logiciel, en matériel ou les deux. En théorie, elles peuvent être implémentées en logiciel, le processeur peut faire tout le travail et envoyer le résultat à une carte d'affichage. Et c'était le cas avant l'invention des premières cartes accélératrices 3D. Le rôle des API 3D était de fournir des morceaux de code et un pipeline graphique, afin de simplifier le travail des développeurs, pas de déporter des calculs sur une carte accélératrice 3D.

D'ailleurs, OpenGl et Direct X sont apparues avant que les premières cartes graphiques grand public soient inventées. Par exemple, les accélérateurs 3D sont arrivés sur le marché quelques mois après la toute première version de Direct X, et Microsoft n'avait pas prévu le coup. OpenGL était lui encore plus ancien et ne servait pas initialement pour les jeux vidéos, mais pour la production d'images de synthèses et dans des applications industrielles (conception assistée par ordinateur, imagerie médicale, autres). OpenGL était l'API plébiscitée à l'époque, car elle était déjà bien implantée dans le domaine industriel, la compatibilité avec les différents OS de l'époque était très bonne, mais aussi car elle était assez simple à programmer.

Les API imposent des contraintes sur le matériel

Plus haut, j'ai dit que les API imposent un ordonnancement précis, décrit par les étapes du pipeline. Le matériel doit respecter cet ordonnancement et faire comme si tout le pipeline graphique décrit par l'API était respecté. Je dis faire comme si, car il se peut que le matériel ne respecte pas cet ordre à la lettre. Il le fera dans les grandes lignes, mais il arrive que la carte graphique fasse certaines opérations en avance, comparé à l'ordre imposé par l'API, pour des raisons de performance.

Typiquement, effectuer du culling ou les tests de profondeur plus tôt permet d'éviter de rejeter de nombreux pixels invisibles à l'écran, et donc d'éliminer beaucoup de calculs inutiles. Mais la carte graphique doit cependant corriger le tout de manière à ce que pour le programmeur, tout se passe comme l'API 3D l'ordonne. Les écarts à l'ordonnancement de l'API sont corrigés d'une manière ou une autre par le hardware, par des circuits spécialisés de remise en ordre.

De manière générale, sans même se limiter à l'ordonnancement des étapes du pipeline graphique, les règles imposées par les API 3D sont des contraintes fortes, qui contraignent les cartes graphiques dans ce qu'elles peuvent faire. De nombreuses optimisations sont rendues impossibles à cause des contraintes des API 3D.

◄ Retour vers « Annexe : le mode texte »

Sommaire du livre

Continuer vers « Les cartes graphiques : architecture de base » ►