Les cartes graphiques/Les unités de texture

Les textures sont des images que l'on va plaquer sur la surface d'un objet, du papier peint en quelque sorte. Les cartes graphiques supportent divers formats de textures, qui indiquent comment les pixels de l'image sont stockés en mémoire : RGB, RGBA, niveaux de gris, etc. Une texture est donc composée de "pixels", comme toute image numérique. Pour bien faire la différence entre les pixels d'une texture, et les pixels de l'écran, les pixels d'une texture sont couramment appelés des texels.

Le placage de textures inverse

Pour rappel, plaquer une texture sur un objet consiste à attribuer un texel à chaque sommet, ce qui est fait lorsque les créateurs de jeu vidéo conçoivent le modèle de l'objet. Chaque sommet est associé à des coordonnées de texture, qui précisent quelle texture appliquer, mais aussi où se situe le texel à appliquer dans la texture. Par exemple, la coordonnée de texture peut dire : je veux le pixel qui est à ligne 5, colonne 27 dans cette texture.

Dans les faits, on n'utilise pas de coordonnées entières de ce type. Les coordonnées de texture sont deux nombres flottants compris entre 0 et 1. La coordonnée 0,0 correspond au texel en bas à gauche, celui de coordonnée 1,1 est tout en haut à droite. Les deux coordonnées de texture sont notées u,v avec DirectX, ou encore s,t dans le cas général : u est la coordonnée horizontale, v la verticale. Le nom donnée à cette technique de description des coordonnées de texture s'appelle l'UV Mapping.

Les API 3D modernes gèrent des textures en trois dimensions, ce qui ajoute une troisième coordonnée de texture notée w. Dans ce qui va suivre, nous allons passer les textures en trois dimensions sous silence. Elles ne sont pas très utilisées, la quasi-totalité des jeux vidéo et applications 3D utilisant des textures en deux dimensions. Par contre, le matériel doit gérer les textures 3D, ce qui le rend plus complexe que prévu. Il faut ajouter quelques circuits pour, de quoi gérer la troisième coordonnée de texture, etc.

Lors de la rastérisation, chaque fragment se voit attribuer un sommet, et donc la coordonnée de texture qui va avec. Si un pixel est situé pile sur un sommet, la coordonnée de texture de ce sommet est attribuée au pixel. Si ce n'est pas le cas, la coordonnée de texture finale est interpolée à partir des coordonnées des trois sommets du triangle rastérisé. L'interpolation en question a lieu dans l'étape de rastérisation, comme nous l'avons vu dans le chapitre précédent. Le fait qu'il y ait une interpolation fait que les coordonnées du pixel gagent à être des nombres flottants. On pourrait faire une interpolation avec des coordonnées de texture entières, mais les arrondis et autres imprécisions de calcul donneraient un résultat graphiquement pas terrible, et empêcheraient d'utiliser les techniques de filtrage de texture que nous verrons dans ce chapitre.

À partir de ces coordonnées de texture, la carte graphique calcule l'adresse du texel qui correspond, et se charge de le lire. Et toute la magie a lieu dans ce calcul d'adresse, qui part de coordonnées de texture flottante, pour arriver à une adresse mémoire. Le calcul de l'adresse du texel se fait en plusieurs étapes, que nous allons voir ci-dessous. La première étape convertit les coordonnées flottantes en coordonnées entières, qui disent à quel ligne et colonne se trouve le texel voulu dans la texture. L'étape suivante transforme ces coordonnées x,y entières en adresse mémoire.

La normalisation des coordonnées

J'ai dit plus haut que les coordonnées de texture sont des coordonnées flottantes, comprises entre 0 et 1. Mais il faut savoir que les pixels shaders peuvent modifier celles-ci pour mettre en œuvre certains effets graphiques. Et le résultat peut alors se retrouver en-dehors de l'intervalle 0,1. C'est quelque chose de voulu et qui est traité par la carte graphique automatiquement, sans que ce soit une erreur. Au contraire, la manière dont la carte graphique traite cette situation permet d'implémenter des effets graphiques comme des textures en damier ou en miroir. Il existe globalement trois méthodes très simples pour gérer cette situation, qui sont appelés des modes d'adressage de texture.

La première méthode est de faire en sorte que le résultat sature. Si une coordonnée est inférieur à 0, alors on la remplace par un zéro. Si elle est supérieure à 1, on la ramène à 1. Avec cette méthode, tout se passe comme si les bords de la texture étaient étendus et remplissaient tout l'espace autour de la texture. Le tout est illustré ci-dessous. Ce mode d'accès aux textures est appelé le clamp.
Une autre solution retire la partie entière de la coordonnée, elle coupe tout ce qui dépasse 1. Pour le dire autrement, elle calcule le résultat modulo 1 de la coordonnée. Le résultat est que tout se passe comme si la texture était répétée à l'infini et qu'elle pavait le plan.
Une autre méthode remplit les coordonnées qui sortent de l’intervalle 0,1 avec une couleur préétablie, configurée par le programmeur.

La conversion des coordonnées de textures flottantes en coordonnées entières

Une fois la normalisation effectuée, les coordonnées de texture sont transformées en coordonnées entières. Pour cela, on multiplie les coordonnées u,v par la résolution de la texture accédée. Pour un écran de résolution ${\text{height,width}}$ , le calcul est le suivant :

x=u\times {\text{width}}

y=v\times {\text{height}}

Le résultat est un nombre avec une partie entière et une partie fractionnaire. La partie entière des deux coordonnées donne la position x,y voulue, et la partie fractionnaire est abandonnée. Elle est utile lors de certaines opérations de filtrage de textures, mais passons cela sous silence pour le moment.

La représentation mémoire des textures

Le calcul de l'adresse d'un texel a besoin de connaitre la position du texel en mémoire, par rapport au début de la texture. Et calculer cette position intra-texture dépend de la manière dont les texels sont stockés en mémoire. Les programmeurs qui lisent ce cours s'attendent certainement à ce que la texture soit stockée en mémoire ligne par ligne, chaque ligne étant stockée pixel par pixel en partant de la gauche. C'est une méthode simple, intuitive, que nous allons voir en premier, mais ce n'est pas celle qui est utilisée de nos jours.

Les textures naïves

En général, les images sont stockées lignes par ligne, ou colonne par colonne. Cela veut dire que le premier pixel en partant d'en haut à gauche est stocké en premier, puis celui immédiatement à sa droite, puis celui encore à droite, et ainsi de suite. Une fois qu'on arrive à la fin d'une ligne, on passe à la ligne suivante, en-dessous. Cette organisation ligne par ligne s'appele l'organisation row major order. On peut faire pareil, mais colonne apr colonne, ce qui donne le column major order.

Maintenant, supposons que la texture commence à l'adresse $A_{\text{texture}}$ , qui est l'adresse du premier texel. La texture a une résolution de ${\text{[width,heigth]}}$ , soit ${\text{width}}$ texels de large, et ${\text{heigth}}$ texels de haut. Par définition, les coordonnées X et Y des texels commencent à 0, ce qui fait que le pixel en haut à gauche a les coordonnées 0,0. L'adresse d'un pixel se calcule facilement si on sait combine d'octets prend un texel en RAM. Supposons que la taille d'un pixel en mémoire soit de T. L'adresse du pixel se calcule comme suit :

A_{\text{pixel}}=A_{\text{texture}}+(width\times T\times X)+(T\times Y)

La formule se comprend assez facilement. On part de l'adresse du début de la texture. Ensuite, on se déplace de Y lignes. La taille d'une ligne en mémoire est de $width\times T$ , ce qui fait que la y-ème ligne se situe $width\times T\times y$ octets plus loin. Ensuite, on se déplace encore de x pixels dans la ligne, ce qui donne un déplacement de $T\times x$ octets. La formule se réecrit comme suit :

A_{\text{pixel}}=A_{\text{texture}}+T\times (width\times Y+X)

Mais cette organisation n'est pas utilisée pour les textures. En effet, les opérations de filtrage de texture que nous allons voir dans ce qui suit, font que le filtrage d'un texel dépend de ses voisins immédiat, que ce soit les voisins du dessus ou du dessous. De même, il est rare que l'on parcoure une texture ligne par ligne, ou colonne par colonne. Cela n'arrive que dans des cas bien précis : une texture vue de face, sans angle, sans filtrage de textures. Mais les textures ne sont pas forcément visibles de face sur l'écran : elles peuvent être penchées, tordues, voire tout simplement déformées par la perspective. L'affichage de la texture ne se fait alors pas ligne par ligne, mais en parcourant la texture en diagonale, l'angle de la diagonale correspondant approximativement à l'angle que fait la verticale de la texture avec le regard. Le fait que la texture n'est pas forcément parcourue ligne par ligne fait que stocker une texture ligne par ligne n'est pas l'idéal. De plus, vu qu'on ne connait pas à l'avance l'angle que fera la diagonale de parcours, on doit ruser.

Les textures tilées

Une première solution à ce problème est celle des textures tilées. Avec ces textures, l'image de la texture est découpée en tiles, des rectangles ou en carrés de taille fixe, généralement des carrés de 4 pixels de côté. Les tiles sont alors mémorisée les unes après les autres dans le fichier de la texture.

Une solution revient à adapter la formule vue plus haut, pour les textures organisées en ligne par ligne. La formule précédente marche donc, mais à condition que l'on change la taille d'un texel par la taille d'une tile, et que la largeur de la texture soit une largeur en nombre de tiles. De plus, on doit adapter les coordonnées des texels pour donner des coordonnées de tile. Généralement, les tiles sont des carrés de N pixels de côté, ce qui fait qu'on peut regrouper les lignes et les colonnes par paquets de N. Il suffit donc de diviser Y et X pour obtenir les coordonnées de la tile, de même que la larguer. La formule pour calculer la position de la énième tile est alors la suivante :

{\text{adresse d'une tile}}={\text{adresse du début de la texture}}+{\text{Taille mémoire d'une tile}}\times \left({{\text{Width}} \over N}\times {Y \over N}+{X \over N}\right)

On peut réécrire le tout comme suit :

{\text{adresse d'une tile}}={\text{adresse du début de la texture}}+K\times \left({Y \over N}+X\right)

, avec K une constante connue à la compilation des ahders.

Les tiles ont une largeur et une longueur égales, afin de simplifier les calculs : on divise X et Y par le même nombre. De plus, leur largeur et leur longueur sont une puissance de deux, afin de simplifier les calculs d'adresse. En faisant cela, la multiplication par la taille d'une tile en mémoire se simplifie : on passe d'une multiplication entière à des décalages de bits. Même chose pour le calcul de l'adresse de la tile à partir des coordonnées x,y : ils impliquent des divisions par une puissance de deux, qui deviennent de simples décalages.

La position d'un pixel dans une tile dépend du format de la texture, mais peut se calculer avec quelques calculs arithmétiques simples. Dans les cas les plus simples, les pixels sont mémorisés ligne par ligne, ou colonne par colonne. Mais ce n'est pas systématiquement le cas. Toujours est-il que les calculs pour déterminer l'adresse sont simples, et ne demandent que quelques additions ou multiplications. Mais avec les formats de texture utilisés actuellement, les tiles sont chargées en entier dans le cache de texture, sans compter que diverses techniques de compression viennent mettre le bazar, comme on le verra dans la suite de cours.

Un avantage de l'organisation en tiles est qu'elle se marie bien avec le parcours des textures. On peut parcourir une texture dans tous les sens, horizontal, vertical, ou diagonal, on sait que les prochains pixels ont de fortes chances d'être dans la même tile. Si on rentre dans une tile par la gauche en haut, on a encore quelques pixels à parcourir dans la tile, par exemple. De même, le filtrage de textures est facilité. On verra dans ce qui va suivre que le filtrage de texture a besoin de lire des blocs de 4 texels, des carrés de 2 pixels de côté. Avec l'organisation en tile, on est certain que les 4 texels seront dans la même tile, sauf s'ils ont le malheur d'être tout au bord d'une tile. Ce dernier cas est assez rare, et il l'est d'autant plus que les tiles sont grandes. Enfin, un dernier avantage est que les tiles sont généralement assez petites pour tenir tout entier dans une ligne de cache. Le cache de texture est donc utilisé à merveille, ce qui rend les accès aux textures plus rapides.

Les textures basées sur des z-order curves

Les formats de textures théoriquement optimaux utilisent une Z-order curve, illustrée ci-dessous. L'idée est de découper la texture en quatre rectangles identiques, et de stocker ceux-ci les uns à la suite des autres. L'intérieur de ces rectangles est lui aussi découpé en quatre rectangles, et ainsi de suite. Au final, l'ordre des pixels en mémoire est celui illustré ci-dessous.

Les texels sont stockés les uns à la suite des autres dans la mémoire, en suivant l'ordre donnée par la Z-order curve. Le calcul d'adresse calcule la position du texel en mémoire, par rapport au début de la texture, et ajoute l'adresse du début de la texture. Mais tout le défi est de calculer la position d'un texel en mémoire, à partir des coordonnées x,y. Le calcul peut sembler très compliqué, mais il n'en est rien. Le calcul demande juste de regarder les bits des deux coordonnées et de les combiner d'une manière particulièrement simple. Il suffit de placer le bit de poids fort de la coordonnée x, suivi de celui de la coordonnée y, et de faire ainsi de suite en passant aux bits suivants.

Calcul de la position d'un élément dans une *Z-order curve* à partir des coordonnées x et y.

L'avantage d'une telle organisation est que la textures est découpées en tiles rectangulaires d'une certaine taille, elles-mêmes découpées en tiles plus petites, etc. Et il se trouve que cette organisation est parfaite pour le cache de texture. L'idéal pour le cache de texture est de charger une tile complète dans le cache de textures. Quand on accède à un texel, on s'assure que la tile complète soit chargée. Mais cela demande de connaitre à l'avance la taille d'une tile. Les formats de texture fournissent généralement une tile carré de 4 pixels de côté, mais cela donnerait un cache trop petit pour être vraiment utile. Avec cette méthode, on s'assure qu'il y ait une tile avec la taille optimale. Les tiles étant découpées en tiles plus petites, elles-mêmes découpées, et ainsi de suite, on s'assure que la texture est découpées en tiles de taille variées. Il y aura au moins une tile qui rentrera tout pile dans le cache.

Le calcul de l'adresse finale

Le calcul de l'adresse d'un texel prend la position du texel par rapport au début de la texture, et ajoute l'adresse du début de la texture. L'adresse mémoire de la texture est mémorisée dans un registre spécialisé. L'adresse est connue au moment où le pilote de la carte graphique place la texture dans la mémoire vidéo, et cette information est transmise au matériel par l'intermédiaire du processeur de commande, puis passée aux processeurs de shaders et à l'unité de texture. Le tout est couplé à d'autres informations, la plus importante étant la taille de la texture en octets, pour éviter de déborder lors des accès à la texture.

Le mip-mapping

Vous pourriez croire qu'il n'y a rien à dire de pertinent sur l'adresse de départ de la texture, mais ce n'est pas le cas. En réalité, c'est l'endroit idéal pour parler d'une technique appelée le mip-mapping, qui a pour but de légèrement améliorer les graphismes des objets lointains, tout en rendant les calculs de texture plus rapides. Le problème résolu par le mip-mapping est le rendu des textures lointaines. Si une texture est plaquée sur un objet lointain, une bonne partie des détails est invisible pour l'utilisateur. Par exemple, un objet assez lointain peut très bien ne prendre que quelques dizaines de pixels à l'écran. Dans ces conditions, plaquer une texture de 512 pixel de côté serait vraiment du gâchis en terme de performance : il faudrait charger tous les pixels de la texture, les traiter, et n'en garder que quelque uns. De plus, ça a tendance à créer des artefacts visuels : les textures affichées ont tendance à pixeliser. Et le mip-mapping permet de réduire ces deux problèmes en même temps.

L'idée est d'utiliser plusieurs exemplaires d'une même texture à des résolutions différentes, chaque exemplaire étant adapté à une certaine distance. Par exemple, une texture sera stocké avec un exemplaire de 512 * 512 pixels, un autre de 256 * 256, un autre de 128 * 128 et ainsi de suite jusqu’à un dernier exemplaire de 32 * 32. Les objets les plus proches utiliseront l'exemplaire à haute résolution, alors que les plus lointains gagneront à utiliser les exemplaires de plus basse résolution. La résolution utilisée diminue d'autant plus que l'objet est situé loin de la caméra. Les objets proches seront rendus avec la texture 512*512, ceux plus lointains seront rendus avec la texture de résolution 256*256, les textures 128*128 seront utilisées encore plus loin, et ainsi de suite jusqu'aux objets les plus lointains qui sont rendus avec la texture la plus petite de 32*32. Chaque exemplaire correspond à un niveau de détail, aussi appelé Level Of Detail (abrévié en LOD).

Le mip-mapping améliore grandement la qualité d'image. L'image d'exemple ci-dessous le montre assez bien.

Évidemment, cette technique consomme de la mémoire vidéo, vu que chaque texture est dupliquée en plusieurs exemplaires, en plusieurs LOD. Dans le détail, la technique du mip-mapping prend au maximum 33% de mémoire en plus (sans compression). Cela vient du fait que chaque LOD prend 4 fois de pixels que l'image immédiatement supérieure : 2 fois moins de pixels en largeur, et 2 fois moins en hauteur. Donc, si je pars d'une texture de base contenant X pixels, la totalité des LODs, texture de base comprise, prendra X + (X/4) + (X/16) + (X/256) + … Un petit calcul de limite donne 4/3 * X, soit 33% de plus.

Pour faciliter les calculs d'adresse, les LOD d'une même texture sont stockées les uns après les autres en mémoire (dans un tableau, comme diraient les programmeurs). Ainsi, pas besoin de se souvenir de la position en mémoire de chaque LOD : l'adresse de la texture de base, et quelques astuces arithmétiques suffisent. Prenons le cas où la texture de base a une taille L. le premier exemplaire est à l'adresse 0, le second niveau de détail est à l'adresse L, le troisième à l'adresse L + L/2, le suivant à l'adresse L + L/2 + L/4, et ainsi de suite. Le calcul d'adresse est alors assez simple et demande juste connaître le niveau de détails souhaité, ainsi que l'adresse de base de la texture. Le niveau de détail voulu est calculé par les pixel shaders, en fonction de la coordonnée de profondeur du pixel à traiter.

Formellement, le mip-mapping est censé être vu avec les autres techniques de filtrage de texture. Mais nous en parlons à part car il s'agit d'une technique de filtrage de texture un peu à part, qui est surtout liée au calcul d'adresse. Les unités de texture ont des circuits dédiés aux filtrage de texture, qui sont relativement séparés des circuits de mip-mapping et de calcul d'adresse, d'où le fait que nous en parlons séparément.

Le cube-mapping

Il n'y a pas que les techniques de mip-mapping qui interférent avec les calculs d'adresse. L'autre technique à le faire est l'environnement-mapping, une technique pour gérer divers effets graphiques liés à l'environnement. L'idée est de plaquer une texture pré-calculée pour simuler l'environnement. Il en existe plusieurs versions différentes, mais la seule utilisée de nos jours est le cube-mapping, où la texture de l'environnement est plaquée sur un cube, d'où son nom. Le cube en question est utilisé différemment suivant ce que l'on cherche à faire avec le cube-mapping. Les deux utilisations principales sont le rendu du ciel et des décors, et les réflexions sur la surface des objets. Dans les deux cas, l'idée est de précalculer ce que l'on voit du point de vue de la caméra. On place la caméra dans la scène 3D, on place un cube centré sur la caméra, le cube est texturé avec ce que l'on voit de l'environnement depuis la caméra/l'objet de son point de vue.

Le rendu du ciel et des décors lointains dans les jeux vidéo se base sur des skybox, à savoir un cube centré sur la caméra, sur lequel on ajoute des textures de ciel ou de décors lointains. Le cube est recouvert par une texture, qui correspond à ce que l'on voit quand on dirige le regard de la caméra vers cette face. Contrairement à ce qu'on pourrait croire, la skybox n'est pas les limites de la scène 3D, les limites du niveau d'un jeu vidéo ou quoique ce soit d'autre de lié à la physique de la scène 3D. La skybox est centrée sur la caméra, elle suit la caméra dans son mouvement. Centrer la skybox sur la caméra permet de simuler des décors très lointains, suffisamment lointain pour qu'on n'ait pas l'illusion de s'en rapprocher en se déplaçant dans la map. De plus, cela évite d'avoir à faire trop de calculs à chaque fois que l'on bouge la caméra. La texture plaquée sur le cube est une texture unique, elle-même découpée en six sous-textures, une par face du cube.

Le cube-mapping est aussi utilisé pour des reflets. L'idée est de simuler les reflets en plaquant une texture pré-calculée sur l'objet réflecteur. La texture pré-calculée est un dessin de l'environnement qui se reflète sur l'objet, un dessin du reflet à afficher. En la plaquant la texture sur l'objet, on simule ainsi des reflets de l'environnement, mais on ne peut pas calculer d'autres reflets comme les reflets objets mobiles comme les personnages. Et il se trouve que la texture pré-calculée est une cubemap. Pour les environnements ouverts, c'est la skybox qui est utilisée, ce qui permet de simuler les reflets dans les flaques d'eau ou dans des lacs/océans/autres. Pour les environnements intérieurs, c'est une cubemap spécifique qui utilisée. Par exemple, pour l'intérieur d'une maison, on a une cubemap par pièce de la maison. Les reflets se calculent en précisant quelle cubemap appliquer sur l'objet en fonction de la direction du regard.

Toujours est-il que les textures utilisées pour le cubemmapping, appelées des cubemaps, sont en réalité la concaténation de six textures différentes. En mémoire vidéo, la cubemap est stockée comme six textures les unes à la suite des autres. Lors du rendu, on doit préciser quelle face du cube utiliser, ce qui fait 6 possibilités. On a le même problème qu'avec les niveaux de détail, sauf que ce sont les faces d'une cubemap qui remplacent les textures de niveaux de détails. L'accès en mémoire doit donc préciser quelle portion de la cubemap il faut accéder. Et l'accès mémoire se complexifie donc. Surtout que l'accès en question varie beaucoup suivant l'API graphique utilisée, et donc suivant la carte graphique.

Les API 3D assez anciennes ne gérent pas nativement les cubemaps, qui doivent être émulées en logiciel en utilisant six textures différentes. Le pixel shader décide donc quelle cubemap utiliser, avec quelques calculs sur la direction du regard. L'accès se fait d'une manière assez simple : le shader choisit quelle texture utiliser. Les API 3D récentes gèrent nativement les cubemaps. Dans le cas le plus simple,pour les versions les plus vielles de ces API, les six faces sont numérotées et l'accès à une cubemap précise quel face utiliser en donnant son numéro. La carte graphique choisit alors automatiquement la bonne texture, mais cela demande de laisser le calcul de la bonne face au pixel shader. D'autres API 3D et cartes graphiques font autrement. Dans les API 3D modenres, les cubemap sont gérées comme des textures en trois dimensions, adressées avec trois coordonnées u,v,w. La carte graphique utilise ces trois coordonnées de manière à en déduire quelle est la face pertinente, mais aussi les coordonnées u,v dans la texture de la face.

L'implémentation matérielle du placage de textures

Pour résumer, la lecture d'un texel demande d'effectuer plusieurs étapes. Dans le cas le plus simple, sans mip-mapping ou cubemapping, on doit effectuer les étapes suivantes :

Il faut d'abord normaliser les coordonnées de texture pour qu'elles tombent dans l'intervalle [0,1] en fonction du mode d'adressage désiré.
Ensuite, les coordonnées u,v doivent être converties en coordonnées entières, ce qui demande une multiplication flottante.
Enfin, l'adresse finale est calculée à partir des coordonnées entières et en ajoutant l'adresse de base de la texture (et éventuellement avec d'autres calculs arithmétiques suivant le format de la texture).

Tout cela pourrait être fait par le pixel shaders, mais cela implique beaucoup de calculs répétitifs et d'opérations arithmétiques assez lourdes, avec des multiplications flottantes, des additions et des multiplications entières, etc. Faire faire tous ces calculs par les shaders serait couteux en performance, sans compter que les shaders deviendraient plus gros et que cela aurait des conséquences sur le cache d'instruction. De plus, certaines de ces étapes peuvent se faire en parallèle, comme les deux premières, ce qui colle mal avec l'aspect sériel des shaders.

Aussi, les processeurs de shaders incorporent une unité de calcul d'adresse spéciale pour faire ces calculs directement en matériel. L'unité de texture contient au minimum deux circuits : un circuit de calcul d'adresse, et un circuit d'accès à la mémoire. Toute la difficulté tient dans le calcul d'adresse, plus que dans le circuit de lecture. Le calcul d'adresse est conceptuellement réalisé en deux étapes. La première étape qui transforme les coordonnées u,v en coordonnées x,y qui donne le numéro de la ligne et de la colonne du texel dans la texture. La seconde étape prend ces deux coordonnées x,y, l'adresse de la texture, et détermine l'adresse de la tile à lire.

L'implémentation du mip-mapping

Le mip-mapping est lui aussi pris en charge par l'unité de calcul d'adresse, car cette technique change l'adresse de base de la texture. La gestion du mip-mapping est cependant assez complexe. Il est possible de laisser le pixel shader calculer quel niveau de détail utiliser, en fonction de la coordonnée de profondeur z du pixel à afficher. La carte graphique détermine alors automatiquement quelle texture lire, quel niveau de détail, automatiquement. Elle détermine aussi la bonne résolution pour la texture, qui est égal à la résolution de la texture de base, divisée par le niveau de détail. Pour résumer, le niveau de détail est envoyé aux unités de texture, qui s'occupent de calculer l'adresse de base et la résolution adéquates. Quelques calculs arithmétiques simples, donc, qui s'implémentent facilement avec quelques circuits.

Mais une autre méthode laisse la carte graphique déterminer le niveau de détail par elle-même. Dans ce cas, cela demande, outre les deux coordonnées de texture, de calculer la dérivée de ces deux coordonnées dans le sens horizontal et vertical, ce qui fait quatre dérivées (deux dérivées horizontales, deux verticales). Les quatre dérivées sont les suivantes :

{\frac {du}{dx}}

,

{\frac {dv}{dx}}

,

{\frac {du}{dy}}

,

{\frac {dv}{dy}}

Un bon moyen pour obtenir ces informations demande de regrouper les pixels par groupes de 4 et de faire la différence entre leurs coordonnées de texture respectives. On peut calculer les deux dérivées horizontales en comparant les deux pixels sur la même ligne, et les deux dérivées verticales en comparant les deux pixels sur la même colonne. Mais cela demande de rastériser les pixels par groupes de 4, par quads. Et c'est ce qui est fait sur les cartes graphiques actuelles, qui rastérisent des groupes de 4 pixels à la fois.

La gestion des accès mémoire

Enfin, l'unité de texture doit tenir compte du fait que la mémoire vidéo met du temps à lire une texture. En théorie, l'unité de texture ne devrait pas accepter de nouvelle demande de lecture tant que celle en cours n'est pas terminée. Mais faire ainsi demanderait de bloquer tout le pipeline, de l'input assembler au unités deshaders, ce qui est tout sauf pratique et nuirait grandement aux performances.

Une solution alternative consiste à mettre en attente les demandes de lectures de texture pendant que la mémoire est occupée. La manière la plus simple d'implémenter des accès mémoire multiples est de les mettre en attente dans une petite mémoire FIFO. Cela implique que les accès mémoire s’exécutent dans l'ordre demandé par le shader et/ou l'unité de rastérisation, il n'y a pas de réorganisation des accès mémoire ou d’exécution dans le désordre des accès mémoire.

Évidemment, quand la mémoire FIFO est pleine, le pipeline est alors totalement bloqué. Le rasteriser est prévenu que l'unité de texture ne peut pas accepter de nouvelle lecture de texture. En pratique, la FIFO est généralement d'une taille respectable et permet de mettre en attente beaucoup de demandes de lecture de texture. Il faut de plus noter qu'il y a une FIFO par processeur de shader sur les cartes graphiques modernes. Quand elle est pleine, le processeur cesse d'exécuter de nouveaux accès mémoire, mais peut continuer à exécuter des shaders dans les autres unités de calcul, pas besoin de bloquer complétement le pipeline.

L'intégration du cache de textures

Il faut noter que les unités de texture incorporent aussi un cache de texture, voire plusieurs. L'intégration des caches de texture avec la mémoire FIFO précédente est quelque peu compliqué, car il faut garantir que les lectures de texture se fassent dans le bon ordre. On ne peut pas exécuter une lecture dans le cache alors que des lectures précédentes sont en attente de lecture en mémoire vidéo. Et cela pose un gros problème : une lecture dans le cache de texture prend quelques dizaines de cycles d'horloge, alors qu'une lecture en mémoire vidéo en prend facilement 400 à 800 cycles, parfois plus. Et cela fait que l'ordre des accès mémoire peut s'inverser.

Prenons par exemple un accès au cache précédé et suivi par deux accès en mémoire vidéo. Le premier démarre au cycle 1, et se termine au cycle numéro 400. L'accès au cache commence au cycle 2 et se termine 20 cycles après, au cycle numéro 22. En clair, la lecture dans le cache s'est terminée avant l'accès mémoire qui le précède. Les textures ne sont donc plus lues dans l'ordre. Et il faut trouver une solution pour éviter cela.

La solution est de retarder les lectures dans le cache tant que tous les accès précédents ne sont pas terminés. Mais pour retarder les lectures en question, il faut d'abord savoir si la lecture atterrit dans le cache ou non, ce qui demande d'accéder au cache. On fait face à un dilemme : on veut retarder les accès au cache, mais les différencier des lectures déclenchant des accès mémoire demande d'accéder au cache en premier lieu. La solution est décrite dans l'article "Prefetching in a Texture Cache Architecture" par Igehy et ses collègues. Elle se base sur deux idées combinées ensemble.

La première idée est de séparer l'accès au cache en deux : une étape qui vérifie si les texels à lire sont dans le cache, et une étape qui accède aux données dans le cache lui-même. Un cache de texture est donc composé de deux circuits principaux. Le premier vérifie la présence des texels dans le cache. Il reçoit l'adresse mémoire à lire, et détermine si une copie de la donnée associée est dans le cache ou non. Pour cela, il utilise un système de tags qu'on ne détaillera pas ici, mais qui donne son nom à l'unité de vérification : l'unité de tag. Ensuite, en plus de l'unité de tags, il y a une mémoire qui stocke les données, la mémoire cache proprement dite. Par simplicité, cette mémoire est une simple mémoire RAM adressable avec des adresses mémoires des plus normales, chaque ligne de cache correspondant à une adresse. Ce genre de cache séparé en deux mémoires est appelé un phased cache, pour ceux qui veulent en savoir plus.

La seconde idée est de retarder l'accès au cache entre les deux phases. La première étape d'un accès mémoire vérifie si la donnée est dans le cache ou non. Puis, on retarde la lecture des données, pour attendre que toutes les lectures précédentes soient terminées. Et enfin, troisième étape : la lecture des texels dans la mémoire cache proprement dite. Les accès mémoire passant par la mémoire vidéo se font de la même manière, à une différence près : la lecture dans le cache est remplacée par la lecture en mémoire vidéo. Tout démarre avec une demande à l'unité de tags, qui vérifie si le texel est dans le cache ou non. Puis on retarde l'accès tant que la mémoire vidéo est occupée, puis on effectue la lecture en mémoire vidéo.

Si ce n'est pas le cas, l'accès mémoire est envoyé à la mémoire vidéo comme précédemment, à savoir qu'il est mis en attente dans une mémoire FIFO, puis envoyé à la mémoire vidéo dès que celle-ci est libre. Mais en sortie de la mémoire, la donnée lue est envoyée dans le cache de texture, par dans l'unité de filtrage. Pour savoir où placer la donnée lue, l'unité de tag a réservé une ligne de cache précise, une adresse bien précise. L'adresse en question est disponible en lisant une autre mémoire FIFO, qui a mis en attente l'adresse en question, en attendant que l'accès mémoire se termine. La donnée est alors écrite dans le cache, puis lue par l'unité de filtrage de textures.

Pour une lecture dans le cache, le déroulement est similaire, mais sans le passage par la mémoire. La lecture fait une demande à l'unité de tag, et celle-ci répond que la donnée est bien dans le cache. Elle place alors l'adresse à lire dans la file d'attente. Une fois que les accès mémoire précédents sont terminés, l'adresse sort de la file d'attente et est envoyée à la mémoire de données. La lecture s'effectue, les texels sont envoyés à l'unité de filtrage de textures. La seule différence avec un phased cache normal est l'insertion de l'adresse à lire dans une FIFO qui vise à mettre en attente

Pour résumer, l'implémentation précédente garantit une exécution des lectures dans leur ordre d'arrivée. Et pour cela, elle retarde les lectures dans le cache tant que les lectures en mémoire précédentes ne sont pas terminées. L'accès au cache est plus rapide que l'accès en mémoire vidéo, mais le retard ajouté pour garantir l'ordre des lectures fait que le temps d'accès est très long.

Le filtrage de textures

Plaquer des textures sans autre forme de procès ne suffit pas à garantir des graphismes d'une qualité époustouflante. La raison est que les sommets et les texels ne tombent pas tout pile sur un pixel de l'écran : le sommet associé au texel peut être un petit peu trop en haut, ou trop à gauche, etc. Une explication plus concrète fait intervenir les coordonnées de texture. Souvenez-vous que lorsque l'on traduit une coordonnée de texture u,v en coordonnées x,y, on obtient un résultat qui ne tombe pas forcément juste. Souvent, le résultat a une partie fractionnaire. Si celle-ci est non-nulle, cela signifie que le texel/sommet n'est pas situé exactement sur le pixel voulu et que celui-ci est situé à une certaine distance. Concrètement, le pixel tombe entre quatre texels, comme indiqué ci-dessous.

Position du pixel par rapport aux texels.

Pour résoudre ce problème, on doit utiliser différentes techniques d'interpolation, aussi appelées techniques de filtrage de texture, qui visent à calculer la couleur du pixel final en fonction des texels qui l'entourent. Il existe de nombreux types de filtrage de textures, qu'il s'agisse du filtrage linéaire, bilinéaire, trilinéaire, anisotropique et bien d'autres.

Tous ont besoin d'avoir certaines informations qui sont généralement fournies par les circuits de calcul d'adresse. La première est clairement la partie fractionnaire des coordonnées x,y. La seconde est la dérivée de ces deux coordonnées dans le sens horizontal et vertical., ce qui fait quatre dérivées (deux dérivées horizontales, deux verticales). Toujours est-il que le filtrage de texture est une opération assez lourde, qui demande beaucoup de calculs arithmétiques. On pourrait en théorie le faire dans les pixels shaders, mais le cout en performance serait absolument insoutenable. Aussi, les cartes graphiques intègrent toutes un circuit dédié au filtrage de texture, le texture sampler. Même les plus anciennes cartes graphiques incorporent une unité de filtrage de texture, ce qui nous montre à quel point cette opération est importante.

On peut configurer la carte graphique de manière à ce qu'elle fasse soit du filtrage bilinéaire, soit du filtrage trilinéaire, on peut configurer le niveau de filtrage anisotropique, etc. Cela peut se faire dans les options de la carte graphique, mais cela peut aussi être géré par l'application. La majorité des jeux vidéos permettent de régler cela dans les options. Ces réglages ne concernent pas la texture elle-même, mais plutôt la manière dont l'unité de texture doit fonctionner. Ces réglages sur l'état de l'unité de texture sont mémorisés quelque part, soit dans l'unité de texture elle-même, soit fournies avec la ressource de texture elle-même, tout dépend de la carte graphique. Certaines cartes graphiques mémorisent ces réglages dans les unités de texture ou dans le processeur de commande, et tout changement demande alors de réinitialiser l'état des unités de texture, ce qui prend un peu de temps. D'autres placent ces réglages dans les ressources de texture elles-mêmes, ce qui rend les modifications de configuration plus rapides, mais demande plus de circuits. D'autres cartes graphiques mélangent les deux options, certains réglages étant globaux, d'autres transmis avec la texture. Bref, difficile de faire des généralités, tout dépend du matériel et le pilote de la carte graphique cache tout cela sous le tapis.

Maintenant que cela est dit, voyons quelles sont les différentes méthodes de filtrage de texture et comment la carte graphique fait pour les calculer.

Le filtrage au plus proche

La méthode de filtrage la plus simple consiste à colorier avec le texel le plus proche. Cela revient tout simplement à ne pas tenir compte de la partie fractionnaire des coordonnées x,y, ce qui est très simple à implémenter en matériel. C'est ce que l'on appelle le filtrage au plus proche, aussi appelé nearest filtering.

Autant être franc, le résultat est assez pixelisé et peu agréable à l’œil. Par contre, le résultat est très rapide à calculer, vu qu'il ne demande aucun calcul à proprement parler. Elle ne fait pas appel à la parti fractionnaire des coordonnées entières de texture, ni aux dérivées de ces coordonnées. On peut combiner cette technique avec la technique du mip-mapping, qui est formellement une technique de filtrage de texture un peu à part. Le résultat est alors déjà bien meilleur, bien que loin d'être satisfaisant. Au passage, toutes les techniques de filtrage de texture peuvent se combiner avec du mip-mapping, certaines ne pouvant pas faire sans.

Le filtrage linéaire

Le plus simple de ces filtrage est le filtrage linéaire, qui effectue une interpolation linéaire entre deux mip-maps, deux niveaux de détails. Pour comprendre l'idée, nous allons prendre une situation très simple, où on souhaite faire une interpolation linéaire entre deux texels. L'interpolation par du principe que la couleur varie entre les deux texels en suivant une fonction affine, illustrée ci-dessous. Ce ne serait évidemment pas le cas dans le monde réel, mais on supposer cela donne une bonne approximation de ce à quoi ressemblerait une texture à plus haute résolution. On peut alors calculer la couleur du pixel par une simple moyenne pondérée par la distance.

Mais où trouver deux pixels pour faire cette moyenne ? C'est là que le mip-mapping rentre en jeu. L'idée est de prendre un texel dans chaque mip-map. Chaque pixel pixel est rendu avec deux niveaux de détail proches, chacun fournissant un texel. Les deux texels sont ensuite interpolés avec la moyenne vu au-dessus, ce qui donne comme résultat moyen intermédiaire entre les deux texels. Le résultat n'est pas très différent de ce qu'on obtient avec une absence d'interpolation et juste du mip-mapping. L'effet visuel est que les transitions entre deux niveaux de détails sont plus lisses, moins abruptes.

Le filtrage bilinéaire

Le filtrage bilinéaire effectue une sorte de moyenne pondérée des quatre texels les plus proches du pixel à afficher. La moyenne est calculée à partir d'interpolations linéaires. Avec 4 pixels, nous allons devoir calculer la couleur de deux points intermédiaires. La couleur de ces deux points se calcule par interpolation linéaire, et il suffit d'utiliser une troisième interpolation linéaire pour obtenir le résultat.

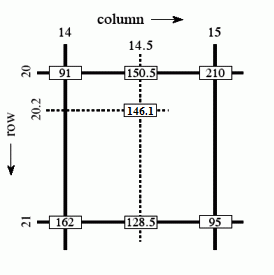
Vous noterez que le filtrage bilinéaire accède à 4 pixels en même temps. Fort heureusement, les textures sont stockées de manière à ce qu'on puisse charger les 4 pixels en une fois. Les 4 pixels sont proches en mémoire, ils sont généralement consécutifs avec un peu de chance. C'est une autre raison pour laquelle on ne stocke pas les textures comme les autres images, à savoir ligne par ligne ou colonne par colonne, mais qu'on les découpe en tiles de petite taille. Le filtrage bilinéaire a de fortes chances que les 4 pixels filtrés soient dans la même tile, la seule exception étant quand ils sont tout juste sur le bord d'une tile.

Le circuit qui permet de faire ce genre de calcul est particulièrement simple. On trouve un circuit de chaque pour chaque composante de couleur de chaque texel : un pour le rouge, un pour le vert, un pour le bleu, et un pour la transparence. Chacun de ces circuit est composé de sous-circuits chargés d'effectuer une interpolation linéaire, reliés comme suit.

La console de jeu Nintendo 64 n'utilise que trois pixels au lieu de quatre dans son interpolation bilinéaire, qui en devient une interpolation quasi-bilinéaire. La raison derrière ce choix est une question de performances, comme beaucoup de décisions de ce genre. Le résultat est un rendu imparfait de certaines textures.

Le filtrage trilinéaire

Avec le mip-mapping, des discontinuités apparaissent lorsqu'une texture est appliquée répétitivement sur une surface, comme quand on fabrique un carrelage à partir de carreaux tous identiques. Par exemple, pensez à une texture de sol : celle-ci est appliquée plusieurs fois sur toute la surface du sol. A une certaine distance, le LOD utilisé change brutalement et passe par exemple de 512*512 à 256*256, ce qui est visible pour un joueur attentif. Le filtrage trilinéaire permet d'adoucir ces transitions. Il consiste à faire « une moyenne » pondérée entre deux niveaux de détails adjacents. Le filtrage trilinéaire effectue d'abord deux filtrages bilinéaires : un sur la texture du niveau de détail adapté, et un autre sur la texture de niveau de détail inférieur. Les deux textures obtenues par filtrage subissent ensuite une interpolation linéaire.

Le circuit de filtrage trilinéaire existe en plusieurs versions. La plus simple, illustrée ci-dessous, effectue deux filtrages bilinéaires en parallèle, dans deux circuits séparés, puis combine leurs résultats avec un circuit d'interpolation linéaire. Seul problème : ce genre de circuit nécessite de charger 8 texels simultanément. Qui plus est, ces 8 texels ne sont pas consécutifs en mémoire,car dans deux niveaux de détails/mip-maps différents. Ce qui fait qu'il n'est pas rare que seuls les 4 premiers pixels soient disponibles rapidement, et que les 4 texels restants mettent du temps avant d'arriver. Les 4 premiers texels doivent donc être mis en attente dans des registres, avant que l'unité de filtrage de texture puisse faire son travail.

Une amélioration du circuit précédent tient compte de cette mise en attente. Il est constitué d'un circuit effectuant un filtrage bilinéaire, de deux registres, d'un interpolateur linéaire, et de quelques circuits de gestion, non-représentés. Son fonctionnement est simple : ce circuit charge 4 texels d'une mip-map, les filtre, et stocke le tout dans un registre. Il recommence l'opération avec les 4 texels de la mip-map de niveau de détail inférieure une fois ces derniers disponibles, puis stocke le résultat dans un autre registre. Enfin, le tout passe par un circuit qui interpole les couleurs finales en tenant compte des coefficients d'interpolation linéaire, mémorisés dans des registres. On économise donc un circuit d'interpolation bilinéaire, sans que les performances soient trop impactées.

Modifier le circuit de filtrage ne suffit pas. Comme je l'ai dit plus haut, la dernière étape d'interpolation linéaire utilise des coefficients, qui lui sont fournis par des registres. Seul problème : entre le temps où ceux-ci sont calculés par l'unité de mip-mapping, et le moment où les texels sont chargés depuis la mémoire, il se passe beaucoup de temps. Le problème, c'est que les unités de texture sont souvent pipelinées : elles peuvent démarrer une lecture de texture sans attendre que les précédentes soient terminées. À chaque cycle d'horloge, une nouvelle lecture de texels peut commencer. La mémoire vidéo est conçue pour supporter ce genre de chose. Cela a une conséquence : durant les 400 à 800 cycles d'attente entre le calcul des coefficients, et la disponibilité des texels, entre 400 et 800 coefficients sont produits : un par cycle. Autant vous dire que mémoriser 400 à 800 ensembles de coefficient prend beaucoup de registres.

Le filtrage anisotrope

D'autres artefacts peuvent survenir lors de l'application d'une texture, la perspective pouvant déformer les textures et entraîner l'apparition de flou. La raison à cela est que les techniques de filtrage de texture précédentes partent du principe que la texture est vue de face. Prenez une texture carrée, par exemple. Vue de face, elle ressemble à un carré sur l'écran. Mais tournez la caméra, de manière à voir la texture de biais, avec un angle, et vous verrez que la forme de la texture sur l'écran est un trapèze, pas un carré. Cette déformation liée à la perspective n'est pas prise en compte par les méthodes de filtrage de texture précédentes. Pour le dire autrement, les techniques de filtrage précédentes partent du principe que les 4 texels qui entourent un pixel forment un carré, ce qui est vrai si la texture est vue de face, sans angle, mais ne l'est pas si la texture n'est pas perpendiculaire à l'axe de la caméra. Du point de vue de la caméra, les 4 texels forment un trapèze d'autant moins proche d'un carré que l'angle est grand.

Pour corriger cela, les chercheurs ont inventé le filtrage anisotrope. En fait, je devrais plutôt dire : LES filtrages anisotropes. Il en existe un grand nombre, dont certains ne sont pas utilisés dans les cartes graphiques actuelles, soit car ils trop gourmand en accès mémoires et en calculs pour être efficaces, soit car ils ne sont pas pratiques à mettre en œuvre. Il est très difficile de savoir quelles sont les techniques de filtrage de texture utilisées par les cartes graphiques, qu'elles soient récentes ou anciennes. Beaucoup de ces technologies sont brevetées ou gardées secrètes, et il faudrait vraiment creuser les brevets déposés par les fabricants de GPU pour en savoir plus. Les algorithmes en question seraient de plus difficiles à comprendre, les méthodes mathématiques cachées derrière ces méthodes de filtrage n'étant pas des plus simple.

La compression de textures

Les textures les plus grosses peuvent aller jusqu'au mébioctet, ce qui est beaucoup. Pour limiter la casse, les textures sont compressées. La compression de texture réduit la taille des textures, ce qui peut se faire avec ou sans perte de qualité. Elle entraîne souvent une légère perte de qualité lors de la compression. Toutefois, cette perte peut être compensée en utilisant des textures à résolution plus grande. Mais il s'agit là d'une technique très simple, beaucoup plus simple que les techniques que nous allons voir dans cette section. Nous allons voir quelque algorithmes de compression de textures de complexité intermédiaire, mais n'allons pas voir l'état de l'art. Il existe des formats de texture plus récents que ceux qui nous allons aborder, comme l'Ericsson Texture Compression ou l'Adaptive Scalable Texture Compression, plus complexes et plus efficaces.

Notons que les textures sont compressées dans les fichiers du jeu, mais aussi en mémoire vidéo. Les textures sont décompressées lors de la lecture. Pour cela, la carte graphique contient alors un circuit, capable de décompresser les textures lorsqu'on les lit en mémoire vidéo. Les cartes graphiques supportent un grand nombre de formats de textures, au niveau du circuit de décompression. Du fait que les textures sont décompressées à la volée, les techniques de compression utilisées sont assez particulières. La carte graphique ne peut pas décompresser une texture entière avant de pouvoir l'utiliser dans un pixel shader. A la place, on doit pouvoir lire un morceau de texture, et le décompresser à la volée. On ne peut utiliser les méthodes de compression du JPEG, ou d'autres formats de compression d'image. Ces dernières ne permettent pas de décompresser une image morceau par morceau.

Pour permettre une décompression/compression à la volée, les textures sont des textures tilées, généralement découpées en tiles de 4 * 4 texels. Les tiles sont compressées indépendamment les unes des autres. Et surtout, avec ou sans compression, la position des tiles en mémoire ne change pas. On trouve toujours une tile tous les T octets, peu importe que la tile soit compressée ou non. Par contre, une tile compressée n'occupera pas T octets, mais moins, là où une tile compressée occupera la totalité des T octets. En clair, compresser une tile fait qu'il y a des vides entre deux tiles dans al mémoire vidéo, mais ne change rien à leur place en mémoire vidéo qui est prédéterminée, peu importe que la texture soit compressée ou non. L'intérêt de la compression de textures n'est pas de réduire la taille de la texture en mémoire vidéo, mais de réduire la quantité de données à lire/écrire en mémoire vidéo. Au lieu de lire T octets pour une tile non-compressée, on pourra en lire moins.

La palette indicée et la technique de Vector quantization

La technique de compression des textures la plus simple est celle de la palette indicée, que l'on a entraperçue dans le chapitre sur les cartes d'affichage. La technique de vector quantization peut être vue comme une amélioration de la palette, qui travaille non pas sur des texels, mais sur des tiles. À l'intérieur de la carte graphique, on trouve une table qui stocke toutes les tiles possibles. Chaque tile se voit attribuer un numéro, et la texture sera composé d'une suite de ces numéros. Quelques anciennes cartes graphiques ATI, ainsi que quelques cartes utilisées dans l’embarqué utilisent ce genre de compression.

Les algorithmes de Block Truncation coding

La première technique de compression élaborée est celle du Block Truncation Coding, qui ne marche que pour les images en niveaux de gris. Le BTC ne mémorise que deux niveaux de gris par tile, que nous appellerons couleur 1 et couleur 2, les deux niveaux de gris n'étant pas le même d'une tile à l'autre. Chaque pixel d'une tile est obligatoirement colorié avec un de ces niveaux de gris. Pour chaque pixel d'une tile, on mémorise sa couleur avec un bit : 0 pour couleur 1, et 1 pour couleur 2. Chaque tile est donc codée par deux entiers, qui codent chacun un niveau de gris, et une suite de bits pour les pixels proprement dit. Le circuit de décompression est alors vraiment très simple, comme illustré ci-dessous.

La technique du BTC peut être appliquée non pas du des niveaux de gris, mais pour chaque composante Rouge, Vert et Bleu. Dans ces conditions, chaque tile est séparée en trois sous-tiles : un sous-bloc pour la composante verte, un autre pour le rouge, et un dernier pour le bleu. Cela prend donc trois fois plus de place en mémoire que le BTC pur, mais cela permet de gérer les images couleur.

Le format de compression S3TC / DXTC

L'algorithme de Color Cell Compression, ou CCC, améliore le BTC pour qu'il gère des couleurs autre que des niveaux de gris. Ce CCC remplace les deux niveaux de gris par deux couleurs. Une tile est donc codée avec un entier 32 bits par couleur, et une suite de bits pour les pixels. Le circuit de décompression est identique à celui utilisé pour le BTC.

Le format de compression de texture utilisé de base par Direct X, le DXTC, est une version amliorée de l'algorithme précédent. Il est décliné en plusieurs versions : DXTC1, DXTC2, etc. La première version du DXTC est une sorte d'amélioration du CCC : il ajoute une gestion minimale de transparence, et découpe la texture à compresser en tiles de 4 pixels de côté. La différence, c'est que la couleur finale d'un texel est un mélange des deux couleurs attribuée au bloc. Pour indiquer comment faire ce mélange, on trouve deux bits de contrôle par texel.

Si jamais la couleur 1 < couleur2, ces deux bits sont à interpréter comme suit :

00 = Couleur1
01 = Couleur2
10 = (2 * Couleur1 + Couleur2) / 3
11 = (Couleur1 + 2 * Couleur2) / 3

Sinon, les deux bits sont à interpréter comme suit :

00 = Couleur1
01 = Couleur2
10 = (Couleur1 + Couleur2) / 2
11 = Transparent

Le circuit de décompression du DXTC ressemble alors à ceci :

Les format DXTC 2, 3, 4 et 5 : l'ajout de la transparence

Pour combler les limitations du DXT1, le format DXT2 a fait son apparition. Il a rapidement été remplacé par le DXT3, lui-même replacé par le DXT4 et par le DXT5. Dans le DXT3, la transparence fait son apparition. Pour cela, on ajoute 64 bits par tile pour stocker des informations de transparence : 4 bits par texel. Le tout est suivi d'un bloc de 64 bits identique au bloc du DXT1.

Dans le DXT4 et le DXT5, la méthode utilisée pour compresser les couleurs l'est aussi pour les valeurs de transparence. L'information de transparence est stockée par un en-tête contenant deux valeurs de transparence, le tout suivi d'une matrice qui attribue trois bits à chaque texel. En fonction de la valeur des trois bits, les deux valeurs de transparence sont combinées pour donner la valeur de transparence finale. Le tout est suivi d'un bloc de 64 bits identique à celui qu'on trouve dans le DXT1.

Le format de compression PVRTC

Passons maintenant à un format de compression de texture un peu moins connu, mais pourtant omniprésent dans notre vie quotidienne : le PVRTC. Ce format de texture est utilisé notamment dans les cartes graphiques de marque PowerVR. Vous ne connaissez peut-être pas cette marque, et c'est normal : elle travaille surtout dans les cartes graphiques embarquées. Ses cartes se trouvent notamment dans l'ipad, l'iPhone, et bien d'autres smartphones actuels.

Avec le PVRTC, les textures sont encore une fois découpées en tiles de 4 texels par 4, mais la ressemblance avec le DXTC s’arrête là. Chacque tile est codée avec :

une couleur codée sur 16 bits ;
une couleur codée sur 15 bits ;
32 bits qui servent à indiquer comment mélanger les deux couleurs ;
et un bit de modulation, qui permet de configurer l’interprétation des bits de mélange.

Les 32 bits qui indiquent comment mélanger les couleurs sont une collection de 2 paquets de 2 bits. Chacun de ces deux bits permet de préciser comment calculer la couleur d'un texel du bloc de 4*4.

◄ Retour vers « Le rasterizeur »

Sommaire du livre

Continuer vers « Les Render Output Target » ►