Les suites et séries/La suite des entiers et les nombres polygonaux
La suite des entiers naturels donne un exemple assez simple de somme partielle. Très facile à étudier, sa somme partielle est aussi très utile pour établir les sommes partielles d'autres suites, comme les suites arithmétiques.
La suite des entiers (nombres triangulaires)
[modifier | modifier le wikicode]La suite des nombres entiers est la suite suivante :
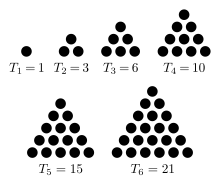
On peut calculer la somme partielle de cette suite, qui n'est autre que la somme des n premiers entiers. La suite formée à partir des sommes partielles donne ce qu'on appelle la suite des nombres triangulaires. Les nombres triangulaires peuvent être représentés par un triangle équilatéral formé par des boules. Le nombre de boules dans le triangle est égal au nombre triangulaire voulu. Le énième terme de la suite des nombres triangulaires donne le nombre de boules pour un triangle de n boules de côté.
La relation de récurrence
[modifier | modifier le wikicode]Cette suite est tout simplement de la somme des n premiers entiers. Cette définition nous permet d'obtenir aisément sa forme récurrente. Il s'agit d'une suite définie par :
Un bon moyen de s'en rendre compte est de calculer les termes de cette suite et de calculer la différence entre termes consécutifs. Le tableau ci-dessous montre que cette différence entre termes consécutifs est égale au rang.
| Terme | 1 | 3 | 6 | 10 | 15 | 21 | 28 | ... |
|---|---|---|---|---|---|---|---|---|
| Rang | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ... |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ... |
La relation paramétrée
[modifier | modifier le wikicode]Calculer la forme paramétrée de cette suite est assez simple pour qui est suffisamment ingénieux. La légende veut que le mathématicien Gauss ait découvert cette formule alors qu’il était au primaire, bien que ce soit sans doute une idée reçue. Cette légende prétend que son professeur avait donné comme exercice le calcul des 100 premiers entiers. Là où ses camarades de classe firent les calculs à la main, Gauss procéda autrement. Il prit la suite des nombres entiers jusqu’à 100 et créa une seconde suite identique, mais de sens inverse. Il additionna alors les deux et trouva ceci :
- 1 + 100 = 101 ;
- 2 + 99 = 101 ;
- 3 + 98 = 101 ;
- … ;
- 49 + 52 = 101 ;
- 50 + 51 = 101 ;
- … ;
- 98 + 3 = 101 ;
- 99 + 2 = 101 ;
- 100 + 1 = 101.
En additionnant la suite des n premiers entiers avec elle-même, il se retrouvait avec 100 fois 101 : . Le calcul de la somme partielle est alors aisé.
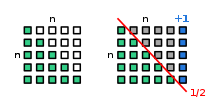
On peut généraliser ce raisonnement pour toute suite de n nombres entiers consécutifs. Pour cette suite, on a :
Donc, si on additionne la suite S avec elle-même, on a :
D'où :
- Pour précision, le terme est ce qu'on appelle un nombre oblong, à savoir le produit de deux entiers consécutifs. Il existe une suite des nombres oblongs, définie par . L'équation démontrée précédemment nous dit donc que le énième nombre oblong est égal au double de la somme des n premiers entiers. En clair, la suite des nombres oblongs est égal au double de la suite des nombres triangulaires.
Les suites arithmétiques
[modifier | modifier le wikicode]

Après avoir vu les multiples des entiers, nous allons voir le cas où chaque entier est multiplié par une constante, avant de se voir ajouter une autre constante. En clair, les suites de la forme :
- , avec k la raison de la suite et le premier terme.
Il se trouve que ces suites ne sont autre que les suites arithmétiques. Nous allons donc calculer la somme partielle d'une suite arithmétique, de la forme :
On peut déduire, avec quelques développements assez simples, que cette somme partielle vaut :
|
Démonstration |
|
La somme partielle d'une suite arithmétique se calcule en additionnant les n premiers termes de la suite : Remplaçons chaque terme par sa valeur paramétrée dans l'équation précédente : Factorisons le terme : Factorisons maintenant : On a vu plus haut que . On a alors : |
|
Démonstration |
|
Partons de la définition de la somme partielle voulue : On applique la formule : Par définition, le terme de droite est égal à : Puis, on applique la formule : On a vu plus haut que : |
On peut aussi reformuler la formule précédente comme suit :
|
Démonstration |
|
Pour cela, partons de la formule précédente : Factorisons : On peut alors utiliser l'équation , ce qui simplifie l'équation précédente en : |
La somme des n premiers nombres pairs et la suite des nombres oblongs
[modifier | modifier le wikicode]Commençons par nous intéresser à la somme des n premiers nombres pairs. Par définition, la suite des nombres pairs, à savoir la somme :
En appliquant la formule sur le produit d'une suite par une constante, on trouve :
En clair, la somme des n premiers pairs est la somme de deux entiers consécutifs. Pour rappel, la somme de deux entiers consécutifs est ce qu'on appelle un nombre oblong. Le résultat précédent nous dit que la somme des n premiers nombres pairs est le énième nombre oblong.
La somme des n premiers nombres impairs
[modifier | modifier le wikicode]Maintenant, étudions le cas de la suite des nombres impairs, dont la somme partielle est la suivante :
La somme des n-1 premiers nombres impairs donne donc le énième carré !
|
Démonstration |
|
La suite des nombres impairs est par définition une suite arithmétique de premier terme 1 et de raison 2. Le énième nombre impair est donc égal à , alors que . En injectant dans la formule générale, on a : |
|
Démonstration |
|
|
On peut remarquer que cette somme partielle donne aussi des nombres figurés, que l'on peut représenter par des figures géométriques, comme pour les nombres triangulaires. Sauf que cette fois-ci, le triangle est remplacé par un carré.

La somme des n premiers nombres de la forme 3n + 1
[modifier | modifier le wikicode]
Maintenant, il est temps de voir la somme partielle de la suite arithmétique de raison 3 et de premier terme 1. Cette série donne aussi des nombres figurés, qui peuvent être représentés par un pentagone. La figure de droite illustre ce point. Cette suite est celle des nombres pentagonaux.
Cette série est obtenue en additionnant les n premiers nombres de la forme 3n + 1. Voici sa formule :
L'application de la formule générale nous donne :
Ce qui se reformule en :
Les autres nombres polygonaux
[modifier | modifier le wikicode]
On pourrait poursuivre et parler des nombres hexagonaux et heptagonaux et de bien d'autres. Mais nous n’allons pas le faire, ce qui serait trop répétitif. Tout ce que l'on peut dire, c'est que les suites de nombres de la forme 4n + 1, 5n + 1, 6n + 1 et autres ont des sommes partielles représentables sous la forme de polygones réguliers (pour rappel, les polygones réguliers sont des figures géométriques avec des côtés de même longueur et des angles identiques). La formule des sommes partielles arithmétiques permet de calculer leur valeur assez simplement. Elle est de la forme :
Ici, k est égal au nombre de côtés du polygone, moins 2. En notant s le nombre de côtés, on a donc :
Ce qui peut aussi s'écrire comme suit :
















































