Les suites et séries/Les séries géométriques
Les séries géométriques sont simplement des séries qui additionnent tous les termes d'une suite géométrique. Toutes ne convergent pas, la plupart divergeant franchement ! Par exemple, la suite géométrique de raison 10 et de premier terme 1 va naturellement diverger, vu que ses termes n'ont de cesse d'augmenter avec le rang. Dans les grandes lignes, il n'y a qu'un seul moyen pour que les termes tendent vers zéro avec le rang : la raison doit être comprise entre -1 et 1. Si c'est le cas, chaque terme sera plus petit (en valeur absolue) que le précédent : les termes diminuant de plus en plus, ils tendent bien vers zéro. Il se trouve que dans ce cas, la série va alors converger. Par contre, une raison de valeur absolue supérieure ou égale à 1 fait diverger la série. Si la raison est égale à 1, la suite est une suite constante, qui va naturellement diverger. Une raison supérieure à 1 va faire que les terme augmentent avec le rang, rendant la série divergente.
Dans la suite du chapitre, nous allons voir le cas général, avant de voir des cas particuliers qui méritent d'être étudiés pour eux même.
Le cas général
[modifier | modifier le wikicode]Pour démontrer le cas général, partons de la formule de la somme partielle d'une suite géométrique, qui est la suivante :
On peut réorganiser les termes comme suit :
Faisons tendre n vers l'infini :
le terme étant constant et indépendant de n, on peut le sortir de la limite :
Si , la limite diverge. Mais si , le terme tend vers 0, ce qui donne :
La suite des puissances des entiers
[modifier | modifier le wikicode]Comme premier exemple de série géométrique, nous allons prendre le cas de la suite des puissances d'un nombre (compris entre 0 et 1), à savoir la suite suivante :
Cette suite n'est autre que la suite définie par la relation de récurrence suivante :
On voit qu'il s'agit d'un cas particulier de suite géométrique, où le premier terme est égal à 1.
La série qui correspond a donc pour résultat :
La suite de l'inverse des puissances des entiers
[modifier | modifier le wikicode]Comme second exemple de série géométrique, nous allons prendre le cas de l'inverse des puissances d'un nombre entier. Par exemple, nous allons étudier la suite de l'inverse des puissances de deux, l'inverse des puissances de trois, etc. Formellement, nous allons étudier les suites définies par :
- ou
La suite de l'inverse des puissances de deux
[modifier | modifier le wikicode]
Pour commencer, nous allons prendre l'exemple de la suite de l'inverse des puissances de deux définie par :
La série associée est la suivante :
Si on applique la formule du dessus, on trouve :
Cette série donne donc un résultat fini quand on fait la somme de tous ses termes : le résultat vaut 2 !
On peut aussi étudier la suite précédente, en remplacant le premier terme par 1/2 et en gardant la même relation de récurrence. On obtient alors la suite définie ainsi :
La formule nous dit que le résultat de la série est tout simplement 1 !

On peut aussi déduire cette limite d'une autre manière. On a vu dans le chapitre sur les sommes partielles que :
En prenant la limite vers l'infini, on retrouve bien le résultat précédent.
Mine de rien, cette série est contre-intuitive : l'intuition nous dit que cette suite devrait diverger, pas converger. Historiquement, le premier a avoir été trahit ainsi par son intuition a été le philosophe Zénon, auteur des célèbres paradoxes de Zénon, censés démontrer que le mouvement est une impossibilité (des trucs de philosophes ! ). Le paradoxe le plus connu est le suivant. Imaginons que me tient à une certaine distance d'un arbre. Pour l'atteindre, je dois parcourir la moitié de la distance qui me sépare de celui-ci. Puis, je dois parcourir la moitié du chemin restant. Puis je dois encore parcourir encore une nouvelle moitié, et ainsi de suite à l'infini. Il est impossible que j'atteigne l'arbre, vu que je devrais traverser une infinité de distances, chacune étant une des moitié mentionnée plus haut. On voit que ce paradoxe est résolu par le calcul vu plus haut : la somme des moitiés converge !

La suite de l'inverse des puissances de quatre
[modifier | modifier le wikicode]On peut maintenant passer au dernier exemple, à savoir la suite de l'inverse des puissances de quatre, définie par :
Cette suite est la suivante :
Si on applique la formule du dessus, on trouve :
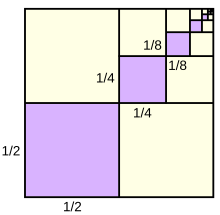
On peut aussi étudier la suite précédente, en remplaçant le premier terme par 1/4 et en gardant la même relation de récurrence. On obtient alors la suite définie ainsi :
La formule nous dit que le résultat de la série est tout simplement 1/3 !
Il existe une belle preuve visuelle de ce résultat, illustré dans le schéma à votre droite, qui illustre le calcul .
Le cas général
[modifier | modifier le wikicode]

On peut étudier les cas de l'inverse des puissances de trois, de cinq, de six, et de bien d'autres. Voici ce que l'on obtient pour les premiers entiers naturels :
Il y a là un motif assez évident et l'on peut généraliser la formule suivante :
Les décimaux périodiques
[modifier | modifier le wikicode]Tous les nombres fractionnaires ont un développement décimal périodique. C'est à dire que si on regarde leurs décimales, on remarque que celles-ci finissent par faire un cycle au bout d'un certain temps. Un même cycle de décimale se répète à l'infini à partir d'un certain rang.
Exemples :
- ...
On ne considère que les séries de décimales répétées non nulles. On peut noter ces nombres en surlignant le groupe de décimales qui se répètent. Par exemple, . Le cas le plus simple est certainement la fraction . En voici d'autres exemples :
Ces nombres peuvent s'étudier assez simplement avec le formalisme des séries. En effet, ces nombres décimaux périodiques peuvent être vus comme le résultat d'une série géométrique et l'on peut déterminer leur fraction à partir de leur développement décimal à partir de la formule d'une série géométrique.
Le développement décimal de l'unité
[modifier | modifier le wikicode]
Le cas le plus étonnant est clairement le cas du nombre . Celui-ci est tout simplement la somme des termes de la suite suivante :
Cette suite est définie comme suit :
- , ou de manière équivalente :
Si l'on souhaite calculer la série qui correspond, on doit retrouver le résultat initial :
Cependant, il est intéressant de regarder le résultat obtenu avec la formule des séries géométriques :
Les deux résultats doivent être égaux, ce qui donne :
Ce résultat fortement contre-intuitif est cependant vérifiable par une petite démonstration assez simple.
|
Démonstration |
|
Partons du nombre :
Multiplions-le par l'inverse de la raison de la suite, à savoir 10.
Soustrayons maintenant le nombre S initial :
Donc, on a :
CQFD! |
Une série de zéros peut se remplacer par une série de 9 en retranchant 1 au chiffre précédent :
Car en utilisant le résultat ci-dessus :
Le développement des décimaux à chiffres périodiques
[modifier | modifier le wikicode]Après avoir vu le cas du développement de l'unité, on peut passer à des décimaux périodiques de la forme : ou . Par exemple, le nombre est la somme totale de la série géométrique suivante : . On voit que cet exemple est une suite géométrique de raison l/10 et de premier terme 7/10. La formule d'une série géométrique nous dit que cette série vaut :
Si on applique le même raisonnement aux nombres dont un seul chiffre est répété infiniment, on trouve :
On voit clairement qu'il y a un certain motif qui se dégage, un motif suffisamment évident pour ne pas le détailler plus.


















































































