Mathc gnuplot/Version imprimable
Une version à jour et éditable de ce livre est disponible sur Wikilivres,
une bibliothèque de livres pédagogiques, à l'URL :
https://fr.wikibooks.org/wiki/Mathc_gnuplot
Introduction
L'étude de ce chapitre peut ce faire à l'aide de cette [Playlist]..
Les notions de mathématiques sont supposées connues.
En pratique
[modifier | modifier le wikicode]Pour le langage C :
Sous linux il faut ajouter la commande -lm dans la ligne de commande pour lier la librairie mathématique à votre code.
Dans Geany il faut aller dans le menu construire/définir les commandes de construction ensuite ajouter la commande -lm
- compile : gcc -Wall -c "%f" -lm
- build ..... : gcc -Wall -o "%e" "%f" -lm
- Copier la bibliothèque, les fichiers h, dans votre répertoire de travail.
- Chaque fichier "*.c" est un exemple à compiler et à exécuter.
Pour gnuplot :
- Linux :
- Exécuter un exemple C.
- Ajouter une nouvelle fenêtre dans votre terminal de travail.
- Vous serez automatiquement dans le bon répertoire pour lancer gnuplot.
- Tapez : gnuplot
- Windows :
- Pour sélectionner le bon répertoire sous Windows
- Choisissez l'icône ChDir (change directory)
- Puis l'icône Open pour sélectionner un fichier de commande de gnuplot.
- Animation :
- Tapotez sur l'icône replot de gnuplot.
Fichiers pour gnuplot
Préambule
[modifier | modifier le wikicode]Quelques fonctions C à connaitre :
f_p=fopen("a.txt","w"); //(write) Créer un fichier en écriture.
f_p=fopen("a.txt","r"); //(read) 0uvrir un fichier en lecture.
f_p=fopen("a.txt","a"); //(append) 0uvrir un fichier en écriture.
// Rajouter le texte en fin de fichier.
printf( "%d",i); // Imprimer sur l'écran.
fprintf(f_p,"%d",i); // Imprimer dans le fichier *f_p
sprintf( s,"%d",i); // Imprimer dans la chaine de caractères s.
Éviter les lettres accentuées dans les fichiers sources (*.c,*.h), cela pose des problèmes pour échanger les fichiers entre Windows et Linux ou à l'international.
Premiers fichiers
[modifier | modifier le wikicode]Un fichier list.txt
[modifier | modifier le wikicode]- Copiez cet exemple dans votre éditeur.
- Sauvez-le sous le nom "c01.c"
- Compilez et exécutez-le.
gcc -lm c01.c -o c01.exe ;./c01.exe
- Éditer le fichier "list.txt"
c01.cUn fichier list.txt |
|---|
/* ------------------------------ */
/* Save as c01.c */
/* ------------------------------ */
#include <stdio.h>
#include <math.h>
/* ------------------------------ */
double f(double x){return(pow(x,2.));}
/* ------------------------------ */
int main(void)
{
FILE *fp; /*Déclarer un pointeur de fichier. */
double a;
/*Ouvrir le fichier en mode écriture.*/
fp = fopen("list.txt","w"); /*fp est un pointeur de fichier */
/*qui pointe sur "list.txt" */
for(a = -5.0; a <= 5.0; a++)
fprintf(fp," %6.3f %6.3f\n",/*Imprimer dans le fichier */
a, f(a));
fclose(fp); /*Fermer le fichier */
printf("\n\n Ouvrir le fichier list.txt "
"\n\n Press return to continue. ");
getchar();
return 0;}
Un fichier de données pour gnuplot
[modifier | modifier le wikicode]Nous ne mettrons pas d'extension pour les fichiers de données avec gnuplot.
- Compilez et exécutez-ce fichier.
- Éditez le fichier "data"
- Dans gnuplot tapez :
plot "data"
c02.cUn fichier de données pour gnuplot |
|---|
/* ------------------------------ */
/* Save as c02.c */
/* ------------------------------ */
#include <stdio.h>
#include <math.h>
/* ------------------------------ */
double f(double x){return(pow(x,2.));}
/* ------------------------------ */
int main(void)
{
FILE *fp = fopen("data","w");
double a = -5.0;
for(; a <= 5.0; a+=.2)
fprintf(fp," %6.3f %6.3f\n",a,f(a));
fclose(fp);
printf(" Dans gnuplot -> plot \"data\" \n\n"
" Press return to continue. \n\n");
getchar();
return 0;
}
Un fichier de commande pour gnuplot
[modifier | modifier le wikicode]L'extension des fichiers de commande de gnuplot est "*.plt" Ici on dessine deux chaines de caractères.
- Compilez et exécutez-ce fichier.
- Éditez le fichier "a_main.plt"
- Dans gnuplot tapez :
load "a_main.plt"
c03.cUn fichier de commande pour gnuplot |
|---|
/* ------------------------------ */
/* Save as c03.c */
/* ------------------------------ */
#include <stdio.h>
#include <math.h>
/* ------------------------------ */
char heq[] = "sin(x)";
char geq[] = "cos(x)";
/* ------------------------------ */
int main(void)
{
FILE *fp = fopen("a_main.plt","w");
fprintf(fp,"# Fichier de commande pour gnuplot \n"
"# En ligne de commande : load \"a_main.plt\"\n"
"#\n"
" set zeroaxis\n"
" plot %s,\\\n"
" %s \n\n"
" reset", geq, heq);
fclose(fp);
printf("\n\n load \"a_main.plt\" with gnuplot."
"\n\n Press return to continue. ");
getchar();
return 0;
}
Cela donne dans le fichier "a_main.plt" :
# Fichier de commande pour gnuplot
# En ligne de commande : load "a_main.plt"
#
set zeroaxis
plot cos(x),\
sin(x)
reset
On peut remarquer que chaque fonction est sur une ligne différente. Important si l'on veut dessiner quatre ou cinq fonctions.
Dessiner une liste et une chaîne de caractères
[modifier | modifier le wikicode]On associe les deux méthodes vues précédemment.
- Compilez et exécutez-ce fichier.
- Éditez le fichier "a_main.plt"
- Dans gnuplot tapez :
load "a_main.plt"
c04.cDessiner une liste et une chaîne de caractères |
|---|
/* ------------------------------ */
/* Save as c04.c */
/* ------------------------------ */
#include <stdio.h>
#include <math.h>
/* ------------------------------ */
double f(double x){return(cos(x));}
/* ------------------------------ */
char feq[] = "cos(x)";
/* ------------------------------ */
int main(void)
{
FILE *fp;
double a = -5.0;
fp = fopen("data","w");
for(; a <= 5.0; a+=.2)
fprintf(fp," %6.3f %6.3f\n", a, f(a));
fclose(fp);
fp = fopen("a_main.plt","w");
fprintf(fp,"# Fichier de commande pour gnuplot \n"
"# En ligne de commande : load \"a_main.plt\"\n"
"#\n"
" set zeroaxis\n"
" plot \"data\",\\\n"
" %s\n"
" reset",feq);
fclose(fp);
printf("\n\n load \"a_main.plt\" with gnuplot."
"\n\n Press return to continue. ");
getchar();
return 0;
}
Cela donne dans le fichier "a_main.plt" :
# Fichier de commande pour gnuplot
# En ligne de commande : load "a_main.plt"
#
set zeroaxis
plot "data",\
cos(x)
reset
Une fonction graphique
[modifier | modifier le wikicode]On met simplement le contenu de la fonction main() dans G_plot().
- Compilez et exécutez-ce fichier..
- Éditez le fichier "a_main.plt"
- Dans gnuplot tapez :
load "a_main.plt"
c05.cUne fonction graphique |
|---|
//* ------------------------------ */
/* Save as c05.c */
/* ------------------------------ */
#include <stdio.h>
#include <math.h>
/* ------------------------------ */
double f(double x){return(cos(x));}
char feq[] = "cos(x)";
/* ------------------------------ */
int G_plot(void)
{
FILE *fp;
double a = -5.0;
fp = fopen("data","w");
for(; a <= 5.0; a+=.2)
fprintf(fp," %6.3f %6.3f\n",a,f(a));
fclose(fp);
fp = fopen("a_main.plt","w");
fprintf(fp,"# Fichier de commande pour gnuplot \n"
"# En ligne de commande : load \"a_main.plt\"\n"
"#\n"
" set zeroaxis\n"
" plot \"data\",\\\n"
" %s\n"
" reset",feq);
fclose(fp);
return 0;
}
/* ------------------------------ */
int main(void)
{
G_plot();
printf("\n\n load \"a_main.plt\" with gnuplot."
"\n\n Press return to continue. ");
getchar();
return 0;
}
Cela donne dans le fichier "a_main.plt" :
# Fichier de commande pour gnuplot
# En ligne de commande : load "a_main.plt"
#
set zeroaxis
plot "data",\
cos(x)
reset
Les ennuis commencent
[modifier | modifier le wikicode]À partir des fichiers précédents, essayer de dessiner la fonction g, sans modifier G_plot() ?
/* ------------------------------ */
double g(double x){return(sin(x));}
char geq[] = "sin(x)";
/* ------------------------------ */
Une solution va être proposée dans le chapitre suivant : Pointeurs de fonctions.
Conclusion
[modifier | modifier le wikicode]Nous avons dessiné des fonctions sous forme de chaînes de caractères et sous la forme de liste de points.
Un problème est apparu : rendre les fonctions graphiques indépendantes de la fonction utilisée.
Pointeurs de fonctions
Préambule
[modifier | modifier le wikicode]En langage C, le nom d'une fonction est un pointeur.
On peut l'utiliser comme argument dans l'appel d'une fonction.
Exemple : G_plot(f); (f() étant une fonction)
Un pointeur de fonction doit avoir le même prototype que la fonction pointée.
- Pour la fonction f(x) :
double f (double x) {return( pow(x,2.));}
double (*P_f)(double x)
- Pour la fonction g(x,y) :
double g (double x,double y) {return(x*y;}
double (*P_g)(double x,double y)
Pour appeler la fonction, nous utiliserons cette méthode :
- Pour la fonction f(x) :
((*P_f)(a)) /* corresponds à un appel de fonction de forme f(a). */
- Pour la fonction g(x,y) :
((*P_g)(a,b)) /* corresponds à un appel de fonction de forme g(a,b). */
Remarque :
- f et g sont des pointeurs et f() et g() sont des fonctions.
double (*P_f)(double x)c'est une déclaration de pointeur de fonction.P_fc'est le pointeur.((*P_f)())c'est un appel à une fonction.
Exemples graphiques (avec gnuplot)
[modifier | modifier le wikicode]Dessiner deux fonctions successivement
[modifier | modifier le wikicode]La fonction Gplt() dessine f(x) et g(x).
c01.cDessiner deux fonctions successivement |
|---|
/* ------------------------------ */
/* Save as c01.c */
/* ------------------------------ */
#include <stdio.h>
#include <math.h>
/* ------------------------------ */
double f(double x){return( pow(x,2.));}
double g(double x){return(2.0*x + 3.0);}
/* ------------------------------ */
void G_plt(
double (*P_f)(double x)
)
{
FILE *fp = fopen("data","w");
double a = -5.0;
for(; a <= 5.0; a += 0.3)
fprintf(fp," %6.3f %6.3f\n",a,((*P_f)(a)));
fclose(fp);
}
/* ------------------------------ */
int main(void)
{
printf(" Type: plot \"data\" ");
G_plt(f);
getchar();
printf(" Type: plot \"data\" ");
G_plt(g);
printf("\n\n Press return to continue.\n");
getchar();
return 0;
}
Solution pour le chapitre précédent
[modifier | modifier le wikicode]La fonction G_plot() dessine la fonction (data) et la chaîne de caractères.
c02.cSolution pour le chapitre précédent |
|---|
/* ------------------------------ */
/* Save as c02.c */
/* ------------------------------ */
#include <stdio.h>
#include <math.h>
/* ------------------------------ */
double f(double x){return(cos(x));}
char feq[] = "cos(x)";
/* ------------------------------ */
double g(double x){return(sin(x));}
char geq[] = "sin(x)";
/* ------------------------------ */
int G_plot(
double (*P_f)(double x),
char Feq[])
{
FILE *fp;
double a = -5.0;
fp = fopen("data","w");
for(; a <= 5.0; a+=.2)
fprintf(fp," %6.3f %6.3f\n",a,((*P_f)(a)));
fclose(fp);
fp = fopen("a_main.plt","w");
fprintf(fp,"# Gnuplot file : load \"a_main.plt\" \n"
" set zeroaxis\n"
" plot \"data\",\\\n"
" %s\n"
" reset",Feq);
fclose(fp);
return 0;
}
/* ------------------------------ */
int main(void)
{
printf(" load \"a_main.plt\" with gnuplot ");
G_plot(f,feq);
getchar();
printf(" load \"a_main.plt\" with gnuplot ");
G_plot(g,geq);
printf("\n\n Press return to continue.\n");
getchar();
return 0;
}
Résultat après le premier appel de G_plot() :
# Gnuplot file : load "a_main.plt"
set zeroaxis
plot "data",\
cos(x)
reset
Résultat après le deuxième appel de G_plot() :
# Gnuplot file : load "a_main.plt"
set zeroaxis
plot "data",\
sin(x)
reset
Exemple numérique
[modifier | modifier le wikicode]Passer des pointeurs de fonctions à une fonction.
Les fonctions f‘ et f‘‘
[modifier | modifier le wikicode]Calculer la dérivée première et seconde d'une fonction.
c03.cLes fonctions f‘ et f‘‘ |
|---|
/* ------------------------------ */
/* Save as c03.c */
/* ------------------------------ */
#include <stdio.h>
#include <math.h>
/* ------ Fonction f ------------ */
double f(double x){return( pow(x,2.));}
/* ------------------------------ */
char feq[] = "x**2";
/* ------ Fonction g ------------ */
double g(double x){return(
pow(cos(x),2.)+sin(x)+x-3);}
/* ------------------------------ */
char geq[] = "cos(x)**2+sin(x)+x-3";
/* ------------------------------
f'(a) = f(a+h) - f(a-h)
-------------
2h
------------------------------ */
double Dx_1(
double (*P_f)(double x),/* Declaration de pointeur de fonction */
double a,
double h
)
{
return( ( ((*P_f)(a+h))-((*P_f)(a-h)) ) / (2.*h) );
}
/* -----------------------------
f''(a) = f(a+h) - 2 f(a) + f(a-h)
----------------------
h**2
------------------------------- */
double Dx_2(
double (*P_f)(double x),/* Declaration de pointeur de fonction */
double a,
double h
)
{
return( (((*P_f)(a+h))-2*((*P_f)(a))+((*P_f)(a-h))) / (h*h) );
}
/* ------------------------------ */
int main(void)
{
double x = 2.;
double h = 0.001;
printf("\n\n");
printf(" f(%.3f) = %.3f \n",x,f(x) );
printf(" f'(%.3f) = %.3f \n",x,Dx_1(f,x,h));
printf("f''(%.3f) = %.3f \n",x,Dx_2(f,x,h));
printf("\n\n");
printf(" g(%.3f) = %.3f \n",x,g(x) );
printf(" g'(%.3f) = %.3f \n",x,Dx_1(g,x,h));
printf("g''(%.3f) = %.3f \n",x,Dx_2(g,x,h));
printf("\n\n Press return to continue.");
getchar();
return 0;
}
Résultat :
f(2.000) = 4.000 f‘(2.000) = 4.000 f‘‘(2.000) = 2.000 . g(2.000) = 0.082 g‘(2.000) = 1.341 g‘‘(2.000) = 0.398 . Press return to continue.
La fonction FoG
[modifier | modifier le wikicode]Ici on passe les deux fonctions f et g à la fonction FoG().
La même fonction peut calculer gof, fog et fof...
c04.cLa fonction FoG |
|---|
/* ------------------------------ */
/* Save as c04.c */
/* ------------------------------ */
#include <stdio.h>
#include <math.h>
/* ------ Fonction f ------------ */
double f(double x){return( pow(x,2.));}
/* ------------------------------ */
char feq[] = "x**2";
/* ------ Fonction g ------------ */
double g(double x){return(2.0*x + 3.0);}
/* ------------------------------ */
char geq[] = "2.0*x + 3.0";
/* - Fonction FoG (g suivie de f)-*/
double FoG(
double (*P_F)(double x),/* Pointeur pour la premiere fonction */
double (*P_G)(double x),/* Pointeur pour la deuxieme fonction */
double a
)
{
return((*P_F)( ((*P_G)(a))) );
}
/* ------------------------------ */
int main(void)
{
double a = 2.0;
printf(" f : x-> %s\n", feq);
printf(" g : x-> %s\n", geq);
printf(" \n\n");
printf(" f(g(%.0f)) = %6.1f\n", a, FoG(f,g,a));
printf(" g(f(%.0f)) = %6.1f\n", a, FoG(g,f,a));
printf(" f(f(%.0f)) = %6.1f\n", a, FoG(f,f,a));
printf("\n\n Press return to continue.\n");
getchar();
return 0;
}
Résultat :
f : x-> x**2 g : x-> 2.0*x + 3.0 . f(g(2)) = 49.0 g(f(2)) = 11.0 f(f(2)) = 16.0 . Press return to continue.
Tableau de pointeurs de fonctions
Préambule
[modifier | modifier le wikicode]Nous avons des fonctions semblables. Nous voulons les associer pour pouvoir les manipuler dans des boucles. Nous allons créer un tableau de pointeurs de fonctions.
Le tableau de pointeurs de fonctions doit être déclaré avec un prototype de la même forme que celui des fonctions.
Tableau de pointeurs de fonctions
[modifier | modifier le wikicode]Les fonctions trigonométriques
[modifier | modifier le wikicode]Nous allons utiliser les fonctions trigonométriques du C.
Déclaration du tableau
[modifier | modifier le wikicode]double (*TrigF[6])(double x) = {cos,sin,tan,atan,asin,acos};
- Toutes les fonctions ont la même forme :
double fonction(double). - Le tableau à la même forme que les fonctions :
double tableau(double). - Il y a six fonctions : cos, sin, tan, atan, asin, acos.
Exemple d'un appel
[modifier | modifier le wikicode] cos(.5) == TrigF[0](.5)
Exemple à tester
[modifier | modifier le wikicode]c01.cExemple à tester |
|---|
/* ------------------------------ */
/* Save as c01.c */
/* ------------------------------ */
#include <stdio.h>
#include <math.h>
/* ------------------------------ */
int main(void)
{
double (*TrigF[6])(double x) = {cos,sin,tan,atan,asin,acos};
double x= .5;
int i= 0;
printf(" Nous avons declare un tableau "
" de pointeurs de fonctions.\n "
" J'ai utilise ici les fonctions predefinie du c.\n");
printf(" cos(%.1f) = %.3f \n", x, cos(x));
printf(" TrigF[%d](%.1f)) = %.3f\n\n",i,x,TrigF[i](x));
printf(" Press return to continue");
getchar();
return 0;
}
Application
[modifier | modifier le wikicode]- Créez un tableau de valeurs des fonctions trigonométriques.
- Imprimez le résultat dans cette ordre (sin,cos,tan,acos,asin,atan)
- Pour .1 <= x <+ .5
Avec le résultat dans un fichier
[modifier | modifier le wikicode]c02.cAvec le résultat dans un fichier |
|---|
/* ------------------------------ */
/* Save as c02.c */
/* ------------------------------ */
#include <stdio.h>
#include <math.h>
/* ------------------------------ */
int main(void)
{
FILE *fp = fopen("list.txt","w");
double (*TrigF[6])(double x) = {atan,asin,acos,tan,cos,sin};
int i= 6;
double x= .1;
fprintf(fp," x || sin cos tan acos asin atan \n");
for(;x<=.5;x+=.1)
{
fprintf(fp," %.1f ||",x);
for(i=6;i;)
fprintf(fp," %.3f ",TrigF[--i](x));
fprintf(fp,"\n");
}
fclose(fp);
printf("\n\n Ouvrir le fichier list.txt\n");
getchar();
return 0;
}
Le résultat :
x || sin cos tan acos asin atan 0.1 || 0.100 0.995 0.100 1.471 0.100 0.100 0.2 || 0.199 0.980 0.203 1.369 0.201 0.197 0.3 || 0.296 0.955 0.309 1.266 0.305 0.291 0.4 || 0.389 0.921 0.423 1.159 0.412 0.381 0.5 || 0.479 0.878 0.546 1.047 0.524 0.464
Remarques :
- Attention à l'ordre des fonctions dans la déclaration du tableau.
- double (*TrigF[6])(double x) = {atan,asin,acos,tan,cos,sin};
Au démarrage :
- La décrémentation se fait dans le tableau. TrigF[--i](x)
- i=6 entre dans le tableau.
- 6 est décrémenté -> 5 (avant l'appel de la fonction --i)
- La sixième fonction est appelée (Sin).
- La numéro cinq. :)
Au final :
- Il entre UN dans le tableau.
- UN est décrémenté -> 0
- La première fonction est appelée (atan).
- La numéro zéro. :))
- i est égal à zéro en rentrant dans la boucle.
- Le cycle est cassé. :(
Avec le résultat à l'écran
[modifier | modifier le wikicode]c03.cAvec le résultat à l'écran |
|---|
/* ------------------------------ */
/* Save as c03.c */
/* ------------------------------ */
#include <stdio.h>
#include <math.h>
/* ------------------------------ */
int main(void)
{
double (*TrigF[6])(double x) = {atan,asin,acos,tan,cos,sin};
int i= 6;
double x= .1;
for(;x<=.5;x+=.1)
{
printf("\n");
for(i=6;i;) printf(" %.3f ",TrigF[--i](x));
}
printf("\n\n Press return to continue.\n");
getchar();
return 0;
}
Les fonctions f‘ et f‘‘
[modifier | modifier le wikicode]Nous voulons créer la fonction Derivate pour calculer les dérivées première et seconde d'une fonction en utilisant un tableau de pointeurs de fonctions.
Voir listing en fin de page.
Déclaration du tableau
[modifier | modifier le wikicode]double (*Derivate[3])(double (*P_f)(double x),double a,double h) = {fx,Df_x,Df_xx};
- Toutes les fonctions (fx,Df_x,Df_xx) ont la même forme :
double fonction(double (*P_f)(double x) double double). - Le tableau a la même forme que les fonctions :
double tableau(double (*P_f)(double x) double double).
Il y a trois fonctions. (0,1,2)= {fx, Df_x, Df_xx}. La fonction fx donne f.
- Supprimez cette fonction et travaillez sur deux fonctions.
- Réfléchissez.
Exemple d'un appel
[modifier | modifier le wikicode] f(x) == Derivate[0](f,x,0.)
- Derivate[0] donne f(x).
- Voir la fonction fx() la première fonction du tableau.
- h = 0 dans cet appel parce qu'il n'est pas utilisé (voir code de fx())
Exemple à tester
[modifier | modifier le wikicode]c04.cExemple à tester |
|---|
/* ------------------------------ */
/* Save as c04.c */
/* ------------------------------ */
#include <stdio.h>
#include <math.h>
/* ------------------------------ */
/* ------------------------------ */
double f(double x){return( pow(x,2.));}
/* ------------------------------ */
char feq[] = "x**2";
/* ------------------------------ */
/* ------------------------------ */
double g(double x){return(
pow(cos(x),2.)+sin(x)+x-3);}
/* ------------------------------ */
char geq[] = "cos(x)**2+sin(x)+x-3";
/* ------------------------------ */
/* ------------------------------ */
double fx(
double (*P_f)(double x),
double a,
double h
)
{
return( ((*P_f)(a)) );
}
/* ------------------------------
f'(a) = f(a+h) - f(a-h)
-------------
2h
------------------------------ */
double Df_x(
double (*P_f)(double x),
double a,
double h
)
{
return( ( ((*P_f)(a+h))-((*P_f)(a-h)) ) / (2.*h) );
}
/* -----------------------------
f''(a) = f(a+h) - 2 f(a) + f(a-h)
----------------------
h**2
------------------------------- */
double Df_xx(
double (*P_f)(double x),
double a,
double h
)
{
return( (((*P_f)(a+h))-2*((*P_f)(a))+((*P_f)(a-h))) / (h*h) );
}
/* ------------------------------ */
int main(void)
{
double (*Derivate[3])(double (*P_f)(double x),
double a,
double h) = {fx,Df_x,Df_xx};
double a = 2;
double h = 0.001;
printf("\n\n");
printf(" f(%.3f) = %.3f = %.3f \n",a, f(a), Derivate[0](f,a,0));
printf(" f'(%.3f) = %.3f = %.3f \n",a,Df_x (f,a,h),Derivate[1](f,a,h));
printf("f''(%.3f) = %.3f = %.3f \n",a,Df_xx(f,a,h),Derivate[2](f,a,h));
printf("\n\n");
printf(" g(%.3f) = %.3f = %.3f \n",a, g(a), Derivate[0](g,a,0));
printf(" g'(%.3f) = %.3f = %.3f \n",a,Df_x (g,a,h),Derivate[1](g,a,h));
printf("g''(%.3f) = %.3f = %.3f \n",a,Df_xx(g,a,h),Derivate[2](g,a,h));
printf("\n\n Press return to continue.");
getchar();
return 0;
}
Fichiers h : Fichiers h partagés
Préambule
[modifier | modifier le wikicode]Vous trouverez dans cette section une suite de fichiers h. Installez ces fichiers dans votre répertoire de travail. Ils seront appelés par le fichier "x_ahfile.h" de chaque exemple.
Ces fichiers ne sont pas utilisés pour la géométrie de la tortue.
En pratique
[modifier | modifier le wikicode]- xdef.h
PI- Déclaration de pi.
clrscrn();- Effacer la fenêtre du terminal Dos.
Pause();- Une pause d'une seconde pour les animations.
NewName();- Créer une liste de noms de fichiers.
- xplt.h
i_WGnuplot();- Contrôler la fenêtre de gnuplot 2d.
i_WsGnuplot();- Contrôler la fenêtre de gnuplot 3d.
i_VGnuplot();- Contrôler la vue de la fonction 3d.
- xspv.h
i_point2d();- Initialiser un point en 2d.
i_point3d();- Initialiser un point en 3d.
i_vector2d();- Initialiser un vecteur en 2d.
i_vector3d();- Initialiser un vecteur en 3d.
- xfx_x.h
- Dérivées de f(x);
- xfxy_x.h
- Dérivées partielles de f(x,y);
- xfxyz_x.h
- Dérivées partielles de f(x,y,z);
Fichiers h : xdef
Préambule
[modifier | modifier le wikicode]Installez ce fichier dans votre répertoire de travail.
xdef.hDéfinitions générales |
|---|
/* ------------------------------------ */
/* Save as : xdef.h */
/* ------------------------------------ */
#ifndef PI
#define PI 3.14159265359
#endif
/* ------------------------------------ */
void clrscrn(void)
{
printf("\n\n\n\n\n\n\n\n\n\n\n"
"\n\n\n\n\n\n\n\n\n\n\n"
"\n\n\n\n\n\n\n\n\n\n\n");
}
/* ------------------------------------ */
void Pause(void)
{
int i=300;
int j;
while(--i){j=600000;while(--j);}
}
/* ------------------------------------ */
/* First file name : */
/* */
/* char fname[]= "a_paaa"; */
/* ------------------------------------ */
char *NewName(
char *name
)
{
if(name[5]<'z')
++name[5];
else if(name[4]<'z')
{
name[5]='a';
++name[4];
}
else if(name[3]<'z')
{
name[5]='a';
name[4]='a';
++name[3];
}
return(name);
}
Fichiers h : xplt
Préambule
[modifier | modifier le wikicode]Installez ce fichier dans votre répertoire de travail.
xplt.hDéfinition d'intervalles pour le tracé |
|---|
/* ------------------------------------ */
/* Save as : xplt.h */
/* ------------------------------------ */
typedef struct
{
double xmini; double xmaxi;
double ymini; double ymaxi;
}W_Ctrl, *PW_Ctrl;
/* ------------------------------------ */
W_Ctrl i_WGnuplot(
double xmini, double xmaxi,
double ymini, double ymaxi
)
{
W_Ctrl w = {xmini,xmaxi,ymini,ymaxi};
return (w);}
/* ------------------------------------ */
typedef struct
{
double xmini; double xmaxi;
double ymini; double ymaxi;
double zmini; double zmaxi;
}Ws_Ctrl, *PWs_Ctrl;
/* ------------------------------------ */
Ws_Ctrl i_WsGnuplot(
double xmini, double xmaxi,
double ymini, double ymaxi,
double zmini, double zmaxi
)
{
Ws_Ctrl w = {xmini,xmaxi,ymini,ymaxi,zmini,zmaxi};
return (w);}
/* ------------------------------------ */
typedef struct
{
double rot_x; double rot_z;
double scale; double scale_z;
}View_Ctrl, *PView_Ctrl;
/* ------------------------------------ */
View_Ctrl i_VGnuplot(
double rot_x, double rot_z,
double scale, double scale_z
)
{
View_Ctrl V = {rot_x,rot_z,scale_z,scale_z};
return (V);}
/* ------------------------------------ */
typedef struct
{
double mini; double maxi;
double step;
}t_Ctrl, *Pt_Ctrl;
/* ------------------------------------ */
t_Ctrl i_time(
double mini, double maxi,
double step
)
{
t_Ctrl t = {mini,maxi,step};
return (t);}
Fichiers h : xspv
Préambule
[modifier | modifier le wikicode]Installez ce fichier dans votre répertoire de travail.
xspv.hDéfinition des types de points et de vecteurs |
|---|
/* ------------------------------------ */
/* Save as : xspv.h */
/* ------------------------------------ */
typedef struct
{
double x; double y;
}point2d, *Ppoint2d;
/* ------------------------------------ */
point2d i_point2d(
double x, double y
)
{
point2d p = {x,y};
return (p);}
/* ------------------------------------ */
typedef struct
{
double x; double y; double z;
}point3d, *Ppoint3d;
/* ------------------------------------ */
point3d i_point3d(
double x, double y, double z
)
{
point3d p = {x,y,z};
return (p);}
/* ------------------------------------ */
typedef struct
{
double i; double j;
}vector2d, *Pvector2d;
/* ------------------------------------ */
vector2d i_vector2d(
double i, double j
)
{
vector2d v = {i,j};
return (v);}
/* ------------------------------------ */
typedef struct
{
double i; double j; double k;
}vector3d, *Pvector3d;
/* ------------------------------------ */
vector3d i_vector3d(
double i, double j, double k
)
{
vector3d v = {i,j,k};
return (v);}
Fichiers h : xfx x
Préambule
[modifier | modifier le wikicode]Installez ce fichier dans votre répertoire de travail.
xfx_x.hDérivation de fonctions df(x)/dx |
|---|
/* ------------------------------------ */
/* Save as : xfx_x.h */
/* ------------------------------------
f'(a) = f(a+h) - f(a-h)
-------------
2h
---------------------------------- */
double fx_x(
double (*P_f)(double x),
double a,
double h
)
{
return( ( ((*P_f)(a+h))-((*P_f)(a-h)) ) / (2.*h) );
}
/* ------------------------------------
f''(a) = f(a+h) - 2 f(a) + f(a-h)
----------------------
h**2
---------------------------------- */
double fx_xx(
double (*P_f)(double x),
double a,
double h
)
{
return( (((*P_f)(a+h))-2*((*P_f)(a))+((*P_f)(a-h))) / (h*h) );
}
Fichiers h : xfxy x
Préambule
[modifier | modifier le wikicode]Installez ce fichier dans votre répertoire de travail.
xfxy_x.hDérivation de fonction df(x,y)/dx |
|---|
/* ------------------------------------ */
/* Save as : xfxy_x.h */
/* ------------------------------------ */
double fxy_x(
double (*P_f)(double x, double y),
double h,
point2d p
)
{
double tplsh;
double tmnsh;
tplsh = ((*P_f)(p.x+h,p.y));
tmnsh = ((*P_f)(p.x-h,p.y));
return(( tplsh-tmnsh)/(2.*h) );
}
/* ------------------------------------ */
double fxy_y(
double (*P_f)(double x, double y),
double h,
point2d p
)
{
double tplsh;
double tmnsh;
tplsh = ((*P_f)(p.x,p.y+h));
tmnsh = ((*P_f)(p.x,p.y-h));
return(( tplsh-tmnsh)/(2.*h) );
}
/* ------------------------------------ */
double fxy_xx(
double (*P_f)(double x, double y),
double h,
point2d p
)
{
double t;
double tplsh;
double tmnsh;
t = ((*P_f)(p.x , p.y));
tplsh = ((*P_f)(p.x+h, p.y));
tmnsh = ((*P_f)(p.x-h, p.y));
return( (tplsh-2*t+tmnsh)/(h*h) );
}
/* ------------------------------------ */
double fxy_yy(
double (*P_f)(double x, double y),
double h,
point2d p
)
{
double t;
double tplsh;
double tmnsh;
t = ((*P_f)(p.x, p.y ));
tplsh = ((*P_f)(p.x, p.y+h));
tmnsh = ((*P_f)(p.x, p.y-h));
return( (tplsh-2*t+tmnsh)/(h*h) );
}
Fichiers h : xfxyz x
Préambule
[modifier | modifier le wikicode]Installez ce fichier dans votre répertoire de travail.
xfxyz_x.hDérivation de fonction df(x,y,z)/dx |
|---|
/* ------------------------------------ */
/* Save as : xfxyz_x.h */
/* ------------------------------------ */
double fxyz_x(
double (*P_f)(double x, double y, double z),
double h,
point3d p
)
{
double tplsh;
double tmnsh;
tplsh = ((*P_f)(p.x+h,p.y,p.z));
tmnsh = ((*P_f)(p.x-h,p.y,p.z));
return(( tplsh-tmnsh)/(2.*h) );
}
/* ------------------------------------ */
double fxyz_y(
double (*P_f)(double x, double y, double z),
double h,
point3d p
)
{
double tplsh;
double tmnsh;
tplsh = ((*P_f)(p.x,p.y+h,p.z));
tmnsh = ((*P_f)(p.x,p.y-h,p.z));
return(( tplsh-tmnsh)/(2.*h) );
}
/* ------------------------------------ */
double fxyz_z(
double (*P_f)(double x, double y, double z),
double h,
point3d p
)
{
double tplsh;
double tmnsh;
tplsh = ((*P_f)(p.x,p.y,p.z+h));
tmnsh = ((*P_f)(p.x,p.y,p.z-h));
return(( tplsh-tmnsh)/(2.*h) );
}
Application : Fonction Heaviside
Préambule
[modifier | modifier le wikicode]La fonction Heaviside dans Wikipedia.
La fonction Heaviside
[modifier | modifier le wikicode]
Présentation
[modifier | modifier le wikicode]Voici une possibilité pour la déclaration de la fonction Heaviside.
/* ------------------------------------ */
double H(
double x)
{
if(x>0.)return(1.);
else return(0.);
}
/* ------------------------------------ */
N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
c01.cLa fonction |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
/* ------------------------------------ */
int main(void)
{
printf(" H : if(x>0) 1 else 0 \n");
G_plot(i_WGnuplot(-2.,20.,-1.,2.),
i_time(-2.,20.,0.001),
H);
printf("\n load \"a_main.plt\" with gnuplot."
"\n Press return to continue ");
getchar();
return 0;
}
Une application
[modifier | modifier le wikicode]Nous allons simplement appeler la fonction Heaviside dans une boucle for.
Pour obtenir une somme : Sum((-1)^n*H(x-n),n=0..20)
c02.cUne application |
|---|
/* ------------------------------------ */
/* Save as : c02.c */
/* ------------------------------------ */
#include "x_ahfile.h"
/* ------------------------------------ */
double v(
double x)
{
double n=0, r=0;
for(;n<20;++n) r += pow(-1,n)*H(x-n);
return(r);
}
char veq[] = "Sum((-1)^n*H(x-n),n=0..20)";
/* ------------------------------------ */
int main(void)
{
printf(" H : if(x>0) 1 else 0 \n\n"
" v : x-> %s \n\n",veq);
G_plot(i_WGnuplot(-2.,20.,-1.,2.),
i_time(-2.,20.,0.001),
v);
printf("\n\n load \"a_main.plt\" with gnuplot."
"\n\n Press return to continue ");
getchar();
return 0;
}
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xplt.h"
/* ------------------------------------ */
#include "fh.h"
#include "g_f.h"
fh.hLa fonction Heaviside |
|---|
/* ------------------------------------ */
/* Save as : fh.h */
/* ------------------------------------ */
double H(
double x)
{
if(x>0.)return(1.);
else return(0.);
}
/* ------------------------------------ */
g_f.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : g_f.h */
/* ------------------------------------ */
void G_plot(
W_Ctrl W,
t_Ctrl T,
double (*P_f1)(double x)
)
{
FILE *fp;
double t;
fp = fopen("a_main.plt","w");
fprintf(fp,"# Gnuplot file : load \"a_main.plt\" \n\n"
" set zeroaxis lt 8\n"
" set grid\n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f] \\\n"
" \"data\" with line lt 3\n"
" reset",
W.xmini,W.xmaxi,W.ymini,W.ymaxi);
fclose(fp);
fp = fopen("data","w");
for(t=T.mini; t<=T.maxi; t+=T.step)
fprintf(fp," %6.3f %6.3f\n",t,(*P_f1)(t));
fclose(fp);
}
Conclusion
[modifier | modifier le wikicode]Certains résultats sont vraiment surprenants en associant la fonction heaviside et la fonction sinus.
Application : Tangente
Préambule
[modifier | modifier le wikicode]La tangente dans Wikipedia.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Dessiner la tangente
[modifier | modifier le wikicode]c01.cDessiner la tangente |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "f2.h"
/* ------------------------------------ */
int main(void)
{
double c = 2;
printf(" f : x-> %s\n\n", feq);
printf(" f': x-> %s\n\n\n",Dfeq);
printf(" With c = %0.3f, the equation of the tangent is :",c);
printf("\n\n y = f'(c) (x-c) + f(c) =");
eq_Tan(c,f,Df);
G_Tan(i_WGnuplot(-7, 7,-2,2),
c,
feq,
f,
Df);
printf(" load \"a_main.plt\" with gnuplot.\n\n"
" Press return to continue");
getchar();
return 0;
}
Le résultat.
f : x-> cos(x) f': x-> (-sin(x)) . With c = 2.000, the equation of the tangent is : . y = f'(c) (x-c) + f(c) = -0.909*x +1.402 . load "a_main.plt" with gnuplot.
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xplt.h"
/* ------------------------------------ */
#include "kg_tan.h"
#include "k_tan.h"
f2.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : f2.h */
/* ------------ f --------------------- */
double f(
double x)
{
return( cos(x));
}
char feq[] = " cos(x)";
/* ------------ f' ------------------- */
double Df(
double x)
{
return( (-sin(x)) );
}
char Dfeq[] = " (-sin(x)) ";
k_tan.hEquation de la tangente |
|---|
/* ------------------------------------ */
/* Save as : k_tan.h */
/* ------------------------------------
y = ax + b [P(xp,yp);(y-yp)=a(x-xp)]
a = f'(x)
b = y - ax
b = y - f'(x)x
b = f(x) - f'(x)x
x=c
a = f'(c)
b = f(c) - f'(c)c
------------------------------------ */
void eq_Tan(
double c,
double (*P_f)(double x),
double (*PDf)(double x)
)
{
printf(" %0.3f*x %+0.3f\n\n\n",
(*PDf)(c), (*P_f)(c) - (*PDf)(c)*c );
}
/* ------------------------------------ */
void eq_Tanf(
FILE *fp,
double c,
double (*P_f)(double x),
double (*PDf)(double x)
)
{
fprintf(fp," %0.3f*x %+0.3f\n\n\n",
(*PDf)(c), (*P_f)(c) - (*PDf)(c)*c );
}
kg_tan.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_tan.h */
/* ------------------------------------ */
void G_Tan(
W_Ctrl w,
double c,
char fEQ[],
double (*P_f)(double x),
double (*PDf)(double x)
)
{
FILE *fp = fopen("a_main.plt","w");
fprintf(fp,"# Gnuplot file : load \"a_main.plt\" \n\n"
" set zeroaxis\n\n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f] \\\n"
" %s, \\\n"
" %0.6f*x %+0.6f lw 3\n"
" reset",
w.xmini,w.xmaxi,w.ymini,w.ymaxi,
fEQ,
(*PDf)(c),
(-(*PDf)(c)* c + (*P_f)(c)));
fclose(fp);
}
Exemple avec la sortie dans le fichier "a_out.txt"
[modifier | modifier le wikicode]c01f.cSortie dans un fichier |
|---|
/* ------------------------------------ */
/* Save as : c01f.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "f2.h"
/* ------------------------------------ */
int main(void)
{
FILE *fp = fopen("a_out.txt","w");
double c = 0;
fprintf(fp," f : x-> %s\n\n", feq);
fprintf(fp," f': x-> %s\n\n\n",Dfeq);
fprintf(fp," With c = %0.3f, the equation of the tangent is :",c);
fprintf(fp,"\n\n y = f'(c) (x-c) + f(c) =");
eq_Tanf(fp,c,f,Df);
G_Tan(i_WGnuplot(-7, 7,-2,2),c,feq,f,Df);
fprintf(fp," load \"a_main.plt\" with gnuplot.");
fclose(fp);
printf(" Read \"a_out.txt\".\n"
" Press return to continue");
getchar();
return 0;
}
Le résultat dans le fichiers "a_out.txt"
f : x-> cos(x) f': x-> (-sin(x)) . With c = 0.000, the equation of the tangent is : . y = f'(c) (x-c) + f(c) = -0.000*x +1.000 . load "a_main.plt" with gnuplot.
| Résultat dans gnuplot |
|---|

|
Application : Champ de tangentes
Préambule
[modifier | modifier le wikicode]La tangente dans Wikipedia.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Dessiner un champ de tangentes 1
[modifier | modifier le wikicode]c01.cDessiner la tangente |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "f1.h"
/* ------------------------------------ */
int main(void)
{
printf(" f : x-> %s \n", feq);
printf(" f': x-> %s\n\n",Dfeq);
printf(" The equation of the tangent is : \n\n");
printf(" y = f'(c) (x-c) + f(c) \n\n");
G_TanA(i_WGnuplot(-10,10,-400,300),
i_time(-24.,24.,1),
feq,
f,
Df);
printf(" load \"a_main.plt\" with gnuplot. \n\n"
" Press return to continue");
getchar();
return 0;
}
| Résultat dans gnuplot |
|---|

|
Dessiner un champ de tangentes 2
[modifier | modifier le wikicode]c02.cDessiner la tangente |
|---|
/* ------------------------------------ */
/* Save as : c02.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "f2.h"
/* ------------------------------------ */
int main(void)
{
printf(" f : x-> %s \n", feq);
printf(" f': x-> %s\n\n",Dfeq);
printf(" The equation of the tangent is : \n\n");
printf(" y = f'(c) (x-c) + f(c) \n\n");
G_TanA(i_WGnuplot(-2*PI, 2*PI,-4,8),
i_time(-2.,2.,.1),
feq,
f,
Df);
printf(" load \"a_main.plt\" with gnuplot. \n\n"
" Press return to continue");
getchar();
return 0;
}
| Résultat dans gnuplot |
|---|

|
Dessiner un champ de normales 3
[modifier | modifier le wikicode]c03.cDessiner un champ de normales 3 |
|---|
/* ------------------------------------ */
/* Save as : c03.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "f3.h"
/* ------------------------------------ */
int main(void)
{
printf(" f : x-> %s \n", feq);
printf(" f': x-> %s\n\n",Dfeq);
printf(" The equation of the tangent is : \n\n");
printf(" y = f'(c) (x-c) + f(c) \n\n");
G_NorA(i_WGnuplot(-2,2,-1,2.4),
i_time(-2,2,.05),
feq,
f,
Df);
printf(" load \"a_main.plt\" with gnuplot. \n\n"
" Press return to continue");
getchar();
return 0;
}
| Résultat dans gnuplot |
|---|

|
Dessiner un champ de normales 4
[modifier | modifier le wikicode]c04.cDessiner un champ de normales 4 |
|---|
/* ------------------------------------ */
/* Save as : c04.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "f1.h"
/* ------------------------------------ */
int main(void)
{
printf(" f : x-> %s \n", feq);
printf(" f': x-> %s\n\n",Dfeq);
printf(" The equation of the tangent is : \n\n");
printf(" y = f'(c) (x-c) + f(c) \n\n");
G_NorA(i_WGnuplot(-2, 2,-1.7,1.7),
i_time(-2.,2.,.05),
feq,
f,
Df);
printf(" load \"a_main.plt\" with gnuplot. \n\n"
" Press return to continue");
getchar();
return 0;
}
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xplt.h"
#include "xdef.h"
/* ------------------------------------ */
#include "kg_tan.h"
f1.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : f1.h */
/* ----------- f ---------------------- */
double f(
double x)
{
return( 3*x*x-2*x-5);
}
char feq[] = " 3*x**2-2*x-5";
/* ------------ f' --------------------- */
double Df(
double x)
{
return( 6*x-2 );
}
char Dfeq[] = " 6*x-2 ";
f2.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : f2.h */
/* ----------- f ---------------------- */
double f(
double x)
{
return( cos(x));
}
char feq[] = " cos(x)";
/* ------------ f' --------------------- */
double Df(
double x)
{
return( (-sin(x)) );
}
char Dfeq[] = " (-sin(x)) ";
f3.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : f3.h */
/* ----------- f ---------------------- */
double f(
double x)
{
return( x*x);
}
char feq[] = " x**2";
/* ------------ f' --------------------- */
double Df(
double x)
{
return( 2*x );
}
char Dfeq[] = " 2*x ";
kg_tan.hLes fonctions graphiques |
|---|
/* ------------------------------------ */
/* Save as : kg_tan.h */
/* ------------------------------------ */
void G_TanA(
W_Ctrl w,
t_Ctrl Pic,
char fEQ[],
double (*P_f)(double x),
double (*PDf)(double x)
)
{
FILE *fp = fopen("a_main.plt","w");
double p = Pic.mini;
fprintf(fp,"# Gnuplot file : load \"a_main.plt\"\n"
" set zeroaxis\n"
" unset key\n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f] \\\n"
" %s, \\\n",
w.xmini,w.xmaxi,w.ymini,w.ymaxi,
fEQ);
for(;p<Pic.maxi;p+=Pic.step)
fprintf(fp," %0.6f*x %+0.6f, \\\n",
(*PDf)(p), (-(*PDf)(p)*p+(*P_f)(p)) );
fprintf(fp," %0.6f*x %+0.6f\n",
(*PDf)(p), (-(*PDf)(p)*p+(*P_f)(p)) );
fprintf(fp," reset");
fclose(fp);
}
/* ------------------------------------ */
void G_NorA(
W_Ctrl w,
t_Ctrl Pic,
char fEQ[],
double (*P_f)(double x),
double (*PDf)(double x)
)
{
FILE *fp = fopen("a_main.plt","w");
double p = Pic.mini;
fprintf(fp,"# Gnuplot file : load \"a_main.plt\"\n"
" set size ratio -1\n"
" set zeroaxis\n\n"
" unset key\n\n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f] \\\n"
" %s, \\\n",
w.xmini,w.xmaxi,w.ymini,w.ymaxi,
fEQ);
for(;p<Pic.maxi;p+=Pic.step)
fprintf(fp," %0.6f*x %+0.6f, \\\n",
(-1/(*PDf)(p)), (1/(*PDf)(p)*p+(*P_f)(p)) );
fprintf(fp," %0.6f*x %+0.6f\n",
(-1/(*PDf)(p)), (1/(*PDf)(p)*p+(*P_f)(p)) );
fprintf(fp," reset");
fclose(fp);
}
Application : Tangente et axes x-y
Préambule
[modifier | modifier le wikicode]La tangente dans Wikipedia.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Dessiner
[modifier | modifier le wikicode]c01.cDessiner les points d'intersection de la tangente avec les axes x/y |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "f2.h"
/* ------------------------------------ */
int main(void)
{
double c = 1;
printf(" f : x-> %s \n", feq);
printf(" Df : x-> %s\n\n",Dfeq);
printf(" With c = %0.3f, the equation of"
" the tangent is :\n\n"
" y = Df(c) (x-c) + f(c) = ",c);
eq_Tan(c,f,Df);
printf(" Find at c = %0.3f\n\n"
" the intersection points of the"
" tangent with the x-y axis.\n\n",c);
printf(" P(%5.3f, %5.3f) P(c, f(c))\n",
c,f(c));
printf(" A(%5.3f, 0.000) A(c-f(c)/Df(c), 0)\n",
c-(f(c))/(Df(c)));
printf(" B( 0, %5.3f) B(0, f(c)-c Df(c))\n",
f(c)-((Df(c))*c));
G_Tan_xy(i_WGnuplot(-7,7,-2,2),
c,
feq,
f,Df);
printf(" load \"a_main.plt\" with gnuplot. \n\n"
" Press return to continue");
getchar();
return 0;
}
Le résultat.
f : x-> cos(x)
Df : x-> (-sin(x))
.
With c = 1.000, the equation of the tangent is :
.
y = Df(c) (x-c) + f(c) = -0.841*x +1.382
.
.
Find at c = 1.000
.
the intersection points of the tangent with the x-y axis.
.
P(1.000, 0.540) P(c, f(c))
A(1.642, 0.000) A(c-f(c)/Df(c), 0)
B( 0, 1.382) B(0, f(c)-c Df(c))
.
load "a_main.plt" with gnuplot.
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xplt.h"
/* ------------------------------------ */
#include "kg_tan.h"
#include "k_tan.h"
f2.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : f2.h */
/* ------------ f --------------------- */
double f(
double x)
{
return( cos(x));
}
char feq[] = " cos(x)";
/* ------------ f' ------------------- */
double Df(
double x)
{
return( (-sin(x)) );
}
char Dfeq[] = " (-sin(x)) ";
k_tan.hEquation de la tangente |
|---|
/* ------------------------------------ */
/* Save as : k_tan.h */
/* ------------------------------------
y = ax + b [P(xp,yp);(y-yp)=a(x-xp)]
a = f'(x)
b = y - ax
b = y - f'(x)x
b = f(x) - f'(x)x
x=c
a = f'(c)
b = f(c) - f'(c)c
------------------------------------ */
void eq_Tan(
double c,
double (*P_f)(double x),
double (*PDf)(double x)
)
{
printf(" %0.3f*x %+0.3f\n\n\n",
(*PDf)(c), (*P_f)(c) - (*PDf)(c)*c );
}
/* ------------------------------------ */
void eq_Tanf(
FILE *fp,
double c,
double (*P_f)(double x),
double (*PDf)(double x)
)
{
fprintf(fp," %0.3f*x %+0.3f\n\n\n",
(*PDf)(c), (*P_f)(c) - (*PDf)(c)*c );
}
kg_tan.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_tan.h */
/* ------------------------------------ */
void G_Tan_xy(
W_Ctrl w,
double c,
char fEQ[],
double (*P_f)(double x),
double (*PDf)(double x)
)
{
FILE *fp;
fp = fopen("a_main.plt","w");
fprintf(fp,"# Gnuplot file : load \"a_main.plt\" \n\n"
" set zeroaxis \n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f] "
" %s,\\\n"
" %0.6f*x %+0.6f,\\\n"
" \"a_p.plt\" lt 1,\\\n"
" \"a_a.plt\" lt 1,\\\n"
" \"a_b.plt\" lt 1\n"
" reset",
w.xmini,w.xmaxi,w.ymini,w.ymaxi,
fEQ,
((*PDf)(c)), (-((*PDf)(c))*c+((*P_f)(c))) );
fclose(fp);
fp = fopen( "a_p.plt","w");
fprintf(fp," %0.6f %0.6f",
c, ((*P_f)(c)));
fclose(fp);
fp = fopen( "a_a.plt","w");
fprintf(fp," %0.6f 0.",
c-((*P_f)(c))/((*PDf)(c)));
fclose(fp);
fp = fopen( "a_b.plt","w");
fprintf(fp," 0. %0.6f",
((*P_f)(c))-(((*PDf)(c))*c));
fclose(fp);
}
Un exemple avec la fonction sin.
| Résultat dans gnuplot |
|---|

|
Application : Tangente de P à l'axes des x
Préambule
[modifier | modifier le wikicode]La tangente dans Wikipedia.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Dessiner
[modifier | modifier le wikicode]c01.cCalculer la longeur de P(c,f(c) à l'axe de x. |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "f2.h"
/* ------------------------------------ */
int main(void)
{
double c = .5;
printf(" f : x-> %s \n", feq);
printf(" Df: x-> %s\n\n",Dfeq);
printf(" With c = %0.3f, the equation of the tangent is :\n\n"
" y = Df(c) (x-c) + f(c) = ",c);
eq_Tan(c,f,Df);
printf(" Find PA, the length of the tangent from P to the x axis.\n\n");
printf(" P(%5.3f, %5.3f) P(c, f(c)) \n",
c,f(c));
printf(" A(%5.3f, 0.000) A(c-f(c)/Df(c), 0)\n\n\n",
c-(f(c)/Df(c)));
printf(" PA = sqrt(f(c)**2*(1 +(1/Df(c)**2))) = %6.3f\n\n\n",
sqrt(pow(f(c),2)*(1+(1/pow(Df(c),2)))));
G_TanPx (i_WGnuplot(-2,4,-1,2),
c,
feq,f,Df);
printf(" load \"a_main.plt\" with gnuplot. \n\n"
" Press return to continue");
getchar();
return 0;
}
Le résultat.
f : x-> cos(x)
Df: x-> (-sin(x))
.
With c = 0.500, the equation of the tangent is :
.
y = Df(c) (x-c) + f(c) = -0.479*x +1.117
.
Find PA, the length of the tangent from P to the x axis.
.
P(0.500, 0.878) P(c, f(c))
A(2.330, 0.000) A(c-f(c)/Df(c), 0)
.
PA = sqrt(f(c)**2*(1 +(1/Df(c)**2))) = 2.030
.
load "a_main.plt" with gnuplot.
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xplt.h"
/* ------------------------------------ */
#include "kg_tan.h"
#include "k_tan.h"
f2.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : f2.h */
/* ------------ f --------------------- */
double f(
double x)
{
return( cos(x));
}
char feq[] = " cos(x)";
/* ------------ f' ------------------- */
double Df(
double x)
{
return( (-sin(x)) );
}
char Dfeq[] = " (-sin(x)) ";
k_tan.hEquation de la tangente |
|---|
/* ------------------------------------ */
/* Save as : k_tan.h */
/* ------------------------------------
y = ax + b [P(xp,yp);(y-yp)=a(x-xp)]
a = f'(x)
b = y - ax
b = y - f'(x)x
b = f(x) - f'(x)x
x=c
a = f'(c)
b = f(c) - f'(c)c
------------------------------------ */
void eq_Tan(
double c,
double (*P_f)(double x),
double (*PDf)(double x)
)
{
printf(" %0.3f*x %+0.3f\n\n\n",
(*PDf)(c), (*P_f)(c) - (*PDf)(c)*c );
}
/* ------------------------------------ */
void eq_Tanf(
FILE *fp,
double c,
double (*P_f)(double x),
double (*PDf)(double x)
)
{
fprintf(fp," %0.3f*x %+0.3f\n\n\n",
(*PDf)(c), (*P_f)(c) - (*PDf)(c)*c );
}
kg_tan.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_tan.h */
/* ------------------------------------ */
void G_TanPx(
W_Ctrl w,
double c,
char fEQ[],
double (*P_f)(double x),
double (*PDf)(double x)
)
{
FILE *fp;
fp = fopen("a_main.plt","w");
fprintf(fp,"# Gnuplot file : load \"a_main.plt\" \n\n"
" set zeroaxis \n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f] \\\n"
" %s,\\\n"
" %0.6f*x %+0.6f,\\\n"
" \"a_xaxe.plt\" with linesp lt 3 \n"
" reset",
w.xmini,w.xmaxi,w.ymini,w.ymaxi,
fEQ,
(*PDf)(c),-(*PDf)(c)*c+(*P_f)(c) );
fclose(fp);
fp = fopen("a_xaxe.plt","w");
fprintf(fp," %0.6f %0.6f\n",c,(*P_f)(c) );
fprintf(fp," %0.6f 0. \n",
c-((*P_f)(c)/(*PDf)(c)));
fclose(fp);
}
Même exemple avec la fonction sin.
| Résultat dans gnuplot |
|---|

|
Application : Tangente de P à l'axes des y
Préambule
[modifier | modifier le wikicode]La tangente dans Wikipedia.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Dessiner
[modifier | modifier le wikicode]c01.cCalculer la longeur de P(c,f(c) à l'axe de y. |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "f2.h"
/* ------------------------------------ */
int main(void)
{
double c = .5;
printf(" f : x-> %s \n", feq);
printf(" Df: x-> %s\n\n",Dfeq);
printf(" With c = %0.3f, the equation of the tangent is :\n\n"
" y = Df(c) (x-c) + f(c) = ",c);
eq_Tan(c,f,Df);
printf(" Find PB, the length of the tangent from P to the y axis.\n\n");
printf(" P(%5.3f, %5.3f) P(c, f(c)) \n",
c, f(c));
printf(" B(0.000, %5.3f) B(0, f(c)-c*Df(c))\n\n",
f(c)-c*Df(c));
printf(" PB = sqrt(c**2*(1+Df(c)**2)) = %6.3f \n\n",
sqrt(c*c*(1+pow(Df(c),2))));
G_TanPy (i_WGnuplot(-2,4,-1,2),
c,
feq,f,Df);
printf(" load \"a_main.plt\" with gnuplot. \n\n"
" Press return to continue");
getchar();
return 0;
}
Le résultat.
f : x-> cos(x)
Df: x-> (-sin(x))
.
With c = 0.500, the equation of the tangent is :
.
y = Df(c) (x-c) + f(c) = -0.479*x +1.117
.
Find PB, the length of the tangent from P to the y axis.
.
P(0.500, 0.878) P(c, f(c))
B(0.000, 1.117) B(0, f(c)-c*Df(c))
.
PB = sqrt(c**2*(1+Df(c)**2)) = 0.554
.
load "a_main.plt" with gnuplot.
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xplt.h"
/* ------------------------------------ */
#include "kg_tan.h"
#include "k_tan.h"
f2.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : f2.h */
/* ------------ f --------------------- */
double f(
double x)
{
return( cos(x));
}
char feq[] = " cos(x)";
/* ------------ f' ------------------- */
double Df(
double x)
{
return( (-sin(x)) );
}
char Dfeq[] = " (-sin(x)) ";
k_tan.hEquation de la tangente |
|---|
/* ------------------------------------ */
/* Save as : k_tan.h */
/* ------------------------------------
y = ax + b [P(xp,yp);(y-yp)=a(x-xp)]
a = f'(x)
b = y - ax
b = y - f'(x)x
b = f(x) - f'(x)x
x=c
a = f'(c)
b = f(c) - f'(c)c
------------------------------------ */
void eq_Tan(
double c,
double (*P_f)(double x),
double (*PDf)(double x)
)
{
printf(" %0.3f*x %+0.3f\n\n\n",
(*PDf)(c), (*P_f)(c) - (*PDf)(c)*c );
}
/* ------------------------------------ */
void eq_Tanf(
FILE *fp,
double c,
double (*P_f)(double x),
double (*PDf)(double x)
)
{
fprintf(fp," %0.3f*x %+0.3f\n\n\n",
(*PDf)(c), (*P_f)(c) - (*PDf)(c)*c );
}
kg_tan.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_tan.h */
/* ------------------------------------ */
void G_TanPy(
W_Ctrl w,
double c,
char fEQ[],
double (*P_f)(double x),
double (*PDf)(double x)
)
{
FILE *fp;
fp = fopen("a_main.plt","w");
fprintf(fp," set zeroaxis\n\n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f] \\\n"
" %s, \\\n"
" %0.6f*x %+0.6f, \\\n"
" \"a_yaxe.plt\" with linesp lt 3\n"
" reset",
w.xmini,w.xmaxi,w.ymini,w.ymaxi,
fEQ,
((*PDf)(c)) ,(-((*PDf)(c))* c + ((*P_f)(c))));
fclose(fp);
fp = fopen("a_yaxe.plt","w");
fprintf(fp," %0.5f %0.5f\n",c,((*P_f)(c)));
fprintf(fp," 0.000 %0.5f",
((*P_f)(c))-(((*PDf)(c))*c));
fclose(fp);
}
Même exemple avec la fonction sin.
| Résultat dans gnuplot |
|---|

|
Application : Sous tangente
Préambule
[modifier | modifier le wikicode]La tangente dans Wikipedia.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Dessiner
[modifier | modifier le wikicode]c01.cCalculer la longeur de la sous tangente. |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "f2.h"
/* ------------------------------------ */
int main(void)
{
double c = .5;
printf(" f : x-> %s \n", feq);
printf(" Df: x-> %s\n\n",Dfeq);
printf(" With c = %0.3f, the equation of the tangent is :\n\n"
" y = Df(c) (x-c) + f(c) = ",c);
eq_Tan(c,f,Df);
printf(" Find AM, the length of the under tangent.\n\n");
printf(" P(%5.3f, %5.3f) P(c, f(c)) \n",
c, f(c));
printf(" A(%5.3f, 0.000) A(c-f(c)/Df(c), 0)\n",
c-(f(c)/Df(c)));
printf(" M(%5.3f, 0.000) M( c, 0)\n\n\n", c);
printf(" AM = sqrt((f(c)**2)/(Df(c)**2)) = %6.3f\n\n\n",
sqrt(f(c)*f(c)*(1/(Df(c)*Df(c)))));
G_TanxM (i_WGnuplot(-2,4,-1,2),
c,
feq,f,Df);
printf(" load \"a_main.plt\" with gnuplot. \n\n"
" Press return to continue");
getchar();
return 0;
}
Le résultat.
f : x-> sin(x)
Df: x-> (cos(x))
.
With c = 0.500, the equation of the tangent is :
.
y = Df(c) (x-c) + f(c) = 0.878*x +0.041
.
Find AM, the length of the under tangent.
.
P(0.500, 0.479) P(c, f(c))
A(-0.046, 0.000) A(c-f(c)/Df(c), 0)
M(0.500, 0.000) M( c, 0)
.
AM = sqrt((f(c)**2)/(Df(c)**2)) = 0.546
.
load "a_main.plt" with gnuplot.
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xplt.h"
/* ------------------------------------ */
#include "kg_tan.h"
#include "k_tan.h"
f2.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : f2.h */
/* ------------ f --------------------- */
double f(
double x)
{
return( cos(x));
}
char feq[] = " cos(x)";
/* ------------ f' ------------------- */
double Df(
double x)
{
return( (-sin(x)) );
}
char Dfeq[] = " (-sin(x)) ";
k_tan.hEquation de la tangente |
|---|
/* ------------------------------------ */
/* Save as : k_tan.h */
/* ------------------------------------
y = ax + b [P(xp,yp);(y-yp)=a(x-xp)]
a = f'(x)
b = y - ax
b = y - f'(x)x
b = f(x) - f'(x)x
x=c
a = f'(c)
b = f(c) - f'(c)c
------------------------------------ */
void eq_Tan(
double c,
double (*P_f)(double x),
double (*PDf)(double x)
)
{
printf(" %0.3f*x %+0.3f\n\n\n",
(*PDf)(c), (*P_f)(c) - (*PDf)(c)*c );
}
/* ------------------------------------ */
void eq_Tanf(
FILE *fp,
double c,
double (*P_f)(double x),
double (*PDf)(double x)
)
{
fprintf(fp," %0.3f*x %+0.3f\n\n\n",
(*PDf)(c), (*P_f)(c) - (*PDf)(c)*c );
}
kg_tan.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_tan.h */
/* ------------------------------------ */
void G_TanxM(
W_Ctrl w,
double c,
char fEQ[],
double (*P_f)(double x),
double (*PDf)(double x)
)
{
FILE *fp;
fp = fopen("a_main.plt","w");
fprintf(fp," set zeroaxis \n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f]\\\n"
" %s,\\\n"
" %0.6f*x %+0.6f,\\\n"
" \"a_px.plt\" with linesp lt 3,\\\n"
" \"a_am.plt\" with linesp lt 4 \n"
" reset",
w.xmini,w.xmaxi,w.ymini,w.ymaxi,fEQ,
((*PDf)(c)),(-(*PDf)(c)*c+(*P_f)(c)));
fclose(fp);
fp = fopen("a_px.plt", "w");
fprintf(fp," %0.6f %0.6f\n", c,((*P_f)(c)));
fprintf(fp," %0.6f 0.",
c-(((*P_f)(c))/((*PDf)(c))) );
fclose(fp);
fp = fopen("a_am.plt", "w");
fprintf(fp," %0.6f 0.\n",
c-(((*P_f)(c))/((*PDf)(c))));
fprintf(fp," %0.6f 0.", c);
fclose(fp);
}
Même exemple avec la fonction sin.
| Résultat dans gnuplot |
|---|

|
Application : Cercle de courbure
Préambule
[modifier | modifier le wikicode]Le cercle de courbure dans Wikipedia.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Dessiner
[modifier | modifier le wikicode]c01.cDessiner un cercle de courbure pour une fonction f(x). |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "fb.h"
/* ------------------------------------ */
int main(void)
{
double x = 0.;
double e = .001;
char Name[FILENAME_MAX] = "a_circle.plt";
circle(Name,
1./K_y_2d(f,x,e),
h_y_2d(f,x,e),
k_y_2d(f,x,e));
G_C_2d(i_WGnuplot(-4.,4.,-2.,2.),
f,x,e,
feq);
clrscrn();
printf(" If a smooth curve C is the graph of y = f(x),\n"
" then the curvature K at P(x,y) is\n\n\n"
" K = |y''| / [1 + y'^2]^(3/2) \n\n\n"
" If P(x,y) is a point on the graph "
"of y = f(x) \n"
" at which K != 0. The point M(h,k)"
" is the center\n"
" of the cuvature for P if \n\n\n"
" h = x - y'[1 + y'^2] / y'' \n"
" k = y + [1 + y'^2] / y'' \n\n\n"
" The radius is r = 1/K \n\n\n"
" Open the file \"a_main.plt\" with Gnuplot.\n\n");
printf("\n Press return to continue");
getchar();
return 0;
}
Le résultat.
| Résultat dans gnuplot |
|---|

|
| Résultat dans gnuplot |
|---|

|
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xplt.h"
#include "xfx_x.h"
/* ------------------------------------ */
#include "kradius.h"
#include "kg_c.h"
#include "kcircle.h"
kradius.hCoordonnées du cercle |
|---|
/* ------------------------------------ */
/* Save as : kradius.h */
/* ------------------------------------ */
double K_y_2d(
double (*P_f)(double x),
double x,
double e
)
{
double a = fx_x((*P_f),x,e);
return(fabs(fx_xx((*P_f),x,e))
/
pow(1+a*a,3./2.));
}
/* ------------------------------------ */
double h_y_2d(
double (*P_f)(double x),
double x,
double e
)
{
double a = fx_x((*P_f),x,e);
return(x - ( ( a*(1+a*a) )
/
fx_xx((*P_f),x,e)));
}
/* ------------------------------------ */
double k_y_2d(
double (*P_f)(double x),
double x,
double e
)
{
double a = fx_x((*P_f),x,e);
return((*P_f)(x) + ( (1+a*a)
/
fx_xx((*P_f),x,e)));
}
fb.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : fb.h */
/* ------------------------------------ */
double f(
double x)
{
return( cos(x));
}
char feq[] = "cos(x)";
kg_c.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_c.h */
/* ------------------------------------ */
void G_C_2d(
W_Ctrl W,
double (*P_f)(double x),
double x,
double e,
char feq[]
)
{
FILE *fp;
fp = fopen("a_main.plt","w");
fprintf(fp," reset\n"
" set zeroaxis lt 8\n"
" set size ratio -1\n"
" set grid\n\n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f]\\\n"
" \"a_radius.plt\" with linespoints,\\\n"
" \"a_circle.plt\" with line,\\\n"
" %s with line\n",
W.xmini,W.xmaxi,W.ymini,W.ymaxi,feq);
fclose(fp);
fp = fopen("a_radius.plt","w");
fprintf(fp," %6.5f %6.5f\n",h_y_2d((*P_f),x,e),
k_y_2d((*P_f),x,e));
fprintf(fp," %6.5f %6.5f\n",x,(*P_f)(x));
fclose(fp);
Pause();
}
kcircle.hLe cercle |
|---|
/* ------------------------------------ */
/* Save as : kcircle.h */
/* ------------------------------------ */
void circle(
char Name[FILENAME_MAX],
double r,
double x,
double y
)
{
FILE *fp = fopen(Name,"w");
double t = 0.;
for(;t<2.01*PI;t+=.1)
fprintf(fp," %6.5f %6.5f\n",r*cos(t)+x,r*sin(t)+y);
fclose(fp);
}
Application : Méthode de Newton
Préambule
[modifier | modifier le wikicode]Méthode de Newton dansWikipedia.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Dessiner
[modifier | modifier le wikicode]c01.cCalculer le point d'intersection entre g et h. |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "f2.h"
/* ------------------------------------ */
int main(void)
{
int n = 5;
double FirstA = 0.5;
clrscrn();
printf(" Use Newton's method to approximate"
" the intersection point of :\n\n");
printf(" g : x-> %s\n\n", geq);
printf(" and\n\n");
printf(" h : x-> %s\n\n", heq);
G_gh(i_WGnuplot(-4,4,-4,4), geq,heq);
printf(" To see the graphs of g and h, open the"
" file \"a_main.plt\" with Gnuplot.\n\n"
" You can see that, the intersection"
" point is between 0.0 and 1.0.\n\n"
" Choose x = %.1f as a first approximation.\n\n",FirstA);
getchar();
clrscrn();
printf(" In fact we want find sin(x) = cos(x)"
" or sin(x) - cos(x) = 0.\n\n"
" We want find a root of\n\n"
" f : x-> %s\n\n", feq);
getchar();
clrscrn();
printf(" As a first approximation x = %.1f \n\n"
" The Newton's method give : \n\n",FirstA);
G_gh_x_0(i_WGnuplot(-4,4,-4,4),
geq,
heq,
g,
Newton_s_Method(FirstA,n,f,Df));
printf("\n\n load \"a_main.plt\" with gnuplot. "
"\n\n Press return to continue");
getchar();
return 0;
}
Le résultat.
Use Newton's method to approximate the intersection point of : g : x-> sin(x) and h : x-> cos(x) . To see the graphs of g and h, open the file "a_main.plt" with Gnuplot. . You can see that, the intersection point is between 0.0 and 1.0. Choose x = 0.5 as a first approximation. In fact we want find sin(x) = cos(x) or sin(x) - cos(x) = 0. We want find a root of . f : x-> sin(x) - cos(x) . As a first approximation x = 0.5 . The Newton's method give : . x[1] = 0.500000000000000 x[2] = 0.793407993026023 x[3] = 0.785397992096516 x[4] = 0.785398163397448 x[5] = 0.785398163397448 . load "a_main.plt" with gnuplot.
| Résultat dans gnuplot |
|---|
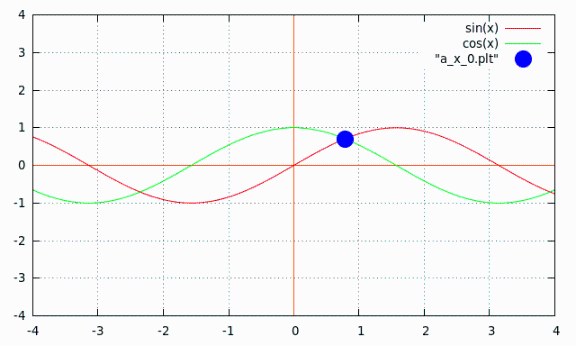
|
Un autre exemple avec :
As a first approximation x = -2.5 . The Newton's method give : . x[1] = -2.500000000000000 x[2] = -2.355194920430497 x[3] = -2.356194490525248 x[4] = -2.356194490192345 x[5] = -2.356194490192345
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xplt.h"
/* ------------------------------------ */
#include "knewton.h"
#include "kg_gh.h"
f2.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : f2.h */
/* ------------------------------------ */
double g(
double x)
{
return(sin(x));
}
char geq [] = "sin(x)";
/* ------------------------------------ */
double Dg(
double x)
{
return(cos(x));
}
char Dgeq [] = "cos(x)";
/* ------------------------------------ */
/* ------------------------------------ */
double h(
double x)
{
return(cos(x));
}
char heq [] = "cos(x)";
/* ------------------------------------ */
double Dh(
double x)
{
return(- sin(x));
}
char Dheq [] = "- sin(x)";
/* ------------------------------------ */
/* ------------------------------------ */
double f(
double x)
{
return(sin(x) - cos(x));
}
char feq [] = "sin(x) - cos(x)";
/* ------------------------------------ */
double Df(
double x)
{
return(cos(x) + sin(x));
}
char Dfeq [] = "cos(x) + sin(x)";
knewton.hMéthode de Newton |
|---|
/* ------------------------------------ */
/* Save as : knewton.h */
/* ------------------------------------
x_n+1 = x_n - f(x_n)
------
f'(x_n)
------------------------------------ */
double Newton_s_Method(
double x,
int imax,
double (*P_f)(double x),
double (*PDf)(double x)
)
{
int i=1;
for(;i<=imax;i++)
{
printf(" x[%d] = %.15f\n",i,x);
x -= ((*P_f)(x))/((*PDf)(x));
}
return(x);
}
kg_gh.hFonctions graphiques |
|---|
/* ------------------------------------ */
/* Save as : kg_gh.h */
/* ------------------------------------ */
void G_gh(
W_Ctrl w,
char geq[],
char heq[]
)
{
FILE *fp = fopen("a_main.plt","w");
fprintf(fp," set zeroaxis lt 8\n"
" set grid\n\n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f] \\\n"
" %s, \\\n"
" %s \n"
" reset",
w.xmini,w.xmaxi,w.ymini,w.ymaxi,
geq,heq);
fclose(fp);
}
/* ------------------------------------ */
void G_gh_x_0(
W_Ctrl w,
char geq[],
char heq[],
double (*P_g)(double x),
double x_0
)
{
FILE *fp = fopen("a_main.plt","w");
FILE *fq = fopen( "a_x_0.plt","w");
fprintf(fp," set zeroaxis lt 8\n"
" set grid\n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f] \\\n"
" %s, \\\n"
" %s, \\\n"
" \"a_x_0.plt\" pt 7 ps 3 \n"
" reset",
w.xmini,w.xmaxi,w.ymini,w.ymaxi,
geq,heq);
fclose(fp);
fprintf(fq," %0.6f %0.6f", x_0,(*P_g)(x_0));
fclose(fq);
}
Application : Tangente d'une courbe
Préambule
[modifier | modifier le wikicode]La tangente dans Wikipedia.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Dessiner la tangente d'une courbe
[modifier | modifier le wikicode]c01.cDessiner la tangente d'une courbe |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "fe.h"
/* ------------------------------------ */
int main(void)
{
printf(" Let C be the curve consisting of all"
" ordered pairs (f(t),g(t)).\n\n"
" With\n\n"
" f : t-> %s\n\n"
" g : t-> %s\n\n", feq, geq);
G_Tan( i_WGnuplot(-10.,10.,-5.,5.),
i_time(0,2.*PI,.05),
2.,
f,g,DgDf);
printf(" To see the curve C, open the file \"a_main.plt\""
" with Gnuplot.\n\n"
"\n Press return to continue");
getchar();
return 0;
}
Le résultat.
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xplt.h"
/* ------------------------------------ */
#include "kg_tan.h"
fe.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : fe.h */
/* ------------------------------------ */
double f(
double t)
{
double a=2;
double k1=3;
return( a*sin(k1*t) );
}
char feq[] = "a*sin(k1*t)";
/* ------------------------------------ */
double Df(
double t)
{
double a=2;
double k1=3;
return( a*cos(k1*t)*k1);
}
char Dfeq[] = "a*cos(k1*t)*k1";
/* ------------------------------------ */
double g(
double t)
{
double b =3;
double k2=1;
return( b*cos(k2*t) );
}
char geq[] = "b*cos(k2*t)";
/* ------------------------------------ */
double Dg(
double t)
{
double b =3;
double k2=1;
return( -b*sin(k2*t)*k2 );
}
char Dgeq[] = "-b*sin(k2*t)*k2";
/* ------------------------------------ */
double DgDf(
double t)
{
return(Dg(t)/Df(t));
}
kg_tan.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_tan.h */
/* ------------------------------------ */
void G_Tan(
W_Ctrl W,
t_Ctrl T,
double c,
double (*P_f) (double t),
double (*P_g) (double t),
double (*PDgDf)(double t)
)
{
FILE *fp;
double t;
fp = fopen("a_main.plt","w");
fprintf(fp," set zeroaxis\n\n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f]\\\n"
" \"data.plt\" with linesp lt 3 pt 1,\\\n"
" %0.6f*x %+0.6f\n"
" reset",
W.xmini,W.xmaxi,W.ymini,W.ymaxi,
(*PDgDf)(c),
(-(*PDgDf)(c)*(*P_f)(c)+(*P_g)(c)));
fclose(fp);
fp = fopen("data.plt","w");
for(t=T.mini; t<=T.maxi; t+=T.step)
fprintf(fp," %6.6f %6.6f\n",(*P_f)(t),(*P_g)(t));
fclose(fp);
}
Application : Tangente et axes x-y d'une courbe
Préambule
[modifier | modifier le wikicode]La tangente dans Wikipedia.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Dessiner
[modifier | modifier le wikicode]c01.cDessiner les points d'intersection de la tangente avec les axes x/y |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "fe.h"
/* ------------------------------------ */
int main(void)
{
double c = PI/2.+.2;
printf(" Let C be the curve consisting of all"
" ordered pairs (f(t),g(t)).\n\n"
" With\n\n"
" f : t-> %s\n\n"
" g : t-> %s\n\n", feq, geq);
printf(" Find at c = %0.3f\n\n"
" the intersection points of "
"the tangent with the x-y axis.\n\n\n",c);
printf(" P(%6.3f, %6.3f) P(c, f(c))\n\n",
c, f(c));
printf(" A(%6.3f, 0) A(f(c)-g(c)/DgDf(c), 0)\n\n",
f(c)-g(c)/DgDf(c));
printf(" B( 0, %6.3f) B(0, g(c)-f(c)*DgDf(c))\n\n\n",
g(c)-f(c)*DgDf(c));
G_Tanxy(i_WGnuplot(-10.,10.,-5.,5.),
i_time(0,2.*PI,.05),
c,
f,g,DgDf);
printf(" To see the curve C, open the file \"a_main.plt\""
" with Gnuplot.\n\n"
"\n Press return to continue");
getchar();
return 0;
}
Le résultat.
Let C be the curve consisting of all ordered pairs (f(t),g(t)). With f : t-> a*sin(k1*t) g : t-> b*cos(k2*t) . Find at c = 1.771 the intersection points of the tangent with the x-y axis. . P( 1.771, -1.651) P(c, f(c)) A(-2.337, 0) A(f(c)-g(c)/DgDf(c), 0) B( 0, -2.029) B(0, g(c)-f(c)*DgDf(c)) . To see the curve C, open the file "a_main.plt" with Gnuplot. Press return to continue
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xplt.h"
/* ------------------------------------ */
#include "kg_tan.h"
fe.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : fe.h */
/* ------------------------------------ */
double f(
double t)
{
double a=2;
double k1=3;
return( a*sin(k1*t) );
}
char feq[] = "a*sin(k1*t)";
/* ------------------------------------ */
double Df(
double t)
{
double a=2;
double k1=3;
return( a*cos(k1*t)*k1);
}
char Dfeq[] = "a*cos(k1*t)*k1";
/* ------------------------------------ */
double g(
double t)
{
double b =3;
double k2=1;
return( b*cos(k2*t) );
}
char geq[] = "b*cos(k2*t)";
/* ------------------------------------ */
double Dg(
double t)
{
double b =3;
double k2=1;
return( -b*sin(k2*t)*k2 );
}
char Dgeq[] = "-b*sin(k2*t)*k2";
/* ------------------------------------ */
double DgDf(
double t)
{
return(Dg(t)/Df(t));
}
kg_tan.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_tan.h */
/* ------------------------------------ */
void G_Tanxy(
W_Ctrl W,
t_Ctrl T,
double c,
double (*P_f) (double t),
double (*P_g) (double t),
double (*PDgDf)(double t)
)
{
FILE *fp;
double t;
fp = fopen("a_main.plt","w");
fprintf(fp," set zeroaxis\n\n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f]\\\n"
" \"data.plt\" with line lt 1,\\\n"
" %0.6f*x %+0.6f, \\\n"
" \"p.plt\" lt 1, \\\n"
" \"px.plt\" lt 1,\\\n"
" \"py.plt\" lt 1 \n"
" reset",
W.xmini,W.xmaxi,W.ymini,W.ymaxi,
(*PDgDf)(c),(-(*PDgDf)(c)*(*P_f)(c)+(*P_g)(c)));
fclose(fp);
fp = fopen("data.plt","w");
for(t=T.mini; t<=T.maxi; t+=T.step)
fprintf(fp," %6.6f %6.6f\n",(*P_f)(t),(*P_g)(t) );
fclose(fp);
fp = fopen("p.plt","w");
fprintf(fp," %0.6f %0.6f", (*P_f)(c), (*P_g)(c) );
fclose(fp);
fp = fopen("px.plt","w");
fprintf(fp," %0.6f 0.",
((*P_f)(c))-((*P_g)(c))/((*PDgDf)(c)) );
fclose(fp);
fp = fopen("py.plt","w");
fprintf(fp," 0. %0.6f",
((*P_g)(c))- (((*PDgDf)(c))*((*P_f)(c))) );
fclose(fp);
}
Application : Tangente de P à l'axes des x d'une courbe
Préambule
[modifier | modifier le wikicode]La tangente dans Wikipedia.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Dessiner
[modifier | modifier le wikicode]c01.cCalculer la longeur de P(f(c),g(c) à l'axe de x. |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "fe.h"
/* ------------------------------------ */
int main(void)
{
double c = PI/4;
printf(" Let C be the curve consisting of all"
" ordered pairs (f(t),g(t)).\n\n"
" With\n\n"
" f : t-> %s\n\n"
" g : t-> %s\n\n", feq, geq);
printf(" With c = %0.3f, the equation of the tangent is :\n\n"
" y = ((Dg/Dy)(c))(x-f(c))+g(c) = ",c);
eq_Tan(f,g,DgDf,c);
printf("\n\n\n");
printf(" Find PA, the length of the tangent from P to the x axis.\n\n");
printf(" P(%6.3f, %6.3f) P(f(c), g(c)) \n",
f(c),g(c));
printf(" A(%6.3f, 0.000) A(f(c)-g(c)/(DgDf)(c), 0)\n\n\n",
f(c)-g(c)/(DgDf)(c));
printf(" PA = sqrt(g(c)**2*(1+(DgDf(c)**2))/(DgDf(c)**2))\n"
" = %6.3f\n\n",
sqrt(pow(g(c),2)*(1/pow(DgDf(c),2)+1)) );
G_TanLx(i_WGnuplot(-10.,10.,-5.,5.),
i_time(0,2.*PI,.05),
c,
f,g,DgDf);
printf(" To see the curve C, open the file \"a_main.plt\""
" with Gnuplot.\n\n"
"\n Press return to continue");
getchar();
return 0;
}
Le résultat.
Let C be the curve consisting of all ordered pairs (f(t),g(t)). . With . f : t-> a*sin(k1*t) g : t-> b*cos(k2*t) . With c = 0.785, the equation of the tangent is : y = ((Dg/Dy)(c))(x-f(c))+g(c) = 0.500*x +1.414 . Find PA, the length of the tangent from P to the x axis. P( 1.414, 2.121) P(f(c), g(c)) A(-2.828, 0.000) A(f(c)-g(c)/(DgDf)(c), 0) . PA = sqrt(g(c)**2*(1+(DgDf(c)**2))/(DgDf(c)**2)) = 4.743 . To see the curve C, open the file "a_main.plt" with Gnuplot.
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xplt.h"
/* ------------------------------------ */
#include "kg_tan.h"
fe.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : fe.h */
/* ------------------------------------ */
double f(
double t)
{
double a=2;
double k1=3;
return( a*sin(k1*t) );
}
char feq[] = "a*sin(k1*t)";
/* ------------------------------------ */
double Df(
double t)
{
double a=2;
double k1=3;
return( a*cos(k1*t)*k1);
}
char Dfeq[] = "a*cos(k1*t)*k1";
/* ------------------------------------ */
double g(
double t)
{
double b =3;
double k2=1;
return( b*cos(k2*t) );
}
char geq[] = "b*cos(k2*t)";
/* ------------------------------------ */
double Dg(
double t)
{
double b =3;
double k2=1;
return( -b*sin(k2*t)*k2 );
}
char Dgeq[] = "-b*sin(k2*t)*k2";
/* ------------------------------------ */
double DgDf(
double t)
{
return(Dg(t)/Df(t));
}
kg_tan.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_tan.h */
/* ------------------------------------ */
void eq_Tan(
double (*P_f) (double t),
double (*P_g) (double t),
double (*PDgDf)(double t),
double c
)
{
printf(" %0.3f*x %+0.3f",
(*PDgDf)(c),(-(*PDgDf)(c)*(*P_f)(c)+(*P_g)(c)));
}
/* ------------------------------------ */
void G_TanLx(
W_Ctrl W,
t_Ctrl T,
double c,
double (*P_f) (double t),
double (*P_g) (double t),
double (*PDgDf)(double t)
)
{
FILE *fp;
double t;
fp = fopen("a_main.plt","w");
fprintf(fp," set zeroaxis\n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f]\\\n"
" \"a_pts.plt\" with line lt 1, \\\n"
" %0.6f*x %+0.6f, \\\n"
" \"axp.plt\" with linesp lt 3 \n"
" reset",
W.xmini,W.xmaxi,W.ymini,W.ymaxi,
(*PDgDf)(c),(-(*PDgDf)(c)*(*P_f)(c)+(*P_g)(c)));
fclose(fp);
fp = fopen("a_pts.plt","w");
for(t=T.mini; t<=T.maxi; t+=T.step)
fprintf(fp," %6.6f %6.6f\n",(*P_f)(t),(*P_g)(t));
fclose(fp);
fp = fopen("axp.plt","w");
fprintf(fp," %0.6f %0.6f\n",(*P_f)(c),(*P_g)(c));
fprintf(fp," %0.6f 0. \n",
(*P_f)(c)-(*P_g)(c)/(*PDgDf)(c));
fclose(fp);
}
Application : Tangente de P à l'axes des y d'une courbe
Préambule
[modifier | modifier le wikicode]La tangente dans Wikipedia.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Dessiner
[modifier | modifier le wikicode]c01.cCalculer la longeur de P(f(c),g(c) à l'axe de y. |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "fe.h"
/* ------------------------------------ */
int main(void)
{
double c = PI/4.;
printf(" Let C be the curve consisting of all"
" ordered pairs (f(t),g(t)).\n\n"
" With\n\n"
" f : t-> %s\n\n"
" g : t-> %s\n\n", feq, geq);
printf(" With c = %0.3f, the equation of the tangent is :\n\n"
" y = ((Dg/Dy)(c))(x-f(c))+g(c) = ",c);
eq_Tan(f,g,DgDf,c);
printf("\n\n\n");
printf(" Find PB, the length of the tangent from P to the y axis.\n\n");
printf(" P(%6.3f, %6.3f) P(f(c), g(c)) \n",
f(c),g(c));
printf(" B(+0.000, %6.3f) B(0, g(c)-f(c)*DgDf(c))\n\n\n",
g(c)-DgDf(c)*f(c));
printf(" PB = sqrt(f(c)**2*(1+DgDf(c)**2))\n"
" = %6.3f\n\n",
sqrt(pow(f(c),2)*(1+pow(DgDf(c),2))));
G_TanLy(i_WGnuplot(-10.,10.,-5.,5.),
i_time(0,2.*PI,.05),
c,
f,g,DgDf);
printf(" To see the curve C, open the file \"a_main.plt\""
" with Gnuplot.\n\n"
"\n Press return to continue");
getchar();
return 0;
}
Le résultat.
Let C be the curve consisting of all ordered pairs (f(t),g(t)). . With . f : t-> a*sin(k1*t) g : t-> b*cos(k2*t) . With c = 0.785, the equation of the tangent y = ((Dg/Dy)(c))(x-f(c))+g(c) = 0.500*x +1.414 . Find PB, the length of the tangent from P to the y axis. . P( 1.414, 2.121) P(f(c), g(c)) B(+0.000, 1.414) B(0, g(c)-f(c)*DgDf(c)) . PB = sqrt(f(c)**2*(1+DgDf(c)**2)) = 1.581 . To see the curve C, open the file "a_main.plt" with Gnuplot.
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xplt.h"
/* ------------------------------------ */
#include "kg_tan.h"
fe.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : fe.h */
/* ------------------------------------ */
double f(
double t)
{
double a=2;
double k1=3;
return( a*sin(k1*t) );
}
char feq[] = "a*sin(k1*t)";
/* ------------------------------------ */
double Df(
double t)
{
double a=2;
double k1=3;
return( a*cos(k1*t)*k1);
}
char Dfeq[] = "a*cos(k1*t)*k1";
/* ------------------------------------ */
double g(
double t)
{
double b =3;
double k2=1;
return( b*cos(k2*t) );
}
char geq[] = "b*cos(k2*t)";
/* ------------------------------------ */
double Dg(
double t)
{
double b =3;
double k2=1;
return( -b*sin(k2*t)*k2 );
}
char Dgeq[] = "-b*sin(k2*t)*k2";
/* ------------------------------------ */
double DgDf(
double t)
{
return(Dg(t)/Df(t));
}
kg_tan.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_tan.h */
/* ------------------------------------ */
void eq_Tan(
double (*P_f) (double t),
double (*P_g) (double t),
double (*PDgDf)(double t),
double c
)
{
printf(" %0.3f*x %+0.3f",
(*PDgDf)(c),(-(*PDgDf)(c)*(*P_f)(c)+(*P_g)(c)));
}
/* ------------------------------------ */
void G_TanLy(
W_Ctrl W,
t_Ctrl T,
double c,
double (*P_f) (double t),
double (*P_g) (double t),
double (*PDgDf)(double t)
)
{
FILE *fp;
double t;
fp = fopen("a_main.plt","w");
fprintf(fp," set zeroaxis\n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f] \\\n"
" \"a_pts.plt\" with line lt 1,\\\n"
" %0.6f*x %+0.6f,\\\n"
" \"ayp.plt\" with linesp lt 3\n"
" reset",
W.xmini,W.xmaxi,W.ymini,W.ymaxi,
(*PDgDf)(c),(-(*PDgDf)(c)*(*P_f)(c)+(*P_g)(c)));
fclose(fp);
fp = fopen("a_pts.plt","w");
for(t=T.mini; t<=T.maxi; t+=T.step)
fprintf(fp," %6.6f %6.6f\n",(*P_f)(t),(*P_g)(t));
fclose(fp);
fp = fopen("ayp.plt","w");
fprintf(fp," %0.6f %0.6f\n",(*P_f)(c),(*P_g)(c));
fprintf(fp," 0. %0.6f \n",
(*P_g)(c)- (*PDgDf)(c)*(*P_f)(c));
fclose(fp);
}
Application : Cercle de courbure d'une courbe
Préambule
[modifier | modifier le wikicode]Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Dessiner
[modifier | modifier le wikicode]c01.cDessiner un cercle de courbure pour une fonction (f(t),g(t)) |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "fb.h"
/* ------------------------------------ */
int main(void)
{
double t = PI;
double e = .001;
char Name[FILENAME_MAX] = "a_circle.plt";
circle(Name,
1./fabs(Kt_2d(f,g,t,e)),
cx_2d(f,g,t,e),
cy_2d(f,g,t,e));
G_C_2d(i_WGnuplot(-4,8,-2,4),
i_time(0.,2*PI,.03),
f,g,t,
e);
printf(" The curvature K of a smooth parametric"
" curve C is :\n\n\n"
" K = |f' g'' - g' f''| / "
"[ (f')^2 - (g')^2 ]^(3/2)\n\n"
" If P(f(t),g(t)) is a point on the curve \n"
" at which K != 0. The point M(h,k)"
" is the center\n"
" of the cuvature for P if \n\n\n"
" h = f - g'[f'^2 + g'^2] / [f'g''-f''g']\n"
" k = g + f'[f'^2 + g'^2] / [f'g''-f''g']\n\n\n"
" The radius is r = 1/|K| \n\n\n"
" Open the file \"a_main.plt\" with Gnuplot.\n\n");
printf("\n Press return to continue");
getchar();
return 0;
}
Le résultat.
| Résultat dans gnuplot |
|---|

|
| Résultat dans gnuplot |
|---|

|
| Résultat dans gnuplot |
|---|
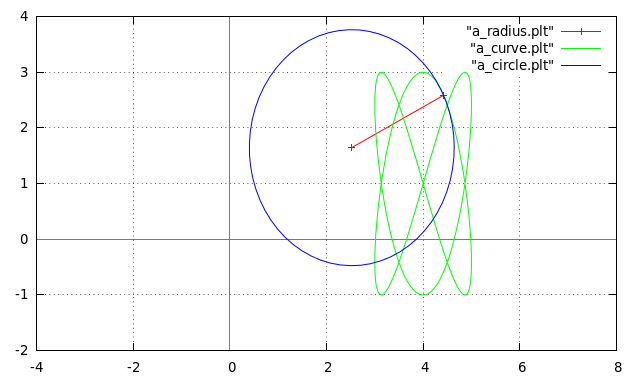
|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xplt.h"
#include "xfx_x.h"
/* ------------------------------------ */
#include "kradius.h"
#include "kg_c.h"
#include "kcircle.h"
kradius.hCoordonnées du cercle |
|---|
/* ------------------------------------ */
/* Save as : kradius.h */
/* ------------------------------------ */
double Kt_2d(
double (*P_f)(double t),
double (*P_g)(double t),
double t,
double e
)
{
double K;
double a;
double b;
a = fx_x((*P_f),t,e);
b = fx_x((*P_g),t,e);
K = fabs(a*fx_xx((*P_g),t,e)-b*fx_xx((*P_f),t,e))
/
pow(a*a+b*b,3./2.);
return(K);
}
/* ------------------------------------ */
double cx_2d(
double (*P_f)(double t),
double (*P_g)(double t),
double t,
double e
)
{
double Num,Den;
Num =( pow(fx_x((*P_f),t,e),2)
+pow(fx_x((*P_g),t,e),2)
)
*fx_x((*P_g),t,e);
Den = fx_x((*P_f),t,e)*fx_xx((*P_g),t,e)-
fx_x((*P_g),t,e)*fx_xx((*P_f),t,e);
return((*P_f)(t)-Num/Den);
}
/* ------------------------------------ */
double cy_2d(
double (*P_f)(double t),
double (*P_g)(double t),
double t,
double e
)
{
double Num,Den;
Num =( pow(fx_x((*P_f),t,e),2)
+pow(fx_x((*P_g),t,e),2)
)
*fx_x((*P_f),t,e);
Den = fx_x((*P_f),t,e)*fx_xx((*P_g),t,e)-
fx_x((*P_g),t,e)*fx_xx((*P_f),t,e);
return((*P_g)(t)+Num/Den);
}
fb.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : fb.h */
/* ------------------------------------ */
double f(
double t)
{
return( 4+sin(2*t) );
}
char feq[] = "4+sin(2*t)";
/* ------------------------------------ */
double g(
double t)
{
return( 1-2*cos(3*t) );
}
char geq[] = "1-2*cos(3*t)";
kg_c.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_c.h */
/* ------------------------------------ */
void G_C_2d(
W_Ctrl W,
t_Ctrl T,
double (*P_f)(double x),
double (*P_g)(double x),
double x,
double e
)
{
FILE *fp;
double i;
fp = fopen("a_main.plt","w");
fprintf(fp," reset\n"
" set zeroaxis lt 8\n"
" set size ratio -1\n"
" set grid\n\n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f]\\\n"
" \"a_radius.plt\" with linespoints,\\\n"
" \"a_curve.plt\" with line,\\\n"
" \"a_circle.plt\" with line\n",
W.xmini,W.xmaxi,W.ymini,W.ymaxi);
fclose(fp);
fp = fopen("a_curve.plt","w");
for(i=T.mini; i<=T.maxi; i+=T.step)
fprintf(fp," %6.3f %6.3f\n",(*P_f)(i),(*P_g)(i));
fclose(fp);
fp = fopen("a_radius.plt","w");
fprintf(fp," %6.5f %6.5f\n",cx_2d((*P_f),(*P_g),x,e),
cy_2d((*P_f),(*P_g),x,e));
fprintf(fp," %6.5f %6.5f\n",(*P_f)(x),(*P_g)(x));
fclose(fp);
Pause();
}
kcircle.hLe cercle |
|---|
/* ------------------------------------ */
/* Save as : kcircle.h */
/* ------------------------------------ */
void circle(
char Name[FILENAME_MAX],
double r,
double x,
double y
)
{
FILE *fp = fopen(Name,"w");
double t = 0.;
for(;t<2.01*PI;t+=.1)
fprintf(fp," %6.5f %6.5f\n",r*cos(t)+x,r*sin(t)+y);
fclose(fp);
}
Application : Courbe de Bézier
Préambule
[modifier | modifier le wikicode]Les courbes de Béziers dans Wikipedia.
Courbe de Béziers
[modifier | modifier le wikicode]Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
c01.cExemple à tester |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
/* ------------------------------------ */
int main(void)
{
printf(" Une courbe de Bezier.\n\n");
G_quadratic_Bezier_lp_2d(
i_WGnuplot(-10,90,-10,50),
i_point2d(20.,10.),
i_point2d(40.,40.),
i_point2d(60.,10.) );
printf("\n\n load \"a_main.plt\" with gnuplot."
"\n\n Press return to continue");
return 0;
}
| Résultat dans gnuplot |
|---|

|
Une application
[modifier | modifier le wikicode]Nous avons essayé de recouvrir un quart de cercle avec une courbe de Béziers. Nous savons que c'est impossible (voir théorie)
c02.cExemple à tester |
|---|
/* ------------------------------------ */
/* Save as : c02.c */
/* ------------------------------------ */
#include "x_ahfile.h"
/* ------------------------------------ */
int main(void)
{
printf(" Une courbe de Bezier.\n\n");
G_quadratic_Bezier_lp_2d(
i_WGnuplot(-0,2,-0,1),
i_point2d(0.,1.),
i_point2d(1.,1.),
i_point2d(1.,0.) );
printf("\n\n load \"a_main.plt\" with gnuplot."
"\n\n Press return to continue");
return 0;
}
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xplt.h"
#include "xspv.h"
/* ------------------------------------ */
#include "kpoly.h"
#include "kbezier.h"
Cette partie ne peut être vue que dans wikiversité.
kpoly.hLes équations de la courbe |
|---|
/* ------------------------------------ */
/* Save as : kpoly.h */
/* ------------------------------------ */
double quadratic_Bezier_x_2d(
double t,
point2d P0,
point2d P1,
point2d P2
)
{
return(
P0.x * pow((1-t),2) * pow(t,0) +
2 * P1.x * pow((1-t),1) * pow(t,1) +
P2.x * pow((1-t),0) * pow(t,2)
);
}
/* ------------------------------------ */
double quadratic_Bezier_y_2d(
double t,
point2d P0,
point2d P1,
point2d P2)
{
return(
P0.y * pow((1-t),2) * pow(t,0) +
2 * P1.y * pow((1-t),1) * pow(t,1) +
P2.y * pow((1-t),0) * pow(t,2)
);
}
/* ------------------------------------ */
kbezier.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kbezier.h */
/* ------------------------------------ */
void G_quadratic_Bezier_lp_2d(
W_Ctrl w,
point2d P0,
point2d P1,
point2d P2
)
{
FILE *fp;
double mini = 0.;
double maxi = 1.;
double step = .01;
double t = mini;
fp = fopen("a_main.plt","w");
fprintf(fp," set zeroaxis lt 8\n"
" set grid \n\n"
" set size ratio -1\n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f] \\\n"
" \"a_pts\" with linesp lt 3 pt 1, \\\n"
" \"a_ctrlpt\" with linesp lt 4 pt 4 \\\n\n"
" reset",w.xmini,w.xmaxi,w.ymini,w.ymaxi);
fclose(fp);
fp = fopen("a_pts","w");
for(t=mini; t<=maxi; t+=step)
fprintf(fp," %6.5f %6.5f\n",quadratic_Bezier_x_2d(t,P0,P1,P2),
quadratic_Bezier_y_2d(t,P0,P1,P2));
fclose(fp);
fp = fopen("a_ctrlpt","w");
fprintf(fp," %6.5f %6.5f\n",P0.x,P0.y);
fprintf(fp," %6.5f %6.5f\n",P1.x,P1.y);
fprintf(fp," %6.5f %6.5f\n",P2.x,P2.y);
fclose(fp);
Pause();
}
Conclusion
[modifier | modifier le wikicode]Nous avons utilisé dans les exemples trois points de contrôles. Ici un exemple avec trois courbes et cinq points de contrôles.
| Résultat dans gnuplot |
|---|

|
Application : Courbe de Bézier rationnelle
Préambule
[modifier | modifier le wikicode]Les courbes de Béziers dans Wikipedia.
Courbes de Béziers rationelles (cubiques)
[modifier | modifier le wikicode]La seule chose qui change avec le chapitre précédent, c'est le fichier "kpoly.h".
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
c01.cExemple à tester |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
/* ------------------------------------ */
int main(void)
{
printf(" Une courbe de Bezier.\n\n");
G_quadratic_Bezier_lp_2d(
i_WGnuplot(-10,90,-10,50),
i_point2d(20.,10.),
i_point2d(40.,40.),
i_point2d(60.,10.)
);
printf("\n\n load \"a_main.plt\" with gnuplot."
"\n\n Press return to continue");
return 0;
}
| Résultat dans gnuplot |
|---|

|
| Courbe du chapitre précédent |
|---|

|
Une application
[modifier | modifier le wikicode]Nous avons essayé de recouvrir un quart de cercle avec une courbe de Béziers. En théorie cela est possible avec les courbes de Béziers rationelles (cubiques).
c02.cExemple à tester |
|---|
/* ------------------------------------ */
/* Save as : c02.c */
/* ------------------------------------ */
#include "x_ahfile.h"
/* ------------------------------------ */
int main(void)
{
printf(" Une courbe de Bezier.\n\n");
G_quadratic_Bezier_lp_2d(
i_WGnuplot(-0,2,-0,1),
i_point2d(0.,1.),
i_point2d(1.,1.),
i_point2d(1.,0.)
);
printf("\n\n load \"a_main.plt\" with gnuplot."
"\n\n Press return to continue");
return 0;
}
| Résultat dans gnuplot |
|---|
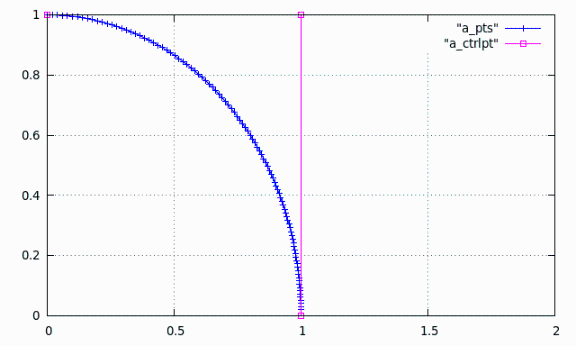
|
| Courbe du chapitre précédent |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xplt.h"
#include "xspv.h"
/* ------------------------------------ */
#include "kpoly.h"
#include "kbezier.h"
Cette partie ne peut être vue que dans wikiversité.
kpoly.hLes équations de la courbe |
|---|
/* ------------------------------------ */
/* Save as : kpoly.h */
/* ------------------------------------ */
double quadratic_Bezier_x_2d(
double t,
point2d P0,
point2d P1,
point2d P2
)
{
return(
(
P0.x * pow((1-t),2) * pow(t,0) +
2 * P1.x * pow((1-t),1) * pow(t,1) +
2 * P2.x * pow((1-t),0) * pow(t,2)
)
/
(
pow((1-t),2) * pow(t,0) +
2 * pow((1-t),1) * pow(t,1) +
2 * pow((1-t),0) * pow(t,2)
)
);
}
/* ------------------------------------ */
double quadratic_Bezier_y_2d(
double t,
point2d P0,
point2d P1,
point2d P2)
{
return(
(
P0.y * pow((1-t),2) * pow(t,0) +
2 * P1.y * pow((1-t),1) * pow(t,1) +
2 * P2.y * pow((1-t),0) * pow(t,2)
)
/
(
pow((1-t),2) * pow(t,0) +
2 * pow((1-t),1) * pow(t,1) +
2 * pow((1-t),0) * pow(t,2)
)
);
}
/* ------------------------------------ */
kbezier.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kbezier.h */
/* ------------------------------------ */
void G_quadratic_Bezier_lp_2d(
W_Ctrl w,
point2d P0,
point2d P1,
point2d P2
)
{
FILE *fp;
double mini = 0.;
double maxi = 1.;
double step = .01;
double t = mini;
fp = fopen("a_main.plt","w");
fprintf(fp," set zeroaxis lt 8\n"
" set grid \n\n"
" set size ratio -1\n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f] \\\n"
" \"a_pts\" with linesp lt 3 pt 1, \\\n"
" \"a_ctrlpt\" with linesp lt 4 pt 4 \\\n\n"
" reset",w.xmini,w.xmaxi,w.ymini,w.ymaxi);
fclose(fp);
fp = fopen("a_pts","w");
for(t=mini; t<=maxi; t+=step)
fprintf(fp," %6.5f %6.5f\n",quadratic_Bezier_x_2d(t,P0,P1,P2),
quadratic_Bezier_y_2d(t,P0,P1,P2));
fclose(fp);
fp = fopen("a_ctrlpt","w");
fprintf(fp," %6.5f %6.5f\n",P0.x,P0.y);
fprintf(fp," %6.5f %6.5f\n",P1.x,P1.y);
fprintf(fp," %6.5f %6.5f\n",P2.x,P2.y);
fclose(fp);
Pause();
}
Application : Fonction vectorielle 3D
Préambule
[modifier | modifier le wikicode]Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Dessiner
[modifier | modifier le wikicode]c01.cDessiner un vecteur tangent et normales unitaire. |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "fa.h"
/* ------------------------------------ */
int main(void)
{
double t = 4.;
printf(" r(t) = f(t)i + g(t)j + h(t)k \n\n");
printf(" With \n\n");
printf(" f : t-> %s \n", feq);
printf(" g : t-> %s \n", geq);
printf(" h : t-> %s\n\n", heq);
printf(" t = %+.2f \n\n", t);
G_Curve_3d(i_time(0.,6.*PI,.01),
f,g,h,
Tf,Tg,Th,
t);
printf(" Draw the velocity and accelerator vectors"
" at the point P(f(t),g(t)), \n\n"
" open the file \"a_main.plt\" with Gnuplot.\n\n");
printf("\n Press return to continue");
getchar();
return 0;
}
Le résultat.
| Résultat dans gnuplot |
|---|

|
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xplt.h"
#include "xfx_x.h"
/* ------------------------------------ */
#include "knfx_x.h"
#include "kg_ctan1.h"
knfx_x.hNormalisé |
|---|
/* ------------------------------------ */
/* Save as : knfx_x.h */
/* ------------------------------------ */
double fx_x_Normalize(
double (*P_f)(double x),
double (*P_g)(double x),
double (*P_h)(double x),
double t,
double e
)
{
double Df=fx_x((*P_f),t,e);
double Dg=fx_x((*P_g),t,e);
double Dh=fx_x((*P_h),t,e);
return(Df/sqrt(Df*Df+Dg*Dg+Dh*Dh));
}
fa.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : fa.h */
/* ------------------------------------ */
double f(
double t)
{
return( cos(t));
}
char feq[] = "cos(t)";
/* ------------------------------------ */
double g(
double t)
{
return( sin(t));
}
char geq[] = "sin(t)";
/* ------------------------------------ */
double h(
double t)
{
return( t);
}
char heq[] = "t";
/* ------------------------------------ */
double Tf(
double t)
{
return(
-(sin(t)/sqrt(2))
);
}
/* ------------------------------------ */
double Tg(
double t)
{
return(
cos(t)/sqrt(2)
);
}
/* ------------------------------------ */
double Th(
double t)
{
return(
1/sqrt(2)
);
}
kg_ctan1.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_ctan1.h */
/* ------------------------------------ */
void G_Curve_3d(
t_Ctrl T,
double (*P_f)(double t),
double (*P_g)(double t),
double (*P_h)(double t),
double (*P_Tf)(double t),
double (*P_Tg)(double t),
double (*P_Th)(double t),
double t
)
{
FILE *fp;
double i;
double e = .001;
fp = fopen("a_main.plt","w");
fprintf(fp," reset\n"
" set zeroaxis lt 8\n"
" set grid\n\n"
" splot \\\n"
" \"a_curve.plt\" with line lt 3,\\\n"
" \"a_radius.plt\" with line lt 2,\\\n"
" \"atangent.plt\" with line lt 4,\\\n"
" \"anormal.plt\" with line lt 1 ");
fclose(fp);
fp = fopen("a_curve.plt","w");
for(i=T.mini; i<=T.maxi; i+=T.step)
fprintf(fp," %6.3f %6.3f %6.3f\n",
(*P_f)(i),
(*P_g)(i),
(*P_h)(i));
fclose(fp);
fp = fopen("a_radius.plt","w");
fprintf(fp," 0 0 0 \n %6.5f %6.5f %6.5f \n",
(*P_f)(t),
(*P_g)(t),
(*P_h)(t));
fclose(fp);
fp = fopen("atangent.plt","w");
fprintf(fp," %6.5f %6.5f %6.5f \n"
" %6.5f %6.5f %6.5f \n",
(*P_f)(t),
(*P_g)(t),
(*P_h)(t),
(*P_f)(t)+fx_x_Normalize((*P_f),(*P_g),(*P_h),t,e),
(*P_g)(t)+fx_x_Normalize((*P_g),(*P_f),(*P_h),t,e),
(*P_h)(t)+fx_x_Normalize((*P_h),(*P_f),(*P_g),t,e) );
fclose(fp);
fp = fopen("anormal.plt","w");
fprintf(fp," %6.5f %6.5f %6.5f \n"
" %6.5f %6.5f %6.5f \n",
(*P_f)(t),
(*P_g)(t),
(*P_h)(t),
(*P_f)(t)+fx_x_Normalize((*P_Tf),(*P_Tg),(*P_Th),t,e),
(*P_g)(t)+fx_x_Normalize((*P_Tg),(*P_Tf),(*P_Th),t,e),
(*P_h)(t)+fx_x_Normalize((*P_Th),(*P_Tf),(*P_Tg),t,e));
fclose(fp);
Pause();
}
Algorithme
[modifier | modifier le wikicode]r(t) = f(t) i + g(t) j + h(t) k T(t) = r'(t) / ||r'(t)|| N(t) = T'(t) / ||T'(t)||
Application : Tangente de f(x,y)
Préambule
[modifier | modifier le wikicode]La tangente dans Wikipedia.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Dessiner la tangente
[modifier | modifier le wikicode]- La méthode consiste à poser :
- x = i (ici i=1).
- D'utiliser la dérivée partielle par rapport à y.
- Puis écrire l'équation de la tangente d'une fonction en y.
c01.cDessiner la tangente |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "fa.h"
/* ------------------------------------ */
int main(void)
{
point2d p = i_point2d(1,2);
double h = .001;
printf(" Draw the equation of the tangent\n\n");
printf(" at the point P(%.0f,%.0f),\n\n",p.x,p.y);
printf(" on the plan x = %.0f for f(x,y).\n\n\n",p.x);
printf(" f : (x,y)-> %s\n\n\n", feq);
printf(" Cartesian form :\n\n"
" z = %f y %+f\n\n",
fxy_y(f,h,p),
f(p.x,p.y)-fxy_y(f,h,p)*p.y);
G_3d_p(i_WGnuplot(-10.,10.,-10.,10.),
i_VGnuplot( 55.,57., 1., 1.),
feq,f,
p);
printf(" Open the file \"a_main.plt\" with gnuplot.\n");
getchar();
return 0;
}
Le résultat.
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xspv.h"
#include "xplt.h"
#include "xfxy_x.h"
/* ------------------------------------ */
#include "kg_3d.h"
fa.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : fa.h */
/* ------------------------------------ */
double f(
double x,
double y)
{
return( (9-x*x-y*y) );
}
char feq[] = "9-x**2-y**2";
kg_3d.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_3d.h */
/* ------------------------------------ */
void G_3d_p(
W_Ctrl W,
View_Ctrl V,
char feq[],
double (*P_f)(double x, double y),
point2d p
)
{
FILE *fp;
double a,b;
double h = .001;
double step = 0.2;
fp = fopen("a_main.plt","w");
fprintf(fp,"set isosamples 50\n"
"set hidden3d\n"
"set xlabel \"X axis\"\n"
"set ylabel \"Y axis\"\n"
"set zlabel \"Z axis\" offset 1, 0\n"
"set view %0.3f, %0.3f, %0.3f, %0.3f \n"
"splot[%0.3f:%0.3f][%0.3f:%0.3f]\\\n"
"\"a_tan.plt\" with linesp lt 1 pt 3,\\\n"
"\"a_p.plt\" pt 20,\\\n"
"%s \n\n",
V.rot_x,V.rot_z,V.scale,V.scale_z,
W.xmini,W.xmaxi,W.ymini,W.ymaxi, feq);
fclose(fp);
fp = fopen("a_p.plt","w");
fprintf(fp," %6.3f %6.3f %6.3f\n",
p.x,p.y, (*P_f)(p.x,p.y));
fclose(fp);
a=fxy_y((*P_f),h,p);
b=((*P_f)(p.x,p.y)-fxy_y((*P_f),h,p)*p.y);
fp = fopen("a_tan.plt","w");
for(p.y=W.ymini; p.y<W.ymaxi;p.y+=step)
fprintf(fp," %6.3f %6.3f %6.3f\n",
p.x,p.y, a*p.y+b);
fclose(fp);
Pause();
}
Application : Gradient
Préambule
[modifier | modifier le wikicode]Le gradient dans Wikipedia.
Présentation
[modifier | modifier le wikicode]Dessiner la courbe de niveau C de f qui contient P et dessiner le gradient au point P.
N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Dessiner le gradient au point P
[modifier | modifier le wikicode]c01.cDessiner le gradient au point P |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "fa.h"
/* ------------------------------------ */
int main(void)
{
double h = .0001;
point2d p = i_point2d(2,1);
vector2d u = grad_fxy(g,h,p);
clrscrn();
printf(" Sketch both the level curve C of f "
"that contains P and grad(P) \n\n");
printf(" f : (x,y)-> %s\n\n", feq);
printf(" with p(%+.3f,%+.3f) \n\n",p.x,p.y);
printf(" In first sketch the graph of f(x,y) = 0\n\n");
G_3d_eq(i_WsGnuplot(-10,10,-10,10,-100,100),
i_VGnuplot( 55.,57.,1.,1.),
feq);
printf(" Open the file \"a_main.plt\" with gnuplot.\n");
getchar();
clrscrn();
printf(" The level curves have the form f(x,y) = k \n");
printf(" with p(%+.3f,%+.3f) k = %+.3f \n\n",
p.x,p.y,f(p.x,p.y));
printf(" The new function is :\n");
printf(" g : (x,y)-> %s\n\n", geq);
printf(" grad(g)]p = %+.3fi %+.3fj\n",u.i,u.j);
printf(" is a vector normal to the function\n");
printf(" g : (x,y)-> %s\n", geq);
printf(" at the point p(%+.3f,%+.3f)\n\n", p.x,p.y);
G_3d_levelcurvegradfxy(i_WsGnuplot(-6,6,-6,6,
g(p.x,p.y),
g(p.x,p.y)+.1),
g,geq,
p);
printf(" Open the file \"a_main.plt\" with gnuplot.\n"
" Press return to continue.\n");
getchar();
return 0;
}
Le résultat.
Sketch both the level curve C of f that contains P and grad(P) . f : (x,y)-> y**2-x**2 . with p(+2.000,+1.000) . In first sketch the graph of f(x,y) = 0 . Open the file "a_main.plt" with gnuplot.
| Résultat dans gnuplot |
|---|

|
The level curves have the form f(x,y) = k with p(+2.000,+1.000) k = -3.000 . The new function is : g : (x,y)-> y**2-x**2+3 . grad(g)]p = -4.000i +2.000j is a vector normal to the function g : (x,y)-> y**2-x**2+3 at the point p(+2.000,+1.000) . Open the file "a_main.plt" with gnuplot. Press return to continue.
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xspv.h"
#include "xplt.h"
#include "xfxy_x.h"
/* ------------------------------------ */
#include "kgrad.h"
#include "kg_3d.h"
#include "kg_grad.h"
fa.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : fa.h */
/* ------------------------------------ */
double f(
double x,
double y)
{
return( ( y*y-x*x) );
}
char feq[] = " y**2-x**2";
/* ------------------------------------ */
double g(
double x,
double y)
{
return( ( y*y-x*x+3) );
}
char geq[] = " y**2-x**2+3";
/* ------------------------------------ */
kgrad.hLe gradient |
|---|
/* ------------------------------------ */
/* Save as : kgrad.h */
/* ------------------------------------ */
vector2d grad_fxy(
double (*P_f)(double x,double y),
double h,
point2d p
)
{
vector2d u;
u.i = fxy_x((*P_f),h,p);
u.j = fxy_y((*P_f),h,p);
return(u);
}
kg_3d.hLa fonction graphique (1) |
|---|
/* ------------------------------------ */
/* Save as : kg_3d.h */
/* ------------------------------------ */
void G_3d_eq(
Ws_Ctrl W,
View_Ctrl V,
char feq[]
)
{
FILE *fp = fopen("a_main.plt","w");
fprintf(fp,"reset\n"
"set samples 40\n"
"set isosamples 40\n"
"set hidden3d\n"
"set view %0.3f, %0.3f, %0.3f, %0.3f \n"
"splot[%0.3f:%0.3f][%0.3f:%0.3f][%0.3f:%0.3f]\\\n"
"%s",
V.rot_x,V.rot_z,V.scale,V.scale_z,
W.xmini,W.xmaxi,W.ymini,W.ymaxi,W.zmini,W.zmaxi,
feq);
fclose(fp);
}
kg_grad.hDessiner la courbe de niveau qui contient P et le gradient au point P |
|---|
/* ------------------------------------ */
/* Save as : kg_grad.h */
/* ------------------------------------ */
void G_3d_levelcurvegradfxy(
Ws_Ctrl W,
double (*P_f)(double x, double y),
char feq[],
point2d p
)
{
FILE *fp;
double h = .0001;
fp = fopen("a_main.plt","w");
fprintf(fp,"reset\n"
"set samples 400\n"
"set isosamples 400\n"
"set view 1.000, 1.000, 1.000, 1.000 \n"
"splot[%0.3f:%0.3f][%0.3f:%0.3f][%0.3f:%0.3f]\\\n"
"%s,\\\n"
"\"a_vect\" with linesp lt 3\n",
W.xmini,W.xmaxi,W.ymini,W.ymaxi,W.zmini,W.zmaxi,
feq);
fclose(fp);
fp = fopen("a_vect","w");
fprintf(fp," %6.3f %6.3f %6.3f\n",
p.x, p.y, ((*P_f)(p.x,p.y)) );
fprintf(fp," %6.3f %6.3f %6.3f\n",
p.x+fxy_x((*P_f),h,p),
p.y+fxy_y((*P_f),h,p),
(*P_f)(p.x,p.y) );
fclose(fp);
}
Application : Vecteur normal
Préambule
[modifier | modifier le wikicode]Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Dessiner le vecteur normale au point P
[modifier | modifier le wikicode]c01.cDessiner le vecteur normale au point P |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "fa.h"
/* ------------------------------------ */
int main(void)
{
printf(" Draw the normal vector at the point P.\n\n"
" f : (x,y)-> %s\n\n", feq);
G_3d_v(i_WsGnuplot(-3,3,-3,3,-.5,2),
i_VGnuplot( 94.,22.,1.,1.),
feq,f,f_z,
i_point2d(1,0.));
printf(" Open the file \"a_main.plt\" with gnuplot.\n"
" Press return to continue.\n");
getchar();
return 0;
}
Le résultat.
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xplt.h"
#include "xspv.h"
#include "xfxyz_x.h"
/* ------------------------------------ */
#include "kg_3dv.h"
fa.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : fa.h */
/* ------------------------------------ */
double f(
double x,
double y)
{
return( (2*exp(-x) * cos(y)) );
}
char feq[] = "2*exp(-x) * cos(y)";
/* ------------------------------------ */
double f_z(
double x,
double y,
double z)
{
return( (2*exp(-x) * cos(y) - z) );
}
char f_zeq[] = "2*exp(-x) * cos(y) - z";
kg_3dv.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_3dv.h */
/* ------------------------------------ */
void G_3d_v(
Ws_Ctrl W,
View_Ctrl V,
char feq[],
double (*P_f) (double x, double y),
double (*P_fz)(double x, double y, double z),
point2d p
)
{
FILE *fp;
point3d p3d = i_point3d(p.x,p.y,(*P_f)(p.x,p.y));
fp = fopen("a_main.plt","w");
fprintf(fp,"reset\n"
"set samples 40\n"
"set isosamples 40\n"
"set hidden3d\n"
"set view %0.3f, %0.3f, %0.3f, %0.3f \n"
"splot[%0.3f:%0.3f][%0.3f:%0.3f][%0.3f:%0.3f]\\\n"
"\"a_ka.plt\" with linespoints,\\\n"
"%s ",
V.rot_x,V.rot_z,V.scale,V.scale_z,
W.xmini,W.xmaxi,W.ymini,W.ymaxi,W.zmini,W.zmaxi,
feq);
fclose(fp);
fp = fopen("a_ka.plt","w");
fprintf(fp," %6.3f %6.3f %6.3f\n",
p.x, p.y, ((*P_f)(p.x,p.y)) );
fprintf(fp," %6.3f %6.3f %6.3f\n",
p.x-fxyz_x((*P_fz),0.0001,p3d),
p.y-fxyz_y((*P_fz),0.0001,p3d),
((*P_f)(p.x,p.y))-fxyz_z((*P_fz),0.0001,p3d));
fclose(fp);
Pause();
}
Application : Plan tangent
Préambule
[modifier | modifier le wikicode]Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Dessiner le plan tangent au point P
[modifier | modifier le wikicode]c01.cDessiner le plan tangent au point P |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "fa.h"
/* ------------------------------------ */
int main(void)
{
printf(" Draw the Tangent plane.\n\n"
" f : (x,y)-> %s\n\n", feq);
G_3d_v( i_WsGnuplot(-4,4,-4,4,-1,2),
i_VGnuplot( 80.,38.,1.,1.),
feq,f,f_z,
i_point2d(2,0.));
printf(" Open the file \"a_main.plt\" with gnuplot.\n"
" Press return to continue.\n");
getchar();
return 0;
}
Le résultat.
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xspv.h"
#include "xplt.h"
#include "xfxy_x.h"
#include "xfxyz_x.h"
/* ------------------------------------ */
#include "kg_3d.h"
fa.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : fa.h */
/* ------------------------------------ */
double f(
double x,
double y)
{
return( cos(x)+cos(y) );
}
char feq[] = "cos(x)+cos(y)";
/* ------------------------------------ */
double f_z(
double x,
double y,
double z)
{
return( cos(x)+cos(y)-z );
}
char f_zeq[] = "cos(x)+cos(y)-z";
fa.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_3d.h */
/* ------------------------------------ */
void G_3d_v(
Ws_Ctrl W,
View_Ctrl V,
char feq[],
double (*P_f) (double x, double y),
double (*P_fz)(double x, double y, double z),
point2d p
)
{
FILE *fp;
point3d P3D = i_point3d(p.x,p.y,(*P_f)(p.x,p.y));
double radius = .5;
fp = fopen("a_main.plt","w");
fprintf(fp,"reset\n"
"set size ratio -1\n"
"set samples 40\n"
"set isosamples 40\n"
"set hidden3d\n"
"set view %0.3f, %0.3f, %0.3f, %0.3f \n"
"splot[%0.3f:%0.3f][%0.3f:%0.3f][%0.3f:%0.3f]\\\n"
" \"a_ka.plt\" with linesp lt 1 lw 4,\\\n"
" \"a_kb.plt\" with linesp lt 1 lw 4 ps 2,\\\n"
"%s lt 3",
V.rot_x,V.rot_z,V.scale,V.scale_z,
W.xmini,W.xmaxi,W.ymini,W.ymaxi,W.zmini,W.zmaxi,
feq);
fclose(fp);
fp = fopen("a_ka.plt","w");
fprintf(fp," %6.3f %6.3f %6.3f\n",
p.x, p.y, (*P_f)(p.x,p.y) );
fprintf(fp," %6.3f %6.3f %6.3f\n",
p.x-fxyz_x((*P_fz),0.0001,P3D),
p.y-fxyz_y((*P_fz),0.0001,P3D),
((*P_f)(p.x,p.y))-fxyz_z((*P_fz),0.0001,P3D));
fclose(fp);
fp = fopen("a_kb.plt","w");
fprintf(fp," %6.3f %6.3f %6.3f\n",
p.x+radius,
p.y+radius,
fxy_x((*P_f),0.0001,p)*(+radius)+
fxy_y((*P_f),0.0001,p)*(+radius)+
(*P_f)(p.x,p.y)
);
fprintf(fp," %6.3f %6.3f %6.3f\n",
p.x-radius,
p.y+radius,
fxy_x((*P_f),0.0001,p)*(-radius)+
fxy_y((*P_f),0.0001,p)*(+radius)+
(*P_f)(p.x,p.y)
);
fprintf(fp," %6.3f %6.3f %6.3f\n",
p.x-radius,
p.y-radius,
fxy_x((*P_f),0.0001,p)*(-radius)+
fxy_y((*P_f),0.0001,p)*(-radius)+
(*P_f)(p.x,p.y)
);
fprintf(fp," %6.3f %6.3f %6.3f\n",
p.x+radius,
p.y-radius,
fxy_x((*P_f),0.0001,p)*(+radius)+
fxy_y((*P_f),0.0001,p)*(-radius)+
(*P_f)(p.x,p.y)
);
fprintf(fp," %6.3f %6.3f %6.3f\n",
p.x+radius,
p.y+radius,
fxy_x((*P_f),0.0001,p)*(+radius)+
fxy_y((*P_f),0.0001,p)*(+radius)+
(*P_f)(p.x,p.y)
);
fprintf(fp," %6.3f %6.3f %6.3f\n",
p.x-radius,
p.y-radius,
fxy_x((*P_f),0.0001,p)*(-radius)+
fxy_y((*P_f),0.0001,p)*(-radius)+
(*P_f)(p.x,p.y)
);
fprintf(fp," %6.3f %6.3f %6.3f\n",
p.x+radius,
p.y-radius,
fxy_x((*P_f),0.0001,p)*(+radius)+
fxy_y((*P_f),0.0001,p)*(-radius)+
(*P_f)(p.x,p.y)
);
fprintf(fp," %6.3f %6.3f %6.3f\n",
p.x-radius,
p.y+radius,
fxy_x((*P_f),0.0001,p)*(-radius)+
fxy_y((*P_f),0.0001,p)*(+radius)+
(*P_f)(p.x,p.y)
);
fclose(fp);
Pause();
}
Commande pause 1
Préambule
[modifier | modifier le wikicode]Créer une animation avec la commande "pause 1" de gnuplot. Ces exemples dans cette page présentent le code sans animation. Pour le troisième exemple voir le chapitre Animation Tangente Pour un autre exemple, voir le chapitre Tangente d'une courbe
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Le cadre
[modifier | modifier le wikicode]c01.cCréer une liste de commande. |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "kg_tan1.h"
/* ------------------------------------ */
int main(void)
{
t_Ctrl Pic = {0,5,1};
G_TanA(Pic);
printf(" Read \"a_main.plt\".\n\n"
" Press return to continue");
getchar();
return 0;
}
Le résultat.
# Gnuplot file : load "a_main.plt"
set zeroaxis
pause 1
pause 1
pause 1
pause 1
pause 1
reset
Dessiner
[modifier | modifier le wikicode]- Dessiner une chaîne de caractères.
/* ------------------------------------ */
/* Save as : c02.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "kg_tan2.h"
#include "f2.h"
/* ------------------------------------ */
int main(void)
{
printf(" f : x-> %s \n", feq);
G_TanA(i_WGnuplot(-7, 7,-2,2),
i_time(0,5,1),
feq);
printf(" load \"a_main.plt\" with gnuplot. \n\n"
" Press return to continue");
getchar();
return 0;
}
Le résultat.
# Gnuplot file : load "a_main.plt"
set zeroaxis
plot [-7.000:7.000] [-2.000:2.000] cos(x)
pause 1
plot [-7.000:7.000] [-2.000:2.000] cos(x)
pause 1
plot [-7.000:7.000] [-2.000:2.000] cos(x)
pause 1
plot [-7.000:7.000] [-2.000:2.000] cos(x)
pause 1
plot [-7.000:7.000] [-2.000:2.000] cos(x)
pause 1
reset
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xplt.h"
f2.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : f2.h */
/* ----------- f ---------------------- */
double f(
double x)
{
return( cos(x));
}
char feq[] = " cos(x)";
kg_tan1.hLa fonction graphique pour c01.c |
|---|
/* ------------------------------------ */
/* Save as : kg_tan1.h */
/* ------------------------------------ */
void G_TanA(
t_Ctrl Pic
)
{
FILE *fp = fopen("a_main.plt","w");
double p;
fprintf(fp,"# Gnuplot file : load \"a_main.plt\" \n\n"
" set zeroaxis\n\n");
for(p=Pic.mini; p<Pic.maxi; p+=Pic.step)
fprintf(fp," pause 1\n\n");
fprintf(fp," reset");
fclose(fp);
}
kg_tan2.hLa fonction graphique pour c02.c |
|---|
/* ------------------------------------ */
/* Save as : kg_tan2.h */
/* ------------------------------------ */
void G_TanA(
W_Ctrl w,
t_Ctrl Pic,
char fEQ[]
)
{
FILE *fp = fopen("a_main.plt","w");
double p ;
fprintf(fp,"# Gnuplot file : load \"a_main.plt\" \n\n"
" set zeroaxis\n\n");
for(p = Pic.mini; p<Pic.maxi; p+=Pic.step)
fprintf(fp," plot [%0.3f:%0.3f] [%0.3f:%0.3f] "
" %s\n"
" pause 1\n\n",
w.xmini,w.xmaxi,w.ymini,w.ymaxi,
fEQ);
fprintf(fp," reset");
fclose(fp);
}
Animer un point
Préambule
[modifier | modifier le wikicode]Créer une animation avec la commande "pause 1" de gnuplot. La position du point est dans les fichiers a_p***. Dans cet exemple la commande "pause 1" a été oublié.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
L'animation
[modifier | modifier le wikicode]c01.cCréer une liste de commande |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "f.h"
/* ------------------------------------ */
int main(void)
{
G_plt(i_WGnuplot(-5,5, -1,10),
i_time(-3.,5., .01),
feq,f);
printf(" open the file \"a_main.plt\" with Gnuplot.\n\n"
" Press return to continue\n");
getchar();
return 0;
}
Le résultat.
# Gnuplot file : load "a_main.plt"
reset
plot[-5.000:5.000] [-1.000:10.000]\
-0.5*x**2 + 1.0*x + 8.0 lt 13,\
"a_paab" pt 7 ps 3
reset
plot[-5.000:5.000] [-1.000:10.000]\
-0.5*x**2 + 1.0*x + 8.0 lt 13,\
"a_paac" pt 7 ps 3
reset
plot[-5.000:5.000] [-1.000:10.000]\
-0.5*x**2 + 1.0*x + 8.0 lt 13,\
"a_paad" pt 7 ps 3
reset
plot[-5.000:5.000] [-1.000:10.000]\
-0.5*x**2 + 1.0*x + 8.0 lt 13,\
"a_paae" pt 7 ps 3
reset
plot[-5.000:5.000] [-1.000:10.000]\
-0.5*x**2 + 1.0*x + 8.0 lt 13,\
"a_paaf" pt 7 ps 3
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xplt.h"
/* ------------------------------------ */
#include "kg_f.h"
f.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : f.h */
/* ------------------------------------ */
double f(
double x)
{
return( -0.5*x*x + 1.0*x + 8.0);
}
char feq[] = "-0.5*x**2 + 1.0*x + 8.0";
kg_f.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_f.h */
/* ------------------------------------ */
void G_plt(
W_Ctrl w,
t_Ctrl Pic,
char feq[],
double (*P_f)(double x)
)
{
FILE *fp1;
FILE *fp2;
double p;
char files[]= "a_paaa";
fp1 = fopen("a_main.plt","w");
fprintf(fp1,"# Gnuplot file : load \"a_main.plt\" \n\n");
for(p=Pic.mini; p<Pic.maxi; p+=Pic.step)
{
fprintf(fp1," reset\n"
" plot[%0.3f:%0.3f] [%0.3f:%0.3f]\\\n"
" %s lt 13,\\\n"
" \"%s\" pt 7 ps 3 \n",
w.xmini,w.xmaxi,w.ymini,w.ymaxi,
feq,
NewName(files));
fp2 = fopen(files,"w");
fprintf(fp2," %+0.6f %+0.6f",p,(*P_f)(p));
fclose(fp2);
}
fclose(fp1);
}
Animer deux points
Préambule
[modifier | modifier le wikicode]Créer une animation avec la commande "pause 1" de gnuplot. La position des deux points sont dans les fichiers a_p***
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
L'animation
[modifier | modifier le wikicode]c01.cCréer une liste de commande. |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "f.h"
/* ------------------------------------ */
int main(void)
{
G_plt(i_WGnuplot(-5,5, -1,10),
i_time(-3.,5., .01),
feq,f);
printf(" open the file \"a_main.plt\" with Gnuplot.\n\n"
" Press return to continue\n");
getchar();
return 0;
}
Le résultat.
# Gnuplot file : load "a_main.plt"
reset
plot[-4.000:6.000] [-1.000:10.000]\
-0.5*x**2 + 1.0*x + 8.0 lt 13,\
"a_paab" pt 7 ps 3
reset
plot[-4.000:6.000] [-1.000:10.000]\
-0.5*x**2 + 1.0*x + 8.0 lt 13,\
"a_paac" pt 7 ps 3
reset
plot[-4.000:6.000] [-1.000:10.000]\
-0.5*x**2 + 1.0*x + 8.0 lt 13,\
"a_paad" pt 7 ps 3
reset
plot[-4.000:6.000] [-1.000:10.000]\
-0.5*x**2 + 1.0*x + 8.0 lt 13,\
"a_paae" pt 7 ps 3
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xplt.h"
/* ------------------------------------ */
#include "xg_f.h"
f.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : f.h */
/* ------------------------------------ */
double f(
double x)
{
return( -0.5*x*x + 1.0*x + 8.0);
}
char feq[] = "-0.5*x**2 + 1.0*x + 8.0";
xg_f.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : xg_f.h */
/* ------------------------------------ */
void G_plt(
W_Ctrl w,
t_Ctrl Pic,
char feq[],
double (*P_f)(double x)
)
{
FILE *fp1;
FILE *fp2;
double p,q;
char files[] = "a_paaa";
fp1 = fopen("a_main.plt","w");
fprintf(fp1,"# Gnuplot file : load \"a_main.plt\" \n\n");
for(p=q=Pic.mini; p<Pic.maxi; p+=Pic.step)
{
fprintf(fp1," reset\n"
" pause %0.2f \n"
" plot[%0.3f:%0.3f] [%0.3f:%0.3f]\\\n"
" %s lt 13,\\\n"
" \"%s\" pt 7 ps 3 \n",
Pic.step,w.xmini,w.xmaxi,w.ymini,w.ymaxi,
feq,
NewName(files));
fp2 = fopen(files,"w");
fprintf(fp2," %+0.6f %+0.6f\n",p,(*P_f)(p));
fprintf(fp2," %+0.6f %+0.6f\n",q,(*P_f)(p));
fclose(fp2);
}
fclose(fp1);
}
Animation : Tangente
Préambule
[modifier | modifier le wikicode]La tangente dans Wikipedia.
Voir l'introduction pour créer une animation avec gnuplot sous windows ou linux.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Animer la tangente
[modifier | modifier le wikicode]Nous utilisons ici la méthode avec la commande "pause 1" de gnuplot.
c01.cAnimer la tangente |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "f2.h"
/* ------------------------------------ */
int main(void)
{
printf(" f : x-> %s \n", feq);
printf(" f': x-> %s\n\n",Dfeq);
printf(" The equation of the tangent is : \n\n");
printf(" y = f'(c) (x-c) + f(c) \n\n");
G_TanA(i_WGnuplot(-7, 7,-2,2),
i_time(-1.5,2,.2),
feq,
f,
Df);
printf(" load \"a_main.plt\" with gnuplot. \n\n"
" Press return to continue");
getchar();
return 0;
}
Le résultat dans a_main.plt
# Gnuplot file : load "a_main.plt"
set zeroaxis
plot [-7.000:7.000] [-2.000:2.000] cos(x), 0.997495*x +1.566980
pause 1
plot [-7.000:7.000] [-2.000:2.000] cos(x), 0.963558*x +1.520124
pause 1
plot [-7.000:7.000] [-2.000:2.000] cos(x), 0.891207*x +1.433924
pause 1
plot [-7.000:7.000] [-2.000:2.000] cos(x), 0.783327*x +1.326604
pause 1
plot [-7.000:7.000] [-2.000:2.000] cos(x), 0.644218*x +1.215795
pause 1
plot [-7.000:7.000] [-2.000:2.000] cos(x), 0.479426*x +1.117295
pause 1
plot [-7.000:7.000] [-2.000:2.000] cos(x), 0.295520*x +1.043993
pause 1
plot [-7.000:7.000] [-2.000:2.000] cos(x), 0.099833*x +1.004988
pause 1
plot [-7.000:7.000] [-2.000:2.000] cos(x), -0.099833*x +1.004988
pause 1
plot [-7.000:7.000] [-2.000:2.000] cos(x), -0.295520*x +1.043993
pause 1
plot [-7.000:7.000] [-2.000:2.000] cos(x), -0.479426*x +1.117295
pause 1
plot [-7.000:7.000] [-2.000:2.000] cos(x), -0.644218*x +1.215795
pause 1
plot [-7.000:7.000] [-2.000:2.000] cos(x), -0.783327*x +1.326604
pause 1
plot [-7.000:7.000] [-2.000:2.000] cos(x), -0.891207*x +1.433924
pause 1
plot [-7.000:7.000] [-2.000:2.000] cos(x), -0.963558*x +1.520124
pause 1
plot [-7.000:7.000] [-2.000:2.000] cos(x), -0.997495*x +1.566980
pause 1
plot [-7.000:7.000] [-2.000:2.000] cos(x), -0.991665*x +1.556986
pause 1
plot [-7.000:7.000] [-2.000:2.000] cos(x), -0.946300*x +1.474681
pause 1
reset
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xplt.h"
/* ------------------------------------ */
#include "kg_tan.h"
f2.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : f2.h */
/* ----------- f ---------------------- */
double f(
double x)
{
return( cos(x));
}
char feq[] = " cos(x)";
/* ------------ f' --------------------- */
double Df(
double x)
{
return( (-sin(x)) );
}
char Dfeq[] = " (-sin(x)) ";
kg_tan.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_tan.h */
/* ------------------------------------
y = ax + b [P(xp,yp);(y-yp)=a(x-xp)]
a = f'(x)
b = y - ax
b = y - f'(x)x
b = f(x) - f'(x)x
x=p
a = f'(p)
b = f(p) - f'(p)p
------------------------------------ */
void G_TanA(
W_Ctrl w,
t_Ctrl Pic,
char fEQ[],
double (*P_f)(double x),
double (*PDf)(double x)
)
{
FILE *fp = fopen("a_main.plt","w");
double p = Pic.mini;
fprintf(fp,"# Gnuplot file : load \"a_main.plt\"\n"
" set zeroaxis\n"
" reset\n\n");
for(;p<Pic.maxi;p+=Pic.step)
fprintf(fp," plot [%0.3f:%0.3f] [%0.3f:%0.3f] "
"%s, "
" %0.6f*x %+0.6f \n"
" pause 1\n\n",
w.xmini,w.xmaxi,w.ymini,w.ymaxi,
fEQ,
(*PDf)(p), (-(*PDf)(p)*p+(*P_f)(p)) );
fprintf(fp," reset");
fclose(fp);
}
Animation : Cercle de courbure
Préambule
[modifier | modifier le wikicode]Cercle de courbure dans Wikipedia.
Voir l'introduction pour créer une animation avec gnuplot sous windows ou linux.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et récupérer aussi ceux du chapitre Dessiner :Cercle de courbure.
Animer
[modifier | modifier le wikicode]c01.cAnimer le cercle de courbure pour une fonction f(x) |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "fb.h"
/* ------------------------------------ */
int main(void)
{
double x = -3.5;
double e = .001;
char Name[FILENAME_MAX] = "a_circle.plt";
for(;x<3.5;x+=.1)
{
circle(Name,
1./K_y_2d(f,x,e),
h_y_2d(f,x,e),
k_y_2d(f,x,e));
G_C_2d(i_WGnuplot(-4.,4.,-2.,2.),
f,x,e,
feq);}
printf(" open the file \"a_main.plt\" with Gnuplot.\n\n"
" Use the command replot of gnuplot \n\n");
return 0;
}
Le résultat.
| Résultat dans gnuplot |
|---|

|
| Résultat dans gnuplot |
|---|

|
| Résultat dans gnuplot |
|---|

|
Animation : Tangente d'une courbe
Préambule
[modifier | modifier le wikicode]La tangente dans Wikipedia.
Voir l'introduction pour créer une animation avec gnuplot sous windows ou linux.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Animer la tangente
[modifier | modifier le wikicode]Nous utilisons ici la méthode avec la commande "pause 1" de gnuplot.
c01.cAnimer la tangente |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "fe.h"
/* ------------------------------------ */
int main(void)
{
printf(" Let C be the curve consisting of all"
" ordered pairs (f(t),g(t)).\n\n"
" With\n\n"
" f : t-> %s\n\n"
" g : t-> %s\n\n", feq, geq);
G_NormalA( i_WGnuplot(-10.,10.,-5.,5.),
i_time( .1,2.*PI,.05),
i_time(0.0,2.*PI,.05),
f,
g,
DgDf);
printf(" To see the curve C, open the file \"a_main.plt\""
" with Gnuplot.\n\n"
"\n Press return to continue");
getchar();
return 0;
}
Le résultat dans a_main.plt
# Gnuplot file : load "a_main.plt"
set zeroaxis
set size ratio -1
plot [-10.000:10.000] [-5.000:5.000]\
"data.plt" with linesp lt 3 pt 1,\
-0.052250*x +3.015895, 19.138612*x -8.326680
pause 1
plot [-10.000:10.000] [-5.000:5.000]\
"data.plt" with linesp lt 3 pt 1,\
-0.082980*x +3.038500, 12.051102*x -7.517315
pause 1
plot [-10.000:10.000] [-5.000:5.000]\
"data.plt" with linesp lt 3 pt 1,\
-0.120357*x +3.076117, 8.308636*x -6.442618
pause 1
plot [-10.000:10.000] [-5.000:5.000]\
"data.plt" with linesp lt 3 pt 1,\
-0.169064*x +3.137218, 5.914933*x -5.156957
pause 1
plot [-10.000:10.000] [-5.000:5.000]\
"data.plt" with linesp lt 3 pt 1,\
-0.237705*x +3.238412, 4.206886*x -3.724725
pause 1
plot [-10.000:10.000] [-5.000:5.000]\
"data.plt" with linesp lt 3 pt 1,\
-0.344572*x +3.415897, 2.902154*x -2.216673
pause 1
plot [-10.000:10.000] [-5.000:5.000]\
"data.plt" with linesp lt 3 pt 1,\
-0.537340*x +3.764826, 1.861020*x -0.705905
pause 1
plot [-10.000:10.000] [-5.000:5.000]\
"data.plt" with linesp lt 3 pt 1,\
-0.993042*x +4.639209, 1.007007*x +0.736221
pause 1
plot [-10.000:10.000] [-5.000:5.000]\
"data.plt" with linesp lt 3 pt 1,\
-3.388779*x +9.393329, 0.295092*x +2.044043
pause 1
plot [-10.000:10.000] [-5.000:5.000]\
"data.plt" with linesp lt 3 pt 1,\
3.303093*x -4.027901, -0.302747*x +3.161169
pause 1
reset
| Résultat dans gnuplot |
|---|

|
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xplt.h"
/* ------------------------------------ */
#include "kg_tan.h"
fe.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : fe.h */
/* ------------------------------------ */
double f(
double t)
{
double a=2;
double k1=3;
return( a*sin(k1*t) );
}
char feq[] = "a*sin(k1*t)";
/* ------------------------------------ */
double Df(
double t)
{
double a=2;
double k1=3;
return( a*cos(k1*t)*k1);
}
char Dfeq[] = "a*cos(k1*t)*k1";
/* ------------------------------------ */
double g(
double t)
{
double b =3;
double k2=1;
return( b*cos(k2*t) );
}
char geq[] = "b*cos(k2*t)";
/* ------------------------------------ */
double Dg(
double t)
{
double b =3;
double k2=1;
return( -b*sin(k2*t)*k2 );
}
char Dgeq[] = "-b*sin(k2*t)*k2";
/* ------------------------------------ */
double DgDf(
double t)
{
return(Dg(t)/Df(t));
}
kg_tan.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_tan.h */
/* ------------------------------------ */
void G_NormalA(
W_Ctrl W,
t_Ctrl C,
t_Ctrl T,
double (*P_f) (double t),
double (*P_g) (double t),
double (*PDgDf)(double t)
)
{
FILE *fp;
double c;
double t;
fp = fopen("a_main.plt","w");
fprintf(fp,"# Gnuplot file : load \"a_main.plt\" \n\n"
" set zeroaxis\n"
" set size ratio -1\n");
for(c=C.mini; c<C.maxi; c+=C.step)
{
fprintf(fp," plot [%0.3f:%0.3f] [%0.3f:%0.3f]\\\n"
" \"data.plt\" with linesp lt 3 pt 1,\\\n"
" %0.6f*x %+0.6f,"
" %0.6f*x %+0.6f\n"
" pause 1\n",
W.xmini,W.xmaxi,W.ymini,W.ymaxi,
(*PDgDf)(c),
(-(*PDgDf)(c)*(*P_f)(c)+(*P_g)(c)),
-1./(*PDgDf)(c),
-1./(-(*PDgDf)(c))*(*P_f)(c)+(*P_g)(c));
}
fprintf(fp," reset");
fclose(fp);
fp = fopen("data.plt","w");
for(t=T.mini; t<=T.maxi; t+=T.step)
fprintf(fp," %6.6f %6.6f\n",
(*P_f)(t),(*P_g)(t));
fclose(fp);
}
Animation : Cercle de courbure d'une courbe
Préambule
[modifier | modifier le wikicode]Cercle de courbure dans Wikipedia.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et de recuperer aussi ceux du chapitre Dessiner : Cercle de courbure d'une courbe.
Animer
[modifier | modifier le wikicode]c01.cAnimer le cercle de courbure pour une fonction (f(t),g(t)). |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "fb.h"
/* ------------------------------------ */
int main(void)
{
double t = 0.;
double e = .001;
char Name[FILENAME_MAX] = "a_circle.plt";
for(;t<2*PI;t+=.03)
{
circle(Name,
1./fabs(Kt_2d(f,g,t,e)),
cx_2d(f,g,t,e),
cy_2d(f,g,t,e));
G_C_2d(i_WGnuplot(-4,8,-2,4),
i_time(0.,2*PI,.03),
f,g,t,
e);
}
printf(" open the file \"a_main.plt\" with Gnuplot.\n\n"
" Use the command replot of gnuplot \n\n");
return 0;
}
Le résultat.
| Résultat dans gnuplot |
|---|

|
| Résultat dans gnuplot |
|---|

|
| Résultat dans gnuplot |
|---|

|
Animation : Cycloïde
Préambule
[modifier | modifier le wikicode]La cycloïde dans Wikipedia.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Animer
[modifier | modifier le wikicode]c01.cAnimer une cycloide |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
/* ------------------------------------ */
int main(void)
{
double x=0;
printf(" Let C be the curve consisting of all ordered \n"
" pairs (f(t),g(t)) \n\n"
" f : t-> %s\n"
" g : t-> %s\n",feq,feq);
printf("\n\n Open the file \"a_main.plt\" with Gnuplot."
"\n\n Use the \"replot\" command of gnuplot.\n\n");
for(;x<4*PI;x+=.1)
G_CurveA(i_WGnuplot(-1.,14,-1.,6.),
i_time(0.,4.*PI,.01),
f,g,
x);
printf(" Press return to continue\n");
getchar();
return 0;
}
Le résultat.
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xplt.h"
/* ------------------------------------ */
#include "curve.h"
#include "kg_curve.h"
curve.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : curve.h */
/* ------------------------------------ */
double f(
double t)
{
return(1*t-sin(t));
}
char feq[] = "1*t-sin(t)";
/* ------------------------------------ */
double g(
double t)
{
return(1-cos(t));
}
char geq[] = "1-cos(t)";
/* ------------------------------------ */
kg_curve.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_curve.h */
/* ------------------------------------ */
void G_CurveA(
W_Ctrl W,
t_Ctrl T,
double (*P_f)(double t),
double (*P_g)(double t),
double x
)
{
FILE *fp;
double t;
fp = fopen("a_main.plt","w");
fprintf(fp," reset\n"
" set zeroaxis lt 8\n"
" set size ratio -1\n"
" set grid\n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f] \\\n"
" \"a_curve.plt\" with line, \\\n"
" \"a_circle.plt\" with line,\\\n"
" \"a_radius.plt\" with linesp",
W.xmini,W.xmaxi,W.ymini,W.ymaxi);
fclose(fp);
fp = fopen("a_curve.plt","w");
for(t=T.mini; t<=T.maxi; t+=T.step)
fprintf(fp," %6.5f %6.5f\n",(*P_f)(t),(*P_g)(t));
fclose(fp);
fp = fopen("a_radius.plt","w");
fprintf(fp," %6.5f 1.000\n",x);
fprintf(fp," %6.5f %6.5f\n",(*P_f)(x),(*P_g)(x));
fclose(fp);
fp = fopen("a_circle.plt","w");
for(t=0;t<2.01*PI;t+=.1)
fprintf(fp," %6.5f %6.5f\n",cos(t)+x,sin(t)+1);
fclose(fp);
Pause();
}
Animation : Cardioïde
Préambule
[modifier | modifier le wikicode]La cardioïde dans Wikipedia.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Animer
[modifier | modifier le wikicode]c01.cAnimer une cardioïde |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
/* ------------------------------------ */
int main(void)
{
double x;
printf(" Let C be the curve consisting of all ordered \n"
" pairs (f(t),g(t)) \n\n"
" f : t-> %s\n"
" g : t-> %s\n",feq,feq);
printf("\n\n Open the file \"a_main.plt\" with Gnuplot."
"\n\n Use the \"replot\" command of gnuplot.\n\n");
for(x=0;x<2.01*PI;x+=.03)
G_C_2d(i_WGnuplot(-10.,10,-5.,5.),
i_time(0.,2.*PI,.1),
f,g,x);
printf(" Press return to continue\n");
getchar();
return 0;
}
Le résultat.
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xplt.h"
/* ------------------------------------ */
#include "curve.h"
#include "kg_curve.h"
curve.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : curve.h */
/* ------------------------------------ */
double f(
double t)
{
double a=1;
return( a*(2*cos(t)-cos(2*t)));
}
char feq[] = "a*(2*cos(t)-cos(2*t))";
/* ------------------------------------ */
double g(
double t)
{
double a=1.;
return( a*(2*sin(t)-sin(2*t)));
}
char geq[] = "a*(2*sin(t)-sin(2*t))";
kg_curve.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_curve.h */
/* ------------------------------------ */
void G_C_2d(
W_Ctrl W,
t_Ctrl T,
double (*P_f)(double t),
double (*P_g)(double t),
double x
)
{
FILE *fp;
double t;
fp = fopen("a_main.plt","w");
fprintf(fp," reset\n"
" set zeroaxis lt 8\n"
" set size ratio -1\n"
" set grid\n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f] \\\n"
" \"a_circle.plt\" with line,\\\n"
" \"b_circle.plt\" with line,\\\n"
" \"a_curve.plt\" with line, \\\n"
" \"a_radius.plt\" with linesp",
W.xmini,W.xmaxi,W.ymini,W.ymaxi);
fclose(fp);
fp = fopen("a_curve.plt","w");
for(t=T.mini; t<=T.maxi; t+=T.step)
fprintf(fp," %6.5f %6.5f\n",(*P_f)(t),(*P_g)(t));
fclose(fp);
fp = fopen("a_radius.plt","w");
fprintf(fp," %6.5f %6.5f\n",2*cos(x)+0,2*sin(x)+0);
fprintf(fp," %6.5f %6.5f\n",(*P_f)(x),(*P_g)(x));
fclose(fp);
fp = fopen("a_circle.plt","w");
for(t=0;t<2.01*PI;t+=.1)
fprintf(fp," %6.5f %6.5f\n",cos(t)+0,sin(t)+0);
fclose(fp);
fp = fopen("b_circle.plt","w");
for(t=0;t<2.01*PI;t+=.1)
fprintf(fp," %6.5f %6.5f\n",
cos(t)+2*cos(x),sin(t)+2*sin(x));
fclose(fp);
Pause();
}
Animation : Rosace
Préambule
[modifier | modifier le wikicode]Coordonnées polaires dans Wikipedia.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Animer
[modifier | modifier le wikicode]c01.cAnimer une rosace |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "fr.h"
/* ------------------------------------ */
int main(void)
{
double maxi;
printf(" r : t-> %s\n\n", req);
printf("\n\n Open the file \"a_main.plt\" with Gnuplot."
"\n\n Use the \"replot\" command of gnuplot.\n\n");
for(maxi=0;maxi<=2.*PI+.1;maxi+=.1)
G_polar(i_WGnuplot(-1.,1.,-1.,1.),
i_time(0,maxi,0.01),
r);
printf("\n Press return to continue");
getchar();
return 0;
}
Le résultat.
| Résultat dans gnuplot |
|---|
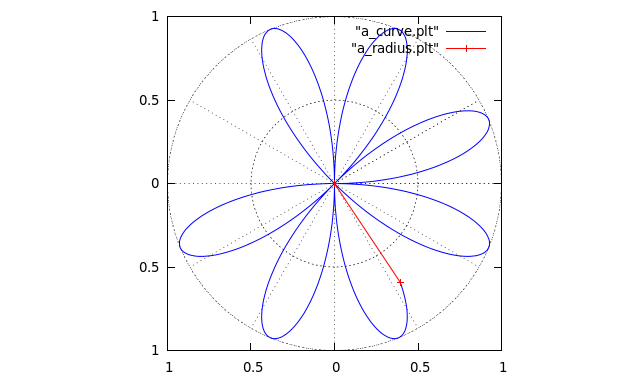
|
| Résultat dans gnuplot |
|---|
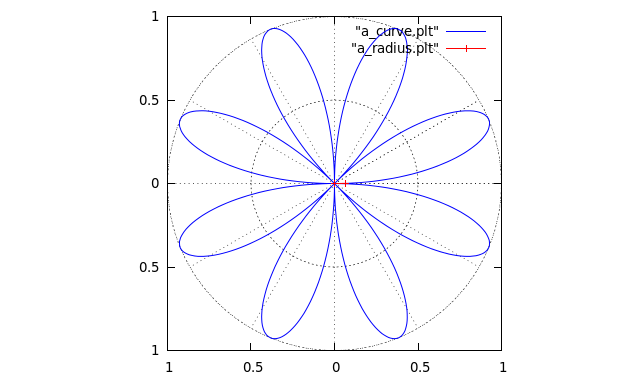
|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xplt.h"
/* ------------------------------------ */
#include "kg_polar.h"
fr.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : fr.h */
/* ------------------------------------ */
double r(
double t)
{
double n=4;
return( sin(n*t));
}
char req[] = "sin(n*t)";
kg_polar.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_polar.h */
/* ------------------------------------ */
void G_polar(
W_Ctrl W,
t_Ctrl T,
double (*P_r)(double k)
)
{
FILE *fp;
double t;
fp = fopen("a_main.plt","w");
fprintf(fp," set size ratio -1\n"
" set polar\n"
" set grid polar\n\n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f] [%0.3f:%0.3f] \\\n"
" \"a_curve.plt\" with line lt 3, \\\n"
" \"a_radius.plt\" with linesp lt 1 pt 1",
0., 2.*PI,W.xmini,W.xmaxi,W.ymini,W.ymaxi);
fclose(fp);
fp = fopen("a_curve.plt","w");
for(t=T.mini; t<=T.maxi; t+=T.step)
fprintf(fp," %6.3f %6.3f\n",t,(*P_r)(t));
fclose(fp);
fp = fopen("a_radius.plt","w");
fprintf(fp," 0. 0. \n %6.3f %6.3f\n",
t-T.step,(*P_r)(t-T.step));
fclose(fp);
Pause();
}
Animation : Vecteur unitaire
Préambule
[modifier | modifier le wikicode]Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Animer
[modifier | modifier le wikicode]c01.cAnimer a un vecteur normale unitaire et un vecteur tangent unitaire. |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "fb.h"
/* ------------------------------------ */
int main(void)
{
double t=0.;
printf(" r(t) = f(t)i + g(t)j \n\n"
" With \n\n"
" f : t-> %s \n"
" g : t-> %s\n\n",feq,geq);
printf("\n\n Open the file \"a_main.plt\" with Gnuplot."
"\n\n Use the \"replot\" command of gnuplot.\n\n");
for(;t<4.*PI;t+=.05)
G_Curve_2d(i_WGnuplot(-2,2,-2,2),
i_time( 0.,4.*PI,.05),
f,g,Tf,Tg,
t);
printf(" Press return to continue\n");
getchar();
return 0;
}
Le résultat.
| Résultat dans gnuplot |
|---|

|
Les fichiers h partagés
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xplt.h"
#include "xfx_x.h"
/* ------------------------------------ */
#include "knfx_x.h"
#include "kg_ctan1.h"
knfx_x.hNormalisé |
|---|
/* ------------------------------------ */
/* Save as : knfx_x.h */
/* ------------------------------------ */
double fx_x_Normalize(
double (*P_f)(double x),
double (*P_g)(double x),
double t,
double e
)
{
double Df=fx_x((*P_f),t,e);
double Dg=fx_x((*P_g),t,e);
return(Df/sqrt(Df*Df+Dg*Dg));
}
fb.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : fb.h */
/* ------------------------------------ */
double f(
double t)
{
return( cos(t)*cos(t));
}
char feq[] = "cos(t)**2";
/* ------------------------------------ */
double g(
double t)
{
return( 2*sin(t));
}
char geq[] = "2*sin(t)";
/* ------------------------------------ */
double Tf(
double t)
{
return(
(-cos(t)*sin(t))
/
sqrt(pow(cos(t),2)*pow(sin(t),2)+pow(cos(t),2)));
}
/* ------------------------------------ */
double Tg(
double t)
{
return(
cos(t)
/
sqrt(pow(cos(t),2)*pow(sin(t),2)+pow(cos(t),2)));
}
/* ------------------------------------ */
kg_ctan1.hLa fonction graphique |
|---|
/* ------------------------------------ */
/* Save as : kg_ctan1.h */
/* ------------------------------------ */
void G_Curve_2d(
W_Ctrl W,
t_Ctrl T,
double (*P_f)(double t),
double (*P_g)(double t),
double (*P_Tf)(double t),
double (*P_Tg)(double t),
double t
)
{
FILE *fp;
double i;
double e=.001;
fp = fopen("a_main.plt","w");
fprintf(fp," reset\n"
" set zeroaxis lt 8\n"
" set grid\n\n"
" set size ratio -1\n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f]\\\n"
" \"a_curve.plt\" with line lt 3,\\\n"
" \"a_radius.plt\" with line lt 2,\\\n"
" \"a_vector.plt\" with line lt 4,\\\n"
" \"a_normal.plt\" with line lt 1 \n",
W.xmini,W.xmaxi,W.ymini,W.ymaxi);
fclose(fp);
fp = fopen("a_curve.plt","w");
for(i=T.mini; i<=T.maxi+T.step; i+=T.step)
fprintf(fp," %6.3f %6.3f\n",(*P_f)(i),(*P_g)(i));
fclose(fp);
fp = fopen("a_radius.plt","w");
fprintf(fp," 0 0 \n %6.5f %6.5f \n",
(*P_f)(t),(*P_g)(t));
fclose(fp);
fp = fopen("a_vector.plt","w");
fprintf(fp," %6.5f %6.5f \n %6.5f %6.5f \n",
(*P_f)(t),
(*P_g)(t),
(*P_f)(t)+fx_x_Normalize((*P_f),(*P_g),t,e),
(*P_g)(t)+fx_x_Normalize((*P_g),(*P_f),t,e) );
fclose(fp);
fp = fopen("a_normal.plt","w");
fprintf(fp," %6.5f %6.5f \n %6.5f %6.5f \n",
(*P_f)(t),
(*P_g)(t),
(*P_f)(t)+fx_x_Normalize((*P_Tf),(*P_Tg),t,e),
(*P_g)(t)+fx_x_Normalize((*P_Tg),(*P_Tf),t,e) );
fclose(fp);
Pause();
}
Animation : Courbe de Bézier
Préambule
[modifier | modifier le wikicode]Les courbes de Béziers dans Wikipedia.
Voir l'introduction pour créer une animation avec gnuplot sous windows ou linux.
Courbes de Béziers cubiques (normale ou rationnelle)
[modifier | modifier le wikicode]L'animation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et les fichiers *.h dans les chapitres Courbe de Bézier ou Courbe de Bézier rationnelle.
Cet exemple fonctionne pour les deux types de courbes (normale,rationnelle).
c01.cCourbe de béziers |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
/* ------------------------------------ */
int main(void)
{
int Pic=80;
printf("\n\n load \"a_main.plt\" with gnuplot."
"\n\n Use replot to see the animation "
"\n\n Press return to continue ");
while(Pic--)
G_quadratic_Bezier_lp_2d(
i_WGnuplot(-10,90,-10,50),
i_point2d(Pic,10.),
i_point2d(40.,40.),
i_point2d(60.,10.));
return 0;
}
Animation : Fonction vectorielle 3D
Préambule
[modifier | modifier le wikicode]Voir l'introduction pour créer une animation avec gnuplot sous windows ou linux.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés. Recuperer aussi ceux du chapitre Dessiner : Fonction vectorielle 3D.
Animer
[modifier | modifier le wikicode]c01.cAnimer un vecteur tangent et normales unitaire |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "fa.h"
/* ------------------------------------ */
int main(void)
{
double t=0;
printf(" r(t) = f(t)i + g(t)j + h(t)k \n\n");
printf(" With \n\n");
printf(" f : t-> %s \n", feq);
printf(" g : t-> %s \n", geq);
printf(" h : t-> %s\n\n", heq);
printf("\n\n Open the file \"a_main.plt\" with Gnuplot."
"\n\n Use the \"replot\" command of gnuplot.\n\n");
for(;t<6.*PI;t+=.05)
G_Curve_3d(i_time(0.,6.*PI,.01),
f,g,h,
Tf,Tg,Th,
t);
printf(" open the file \"a_main.plt\" with Gnuplot.\n\n"
" Use the command replot of gnuplot \n\n");
return 0;
}
Le résultat.
| Résultat dans gnuplot |
|---|

|
| Résultat dans gnuplot |
|---|

|
Animation : Tangente de f(x,y)
Préambule
[modifier | modifier le wikicode]La tangente dans Wikipedia.
Voir l'introduction pour créer une animation avec gnuplot sous windows ou linux.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés. Recuperer aussi ceux du chapitre Dessiner : Tangente de f(x,y).
Dessiner la tangente
[modifier | modifier le wikicode]- La méthode consiste à poser :
- x = i (ici i=1).
- D'utiliser la dérivée partielle par rapport à y.
- Puis écrire l'équation de la tangente d'une fonction en y.
c01.cDessiner la tangente |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "fa.h"
/* ------------------------------------ */
int main(void)
{
double n = -10;
while((n+=.2)<10)
G_3d_p( i_WGnuplot(-10.,10.,-10.,10.),
i_VGnuplot( 55.,57., 1., 1.),
feq,f,
i_point2d(1,n));
printf(" Open the file \"a_main.plt\" with Gnuplot.\n\n"
" Use the \"replot\" command of gnuplot. \n\n"
" Press return to continue. \n\n");
return 0;
}
Le résultat.
| Résultat dans gnuplot |
|---|

|
| Résultat dans gnuplot |
|---|

|
| Résultat dans gnuplot |
|---|

|
Animation : Vecteur normal
Préambule
[modifier | modifier le wikicode]Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés. Récupérer aussi ceux du chapitre Dessiner : Vecteur normal.
Dessiner le vecteur normale au point P
[modifier | modifier le wikicode]c01.cDessiner le vecteur normale au point P |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "fa.h"
/* ------------------------------------ */
int main(void)
{
double n = 0;
printf(" Draw the normal vector at the point P.\n\n"
" f : (x,y)-> %s\n\n", feq);
while((n+=.05)<2.8)
G_3d_v(i_WsGnuplot(-3,3,-3,3,-.5,2),
i_VGnuplot( 94.,22.,1.,1.),
feq,f,f_z,
i_point2d(n,0.));
printf(" Open the file \"a_main.plt\" with Gnuplot.\n\n"
" Use the \"replot\" command of gnuplot. \n\n"
" Press return to continue. \n\n");
getchar();
return 0;
}
Le résultat.
| Résultat dans gnuplot |
|---|

|
| Résultat dans gnuplot |
|---|
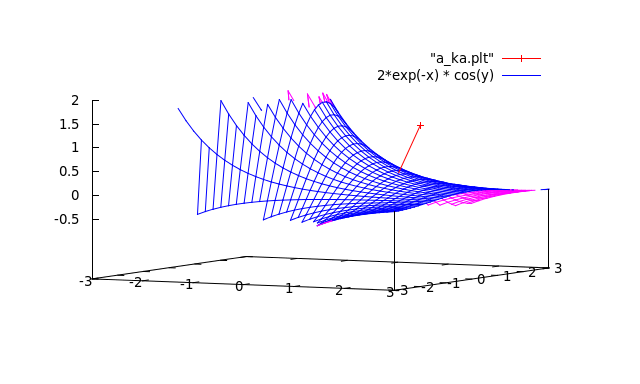
|
| Résultat dans gnuplot |
|---|

|
Animation : Plan tangent
Préambule
[modifier | modifier le wikicode]Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés. Récupérer aussi ceux du chapitre Dessiner : Plan tangent'.
Animer le plan tangent au point P
[modifier | modifier le wikicode]c01.cAnimer le plan tangent au point P |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "fa.h"
/* ------------------------------------ */
int main(void)
{
double n = 0;
printf(" Draw the Tangent plane.\n\n"
" f : (x,y)-> %s\n\n", feq);
while((n+=.05)<3.8)
G_3d_v( i_WsGnuplot(-4,4,-4,4,-1,2),
i_VGnuplot( 80.,38.,1.,1.),
feq,f,f_z,
i_point2d(n,0.));
printf(" Open the file \"a_main.plt\" with Gnuplot.\n\n"
" Use the \"replot\" command of gnuplot. \n\n"
" Press return to continue. \n\n");
getchar();
return 0;
}
Le résultat.
| Résultat dans gnuplot |
|---|

|
| Résultat dans gnuplot |
|---|

|
| Résultat dans gnuplot |
|---|

|
Présentation de la librairie
Préambule
[modifier | modifier le wikicode]La géométrie de la tortue dans Wikipedia.
Dans ce chapitre, nous présenterons un exemple (c01.c) et la librairie (*.h). Le code des fonctions de la librairie ne sont pas à étudier. Dans un premier temps, amusez-vous simplement avec ces fonctions.
L'étude de ce chapitre peut ce faire à l'aide de cette [Playlist]..
Présentation
[modifier | modifier le wikicode]- Les commandes d'initialisation :
- **U = GINIT(-10.,10.,-10.,10.);
- création de la matrice.
- initialisation de la fenêtre de gnuplot
- F_mR(U); Destruction de la matrice.
- **U = GINIT(-10.,10.,-10.,10.);
- Les commandes de déplacement :
- SETUP(U,angle,x,y); Positionner la tortue.
- GO(U,+P); Avancer de P pas.
- GO(U,-P); Reculer de P pas.
- TU(U,+D); Tourner de D degrés sur la droite.
- TU(U,-D); Tourner de D degrés sur la gauche.
- La direction:
- Les angles positifs tournent dans le sens des aiguilles d'une montre.
- L'angle 0 est le nord.
- La direction est mémorisée.
- Les angles positifs tournent dans le sens des aiguilles d'une montre.
Dessiner
[modifier | modifier le wikicode]c01.cDessiner un carré |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-10.,10.,-10.,10.);
int i = 4;
clrscrn();
for(;i--;)
{GO(U,5.);TU(U,90.);}
F_mR(U);
printf(" * open the file main.plt with Gnuplot.\n\n\n");
getchar();
return 0;
}
Le résultat :
# Gnuplot file : load "a_main.plt"
set zeroaxis
set size ratio -1
plot [-10.000:10.000] [-10.000:10.000] \
"data.plt" with linesp pt 0
| Résultat dans gnuplot |
|---|

|
Les fichiers h partagés
[modifier | modifier le wikicode]v_a.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : v_a.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <stddef.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
/* ------------------------------------ */
#include "vdefine.h"
#include "vmatini.h"
#include "vmatbas.h"
#include "vmatcop.h"
#include "vmatrot.h"
vdefine.hDéclaration des defines |
|---|
/* ------------------------------------ */
/* Save as : vdefine.h */
/* ------------------------------------ */
#define C0 0
#define C1 1
#define C2 2
#define C3 3
#define C4 4
#define C5 5
#define R0 0
#define R1 1
#define R2 2
#define R3 3
#define R4 4
#define R5 5
#define OF 0
#define R_SIZE 0
#define C_SIZE 1
#define C_SIZE_A 2
#define FIRST 1
#ifndef PI
#define PI 3.14159265359
#endif
#define MAX(A,B) ((A)>(B) ? (A):(B) )
void clrscrn(void)
{
printf("\n\n\n\n\n\n\n\n\n\n\n"
"\n\n\n\n\n\n\n\n\n\n\n"
"\n\n\n\n\n\n\n\n\n\n\n");
}
L'étude sur les matrices fait partie d'un autre livre.
vmatini.hCréation et destruction d'une matrice |
|---|
/* ------------------------------------ */
/* Save as : vmatini.h */
/* -------------------------------------*/
double **I_mR(
int r,
int c
)
{
int i = R0;
int ar = r + C1;
int ac = c + C1;
double **A = malloc(ar * sizeof(*A));
for(; i<ar; i++)
A[i] = malloc(ac * sizeof(**A));
A[R_SIZE][OF] = ar;
A[C_SIZE][OF] = ac;
return(A);
}
/* ------------------------------------ */
void F_mR(
double **A
)
{
int i=R0;
int r=A[R_SIZE][OF];
if(A) for(;i<r;i++) free(A[i]);
free(A);
}
vmatbas.hAdditionner et multiplier des matrices |
|---|
/* ------------------------------------ */
/* Save as : vmatbas.h */
/* ------------------------------------ */
double **add_mR(
double **A,
double **B,
double **AplsB
)
{
int r;
int c;
for (r=FIRST;r<A[R_SIZE][OF];r++)
for(c=FIRST;c<A[C_SIZE][OF];c++)
AplsB[r][c]=A[r][c]+B[r][c];
return(AplsB);
}
/* ------------------------------------ */
double **mul_mR(
double **A,
double **B,
double **AB
)
{
int i,j,k;
for (k=FIRST; k<A[R_SIZE][OF];k++)
for (j=FIRST; j<B[C_SIZE][OF];j++)
for(i=FIRST,AB[k][j]=0;i<A[C_SIZE][OF];i++)
AB[k][j]+=A[k][i]*B[i][j];
return(AB);
}
vmatcop.hCopier une matrice |
|---|
/* ------------------------------------ */
/* Save as : vmatcop.h */
/* ------------------------------------ */
double ** c_mR(
double **A,
double **B
)
{
int r;
int c;
for( r=FIRST;r<A[R_SIZE][OF];r++)
for(c=FIRST;c<A[C_SIZE][OF];c++)
B[r][c]=A[r][c];
return(B);
}
/* ------------------------------------ */
double **c_a_A_mR(
double a[],
double **A
)
{
int r;
int c;
int i=0;
for( r=FIRST; r<A[R_SIZE][OF]; r++)
for(c=FIRST; c<A[C_SIZE][OF]; c++)
A[r][c] = a[i++];
return(A);
}
vmatrot.hMatrice de rotation |
|---|
/* ------------------------------------ */
/* Save as : vmatrot.h */
/* ------------------------------------ */
double **rot2D_mR(
double **A,
double alpha
)
{
A[1][1]=cos(alpha);A[1][2]=-sin(alpha);
A[2][1]=sin(alpha);A[2][2]= cos(alpha);
return(A);
}
y_o.hLa librairie de géométrie de la tortue standard |
|---|
/* ------------------------------------ */
/* Save as : y_o.h */
/* ------------------------------------ */
void PD(
double **A
)
{
FILE * fp = fopen("data.plt","a");
fprintf(fp," %+.3f %+.3f \n",
A[R1][C1],A[R2][C1]);
fclose(fp);
}
/* ------------------------------------ */
void PU(
double **A
)
{
FILE *fp = fopen("data.plt","a");
fprintf(fp,"\n %+.3f %+.3f \n",
A[R1][C1],A[R2][C1]);
fclose(fp);
}
/* ------------------------------------ */
double **Ginit(
double **U,
double xmin,
double xmax,
double ymin,
double ymax
)
{
FILE *fp;
fp = fopen("a_main.plt","w");
fprintf(fp,"# Gnuplot file : load \"a_main.plt\" \n"
"reset\n"
"set zeroaxis\n"
"set size ratio -1\n"
"plot [%0.3f:%0.3f] [%0.3f:%0.3f] \\\n"
"\"data.plt\" with linesp pt 0\n"
,xmin,xmax,ymin,ymax);
fclose(fp);
fp = fopen("data.plt","w");
fclose(fp);
U[R0][C1] = 0.;/* angle */
U[R1][C1] = 0.;/* x */
U[R2][C1] = 0.;/* y */
PD(U);
return(U);
}
/* ------------------------------------ */
double **GINIT(
double xmin,
double xmax,
double ymin,
double ymax
)
{
return( Ginit(I_mR(R2,C1),xmin,xmax,ymin,ymax) );
}
/* ------------------------------------ */
void SET(
double **U,
double angle,
double x,
double y
)
{
U[R0][C1] = angle;
U[R1][C1] = x;
U[R2][C1] = y;
PD(U);
}
/* ------------------------------------ */
void SETUP(
double **U,
double angle,
double x,
double y
)
{
U[R0][C1] = angle;
U[R1][C1] = x;
U[R2][C1] = y;
PU(U);
}
/* ------------------------------------ */
void GO(
double **U,
double Step
)
{
double **T = I_mR(R2,C2);
double **B = I_mR(R2,C1);
double **C = I_mR(R2,C1);
double angle=U[R0][C1];
B[R1][C1] = 0.;
B[R2][C1] = Step;
rot2D_mR(T,PI/180.*(-angle));
mul_mR(T,B,C);
c_mR(U,B);
add_mR(B,C,U);
PD(U);
F_mR(C);
F_mR(B);
F_mR(T);
}
/* ------------------------------------ */
void GU(
double **U,
double Step
)
{
double **T = I_mR(R2,C2);
double **B = I_mR(R2,C1);
double **C = I_mR(R2,C1);
double angle=U[R0][C1];
B[R1][C1] = 0.;
B[R2][C1] = Step;
rot2D_mR(T,PI/180.*(-angle));
mul_mR(T,B,C);
c_mR(U,B);
add_mR(B,C,U);
PU(U);
F_mR(C);
F_mR(B);
F_mR(T);
}
/* ------------------------------------ */
void TU(
double **U,
double angle
)
{
U[R0][C1]+=angle;
}
Application : Quelques exemples
Préambule
[modifier | modifier le wikicode]La géométrie de la tortue dans Wikipedia.
Présentation
[modifier | modifier le wikicode]Quelques exemples.
Dessiner
[modifier | modifier le wikicode]Petits drapeaux
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c01.cPetits drapeaux |
|---|
/* ------------------------------------ */
/* save as : c01.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
void shape(
double **U,
double step,
int side
)
{
double angle=360./side;
for(;side--;)
{GO(U,step);TU(U,angle);}
}
/* ------------------------------------ */
void fun(
double **U,
double step
)
{
int a=20;
int i=360/a;
for(;i--;)
{
GO(U, step);
shape(U,1,4);
shape(U,1,3);
GO(U,-step);
TU(U, 1*a);
}
}
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-10.,10.,-10.,10.);
fun(U,6.);
F_mR(U);
printf(" * open the file a_main.plt with Gnuplot.\n\n\n");
return 0;
}
| Résultat dans gnuplot |
|---|

|
Petit jeux sur les rectangles
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c02.cPetit jeux sur les rectangles |
|---|
/* ------------------------------------ */
/* save as : c02.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
void side(
double **U,
double size
)
{
GO(U,size);TU(U,90.);
}
/* ------------------------------------ */
void rectangle(
double **U,
double size1,
double size2
)
{
int i=2;
for(;i--;)
{
side(U,size1);
side(U,size2);
}
}
/* ------------------------------------ */
int main(void)
{
double i = 360.;
double n = 16.;
double **U = GINIT(-15.,15.,-15.,15.);
for(;(i-=n)>=0.;)
{
TU(U,n);rectangle(U,5.,10.);
}
F_mR(U);
printf(" * open the file a_main.plt with Gnuplot.\n\n\n");
fflush(stdout);
return 0;
}
| Résultat dans gnuplot |
|---|

|
Petit jeux sur les formes
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c03.cPetit jeux sur les formes |
|---|
/* ------------------------------------ */
/* save as : c03.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
void shape(
double **U,
double step,
int side
)
{
double angle=360./side;
for(;side--;)
{GO(U,step);TU(U,angle);}
}
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-10.,10.,-10.,10.);
SETUP(U,30,-5,5);
shape(U,2,3);
GO(U,3.);
SETUP(U, 0, 5,5);
shape(U,2,4);
GO(U,3.);
SETUP(U,72.-90.,-5,-5);
shape(U,2,5);
GO(U,3.);
SETUP(U,10-90, 5,-5);
shape(U,.2,36);
GO(U,3.);
F_mR(U);
printf(" * open the file a_main.plt with Gnuplot.\n\n\n");
fflush(stdout);
return 0;
}
| Résultat dans gnuplot |
|---|

|
Application : Soleil 1
Préambule
[modifier | modifier le wikicode]La géométrie de la tortue dans Wikipedia.
Présentation
[modifier | modifier le wikicode]Quelques exemples.
Dessiner
[modifier | modifier le wikicode]Soleils 0
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c00.cSoleils 0 |
|---|
/* ------------------------------------ */
/* Save as : c00.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
void fun(
double **U,
double step
)
{
int i=360/10;
for(;i--;)
{
GO(U, step);
GO(U,-step);
TU(U, 10.);
}
}
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-10.,10.,-10.,10.);
// clrscrn();
SETUP(U,0.,-5, 5);fun(U,3.);
SETUP(U,0., 5, 5);fun(U,3.);
SETUP(U,0.,-5,-5);fun(U,3.);
SETUP(U,0., 5,-5);fun(U,3.);
SETUP(U,0., 0,-0);fun(U,3.);
F_mR(U);
printf(" * open the file a_main.plt with Gnuplot.\n\n\n");
fflush(stdout);
return 0;
}
| Résultat dans gnuplot |
|---|

|
Soleil 1
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c01.cSoleil 1 |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
void fun(
double **U,
double step
)
{
int i=360/10;
int a=1;
for(;i--;)
{
a= (a==1)?2:1;
GO(U, a*step);
GO(U,-a*step);
TU(U, 10.);
}
}
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-10.,10.,-10.,10.);
clrscrn();
fun(U,4.);
F_mR(U);
printf(" * open the file main.plt with Gnuplot.\n\n\n");
getchar();
return 0;
}
| Résultat dans gnuplot |
|---|
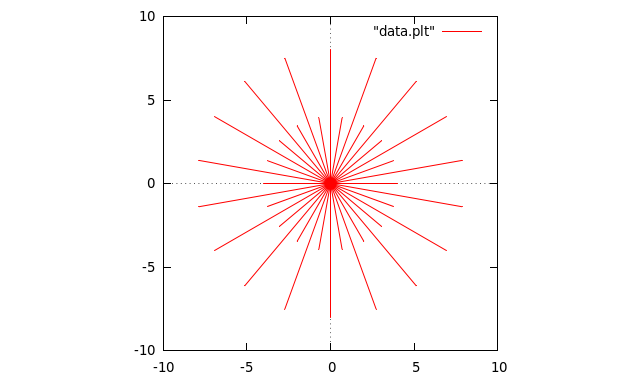
|
Soleil 2
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c01.cSoleil 2 |
|---|
/* ------------------------------------ */
/* Save as : c02.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
void fun(
double **U,
double step
)
{
int i=360/10;
double a=2.;
for(;i--;)
{
(a>2.) ? (a=1.):(a+=0.2);
GO(U, a*step);
GO(U,-a*step);
TU(U, 10.);
}
}
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-10.,10.,-10.,10.);
clrscrn();
fun(U,4.);
F_mR(U);
printf(" * open the file main.plt with Gnuplot.\n\n\n");
getchar();
return 0;
}
| Résultat dans gnuplot |
|---|

|
Soleil 3
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c01.cSoleil 3 |
|---|
/* ------------------------------------ */
/* Save as : c03.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
void fun(
double **U,
double step
)
{
int i=18;
int a=1;
for(;i--;)
{
a= (a==1)?3:1;
GO(U, step);
GO(U,-step);
TU(U, a*10.);
}
}
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-10.,10.,-10.,10.);
clrscrn();
fun(U,8.);
F_mR(U);
printf(" * open the file main.plt with Gnuplot.\n\n\n");
getchar();
return 0;
}
| Résultat dans gnuplot |
|---|

|
Soleil 4
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c01.cSoleil 4 |
|---|
/* ------------------------------------ */
/* Save as : c04.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
void fun(
double **U,
double step
)
{
int i=113;
int a=0;
for(;i--;)
{
(a) ? (a-=2):(a=60);
GO(U, step);
GO(U,-step);
TU(U, a*.1);
}
}
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-10.,10.,-10.,10.);
clrscrn();
fun(U,8.);
F_mR(U);
printf(" * open the file main.plt with Gnuplot.\n\n\n");
fflush(stdout);
getchar();
return 0;
}
| Résultat dans gnuplot |
|---|

|
Application : Soleil 2
Préambule
[modifier | modifier le wikicode]La géométrie de la tortue dans Wikipedia.
Présentation
[modifier | modifier le wikicode]Quelques exemples.
Dessiner
[modifier | modifier le wikicode]Soleils 0
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c00.cSoleils 0 |
|---|
/* ------------------------------------ */
/* Save as : c00.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
void fun(
double **U,
double step
)
{
int i=180;
double a=1.;
for(;i--;)
{
(a>2.) ? (a=1.):(a+=0.04);
GO(U, a*step);
TU(U, 45.);
GO(U, step);
GO(U,- step);
TU(U, -45.);
GO(U,-a*step);
TU(U, 2.);
}
}
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-10.,10.,-10.,10.);
// clrscrn();
fun(U,3.);
F_mR(U);
printf(" * open the file a_main.plt with Gnuplot.\n");
return 0;
}
| Résultat dans gnuplot |
|---|

|
Soleils 1
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c00.cSoleils 1 |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
void fun(
double **U,
double step
)
{
int i=180;
double a=1.;
for(;i--;)
{
(a>2.) ? (a=1.):(a+=0.04);
GO(U, a*step);
TU(U, 45.);
GO(U, step);
TU(U, 45.);
GO(U, step);
GO(U,- step);
TU(U, -45.);
GO(U,- step);
TU(U, -45.);
GO(U,-a*step);
TU(U, 2.);
}
}
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-10.,10.,-10.,10.);
clrscrn();
fun(U,3.);
F_mR(U);
printf(" * open the file main.plt with Gnuplot.\n\n\n");
return 0;
}
| Résultat dans gnuplot |
|---|
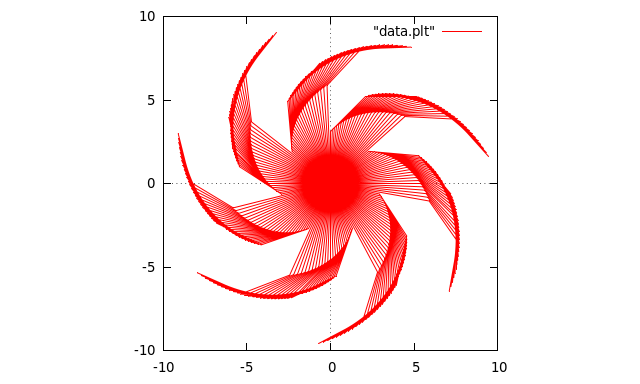
|
Soleils 2
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c00.cSoleils 2 |
|---|
/* ------------------------------------ */
/* Save as : c02.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
void fun(
double **U,
double step
)
{
int i=180;
double a=1.;
for(;i--;)
{
(a>2.) ? (a=1.):(a+=0.04);
GO(U, a*step);
TU(U, 45.);
GO(U, step);
TU(U, -45.);
GO(U, step);
GO(U,- step);
TU(U, 45.);
GO(U,- step);
TU(U, -45.);
GO(U,-a*step);
TU(U, 2.);
}
}
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-12.,12.,-12.,12.);
// clrscrn();
fun(U,3.);
F_mR(U);
printf(" * open the file a_main.plt with Gnuplot.\n");
return 0;
}
| Résultat dans gnuplot |
|---|

|
Soleils 3
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c00.cSoleils 3 |
|---|
/* ------------------------------------ */
/* Save as : c03.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
void fun(
double **U,
double step
)
{
int i=180;
double a=1.;
for(;i--;)
{
(a>2.) ? (a=1.):(a+=0.04);
GO(U, a*step);
TU(U, 45.);
GO(U, step);
TU(U, -90.);
GO(U, step/2.);
GO(U,- step/2.);
TU(U, 90.);
GO(U,- step);
TU(U, -45.);
GO(U,-a*step);
TU(U, 2.);
}
}
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-12.,12.,-12.,12.);
// clrscrn();
fun(U,3.);
F_mR(U);
printf(" * open the file a_main.plt with Gnuplot. \n");
return 0;
}
| Résultat dans gnuplot |
|---|

|
Soleils 4
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c00.cSoleils 4 |
|---|
/* ------------------------------------ */
/* Save as : c04.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
void fun(
double **U,
double step
)
{
int i=180;
double a=1.;
for(;i--;)
{
(a>2.) ? (a=1.):(a+=0.04);
GO(U, a*step);
TU(U, 45.);
GO(U, a*step);
TU(U, -90.);
GO(U, step);
GO(U, -step);
TU(U, 90.);
GO(U,-a*step);
TU(U, -45.);
GO(U,-a*step);
TU(U, 2.);
}
}
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-12.,12.,-12.,12.);
// clrscrn();
fun(U,3.);
F_mR(U);
printf(" * open the file a_main.plt with Gnuplot.\n\n\n");
return 0;
}
| Résultat dans gnuplot |
|---|
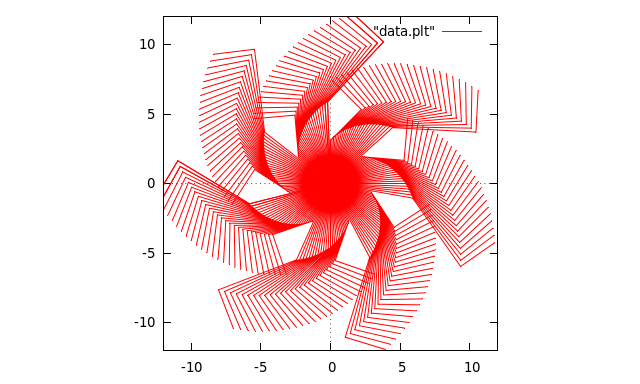
|
Application : Quelques polygones
Préambule
[modifier | modifier le wikicode]La géométrie de la tortue dans Wikipedia.
Présentation
[modifier | modifier le wikicode]Quelques exemples.
Dessiner
[modifier | modifier le wikicode]Jeux sur les polygones 1
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c01.cJeux sur les polygones 1 |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
void poly(
double **U,
double d,
double a,
double phasechange,
double n
)
{
double phase=0.;
for(;n-->0;)
{
GO(U,d*cos(phase));
TU(U,-a);
phase+=phasechange;
}
}
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-10.,10.,-10.,10.);
clrscrn();
/* poly(U, d, a, phasechange, n) */
SETUP(U,0.,-8, 4 );poly(U, 1.5, 45., 1.,500.);
SETUP(U,0., 3, 1 );poly(U, 7. , 45., 3.,100.);
SETUP(U,0.,-1,-6.5);poly(U, 3. , 45., 6.,100.);
SETUP(U,0., 3,-7 );poly(U, 5. , 45., 8.,500.);
F_mR(U);
printf(" * open the file a_main.plt with Gnuplot.\n\n\n");
return 0;
}
| Résultat dans gnuplot |
|---|

|
Jeux sur les polygones 2
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c02.cJeux sur les polygones 2 |
|---|
/* ------------------------------------ */
/* Save as : c02.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
void poly(
double **U,
double d,
double a,
double phasechange,
double n
)
{
double phase=0.;
for(;n-->0;)
{
GO(U,d*cos(phase));
TU(U,-a);
phase+=phasechange;
}
}
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-10.,10.,-10.,10.);
clrscrn();
/* poly(U, d, a, phasechange, n) */
SETUP(U,0.,-7., 2.5);poly(U, 5. , 45., 11.,300.);
SETUP(U,0., 8., 4. );poly(U, 2. , 45., 13.,500.);
SETUP(U,0.,-1.,-7. );poly(U, 3. , 45., 19.,500.);
SETUP(U,0., 3.,-8. );poly(U, 6. , 45., 17.,500.);
F_mR(U);
printf(" * open the file a_main.plt with Gnuplot.\n\n\n");
return 0;
}
| Résultat dans gnuplot |
|---|

|
Jeux sur les polygones 3
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c03.cJeux sur les polygones 3 |
|---|
/* ------------------------------------ */
/* Save as : c03.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
void poly(
double **U,
double d,
double a,
double phasechange,
double n
)
{
double phase=0.;
for(;n-->0;)
{
GO(U,d*cos(phase));
TU(U,-a);
phase+=phasechange;
}
}
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-10.,10.,-10.,10.);
clrscrn();
/* poly(U, d, a, phasechange, n) */
SETUP(U,0.,-6., 1. );poly(U,7. , 45., 22.,100.);
SETUP(U,0., 2., 4. );poly(U,2.5, 45., 24.,400.);
SETUP(U,0.,-1.,-6. );poly(U,3. , 45., 25.,600.);
SETUP(U,0., 2.,-7. );poly(U,4.5, 45., 30.,290.);
F_mR(U);
printf(" * open the file a_main.plt with Gnuplot.\n\n\n");
return 0;
}
| Résultat dans gnuplot |
|---|

|
Application : Dessiner en pointillés
Préambule
[modifier | modifier le wikicode]La géométrie de la tortue dans Wikipedia.
Présentation
[modifier | modifier le wikicode]Quelques exemples en pointillés.
- Les commandes :
- GO(U,+P); Avancer de P pas.
- GO(U,-P); Reculer de P pas.
- GU(U,+P); Avancer de P pas sans laisser de trace.
- GU(U,-P); Reculer de P pas sans laisser de trace.
Dessiner
[modifier | modifier le wikicode]Premier exemple
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c01.cPremier exemple |
|---|
/* ------------------------------------ */
/* save as : c01.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
void circle(
double **U,
double r,
double deg
)
{
double i=360;
int j=1;
for(;(i-=deg)>=0;)
{
if((j*=-1)>0)GO(U,r);
else GU(U,r);
TU(U,deg);
}
}
/* ------------------------------------ */
void circleS(
double **U
)
{
int i=9;
for(;i--;)
{
circle(U,1.,5.);
TU(U,40.);
}
}
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-30.,30.,-30.,30.);
clrscrn();
circleS(U);
F_mR(U);
printf(" * open the file main.plt with Gnuplot.\n\n\n");
return 0;
}
| Résultat dans gnuplot |
|---|

|
Deuxième exemple
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c02.cDeuxième exemple |
|---|
/* ------------------------------------ */
/* save as : c02.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
void arcR(
double **U,
double r,
double deg
)
{
int i=0;
for(;i++<deg;)
{
if(fmod(i,2))GO(U,r);
else GU(U,r);
TU(U,1.);
}
}
/* ------------------------------------ */
void petal(
double **U,
double size
)
{
arcR(U,size,60.);
TU(U,120.);
arcR(U,size,60.);
TU(U,120.);
}
/* ------------------------------------ */
void flower(
double **U,
double size
)
{
int i=6;
for(;i--;)
{
petal(U,size);
TU(U,60.);
}
}
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-500.,500.,-500.,500.);
clrscrn();
flower(U,10.);
F_mR(U);
printf(" * open the file main.plt with Gnuplot.\n\n\n");
return 0;
}
| Résultat dans gnuplot |
|---|

|
Troisième exemple
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c03.cTroisième exemple |
|---|
/* ------------------------------------ */
/* save as : c03.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
void arcR(
double **U,
double r,
double deg
)
{
int i=0;
for(;i++<deg;)
{
if(fmod(i,2))GO(U,r);
else GU(U,r);
TU(U,4.);
}
}
/* ------------------------------------ */
void arcL(
double **U,
double r,
double deg
)
{
for(;deg-->=0;)
{
GO(U,r);
TU(U,-4.);
}
}
/* ------------------------------------ */
void ray(
double **U,
double r
)
{
int i=2;
for(;i--;)
{
arcL(U,r,45./2.);
arcR(U,r,45./2.);
}
}
/* ------------------------------------ */
void sun(
double **U,
double size
)
{
int i=9;
for(;i--;)
{
ray(U,size);
TU(U,160.);
}
}
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-270.,80.,-40.,300.);
sun(U,4.);
F_mR(U);
printf(" * open the file main.plt with Gnuplot.\n\n\n");
return 0;
}
| Résultat dans gnuplot |
|---|
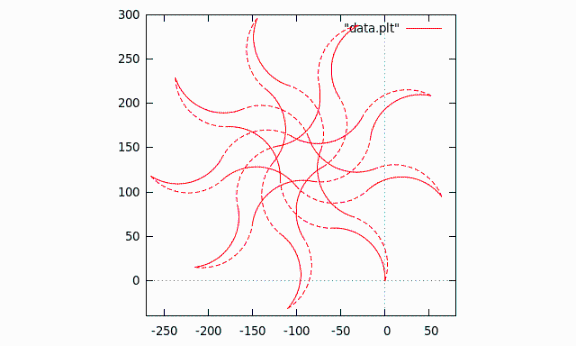
|
Application : Fonctions récursives
Préambule
[modifier | modifier le wikicode]La géométrie de la tortue dans Wikipedia.
Présentation
[modifier | modifier le wikicode]- F_mR(tree(U,50.));
- Cette méthode est utilisée ici pour montrer la sortie finale des fonctions.
- C'est à dire return(U);
Dessiner
[modifier | modifier le wikicode]Un arbre
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c01.cUn arbre |
|---|
/* ------------------------------------ */
/* save as : c01.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
double **tree( double **U,double size);
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-40.,40.,-0.,80.);
F_mR(tree(U,50.));
printf(" * open the file main.plt with Gnuplot.");
return 0;
}
/* ------------------------------------ */
double **tree(
double **U,
double size
)
{
if(size<5.){GO(U,size);GO(U,-size);return(0);}
GO(U,size/3.);TU(U,-30.);
tree(U,size*2./3.);
TU(U,30.);GO(U,size/6.);TU(U,25.);
tree(U,size/2.);
TU(U,-25.);GO(U,size/3.);TU(U,25.);
tree(U,size/2.);
TU(U,-25.);GO(U,size/6.);GO(U,-size);
return(U);
}
| Résultat dans gnuplot |
|---|

|
Petit jeux sur les triangles
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c02.cPetit jeux sur les triangles |
|---|
/* ------------------------------------ */
/* save as : c02.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
double **sqr(double **U,double size);
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-150.,400.,-50.,500.);
F_mR(sqr(U,400.));
printf(" * open the file main.plt with Gnuplot.");
return 0;
}
/* ------------------------------------ */
double **sqr(
double **U,
double size
)
{
int i=3;
if(size<10.) return(0);
for(;i--;)
{
TU(U,-60.);
sqr(U,size/4.);
TU(U,60.);GO(U,size);TU(U,120.);
}
return(U);
}
| Résultat dans gnuplot |
|---|

|
Petit jeux sur les carrés
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c03.cPetit jeux sur les carrés |
|---|
/* ------------------------------------ */
/* save as : c03.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
double **sqr(double **U,double size);
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-200.,600.,-200.,600.);
F_mR(sqr(U,400.));
printf(" * open the file main.plt with Gnuplot.");
return 0;
}
/* ------------------------------------ */
double **sqr(
double **U,
double size
)
{
int i=4;
if(size<10.) return(0);
for(;i--;)
{
TU(U,-90.);
sqr(U,size/4.);
TU(U,90.);GO(U,size);TU(U,90.);
}
return(U);
}
| Résultat dans gnuplot |
|---|

|
Courbe de Hilbert
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c04.cCourbe de Hilbert |
|---|
/* ------------------------------------ */
/* save as : c04.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
double **hilbert(double **U,double size,
double level,double parity);
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-32., 1.,-1.,32.);
F_mR(hilbert(U,1.,5.,1.));
printf(" * open the file main.plt with Gnuplot.");
return 0;
}
/* ------------------------------------ */
double **hilbert(
double **U,
double size,
double level,
double parity
)
{
if(--level<0.)return(0);
TU(U,parity*(-90));
hilbert(U,size,level,-parity);
GO(U,size);TU(U,parity*90);
hilbert(U,size,level,parity);
GO(U,size);
hilbert(U,size,level,parity);
TU(U,parity*90);GO(U,size);
hilbert(U,size,level,-parity);
TU(U,parity*(-90));
return(U);
}
| Résultat dans gnuplot |
|---|

|
Application : Triangles
Préambule
[modifier | modifier le wikicode]La géométrie de la tortue dans Wikipedia.
Présentation
[modifier | modifier le wikicode]Quelques exemples avec des fonctions récursives. Petits jeux sur les triangles.
Dessiner des triangles
[modifier | modifier le wikicode]Exemple 1
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c01.cExemple 1 |
|---|
/* ------------------------------------ */
/* save as : c01.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
double **triangle(double **U,double size);
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-12.,355.,-5.,410.);
F_mR(triangle(U,400.));
printf(" * open the file main.plt with Gnuplot.");
return 0;
}
/* ------------------------------------ */
double **triangle(
double **U,
double size
)
{
int i=3;
if(size<10.) return(0);
for(;i--;)
{
triangle(U,size/2.);
GO(U,size);TU(U,120.);
}
return(U);
}
| Résultat dans gnuplot |
|---|
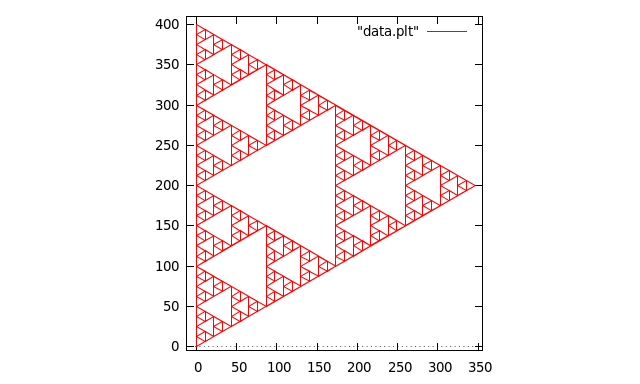
|
Exemple 2
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c02.cExemple 2 |
|---|
/* ------------------------------------ */
/* save as : c02.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
double **triangle(double **U,double size);
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-200.,350.,-120.,410.);
F_mR(triangle(U,200.));
printf(" * open the file main.plt with Gnuplot.");
return 0;
}
/* ------------------------------------ */
double **triangle(
double **U,
double size
)
{
int i=3;
if(size<10.) return(0);
for(;i--;)
{
GO(U,size);
triangle(U,size/2.);
TU(U,120.);
}
return(U);
}
| Résultat dans gnuplot |
|---|

|
Exemple 3
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c03.cExemple 3 |
|---|
/* ------------------------------------ */
/* save as : c03.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_o.h"
/* ------------------------------------ */
double **triangle(double **U,double size);
/* ------------------------------------ */
int main(void)
{
double **U = GINIT(-200.,180.,-100.,310.);
F_mR(triangle(U,200.));
printf(" * open the file main.plt with Gnuplot.");
return 0;
}
/* ------------------------------------ */
double **triangle(
double **U,
double size
)
{
int i=3;
if(size<10.) return(0);
for(;i--;)
{
GO(U,size/2.);TU(U,-120.);
triangle(U,size/2.);
TU(U,120.);GO(U,size/2.);
TU(U,120.);
}
return(U);
}
| Résultat dans gnuplot |
|---|

|
Présentation de la librairie vectorielle
Préambule
[modifier | modifier le wikicode]La géométrie de la tortue dans Wikipedia.
Dans ce chapitre, nous présenterons un exemple (c01.c) et la librairie (*.h). Les fonctions de la librairie ne sont pas à étudier. Dans un premier temps, amusez-vous simplement avec ces fonctions.
L'étude de ce chapitre peut ce faire à l'aide de cette [Playlist]..
Présentation
[modifier | modifier le wikicode]Les commandes d'initialisation :
- **U = G_main(-10.,10.,-10.,10.);
- création de la matrice.
- Initialisation de la fenêtre de gnuplot
- F_mR(U); Destruction de la matrice.
Les commandes de déplacement :
- SETUP(U,angle,x,y); Positionner la tortue.
- vo(U,0,+P); Avancer de P unités.
- vo(U,0,-P); Reculer de P unités.
- vo(U,D,0); Contrôler la "D"irection.
La direction :
- Suit les règles du cercle trigonométrique mais en degrés. Les angles positifs sont mesurés dans le sens inverse des aiguilles d'une montre, à partir de l'axe des x positifs.
- À chaque déplacement il faut lui indiquer une direction.
Dessiner
[modifier | modifier le wikicode]Dessiner un carré.
c01.cDessiner un carré. |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_r.h"
/* ------------------------------------ */
int main(void)
{
double **U = G_main(-10.,10.,-10.,10.);
double angle = 0.;
double side = 5.;
for(;angle<360;angle+=90)
vo(U,angle,side);
F_mR(U);
printf(" * open the file a_main.plt with Gnuplot.\n\n\n");
return 0;
}
Le résultat :
# Gnuplot file : load "a_main.plt"
set zeroaxis
set size ratio -1
plot [-10.000:10.000] [-10.000:10.000] \
"data.plt" with linesp pt 0
| Résultat dans gnuplot |
|---|

|
Les fichiers h partagés
[modifier | modifier le wikicode]v_a.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : v_a.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <stddef.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
/* ------------------------------------ */
#include "vdefine.h"
#include "vmatini.h"
#include "vmatbas.h"
#include "vmatcop.h"
#include "vmatrot.h"
vdefine.hDéclaration des defines |
|---|
/* ------------------------------------ */
/* Save as : vdefine.h */
/* ------------------------------------ */
#define C0 0
#define C1 1
#define C2 2
#define C3 3
#define C4 4
#define C5 5
#define R0 0
#define R1 1
#define R2 2
#define R3 3
#define R4 4
#define R5 5
#define OF 0
#define R_SIZE 0
#define C_SIZE 1
#define C_SIZE_A 2
#define FIRST 1
#ifndef PI
#define PI 3.14159265359
#endif
#define MAX(A,B) ((A)>(B) ? (A):(B) )
void clrscrn(void)
{
printf("\n\n\n\n\n\n\n\n\n\n\n"
"\n\n\n\n\n\n\n\n\n\n\n"
"\n\n\n\n\n\n\n\n\n\n\n");
}
L'étude sur les matrices fait partie d'un autre livre.
vmatini.hCréation et destruction d'une matrice |
|---|
/* ------------------------------------ */
/* Save as : vmatini.h */
/* -------------------------------------*/
double **I_mR(
int r,
int c
)
{
int i = R0;
int ar = r + C1;
int ac = c + C1;
double **A = malloc(ar * sizeof(*A));
for(; i<ar; i++)
A[i] = malloc(ac * sizeof(**A));
A[R_SIZE][OF] = ar;
A[C_SIZE][OF] = ac;
return(A);
}
/* ------------------------------------ */
void F_mR(
double **A
)
{
int i=R0;
int r=A[R_SIZE][OF];
if(A) for(;i<r;i++) free(A[i]);
free(A);
}
vmatbas.hAdditionner et multiplier des matrices |
|---|
/* ------------------------------------ */
/* Save as : vmatbas.h */
/* ------------------------------------ */
double **add_mR(
double **A,
double **B,
double **AplsB
)
{
int r;
int c;
for (r=FIRST;r<A[R_SIZE][OF];r++)
for(c=FIRST;c<A[C_SIZE][OF];c++)
AplsB[r][c]=A[r][c]+B[r][c];
return(AplsB);
}
/* ------------------------------------ */
double **mul_mR(
double **A,
double **B,
double **AB
)
{
int i,j,k;
for (k=FIRST; k<A[R_SIZE][OF];k++)
for (j=FIRST; j<B[C_SIZE][OF];j++)
for(i=FIRST,AB[k][j]=0;i<A[C_SIZE][OF];i++)
AB[k][j]+=A[k][i]*B[i][j];
return(AB);
}
vmatcop.hCopier une matrice |
|---|
/* ------------------------------------ */
/* Save as : vmatcop.h */
/* ------------------------------------ */
double ** c_mR(
double **A,
double **B
)
{
int r;
int c;
for( r=FIRST;r<A[R_SIZE][OF];r++)
for(c=FIRST;c<A[C_SIZE][OF];c++)
B[r][c]=A[r][c];
return(B);
}
/* ------------------------------------ */
double **c_a_A_mR(
double a[],
double **A
)
{
int r;
int c;
int i=0;
for( r=FIRST; r<A[R_SIZE][OF]; r++)
for(c=FIRST; c<A[C_SIZE][OF]; c++)
A[r][c] = a[i++];
return(A);
}
vmatrot.hMatrice de rotation |
|---|
/* Save as : vmatrot.h */
/* ------------------------------------ */
double **rot2D_mR(
double **A,
double alpha
)
{
A[1][1]=cos(alpha);A[1][2]=-sin(alpha);
A[2][1]=sin(alpha);A[2][2]= cos(alpha);
return(A);
}
y_r.hLa librairie de géométrie de la tortue vectorielle |
|---|
/* ------------------------------------ */
/* Save as : y_r.h */
/* ------------------------------------ */
void pd(
double **A
)
{
FILE *fp = fopen("data.plt","a");
fprintf(fp," %+.3f %+.3f\n",A[R1][C1],A[R2][C1]);
fclose(fp);
}
/* ------------------------------------ */
void pu(
double **A
)
{
FILE *fp = fopen("data.plt","a");
fprintf(fp,"\n %+.3f %+.3f\n",A[R1][C1],A[R2][C1]);
fclose(fp);
}
/* ------------------------------------ */
double **g_main(
double **A,
double xmin,
double xmax,
double ymin,
double ymax
)
{
FILE *fp;
fp = fopen("a_main.plt","w");
fprintf(fp,"# Gnuplot file : load \"a_main.plt\" \n"
"reset\n"
"set zeroaxis\n"
"set size ratio -1\n"
"plot [%0.3f:%0.3f] [%0.3f:%0.3f] \\\n"
"\"data.plt\" with linesp pt 0\n"
,xmin,xmax,ymin,ymax);
fclose(fp);
fp = fopen("data.plt","w");
fclose(fp);
A[R1][C1] = 0.;
A[R2][C1] = 0.;
pd(A);
return(A);
}
/* ------------------------------------ */
double **G_main(
double xmin,
double xmax,
double ymin,
double ymax
)
{
return(g_main(I_mR(R2,C1),xmin,xmax,ymin,ymax));
}
/* ------------------------------------ */
void set(
double **A,
double x,
double y
)
{
A[R1][C1] = x;
A[R2][C1] = y;
pd(A);
}
/* ------------------------------------ */
void setup(
double **A,
double x,
double y
)
{
A[R1][C1] = x;
A[R2][C1] = y;
pu(A);
}
/* ------------------------------------ */
void vo(
double **A,
double alpha,
double side
)
{
double **T = I_mR(R2,C2);
double **B = I_mR(R2,C1);
double **C = I_mR(R2,C1);
B[R1][C1] = side;
B[R2][C1] = 0.;
rot2D_mR(T,PI/180.*(alpha));
mul_mR(T,B,C);
c_mR(A,B);
add_mR(B,C,A);
pd(A);
F_mR(C);
F_mR(B);
F_mR(T);
}
/* ------------------------------------ */
void vu(
double **A,
double alpha,
double side
)
{
double **T = I_mR(R2,C2);
double **B = I_mR(R2,C1);
double **C = I_mR(R2,C1);
B[R1][C1] = side;
B[R2][C1] = 0.;
rot2D_mR(T,PI/180.*(alpha));
mul_mR(T,B,C);
c_mR(A,B);
add_mR(B,C,A);
pu(A);
F_mR(C);
F_mR(B);
F_mR(T);
}
Vectorielle : Quelques exemples
Préambule
[modifier | modifier le wikicode]La géométrie de la tortue dans Wikipedia.
Présentation
[modifier | modifier le wikicode]- Quelques exemples .
Dessiner
[modifier | modifier le wikicode]Petits jeux sur les pentagones
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c01.cPetits jeux sur les pentagones |
|---|
/* ------------------------------------ */
/* save as : c01.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_r.h"
/* ------------------------------------ */
void shape(
double **U,
double side,
int nbside,
double angle0
)
{
double i=nbside;
double shapeangle=360./nbside;
for(;i--;angle0+=shapeangle)
vo(U,angle0,side);
}
/* ------------------------------------ */
int main(void)
{
double side = 3.;
double nbside = 5.;
double angle = 0.;
double **U = G_main(-10.,10.,-10.,10.);
setup(U,-5,5);
for(angle=0; angle<360; angle+=6)
shape(U,side,nbside,angle);
setup(U,5.,5.);
for(angle=0; angle<360; angle+=12)
shape(U,side,nbside,angle);
setup(U,-5.,-5.);
for(angle=0; angle<360; angle+=36)
shape(U,side,nbside,angle);
setup(U,5.,-5.);
for(angle=0; angle<360; angle+=72)
shape(U,side,nbside,angle);
F_mR(U);
printf(" * open the file a_main.plt with Gnuplot. \n");
return 0;
}
| Résultat dans gnuplot |
|---|
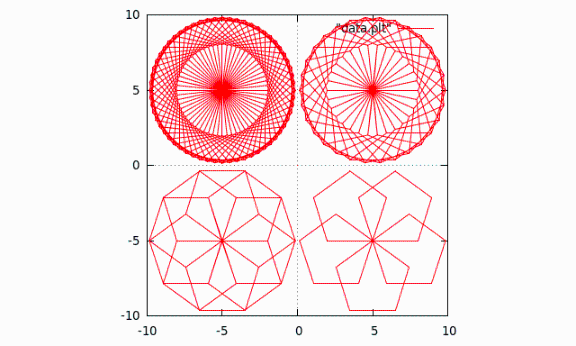
|
Une feuille
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c02.cUne feuille |
|---|
/* ------------------------------------ */
/* save as : c02.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_r.h"
/* ------------------------------------ */
double **tree(
double **U,
double brancheangle,
double branchelength,
double branchebranche,
double step,
double angletrunc
)
{
double j=angletrunc;
double i=branchelength;
vo(U,+90.,branchelength);
for(;i>0;i-=step,j+=angletrunc)
{
vo(U, brancheangle+90., i);
vo(U, brancheangle+90., -i);
vo(U,-brancheangle+90., i);
vo(U,-brancheangle+90., -i);
vo(U, j+90., i/branchebranche);
}
return(U);
}
/* ------------------------------------ */
int main(void)
{
double **U = G_main(-40.,40.,-40.,40.);
double branchebranche = 4.;
double branchelength = 10.;
double brancheangle = -45.;
double step = .5;
setup(U,-20.,0.);
tree(U,brancheangle,branchelength,branchebranche,step,2);
setup(U,0.,0.);
tree(U,brancheangle,branchelength,branchebranche,step,4);
setup(U,20.,0.);
tree(U,brancheangle,branchelength,branchebranche,step,6);
setup(U,-20.,-40.);
tree(U,brancheangle,branchelength,branchebranche,step,8);
setup(U,0.,-40.);
tree(U,brancheangle,branchelength,branchebranche,step,10);
setup(U,20.,-40.);
tree(U,brancheangle,branchelength,branchebranche,step,12);
F_mR(U);
return 0;
}
| Résultat dans gnuplot |
|---|
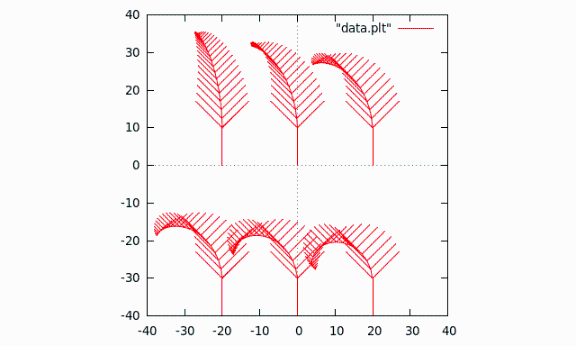
|
Petit jeux sur les polygones 1
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c03.cPetit jeux sur les polygones 1 |
|---|
/* ------------------------------------ */
/* save as : c03.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_r.h"
/* ------------------------------------ */
void duopoly(
double **U,
double **Sides,
double **Angles,
double alpha,
int n
)
{
int i=1;
int c;
for(;i++<n;)
for(c=C1;c<Angles[C_SIZE][OF];c++)
vo(U,i*(Angles[R1][c])+alpha,Sides[R1][c]);
}
/* ------------------------------------ */
int main(void)
{
double alpha =-0;
double a[2] ={ 45., 46.};
double s[2] ={ 140., 140.};
double **U = G_main(-1000.,1000.,-1000.,1000.);
double **A = c_a_A_mR(a,I_mR(R1,C2));
double **S = c_a_A_mR(s,I_mR(R1,C2));
setup(U,-150, 350.);
duopoly(U,S,A,alpha,152);
setup(U, 800, 350.);
duopoly(U,S,A,alpha,200);
setup(U,-150,-600.);
duopoly(U,S,A,alpha,275);
setup(U, 800,-600.);
duopoly(U,S,A,alpha,400);
F_mR(U);
return 0;
}
| Résultat dans gnuplot |
|---|

|
Petit jeux sur les polygones 2
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c04.cPetit jeux sur les polygones 2 |
|---|
/* ------------------------------------ */
/* save as : c04.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_r.h"
/* ------------------------------------ */
void duopoly(
double **U,
double **Sides,
double **Angles,
double alpha,
int n
)
{
int i=1;
int c;
for(;i++<n;)
for(c=C1;c<Angles[C_SIZE][OF];c++)
vo(U,i*(Angles[R1][c])+alpha,Sides[R1][c]);
}
/* ------------------------------------ */
int main(void)
{
double alpha =-0;
double a[2] ={ 45., 46.};
double s[2] ={ 140., -140.};
double **U = G_main(-1000.,1000.,-1000.,1000.);
double **A = c_a_A_mR(a,I_mR(R1,C2));
double **S = c_a_A_mR(s,I_mR(R1,C2));
setup(U,-550, 450.);
duopoly(U,S,A,alpha,152);
setup(U, 500, 450.);
duopoly(U,S,A,alpha,200);
setup(U,-550,-500.);
duopoly(U,S,A,alpha,275);
setup(U, 500,-500.);
duopoly(U,S,A,alpha,400);
F_mR(U);
return 0;
}
| Résultat dans gnuplot |
|---|

|
Petit jeux sur les polygones 3
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c05.cPetit jeux sur les polygones 3 |
|---|
/* ------------------------------------ */
/* save as : c05.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_r.h"
/* ------------------------------------ */
void duopoly(
double **U,
double **Sides,
double **Angles,
double alpha,
int n
)
{
int a=1;
int i=1;
int c;
for(;i++<n;)
for(c=C1;c<Angles[C_SIZE][OF];c++)
if(a)
{vu(U,i*(Angles[R1][c])+alpha,Sides[R1][c]);
a=0;}
else
{vo(U,i*(Angles[R1][c])+alpha,Sides[R1][c]);
a=1;}
}
/* ------------------------------------ */
int main(void)
{
double alpha =-0;
double a[2] ={ 45., 46.};
double s[2] ={ 140., -140.};
double **U = G_main(-1000.,1000.,-1000.,1000.);
double **A = c_a_A_mR(a,I_mR(R1,C2));
double **S = c_a_A_mR(s,I_mR(R1,C2));
setup(U,-550, 450.);
duopoly(U,S,A,alpha,152);
setup(U, 500, 450.);
duopoly(U,S,A,alpha,200);
setup(U,-550,-500.);
duopoly(U,S,A,alpha,275);
setup(U, 500,-500.);
duopoly(U,S,A,alpha,400);
F_mR(U);
return 0;
}
| Résultat dans gnuplot |
|---|

|
Vectorielle : Quelques exemples 2
Préambule
[modifier | modifier le wikicode]La géométrie de la tortue dans Wikipedia.
Présentation
[modifier | modifier le wikicode]- Quelques exemples .
Dessiner
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c01.cPetits jeux sur les polygones |
|---|
/* ------------------------------------ */
/* save as : c01.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_r.h"
/* ------------------------------------ */
void poly(
double **U,
double **Sides,
double **Angles,
double alpha,
int n
)
{
int i=1;
int c;
for(;i++<n;)
for(c=C1;c<Angles[C_SIZE][OF];c++)
vo(U,i*(Angles[R1][c])+alpha,Sides[R1][c]);
}
/* ------------------------------------ */
int main(void)
{
double a[2] ={ 19.,-20.};
double s[2] ={ 60., 60.};
double alpha =-90;
double **U = G_main(-1000.,1000.,-1000.,1000.);
double **A = c_a_A_mR(a,I_mR(R1,C2));
double **S = c_a_A_mR(s,I_mR(R1,C2));
setup(U,-500,450.);
poly(U,S,A,alpha,50);
setup(U, 500,450.);
poly(U,S,A,alpha,100);
setup(U, -500,-600.);
poly(U,S,A,alpha,200);
setup(U,500,-600.);
poly(U,S,A,alpha,400);
F_mR(U);
return 0;
}
| Résultat dans gnuplot |
|---|
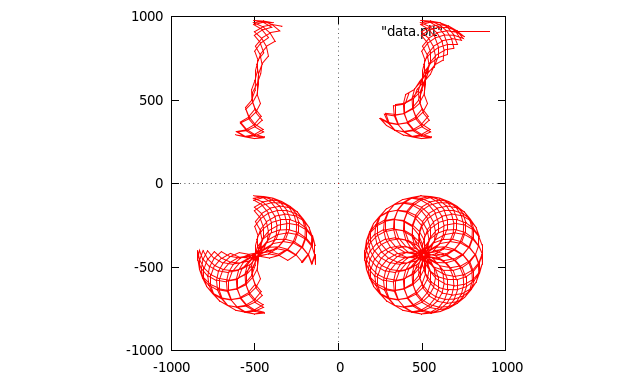
|
N'oubliez pas les fichiers h de la librairie.
c02.cUne étoiles |
|---|
/* ------------------------------------ */
/* save as : c02.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_r.h"
/* ------------------------------------ */
void poly(
double **U,
double **Sides,
double **Angles,
double alpha,
int n
)
{
int i=1;
int c;
for(;i++<n;)
for(c=C1;c<Angles[C_SIZE][OF];c++)
vo(U,i*(Angles[R1][c])+alpha,Sides[R1][c]);
}
/* ------------------------------------ */
int main(void)
{
double a[4] ={ 7., -8., 9., -10.};
double s[4] ={ 30., 30., 30., 30.};
double **U = G_main(-1000.,1000.,-1000.,1000.);
double **A = c_a_A_mR(a,I_mR(R1,C4));
double **S = c_a_A_mR(s,I_mR(R1,C4));
setup(U, 200,-100.);
poly(U,S,A,-0.,400.);
F_mR(U);
return 0;
}
| Résultat dans gnuplot |
|---|
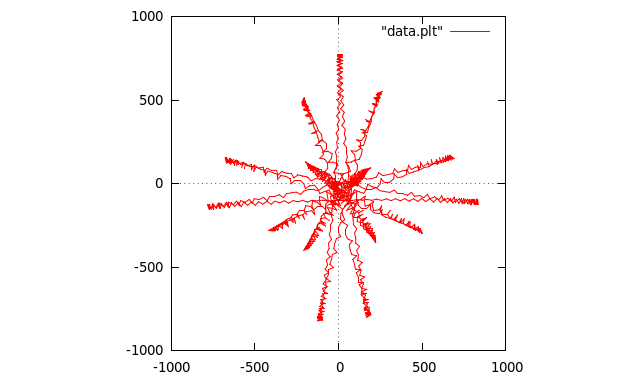
|
N'oubliez pas les fichiers h de la librairie.
c03.cPetit jeux sur les polygones |
|---|
/* ------------------------------------ */
/* save as : c03.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_r.h"
/* ------------------------------------ */
void poly(
double **U,
double **Sides,
double **Angles,
double alpha,
double n
)
{
int i;
int c;
for(i=1;i<n;++i)
for(c=FIRST; c<Angles[C_SIZE][OF]; c++)
vo(U,i*(Angles[FIRST][c])+alpha,Sides[FIRST][c]);
}
/* ------------------------------------ */
int main(void)
{
double alpha =-90;
double a[3] ={ -12., 13.,-12.};
double s[3] ={ 10., 20., 30.};
double **U = G_main(-1000.,1000.,-1000.,1000.);
double **A = c_a_A_mR(a,I_mR(R1,C3));
double **S = c_a_A_mR(s,I_mR(R1,C3));
setup(U,-500,450.);
poly(U,S,A,alpha,50);
setup(U, 500,450.);
poly(U,S,A,alpha,100);
setup(U, -500,-600.);
poly(U,S,A,alpha,200);
setup(U, 500,-600.);
poly(U,S,A,alpha,400);
F_mR(U);
return 0;
}
| Résultat dans gnuplot |
|---|

|
Vectorielle : Fonctions récursives
Préambule
[modifier | modifier le wikicode]La géométrie de la tortue dans Wikipedia.
Présentation
[modifier | modifier le wikicode]Les fonctions récursives.
Dessiner
[modifier | modifier le wikicode]Un arbre
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c01.cUn arbre |
|---|
/* ------------------------------------ */
/* save as : c01.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_r.h"
/* ------------------------------------ */
double **fun(double **U,double side,double angle);
/* ------------------------------------ */
int main(void)
{
double angle = 90.;
double side = 200.;
double **U = G_main(-150.,150.,-0.,300.);
F_mR(fun(U,angle,side));
printf(" * open the file main.plt with Gnuplot.");
return 0;
}
/* ------------------------------------ */
double **fun(
double **U,
double angle,
double side
)
{
if(side<5)
{
vo(U,angle, side);
vo(U,angle,-side);
return(0);
}
vo(U,angle, side/3.);
angle+=-30;
fun(U,angle,side*2./3.);
angle+= 30;
vo(U,angle, side/6.);
angle+= 25;
fun(U,angle,side/2.);
angle+=-25;
vo(U,angle, side/3.);
angle+= 25;
fun(U,angle,side/2.);
angle+=-25;
vo(U,angle, side/6.);
vo(U,angle, -side);
return(U);
}
| Résultat dans gnuplot |
|---|

|
Un arbre (2)
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c02.cUn arbre (2) |
|---|
/* ------------------------------------ */
/* save as : c02.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_r.h"
/* ------------------------------------ */
double **fun(double **U,
double side,double angle,double tangle);
/* ------------------------------------ */
int main(void)
{
double angle = 90.;
double side = 200.;
double tangle = 90.;
double **U = G_main(-400.,550.,-200.,500.);
F_mR(fun(U,angle,side,tangle));
printf(" * open the file main.plt with Gnuplot.");
return 0;
}
/* ------------------------------------ */
double **fun(
double **U,
double angle,
double side,
double tangle
)
{
if(side<2) return(0);
angle+=-tangle/2.;
vo(U,angle, side);
fun(U,angle,side/1.4,tangle);
vo(U,angle,-side);
angle+=tangle;
vo(U,angle, side);
fun(U,angle,side/2.,tangle);
vo(U,angle,-side);
angle+=-tangle/2.;
return(U);
}
| Résultat dans gnuplot |
|---|
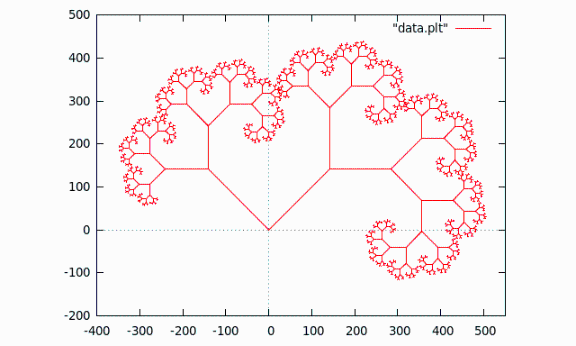
|
Un flocon
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c03.cUn flocon |
|---|
/* ------------------------------------ */
/* save as : c03.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_r.h"
/* ------------------------------------ */
double **fun2(double **U,
double angle,double side,double i);
int fun(double **U,
double angle,double side,double i);
/* ------------------------------------ */
int main(void)
{
double angle = 0.;
double side = 100.;
double i = 10.;
double **U = G_main(-120.,20.,-40.,120.);
F_mR(fun2(U,angle,side,i));
printf(" * open the file main.plt with Gnuplot.");
return 0;
}
/* ------------------------------------ */
int fun(
double **U,
double angle,
double side,
double i
)
{
if(i<1)
{
vo(U,angle,side);
return (0);
}
fun(U,angle,side/3.,--i);angle+=-60;
fun(U,angle,side/3.,--i);angle+=120;
fun(U,angle,side/3.,--i);angle+=-60;
fun(U,angle,side/3.,--i);
return (0);
}
/* ------------------------------------ */
double **fun2(
double **U,
double angle,
double side,
double i
)
{
int j;
for(j=3; j>0; --j)
{
angle+=120;fun(U,angle,side,i);
}
return(U);
}
| Résultat dans gnuplot |
|---|

|
Annexe : Commandes de bases (gnuplot)
Préambule
[modifier | modifier le wikicode]Dans ce chapitre, nous voyons les premières commandes pour dessiner des fonctions de la forme f(x).
En pratique
[modifier | modifier le wikicode]test
[modifier | modifier le wikicode]Cet exemple donne les informations de base.
# ---------------------
# save this file as : a_main.plt
# Then into gnuplot : load "a_main.plt"
#
#
test
reset
# ---------------------
Le passage à la ligne
[modifier | modifier le wikicode]# ---------------------
# save this file as : a_main.plt
# Then into gnuplot : load "a_main.plt"
#
# \n -> \
#
plot cos(x),\
sin(x),\
.4,\
-.4
reset
# ---------------------
Chaine de caractères
[modifier | modifier le wikicode]linetype | lt <0..15>
[modifier | modifier le wikicode]Chaque nombre correspond à une couleur différente. (voir test)
# ---------------------
# save this file as : a_main.plt
# Then into gnuplot : load "a_main.plt"
#
# linetype | lt <0..15>
#
plot cos(x) lt 1,\
sin(x) lt 2,\
.4 lt 3,\
-.4 lt 3
reset
# ---------------------
linewidth | lw <1.. 6>
[modifier | modifier le wikicode]Chaque nombre correspond à une épaisseur différente.
# ---------------------
# save this file as : a_main.plt
# Then into gnuplot : load "a_main.plt"
#
# # linewidth | lw <1.. 6>
#
plot cos(x) lt 1 lw 1,\
sin(x) lt 2 lw 3,\
.4 lt 3 lw 4,\
-.4 lt 3 lw 6
reset
# ---------------------
Liste de points
[modifier | modifier le wikicode]plot "data"
[modifier | modifier le wikicode]Dessiner une liste de points.
# ---------------------
# save this file as : a_main.plt
# Then into gnuplot : load "a_main.plt"
#
#
plot "data"
reset
# ---------------------
Créer un fichier "data" avec ces données :
-5 25 -4 16 -3 9 -2 4 -1 1 0 0 1 1 2 4 3 9 4 16 5 25
pointtype | pt <0..15>
[modifier | modifier le wikicode]Chaque nombre correspond à un dessin différent de points. (voir test)
# ---------------------
# save this file as : a_main.plt
# Then into gnuplot : load "a_main.plt"
#
# pointtype | pt <0..15>
#
plot "data" pt 10
reset
# ---------------------
pointsize | ps <1.. >
[modifier | modifier le wikicode]Chaque nombre correspond taille de points différents. (voir test)
# ---------------------
# save this file as : a_main.plt
# Then into gnuplot : load "a_main.plt"
#
# pointsize | ps <1.. >
#
plot "data" pt 10 ps 3
reset
# ---------------------
with linesp
[modifier | modifier le wikicode]Les points sont réliés par des segments.
# ---------------------
# save this file as : a_main.plt
# Then into gnuplot : load "a_main.plt"
#
# linetype | lt <0..15> (color)
# linewidth | lw <1.. 6> (size)
# pointsize | ps <1.. > (size)
#
plot "data" with linesp lt 3 lw 3 ps 3
reset
# ---------------------
pt 0
[modifier | modifier le wikicode]Sans les points.
# ---------------------
# save this file as : a_main.plt
# Then into gnuplot : load "a_main.plt"
#
# linetype | lt <0..15> (color)
# linewidth | lw <1.. 6> (size)
# pointsize | ps <1.. > (size)
#
plot "data" with linesp lt 3 lw 3 ps 3 pt 0
reset
# ---------------------
Commandes générales
[modifier | modifier le wikicode]set zeroaxis lt 8 lw 3
[modifier | modifier le wikicode]# ---------------------
# save this file as : a_main.plt
# Then into gnuplot : load "a_main.plt"
#
# linetype | lt <0..15> (color)
# linewidth | lw <1.. 6> (size)
#
set zeroaxis lt 8 lw 3
plot sin(x),\
cos(x)
reset
# ---------------------
set grid lt 8 lw 3
[modifier | modifier le wikicode]# ---------------------
# save this file as : a_main.plt
# Then into gnuplot : load "a_main.plt"
#
# linetype | lt <0..15> (color)
# linewidth | lw <1.. 6> (size)
# pointsize | ps <1.. > (size)
#
set grid lt 8 lw 3
plot sin(x),\
cos(x)
reset
# ---------------------
complet
[modifier | modifier le wikicode]# ---------------------
# save this file as : a_main.plt
# Then into gnuplot : load "a_main.plt"
#
# linetype | lt <0..15> (color)
# linewidth | lw <1.. 6> (size)
# pointsize | ps <1.. > (size)
#
set zeroaxis lt 8 lw 3
set grid
plot [-6.:6.] [-1.4:1.4]\
sin(x),\
cos(x)
reset
# ---------------------
Annexe : Commandes de bases 3d (gnuplot)
Préambule
[modifier | modifier le wikicode]Dans ce chapitre, nous voyons les premières commandes pour dessiner des fonctions en 3d.
En pratique
[modifier | modifier le wikicode]splot[x][y][z] (La fonction)
[modifier | modifier le wikicode]# ---------------------
# save this file as : a_main.plt
# Then into gnuplot : load "a_main.plt"
#
reset
splot [0:2*pi][0:2*pi][-1:1]\
cos(x)*cos(y)
# ---------------------
set hidden (Faces cachées)
[modifier | modifier le wikicode]# ---------------------
# save this file as : a_main.plt
# Then into gnuplot : load "a_main.plt"
#
reset
set hidden
splot [0:2*pi][0:2*pi][-1:1]\
cos(x)*cos(y)
# ---------------------
set view rot_x, rot_z, scale, scale_z (Imposer une vue)
[modifier | modifier le wikicode]# ---------------------
# save this file as : a_main.plt
# Then into gnuplot : load "a_main.plt"
#
reset
set hidden
set view 55.,57., 1., 1.
splot [0:2*pi][0:2*pi][-1:1]\
cos(x)*cos(y)
# ---------------------
set xlabel "X axis" (Nommer les axes)
[modifier | modifier le wikicode]# ---------------------
# save this file as : a_main.plt
# Then into gnuplot : load "a_main.plt"
#
reset
set hidden
set xlabel "X axis"
set ylabel "Y axis"
set view 55.,57., 1., 1.
splot [0:2*pi][0:2*pi][-1:1]\
cos(x)*cos(y)
# ---------------------
 GFDL GFDL
|
Vous avez la permission de copier, distribuer et/ou modifier ce document selon les termes de la licence de documentation libre GNU, version 1.2 ou plus récente publiée par la Free Software Foundation ; sans sections inaltérables, sans texte de première page de couverture et sans texte de dernière page de couverture. |


