Tribologie/Modélisation des actions de contact
Un peu d'histoire
[modifier | modifier le wikicode]Pendant très longtemps, les traités de mécanique rationnelle se sont bornés à étudier des systèmes matériels dénués de tout frottement. Joseph-Louis Lagrange, dans sa Mécanique analytique, semble avoir été le premier à distinguer, parmi les forces extérieures appliquées aux systèmes mécaniques,
- les forces actives, que nous appellerions aujourd'hui actions directes, qui pour une large part sont le résultat d'une volonté ou d'une imposition,
- les forces de liaison, ou actions de contact, qui sont imposées ou subies en raison de la nécessité d'imposer certaines conditions de fonctionnement aux composants mis en jeu.
Paul Painlevé, dans ses Leçons sur le frottement, écrit :
- La plupart des traités de mécanique rationnelle sont consacrés exclusivement aux systèmes dénués de frottement. Le frottement n'apparaît que dans quelques applications particulières. Est-il impossible de développer, pour les systèmes doués de frottement, une théorie générale analogue, par exemple, à celle que constitue l'application des équations de Lagrange aux systèmes sans frottement ? À coup sûr les lois empiriques du frottement ont des formes différentes suivant la nature des liaisons ; elles possèdent néanmoins assez de caractères communs, la marche qu'il convient de suivre dans les cas particuliers, les difficultés qui s'y rencontrent, offrent assez d'analogies pour qu'une telle théorie ait son utilité tant au point de vue rationnel qu'au point de vue des applications.
Les actions de contact
[modifier | modifier le wikicode]Il n'y a que deux manières d'appliquer des efforts mécaniques, que ce soit sur un solide unique ou sur un système matériel plus complexe :
- à distance (poids et plus généralement forces de gravitation, actions magnétiques, électrostatiques, ...)
- par contact avec d'autres objets ou systèmes matériels.
Lorsque l'on fait l'inventaire des efforts extérieurs appliqués sur un système matériel, il faut donc répondre complètement et exactement à deux questions :
- par quoi ce système est-il attiré ou repoussé ?
- à quoi ce système touche-t-il ?
Le terme général actions de contact désigne l'ensemble des efforts extérieurs, forces et moments, appliqués sur un système mécanique par d'autres objets qui le touchent. Ce sont ces efforts que nous allons tenter de représenter ici, sous la forme de modèles. La plupart du temps, leur répartition est très complexe et il est difficile voire impossible de les modéliser autrement que par des méthodes statistiques : par exemple, le comportement « global » d'un pneumatique sur une chaussée peut être étudié sans trop de problème, mais il est très difficile de définir les caractéristiques du contact, à l'instant « t », entre les sculptures du pneumatique et les aspérités du revêtement. Pour être efficace, il faut souvent renoncer à tout connaître. Reste à déterminer précisément les limites de l'étude ...
Il est bien rare qu'une machine puisse fonctionner sans que l'on ait tenu compte des résistances passives. L'ingénieur doit donc :
- les mettre à profit pour garantir l'adhérence d'une roue sur le sol, l'efficacité d'un frein ou d'un embrayage, la tenue en service d'un assemblage boulonné, ...
- ou les combattre, afin d'améliorer les rendements mécaniques, d'économiser l'énergie, d'obtenir de meilleures performances ...
Dans les deux cas, il doit être capable de définir et de quantifier les phénomènes susceptibles de se produire, ce qui suppose qu'il sache créer des modèles rendant compte aussi fidèlement que possible de la réalité.
Les mouvements relatifs des surfaces
[modifier | modifier le wikicode]Le mouvement relatif général de deux solides qui se touchent peut être considéré, en tout point de leur surface de contact, comme la combinaison de trois mouvements « élémentaires » définis selon les modalités habituelles de la cinématique : ce sont le glissement, le pivotement et le roulement.
Selon les cas, en théorie, chacun de ces trois mouvements peut être empêché ou plus ou moins contrarié, indépendamment des deux autres, par l'adhérence et/ou le frottement. C'est ainsi que dans des conditions normales, les roues d'un véhicule roulent sans glisser sur le sol. Différentes sortes de frottements freinent légèrement le mouvement de roulement tandis que l'adhérence empêche le glissement.
Il faut toutefois remarquer ici que les corps réels ne sont jamais des solides parfaits ; ainsi, des déformations parfois importantes se produisent dans les zones de contact et il en résulte des interactions qui font varier les comportements des systèmes. Par exemple, sans direction assistée, il est beaucoup plus facile de tourner le volant d'une automobile lorsqu'elle se déplace que lorsqu'elle est arrêtée : le fait que le pneu roule lui permet de pivoter plus facilement.
Attention à bien définir le vocabulaire utilisé et les mouvements eux-mêmes, en fonction des circonstances et des besoins. Si nous introduisons ici la notion de rotation, il est clair que le roulement et le pivotement ne peuvent se produire que si l'un des corps tourne par rapport à l'autre. En revanche une rotation n'entraînera pas forcément l'existence de mouvements de roulement et de pivotement au niveau des surfaces de contact. Par exemple, les mouvements relatifs possibles d'une tige cylindrique montée dans un alésage de même diamètre (liaison pivot glissant) sont une translation et une rotation. Au niveau de n'importe quel point de la surface de contact, chacun de ces mouvements provoque un glissement mais jamais de roulement ni de pivotement.
Adhérence et glissement
[modifier | modifier le wikicode]
|
| Schéma |
Un bloc parallélépipédique est pressé sur un plan par une force normale (son poids ou toute autre force imposée). Naturellement, cette force est compensée par l'ensemble des actions exercées par le plan sur le bloc, actions qui n'ont pas été dessinées ici puisque le bloc n'est pas isolé.
Rappelons qu'il ne faut jamais représenter les actions de contact sur un plan d'ensemble.
Appliquons maintenant au bloc une force parallèle au plan.
Cette fois, le bloc a été isolé, ce qui nous permet de dessiner la résultante de toutes les petites forces élémentaires qu'il reçoit de la part du plan. Tant que reste faible, rien ne bouge, le bloc est en équilibre : les trois forces ont des supports coplanaires, concourants, et leur somme est nulle. Remarquons en passant que le point d'application de la résultante n'est pas au centre du bloc mais légèrement décalé « vers l'avant ».

|
| Poussée sans glissement |
Le fait que la poussée ne provoque aucun mouvement prouve qu'il existe dans le contact des forces suffisantes pour maintenir le bloc immobile. On dit alors qu'il y a adhérence (et non pas adhésion, terme utilisé dans le cas du collage).
La résultante est dans le même plan que et , elle est située, par rapport à la normale, du côté qui lui permet de contrebalancer l'effet de .
L'angle de avec la normale n'a pas une valeur fixe, il est d'autant plus grand que la poussée est plus forte mais il ne peut en aucun cas dépasser une certaine valeur dite angle limite d'adhérence ou plus simplement angle d'adhérence.
Si l'on fait tourner la direction de autour de la normale, « suit le mouvement » et la conclusion est la même. Il s'ensuit que la résultante se trouve dans ou à la limite sur un cône de révolution dont l'axe est perpendiculaire au plan et dont le demi-angle au sommet vaut . Ce cône est appelé cône d'adhérence.
Le facteur d'adhérence , ou coefficient d'adhérence, est la limite supérieure du rapport des normes de l'effort tangentiel et de l'effort normal (ce facteur caractérise la limite entre adhérence et glissement, entre système statique et système dynamique) :

|
| Glissement |
Supposons maintenant que nous poussions suffisamment fort pour faire glisser le bloc. Si celui-ci a une vitesse constante , alors nous pouvons à nouveau faire comme s'il était en équilibre, c'est-à-dire que les trois forces , et qui s'exercent sur lui sont toujours coplanaires, concourantes, et leur somme est nulle.
Nous constatons cette fois que la résultante est toujours inclinée du même angle de frottement φ par rapport à la normale, c'est-à-dire qu'elle se trouve toujours sur un cône d'axe normal au plan et de demi angle au sommet φ, que nous appellerons cône de frottement.
Le facteur de frottement ou coefficient de frottement f est cette fois égal au rapport (constant) des normes de l'effort tangentiel et de l'effort normal :
| S'il y a glissement la force de contact est sur le cône de frottement le coefficient de frottement correspond à une égalité |
|
| S'il n'y a pas glissement la force de contact est dans ou à la limite sur le cône d'adhérence le coefficient d'adhérence correspond à une inégalité |
Dans la plupart des problèmes de mécanique rationnelle qui font intervenir le frottement, on fait l'hypothèse que les deux coefficients d'adhérence et de frottement sont égaux et constants. Ce n'est évidemment qu'une approximation plus ou moins grossière.
Le coefficient de frottement, comme nous le verrons, dépend d'une foule de paramètres parfois invraisemblables. Pour deux matériaux donnés, il peut varier dans d'énormes proportions selon la vitesse de glissement, la température, la lubrification, ...
Généralement le coefficient d'adhérence est plus important que le coefficient de frottement. Il s'ensuit qu'il est plus difficile de provoquer un mouvement que de le maintenir une fois qu'il a démarré. Cependant, un coefficient de frottement qui diminue quand la vitesse augmente est générateur de vibrations, c'est pourquoi l'on recherche souvent des couples de matériaux dont le coefficient de frottement croît légèrement quand la vitesse de glissement augmente ; c'est le cas, par exemple, pour les embrayages et les freins des véhicules.
En réalité, le frottement dit « statique » ne l'est jamais parfaitement. Même si deux pièces en contact semblent rester parfaitement immobiles l'une par rapport à l'autre, le moindre effort tangentiel provoque de petits mouvements de glissement localisés sur un nombre plus ou moins important de contacts d'aspérités. Il s'ensuit que le déplacement relatif d'une pièce par rapport à l'autre provoqué par un tel effort n'est jamais parfaitement réversible ; les pièces ne reviennent jamais parfaitement à leur position initiale car la récupération élastique de ce déplacement ne se fait plus dans les zones qui ont glissé.
Détermination rapide du coefficient d'adhérence
[modifier | modifier le wikicode]Imaginons un objet fait d'un matériau A reposant sur un plan horizontal fait d'un matériau B. Si l'on incline légèrement le plan, rien ne se passe puisque la résultante des actions de contact, directement opposée au poids de l'objet, se situe dans le cône d'adhérence.
En continuant d'incliner le plan, très progressivement, il arrive un moment où cette résultante se trouve juste sur le cône d'adhérence, on se trouve alors à la limite du glissement. La moindre inclinaison supplémentaire provoquera alors le glissement, puisque la résultante des efforts de contact ne pourra plus s'opposer au poids. L'angle limite d'inclinaison du plan n'est autre que l'angle d'adhérence des deux matériaux A et B, dans l'état où ils se trouvent (qualité de la surface, lubrification éventuelle, etc.).
Le « paradoxe de Painlevé »
[modifier | modifier le wikicode]Certains cas particuliers ont été signalés par Paul Painlevé et Amédée de Saint-Germain en 1895. Le mouvement commençant d'un système est généralement déterminé par les conditions initiales mais ce n'est pas toujours le cas. En particulier, lorsque les liaisons sont surabondantes, il y a souvent plusieurs mouvements commençants possibles.
Cet aspect des choses est connu depuis Bouligand sous le nom de « paradoxe de Painlevé ».
Contacts infinitésimaux
[modifier | modifier le wikicode] |
| Points réels de contact |
Dans le cas du frottement à sec (on parle de frottement immédiat, par opposition au frottement médiat qui fait intervenir un lubrifiant), l'aire réelle du contact de deux corps est toujours extrêmement petite par rapport à l'aire apparente définie par exemple sur un dessin technique. De plus, elle est très fragmentée : les pièces ne se touchent qu'en quelques points seulement, au moins trois non alignés, davantage si les pièces sont fortement pressées l'une contre l'autre
Pour envisager le problème à l'échelle infinitésimale, il faut supposer qu'il existe pour l'aire de contact S une échelle d'observation telle que les phénomènes qui se produisent à l'interface donnent l'impression d'être continus.
 |
| Élément de surface dS |
Dans ces conditions, il est possible de diviser S en éléments dS assez petits pour que l'on puisse considérer :
- que la pression de contact qu'ils subissent est uniforme,
- que la vitesse de glissement est la même en tous les points.
Ces deux hypothèses conduisent à assimiler chaque élément dS à une petite portion de plan située autour d'un point central M et à laquelle on associe un vecteur unitaire normal extérieur à la matière.
 |
| Forces s'appliquant sur dS |
On représente ici par la force élémentaire appliquée par la pièce A sur la pièce B, au niveau de l'élément de surface dS. Cette force peut toujours être « décomposée » d'une manière unique en une force normale dirigée suivant et une force tangentielle située dans le plan de la surface dS.
Bien évidemment
Si l'on appelle p la pression de contact au niveau de dS, alors on peut aussi écrire :
La composante tangentielle donnera quant à elle une contrainte tangentielle. En plus des pressions de contact comptées dans la direction perpendiculaire au petit élément de surface, le frottement engendre donc un effet de cisaillement.
L'étude globale devrait théoriquement se faire en intégrant les effets de toutes les petites forces de contact élémentaire, mais il est clair que si la surface de contact de deux corps est un tant soit peu complexe, les calculs deviennent très vite inextricables. Tout l'art consistera donc à créer des modèles d'étude pas trop éloignés de la réalité.
Oscillations de relaxation, stick-slip
[modifier | modifier le wikicode]Les lois du frottement, appelées plus ou moins à tort « loi de Coulomb », et sur lesquelles nous reviendrons dans le chapitre suivant, stipulent que le facteur de frottement ne dépend que de la nature des matériaux en présence et de l'état de leur surface, et qu'il est indépendant de facteurs comme la pression de contact, la vitesse de glissement, la température, etc. Ce n'est évidemment qu'une approximation souvent grossière.
Le facteur d'adhérence est généralement supérieur, parfois de beaucoup, au facteur de frottement. Nous allons montrer comment cela favorise l'apparition d'un phénomène de glissement saccadé que les anglo-saxons nomment stick-slip (littéralement colle-glisse) et qui est une oscillation de relaxation. Les exemples ci-dessous vont illustrer ce phénomène :
Glissement d'une masse poussée par un système élastique
[modifier | modifier le wikicode]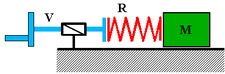 |
| Schéma du dispositif |
Une masse M de poids 100 N peut glisser sur un plan horizontal sous la poussée d'un ressort R que l'on comprime en faisant tourner très lentement une vis V. On admettra que le facteur d'adhérence vaut 0,3 et le facteur de frottement 0,25 ; la raideur du ressort est k = 1 N/mm.
Lorsque la force fournie par le ressort atteint 30 N, la masse démarre. Le ressort est alors comprimé d'une quantité X = 30 mm et son énergie potentielle vaut :
Dès le début du glissement, la résistance à l'avancement n'est plus que de 25 N ; comme la force appliquée par le ressort vaut 30 N, la masse M va « bondir », puis s'arrêter après avoir parcouru une certaine distance d. À la fin de ce mouvement, l'énergie potentielle du ressort vaut :
La variation de l'énergie potentielle du ressort entre le début et la fin du mouvement correspond au travail des forces de frottement le long du parcours :
On en tire :
On remarquera que lorsque la masse s'est arrêtée, la tension du ressort ne vaut plus que 20 N. Il faudra faire avancer la vis de 10 mm pour provoquer un nouveau déplacement. Si la vis tourne lentement et d'un mouvement continu, la masse avance par bonds successifs de 10 mm.
Vous pourrez reproduire facilement ce phénomène en tirant une masse par l'intermédiaire d'un élastique. Vous constaterez que les bonds sont d'autant plus longs que l'élastique est plus mou et qu'ils dépendent aussi des matériaux en présence.
Ce type de mouvement est responsable des sons musicaux émis par les instruments de musique à cordes frottées de la famille du violon, du grincement des portes dans les gonds desquelles « les gouttes d'huile se coincent », du crissement de la craie sur le tableau, du chant des grillons et des sauterelles, des bruits stridents émis par les freins de certains poids lourds, etc.
On comprend mieux désormais le titre de ce paragraphe. Oscillation de relaxation signifie que pendant une phase du mouvement, le système accumule une énergie potentielle qui se libère, se relaxe, brutalement, pendant la phase suivante.
Crissement d'une craie sur un tableau
[modifier | modifier le wikicode] |
En tenant la craie de cette manière, fermement et en appuyant sur l'extrémité qui écrit, l'élasticité de la main n'intervient pratiquement pas ; c'est ainsi que l'on écrit sans bruit et en déposant un maximum de craie sur le tableau |
 |
Si l'on tient la craie plus souplement, par l'extrémité qui n'écrit pas, et en l'inclinant « dans le sens inverse de la marche », le système devient déformable et apte à emmagasiner de l'énergie potentielle. La craie sautille bruyamment sur le tableau, trace un magnifique pointillé ... et s'use moins que précédemment. Merci Monsieur Coriolis (voir ici) ! |
 |
Il faut évidemment comparer les deux traits ... |
 |
... et ne pas hésiter à s'approcher. Le trait de gauche n'est continu que de loin, il présente en fait les nombreuses stries orientées dans la direction du mouvement qui résultent de l'usure abrasive. À droite, on s'aperçoit que tous les petits traits ont la même structure : une trace d'impact bien marquée suivie d'une trace de frottement plus légère, qui précède la phase de « décollage » de la craie. |
Traces d'usure
[modifier | modifier le wikicode]Les phénomènes que nous venons de décrire à partir d'objets dont les dimensions sont relativement importantes se produisent aussi à des échelles beaucoup plus petites, par exemple lors du contact des aspérités d'une pièce. C'est pourquoi on trouve dans de nombreuses traces d'usure les figures plus ou moins périodiques caractéristiques du stick slip. Lors des essais d'usure, le changement du bruit émis par les échantillons en contact peut être un élément d'information important, car il traduit immanquablement un changement de régime de frottement, changement qui n'est pas forcément perçu par les instruments de mesure utilisés dans le montage.
Sismologie
[modifier | modifier le wikicode]
L'un des phénomènes qui se produisent lors des tremblements de terre est en tous points analogue au stick-slip que l'on rencontre en mécanique. On sait que la croûte terrestre est constituée de « plaques » qui se déplacent les unes par rapport aux autres selon différents processus. Ces plaques peuvent en effet glisser l'une contre l'autre selon des surfaces de fracture ou « failles », ou encore passer l'une sous l'autre dans un mouvement dit de « subduction ».
Les déplacements relatifs sont très lents et se font d'abord grâce à une déformation progressive des roches en contact de part et d'autre des surfaces de glissement. Lors de cette déformation, qui est partiellement élastique, d'énormes quantités d'énergie potentielle sont accumulées. Simultanément, les contraintes de cisaillement augmentent au niveau des surfaces de contact. Lorsque la limite d'adhérence de ces surfaces est atteinte, un glissement brutal se produit, l'énergie emmagasinée dans les roches se trouve brutalement libérée, avec les conséquences que l'on sait : bâtiments détruits, ouverture de crevasses dans le sol, etc.
Depuis quelques années, on commence à s'inquiéter des conséquences de l'action humaine sur l'apparition des séismes. Celui qui s'est produit à Pawnee, dans l'Oklahoma, en septembre 2016, a atteint une magnitude de 5,7 ; le mécanisme de la rupture a été étudié par l'Institut de physique du globe de Paris, en associant les observations de terrain classiques, les données satellitaires et une modélisation numérique. Il est désormais démontré que les activités humaines peuvent « réveiller » des failles dormantes situées à plusieurs kilomètres et de déstabiliser les sols sur des zones très étendues.
À cause de la fracturation hydraulique pratiquée à grande échelle pour l'exploitation pétrolière, l’État de l'Oklahoma est devenu plus instable que la Californie ! Avant 2009, il subissait moins d'un séisme de magnitude égale ou supérieure à 3 par an ; on en a compté environ 600 en 2014 et plus de 800 en 2015. L'action de la population et de la presse a conduit les autorités de l'Oklahoma à prendre des mesures de régulation grâce auxquelles le nombre de séismes a légèrement baissé, environ 500 « seulement » en 2016, mais trois d'entre eux ont atteint une magnitude supérieure à 5 et occasionné des dégâts matériels.
Frottement de pivotement
[modifier | modifier le wikicode]
|
| Frottement de pivotement |
Il s'agit d'un cas particulier du frottement de glissement, avec une vitesse de glissement variable dans la zone d'appui.
Une bille, qui repose ici dans une alvéole en forme de calotte sphérique, est chargée verticalement par une force . Pour la faire tourner à la vitesse par rapport au support, il faut lui appliquer un couple .
Ce couple, créé par les résistances passives, freine d'autant plus la rotation que le facteur de frottement est plus élevé et que l'appui est plus étendu et plus chargé. Il dépend en outre de la façon dont se répartissent les pressions de contact entre la sphère et le support.
Il est toujours possible d'écrire le couple de frottement de pivotement sous la forme suivante :

|
| Rayon de pivotement |
Tout se passe comme si le contact des deux objets se faisait sur une couronne circulaire de rayon moyen R.
Ce rayon fictif R est le facteur de frottement de pivotement.
Si le couple « moteur » est insuffisant, la bille ne tourne pas, il y a adhérence, dans ce cas :
| Le facteur de frottement de pivotement est une longueur, contrairement au facteur de frottement de glissement qui n'a aucune dimension |
Sous sa simplicité apparente, ce petit problème cache beaucoup de choses :
- Si le couple est très faible, l'adhérence règne partout dans le contact, les surfaces ne glissent nulle part mais l'ensemble du système se déforme très légèrement à cause de l'élasticité des matériaux. La bille tourne d'un très petit angle avant de s'immobiliser.
- Si le couple est un peu plus important, alors les déformations élastiques augmentent et l'on commence à voir des glissements dans les zones du contact les plus éloignées de l'axe. Le frottement dans ces zones externes, associé aux forces d'adhérence dans la zone centrale, immobilise la bille. Les déplacements qui se sont produits font que si le couple se relâche, la bille ne revient pas exactement à sa position initiale, des forces de cisaillement subsistent dans le contact.
- Si le couple augmente encore, la zone de glissement s'étend à tout le contact et la bille tourne en permanence. Le problème devient soudain ... beaucoup plus simple et facile à étudier !
Dans tout contact apparemment immobile, il y a pratiquement toujours des zones dans lesquelles se produisent des glissements tandis que partout ailleurs règnent des efforts de cisaillement inférieurs à la limite à partir de laquelle le glissement se produit.
Pour comprendre ce phénomène, une expérience très simple suffit : pressons nos deux mains l'une contre l'autre, paume contre paume, doigts étendus et serrés. Normalement, par symétrie, leur contact est une surface plane. Lorsque nous les faisons tourner de quelques degrés l'une par rapport à l'autre autour du « poil dans la main », les premiers glissements se produisent au bout des doigts tandis qu'au niveau des paumes, l'élasticité des « tissus mous » autorise la rotation des structures osseuses sans pour autant que le glissement se produise. Une fois que les doigts ont glissé, ils ne reprennent pas spontanément leur position initiale, on ne peut les y ramener que par l'application d'un couple de sens contraire au précédent.
Pivotement dans un contact ponctuel « hertzien »
[modifier | modifier le wikicode]Deux solides bombés parfaitement indéformables mis en contact l'un avec l'autre devraient théoriquement se toucher par un seul point. Évidemment cette représentation est fausse car le moindre effort normal donnerait une pression infinie, ce qui est physiquement impossible. On l'utilise néanmoins à l'échelle macroscopique, lorsque les zones de contact sont très petites par rapport aux dimensions des pièces mises en jeu.
En réalité, les matériaux étant toujours plus ou moins déformables, le contact s'établit selon une petite surface dont l'aire augmente, mais pas de façon linéaire, lorsque l'effort normal croît.

|
| Pressions de Hertz |
Dans certaines conditions bien définies, que nous verrons plus loin, on peut parler de contact hertzien « ponctuel », par exemple celui d'une bille sur un plan). D'après la théorie de l'ingénieur Hertz, cette surface est en général une petite ellipse ou parfois un cercle ; la pression de contact, maximale au centre, diminue graduellement selon une loi elliptique jusqu'à la périphérie. Le diagramme donnant la répartition des pressions sur l'appui est donc un demi-ellipsoïde.
On montre que dans ces conditions, le couple de frottement de pivotement est proportionnel au périmètre L de la zone d'appui ; f est bien sûr le facteur de frottement et P la charge normale au contact.
Cas d'une collerette d'appui
[modifier | modifier le wikicode]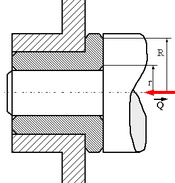
|
| Collerette d'appui |
Un cas particulier très fréquent est celui d'une collerette d'appui. La portée des deux pièces se fait sur une couronne circulaire de petit rayon r et de grand rayon R chargée de supporter l'effort axial Q.
Si l'on suppose parfaite la congruence (du latin congruus, qui s'accorde, qui convient) des deux surfaces de l'axe et du coussinet, la pression de contact est constante dans toute l'aire de contact. En admettant également que le facteur de frottement ait la même valeur f en tout point, il est facile de calculer le couple de pivotement :
Re est parfois appelé « rayon équivalent », tandis que le produit f.Re n'est autre que le facteur de frottement de pivotement.
Si R et r sont voisins, compte tenu de l'imprécision inévitable sur la valeur du facteur de frottement de glissement, on peut remplacer sans trop d'états d'âme le rayon équivalent par le rayon moyen Rm :
Frottement de roulement
[modifier | modifier le wikicode]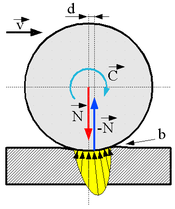
|
| Roulement |
Une bille ou un rouleau qui roule sans glisser sur un plan horizontal, sans recevoir d'énergie extérieure, ralentit et finit par s'arrêter sous l'effet des frottements internes aux pièces. On peut maintenir la vitesse constante par application d'un couple parallèle à l'axe de la rotation.
La zone d'appui, plus ou moins étendue, subit des pressions qui peuvent être relativement faibles (pneumatiques automobiles ...) ou très élevées (couramment 3000 à 3500 MPa dans les roulements à billes ou à rouleaux). Le corps roulant (supposé, sur ce schéma, moins déformable que le support) et la piste s'affaissent toujours plus ou moins lors de la mise en contact, puis reprennent leur forme initiale, du moins si les déformations sont restées élastiques. Dans le cas contraire, le corps roulant laisse une « ornière » dans la piste, comme fait une roue qui parcourt un sol meuble.
Comme les matériaux réels ne sont jamais parfaitement élastiques, le retour à la forme initiale, même quand il est total, n'est pas instantané. Un « bourrelet » (b) se forme à l'avant du corps roulant, tandis qu'à l'arrière les surfaces se séparent un peu trop vite ; tout se passe comme si le corps roulant montait une pente sans fin. De ce fait, les forces de contact sont plus élevées à l'avant de la zone de contact qu'à l'arrière et leur résultante n'est pas directement opposée à la charge normale mais décalée vers l'avant d'une certaine distance d telle que :
Les valeurs de et sont ici, bien évidemment, des normes. La distance d est le facteur de frottement de roulement, ou encore coefficient de frottement de roulement.
| Le facteur de frottement de roulement est une longueur, contrairement au facteur de frottement de glissement qui n'a aucune dimension |

|
| Bloc sur rouleaux |
Il est souvent intéressant de considérer le frottement de roulement d'une manière plus globale, combiné ou non à d'autres formes de frottement. Ainsi, lors de l'avancement d'un objet de poids monté sur des rouleaux, la poussée tient-elle compte globalement des frottements de roulement dans l'ensemble des zones de contact.
Dans le cas d'un véhicule sur roues, la poussée intègre non seulement les frottements de roulement des bandages ou des pneus sur le sol, mais encore les frottements de roulement ou de glissement des essieux dans leurs paliers, les frottements de glissement dans les joints d'étanchéité, etc.
Cela donne par exemple, par tonne de véhicule, des valeurs de de l'ordre de :
- 300 N pour une automobile,
- 150 N pour un poids lourd (jusqu'à 80),
- 30 N pour un véhicule sur rail (jusqu'à 17 pour le TGV).
Ces valeurs ne tiennent compte que du roulement et n'intègrent ni la pente éventuelle de la piste ni la résistance de l'air. Elles indiquent toutefois que sur un parcours horizontal et à vitesse modérée, de 80 à 100 km/h, à masse égale, le transport de marchandises par la route consomme de 5 à 10 fois plus d'énergie que le transport ferroviaire.
Frottements combinés
[modifier | modifier le wikicode]
|
| Contact de deux objets |
Dans de nombreux cas, les mouvements relatifs des solides sont combinés, et il en va de même pour les résistances passives. Considérons par exemple deux solides quelconques : A, fixe par convention, nous servira de repère et B, mobile, en contact avec A par une certaine surface S que nous considérons ici comme très petite et plane.
En un point de cette surface nous pouvons exprimer les éléments de réduction du torseur cinématique représentant le mouvement de B par rapport à A :
- un vecteur « rotation » , qu'il vaut mieux appeler taux de rotation,
- la vitesse de glissement , qui est la vitesse du point coïncidant avec le point à l'instant t.

|
| Vitesses |
Il est toujours possible de « décomposer » de manière unique le vecteur taux de rotation en deux parties :
- le taux de pivotement dirigé selon la normale à la surface S,
- le taux de roulement perpendiculaire à cette normale et donc situé dans le plan de S, qui n'est autre que le plan tangent commun aux deux surfaces.
Les efforts appliqués par A sur B doivent être reliés, autant que faire se peut, aux mouvements de B par rapport à A. Ils sont composés d'une force , résultante des forces appliquées sur la surface S, et d'un couple .
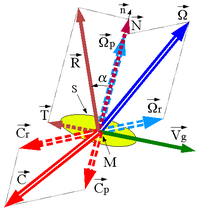
|
| Résistances passives |
- la force comporte une partie normale transmise par l'appui (c'est sa fonction !) et une partie tangentielle qui s'oppose au mouvement, et que l'on appelle pour cela force de frottement :
- - si les surfaces glissent, a le même support que la vitesse de glissement mais elle est de sens contraire. Dans ces conditions, .
- - si les surfaces ne glissent pas, alors il n'y a pas de vecteur , la force reste bien entendu tangentielle mais on ne connaît pas a priori sa direction ; sa norme est telle que
- Le couple peut être conçu comme la somme de deux composantes :
- - un couple de résistance au pivotement de même support que mais de sens contraire,
- - un couple de résistance au roulement de même support que mais de sens contraire.
L'absence de pivotement ne signifie pas que le couple de résistance au pivotement est nul. C'est peut-être ce couple, justement, qui empêche le mouvement correspondant. S'il existe, il est normal à la surface S et sa direction est donc connue, mais on ne connaît pas son sens.
En l'absence de mouvement de roulement, le couple de résistance au roulement existe probablement, il est de toute manière tangentiel, donc dans le plan de S, mais on ne connaît pas sa direction.
Le glissement, le pivotement et le roulement sont le plus souvent indépendants (mais pas toujours) et a priori rien ne relie les trois efforts fondamentaux qui tendent à s'opposer à ces mouvements.

|
| Contact bille-gorge |
Pour prendre un exemple pratique, examinons le contact d'une bille qui peut se déplacer dans une piste cylindrique de même rayon.
Si ces deux pièces étaient parfaitement réalisées et parfaitement rigides, leur contact se ferait selon un arc de cercle. En pratique, on ne peut pas plus réaliser deux surfaces géométriquement exactes que deux rayons parfaitement identiques. Même si ce bel ordonnancement pouvait exister, les déformations et l'usure auraient d'ailleurs tôt fait de le détruire.
Comme on ne peut évidemment pas compter sur les miracles pour faire fonctionner les machines, il faut réaliser délibérément deux rayons légèrement différents.
- Si le plus grand est celui de la bille, alors celle-ci porte sur les deux arêtes latérales de la piste, ce qui n'est pas génial ...
- Si c'est celui de la piste, alors la portée se fait théoriquement en un seul point de la génératrice médiane mais pratiquement elle a lieu selon une surface très allongée semblable à une ellipse que l'on aurait incurvée pour qu'elle épouse la piste. Naturellement, plus la bille est chargée et plus la surface de contact est importante.

|
| Ellipse de contact |
Si la bille pivote autour d'un axe normal au contact en son centre, seul le point central est immobile ; tous les autres points sont le siège d'un glissement à une vitesse d'autant plus grande qu'ils sont plus éloignés de l'axe.
Si la bille roule sur la piste, on conçoit immédiatement que cela ne peut pas se faire sans glissement Si la bille porte au centre, elle avance en un tour d'une longueur égale au périmètre du cercle central C. Si elle porte sur les arêtes latérales, elle avance en un tour du périmètre des cercles B. Si le contact se fait selon un arc, elle avance d'une longueur intermédiaire entre ces deux périmètres.

|
| Mouvements combinés |
Dans ce dernier cas, l'axe instantané de rotation de la bille se situe à un niveau intermédiaire entre le fond et les bords de la piste. En I et I' le vecteur taux de rotation n'est pas perpendiculaire au contact, mais oblique ; on peut le considérer comme la somme de deux composantes, un taux de pivotement et un taux de roulement .
- Les deux points I et I' de la bille sont immobiles à l'instant t, il s'y produit du pivotement et du roulement mais aucun glissement.
- À l'intersection du plan de symétrie et de la surface de contact, sur le « petit diamètre » de la zone de contact, il y a du roulement et du glissement mais pas de pivotement.
- Partout ailleurs dans le contact, les trois mouvements de glissement, de pivotement et de roulement se produisent ensemble et leurs trois valeurs varient selon des lois différentes d'un point à un autre.

|
| Ellipse de contact |
A priori l'usure d'un tel contact est d'autant plus grande, en un point donné, que la pression et la vitesse de glissement sont plus élevées.
- Si le rayon de la bille n'est que très légèrement inférieur à celui de la piste, l'"ellipse" de contact peut avoir une aire relativement importante et le système possède alors une capacité de charge élevée. En revanche les vitesses de glissement, et donc les pertes par frottement, peuvent prendre des valeurs prohibitives.
- Si le rayon de la bille est nettement inférieur à celui de la piste, alors l'axe instantané de rotation se rapproche du « fond » de cette dernière, le pivotement et le glissement tendent à disparaître, le mouvement devient plus facile car la résistance au roulement est généralement plus faible que les deux autres. Par contre, la capacité de charge baisse par suite de l'inévitable diminution de l'aire de contact.
- Dans des conditions données de charge et de vitesse, le constructeur doit trouver un compromis acceptable en tenant compte d'autres éléments comme les matériaux, la lubrification ... On aura compris que l'un des éléments essentiels de ce compromis se mesure en centièmes de mm, voire en micromètres, son maniement est assez subtil, il s'agit bien sûr de la différence des rayons.
Chocs avec frottement
[modifier | modifier le wikicode]Lorsque deux corps animés de vitesses différentes en grandeur et/ou en direction se rencontrent, il se produit un phénomène appelé choc ou percussion
On considère généralement en mécanique qu'un choc engendre des efforts très importants qui agissent pendant un temps très court, voire de façon quasi instantanée. Pendant ce laps de temps, les objets subissent des changements brusques de vitesse mais leurs positions ne varient pas notablement.
Les premières études de chocs sans frottement sont dues à Newton. Poisson, vers 1820, a traité divers cas particuliers, mais toujours sans frottement. Beaucoup d'autres auteurs ont travaillé sur ce thème, parmi lesquels Cournot, Coriolis (1835), Phillips (1849), Darboux (1874), Joukovsky (1878), Ostrogradsky, Soula et Villa (1923). Delassus et Pérès ont étudié des situations plus complexes, comme les chocs avec glissement suivi de roulement.
La tendance actuelle est d'étudier les chocs à l'aide d'ordinateurs, par des méthodes numériques. La prise en compte du frottement se fait toujours, faute de mieux, en supposant que le facteur de frottement reste constant dans toute la zone de contact et pendant toute la durée, du choc, ce qui ne peut constituer au mieux qu'une approximation, mais rend finalement assez bien compte tout de même des phénomènes réels (à condition, évidemment, d'adopter une bonne valeur).
Les bons joueurs de billard n'ont pas besoin de calculs complexes pour évaluer les divers effets du frottement lors du choc des boules ...
« Extinction du frottement »
[modifier | modifier le wikicode]P. Appell a fait remarquer, en 1905, que le mouvement d'un système qui subit le frottement s'effectue toujours de façon que le travail des forces de frottement diminue de plus en plus, comme si ce système cherchait à échapper au frottement. Une boule de billard à laquelle on donne de l'effet commence par glisser en roulant, mais très vite le glissement cesse et seul le roulement se poursuit jusqu'à l'arrêt complet.
L. Lecornu, dans des mémoires adressés à l'Académie des Sciences en 1906 et 1907 et intulés « Sur l'extinction du frottement », indique que dans les systèmes frottants abandonnés à eux-mêmes, «le travail de frottement, rapporté à l'unité de temps, va constamment en diminuant et qu'à l'état final le travail du frottement est devenu minimal. »
Notons que le travail rapporté à l'unité de temps n'est autre que la puissance.
Lecornu a repris et développé cette idée en 1937.
Ambiguïtés et paradoxes, arc-boutement, broutage
[modifier | modifier le wikicode]P. Painlevé a montré que les lois du frottement sont souvent grossièrement approchées par rapport aux phénomènes réels et qu'elles peuvent conduire à des résultats ambigus ou paradoxaux.
- Dans les cas les plus simples où l'on prend en compte le frottement, les composantes normales des forces aux appuis sont indépendantes du coefficient de frottement. Par exemple, si l'on fait glisser un objet sur un plan horizontal, la résultante des forces appliquées par le plan sur l'objet a toujours une composante verticale ascendante directement opposée au poids, donc constante, quelle que soit l'intensité du frottement entre cet objet et le plan.
- Dans des cas plus généraux, il arrive au contraire que les composantes normales prennent des valeurs qui dépendent du coefficient de frottement. Dans ce cas, tant pour le frottement de glissement que pour la rupture d'un équilibre, des faits singuliers d'indétermination, de mouvements saccadés ou d'impossibilité peuvent se produire.
Indéterminations
[modifier | modifier le wikicode]Dans bien des cas le mouvement d'un objet soumis au frottement ou à l'adhérence est totalement imprévisible. Prenons par exemple une simple bande de plastique un peu épais, plions-la en deux et posons-la en forme de (lambda majuscule) sur un plan. Très vite, le plastique se « relâche », la bande glisse, se stabilise, glisse à nouveau, se restabilise, et ainsi de suite ; des périodes de « repos » de plus en plus longues séparent des mouvements brusques.
 |
 |
 |
 |
Il est facile d'observer qu'au début d'un mouvement, le glissement n'est pas symétrique : l'un des « pieds » du glisse avant l'autre, sans que l'on puisse prévoir lequel glissera en premier. Il est également presque impossible de prévoir à quel instant un mouvement aura lieu ; même si l'on pouvait facilement évaluer les contraintes qui règnent dans le plastique, cette question resterait pratiquement sans réponse.
(mais vous pouvez compléter si vous le souhaitez !)
Paradoxes
[modifier | modifier le wikicode]Mouvements de broutement
[modifier | modifier le wikicode]Ils ont été étudiés plus haut dans la partie consacrée aux « oscillations de relaxation ». Dans la mesure où ces mouvements produisent des bruits et des vibrations presque toujours indésirables, on tâche de les éviter en utilisant le frottement de roulement ou le frottement fluide, et de toute manière en faisant en sorte que les frottements aillent en croissant lorsque les vitesses augmentent, et jamais l'inverse.
Ceci est particulièrement vrai pour les freins et les embrayages, à propos desquels on trouvera des données constructives dans le chapitre Tribologie - Applications pratiques.
Arc-boutement
[modifier | modifier le wikicode]
Le phénomène d'arc-boutement se produit dans un système mécanique lorsque la configuration de celui-ci est telle que l’adhérence empêche tout mouvement et maintient donc l'équilibre, quelle que soit l’intensité des actions mécaniques extérieures.
Un exemple classique et connu de tous est celui du tiroir de commode qui se met légèrement en biais et se « coince » lorsque l'on veut le refermer. Chacun sait que ce n'est pas en poussant plus fort que l'on peut atteindre le but recherché. L'expérience personnelle indique que le tiroir s'immobilise d'autant plus facilement que son guidage est moins profond que large, que le tiroir est chargé d'un seul côté, que l'on ne pousse pas dans l'axe, etc.
De nombreux outils, mécanismes ou dispositifs, comme la clé du plombier ou le serre-joint du menuisier, utilisent l'arc-boutement pour assurer l'immobilisation de certains éléments.
L'arc-boutement peut parfois survenir de façon brutale dans des mécanismes trop usés ou mal lubrifiés et il peut se révéler fort dangereux lorsque des éléments de forte inertie se trouvent soudain immobilisés. Les risques sont diminués en utilisant des guidages par roulement plutôt que des guidages par glissement et, par ailleurs, les mécaniciens expérimentés savent qu'il faut toujours substituer, lorsque c'est possible, les guidages en rotation aux guidages en translation ; autrement dit, il vaut toujours mieux utiliser des pivots plutôt que des glissières.
Les alpinistes et les grimpeurs utilisent souvent des coinceurs pour s'assurer en en bloquant un dans une fissure. Beaucoup de ces dispositifs utilisent le principe de l'arc-boutement, à l'exemple du coinceur à deux cames représenté ci-contre. Les pièces de ce dispositif ont une forme telle que plus on tire sur la tige, plus les cames appuient sur les parois, sans pour autant glisser car les angles des forces d'appui restent toujours inférieurs à l'angle d'adhérence défini plus haut.
En tournant, les cames peuvent s'adapter à des fentes de diverses largeurs. Le profil des surfaces d'appui est défini par une spirale logarithmique ; on sait qu'en tout point de cette courbe, la tangente fait un angle constant avec le rayon vecteur, cette propriété étant utilisée pour bien d'autres applications telles que les lames de sécateurs ou le profil en long des salles de cinéma.