Électricité/Le transformateur monophasé

Électricité

La physique de l’électricité

• Les grandeurs électriques : intensité, tension, puissance
• Le passage du courant dans un solide : la résistance

Les circuits électriques

• Les dipôles : générateurs et récepteurs
• Les circuits électriques
• Les lois des circuits électriques

Le régime continu et les circuits résistifs/linéaires

• Les résistors
• Les générateurs : piles, batteries et autres
• Les associations de résistors
• Les circuits linéaires et leurs lois
• Les quadripôles linéaires

Le régime transitoire : bobines et condensateurs

• Le condensateur
• La bobine
• Bobines et condensateurs en série/parallèle
• Les circuits RL, RC, LC et RLC

Le régime alternatif

• Le continu et l'alternatif
• Le régime sinusoïdal
• L'impédance : l'équivalent sinusoïdal de la résistance
• Les quadripôles en régime sinusoïdal
• Le transformateur monophasé
• Les redresseurs

Annexes

• Notions de sécurité électrique

Généralités sur le transformateur

Qu'est-ce qu'un transformateur ?

Un transformateur a pour but de modifier les amplitudes des grandeurs électriques alternatives : il transforme des signaux de tension et de courant de fréquence donnée en signaux de même fréquence mais de valeurs efficaces différentes.

L'une des particularités du transformateur est qu'il a un rendement très élevé, souvent proche de 100 % : dans les gros transformateurs, on a moins de 1 % de pertes. Pour simplifier, nous ne considérerons ici que le cas du transformateur monophasé, mais les principes physiques abordés s'appliquent aussi au cas du transformateur triphasé.

Pourquoi utiliser un transformateur ?

Le transformateur joue un rôle important dans le transport et la distribution de l'énergie électrique. En effet, si l'on s'intéresse aux pertes en ligne lors d'un transport de puissance électrique, et plus particulièrement aux pertes par effet Joule, ces-dernières sont, quel que soit le conducteur, d'autant plus importantes que le courant électrique est élevé. Or, à puissance transportée constante, l'utilisation d'une tension plus élevée implique un courant électrique plus faible puisque, d'une manière générale et quel que soit le nombre de phases utilisées, la puissance électrique $P_{elec}$ est proportionnelle au produit de la tension $V$ par le courant $I$ :

$P_{elec}\propto V\times I\qquad (6)$

De fait, afin de limiter au maximum les pertes en ligne, il faut transporter un courant aussi faible que possible : quand les distances deviennent importantes, le transport de l'énergie électrique ne peut se faire qu'à très haute tension. Il est donc nécessaire d'élever la tension fournie par les générateurs avant de la transporter, et pour cela d'utiliser des transformateurs.

D'un autre côté, les tensions élevées demandent une maîtrise plus importante. Pour des raisons de sécurité, tournant notamment autour de problèmes d'isolation des conducteurs, ou lorsqu'il n'est pas nécessaire de transporter l'énergie sur de longues distances, on n'a pas toujours recours à l'utilisation des hautes tensions. En particulier, il n'est pas envisageable de câbler les bâtiments avec des tensions très élevées : une fois le transport effectué, l'énergie électrique doit être distribuée sous la forme de basses tensions et l'on doit par conséquent avoir là aussi recours à un transformateur.

En résumé, le transformateur permet à l'énergie électrique d'être transportée à longue distance de façon économique et distribuée dans les industries et les habitations.

Constitution d'un transformateur monophasé

Comme nous pouvons le voir sur la Fig. 2, un transformateur monophasé est constitué :

• d'un circuit magnétique fermé ;
• de deux circuits électriques sans liaison entre eux, enroulés autour du circuit magnétique.

Fig. 2 : Schéma de principe d'un transformateur monophasé

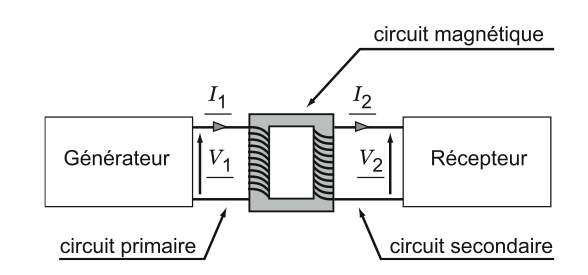
Le circuit électrique lié au générateur est appelé le circuit primaire, celui qui est lié au récepteur est appelé le circuit secondaire.

Appelons $V_{1}$ la valeur efficace de ${\underline {V_{1}}}$ au primaire et $V_{2}$ la valeur efficace de ${\underline {V_{2}}}$ au secondaire alors :

• Si $V_{1}<V_{2}$, le transformateur est dit élévateur de tension ;
• Si $V_{1}>V_{2}$, le transformateur est dit abaisseur de tension ;
• Si $V_{1}=V_{2}$, le transformateur est un transformateur d'isolement ;

Remarque : Il existe une isolation galvanique entre le primaire et le secondaire : un défaut électrique au niveau du secondaire n'est pas détectable par un dispositif différentiel présent au primaire. Pour protéger l'utilisateur d'un transformateur, il faut placer une protection différentielle au secondaire.

Principe de fonctionnement

L'enroulement primaire est soumis à une tension sinusoïdale. Il est donc traversé par un courant sinusoïdal et donne naissance à travers le circuit magnétique à un flux sinusoïdal. Ce flux engendre alors une force électromotrice induite ${\underline {E_{1}}}$ dans l'enroulement primaire et ${\underline {E_{2}}}$ dans l'enroulement secondaire. Au niveau des bornes du secondaire apparaît alors une tension sinusoïdale dont la fréquence est la même que celle de la tension appliquée au primaire, mais dont l'amplitude est différente.

Fig. 3 : Principe de fonctionnement du transformateur. On utilise la convention récepteur pour le primaire (le sens positif de ${\underline {V_{1}}}$ est pris en opposition avec celui de ${\underline {I_{1}}}$) et générateur pour le secondaire (le sens positif de ${\underline {V_{2}}}$ est pris dans le même sens que celui de ${\underline {I_{2}}}$)

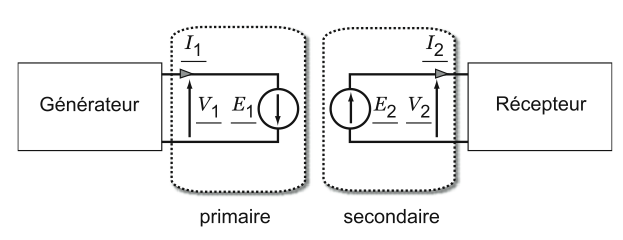
Le comportement du transformateur peut alors être appréhendé par le schéma reporté sur la Fig. 3.

Convention de signe

Les conventions de signe que nous utiliserons dans le cas du transformateur monophasé sont celles reportées sur la Fig. 3 :

• en ce qui concerne les forces électromotrices (f.é.m) ${\underline {E_{1}}}$ et ${\underline {E_{2}}}$, nous prenons comme convention le fait que des f.é.m positives tendent à faire circuler des courants positifs ;
• en ce qui concerne la tension d'entrée du primaire ${\underline {V_{1}}}$ et le courant ${\underline {I_{1}}}$, puisque l'enroulement primaire absorbe l'énergie du générateur, il se comporte comme un récepteur : ${\underline {V_{1}}}$ et ${\underline {I_{1}}}$ sont donc liés par la convention des récepteurs et leurs sens positifs sont pris en opposition ;
• en ce qui concerne la tension de sortie du secondaire ${\underline {V_{2}}}$ et le courant ${\underline {I_{2}}}$, puisque l'enroulement secondaire se comporte comme un générateur et fournit de l'énergie au récepteur, ils sont reliés par la convention des générateurs et le sens positif de ${\underline {V_{2}}}$ est pris dans le même sens que celui de ${\underline {I_{2}}}$.

Formule de Boucherot pour le transformateur

L'une des propriétés du transformateur est d'être une machine statique à flux forcé. En effet, au primaire, le générateur impose la tension ${\underline {V_{1}}}$ ainsi que la fréquence $f$. Le nombre de spires $N_{1}$ est quant à lui fixé. Par conséquent, le flux ${\underline {\phi }}$ voit sa valeur imposée en module et phase par le générateur. Les différentes grandeurs que nous venons de citer sont reliées par la formule de Boucherot :

$V_{1}=4,44\ N_{1}\ f\ {\phi _{max}}\qquad (7)$

où $V_{1}$ est la valeur efficace de la tension au primaire, $N_{1}$ le nombre de spires de l'enroulement primaire, $f$ la fréquence du flux et $\Phi _{max}$ la valeur maximale du flux magnétique.

Remarque : Le transformateur est une machine à flux forcé : alimenté par une tension efficace constante, il fournit au secondaire une tension sinusoïdale de valeur efficace constante.

Symboles électriques du transformateur

Dans un schéma électrique, le transformateur peut être représenté par l'un des deux symboles reportés dans les volets (a) et (b) de la Fig. 4.

Fig. 4 : Symboles électriques du transformateur monophasé.

Dans ce wikilivre, nous utiliserons le symbole reporté dans le volet (a) de la Fig. 4.

Le transformateur parfait (ou idéal)

Définition du transformateur parfait (ou idéal)

On appelle transformateur parfait, ou idéal, un transformateur vérifiant les conditions suivantes :

• Les pertes dans le fer, c'est-à-dire les pertes par hystérésis et les courants de Foucault sont nulles. Le noyau est infiniment perméable au champ magnétique et sa réluctance ${\mathcal {R}}$, grandeur décrivant la résistance d'un circuit magnétique à sa pénétration par un champ magnétique, est nulle.
• La résistance des enroulements primaires et secondaires est nulle.
• Il n'y a pas de pertes de flux magnétique : tout le flux présent dans le noyau sert à magnétiser l'enroulement secondaire.

Du point de vue des grandeurs électriques, cela veut dire que :

• Si le secondaire est à vide, et donc si ${\underline {I_{2}}}=0$, alors le courant qui traverse le primaire est nul, c'est-à-dire que ${\underline {I_{1}}}=0$ ;
• Le secondaire se comporte comme un générateur parfait, de résistance interne nulle, de sorte que la valeur efficace de la tension au secondaire $V_{2}$ est constante quand le courant au secondaire $I_{2}$ varie, en valeur efficace, de 0 à sa valeur nominale $I_{2n}$ ;
• Le rendement du transformateur est de $\eta =1=100\%$.

Expression des f.é.m dans le transformateur parfait

D'après la loi de Faraday, les forces électromotrices ${\underline {E_{1}}}$ et ${\underline {E_{2}}}$ dépendent de la variation du flux magnétique ${\underline {\phi }}$ selon la relation :

${\underline {E_{1}}}=-N_{1}{\frac {d{\underline {\phi }}}{dt}}\qquad (8)$

et

${\underline {E_{2}}}=-N_{2}{\frac {d{\underline {\phi }}}{dt}}\qquad (9)$

où $N_{1}$ et $N_{2}$ sont respectivement le nombre de spires des enroulements primaire et secondaire.

Equation de la tension dans le cas idéal

Dans le cas idéal, la tension au primaire vérifie la relation :

${\underline {V_{1}}}=-{\underline {E_{1}}}=N_{1}{\frac {d{\underline {\phi }}}{dt}}\qquad (10)$

et celle au secondaire vérifie :

${\underline {V_{2}}}={\underline {E_{2}}}=-N_{2}{\frac {d{\underline {\phi }}}{dt}}\qquad (11)$

De fait, à condition que $d{\underline {\phi }}/dt\neq 0$, on peut ramener ces deux expressions à :

${\frac {\underline {V_{2}}}{\underline {V_{1}}}}=-{\frac {N_{2}}{N_{1}}}=-m\qquad (12)$

où $m$ est appelé le rapport de transformation. Si l'on remplace les valeurs temporelles de la tension par des valeurs efficaces, la précédente équation se ramène, dans le cas idéal, à :

${\frac {V_{2}}{V_{1}}}=m\qquad (13)$

Remarque : le fait que l'on doive avoir $d{\underline {\phi }}/dt\neq 0$ implique que le transformateur ne peut fonctionner qu'en régime alternatif.

Equation d'intensité

Dans le cas général, le courant au primaire et celui au secondaire sont reliés à tout instant par la relation d'Hopkinson :

$N_{1}{\underline {I_{1}}}+N_{2}{\underline {I_{2}}}={\mathcal {R}}{\underline {\phi _{m}}}\qquad (14)$

où ${\underline {\phi _{m}}}$ est le flux mutuel (dans le cas idéal ${\underline {\phi _{m}}}={\underline {\phi }}$) et où ${\mathcal {R}}$ est la réluctance du circuit magnétique. Cette grandeur décrit l'opposition du noyau au passage du champ magnétique : elle est par conséquent liée à la notion de pertes dans le fer. Or, nous sommes dans le cas d'un transformateur idéal et, de fait, la réluctance du circuit noyau est nulle et la précédente équation s'écrit sous la forme :

$N_{1}{\underline {I_{1}}}+N_{2}{\underline {I_{2}}}=0\qquad (15)$

Ceci implique que :

${\frac {\underline {I_{2}}}{\underline {I_{1}}}}=-{\frac {N_{1}}{N_{2}}}=-{\frac {1}{m}}\qquad (16)$

Si, à présent, on remplace les grandeurs temporelles par des grandeurs efficaces, on aboutit à la relation, valable dans le cas idéal :

${\frac {I_{2}}{I_{1}}}=-{\frac {1}{m}}\qquad (17)$

Remarque : Le rapport de transformation des intensités est l'inverse de celui des tensions en valeur absolue.

Propriétés du transformateur parfait

Déphasages : diagramme de Fresnel

Nous reportons sur la Fig. 5 le diagramme vectoriel associé aux équations (12) et (16) en prenant comme grandeur de référence le flux magnétique. Ce diagramme de Fresnel représente donc les différentes grandeurs électriques dans le cas du transformateur idéal à travers leurs valeurs efficaces et leurs déphasages.

D'après les équations sus-citées, les grandeurs ${\underline {V_{1}}}$ et ${\underline {V_{2}}}$ sont alignées, et il en va de même pour les grandeurs ${\underline {I_{1}}}$ et ${\underline {I_{2}}}$.

Fig. 5 : Diagramme de Fresnel dans le cas d'un transformateur idéal.

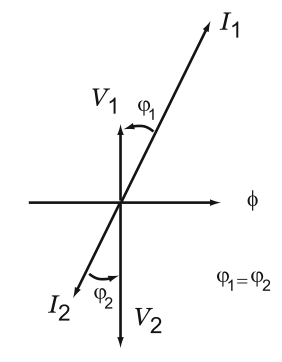
Par conséquent, les déphasages $\varphi _{1}$ et $\varphi _{2}$ sont nécessairement les mêmes.

Lois de conservation

À partir des équations (13) et (17), nous pouvons écrire que :

$V_{2}\times I_{2}=mV_{1}\times {\frac {1}{m}}I_{1}=V_{1}\times I_{1}\qquad (18)$

et, de fait, si l'on appelle $S_{1}$ la puissance apparente absorbée au primaire et $S_{2}$ celle fournie au secondaire, alors :

$S_{1}=S_{2}\qquad (19)$

De plus, nous avons vu que le transformateur conserve le déphasage $\varphi$. Or, la puissance active $P$ s'exprime comme

$P=S\cos \varphi \qquad (20)$

tandis que la puissance réactive $Q$ vérifie :

$Q=S\sin \varphi \qquad (21)$

On remarque au passage que $P$, $Q$ et $S$ sont reliées par la relation :

$S={\sqrt {P^{2}+Q^{2}}}\qquad (22)$

Comme $S$ et $\varphi$ sont conservés, il en va de même pour $P$ et $Q$. Par conséquent, dans le cas du transformateur idéal :

$P_{1}=P_{2}\qquad (23)$

et

$Q_{1}=Q_{2}\qquad (24)$

Le transformateur idéal conserve les puissances active, réactive et apparente. Il conserve aussi le déphasage.