Électricité/Les quadripôles en régime sinusoïdal
Si l'on envoie une tension sinusoïdale sur l'entrée d'un quadripôle, celui-ci va fournir une tension sinusoïdale de même fréquence à sa sortie (même chose pour un courant, mais nous utiliserons des tensions dans ce qui suit, pour simplifier les explications). Par contre, les deux signaux ne seront pas forcément en phase et n'ont pas la même amplitude. Décrire le comportement du filtre demande d'étudier deux paramètres :
- le déphasage entre entrée et sortie ;
- le rapport entre amplitude d'entrée et de sortie.
La transmittance
[modifier | modifier le wikicode]On peut calculer le rapport entre la tension d'entrée et la tension de sortie . Celui-ci s'appelle la fonction de transfert, bien que le terme transmittance soit aussi très utilisé, et se note . La transmittance d'un quadripôle n'est évidemment pas la même selon la fréquence, ce qui traduit le fait que certaines fréquences sont atténuées et d'autres amplifiées. Voici sa formule de calcul.
Si on utilise des phaseurs pour les tensions d'entrée et de sortie, leur rapport est un nombre complexe, qui dépend de la fréquence du signal d'entrée/sortie. La transmittance ainsi calculée est appelée la transmittance complexe et se note .
Vu qu'il s'agit d'un nombre complexe, la transmittance possède un module et un argument, dont les interprétations sont les suivantes :
- Le module est le rapport entre amplitudes d'entrée et de sortie.
- L'argument est le déphasage entre signal de sortie et d'entrée.
L'atténuation et l'amplification
[modifier | modifier le wikicode]Le module de la transmittance porte le nom d'atténuation ou d'amplification selon les cas. L'amplification/atténuation se définit comme le rapport des valeurs efficaces du signal de sortie et d'entrée. On peut aussi la voir comme le rapport entre les amplitudes maximales de la sortie et de l'entrée, ce qui est équivalent pour des signaux sinusoïdaux. Elle n'est évidemment pas la même selon la fréquence, ce qui traduit le fait que certaines fréquences sont atténuées et d'autres amplifiées.
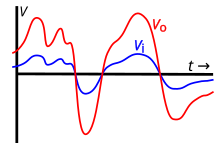
Le nom d'atténuation/amplification vient du fait que le quadripôle peut soit atténuer ou amplifier son entrée. Dans le premier cas, la tension de sortie est inférieure à la tension d'entrée : cette dernière est alors atténuée. Dans le deuxième cas, la tension de sortie est supérieure à celle d'entrée, ce qui fait que la tension d'entrée a été amplifiée. Tous les quadripôles ne peuvent pas amplifier un signal : seuls ceux alimentés par autre chose que le signal d'entrée le peuvent. Ceux-ci sont appelés des quadripôles actifs, là où les autres sont des quadripôles passifs. La différence entre les deux tient au fait que les quadripôles actifs contiennent des composants actifs (générateurs, autres), là où les autres sont composés exclusivement de récepteurs passifs (résistances, condensateurs, bobines, autres).
Le gain d'un quadripôle
[modifier | modifier le wikicode]Il est fréquent d'utiliser des diagrammes qui relient l'amplification/atténuation à la fréquence. Analyser ces diagrammes est cependant assez compliqué si l'on utilise une échelle linéaire. Par exemple, la courbe tracée par un simple condensateur ou une bobine donnent une courbe exponentielle. Pour éviter un tel écueil, il est d'usage d'utiliser une courbe logarithmique afin que l'amplification causée par les récepteurs non-linéaires (condensateur et bobine) donnent des droites. Pour cela, on calcule une fonction dérivée du logarithme de l'amplification : le gain. Celui-ci vaut :
Les diagrammes de Bode
[modifier | modifier le wikicode]Si on trace le gain en fonction de la fréquence, on obtient un diagramme appelé diagramme de Bode. Son étude donne de nombreuses indications sur le filtre étudié. On peut remarquer que celui-ci utilise le gain et non l'amplification. La raison en est que les courbes usuelles donnent des droites, là où elles donneraient des courbes exponentielles sur la plupart des filtres. Voici un exemple de diagramme de Bode :

Il est possible de fusionner les deux diagrammes de Bode en un seul, ce qui peut être fait de plusieurs manières.
La première méthode se base sur le fait que la phase est déterminée par la fréquence : à toute fréquence correspond une phase. Cette méthode consiste à donner le gain en fonction de la phase, et de tracer le tout sous la forme d'un diagramme semi-logarithmique (échelle logarithmique pour le gain, linéaire pour la phase). Le graphe obtenu est appelé diagramme de Black du circuit.
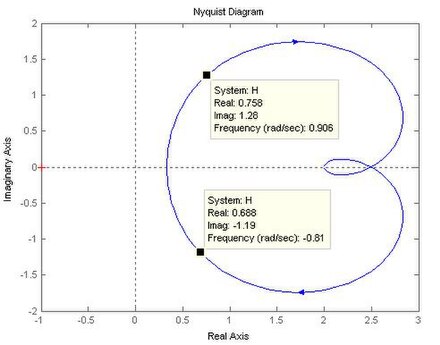
Une seconde méthode consiste à représenter la transmittance sur un graphe dans le plan complexe. Rappelons que la transmittance est un ensemble de nombres complexes (un par fréquence) dont le module est le gain et la phase est l'argument. Avec ces nombres complexes, on peut tracer une courbe sur le plan complexe, courbe dont chaque point correspond à la transmittance observée pour une fréquence bien précise. Le résultat est appelé le diagramme de Nyquist. La forme de ce diagramme de Nyquist donne des indications sur la stabilité du circuit considéré,