Cristallographie géométrique/Groupes ponctuels de symétrie

Les opérations de symétrie ponctuelle d'un objet forment un groupe mathématique. Il existe en tout 10 groupes de symétrie ponctuelle compatibles avec les translations de réseau dans l'espace à deux dimensions et 32 dans l'espace à trois dimensions. Deux notations existent pour désigner les groupes ponctuels de symétrie, la notation de Hermann-Mauguin, utilisée en cristallographie, et la notation de Schoenflies, utilisée en chimie et en spectroscopie.

Groupe ponctuel de symétrie

Les opérations de symétrie ponctuelle d'un objet, munies de la loi de composition • où a•b représente l'application de l'opération b suivie de l'opération a, forment un groupe. Ce groupe possède donc les propriétés suivantes :

• la composition de deux opérations de symétrie ponctuelle d'un groupe est une opération de symétrie ponctuelle qui est aussi membre du groupe : le groupe est clos ;
• la loi de composition est associative : (a•b)•c=a•(b•c), puisque la loi de multiplication de matrices carrées, représentatives des opérations de symétrie, est associative ;
• il existe un élément neutre du groupe, l'opération identité, notée 1, telle que pour toute opération de symétrie ponctuelle du groupe, 1•a=a•1 ;
• tout élément de symétrie ponctuelle a possède un inverse a⁻¹ tel que a•a⁻¹=a⁻¹•a=1. Par exemple, si a est une rotation d'angle θ, a⁻¹ est la rotation d'angle −θ.

Cette définition d'un groupe ponctuel de symétrie est générale et ne se limite pas aux opérations de symétrie compatibles avec les translations de réseau.

Table de multiplication d'un groupe

Afin de visualiser l'ensemble des éléments g_i d'un groupe ponctuel de symétrie G, ou de vérifier que le groupe G est clos, il est souvent pratique d'utiliser sa table de multiplication, écrite sous forme de tableau dont les éléments sont toutes les composées des éléments g_i et g_j du groupe. Comme G est un groupe, tous les éléments du tableau sont des éléments de G.

G	g1	g2	…	gi	…	gn
g1	g1•g1=g12	g1•g2	…	g1•gi	…	g1•gn
g2	g2•g1	g22	…	g2•gi	…	g2•gn
…	…	…	…	…	…	…
gi	gi•g1	gi•g2	…	gi2	…	gi•g1
…	…	…	…	…	…	…
gn	gn•g1	gn•g2	…	gn•gi	…	gn2

Si le tableau est symétrique par rapport à sa diagonale (indiquée en bleu clair ci-dessus), cela signifie que pour tout couple d'éléments g_i et g_j du groupe, g_i•g_j=g_j•g_i : le groupe est alors abélien et tous les éléments du groupe commutent entre eux. Un exemple de groupe abélien est donné dans la section « ordre d'un groupe ». Un groupe non abélien est présenté dans la section « sous-groupes ».

D'autre part, deux groupes sont isomorphes si la structure de leurs tables de multiplication est identique.

Une façon pratique d'établir la table de multiplication d'un groupe est de commencer à reporter dans la première ligne et la première colonne les éléments connus du groupe, en utilisant le même ordre en ligne et en colonne. Si de nouveaux éléments apparaissent lors de la composée de deux éléments, on ajoute de nouvelles lignes et colonnes au tableau jusqu'à ce qu'aucun nouvel élément n'apparaisse. Lors de la construction de la table de multiplication d'un groupe, chaque élément du groupe doit apparaître dans chaque ligne et chaque colonne du tableau, et ceci une seule fois par ligne et par colonne.

Notation des groupes ponctuels de symétrie

La notation de Hermann-Mauguin est une notation « orientée » : le symbole du groupe contient les éléments de symétrie qui sont contenus dans chaque direction de symétrie, dans l'ordre suivant :

• 1^ère direction de symétrie ;
• 2^ème direction de symétrie ;
• éventuellement, 3^ème direction de symétrie.

La notation de Hermann-Mauguin dépend du système cristallin utilisé. Elle permet une identification rapide de celui-ci, selon la position des éléments de symétrie caractéristiques du système.

Par exemple, si dans le système orthorhombique il existe un plan miroir perpendiculaire à la direction [100] (première direction de symétrie), un plan miroir perpendiculaire à la direction [010] (deuxième direction de symétrie) et un axe de rotation d'ordre 2 parallèle à la direction [001] (troisième direction de symétrie), la notation de Hermann-Mauguin du groupe généré par les trois opérations associées, m_[100], m_[010] et 2_[001], est mm2. Les symboles pour les éléments de symétrie sont les mêmes que ceux pour les opérations de symétrie vus au début de ce chapitre. L'orientation de l'élément d'une opération de symétrie est indiquée en indice. Cette dernière précision n'est cependant pas nécessaire dans la notation de Hermann-Mauguin du groupe car elle est contenue dans la position du symbole.

Si plusieurs opérations de symétrie coexistent le long d'une même direction de symétrie, celle d'ordre le plus élevé est choisie pour le symbole du groupe ponctuel. Par exemple, la composée d'une rotation d'ordre 4 avec elle-même est une rotation d'ordre 2 et d'axe identique à celui de la rotation d'ordre 4 : le symbole de Hermann-Mauguin dans cette direction de symétrie est 4. Dans le cas où une direction de symétrie contient à la fois un axe de rotation d'ordre n qui lui est parallèle et un plan miroir qui lui est perpendiculaire, on note alors la symétrie dans cette direction n/m. Par exemple, si un axe de rotation d'ordre 2 est perpendiculaire à un plan miroir, le symbole de Hermann-Mauguin associé à cette direction est 2/m. Dans le cas où seule l'identité est présente dans la troisième direction de symétrie, ou dans la deuxième et troisième direction, on omet généralement d'indiquer l'identité. Ainsi, le groupe généré par la seule rotation d'ordre 6 appartient forcément au système cristallin hexagonal : l'axe de rotation est parallèle à la première direction de symétrie [001]. Comme les deux autres directions de symétrie ne contiennent que l'identité, on note le groupe 6 au lieu de 611.

La notation de Hermann-Mauguin est donc très bien adaptée pour décrire la symétrie ponctuelle des cristaux. Il est possible de décrire la symétrie d'une molécule contenant des éléments de symétrie non cristallographiques avec la notation de Hermann-Mauguin : on utilise toujours des directions de symétrie de la molécule, mais on ne peut plus dans ce cas faire la correspondance avec un système cristallin.

La notation de Schoenflies est une notation moins orientée que celle de Hermann-Mauguin. Son symbole principal est l'opération de symétrie d'ordre le plus élevé, les autres sont notées par rapport à celle-ci. Elle utilise des symboles différents pour les opérations de symétrie :

• l'inversion est notée i ;
• une rotation d'ordre n est notée C_n ;
• une roto-inversion d'ordre n supérieur à 2 est notée S_n ;
• une réflexion est notée σ_v si son plan miroir contient l'axe principal de symétrie et σ_h si il y est perpendiculaire.

Dans l'exemple précédent du groupe noté mm2 dans la notation de Hermann-Mauguin, la notation de Schoenflies du groupe est ainsi C_2v : l'axe de la rotation d'ordre 2 est considéré comme l'axe de la symétrie principale et les plans miroirs des deux réflexions contiennent cet axe.

D'autre part, la lettre C ou S peut être remplacée par une autre lettre en fonction de la symétrie de l'objet étudié. La signification de ces lettres est la suivante :

• C indique que le groupe est cyclique (voir plus loin) ;
• S indique que les seules opérations de symétrie sont des roto-inversions (la lettre S vient du mot Spiegel qui signifie « miroir » en allemand ; Schoenflies était allemand) ;
• D indique qu'il existe des rotations d'ordre 2 d'axe perpendiculaire à l'axe principal de symétrie (la lettre D vient du mot « drièdre ») ;
• T indique que le groupe possède les rotations du tétraèdre (sans roto-inversion), avec éventuellement des réflexions (T_d et T_h) ;
• O indique que le groupe possède les rotations de l'octaèdre ;
• I est le symbole du groupe icosaédrique, qui contient entre autres des rotations d'ordre 5.

La figure ci-dessous décrit la méthode pour déterminer la notation de Schoenflies d'un groupe ponctuel de symétrie.

Nous utiliserons par la suite principalement la notation de Hermann-Mauguin, celle de Schoenflies sera éventuellement donnée à titre indicatif.

Ordre d'un groupe

Définition

L'ordre d'un groupe ponctuel de symétrie est le nombre d'éléments que ce groupe contient.

Il faut ici faire attention à ne pas confondre cette notion avec celle de l'ordre d'une opération de rotation ou de roto-inversion. Considérons par exemple le groupe généré par la roto-inversion d'ordre 3 d'axe parallèle à [001]. Pour rappeler que la rotation a lieu dans le sens trigonométrique, cette opération est notée ${\bar {3}}_{[001]}^{+}\,$. L'opération inverse est la roto-inversion d'angle 240° et d'axe parallèle à [001], notée ${\bar {3}}_{[001]}^{-}\,$. Leurs matrices représentatives sont

${\begin{array}{ll}\mathbf {M} _{{\bar {3}}_{[001]}^{+}}={\begin{bmatrix}0&1&0\\-1&1&0\\0&0&-1\end{bmatrix}},&\mathbf {M} _{{\bar {3}}_{[001]}^{-}}={\begin{bmatrix}1&-1&0\\1&0&0\\0&0&-1\end{bmatrix}}.\end{array}}$

En effet,

${\begin{bmatrix}0&1&0\\-1&1&0\\0&0&-1\end{bmatrix}}\cdot {\begin{bmatrix}1&-1&0\\1&0&0\\0&0&-1\end{bmatrix}}={\begin{bmatrix}1&-1&0\\1&0&0\\0&0&-1\end{bmatrix}}\cdot {\begin{bmatrix}0&1&0\\-1&1&0\\0&0&-1\end{bmatrix}}={\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}.$

La table de multiplication de ce groupe est

	${\bar {3}}_{[001]}^{+}$	${\bar {3}}_{[001]}^{-}$	$1\,$	$3_{[001]}^{+}$	$3_{[001]}^{-}$	${\bar {1}}$
${\bar {3}}_{[001]}^{+}$	$\color {Blue}3_{[001]}^{-}$	$1\,$	${\bar {3}}_{[001]}^{+}$	${\bar {3}}_{[001]}^{-}$	${\bar {1}}$	$3_{[001]}^{+}$
${\bar {3}}_{[001]}^{-}$	$1\,$	$\color {Blue}3_{[001]}^{+}$	${\bar {3}}_{[001]}^{-}$	${\bar {1}}$	${\bar {3}}_{[001]}^{+}$	$3_{[001]}^{-}$
$1\,$	${\bar {3}}_{[001]}^{+}$	${\bar {3}}_{[001]}^{-}$	$\color {Blue}1\,$	$3_{[001]}^{+}$	$3_{[001]}^{-}$	${\bar {1}}$
$3_{[001]}^{+}$	${\bar {3}}_{[001]}^{-}$	${\bar {1}}$	$3_{[001]}^{+}$	$\color {Blue}3_{[001]}^{-}$	$1\,$	${\bar {3}}_{[001]}^{+}$
$3_{[001]}^{-}$	${\bar {1}}$	${\bar {3}}_{[001]}^{+}$	$3_{[001]}^{-}$	$1\,$	$\color {Blue}3_{[001]}^{+}$	${\bar {3}}_{[001]}^{-}$
${\bar {1}}$	$3_{[001]}^{+}$	$3_{[001]}^{-}$	${\bar {1}}$	${\bar {3}}_{[001]}^{+}$	${\bar {3}}_{[001]}^{-}$	$\color {Blue}1\,$

Ainsi, l'ordre du groupe généré par une roto-inversion d'ordre 3 est 6. Dans la notation de Hermann-Mauguin, ce groupe est noté ${\bar {3}}$. Il s'agit d'un groupe du système cristallin trigonal puisqu'il ne contient qu'un seul axe de roto-inversion d'ordre 3. D'autre part, ce groupe est abélien.

Pour certaines opérations de symétrie non cristallographiques, l'ordre du groupe généré peut être infini : il suffit par exemple que l'angle de la rotation (exprimé en degrés) soit un nombre irrationnel. Dans ce cas, l'utilisation de la table de multiplication n'est pas appropriée.

C'est l'ordre du groupe généré par une opération de symétrie qui détermine le degré de symétrie de l'opération, et pas l'ordre de l'opération lui-même. Par exemple, l'ordre du groupe généré par la roto-inversion d'ordre 4 est 4, alors que l'ordre du groupe généré par la roto-inversion d'ordre 3 est 6 : la roto-inversion d'ordre 3 possède un degré de symétrie plus élevée que la roto-inversion d'ordre 4.

Projection stéréographique d'un groupe ponctuel de symétrie

Les groupes ponctuels de symétrie peuvent être représentés en utilisant la projection stéréographique des éléments de symétrie attachés aux opérations de symétrie. Le point d'intersection commun à tous les éléments de symétrie est placé au centre de la sphère de projection. La première direction de symétrie est choisie comme l'axe nord-sud de la sphère de projection et est donc perpendiculaire au plan de la projection. Les autres directions de symétrie sont indiquées par un trait en dehors du disque de projection, ou à l'intérieur dans les cas où elles ne sont pas perpendiculaires à la première direction de symétrie. Par convention dans les systèmes réticulaires orthorhombique, tétragonal, hexagonal et cubique, la direction [010] (b) est choisie horizontale et pointant vers la droite dans le plan de projection. Dans le système monoclinique, [010] étant l'unique direction de symétrie, elle est choisie perpendiculaire au plan de projection et la direction [001] est alors la direction horizontale.

Les images a), b) et c) suivantes montrent les projections stéréographiques pour les groupes ponctuels de symétrie 2/m, 422 et ${\bar {3}}$. Les points d'intersection des éléments de symétrie avec la sphère de projection ne sont pas représentés par une croix ou un rond, comme ce serait le cas dans le cas de la projection d'une droite, mais par le symbole de l'opération de symétrie correspondante. Si le groupe ponctuel de symétrie est centrosymétrique, le centre d'inversion est situé au centre de la sphère de projection. Il n'intersecte pas la sphère mais il est quand même représenté au centre du disque de projection, comme dans l'image d) ci-dessous.

• 
  a) Groupe 2/m
• 
  b) Groupe 422
• 
  c) Groupe ${\bar {3}}$
• 
  d) Groupe ${\bar {1}}$

Il est également possible d'indiquer l'action des opérations de symétrie du groupe sur un pôle quelconque, comme dans l'image d) ci-dessus. Lorsque le pôle est choisi en position générale, le nombre total de pôles générés par toutes les opérations de symétrie du groupe, incluant le pôle de départ (généré par l'identité), est égal à l'ordre du groupe. La projection stéréographique permet donc de retrouver facilement l'ordre d'un groupe et de vérifier visuellement une table de multiplication.

Groupes cycliques

Un groupe cyclique est un groupe généré à partir d'un élément a et qui ne contient comme autres éléments que des composées de a avec lui-même : a², a³, etc. L'identité étant l'élément neutre de tout groupe, il existe un entier m tel que a^m=1 : l'ordre d'un groupe cyclique est cet entier m.

Dans l'exemple du groupe ${\bar {3}}1$ précédent, il s'agit d'un groupe cyclique d'ordre 6 :

${\begin{array}{lll}({\bar {3}}^{+})^{1}={\bar {3}}^{+},\,&({\bar {3}}^{+})^{2}={\bar {3}}^{+}\cdot {\bar {3}}^{+}=3^{-},\,&({\bar {3}}^{+})^{3}={\bar {3}}^{+}\cdot 3^{-}={\bar {1}},\\[1ex]({\bar {3}}^{+})^{4}={\bar {3}}^{+}\cdot {\bar {1}}=3^{+},\,&({\bar {3}}^{+})^{5}={\bar {3}}^{+}\cdot 3^{+}={\bar {3}}^{-},\,&({\bar {3}}^{+})^{6}={\bar {3}}^{+}\cdot {\bar {3}}^{-}=1.\end{array}}$

Généralisation

Toute opération de rotation ou de roto-inversion est un élément générateur d'un groupe cyclique.

Un groupe cyclique est toujours abélien. La réciproque n'est pas vraie : tout groupe abélien n'est pas forcément cyclique.

Sous-groupes

Chaque groupe G possède deux sous-groupes triviaux : le groupe lui-même et celui ne contenant que l'identité. Les sous-groupes H_i d'un groupe G ont une symétrie inférieure à celle de G, sauf dans le cas du sous-groupe trivial G. En particulier, le système cristallin attaché à un sous-groupe peut être différent de celui du groupe.

Définition

Un sous-groupe H de G est dit « maximal » si il n'est pas sous-groupe d'un autre sous-groupe K de G, autrement dit si il n'existe pas de sous-groupe K de G tel que H<K<G (le sous-groupe trivial G n'est pas pris en compte).

Certaines propriétés d'un sous-groupe H de G se retrouvent dans G :

• si H est centrosymétrique, G l'est aussi ;
• si H est non abélien, alors G est non abélien.

L'inverse de ces relations n'est pas toujours vrai. Par contre, si H est cyclique, G ne l'est pas forcément, mais les sous-groupes d'un groupe cyclique sont aussi des groupes cycliques. De même, les sous-groupes d'un groupe abélien sont des groupes abéliens.

Lorsque la table de multiplication d'un groupe ponctuel de symétrie G a été établie, il est possible de reconnaître facilement ses sous-groupes H_i selon l'arrangement des opérations de symétrie dans le tableau.

Considérons par exemple dans le système tétragonal le groupe formé par la rotation d'ordre 4 autour de [001] et la rotation d'ordre 2 autour de [100]. Comme nous l'avons vu plus haut pour les rotations en général, la rotation d'ordre 4 autour de [001] forme un groupe cyclique, noté 4. Combinée à la rotation d'ordre 2 autour de [100], elle forme le groupe 422 d'ordre 8, dont 4 est un sous-groupe et est indiqué en rouge dans la table de multiplication de 422 ci-dessous. La rotation d'ordre 2 autour de [110] dans la troisième direction de symétrie tétragonale résulte de la composée de 2_[100] et de 4_[001]. D'autre part, le groupe 422 est non abélien. Les éléments du tableau non symétriques par rapport à la diagonale sont indiqués en bleu.

	$1\,$	$4_{[001]}^{+}$	$2_{[001]}\,$	$4_{[001]}^{-}$	$2_{[100]}\,$	$2_{[010]}\,$	$2_{[110]}\,$	$2_{[1{\bar {1}}0]}$
$1\,$	$\color {Red}1\,$	$\color {Red}4_{[001]}^{+}$	$\color {Red}2_{[001]}\,$	$\color {Red}4_{[001]}^{-}$	$2_{[100]}\,$	$2_{[010]}\,$	$2_{[110]}\,$	$2_{[1{\bar {1}}0]}$
$4_{[001]}^{+}$	$\color {Red}4_{[001]}^{+}$	$\color {Red}2_{[001]}\,$	$\color {Red}4_{[001]}^{-}$	$\color {Red}1\,$	$\color {Blue}2_{[110]}\,$	$\color {Blue}2_{[1{\bar {1}}0]}$	$\color {Blue}2_{[010]}\,$	$2_{[100]}\,$
$2_{[001]}\,$	$\color {Red}2_{[001]}\,$	$\color {Red}4_{[001]}^{-}$	$\color {Red}1\,$	$\color {Red}4_{[001]}^{+}$	$2_{[010]}\,$	$2_{[100]}\,$	$2_{[1{\bar {1}}0]}$	$2_{[110]}\,$
$4_{[001]}^{-}$	$\color {Red}4_{[001]}^{-}$	$\color {Red}1\,$	$\color {Red}4_{[001]}^{+}$	$\color {Red}2_{[001]}\,$	$\color {Blue}2_{[1{\bar {1}}0]}$	$\color {Blue}2_{[110]}\,$	$\color {Blue}2_{[100]}\,$	$\color {Blue}2_{[010]}\,$
$2_{[100]}\,$	$2_{[100]}\,$	$\color {Blue}2_{[1{\bar {1}}0]}$	$2_{[010]}\,$	$\color {Blue}2_{[110]}\,$	$1\,$	$2_{[001]}\,$	$\color {Blue}4_{[001]}^{-}$	$\color {Blue}4_{[001]}^{+}$
$2_{[010]}\,$	$2_{[010]}\,$	$\color {Blue}2_{[110]}\,$	$2_{[100]}\,$	$\color {Blue}2_{[1{\bar {1}}0]}$	$2_{[001]}\,$	$1\,$	$\color {Blue}4_{[001]}^{+}$	$\color {Blue}4_{[001]}^{-}$
$2_{[110]}\,$	$2_{[110]}\,$	$\color {Blue}2_{[100]}\,$	$2_{[1{\bar {1}}0]}$	$\color {Blue}2_{[010]}\,$	$\color {Blue}4_{[001]}^{+}$	$\color {Blue}4_{[001]}^{-}$	$1\,$	$2_{[001]}\,$
$2_{[1{\bar {1}}0]}$	$2_{[1{\bar {1}}0]}$	$2_{[010]}\,$	$2_{[110]}\,$	$\color {Blue}2_{[100]}\,$	$\color {Blue}4_{[001]}^{-}$	$\color {Blue}4_{[001]}^{+}$	$2_{[001]}\,$	$1\,$

Ainsi, le groupe 422 possède cinq sous-groupes :

• sous-groupes de symétrie tétragonale : 422 et 4 ;
• sous-groupe de symétrie orthorhombique : 222 ;
• sous-groupe de symétrie monoclinique : 2 ;
• sous-groupe de symétrie triclinique : 1.

Parmi ces cinq sous-groupes, 4 et 222 sont des sous-groupes maximum de 422.

Pour chaque système cristallin, le groupe ponctuel de symétrie maximale est appelé « holoédrie ». Il s'agit par exemple du groupe 2/m dans le système monoclinique. Un sous-groupe d'une holoédrie contient moins d'éléments que celle-ci et est appelé pour cette raison « mériédrie ».

• Une « hémiédrie » est une mériédrie d'ordre égal à la moitié de l'ordre de l'holoédrie.
• Une « tétartoédrie » est une mériédrie d'ordre égal au quart de l'ordre de l'holoédrie.
• Une « ogdoédrie » est une mériédrie d'ordre égal au huitième de l'ordre de l'holoédrie.

Décomposition d'un groupe en classes

La relation entre un groupe G et un de ses sous-groupes H est caractérisée par l'« index » [i] du sous-groupe H dans G, noté entre crochets. L'index de H dans G est le nombre de classes de G lors de sa décomposition en classes par rapport à son sous-groupe H. Il existe deux possibilités pour décomposer un groupe en classes :

• la décomposition en classes à gauche ;
• la décomposition en classes à droite.

La valeur de l'index [i] de H dans G est la même dans les deux cas.

La décomposition en classes s'effectue de la façon suivante :

• le sous-groupe H constitue la première classe du groupe G ;
• si g_i est un élément de G mais pas de H, la deuxième classe est formée par :
  • la composition de g_i avec tous les éléments de H, g_i•H, dans le cas de la décomposition en classes à gauche (« à gauche de H »),
  • la composition de tous les éléments de H avec g_i, H•g_i, dans le cas de la décomposition en classes à droite (« à droite de H »),
• si g_j est un élément de G mais pas de H, et si g_j n'appartient pas à la deuxième classe, la troisième classe est formée de manière similaire à la deuxième classe avec g_j ;
• ainsi de suite jusqu'au classement de tous les éléments de G.

Les classes de G possèdent les propriétés suivantes :

• toutes les classes de G contiennent le même nombre d'éléments, qui est égal à l'ordre de H ;
• une seule classe de G possède une structure de groupe, celle du sous-groupe H ;
• chaque élément de G n'appartient qu'à une seule classe : l'intersection de deux classes est l'ensemble vide.

Le théorème de Lagrange permet de déterminer rapidement l'index [i] d'un sous-groupe H dans le groupe G.

Théorème de Lagrange

Si H est un sous-groupe de G, l'index [i] de H dans G est égal au rapport des ordres de G et H : $[i]={\frac {n_{\mathbf {G} }}{n_{\mathbf {H} }}}.$

L'index est toujours un nombre entier et peut être infini. Dans l'exemple précédent du groupe 422, ses sous-groupes propres 4 et 222 ont un index de [2] et le sous-groupe 2 a un index de [4] dans 422. La décomposition du groupe 422 en classes à droite et à gauche par rapport à son sous-groupe 2_[100], généré par la rotation d'ordre 2 d'axe [100], est donnée ci-dessous.

Classes à gauche				Classes à droite
$2_{[100]}$	$4_{[001]}^{+}\cdot 2_{[100]}$	$2_{[001]}\cdot 2_{[100]}$	$4_{[001]}^{-}\cdot 2_{[100]}$	$2_{[100]}$	$2_{[100]}\cdot 4_{[001]}^{+}$	$2_{[100]}\cdot 2_{[001]}$	$2_{[100]}\cdot 4_{[001]}^{-}$
$1\,$	$4_{[001]}^{+}$	$2_{[001]}$	$4_{[001]}^{-}$	$1\,$	$4_{[001]}^{+}$	$2_{[001]}$	$4_{[001]}^{-}$
$2_{[100]}$	$2_{[110]}$	$2_{[010]}$	$2_{[1{\bar {1}}0]}$	$2_{[100]}$	$2_{[1{\bar {1}}0]}$	$2_{[010]}$	$2_{[110]}$

Les classes à droite et à gauche sont ici différentes car elles ne contiennent pas toutes les mêmes éléments. Si G est un groupe abélien, ses classes à gauche sont identiques à ses classes à droite, quel que soit le sous-groupe utilisé pour la décomposition.

Classe cristalline

Le concept de « classe cristalline » permet de regrouper les groupes d'espace qui possèdent des propriétés de symétrie similaires. Les groupes d'espace seront vus dans un chapitre dédié ; l'introduction des classes cristallines est faite ici pour une description complète des groupes ponctuels de symétrie dans les sections suivantes.

On distingue deux types de classes cristallines :

• une « classe cristalline géométrique », ou « classe cristalline », regroupe tous les groupes d'espace de même symétrie ponctuelle. Il en existe autant que de groupes ponctuels de symétrie : 2 dans l'espace unidimensionnel, 10 dans l'espace bidimensionnel et 32 dans l'espace tridimensionnel ;
• une « classe cristalline arithmétique » regroupe tous les groupes d'espace de même symétrie ponctuelle et de même réseau de Bravais. Il en existe 2 dans l'espace unidimensionnel, 13 dans l'espace bidimensionnel et 73 dans l'espace tridimensionnel.

Chaque classe cristalline géométrique possède deux désignations, selon la nomenclature utilisée :

• la nomenclature de Friedel utilise les relations de groupe/sous-groupe : holoédrie, hémiédrie, etc. ;
• la nomenclature de Groth utilise le nom de la forme cristalline générée par le groupe ponctuel de symétrie sur un pôle en position générale.

La nomenclature de Friedel est indiquée dans les listes des groupes ponctuels de symétrie ci-dessous. Celle de Groth sera vue dans le chapitre sur la morphologie des cristaux.

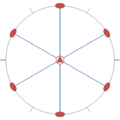
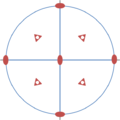
Les 10 groupes ponctuels de symétrie bidimensionnels

Relations de groupe/sous-groupe maximum.

L'holoédrie du système monoclinique est le groupe cyclique 2, d'ordre 2 et généré par la rotation d'ordre 2. Sa seule hémiédrie est le groupe de l'identité 1, d'ordre 1.

L'holoédrie du système orthorhombique est 2mm, contenant deux réflexions dont les droites miroir sont orthogonales entre elles et s'intersectent au centre de rotation. Ce groupe est abélien et non cyclique, son ordre est 4. Sa seule hémiédrie dans le système orthorhombique est le groupe cyclique m, d'ordre 2 et généré par une seule réflexion.

L'holoédrie du système tétragonal est le groupe non abélien 4mm, d'ordre 8. Elle contient quatre réflexions, dont deux sont de droites miroir perpendiculaires aux directions <10> et deux sont de droites miroir perpendiculaires aux directions <11> : les quatre droites miroir forment des angles de 45° entre elles et s'intersectent au centre de rotation d'ordre 4. La seule hémiédrie de ce groupe dans le système tétragonal est le groupe cyclique 4, d'ordre 4.

L'holoédrie du système hexagonal est le groupe non abélien 6mm, d'ordre 12. Elle contient six réflexions, dont trois sont de droites miroirs perpendiculaires aux directions <10> et trois sont de droites miroirs perpendiculaires aux directions <21> : les six droites miroirs forment un angle de 30° entre elles et s'intersectent au centre de rotation d'ordre 6. Le groupe 6mm possède deux hémiédries dans le système hexagonal, le groupe non abélien 3m et le groupe cyclique 6, tous deux d'ordre 6. Le groupe 3m contient trois réflexions de droites miroir perpendiculaires aux directions <21>, formant un angle de 60° entre elles et s'intersectant au centre de rotation d'ordre 3. Le groupe 6mm possède aussi une tétartoédrie dans le système hexagonal, le groupe cyclique 3 d'ordre 3.

Les relations de groupe/sous-groupe maximum entre les groupes ponctuels de symétrie cristallographiques sont montrées dans la figure ci-dessus. Les groupes sont classés du haut vers le bas selon leur ordre décroissant.

• 
  1
• 
  2
• 
  m
• 
  2mm
• 
  4
• 
  4mm
• 
  3
• 
  3m
• 
  6
• 
  6mm

Les 32 groupes ponctuels de symétrie tridimensionnels

Les groupes ponctuels de symétrie dans l'espace tridimensionnel sont au nombre de 32 : 2 dans le système cristallin triclinique, 3 dans le système cristallin monoclinique, 3 dans le système cristallin orthorhombique, 7 dans le système cristallin tétragonal, 5 dans le système cristallin trigonal, 7 dans le système cristallin hexagonal et 5 dans le système cristallin cubique.

Les opérations de symétrie compatibles avec le système triclinique sont l'identité et l'inversion. Le groupe généré par l'inversion constitue donc l'holoédrie triclinique et est noté ${\bar {1}}$. Il s'agit d'un groupe centrosymétrique et cyclique d'ordre 2. Sa seule mériédrie est l'hémiédrie triclinique formée par le groupe 1 de l'identité, groupe cyclique non centrosymétrique d'ordre 1.

Dans le système monoclinique, il peut y avoir au maximum un axe de rotation d'ordre 2 perpendiculaire à un plan miroir. L'holoédrie monoclinique est donc 2/m. Il s'agit d'un groupe centrosymétrique abélien non cyclique d'ordre 4. Le groupe 2/m possède deux hémiédries dans le système monoclinique, qui sont des groupes cycliques non centrosymétriques d'ordre 2 : l'hémiédrie « holoaxe » monoclinique 2 et l'« antihémiédrie » monoclinique m. Une hémiédrie holoaxe est une hémiédrie qui ne contient que des opérations de symétrie de première espèce ; une antihémiédrie contient des opérations de symétrie de seconde espèce.

Ci-dessous sont représentées les projections stéréographiques des groupes ponctuels tricliniques et monocliniques. Les notations de Schoenflies sont indiquées entre parenthèses.

• Groupes ponctuels tricliniques et monocliniques
• 
  $1\,(C_{1})$
• 
  ${\bar {1}}\,(C_{i})$
• 
  $2\,(C_{2})$
• 
  $m\,(C_{s})$
• 
  ${\frac {2}{m}}\,(C_{2h})$

Dans le système orthorhombique, chaque direction de symétrie peut contenir au maximum un axe de rotation d'ordre 2 perpendiculaire à un plan miroir. L'holoédrie orthorhombique est donc 2/m 2/m 2/m. Comme deux réflexions de plans miroirs orthogonaux génèrent une rotation d'ordre 2, le groupe 2/m 2/m 2/m est généralement noté sous sa forme raccourcie : mmm. Il s'agit d'un groupe centrosymétrique abélien non cyclique d'ordre 8. Il possède deux hémiédries dans le système orthorhombique : l'hémiédrie holoaxe orthorhombique 222 et l'antihémiédrie orthorhombique mm2, groupes abéliens non centrosymétriques et non cycliques d'ordre 4.

L'holoédrie tétragonale est 4/m 2/m 2/m, ou 4/mmm en notation raccourcie. Il s'agit d'un groupe centrosymétrique non abélien d'ordre 16. Elle possède quatre hémiédries d'ordre 8 et deux tétartoédries d'ordre 4 dans le système tétragonal. La « parahémiédrie » tétragonale 4/m est ainsi nommée car elle contient une rotation d'axe perpendiculaire à un plan miroir. Il s'agit d'un groupe centrosymétrique abélien non cyclique. Les trois autres hémiédries sont des groupes non centrosymétriques et non abéliens : l'hémiédrie holoaxe tétragonale 422, l'antihémiédrie à axe quaternaire 4mm et l'antihémiédrie sphénoédrique ${\bar {4}}2m$, qui est identique, par rotation de 45° des directions <100>, au groupe ${\bar {4}}m2\,{}$. Les deux tétartoédries sont la tétartoédrie à axe quaternaire 4 et la tétartoédrie sphénoédrique ${\bar {4}}$, toutes deux groupes cycliques non centrosymétriques. Les mériédries sphénoédriques font référence à la forme créée par une anti-rotation d'ordre 4 sur un pôle général, le sphénoèdre (le tétraèdre est un sphénoèdre particulier dont tous les côtés ont la même longueur).

• Groupes ponctuels orthorhombiques et tétragonaux
• 
  $222\,(D_{2})$
• 
  $mm2\,(C_{2v})$
• 
  ${\frac {2}{m}}{\frac {2}{m}}{\frac {2}{m}}\,(D_{2h})$
• 
  $4\,(C_{4})$
• 
  ${\bar {4}}\,(S_{4})$
• 
  $422\,(D_{4})$
• 
  $4mm\,(C_{4v})$
• 
  ${\bar {4}}2m\,(D_{2d})$
• 
  ${\frac {4}{m}}\,(C_{4h})$
• 
  ${\frac {4}{m}}{\frac {2}{m}}{\frac {2}{m}}\,(D_{4h})$

Pour le système cristallin trigonal, l'ordre de rotation ou roto-inversion le plus élevé est 3 : l'holoédrie est le groupe centrosymétrique non abélien ${\bar {3}}m$, d'ordre 12. Elle est généralement appelée « holoédrie rhomboédrique », bien qu'il s'agisse d'un groupe ponctuel de symétrie indépendant du système réticulaire utilisé. Ce groupe est aussi une hémiédrie d'un groupe ponctuel hexagonal. Pour cette raison, deux possibilités existent pour chaque groupe ponctuel de symétrie trigonal dans la nomenclature de Friedel. L'holoédrie rhomboédrique est aussi appelée « parahémiédrie hexagonale à axe ternaire ». Elle possède trois hémiédries d'ordre 6 et une tétartoédrie d'ordre 3 dans le système trigonal. Deux hémiédries sont des groupes non centrosymétriques et non abéliens : l'hémiédrie rhomboédrique holoaxe 32 (ou tétartoédrie hexagonale holoaxe à axe ternaire) et l'antihémiédrie rhomboédrique 3m (ou antitétartoédrie hexagonale). La parahémiédrie rhomboédrique (ou paratétartoédrie hexagonale) est le groupe cyclique centrosymétrique ${\bar {3}}$. La tétartoédrie rhomboédrique 3 (ou ogdoédrie hexagonale) est un groupe cyclique non centrosymétrique. Le groupe ponctuel de symétrie 3/m ne fait pas partie du système cristallin trigonal mais du système cristallin hexagonal : il s'agit en fait du groupe ${\bar {6}}$.

Les projections stéréographiques des groupes ponctuels trigonaux sont données ci-dessous avec les axes du réseau hexagonal et non rhomboédrique ; ce choix ne change bien sûr pas la position relative des éléments de symétrie.

• Groupes ponctuels trigonaux
• 
  $3\,(C_{3})$
• 
  ${\bar {3}}\,(S_{6})$
• 
  $32\,(D_{3})$
• 
  $3m\,(C_{3v})$
• 
  ${\bar {3}}m\,(D_{3d})$

${\frac {6}{m}}{\frac {2}{m}}{\frac {2}{m}}\,(D_{6h})$

L'holoédrie hexagonale est 6/m 2/m 2/m, ou 6/mmm en notation raccourcie. Il s'agit d'un groupe centrosymétrique non abélien d'ordre 24. Elle possède quatre hémiédries d'ordre 12 et deux tétartoédries d'ordre 6 dans le système cristallin hexagonal.

Trois hémiédries sont des groupes non centrosymétriques et non abéliens : l'hémiédrie holoaxe hexagonale 622, l'antihémiédrie à axe sénaire 6mm et l'antihémiédrie trigonoédrique ${\bar {6}}m2$. Ce dernier groupe est identique au groupe ${\bar {6}}2m$. L'orientation des directions <100> a été choisie de façon à avoir la même position relative des plans miroirs que dans le groupe ponctuel trigonal 3m, ce qui facilite l'étude de la relation de groupe/sous-groupe entre ces deux groupes. La quatrième hémiédrie est la parahémiédrie à axe sénaire 6/m, qui est un groupe centrosymétrique abélien non cyclique.

Les deux tétartoédries hexagonales sont des groupes cycliques non centrosymétriques : la tétartoédrie à axe sénaire 6 et l'antitétartoédrie trigonoédrique ${\bar {6}}$.

Les mériédries trigonoédriques font référence à la forme créée par une anti-rotation d'ordre 6 sur un pôle général, le trigonoèdre (il s'agit d'un terme peu usité pour désigner la bipyramide trigonale).

• Mériédries hexagonales
• 
  $6\,(C_{6})$
• 
  ${\bar {6}}\equiv {\frac {3}{m}}\,(S_{3})$
• 
  $622\,(D_{6})$
• 
  $6mm\,(C_{6v})$
• 
  ${\bar {6}}m2\,(D_{3h})$
• 
  ${\frac {6}{m}}\,(C_{6h})$

Tous les groupes ponctuels de symétrie cubiques sont non abéliens. L'holoédrie cubique est le groupe $4/m\,{\bar {3}}\,2/m$ de notation raccourcie $m{\bar {3}}m$. Ce groupe a été noté m3m dans le passé, ce qui ne faisait pas apparaître la présence de roto-inversions d'ordre 3. Il s'agit d'un groupe centrosymétrique d'ordre 48. L'holoédrie cubique possède trois antihémiédries d'ordre 24 et une tétartoédrie d'ordre 12 dans le système cubique. Deux hémiédries ne sont pas centrosymétriques : l'hémiédrie holoaxe cubique 432 et l'antihémiédrie cubique ${\bar {4}}3m$. La parahémiédrie cubique est centrosymétrique, il s'agit du groupe $2/m\,{\bar {3}}$, de notation raccourcie $m{\bar {3}}$.

La tétartoédrie cubique 23 est un groupe non centrosymétrique.

• Groupes ponctuels cubiques
• 
  $23\,(T)$
• 
  ${\frac {2}{m}}{\bar {3}}\,(T_{h})$
• 
  $432\,(O)$
• 
  ${\bar {4}}3m\,(T_{d})$
• 
  ${\frac {4}{m}}{\bar {3}}{\frac {2}{m}}\,(O_{h})$