Cristallographie géométrique/Translations de réseau
- Ce chapitre présente les caractéristiques des réseaux cristallins, donne les bases de la description mathématique des réseaux et esquisse la classification des réseaux selon les systèmes cristallins, systèmes réticulaires et familles cristallines.
Un cristal est composé d'un motif qui se répète à l'identique et remplit tout l'espace occupé par le cristal. Pour décrire un cristal, il faut donc décrire le motif en question, et comment celui-ci remplit l'espace. Une autre manière de le dire est qu'il découpe l'espace occupé par le cristal, en cellules qui contiennent chacune un motif. Le découpage de l'espace décrit comment le motif est répété, là où il faut placer le motif en question dans l'espace. Le problème est qu'il existe une infinité de manière de faire ainsi, qui donnent le même cristal et sont toutes plus ou moins équivalentes. Aussi, les cristallographes utilisent quelques conventions pour découper l'espace en cellules, ainsi que pour définir le motif.

Toutes ces méthodes se basent sur le même principe. Premièrement, elles placent des points dans l'espace, qui servent de points de repère pour placer les cellules, et qui sont agencés selon une organisation périodique. Les points en question sont appelés des nœuds. L'ensemble de ces nœuds forme ce qu'on appelle un réseau cristallin. Notons que les nœuds du réseau ne sont pas forcément les positions des atomes : on peut avoir des atomes qui sont localisés à coté des nœuds, dans une cellule, et des nœuds peuvent ne pas être associé à un atome. Les nœuds servent non pas à indiquer la position des atomes, mais servent de quadrillage pour découper l'espace en cellules, en motifs périodiques.
Ensuite, les nœuds sont connectés entre eux par des arêtes et des faces, qui délimitent la cellule de base. Avec les conventions cristallographiques habituelles, chaque cellule est un parallélogramme, appelé une maille. La raison est que le parallélogramme permet de paver l'espace : il est parfaitement possible de remplir un espace infini de parallélogrammes identiques collés les uns à coté des autres. Il y a d'autres méthodes pour découper l'espace en volumes identiques, mais celle du parallélogramme est particulièrement pratique. Cette praticité tient dans le fait qu'on peut passer d'un parallélogramme à un autre par une simple translation, sans faire intervenir de rotations ou d'autres opérations de symétrie. Ce n'est pas le cas si on pave l'espace avec d'autres formes, pour lesquelles les cellules ne sont pas dans le même sens.

Le réseau cristallin
[modifier | modifier le wikicode]Comme on l'a dit plus haut, un réseau cristallin est un ensemble de points organisés de manière périodique dans l'espace. Dans un cristal, les nœuds d'un réseau ne correspondent pas à des atomes, ce sont des objets mathématiques qui permettent de décrire le réseau cristallin. Il peut arriver qu'un nœud du réseau coïncide avec la position d'un atome, selon l'origine choisie du réseau, mais ces deux concepts sont différents. En deux dimensions, les réseaux les plus utilisés sont les suivants :
-
Réseau triangulaire
-
Réseau carré
-
Réseau rectangulaire
-
Réseau rhombique (losanges)
-
Réseau oblique (parallélogrammes quelconques)
Pour déterminer la position des nœuds dans l'espace, l'idée est de choisir un nœud origine et de localiser tous les autres nœuds par rapport à ce nœud origine. L'origine du réseau est choisie arbitrairement, puisque chaque nœud du réseau est équivalent aux autres. Si l'on part de ce nœud origine, la position d'un autre nœud est donnée par un vecteur qui part du nœud origine et pointe le nœud voulu. Le réseau cristallin définit un ensemble de vecteurs, chaque vecteur correspond à un autre nœud du réseau localisé à partir du nœud origine. Les nœuds d'un réseau sont des points de l'espace situés aux extrémités de tous les vecteurs du réseau centrés sur une origine commune.
 |
 |
Les vecteurs de base d'un réseau cristallin
[modifier | modifier le wikicode]Tous les vecteurs du réseau sont une combinaison linéaire de plusieurs vecteurs de base, linéairement indépendants : trois vecteurs pour un cristal en trois dimensions, deux pour un cristal en deux dimensions. Notons que ces vecteurs de base ne forment pas forcément un système orthonormal. On peut ainsi définir la position de tous les nœuds avec ces trois vecteurs de base et la position d'un nœud quelconque, choisit comme origine du réseau, n'importe lequel faisant l'affaire.
Le réseau est décrit par des vecteurs de base linéairement indépendants, qui ne forment pas forcément un système orthonormal. De manière générale, dans un espace à n dimensions, un réseau est décrit par n vecteurs de base ei linéairement indépendants. Le choix des vecteurs de base d'un réseau n'est pas unique. Tout vecteur τ pouvant s'écrire comme une combinaison linéaire des vecteurs de base du réseau ei avec des coefficients entiers mi est un vecteur du réseau. Les coordonnées des nœuds exprimées dans la base des vecteurs ei sont entières.
|
Définition |
|
Un réseau d'un espace à n dimensions est un ensemble infini de vecteurs qui sont des combinaisons linéaires de ses n vecteurs de base ei : {m1e1 + m2e2 + … + mnen} où les mi sont des nombres entiers et i est compris entre 1 et n. |
Dans l'espace à trois dimensions, il existe pour chaque réseau une infinité de triplets de vecteurs de base linéairement indépendants. Un triplet de vecteurs de base est toujours choisi de façon à former un trièdre direct. Les vecteurs de base dans l'espace à trois dimensions sont notés a, b et c dans ce qui suit.
Le système de coordonnées dans un cristal
[modifier | modifier le wikicode]
Le système de coordonnées pour repérer les nœuds est défini par les vecteurs de base a, b et c du réseau cristallin. Les vecteurs de base sont toujours choisis de façon à former un trièdre direct. Dans le cas général, les vecteurs de base peuvent être de longueurs différentes et former des angles non égaux à 90°. Le système de cordonnées du réseau n'est pas orthogonal, sauf dans les systèmes cristallins orthorhombique, tétragonal et cubique. L'utilisation de ce système de coordonnées, plutôt que d'un système orthonormé, permet de mieux rendre compte de la symétrie du réseau et de simplifier certains calculs. En particulier, l'écriture des matrices représentatrices des opérations de symétrie dans le cristal est facilitée (voir le chapitre sur la symétrie ponctuelle).
Dans un système de coordonnées non orthogonal, une coordonnée d'un point se lit sur l'axe correspondant en y projetant le point parallèlement aux autres axes. La position d'un point A quelconque dans un cristal est définie par son vecteur position rA :
- , où les coordonnées xA, yA et zA du point A sont des nombres réels.
Tout vecteur t s'écrit comme une combinaison linéaire des vecteurs de base du réseau :
Si t est un vecteur du réseau, ses composantes u, v et w sont des nombres entiers.
Les vecteurs d'un réseau représentent des translations
[modifier | modifier le wikicode]Le réseau cristallin, même décrit comme un ensemble de points, est périodique. Concrètement, cela veut dire que si on effectue certaines translations bien précises, le réseau initial et le réseau translaté sont identiques (sous réserve que les deux soient infinis). On dit que ces translations laissent le cristal invariant (sous réserve qu'il soit infini). Reste à définir quelles sont ces translations et les vecteurs translations associés.
Quand cela arrive, tous les nœuds du réseau initial se retrouvent sur un autre nœud du réseau translaté. Le vecteur qui décrit la translation part donc d'un nœud initial, et termine sur le nœud d'arrivée. Maintenant, prenons le nœud de départ comme origine : le vecteur position du nœud d'arrivée est le même que le vecteur de la translation. En clair, tout vecteur du réseau peut s'interpréter comme un vecteur de position, mais aussi comme la translation qu'il faut faire pour passer du nœud origine au nœud de destination. Les vecteurs d'un réseau définissent donc les opérations de translation t qui laissent le réseau invariant. Ces opérations de translation sont des opérations de symétrie du réseau. Deux points A et B sont équivalents par symétrie de translation si il est possible de passer du point A au point B par une translation d'un vecteur τ du réseau. Il est alors possible de passer du point B au point A en effectuant la translation inverse de vecteur −τ.
Le cristal est définit par une combinaison d'un réseau et du motif de base. En effet, un cristal est invariant par translation, ce qui veut dire que si l'on part d'un motif bien précis, on retombe sur le même motif si l'on effectue certaines translations bien précises. On peut décrire un cristal en écrivant toutes les translations en question et le motif de base. Et les translations en question sont celles qui permettent de passer d'un nœud à un autre. Les atomes constituant le motif sont indépendants les uns des autres, c'est-à-dire qu'il n'existe aucune translation du réseau permettant de passer d'un atome à un autre à l'intérieur du motif. Les coordonnées des atomes exprimées dans la base des vecteurs ei sont des nombres réels.
Un vecteur de translation τ du réseau est une combinaison linéaire des vecteurs de base :
- , où u, v et w sont des nombres entiers.
Le vecteur position r d'un atome de coordonnées x, y et z dans la base d'un réseau tridimensionnel s'écrit :
- , mais avec x, y ou z qui sont des nombres réels, pas forcément entier.

Les mailles cristallines
[modifier | modifier le wikicode]Une maille permet de paver l'espace de façon continue, sans donner lieu à des recouvrements ou à des espaces vacants. La connaissance de la maille et de son contenu (les atomes) permet par translations de reconstruire la totalité du cristal : il suffit de décrire la maille pour décrire le cristal. Il s'agit donc d'un concept fondamental en cristallographie. Le pavage de l'espace se fait par translations de la maille, suivant les vecteurs qui sont des combinaisons linéaires des vecteurs de base du réseau. Dans l'espace à trois dimensions, un triplet {a, b, c} de vecteurs de base du réseau définit un parallélépipède : la maille du réseau. Dans l'espace à deux dimensions, la maille est un parallélogramme défini par un doublet de vecteurs de base {a, b}.
|
Définition |
|
Une maille est un élément de volume sous-tendu par des vecteurs de base du réseau permettant de reconstituer entièrement l'espace par application de toutes les opérations de translation du réseau, sans donner lieu à des recouvrements ou à des espaces vacants. |
Les paramètres d'une maille
[modifier | modifier le wikicode]Les paramètres qui définissent la maille sont les trois longueurs des côtés et les trois angles entre ces longueurs.
Les longueurs de ses arêtes sont données par les longueurs a, b et c des vecteurs de base (a et b dans l'espace bidimensionnel). En cristallographie, les longueurs des vecteurs de la maille sont exprimés en ångström (1 Å vaut 10-10 m) et les angles en degrés.
Les trois angles α, β et γ (γ dans l'espace bidimensionnel) entre les vecteurs de base sont définis comme suit :
- α est l'angle entre les vecteurs b et c,
- β est l'angle entre les vecteurs a et c,
- γ est l'angle entre les vecteurs a et b.
Les coordonnées des atomes dans la maille sont des nombres réels x, y et z tels que 0≤x<1, 0≤y<1 et 0≤z<1. Le vecteur position r d'un atome dans la maille s'écrit en fonction des vecteurs de base :
La maille est donc définie pour chaque coordonnée dans l'intervalle [0,1[. À l'intérieur de la maille, il n'existe pas de positions équivalentes par translation des vecteurs a, b ou c.
Les types de mailles : mailles primitives et multiples
[modifier | modifier le wikicode]
Comme il existe une infinité de triplets de vecteurs de base, il existe une infinité de mailles pour un réseau donné. Dans toutes ces mailles, on peut distinguer deux types bien précis.
La maille primitive est la maille dont le volume est le plus petit, celle qui contient le moins d'atomes possibles, celle dont le motif est le plus simple. Une maille primitive est une maille qui ne contient qu'un seul nœud du réseau. C'est la maille de volume minimal qui permet de décrire un réseau. La maille primitive a pour particularité qu'elle a un point du réseau à chaque sommet mais pas dans ses faces ou dans son volume. En particulier, aucune translation d'un vecteur du réseau n'est applicable à l'intérieur de la maille primitive. Chaque réseau peut être décrit par une infinité de mailles primitives, qui ont toutes le même volume.
Une maille multiple (ou centrée) est une maille non-primitive. Autrement dit, elle contient plusieurs nœuds du réseau à l'intérieur de la maille, sur ses faces ou dans son volume. Il est donc possible de trouver des positions équivalentes par translations du réseau à l'intérieur d'une maille multiple.
Pour illustrer la différence, voici ce que cela donne pour un réseau en deux dimensions orthogonal, illustré dans le schéma ci-dessous. La maille primitive est un simple losange, sans points à l'intérieur. La maille multiple en rouge est un rectangle avec un point au centre, au milieu de ses diagonales. On voit aussi que la surface de la maille primitive est plus faible que celle de la maille conventionnelle, ce qui arrive souvent en deux dimensions (pareil pour le volume en trois dimensions). La maille multiple en rouge est une maille double car elle contient exactement deux nœuds :
- le nœud au centre de la maille ;
- le nœud à l'origine de la maille. La maille étant définie dans l'intervalle [0,1[, les nœuds situés aux autres sommets du rectangle, de coordonnées (1,0), (0,1) et (1,1), ne sont pas pris en compte car ils appartiennent aux mailles voisines dans le réseau.

- Une maille ne peut contenir qu'un nombre entier de nœuds du réseau.
La maille conventionnelle
[modifier | modifier le wikicode]La maille conventionnelle est la maille qui permet de rendre compte au mieux de la symétrie du réseau. Ce point est très utile quand on doit faire des calculs impliquant la structure d'un cristal, les symétries permettant de fortement simplifier certains calculs de la physique du solide. Ce type de maille autorise la présence de points du réseau sur ses faces ou dans son volume, mais ce n'est pas une nécessité et tout dépend du cristal considéré. Elle peut être autant une maille primitive qu'une maille multiple : tout dépend du réseau.
Les critères suivants permettent de trouver la maille conventionnelle pour décrire un réseau.
- Les vecteurs de base doivent avoir une longueur la plus courte possible.
- Les vecteurs de base sont choisis de façon à former des angles obtus.
- Si les nœuds du réseau forment des directions perpendiculaires entre elles, ces directions doivent être choisies pour trouver les vecteurs de base.
- Lorsqu'une maille multiple existe qui donne lieu à des vecteurs de base perpendiculaires entre eux, il vaut mieux choisir la maille multiple, sauf si des angles de 120° sont présents.
- Limiter le nombre de nœuds dans une maille. Dans un espace à deux dimensions, ne pas aller au-delà de deux nœuds par maille. Dans un espace à trois dimensions, ne pas aller au-delà de quatre nœuds par maille.
Les critères de choix de la meilleure maille pour un réseau donné dépendent de la symétrie du réseau et seront détaillés dans le chapitre sur les groupes d'espace.
La maille de Wigner-Seitz
[modifier | modifier le wikicode]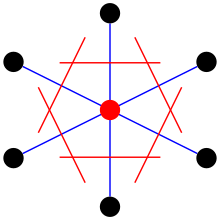
La maille de Wigner-Seitz est une des nombreuses mailles primitives d'un cristal. Chaque maille de ce type entoure un nœud du réseau, appelé le nœud enclos. Elle est définie de telle manière que tout point dans cette maille est plus proche du nœud enclos que des autres.
Elle s'obtient de la manière suivante :
- Pour commencer, il faut tracer toutes les segments possible qui relient deux nœuds.
- Ensuite, on trace ou les plans médiateurs de ces segments (les médiatrices si on travaille dans le plan).
- Le volume obtenu ainsi, coincé par les plans médiateurs, est la maille de Wigner-Seitz.
La procédure est illustrée ci-dessous dans un exemple à deux dimensions.

En deux dimensions, les mailles de Wigner-Seitz sont limitées à des hexagones, des losanges ou des carrés.

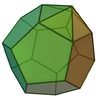
En trois dimensions, la forme d'une maille de Wigner-Seitz peut prendre l'une des cinq formes pré-établies suivantes :
| Maille | 
|

|

|
|

|
|---|---|---|---|---|---|
| Pavage de l'espace par la maille | 
|

|

|

|

|
Les systèmes réticulaires
[modifier | modifier le wikicode]Il est possible de classer les réseaux selon leurs morphologies. La forme de la maille et les conditions sur ses paramètres déterminent le système réticulaire d'un réseau.
Les systèmes réticulaires en deux dimensions
[modifier | modifier le wikicode]En deux dimensions, il existe quatre systèmes réticulaires, qui portent le même nom dans les trois classifications.
- Dans le système réticulaire monoclinique, les paramètres de maille sont tous quelconques : a≠b, γ≠90°.
- Dans le système réticulaire orthorhombique, les paramètres de maille sont a≠b et γ=90° : les vecteurs de base sont orthogonaux.
- Dans le système réticulaire tétragonale, les paramètres de maille sont a=b et γ=90°. En français, le terme « quadratique » est plus utilisé que le terme « tétragonal ». Ce deuxième terme sera cependant utilisé par la suite dans cet ouvrage, car c'est le terme standard dans les tables internationales de cristallographie. Il permet également une meilleure identification des réseaux de Bravais tétragonaux, qui sont notés par la lettre « t ».
- Dans le système réticulaire hexagonal, les paramètres de maille sont a=b et γ=120°.
| Nom | Paramètres de maille | Schéma de la maille | |
|---|---|---|---|
| Monoclinique | a≠b | γ≠90° | 
|
| Orthorhombique | γ=90° | 
| |
| Tétragonale | a=b | 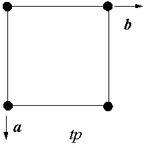
| |
| Hexagonale | γ=120° | 
| |
Les systèmes réticulaires en trois dimensions
[modifier | modifier le wikicode]En trois dimensions, il existe 7 systèmes réticulaires, appelés système triclinique, monoclinique, orthorhombique, tétragonale, cubique, rhomboédrique et hexagonale.
- Dans le système réticulaire triclinique, les paramètres de maille sont tous quelconques : a≠b≠c, α≠β≠γ≠90°. Ce système est aussi appelé « anortique » car les vecteurs de base du réseau ne sont pas orthogonaux.
- Dans le système réticulaire monoclinique, il existe une direction perpendiculaire aux deux autres. Par convention, cette direction est notée b. Les paramètres de maille sont a≠b≠c, α=γ=90°≠β.
- Dans le système réticulaire orthorhombique, les trois vecteurs de base, de longueurs différentes, forment des angles droits. Les paramètres de maille sont a≠b≠c, α=β=γ=90°.
- Dans le système réticulaire tétragonale, les trois vecteurs de base forment des angles droits et deux des vecteurs de base sont de même longueur. Par convention, le vecteur de longueur différente est appelé c. Les paramètres de maille sont a=b≠c, α=β=γ=90°.
- Dans le système réticulaire cubique, les vecteurs de base sont orthogonaux et de même longueur : a=b=c, α=β=γ=90°.
- Dans le système réticulaire rhomboédrique, la maille primitive est un rhomboèdre, dont les vecteurs de base ont la même longueur et forment le même angle entre eux, différent de 90°. Dit autrement, on a : a=b=c, α=β=γ≠90°.
- Dans le système réticulaire hexagonal, la maille a seulement deux longueurs et deux angles identiques, ce qui donne une maille qui a pour paramètres : a=b≠c, α=β=90° et γ=120°.
Les autres classifications des réseaux cristallins : système cristallin et famille cristalline
[modifier | modifier le wikicode]Outre la classification en systèmes réticulaires, il est possible de classer les réseaux en fonction de leurs propriétés de symétrie du réseau. La classification des réseaux basée sur la symétrie sera revue dans le chapitre sur la symétrie ponctuelle. Pour le moment, nous allons simplement dire qu'il existe deux types de classifications en fonction des symétries :
- Les familles cristallines regroupent les réseaux qui ont les mêmes propriétés de symétrie. Deux réseaux appartiennent à la même famille cristalline si leurs mailles ne diffèrent que par le nombre de nœuds qu'elles contiennent.
- Les systèmes cristallins classent les réseaux selon leurs symétries, indépendamment de la maille choisie pour les décrire.
Dans l'espace à deux dimensions, familles cristallines, systèmes cristallins et systèmes réticulaires se confondent. Aussi, nous n'allons parler que du cas à trois dimensions.
Dans l'espace à trois dimensions, il existe six familles cristallines, sept systèmes cristallins et sept systèmes réticulaires. Le systèmes réticulaires triclinique, monoclinique, orthorhombique, tétragonal et cubiques sont aussi des familles cristalline et des systèmes cristallins. Ce n'est que pour la famille cristalline hexagonale que la nomenclature change. Le tout est résumé dans le tableau ci-dessous, qui illustre bien les explications qui vont suivre.
La famille hexagonale regroupe les systèmes cristallins trigonal et hexagonal, et les systèmes réticulaires rhomboédrique et hexagonal. Il convient de bien faire la distinction entre système réticulaire et système cristallin. Plusieurs ouvrages mentionnent par erreur un système cristallin rhomboédrique, qui n'existe pas. Les deux systèmes cristallins trigonal et hexagonal ne recoupent pas exactement les deux systèmes réticulaires hexagonal et rhomboédrique. Pour comprendre la différence, il identifier un sous-type bien précis de maille hexagonal. Celui-ci identifie une maille triple de forme prismatique, système réticulaire hexagonal. Cette maille contient trois nœuds : un au sommet de la maille et deux à l'intérieur de la maille, de coordonnées (2/3,1/3,1/3) et (1/3,2/3,2/3). Dans ce cas, le système réticulaire est hexagonal. le système cristallin trigonal regroupe ce sous-type et le système réticulaire rhomboédrique. les autres mailles forment le système cristallin hexagonal.




















