Cristallographie géométrique/Introduction
La cristallographie est la science qui étudie les matériaux cristallins : leurs structures atomiques, les relations entre structures et propriétés et la classification des structures cristallines. Il s'agit d'une science interdisciplinaire : elle est appliquée dans les domaines de la physique, de la chimie, de la biologie, de la minéralogie… Elle utilise la diffraction des rayons X, neutrons ou électrons par les cristaux, qui n'est pas l'objet de ce livre.
La cristallographie géométrique présentée ici s'occupe de la symétrie dans les cristaux : principalement sont traités les groupes ponctuels de symétrie, qui peuvent être utilisés aussi pour des molécules isolées, la morphologie des cristaux et les groupes d'espace. Le chapitre de cristallochimie est consacré à la description géométrique des différentes structures cristallines, en particulier les empilements compacts, les polyèdres de coordination, l'isomorphisme et le polymorphisme, puis nous discuterons des transitions de phase structurales dans les cristaux. Enfin, le chapitre sur les propriétés physiques décrit dans quelles conditions de symétrie un cristal peut présenter certaines propriétés : ferroélectricité, génération de seconde harmonique pour les lasers…
L'état cristallin
[modifier | modifier le wikicode]La matière est généralement divisée en trois états :
- les gaz, qui ne possèdent pas de forme propre ni de volume propre et tend à occuper tout l'espace à sa disposition ;
- les liquides sont aussi désordonnés et ne possèdent pas de forme propre ;
- un solide est constitué d'atomes fortement liés qui ne peuvent pas se déplacer librement : il possède une forme et un volume propre.
Cette classification est très simple, facile à comprendre, très pédagogique, mais elle est incomplète et imparfaite sur de nombreux points. Un de ces points est que l'état solide est défini par deux propriétés dites rhéologique : le fait qu'il ait une forme et un volume propre, qu'il ne prend pas la forme de son contenant, que son volume soit (presque) constant. Mais cette définition regroupe des matériaux qui n'ont rien à voir entre eux. Du bois n'a pas grand-chose à voir avec du métal, ou avec du ciment. Les solides peuvent eux-mêmes être classés en plusieurs catégories et ces classifications sont très nombreuses. On peut les classer suivant leurs propriétés mécaniques (fragilité, dureté, seuil de plasticité, résistance aux chocs, et bien d'autres), électrique (conduit-il le courant électrique et si oui, comment), magnétique (comment il réagit à un aimant), et bien d'autres. Ces classifications sont formellement l'objet de la science des matériaux ou de la physique du solide. Mais il faut savoir qu'on peut aussi classer les solides suivant la manière dont les atomes sont disposés dans le solide.
Les atomes d'un solide ne sont pas disposés de la même manière que dans un liquide ou un gaz. Dans l'état gazeux, les atomes sont très faiblement liés entre eux et bougent librement dans le gaz. Les atomes d'un gaz sont toujours en mouvement et leur distance moyenne de déplacement (ou libre parcours moyen) dépend de la température. L'ensemble est donc complètement désordonné. Les interactions entre atomes s'effectuent sous forme de chocs. Dans un liquide, les atomes peuvent là encore bouger dans tout le volume du liquide, mais les interactions entre atomes sont plus fortes, ce qui rapproche les atomes. La distance interatomique moyenne est plus courte et le libre parcours moyen des atomes est plus court. Un liquide est donc beaucoup moins compressible qu'un gaz. Les atomes dans un liquide forment un ordre à courte distance, mais l'ordre à longue distance n'existe pas vraiment. Dans un solide, les atomes ne peuvent pas se déplacer dans tout le solide et sont coincés autour d'une position bien précise. Ils vibrent autour d'une position moyenne bien définie, l'amplitude de cette vibration augmentant avec la température. Un solide est donc plus organisé qu'un liquide ou un solide. Mais tous les solides ne sont pas égaux de ce point de vue.
Les cristaux et les solides amorphes
[modifier | modifier le wikicode]
Dans les grandes lignes, on peut opposer des solides relativement désorganisés aux solides parfaitement organisés. Les solides désorganisés sont appelés les solides amorphes. Dans ces solides, les atomes sont disposés presque aléatoirement dans l'espace, le presque signifiant que les atomes sont proches les uns des autres. Un bon exemple de ce genre de solide est le verre, qui est un solide amorphe composé uniquement de silice (mélange d'oxygène et de silicium). Le fait que les atomes soient proches signifie qu'il y a un ordre à courte distance, mais un désordre sur des distances plus longues. L'ordre se résume aux liaisons chimiques d'un atome avec ses voisins, mais guère plus. À l'inverse, un cristal a une organisation très précise, que ce soit à courte ou longue distance. Les atomes y sont disposés suivant un plan très précis, basé sur un motif en trois dimensions qui est répété dans tout le cristal.
|
Définition |
|
Un cristal est un solide dans lequel les atomes sont ordonnés de façon périodique dans les trois directions de l'espace. |
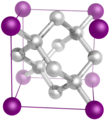
Un bon exemple est tout simplement le sel de table, qui est un cristal comme un autre. La structure atomique du sel est composée de plusieurs cubes collés les uns aux autres, tous les sommets de chaque cube étant occupés pour moitié par un atome de sodium, pour moitié par un atome de chlore.

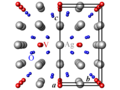
Un autre exemple est la glace, qui est un cristal. Elle cristallise à température et pression normale, ce qui donne le motif suivant :

Il existe d'autres matériaux solides qui ne sont, d'après la définition précédente, ni des cristaux ni des solides amorphes : ce sont les solides à structure ordonnée non périodique. On peut les voir comme des intermédiaires entre cristaux et solides amorphes, dans le sens où ces solides ont un ordre à courte et longues distances, avec des atomes qui sont disposés dans l’espace suivant une règle bien précise, mais que l'agencement des atomes n'est pas périodique. On distingue généralement trois classes de structures apériodiques : les structures modulées, les structures composites et les quasi-cristaux[1]. Ces matériaux ne peuvent pas être décrits par les concepts de la cristallographie géométrique détaillés dans ce livre, ce qui fait qu'ils ne seront pas traités ici.
La forme des cristaux
[modifier | modifier le wikicode]L'arrangement des atomes dépend du cristal, ce qui fait que les cristaux sont très nombreux et assez différents les uns des autres. Un des buts de la cristallographie géométrique est de décrire comment sont disposés les atomes d'un cristal dans l'espace, quel est le motif de base du cristal, comment celui-ci se répète dans l'espace. Et cela a une grande importance, car elle détermine, au moins partiellement, les propriétés électriques, mécaniques ou magnétiques du cristal. La classification des solides et des cristaux est donc fondamentale pour la science des matériaux et la physique du solide.

L'agencement répétitif des atomes du cristal est parfois trahi par sa forme. À l'état naturel, les roches contiennent souvent de nombreux cristaux aux formes assez caractéristiques. Les plus beaux exemples de cristaux ont une forme cubique, en forme de pavé, d'octaèdre, de pyramide, d'obélisque, ou autre. La forme de tels cristaux a souvent un lien direct avec l'agencement des atomes dans le cristal. Par exemple, les cristaux de sel ont une forme cubique et il se trouve que les atomes sont organisés comme tel dans le sel.
- Forme et arrangement atomique des cristaux de sel
-
Cristaux de sel.
-
Arrangement des atomes dans un cristal de sel.
Mais attention : les contre-exemples à cette règle sont nombreux. Par exemple, prenons la pyrite, un minéral assez fréquent composé de sulfure de fer (). L'arrangement des atomes de ce minéral est proche de celui du sel : des cubes collés les uns aux autres, dont la moité est occupée par des atomes de Fer et l'autre par des atomes de Soufre. Et pourtant, on peut trouver des cristaux cubiques, mais aussi octaédriques, et bien d'autres. Évidemment, un cristal de pyrite ne peut prendre que quelques formes bien précises, qui sont compatibles avec l'arrangement atomique cubique. Il y a donc un lien entre arrangement atomique et forme du cristal, mais ce lien n'est pas aussi direct que l'on pourrait le croire.
- Forme des cristaux de pyrite.
-
Cristal cubique de pyrite.
-
Cristal octaédrique de pyrite.
-
Formes possibles d'un cristal de pyrite.
De même, des minéraux distincts peuvent avoir des formes différentes, mais le même arrangement cristallin. Un bon exemple est donné par les cristaux de boléite et de magnétite. Ces trois minéraux ont un arrangement atomique cubique, comme la pyrite et le sel, mais cristallisent dans des formes différentes. La boléite présente en général des cristaux de forme cubique, alors que la magnétite cristallise préférentiellement en cristaux octaédriques.
- Morphologie de cristaux de symétrie cubique
-
La boléite présente en général des cristaux de forme cubique.
-
Les cristaux de magnétite ont une forme octaédrique.
-
La forme de ses cristaux est à l'origine du nom de la tétraédrite.
Tous les cristaux montrent des formes bien précises, avec des faces et des arêtes bien délimitées. Les faces d'un cristal correspondent à des plans d'atomes assez denses dans la structure, c'est-à-dire des plans dans lesquels se trouvent beaucoup de liaisons chimiques, ce qui assure la stabilité des faces. Le volume du cristal n'est pas borné et les arêtes et faces peuvent avoir des dimensions très variables d'un cristal à l'autre. Par exemple, deux cristaux cubiques de pyrite peuvent avoir des tailles très différentes, l'un étant visible à l’œil nu et l'autre microscopique. Par contre, les angles que font les faces d'un cristal sont systématiquement les mêmes d'un cristal à l'autre. Cette observation est aujourd'hui appelée la loi de constance des angles.
« Quelles que soient les dimensions relatives de deux faces déterminées d'un même cristal, elles présentent toujours entre elles le même angle dièdre. »
La formation des cristaux
[modifier | modifier le wikicode]Les cristaux se forment progressivement, généralement à partir d'une solution fluide concentrée en éléments chimiques. Un premier cristal minuscule se forme, puis grossit petit à petit par accumulation d'atomes sur ses faces. Des couches d'atomes s'accumulent sur chaque face, en se recouvrant progressivement. Les faces grossissent donc, ce qui fait augmenter le cristal de volume, mais ce processus ne peut pas changer l'angle entre les faces. La vitesse de croissance d'une face est la vitesse à laquelle une nouvelle couche d'atomes est ajoutée en surface, c'est donc la vitesse de croissance du cristal perpendiculairement à la face et pas parallèlement. Au passage, il est fréquent qu'une face grossisse plus vite qu'une autre, si les conditions sont réunies. Les faces qui croissent le plus vite disparaissent généralement de la morphologie du cristal et se réduisent à des arêtes ou des sommets[2],[3].


Tout cela explique que les cristaux naturels n'ont pas toujours des formes parfaites à l'état naturel, c'est même peu fréquent. La plupart des cristaux trouvés à l'état naturel se sont formés sous l'action de processus géologiques ou biologique imparfaits, qui ne donnent pas forcément de beaux cristaux à la forme bien nette. La croissance de chaque face se fait à une vitesse très différente ce qui déforme le cristal, la croissance de certaines faces peut être bloquée par des obstacles mécaniques : les raisons sont nombreuses. Par exemple, les cristaux de pyrite se développent souvent dans les vides d'une roche, ce qui fait qu'ils prennent tout l'espace disponible lors de leur formation et ne peuvent pas prendre une belle forme cubique ou octaédrique. Il n'est aussi pas rare que des cristaux distincts s’interpénètrent, ce qui donne des macles assez jolies à regarder. Cela vient du fait que plusieurs cristaux ont grossi chacun dans leur coin avant de se cogner les uns aux autres, avant de fusionner ensemble.
Les cristaux sont anisotropes
[modifier | modifier le wikicode]Les cristaux se distinguent des autres états de la matière sur leur caractère anisotrope. Les liquides, gaz et solides amorphes sont dits isotropes, c’est-à-dire que leurs propriétés physiques sont les mêmes peut importe la direction dans laquelle on les mesure. Par exemple, la résistance aux chocs d'un solide amorphe comme le verre est approximativement la même peu importe à quel endroit ou dans quelle direction à la mesure. De même, le verre n'a pas d'axe dans lequel la conductivité thermique serait plus grande que dans les autres directions. Mais c'est complètement différent pour les cristaux.
Du fait de la périodicité des atomes dans les cristaux, il existe plusieurs directions différentes le long desquelles l'arrangement atomique est différent. En conséquence, les propriétés physiques des cristaux (morphologie, clivage, dureté, conductivités thermique et électrique, dilatation thermique, déformation élastique, etc.) dépendent de la direction dans laquelle elles sont mesurées. Par exemple, les cristaux ont tendance à plus facilement casser suivants certains plans, dont l'orientation dépend de l'organisation des atomes dans le cristal. De même, certains cristaux conduisent plus facilement le courant dans certaines directions, orientés parallèlement ou perpendiculairement à l'arrangement atomique du cristal. Pour cette raison, les cristaux sont anisotropes, alors que les matériaux amorphes présentent des propriétés isotropes. Une définition plus ancienne des cristaux les décrit d'ailleurs comme des corps homogènes et anisotropes.
Il est parfois dit que les cristaux d'arrangement cubique, comme la pyrite ou le sel, sont isotropes. Mais dans les faits, cela n'est pas vrai pour toutes leurs propriétés physiques. Notamment, les faces d'un cristal ont une vitesse de croissance différente selon la direction (l'environnement chimique du cristal et les conditions de température et de pression lors de sa croissance jouent aussi un rôle). La croissance cristalline est ainsi anisotrope pour tous les cristaux, et les cristaux d'arrangement cubique ne font pas exception.
La diffraction des ondes montre particulièrement le caractère anisotrope des cristaux. Si la longueur d'onde choisie est du même ordre de grandeur que les distances interatomiques, la périodicité des atomes dans un cristal provoque des interférences dans l'onde diffusée. Ce phénomène est appelé « diffraction » et est similaire à la diffraction de la lumière visible par un réseau en optique. On observe une intensité diffractée dans certaines directions bien définies de l'espace (les réflexions), correspondant aux interférences constructives, alors qu'aucune intensité n'est présente dans le reste de l'espace à cause des interférences destructives. Un matériau amorphe diffuse au contraire les ondes de manière continue dans tout l'espace et son diffractogramme présente des maxima beaucoup plus larges.
Au passage, précisons que les solides à structures ordonnées non-périodique donnent lieu à une figure de diffraction discrète lors d'expériences de diffraction de rayons X, de neutrons ou d'électrons, comme les cristaux classiques,. Ceci a conduit l'union internationale de cristallographie à poser une nouvelle définition plus large du concept de cristal en 1992[4], qui ne sera pas utilisée dans le reste du livre.
|
Définition |
|
Un cristal est un solide dont la figure de diffraction est de nature discrète. |
La stabilité des cristaux et leur polymorphisme
[modifier | modifier le wikicode]
Certains composés chimiques peuvent cristalliser dans plusieurs arrangements atomiques différents. Un exemple du quotidien est le carbone, qui peut cristalliser dans deux phases cristallines différentes. Le carbone peut tout d'abord cristalliser en graphite, la substance qui compose les mines de crayon. Le cristal de graphite est composé de plusieurs feuillets empilés les uns sur les autres, chaque feuillet étant composé d'un arrangement hexagonal d'atomes de carbone semblable à une ruche d'abeilles. Notons dans les schémas ci-dessous que deux feuillets superposés sont légèrement décalés les uns des autres. L'autre forme cristalline du carbone n'est autre que le diamant, dont la structure cristalline ne contient pas de feuillet et est beaucoup plus compacte. Cela explique que le diamant soit plus dense et plus solide que le graphite. Là où les feuillets du graphite se désolidarisent facilement, la structure compacte du diamant résiste bien mieux.
La structure d'un cristal dépend des conditions de température et de pression auquel il s'est formé et/ou il est exposé. Par exemple, la silice (SiO2) peut cristalliser avec différentes structures, la plus connue étant celle du quartz α. Sous pression atmosphérique, le quartz α, de symétrie trigonale, se transforme vers 573 °C en quartz β, de symétrie hexagonale. Au-dessus de 1 470 °C, la cristobalite est la forme stable de SiO2. Un autre exemple est celui de la glace, qui peut cristalliser dans plus d'une dizaine d'arrangements cristallin différents, en fonction de la pression et de la température.
Ci-dessous est illustré le polymorphisme du vanadate d'argent Ag3VO4. Entre la température ambiante et 620 °C, Ag3VO4 subit deux transitions de phase structurales et a donc trois polymorphes qui se distinguent par l'arrangement des atomes dans le cristal[5] :
- le Ag3VO4-α, stable à température ambiante ;
- le Ag3VO4-β, stable entre 92 °C et 414 °C ;
- le Ag3VO4-γ, stable au-delà de 414 °C, avec des atomes d'oxygène désordonnés.
Si un même matériau peut cristalliser dans des formes différentes, c'est une question d'énergie et de thermodynamique. Un cristal cristallise dans un arrangement tel que son énergie libre soit minimale, mais l'arrangement de moindre énergie dépend des conditions de température et de pression. Il n'est pas le même suivant que la température soit élevée ou faible, que la pression soit forte ou non. Ainsi, la stabilité d'une structure cristalline dépend du domaine de température ou de pression considéré. Le passage d'un polymorphe à un autre lors de la variation d'une grandeur thermodynamique intensive comme la température ou la pression est appelé « transition de phase structurale ».

Typiquement, les fortes pressions tendent à rapprocher les atomes les uns des autres, ce qui favorise les arrangements compacts où les atomes sont collés les uns aux autres. Les fortes températures favorisent au contraire des arrangements plus espacés, moins compacts. Mais ces deux règles sont parfois mises en défaut. Prenons le cas du fer, par exemple. À pression ambiante, il cristallise dans deux arrangements cristallins distincts : un arrangement dit cubique centré à température ambiante, et un arrangement dit cubique à face centrées à haute température. Le premier est paradoxalement moins compact que le second. Ainsi, si on chauffe du fer au-delà de 910°c, le fer change d'arrangement atomique et passe à un arrangement plus dense.
Il existe aussi des composés chimiques qui existent sous forme cristalline et amorphe, et le dioxyde de silicium SiO2 en est encore une fois un bon exemple : il existe un verre de silice amorphe. L'arrangement périodique des atomes dans un cristal est celui pour lequel l'énergie libre totale du système est minimal. Un cristal est thermodynamiquement stable, au contraire des matériaux amorphes qui ne le sont pas. Les solides amorphes tendent donc à évoluer progressivement vers une forme cristalline, les atomes se déplaçant lentement mais sûrement vers leur position d'équilibre. Cependant, précisons que si les solides amorphes ne sont pas stables à proprement parler, leur évolution est tellement lente qu'on peut les considérer comme presque stables : ils sont dits métastables. Pour l'illustrer, reprenons l'exemple du quartz. Dans les conditions normales de température et de pression, la structure du quartz α est stable, alors que celle de la stishovite (son polymorphe de haute pression), n'est que métastable. La stishovite évolue donc en quartz α dans des conditions normales de température et de pression, mais cette transformation est très lente et peut durer quelques milliers d'années.
Les cristaux réels ont des défauts dans leur organisation cristalline
[modifier | modifier le wikicode]Les cristaux vu plus haut sont des cristaux parfaits, où des atomes identiques sont ordonnés de façon périodique à l'infini dans les trois directions de l'espace. Un tel cristal n'existe pas dans le monde réel, car tous les cristaux réels ont des défauts qui perturbent la parfaite organisation périodique du cristal. Les défauts les plus simples sont les défauts ponctuels, où des atomes manquants à un point bien précis du cristal, un atome étranger inséré quelque part, des atomes déplacés, etc. Mais il existe d'autres défauts plus complexes, dont la géométrie est est à une, deux ou trois dimensions. On fait ainsi la distinction entre :
- défauts ponctuels, de dimension 0 (lacunes, atomes interstitiels) ;
- défauts linéaires, de dimension 1 (dislocations) ;
- défauts de dimension 2 (joints de grains dans les polycristaux) ;
- défauts volumiques (macles, pores).
Les défauts sont présents dans tous les cristaux. Ils ne gênent généralement pas lors d'expériences de caractérisation et sont même nécessaires : sans défaut, les réflexions de diffraction d'un cristal seraient trop fines pour être mesurées correctement et l'analyse de leurs intensités devrait faire appel à la théorie dynamique de la diffraction, qui n'est pas implémentée dans la majorité des programmes dédiés. D'autre part, les défauts font partie du mécanisme de certaines propriétés physiques. C'est le cas pour la conductivité électrique d'origine ionique : les ions soumis à un champ électrique se déplacent dans le cristal par l'intermédiaire de lacunes. Les déformations plastiques dans les cristaux sont expliqués par le glissement de plans atomiques, qui est facilité par la présence de défauts.
Les modèles de cristaux parfaits sont utilisés comme un modèle idéal, qui permet d'approximer le comportement d'un cristal réel. On l'utilise par exemple pour calculer les états quantiques d'électrons soumis à un potentiel périodique (ondes de Bloch).
Histoire de la cristallographie
[modifier | modifier le wikicode]Par leurs formes géométriques naturelles, les cristaux ont toujours été une source de fascination, en particulier les gemmes et les pierres précieuses. Ils sont étudiés dès l'Antiquité : le philosophe Théophraste, né vers 372 avant J.-C. et mort vers 288 avant J.-C., décrit des cristaux de grenat, un minéral qu'il nomme anthrax. Strabon (né vers 58 avant J.-C. et mort en 21 ou 25 après J.-C.) étudie des cristaux de quartz en provenance d'Inde, pour lesquels il invente le nom de Krystallos. Au Ier siècle, Pline l'Ancien consacre une partie de son ouvrage Histoire naturelle à la description des minéraux. Vers la fin de la Renaissance, Johannes Kepler s'interroge dans De nive sexangula (1611) sur la régularité des flocons de neige et suppose que leur formation provient d'un empilement compact régulier de constituants élémentaires.
-
Cristaux de grenat en provenance d'Aggeneys en Afrique du Sud.
-
Cristaux de quartz en provenance du Minas Gerais au Brésil.
-
Cristaux cubiques de pyrite en provenance du Pérou.
L'étude géométrique systématique des cristaux commence réellement avec les travaux de Sténon, qui remarque en 1669 que les angles entre des faces adjacentes de cristaux de quartz d'origines différentes sont constants. Ces résultats sont généralisés à tous les cristaux par Domenico Guglielmini entre 1688 et 1705 et par Jean-Baptiste Romé de L'Isle près d'un siècle plus tard avec l'invention du goniomètre, ce qui permet à ce dernier de formuler sa « loi de constance des angles ».

En 1784, René Just Haüy montre que les cristaux sont constitués d'empilement d'unités de volume de matière, qu'il désigne par « molécules intégrantes ». Grâce à ce concept, obtenu par sa « loi des troncatures », il explique la forme des cristaux, démontre la loi de constance des angles de Romé de L'Isle et tente une classification des cristaux en fonction de leur morphologie. Ce faisant, il montre qu'il n'existe qu'un nombre fini de formes des molécules intégrantes permettant de reconstruire les différentes morphologies observées et que certaines formes, comme les prismes pentagonaux ou octogonaux, ne peuvent pas servir à construire un cristal (cette impossibilité est démontrée par le théorème de restriction cristallographique). Il montre aussi qu'il existe des cristaux dont la forme ne contient que la moitié des éléments de symétrie de la molécule intégrante : c'est l'« hémimorphisme ». Par exemple, un tétraèdre peut être obtenu à partir d'un cube en tronquant quatre de ses sommets non voisins (voir la figure ci-contre), et il existe deux façons d'obtenir un tétraèdre à partir d'un cube, en fonction des sommets tronqués : ces deux tétraèdres sont des images l'un de l'autre dans un miroir. Haüy nomme les deux formes obtenues par hémiédrie « plagièdre droit » et « plagièdre gauche », connus aujourd'hui sous le nom d'« énantiomères ». L'idée des molécules intégrantes de Haüy est reprise par son élève Gabriel Delafosse qui en déduit l'existence d'une « maille élémentaire », à la base de la cristallographie géométrique actuelle.
L'invention par William Hyde Wollaston en 1809 du goniomètre à réflexion, qui permet des mesures d'angles d'une bien meilleure précision, marque un nouveau pas dans l'histoire de la minéralogie et de la cristallographie. En 1815, Christian Samuel Weiss décrit les sept systèmes cristallins possibles. L'utilisation du goniomètre à réflexion amène en particulier Eilhard Mitscherlich, assisté par Gustav Rose, à découvrir l'isomorphisme en 1819 et le polymorphisme en 1824. De ces découvertes s'inspirent pendant presque un siècle les travaux suivants sur la relation entre la forme des cristaux et leur composition chimique, du domaine de la cristallochimie. On peut noter entre autres la (re)découverte de la « dissymétrie moléculaire » (ou énantiomorphisme) par Louis Pasteur en 1848 ainsi que sa méthode expérimentale pour isoler les deux énantiomorphes du paratartrate, qui conduit à la naissance du domaine de la stéréochimie. Hermann Kopp étudie les cristaux mixtes isomorphes, dans lesquels des molécules peuvent être substituées par d'autres, et montre en 1840 que la probabilité pour deux molécules de former des cristaux mixtes est plus grande si leurs tailles sont semblables. Ces résultats sont développés par Paul Heinrich von Groth qui met en évidence un changement graduel de la morphologie des cristaux mixtes lors d'une substitution isomorphe. En 1849, Auguste Bravais décrit les propriétés de la maille élémentaire et montre qu'il n'existe que 14 mailles élémentaires dans l'espace à trois dimensions. La deuxième moitié du XIXe siècle voit également l'élaboration de classifications des minéraux en fonction de leurs compositions chimiques et/ou de leurs formes cristallines, comme la classification de Gustav Rose et celle de James Dana. À la fin du XIXe siècle, les fondements mathématiques de la théorie sur la symétrie des cristaux, dont la liste des 230 groupes d'espace, sont développés de façon indépendante par Arthur Schoenflies, William Barlow et Evgraf Fedorov.
La découverte des atomes au début du XXe siècle permet finalement de comprendre la nature des cristaux. William Barlow et William Pope émettent l'hypothèse, en 1906, que la forme des cristaux est définie par l'arrangement d'atomes sphériques qui en sont les constituants élémentaires. Les expériences de diffraction des rayons X par les cristaux menées par Max von Laue en 1912 et les travaux successifs de William Lawrence Bragg et William Henry Bragg sur le chlorure de sodium NaCl confirment cette hypothèse et ouvrent la voie à la détermination de la structure atomique des cristaux. En 1926, Victor Goldschmidt montre que la formation de cristaux mixtes a lieu lorsque les rayons ioniques des éléments substitués dans le cristal sont très proches, comme par exemple dans la série forstérite (Mg2SiO4) - fayalite (Fe2SiO4). Au début des années 1930, Carl Hermann et Charles Mauguin se consacrent à l'étude des 32 classes cristallines et des 230 groupes d'espace, développant une notation symbolique toujours utilisée internationalement : les symboles de Hermann-Mauguin. L'amélioration au cours du XXe siècle des techniques de diffraction des rayons X, des neutrons et des électrons, la construction de synchrotrons et de sources de neutrons à des fins scientifiques et les progrès en informatique font de la détermination d'une structure cristalline une technique de routine en cristallographie. Depuis la découverte des rayons X par Wilhelm Röntgen en 1895, les prix Nobel jalonnent l'histoire de la cristallographie dans plusieurs disciplines scientifiques.
| Année | Discipline | Lauréats | Travaux récompensés |
|---|---|---|---|
| 1901 | physique | Wilhelm Röntgen | En témoignage des services extraordinaires rendus par sa découverte des remarquables rayons ultérieurement nommés d'après lui |
| 1914 | physique | Max von Laue | Pour sa découverte de la diffraction des rayons X par les cristaux |
| 1915 | physique | William Henry Bragg, William Lawrence Bragg |
Pour leurs contributions à l'analyse de la structure cristalline au moyen des rayons X |
| 1929 | physique | Louis de Broglie | Pour sa découverte de la nature ondulatoire des électrons |
| 1937 | physique | Clinton Davisson, George Thomson |
Pour leur découverte expérimentale de la diffraction des électrons par les cristaux |
| 1946 | chimie | James Sumner, John Northrop, Wendell Stanley |
Pour la découverte de la cristallisation des enzymes, pour la préparation d'enzymes et de protéines virales sous forme purifiée |
| 1962 | chimie | Max Perutz, John Kendrew |
Pour leurs travaux sur la structure des protéines globulaires |
| 1962 | médecine | Francis Crick, James Watson, Maurice Wilkins |
Pour leurs découvertes sur la structure moléculaire des acides nucléiques et sa signification pour la transmission de l'information pour la matière vivante |
| 1964 | chimie | Dorothy Crowfoot Hodgkin | Pour la détermination par les techniques des rayons X de la structure d'importantes substances biologiques |
| 1973 | chimie | Ernst Fischer, Geoffrey Wilkinson |
Pour leurs travaux de pionniers, réalisés indépendamment, sur les composés organométalliques appelés composés sandwich |
| 1976 | chimie | William Lipscomb | Pour ses travaux sur la structure des boranes, qui ont apporté un nouvel éclairage sur la liaison chimique |
| 1982 | chimie | Aaron Klug | Pour avoir développé la microscopie électronique cristallographique et pour avoir déterminé la structure des complexes acides-nucléiques protéines biologiquement importants |
| 1985 | chimie | Herbert Hauptman, Jerome Karle |
Pour leurs réalisations remarquables dans la mise au point de méthodes directes de détermination des structures cristallines |
| 1988 | chimie | Johann Deisenhofer, Robert Huber, Hartmut Michel |
Pour la détermination de la structure tridimensionnelle d'un site de la réaction photosynthétique |
| 1994 | physique | Clifford Shull | Pour la mise au point de la technique de diffraction neutronique |
| 2003 | chimie | Roderick MacKinnon | Pour avoir été le premier à résoudre par cristallographie aux rayons X la structure de canaux ioniques (en particulier un canal potassium) dans les membranes cellulaires |
| 2009 | chimie | Venkatraman Ramakrishnan, Thomas Steitz, Ada Yonath |
Pour leurs études de la structure et de la fonction du ribosome |
| 2011 | chimie | Dan Shechtman | Pour sa découverte des quasi-cristaux |
Les applications de la cristallographie
[modifier | modifier le wikicode]La cristallographie est le plus souvent utilisée pour la détermination de structures cristallines par diffraction de rayons X, de neutrons ou d'électrons : il est possible de retrouver la position des atomes dans la maille à partir des intensités des ondes diffractées par un cristal. Cette application de la cristallographie ne se limite pas à la seule détermination de structures atomiques. La diffraction de neutrons donne aussi des informations sur la distribution des moments magnétiques dans un matériau. La diffraction par un cristal est une technique importante dans plusieurs disciplines scientifiques, puisque la connaissance de la structure d'un cristal permet d'expliquer ses propriétés physico-chimiques :
- en physique, les modèles établis pour prédire le comportement de matériaux sous certaines conditions de température ou de pression se basent sur la connaissance de leurs structures ;
- en physico-chimie des surfaces, il est souvent observé que la structure atomique en surface (quelques couches atomiques) diffère de celle du matériau en volume : on parle de reconstruction. L'étude de la structure des surfaces par diffraction d'électrons est importante pour comprendre leurs propriétés de catalyse ou d'adsorption de molécules ;
- en biologie, la diffraction sur des macromolécules cristallisées livre des informations sur la structure de nombreuses molécules (ADN, protéines…), comme la localisation et la forme des sites actifs dans les enzymes.
Vers la fin du XXe siècle se sont développées des techniques de diffraction permettant de suivre l'évolution d'un système en temps. Par exemple, lors d'une illumination d'un cristal par un laser, certains atomes peuvent être amenés dans un état excité ou même former de nouvelles liaisons chimiques, la vitesse du retour à l'état fondamental étant très variable. Il est actuellement possible d'étudier in situ par diffraction des phénomènes dynamiques induits d'une durée de quelques femtosecondes[7],[8]. Les applications possibles sont l'étude des transferts d'atomes dans les sites actifs de protéines ou celle des transitions de spin dans les composés moléculaires.

Dans un matériau « polycristallin », plusieurs cristallites ou « monocristaux » d'orientations différentes sont arrangés côte à côte. Des exemples de matériaux polycristallins sont les poudres, les couches minces ou les aciers. La texture d'un polycristal, c'est-à-dire l'orientation relative des monocristaux qui le constituent, peut être déterminée par diffraction. Elle donne des informations sur la formation du polycristal ou sur les déformations plastiques qu'il a subies : l'application d'une pression sur un matériau polycristallin change l'orientation relative de ses cristallites. Dans le cas des poudres, la texture ou « orientation préférentielle » résulte de la forme anisotrope des cristallites, en plaquettes ou en aiguilles par exemple. En géologie, la texture d'une roche renseigne sur ses déformations successives et permet de reconstruire l'histoire des déplacements des plaques tectoniques. D'autre part, la texture des minéraux à l'intérieur du manteau terrestre joue un rôle dans la transmission des ondes sismiques. La découverte en laboratoire de la phase post-pérovskite de MgSiO3 en 2004[9] par diffraction sur poudre, sous des conditions de pression et de température similaires à celles régnant à l'interface entre le manteau inférieur et le noyau terrestre, et les travaux successifs sur la texture de cette phase ont apporté des éléments importants pour comprendre la propagation anisotrope des ondes sismiques à la discontinuité de Gutenberg.
La diffraction est aussi utilisée pour étudier la distribution des contraintes dans un matériau. Ceci est par exemple utile lors de l'optimisation de procédés de fabrication de pièces mécaniques : si plusieurs méthodes sont possibles, celle à privilégier est celle qui limite les contraintes dans le matériau afin de limiter les risques de cassure et de prolonger la durée de vie de la pièce. En géologie, la formation de failles ou de plis trouve son origine dans les contraintes présentes dans les roches.
Références
[modifier | modifier le wikicode]- ↑ anglais Sander van Smaalen, Incommensurate Crystallography, Oxford University Press, coll. « IUCr Monographs on Crystallography » (no 21), 2007, chap. 1 (« Structure and diffraction of aperiodic crystals »), p. 2 (ISBN 978-0-19-857082-0)
- ↑ anglais M. Szurgot, « Velocities of Disappearance and Lifetime of Faces of Growing Crystals », dans Crystal Research and Technology, vol. 26, no 5, 1991, p. 555-562, lien doi
- ↑ anglais Jolanta Prywer, « Three-dimensional model of faces disappearance in crystal habit », dans Journal of Crystal Growth, vol. 155, no 3-4, 1995, p. 254-259, lien doi
- ↑ « Report of the Executive Committee for 1991 », dans Acta Crystallographica Section A, vol. 48, no 6, 1992, p. 922-946, en particulier p. 928, lien doi
- ↑ anglais R.E. Dinnebier, A. Kowalevsky, H. Reichert et M. Jansen, « Polymorphism of Ag3VO4 », dans Zeitschrift für Kristallographie, vol. 222, no 8, 2007, p. 420-426, lien doi
- ↑ Tableau réalisé à partir des articles de Wikipédia Prix Nobel de chimie, Prix Nobel de physique et Prix Nobel de physiologie ou médecine dans leurs versions du 16 novembre 2011
- ↑ anglais Jacqueline M. Cole, « Photocrystallography », dans Acta Crystallographica Section A, vol. 64, no 1, 2008, p. 259-271, lien DOI
- ↑ anglais Zeitschrift für Kristallographie, vol. 223, no 4-5 : « Photocrystallography », 2008, voir le sommaire en ligne
- ↑ anglais Motohiko Murakami, Kei Hirose, Katsuyuki Kawamura, Nagayoshi Sata et Yasuo Ohishi, « Post-Perovskite Phase Transition in MgSiO3 », dans Science, vol. 304, no 5672, 2004, p. 855-858, lien DOI