Cristallographie géométrique/Symétrie ponctuelle

Cristallographie géométrique

Table des matières
Introduction Translations de réseau Calculs dans les réseaux Changement de base Projection stéréographique Symétrie ponctuelle Groupes ponctuels de symétrie Symétrie de corps simples et molécules Morphologie des cristaux Symétrie translatoire Réseaux de Bravais Groupes d'espace Propriétés physiques des cristaux Cristallochimie Transitions de phase

La symétrie ponctuelle désigne l'ensemble des applications linéaires qui laissent invariant un objet de dimension finie : polyèdre ou molécule par exemple. Les éléments de symétrie d'un objet passent tous par son centre et ont donc au moins un point en commun, le centre de l'objet, d'où le nom de « symétrie ponctuelle ». Les opérations de translation ne font pas partie des opérations de symétrie ponctuelle.

En cristallographie, la symétrie ponctuelle d'un cristal doit aussi laisser le réseau invariant : on ne considère que les isométries, qui conservent les longueurs. D'autre part, seul un petit nombre d'opérations de symétrie est compatible avec les translations de réseau : c'est le « théorème de restriction cristallographique ». La symétrie ponctuelle d'un cristal impose des restrictions sur les paramètres de sa maille conventionnelle.

Opérations et éléments de symétrie ponctuelle


Définition
Une opération de symétrie est une application linéaire qui associe à tout point de l'espace un point image. Un élément de symétrie est l'ensemble des points fixes de l'opération de symétrie associée, qui restent inchangés par l'application de l'opération de symétrie : il peut s'agir d'un point, d'une droite ou d'un plan par rapport auquel est effectuée l'opération de symétrie.

Une opération de symétrie ne possède qu'un seul élément de symétrie. Les éléments de symétrie d'un objet passant tous par son centre, on choisit ce point comme origine de l'espace.

Identité

L'identité est une opération, notée 1, qui associe à tout point P de l'espace le point P lui-même comme image. Il s'agit d'une opération sans effet. Tous les points de l'espace sont points fixes de l'identité. Si le point P a pour coordonnées (x,y,z), son image a aussi pour coordonnées (x,y,z). Tout objet est invariant par l'application de l'identité.

Réflexion

La réflexion est notée m et associe à tout point P de l'espace un point P' qui est son image par rapport à un plan, de la même façon qu'une image dans un miroir. Pour cette raison, le plan de la réflexion est appelé « plan miroir » en cristallographie. Le point P' est tel que sa distance au plan miroir est la même que celle du point P et la droite (PP') est perpendiculaire au plan miroir. Les points fixes de la réflexion constituent le plan miroir.

Soit un point P de l'espace de coordonnées (x,y,z) dans un système de coordonnées cartésien. Son image P' par réflexion par rapport au plan (x,y), perpendiculairement à l'axe z, a pour coordonnées (x,y,−z). Son image P'' par réflexion par rapport au plan (x,z), perpendiculairement à l'axe y, a pour coordonnées (x,−y,z).

La réflexion conserve les distances et est donc une isométrie. Elle ne conserve pas la chiralité des objets. La chiralité est d'ailleurs définie par la réflexion par rapport à un plan : un objet chiral est un objet qui ne se superpose pas à son image dans un miroir.

Dans l'espace à deux dimensions, la réflexion s'effectue par rapport à une droite appelée « droite miroir ».

Réflexion.
Réflexion.
Réflexion dans le plan.
Changement de chiralité.

Rotation

Une rotation d'angle θ est une opération qui associe à tout point P de l'espace un point image P' qui est tourné de l'angle θ par rapport à l'axe de la rotation. L'angle de la rotation est exprimé en degrés. La rotation s'effectue dans le sens trigonométrique autour de l'axe et dans le plan contenant le point P et perpendiculaire à l'axe. Les points fixes d'une rotation constituent l'axe de la rotation. La figure a) ci-dessous montre l'application d'une rotation d'angle γ autour de la direction z sur les axes x et y dans un système de coordonnées cartésien.

La rotation est une isométrie : elle conserve les distances. En particulier, la distance du point P à l'axe de rotation est la même que la distance de son image P' à l'axe. D'autre part, la rotation conserve la chiralité des objets, comme illustré dans les figures b) et c) ci-dessous : l'image par rotation d'un objet lévogyre est un objet lévogyre.

a) Rotation autour de l'axe z des axes x et y.
b) Rotation.
c) Rotation et chiralité.

L'ordre n d'une rotation est défini comme le nombre de rotations successives à appliquer au point P pour revenir à la position initiale. Par exemple, une rotation de 180° autour d'un axe est une rotation d'ordre 2 : l'application sur P de deux rotations successives de 180° autour du même axe redonne P. Si l'angle de rotation θ est un diviseur de 360°, l'ordre de la rotation est n=360/θ. La rotation d'ordre 1 est une rotation d'angle 360° et est donc l'identité. Une rotation est notée par son ordre, n.

Il est parfois utile de décrire une rotation par l'angle θ−360° au lieu de θ. Considérons par exemple une rotation d'angle 240° dans le sens trigonométrique et un point P de départ sur lequel sera appliquée la rotation de façon successive. Pour simplifier, nous utiliserons un système de coordonnées polaires : P a alors pour coordonnées (ρ,φ). L'image de P par la rotation d'angle 240° a pour coordonnées (ρ,φ+240°), la deuxième image suivante (ρ,φ+480°), qui est identique à (ρ,φ+120°), la troisième image a pour coordonnées (ρ,φ+360°) et est donc le point P de départ. La rotation d'angle 240° dans le sens trigonométrique est donc d'ordre 3 et est identique à la rotation d'angle 120° dans le sens horaire, c'est-à-dire à une rotation d'angle −120°. Dans les cas où la distinction est nécessaire, on écrit une rotation d'ordre n dans le sens trigonométrique n⁺ et une rotation d'ordre n dans le sens horaire n⁻.

Dans l'espace bidimensionnel, la rotation s'effectue autour d'un point appelé « centre de rotation ».

Inversion

L'inversion en cristallographie est notée ${\bar {1}}\,$ et correspond à la symétrie centrale en mathématiques. Elle s'effectue par rapport à un centre d'inversion. Le point fixe de l'inversion est ce centre d'inversion.

L'inversion associe à tout point P de l'espace un point image P' qui lui est symétrique par rapport au centre d'inversion situé sur l'origine O et tel que O est au centre du segment [PP']. Si le point P a pour coordonnées (x,y,z), son image P' a alors pour coordonnées (−x,−y,−z).

L'inversion est une isométrie car elle conserve les distances. L'inversion ne conserve pas la chiralité : un objet lévogyre a pour image par inversion un objet dextrogyre. Par exemple, l'image par inversion d'une hélice tournant vers la gauche est une hélice tournant vers la droite.

Un objet possédant un centre d'inversion est dit « centrosymétrique ». La présence d'un centre d'inversion est incompatible avec le caractère de chiralité : tout objet centrosymétrique est achiral.

Dans l'espace à deux dimensions, l'inversion est assimilable à une rotation d'ordre 2 autour d'un point, elle conserve alors la chiralité. Ainsi, la conservation de la chiralité d'une opération dépend de la dimension de l'espace utilisé. De façon générale, l'inversion est une rotation dans les espaces de dimension paire.

Roto-inversion

La roto-inversion est la composée d'une rotation d'ordre n autour d'un axe et de l'inversion par rapport à un point de l'axe. Ces deux opérations de symétrie commutent : l'ordre dans lequel elles sont effectuées ne change pas le résultat de la roto-inversion. Il n'existe qu'un seul point fixe de la roto-inversion, qui est le centre d'inversion utilisé pour la composée. Une roto-inversion est notée ${\bar {n}}$ .

La figure ci-contre montre le principe de la roto-inversion dans le cas d'une rotation d'ordre 2. L'image du triangle ABC par la roto-inversion est le triangle A''B''C''. Afin de construire l'image du triangle ABC, on détermine d'abord son image intermédiaire par la rotation d'ordre 2, qui est le triangle A'B'C', puis on applique l'inversion sur A'B'C' pour obtenir A''B''C''. Il aurait aussi été possible d'effectuer d'abord l'inversion sur ABC, puis la rotation sur l'image intermédiaire d'ABC par inversion pour obtenir A''B''C''. Dans les deux cas, l'image intermédiaire n'est qu'une aide de construction et n'existe pas pour la roto-inversion.

La roto-inversion n'est ni une rotation ni une inversion mais la composée de ces deux opérations. En particulier, un objet possédant un centre de roto-inversion d'ordre 2, comme le tétraèdre, n'est pas centrosymétrique et ne possède pas d'axe de rotation d'ordre 2.

Il existe des cas particuliers de la roto-inversion :

la roto-inversion d'ordre 1 est la composée d'une rotation d'angle 360° et d'une inversion, il s'agit donc d'une inversion ;
la roto-inversion d'ordre 2 donnée en exemple est en fait une réflexion par rapport au plan miroir perpendiculaire à l'axe de rotation et passant par le centre d'inversion : ${\bar {2}}\equiv m$ .

L'ordre d'une roto-inversion est l'ordre de sa rotation associée. Du fait de l'utilisation de l'inversion, la roto-inversion ne conserve pas la chiralité dans l'espace à trois dimensions. Un objet contenant un centre de roto-inversion est achiral.

La roto-inversion d'angle θ autour d'un axe peut aussi être vue comme la composée d'une rotation d'angle θ−180° autour du même axe et d'une réflexion par rapport à un plan miroir perpendiculaire à l'axe et contenant le centre d'inversion. Pour cette raison, cette opération est aussi appelée « roto-réflexion ». Il faut cependant faire attention à l'angle utilisé : une roto-réflexion d'angle θ est une roto-inversion d'angle θ+180°. La décomposition de cette opération de symétrie en rotation et réflexion est plus utilisée en chimie.

La roto-inversion n'existe pas dans l'espace bidimensionnel.

Représentation graphique des éléments de symétrie

Les symboles pour la représentation graphique des éléments de symétrie ont été standardisés dans les tables internationales de cristallographie^[1] et sont rassemblés dans le tableau ci-dessous. Ces symboles sont utilisés dans le cas où l'axe de rotation ou de roto-inversion est perpendiculaire au plan du dessin, lorsque l'on projette les éléments de symétrie d'un objet sur un plan. Il existe d'autres symboles correspondant à des orientations différentes des axes, que nous verrons dans le chapitre sur les groupes d'espace. Nous utiliserons pour l'instant ces symboles indépendamment de l'orientation des axes.

Ulrich Müller de l'université de Marbourg en Allemagne a mis au point une police de caractères permettant d'utiliser les symboles graphiques des éléments de symétrie dans des programmes de traitement de texte comme Microsoft Word ou LaTeX, téléchargeable gratuitement sur le site de l'Union internationale de cristallographie^[2].

n = 360/θ	1	2	3	4	6
Rotations	1	2	3	4	6
Rotations
Roto-inversions	${\bar {1}}$	$m\equiv {\bar {2}}$	${\bar {3}}$	${\bar {4}}$	${\bar {6}}$
Roto-inversions

Position générale, position spéciale

À partir des éléments de symétrie définis plus haut, on distingue deux types de positions pour un point appartenant à un objet symétrique :

un point est en « position générale » s'il n'appartient à aucun élément de symétrie ponctuelle de l'objet : l'application des opérations de symétrie de l'objet sur ce point produit un point image sur une autre position, elle aussi générale ;
un point est en « position spéciale » si il est situé sur un élément de symétrie ponctuelle : l'application de l'opération de symétrie attachée à l'élément de symétrie laisse ce point invariant, le point image est alors confondu avec le point de départ.

Symétrie ponctuelle et réseaux

Dans un cristal, la symétrie ponctuelle de la maille doit être compatible avec les opérations de translation du réseau. Il existe une infinité d'opérations de rotation, mais seulement quelques unes s'accordent avec un réseau, ce que nous verrons en démontrant le théorème de restriction cristallographique. Ces opérations de symétrie sont les « opérations de symétrie cristallographiques ». La symétrie ponctuelle de la maille détermine le système cristallin du réseau. En particulier, l'orientation des éléments de symétrie dans la maille permet de définir des « directions de symétrie » qui seront utilisées pour l'écriture des groupes ponctuels de symétrie dans la notation de Hermann-Mauguin. Certaines opérations de symétrie ne peuvent exister que dans certains systèmes cristallins. Leurs écritures matricielles dépendent du système cristallin choisi. À partir de la représentation matricielle des opérations de symétrie, il est possible de les classer en fonction de leurs propriétés, qui sont indépendantes du système cristallin.

Théorème de restriction cristallographique

Ce théorème ne concerne que les opérations de rotation et de roto-inversion. En effet, la réflexion par rapport à un plan est compatible avec un réseau à partir du moment où au moins deux des vecteurs de base sont orthogonaux entre eux, comme dans le réseau bidimensionnel orthorhombique ou le réseau tridimensionnel monoclinique. L'identité et l'inversion sont compatibles avec tout réseau. Les restrictions de réseau sur les opérations de rotation sont alors les mêmes que sur les opérations de roto-inversion.

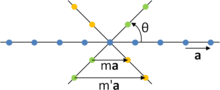
Nous considérons un réseau bidimensionnel quelconque, de vecteurs de base a et b. Dans la figure ci-contre, on se concentre sur la rangée réticulaire [10], le long de laquelle les nœuds du réseau sont équidistants de a.

Soit une opération de rotation d'angle θ autour d'un point. L'ordre de la rotation est n=360/θ. Cette rotation est une opération de symétrie du réseau si l'image d'un nœud par la rotation est aussi un nœud du réseau. L'image de la rangée réticulaire [10] par la rotation est dans ce cas une autre rangée réticulaire, représentée en vert dans la figure. Les nœuds de la rangée image sont également équidistants de a.

D'autre part, la rotation inverse d'angle −θ est aussi une opération de symétrie du réseau car toute rotation est un élément générateur d'un groupe (voir plus loin). L'image de la rangée réticulaire [10] par la rotation inverse est la rangée réticulaire représentée en orange dans la figure, dans laquelle les nœuds sont équidistants de a.

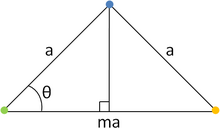
Si le centre de la rotation est un élément de symétrie du réseau, il existe une infinité de centres de rotation qui sont des éléments de symétrie du réseau, par l'application de la translation de vecteur a. La rotation d'angle θ et sa rotation inverse définissent ainsi des rangées réticulaires parallèles à [10]. Afin de garder la symétrie de réseau par les translations de vecteurs nb, les nœuds de ces rangées parallèles doivent aussi être équidistants de a. La distance entre deux nœuds quelconques d'une rangée parallèle est alors un multiple de a : ma, m'a, etc. Cette situation est décrite par la deuxième figure. Dans le triangle isocèle de côtés a, a et ma ainsi obtenu, on trouve la relation :

\cos {\theta }={\frac {{\frac {1}{2}}ma}{a}}={\frac {m}{2}},

où m est un nombre entier. La fonction cosinus donnant des valeurs comprises entre −1 et +1, cette relation implique que seuls cinq ordres de rotation sont compatibles avec les translations de réseau, résumés dans le tableau ci-dessous.

m	–2	–1	0	1	2
cos θ	–1	–1/2	0	1/2	1
θ	180°	± 120°	± 90°	± 60°	360°
n	2	3	4	6	1

Il est démontrable que ces restrictions sur les ordres des rotations sont les mêmes dans l'espace bidimensionnel et dans l'espace tridimensionnel. Par contre, cela n'est plus vrai dans des espaces de dimension supérieure.


Théorème de restriction cristallographique
Dans les espaces à deux et à trois dimensions, les seules rotations et roto-inversions compatibles avec les translations de réseau sont celles d'ordre 1, 2, 3, 4 et 6.

Le théorème de restriction cristallographique n'est valable que pour les réseaux. Le motif d'un cristal peut très bien avoir une symétrie ponctuelle quelconque, comme une rotation d'ordre 5 par exemple, mais l'arrangement des motifs à l'intérieur du cristal respecte la restriction sur les rotations. Par contre, les quasi-cristaux possèdent des symétries interdites par le théorème de restriction cristallographique mais ils ne possèdent pas de symétrie de translation et donc pas de réseau : il est impossible de définir une maille pour un quasi-cristal.

Motif de symétrie d'ordre 5 dans un réseau.
Structure d'un quasi-cristal.
Quasi-cristal : alliage Ho-Mg-Zn.

Systèmes réticulaires, systèmes cristallins et directions de symétrie

Nous allons revoir les notions de systèmes réticulaires et cristallins introduites dans le chapitre sur les translations de réseau à la lumière des opérations de symétrie présentées ici. Un cristal peut posséder d'autres symétries, celles à composante translatoire, qui seront vues dans un autre chapitre. Les résultats généraux donnés ici ne changent cependant pas en les prenant en compte.

Une opération de symétrie compatible avec les opérations de translation du réseau laisse le réseau invariant. Cela est vrai pour les nœuds du réseau et aussi pour ses vecteurs de base. Les opérations de symétrie imposent donc des restrictions sur les paramètres de la maille conventionnelle du réseau. Dans le reste de cette section, nous nous intéresserons aux éléments de symétrie caractéristiques des systèmes cristallins, c'est-à-dire ceux qui sont nécessaires pour les définir. La symétrie du réseau cristallin n'est pas forcément la symétrie du cristal car le motif à l'intérieur de la maille peut briser sa symétrie. Par exemple, tout réseau tridimensionnel est centrosymétrique : pour chaque vecteur de base a, b et c existent les vecteurs opposés −a, −b et −c. L'arrangement des atomes dans un cristal n'est lui pas toujours centrosymétrique : la présence d'un atome à la position (x,y,z) n'est pas forcément accompagnée par celle d'un même atome à la position (−x,−y,−z). Cependant, un cristal appartenant à un système cristallin particulier possède au moins les éléments de symétrie nécessaires à la définition du système cristallin.


Définition
Une direction de symétrie d'un cristal est une direction de son réseau dans laquelle il existe un élément de symétrie. Si il s'agit d'un axe de rotation, la direction de symétrie est parallèle à l'axe ; si il s'agit d'un plan miroir, elle lui est perpendiculaire.

Réseaux bidimensionnels

Les opérations de symétrie ponctuelle que l'on peut rencontrer dans un cristal bidimensionnel sont l'identité, la réflexion par rapport à une droite et les rotations d'ordre 2, 3, 4 et 6 autour d'un point.

Maille monoclinique
Maille orthorhombique
Maille tétragonale
Maille hexagonale

La maille d'un cristal monoclinique a pour paramètres a≠b et γ quelconque. Le réseau ne peut donc pas contenir de centre de rotation d'ordre supérieur à 2, car dans ce cas les vecteurs a et b devraient être de même longueur. D'autre part, il n'est pas possible de trouver une droite miroir dans le réseau, car cela conduirait à des vecteurs a et b orthogonaux. Les seuls éléments de symétrie possibles dans le système monoclinique sont donc l'identité et la rotation d'ordre 2. Le centre de la rotation étant un point, le réseau monoclinique ne possède pas de direction de symétrie privilégiée dans le plan. La seule « direction » de symétrie du cristal est celle perpendiculaire au plan et contenant le centre de la rotation d'ordre 2, si il existe.


Définition
Par convention, la première direction de symétrie d'un réseau bidimensionnel est celle qui est orthogonale au réseau.

La présence d'une droite miroir perpendiculaire à l'un des deux vecteurs de base du réseau conduit à des angles de 90°. Un réseau contenant une droite miroir est donc forcément au moins orthorhombique, mais il peut aussi être tétragonal ou hexagonal (dans le réseau hexagonal, les directions [10] et [12] sont orthogonales par exemple).

La maille d'un cristal orthorhombique a pour paramètres a≠b et γ=90°. L'angle entre a et b étant exactement 90°, le réseau orthorhombique doit forcément contenir au moins une droite miroir, perpendiculaire à l'un des vecteurs de base. Les éléments de symétrie compatibles avec un réseau monoclinique le sont aussi avec un réseau orthorhombique. Comme dans tout réseau bidimensionnel, la première direction de symétrie est celle perpendiculaire au plan. La deuxième direction de symétrie est perpendiculaire à la droite miroir ; par convention, il s'agit de la direction [10] dans le système orthorhombique. La troisième direction de symétrie est alors [01], perpendiculairement à laquelle il peut se trouver une autre droite miroir.

La présence d'un centre de rotation d'ordre 4 dans un réseau se traduit par des paramètres de maille a et b égaux et un angle γ de 90°. Cette situation ne se rencontre que dans le système tétragonal (dans le réseau hexagonal, on a bien a=b, mais γ=120° ; les directions [10] et [12] du réseau hexagonal sont orthogonales, mais leurs vecteurs primitifs ne sont pas de même longueur). Le système cristallin tétragonal est caractérisé par la présence d'un centre de rotation d'ordre 4. Les éléments de symétrie compatibles avec un réseau orthorhombique le sont aussi avec un réseau tétragonal. Les directions de symétrie du système tétragonal sont différentes de celles du système orthorhombique : les vecteurs de base a et b étant équivalents par la rotation d'ordre 4, les directions [10] et [01] le sont aussi. À tout élément de symétrie trouvé dans la deuxième direction de symétrie [10] correspond un élément de même symétrie dans la direction [01]. Par exemple, si une droite miroir est perpendiculaire à a dans un cristal tétragonal, alors il existe une droite miroir perpendiculaire à b. La deuxième direction de symétrie s'écrit <10> pour montrer qu'il s'agit d'une famille de directions équivalentes. D'autre part, comme a=b, il est aussi possible d'avoir une droite miroir perpendiculaire à la direction [11]. La troisième direction de symétrie du système tétragonal est la direction <11>.

Les rotations d'ordre 3 et 6 sont les seules qui conduisent aux paramètres a=b et γ=120° de la maille hexagonale. Un réseau hexagonal possède au moins un centre de rotation d'ordre 3, il peut aussi posséder un centre de rotation d'ordre 6. Les éléments de symétrie compatibles avec un réseau monoclinique le sont aussi avec un réseau hexagonal. La deuxième direction de symétrie du système hexagonal est la direction <10>, perpendiculairement à laquelle peut se trouver une droite miroir. La troisième direction de symétrie est la direction <12>. La famille de directions <10> contient trois directions équivalentes par symétrie, comme la famille <12>.

Le tableau suivant résume les directions de symétrie des systèmes cristallins bidimensionnels et les éléments de symétrie qui peuvent s'y trouver. Les éléments écrits en gras sont ceux qui définissent le système cristallin, les autres peuvent éventuellement s'y ajouter.

Système cristallin	Directions de symétrie
Système cristallin	1^ère direction	2^ème direction	3^ème direction
Monoclinique	centre de rotation d'ordre 2, identité	-	-
Orthorhombique	centre de rotation d'ordre 2, identité	[10] : droite miroir, identité	[01] : droite miroir, identité
Tétragonal	centre de rotation d'ordre 4	<10> : droite miroir, identité	<11> : droite miroir, identité
Hexagonal	centre de rotation d'ordre 3 ou 6	<10> : droite miroir, identité	<21> : droite miroir, identité

Réseaux tridimensionnels

Dans l'espace à trois dimensions, la première direction de symétrie est généralement celle selon laquelle on trouve les éléments de symétrie d'ordre le plus grand. Il serait très fastidieux de reprendre la discussion dans le cas des réseaux bidimensionnels à trois dimensions. Le tableau suivant résume les directions de symétrie des systèmes cristallins tridimensionnels avec les éléments de symétrie ponctuelle que l'on peut y rencontrer :

axes de rotation d'ordre 1 (identité), 2, 3, 4 et 6 ;
axes de roto-inversion d'ordre 1 (inversion), 2 (réflexion), 3, 4 et 6.

Si une rotation d'ordre n est compatible avec un système cristallin, la roto-inversion d'ordre n l'est aussi. Pour simplifier le tableau, seul l'ordre des opérations est indiqué. Les éléments écrits en gras sont ceux qui définissent le système cristallin, les autres peuvent éventuellement s'y ajouter.

Système cristallin		Directions de symétrie
Système cristallin		1^ère direction	2^ème direction	3^ème direction
Triclinique		- : 1	- : 1	- : 1
Monoclinique		[010] : 2, 1	- : 1	- : 1
Orthorhombique		[100] : 2, 1	[010] : 2, 1	[001] : 2, 1
Tétragonal		[001] : 4, 2, 1	<100> : 2, 1	<110> : 2, 1
Trigonal	Maille rhomboédrique	[111] : 3, 1	$<1{\bar {1}}0>$ : 2, 1	- : 1
Trigonal	Maille hexagonale	[001] : 3, 1	<100> : 2, 1	- : 1
Hexagonal		[001] : 6, 2, 1	<100> : 2, 1	<210> : 2, 1
Cubique		[100] : 4, 2, 1	<111> : 3, 1	<110> : 2, 1

Le système triclinique ne possède pas de direction de symétrie, l'opération de symétrie maximum compatible est l'inversion.

Le système monoclinique se caractérise par une seule direction de symétrie, le long de laquelle peuvent se trouver un axe de rotation d'ordre 2, un plan miroir ou les deux.

Le système orthorhombique possède trois directions de symétrie perpendiculaires entre elles, le long desquelles se trouvent au moins un axe de rotation d'ordre 2 ou un plan miroir.

Le système tétragonal est caractérisé par la présence d'un axe de rotation d'ordre 4. Dans les autres directions de symétrie ne peuvent se trouver que des éléments de symétrie d'ordre maximal 2.

Le système trigonal ne possède que deux directions de symétrie, dont la première contient un axe de rotation d'ordre 3. La deuxième direction de symétrie ne peut contenir que des éléments de symétrie d'ordre maximal 2.

Le système hexagonal se caractérise par la présence d'un axe de rotation d'ordre 6. Dans les autres directions de symétrie ne peuvent se trouver que des éléments de symétrie d'ordre maximal 2.

Le système cubique possède quatre directions équivalentes <111> le long desquelles se trouve un axe de symétrie d'ordre 3. Il se distingue ainsi du système trigonal pour lequel l'axe d'ordre 3 n'existe que dans la seule direction [111] (maille rhomboédrique) ou [001] (maille hexagonale). La première direction de symétrie est celle qui peut contenir un axe de symétrie d'ordre 4 : il s'agit de la direction <100>. L'axe de rotation d'ordre 3 est parallèle à la deuxième direction de symétrie <111>. Dans la troisième direction de symétrie ne peuvent se trouver que des éléments de symétrie d'ordre maximal 2. La direction <100> n'est pas forcément celle qui contient les éléments de plus haute symétrie : en effet, si un axe de roto-inversion d'ordre 3 est présent le long de <111>, sa symétrie associée est plus élevée que la rotation d'ordre 4 le long de <100> (voir la section ordre d'un groupe du chapitre suivant).

Maille et symétrie

La présence d'éléments de symétrie ponctuelle dans le réseau impose des conditions sur le système cristallin et donc sur les paramètres de maille d'un cristal. L'inverse n'est pas vrai : un cristal d'un système cristallin donné peut avoir des paramètres de maille correspondant à ceux d'un système cristallin de symétrie supérieure.

Par exemple, il est possible d'avoir un cristal monoclinique de paramètres de maille a≠b≠c et α=β=γ=90° : l'orthogonalité des trois vecteurs de base est alors « accidentelle » et la symétrie de la structure atomique dans le cristal est monoclinique. Très souvent, une telle maille mimant une symétrie supérieure de celle du cristal indique une « pseudo-symétrie » : seulement quelques détails dans la structure d'un cristal dévient de la symétrie supérieure. Cela peut être le cas lorsque l'on étudie la structure du cristal près d'une transition de phase : une faible élévation de la température amène alors le cristal dans la symétrie supérieure. Si c'est le cas, il n'est pas rare d'observer la présence de macles en-dessous de la température de transition de phase dans le cristal.

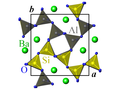
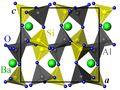
Parmi les structures publiées dans la littérature scientifique, on peut citer la paracelsiane^[3], un minéral rare de formule chimique BaAl₂Si₂O₈, de système cristallin monoclinique et de paramètres de maille a=9,065 Å, b=9,568 Å, c=8,578 Å et β=90°. Les images ci-dessous montrent la structure cristalline de la paracelsiane à température ambiante, projetée le long des trois directions [001], [010] et [100], respectivement. Les atomes de baryum sont représentés en vert, ceux de silicium en jaune, ceux d'aluminium en gris et ceux d'oxygène en bleu (il s'agit de couleurs arbitraires pas forcément utilisées en chimie). Les atomes de silicium et d'aluminium sont entourés par quatre atomes d'oxygène et sont pour cette raison représentés avec leurs polyèdres de coordination. La maille conventionnelle du cristal est indiquée en noir.

Structure cristalline de la paracelsiane
Projection dans le plan (a,b).
Projection dans le plan (a,c).
Projection dans le plan (b,c).

Écriture matricielle des opérations de symétrie

Nous allons maintenant nous intéresser à la représentation matricielle des opérations de symétrie ponctuelle dont l'élément de symétrie passe par l'origine. Connaissant les directions de symétrie des différents systèmes réticulaires, il n'est nécessaire de considérer que quelques cas. Seules les opérations de l'espace tridimensionnel sont traitées, celles pour l'espace bidimensionnel s'en déduisent facilement.

Si le point P de coordonnées (x,y,z) a pour image par une opération de symétrie le point P' de coordonnées (x',y',z'), la transformation s'écrit

{\begin{bmatrix}x'\\y'\\z'\end{bmatrix}}=\mathbf {M} {\begin{bmatrix}x\\y\\z\end{bmatrix}}={\begin{bmatrix}M_{11}&M_{12}&M_{13}\\M_{21}&M_{22}&M_{23}\\M_{31}&M_{32}&M_{33}\end{bmatrix}}{\begin{bmatrix}x\\y\\z\end{bmatrix}}

où M est la représentation matricielle de l'opération de symétrie.

Les écritures matricielles de l'identité et de l'inversion ne dépendent pas du système de coordonnées choisi :

{\begin{array}{ll}\mathbf {M} _{1}={\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}},&\mathbf {M} _{\bar {1}}={\begin{bmatrix}-1&0&0\\0&-1&0\\0&0&-1\end{bmatrix}}.\end{array}}

Rotations

Rotation d'ordre 2

Dans les systèmes orthorhombique, tétragonal et cubique, une rotation d'ordre 2 d'axe parallèle à un des vecteurs de base s'écrit :

{\begin{array}{lll}\mathbf {M} _{2}^{[100]}={\begin{bmatrix}1&0&0\\0&-1&0\\0&0&-1\end{bmatrix}},&\mathbf {M} _{2}^{[010]}={\begin{bmatrix}-1&0&0\\0&1&0\\0&0&-1\end{bmatrix}},&\mathbf {M} _{2}^{[001]}={\begin{bmatrix}-1&0&0\\0&-1&0\\0&0&1\end{bmatrix}}.\end{array}}

Dans le système monoclinique, il n'existe que la rotation d'axe parallèle à [010]. Il s'agit d'une écriture matricielle en blocs : seules les composantes d'un vecteur non parallèles à l'axe de rotation sont changées par l'application de la rotation.

La matrice d'une rotation d'ordre 2 et d'axe parallèle à un des vecteurs de base du plan (001) est différente dans le système réticulaire hexagonal, car les vecteurs de base a et b ne sont pas orthogonaux. Les directions [100], [010] et [110] étant équivalentes, on a :

{\begin{array}{lll}\mathbf {M} _{2}^{[100]}={\begin{bmatrix}1&-1&0\\0&-1&0\\0&0&-1\end{bmatrix}},&\mathbf {M} _{2}^{[010]}={\begin{bmatrix}-1&0&0\\-1&1&0\\0&0&-1\end{bmatrix}},&\mathbf {M} _{2}^{[110]}={\begin{bmatrix}0&1&0\\1&0&0\\0&0&-1\end{bmatrix}}.\end{array}}

Dans les systèmes tétragonal et cubique, il peut se trouver un axe de rotation d'ordre 2 dans la direction <110> (correspondant à la diagonale d'une face carrée de la maille) :

{\begin{array}{ll}\mathbf {M} _{2}^{[110]}={\begin{bmatrix}0&1&0\\1&0&0\\0&0&-1\end{bmatrix}},&\mathbf {M} _{2}^{[1{\bar {1}}0]}={\begin{bmatrix}0&-1&0\\-1&0&0\\0&0&-1\end{bmatrix}},\end{array}}

{\begin{array}{ll}\mathbf {M} _{2}^{[101]}={\begin{bmatrix}0&0&1\\0&-1&0\\1&0&0\end{bmatrix}},&\mathbf {M} _{2}^{[10{\bar {1}}]}={\begin{bmatrix}0&0&-1\\0&-1&0\\-1&0&0\end{bmatrix}},\end{array}}

{\begin{array}{ll}\mathbf {M} _{2}^{[011]}={\begin{bmatrix}-1&0&0\\0&0&1\\0&1&0\end{bmatrix}},&\mathbf {M} _{2}^{[01{\bar {1}}]}={\begin{bmatrix}-1&0&0\\0&0&-1\\0&-1&0\end{bmatrix}}.\end{array}}

Seules les deux premières rotations sont compatibles avec le système tétragonal, les quatre autres n'existent que dans le système cubique.

Dans le système réticulaire hexagonal, la troisième direction de symétrie <210> peut aussi contenir un axe de rotation d'ordre 2 :

{\begin{array}{lll}\mathbf {M} _{2}^{[210]}={\begin{bmatrix}1&0&0\\1&-1&0\\0&0&-1\end{bmatrix}},&\mathbf {M} _{2}^{[120]}={\begin{bmatrix}-1&1&0\\0&1&0\\0&0&-1\end{bmatrix}},&\mathbf {M} _{2}^{[{\bar {1}}10]}={\begin{bmatrix}0&-1&0\\-1&0&0\\0&0&-1\end{bmatrix}}.\end{array}}

Enfin, la matrice d'une rotation d'ordre 2 d'axe parallèle à la deuxième direction de symétrie $<1{\bar {1}}0>$ dans le système réticulaire rhomboédrique s'écrit :

{\begin{array}{lll}\mathbf {M} _{2}^{[1{\bar {1}}0]}={\begin{bmatrix}0&-1&0\\-1&0&0\\0&0&-1\end{bmatrix}},&\mathbf {M} _{2}^{[10{\bar {1}}]}={\begin{bmatrix}0&0&-1\\0&-1&0\\-1&0&0\end{bmatrix}},&\mathbf {M} _{2}^{[01{\bar {1}}]}={\begin{bmatrix}-1&0&0\\0&0&-1\\0&-1&0\end{bmatrix}}.\end{array}}

Ces trois dernières matrices sont identiques à celles du système cubique.

Le déterminant de la matrice d'une rotation d'ordre 2 est toujours égal à 1 ; sa trace est aussi invariante et vaut −1.


Généralisation
Le déterminant et la trace de la matrice d'une opération de symétrie ne dépendent pas de la position ou de l'orientation de son élément de symétrie.

Rotation d'ordre 3

Dans le système réticulaire hexagonal, les rotations d'ordre 3 sont d'axe parallèle à la première direction de symétrie [001]. La représentation matricielle d'une rotation d'ordre 3 d'axe passant par l'origine est :

\mathbf {M} _{3}^{[001]}={\begin{bmatrix}0&-1&0\\1&-1&0\\0&0&1\end{bmatrix}}.

L'écriture matricielle d'une rotation d'ordre 3 parallèle à la première direction de symétrie [111] dans le système réticulaire rhomboédrique est :

\mathbf {M} _{3}^{[111]}={\begin{bmatrix}0&0&1\\1&0&0\\0&1&0\end{bmatrix}}.

Dans le système cubique, les axes des rotations d'ordre 3 sont parallèles aux quatre diagonales de la maille, c'est-à-dire aux quatre directions <111> qui constituent la deuxième direction de symétrie :

{\begin{array}{lr}\mathbf {M} _{3}^{[111]}={\begin{bmatrix}0&0&1\\1&0&0\\0&1&0\end{bmatrix}},&\mathbf {M} _{3}^{[{\bar {1}}1{\bar {1}}]}={\begin{bmatrix}0&0&1\\-1&0&0\\0&-1&0\end{bmatrix}},\\[4ex]\mathbf {M} _{3}^{[1{\bar {1}}{\bar {1}}]}={\begin{bmatrix}0&0&-1\\-1&0&0\\0&1&0\end{bmatrix}},&\mathbf {M} _{3}^{[{\bar {1}}{\bar {1}}1]}={\begin{bmatrix}0&0&-1\\1&0&0\\0&-1&0\end{bmatrix}}.\end{array}}

On remarque en particulier que la matrice de la rotation d'ordre 3 d'axe parallèle à [111] est identique dans les systèmes réticulaires rhomboédrique et cubique. En effet, une maille rhomboédrique peut être vue comme une maille cubique qui a été déformée par compression ou étirement le long d'une de ses diagonales : la symétrie le long de cette diagonale reste inchangée par la déformation.

Le déterminant d'une matrice d'une rotation d'ordre 3 est égal à 1 ; sa trace vaut 0.

Rotation d'ordre 4

Les rotations d'ordre 4 sont d'axe parallèle à la première direction de symétrie dans les systèmes tétragonal et cubique. Il s'agit de la direction [001] dans le système tétragonal et des directions équivalentes [100], [010] et [001] dans le système cubique.

{\begin{array}{lll}\mathbf {M} _{4}^{[001]}={\begin{bmatrix}0&-1&0\\1&0&0\\0&0&1\end{bmatrix}},&\mathbf {M} _{4}^{[010]}={\begin{bmatrix}0&0&1\\0&1&0\\-1&0&0\end{bmatrix}},&\mathbf {M} _{4}^{[001]}={\begin{bmatrix}0&-1&0\\1&0&0\\0&0&1\end{bmatrix}}.\end{array}}

Le déterminant d'une matrice d'une rotation d'ordre 4 est égal à 1 ; sa trace vaut 1.

Rotation d'ordre 6

La rotation d'ordre 6 ne se rencontre que dans le système cristallin hexagonal, avec un axe de rotation parallèle à la direction [001]. Sa représentation matricielle est

\mathbf {M} _{6}^{[001]}={\begin{bmatrix}1&-1&0\\1&0&0\\0&0&1\end{bmatrix}}.

Le déterminant de la matrice d'une rotation d'ordre 6 est égal à 1 ; sa trace vaut 2.

Composition d'opérations de symétrie

Deux opérations de symétrie a et b sont composées si elles sont effectuées l'une après l'autre. Pour trouver la représentation matricielle M_ba de la composition de deux opérations a et b, il suffit d'effectuer le produit des deux matrices M_a et M_b en respectant l'ordre dans lequel les opérations sont effectuées :

\mathbf {M} _{ba}=\mathbf {M} _{a}\cdot \mathbf {M} _{b}.

Les opérations de symétrie ne commutent généralement pas. Il faut faire attention à l'ordre des matrices lorsque l'on compose plusieurs opérations de symétrie. Par exemple, dans le système réticulaire hexagonal, si on effectue d'abord une rotation d'ordre 3, d'axe [001], et ensuite une rotation d'ordre 2, d'axe [100], la matrice de la composition s'écrit

\mathbf {M} _{2}^{[100]}\cdot \mathbf {M} _{3}^{[001]}={\begin{bmatrix}1&-1&0\\0&-1&0\\0&0&-1\end{bmatrix}}\cdot {\begin{bmatrix}0&-1&0\\1&-1&0\\0&0&1\end{bmatrix}}={\begin{bmatrix}-1&0&0\\-1&1&0\\0&0&-1\end{bmatrix}}=\mathbf {M} _{2}^{[010]}.

Si on effectue d'abord la rotation d'ordre 2 et ensuite celle d'ordre 3, la matrice de la composition s'écrit

\mathbf {M} _{3}^{[001]}\cdot \mathbf {M} _{2}^{[100]}={\begin{bmatrix}0&-1&0\\1&-1&0\\0&0&1\end{bmatrix}}\cdot {\begin{bmatrix}1&-1&0\\0&-1&0\\0&0&-1\end{bmatrix}}={\begin{bmatrix}0&1&0\\1&0&0\\0&0&-1\end{bmatrix}}=\mathbf {M} _{2}^{[110]}.

Non-commutativité de rotations d'axes différents.

On obtient dans les deux cas des résultats différents. La composition consistant à effectuer une rotation d'ordre 3 d'axe [001] suivie d'une rotation d'ordre 2 d'axe [100] est équivalente à une rotation d'ordre 2 d'axe [010] ; le changement de l'ordre de ces deux opérations conduit à une rotation d'ordre 2 d'axe [110].

Les opérations de rotation d'axes différents ne commutent pas. Ceci est illustré dans la figure ci-contre, où l'on voit que la rotation successive d'un objet de 90° autour de l'axe x puis autour de l'axe y est différente de la rotation successive autour de l'axe y puis autour de l'axe x.

Par contre, les rotations autour d'un même axe commutent : la composée d'une rotation d'angle θ₁ autour d'un axe et d'une rotation d'angle θ₂ autour du même axe est une rotation d'angle θ₁+θ₂ autour de cet axe.

Parmi les compositions d'opérations de symétrie, certaines sont particulièrement importantes :

la composition d'une rotation d'ordre 2 et d'une réflexion de plan miroir perpendiculaire à l'axe de rotation est l'inversion. En effet, la roto-inversion d'ordre 2, équivalente à une réflexion, est par définition la composée d'une rotation d'ordre 2 et d'une inversion. Un objet contenant un axe de rotation d'ordre 2 perpendiculaire à un plan miroir est donc toujours centrosymétrique ;
la composition d'une rotation d'ordre 3 et d'une réflexion de plan miroir perpendiculaire à l'axe de rotation est une roto-inversion d'ordre 6 ;
la droite d'intersection de deux plans miroirs orthogonaux est un axe de rotation d'ordre 2 ;
la droite d'intersection de trois plans miroirs tautozonaux formant des angles de 60° entre eux est un axe de rotation d'ordre 3 ;
la droite d'intersection de quatre plans miroirs tautozonaux formant des angles de 45° entre eux est un axe de rotation d'ordre 4 ;
la droite d'intersection de six plans miroirs tautozonaux formant des angles de 30° entre eux est un axe de rotation d'ordre 6 ;
si un axe de rotation d'ordre n est contenu dans un plan miroir, alors il existe :
- au moins n/2 plans miroirs tautozonaux qui s'intersectent le long de l'axe de rotation si n est pair : ces plans forment un angle de 360/n entre eux ; l'axe de zone est l'axe de la rotation,
- au moins n plans miroirs tautozonaux qui s'intersectent le long de l'axe de rotation si n est impair : ces plans forment un angle de 180/n entre eux ; l'axe de zone est l'axe de la rotation.

Roto-inversions

Les représentations matricielles des opérations de roto-inversion d'ordre n s'obtiennent en composant la matrice de la rotation d'ordre n avec la matrice de l'inversion. La matrice d'une roto-inversion d'ordre n s'obtient à partir de celle d'une rotation d'ordre n en changeant le signe de toutes ses composantes. L'inversion commute avec toutes les opérations de symétrie.

Par exemple, la matrice d'une roto-inversion d'ordre 3 d'axe parallèle à la direction [001] dans le système réticulaire hexagonal est

\mathbf {M} _{\bar {3}}^{[001]}={\begin{bmatrix}-1&0&0\\0&-1&0\\0&0&-1\end{bmatrix}}\cdot {\begin{bmatrix}0&-1&0\\1&-1&0\\0&0&1\end{bmatrix}}={\begin{bmatrix}0&1&0\\-1&1&0\\0&0&-1\end{bmatrix}}.

Nous avons vu dans le cas des rotations que le déterminant de la matrice représentative est toujours égal à 1. Du fait de la composition avec l'inversion, le déterminant de la matrice représentative d'une roto-inversion est toujours égal à −1 dans l'espace à trois dimensions (en fait, c'est le cas dans tous les espaces de dimension impaire). D'autre part, la trace de la matrice d'une roto-inversion d'ordre n est l'opposé de celle d'une rotation d'ordre n.

Classement des opérations de symétrie

Le déterminant et la trace de la matrice d'une opération de symétrie permet d'identifier la nature de l'opération. Les opérations de symétrie sont classées en fonction de leurs déterminants :

une opération de symétrie de première espèce a un déterminant égal à 1 et conserve la chiralité, il s'agit des rotations pures ;
une opération de symétrie de seconde espèce a un déterminant égal à −1 et ne conserve pas la chiralité, il s'agit des roto-inversions.

Invariants des opérations de symétrie
Opération de symétrie	1^ère espèce					2^ème espèce
Opération de symétrie	1	2	3	4	6	${\bar {1}}$	${\bar {2}}\equiv m$	${\bar {3}}$	${\bar {4}}$	${\bar {6}}$
Déterminant	1	1	1	1	1	−1	−1	−1	−1	−1
Trace	3	−1	0	1	2	−3	1	0	−1	−2

Notes et références

↑ (en) International Tables for Crystallography, vol. A : Space-group symmetry, Theo Hahn, Kluwer Academic Publishers, 2005 (réimpr. corrigée), 5^e éd. (ISBN 978-0-470-68908-0), chap. 1.4 (« Graphical symbols for symmetry elements in one, two and three dimensions »), p. 9
↑ http://www.iucr.org/resources/symmetry-font
↑ anglais G. Chiari, G. Gazzoni, J.R. Craig, G.V. Gibbs, S.J. Louisnathan, « Two independent refinements of the structure of paracelsian », dans American Mineralogist, vol. 70, n^o 9-10, 1985, p. 969-974, [lire en ligne]

Projection stéréographique

<<

Cristallographie géométrique

>>

Groupes ponctuels de symétrie

[1] (en) International Tables for Crystallography, vol. A : Space-group symmetry, Theo Hahn, Kluwer Academic Publishers, 2005 (réimpr. corrigée), 5^e éd. (ISBN 978-0-470-68908-0), chap. 1.4 (« Graphical symbols for symmetry elements in one, two and three dimensions »), p. 9

[2] ttp://www.iucr.org/resources/symmetry-font

[3] s G. Chiari, G. Gazzoni, J.R. Craig, G.V. Gibbs, S.J. Louisnathan, « Two independent refinements of the structure of paracelsian », dans American Mineralogist, vol. 70, n^o 9-10, 1985, p. 969-974, [lire en ligne]

[1]

[2]

[3]