Mathc gnuplot/Application : Méthode de Newton
Apparence
Préambule
[modifier | modifier le wikicode]Méthode de Newton dansWikipedia.
Présentation
[modifier | modifier le wikicode]N'oubliez pas les fichiers *.h partagés et ceux de ce chapitre.
Dessiner
[modifier | modifier le wikicode]c01.cCalculer le point d'intersection entre g et h. |
|---|
/* ------------------------------------ */
/* Save as : c01.c */
/* ------------------------------------ */
#include "x_ahfile.h"
#include "f2.h"
/* ------------------------------------ */
int main(void)
{
int n = 5;
double FirstA = 0.5;
clrscrn();
printf(" Use Newton's method to approximate"
" the intersection point of :\n\n");
printf(" g : x-> %s\n\n", geq);
printf(" and\n\n");
printf(" h : x-> %s\n\n", heq);
G_gh(i_WGnuplot(-4,4,-4,4), geq,heq);
printf(" To see the graphs of g and h, open the"
" file \"a_main.plt\" with Gnuplot.\n\n"
" You can see that, the intersection"
" point is between 0.0 and 1.0.\n\n"
" Choose x = %.1f as a first approximation.\n\n",FirstA);
getchar();
clrscrn();
printf(" In fact we want find sin(x) = cos(x)"
" or sin(x) - cos(x) = 0.\n\n"
" We want find a root of\n\n"
" f : x-> %s\n\n", feq);
getchar();
clrscrn();
printf(" As a first approximation x = %.1f \n\n"
" The Newton's method give : \n\n",FirstA);
G_gh_x_0(i_WGnuplot(-4,4,-4,4),
geq,
heq,
g,
Newton_s_Method(FirstA,n,f,Df));
printf("\n\n load \"a_main.plt\" with gnuplot. "
"\n\n Press return to continue");
getchar();
return 0;
}
Le résultat.
Use Newton's method to approximate the intersection point of : g : x-> sin(x) and h : x-> cos(x) . To see the graphs of g and h, open the file "a_main.plt" with Gnuplot. . You can see that, the intersection point is between 0.0 and 1.0. Choose x = 0.5 as a first approximation. In fact we want find sin(x) = cos(x) or sin(x) - cos(x) = 0. We want find a root of . f : x-> sin(x) - cos(x) . As a first approximation x = 0.5 . The Newton's method give : . x[1] = 0.500000000000000 x[2] = 0.793407993026023 x[3] = 0.785397992096516 x[4] = 0.785398163397448 x[5] = 0.785398163397448 . load "a_main.plt" with gnuplot.
| Résultat dans gnuplot |
|---|
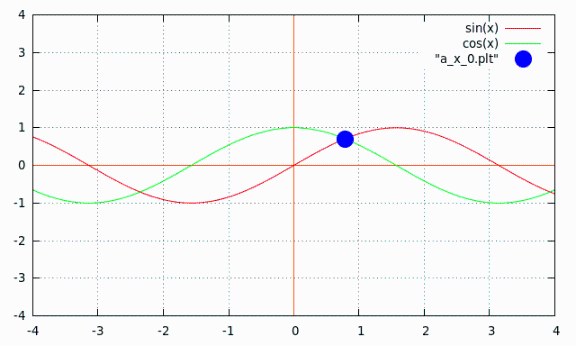
|
Un autre exemple avec :
As a first approximation x = -2.5 . The Newton's method give : . x[1] = -2.500000000000000 x[2] = -2.355194920430497 x[3] = -2.356194490525248 x[4] = -2.356194490192345 x[5] = -2.356194490192345
| Résultat dans gnuplot |
|---|

|
Les fichiers h de ce chapitre
[modifier | modifier le wikicode]x_ahfile.hAppel des fichiers |
|---|
/* ------------------------------------ */
/* Save as : x_ahfile.h */
/* ------------------------------------ */
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>
#include <math.h>
#include <string.h>
/* ------------------------------------ */
#include "xdef.h"
#include "xplt.h"
/* ------------------------------------ */
#include "knewton.h"
#include "kg_gh.h"
f2.hLa fonction à dessiner |
|---|
/* ------------------------------------ */
/* Save as : f2.h */
/* ------------------------------------ */
double g(
double x)
{
return(sin(x));
}
char geq [] = "sin(x)";
/* ------------------------------------ */
double Dg(
double x)
{
return(cos(x));
}
char Dgeq [] = "cos(x)";
/* ------------------------------------ */
/* ------------------------------------ */
double h(
double x)
{
return(cos(x));
}
char heq [] = "cos(x)";
/* ------------------------------------ */
double Dh(
double x)
{
return(- sin(x));
}
char Dheq [] = "- sin(x)";
/* ------------------------------------ */
/* ------------------------------------ */
double f(
double x)
{
return(sin(x) - cos(x));
}
char feq [] = "sin(x) - cos(x)";
/* ------------------------------------ */
double Df(
double x)
{
return(cos(x) + sin(x));
}
char Dfeq [] = "cos(x) + sin(x)";
knewton.hMéthode de Newton |
|---|
/* ------------------------------------ */
/* Save as : knewton.h */
/* ------------------------------------
x_n+1 = x_n - f(x_n)
------
f'(x_n)
------------------------------------ */
double Newton_s_Method(
double x,
int imax,
double (*P_f)(double x),
double (*PDf)(double x)
)
{
int i=1;
for(;i<=imax;i++)
{
printf(" x[%d] = %.15f\n",i,x);
x -= ((*P_f)(x))/((*PDf)(x));
}
return(x);
}
kg_gh.hFonctions graphiques |
|---|
/* ------------------------------------ */
/* Save as : kg_gh.h */
/* ------------------------------------ */
void G_gh(
W_Ctrl w,
char geq[],
char heq[]
)
{
FILE *fp = fopen("a_main.plt","w");
fprintf(fp," set zeroaxis lt 8\n"
" set grid\n\n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f] \\\n"
" %s, \\\n"
" %s \n"
" reset",
w.xmini,w.xmaxi,w.ymini,w.ymaxi,
geq,heq);
fclose(fp);
}
/* ------------------------------------ */
void G_gh_x_0(
W_Ctrl w,
char geq[],
char heq[],
double (*P_g)(double x),
double x_0
)
{
FILE *fp = fopen("a_main.plt","w");
FILE *fq = fopen( "a_x_0.plt","w");
fprintf(fp," set zeroaxis lt 8\n"
" set grid\n"
" plot [%0.3f:%0.3f] [%0.3f:%0.3f] \\\n"
" %s, \\\n"
" %s, \\\n"
" \"a_x_0.plt\" pt 7 ps 3 \n"
" reset",
w.xmini,w.xmaxi,w.ymini,w.ymaxi,
geq,heq);
fclose(fp);
fprintf(fq," %0.6f %0.6f", x_0,(*P_g)(x_0));
fclose(fq);
}

