Mathc gnuplot/Vectorielle : Fonctions récursives
Apparence
Préambule
[modifier | modifier le wikicode]La géométrie de la tortue dans Wikipedia.
Présentation
[modifier | modifier le wikicode]Les fonctions récursives.
Dessiner
[modifier | modifier le wikicode]Un arbre
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c01.cUn arbre |
|---|
/* ------------------------------------ */
/* save as : c01.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_r.h"
/* ------------------------------------ */
double **fun(double **U,double side,double angle);
/* ------------------------------------ */
int main(void)
{
double angle = 90.;
double side = 200.;
double **U = G_main(-150.,150.,-0.,300.);
F_mR(fun(U,angle,side));
printf(" * open the file main.plt with Gnuplot.");
return 0;
}
/* ------------------------------------ */
double **fun(
double **U,
double angle,
double side
)
{
if(side<5)
{
vo(U,angle, side);
vo(U,angle,-side);
return(0);
}
vo(U,angle, side/3.);
angle+=-30;
fun(U,angle,side*2./3.);
angle+= 30;
vo(U,angle, side/6.);
angle+= 25;
fun(U,angle,side/2.);
angle+=-25;
vo(U,angle, side/3.);
angle+= 25;
fun(U,angle,side/2.);
angle+=-25;
vo(U,angle, side/6.);
vo(U,angle, -side);
return(U);
}
| Résultat dans gnuplot |
|---|

|
Un arbre (2)
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c02.cUn arbre (2) |
|---|
/* ------------------------------------ */
/* save as : c02.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_r.h"
/* ------------------------------------ */
double **fun(double **U,
double side,double angle,double tangle);
/* ------------------------------------ */
int main(void)
{
double angle = 90.;
double side = 200.;
double tangle = 90.;
double **U = G_main(-400.,550.,-200.,500.);
F_mR(fun(U,angle,side,tangle));
printf(" * open the file main.plt with Gnuplot.");
return 0;
}
/* ------------------------------------ */
double **fun(
double **U,
double angle,
double side,
double tangle
)
{
if(side<2) return(0);
angle+=-tangle/2.;
vo(U,angle, side);
fun(U,angle,side/1.4,tangle);
vo(U,angle,-side);
angle+=tangle;
vo(U,angle, side);
fun(U,angle,side/2.,tangle);
vo(U,angle,-side);
angle+=-tangle/2.;
return(U);
}
| Résultat dans gnuplot |
|---|
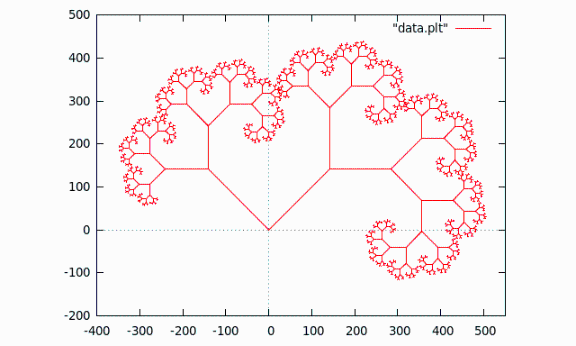
|
Un flocon
[modifier | modifier le wikicode]N'oubliez pas les fichiers h de la librairie.
c03.cUn flocon |
|---|
/* ------------------------------------ */
/* save as : c03.c */
/* ------------------------------------ */
#include "v_a.h"
#include "y_r.h"
/* ------------------------------------ */
double **fun2(double **U,
double angle,double side,double i);
int fun(double **U,
double angle,double side,double i);
/* ------------------------------------ */
int main(void)
{
double angle = 0.;
double side = 100.;
double i = 10.;
double **U = G_main(-120.,20.,-40.,120.);
F_mR(fun2(U,angle,side,i));
printf(" * open the file main.plt with Gnuplot.");
return 0;
}
/* ------------------------------------ */
int fun(
double **U,
double angle,
double side,
double i
)
{
if(i<1)
{
vo(U,angle,side);
return (0);
}
fun(U,angle,side/3.,--i);angle+=-60;
fun(U,angle,side/3.,--i);angle+=120;
fun(U,angle,side/3.,--i);angle+=-60;
fun(U,angle,side/3.,--i);
return (0);
}
/* ------------------------------------ */
double **fun2(
double **U,
double angle,
double side,
double i
)
{
int j;
for(j=3; j>0; --j)
{
angle+=120;fun(U,angle,side,i);
}
return(U);
}
| Résultat dans gnuplot |
|---|

|

