Calcul différentiel et intégral pour débutants

Thierry Dugnolle

Ce livre présente les éléments du calcul différentiel et intégral pour le grand débutant, c'est à dire au niveau d'un lycéen qui aurait peut-être un peu oublié, ou pas toujours compris, les mathématiques du collège.

On peut dire du calcul différentiel qu'il étudie les variations des grandeurs, alors que le calcul intégral étudie des accumulations de grandeurs. Mais ces définitions ne sont pas vraiment éclairantes tant qu'on ne connaît pas la théorie.

L'analyse est la science des systèmes de nombres réels. Analyser veut dire identifier les parties d'un tout et la façon dont elles s'assemblent. L'analyse ultime doit identifier les constituants ultimes. Or tout ce qui est réel peut être représenté par un système de nombres réels. Les nombres réels peuvent donc être considérés comme les constituants ultimes de tout ce qui est réel. C'est pourquoi la science des systèmes de nombres réels peut être appelée l'analyse.

Pour étudier les systèmes de nombres réels, on se sert toujours, ou presque toujours, du calcul des fonctions dérivées et des intégrales. Le calcul différentiel et intégral est le principal outil de l'analyse, à tel point qu'on peut dire qu'il est l'analyse.

Résumé :

Le premier chapitre présente les principaux concepts nécessaires pour aborder l'analyse : la droite $\mathbb {R}$ des nombres réels, les fonctions de $\mathbb {R}$ dans $\mathbb {R}$ et la pente d'une droite.

Le second chapitre entre dans le vif du sujet en définissant la fonction dérivée d'une fonction de $\mathbb {R}$ dans $\mathbb {R}$. Un nombre dérivé est défini géométriquement comme la pente de la tangente à la courbe qui représente la fonction que l'on dérive. Il est défini analytiquement comme la limite du taux de variation de la fonction lorsque l'intervalle de variation tend vers zéro. Le calcul différentiel est le calcul des nombres dérivés.

Le troisième chapitre montre comment définir rigoureusement la limite d'une fonction, ce qui est nécessaire pour définir rigoureusement les nombres dérivés.

Le quatrième chapitre présente les règles les plus élémentaires du calcul différentiel. Elles suffisent pour calculer toutes les fonctions dérivées utilisées dans ce petit livre.

Le cinquième chapitre montre que la vitesse est la fonction dérivée de la position.

Le sixième chapitre définit les intégrales des fonctions de $\mathbb {R}$ dans $\mathbb {R}$ et explique le théorème fondamental de l'analyse, qui montre comment le calcul des dérivées permet de calculer des intégrales.

Le dernier chapitre montre comment le calcul différentiel et intégral permet de prouver la loi de Galilée, que la distance parcourue en chute libre est proportionnelle au carré du temps écoulé depuis un lâcher sans vitesse initiale, et la forme parabolique des trajectoires des projectiles et des jets d'eau.

Préliminaires

La droite( $\mathbb {R}$ )des nombres réels, le plan $\mathbb {R} ^{2}$ et l'espace $\mathbb {R} ^{3}$

$\mathbb {R}$ est l'ensemble des nombres réels. Ce sont tous les nombres positifs qui peuvent servir à mesurer des longueurs, plus les nombres négatifs correspondants, plus le zéro. On peut toujours les écrire comme des nombres à décimales, mais la suite des décimales peut être infinie. Par exemple, $1/3=0.3333333...$

Si on se donne une ligne droite, un point O sur cette droite, que l'on choisit comme origine, un sens (de la gauche vers la droite, ou l'inverse) et une unité de longueur, chaque point de la droite est représenté par un unique nombre réel :

C'est pourquoi $\mathbb {R}$ est parfois appelé la droite des nombres réels. On peut penser à chaque nombre réel comme à un point sur une droite.

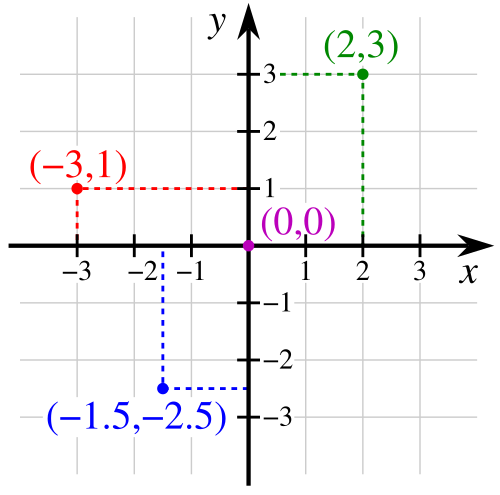
Si on se donne un plan, un point O dans ce plan, que l'on choisit comme origine, deux lignes droites perpendiculaires qui se coupent en O, un sens sur chacune de ces droites et une unité de longueur, chaque point du plan est représenté par un unique couple de nombres réels :

Les deux droites orientées sont appelés des axes, et elles forment un repère cartésien du plan.

L'ensemble de tous les couples de nombres réels est appelé $\mathbb {R} ^{2}$. Comme on peut penser à chaque couple $(x,y)$ de nombres réels comme à un point dans un plan, on dit parfois de $\mathbb {R} ^{2}$ qu'il est un plan. $x$ est parfois appelé l'abscisse et $y$ l'ordonnée du point $(x,y)$.

Si on se donne trois droites mutuellement perpendiculaires, on définit de même un repère cartésien de l'espace à trois dimensions :

On identifie parfois l'espace à l'ensemble $\mathbb {R} ^{3}$ des triplets de nombres réels, parce qu'on peut penser à chaque triplet $(x,y,z)$ de nombres réels comme à un point de l'espace.

Tous les points, qu'ils soient les points d'une droite, d'un plan ou de l'espace peuvent être identifiés par des nombres réels, ou par des couples, ou des triplets de ces nombres. Les figures géométriques, et donc la forme de tous les corps matériels, peuvent toujours être définies comme des ensembles de points, donc comme des ensembles de nombres réels, ou de couples, ou de triplets de nombres réels (et même les quadruplets, et les n-uplets de nombres réels, pour n'importe quel entier positif n, mais c'est plus difficile à comprendre). René Descartes (mathématicien, physicien, biologiste, psychologue, théologien, philosophe... 1596-1650) est le premier à avoir bien compris que la science des figures géométriques est une partie de la science des systèmes de nombres, et à l'avoir clairement expliqué. Cartésien nomme ce qui a été donné par Descartes, ou ce qui est digne de lui.

Plus de deux millénaires avant Descartes, Pythagore (600 avant J-C, environ) a eu la même intuition quand il a affirmé que « tout est nombre ».

Un vecteur est, par définition, quelque chose qui détermine une direction, un sens et une longueur.

Les couples $(x,y)$ (ou les triplets $(x,y,z)$) de nombres réels sont appelés des vecteurs, parce qu'ils déterminent une direction, un sens et une longueur, c'est à dire la direction, le sens et la longueur qui vont de $(0,0)$ à $(x,y)$ (ou de $(0,0,0)$ à $(x,y,z)$) . Même les nombres réels $x$ peuvent être appelés des vecteurs, parce qu'ils déterminent un sens et une longueur sur la droite $\mathbb {R}$ des nombres réels, c'est à dire le sens et la longueur qui vont de $0$ à $x$.

Les fonctions de $\mathbb {R}$ dans $\mathbb {R}$ et leurs représentations graphiques

Les modèles mathématiques de la réalité sont en général définis avec des nombres, ce sont des systèmes de nombres. Parmi les systèmes de nombres, les fonctions de $\mathbb {R}$ dans $\mathbb {R}$ sont parmi les plus élémentaires et les plus importants.

On dit d'une grandeur $y$ qu'elle est fonction d'une grandeur $x$ lorsque la détermination de $x$ suffit pour déterminer $y$. Par exemple, $x$ peut être l'âge d'un enfant et $y$ sa taille (sa hauteur). On écrit alors $y=h(x)$ (qu'il faut lire "h de x") et on dit que la hauteur $h$ est une fonction de l'âge $x$. On dit de $x$ qu'elle est la variable et de $h(x)$ qu'elle est la valeur de la fonction $h$.

Lorsqu'une fonction est définie avec une formule de calcul, il suffit de calculer pour trouver ses valeurs. Si par exemple la fonction $f$ est définie par $f(x)=x^{3}-9x$, on peut calculer un tableau des valeurs de la fonction $f$ :

x	-4	-3	-2	-1	0	1	2	3	4
f(x)	-28	0	10	8	0	-8	-10	0	28

La valeur $f(x)=x^{3}-9x$ de la fonction $f$ est définie pour tout nombre réel $x$. On dit alors que le domaine de définition de $f$ est égal à $\mathbb {R}$ tout entier. Mais ce n'est pas toujours le cas. Par exemple, la fonction $g$ définie par $g(x)=1/x$ n'est pas définie pour $x=0$, parce qu'on ne peut pas diviser par zéro. Le domaine de définition de $g$ est $\mathbb {R}$ privé de zéro, que l'on note $\mathbb {R} ^{*}=\mathbb {R} -\{0\}$.

La représentation graphique, ou le graphe, d'une fonction $f$ de $\mathbb {R}$ dans $\mathbb {R}$ est l'ensemble de tous les points $(x,y)$ tels que $y=f(x)$. On peut dire aussi que c'est l'ensemble de tous les points $(x,f(x))$ pour tous les $x$ dans le domaine de définition de $f$.

Un tableau des valeurs peut aider à tracer la représentation graphique de $f$ :

Mais il faut pour cela calculer $f(x)$ pour de nombreuses valeurs de $x$. Nous verrons que l'étude des variations de $f$ à partir de sa fonction dérivée aide considérablement à tracer sa représentation graphique.

La pente d'une droite

Une fonction $f$ de $\mathbb {R}$ dans $\mathbb {R}$ définie par $f(x)=px+q$ où $p$ et $q$ sont des nombres réels, des constantes, est appelée une fonction affine. Son graphe est une droite, plus ou moins inclinée par rapport à l'horizontale, mais jamais verticale. $p$ mesure cette inclinaison. Nous allons montrer qu'elle est la pente, ou le coefficient directeur, de cette droite.

La pente d'une droite non verticale, tracée dans un repère cartésien, est le rapport ${\frac {\Delta y}{\Delta x}}$ où $\Delta x$ mesure le déplacement dans la direction horizontale, et $\Delta y$ le déplacement dans la direction verticale, d'un point mobile qui reste sur la droite.

Si par exemple une côte oblige à s'élever verticalement de 10 m lorsqu'on avance horizontalement de 100 m, sa pente est de 10%=10/100=0.1. Une côte à 90° par rapport à l'horizontale a une pente de 100 %. On peut dire d'une ligne verticale qu'elle a une pente infinie.

Soient $x_{1}$ et $x_{2}$ deux nombres réels différents. $(x_{1},f(x_{1}))$ et $(x_{2},f(x2))$ sont deux points du graphe de $f$. La droite qui les joint a pour pente ${\frac {f(x_{2})-f(x_{1})}{x_{2}-x_{1}}}$. Si $f$ est définie par $f(x)=px+q$ alors cette pente est égale à :

${\frac {px_{2}+q-(px_{1}+q)}{x_{2}-x_{1}}}={\frac {p(x_{2}-x_{1})}{x_{2}-x_{1}}}=p$

Si $p$ est positif, alors $f$ est croissante : il faut s'élever quand on se déplace sur la droite dans la direction des $x$ positifs.

Si $p$ est négatif, alors $f$ est décroissante : il faut descendre quand on se déplace sur la droite dans la direction des $x$ positifs.

Exercices

• Calculer les valeurs de $f$ définie par $f(x)=x^{2}=x\times x$ pour $x=-2,-1,0,0.5,1,2,3$ et $4$ et représenter graphiquement $f$ sur du papier quadrillé.

• Calculer la pente de la droite qui relie les points $(1,f(1))$ et $(2,f(2))$

Solutions

La fonction dérivée d'une fonction de $\mathbb {R}$ dans $\mathbb {R}$

Définition géométrique

Soit $f$ une fonction de $\mathbb {R}$ dans $\mathbb {R}$. On dit que $f$ est dérivable en $x_{0}$ lorsque le graphe de $f$ admet une tangente au point $(x_{0},f(x_{0}))$. Une tangente est une ligne droite "qui s'ajuste exactement, qui colle" à la courbe au point considéré :

Soit $x$ un nombre différent de $x_{0}$. Lorsque $x$ s'approche de $x_{0}$, la droite qui joint les points $(x_{0},f(x_{0}))$ et $(x,f(x))$ s'approche de plus en plus de la tangente du graphe de $f$ en $x_{0}$ :

Une fonction n'est pas toujours dérivable. Par exemple, soit $f$ la fonction valeur absolue, $f(x)=|x|$, c'est à dire que $f(x)=x$ si $x\geq 0$, et $f(x)=-x$ si $x\leq 0$. Son graphe a un point anguleux :

$f$ n'est pas dérivable en $0$ parce que son graphe n'a pas une unique tangente au point $(0,0)$. Il en a deux, une à gauche et l'autre à droite. Dans ce cas on dit de $f$ qu'elle n'est pas dérivable en $0$, mais qu'elle y est quand même dérivable à gauche, et dérivable à droite.

Lorsque $f$ est dérivable en $x_{0}$, le nombre dérivé de $f$ en $x_{0}$, noté $f'(x_{0})$ ($f'$ se lit f prime), est par définition la pente de la tangente du graphe de $f$ au point $(x_{0},f(x_{0}))$.

$f'$ est la fonction dérivée de $f$. Le domaine de définition de $f'$ est l'ensemble de tous les $x$ où $f$ est dérivable. $f'(x)$ est la pente de la tangente au graphe de $f$ en $x$, lorsqu'elle existe :

Définition analytique

Une définition analytique est une définition avec une formule de calcul.

Pour définir $f'(x_{0})$ avec une formule, on commence par définir le taux de variation $T_{v}$ de $f$ entre $x_{0}$ et $x=x_{0}+\epsilon$ :

$T_{v}(\epsilon )={\frac {f(x)-f(x_{0})}{x-x_{0}}}={\frac {f(x_{0}+\epsilon )-f(x_{0})}{\epsilon }}$

$f'(x_{0})$ est la limite de $T_{v}(\epsilon )$ quand $\epsilon$ tend vers $0$. On peut aussi dire que c'est la limite de $T_{v}$ quand $x$ tend vers $x_{0}$.

$f'(x_{0})=\lim _{\epsilon \to 0}{\frac {f(x_{0}+\epsilon )-f(x_{0})}{\epsilon }}=\lim _{x\to x_{0}}{\frac {f(x)-f(x_{0})}{x-x_{0}}}$

Mais pour bien comprendre cette définition, il faut savoir définir la limite d'une fonction en $x_{0}$, ou en zéro. Cette définition est présentée un peu plus loin.

Pour calculer un nombre dérivé, on calcule la limite du quotient entre deux différences, celle entre $f(x)$ et $f(x_{0})$ d'une part, celle entre $x$ et $x_{0}$ d'autre part. C'est pourquoi on dit du calcul des dérivées qu'il est un calcul des différences, ou qu'il est un calcul différentiel. Il faut entendre par là qu'on calcule des taux de variation.

Les variations d'une fonction dépendent du signe de sa dérivée

Comme $f'(x)$ est la pente de la tangente du graphe de $f$ en $x$, il est positif (strictement, c'est à dire $>0$) si et seulement si $f$ est croissante au voisinage de $x$. Il est négatif ($<0$) si et seulement si $f$ est décroissante au voisinage de $x$.

Si on connaît la fonction dérivée $f'$ d'une fonction $f$, il suffit d'étudier le signe, positif ou négatif, de $f'$ pour connaître le sens de variation de $f$. Cette règle est souvent très utile. Elle permet en particulier de trouver les sommets (les maximums) et les creux (les minimums) de la représentation graphique d'une fonction, parce qu'au voisinage d'un sommet, la fonction est d'abord croissante puis décroissante, tandis qu'au voisinage d'un creux, elle est d'abord décroissante puis croissante. Les extremums sont donc des points où $f'(x)$ change de signe.

Exercices

• Calculer les valeurs de $f$ définie par $f(x)=x^{2}=x\times x$ pour $x=1,2,1.5,1.1$ et $1.01$

• Calculer le taux de variation de $f$ entre $x=1$ et $x=2$, puis entre $x=1$ et $x=1.5$, entre $x=1$ et $x=1.1$ et enfin entre $x=1$ et $x=1.01$

• Calculer le taux de variation de $f$ entre $x$ et $x+\epsilon$ : ${\frac {f(x+\epsilon )-f(x)}{\epsilon }}$

Il faut se souvenir de l'identité remarquable $(a+b)^{2}=a^{2}+2ab+b^{2}$

Quelle est la limite de ce taux de variation quand $\epsilon$ tend vers zéro ? Que vaut cette limite si $x=1$ ?

• Avec les règles du calcul différentiel, présentées au chapitre 4, on peut prouver que la dérivée de $g$ définie par $g(x)=-x^{2}+2x$ est $g'(x)=-2x+2$

Étudier le signe de $g'$ et trouver alors l'extremum de $g$. Est-ce un maximum ou un minimum ?

• La dérivée de $h(x)=x^{3}-9x$ ($h$ a été représentée graphiquement un peu plus haut) est $h'(x)=3x^{2}-9=3(x^{2}-3)$

Étudier le signe de $h'$

Il faut se souvenir de l'identité remarquable $(a+b)(a-b)=a^{2}-b^{2}$ et de $3=({\sqrt {3}})^{2}$

Trouver alors les extremums de $h$

Vérifier les résultats avec la représentation graphique de $h$

Solutions

La continuité et la limite d'une fonction en un point

Ce chapitre est le plus difficile de ce petit livre. Pourtant au commencement il n'en a pas l'air, parce qu'on comprend ce qu'est la limite d'une fonction simplement en comprenant ce qu'est l'extrémité d'une ligne. Cela semble plutôt trivial. Mais la définition logiquement rigoureuse de la limite d'une fonction, la définition en $\epsilon \delta$, est d'une importance fondamentale. Elle va au cœur du sujet. C'est à partir d'elle que les mathématiciens ont pu développer avec des preuves exactes et rigoureuses tout le calcul différentiel et intégral.

Discontinuité et continuité

Soit $H$ la fonction définie par :

• $H(x)=0$ si $x<0$
• $H(0)=1/2$
• $H(x)=1$ si $x>0$

Son graphe est :

$H$ admet deux limites en zéro, une à droite et l'autre à gauche. Quand $x$ tend vers $0$ par valeurs supérieures, $H(x)$ tend vers $1$. Quand $x$ tend vers $0$ par valeurs inférieures, $H(x)$ tend vers $0$. On écrit :

$\lim _{x\to 0,x>0}H(x)=1$

$\lim _{x\to 0,x<0}H(x)=0$

Ces deux limites sont différentes entre elles, et différentes de $H(0)$ parce que $H$ est discontinue en $0$. $H(x)$ fait un saut, de zéro à un, lorsque $x$ passe des valeurs inférieures aux valeurs supérieures à zéro.

Une fonction est continue au point $x_{0}$, par définition, lorsqu'elle admet une unique limite en $x_{0}$ égale à $f(x_{0})$.

Il faut bien sûr définir la limite d'une fonction pour que sa continuité soit ainsi définie. C'est le rôle de la définition en $\epsilon \delta$ présentée ci-dessous.

Soit $f$ la fonction définie par $f(x)=x/x$. $f$ est définie pour tout nombre réel $x$ et est égal à $1$, sauf pour $x=0$, parce qu'on ne peut pas diviser par zéro. Mais $f$ admet quand même une limite en zéro, égale à un. Si on la représente graphiquement, on obtient une fonction constante :

où il faut supprimer le point $(0,1)$, parce que $f(x)$ n'est pas défini pour $x=0$.

$f$ n'est pas continue en $0$, parce qu'elle n'y est pas définie, mais il est facile de la prolonger par continuité, en posant, $f(0)=1$. Elle est alors partout continue.

La définition en $\epsilon \delta$ de la limite d'une fonction

Voici enfin la définition formelle de la limite d'une fonction de $\mathbb {R}$ dans $\mathbb {R}$ :

Une fonction $f$ de $\mathbb {R}$ dans $\mathbb {R}$ admet la limite $L$ quand $x$ tend vers $x_{0}$ si et seulement si :

Pour tout $\epsilon >0$, il existe $\delta >0$ tel que $|x-x_{0}|<\delta$ entraîne $|f(x)-L|<\epsilon$.

Et on écrit alors :

$\lim _{x\to x_{0}}f(x)=L$

Il faut penser à $\epsilon$ comme à un petit nombre positif, proche de zéro. C'est d'ailleurs pour cela qu'on l'appelle $\epsilon$. Exiger que $|f(x)-L|<\epsilon$ revient alors à exiger que $f(x)$ soit très proche de $L$. On demande que $f(x)$ s'approche d'aussi près qu'on le veut de $L$ dès que $x$ s'approche suffisamment de $x_{0}$.

Vérifions que cette définition est en accord avec nos intuitions sur la continuité :

• $H$ peut-elle avoir une limite $L$ en zéro ? Pour cela, il faut que $|H(x)-L|$ s'approche de zéro quand $x$ tend vers zéro, mais si $L$ est différent de zéro et de un, $|H(x)-L|\geq min(|1-L|,|L|)>0$ et ne peut donc pas s'approcher de zéro ($min(a,b)$ est le plus petit des nombres $a$ et $b$).
  Plus formellement, il existe $\epsilon =min(|1-L|,|L|)>0$ tel que $|H(x)-L|>\epsilon$ pour tout $x$. Donc $H$ ne peut pas avoir de limite autre que $0$ ou $1$. Supposons que $L=1$. Alors si $x<0$, $|H(x)-L|=1$ et ne peut pas être plus petit que $\epsilon$ si celui-ci est plus petit que $1$. De même si $L=0$, $|H(x)-L|=1$ lorsque $x>0$ et ne peut pas non plus être plus petit que $\epsilon$. On en conclut que $H$ n'admet pas de limite en zéro.

• Soit $f$ la fonction définie par $f(x)=x/x=1$ pour tout $x\neq 0$. Montrons qu'elle tend vers $1$ quand $x$ tend vers $0$. $|f(x)-1|=0<\epsilon$ pour tout $x\neq 0$ et tout $\epsilon >0$. N'importe quel nombre $\delta >0$ est donc tel que $|x|<\delta$ entraîne $|f(x)-1|<\epsilon$.

Exercices

• La fonction valeur absolue est définie par $|x|=x$ si $x\geq 0$ et $|x|=-x$ si $x\leq 0$

Appelons $f$ cette fonction valeur absolue : $f(x)=|x|$

La règle de la dérivée d'une fonction affine (chapitre suivant) montre que $f'(x)=1$ si $x\geq 0$ et $f'(x)=-1$ si $x\leq 0$

Quelle est la limite de $f'$ à gauche de $0$ ? Et à droite de $0$ ?

$f'$ est-elle continue en $0$ ?

$f$ est-elle dérivable en $0$ ?

Solutions

Règles élémentaires pour le calcul des dérivées

La définition en $\epsilon \delta$ permet de définir rigoureusement les nombres dérivés et donc les fonction dérivées, mais elle est difficile à utiliser. En pratique, on calcule les fonctions dérivées en se servant de règles de dérivation. Historiquement, ces règles ont précédé de plus d'un siècle la définition en $\epsilon \delta$. Elles ont été trouvées en tâtonnant et avec des arguments peu rigoureux, parce qu'il fallait raisonner sur des divisions par des nombres qui s'approchent de zéro. On appelait ces nombres des quantités infiniment petites et on parlait de calcul infinitésimal. Dans cette section on présente ces règles sans les démontrer ou en donnant seulement quelques indications sur les preuves. Mais toutes ces règles peuvent être rigoureusement prouvées à partir de la définition en $\epsilon \delta$.

La dérivée d'une fonction constante

Soit $f$ la fonction définie par $f(x)=A$ où $A$ est une constante.

${\frac {f(x+\epsilon )-f(x)}{\epsilon }}={\frac {A-A}{\epsilon }}=0$ pour tout $\epsilon \neq 0$. Donc :

$f'(x)=\lim _{\epsilon \to 0}{\frac {f(x+\epsilon )-f(x)}{\epsilon }}=0$ pour tout $x\in \mathbb {R}$

On pouvait s'y attendre puisqu'une fonction constante est représentée par une droite horizontale.

La dérivée d'une fonction affine

Soit $f$ la fonction définie par $f(x)=px+q$ où $p$ et $q$ sont des constantes.

${\frac {f(x+\epsilon )-f(x)}{\epsilon }}={\frac {p(x+\epsilon )+q-(px+q)}{\epsilon }}={\frac {p\epsilon }{\epsilon }}=p$ pour tout $\epsilon \neq 0$. Donc :

$f'(x)=\lim _{\epsilon \to 0}{\frac {f(x+\epsilon )-f(x)}{\epsilon }}=p$ pour tout $x\in \mathbb {R}$

On pouvait s'y attendre puisque $p$ est la pente de la droite qui représente $f$.

La dérivée d'une somme

Si $f$ et $g$ sont deux fonctions dérivables en $x_{0}$ alors leur somme est aussi dérivable en $x_{0}$ et son nombre dérivé est $(f+g)'(x_{0})=f'(x_{0})+g'(x_{0})$.

On dit aussi que la dérivée d'une somme est la somme des dérivées et on écrit plus simplement :

$(f+g)'=f'+g'$

La dérivée d'un produit par une constante

Si $f$ est une fonction dérivable en $x_{0}$ alors son produit par une constante $A$ est aussi dérivable en $x_{0}$ et le nombre dérivé du produit est $(Af)'(x_{0})=Af'(x_{0})$.

On écrit plus simplement :

$(Af)'=Af'$

La dérivée d'un produit

Si $f$ et $g$ sont deux fonctions dérivables en $x_{0}$ alors leur produit est aussi dérivable en $x_{0}$ et son nombre dérivé est $(fg)'(x_{0})=f(x_{0})g'(x_{0})+f'(x_{0})g(x_{0})$.

On écrit plus simplement :

$(fg)'=fg'+f'g$

Attention, la dérivée d'un produit n'est pas le produit des dérivées.

Ces règles suffiront pour les calculs du présent livre, qui reste volontairement à un niveau élémentaire. Elles doivent être complétées par deux autres règles (dérivées d'un quotient et d'une fonction composée) pour pouvoir calculer les dérivées de la plupart des fonctions habituellement définies.

Exercices

• Trouver les fonctions dérivées des fonctions suivantes :

$f_{1}(x)=0,f_{2}(x)=5,f_{3}(x)=x,f_{4}(x)=2x,f_{5}(x)=3x-5,f_{6}(x)=x^{2},f_{7}(x)=-4x^{2},$

$f_{8}(x)=-4x^{2}+5,f_{9}(x)=-x^{2}+2x,f_{10}(x)=x^{3},f_{11}(x)=x^{3}/3,f_{12}(x)=x^{3}-9x,f_{13}(x)=x^{4}$

• Vérifier que la règle de la dérivée d'un produit par une constante $(Af)'=Af'$ est un cas particulier de la règle du produit des dérivées $(fg)'=f'g+fg'$

• On veut prouver que $(x^{n})'=nx^{n-1}$ pour tout entier $n\geq 1$

Par commodité on définit les $f_{n}$, où $n$ est un entier et $n\geq 1$ par $f_{n}(x)=x^{n}$. On veut donc prouver que $f'_{n}(x)=nx^{n-1}$

Montrer que la formule est vraie pour $n=1$

On rappelle que par définition $x^{0}=1$ et $x^{1}=x$

Montrer que si la formule est vraie pour $n$ alors elle reste vraie pour $n+1$

Il faut pour cela se servir de la règle pour la dérivée d'un produit.

Ces deux conditions suffisent pour conclure que la formule est vraie pour tout entier $n\geq 1$ : d'après la première condition la formule est vraie pour $n=1$, d'après la seconde condition elle est donc vraie pour $n=2$, mais encore d'après cette même condition elle est alors vraie pour $n=3$ et ainsi de suite, à l'infini. On appelle une telle preuve un raisonnement par récurrence.

Solutions

La vitesse est la dérivée de la position

Les mouvements et les fonctions de $\mathbb {R}$ dans $\mathbb {R}$

Lorsqu'un mobile est contraint de se déplacer sur une droite, comme un train sur des rails, sa position peut être déterminée par un seul nombre. Il suffit de se donner un repère (une origine, un sens, et une unité de longueur) sur la droite.

Le mouvement du mobile est déterminé par la succession de toutes ses positions $x(t)$ à tous les instants $t$ du temps. Comme la position dépend du temps, $x$ est une fonction de $t$. $x$ est la fonction de $\mathbb {R}$ dans $\mathbb {R}$ qui à tout $t$ associe la position $x(t)$.

Inversement n'importe quelle fonction $f$ de $\mathbb {R}$ dans $\mathbb {R}$, dès qu'elle est continue, peut être interprétée comme la représentation d'un mouvement. Il suffit d'interpréter $f(t)$ comme la position d'un certain mobile à l'instant $t$.

Le graphe d'une fonction de $\mathbb {R}$ dans $\mathbb {R}$ qui représente un mouvement peut être considéré comme une sorte de partition tandis que le mouvement lui-même est la musique.

Si le point mobile se déplace dans un plan, ou sur une surface, il faut deux nombres réels $x(t)$ et $y(t)$ pour déterminer sa position à chaque instant $t$, il faut donc deux fonctions de $\mathbb {R}$ dans $\mathbb {R}$, $x$ et $y$, pour déterminer complètement le mouvement. $(x(t),y(t))$ est la position du point mobile à l'instant $t$.

Si le point mobile se déplace dans l'espace, il faut trois nombres réels $x(t)$, $y(t)$ et $z(t)$ pour déterminer sa position à chaque instant $t$, il faut donc trois fonctions de $\mathbb {R}$ dans $\mathbb {R}$, $x$, $y$ et $z$ pour déterminer complètement le mouvement.

S'il s'agit d'un corps mobile dans l'espace, la description de son mouvement est plus compliquée. Il faut six fonctions de $\mathbb {R}$ dans $\mathbb {R}$ pour décrire le mouvement d'un corps parfaitement rigide, trois pour décrire le mouvement de son centre de masse, et trois autres pour décrire la rotation autour de ce centre.

Vitesse moyenne et vitesse instantanée

Soit $x$ une fonction de $\mathbb {R}$ dans $\mathbb {R}$ qui décrit le mouvement d'un mobile contraint de se déplacer sur une droite. Le taux de variation de $x$ entre les instants $t_{1}$ et $t_{2}$ est défini par :

$T_{v}(t_{1},t_{2})={\frac {x(t_{2})-x(t_{1})}{t_{2}-t_{1}}}$

C'est la vitesse moyenne du mobile entre $t_{1}$ et $t_{2}$

Si $t_{2}$ tend vers $t_{1}$, ce taux de variation tend vers le nombre dérivé de $x$ en $t_{1}$ :

$\lim _{t_{2}\to t_{1}}T_{v}(t_{1},t_{2})=x'(t_{1})$

C'est la vitesse instantanée du mobile à l'instant $t_{1}$

$x'$, la fonction dérivée de la fonction position $x$ est donc la vitesse instantanée du mobile.

Si le point mobile se déplace dans un plan, $(x'(t),y'(t)$ est le vecteur vitesse à l'instant $t$. Si le point mobile se déplace dans l'espace, son vecteur vitesse instantanée est $(x'(t),y'(t),z'(t))$

Le vecteur vitesse instantanée est donc toujours la dérivée du vecteur position.

Exercices

• Le dernier chapitre montrera que la distance parcourue, en mètres, par un corps en chute libre, lâché sans vitesse initiale, est à peu près égale à $x(t)=5t^{2}$ où $t$ est le temps écoulé, en secondes, à partir du lâcher. On a négligé les frottements contre l'air. C'est une assez bonne approximation pour le début de la chute, mais dès que la vitesse est assez grande, le freinage par l'air ne peut plus être négligé.

Calculer $x'(t),x'(0),x'(1)$ et $x'(2)$ en m/s et en km/h.

Il faut se rappeler que 1m/s=3.6km/h.

Si le mobile est lâché d'une hauteur de 10m, combien de temps lui faut-il pour arriver en bas ?

Quelle est sa vitesse (en m/s et en km/h) à l'instant de l'impact sur le sol ?

Solutions

Calcul intégral

Les intégrales d'une fonction de $\mathbb {R}$ dans $\mathbb {R}$

Si $f$ est une fonction de $\mathbb {R}$ dans $\mathbb {R}$ définie sur l'intervalle $[a,b]$, et si elle est suffisamment régulière, c'est à dire continue, ou pas trop discontinue, alors elle permet de délimiter une aire, l'aire comprise entre la courbe qui la représente et l'axe horizontal :

Cette aire est par définition l'intégrale de $f$ entre $a$ et $b$. Elle est notée comme suit, pour des raisons qui vont apparaître bientôt :

$\int _{a}^{b}f(x)dx$

ce qui se lit, intégrale, ou somme, de f de x dé x entre a et b.

Il faut compter positivement une aire au dessus de l'axe horizontal et négativement une aire en dessous :

Pour calculer cette aire on procède par approximations successives, en mesurant les aires de rectangles qui touchent la courbe :

Cette méthode de calcul explique la notation $\int _{a}^{b}f(x)dx$. $dx$ représente la largeur des rectangles que l'on additionne. Il faut le concevoir comme un petit nombre que l'on fait tendre vers zéro. Plus $dx$ est proche de zéro, plus les rectangles sont nombreux, plus ils s'ajustent finement à la courbe et meilleure est l'approximation. Si un rectangle touche la courbe au point d'abscisse $x$, $f(x)$ est sa hauteur, son aire est donc $f(x)dx$. $\int$ est une sorte de S étiré qui veut dire somme. Intégrer veut dire sommer, additionner, accumuler.

La méthode par approximations successives permet de définir rigoureusement les intégrales, par passage à la limite, c'est à dire en faisant tendre $dx$ vers zéro et en étudiant la limite, si elle existe, de la somme des $f(x)dx$. Mais elle est souvent d'une utilisation difficile. On s'en sert surtout pour prouver les théorèmes qui nous servent à justifier nos calculs. En pratique on calcule presque toujours les intégrales en se servant du théorème fondamental de l'analyse. Il montre que savoir calculer des dérivées suffit pour calculer des intégrales.

Le théorème fondamental de l'analyse

Si $F$ est une fonction de $\mathbb {R}$ dans $\mathbb {R}$ définie et dérivable sur l'intervalle $[a,b]$ et si l'intégrale de $F'$ entre $a$ et $b$ existe alors elle est égale à $F(b)-F(a)$ : $\int _{a}^{b}F'(x)dx=F(b)-F(a)$

Pour comprendre intuitivement ce théorème il suffit de comprendre que $F(b)-F(a)$ est une grande différence qui résulte d'une accumulation de petites différences, les $F'(x)dx$ :

$F'(x)$ est à peu près égal à ${\frac {F(x+dx)-F(x)}{dx}}$ lorsque $dx$ est très petit, $F'(x)dx$ est donc à peu près égal à $F(x+dx)-F(x)$.

Or $F(b)-F(a)=F(b)-F(b-dx)+F(b-dx)-F(b-2dx)+...$

$...+F(a+2dx)-F(a+dx)+F(a+dx)-F(a)$

où l'on a choisi $dx=(b-a)/N$ et $N$ est un entier que l'on peut choisir aussi grand que l'on veut, pour que $dx$ puisse être aussi petit qu'on le veut.

Donc, dès que $N$ est assez grand, $F(b)-F(a)$ est à peu près égal à la somme des $F'(x)dx$ pour toutes les valeurs de $x$ égales à $a+ndx$ où n est un entier tel que $0\leq n<N$.

Si on fait tendre $N$ vers l'infini alors $dx$ tend vers $0$ et la somme des $F'(x)dx$ tend vers l'intégrale $\int _{a}^{b}F'(x)dx$.

Les fonctions primitives d'une fonction de $\mathbb {R}$ dans $\mathbb {R}$

$F$ est une fonction primitive de $f$ si et seulement si $f$ est la fonction dérivée de $F$, $f=F'$.

Une primitive pourrait être appelée une antidérivée (en anglais on l'appelle antiderivative).

Par exemple $F$ définie par $F(x)=x^{2}/2$ est une primitive de $f$ définie par $f(x)=x$.

Une fonction $f$ qui admet une primitive $F$ en admet toujours une infinité, parce que $F+A$ est aussi une primitive de $f$ pour n'importe quelle constante $A$ (il faut se souvenir que la dérivée d'une constante est nulle, et que la dérivée d'une somme est la somme des dérivées).

Le théorème fondamental de l'analyse montre que la connaissance d'une primitive de $f$ suffit pour calculer les intégrales de $f$.

Exercices

• $A$ est une constante. Calculer les dérivées des fonctions suivantes : $f(x)=Ax,g(x)=Ax^{2}/2,h(x)=Ax^{3}/3$

• Calculer $\int _{0}^{b}Adx$. Vérifier que l'on retrouve l'aire d'un rectangle.

• Calculer $\int _{0}^{b}Axdx$. Pour $A=1$, vérifier que l'on retrouve l'aire d'un demi-carré.

• Calculer $\int _{0}^{b}Ax^{2}dx$

Solutions

La chute des corps et la loi de Galilée

Ce chapitre explique pourquoi les corps en chute libre ont des trajectoires paraboliques, ou presque paraboliques.

Comment trouver la position si on connaît la vitesse ?

Soit un mobile contraint de se déplacer sur une droite. On suppose qu'on connaît sa vitesse $v(t)$ à tous les instants $t$ et sa position initiale $x(0)$ à l'instant $0$. Cela suffit pour calculer sa position $x(t)$ à tous les instants :

À partir de $x(0)$ et $v(0)$ on calcule $x(dt)\approx x(0)+v(0)dt$

À partir de $x(dt)$ et $v(dt)$ on calcule $x(2dt)\approx x(dt)+v(dt)dt$

Plus généralement, à partir de $x(ndt)$ et $v(ndt)$ on calcule $x((n+1)dt)\approx x(ndt)+v(ndt)dt$

Plus $dt$ est petit, meilleure est l'approximation.

Le théorème fondamental de l'analyse montre que $x(t)=x(0)+\int _{0}^{t}v(t)dt$ puisque $v=x'$

Le calcul précédent conduit à trouver une valeur approchée de $\int _{0}^{t}v(t)dt$

Si on connaît $v(t)$ par une formule analytique et si on connaît une de ses primitives, le théorème fondamental de l'analyse suffit pour trouver $x(t)$ à tous les instants $t$

L'accélération est la dérivée de la vitesse

L'accélération est la vitesse de variation de la vitesse. Elle est positive quand la vitesse augmente et négative (décélération) quand la vitesse diminue.

Comme la vitesse de variation d'une fonction qui dépend du temps est sa dérivée, l'accélération est la fonction dérivée de la fonction vitesse :

$a=v'$

Si $f'$ est dérivable, sa dérivée $f''$ (lire f seconde) est la dérivée seconde de $f$. L'accélération est donc la dérivée seconde de la position :

$a=x''$

La chute libre à la surface de la Terre

En première approximation on peut considérer que l'accélération de tous les corps en chute libre à la surface de la Terre est partout égale à 10 m/s/s (qui se lit mètre par seconde par seconde) et dirigée vers le centre de la Terre. C'est une conséquence de la loi de la gravitation universelle de Newton. L'accélération d'un corps attiré par la Terre est inversement proportionnelle au carré de la distance au centre de la Terre. Comme à la surface la distance au centre varie peu, l'accélération est approximativement constante.

Chute libre veut dire que le mobile est seulement soumis à la force d'attraction de la Terre. On néglige les frottements contre l'air.

Soit une pierre, lâchée sans vitesse initiale du sommet d'une tour. On appelle $y(t)$ la distance en mètres parcourue au bout de $t$ secondes. On a donc $y(0)=0$, $v_{y}(0)=y'(0)=0$ et $a_{y}(t)=v'_{y}(t)=y''(t)=10$ quel que soit $t$

Comme on connaît la vitesse initiale $v_{y}(0)=0$ et l'accélération $a_{y}(t)=10$ à tous les instants $t$, on peut en déduire la vitesse à tous les instants :

$v_{y}(T)=v_{y}(0)+\int _{0}^{T}a_{y}(t)dt=\int _{0}^{T}10dt=10T$

Comme on connaît maintenant la position initiale $y(0)=0$ et la vitesse $v_{y}(t)=10t$ à tous les instants $t$, on peut en déduire la position à tous les instants :

$y(T)=y(0)+\int _{0}^{T}v_{y}(t)dt=\int _{0}^{T}10tdt=5T^{2}$

On prouve ainsi la loi de Galilée : la distance parcourue en chute libre est proportionnelle au carré du temps écoulé depuis un lâcher initial au repos.

Exercice

• On suppose que le corps en chute libre a une vitesse initiale verticale $V$ différente de $0$

On a donc $y(0)=0$ et $y'(0)=v_{y}(0)=V$

Calculer $v_{y}(T)$ pour tout $T$

Calculer $y(T)$ pour tout $T$

Il vaut mieux savoir que l'intégrale d'une somme est la somme des intégrales :

$\int _{a}^{b}(f(t)+g(t))dt=\int _{a}^{b}f(t)dt+\int _{a}^{b}g(t)dt$

Solutions

Les trajectoires paraboliques

Un corps lâché sans vitesse initiale tombe en ligne droite vers le centre de la Terre. Si on lui donne initialement une vitesse qui s'écarte de la verticale, sa trajectoire de chute libre est une parabole.

Une parabole est la représentation graphique d'une fonction définie par $f(x)=ax^{2}$, où $a$ est une constante différente de zéro.

Par exemple, si $a=1$ :

Pour décrire la trajectoire du mobile, on a besoin de deux coordonnées, $x(t)$ et $y(t)$. $x(t)$ mesure la position dans la direction horizontale, $y(t)$ dans la direction verticale.

Si on néglige les frottements, il n'y a pas de force dans la direction horizontale. L'accélération $a_{x}(t)=x''(t)$ dans cette direction est donc toujours nulle. La vitesse $v_{x}(t)=x'(t)$ reste donc constante et égale à la vitesse $v_{x}(0)$ donnée initialement au mobile. On en déduit que :

$x(T)=x(0)+\int _{0}^{T}v_{x}(t)dt=\int _{0}^{T}v_{x}(0)dt=v_{x}(0)T$

Si la vitesse initiale du mobile est horizontale, $v_{y}(0)=0$, $v_{y}(T)=10T$ et

$y(T)=5T^{2}$

on en déduit que

$y(T)=5(x(T)/v_{x}(0))^{2}={\frac {5}{v_{x}(0)^{2}}}x(T)^{2}$

et on peut conclure que la trajectoire du mobile est une parabole. Elle est orientée vers le bas, parce que l'axe des $y$ choisi pour ce calcul est orienté vers le bas. Le mobile passe par le sommet de la parabole à l'instant $t=0$, lorsque sa vitesse est horizontale.