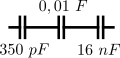Préparation au certificat d'opérateur du service amateur/Condensateurs

Résistances

Bobines

Préparation au certificat d'opérateur du service amateur

Outils mathématiques[modifier | modifier le wikicode]

Les briques de base[modifier | modifier le wikicode]

Réglementation[modifier | modifier le wikicode]

Technique[modifier | modifier le wikicode]

Bases d'électricité[modifier | modifier le wikicode]

Radioélectricité[modifier | modifier le wikicode]

Annexes[modifier | modifier le wikicode]

[ Modifier le sommaire ]

Résistances

Bobines


*Savoirs fondamentaux du chapitre (Arrêté du 21 septembre 2000)*
Le dipôle condensateur : Capacité L'unité : le farad La relation entre capacité, dimensions et diélectrique (aspect quantitatif uniquement) : $X_{C}={\frac {1}{2\pi FC}}={\frac {1}{C\omega }}$ Déphasage entre la tension et le courant Caractéristiques des condensateurs, condensateurs fixes et variables : à air, au mica, au plastique, à la céramique et condensateurs électrolytiques Coefficient de température Courant de fuite

Après avoir appris les bases de l'électricité, nous allons nous intéresser à des composants plus intéressants que des résistances. Ce chapitre et le suivant vous proposent d'étudier les condensateurs et les bobines, éléments de base des circuits électroniques.

Le condensateur[modifier | modifier le wikicode]

Un condensateur est formé de deux armatures métalliques en vis-à-vis, isolées électriquement par un matériau diélectrique^[1]. Il a la particularité d'être capable d'accumuler les électrons (donc de se charger) et de les restituer par la suite (donc de se décharger) : il se comporte comme un réservoir de charges électriques.

Essayons par exemple de soumettre un condensateur à un premier échelon de tension positif et mesurons la tension à ses bornes (cas A sur la figure) : nous observons nettement un retard à l'établissement de la tension^[2], dû au temps de charge du condensateur. Les électrons, plutôt que de poursuivre dans le circuit, s’emmagasinent dans le dipôle. Puis, si on coupe l'alimentation, on constate un retard au retour à une tension nulle : le condensateur est en train de se décharger et de déverser les charges qu'il a accumulées dans le circuit jusqu'à ce qu'il soit entièrement vide.

Le condensateur fonctionne grâce à l'effet électrostatique. Son explication complète est complexe, dépasse le cadre de l'ouvrage et n'est pas exigible à l'examen : nous ne nous y attarderons pas.

La capacité du condensateur à emmagasiner l'énergie, appelée... capacité, se note $C$ et se mesure en farads (symbole $F$ ). Le farad étant une unité très grande, ses sous-multiples sont largement utilisés (picofarad $pF$ , nanofarad $nF$ , microfarad $\mu F$ ) ; la capacité est notée sur le condensateur. Plus la capacité est grande, plus le condensateur peut stocker des charges et « s'opposer » aux variations de tension à ses bornes. C'est-à-dire qu'un condensateur, placé dans un circuit, permet d'atténuer les éventuelles variations subites de la tension : si celle-ci baisse, il se décharge ; si à l'inverse, elle augmente, il se charge pour maintenir une tension quasi-constante.

Le dipôle est, outre la capacité, caractérisé par une distance entre ses lames (ou épaisseur du diélectrique) notée $E$ , une surface des armatures $A$ (ou $S$ ) et une constante $d$ propre au diélectrique. On définit $Q$ comme la quantité de charges électriques emmagasinée sur une des armatures métalliques (en coulombs). On a alors les relations suivantes :

Q=C\cdot U

{\mathcal {E}}_{C}={\frac {1}{2}}Q\cdot U={\frac {1}{2}}C\cdot U^{2}={\frac {1}{2}}2C\cdot Q^{2}

De ces formules, on déduit que plus la tension $U$ est grande, plus la quantité $Q$ de charges électriques emmagasinées est grande.

Les condensateurs peuvent se monter en série comme en parallèle. Dans ces situations, il est demandé de savoir calculer la capacité équivalente (notée $C_{eq}$ ) :

en parallèle, la capacité équivalente est égale à la somme des capacités : $C_{eq}=C_{1}+C_{2}+...$ ;
en série, l'inverse de la capacité équivalente est égale à la somme des inverses des capacités : ${\frac {1}{C_{eq}}}={\frac {1}{C_{1}}}+{\frac {1}{C_{2}}}+...$


Exemple : montages série et parallèle

Il est possible de déterminer la capacité $C$ d'un condensateur grâce à la formule $C={\frac {\epsilon \cdot A}{d}}$ , dans laquelle $\epsilon$ est la permittivité du diélectrique^[3], $A$ est l'aire en vis-à-vis et $d$ la distance séparant les deux armatures.

Différents modèles de condensateurs sont proposés par les fabricants. Un premier modèle est variable et peut donc être réglé en capacité. Un second présente un diélectrique chimique. Des précautions particulières sont à observer lors de la manipulation de ce dernier type : un condensateur chimique est polarisé, et peut chauffer voire exploser si ses bornes sont inversées dans le circuit.

Altération des condensateurs[modifier | modifier le wikicode]

La capacité des condensateurs varie avec la température : on parle de déviation en température. Cette variation dépend entièrement du type de condensateur ; elle est représentée par le coefficient de température.

En outre, chaque condensateur (sauf les condensateurs à air) présente un courant de fuite. En effet, si on charge un condensateur avant de le déconnecter, il se décharge lentement.

Charge du condensateur initialement déchargé[modifier | modifier le wikicode]

Considérons le montage ci-contre, avec un condensateur initialement déchargé. Lorsque l'inverseur est en position $A$ , le condensateur est relié au générateur et se charge. Lorsque l'inverseur est basculé en position $B$ , le condensateur va se décharger dans la résistance. Quel peut être le temps de charge ? Partons des formules vues dans le chapitre sur les puissances, nous déduisons que $t={\frac {Q}{I}}$ . Or, $Q=C\cdot U$ et $I={\frac {U}{R}}$ . En remplaçant dans l'expression du temps, on trouve $t=R\cdot C$ . Cette quantité est appelée constante de temps du condensateur et se note $\tau$ ^[4] (en secondes). Connaître le temps caractéristique permet d'esquisser le graphe de charge du condensateur : au bout d'un temps $\tau$ , le condensateur est chargé aux 2 tiers de la tension à ses bornes (63 % de E) (et donc la tension traversant la résistance vaut 63 % de E) ; au bout de $2\tau$ le condensateur est chargé à 87 % de la tension à ses bornes ; au bout de $3\tau$ , le condensateur est chargé à 95 % de la tension à ses bornes. On le considère chargé au bout de $5\tau$ .


Exemple : détermination de l'allure de la charge
Soit un condensateur $A$ de capacité 50 μF monté en série avec une résistance de 120 Ω. On le charge sous une tension de 15 V. Déterminez sa constante de temps $\tau$ . Quelle sera la valeur de la tension aux bornes de la résistance au bout d'un temps $2\tau$ ? $\tau =R\cdot C=120\times 50\cdot 10^{-6}=0,006$ secondes. Par propriété de la constante de temps, au bout d'un temps $2\tau$ , la tension traversant la résistance vaut 95 % de la tension aux bornes du condensateur, soit $0,95\times 15=14,25$ volts. Au bout de combien de temps le condensateur sera-t-il chargé ? Le condensateur sera chargé au bout de $5\tau$ soit 0,03 secondes. On considère maintenant un second condensateur, nommé $B$ , de constante de temps $\tau '=0,05$ secondes. Les deux condensateurs $A$ et $B$ sont initialement déchargés, puis on les charge séparément sous une tension de 20 V. Lequel des deux sera le plus rapidement chargé ? Celui qui a la plus petite constante de temps atteindra plus vite un état chargé. C'est donc le condensateur $A$ .

Décharge du condensateur initialement chargé[modifier | modifier le wikicode]

On reprend le circuit du paragraphe précédent, mais en considérant le condensateur comme initialement chargé sous une tension $E$ . On bascule l'interrupteur sur $B$ afin de le décharger dans la résistance. La décharge se passe inversement à la charge : au bout d'un temps $\tau$ ^[5], le condensateur est déchargé à 63 % (la tension aux bornes de la résistance vaut 37 % de E) ; au bout de $2\tau$ le condensateur est déchargé à 87 % (la tension aux bornes de la résistance vaut 13 % de E) ; le condensateur est considéré comme déchargé au bout de $5\tau$ (la tension aux bornes de la résistance est nulle).


Exemple : détermination de l'allure de la décharge
Soit un condensateur $A$ de capacité 150 μF monté en série avec une résistance de 10 kΩ. On le considère chargé sous une tension de 15 V. On étudie sa décharge dans la résistance. Déterminez sa constante de temps $\tau$ . Quelle sera la valeur de la tension aux bornes de la résistance au bout d'un temps $2\tau$ ? $\tau =R\cdot C=120\cdot 10^{3}\times 150\cdot 10^{-6}=18$ secondes. Par propriété de la constante de temps, au bout d'un temps $2\tau$ , la tension traversant la résistance vaut 13 % de la tension initiale aux bornes du condensateur, soit $0,13\times 15=1,95$ volts. Au bout de combien de temps le condensateur sera-t-il déchargé ? Le condensateur sera chargé au bout de $5\tau$ soit 90 secondes. On considère maintenant un second condensateur, nommé $B$ , de constante de temps $\tau '=10$ secondes. Les deux condensateurs $A$ et $B$ sont initialement chargés sous une tension de 20 V, puis on les décharge séparément. Lequel des deux sera le plus rapidement déchargé ? Celui qui a la plus petite constante de temps atteindra plus vite un état déchargé. C'est donc le condensateur $B$ .

Familles de condensateurs[modifier | modifier le wikicode]

Nous avons évoqué plus haut l'existence de familles de condensateurs en fonction de leur composition : nous allons maintenant en étudier quelques-unes. Il ne s'agit pas de faire la liste de tous les types, mais seulement de présenter les plus courants demandés pour l'examen.

Impédance du condensateur[modifier | modifier le wikicode]

L'impédance du condensateur parfait (notée $Z_{C}$ ) varie avec la fréquence du courant traversant le dipôle. L'impédance du condensateur est donnée par la formule $Z_{C}={\frac {1}{C\omega }}$ ^[6]. Comment évolue l'impédance quand on fait varier la fréquence ?

Si la fréquence est grande, alors $\omega$ prend une grande valeur. Dans la formule de l'impédance, le dénominateur devenant grand, le quotient devient petit et se rapproche de 0, c'est-à-dire que l'impédance est presque nulle. Souvenons-nous que l'impédance correspond à la résistance en régime sinusoïdal ; on peut donc dire que la résistance du condensateur est nulle à haute fréquence et donc on retient qu'à haute fréquence, le condensateur se comporte comme un fil ( $Z_{C}=0$ ) ;
Si la fréquence est petite, alors $\omega$ prend une petite valeur. Pour le condensateur, le dénominateur se rapprochant de 0, le quotient devient très grand et se rapproche de l'infini, c'est-à-dire que l'impédance est très grande : on peut donc dire que la résistance du condensateur est très grande, et donc qu'il ne laisse pas passer le courant électrique. On retient qu'à basse fréquence, le condensateur se comporte comme un interrupteur ouvert ( $Z_{C}=\infty$ ).

Exercices[modifier | modifier le wikicode]

Calculs de capacités équivalentes[modifier | modifier le wikicode]

Pour chaque circuit ci-dessous, calculez sa capacité équivalente $C_{eq}$ .

Circuit A
Circuit B
Circuit C
Circuit D

Étude d'un condensateur[modifier | modifier le wikicode]

On considère le condensateur ci-contre. Fréquence du signal : 230 MHz.

Déterminez son impédance.
Quelle est la quantité de charges électriques emmagasinée ?
À quoi correspond le temps caractéristique ?
On adjoint au condensateur en série une résistance de $0,5~\Omega$ . Déterminez son temps caractéristique $\tau$ , en secondes.

Notes[modifier | modifier le wikicode]

↑ Milieu qui ne peut pas conduire le courant électrique : le vide, le verre et de nombreux plastiques.
↑ C'est-à-dire qu'un certain laps de temps s'écoule pour que la tension aux bornes du condensateurs atteigne la valeur finale imposée par l'échelon de tension.
↑ La permittivité est une constante propre à chaque milieu qui décrit la réponse de ce milieu à un champ électrique appliqué.
↑ T minuscule grec, appelé « tau ».
↑ La constante de temps ne varie pas à la décharge : elle est liée uniquement à $R$ et $C$ , grandeurs invariantes et propres au condensateur.
↑ Pour mémoire, $\omega$ désigne la pulsation (en radians par seconde) égale à $2\pi F$ .

[1] Milieu qui ne peut pas conduire le courant électrique : le vide, le verre et de nombreux plastiques.

[2] C'est-à-dire qu'un certain laps de temps s'écoule pour que la tension aux bornes du condensateurs atteigne la valeur finale imposée par l'échelon de tension.

[3] La permittivité est une constante propre à chaque milieu qui décrit la réponse de ce milieu à un champ électrique appliqué.

[4] T minuscule grec, appelé « tau ».

[5] La constante de temps ne varie pas à la décharge : elle est liée uniquement à $R$ et $C$ , grandeurs invariantes et propres au condensateur.

[6] Pour mémoire, $\omega$ désigne la pulsation (en radians par seconde) égale à $2\pi F$ .

[1]

[2]

[3]

[4]

[5]

[6]