Photographie/Optique/Les principes de l'optique géométrique
| ||||
|
plan du chapitre en cours
|
navigation rapide
Fabricants et marques de produits et de matériels Personnalités du monde de la photographie Éditeurs de cartes postales photographiques Thèmes ▪
Bibliographie
■ préface - SOMMAIRE COMPLET ■ notions fondamentales et conseils pour les débutants ■ aspects esthétiques, thèmes photographiques ■ références scientifiques ■ photométrie, colorimétrie, optique ■ appareils, objectifs, éclairage, accessoires, entretien ■ procédés chimiques ■ procédés numériques ■ caractéristiques physiques des images, densité, netteté ■ compléments techniques et pratiques ■ photographie et vie sociale, histoire, enseignement,institutions, droit... | |||
L'étude complète de la propagation de la lumière tient compte de sa double nature ondulatoire et corpusculaire, elle n'est pas du tout facile !
L'optique géométrique donne des interprétations simplifiées mais suffisantes pour aborder presque toutes les questions qui intéressent un photographe, en particulier la formation des images. Elle utilise un artifice sans existence réelle, mais très commode, le rayon lumineux, qui est une droite ou une portion de droite parcourue par la lumière. Cependant, certains résultats doivent être retouchés par d'autres méthodes, en particulier pour l'étude de la netteté des images.
Principe de propagation rectiligne
[modifier | modifier le wikicode]Le principe de propagation rectiligne est vérifié par de nombreuses expériences. On peut par exemple observer une source lumineuse à travers des petits trous percés dans une série de parois opaques et alignés à l'aide d'un fil à plomb.
Un faisceau lumineux est constitué par un ensemble de rayons lumineux. Si ces rayons sont émis par un même point lumineux S, le faisceau est dit conique, homocentrique ou encore isogène. Un tel faisceau est toujours divergent car les rayons lumineux s'écartent quand on s'éloigne de la source.

Lorsqu'un faisceau lumineux rencontre de petites particules en suspension, de la poussière, de la brume, de la fumée, une partie de la lumière est diffusée, ce qui permet de le localiser. Le photographe avisé ne manquera pas de tirer habilement parti de cette situation, comme ont si bien su le faire les auteurs des photographies ci-dessous :
-
Jack Delano, Salle d'attente de l'Union Station, Chicago
-
Lucas Löffler, Antelope Cañon, USA
-
coupole de la basilique de Santa Maria Maggiore à Rome
-
Movila Vlad, vieille église à Tbilissi
Vus « de l'intérieur », les faisceaux parallèles présentent un point de fuite (qu'il faut masquer ou placer hors du cadre sous peine d'éblouissement). Ils semblent donc divergents mais cette divergence apparente n'est en pratique qu'un effet de perspective qui se comprend facilement en imaginant que l'on regarde dans un tuyau.
 |
 |
Comme nous le verrons, des systèmes optiques appropriés peuvent produire des faisceaux parallèles et des faisceaux convergents.
Lorsque la lumière solaire arrive perpendiculairement à l'axe de l'appareil, c'est-à-dire latéralement, les traces des rayons deviennent parallèles sur l'image. C'est presque le cas sur la photographie ci-dessous ; le point de fuite des rayons, qui est en réalité leur point de départ, se trouve rejeté très loin à droite.

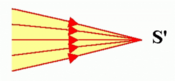
Si le point S' est situé sur un objet opaque, le faisceau ne va évidemment pas plus loin. Sinon, les rayons ne font que s'y croiser et le faisceau devient divergent, tout se passe comme si S' était une source lumineuse.

L'ouverture d'un faisceau lumineux conique correspond à l'angle solide défini par les rayons extrêmes, elle se mesure donc en stéradians. Si le faisceau a la forme d'un cône de révolution, on peut aussi définir l'ouverture par le demi-angle au sommet de ce cône. Un faisceau parallèle doit être caractérisé par l'aire de sa section droite, puisque son ouverture est nulle.
On appelle pinceau lumineux un faisceau dont l'ouverture est très faible ou nulle et dont les dimensions transversales sont très petites.
Principe d'indépendance des rayons lumineux
[modifier | modifier le wikicode]Le principe d'indépendance des rayons lumineux peut s'énoncer ainsi : Un milieu transparent peut transporter simultanément des rayons lumineux issus d'une même source ou de plusieurs sources, dont les propagations sont indépendantes.
Cela signifie par exemple que deux ou plusieurs faisceaux lumineux peuvent être traversés les uns par les autres sans qu'aucun d'eux soit modifié en quoi que ce soit. En particulier, leurs directions, leurs intensités et leurs couleurs sont conservées.

Sur la photographie de Jack Delano, par exemple, la lumière provenant des petites ouvertures rectangulaires traverse sans déviation les rayons provenant des ouvertures de la partie supérieure.