Photographie/Optique/Stigmatisme, objets et images

Un livre de Wikibooks.

< Photographie | Optique

Aller à : Navigation, rechercher

PHOTOGRAPHIE

Un wikilivre pour ceux qui veulent apprendre la photographie de façon méthodique et approfondie.

Enrichissez-le en mettant votre propre savoir à la disposition de tous.

Si vous ne savez pas où intervenir, utilisez cette page.

Voyez aussi le « livre d'or ».

plan du chapitre en cours

Optique

▼ propagation de la lumière

▼ systèmes optiques

Niveau

A - débutant
B - lecteur averti
C - compléments

Avancement

Projet
Ébauche

des articles

En cours
Avancé
Terminé

Quoi de neuf
Docteur ?

dernières mises à jour

Les plus récentes sont en tête de liste !

ajouter une rubrique [1]

clubs - expositions - stages

navigation rapide

accès directs B ▪ F ▪ G ▪ In ▪ M ▪ P ▪ R ▪ T

■ préface - SOMMAIRE COMPLET

■ conseils pour bien débuter en photographie

■ aspects esthétiques, thèmes photographiques

■ références scientifiques

■ photométrie, optique

■ matériel, fournitures, accessoires, entretien

■ procédés chimiques

■ procédés numériques

■ caractéristiques physiques des images

■ compléments techniques et pratiques

■ photographie et vie sociale

■ personnalités

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

■ glossaire

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

■ annexes

Sections

1 Définitions
2 Stigmatisme parfait, stigmatisme approché
3 Objets et images réels et virtuels
- 3.1 Cas d'un seul système optique
- 3.2 Cas d'une succession de systèmes optiques
4 Où l'on retrouve le principe de Fermat
5 Conditions de Gauss

[modifier] Définitions

Tout système optique comporte une face d'entrée où pénètre un faisceau incident et une face de sortie d'où sort un faisceau émergent.

Un système optique est dit stigmatique pour deux points A et A' si, recevant un faisceau lumineux conique de sommet A, il le transforme en un autre faisceau conique de sommet A'.

A et A' sont appelés points réciproques, ou encore points conjugués. Le sommet A du faisceau entrant est un point objet, le sommet A' du faisceau sortant est un point image.

Si l'on change le sens de parcours de la lumière, les deux faisceaux entrant et sortant sont conservés mais parcourus en sens inverse. De fait, chacun peut facilement constater qu'il est possible, mais sans doute pas très adroit, d'observer une scène éloignée "par le petit bout de la lorgnette".

Remarque : dans certains cas, notamment en astronomie, la notion de stigmatisme ne s'applique que dans un sens. Les étoiles sont des objets gigantesques mais si éloignés que quelle que soit la puissance de l'instrument avec lequel on les observe, elles apparaissent toujours sous la forme d'un point de diamètre apparent non mesurable. Si l'image d'une étoile se forme, à la sortie d'un instrument, en un point A', on dira qu'il y a stigmatisme, mais il serait absurde de penser que la lumière issue de A' pourrait converger en un point A bien défini à quelques dizaines ou milliers d'années-lumière.

[modifier] Stigmatisme parfait, stigmatisme approché

Le stigmatisme est évidemment l'une des propriétés les plus importantes des systèmes optiques. Un instrument idéal, parfaitement stigmatique pour tous les points d'une certaine région de l'espace, donnerait une image parfaitement nette de tous les objets situés dans cette région. Hélas, il est impossible de réaliser un tel instrument, sauf si l'on n'utilise que des miroirs plans. Le miroir plan est en effet le seul système optique parfaitement stigmatique pour tous les points de l'espace, puisque l'image et l'objet sont symétriques.

En pratique, l'imperfection des systèmes récepteurs de lumière (œil, surface sensible photographique, capteur électronique, ...) permet de se contenter d'un stigmatisme approché. En effet, à partir d'un certain niveau de qualité, les défauts des images ne sont plus perçus et tout se passe comme s'ils n'existaient pas. Nous y reviendrons au chapitre 14 consacré à la netteté des images photographiques.

[modifier] Objets et images réels et virtuels

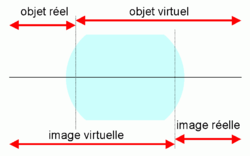
La question des objets et des images réels et virtuels est l'une des premières difficultés sérieuses pour les débutants en optique.

[modifier] Cas d'un seul système optique

OR IR		Les rayons incidents proviennent tous d'un point A situé devant la face d'entrée du système optique, ce point est un objet réel. Les rayons émergents passent tous par un point A' situé derrière la face de sortie du système optique, formant une image réelle.
Les surfaces sensibles photographiques (films ou capteurs) et la rétine de l'œil ont besoin de recevoir des images réelles où se concentre la lumière issue des points-objets. Le système optique est alors un objectif ou l'ensemble des parties réfringentes de l'œil.
OR IV		Nous avons toujours un objet réel A mais ce sont les prolongements des rayons émergents qui passent par le point A' situé devant la face de sortie du système, formant alors une image virtuelle.
Cette configuration est celle de tous les instruments d'optique destinés à l'observation visuelle : loupes, lunettes, télescopes, microscopes, etc. L'image virtuelle est souvent rejetée à l'infini.
OV IR		Ce sont les prolongements des rayons incidents qui passent par un point A situé derrière la face d'entrée du système, ce point constitue un objet virtuel. Les rayons du faisceau émergent convergent en A' derrière la face de sortie, formant une image réelle.
Le faisceau entrant convergent provient nécessairement d'un autre système optique.
OV IV		Quatrième et dernière possibilité, un objet virtuel et une image virtuelle.
Même remarque que dans le cas précédent.
		Il faut se rappeler la règle simple illustrée ci-contre : Si les rayons entrants ou leurs prolongements passent par un point situé devant la première surface de verre du système optique, alors l'objet est réel, sinon il est virtuel. Si les rayons sortants ou leurs prolongements passent par un point situé derrière la dernière surface de verre du système optique, alors l'image est réelle, sinon elle est virtuelle. Autrement dit, la face d'entrée d'un système optique sépare l'espace objet en deux parties, réelle du côté où arrive la lumière, virtuelle de l'autre, la face de sortie sépare l'espace image en deux parties, réelle du côté où sort la lumière, virtuelle de l'autre.
Lorsque les rayons d'un faisceau sont parallèles, le sens de parcours de la lumière et l'usage normal de l'instrument permettent en général de lever très vite les quelques ambiguïtés qui pourraient apparaître. Le cas des systèmes afocaux, qui transforment un faisceau de rayons parallèles en un autre faisceau parallèle différemment incliné, sera examiné plus loin.

[modifier] Cas d'une succession de systèmes optiques

Attention ! Pour éviter toute confusion lorsque la lumière passe d'un système optique à un autre, l'objet et l'image doivent être définis systématiquement pour CHAQUE système. l'image donnée par un système devient toujours un objet pour le suivant, le caractère réel ou virtuel peut être conservé ou non, selon les cas.
	Ici, l'image réelle A' fournie par le premier système optique S devient un objet réel pour le second système S'.
Un projecteur de cinéma ou de diapositives S forme l'image réelle du film sur un écran de projection. Celui-ci, en diffusant la lumière qu'il reçoit, devient un objet réel pour l'œil S' du spectateur. C'est une situation normale. L'œil S' placé dans cette position derrière une loupe ou une lunette déréglée S observe, dans un champ très réduit, un objet retourné et beaucoup plus petit que celui qui est placé « en chair et en os » devant l'instrument. Ce n'est évidemment pas une façon très futée d'utiliser le matériel ...
	L'image virtuelle A' fournie par le premier système optique S est encore un objet réel pour le second système S'.
S'il reçoit un faisceau lumineux convergent, l'œil normal ne peut pas l'utiliser car ses capacités d'accommodation ne sont pas suffisantes. Pour voir net, il ne doit recevoir que des faisceaux divergents ou parallèles comme ceux qui lui arrivent directement des objets ; quand la lumière lui parvient à travers un instrument d'optique, celui-ci doit produire une image virtuelle située à une distance finie ou mieux, à l'infini, pour éviter la fatigue oculaire. Certains photographes pratiquent la digiscopie en fixant un appareil photo numérique à la place de l'œil, derrière une lunette munie de son oculaire. Cette méthode permet d'obtenir assez facilement d'énormes rapports de grandissement, il faut toutefois que l'appareil et surtout la lunette soient d'excellente qualité.

Remarque : Dans le langage courant, ou pour aller plus vite, on utilise souvent des expressions impropres comme l'œil examine l'image projetée sur un écran. Généralement ces expressions ne prêtent guère à confusion mais elles doivent cependant être proscrites lors de l'étude approfondie des systèmes optiques, puisqu'en toute rigueur la lumière qui entre dans un système provient, par définition, d'un objet.

[modifier] Où l'on retrouve le principe de Fermat

Tout ceci ne nous donne évidemment pas les conditions pour que l'image d'un point soit un point, ou presque un point. Nous allons pour cela prendre un chemin détourné, la meilleure façon d'aller d'un endroit à un autre n'est pas toujours la ligne droite, y compris pour la pensée.

Voici d'abord un jardinier qui veut créer un massif elliptique de grand rayon a et de petit rayon b, ou de longueur 2a et de largeur 2b. Sur le grand diamètre, il plantera deux piquets en F et F' à une distance du centre qui vaudra :

$f = OF = OF' = \sqrt{a^2-b^2}$

Par exemple, si a = 7 m et b = 4 m, alors il trouvera f = 5,74 m.

Il se munira ensuite d'une corde de longueur 2a dont il fixera une extrémité en F et l'autre en F'. Avec un bâton, tout en maintenant la corde tendue, il tracera sur le sol une ellipse, courbe bien connue des mathématiciens et des physiciens car elle intervient dans de très nombreux domaines. Tout point M de cette ellipse est tel que la somme de ses distances aux deux points fixes F et F', appelés foyers, est constante :

MF + MF' = 2a

Un cercle vu "en perspective", en biais, nous apparaît sous la forme d'une ellipse. Inversement, le dessin d'une ellipse vu sous un angle adéquat prend la forme d'un cercle (un vieux truc de dessinateur pour vérifier qu'une ellipse tracée à main levée n'est pas un « patatoïde »).

Voici maintenant un chercheur de haut niveau spécialiste des matériaux réfractaires. Notre homme étudie une céramique révolutionnaire ; il en possède un échantillon gros comme un grain de blé, échantillon qu'il veut porter à 3 000 °C en un centième de seconde, tout en évitant de le polluer. Les méthodes classiques, chauffer le produit par une flamme ou dans un creuset, ne sont ni assez brutales ni assez propres. On réalise ce choc thermique dans un four à image en forme d'ellipsoïde de révolution dont la surface intérieure est traitée pour en faire un miroir. À l'un des foyers, on fait éclater un arc électrique, à l'autre, se trouve l'échantillon à tester qui reçoit aussitôt le rayonnement.

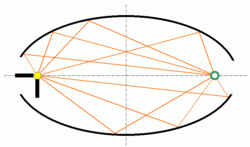
Le principe de FERMAT nous dit que la lumière qui va d'un foyer à l'autre en se réfléchissant sur l'ellipsoïde emprunte un chemin dont le temps de parcours est minimal ou maximal. Or, tous les trajets possibles de type FMF' ont exactement la même longueur et sont effectués dans le même milieu, leurs temps de parcours par la lumière sont identiques et c'est pourquoi tous les rayons émis en F convergent en F' !

Ce miroir ellipsoïdal est donc rigoureusement stigmatique pour ses deux foyers. Pour tous les autres points, au mieux, le stigmatisme ne peut être qu'approché. Pour une sphère, les deux foyers sont confondus au centre, lequel est donc rigoureusement stigmatique avec ... lui-même. On trouve au Palais de la Découverte à Paris une sphère réfléchissante creuse dans l'ouverture de laquelle les visiteurs peuvent passer la tête. Lorsque celle-ci est au centre, les rayons infrarouges qu'elle émet lui reviennent et il fait alors très, très chaud ...

La recherche du stigmatisme n'est rien d'autre que la recherche de trajets optiques de même durée pour aller d'un point à un autre ...

[modifier] Conditions de Gauss

Dans le cas général, l'image d'un point est une figure à trois dimensions plus ou moins compliquée. On peut tout de même étudier les systèmes optiques de façon relativement simple à condition de faire quelques hypothèses simplificatrices :

on ne considère que les points appartenant à l'axe optique ou très proches de lui,
on limite l'ouverture du système de manière à ne conserver que des rayons utiles presque parallèles à l'axe (rayons dit paraxiaux),
on limite le champ du système, c'est-à-dire la portion de l'espace où doit se trouver un objet non plan pour que l'on puisse en obtenir une image utilisable,
l'épaisseur des lentilles est petite devant les rayons des dioptres, de façon que ces derniers soient rencontrés presque perpendiculairement par la lumière.

Dans de telles conditions, l'image d'un point est un volume limité que l'on suppose assez petit pour que son étendue ne soit pas discernable dans les conditions normales de l'observation. On a réalisé alors un stigmatisme approché et l'on dit que le système étudié travaille dans l'approximation de Gauss ou dans les conditions de Gauss.

Optique

▼ propagation de la lumière

▼ systèmes optiques

Photographie/Optique/Stigmatisme, objets et images

Un livre de Wikibooks.

Sections

[modifier] Définitions

[modifier] Stigmatisme parfait, stigmatisme approché

[modifier] Objets et images réels et virtuels

[modifier] Cas d'un seul système optique

[modifier] Cas d'une succession de systèmes optiques

[modifier] Où l'on retrouve le principe de Fermat

[modifier] Conditions de Gauss

Affichages

Outils personnels

Rechercher

Bibliothèque

Navigation

Aide

Imprimer / exporter

Boîte à outils